Automated identification of pulmonary arteries and veins depicted in non-contrast chest CT scans

Abstract

We present a novel integrative computerized solution to automatically identify and differentiate pulmonary arteries and veins depicted on chest computed tomography (CT) without iodinated contrast agents. We first identified the central extrapulmonary arteries and veins using a convolutional neural network (CNN) model. Then, a computational differential geometry method was used to automatically identify the tubular-like structures in the lungs with high densities, which we believe are the intrapulmonary vessels. Beginning with the extrapulmonary arteries and veins, we progressively traced the intrapulmonary vessels by following their skeletons and differentiated them into arteries and veins. Instead of manually labeling the numerous arteries and veins in the lungs for machine learning, this integrative strategy limits the manual effort only to the large extrapulmonary vessels. We used a dataset consisting of 120 chest CT scans acquired on different subjects using various protocols to develop, train, and test the algorithms. Our experiments on an independent test set (n=15) showed promising performance. The computer algorithm achieved a sensitivity of ~98% in labeling the pulmonary artery and vein branches when compared with a human expert’s results, demonstrating the feasibility of our computerized solution in pulmonary artery/vein labeling.

Graphical Abstract

I. INTRODUCTION

Pulmonary veins and arteries constitute a low-pressure vascular system responsible for transporting oxygenated and deoxygenated blood to and from the heart, respectively. Many disease states are associated with the pulmonary vasculature, including pulmonary embolism (PE), pulmonary hypertension (PH), hypoxic pulmonary vasoconstriction, pulmonary arteriovenous malformations, and cancer (Papagiannis, Apostolopoulou et al. 2002, Grosse and Grosse 2010, Estepar, Kinney et al. 2013, Shovlin 2014, Cummings and Bhalla 2015, Khincha, Bertuch et al. 2017, Wang, Leader et al. 2017, Tellapuri, Park et al. 2019, Gao, Shen et al. 2020). Identifying and differentiating pulmonary arteries and veins are essential for quantitative analyses of the relevant diseases and the study of vascular changes, which may serve as biomarkers for early detection and disease progression (Estepar, Kinney et al. 2013). Additionally, differentiating pulmonary arteries and veins may also facilitate surgical planning for tumor resection to prevent possible complications (Ma and Liu 2016, Yang, Xie et al. 2016, Le Moal, Peillon et al. 2018). Computed tomography (CT) is the most widely used imaging modality for visualizing, diagnosing, and treating various lung diseases. However, discriminating pulmonary arteries and veins depicted on CT scans can be challenging, as these vessels densely populate the lungs and are often intertwined (Fig. 1). Although iodinated contrast agents may improve differentiating arteries and veins, there is no reliable approach to synchronize contrast dynamics such that the pulmonary arteries or veins are selectively opacified. Hence, it remains challenging to separate pulmonary arteries and veins without tracking them distally from the hila.

Figure 1.

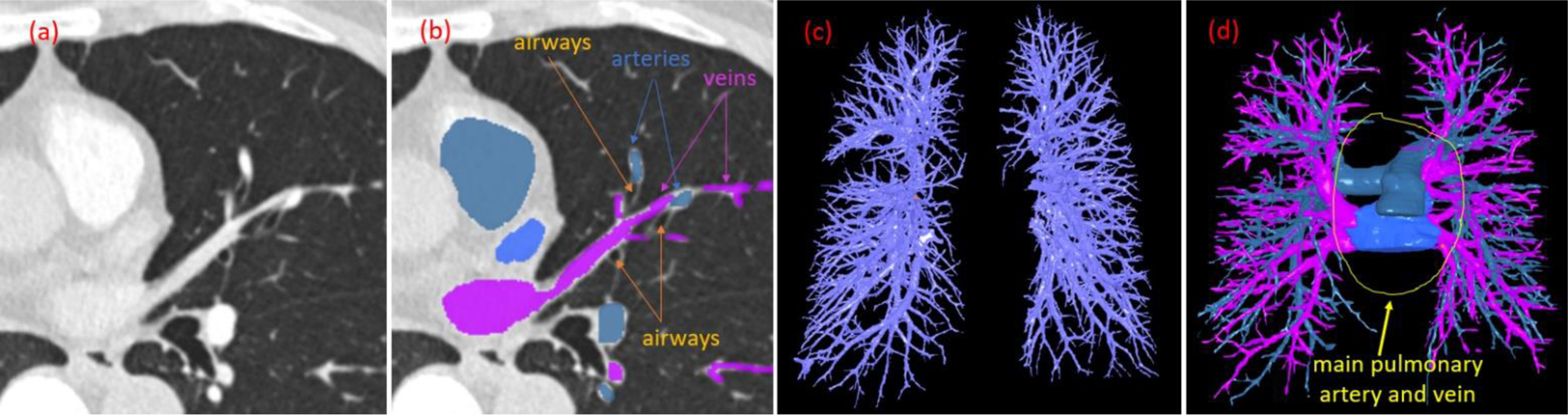
Illustration of pulmonary arteries and veins. (a) Contrast-enhanced chest CT scan showing left upper lobe vessels; (b) The arteries, veins, and airways labeled manually; (c) The intrapulmonary vessels without differentiation of the arteries and veins; and (d) Inclusion of the extrapulmonary artery and vein.

To address these challenges, a limited number of investigations have focused on developing automated procedures to identify pulmonary arteries or veins (Mekada, Nakamura et al. 2006, Zhou, Chan et al. 2007, Saha, Gao et al. 2010, Gao, Grout et al. 2012, Estepar, Kinney et al. 2013, Park, Lee et al. 2013, Stoecker, Welter et al. 2013, Charbonnier, Brink et al. 2016, Kitamura, Li et al. 2016, Payer, Pienn et al. 2016, Nardelli, Jimenez-Carretero et al. 2018, Jimenez-Carretero, Bermejo-Pelaez et al. 2019, Zhang, Sun et al. 2019). Most published approaches make assumptions regarding lung anatomy, specifically the proximity of arteries and airways, along with sophisticated image analyses to separate the arteries from the veins (Saha, Gao et al. 2010, Payer, Pienn et al. 2016). These employed image analysis techniques included the Voronoi diagram (Mekada, Nakamura et al. 2006), tubular filter (Zhang, Sun et al. 2019), graph-cut (Jimenez-Carretero, Bermejo-Pelaez et al. 2019), and distance transform (Gao, Grout et al. 2012). Because it is not easy to reliably quantify the proximity of arteries and airways in practice (Fig. 1), most of these algorithms only worked on contrast-enhanced CT images, exhibited limited performance, and additional manual interaction or refinement was often required (Gao, Grout et al. 2012). Even for the large airways, especially around the hilum regions, it is difficult to determine the “proximity” of the arteries and veins to the large airways due to their complex intertwining relation. Consequently, the available approaches primarily focused on identifying and separating lung arteries and veins in the lungs (Fig. 1C) but ignored the larger components (i.e., main pulmonary artery and veins) outside of the lungs (Fig. 1D). Additionally, for the analyses of specific diseases (e.g., PE), it is often necessary to locate the central pulmonary arteries and veins, where severe obstructions often occur. The lack of investigative effort in this regard is attributed primarily to the low contrast between these mediastinal pulmonary vessels and the background. To the best of our knowledge, there are no commercial computer tools available in clinical practice that that can be used to reliably and automatically identify pulmonary arteries and veins from chest CT scans, especially in the absence of contrast. This reality suggests the complexity of this problem and the lack of reliable algorithms in this regard.

Deep learning technology, specifically the convolutional neural networks (CNNs), has emerged as a new approach to many challenging medical image analysis problems and has demonstrated exciting performance in segmenting a large variety of biological structures depicted on two- or three-dimensional (2-D / 3-D) images (Gulshan, Peng et al. 2016, Coudray, Ocampo et al. 2018, Ardila, Kiraly et al. 2019, Falk, Mai et al. 2019, Hwang, Park et al. 2019, Lundervold and Lundervold 2019, Wang, Liu et al. 2019, Zhen, Chen et al. 2019, Wang, Yu et al. 2020, Yu, Yang et al. 2020). However, deep learning technology requires a relatively large dataset with verified “ground truth” to develop machine learning software. Given the large number of vessels in the lungs and, in particular, the similar appearance of intertwined arteries and veins on CT images, it is extremely challenging and time-consuming to manually and accurately label these vessels. Nardelli et al. (Nardelli, Jimenez-Carretero et al. 2018) tested the feasibility of a CNN model to detect pulmonary arteries and veins and reported an overall accuracy of 96% based on voxel count on a dataset consisting of 18 chest CT scans without contrast. However, only the superior and inferior lobes of the right lung were included in their study, which may have been due to the challenge of labeling the large number of vessels in the lungs. Even if intrapulmonary vessels are labeled, the memory limit of the graphical processing unit (GPU) will prevent the feed of the entire CT into the GPU. Consequently, the entire CT scan needs to be divided into a number of volumetric patches separately for deep learning. It may not be easy to reliably trace and differentiate the small arteries from the small veins in the peripheral volumetric patches.

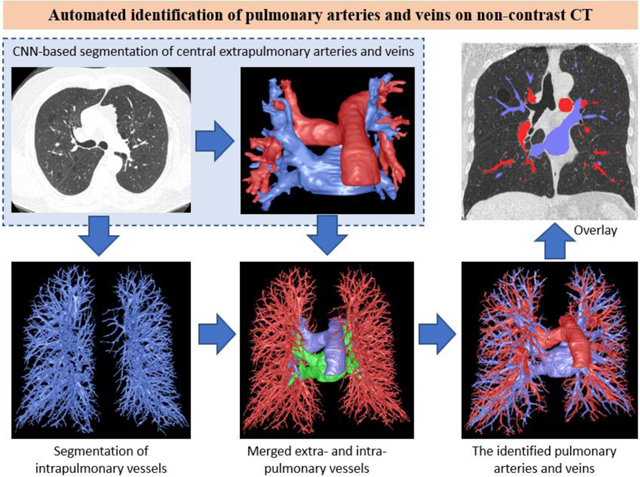
In this study, we present a novel integrative strategy to automatically segment the pulmonary arteries and veins depicted on non-contrast chest CT scans. The unique characteristic of this strategy is integrating both the CNN and computational differential geometry techniques. The CNN-based method was used to identify and differentiate the central extrapulmonary arteries and veins. The computational geometric method was used to segment the intrapulmonary vessels without differentiating arteries and veins. Thereafter, we integrated the results of both methodologies and employed a skeletonization procedure to progressively trace the vessels in the lungs from the main arteries and veins to the smaller vessels. Our innovative approach significantly relieves the efforts of manually labeling the pulmonary vasculature, particularly smaller arteries and veins, for machine learning. We demonstrate for the first time a novel integrative and progressive strategy to differentiate pulmonary arteries and veins depicted on non-contrast chest CT scans.

II. METHODS AND MATERIALS

A. Datasets

We created a dataset consisting of 120 non-contrast chest CT scans to develop, train, and test the algorithm for segmenting the extrapulmonary arteries and veins. The CT scans without iodinated contrast agents were randomly selected from the Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI) (LIDC-IDRI) in the Cancer Imaging Archive (TCIA). These CT scans were acquired using different scanners and protocols (Table 1). We only used the CT scans with a slice thickness of ≤ 1.5 mm because a higher slickness significantly affects the visualization of vessels. All CT scans were reconstructed with a matrix of 512×512 and encompassed the entire lung field. A detailed description of the LIDC-IDRI dataset and its acquisition protocols can be found in (Armato, McLennan et al. 2011).

Table 1:

Subject demographics and dataset distribution (n=120)

Age, year (SD)	62.3 (7.9)
Male, n (%)	69 (57.5)
Scanner manufacturer and model
GE Medical Systems (LightSpeed), n (%)	64 (53.3)
Simens (Definition and Emotion), n (%)	18 (15.0)
Phillips (Brilliance), n (%)	27 (22.5)
Toshiba (Aquilion), n (%)	11 (9.2)
Sub-groups
Training	90
Internal validation	15
Independent test	15
Slice thicknesses
≤ 1.0 mm	76
> 1.0 mm and ≤1.5 mm	44

Abbreviations: SD – standard deviation

An experienced (> 10 years) thoracic radiologist (JS) manually labeled the central extrapulmonary arteries and veins depicted on the CT scans using our in-house software. This annotation software supports various 2-D and 3-D operations, such as local region thresholding, flooding or region growing, dilation and erosion operators, noise or small region removal outline interpolation between neighboring slices, free-form delineation, and overlay editing. A user can label the regions of interest in separate slices and then perform the automated interpolation. We made certain that the hilar arteries and veins were specifically labeled so that they could be merged with the intrapulmonary vessels. The dataset was split randomly into three sub-groups: (1) training (n=90), (2) internal validation (n=15), and (3) independent testing (n=15). The independent test set was used as the reference standard to validate the performance of the final algorithm to identify the arteries and veins. The radiologist also labeled the intrapulmonary vessels in the independent test set with the assistance of in-house software. When labeling the intrapulmonary vessels, the radiologist traced the vessels and used a painting operation to mark the arteries and veins with a high density in two different overlays. No sophisticated algorithms were used to facilitate the labeling.

B. Scheme overview

The developed scheme was formed by four main components (Fig. 2): (1) identifying the extrapulmonary arteries and veins using a U-Net architecture (Ronneberger, Fischer et al. 2015, Falk, Mai et al. 2019), (2) identifying the intrapulmonary vessels using a computational differential geometry solution, (3) skeletonizing the intrapulmonary vessels, which guides the tracing of neighboring vessel branches, and (4) tracing the skeletons of the intrapulmonary vessels in order to differentiate between arteries and veins starting from the extrapulmonary arteries and veins. The extrapulmonary arteries and veins were identified separately to provide the seeds for tracing the small arteries and veins. Also, manually labeling only the extrapulmonary arteries and veins is significantly faster than labeling all the pulmonary arteries and veins in the CT scans.

Figure 2.

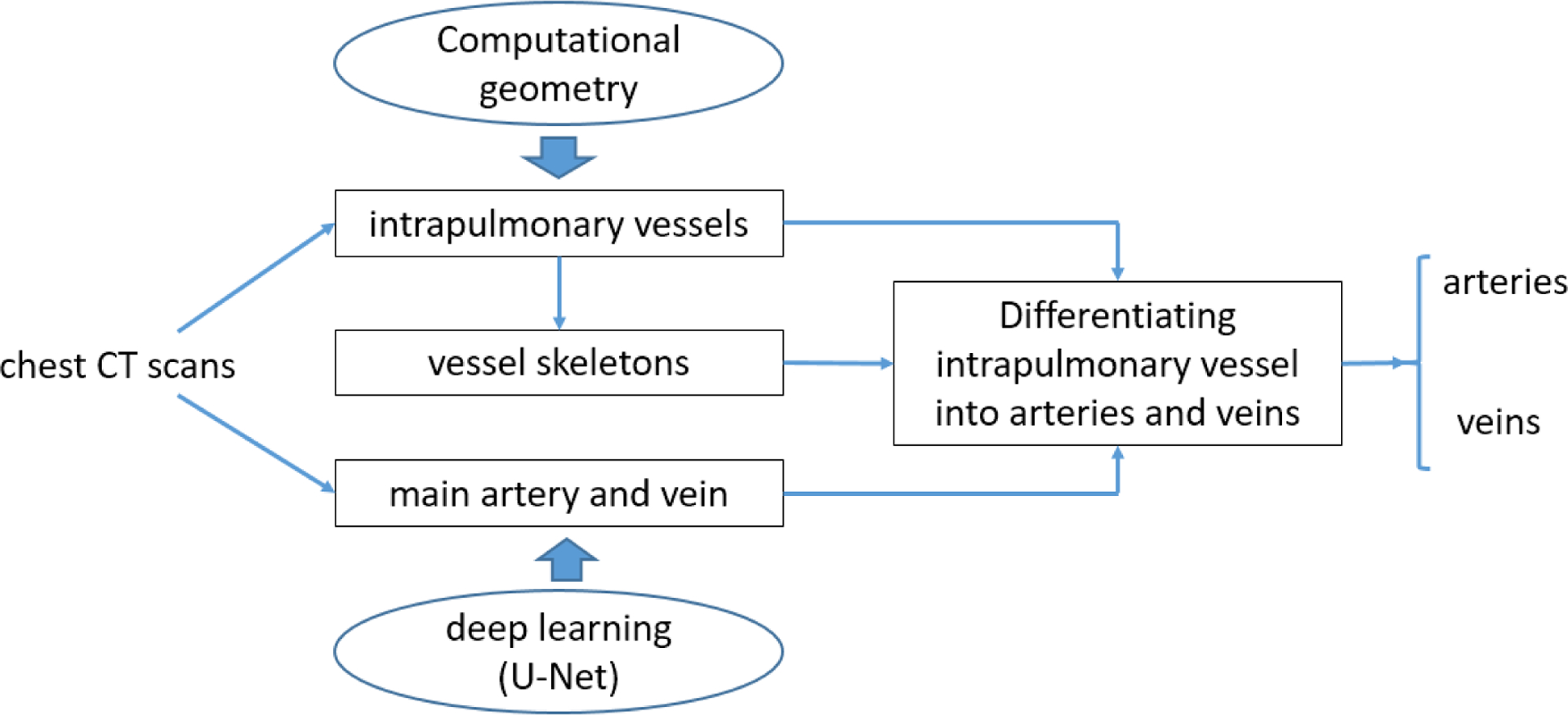
Schematic flowchart for identifying pulmonary arteries and veins.

C. Segmentation of central extrapulmonary arteries and veins using deep learning

To segment the central extrapulmonary arteries and veins, we implemented and tested several U-Net models, including the classical U-Net (Ronneberger, Fischer et al. 2015), R2Unet (Alom, Yakopcic et al. 2019), Attention U-Net (Oktay, Schlemper et al. 2018), and U-Net++ (Zhou, Rahman Siddiquee et al. 2018). The implementation of the segmentation scheme consisted of the following steps (Figure 3).

Figure 3.

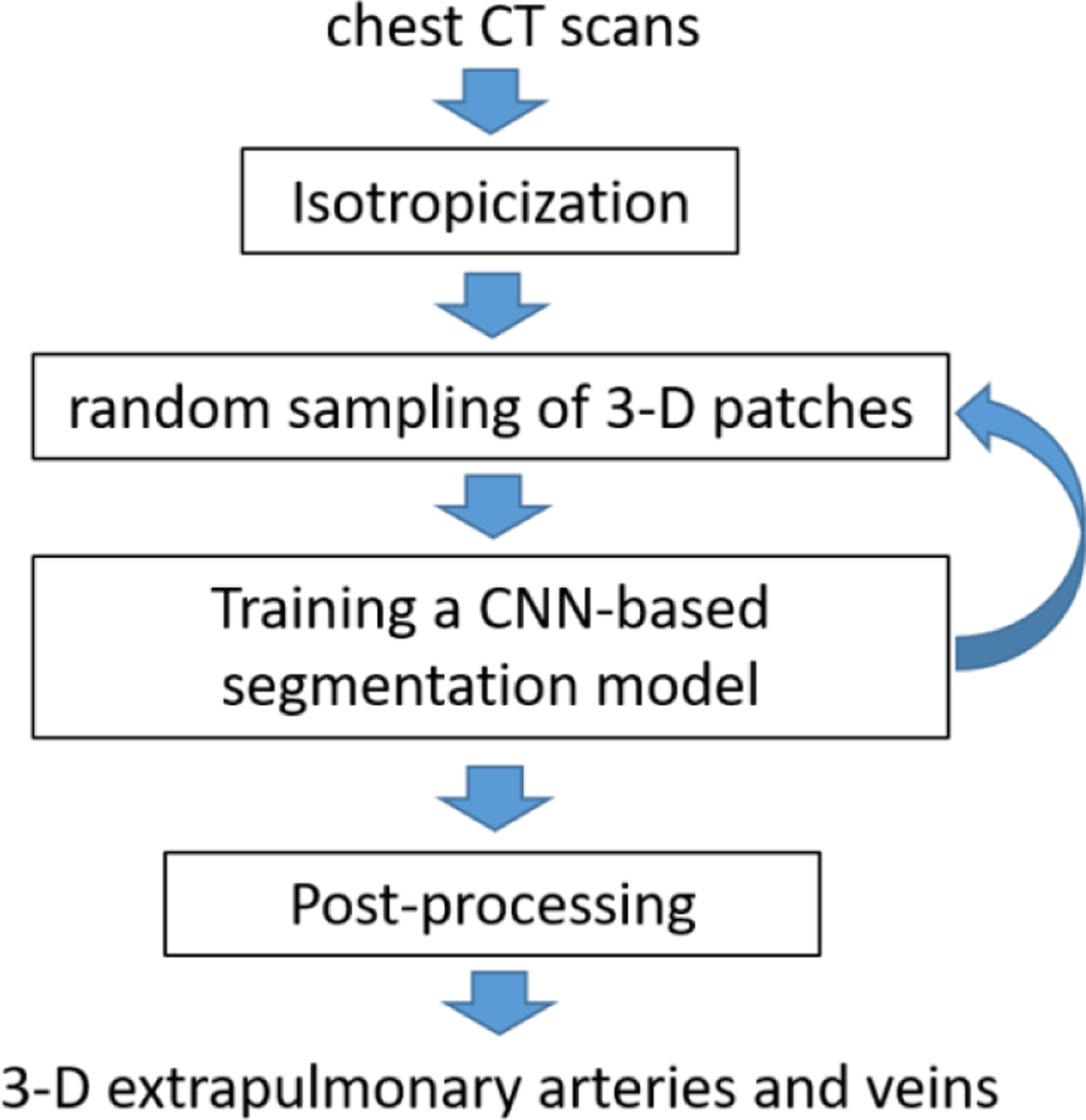
The implementation of the CNN-based segmentation scheme.

(1). Image isotropicization:

Image voxels in a chest CT scan are often not isotropic secondary to the image thickness relative to the in-plane resolution. Therefore, the CT image voxels were sub-sampled to create isotropic voxels. Since the dimensions of the central extrapulmonary arteries and veins are relatively large, a relatively low isotropic resolution (i.e., 1.5 mm) was used to speed up the training and increase efficiency.

(2). Random sampling of 3-D image patches:

The memory limit of the GPU and the difference in the number of images in the CT scans make it impossible to feed the entire CT scans into the deep learning architecture. To address this issue, the CT images were randomly cropped into a number of cubic sub-volumes or patches (e.g., 64×64×64 mm³) and used to train a CNN-based segmentation model. There can be a significant difference between the size of the background (i.e., vessels) and the size of the foreground (i.e., non-vessels), which can lead to imbalanced sampling and thus cause biased training. Although our interest is the foreground, namely the vessels, we should not ignore the background. In other words, we need the computer to learn the characteristics of the background as well as the foreground to fully train a CNN model. Only learning the foreground will lead to a biased CNN model. Also, considering the background can increase the diversity of the 3-D patches and thus the robustness of the trained CNN model. To balance the foreground and background samples, two paired cubic sub-volumes were generated for each sampling operation. One was centered on the foreground (i.e., vessels), and the other was centered on the background (i.e., non-vessels). When a sufficient number of samplings are performed, the sampled sub-volumes are expected to cover the entire CT scan. During the training of a CNN-based segmentation model, which typically involves many epochs, there should be a sufficient number of samplings.

(3). Training of a CNN model:

Four different CNN models were trained to segment the central pulmonary arteries and veins using the dataset described in Section II.A. The classical U-Net has demonstrated promising performance in segmenting various anatomical structures depicted on 2-D or 3-D images (Wang, Zhao et al. 2019, Wang, Wang et al. 2020, Weston, Korfiatis et al. 2020, Wu, Fang et al. 2020, Zhang, Wu et al. 2020). All other three models are well-known variants of the U-Net architecture (Oktay, Schlemper et al. 2018, Zhou, Rahman Siddiquee et al. 2018, Alom, Yakopcic et al. 2019). In architecture, these U-Net models are typically formed by two paths, namely an encoding (or down-sampling) path and a decoding (or up-sampling) path. In our implementation, both paths had four convolutional layers, and each layer was formed by two 3×3×3 convolutions and a 2×2×2 maximum pooling. The down-sampling and up-sampling layers with the same resolution were concatenated. At the end of each layer, there was a dropout layer with a dropout rate of 0.2. The stochastic gradient descent (SGD) algorithm was used to optimize the network with a batch size of 16 paired sub-volumes, a momentum of 0.95, and an initial learning rate of 0.001. The rate was decreased by a factor of 10 for every 10 epochs. The number of training epochs was 150, and the threshold for predicting probabilities was 0.5. Geometric and intensity augmentations were performed to improve the reliability of the trained model. The geometric augmentations, such as rotation [−90, 90], vertical/horizontal flipping, translation [0.2, 0.8], and scaling [0.9, 1.1], were applied to both the images and the labeled masks. The intensity augmentations, such as random intensity shift with a range of [−50, 50] Hounsfield unit (HU), image blurring, and Gaussian noise addition, were applied only to the images. All these models were implemented using the Keras library.

(4). Post-processing:

When applying the trained model to a non-contrast CT scan, there could be false-positive detections. The false positives are primarily attributed to the image patch strategy, namely the limited field of view of the sub-volume. When we identify the extrapulmonary vessels, we also would like to identify the intrapulmonary vessels near the hilum, which have much smaller dimensions as compared with the extrapulmonary vessels. Hence, we used an isotropic resolution of 1.5 mm. A higher image resolution will lead to a smaller field of view, which may, in return, lead to more false positives. A lower image resolution will lead to a larger field of view but may cause the missing of relatively small intrapulmonary vessels near the hilum. To eliminate the false positive detections, the first two largest regions, which were assumed to be the corresponding extrapulmonary artery and vein, were retained, and all other detections were removed.

C. Segmentation of intrapulmonary vessels using a computational differential geometry solution

Although there is high contrast between the pulmonary vessels and lung parenchyma, a simple thresholding operation does not produce a reasonable segmentation of the pulmonary vessels. First, it is impossible to determine an optimal threshold because the density of the pulmonary vessels typically decreases in the lung periphery. Second, the computed x-ray attenuation of many abnormal lung tissues (e.g., interstitial lung disease (ILD) or lung tumors) can be similar to the computed attenuation of the vessels. In geometry, as compared to other normal and abnormal lung structures, the intrapulmonary vessels have a convex cylinder-like shape and appear as high-density regions on CT images. Although the airways are also tubular structures ventilating the lungs, the airway lumen appears as low-density regions on the CT images and has a concave shape description. To leverage this unique geometric property associated with intrapulmonary vessels, we developed a computational geometry solution to automatically identify the structures with a convex cylinder-like shape in the lungs (Fig. 4). For the sake of clearly visualizing the segmentation procedures, we used a sub-volume of a chest CT scan to explain the involved steps (Fig. 4).

Figure 4.

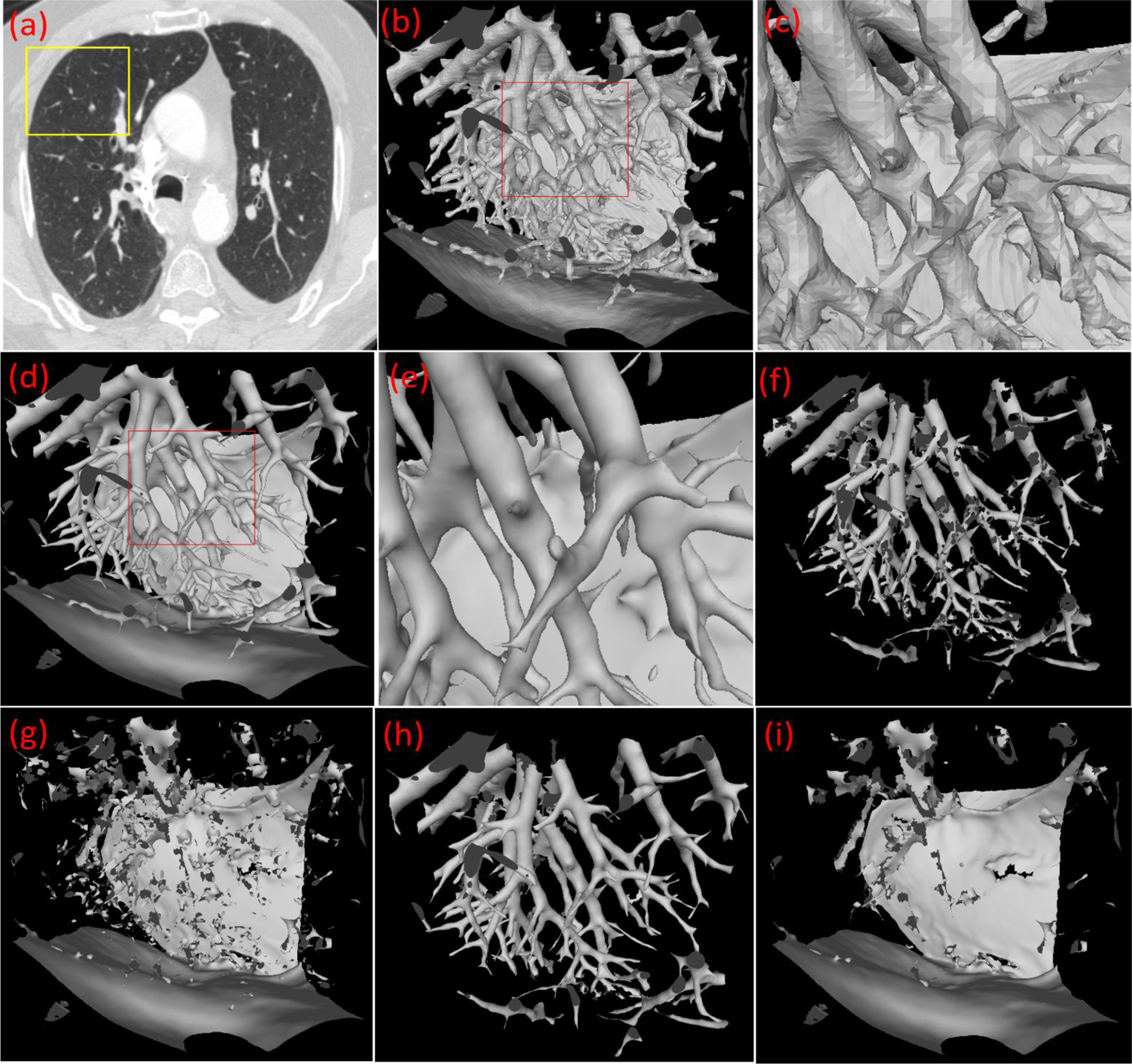
Illustration of the developed computational geometry solution for identifying intrapulmonary vessels. (a) a CT scan, (b) the 3-D surface model of the local region as indicated by the box in (a), (c) the local enlargement of the surface model in (b), (d) the surface model after the application of the Laplacian smoothing, (e) the local enlargement of the surface model in (d), (f) the surface model after filtering the triangles based on the principal curvature analyses, (g) the filtered surface model, (h) the surface model after picking up the small patches from (g), and (i) the final filtered surface model after the pick-up operation.

(1). 3-D geometric surface modeling.

Given a chest CT scan (Fig. 4(a)), the anatomical structures were reconstructed as 3-D geometric surfaces in the form of a triangle mesh using the well-known marching cubes algorithm (MCA) (Lorensen and Cline 1987) (Fig. 4(b)–(c)). To produce a triangle mesh with a similar triangle size and thus enable a more accurate computation for its properties (e.g., curvature), the CT images were subsampled to create isotropic images before applying the MCA. A higher resolution of the isotropic images enables the detection of smaller vessels due to more triangles but involves a higher computational cost.

(2). Laplacian smoothing of the geometric surface.

The geometric surface was smoothed using the Laplacian algorithm (Liu, Chen et al. 2017), which moved the vertex towards the centroid of its neighbor vertices progressively (Fig. 4(d)–(e)). Mathematically, the Laplacian smoothing can be described as:

$$v_i^{\prime }=\frac{{\sum }_j^k{w}_j{c}_j}{{\sum }_j^k{w}_j}$$ (1)

where $v_i^{\prime }$ is the new position of a vertex v_i after applying the Laplacian operation, k is the number of the neighboring triangles surrounding v_i, C_j is the center of the j^th neighboring triangle, and w_j is the area of the j^th neighboring triangle. Unlike traditional image smoothing operations (e.g., Gaussian filter) in image space, the smoothing operation in geometric space does not smooth or remove critical structural details (e.g., removing small vessels).

(3). Computing principal curvatures and directions.

The finite-difference algorithm proposed by Rusinkiewicz (Rusinkiewicz 2004) was used to estimate the principal curvatures and the principal directions of the vertices in the triangle mesh. Unlike local surface fitting methods (Goldfeather and Interrante 2004), which typically involve a very high computational cost, the basic idea of the Rusinkiewicz algorithm is to estimate the surface curvatures at a vertex by performing a differential and weighted analysis of the relative positions of the immediately adjacent vertices. This algorithm leverages the fact that a triangle has three edges. By these edges, the normal vectors of the three vertices can be computed and then used to compute the normal differences between neighboring triangles. A detailed description of the Rusinkiewicz algorithm can be found in (Rusinkiewicz 2004). The advantage of this algorithm is the computational efficiency and independence on the topology of the triangle mesh.

(4). Non-vessel surface filtering.

The triangles that did not meet the conditions for being part of a convex cylinder shape were removed (Fig. 4(f)–(g)). We simplified the shapes of the structures in a biological system into three distinct shapes, including (i) a blob-like shape, (ii) a planar-like shape, and (iii) a cylinder-like shape with distinct differential geometry properties (Table 2). For a sphere-like shape, such as a nodule, the minimal curvatures of the points on its surface are typically not close to zero and the principal directions associated with the minimal curvatures are often randomly distributed. For a planar-like shape, such as the lung surface, the maximum curvatures are typically small, and the principal directions associated with the minimal curvatures are randomly distributed. For a cylindrical structure, the minimal curvature of a point on its surface is close to zero, and the maximal curvature is one divided by the radius of the curvature. The curvature is the second derivative and sensitive to image noise or artifacts. Fortunately, there are principal directions associated with these maximal and minima curvatures. For any point on a cylinder-like structure, the principal directions associated with their minimal curvatures are parallel to each other along the cylinder’s axis, and the principal directions associated with the maximal curvatures are perpendicular to the cylinder’s axis. Structures that satisfied all of the following conditions were classified as lung vessels:

1. The minimal curvature is close to zero, e.g., < 0.01.

2. The maximum curvature (or the radius of the vessels) is within a certain range, e.g., [0.1, 2], which suggests the size range of the intrapulmonary vessels.

3. The principal direction associated with the minimal curvatures of the neighboring points are parallel to each other. This can be assessed by computing the cross-products of the neighboring principal directions associated with the minimal curvature.

Table 2:

Summary of the differential geometry properties of the basic solid shapes

Basic shape	Minimal curvature	Maximal curvature	Minimum curvature directions
cylinder-like shape	~0	> 0, in a range [c1, c2]	parallel
blob-like shape	> 0, in a range [c1, c2]	> 0, in a range [c1, c2]	random
planar-like shape	~0	~0	random

Note: For non-solid shapes, such as the airways, the maximal curvature on the surface is negative.

(5). Identifying the false-negative regions (i.e., the incorrectly removed surface).

The removed triangle patches that matched the holes in Fig. 4(f) were identified and classified as part of the lung vessels. Although both principal curvatures and directions were used to identify the surfaces associated with lung vessels, it was unavoidable to incorrectly remove the part of the vessels as non-vessel regions, as the holes shown in Fig. 4(f). The incorrectly removed regions are typically small and matched with the holes (Fig. 4(f) and 4(g)).

Finally, the identified lung vessel surfaces were mapped to the image space as the overlay of the lung vessels.

In the first step, there is an important parameter associated with the Marching Cubes algorithm (Lorensen and Cline 1987), namely the isovalue for the surface modeling. Different isovalues will lead to different surface models. A smaller isovalue typically leads to the identification of small vessels with lower densities. Since the density of intrapulmonary vessels varies significantly, a multiple-scale strategy was used to address the variability in vessel appearance. The above procedure was repeated multiples times for different isovalues or thresholds ranging from −700 HU to −200 HU at 50 HU intervals. At each isovalue, we mapped the identified vessels from the geometric space to the image space. In this way, the vessel surfaces obtained at multiple isovalues are merged or combined as a union operation in the form of an overlay of the CT images. Notably, the differential geometry algorithm only identified the regions with a cylinder-like shape in the lungs and did not differentiate the arteries from the veins (Fig. 5(d)). The large intrapulmonary vessels near the hilum regions were typically missed due to their complex geometric shapes, which tend to appear as blob-like shapes instead of cylinder-like shapes. The procedure for segmenting extrapulmonary vessels (Section II.C) was used to detect the large intrapulmonary vessels that were missed by the differential geometry algorithm. The lungs were segmented from the CT images using our previously developed scheme (Pu, Paik et al. 2011) before performing the above procedures to limit the computation within the lung regions.

Figure 5.

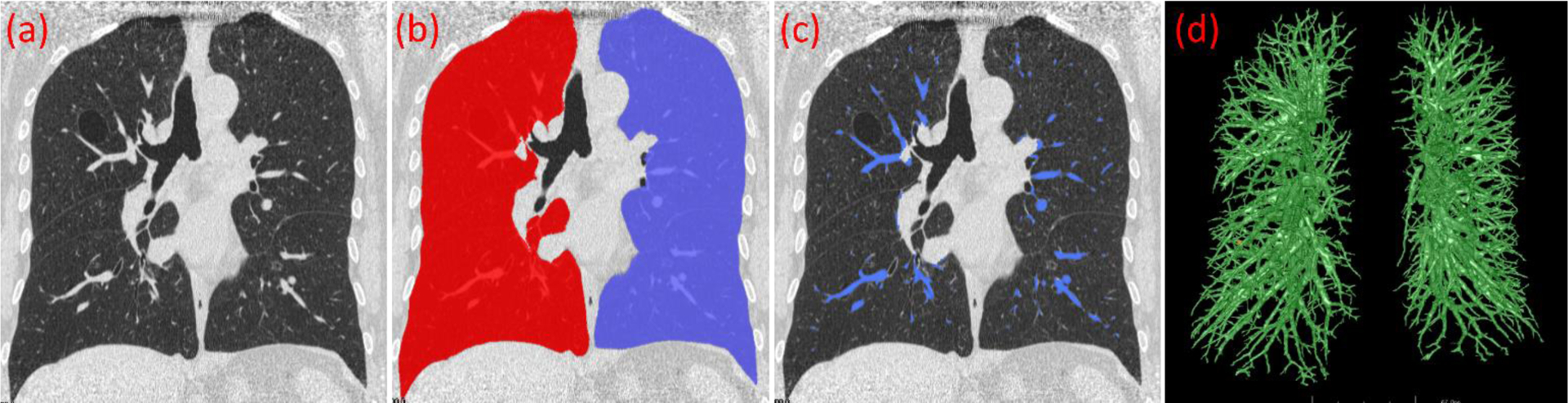
Intrapulmonary vessels identified using the developed differential geometry method and multiple thresholds [−700 HU, −200 HU]. (a) original CT image, (b) segmented lung, (c) intrapulmonary vessels detected, and (d) 3-D visualization of the detected vessels.

D. Differentiation of intrapulmonary arteries and veins

After the identification of intrapulmonary vessels, we developed a scheme to use the central extrapulmonary arteries and veins as the seeds to progressively trace intrapulmonary vessels and differentiate them into arteries and veins. The differentiation consisted of the following steps.

(1). Merge the extra-pulmonary arteries and veins with the intrapulmonary vessels.

In order to trace the pulmonary arteries and veins starting from the main vessels, the extrapulmonary and intrapulmonary vessels were merged by mapping them into the same image space. During the mapping, the central extrapulmonary arteries and veins retained their labels regardless of whether or not they overlapped with the intrapulmonary vessels (Fig. 6(a)). Although we expected that the extrapulmonary arteries and veins could be completely connected with the intrapulmonary vessels, there might be some small gaps between the intrapulmonary vessels near the hilum and the extrapulmonary arteries and veins, which may cause an interruption to the tracing operation. To avoid this interruption, a dilated operation was used to bridge these possible gaps by only including regions with high densities in the lungs near the hilum.

Figure. 6.

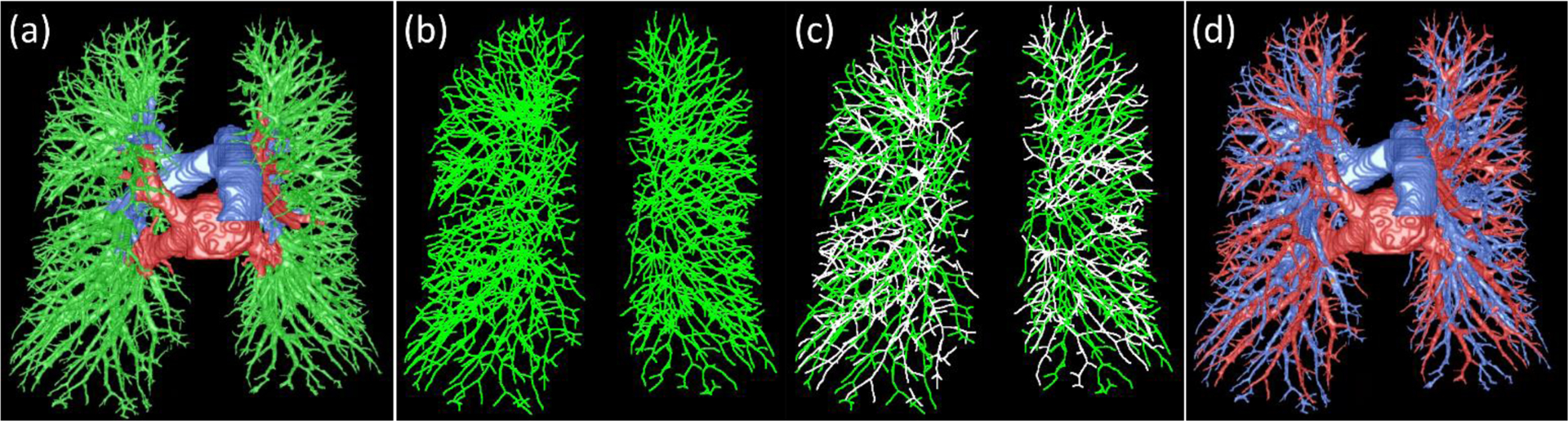
Illustration of the procedure for differentiating the intrapulmonary arteries and veins. (a) the merge of the intra- and extra-pulmonary vessels, (b) the skeletonization of the intra-pulmonary vessels, (c) the differentiation of the intra-pulmonary vessel skeletons, and (d) the final differentiation of the lung arteries and veins.

(2). Skeletonization of the intrapulmonary vessels.

The skeletonization is an operation to simplify the representation of the vessels as a number of individual branches or line segments. The objective is to make it easy to analyze the relationship between neighboring vessel branches and thus enable a more reliable tracing of the vessels. In the implementation, we used the algorithm developed by Cornea et al. (Cornea ND 2005) to automatically extract the vessel skeletons by reconstructing a “repulsive force field” to characterize the centerline of the vessel (Fig. 6(b)). The unique strength of this skeletonization algorithm is the ability to extract a skeleton of an arbitrary object at a specified level of detail and to concurrently detect the critical points (corresponding to the endpoints of the vessel branch). The lung vessels are represented as a number of individual branches after skeletonization. The orientation of each vessel branch is computed based on its two endpoints.

(3). The distance field of the intrapulmonary vessels.

In addition to the vessel branch orientation, we also computed the distance field of the intrapulmonary vessels. The objective is to efficiently obtain the size of the vessels at a point on the vessel skeletons. The distance field of the vessels was computed using the fast transformation method (Felzenszwalb and Huttenlocher 2004). The averaged distance of the skeleton points on each branch was used to denote the size (i.e., the average radius of the cross-section) of the branch.

(4). Tracing the arteries and veins starting from the vessels near the hilum.

In practice, the pulmonary lung arteries and veins are intertwined as they course throughout the lung. The intertwined vessels, with a minimal HU value gradient at the vessel walls, can merge and depict arteries and veins on a CT image, as indicated by the arrow “A” in Fig. 7b. The local artery and vein fusion is the most common and challenging issue that affects the tracing of arteries or veins. Meanwhile, the skeletonization procedure may also result in small “noisy” skeletons around the branching regions when the fusion region is close to the branching or bifurcation regions, as indicated by “B” in Fig. 7b and 7d. Another situation that may cause issues for skeleton-based tracing is the disconnection of the vessel branch skeleton (as indicated by arrow C Fig. 7). No matter what kind of situation, the neighboring consequent vessel branches with the same label (i.e., either arteries or veins) have several properties: (i) they have a similar orientation, (ii) their two neighboring endpoints should be within a certain distance, and (iii) they have a similar size (radius). Hence, we leveraged these characteristics to address the labeling challenges described above with the help of the skeletons and the distance field of the vessels. First, as an initialization step, we labeled the skeletons of the intrapulmonary vessels that were directly attached to the extrapulmonary arteries and veins. Also, the unlabeled branches should have a certain level of overlap in volume (e.g., 25%) with the identified extrapulmonary arteries or veins. Second, we computed the orientations and sizes of the initially labeled vessel branched. Third, given an endpoint of a labeled vessel branch (i.e., reference branch), we identified all neighboring vessels branches (i.e., the candidate branches) (e.g., within 3 mm to the endpoint of the reference branch). From these candidate branches, we firstly identified those that shared the same endpoint with the reference branch, had a similar orientation with the reference branch, and had a certain length (e.g., 5 mm). The length criterion was used to exclude the possible “noisy” branches, such as the branch indicated by arrow B in Fig. 7c. The identified vessels were assigned with the label (i.e., artery or vein) of the reference branch. For example, assuming that branch 1 in Fig. 7c is the reference branch, we can assign the label of brach 1 to branches “3” and “5”. The branch, as indicated by arrow A in Fig. 7d, would not be labeled. Second, we checked each one in the remaining unlabeled branches to assess its distance and orientation with the neighboring labeled vessels. If a branch is close and has a similar orientation to the reference branch, it is assigned the same label as the reference branch. For example, in Fig. 7c, branch “4” will be assigned with the label as branch “2”. We repeated the above procedures until there were no branches that could be labeled further. However, there could be unlabeled vessel branches left. Given each left branch (e.g., the branch as indicated by arrow C in Fig. 7), we identified its closest labeled branch with the most similar orientation based on the branch endpoints. The branch was assigned with the label of the nearest branch. Finally, the intrapulmonary vessels were fully labeled (Fig. 6(d)).

Figure 7.

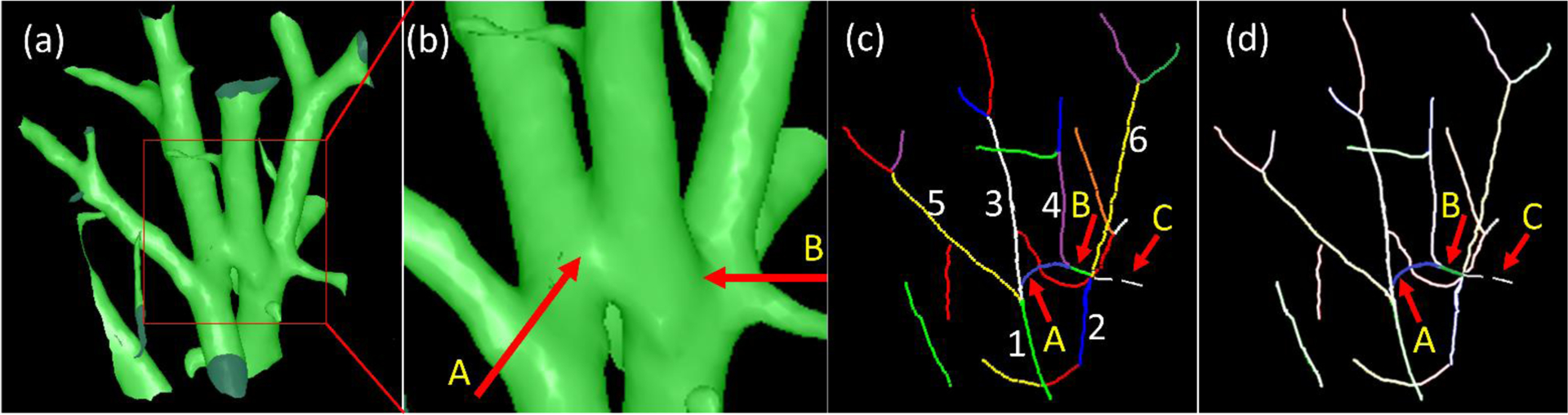
An example to illustrate the challenge of tracing the lung arteries and veins. (a) the 3-D surface model of the lung vessels in a local region, (b) the local enlargement of the region as indicated by the box in (a), (c) the skeletons of the vessel branches in (a) and each skeleton indicates a vessel branch, and (d) the highlight of the two skeletons (i.e., A and B) associated with the challenge of vessel tracing. Arrow C illustrated a disconnected branch as the result of skeletonization. In (c), “1”–”6” indicated four different branches.

E. Performance validation

To evaluate the performance of the developed scheme in differentiating lung arteries and veins, we first computed the Dice coefficient to assess the agreement between the computer output and the manual labeling by the radiologist for identifying the central extrapulmonary vessels. The Dice coefficient is defined as:

$$D(A,B)=\frac{2\left|A\cap B\right|}{\left|A\right|+\left|B\right|}$$ (2)

where A is the computerized results and B is the labeled results by the radiologists. The vessels labeled by the radiologist were used as the reference standard in assessing the computer’s performance for detecting intrapulmonary arteries and veins. In particular, we divided the extrapulmonary vessels into two parts based on whether the vessels are within the lung volume or not, namely the large ones outside the lungs (denoted as “mediastinal vessels”) and the small ones within the lung volume (denoted as “hilum vessel”) (Fig. 8). We evaluated the performance of the U-Net and its several state-of-art variants in identifying these two parts. All the CNN models were trained using the same parameters, such as patch size, learning rate, and early stop conditions. A paired-samples t-test was performed to assess the performance difference of these CNN models. A p-value of less than 0.05 was considered statistically significant. IBM SPSS v25 was used for the statistical analyses.

Figure 8.

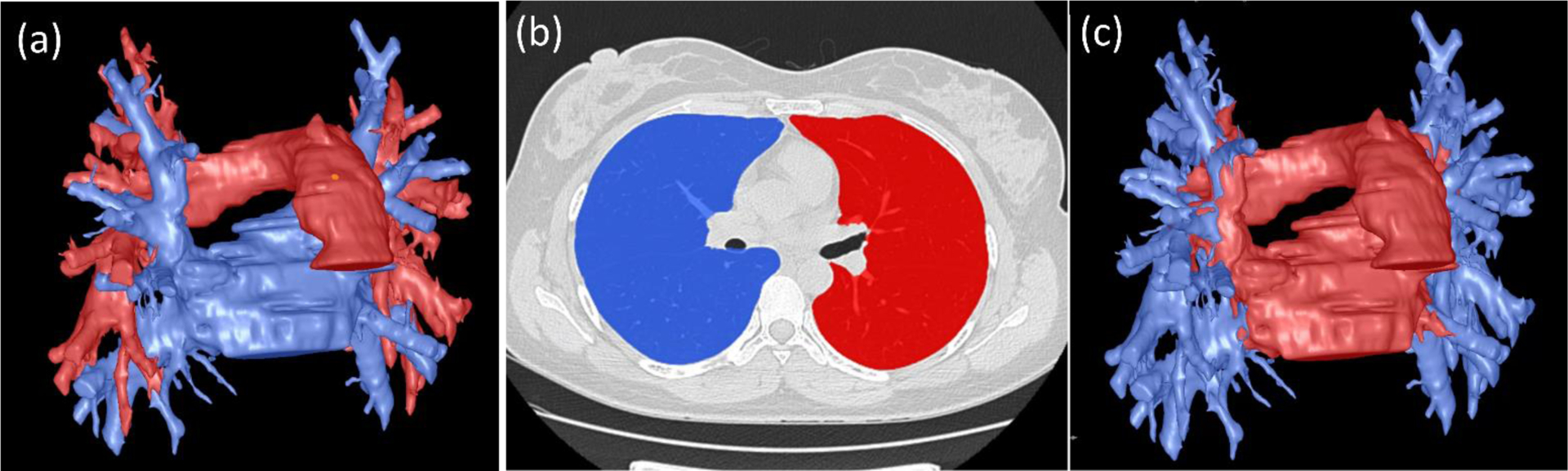
Separating extrapulmonary vessels (a) into two parts based on whether the vessels are within the lung volume (b), including (1) mediastinal vessels (red) and (2) hilum vessels (blue) in (c).

Second, we computed the sensitivity of the computer algorithm to correctly label the artery and vein branches in the reference standard. Meanwhile, considering that the computer algorithm might identify more small vessels than the human expert, we asked a radiologist (IO) to visual trace and review the computerized results in the independent test set (n=15). The artery and vein branches incorrectly labeled by the computerized algorithm were marked using our in-house software. The sensitivities of the computer algorithm in segmenting arteries and veins were computed to evaluate the performance of the computer algorithm related to the intrapulmonary vessel labeling.

III. RESULTS

We summarized the performance of the classical U-Net and its several variants in identifying extrapulmonary arteries and veins in Table 3 and Appendix Table A–B, respectively. There was a strong agreement between the radiologist’s manual and CNN-based computer segmentations of the extrapulmonary vessels. The average Dice coefficients of agreement between the manual and computer segmentation for the central extrapulmonary veins and arteries were 0.919±0.017 (range: 0.883–0.948) and 0.907±0.012 (range: 0.886–0.924), respectively. The U-Net model demonstrated much higher performance in identifying the vessels near the hilum (0.924±0.011) as compared to the mediastinal vessels (0.913±0.007) (p<0.05). Notably, although the R2Uet demonstrated the best performance, there was no significant difference between the performance of the classical U-Net and its variants (p>0.05) in identifying extrapulmonary vessels. The average Dice coefficients of the U-Net model for the cases with a slice thickness of 0.625 mm, 1.25 mm, and 1.50 mm were 0.916±0.023, 0.923±0.010, and 0.921±0.002 for the veins, and 0.911±0.012, 0.902±0.011, and 0.907±0.013 for the arteries, respectively.

Table 3.

The performance of the U-Net in identifying extrapulmonary arteries and veins on the independent test set.

Case	Dice coefficient
	vein	artery	hilum vessels	mediastinal vessels
1*	0.937	0.917	0.931	0.918
2*	0.929	0.908	0.937	0.911
3ǂ	0.948	0.921	0.944	0.917
4#	0.919	0.897	0.922	0.909
5ǂ	0.924	0.905	0.931	0.909
6*	0.918	0.886	0.913	0.903
7*	0.915	0.900	0.916	0.919
8ǂ	0.896	0.916	0.906	0.910
9ǂ	0.909	0.893	0.913	0.911
10#	0.922	0.916	0.929	0.916
11ǂ	0.911	0.924	0.915	0.921
12*	0.926	0.895	0.928	0.906
13ǂ	0.943	0.924	0.939	0.930
14ǂ	0.883	0.903	0.910	0.912
15*	0.911	0.903	0.922	0.914
mean	0.919±0.017	0.907±0.012	0.924±0.011	0.913±0.007
ST = 0.625 mm	0.916±0.024	0.911±0.012	0.924±0.016	0.915±0.008
ST = 1.25 mm	0.923±0.010	0.902±0.011	0.924±0.010	0.913±0.006
ST = 1.5 mm	0.921±0.002	0.907±0.013	0.926±0.005	0.913±0.005

^ǂ:cases with a slice thickness of 0.625 mm

^*:cases with a slice thickness of 1.25 mm

^#:cases with a slice thickness of 1.50 mm

ST: slice thickness

The developed computerized scheme identified an average branch count for the intrapulmonary veins and arteries of 1459.6±620.9 (range: 597–2890) and 1414.5±779.5 (range: 595–2923), respectively (Table 4). More vessels were identified for the cases with smaller slice thicknesses. For the cases with a slice thickness of 0.625 mm, the computer algorithm detected an average vessel branch count of veins and arteries of 1879.0±544.7 and 1965.3±886.8, respectively. In contrast, for the cases with a slice thickness of 1.25 mm, the computer algorithm detected an average vessel branch count of veins and arteries of 1131.4±128.4 and 991.0±232.4, respectively. The radiologist manually identified an average branch count of veins and arteries of 347.5±124.2 (range: 231–661) and 294.4±77.4 (range: 206–496), respectively (Table 4). The computer algorithm identified all of the intrapulmonary veins and arteries manually outlined by the radiologist. On average, the computer algorithm detected 98.2±0.98% (range: 96.7–100.0%) and 98.1±1.07% (range: 95.3–99.6%) of the veins and arteries, respectively, manually identified by the radiologists (Table 5). As compared with manual results, the computerized scheme identified many smaller vessels (Fig. 9), which were difficult for manual delineation. An example in Fig. 10 showed the computerized results by progressively visualizing the lung arteries and veins. The examples in Figs. 11–12 showed the computerized results and the manual results when the CT examinations had different slice thicknesses. The partial fusion was the primary reason that caused the incorrect differentiation of lung arteries and veins, as the example in Fig. 13 illustrated. The radiologist’s review of the computerized results showed that the computer algorithm correctly labeled 97.1±0.9% (range: 95.8–98.8%) and 97.4±0.9% (range: 95.1–98.7%) of the detected veins and arteries, respectively (Table 5). Correspondingly, an average of 43.20±23.00 vein branches were incorrectly labeled as arteries, and 39.33±28.43 artery branches were incorrectly labeled as veins.

Table 4:

The summary of the vessel branches identified by the developed algorithms and the manual annotation in the independent test set (n=15)

Case	Intrapulmonary vessel detected (count)
	Computer		Radiologist
	vein	artery	vein	artery
1*	1023	833	464	346
2*	1157	1159	492	496
3ǂ	2890	2848	426	352
4#	857	994	242	297
5ǂ	1310	753	661	304
6*	1302	1317	274	206
7*	1189	817	213	215
8ǂ	1822	1889	373	263
9ǂ	1523	1138	377	311
10#	597	595	227	236
11ǂ	2452	2061	367	365
12*	1057	820	249	212
13ǂ	1804	2923	261	311
14ǂ	1925	2241	254	213
15*	986	829	333	289
mean	1459.6±620.9	1414.5±779.5	347.5±124.2	294.4±77.6
ST = 0.625 mm	1879.0±544.7	1965.3±886.8	393.0±148.5	292.3±48.1
ST = 1.25 mm	1131.4±128.4	991.0±232.4	355.2±120.3	310.4±118.5
ST = 1.5 mm	727.0±183.8	794.5±282.1	234.5±10.6	266.5±43.1

^ǂ:cases with a slice thickness of 0.625 mm

^*:cases with a slice thickness of 1.25 mm

^#:cases with a slice thickness of 1.50 mm

ST: slice thickness

Table 5:

The performance of the developed algorithms in labeling intrapulmonary vessels in the independent test set (n=15)

Case	Manual annotation as the reference standard				Visually review of the computerized results
	Computer detected (%)		Computer missed (count)		Computer detected (%)		Computer label errors (count)
	vein	artery	vein	artery	vein	artery	vein	artery
1*	98.7	98.6	6	5	96.4	96.3	37	31
2*	99.0	98.6	5	7	97.1	97.2	34	32
3ǂ	98.6	98.9	6	4	97.1	97.2	84	79
4#	98.4	98.3	4	5	97.9	97.9	18	21
5ǂ	99.6	98.7	3	4	98.5	98.1	19	14
6*	98.5	98.6	4	3	96.9	97.4	40	34
7*	96.7	96.3	7	8	95.9	97.6	49	20
8ǂ	98.1	98.5	7	4	97.3	98.0	50	38
9ǂ	97.6	97.4	9	8	96.3	96.2	57	43
10#	100.0	99.6	0	1	98.8	98.7	7	8
11ǂ	98.1	97.5	7	9	97.6	97.4	59	53
12*	97.7	98.1	6	4	97.1	97.9	31	17
13ǂ	96.9	98.1	8	6	96.5	97.5	63	74
14ǂ	96.9	95.3	8	10	95.8	95.1	81	109
15*	99.1	98.6	3	4	98.1	97.9	19	17
mean	98.3±1.0	98.1±1.1	5.5±2.4	5.5±2.5	97.1±0.9	97.4±0.9	43.2±23.0	39.3±28.4
ST = 0.625 mm	98.0±1.1	97.8±1.3	6.8±2.1	6.0±2.5	96.9±1.0	97.0±1.2	59.0±23.7	59.5±34.2
ST = 1.25 mm	98.4±1.0	98.1±1.0	5.0±1.6	5.4±2.1	96.9±0.8	97.3±06	35.8±10.9	26.8±7.7
ST = 1.5 mm	99.2±1.1	99.0±0.9	2.0±2.8	3.0±2.8	98.4±0.6	98.3±0.6	12.5±7.8	14.5±9.2

^ǂ:cases with a slice thickness of 0.625 mm

^*:cases with a slice thickness of 1.25 mm

^#:cases with a slice thickness of 1.50 mm.

ST: slice thickness

Figure 9.

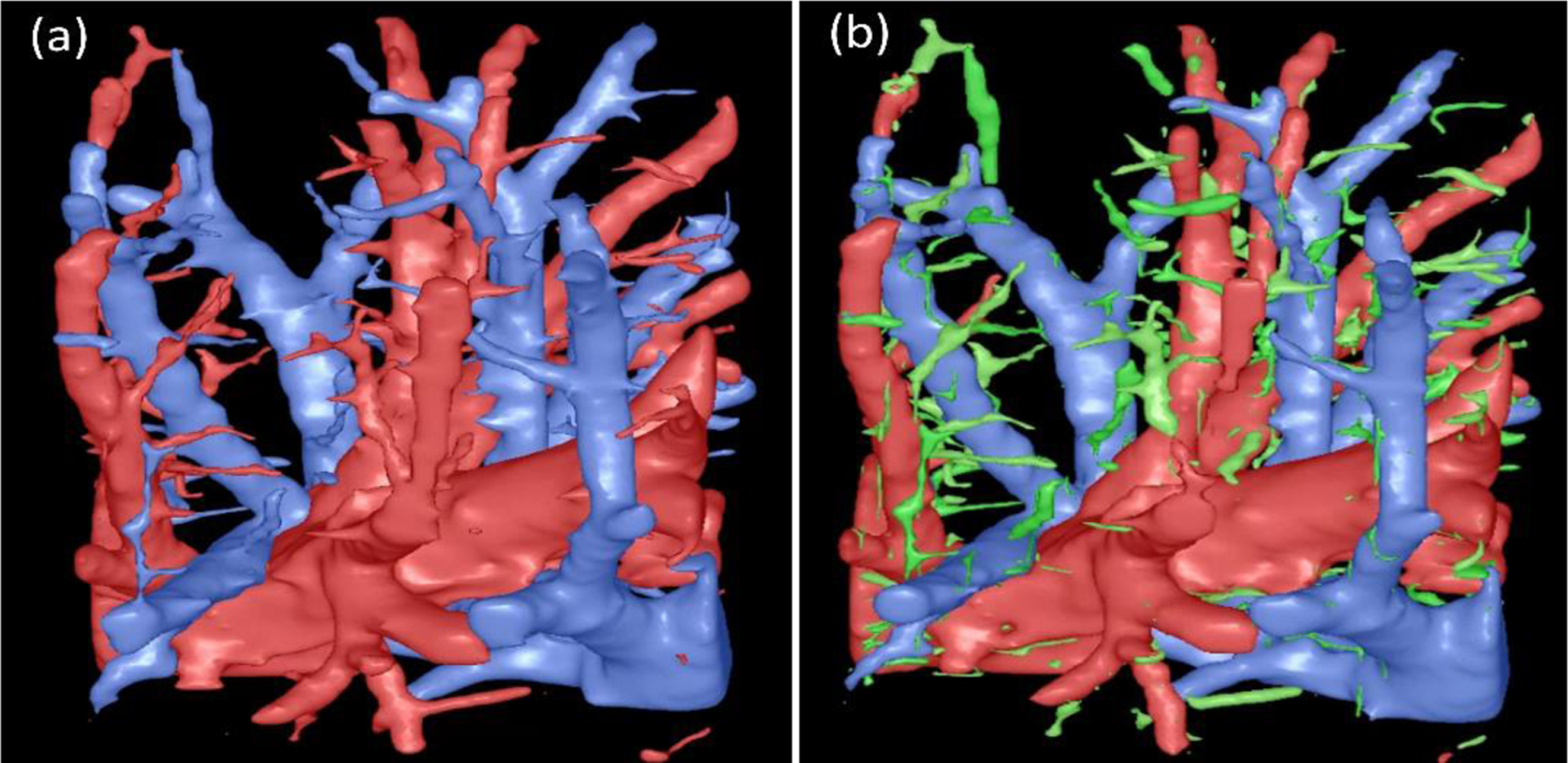
The vessels identified by the computerized scheme (a) and the manual operation (b). The regions in green were vessel branches identified by the computerized scheme but not labeled by the radiologist.

Figure 10.

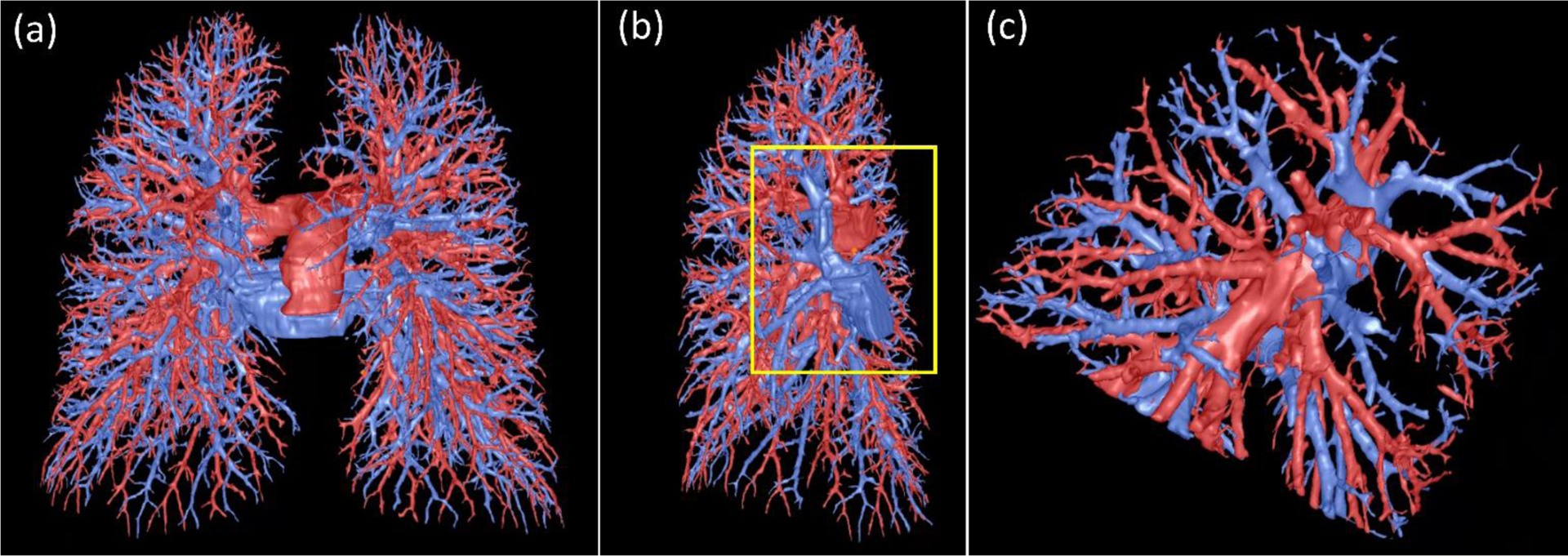
Visualization of the computerized results. (a) the global view of the lung artery and vein labeling, (b) the view of the right lung, and (c) the local enlargement of the region as indicated by the box in (b).

Figure 11.

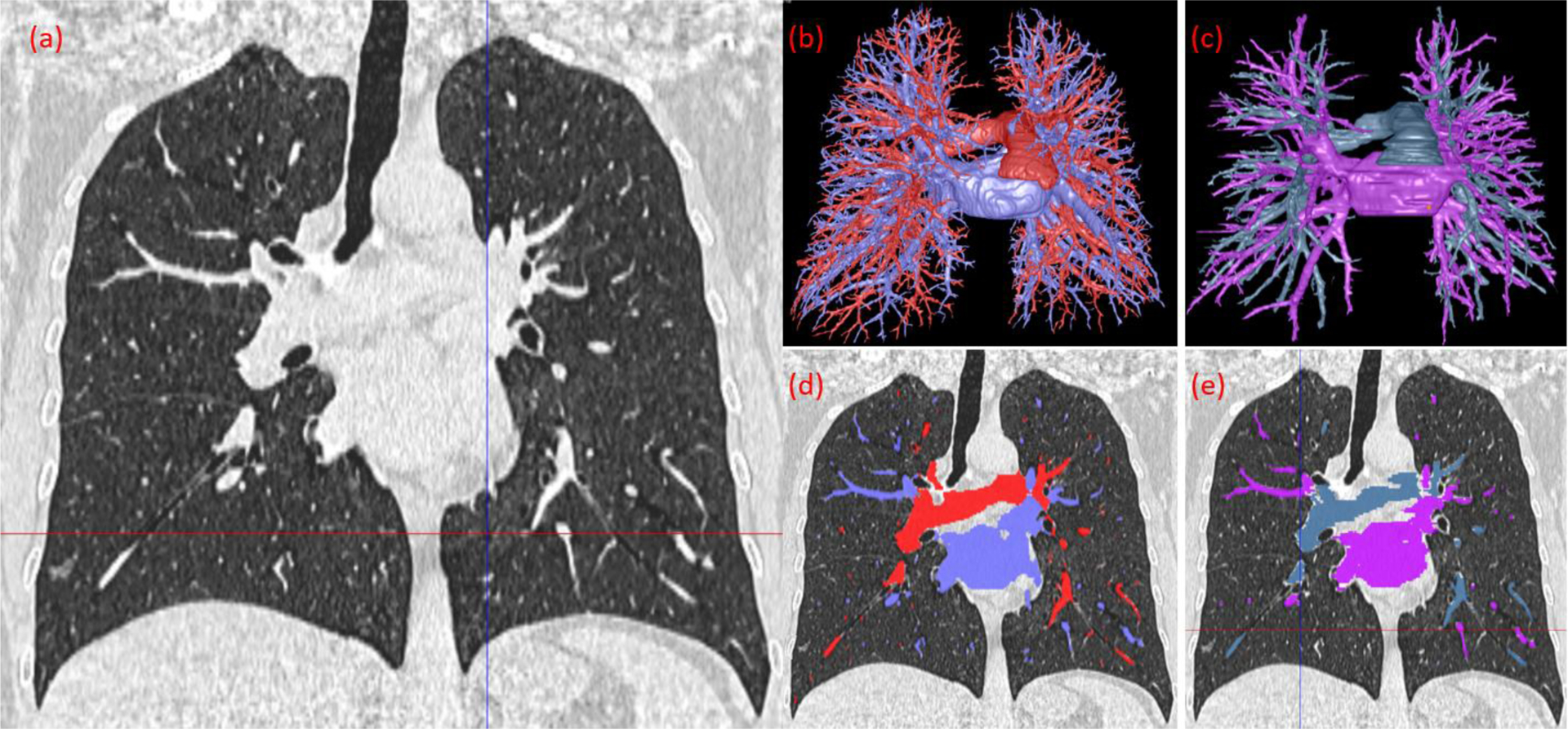
The computerized results and radiologist’s manual segmentation of the arteries and veins. (a) CT image of the lungs in the coronal view, image thickness of 1.25 mm. (b) 3-D visualization of the computer’s segmentation. (c) 3-D visualization of the radiologist’s segmentation. (d) Overlay of the computer’s segmentation on the CT image. (e) Overlay of the radiologist’s segmentation on the CT image.

Figure 12.

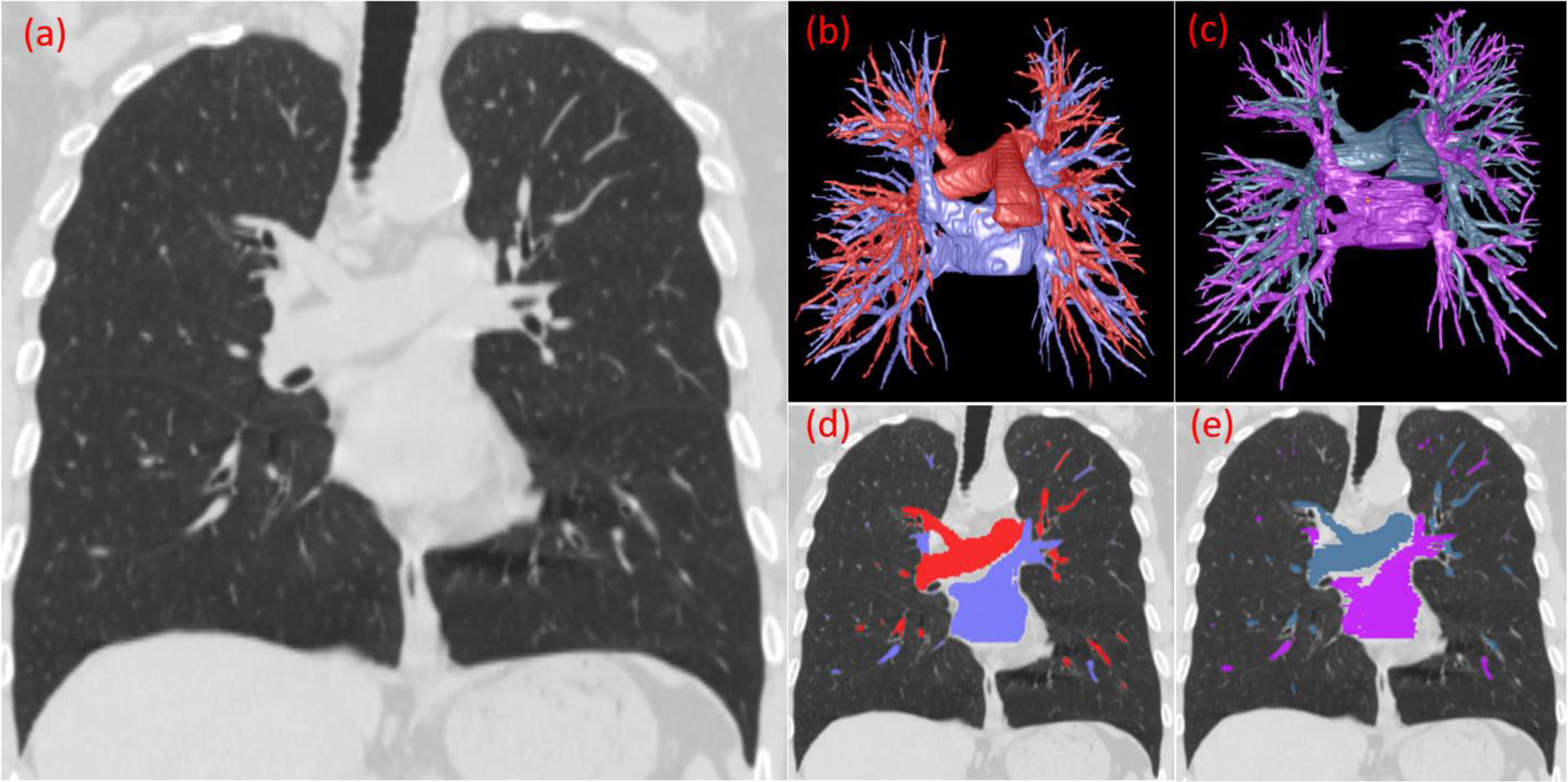
The computerized results and radiologist’s manual segmentation of the arteries and veins. (a) CT image of the lungs in the coronal view, image thickness of 1.5 mm. (b) 3-D visualization of the computer’s segmentation. (c) 3-D visualization of the radiologist’s segmentation. (d) Overlay of the computer’s segmentation on the CT image. (e) Overlay of the radiologist’s segmentation on the CT image.

Figure 13.

An example illustrating the incorrect differentiation of intrapulmonary arteries and veins. (a) the arteries and veins labeled by the computerized scheme, where the vessels indicated by arrow A were incorrectly labeled as the follow-up branch of the vessel as indicated by arrow B, (b) the local enlargement of the regions indicated by A and B, and (c) the arteries and veins labeled by the radiologist.

The radiologist labeled the central extrapulmonary arteries and veins in approximately 30 minutes per CT scan. In contrast, the radiologist needed 6 to 8 hours to label the intrapulmonary arteries and veins with the help of our in-house software. Although it took ~ 30 hours to train the CNN-based algorithm, only 2 to 3 minutes was required to automatically identify the arteries and veins depicted on a single CT scan. This was accomplished using a high-end GPU (NVIDIA TITAN Xp). If the prediction model was run on a CPU (Intel (R) Xeon W-2123 CPU @ 3.60 GHz), it would take about ~20 minutes to identify the arteries and veins.

IV. DISCUSSION

Our novel computer algorithm to automatically segment the pulmonary arteries and veins depicted on chest CT scans had several unique characteristics. First, the algorithm integrated a CNN-based method and a computational differential geometry method that significantly relieves the time-consuming and error-prone manual efforts to generate a large dataset with “ground truth” for machine learning. In the lungs, there are a large number of vessels. It is extremely challenging (if not improbable) to manually delineate and differentiate them into arteries and veins. We used a CNN approach to identify the central extrapulmonary arteries and veins and a differential geometry approach to delineate the vessels in the lungs. The small vessels were progressively labeled as arteries or veins in the lungs, beginning with the extrapulmonary vessels. Second, the algorithm automatically segmented the extrapulmonary arteries and veins and strongly correlated with a radiologist’s manual segmentation (Dice coefficient > 0.91). The segmentation of extrapulmonary arteries and veins will facilitate the study of pulmonary vascular disease (e.g., PE and PH). To our knowledge, current algorithms for segmenting pulmonary arteries and veins (Mekada, Nakamura et al. 2006, Zhou, Chan et al. 2007, Saha, Gao et al. 2010, Gao, Grout et al. 2012, Estepar, Kinney et al. 2013, Park, Lee et al. 2013, Stoecker, Welter et al. 2013, Charbonnier, Brink et al. 2016, Kitamura, Li et al. 2016, Payer, Pienn et al. 2016, Nardelli, Jimenez-Carretero et al. 2018, Jimenez-Carretero, Bermejo-Pelaez et al. 2019, Zhang, Sun et al. 2019) only attempt to segment the intrapulmonary vessels. The labeling procedure in other available methods primarily depends on the anatomical knowledge of the lung, such as the proximity of airways and arteries, because they were not guided by the segmentation results of the extrapulmonary arteries and veins. Also, identifying the airway tree is a prerequisite to assessing the proximity of the airways and arteries, which can be poorly depicted on the chest CT images, especially in the presence of airway-related disease (e.g., COPD and asthma). Our algorithm avoids this problem, because it does not rely on knowing the proximity of airways and arteries. Third, the algorithm is designed to process non-contrast CT images. This characteristic has important clinical implications, because iodinated contrast agents carry a significant risk of renal damage, as well as allergic reactions.

We developed and tested several CNN models for segmenting the extrapulmonary vessels. Like many other algorithms that involved multiple procedures, the performance of the initial step (i.e., the segmentation of extrapulmonary arteries and veins) is critical for the performance of the entire algorithm. If the extrapulmonary vessels cannot be correctly identified, it is almost impossible to ensure accurate labeling of the intrapulmonary vessels. As our experiments showed, the CNN-based method demonstrated reliable and accurate performance in identifying the extrapulmonary vessels. We also found that there were no significant differences among the performance of these CNN models (Tables A and B in the appendix). Although the R2Unet and UNet++ demonstrated better performance on the independent test set, their computational cost for training the models was much higher than the classical U-Net. Hence, we suggested the use of the classical U-Net for this specific purpose. Despite the low contrast or fuzzy boundaries between extrapulmonary vessels and their surrounding tissues, the CNN models demonstrated very promising performance and could accurately locate the arteries and veins. It is difficult to explain why a CNN model can handle such a challenging situation since it works as a “black-box.” A possible explanation is that a CNN model abstracts image features progressively from low levels to higher levels via 3-D convolutional operations until the last layer (typically fully connected), representing the semantic conclusion of the machine learning. During this progressive learning, tens of millions of parameters are involved in the 3-D convolutional operations to facilitate identifying the boundaries (i.e., regions with relatively high contrast) of the objects depicted on CT images. Notably, the CNN models demonstrated a consistently better performance in locating the arteries and veins near the hilum than in locating the mediastinal arteries and veins (Table 3). This may be primarily attributed to the higher contrast between the vessels near the hilum and the surrounding lung tissues.

There have been many CNN models developed for segmenting a variety of biological structures depicted on medical images (Vigneault, Xie et al. 2018, Vigueras-Guillen, Sari et al. 2019, Ushinsky, Bardis et al. 2020, Wang, Wang et al. 2020). A large portion of the approaches are somewhat variants of the classical U-Net model. Our results demonstrated that the classical U-Net architecture performed extremely well in comparison with a radiologist’s manual segmentation of the extrapulmonary arteries and veins (average dice coefficient of 0.91 and 0.92 for arteries and veins, respectively). As our experiments showed, their performance improvement was actually limited when compared with the classical U-Net model when applied to segmenting extrapulmonary vessels (Appendix Table A and B). In most situations, the size and diversity of the data matter significantly more than the CNN architecture based on our experience (Liu, Wang et al. 2019, Wang, Liu et al. 2019, Zhen, Chen et al. 2019, Pu, Leader et al. 2020, Wang, Yu et al. 2020, Yu, Yang et al. 2020).

When we trained the patch-based CNN model, although our interest was the foreground, namely the vessels, we should not ignore the background. In other words, we need the computer to learn the characteristics of the background as well as the foreground to properly train a CNN model. Only learning the foreground will lead to a biased CNN model. Also, considering the background will increase the diversity of the 3-D patches and thus the robustness of the trained CNN model.

There might be some small false positive detections when the trained CNN model was used to segment the extrapulmonary vessels. To address this issue, we used a simple size-based filter as a post-processing operation to remove the false positives. The false positives were primarily caused by the 3-D patch strategy, namely the limited field of view of the 3-D patch. When we identified the extrapulmonary vessels, we also would like to identify the intrapulmonary vessels near the hilum, which have much smaller dimensions than the extrapulmonary vessels. Hence, we used an isotropic resolution of 1.5 mm. A higher image resolution will lead to a smaller field of view, which may, in return, lead to more false positives. A lower image resolution will lead to a larger field of view but may cause the missing of relatively small intrapulmonary vessels near the hilum.

As demonstrated by our experiments, the branch number detected by the computer algorithm varied significantly across the chest CT scans, ranging from 600 to 2,800 for both veins and arteries (Table 1). This may have been caused by multiple factors, such as the biological differences between the subjects, image acquisition protocols (e.g., image slice thickness and dosage), and respiratory effort (correct breath-hold maneuver performed during image acquisition). Typically, the algorithms detect more vessels for the cases with smaller image slice thickness (e.g., Table 4). However, based on our experiment on a relatively small dataset (Table 5), the image slice thickness had a limited impact on the accuracy of intrapulmonary vessel labeling. In addition, the lungs are dynamic structures. Different respiration stages may lead to different image qualities on CT images and thus different levels of the visualization of the intrapulmonary vessels. All these factors can affect the depiction of small pulmonary vessels on CT images and subsequently their segmentation and quantifications. Hence, it is not surprising that the number of the identified vessels varies across these scans. Meanwhile, the large number of pulmonary vessel branches suggests the challenge to manually differentiate the arteries and veins. This could be the reason that Nardelli et al. (Nardelli, Jimenez-Carretero et al. 2018) developed and tested their CNN algorithm only on the right superior and lower lobes of 18 chest CT scans.

We developed a computational differential geometry solution to automatically segment the intrapulmonary vessels by identifying the surface regions that satisfy the criteria for a cylinder-like shape. The novelty of this solution lies in: (1) the geometric representation of the entire lung structures and (2) the way to identify the vessel surfaces. For example, the Laplacian smoothing operation is performed on the geometric surfaces instead of the original images to preserve small vessels. The differential geometry analyses were applied to the geometric surface instead of the original images. Several computer algorithms have been developed for computing differential geometry properties directly from an image by analyzing the changes of adjacent pixels or voxels (Wernersson, Hendriks et al. 2011, Gong and Sbalzarini 2013). However, the image-based operations (e.g., Gaussian filter) can smear out the detailed information related to small vessels. In contrast, we computed the principal curvatures and the principal directions in the geometric space based on the triangle mesh. The geometric smoothing kept the triangle meshes and their topology because the triangles in the surface models were not removed and only their locations were adjusted to smooth the surface models. Also, a dynamic range of the HU-value threshold was used to detect different scales of pulmonary vessels, as demonstrated by the examples in Figs. 9, 10, and 13. We believe that this dynamic threshold has practical implications because different applications may require different levels of pulmonary vessel detail.

When differentiating the intrapulmonary vessels, we developed a scheme to trace the arteries and veins along their skeletons separately, beginning with the identified extrapulmonary vessels. The tracing criteria were primarily based on the orientation and distance of the neighboring skeletons. Our experiments showed that this scheme demonstrated a promising performance and could accurately differentiate ~98% of the vessels, which outperformed most of the available algorithms (Charbonnier, Brink et al. 2016, Nardelli, Jimenez-Carretero et al. 2018, Jimenez-Carretero, Bermejo-Pelaez et al. 2019). However, in practice, there were still situations where the vessels were incorrectly labeled, as demonstrated by the example in Fig. 13. Given the complex spatial relationship between lung arteries and veins, it is difficult, even impossible, to have a scheme that can ensure 100% accuracy of lung artery and vein labeling. Hence, a practical solution to address the mislabeled vessels is to develop an interactive scheme that can allow a user to easily specify the mislabeled branches and make the corrections.

We used a relatively small dataset of 15 non-contrast chest CT scans to evaluate the performance of our segmentation algorithm because it is difficult to establish a large dataset in which a meaningful number of arteries and veins could be manually labeled. Although Nardelli et al. used 18 cases as an independent test set in their study (Nardelli, Jimenez-Carretero et al. 2018), only the superior and inferior lobes of the right lung were labeled by the radiologist. Also, Charbonnier et al. (Charbonnier, Brink et al. 2016) only used 10 fully annotated cases to test the performance of their algorithms, where only the intrapulmonary vessels were labeled and tested. Although Charbonnier et al. claimed that they “fully” annotated 10 cases, it is still difficult to ensure that the small vessels are fully identified and labeled. In practice, it is extremely difficult for a human expert to manually, accurately, and comprehensively label so many small vessels in the lungs as the computational geometry solution we developed (Figs. 9–10). This reality makes it challenging to develop a reliable ground truth, where the arteries and veins are fully labeled, for a fair and consistent evaluation of different computerized schemes. Additionally, it was impractical to assess false positive detection by the computer algorithm because of the large number of computer detections (Figs. 9 and 13). Simply measuring the false-positive labeling by using manual labeling as the ground truth may not faithfully reflect the performance of an algorithm in lung artery and vein labeling. Therefore, we primarily addressed the computer algorithm’s ability to detect and label the manually segmented vessels. More than 98% of the manually segmented arteries and veins were correctly labeled (Table 5). We also asked a radiologist (IO) to trace and review the computerized results. Our experiments showed that more than 97% of the veins and arteries detected by the computer algorithms, which were far more than the manually segmented vessels, were correctly labeled (Table 5). All these demonstrate the feasibility and performance of our automatic pulmonary vessel segmentation scheme.

V. CONCLUSION

We developed and validated a novel computer algorithm to automatically identify the pulmonary arteries and veins depicted on non-contrast chest CT scans. Both the central extrapulmonary and intrapulmonary arteries and veins were automatically and successfully segmented. There was strong agreement between the computer and manual segmentations of the intra- and extra-pulmonary vessels. The intrapulmonary vessels were automatically segmented well beyond the manual segmentation and reached out to the lung periphery. The algorithm is independent of any specific anatomical knowledge or manual seeding.

Highlights:

• A novel strategy to efficiently and accurately identify pulmonary arteries and veins on non-contrast CT

• Segmentation of both intra- and extra-pulmonary arteries and veins

• The combination of a CNN-based method and a computational differential geometry method

• Demonstrate a very promising performance on 15 CT scans without iodinated contrast agents

Appendix

Table A.

The performance of several U-Net variants in identifying extrapulmonary arteries and veins on the independent test set. The radiologist’s manual outlines were used as the reference standard.

Case	Dice coefficient
	R2UNet		Attention U-Net		U-Net++
	vein	artery	vein	artery	vein	artery
1	0.931	0.918	0.919	0.899	0.933	0.921
2	0.937	0.911	0.914	0.887	0.933	0.919
3	0.944	0.917	0.911	0.901	0.947	0.931
4	0.922	0.909	0.910	0.900	0.919	0.909
5	0.931	0.909	0.902	0.891	0.924	0.912
6	0.913	0.903	0.905	0.885	0.916	0.912
7	0.916	0.919	0.905	0.897	0.915	0.921
8	0.906	0.910	0.910	0.909	0.901	0.914
9	0.913	0.911	0.900	0.889	0.912	0.903
10	0.929	0.916	0.913	0.910	0.919	0.922
11	0.915	0.921	0.922	0.910	0.918	0.918
12	0.928	0.906	0.916	0.899	0.932	0.911
13	0.939	0.930	0.927	0.923	0.931	0.910
14	0.910	0.912	0.899	0.897	0.900	0.907
15	0.922	0.914	0.903	0.902	0.914	0.911
Mean	0.924±0.011	0.913±0.007	0.910±0.008	0.900±0.010	0.921±0.013	0.915±0.007

Table B.

The performance of several U-Net variants in identifying the mediastinal and hilum vessels on the independent test set. The radiologist’s manual outlines were used as the reference standard.

Case	Dice coefficient
	R2UNet		Attention U-Net		U-Net++
	mediastinal	hilum	mediastinal	hilum	mediastinal	hilum
1	0.944	0.910	0.946	0.880	0.950	0.918
2	0.933	0.915	0.924	0.878	0.941	0.914
3	0.949	0.909	0.944	0.892	0.944	0.932
4	0.922	0.912	0.926	0.900	0.918	0.909
5	0.928	0.915	0.910	0.881	0.934	0.910
6	0.930	0.900	0.912	0.867	0.929	0.910
7	0.929	0.908	0.913	0.890	0.938	0.918
8	0.942	0.902	0.923	0.903	0.938	0.909
9	0.927	0.910	0.920	0.879	0.922	0.900
10	0.924	0.922	0.906	0.914	0.936	0.914
11	0.930	0.904	0.951	0.900	0.928	0.913
12	0.936	0.904	0.926	0.897	0.935	0.914
13	0.944	0.920	0.922	0.923	0.944	0.885
14	0.925	0.905	0.915	0.876	0.915	0.903
15	0.941	0.906	0.918	0.895	0.913	0.910
Mean	0.934±0.008	0.909±0.006	0.924±0.013	0.892±0.015	0.932±0.011	0.910±0.010