Protein-ligand binding affinity prediction based on profiles of intermolecular contacts

Graphical abstract

Abstract

As a key element in structure-based drug design, binding affinity prediction (BAP) for putative protein-ligand complexes can be efficiently achieved by the incorporation of structural descriptors and machine-learning models. However, developing concise descriptors that will lead to accurate and interpretable BAP remains a difficult problem in this field. Herein, we introduce the profiles of intermolecular contacts (IMCPs) as descriptors for machine-learning-based BAP. IMCPs describe each group of protein-ligand contacts by the count and average distance of the group members, and collaborate closely with classical machine-learning models. Performed on multiple validation sets, IMCP-based models often result in better BAP accuracy than those originating from other similar descriptors. Additionally, IMCPs are simple and concise, and easy to interpret in model training. These descriptors highly conclude the structural information of protein-ligand complexes and can be easily updated with personalized profile features. IMCPs have been implemented in the BAP Toolkit on github ( https://github.com/debbydanwang/BAP).

1. Introduction

Binding affinity prediction (BAP) is one of the key problems in structure-based drug design (SBDD) [1], [2]. BAP is generally oriented toward putative protein-ligand complexes, and aims to create a bridge between the structures of these complexes and the binding affinities in them. Scoring functions (SFs) are well-acknowledged, efficient BAP approaches among many others [3], [4], however, they mostly prioritize prediction efficiency over accuracy. Accurate BAP remains a challenging problem in SBDD [5].

SFs, whether classical or machine-learning [6], rely heavily on the descriptors extracted from complexes’ structures. Classical SFs adopt a simple linear combination of interaction energy terms (descriptors) to predict binding affinity [7], [8], [9], which hardly yields a high BAP accuracy. In contrast, a wide range of descriptors and machine-learning methods have been employed to construct machine-learning SFs, often leading to more accurate BAP [5], [10].

In recent years, the descriptors for BAP either become more specialized and method-oriented, or stay simple and generic. Descriptors (e.g. voxel representations) used by deep-learning SFs are examples of the former [11], [12]. But these SFs only result in marginal accuracy improvement in BAP, hardly compensating the increasingly complex descriptors and less interpretability of model details. On the contrary, simple descriptors have gained widespread popularity due to the easier manipulation, better collaboration with classical machine-learning models and higher interpretability of SFs. The arguably first machine-learning SF, RF-Score, simply adopts 36 types of atom-pair counts as descriptors and has achieved a good BAP accuracy [13]. Here we term these descriptors as intermolecular contacts (IMCs). Inspired by RF-Score, Zheng et al. further subdivided these IMCs through mapping their distances into different distance bins (IMCiDBs), and constructed an accurate deep-learning SF based on these descriptors [14]. Later, IMCiDBs were slightly modified to represent the contacts between protein residues and ligand atoms in different distance bins [15]. Extended connectivity interaction features (ECIFs) are another group of descriptors that originate from IMCs and perform well in BAP. Different from using simply the atom types to define IMCs (e.g. $C-O$ contacts), atoms’ connectivity information was taken into account to subdivide IMCs into ECIFs (e.g. $C/{\mathit{connectivity}}_1-O/{\mathit{connectivity}}_2$ contacts). IMCs can be regarded as a special type of protein-ligand interaction fingerprints (IFPs) [16], and a variety of IFPs have been developed in past decades for BAP. P’erez-Nueno et al. considered pairs of IMCs, classified these pairs into different categories and counted the members in each category to construct the atom-pair-based interaction fingerprints (APIFs) [17]. Da et al. developed the structural protein-ligand interaction fingerprints (SPLIFs), by considering the environments of the endpoint atoms in each IMC and mapping the environment pairs into specific fingerprint positions [18]. Based on SPLIFs, W’ojcikowski et al. adopted multiple pairs of radii, rather than a fixed pair, for extracting atomic environments, leading to the proposal of protein-ligand extended connectivity fingerprint (PLEC FP) [19]. By separately considering the environments of the endpoint atoms in each IMC and mapping them to two fingerprint fragments, we proposed the proteo-chemometrics interaction fingerprints (PrtCmm IFPs) in an earlier work [20]. Some of these IFPs have been shown to collaborate nicely with classical machine-learning methods for accurate BAP [19], [20].

Although aforementioned descriptors have been demonstrated to perform well in BAP, they either result in SFs that are not accurate enough (e.g. IMCs) or form feature sets that are very large and redundant (e.g. IFPs). Reaching a balance between BAP accuracy and the complexity of descriptors thus remains an active area of research. Herein, we expand IMCs to IMC profiles (IMCPs) by taking into account the average distance for each type of IMCs, which improves the BAP accuracy but keeps the descriptors’ simplicity and model interpretability.

2. Method and algorithm

2.1. Intermolecular contact profiles (IMCPs)

Using the counts of different types of IMCs as descriptors and random forests (RFs) as regression methods, RF-Score has been constructed through a training process on the data from PDBbind database [13], [21], [22]. Given a protein-ligand complex structure, the contacting atoms are first identified by setting a distance threshold ($<12\AA$). The IMCs between the protein and ligand are then categorized into a series of groups, based on the types of their endpoint atoms. 4 types of protein atoms ($\{C,N,O,S\}$) and 9 types of ligand atoms ($\{C,N,O,F,P,S,\mathit{Cl},\mathit{Br},I\}$) are considered, forming 36 groups of IMCs ($\{C-C,C-N,C-O,\dots ,S-\mathit{Br},S-I\}$). The counts of these IMCs constitute the descriptors of RF-Score,

$${\mathbf{D}}^{\mathbf{IMC}}=(n_{C-C},n_{C-N},n_{C-O},\dots ,n_{S-\mathit{Br}},n_{S-I})$$ (1)

After extracting ${\mathbf{D}}^{\mathbf{IMC}}$ for each of the training complexes, RFs can be employed to find the relation between ${\mathbf{D}}^{\mathbf{IMC}}$ and the experimental binding affinities. This leads to the birth of RF-Score, which is simple but efficient.

In ${\mathbf{D}}^{\mathbf{IMC}}$, each IMC group (type of $x-y$) is profiled by the number of group members ($n_{x-y}$), which is apparently a coarse representation. Using more features to profile each group will promisingly results in more powerful descriptors for SFs. The average distance of each IMC group, as a common metric (Eq. 2), can be incorporated as a profile feature (Eq. 3).

$${\overline{d}}_{x-y}=\frac{{\displaystyle \sum _i}{d}_{x-y}^i}{n_{x-y}}$$ (2)

$${\mathbf{D}}^{\mathbf{IMCP}}=(\{n_{C-C},{\overline{d}}_{C-C}\},\{n_{C-N},{\overline{d}}_{C-N}\},\{n_{C-O},{\overline{d}}_{C-O}\},\dots ,\{n_{S-\mathit{Br}},{\overline{d}}_{S-\mathit{Br}}\},\{n_{S-I},{\overline{d}}_{S-I}\})$$ (3)

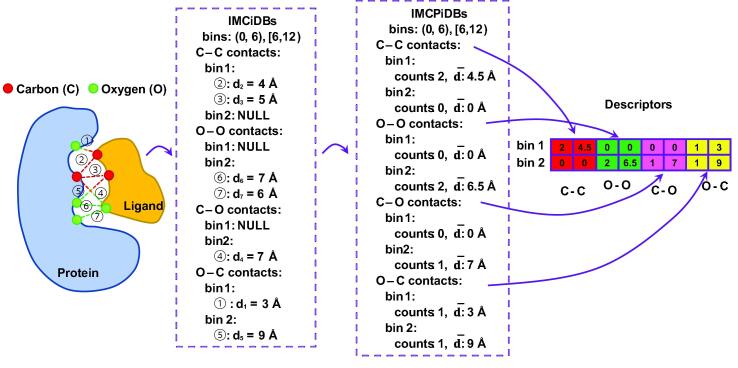
For a simplified scenario where only Carbon and Oxygen atoms in the protein and ligand are considered, the procedure to extract ${\mathbf{D}}^{\mathbf{IMCP}}$ is outlined in Fig. 1.

Fig. 1.

An outline of IMCP extraction.

Above is an oversimplified scenario for ${\mathbf{D}}^{\mathbf{IMCP}}$-extraction. In real cases, a protein-ligand complex may contain much more IMCs than above. Fig. 2 shows the frequency of IMCs in complexes from a dataset generally used for descriptor-extraction and SF-construction (PDBbind refined set). The average distance of each IMC group, which is a common statistical metric of the distance distribution, shows the average contacting level of this specific type of IMCs.

Fig. 2.

Frequency of IMCs (distances $<12\AA$) in complexes from the PDBbind refined set (v2020).

2.2. Intermolecular-contact profiles in distance bins (IMCPiDBs)

IMCPs can be further refined referring to the idea of IMCiDBs, which were the descriptors to construct Onionnet [14]. In this method, the space between a pair of protein and ligand is partitioned by a series of boundaries ($\{b_0,b_1,\dots ,b_n\}$), and two consecutive boundaries form a distance bin $[b_{i-1},b_i)$. According to these distance bins ($\{{\mathit{bin}}_i|{\mathit{bin}}_i=[b_{i-1},b_i)\text{;}i=1,\dots ,n\}$), each IMC of type $x-y$ can be further assigned to a subgroup ${\mathit{bin}}_i$ if its distance fulfills $b_{i-1}⩽d^{\mathit{IMC}}<b_i$. Suppose p types of protein atoms ($x_1,x_2,\dots ,x_p$) and q types of ligand atoms ($y_1,y_2,\dots ,y_q$) are considered, then the following group of descriptors ($p\times q\times n$) are formed,

$$\begin{array}{cc}{\mathbf{D}}^{\mathbf{IMCiDB}}=\hfill & (n_{x_1,y_1}^{{\mathit{bin}}_1},\dots ,n_{x_1,y_q}^{{\mathit{bin}}_1},\dots ,n_{x_p,y_1}^{{\mathit{bin}}_1},\dots ,n_{x_p,y_q}^{{\mathit{bin}}_1},\hfill \\ \hfill & \dots \hfill \\ \hfill & n_{x_1,y_1}^{{\mathit{bin}}_n},\dots ,n_{x_1,y_q}^{{\mathit{bin}}_n},\dots ,n_{x_p,y_1}^{{\mathit{bin}}_n},\dots ,n_{x_p,y_q}^{{\mathit{bin}}_n})\hfill \end{array}$$ (4)

${\mathbf{D}}^{\mathbf{IMC}}$ employed by RF-Score is a special case of ${\mathbf{D}}^{\mathbf{IMCiDB}}$, where $n=1$ (${\mathit{bin}}_1=(0,12\AA )$), $p=4$ and $q=9$. In the Onionnet work, 8 atom types for both protein and ligand atoms $\{C,N,O,H,P,S,\mathit{HAX},\mathit{DU}\}$, where HAX indicates halogen atoms ($\{F,\mathit{Cl},\mathit{Br},I\}$) and DU the remaining atoms, were adopted. 60 distance bins, including $(0,1),[1.0,1.5),[1.5,2.0),\dots ,[29.5,30.0)$ and $[30.0,30.5)$, were used.

Similar to IMCPs, IMCPiDBs can be extracted by profiling the atoms in each subgroup (type of $x-y$ and distance bin of ${\mathit{bin}}_i$) using the atom counts and average distance, in Eq. 5.

$$\begin{array}{cc}{\mathbf{D}}^{\mathbf{IMCPiDB}}=\hfill & (\{n_{x_1,y_1}^{{\mathit{bin}}_1},{\overline{d}}_{x_1,y_1}^{{\mathit{bin}}_1}\},\dots ,\{n_{x_1,y_q}^{{\mathit{bin}}_1},{\overline{d}}_{x_1,y_q}^{{\mathit{bin}}_1}\},\dots ,\{n_{x_p,y_1}^{{\mathit{bin}}_1},{\overline{d}}_{x_p,y_1}^{{\mathit{bin}}_1}\},\dots ,\{n_{x_p,y_q}^{{\mathit{bin}}_1},{\overline{d}}_{x_p,y_q}^{{\mathit{bin}}_1}\},\hfill \\ \hfill & \dots \hfill \\ \hfill & \{n_{x_1,y_1}^{{\mathit{bin}}_n},{\overline{d}}_{x_1,y_1}^{{\mathit{bin}}_n}\},\dots ,\{n_{x_1,y_q}^{{\mathit{bin}}_n},{\overline{d}}_{x_1,y_q}^{{\mathit{bin}}_n}\},\dots ,\{n_{x_p,y_1}^{{\mathit{bin}}_n},{\overline{d}}_{x_p,y_1}^{{\mathit{bin}}_n}\},\dots ,\{n_{x_p,y_q}^{{\mathit{bin}}_n},{\overline{d}}_{x_p,y_q}^{{\mathit{bin}}_n}\})\hfill \end{array}$$ (5)

For a simplified scenario where we only consider Carbon and Oxygen atoms for IMCs and adopt two distance bins ($(0,6\AA ),[6\AA ,12\AA )$), the procedure to extract ${\mathbf{D}}^{\mathbf{IMCPiDB}}$ is outlined in Fig. 3.

Fig. 3.

An outline of IMCPiDB extraction.

On the other hand, smaller distance bins often contain less IMCs, which makes averaging the IMC distances has less statistical meaning. In an extreme case where the bins are tiny and each only contains one or zero IMC, the average distance of a specific type of IMCs in each bin will degrade into the boundaries of the bin. In this regard, a small number of bins is useful for extracting more meaningful ${\mathbf{D}}^{\mathbf{IMCPiDB}}$.

2.3. ICMP-based SFs

When ${\mathbf{D}}^{\mathbf{IMCP}}$ or ${\mathbf{D}}^{\mathbf{IMCPiDB}}$ is regarded as a set of simple 1D descriptors, it can be fed into classical machine-learning algorithms, such as RFs [13], [23], [24], for BAP. Inspired by RF-Score, we first build ICMP- and ICMPiDB-based SFs with the assistance of RFs. As the binding affinities to be predicted are continuous values, RF regression models are required here. An RF regression model is composed of a forest of regression trees, and outputs the average of the predictions from these individual trees. To prevent overfitting, each tree draws a random sample from the whole training data when generating its splits, and randomly selects a number of features to split each tree node. The number of trees ($n_{\mathit{tree}}$), which was fixed on 500 in the RF-Score work [13], is one of the key parameters in RF construction, and we tuned this parameter in this work. Beside RFs, gradient boosted decision trees (GBDTs) are another type of widely-applied regression models for BAP. A GBDT model fits a weak learner (tree) in each stage to reduce the loss, and uses the weighted sum of the predictions from these trees. Such models were also employed in this work, with the boosting stages ($n_{\mathit{stage}}$) regarded as a key parameter for tuning.

Beyond 1D descriptors, ${\mathbf{D}}^{\mathbf{IMCPiDB}}$ can also be arranged as 2D descriptors, corresponding to dimensions of $n\times (p\times q\times 2)$ or $n\times (p\times q)\times 2$ (2 channels). Guided by Onionnet that uses IMCiDBs and convolutional neural networks (CNNs) for BAP, 2D ${\mathbf{D}}^{\mathbf{IMCPiDB}}$ are expected to collaborate friendly with deep-learning algorithms in SF-construction. The CNN architecture employed by Onionnet includes three convolutional layers (with 32, 64 and 128 filters respectively), one feature-flattening layer and four fully-connected layers (with 400, 200, 100 and 1 unit respectively) to output the final prediction. In the convolutional layers, kernel size of 4 and stride of 1 were adopted uniformly. The rectified linear units (ReLU) activation function was employed for both the convolutional and fully-connected layers. A customized loss function (Eq. 8), which combines the correlation between the experimental and predicted affinities (corr, Eq. 6) and the root-mean-square error (RMSE, Eq. 7), was used when training the CNN model.

$$\mathit{corr}=\frac{{\sum }_{i=1}^n(y_i^{\mathit{pred}}-{\overline{y}}^{\mathit{pred}})(y_i^{\mathit{exp}}-{\overline{y}}^{\mathit{exp}})}{\sqrt{{\sum }_{i=1}^n{(y_i^{\mathit{pred}}-{\overline{y}}^{\mathit{pred}})}^2}\sqrt{{\sum }_{i=1}^n{(y_i^{\mathit{exp}}-{\overline{y}}^{\mathit{exp}})}^2}}$$ (6)

$$\mathit{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{(y_i^{\mathit{pred}}-y_i^{\mathit{exp}})}^2}{n}}$$ (7)

$$\mathit{loss}=0.8\times (1-\mathit{corr})+0.2\times \mathit{RMSE}$$ (8)

Besides, an SGD optimizer, a batch size of 128, L2 regularization added to the hidden layers and an early-stopping strategy were adopted during the training process. In this work, we adopted this architecture but altered the optimizer to Adam for an easier convergence.

3. Implementation

3.1. Training and validation data

Training a machine-learning SF is generally accomplished on a set of protein-ligand complex structures with known binding affinities (experimental, $K_d$ or $K_i$), and the trained SF will be evaluated on separate validation sets to measure its generalization ability. The training and validation sets should never overlap for a fair evaluation. The PDBbind database ( http://www.pdbbind.org.cn/), which originates from the Protein Data Bank (PDB) [25] and recruits experimental binding data for the structures in PDB, is highly accessed for BAP works [13], [26], [12], [19], [14], [15], [27]. The PDBbind refined set of the newest version ($v2020$) was employed as our training data in this work. The CASF-2016 set in PDBbind and the three high-quality (HiQ) sets in the community structure activity resource (CSAR) database ( http://www.csardock.org [28]) were used for evaluating and comparing machine-learning SFs. The sizes of training and validation sets are listed as follows.

• •PDBbind refined set ($v2020$): 5,316 complexes. When training each type of SFs, this set was further randomly partitioned ($90\%:10\%$) for parameter-tuning, with 90% of data for SF construction and 10% for parameter evaluation.
• •CASF-2016 set: 285 complexes.
• •CSAR-HiQ Set 1: 176 complexes.
• •CSAR-HiQ Set 2: 167 complexes.
• •CSAR-HiQ Set 3: 123 complexes.

The overlapping complexes between the training and four validation sets were removed from the training set. Treating a machine-learning SF as a regression model, the independent variables are the structural descriptors extracted from the protein-ligand complexes and the dependent variable is $-\mathit{log}(K_{d/i})$. Given a descriptor model and a machine-learning method, the parameter-tuning phase includes 1) constructing SFs with different parameters (e.g. $n_{\mathit{tree}}$ for RFs) on 90% of the training data, and 2) selecting the SF that performs best on the rest 10% of training data. This selected SF will be further evaluated on the four validation sets, yielding its generalization performance. In this work, the performance of an SF was evaluated according to corr (Eq. 6) and RMSE (Eq. 7).

3.2. Comparison between IMCP-based SFs and RF-Score

As RF-Score was commonly regarded as a benchmark BAP method, we first compared our IMCP-based SFs with RF-Score. To make a fair comparison, RFs were adopted to build IMCP-based SFs. When training IMCP-based SFs and RF-Score, the parameters of RFs were uniformly tuned ($n_{\mathit{tree}}$ from 300 to 700 at a step of 100). In addition to model parameters, the distance threshold for IMC- or IMCP-extraction can also influence the BAP accuracy. Herein, we compared IMCP-based SFs and RF-Score with regard to different distance thresholds ($4.5\AA ,6\AA ,10\AA ,12\AA ,15\AA ,18\AA ,21\AA ,24\AA ,27\AA ,30\AA$ and $30.5\AA$), with the commonly used values ($4.5\AA ,12\AA$ and $30.5\AA$) taken into consideration. Referring to the original work of RF-Score, IMCs were grouped according to 4 types of protein atoms ($\{C,N,O,S\}$) and 9 types of ligand atoms ($\{C,N,O,F,P,S,\mathit{Cl},\mathit{Br},I\}$). The comparisons between IMCP-based SFs and RF-Score on corr and RMSE are presented in Fig. 4, where performances of these SFs in the parameter-tuning phase (tested on 10% of training data) and on the four validation sets (CASF-2016 set and CSAR-HiQ Sets 1$\sim$3) are shown. We can see that IMCP-based SFs consistently outperform RF-Score in all the examined scenarios, in both parameter-tuning and validation phases. This demonstrates that using more detailed profiles of IMCs instead of using simply the counts can improve the BAP accuracy. As shown in Fig. 4, distance thresholds such as $10\AA$ and $18\AA$ for generating IMCP-based SFs can lead to relatively better BAP accuracies for all the validation sets. Distance thresholds such as $6\AA$ result in better RF-Score performance for the validation sets. For easier interpretation, only the validation results of SFs are presented hereinbelow.

Fig. 4.

Comparisons between IMC- and IMCP-based SFs in the parameter-tuning and validation phases. Different distance thresholds for extracting IMCs and IMCPs are examined, and RFs are used for constructing the SFs. These SFs are evaluated according to the correlation and root-mean-square error between the experimental and predicted affinities.

3.3. Comparison between IMCPiDB- and IMCiDB-based SFs

By partitioning the space between a pair of protein and ligand into a series of distance bins, IMCiDBs and IMCPiDBs can be extracted. They were grouped based on 8 atom types ($\{C,N,O,H,P,S,\mathit{HAX},\mathit{DU}\}$) for both protein and ligand atoms, and a number of distance bins. To further investigate the importance of profiling the IMCs in a bin using their average distance, we extracted another sets of descriptors (denoted as IMCiDB2) by replacing the average distance (${\overline{d}}_{x_j,y_k}^{{\mathit{bin}}_i}$) with the midpoint of the bin ($\frac{b_{i-1}+b_i}{2}$) in ${\mathbf{D}}^{\mathbf{IMCPiDB}}$ (Eq. 5). Different sets of distance bins were used to generated ${\mathbf{D}}^{\mathbf{IMCPiDB}},{\mathbf{D}}^{\mathbf{IMCiDB}}$ and ${\mathbf{D}}^{\mathbf{IMCiDB}\mathbf{2}}$ in this work.

IMCPiDBs and IMCiDBs can be simply regarded as 1D descriptors. We adopted RFs to absorb them and construct SFs for BAP. In addition to the set of distance bins (60 bins; $\{(0,1),[1.0,1.5),[1.5,2.0),\dots ,[30.0,30.5)\}$) used in the Onionnet work [14], other sets of distance bins were also considered in descriptor extraction and SF construction, as follows.

• •2 bins: $\{(0,15),[15,30)\}$.
• •3 bins: $\{(0,10),[10,20),[20,30)\}$.
• •4 bins: $\{(0,7.5),[7.5,15),[15,22.5),[22.5,30)\}$.
• •5 bins: $\{(0,6),[6,12),[12,18),[18,24),[24,30)\}$.
• •6 bins: $\{(0,5),[5,10),[10,15),[15,20),[20,25),[25,30)\}$.
• •8 bins: $\{(0,3.75),[3.75,7.5),[7.5,11.25),\dots ,[26.25,30)\}$.
• •10 bins: $\{(0,3),[3,6),[6,9),\dots ,[27,30)\}$.
• •15 bins: $\{(0,2),[2,4),[4,6),\dots ,[28,30)\}$.
• •30 bins: $\{(0,1),[1,2),[2,3),\dots ,[29,30)\}$.

The performances of SFs are displayed in Fig. 5. Compared to the marginal performance difference between IMCiDB- and IMCiDB2-based SFs, that between IMCiDB- and IMCPiDB-based SFs is more evident. This demonstrates the importance of using the average distance of IMCs as a profiling feature in SF-construction. In addition, as smaller bins contain less IMCs that averaging their distances is less statistically meaningful, a smaller number of bins often result in more useful IMCPiDBs and more accurate BAP. This can be observed in Fig. 5, where IMCPiDBs generated based on more bins commonly lead to worse predictions. Considering the number of bins for extracting IMCPiDBs as a parameter, an optimal number can be obtained in the parameter-tuning phase. Accordingly, an optimal number of 3 bins ($\{(0,10),[10,20),[20,30)\}$) was derived in our work, leading to the following scoring performances.

• •CASF-2016: $\mathit{corr}=0.791/\mathit{RMSE}=1.452$.
• •CSAR-HiQ Set 1: $\mathit{corr}=0.738/\mathit{RMSE}=1.602$.
• •CSAR-HiQ Set 2: $\mathit{corr}=0.769/\mathit{RMSE}=1.428$.
• •CSAR-HiQ Set 3: $\mathit{corr}=0.646/\mathit{RMSE}=1.352$.

Fig. 5.

Comparisons between IMCiDB-, IMCiDB2- and IMCPiDB-based SFs. Different sets of distance bins for extracting descriptors are examined, and RFs are used for constructing the SFs. These SFs are evaluated according to the correlation and root-mean-square error between the experimental and predicted affinities.

IMCPiDBs and IMCiDBs can also be arranged as 2D descriptors. Given n distance bins and 64 contact types (8 types for both the protein and ligand atoms), IMCiDBs can be organized as $n\times 64$-shaped features, and IMCPiDBs as $n\times 128$- or $n\times 64\times 2$-shaped (2 channels) features. Representative sets of distance bins (15, 30 and 60) were used for extracting such descriptors, which were fed into two deep-learning models for SF construction. The first model (CNN1) is the one proposed in the Onionnet work, including three convolutional layers, one feature-flattening layer and four fully-connected layers. The other model (CNN2) possesses four additional dropout layers, with one between the feature-flattening layer and the first fully-connected layer, and the other three each between two consecutive fully-connected layers. Incorporating each type of descriptors and each CNN model results in a specific deep-learning SF, whose performance is presented in Fig. 6. As shown in this figure, these deep-learning SFs perform generally worse than aforementioned classical machine-learning SFs. This implies the inapplicability of these simple descriptors to complex deep-learning models. Moreover, these SFs have encountered severe overfitting problems, as revealed by the poor performances on the CASF-2016 set. Adding dropout layers can marginally mitigate the situation for IMCPiDB-based SFs, while no clear trends among other SFs are found. In this regard, the architecture of deep-learning models should be carefully developed to combat with the overfitting problem. The best predictions for the four validation sets belong to the following models.

• •CASF-2016: IMCiDBs (30 bins) combined with CNN2 model, $\mathit{corr}=0.345/\mathit{RMSE}=1.594$.
• •CSAR-HiQ Set 1: IMCPiDBs (15 bins) combined with CNN2 model, $\mathit{corr}=0.686/\mathit{RMSE}=1.692$.
• •CSAR-HiQ Set 2: IMCPiDBs (60 bins) combined with CNN2 model, $\mathit{corr}=0.690/\mathit{RMSE}=1.543$.
• •CSAR-HiQ Set 3: IMCPiDB_2Cs (30 bins) combined with CNN2 model, $\mathit{corr}=0.663/\mathit{RMSE}=1.332$.

Fig. 6.

Comparisons between IMCiDB- and IMCPiDB-based SFs. Different sets of distance bins are used for extracting IMCiDBs and IMCPiDBs, which are arranged as two-dimensional descriptors (IMCiDB: $n\times 64$, IMCPiDB: $n\times 128$, IMCPiDB_2C: $n\times 64\times 2\text{;}n=15,30,60$). Two deep-learning models (CNN1 and CNN2) are used for constructing the SFs. These SFs are evaluated according to the correlation and root-mean-square error between the experimental and predicted affinities.

3.4. Comparisons among different SFs

To further evaluate the roles of IMC-related descriptors in BAP, we compared SFs that are based on different descriptors, including IMCPs (proposed), IMCPiDBs (proposed), IMCs, IMCiDBs, ECIFs, APIFs, SPLIFs and PLEC FPs. The details for extracting these descriptors are tabulated in Table 1. For IMCPs, IMCPiDBs, IMCs and IMCiDBs, the distance thresholds and bins were selected according to their performances in BAP for CASF-2016 set (Fig. 4, Fig. 5). For the remaining descriptors, the suggested parameters in their original works were adopted. RFs and GBDTs were employed to train SFs. During the training phase, $n_{\mathit{tree}}$ was tuned from 300 to 700 at a step of 100 for RFs, and $n_{\mathit{stage}}$ was tuned from 300 to 700 at a step of 100 for GBDTs. Specifically, the length of fingerprint (descriptors) was regarded as a parameter ($2^l,l=3,4,\dots ,12$) when training SPLIF- and PLEC FP-based SFs.

Table 1.

Details of the descriptors used for developing machine-learning SFs.

Descriptor	Distance threshold ($\AA$)	Number of distance bins	Length of descriptorsa	Other parameters	References
IMCP	18	1	72	–	proposed
IMCPiDB	30	8	1,024	–	proposed
IMC	10	1	36	–	[13]
IMCiDB	30	30	1,920	–	[14]
ECIF	6	1	489	–	[27]
APIF	10	1	294	–	[17], [29]
SPLIF	4.5	1	$2^l$	$R_{\mathit{protein}}=1,R_{\mathit{ligand}}=1$	[18]
PLEC FP	4.5	1	$2^l$	$R_{\mathit{protein}}=5,R_{\mathit{ligand}}=1$	[18]

^aThe length of SPLIF or PLEC FP was tuned ($2^l,l=3,4,\dots ,12$) during the training process, and the best performer was retained.

Moreover, to provide comparisons between above machine-learning SFs with classical SFs (employed by docking programs), we scored the complexes in the validation sets using AutoDOCK Vina [30]. Two AutoDOCK SFs, using either Vina [30] or Vinardo [31] force fields, were investigated. For each protein-ligand complex, the docking grid space was automatically centered around the ligand with fixed dimensions ($20\AA \times 20\AA \times 20\AA$). To align with the predictions ($-\mathit{log}(K_{d/i})$) by machine-learning SFs, the original AutoDOCK scores (in kcal/mol) were rescaled to $-\mathit{log}(K_{d/i})$ according to $\mathrm{\Delta }G={\mathit{RTlnK}}_d$ ($T=300K$).

The performances of different SFs are now presented in Fig. 7. As shown in this figure, the classical SFs evidently underperform the machine-learning SFs. For machine-learning SFs, those developed from RFs generally perform better than those from GBDTs. In the SFs developed from RFs, those based on IMCPs, IMCPiDBs and IMCiDBs are the top three best performers on CASF-2016 set, CSAR-HiQ Set 1 and CSAR-HiQ Set 2. For CSAR-HiQ Set 3, the RFs based on ECIFs, PLEC FPs and IMCPiDBs are ranked the top three. This indicates that IMCPiDBs, IMCiDBs and IMCPs collaborate nicely with classical machine-learning methods in BAP works. Beyond that, the lengths of IMCPiDBs and especially IMCPs are shorter than that of IMCiDBs (Table 1), showing the simplicity and conciseness of IMCPiDBs and IMCPs as descriptors. Overall, the descriptors proposed in this work (IMCPiDBs and IMCPs) are simple but promising for BAP.

Fig. 7.

Comparisons among machine-learning SFs that are based on different descriptors, including IMCPs, IMCPiDBs, IMCs, IMCiDBs, ECIFs, APIFs, SPLIFs and PLEC FPs. RFs and GBDTs are used for constructing these SFs. AutoDOCK SFs (using Vina or Vinardo force fields) are also examined for comparisons between classical SFs and machine-learning SFs. All the SFs are evaluated based on the correlation and root-mean-square error between the experimental and predicted affinities.

3.5. Interpretability of IMCP-based SFs

Most of current machine-learning SFs, especially deep-learning SFs, lack of model interpretability. However, simple descriptors, such as IMCPs proposed in this work, are easy to interpret for the constructed SFs. Herein, we investigated the importance of IMCPs for training the SFs in Fig. 4. The top 20 important descriptors with regard to a number of distance thresholds ($10\AA ,12\AA ,18\AA$ and $24\AA$) are displayed in Fig. 8. In these scenarios, the top 20 descriptors are highly superposed, and the 14 mutual important descriptors include $n_{C-C},{\overline{d}}_{C-C},n_{C-N},{\overline{d}}_{C-N},n_{C-O},{\overline{d}}_{C-O},n_{N-C},{\overline{d}}_{N-C},n_{N-O},{\overline{d}}_{N-O},n_{O-C},{\overline{d}}_{O-C},n_{O-N}$ and $n_{O-O}$. These mutual important descriptors are composed of 8 counts and 6 average distances of IMCs, showing that efficiently profiling the IMCs is necessary for accurate BAP. For the top 10 or 30 important descriptors, 5 ($n_{C-C},{\overline{d}}_{C-C},n_{C-N},n_{N-C}$ and ${\overline{d}}_{C-O}$) or 27 descriptors ($n_{C-C},{\overline{d}}_{C-C},n_{C-N},{\overline{d}}_{C-N},n_{C-O},{\overline{d}}_{C-O},n_{C-S},{\overline{d}}_{C-S},n_{N-C},{\overline{d}}_{N-C},n_{N-N},{\overline{d}}_{N-N},n_{N-O},{\overline{d}}_{N-O},n_{O-C},{\overline{d}}_{O-C},n_{O-N},{\overline{d}}_{O-N},n_{O-O},{\overline{d}}_{O-O},n_{S-C},{\overline{d}}_{S-C},n_{S-N},{\overline{d}}_{S-N},n_{S-O},{\overline{d}}_{S-O}$ and $n_{N-S}$) are mutual for the four scenarios.

Fig. 8.

The top 20 important IMCPs for constructing SFs based on RFs. n$(x-y)$ indicates the counts of contacts with type $x-y$ and d$(x-y)$ the average distance of contacts with type $x-y$. Each subfigure corresponds to a specific distance threshold ($10\AA ,12\AA ,18\AA$ or $24\AA$).

3.6. Examples of predictions

To further evaluate the predictions by the proposed machine-learning SFs, some examples predicted by a representative SF were investigated. This SF was constructed based on IMCPs (distance threshold: $12\AA$) and RFs, and trained on the PDBbind refined set (Fig. 4). The validation samples (from CASF-2016 set and CSAR-HiQ Sets 1$\sim$3) were grouped according to the target proteins. Several large groups are listed as follows.

• •Group 1: HIV-1 PROTEASE with ligands
• •Group 2: HEAT SHOCK PROTEIN HSP90-ALPHA with ligands
• •Group 3: BETA-SECRETASE 1 with ligands
• •Group 4: COAGULATION FACTOR XA with ligands
• •Group 5: ESTROGEN RECEPTOR with ligands
• •Group 6: CELL DIVISION PROTEIN KINASE 2 with ligands
• •Group 7: ALPHA-MANNOSIDASE II with ligands
• •Group 8: UROKINASE-TYPE PLASMINOGEN ACTIVATOR with ligands
• •Group 9: CARBONIC ANHYDRASE 2 with ligands

The predicted (by the representative SF) and experimental binding affinities of the samples in these groups are now presented in Fig. 9. Given ‘$y=x$’ as a perfect prediction trendline, the predictions for Groups 6 ($y=0.60x+2.62$) and 9 ($y=0.55x+3.37$) are more favorable than those for Groups 4 ($y=0.01x+7.66$) and 5 ($y=0.11x+6.12$). Looking back on the training set (PDBbind refined set) used for constructing the SF, it contains more samples belonging to Groups 6 (165 samples) and 9 (408 samples) than those belonging to Groups 4 (50 samples) and 5 (61 samples). This to some extent verifies the strong dependence of the scoring performances of SFs on the training data.

Fig. 9.

Some examples of the validation results of a representative machine-learning SF. IMCPs (distance threshold: $12\AA$) allied with RFs are used to construct the SF.

4. Conclusion and discussion

In this work, we have proposed the profiles of intermolecular contacts as descriptors for BAP. These descriptors are simple and easy to generate, and collaborate nicely with classical machine-learning algorithms in SF-construction. Compared to other similar descriptors, the proposed IMCPs often lead to a better BAP accuracy, while keeping a simple form. Opposite to many black-box machine-learning SFs, the IMCP-based SFs are easier to interpret. According to the feature-importance evaluation, we noticed that the counts and average distances of IMCs are both effective profile features for SF-construction, and IMCs such as $C-C$ and $C-N$ are more important among others. In future studies, additional profile features can be explored to describe the IMCs more elaborately.

One major limitation of machine-learning SFs is that constructing them relies on the quantity and quality of training data. The latest PDBbind database provides binding affinity data for 19,443 protein-ligand complexes (the general set). Comprehensively considering factors such as structural resolution, protein coverage and ligand diversity, the developers of PDBbind have further filtered these samples into the refined set (5,316 complexes, generally used as training data) by multistep quality control. Although such training data are not perfect, they have benefitted many SF-construction works that were proven to be efficient in rescoring of docking poses, virtual screening and lead optimization. As we have entered the age of big data, more and qualified data will be produced and join as new training data, which will promote the development of machine-learning SFs further.

Funding

This work was support by Hong Kong Research Grants Council (Project UGC/FDS16/M08/18).

CRediT authorship contribution statement

Debby D. Wang: Conceptualization, Methodology, Software, Writing – original draft. Moon-Tong Chan: Investigation, Validation, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.