Jointly Leveraging Decorrelation and Sparsity for Improved Feedback Cancellation in Hearing Aids

Abstract

We propose a new adaptive feedback cancellation (AFC) system in hearing aids (HAs) based on a well-posed optimization criterion that jointly considers both decorrelation of the signals and sparsity of the underlying channel. We show that the least squares criterion on subband errors regularized by a p-norm-like diversity measure can be used to simultaneously decorrelate the speech signals and exploit sparsity of the acoustic feedback path impulse response. Compared with traditional subband adaptive filters that are not appropriate for incorporating sparsity due to shorter sub-filters, our proposed framework is suitable for promoting sparse characteristics, as the update rule utilizing subband information actually operates in the fullband. Simulation results show that the normalized misalignment, added stable gain, and other objective metrics of the AFC are significantly improved by choosing a proper sparsity promoting factor and a suitable number of subbands. More importantly, the results indicate that the benefits of subband decomposition and sparsity promoting are complementary and additive for AFC in HAs.

I. Introduction

The acoustic feedback or so-called howling effect induced by the strong coupling between the receiver (loudspeaker) and the microphone in hearing aids (HAs) deteriorates the intelligibility, quality and maximum stable gain of the input. To mitigate this feedback problem, adaptive feedback cancellation (AFC) is commonly employed to continuously identify or approximate the time-varying impulse response (IR) of the acoustic feedback path [1]. Due to the strong correlation between the microphone and the receiver signals [2], adaptive filters without decorrelation capability in AFC give biased estimates and result in degraded performance in convergence, e.g., the classic least mean square (LMS) and the well-known normalized LMS (NLMS) [3]–[5]. More importantly, adaptive filters without leveraging sparsity of the acoustic feedback path are prone to have slower initial convergence rate [6]–[8].

Therefore, to improve the performance of AFC, both decorrelation and sparsity may be jointly exploited. However, in the AFC literature, many works have been dedicated to either decorrelation [9]–[18] or promoting sparsity [7], [8]; a joint exploration on both is lacking. Recently, a sparsity promoting, subband AFC [19] was developed based on solving a constrained optimization problem with ℓ₁ norm penalty. However, there are still several aspects that deserve further investigations. On the theoretical part, the cost function considered in [19] was based on the least perturbation principle which is not as straightforward as direct minimization on subband errors. On the experimental part, the effect of using different degrees of decorrelation and sparsity promoting on AFC was not studied (only evaluated on four subbands). Moreover, the additional benefit that the widely used prediction error method (PEM) [14]–[16] adding to the subband system for deccorrelation was not quantified.

Based on our previous work [20] which only studied a theoretical problem, in this paper, we extend the joint framework for leveraging decorrelation and sparsity to a real-world application in HAs. We propose and evaluate a new AFC system in HAs based on a well-posed optimization criterion that simultaneously explores decorrelation and sparsity. Using different speech input signals, feedback paths and amplifications, we extensively study the efficacy of AFC using different numbers of subbands and degrees of promoted sparsity. In addition, we study the benefits of using the PEM on top of our system. Both commonly used AFC evaluation criteria and objective evaluations on intelligibility and quality are presented on a large speech corpus to illustrate the effectiveness of the proposed AFC framework. We show that the benefits of decorrelation and sparsity promoting for AFC are additive and complementary.

II. Background

To address the bias issue in AFC systems, several methods have been proposed [9]–[16], [21]. One of the bias reduction methods in AFC is the usage of subband adaptive filters (SAFs) [6], [17], [18], [22]. A conventional SAF for AFC like that in [17] utilizes an independent adaptive filter for each subband. However, SAFs are known to suffer from the aliasing problem and band-edge effects [6]. To avoid these issues, a family of new SAFs or normalized subband adaptive filters (NSAFs) [23]–[25] which compute the gradient before the subband projection were proposed. For example, in [18], a delayless NSAF on top of the PEM was introduced to improve AFC. Besides, the acquisition of fullband filter taps in NSAFs is important since inducing sparsity on shorter sub-filters does not seem logical in conventional SAFs.

On the other hand, to achieve faster convergence rate of the AFC filter, the sparse characteristics of the acoustic feedback path may be taken into account [6]–[8]. This can be carried out by utilizing the proportionate adaptation scheme originated from the proportionate NLMS (PNLMS) [26] algorithm. In the adaptive filtering literature, the PNLMS [26] was introduced to improve convergence behavior by intuitively assigning a step size proportional to the magnitude of the estimated coefficient to each filter tap. Many proportionate-type NLMS (PtNLMS) algorithms [27] were later proposed to enhance PNLMS. Based on PtNLMS, a family of proportionate-type NSAFs (PtNSAFs) [28]–[30] have been proposed on top of NSAF to speed up convergence as they exploit the sparse structure of the fullband filter taps and reduce signal correlation. Finally, the update rule recently proposed in [20] is a generalization of PtNSAFs. The criterion is straightforward in a sense that it minimizes errors in each subband but penalizes a weighted norm in the fullband.

III. The Proposed AFC Framework

The proposed AFC framework is depicted in Fig. 1. The microphone signal d(n) is the sum of the speech signal x(n) and the feedback signal y(n), i.e., d(n) = x(n) + y(n). u(n) denotes the receiver signal which is given by passing the feedback-compensated signal e(n) through the HA processing G(z). Assuming that the acoustic feedback path is a finite impulse response (FIR) filter F(z), we have y(n) generated by filtering u(n) through F(z). The goal of AFC is to have the estimated feedback signal $\widehat{y}(n)$ close to y(n) by continuously adapting the filter S(z). Together with a set of fixed analysis filters H_i(z), i = 1, 2, …, M, the prediction-error filter A(z) from PEM forms a time-varying analysis filter bank, i.e., A(z)H_i(z) where the coefficients in A(z) are adapted by using the linear prediction of e(n). Notice that the synthesis filters are not needed in our proposed framework. The subband error signals are computed and then aggregated together to update the fullband filter taps. The block of coefficient adaptation in Fig. 1 is the core of the AFC and a novel update rule in this block is discussed in the following paragraphs.

Fig. 1:

Block diagram of the proposed AFC framework.

We propose the following optimization criterion to jointly exploit sparsity and achieve decorrelation:

$$J(s)=\sum _{i=1}^M{e}_i^2(n)+\tau \Vert s{\Vert }_p^p$$ (1)

where τ → 0⁺ is a regularization parameter, $e_i\text{(}n\text{)=}{d}_i(n)-u_i^T(n)s$ is the i^th subband error scalar; d_i(n) and u_i(n) are the i^th subband desired scalar and the i^th subband input vector, respectively. M is the number of subbands and the optimization variable $s={\left[\begin{array}{llll}{s}_1\hfill & s_2\hfill & \cdots \hfill & s_L\hfill \end{array}\right]}^T\in {ℝ}^L$ denotes the adaptive filter of length L. We have used the p-norm-like diversity measure $\Vert s{\Vert }_p^p={\sum }_{i=1}^L{\left|s_i\right|}^p$ for promoting sparsity where the parameter p ∈ (0, 2] controls the degree of sparsity promoting [31], [32]. By minimizing the cost function (1) using the reweighted ℓ₂ framework [31], affine scaling transformation [32] and the regularized Newton’s method [20], the resulting LMS-like update rule is given by

$$s(n+1)=s(n)+\mu W(n)U(n)\Phi (n)e(n)$$ (2)

where $e(n)={\left[\begin{array}{llll}{e}_1(n)\hfill & e_2(n)\hfill & \cdots \hfill & e_M(n)\hfill \end{array}\right]}^T\in {ℝ}^M$ is the subband error vector and s(n) = [s₁(n) s₂(n) ⋯ s_L(n)]^T is the adaptive filter. The subband input data matrix is given by $U(n)=\left[\begin{array}{llll}{u}_1(n)\hfill & u_2(n)\hfill & \cdots \hfill & u_M(n)\hfill \end{array}\right]\in {ℝ}^{L\times M}$ where the columns are subband signals.

For the proportionate matrix W(n) = diag{w₁(n), w₂(n), ⋯, w_L(n)}, it is given by

$$w_i(n)={\left(|s_i(n)|+c\right)}^{2-p},i=1,2,\cdots ,L$$ (3)

where c > 0 is a regularization constant for avoiding stagnation and instability. The suggested range of the parameter p for sparse, compressible (quasi-sparse) and dispersive solutions are [1.0, 1.2], (1.2, 1.8) and [1.8, 2.0], respectively [7].

For the whitening matrix Φ(n), a time-varying diagonal regularization matrix Δ(n) can be employed as

$$\Phi (n)={\left[\Delta (n)+U^T(n)W(n)U(n)\right]}^{-1}\in {ℝ}^{M\times M}$$ (4)

where Δ(n) = diag{δ₁(n), δ₂(n), ⋯, δ_M(n)} and δ_i, i = 1, 2, …, M depends on the estimated time-varying variance of the subband error e_i(n). However, the proper estimation of δ_i needs further investigations and empirical research. In this paper, we use Δ(n) = δI where δ > 0 is a samll constant.

In sum, (2), (3) and (4) give the proposed Sparsity-promoting Normalized Subband Adaptive Filter algorithm (S-NSAF). Indeed, the proposed update rule (2) is a generalized framework for some well-known adaptive filtering algorithms including NLMS, affine projection algorithm (APA), etc. We hereby summarize the behaviors in TABLE I.

TABLE I:

Different cases of S-NSAF. For the correspondence to NSAF and PtNSAF, Φ(n) needs to be approximated by a diagonal matrix using a proper analysis filter bank.

	M = 1	M > 1, H ≠ I	M > 1, H = I
p = 2	NLMS [4]	NSAF [23]	APA [33]
2 > p > 0	PtNLMS [27]	PtNSAF [29]	PtAPA [34]

Different from the direct combination method, i.e., the PEM-based PtNLMS for AFC [35], our proposed AFC framework jointly combines decorrelation (first term in (1)) and tunable sparsity exploiting (second term in (1)) in one cost function and update rule. The PEM in our framework can be considered as a way to establish a time-varying analysis filter bank for better decorrelation.

IV. Simulation Results

In this section, we evaluate the performance of using S-NSAF for AFC in HAs. To be more specific, the effects of using different numbers of subbands M and different degrees of sparsity promoting, namely, the p value, are jointly investigated. In addition, the relationship between the PEM and the proposed method is studied.

Experimental Setup:

The experiments were conducted at 16 kHz with the input speech signal x(n) from the TIMIT dataset [36] and two feedback paths measured from the real-world setup as shown in Fig. 3. In order to get realistic simulations of human experiences, long speech signals (89.11 seconds) created by concatenating speech files were used.

Fig. 3:

The truncated FIR filters of different feedback paths were measured from a HA on a dummy head. (a) represents the IRs and (b) shows the magnitudes of the frequency responses.

The forward path, i.e., the HA processing, was simulated by G(z) = gz^−d where g was the gain in the linear scale and d was the samples of delay corresponding to a fixed latency of 8 milliseconds. In the setting of the S-NSAF, the length L = 100 was set to the same size as the truncated FIR filter in Fig. 3 and all taps were initialized by 0. For PEM, the order of the prediction-error filter A(z) was 20 and the filter was updated every 10 milliseconds via Levinson-Durbin recursion with the window length of 160 samples [18]. The analysis filter bank H is a cosine-modulated pseudo-quadrature mirror filter (QMF) bank. M = 1, 2, 4 were chosen to be evaluated. We maintain the same length N = 16 of the analysis filters for M = 2 and M = 4. The p values which were chosen to be tested are 1.5 [7] and 2.0. For regularizations, we used δ = 10⁻⁵ and c = 10⁻³ for all simulations. The step size is given by $\mu =\frac{1}{M}\times {10}^{-3}$ so that the comparison is fair for adaptive filters using different M. All curves in Fig. 2 and Fig. 4 were ensemble averaged over 100 different speech signals. During all experiments, a sudden change of the feedback path was introduced at half time where this new path was given by the one with obstruction in Fig. 3.

Fig. 2:

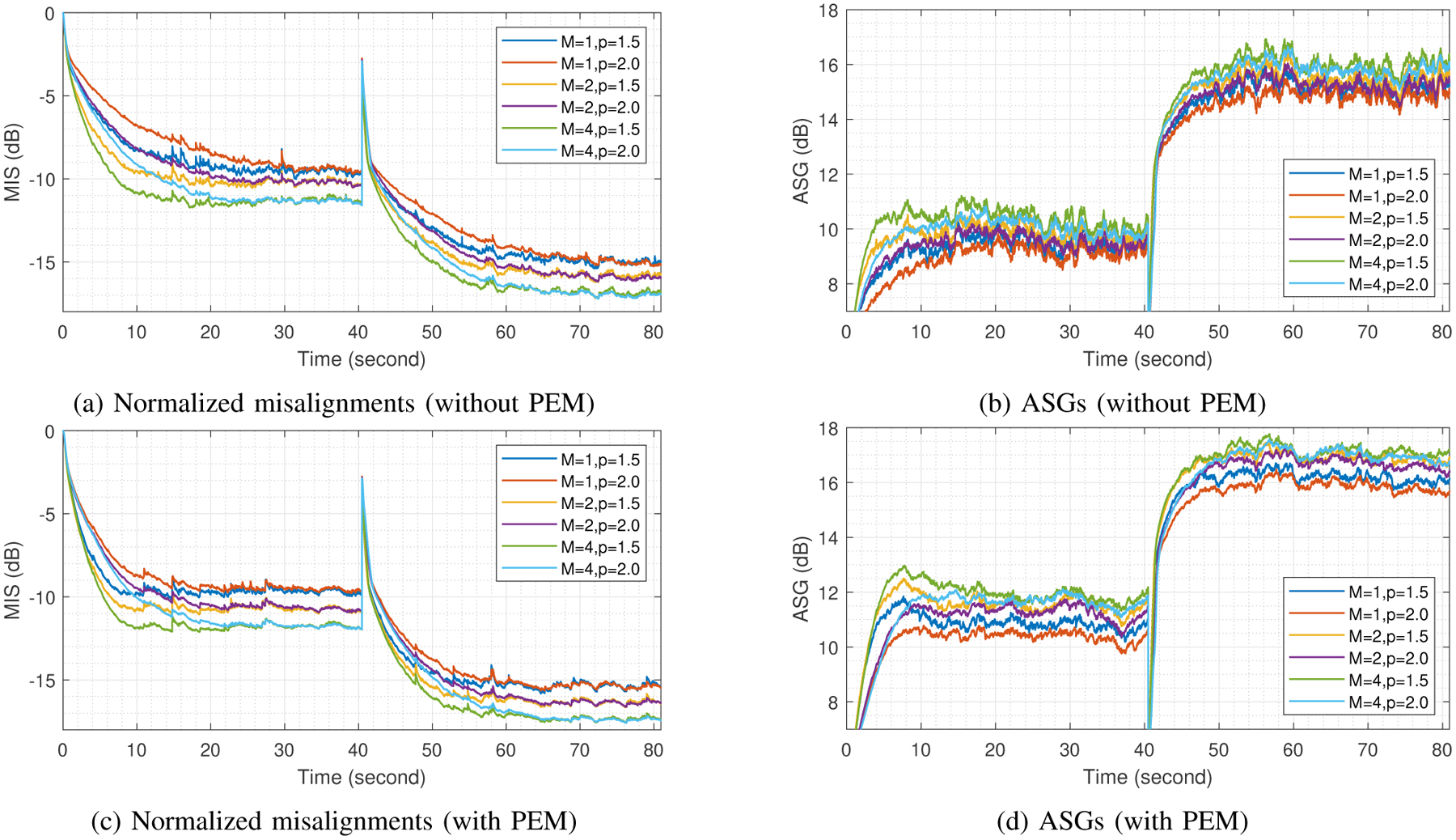
The performance of AFC is better with higher M for a given p; and p = 1.5 is better than p = 2.0 for a given M, in terms of normalized misalignment and ASG. Noticeably, the case of M = 4 and p = 1.5 outperforms all the other cases. If the PEM is used, the performance can be further enhanced; there is approximately ASG improvement of 2.0 dB in all cases.

Fig. 4:

In (a), the speech intelligibility is better with higher M for a given p; and p = 1.5 is better than p = 2.0 for a given M. In (b), the speech quality is improved by choosing higher M; and the p value seems to be irrelevant. If the PEM is used, the performance gaps between different M reduce in terms of STOI and HASQI.

Evaluation Metrics:

To evaluate the performance of the proposed AFC using S-NSAF, the normalized misalignment (MIS), added stable gain (ASG) [14], [37], short-time objective intelligibility (STOI) [38], [39] and hearing-aid speech quality index (HASQI) [40] were used. The normalized misalignment and ASG given by (5) were evaluated for a fixed HA processing G(z) with the gain value set to 20 in dB scale. On the other hand, the objective metrics including STOI and HASQI were used to quantify the performance of AFC for different values of gain g in the HA processing G(z). Measuring AFC performance in different gain values is critical since the gain in HAs is subject to change in real-world scenarios. The STOI and HASQI were computed via the comparison between the input speech signal x(n) and the feedback-compensated signal e(n). They both are scores of a single scalar which ranges from 0 to 1, where the higher the score, the better the intelligibility or quality.

$$\begin{gathered} \text{MIS}=10{\text{log}}_{10}\frac{{\int }_0^{\pi }{\left|S\left(e^{j\omega }\right)-F\left(e^{j\omega }\right)\right|}^{2}d\omega }{{\int }_0^{\pi }{|F\left(e^{j\omega }\right)|}^{2}d\omega } \\ \text{ASG}=10{\text{log}}_{10}\frac{{\text{max}}_{\omega }{\left|F\left(e^{j\omega }\right)\right|}^2}{{\text{max}}_{\omega }{|S\left(e^{j\omega }\right)-F\left(e^{j\omega }\right)|}^2} \end{gathered}$$ (5)

Misalignments and ASGs under a fix gain:

We first consider the case where the PEM is not incorporated. In this case, increasing M is the only way to further decorrelate the signals. In Fig. 2(a) and Fig. 2(b), it is obvious that the performance of AFC is better with higher M for a given p; and p = 1.5 is better than p = 2.0 for a given M. Noticeably, the case of M = 4 and p = 1.5 outperforms all the other cases in terms of normalized misalignment and ASG. On the other hand, M = 1 and p = 2.0, i.e., the NLMS, is the worst case since it has nothing to do with decorrelation and sparsity promoting of the sparse feedback path. We observe that a better decorrelation scheme can be potentially achieved by choosing a larger M (here we have shown this up to M = 4). In addition, the benefits of subband decomposition and sparsity promoting are additive and complementary for AFC.

Now consider the situation where the PEM is incorporated. In Fig. 2(c) and Fig. 2(d), we observe the same conclusions we have drawn from Fig. 2(a) and Fig. 2(b). However, notice that the performance of AFC is further enhanced with PEM. Comparing Fig. 2(b) to Fig. 2(d), there is approximately ASG improvement of 2.0 dB in all cases if the PEM is used. This means that the decorrelation performed by subband decomposition can even be improved by employing PEM on top of it. To be more specific, the combination of the analysis filter bank and the prediction-error filter induces a time-varying analysis filter bank which gives a better approximation to the input spectrum; the bias reduction is then enhanced in AFC.

STOI and HASQI under different gains:

In Fig. 4(a), we observe that the speech intelligibility is better with higher M for a given p; and p = 1.5 is better than p = 2.0 for a given M. In Fig. 4(b), we find that the speech quality is improved by choosing higher M; and the p value seems to be irrelevant. When the PEM is incorporated as in Fig. 4(c) and Fig. 4(d), the performance gaps between different M reduce in terms of STOI and HASQI. However, the incorporation of the PEM does not seem to necessarily improve the performance for M = 4 here. According to Fig. 4(c), the p value has larger impact on speech intelligibility when the gain is increased.

V. Conclusion

Different from our previous work [20] which was only evaluated in a theoretical system identification setting, a new formulation of jointly exploring sparsity promoting and decorrelation is proposed for practical AFC applications. In the proposed method, the effectiveness of using different degrees of sparsity promoting and number of subbands are studied extensively with a large speech corpus and different feedback paths. The simulation results show that higher number of subbands (up to a certain level) and a proper degree of sparsity promoting give superior AFC performance in terms of commonly used metrics regardless of the incorporation of the PEM. Compared with the ordinary AFC using the NLMS, our proposed method improves ASG by 2 to 3 dB, STOI and HASQI from 0.91 to 0.94 and 0.76 to 0.81, respectively.