Summary
Unobserved confounding presents a major threat to causal inference in observational studies. Recently, several authors have suggested that this problem could be overcome in a shared confounding setting where multiple treatments are independent given a common latent confounder. It has been shown that under a linear Gaussian model for the treatments,the causal effect is not identifiable without parametric assumptions on the outcome model. In this note, we show that the causal effect is indeed identifiable if we assume a general binary choice model for the outcome with a non-probit link. Our identification approach is based on the incongruence between Gaussianity of the treatments and latent confounder and non-Gaussianity of a latent outcome variable. We further develop a two-step likelihood-based estimation procedure.
Keywords: Binary choice model, Latent ignorability, Unmeasured confounding
1. Introduction
Unmeasured confounding poses a major challenge to causal inference in observational studies. Without further assumptions, it is often impossible to identify the causal effects of interest. Classical approaches to mitigating bias due to unmeasured confounding include instrumental variable methods (Angrist et al., 1996; Hernán & Robins, 2006; Wang & Tchetgen Tchetgen, 2018), causal structure learning (Drton & Maathuis, 2017), invariance prediction (Peters et al., 2016), negative controls (Kuroki & Pearl, 2014; Miao et al., 2018), and sensitivity analysis (Cornfield et al., 1959).
Several recent publications have suggested an alternative approaches to this problem that assume shared confounding between multiple treatments and independence of treatments given the confounder (Tran & Blei, 2017; Ranganath & Perotte, 2019; Wang & Blei, 2019a,b). These approaches leverage information in a potentially high-dimensional treatment to aid causal identification. Such settings are prevalent in many contemporary areas, such as genetics, recommendation systems and neuroimaging studies. Unfortunately, in general the shared confounding structure is not sufficient for causal identification. D’Amour (2019, Theorem 1) showed that under a linear Gaussian treatment model, except in trivial cases, the causal effects are not identifiable without parametric assumptions on the outcome model.To address this nonidentifiability problem,D’Amour (2019) and Imai & Jiang (2019) suggested collecting auxiliary variables such as negative controls or instrumental variables. Along these lines, Wang & Blei (2019b) showed that the deconfounder algorithm of Wang & Blei (2019a) is valid given a set of negative controls, and Veitch et al. (2019) further found a negative control in network settings.
The present work contributes to this discussion by establishing a new identifiability result for causal effects, assuming a general binary choice outcome model with a non-probit link in addition to a linear Gaussian treatment model. Our result provides a counterpart to the nonidentifiability result of D’Amour (2019, Theorem 1).We use parametric assumptions in place of auxiliary data for causal identification. This is similar in spirit to Heckman’s selection model (Heckman, 1979) for correcting bias from nonignorable missing data. In contrast to the case with normally distributed treatments and outcome, in general the observed data distribution may contain information beyond the first two moments, thereby providing many more nontrivial constraints for causal identification (Bentler, 1983; Bollen, 2014). In particular, our approach leverages the incongruence between Gaussianity of the treatments and latent confounder and non-Gaussianity of a latent outcome variable to achieve causal identification. A referee pointed out that this is related to previous results of Peters et al. (2009) and Imai & Jiang (2019, §2.1) in other contexts of causal inference. Our identification approach is accompanied by a simple likelihood-based estimation procedure, and we illustrate the method through synthetic and real data analyses in the Supplementary Material.
2. Framework
Let be a p-vector of continuous treatments, Y an outcome, and X a q-vector of observed pre-treatment variables. The observed data are independent samples from a superpopulation. Under the potential outcomes framework, Y is the potential outcome had the patient received treatment . We are interested in identifying and estimating the mean potential outcome . We make the stable unit treatment value assumption, under which Y(a) is well-defined and if A = a.
We assume the shared confounding structure under which the treatments are conditionally independent given the baseline covariates X and a scalar latent confounder U. Figure 1 provides a graphical illustration of the setting.
Fig.1.
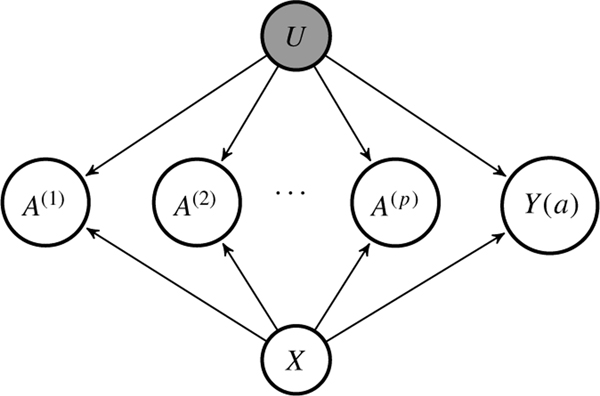
A graphical illustration of the shared confounding setting. The latent ignorability assumption is encoded by the absence of arrows between and Y(a) for . The grey node indicates that U is unobserved.
Assumption 1 (Latent ignorablity).
For all a, .
Under Assumption 1, we have
| (1) |
We consider a latent factor model for the treatments:
| (2) |
where and Wang & Blei (2019a) suggested first constructing an estimate of U, the so-called deconfounder, and then using (1) to identify the mean potential outcomes and causalcontrasts.However,aspointedoutbyD’Amour(2019), Assumption 1 and model (2) are not sufficient for identification of . See also Example S1 in the Supplementary Material for a counterexample where Y follows a Gaussian structural equation model.
3. Identification with a binary outcome
We now study the identification problem with a binary Y, thereby operating under a different set of assumptions from those in Example S1. To fix ideas, we first consider the case without measured covariates X and later extend the results to the case with X. We assume that treatments A follow the latent factor model (2). We also assume the following binary choice model:
| (3) |
where an auxiliary latent variable T, independent of (A, U), has a known cumulative distribution function G. Equivalently, model (3) can be written as . This class of models is general and includes common models for the binary outcome. For example, when T follows a logistic distribution with mean 0 and scale 1, model (3) becomes a logistic model; when T follows a standard normal distribution, model (3) is a probit model; when T follows a central t distribution, model (3) is a robit model (Liu, 2004; Ding, 2014).
Our main identification result is summarized in Theorem 1.
Theorem 1.
Suppose that Assumption 1, models (2) and (3) and the following conditions hold:
there exist at least three elements of that are nonzero, and there exists at least one such that and its sign is known a priori;
is not a constant function of a.
Then the parameters and hence are identifiable if and only if T is not deterministic or normally distributed.
Theorem 1 entails that identifiability of causal effects is guaranteed as long as the outcome follows a nontrivial binary choice model with any link function other than the probit. Condition (i) of the theorem is plausible when the latent confounder U affects at least three treatments, for at least one of which subjectspecific knowledge allows the signs of θj and γ to be determined. Condition (ii) requires that the observed outcome means differ across treatment levels, and can be checked from the observed data.
We now present an outline of our identification strategy leading to Theorem 1. Under model (2), follows a joint multivariate normal distribution
where . Therefore follows a univariate normal distribution with mean and variance .
The starting point of our identification approach is the following orthogonalization of . Let be the standardized latent confounder conditional on A. Then and Z follows a standard normal distribution. Model (3) then implies that
| (4) |
where and (A,T,Z) are jointly independent.
The unknown parameters can then be identified in three steps.In the first step,we prove the identifiability of θ and using standard results from factor analysis (Anderson & Rubin, 1956). In the second step, we study the binary choice model (4), and show that both c2 and the distribution of are identifiable up to a positive scale parameter. In the third step, we show that when the distribution of T is nondeterministic and non-Gaussian, one can leverage the incongruence between the Gaussianity of Z and the non-Gaussianity of T to identify c1, c3 and the scale parameter in the second step. The key to this step is the following lemma. Finally, we identify α,β,γ and hence from c1, c2, c3, θ and .
Lemma 1.
Suppose and that T is independent of Z, where Z follows a standard normal distribution and c1 and c3 are constants. The following statements are equivalent.
There exist , and such that , and , where means that the random variables E and F have the same distribution.
The random variable T is either deterministic or normally distributed.
Remark 1.
In this paper we only allow U to be a scalar. In this case, θ is identified up to its sign from the factor model, and it may be possible to identify the sign of θ from subject-matter knowledge. However, if U is a multi-dimensional vector, then the factor model (2) becomes , where is the loading matrix. In this case, is only identifiable up to a rotation. Consequently, in general, there are infinitely many causal effect parameters that are compatible with the observed data distribution; see Miao et al. (2020) for related discussions.
Remark 2.
Example S1 in the Supplementary Material shows that when the continuous outcome Y follows a Gaussian structural model, is not identifiable. Intuitively, the binary outcome in a probit regression can be obtained by dichotomizing a continuous outcome following a Gaussian distribution, and there is no reason to believe that dichotomization improves identifiability. So it should not be surprising that is not identifiable in the probit case.
In the presence of baseline covariates X, we assume that
| (5) |
| (6) |
where . We also assume that
| (7) |
where with and being the covariances of A and X, respectively. Then , follows a univariate normal distribution with mean and variance . Identifiability of can then be obtained as in Theorem 1, except that now we replace (ii) of Theorem 1 with the following weaker condition:
(ii*) depends on a or x or both. Furthermore, if depends only on a subset of x, say , then at least one of has full support in .
Theorem 2.
Suppose that Assumption 1, (5)–(7), and conditions (i) and (ii) of Theorem 1 hold. Then the parameters and hence E{Y(a)} are identifiable if and only if T is not deterministic or normally distributed.
The proof of Theorem 2 is similar to that of Theorem 1 and hence omitted.
4. Discussion
When the causal effects are identifiable,one canuse the following likelihood-based procedure to estimate the model parameters. Asymptotic normality and the resulting inference procedures follow directly from standard M-estimation theory.
Step 1. LetA* be the residual of a linear regression of A on X. Obtain the maximum likelihood estimators and based on a factor analysis on A*, using an off-the-shelf package such as the factanal function in R (R Development Core Team, 2022).When there are no observed confounders X, one can use A instead of A* and perform factor analysis.
Step 2. Estimate by maximizing the conditional likelihood , where .
In the Supplementary Material, we report numerical results from analyses of synthetic data and real datasets. In a recent note, Grimmer et al. (2020) showed that the deconfounder algorithm of Wang & Blei (2019a) may not consistently outperform naive regression, ignoring the unmeasured confounder when the outcome and treatments follow Gaussian models. In constrast, our numerical results suggest that under our identification conditions, the likelihood-based estimates outperform naive regression estimates. Furthermore, these estimates exhibit some robustness against violations of the binary choice model specification. Nevertheless, we end with a cautionary remark that our results show that identification of causal effects in the multi-cause setting requires additional parametric structural assumptions, including the linear Gaussian treatment model, the binary choice outcome model, and a scalar confounder.
Supplementary Material
Acknowledgement
The authors thank the editor, associate editor and referees for their helpful comments and suggestions.The authors also thank Jiaying Gu, Stanislav Volgushev and Ying Zhou for insightful discussions that have improved the main identification theorem. Kong and Wang were partially supported by the Natural Sciences and Engineering Research Council of Canada.
Appendix
Proof of Theorem 1
We use the following notation. Let and define and analogously. Also write .
We first establish the identifiability results for and . When by condition (i) of Theorem 1 there exist at least three nonzero elements of . By Anderson & Rubin (1956, Theorem 5.5) one can identify θ up to sign and uniquely identify . As U is latent with a symmetric distribution around zero, without loss of generality we may assume we know γ > 0 so that the sign of θj in condition (i) is determined accordingly; otherwise, we may redefine U to be its negative, and all the assumptions in Theorem 1 then hold if we also redefine θj and γ to be their respective negatives. It follows that both θ and are identifiable.
We now study the binary choice model (4). This is a nontraditional binary choice model as the right-hand side of the inequality involves a latent variable Z. We therefore let so that , and model (4) becomes
| (A1) |
This is a binary choice model that was first introduced in economics (e.g., Cosslett, 1983; Gu & Koenker, 2020) and recently studied in statistics (e.g., Tchetgen Tchetgen et al., 2018). Condition (ii) of Theorem 1 implies that there exists j such that . Without loss of generality we assume .
To identify the sign of and the distribution of observe that (A1) implies
| (A2) |
where the second equality holds because . Since A follows a multivariate Gaussian distribution, (1) (A2) holds for any . Setting in (A2), we can identify for any . Condition (ii) and (A2) guarantee that this is a monotone nonconstant function of a. It is easy to see that if and only if is an increasing function of a(1) so that the sign of is identifiable. Thus the distribution of is identifiable.
We now show that is identifiable. Without loss of generality we assume . If we let , then (A2) implies that for any ,
Consequently, the distribution, and hence the expectation, of is identifiable. It follows that for we can also identify
where the equality holds because .
We now turn to the third step of the proof. Lemma 1 implies that , c1 and are all identifiable if and only if T is not deterministic or normally distributed. The sign of can then be determined from the sign of γ, as . Thus, the parameters and hence are identifiable if and only if T is not deterministic or normally distributed, which finishes the proof.
Proof of Lemma 1
Without loss of generality we assume C = 1. Let .
We first show that (II) implies (I). Suppose , where if T is normally distributed and 0 if T is deterministic. Then and . It is easy to verify that if and , then .
We next show that (I) implies (II). We start by showing that . Suppose otherwise; then . We then have that for all and hence , where is the characteristic function of T. As a result, , which implies This is a contradiction.
We now let and so that . We first consider the case where . By a similar characteristic function argument to that above, , so T is a constant almost surely. We next consider the case where . Without loss of generality we assume . By a similar characteristic function argument to that above, we have
| (A3) |
where and with and . Equation (A3) implies that
| (A4) |
Consequently,
| (A5) |
where are independent and identically distributed and are independent of T. We will now show that . Suppose otherwise; then . Let denote the modulus of a complex number. For any t > 0, by (A4) and the property of a normal distribution we have that as . This is a contradiction, as by the continuity of the characteristic function we have .
We can now see that in (A5), as , in probability and in distribution. Therefore, . Thus the proof is complete.
Footnotes
Supplementary material
Supplementary Material available at Biometrika online includes examples, simulation results, and two data illustrations.
Contributor Information
DEHAN KONG, Department of Statistical Sciences, University of Toronto,700 University Avenue, Toronto, Ontario M5G 1X6, Canada.
SHU YANG, Department of Statistics, North Carolina State University, 2311 Stinson Drive, Raleigh, North Carolina 27695, U.S.A..
LINBO WANG, Department of Statistical Sciences, University of Toronto, 700 University Avenue, Toronto, Ontario M5G 1X6, Canada.
References
- Anderson TW & Rubin H. (1956). Statistical inference in factor analysis. In Proc. 3rd Berkeley Sympos. Mathematical Statistics and Probability, vol. 5. Berkeley, California: University of California Press, pp. 111–50. [Google Scholar]
- Angrist JD, Imbens GW & Rubin DB (1996). Identification of causal effects using instrumental variables. J. Am. Statist. Assoc 91, 444–55. [Google Scholar]
- Bentle PM. (1983). Simultaneous equation systems as moment structure models: With an introduction to latent variable models. J. Economet 22, 13–42. [Google Scholar]
- Bollen KA (2014). Structural Equations with Latent Variables. NewYork: John Wiley & Sons. [Google Scholar]
- Cornfield J, Haenszel W, Hammond EC, Lilienfeld AM, Shimkin MB & Wynder EL (1959). Smoking and lung cancer: Recent evidence and a discussion of some questions. J. Nat. Cancer Inst 22, 173–203. [PubMed] [Google Scholar]
- Cosslett SR (1983). Distribution-free maximum likelihood estimator of the binary choice model. Econometrica 51, 765–82. [Google Scholar]
- D’Amour A. (2019). On multi-cause approaches to causal inference with unobserved counfounding: Two cautionary failure cases and a promising alternative. Proc. Mach. Learn. Res 89, 3478–86. [Google Scholar]
- Ding P. (2014). Bayesian robust inference of sample selection using selection-t models. J. Mult. Anal 124, 451–64. [Google Scholar]
- Drton M. & Maathuis MH (2017). Structure learning in graphical modeling. Annu. Rev. Statist. Appl 4, 365–93. [Google Scholar]
- Grimmer J, Knox D. & Stewart BM (2020). Naive regression requires weaker assumptions than factor models to adjust for multiple cause confounding. arXiv: 2007.12702.
- Gu J. & Koenker R. (2020). Nonparametric maximum likelihood methods for binary response models with random coefficients. J. Am. Statist. Assoc to appear, DOI: 10.1080/01621459.2020.1802284. [DOI]
- Heckman JJ (1979). Sample selection bias as a specification error. Econometrica 47, 153–61. [Google Scholar]
- Hernán MA & Robins JM (2006). Instruments for causal inference: An epidemiologist’s dream? Epidemiology 17, 360–72. [DOI] [PubMed] [Google Scholar]
- Imai K. & Jiang Z. (2019). Discussion of ‘The blessings of multiple causes’ by Wang and Blei. arXiv: 1910.06991.
- Kuroki M. & Pearl J. (2014). Measurement bias and effect restoration in causal inference. Biometrika 101, 423–37. [Google Scholar]
- Liu C. (2004). Robit regression: A simple robust alternative to logistic and probit regression. In Applied Bayesian Modeling and Casual Inference from Incomplete-Data Perspectives. London: Wiley, pp. 227–38. [Google Scholar]
- Miao W, Geng Z. & Tchetgen Tchetgen EJ (2018). Identifying causal effects with proxy variables of an unmeasured confounder. Biometrika 105, 987–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao W, Hu W, Ogburn E. & Zhou X. (2020). Identifying effects of multiple treatments in the presence of unmeasured confounding. arXiv: 2011.04504v3.
- Peters J, Bühlmann P. & Meinshausen N. (2016). Causal inference by using invariant prediction: Identification and confidence intervals. J. R. Statist. Soc. B 78, 947–1012. [Google Scholar]
- Peters J, Janzing D, Gretton A. & Schölkopf B. (2009). Detecting the direction of causal time series. In Proc. 26th Annu. Int. Conf. Machine Learning. NewYork: Association for Computing Machinery, pp. 801–8. [Google Scholar]
- R Development Core Team (2022). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Ranganath R. & Perotte A. (2019). Multiple causal inference with latent confounding. arXiv: 1805.08273v3.
- Tchetgen Tchetgen EJ, Wang L. & Sun B. (2018). Discrete choice models for nonmonotone nonignorable missing data: Identification and inference. Statist. Sinica 28, 2069–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran D. & Blei DM (2017). Implicit causal models for genome-wide association studies. arXiv: 1710.10742.
- Veitch V, Wang Y. & Blei D. (2019). Using embeddings to correct for unobserved confounding in networks. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019). La Jolla, California: Neural Information Processing Systems Foundation, pp. 13792–802. [Google Scholar]
- Wang L. & Tchetgen Tchetgen E. (2018). Bounded, efficient and multiply robust estimation of average treatment effects using instrumental variables. J. R. Statist. Soc. B 80, 531–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. & Blei DM (2019a). The blessings of multiple causes. J. Am. Statist. Assoc 114, 1574–96. [Google Scholar]
- Wang Y. & Blei DM (2019b). Multiple causes: A causal graphical view. arXiv: 1905.12793.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


