Fast Quantitative Low-Field Magnetic Resonance Imaging With OPTIMUM—Optimized Magnetic Resonance Fingerprinting Using a Stationary Steady-State Cartesian Approach and Accelerated Acquisition Schedules

Objective

The aim of the proposed work is to develop model-based, fast multiparametric magnetic resonance imaging (MRI) in field regimes where signal-to-noise ratio is poor, such as encountered at low-field and in low γ nuclei.

Materials and Methods

A custom, optimized MRI pipeline was developed at low field (0.1 T) that relies on the magnetic resonance fingerprinting framework, called OPTIMUM. An optimization algorithm was used to select a short acquisition schedule (n = 18 images) that favors maximal discrimination across varying magnetic properties (T₁, T₂) and off-resonance effects while maintaining high transverse magnetization at the steady state. In the presented study, a stationary balanced steady-state approach was investigated that allows for Cartesian (used here) and non-Cartesian acquisition schemes. Images were collected in calibrated samples containing different concentrations of manganese(II) chloride (MnCl₂) in deionized water and compared with gold standard techniques (ie, inversion recovery for T₁, Carr-Purcell-Meiboom-Gill for T₂). Images were then collected in vivo in the human hand and wrist.

Results

OPTIMUM successfully provided sets of quantified maps (T₁, T₂, T₂*, M₀, ΔB₀, B₁⁺) in calibrated samples and in vivo in the human hand and wrist in 3 dimensions, in ~8.5 minutes, with a voxel resolution of [1.5 ×1.5 × 6.5] mm³. Relaxation parameters (T₁, T₂) scale linearly with [MnCl₂] and are in good agreement with the calibrations performed for T₁, with a consistent trend to underestimate T₂.

Conclusion

We show that low-field MRI can benefit from innovative multiparametric approaches to gain speed and become realistic in clinical environments. For the first time, we report simultaneous, multiparametric imaging (6 quantitative maps) in 3 dimensions, in vivo in the human hand and wrist, obtained in just 8.5 minutes. It is sometimes overlooked that low magnetic fields provide higher dispersion of nuclear spin relaxation rates. Rapid quantification such as offered by OPTIMUM could be an enabling technology to explore new metrics and contrasts in point-of-care MRI diagnosis, making it an important step toward broad democratization.

Magnetic resonance imaging (MRI) in radiology has steadily moved toward stronger magnetic fields to provide finer image resolution of body parts and function within the minimum acquisition time. This technical approach prioritizes sensitivity gain from increased nuclear polarization over weight, power requirements, or siting infrastructure considerations. Consequently, MRI scanners in radiology suites offer high performance but stay confined in a highly controlled environment that translates in tremendous costs and little (or no) flexibility. The prospect of agile MRI technology could be relevant in many areas though, from interventional settings to intensive care units where patients at risk need ongoing MRI monitoring.

The MRI community currently observes a resurgence of interest for low field (LF) that could enable such a paradigm change^1–5 and whose potential clinical value spans a very broad range whether on the upper (>0.2 T) or lower (<0.2 T) bound of the spectrum. If promising, such technologies face continuous challenges to reach clinical value that may trigger mass adoption. The intrinsically lower signal-to-noise ratio (SNR) per unit time calls for efficient acquisition schemes, supported by original reconstruction and processing pipelines, and innovative hardware solutions.

Often overlooked, nuclear relaxation mechanisms (longitudinal, T₁, and transverse, T₂ and T₂*) also play a major role in LF, with potential to unveil a diversity of clinically relevant, new endogenous contrasts. Largely unexplored, T₁ relaxation is known to exhibit higher dispersion at LF, as could be observed in the brain tissue,⁶ whereas prolonged T₂ and T₂* inherently offer larger dynamic ranges. Unfortunately, spatial quantification of relaxation properties is generally unused at clinical fields (1.5–3 T) because of the additional acquisition time implied, and it is even harder to envision at LF to very-LF regimes. Indeed, T₁ and T₂ characterization relies on the calculation of time constants in the form of exponential decay/recovery curves, whose sampling strategy is adapted to the type of tissue or material investigated. In numerous applications, it is required to cover broad ranges of time constants that can result in prohibitive acquisition times. Hence, a general lack of quantitative data is commonly observed in clinical practice.

Promising methods exist that allow quickly probing of multiple properties of matter at once,^7–10 but rarely provide simultaneous quantification of an extensive range of typical MRI parameters such as T₁, T₂, T₂*, ΔB₀, or the transmit bias field B₁⁺. Magnetic resonance fingerprinting (MRF),¹¹ introduced in 2013, is a model-based approach of MRI providing a set of quantitative nuclear magnetic resonance (NMR) maps at once, from a single magnetic resonance (MR) acquisition. Magnetic resonance fingerprinting consists of transient state sequences where a series of highly undersampled images are successively acquired while varying imaging parameters flip angle (FA) and repetition time (TR) simultaneously. Multiparametric maps are obtained by matching the acquired, time-varying signal pixelwise to a precomputed database of simulated MR signals. Since its introduction, MRF has gained considerable interest, and there have been many developments to improve it robustness, reliability, and expand its use.

Considering LF MRI, MRF transformed to fit this particular regime (ie, high T₁ dispersion, Johnson noise dominated) and constraints (ie, low SNR, inhomogeneous fields, limited hardware performance) could make quantitative imaging clinically relevant. The MRF pipeline currently relies (most commonly) on hundreds^12,13 to thousands¹¹ of time-varying images acquired with a single-shot, highly undersampled spiral sampling of k-space (ie, non-Cartesian) following an inversion pulse. In multishot acquisitions, a delay is generally added at the end of each time series to allow for magnetization recovery. Such peculiarities make MRF a challenge to deploy at LF, in particular, on the lower end of the LF spectrum. Besides, single-shot spiral imaging is nontrivial to implement on noncommercial research LF systems; multishot (Cartesian or non-Cartesian) alternatives will translate into prohibitive acquisition times; and single-shot acquisitions are most likely to be banned considering the shortened T₁ values, reduced sensitivity, and increased field inhomogeneity (ie, shortened T₂*) one shall expect in small footprint LF magnets.

Yet, approaches exist that have separately tackled some of these limitations. Cartesian and spiral sampling schemes have been used without delay between consecutive time series, resulting in stationary fingerprints.^14,15 The resulting, recurring patterns of signal changes can be repeated indefinitely and used for matching, whereas speed is not sacrificed by long recovery times between acquisitions. Besides, Cartesian acquisition allows for flexible and straightforward image reconstruction.^14,16–19 Optimization strategies have been leveraged to increase the separation between signals with different relaxation properties, with the extra benefit of reducing the total number of images required and, hence, acquisition times.^{16–18,20,21} Better discrimination across tissue relaxation properties seems quite potent as MR fingerprints are generally highly correlated regardless of the time series length. Focusing on the latter has allowed drastically reducing the number of required images per time series (down to ≤30), opening up for alternate acquisition strategies such as echo-planar imaging^16–18 while maintaining speed.

Here, we propose OPTIMUM and divert from the original MRF pipeline based on the combination of 3 major changes tailored to LF applications. First, subsampled 3D Cartesian acquisition is performed that allows for straightforward, robust data gridding before image reconstruction. Second, a stationary regime of unique, time-varying, short signal patterns is reached at the steady state for each image voxel. Third, the FA and TR schedule used here was optimized to emphasize signal discrimination at stationary state, across different tissue magnetic properties while bringing robustness to off-resonance and low-SNR conditions.

If promising, a limitation of previously published MRF optimizations lies in the optimization being performed on-resonance, with high SNR. Yet, off-resonance effects can lead to completely different signal patterns that may defeat the optimization performed, even in unbalanced sequences, and a low SNR as encountered at LF could equally jeopardize MRF outcomes. Here, criteria on the amount of transverse magnetization at the steady state were included in our optimization in conjunction with a fully balanced steady state (bSSFP) sequence. Interestingly, MRF originally used bSSFP but quickly departed from it because of off-resonance artifacts. At LF, however, bSSFP provides higher steady-state transverse magnetization (compared with high fields) from reduced T₁ and prolonged T₂ values, making it an imaging sequence of choice.²² Considering TR ≪ T₁, T₂, the available signal at steady state is mainly driven by the ratio T₁/T₂ of the imaged sample,²³ which becomes beneficial as static field B₀ goes down.

With OPTIMUM, we could evaluate results at 100 mT (4.25 MHz) in calibrated samples, with T₁/T₂ ranging from 40/15 to 1700/960 milliseconds, and perform quantitative imaging in vivo in the human hand and wrist, providing a set of 6 quantitative maps (T₁, T₂, T₂*, M₀, ∆B₀, and B₁⁺). The results presented were obtained from an 8.5-minute, 3-dimensional (3D) scan, in a small footprint dedicated MRI scanner²⁴ for musculoskeletal applications. To the best of our knowledge, this is the first time that such a set of quantitative maps can be obtained at LF, in 3D, in vivo in human tissue, and with clinically acceptable times.

In the quest for clinical benefits and further medical value, we anticipate that such technique developments may play a critical role in the democratization of LF MRI, from point-of-care, dedicated devices to multipurpose whole body systems.

MATERIALS AND METHODS

OPTIMUM: OPTImized MUltiparametric MRI for Better Tissue Discrimination

Magnetic resonance fingerprinting relies on pattern matching of an acquired NMR signal to a database of simulated signals.¹¹ The simulated signal showing the highest correlation with the acquired one is identified as the best match, and corresponding NMR properties such as T₁, T₂, off-resonance, and proton density are extracted. Essential to an accurate matching is making sure that, for a given schedule of FAs and TRs, acquired NMR signal trajectories (so called “MR fingerprints”) are unique signatures of specific tissue properties. Tissues with different properties that present similar signal evolutions are intrinsically impossible to distinguish, with a risk that MRF will fail. This risk is partially tamed at clinical fields where sufficient SNR may allow distinguishing between correlated signals, but it is particularly exacerbated at LF. Cohen^16,18 showed that signal correlation for a given schedule of FAs and TRs can be evaluated by calculating the dot product matrix H of an optimized dictionary D: H = D · D, and optimization schemes were assessed so to diagonalize H for a range of T₁ and T₂ values. Here, OPTIMUM follows a rebooted, similar strategy, accounting for (crucial) off-resonance, converting it to stationary fingerprints, and compromising between discriminatory power and SNR efficiency.

A first pool of n = 10,000 random schedule candidates was generated with MATLAB (MathWorks, Natick, MA) with each 18 FAs/TRs and a fixed echo time (TE) of 9 milliseconds. Echo time was empirically chosen above the minimum achievable (5 milliseconds) to compromise between sufficiently long gradient ramp and plateau times (ie, accounting for hardware limitations), good discriminatory power, and reasonable acquisition times. The explored range for TR was 15 to 40 milliseconds in steps of 5 milliseconds, set by our fixed TE and a target acquisition time of less than 10 minutes, and 0 to 180 degrees for FA with steps of 10 degrees. Dictionaries were simulated accounting for 50 consecutive series of 18 TRs to reach a stationary state across a broad range of magnetic properties. For each FA/TR schedule candidate, 4 dot product matrices H were calculated for 10 pairs of T₁/T₂ properties (Table 1) on-resonance and off-resonance, with δf = 0, 10, 25 (1/max TR), and 67(1/min TR) Hz. Including off-resonance is quite essential as the latter plays a dominant role in the alteration of bSSFP-based MRF signals,¹² beyond the effect of T₁ and T₂ relaxation rates and considering that typical magnetic field homogeneity easily reaches hundreds of hertz in clinical setups.

TABLE 1.

Set of T₁/T₂ Pairs Used in the Described Optimization for OPTIMUM

T1, ms	45	88	130	190	220	280	330	380	450	500
T2, ms	19	39	55	83	100	130	150	170	200	230

The selection criteria for the best FA/TR schedule were twofold. First, the mean and standard deviation of the stationary fingerprint magnitude signals |S_st(D)| over the last 18 TRs were computed in each simulated dictionary, namely, $\overline{\left|S_{\mathit{st}}\left(D\right)\right|}$ and σ. On a scale from 0 to 1 (1 being 100% of net magnetization M₀), we noticed that $\overline{\left|S_{\mathit{st}}\left(D\right)\right|}$ can be rather low (<0.01) in our conditions. Here, only dictionaries with both $\overline{\left|S_{\mathit{st}}\left(D\right)\right|}\ge 0.05$ and σ ≤ 0.05 were retained to promote a minimum SNR across all simulated signals. In the pool of selected dictionaries, entries in H below a correlation threshold of 0.7 (0 = noncorrelated, 1 = fully correlated) were counted, and the schedule resulting in the largest number of entries was kept. After this initial selection, the FAs in the best schedule candidate were individually challenged in an ordered, iterative manner, by adding or subtracting 10 degrees. For each iteration, a new correlation matrix H was computed. If better (both on SNR and discriminatory aspects), the modification was kept and the FA was further incremented/decremented, or else discarded moving to the next FA in the list. The process was continuously repeated over the entire list of FA until no further improvement was observed. The same iterative approach on TR consistently resulted in prolonged values and hence was not used to maintain reasonably short acquisition times.

The discriminatory performance of the selected OPTIMUM schedule was then compared with simulated schedules from the original MRF approach, also based on bSSFP. For each approach, an array of dot product matrices H was computed with δf = −100:0.1:100 Hz, using the magnetic properties described in Table 1. For each set of magnetic properties, the mean and standard deviation on the calculated correlation coefficients was obtained, aiming at diagonalizing H while maintaining low standard deviation scores.

LF OPTIMUM Acquisitions

The OPTIMUM sequence used here is described in Figure 1A, using a Cartesian acquisition and a schedule of n = 18 TRs/FAs. Each k-space line was sequentially acquired over the 18 FAs/TRs before moving to the next without pause. The latter strategy ensures that, for each phase encode step, k-space lines are rigorously acquired with the same timing (ie, same TE/TR) and prevent potential filtering effects of k-space that may arise in single-shot strategies. A generic acquisition strategy was used for both phantom and in vivo measurements, with parameters as follows: sampling rate of 50% following a Gaussian probability density function (Fig. 1B), matrix size 90 × 81 × 15, voxel size [1.5 × 1.5 × 6.5] mm³ and corresponding field of view [135 × 122.5 × 98] mm³, bandwidth = 15,000 Hz, number of averages = 2, for a total acquisition time of ~8.5 minutes. Nonsampled k-lines in all acquisitions were zero-filled. At 0.1 T, hence more than 15 times lower field strength than the original MRF work (ie, ~15^3/2 lower sensitivity¹), with no magnetic nor radiofrequency shielding, the optimized 18 FA/TR schedule used here brings the acquisition of a single 2D partition to 34 seconds, compared with 12 seconds in the original MRF study.

FIGURE 1.

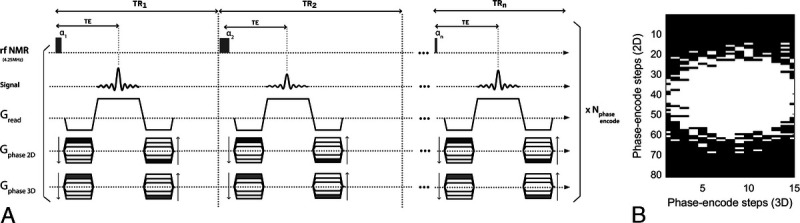
OPTIMUM pulse sequence diagram and undersampling pattern used for imaging. A, The acquisition scheme relies on a balanced steady-state approach with Cartesian sampling of k-space operating in a sequential fashion. B, A 50% sampling scheme was applied following a Gaussian probability density function.

LF MRI System

All experiments were performed on a small footprint, biplanar 0.1 T MRI scanner²⁴ (Fig. 2A), in combination with a 60 × 120–mm² inside diameter, 120-mm-long transmit/receive solenoid coil (Fig. 2B), capacitively tuned and inductively matched at F₀ = 4.256 MHz. The MRI scanner features a transverse, horizontal static magnetic field B₀ and a 17-cm bore. The 0.1 T resistive magnet (EAR54L, Drusch & Cie, Rueil-Malmaison, France) is water cooled and powered by a separated power unit including the magnet main power supply and the gradient power amplifiers. The scanner is equipped with a set of 3 biplanar gradients (x, y, z) which can presently achieve a calibrated maximum gradient strength of 10 mT/m. The console used to drive the MRI hardware and for signal collection is a Cameleon3 (RS2D, Strasbourg, France) respectively equipped with 2 radiofrequency transmit and 4 receive channels. Radiofrequency transmit operations were performed via a 500 W pulsed amplifier (BT00500-ALphaS, Tomco Technologies, Stepney, Australia) connected to the coil via a passive transcoupler (NMR Service GmbH, Erfurt, Germany). For receive operations, the used transmit/receive solenoid coil (Fig. 2B) was connected to a custom low-noise preamplifier developed in-house.²⁵

FIGURE 2.

Experimental setup. View of (A) the small footprint, biplanar 0.1 T scanner and (B) the transmit/receive solenoid coil used.

Dictionary Design

As we are using a fully balanced MR acquisition strategy, our computed dictionary relies on the Bloch formalism as described by Ma et al.¹¹ Dictionaries were simulated using Matlab with 4 dimensions: T₁, T₂, ∆B₀, and FA homogeneity (B₁⁺) as a scaling factor of the desired, nominal FAs. For matching, T₁ ranged from 5 to 1900 milliseconds (in increments of 5 milliseconds from 5 to 150 milliseconds, in increments of 10 milliseconds from 160 to 400 milliseconds, in increments of 25 milliseconds from 425 to 1000 milliseconds, and in increments of 50 milliseconds from 1050 to 1900 milliseconds). T₂ in the simulated dictionary ranges from 4 to 1000 milliseconds (in increments of 2 milliseconds from 4 to 60 milliseconds, in increments of 5 milliseconds from 65 to 200 milliseconds, in increments of 10 milliseconds from 220 to 500 milliseconds, and in increments of 25 milliseconds from 525 to 1000 milliseconds). Static magnetic field ∆B₀ variations are included as off-resonance frequencies ranging between ±80 Hz in steps of 1 Hz. Flip angle homogeneity ranges from 65% to 125% of nominal FAs with increments of 5%. Data matching to recover OPTIMUM maps from a ~8 M entries dictionary required ~1.5 minutes on a desktop computer equipped with a 2176 core/8 GB DDR6 memory GPU engine (GEFORCE RTX 2060 Super, NVIDIA, Santa Clara, CA). Getting both T₂ and off-resonance maps from the MRF pipeline, we could infer a voxel wise estimation of T₂* and hence add a sixth quantified map to the MRF reconstructed set following $\frac{1}{T_2^{*}}=\frac{1}{T_2}+\frac{1}{T_2^{\prime }}$ and assuming $\frac{1}{T_2^{\prime }}=\frac{\gamma }{2\pi }\times \mathrm{\Delta }{B}_0$.

Validation in Phantoms

OPTIMUM at 0.1 T was validated in 2 calibrated, 6-bottle phantoms made of borosilicate glass with Teflon caps (30 mL, ∅2 cm ID) containing MnCl₂ in deionized water at different concentrations. For each solution, T₁ and T₂ relaxation rates were respectively measured from gold standard inversion recovery and echo-train-based (CPMG) spectroscopic experiments (parameters in Table 2), with probed relaxation rates ranging from T₁/T₂ = 43/19 milliseconds to 1700/960 milliseconds (Table 3). Static magnetic field homogeneity B₀, T₂*, and $B_1^{+}$ obtained with OPTIMUM were compared with ground truth experiments in one of the calibrated 6-bottle phantoms. A 3D gradient echo sequence with varying TEs (TE, 6:5:31 milliseconds; TR, 40 milliseconds) and the same geometry was performed that allowed to fit T₂* voxel-wise. The first 2 echoes of the latter imaging sequence were used to infer a reference B₀ map. A dual flip-angle (90°/45°), 3D gradient echo approach using the same geometry was used to obtain a reference $B_1^{+}$ map, with parameters of TE of 6 milliseconds and TR of 1.6 seconds (ie, ~5 times the expected longer T₁ in the investigated calibrated phantom). OPTIMUM robustness to off-resonance was challenged by performing experiments in different off-resonance conditions. Respectively, OPTIMUM was performed at 13 and 35 Hz off-resonance that can be achieved by manually varying the magnetic field of the resistive 0.1 T scanner, and ultimately at 35 Hz off-resonance with an altered shim.

TABLE 2.

Sets of Parameters Used in the Spectroscopic Experiments to Quantify T₁ and T₂

	Inversion Recovery (T1)		CPMG (T2)
Sol. ID	Inversion Time (ms)	No. Steps	TE, δTE (ms)	ETL
1	10	101	5	76
2	10	101	5	101
3	20	101	5	201
4	40	71	5	301
5	45	71	5	401
6	60	71	5	401
7	60	71	5	401
8	60	71	5	401
9	150	51	5	601
10	200	51	5	601
11	200	51	5	601
12	200	51	5	1001

The CPMG sequence used had TE = δTE = 5 milliseconds, and variable ETLs.

ETL indicates echo train length; TE, echo time.

TABLE 3.

OPTIMUM Accuracy in a Calibrated Phantom

Sol. ID	[MnCl2] (mM)	T1 (ms)	T1 OPTIMUM (ms)	T2 (ms)	T2 OPTIMUM (ms)
1	1.35	43 ± 0.7	43.9 ± 3	19 ± 0.3	15.5 ± 1.5
2	0.65	89 ± 1	85.5 ± 7	39 ± 1	28.5 ± 2
3	0.45	127 ± 2	125.6 ± 8	57 ± 0.2	38.5 ± 3
4	0.3	185 ± 4	194.8 ± 13	83 ± 0.5	53 ± 5
5	0.25	221 ± 5	241 ± 13	101 ± 0.2	66 ± 5
6	0.16	333 ± 6	354 ± 27	152 ± 0.3	94 ± 6
7	0.14	378 ± 8	313 ± 48	170 ± 0.3	77 ± 13
8	0.10	496 ± 9	503 ± 55	231 ± 1	146 ± 31
9	0.07	664 ± 13	709 ± 110	315 ± 1	176 ± 30
10	0.055	807 ± 17	982 ± 148	384 ± 1	261 ± 51
11	0.04	1016 ± 29	1083 ± 228	492 ± 1.5	365 ± 66
12	0.015	1723 ± 25	433 ± 296	960 ± 1.5	259 ± 158

Multiparametric Imaging In Vivo

OPTIMUM was performed in vivo in the human hand and wrist. Axial images were acquired in 3D in 8.5 minutes with parameters identical to the phantom measurements. A total of 6 quantified maps could be inferred (M₀, T₁, T₂, T₂*, ∆B₀ and B₁). Signal trajectories were compared across different tissue types (eg, bone marrow, bone, tendon, and muscle).

RESULTS

OPTIMUM

When we compare the discriminatory power of our optimized schedule against the original MRF types of pseudo-random schedules (type 1 and 2) described by Ma et al¹¹ (Fig. 3), it seems that all schedules perform reasonably well on resonance (ΔB₀= 0 Hz) for our set of T₁/T₂ values (Table 1), with sensibly better performance for OPTIMUM. Type 1 and 2 MRF schedules exhibit a mean correlation of 0.85 ± 0.16 and 0.83 ± 0.19, respectively, whereas OPTIMUM provides 0.67 ± 0.33. Off-resonance, however, both type 1 and 2 schedules show reduced discriminatory power, even for species an order of magnitude apart, when OPTIMUM maintains similar performance. This can be seen for a given frequency offset (here 33 Hz, randomly picked) and similarly over an averaged correlation matrix across 2000 frequency offsets (−100:0.1:100 Hz). At 33 Hz off-resonance, type 1 and 2 MRF schedules show a mean correlation of 0.97 ± 0.035 and 0.99 ± 0.012, respectively, whereas OPTIMUM exhibits 0.71 ± 0.31. Over the averaged 2000 frequency offsets, type 1 and type 2 MRF schedules show a mean correlation of 0.93 ± 0.082 and 0.95 ± 0.057, respectively, whereas OPTIMUM exhibits 0.73 ± 0.31. The latter trend is further confirmed by the corresponding standard deviations, showing high discrepancies (>0.4) in type 1 and 2 schedules versus a maintained low value with OPTIMUM (<0.2). We observe nonetheless that both optimized and pseudo-random acquisition strategies lack discriminatory power for T₁/T₂ greater than 330/150 milliseconds, even at resonance.

FIGURE 3.

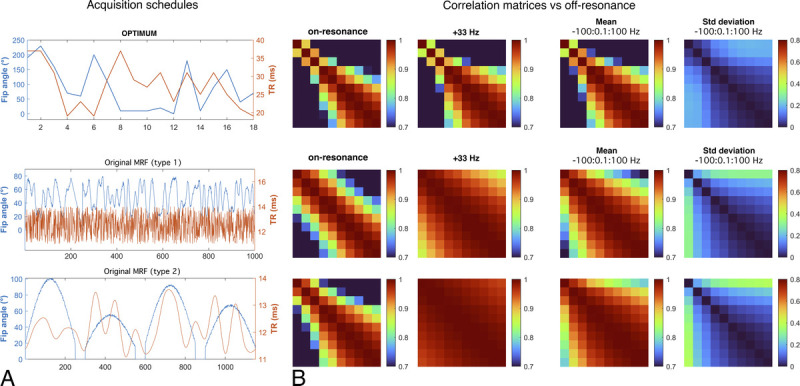
Acquisition schedules and correlation matrices H computed as a function of off-resonance. Top row: OPTIMUM with 18 FAs/TRs exhibits good discriminatory power (diagonalized H) across a broad range of off-resonance frequencies, with maintained low standard deviation. Central to bottom row: original MRF schedules with ≥1000 FAs/TRs exhibit reasonable discriminatory power on-resonance, and lower overall performance off-resonance. Correlation matrices were all calculated with the same 10 pairs of T₁/T₂ properties (Table 1).

Validation in Calibrated Phantoms

Over the investigated broad range of relaxation rates, LF OPTIMUM seems to be in rather good agreement with gold standard experiments for 11 of 12 samples tested (Fig. 4), with comparable T₁ values retrieved (y_T1 = 1.092 · x_T1) and a tendency to underestimate T₂ (y_T2 = 0.70 · x_T2), in particular at long relaxation rates. We note that the extracted T₁ and T₂ standard deviations for each sample also increases with increased T₁ and T₂, noticeably for T₁/T₂ 380/170 milliseconds or greater, as can be equally observed on the corresponding mean T₁ and T₂ maps. For both T₁ and T₂, we notice an outlier value retrieved in the 12th sample tested with the longest T₁/T₂ probed (1700/960 milliseconds), with both highly underestimated retrieved values and the largest standard deviation across the sample. The latter data point was not used in the calculation of linear regressions. Calibrated B₀ and $B_1^{+}$ also show good agreement with OPTIMUM (Figs. 5A, B). Subtle discrepancies can be observed with respect to B₀ that originate from slightly different shimming conditions. The calibration 6-echo scan performed to retrieve T₂* was compared with the one inferred with OPTIMUM (Fig. 6), yet using a corrected $T_{2\text{corr}}=\frac{T_{2\text{optimum}}}{0.7}$ as the latter shows a tendency to be underestimated (y_T2 = 0.70 · x_T2). The OPTIMUM inferred T₂* maps are in good agreement with the calibration experiment (Fig. 6A) when confidence in the performed voxel-wise fit is good (Fig. 6B). Discrepancies arise, particularly pronounced in sample tubes 4 and 5 (>50%), in areas exhibiting poor fitting performance (ie, low R²). Robustness to off-resonance is reported in Figure 7. At 35 Hz off-resonance and with an altered shim (Fig. 7A), OPTIMUM can retrieve relaxation parameters in the calibrated phantom while depicting the expected change in static magnetic field. It shows similarly good performance in all the off-resonance scenarios investigated (13 Hz, 35 Hz, and 35 Hz + altered shim conditions) in comparison with the reference on-resonance experiment (Fig. 7B).

FIGURE 4.

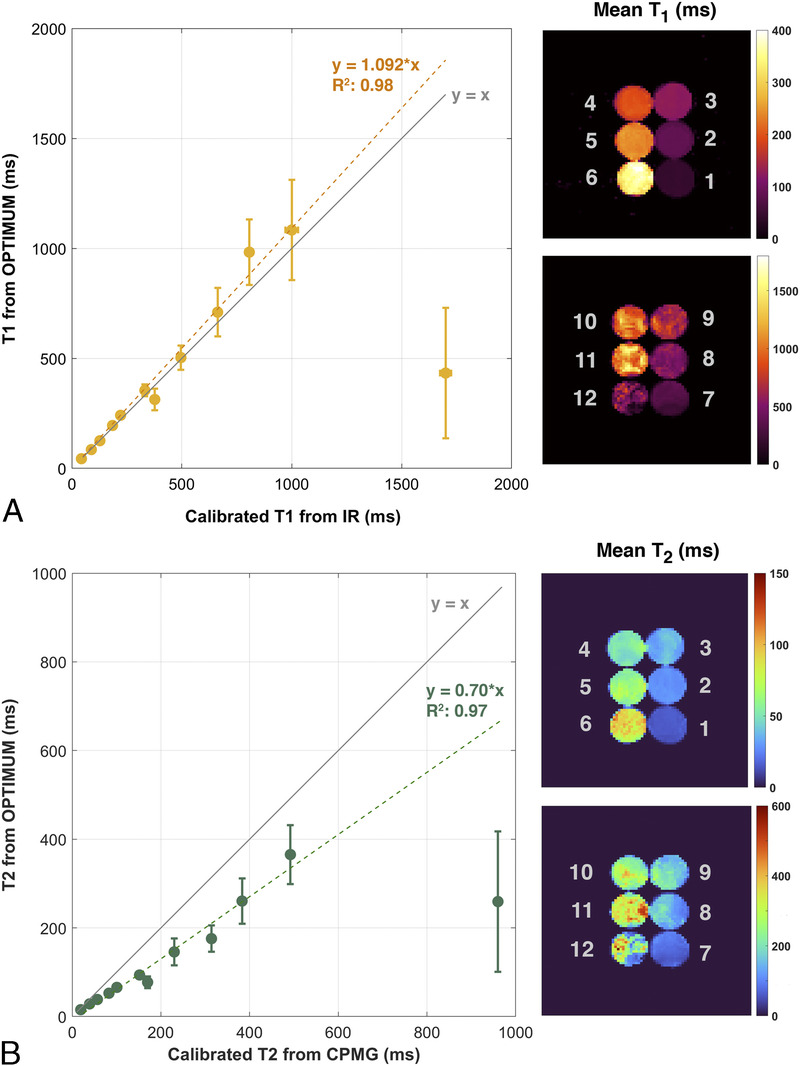
Comparison of LF OPTIMUM with gold standard spectroscopic measurements. T₁ (A) and T₂ (B) values retrieved in calibrated phantoms compared with standard inversion-recovery and spin echo techniques, and their corresponding mean relaxation maps over the phantom volumes.

FIGURE 5.

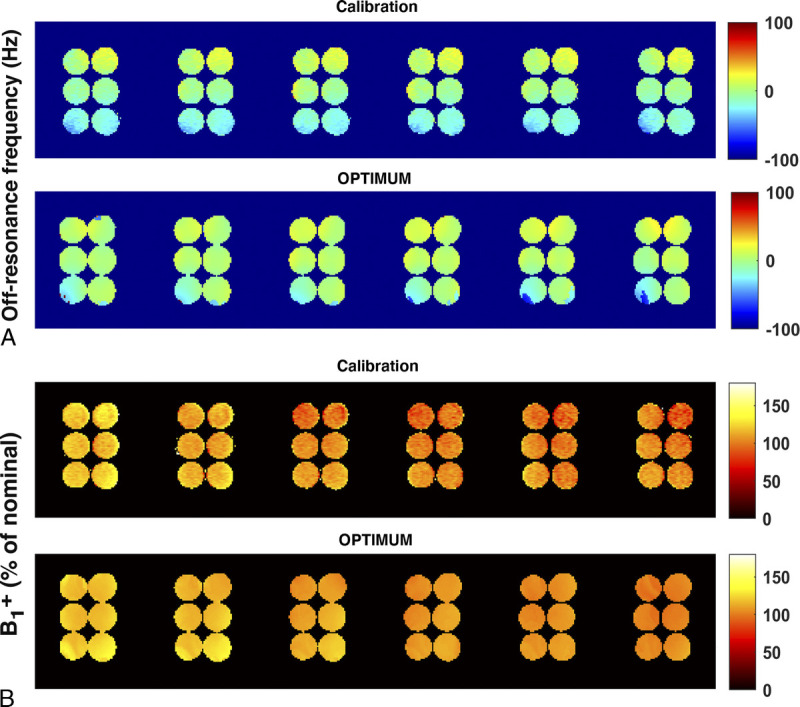
Comparison of calibrated static magnetic field and radiofrequency FA homogeneity with OPTIMUM. (A) Off-resonance frequency (in Hz) and (B) B₁⁺ (in percentage of nominal FA) displayed for 6 central slices.

FIGURE 6.

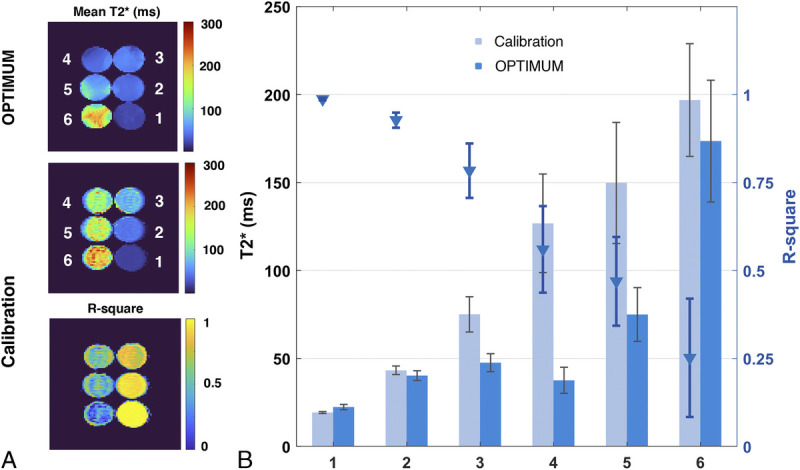
Comparison of calibrated T₂* with OPTIMUM. A, Mean T₂* and R-square maps resulting from voxel wise curve fitting vs OPTIMUM. B, Corresponding bar graphs reported for each sample.

FIGURE 7.

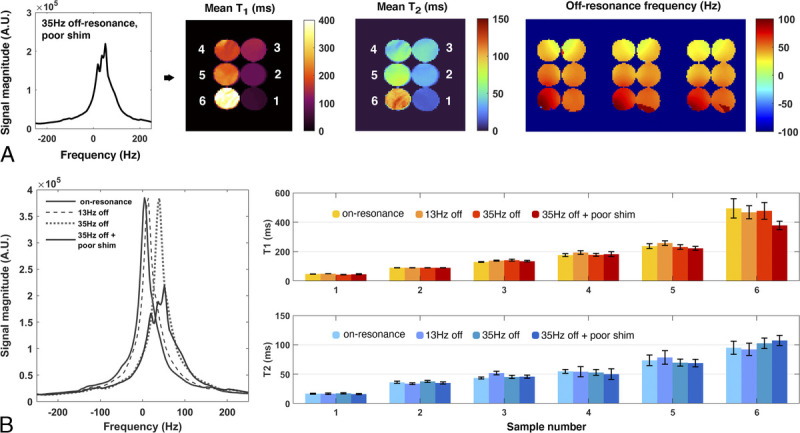
Assessment of OPTIMUM robustness to off-resonance. A, Mean T₁, T₂ maps, and off-resonance (3 central slices displayed) in a 35 Hz off-resonance scenario with altered shim. B, Reported mean T₁ and T₂ values in 4 distinct scenarios, respectively, on-resonance, 13 Hz and 35 Hz off-resonance, and 35 Hz off-resonance in combination with an altered shim.

Multiparametric Imaging In Vivo

Quantitative maps acquired in the hand and wrist allow successfully distinguishing main anatomical structures (Fig. 8A) and their associated relaxation properties, reported in Table 4. Bones, tendons, and large blood vessels, as well muscle, skin, and fatty tissue, can be observed. Magnetic field inhomogeneity reaches a maximum of ±80 Hz across the limb, equivalent to 19 ppm at 4.256 MHz (100 mT). The extracted B₁⁺ maps reflect accurately the expected profile from the coil used, with higher FAs closer to the coil wire, at the periphery of the imaged object. Tissue species such as bone marrow and muscle exhibit very different signal evolutions (Fig. 8B), whereas tendon seems rather close to bone. With T₁/T₂~1, bone marrow exhibits the highest and most recurring signal on the OPTIMUM time series recorded (Fig. 8C), which is expected from the bSSFP nature of the sequence.

FIGURE 8.

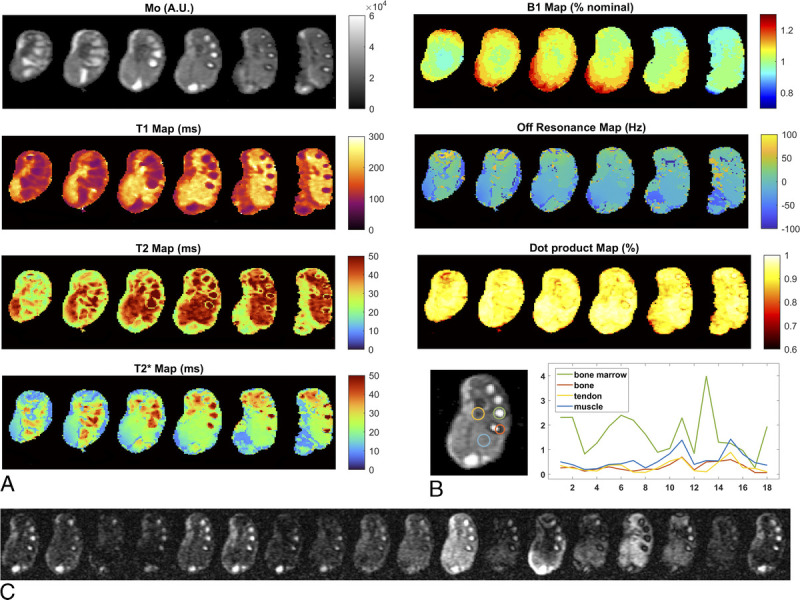
LF OPTIMUM results in vivo at 0.1 T. A, Quantified maps in the human hand/wrist that includes proton density M₀, T₁, T₂, T₂*, B₀, FA homogeneity B₁⁺, and matching efficiency (dot product map) for 6 central slices. Matrix size is 90 × 81 × 15, corresponding voxel size is [1.5 × 1.5 × 6.5] mm³. Total imaging time is 8.5 minutes with number of averages = 2. B, Signal evolution (ie, MR fingerprints) reported for different tissue types in a central slice. (C) Corresponding MR image series.

TABLE 4.

Compilation of T₁, T₂, and T₂* With OPTIMUM for a Selection of Tissue Types

Tissue Type	T1 (ms)	T2 (ms)	T 1 /T 2	T2* (ms)
Muscle	237 ± 16	48 ± 4	5	22.5 ± 0.8
Tendon	202 ± 22	41 ± 4	5	24 ± 1.6
Bone	171 ± 4	39 ± 3	4.4	26 ± 5
Bone marrow	98 ± 6	69 ± 6	1.4	49 ± 3
Fat layer	131 ± 14	30 ± 5	4.4	25 ± 5

DISCUSSION

Relying on both a high duty cycle for data acquisition and favorable, reduced T₁/T₂ ratios at lower magnetic fields, bSSFP running under the hood of OPTIMUM is a very efficient way to rationalize SNR per unit time. bSSFP alone can bring high SNR but limited contrast, and a high sensitivity to off-resonance artifacts. Here, off-resonance can be used as a discriminatory feature for matching purposes, and the high SNR/unit time is key to acceptable acquisition times.

The optimization performed and subsequent reduction of the acquisition schedule were aimed to bring good discriminatory performance across a range of relaxation rates relevant to LF MRI (Table 1). The latter allows porting the MRF framework to straightforward Cartesian acquisitions, without heavily impacting acquisition times. With no particular calibration nor preliminary processing, the acquired, undersampled raw data are then zero-filled before a 3D Fourier transform is applied (Fig. 8C), hence providing a robust and straightforward reconstruction pipeline before matching to a precomputed dictionary. Simulations show that OPTIMUM maintains good discriminatory power across the investigated range of relaxation rates (Fig. 3B), both on- and off-resonance, whereas regular MRF approaches tend to generally worsen off-resonance. Robustness to off-resonance is further confirmed in experiments (Fig. 7), where both magnetic properties and static magnetic field maps can be accurately retrieved, even in altered shim conditions. The length of the acquisition schedule, as a result, should not be seen as a validity criterion to obtain good signal discrimination.

We hypothesize that optimization is critical to LF regimes where the combination of low SNR and highly correlated signals may simply defeat the technique. However, as regular MRF seems to perform well at clinical fields, it would be interesting to rigorously assess the impact of such an optimization, whether it is beneficial to discriminate better across species or if the inherently higher SNR allows to navigate through signal similarities. To that end, optimizations could be performed over both short and large trajectories, for stationary or transient state approaches, and compared with nonoptimized MRF for different SNR regimes. Scaling-up at larger FA/TR schedules may require larger computational time, or further compartmenting of computational tasks to be effective, yet that shall not hinder generic MRF applications, being only a 1-time operation.

OPTIMUM validation in calibrated phantoms demonstrates the expected linear relationship between manganese chloride concentration and the retrieved T₁ and T₂ relaxation rates, at the exception of 1 outlier data point (T₁/T₂ = 1700/960 milliseconds). With reasonably good T₁ estimates (Fig. 4A), we tend to consistently underestimate T₂ (Fig. 4B). A plausible cause to such underestimation could be intravoxel phase dispersion, as demonstrated by Chiu et al,²⁶ that needs to be further investigated. The type of optimization, the range of sequence parameters (FA, TR), the set of relaxation rates, and further, the dictionary used for the matching may also be in cause. In the meantime, one could imagine to simply correct T₂ maps in postprocessing for more realistic estimates (at least in phantom experiments), so long that the observed trend proves stable. After such correction, we notice that T₂* maps from OPTIMUM are in reasonably good agreement with T₂* maps generated from a multiecho, calibration sequence (Fig. 6). Discrepancies can, however, arise when curve-fitting exhibits poor performance. The latter highlights the difficulty in performing and trusting a single calibration scan with a broad range of relaxation parameters (here, from T₁/T₂ = 43/19 milliseconds to 333/152 milliseconds). Instead, several calibration scans would be needed that would inevitably impact the overall experiment time.

Overall, OPTIMUM shows larger standard deviations with increasing relaxation rates (Fig. 4), noticeably in sample 7 to 12 (deviations >15%), both in the plots and corresponding maps displayed. An explanation could be the low discriminatory performance of OPTIMUM when T₁/T₂ goes from 330/150 milliseconds to 500/230 milliseconds (Fig. 3B), with corresponding mean correlation scoring very high, from 96% to 99.5%. It is also possible that too many banding artifacts arise, impeding SNR and hence preventing good matching performance.¹² Alternatively, the simulated dictionaries could be enriched with a higher density of parameters or with additional parameters for higher accuracy. In the latter case, innovative approaches^27–30 will then be needed to keep the reconstruction time low, bringing options to rationalize acquired datasets over longer time periods. Overall, it is quite reasonable, however, that the observed performance drop occurs where the optimization performs the least, and future work on the optimization at longer relaxation times should beneficially improve performance.

In vivo, we successfully report on fast quantitative imaging in the human hand and wrist at 0.1 T, providing a total of 6 quantified metrics in 3D. Major anatomical structures can be resolved, and their corresponding relaxation rates mapped. Comparison with T₁ and T₂ relaxometry in vivo in humans is not trivial as the literature is scarce, but OPTIMUM shows quantified values in the skeletal muscle and fat in reasonably good agreement with previous work in animal and humans (generally only T₁ is available) that compiles living and postmortem measurements.^31–33

CONCLUSION

Largely unexplored in vivo, relaxation dynamics are increasingly influenced by molecular interactions at lower fields and present inherently larger dispersion that could result in unique contrasts.^19,34 As the interest in LF MRI research resurfaces, time-efficient quantification of magnetic properties in tissue will become more and more essential to address fundamental questions on the diagnosis potential of lower field strengths. Relying on the grounds of MRF, OPTIMUM brings an added, tailored layer to LF MRI. From the optimized, enhanced discrimination across NMR signals within a broad range of static field inhomogeneities, it allows navigating in low-SNR regimes. From its reduced amount of temporal steps, it allows mitigating total acquisition times while giving the choice to use Cartesian (privileged here for robustness) or non-Cartesian acquisition schemes. As such, OPTIMUM is currently the only technique capable to characterize simultaneously M₀, T₁, T₂, T₂*, B₀, and B₁⁺ in 3D, with acquisition times acceptable for clinical routine. Leveraging SNR efficient sequences and transferring the complexity associated with quantitative MR in silico, OPTIMUM is compelling with simpler and scalable technologies that could shape the future of mobile diagnostics in radiology. It could be central to the contemporary investigation of novel contrasts, from markers of ischemic/hemorrhagic stroke in the intensive care unit, of inflammation in MSK applications, to subtle underlying changes for the screening or staging of cancer.