Background
Radiomics can yield minable information from medical images, which can facilitate computer-aided diagnosis. However, the lack of repeatability and reproducibility of radiomic features (RFs) may hinder their generalizability in clinical applications.
Objectives
The aims of this study were to explore 3 main sources of variability in RFs, investigate their influencing magnitudes and patterns, and identify a subset of robust RFs for further studies.
Materials and Methods
A chest phantom with nodules was scanned with different computed tomography (CT) scanners repeatedly with varying acquisition and reconstruction parameters (April-May 2019) to evaluate 3 sources of variability: test-retest, inter-CT, and intra-CT protocol variability. The robustness of the RFs was measured using the concordance correlation coefficient, dynamic range, and intraclass correlation coefficient (ICC). The influencing magnitudes and patterns were analyzed using the Friedman test and Spearman rank correlation coefficient. Stable and informative RFs were selected, and their redundancy was eliminated using hierarchical clustering. Clinical validation was also performed to verify the clinical effectiveness and potential enhancement of the generalizability of radiomics research.
Results
A total of 1295 RFs that showed all 3 sources of variability were included. The reconstruction kernel and the iteration level showed the greatest (ICC, 0.35 ± 0.31) and the least (ICC, 0.63 ± 0.27) influence on magnitudes. The different sources of variability showed relatively consistent patterns of influence (false discovery rate <0.001). Finally, we obtained a subset of 19 stable, informative, and nonredundant RFs under all 3 sources of variability. These RFs exhibited clinical effectiveness and showed better prediction performance than unstable RFs in the validation dataset (P = 0.017, Delong test).
Conclusions
The stability of RFs was affected to different degrees by test-retest and differences in CT manufacturers and models and CT acquisition and reconstruction parameters, but the influences of these factors showed relatively consistent patterns. We also obtained a subset of 19 stable, informative, and nonredundant RFs that should be preferably used to enhance the generalizability of further radiomics research.
Key Words: radiomics, computed tomography, CT, repeatability, reproducibility, phantom, stability, robustness
Radiomics is a new discipline that enables the extraction of massive, quantitative, and minable information from medical images, including computed tomography (CT), magnetic resonance imaging (MRI), and positron emission tomography CT.1 Using high-throughput computer algorithms, the underlying radiographic information in medical images, which has been difficult to quantify manually, is translated into radiomic features (RFs). Several radiogenomic studies2–4 have identified connections between RFs and genomic information, molecular pathways, pathophysiological states, and clinical factors. In combination with other sources of medical data, high-dimensional RFs can facilitate precision medicine by serving as a predictive signature in clinical decision support systems for objectively capturing the radiographic phenotype5 in routine medical images.
To date, radiomics studies have focused more on cancer research since radiomics approaches hold the potential of serving as virtual biopsy,6 offering the advantage of constantly characterizing the spatial and temporal heterogeneity of the tumor and its microenvironment. Even though biopsy is treated as the gold standard in cancer diagnosis, it can only show limited characteristics of the tumor from only a small part of a lesion at 1 time point. In contrast, radiomics can routinely quantify tumor phenotypes from every part of all suspicious lesions in a noninvasive manner.7 To date, radiomics has shown great potential for precision medicine in computer-aided screening,8,9 diagnosis,10 treatment guidance,11 and prognosis prediction.12,13
Nevertheless, both clinical and phantom studies have revealed a lack of repeatability and reproducibility in radiomics research, which may hinder its generalizability in clinical applications.14,15 Radiomic features showed sensitivity and variability related to differences in manufacturers,16 scanners,17 and acquisition and reconstruction parameters,18–20 including pitch value, tube voltage, tube current, slice thickness, resolution, field of view (FOV), reconstruction method,20 reconstruction kernel, and radiation dose. Radiomic features also showed variability in test-retest datasets21 and various radiomics software.22 Many efforts have been made to investigate and solve this problem.16–19,22,23 The lack of robustness in RFs makes it difficult for researchers to repeat and reproduce radiomics achievements, and prompt solutions are required to address these limitations. The repeatability and reproducibility of RFs have been strictly defined, with “repeatability” referring to multiple measurements with RFs in the same subject with the same equipment, imaging acquisition settings, and operators over a short time frame, and “reproducibility” referring to measurement of RFs with different equipment, imaging acquisition settings, or operators in the same or different subjects.24,25
To explore this problem, we designed a multicenter phantom study under 3 different conditions introducing variability: test-retest, inter-CT, and intra-CT protocols, each of which was related to a different source of variability. First, we investigated, quantified, and compared the influencing magnitudes and patterns of these factors on the stability of the RFs. Second, we filtered a subset of RFs in which all features were robust under these influencing factors. Finally, clinical validation was performed to verify whether the aforementioned subset was clinically effective and whether it could enhance the generalizability of radiomics research.
MATERIALS AND METHODS
Study Design
Three sources of variability were included in this study (Fig. 1): test-retest, inter-CT, and intra-CT protocol variability. Among them, test-retest variability refers to the RF variability caused by different CT acquisitions, inter-CT variability is caused by differences in CT manufacturers and models, and intra-CT protocol variability is caused by differences in CT acquisition and reconstruction parameters. The targeted CT acquisition and reconstruction parameters included pitch, rotation time, tube voltage, tube current, FOV, slice thickness, slice interval, reconstruction kernel, and iteration level. For each scanner, the most recommended reconstruction method for thoracic imaging was used to ensure optimal image quality; therefore, instead of the reconstruction method, we included the iteration level of the targeted scanner's routine lung reconstruction method in our intra-CT protocol trial.
FIGURE 1.
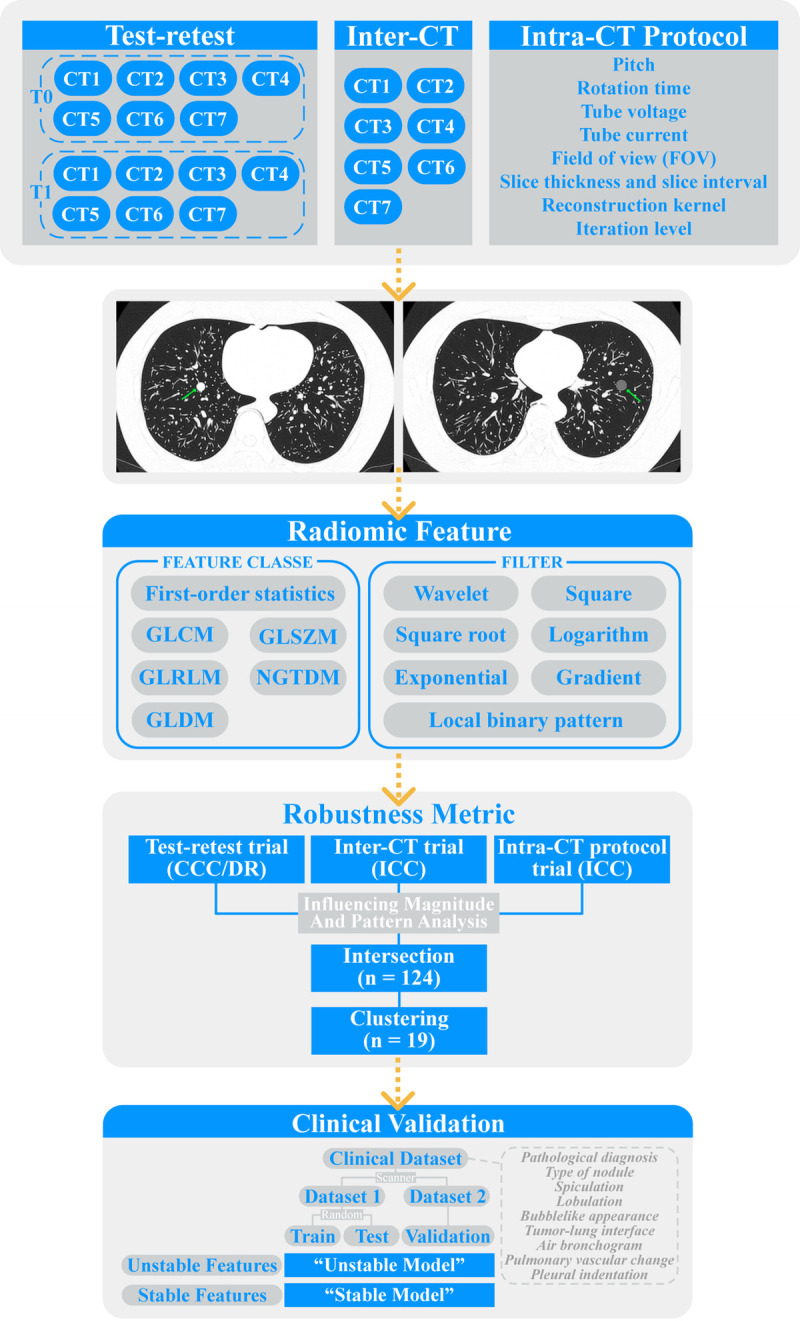
Flowchart of the overall study design. The overall study was divided into 3 parts: test-retest, inter-CT, and intra-CT protocol trials. In the test-retest trial, data were compared between different time points (T0 and T1) to calculate CCC and DR. In the inter-CT trial, data were compared between different CT scanners to calculate ICC. In the intra-CT protocol trial, data were compared under varying CT acquisition and reconstruction parameters to calculate ICC. GLCM, gray level cooccurrence matrix; GLSZM, gray level size zone matrix; GLRLM, gray level run length matrix; NGTDM, neighboring gray tone difference matrix; GLDM, gray level dependence matrix.
Correspondingly, the overall phantom study was divided into test-retest, inter-CT, and intra-CT protocol trials (Fig. 1). In the test-retest trial, the same set of CT scanners and their corresponding routine thoracic imaging acquisition protocols for lung nodules (baseline protocols) were repeatedly used on 2 different days. In the inter-CT trial, 7 different CT scanners with baseline protocols were used. In the intra-CT protocol trial, a CT scanner with its baseline protocol was chosen. Subsequently, the above-mentioned CT acquisition and reconstruction parameters were adjusted one by one with other parameters fixed on the baseline protocol to obtain different CT images after adjustment of different parameters.
Phantom
An anthropomorphic thorax phantom named chest phantom N-1 LUNGMAN26,27 (Kyoto Kagaku Co, Kyoto, Japan; Figs. 2A, B) with simulated nodules was used. The phantom consisted of 3 parts: body model, the internal structure of the lung, and simulated nodules, reproducing the anatomical structures of the lung. The simulated nodules were 9 spherical nodules with 3 CT attenuation values (−800, −630, and 100 Hounsfield units) and 3 sizes (8, 10, and 12 mm in diameter). In accordance with the instruction manual, the 9 simulated nodules were randomly attached to the internal structure of the lung by using double-sided adhesive tape and tweezers. The CT images of the phantom (Figs. 2C, D) were close to the CT images of the human lung. However, the lung nodules were more conspicuous than they would appear on the patient images because the phantom lacked lung parenchyma.
FIGURE 2.
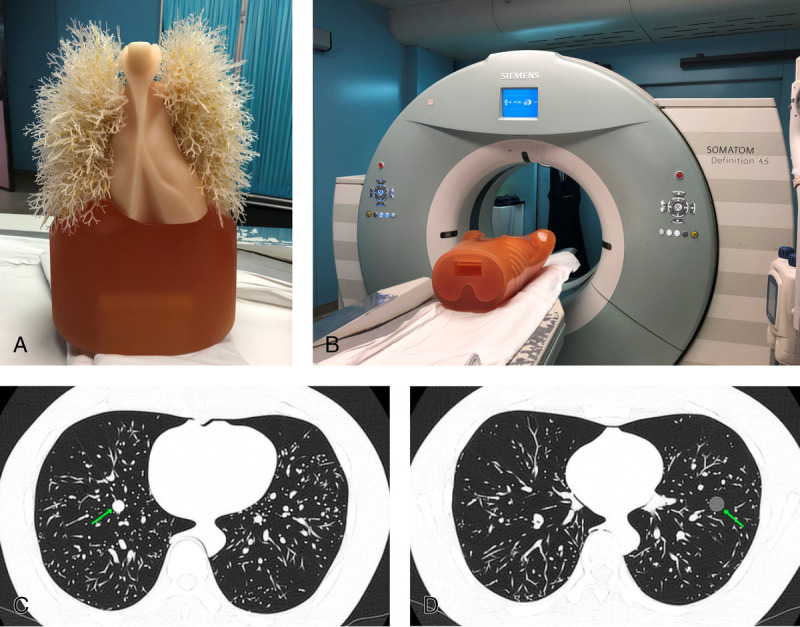
The anthropomorphic thorax phantom (A) scanned by SOMATOM Definition AS (Siemens Healthineers) (B). CT images of the phantom with simulated nodules (arrow; CT attenuation values: 100 [C] and −630 [D] Hounsfield units) scanned by Aquilion ONE TSX-301C (Toshiba, Japan) with the baseline acquisition protocol.
Image Acquisition
Three hospitals at 4 different sites were included: Shanghai Public Health Clinical Center (Jinshan District), Shanghai Public Health Clinical Center (Hongkou District), Zhongshan Hospital of Fudan University, and Shanghai Sixth People's Hospital. For the test-retest and inter-CT trials, because of the limitations imposed by vendor-specific CT acquisition and reconstruction parameters, CT acquisition protocols for different scanners cannot be identical. Therefore, the routine thoracic imaging acquisition protocol for lung nodules of each scanner in each hospital was adopted as the baseline protocol (Table 1). For the intra-CT protocol trial, Aquilion ONE TSX-301C was selected to obtain CT images with varying acquisition and reconstruction parameters (Table 2), and the intra-CT protocol trial was repeated twice to obtain a more general result. The varying scope of acquisition and reconstruction parameters were chosen based on previous studies16,18,19,28,29 and radiologists' previous knowledge. For example, tube voltage (baseline level: 120 kVp) was adjusted to 80 kVp and 135 kVp, because 80 kVp was usually used in low-dose CT and 135 kVp was used for high doses in the corresponding hospital. Finally, 44 sets of CT images were obtained (April-May 2019).
TABLE 1.
CT Acquisition Protocols for the Test-Retest and Inter-CT Trials
| Site | CT Scanner (Manufacturer) | Pitch* | Rotation Time (s) | Tube Voltage (kVp) | Tube Current (mA·s) | FOV (mm) | Slice Thickness (mm)* | Slice Interval (mm)* | Reconstruction Kernel† | Reconstruction Method‡ |
|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai Public Health Clinical Center (Jinshan District) | Aquilion ONE TSX-301C (Toshiba) | 0.813 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | FC56 | AIDR 3D (standard) |
| Shanghai Public Health Clinical Center (Jinshan District) | SCENARIA (Hitachi) | 0.8281 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | 66 | Intelli IP (Lv.2) |
| Shanghai Public Health Clinical Center (Hongkou District) | Brilliance 64 (Philips) | 0.891 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | L | Standard (enhancement = 1.0) |
| Zhongshan Hospital of Fudan University | SOMATOM Definition AS (Siemens Healthineers) | 0.9 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | B60f | ADMIRE (strength = 3) |
| Zhongshan Hospital of Fudan University | Aquilion ONE TSX-301A (Toshiba) | 0.828 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | FC56 | AIDR 3D (standard) |
| Zhongshan Hospital of Fudan University | UCT550 (United Imaging Healthcare) | 0.8875 | 0.5 | 120 | 75 | 350 | 1.0 | 1.0 | SHARPC | Adaptive filter function (enhancement = 2.5) |
| Shanghai Sixth People's Hospital | Revolution CT (GE Healthcare) | 0.992 | 0.5 | 120 | 75 | 350 | 1.25 | 1.25 | LUNG | ASiR (Plus/SS40) |
The number of decimal places was consistent with the corresponding CT scanner control panel.
* The pitch value, slice thickness, and slice interval of each CT scanner can only be selected from several fixed values, which cannot be identical. Subsequently, we selected the closest value of each CT scanner as the baseline level.
† Because different manufacturers had different reconstruction kernels, the reconstruction kernel of each scanner routinely used for thoracic imaging was chosen as the baseline level.
‡ For each scanner, the most recommended reconstruction method for thoracic imaging was used to ensure optimal image quality.
CT indicates computed tomography; FOV, field of view.
TABLE 2.
The Adjustment Range of CT Acquisition and Reconstruction Parameters for the Intra-CT Protocol Trial*
| Pitch | Rotation Time (s) | Tube Voltage (kVp) | Tube Current (mA·s) | FOV (mm) | Slice Thickness/Slice Interval (mm/mm)† | Reconstruction Kernel | Iteration Level‡ |
|---|---|---|---|---|---|---|---|
| 0.637 | 0.5 | 80 | 25 | 350 | 1.0/1.0 | FC17 | Mild |
| 0.813 | 0.75 | 120 | 75 | 400 | 2.0/2.0 | FC56 | Standard |
| 1.388 | 135 | 100 | 5.0/5.0 | FC86 | Strong | ||
| Enhanced |
The number of decimal places was consistent with the CT scanner control panel.
* Aquilion ONE TSX-301C was chosen for the intra-CT protocol trial.
† Slice interval was not adjusted as an independent CT acquisition parameter but corresponded to the slice thickness to simulate realistic clinical CT acquisition scenarios.
‡ Different iteration levels of reconstruction method AIDR 3D were included.
CT indicates computed tomography; FOV, field of view.
The 44 sets of CT images were then shared across different trials. For the test-retest trial, we obtained 2 scans per CT scanner, totaling 14 scans. For the inter-CT trial, we obtained 7 scans per examination, totaling 14 scans, allowing a different analysis of the same data as that in the test-retest trial. For the intra-CT protocol trial, the baseline CT images were shared each time we investigated different acquisition and reconstruction parameters: pitch (adjusted twice, 3 scans per time summed 6 scans), rotation time (adjusted once, 2 scans per time summed 4 scans), tube voltage (adjusted twice, 3 scans per time summed 6 scans), tube current (adjusted twice, 3 scans per time summed 6 scans), FOV (adjusted once, 2 scans per time summed 4 scans), slice thickness/slice interval (adjusted twice, 3 scans per time summed 6 scans), reconstruction kernel (adjusted twice, 3 scans per time summed 6 scans), and iteration level (adjusted 3 times, 4 scans per time summed 8 scans).
Image Segmentation and Feature Extraction
Homemade software and segmentation tools were used for the semiautomatic segmentation. To minimize the influence of segmentation15 and amplify the effectiveness of RFs with internal segmentation,11 internal square segmentation was chosen. For 8-, 10-, and 12-mm-diameter nodules, square regions with lengths of 6, 8, and 10 mm were selected in their maximum cross-section layer by a chest radiologist with 7 years of experience in CT and MRI scan interpretation (see Fig. S1, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the CT images of 3 simulated nodules with their internal square segmentations in the inter-CT trial). A chest radiologist with 20 years of experience in CT and MRI scan interpretation manually confirmed that all segmented regions were contained within the nodule.
PyRadiomics (version 2.2.0) with default calculation settings,30 an open-source library implemented in Python capable of extracting a large panel of features from medical images, was used to extract the RFs. Original and filtered RFs were extracted (Fig. 1). However, because of the fixed-shape segmentation, all morphological RFs were excluded. Finally, 1295 RFs were included in our analysis. More details of the RFs from PyRadiomics have been described previously.30
Clinical Validation
A clinical validation dataset31 with CT images containing 384 ground-glass nodules measuring 5 to 10 mm in diameter (353 patients; men: 87, women: 266; age: 51.2 ± 11.4 years) was used in this study. Pathological diagnosis, 8 CT semantic features of radiological importance in the radiologists' prior knowledge,32 and CT RFs were collected in this dataset (see Table S1, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the characteristics of the clinical dataset). The correlation of RFs with both pathological diagnosis and semantic features was analyzed to explore the clinical effectiveness of each robust RF.
For further validation of the results of stability analyses, the entire dataset was divided into 2 parts with nonoverlapping CT scanners (see Table S2, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the CT scanners and acquisition parameters used for the clinical dataset); the larger part was randomly divided into a training dataset and a testing dataset, and the smaller part was used as a validation dataset. Subsequently, we trained 2 prediction models for pathological diagnosis with unstable RFs and robust RFs separately and compared their performance to validate whether our stability results could enhance the generalizability of radiomics research (Fig. 1).
Statistical Analysis
The concordance correlation coefficient (CCC)33 with a cutoff value of 0.85 and the intraclass correlation coefficient (ICC)34,35 (based on a single-rating [k = 1], absolute-agreement, 2-way mixed-effects model) with a cutoff value of 0.7536 were calculated for repeatability and reproducibility measurements. The dynamic range (DR)37 with a cutoff value of 0.90 was calculated for informativeness measurement. The Friedman test and pairwise Wilcoxon signed-rank test were used to compare the magnitude of the influence of different acquisition and reconstruction parameters. The Spearman rank correlation coefficient was used to analyze the consistency of the influencing patterns of different sources of variability. Hierarchical clustering based on Euclidean distance was used to eliminate redundant RFs, and in each cluster, the RF with the largest DR was selected as the representative RF.
For clinical validation, the Wilcoxon rank-sum test was used to explore the discriminative effectiveness of the representative RFs. The least absolute shrinkage and selection operator (LASSO) and logistic regression were used to establish prediction models for pathological diagnosis. Receiver operating characteristic analysis was also conducted, and the area under the curve (AUC) values were compared with the Delong test. A P value less than 0.05 was considered to indicate a statistically significant difference. Multiple tests were corrected using the false discovery rate (FDR) method. All statistical analyses were performed using R software (version 4.0.3; R Foundation for Statistical Computing, Vienna, Austria).
RESULTS
The Variability of RFs
The CCC, DR, and ICC for the 3 sources of variability were calculated to quantify the robustness and informativeness of each RF (Fig. 3A). For the test-retest variability, the ratio of repeatable RFs was 20.93% (271/1295; CCC, 0.56 ± 0.31), and the ratio of informative RFs was 20.39% (264/1295; DR, 0.83 ± 0.08). For inter-CT variability, the ratio of reproducible RFs was 20.54% (266/1295, ICC: 0.46 ± 0.30). For intra-CT protocol variability, different CT acquisition and reconstruction parameters showed different magnitudes of influence (Table 3).
FIGURE 3.
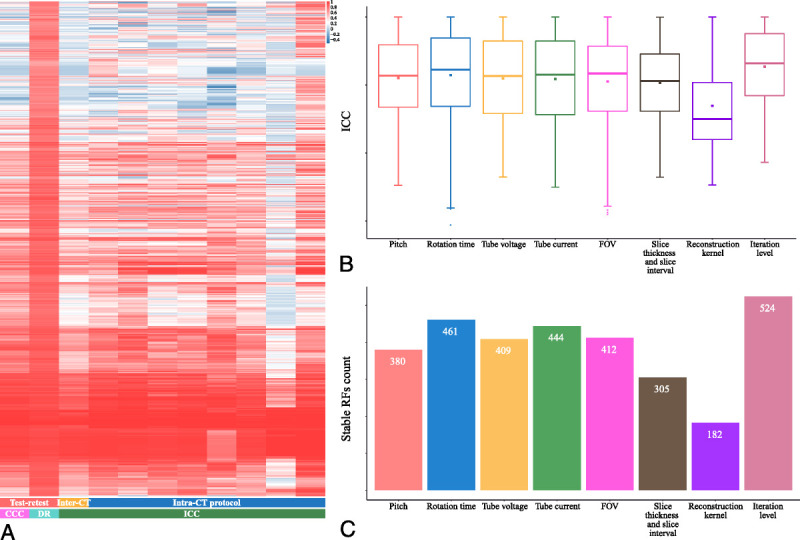
A, Overview of the variability of RFs. Each row is one RF; each column is one variability measurement from one trial. Unsupervised clustering of RFs was used on the y axis. Of the intra-CT protocol trial, from left to right, followed by pitch, rotation time, tube voltage, tube current, FOV, slice thickness and slice interval, reconstruction kernel, and iteration level. Boxplot (B) of the ICC values and bar graph (C) of the stable RF count under varying CT acquisition and reconstruction parameters.
TABLE 3.
Robustness Measurement Results of Each Trial
| Trial | Measurement | Value* | Ratio† |
|---|---|---|---|
| Test-retest | CCC | 0.56 ± 0.31 | 271/1295 (20.93%) |
| Test-retest | DR | 0.83 ± 0.08 | 264/1295 (20.39%) |
| Inter-CT | ICC | 0.46 ± 0.30 | 266/1295 (20.54%) |
| Pitch (intra-CT protocol) | ICC | 0.55 ± 0.30 | 380/1295 (29.34%) |
| Rotation time (intra-CT protocol) | ICC | 0.57 ± 0.32 | 461/1295 (35.60%) |
| Tube voltage (intra-CT protocol) | ICC | 0.55 ± 0.30 | 409/1295 (31.58%) |
| Tube current (intra-CT protocol) | ICC | 0.54 ± 0.32 | 444/1295 (34.29%) |
| FOV (intra-CT protocol) | ICC | 0.53 ± 0.33 | 412/1295 (31.81%) |
| Slice thickness and slice interval (intra-CT protocol) | ICC | 0.52 ± 0.29 | 305/1295 (23.55%) |
| Reconstruction kernel (intra-CT protocol) | ICC | 0.35 ± 0.31 | 182/1295 (14.05%) |
| Iteration level (intra-CT protocol) | ICC | 0.63 ± 0.27 | 524/1295 (40.46%) |
* Data are provided as mean ± SD.
† Data are expressed as numerator/denominator (percentage). The cutoff values were 0.85, 0.90, and 0.75 for CCC, DR, and ICC, respectively.
CCC indicates concordance correlation coefficient; CT, compute tomography; DR, dynamic range; FOV, field of view; ICC, intraclass correlation coefficient.
The Influencing Magnitudes of CT Acquisition and Reconstruction Parameters
For different CT acquisition and reconstruction parameters, their influencing magnitudes showed statistically significant differences (FDR < 0.001, Friedman test). Using the pairwise Wilcoxon signed-rank test (see Table S3, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the results of the pairwise comparison), the influencing magnitudes were ranked: the reconstruction kernel showed the greatest influence with lower ICC and fewer reproducible RFs (ICC, 0.35 ± 0.31, 182/1295, 14.05%), the second was the slice thickness and slice interval (ICC, 0.52 ± 0.29, 305/1295, 23.55%), the third was the FOV (ICC, 0.53 ± 0.33, 412/1295, 31.81%), the fourth were the pitch (ICC, 0.55 ± 0.30, 380/1295, 29.34%), tube current (ICC, 0.54 ± 0.32, 444/1295, 34.29%), and tube voltage (ICC, 0.55 ± 0.30, 409/1295, 31.58%), the fifth was the rotation time (ICC, 0.57 ± 0.32, 461/1295, 35.60%), and the iteration level showed the least influence on the reproducibility of RFs with higher ICC and more reproducible RFs (ICC, 0.63 ± 0.27, 524/1295, 40.46%) (Figs. 3B, C).
The Influencing Patterns of Different Sources of Variability
The influencing patterns were analyzed using Spearman rank correlation coefficients calculated with CCC or ICC values of each RF from each pair of sources of variability. The higher the Spearman rank correlation coefficient, the more consistent the influencing patterns of the 2 sources of variability, which meant that the RFs that were more stable under 1 of the 2 sources of variability (ICC ranked higher in all RFs) were more likely to be stable under the other source of variability. The Spearman rank correlation coefficient matrix (Fig. 4A) showed that the influencing patterns of all sources of variability were positively correlated with each other with statistical significance (FDR < 0.001; see Table S4, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the FDR values of the Spearman rank correlation coefficients). Overall, all sources of variability showed relatively consistent influencing patterns on RFs (all blue in Fig. 4A), with the reconstruction kernel and the iterative level differing more from the others (2 lighter blue columns in Fig. 4A). Among them, the tube voltage and tube current showed the most consistent influencing patterns (ρ = 0.93, FDR < 0.001) with the ICC ranking distribution near the 45-degree diagonal (Fig. 4B). The RFs with higher ICC values under varying tube voltage settings tended to show higher ICC values under varying tube current settings, and vice versa. However, the FOV and reconstruction kernel showed the most inconsistent influencing patterns (ρ = 0.56, FDR < 0.001) with a scattered ICC ranking distribution (Fig. 4C). The RFs with higher ICC under varying FOV settings did not necessarily show a higher ICC under varying reconstruction kernel settings.
FIGURE 4.

A, Spearman rank correlation coefficient matrix of the influencing patterns of all sources of variability. B, Scatterplot of the ICC rankings under varying tube voltage and tube current settings. Each point corresponds to an RF, and the horizontal and vertical coordinates are the ICC rankings under the corresponding source of variability. Different colors correspond to the filter to which the RF belongs. C, Scatterplot of the ICC rankings under varying FOV and reconstruction kernel settings.
A Subset of Representative Robust RFs
Stable and informative RFs from each source of variability were selected. Their intersection yielded 124 RFs that showed stability and greater informativeness under all sources of variability (Fig. 5). The total intersection consisted of original RFs (9/124, 7.26%), wavelet-filtered RFs (22/124, 17.74%), square-filtered RFs (13/124, 10.48%), square-root-filtered RFs (10/124, 8.06%), logarithm-filtered RFs (8/124, 6.45%), exponential-filtered RFs (29/124, 23.39%), and local binary pattern–filtered RFs (24/124, 19.35%) (Fig. 5C). Hierarchical clustering was then used to remove redundancies in the above 124 RFs (see Fig. S2, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the dendrogram showing the progression of the hierarchical clustering). Nineteen RFs with the largest DRs in each cluster were selected as representative RFs (Table 4; see Table S5, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the robustness measurement results of the 19 representative RFs). These included 2 original RFs, 3 wavelet-filtered RFs, 5 square-filtered RFs, 2 square-root-filtered RFs, 2 logarithm-filtered RFs, 4 exponential-filtered RFs, and 1 local binary pattern-filtered RF. In addition, the subset contained 12 first-order RFs and 7 texture RFs. The scatterplot (Fig. 6A) showed that the wavelet-LLL-filtered root mean squared as one of the representative RFs was concentrated and nonoverlapping in the 9 simulated nodules and could distinguish different nodules. Meanwhile, the wavelet-HLH-filtered informational measure of correlation2 as a representative of unstable RFs was scattered and overlapped with each other in the 9 simulated nodules and could hardly distinguish different nodules (Fig. 6B). The corresponding Bland-Altman plot (Figs. 6C, D) based on data from the test-retest trial also showed that in comparison with the unstable wavelet-HLH-filtered informational measure of correlation2, the mean difference line (solid blue line) of the stable wavelet-LLL-filtered root mean squared was relatively closer to zero (solid red line), with a narrower 95% confidence interval (CI) (dashed blue line). Thus, we obtained a stable, informative, and nonredundant subset of RFs.
FIGURE 5.
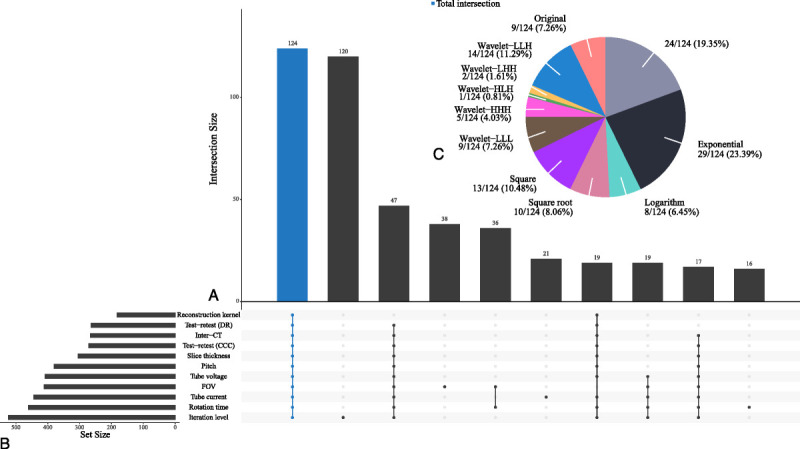
A, Venn diagram. Each bar in the bar graph represents the number of RFs that are stable in the groups corresponding to the bottom bright spot and unstable in the others. B, Bar graph of stable RF counts in each group. C, Pie chart of the composition of the total intersection. The number is expressed as the group quantity/total quantity (percentage).
TABLE 4.
19 Representative RFs
| Filter | Representative RF |
|---|---|
| Original | Energy Mean |
| Wavelet-LLH | wavelet.LLH_original_firstorder_90Percentile wavelet.LLH_original_firstorder_Range |
| Wavelet-LLL | wavelet.LLL_original_firstorder_RootMeanSquared |
| Square | square_original_firstorder_Energy square_original_firstorder_Median square_original_gldm_GrayLevelNonUniformity square_original_gldm_LargeDependenceLowGrayLevelEmphasis square_original_glrlm_LongRunLowGrayLevelEmphasis |
| Square root | squareroot_original_firstorder_Energy squareroot_original_glrlm_GrayLevelNonUniformity |
| Logarithm | logarithm_original_firstorder_Entropy logarithm_original_glcm_Imc2 |
| Exponential | exponential_original_firstorder_Maximum exponential_original_firstorder_Minimum exponential_original_glrlm_RunEntropy exponential_original_glrlm_RunLengthNonUniformityNormalized |
| Local binary pattern | lbp.2D_original_firstorder_Energy |
RF indicates radiomic feature.
FIGURE 6.
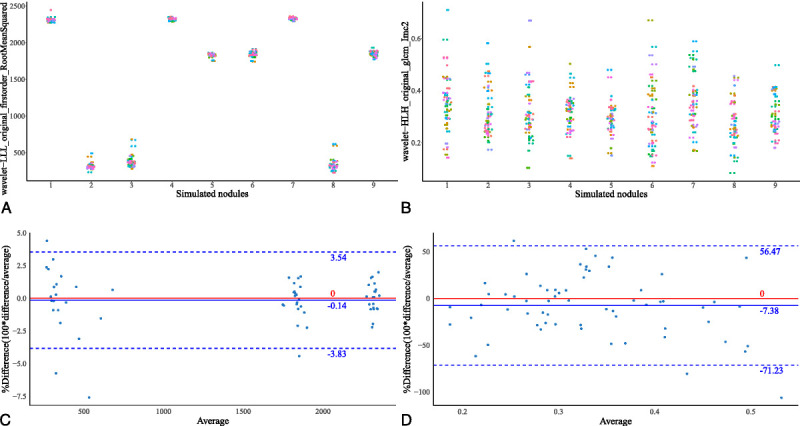
Scatterplots of wavelet-LLL-filtered root mean squared (A) and wavelet-HLH-filtered informational measure of correlation2 (B) in 9 simulated nodules: nodule 1: −800 HU, 8 mm; nodule 2: 100 HU, 12 mm; nodule 3: 100 HU, 8 mm; nodule 4: −800 HU, 12 mm; nodule 5: −630 HU, 12 mm; nodule 6: −630 HU, 8 mm; nodule 7: −800 HU, 10 mm; nodule 8: 100 HU, 10 mm; nodule 9: −630 HU, 10 mm (CT attenuation value, diameter). Bland-Altman plots of wavelet-LLL-filtered root mean squared (C) and wavelet-HLH-filtered informational measure of correlation2 (D). HU, Hounsfield units.
Clinical Validation
Clinical Effectiveness of the Representative Subset
To verify the clinical effectiveness of the 19 representative robust RFs, their correlations with pathological diagnosis and 8 CT semantic features were analyzed (Fig. 7). For the pathological diagnosis, 16 of 19 RFs showed statistically significant differences when differentiating invasive adenocarcinoma (IAC) from adenocarcinoma in situ (AIS) and minimally invasive adenocarcinoma (MIA) (FDR < 0.05, Wilcoxon rank-sum test; see Table S6, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the results of differential analysis), with the highest AUC reaching 0.722 (95% CI, 0.664-0.780; see Table S7, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the AUC values of 19 representative RFs in pathological diagnosis and semantic features). For each of the 8 CT semantic features, at least 3 RFs of the subset showed statistically significant differences between the groups. When the mean value was used to distinguish the type of nodule, we obtained the highest AUC (AUC, 0.845; 95% CI, 0.801-0.889; see Table S7, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the AUC values of 19 representative RFs in pathological diagnosis and semantic features). Among the 8 semantic features, the RFs showed better performance in distinguishing the type of nodule, spiculation, lobulation, bubblelike appearance, pulmonary vascular change, and pleural indentation (columns with more asterisks in Fig. 7) than the tumor-lung interface and air bronchogram (columns with fewer asterisks in Fig. 7).
FIGURE 7.
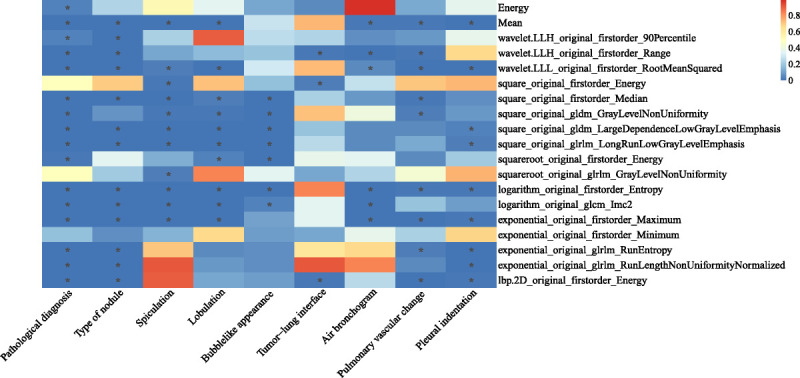
FDR matrix of the differential analysis results of 19 representative RFs in the pathological diagnosis and 8 CT semantic features of the clinical dataset. The asterisk in the cell represents FDR <0.05.
Enhancement of the Generalizability of the Representative Subset
To validate the effects of our stability results on generalizability, we trained 2 logistic regression models for differentiating IAC from AIS and MIA with 1171 unstable RFs (excluding the intersection of 124 RFs from a total of 1295 RFs) and the 19 representative RFs separately. Because of their large number, the 1171 unstable RFs were selected by LASSO (see Fig. S3, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the RF selection process with the LASSO regression model) to obtain the optimal RFs to establish an “unstable model” with logistic regression (see Table S8, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the coefficients of the “unstable model”). As for the 19 representative RFs, logistic regression was directly used for establishment of the “stable model” (see Table S9, Supplemental Digital Content, http://links.lww.com/RLI/A653, which demonstrates the coefficients of the “stable model”). A comparison of the Receiver operating characteristics of the 2 models showed different results for the different datasets. The “unstable model” outperformed the “stable model” in the training dataset (Fig. 8A; see Figs. S4A, B, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the predicted risk scores of the 2 models in the training dataset) and the testing dataset (Fig. 8B; see Figs. S4C, D, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the predicted risk scores of the 2 models in the testing dataset) without statistical significance. However, the “stable model” outperformed the “unstable model” in the validation dataset (Fig. 8C; see Figs. S4E, F, Supplemental Digital Content, http://links.lww.com/RLI/A653, which illustrates the predicted risk scores of the 2 models in the validation dataset) with statistical significance (P = 0.017, Delong test; AUC for the “unstable model,” 0.548, 95% CI, 0.414-0.683; AUC for the “stable model,” 0.723, 95% CI, 0.604-0.843).
FIGURE 8.
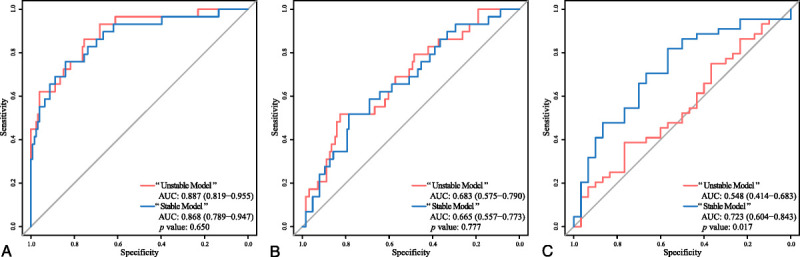
ROC curves of the “unstable model” and the “stable model” in the training dataset (A), the testing dataset (B), and the validation dataset (C). ROC, receiver operating characteristic; AUC, area under curve.
DISCUSSION
Radiomics can obtain massive, quantitative, and minable information from medical images such as CT scans,38 which can facilitate precision medicine.39 However, the lack of repeatability and reproducibility of RFs may hinder their generalizability in clinical applications.40 We designed a multicenter phantom study to explore the 3 main sources of variability in radiomics in simulated clinical scenarios. The results showed that test-retest scenarios, differences in CT manufacturers and models, and differences in CT acquisition and reconstruction parameters cause different degrees of variability in RFs. Among them, the reconstruction kernel, slice thickness, slice interval, and FOV showed greater influence than the other sources. Nevertheless, the influencing patterns of the above sources of variability were positively correlated. Subsequently, by performing intersection and hierarchical clustering, we obtained a subset of stable, informative, and nonredundant RFs with clinical discriminant power. This subset of representative RFs was also proven to have the potential to enhance the generalizability of radiomics research.
The test-retest trial showed a lower level of repeatability than other studies.18,37,41 Berenguer et al18 showed a repeatability ratio of 91% (161/177 RFs) in the test-retest analysis. Balagurunathan et al37 found that 30.14% (66/219) of RFs showed good CCC and acceptable DR. Mahon et al41 found that 54.4% (for tumors) and 78.5% (for normal tissues) of 59 texture features were considered repeatable. The possible reasons for our lower level of repeatability might be the inclusion of more CT manufacturers and models in our study, the longer test-retest time interval than that in previous studies,37 and the greater number of RFs analyzed in our study. Moreover, in the test-retest trial, we only performed the repetition twice on different days while trying to capture all the variabilities that could happen in a test-retest situation at once. Adding repetition time may have helped us obtain a more solid result for the average repeatability at different time intervals with or without position changes. The same reasons could also explain the lower level of reproducibility in the inter-CT trial.18
For the intra-CT protocol trial, we quantified and compared the magnitude of influence of different CT acquisition and reconstruction parameters and obtained their influence magnitude rankings. We found that the reconstruction kernel, slice thickness, slice interval, and FOV had a greater influence on the reproducibility of RFs, where slice thickness, slice interval, and FOV contributed to voxel size. Ultimately, it was the reconstruction kernel and the voxel size that had a major influence, which was consistent with the findings of previous studies.16,19,28,29,42 This result could provide a reference for subsequent multicenter radiomics research and also facilitate the establishment of a standard CT acquisition procedure for radiomics research. Uniform setting of the reconstruction kernel and voxel size has been recommended to receive more attention, whereas uniform setting of other parameters can be slightly relaxed when strict standardization could not be implemented. However, we did not include the reconstruction method in the intra-CT protocol trial. Because reconstruction parameters such as reconstruction kernel showed a greater influence on RFs, the impact of the reconstruction method on RFs needs further investigation.
On the basis of the positive relationship of influencing patterns between sources of variability, we confirmed that the stability results from different sources of variability could be generalized. Even though only limited sources of variability were included in our study, our subset of representative RFs had the potential to be extended to more sources of variability that had not been included in this study or had not yet been found.
While the subset of representative RFs showed stability under all sources of variability, they also showed clinical effectiveness with statistical significance in differentiating pathological diagnosis and predicting the appearance of CT semantic features. We further compared the performances of the representative RFs and unstable RFs on the clinical dataset in distinguishing IAC from AIS and MIA. Although the “unstable model” showed higher AUC values than the “stable model” in the training and testing dataset, the “stable model” beat the “unstable model” with statistical significance in the validation dataset, which shared no overlapping CT scanners with the training and testing datasets. However, both of them performed poorly in the validation dataset, which may have been caused by the elimination of morphological RFs in our results in the first place. In addition, the main reason for the decrease in the “unstable model” may be the different distribution of AIS, MIA, and IAC in the training dataset and the validation dataset. The better generalization of the “stable model” indicated that better generalization of radiomics research might be achieved with the preferred usage of our subset of representative RFs.
This study had several advantages. First, as a multicenter prospective study, we included almost all mainstream CT manufacturers in China (GE, Philips, Siemens, Toshiba, Hitachi, and United Imaging Healthcare) and analyzed both their test-retest and inter-CT variability. Second, we studied most of the acquisition and reconstruction parameters encountered in the daily CT acquisition procedure according to their actual clinical adjustment ranges and obtained their influence rankings. With these 2 efforts, we simulated realistic clinical CT acquisition scenarios, which can improve the clinical transformation capability of our results and enhance their guiding value for subsequent radiomics research. Third, we included as many RFs as possible, including first-order RFs, texture RFs, and filtered RFs, to determine more stable RFs. Fourth, by comparison of influencing patterns, the generalization of our stable RFs to a wider range of influencing factors was verified. Last, but most importantly, we not only obtained a subset of representative RFs with clinical effectiveness but also validated their enhancement for the generalizability of radiomics research.
This study also had some limitations. First, to eliminate the influence of segmentation, we adopted 2D square segmentation and strictly limited it to the interior of the simulated nodules according to the results of previous studies.11 Second, our phantom lacked lung parenchyma and our simulated nodules were all pure with limited CT attenuation values and sizes, and their position might change slightly during phantom movement, which might have had an unknown impact. Third, because all CT scanners are currently in clinical use in hospitals and the test time was limited, the study of CT acquisition and reconstruction parameters was performed on only 1 CT scanner. Fourth, the limited number of repetitions in the test-retest trial may hinder the reliability of our repeatability results. Fifth, as morphological RFs were eliminated in the first place in our study, their repeatability and reproducibility required further study. Lastly, although we validated our results in a clinical cancer dataset, the generalizability of our study to other lung diseases remains unknown.
Recent phantom studies on radiomics robustness have often used the Credence Cartridge Radiomics phantom,16,17 chest phantom N-1 LUNGMAN,26,27 and the NEMA image quality phantom.43,44 We chose the chest phantom N-1 LUNGMAN to simulate the real lung CT image as possible. However, because the phantom lacked lung parenchyma, a gap still exists between our phantom images and real patient images. For further study of radiomics robustness, phantoms are needed to achieve better simulation of patient lung images, especially better simulation of lung nodules not only on attenuation values and diameters but also on texture and shape. Although only spherical nodules were used in our study, the same phantom manufacturer also offers spiculated, lobulated, and subsolid nodules, which could help in the investigation of morphological RFs in future studies. However, the lack of lung parenchyma remains a question. To the best of our knowledge, 3D-printed phantoms45–47 for lung radiomics may be a solution because they could reproduce an individual patient's CT images with high precision of anatomic details and radiation attenuation properties.
In conclusion, this study evaluated the 3 main sources of variability in RFs: test-retest, CT manufacturers and models, and CT acquisition and reconstruction parameters. We obtained an influence ranking of acquisition and reconstruction parameters and proved the consistency of the influence patterns of sources of variability. We also obtained a subset of stable, informative, and nonredundant RFs with clinical effectiveness that could potentially enhance the generalizability of radiomics research. For retrospective research, we suggest the preferred use of the representative subset to enhance generalizability and clinical transformation ability. The inclusion criteria for robust RFs could be relaxed or other unstable RFs could be included after these RFs are included. For prospective research, on the basis of the influence rankings, we suggested that acquisition and reconstruction parameters with greater influences need stricter control in subsequent studies and more urgent standardization in the ongoing establishment of standard processes in radiomics research.22
Supplementary Material
ACKNOWLEDGMENTS
The authors thank the Medical Research Data Center of Fudan University for their support in computational power. The authors also thank Chaoyu Zhu, Yunhe Liu, and Yunpeng Wang for their assistance in acquiring the CT scans of the phantom and their helpful comments. The authors would like to thank Editage (www.editage.com) for English language editing.
Footnotes
Xueqing Peng and Shuyi Yang contributed equally to this work.
Funding information: Supported by the National Natural Science Foundation of China (#91846302), Shanghai Committee of Science and Technology, China (grant no. 18511102704), National Key Research and Development Program of China (grant nos. 2018YFC0910700 and 2016YFB0201702), Shanghai Municipal Commission of Health and Family Planning, China (grant no. 2018ZHYL0104), National Natural Science Foundation of China (General Program) (grant no. 82172030), Ningbo Medical Science and Technology Project, China (grant no. 2018A14), and Clinical Research Plan of SHDC, China (grant no. SHDC2020CR3080B).
Conflicts of interest and sources of funding: none declared.
Supplemental digital contents are available for this article. Direct URL citations appear in the printed text and are provided in the HTML and PDF versions of this article on the journal’s Web site (www.investigativeradiology.com).
Contributor Information
Xueqing Peng, Email: 18111510058@fudan.edu.cn.
Shuyi Yang, Email: yangsyyx0914@163.com.
Lingxiao Zhou, Email: lingxiaoz@szu.edu.cn.
Yu Mei, Email: mei9501@163.com.
Lili Shi, Email: lilishi8668@163.com.
Rengyin Zhang, Email: zhangrengyin@shphc.org.cn.
Fei Shan, Email: shanfei_2901@163.com.
REFERENCES
- 1.Gillies RJ, Kinahan PE, Hricak H. Radiomics: images are more than pictures, they are data. Radiology. 2016;278:563–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Segal E Sirlin CB Ooi C, et al. Decoding global gene expression programs in liver cancer by noninvasive imaging. Nat Biotechnol. 2007;25:675–680. [DOI] [PubMed] [Google Scholar]
- 3.Diehn M Nardini C Wang DS, et al. Identification of noninvasive imaging surrogates for brain tumor gene-expression modules. Proc Natl Acad Sci U S A. 2008;105:5213–5218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Grossmann P Stringfield O El-Hachem N, et al. Defining the biological basis of radiomic phenotypes in lung cancer. Elife. 2017;6:e23421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bi WL Hosny A Schabath MB, et al. Artificial intelligence in cancer imaging: clinical challenges and applications. CA Cancer J Clin. 2019;69:127–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lambin P Leijenaar RTH Deist TM, et al. Radiomics: the bridge between medical imaging and personalized medicine. Nat Rev Clin Oncol. 2017;14:749–762. [DOI] [PubMed] [Google Scholar]
- 7.Aerts HJ. The potential of radiomic-based phenotyping in precision medicine: a review. JAMA Oncol. 2016;2:1636–1642. [DOI] [PubMed] [Google Scholar]
- 8.Hawkins S Wang H Liu Y, et al. Predicting malignant nodules from screening CT scans. J Thorac Oncol. 2016;11:2120–2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Drukker K Giger ML Joe BN, et al. Combined benefit of quantitative three-compartment breast image analysis and mammography radiomics in the classification of breast masses in a clinical data set. Radiology. 2019;290:621–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhao W Yang J Sun Y, et al. 3D deep learning from CT scans predicts tumor invasiveness of subcentimeter pulmonary adenocarcinomas. Cancer Res. 2018;78:6881–6889. [DOI] [PubMed] [Google Scholar]
- 11.Lu H Arshad M Thornton A, et al. A mathematical-descriptor of tumor-mesoscopic-structure from computed-tomography images annotates prognostic- and molecular-phenotypes of epithelial ovarian cancer. Nat Commun. 2019;10:764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang Y Liu Z He L, et al. Radiomics signature: a potential biomarker for the prediction of disease-free survival in early-stage (I or II) non–small cell lung cancer. Radiology. 2016;281:947–957. [DOI] [PubMed] [Google Scholar]
- 13.Hosny A Parmar C Coroller TP, et al. Deep learning for lung cancer prognostication: a retrospective multi-cohort radiomics study. PLoS Med. 2018;15:e1002711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fornacon-Wood I Faivre-Finn C O'Connor JPB, et al. Radiomics as a personalized medicine tool in lung cancer: Separating the hope from the hype. Lung Cancer. 2020;146:197–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van Timmeren JE Cester D Tanadini-Lang S, et al. Radiomics in medical imaging—“how-to” guide and critical reflection. Insights Imaging. 2020;11:91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mackin D Ger R Gay S, et al. Matching and homogenizing convolution kernels for quantitative studies in computed tomography. Invest Radiol. 2019;54:288–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mackin D Fave X Zhang L, et al. Measuring computed tomography scanner variability of radiomics features. Invest Radiol. 2015;50:757–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Berenguer R Pastor-Juan MDR Canales-Vazquez J, et al. Radiomics of CT features may be nonreproducible and redundant: influence of CT acquisition parameters. Radiology. 2018;288:407–415. [DOI] [PubMed] [Google Scholar]
- 19.Orlhac F Frouin F Nioche C, et al. Validation of a method to compensate multicenter effects affecting CT radiomics. Radiology. 2019;291:53–59. [DOI] [PubMed] [Google Scholar]
- 20.Solomon J Mileto A Nelson RC, et al. Quantitative features of liver lesions, lung nodules, and renal stones at multi-detector row CT examinations: dependency on radiation dose and reconstruction algorithm. Radiology. 2016;279:185–194. [DOI] [PubMed] [Google Scholar]
- 21.Gu J Zhu J Qiu Q, et al. The feasibility study of megavoltage computed tomographic (MVCT) image for texture feature analysis. Front Oncol. 2018;8:586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zwanenburg A Vallieres M Abdalah MA, et al. The image biomarker standardization initiative: standardized quantitative radiomics for high-throughput image-based phenotyping. Radiology. 2020;295:328–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Orlhac F Boughdad S Philippe C, et al. A postreconstruction harmonization method for multicenter radiomic studies in PET. J Nucl Med. 2018;59:1321–1328. [DOI] [PubMed] [Google Scholar]
- 24.O'Connor JP Aboagye EO Adams JE, et al. Imaging biomarker roadmap for cancer studies. Nat Rev Clin Oncol. 2017;14:169–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Traverso A Wee L Dekker A, et al. Repeatability and reproducibility of radiomic features: a systematic review. Int J Radiat Oncol Biol Phys. 2018;102:1143–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xie X Zhao Y Snijder RA, et al. Sensitivity and accuracy of volumetry of pulmonary nodules on low-dose 16- and 64-row multi-detector CT: an anthropomorphic phantom study. Eur Radiol. 2013;23:139–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhao B Tan Y Tsai WY, et al. Exploring variability in CT characterization of tumors: a preliminary phantom study. Transl Oncol. 2014;7:88–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kim YJ Lee HJ Kim KG, et al. The effect of CT scan parameters on the measurement of CT radiomic features: a lung nodule phantom study. Comput Math Methods Med. 2019;2019:8790694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Prayer F Hofmanninger J Weber M, et al. Variability of computed tomography radiomics features of fibrosing interstitial lung disease: a test-retest study. Methods. 2021;188:98–104. [DOI] [PubMed] [Google Scholar]
- 30.van Griethuysen JJM Fedorov A Parmar C, et al. Computational radiomics system to decode the radiographic phenotype. Cancer Res. 2017;77:e104–e107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shi L Shi W Peng X, et al. Development and validation a nomogram incorporating CT radiomics signatures and radiological features for differentiating invasive adenocarcinoma from adenocarcinoma in situ and minimally invasive adenocarcinoma presenting as ground-glass nodules measuring 5-10 mm in diameter. Front Oncol. 2021;11:618677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhan Y Peng X Shan F, et al. Attenuation and morphologic characteristics distinguishing a ground-glass nodule measuring 5-10 mm in diameter as invasive lung adenocarcinoma on thin-slice CT. AJR Am J Roentgenol. 2019;213:W162–W170. [DOI] [PubMed] [Google Scholar]
- 33.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–268. [PubMed] [Google Scholar]
- 34.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. [DOI] [PubMed] [Google Scholar]
- 35.McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychol Methods. 1996;1:30–46. [Google Scholar]
- 36.Koo TK, Li MY. A Guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med. 2016;15:155–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Balagurunathan Y Kumar V Gu Y, et al. Test-retest reproducibility analysis of lung CT image features. J Digit Imaging. 2014;27:805–823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wildberger JE, Prokop M. Hounsfield's legacy. Invest Radiol. 2020;55:556–558. [DOI] [PubMed] [Google Scholar]
- 39.Makowski MR Bressem KK Franz L, et al. De novo radiomics approach using image augmentation and features from T1 mapping to predict Gleason scores in prostate cancer. Invest Radiol. 2021;56:661–668. [DOI] [PubMed] [Google Scholar]
- 40.Hagiwara A Fujita S Ohno Y, et al. Variability and standardization of quantitative imaging: monoparametric to multiparametric quantification, radiomics, and artificial intelligence. Invest Radiol. 2020;55:601–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mahon RN, Hugo GD, Weiss E. Repeatability of texture features derived from magnetic resonance and computed tomography imaging and use in predictive models for non–small cell lung cancer outcome [published online ahead of print April 12, 2019]. Phys Med Biol. [DOI] [PubMed] [Google Scholar]
- 42.Mackin D Fave X Zhang L, et al. Harmonizing the pixel size in retrospective computed tomography radiomics studies. PLoS One. 2017;12:e0178524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Papp L Rausch I Grahovac M, et al. Optimized feature extraction for radiomics analysis of (18)F-FDG PET imaging. J Nucl Med. 2019;60:864–872. [DOI] [PubMed] [Google Scholar]
- 44.Pfaehler E Beukinga RJ de Jong JR, et al. Repeatability of 18 F-FDG PET radiomic features: a phantom study to explore sensitivity to image reconstruction settings, noise, and delineation method. Med Phys. 2019;46:665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Muenzfeld H Nowak C Riedlberger S, et al. Intra-scanner repeatability of quantitative imaging features in a 3D printed semi-anthropomorphic CT phantom. Eur J Radiol. 2021;141:109818. [DOI] [PubMed] [Google Scholar]
- 46.Jimenez-Del-Toro O Aberle C Bach M, et al. The discriminative power and stability of radiomics features with computed tomography variations: task-based analysis in an anthropomorphic 3D-printed CT phantom [published online ahead of print May 14, 2021]. Invest Radiol. [DOI] [PubMed] [Google Scholar]
- 47.Jahnke P Limberg FR Gerbl A, et al. Radiopaque three-dimensional printing: a method to create realistic CT phantoms. Radiology. 2017;282:569–575. [DOI] [PubMed] [Google Scholar]


