Abstract
Objective:
Neuromodulation of visceral nerves is being intensively studied for treating a wide range of conditions, but effective translation requires increasing the efficacy and predictability of neural interface performance. Here we use computational models of rat visceral nerve to predict how neuroanatomical variability could affect both electrical stimulation and recording with an experimental planar neural interface.
Approach:
We developed a hybrid computational pipeline, Visceral Nerve Ensemble Recording & Stimulation (ViNERS), to couple finite-element modelling of extracellular electrical fields with biophysical simulations of individual axons. Anatomical properties of fascicles and axons in rat pelvic and vagus nerves were measured or obtained from public datasets. To validate ViNERS, we simulated pelvic nerve stimulation and recording with an experimental four-electrode planar array.
Main results:
Axon diameters measured from pelvic nerve were used to model a population of myelinated and unmyelinated axons and simulate recordings of electrically evoked single-unit field potentials (SUFPs). Across visceral nerve fascicles of increasing size, our simulations predicted an increase in stimulation threshold and a decrease in SUFP amplitude. Simulated threshold changes were dominated by changes in perineurium thickness, which correlates with fascicle diameter. We also demonstrated that ViNERS could simulate recordings of electrically-evoked compound action potentials (ECAPs) that were qualitatively similar to pelvic nerve recording made with the array used for simulation.
Significance:
We introduce ViNERS as a new open-source computational tool for modelling large-scale stimulation and recording from visceral nerves. ViNERS predicts how neuroanatomical variation in rat pelvic nerve affects stimulation and recording with an experimental planar electrode array. We show ViNERS can simulate ECAPS that capture features of our recordings, but our results suggest the underlying NEURON models need to be further refined and specifically adapted to accurately simulate visceral nerve axons.
Keywords: Computational, Modellings, Stimulations, Recordings, Pelvic Nerve
Introduction
Bioelectronic therapies targeting the peripheral visceral nervous system are now well established for the treatment of lower urinary tract (LUT) disorders (Jaqua and Powell, 2017), and are being investigated for a wide range of other conditions (Horn et al., 2019). However, many promising therapies developed using animal models in preclinical studies fail to translate into the clinic (Byku and Mann, 2016). Contributing factors include suboptimal neural interface design, lack of stimulus specificity, and a ‘one size fits all’ approach to clinical neuromodulation. Computational modelling has been important for accelerating the design of neural interfaces (Sperry et al., 2018; Romeni et al., 2020; Ward et al., 2020a; Larson and Meng, 2020; Leventhal and Durand, 2003), improving our understanding of stimulus specificity (Bucksot et al., 2021; Leventhal and Durand, 2003; Romeni et al., 2020), and understanding how subject-specific variation in nerve anatomy affects peripheral nerve stimulation (Grinberg et al., 2008; Musselman et al., 2021; Pelot et al., 2019). Accordingly, many computational models have been used to study neural interfaces for delivering neuromodulation (e.g. Rattay, 1986; Leventhal and Durand, 2003; Johnson et al., 2007; Grinberg et al., 2008; Grill, 2015; Raspopovic et al., 2017; Gaines et al., 2018; Lubba et al., 2019; Pelot et al., 2019; Gupta et al., 2020; Romeni et al., 2020; Bucksot et al., 2021; Musselman et al., 2021).
The dynamic physiology of the peripheral visceral nervous system can lead to the same stimulus having different effects, depending on factors such as the state of the nerve, the innervated organ, or the relevant central control circuits (Zanos, 2018). In order to help patients engage in dynamic behaviors such as micturition (Payne et al., 2020), the efficacy of neural interfaces applied to visceral nerves may be improved by recording neural activity to control delivery of neuromodulation (Bouton and Czura, 2018; Larson and Meng, 2020). An example of such an approach is closed-loop control by monitoring electrically-evoked compound actions potentials (ECAPs) for self-calibration of stimulation parameters, an approach which has been applied extensively in cochlear interfaces (DeVries et al., 2016), the vagus nerve (Ward et al., 2015, 2020a) and spinal cord stimulation (Parker et al., 2017). However, in comparison to the many models of neuromodulation, far fewer models have addressed the problem of optimizing neural recording performance (Struijk, 1997; Karimi and Seydnejad, 2015; Lubba et al., 2019; Smets et al., 2021; Buccino and Einevoll, 2021). Furthermore, the available open source models use significant simplifications of the electrode-nerve interface geometry, such as the assumption of circular symmetry for nerves in cuff electrodes (e.g. Struijk, 1997; Lubba et al., 2019), which limit their predictive power for new devices and neuromodulation targets. The commercial package Sim4Life (Zurich MedTech, Switzerland) has recently introduced capabilities for modelling nerve recording using predefined axon models in addition to the ability to simulate extracellular nerve stimulation, and other commercial simulation platform providers such as COMSOL Multiphysics (COMSOL Inc., Burlington, MA) are following suit.
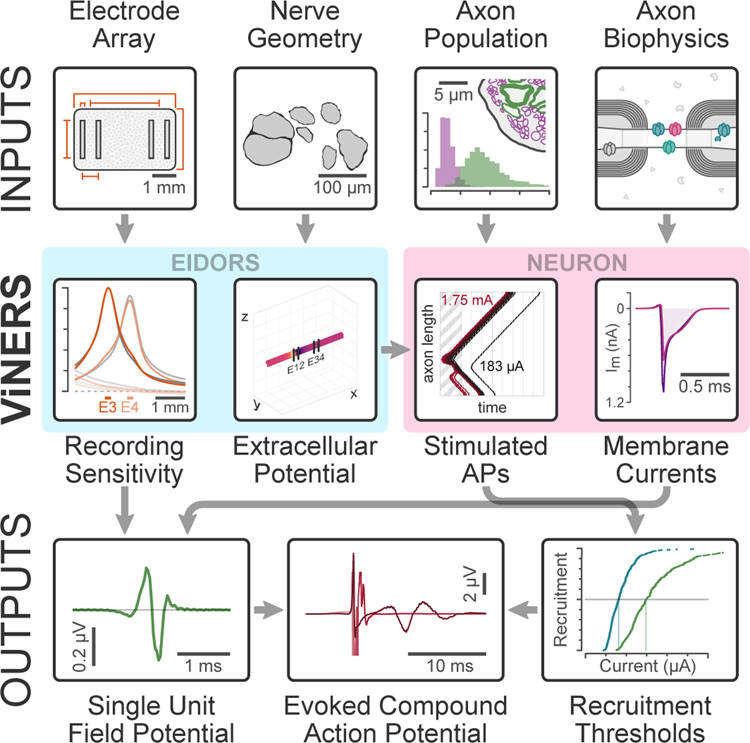
There is an unmet need for a wider range of computational tools that can be used for large-scale modelling of both electrical stimulation and recording with accurate models of neural interfaces on peripheral nerves, and in particular visceral nerves. To address this need, we present Visceral Nerve Ensemble Recording and Stimulation (ViNERS), an automated, open source, MATLAB+NEURON-based pipeline (available at [https://dx.doi.org/10.26275/chfk-eugm]). ViNERS combines multidomain electro-anatomical electric field models and biophysical models of individual myelinated and unmyelinated visceral axons to compute nerve-electrode coupling, electrical stimulation thresholds, action potential firing, and single-unit field potentials (SUFPs). These can be combined to simulate ECAPs and ensemble activity recordings using realistic neural interface and peripheral nerve geometries (Figure 1).
Figure 1. Schematic overview of ViNERS.
This diagram shows the necessary inputs (electrode array design specifications, target nerve anatomy, characteristics of the axon populations comprising the target nerve, and biophysical axon models), intermediate steps (extracellular potentials and sensitivity functions, computed using EIDORS, as well as stimulus-evoked spike-times and axonal membrane current profiles, computed using NEURON), and outputs (single-unit field potentials (SUFPs), simulated evoked compound action potential (ECAP) waveforms, and extracellular stimulus threshold recruitment curves) of ViNERS.
In comparison to peripheral somatic (non-visceral) nerves, much less is known about how variations in anatomy and physiology of peripheral visceral nerves affect the efficacy of therapeutic neuromodulation and neural recording performance with neural interfaces of different designs. Relevant differences in nerves that are candidate therapeutic targets include the predominance of small diameter myelinated (Aδ-fiber) and unmyelinated (C-fiber) axons, representation of spinal cord autonomic preganglionic axons (absent in most somatic nerves) and differences in size and fascicular structure. We used ViNERS to predict how biological variation in the neuroantaomical properties of pelvic and vagus nerves influence recordings of single-unit field potentials (SUFPs) and extracellular stimulation thresholds, based on the typical myelinated and unmyelinated axons and fascicles present in rat pelvic nerve (Hulsebosch and Coggeshall, 1982; Keast, 2006; Bertrand et al., 2020).
To validate ViNERS, we modelled ECAP recordings from the pelvic nerve in awake rats (Payne et al., 2020) using a four-electrode planar electrode array interface. The pelvic nerve is a multi-fasciculated visceral nerve that contains a majority of the primary sensory and autonomic (sacral spinal preganglionic) axons required for controlling lower urinary tract function during storage and voiding (micturition), as well as other important equivalent projections that regulate large intestine and reproductive organs (Hulsebosch and Coggeshall, 1982; Keast, 2006). Bladder pressure and volume may be estimated from recordings of afferent activity in the pelvic (Payne et al., 2020) and pudendal (Wenzel et al., 2006) nerves as well as the connected sacral dorsal root ganglia (Jabbari and Erfanian, 2019; Ouyang et al., 2019). We will demonstrate that for both recording and neuromodulation, neural interface performance depends on the anatomy and electrical properties of the visceral nerve and surrounding tissue, as well as the geometry of the implanted device.
Methods
We conducted a hybrid computational and neuroanatomical study to measure the required inputs (fascicle cross-sectional profiles, obtained with light microscopy, and distributions of axon diameters and g-ratios, obtained with electron microscopy) to simulate electrical stimulation and ensemble recordings of visceral nerve activity. Using ViNERS, we reproduced previous results (Grinberg et al., 2008; Koole et al., 1997; Pelot et al., 2019) regarding the influence of fascicle diameter and perineurium thickness on nerve stimulation and extended those results to predict the influence of these parameters on nerve recording. Finally, to validate ViNERS, we simulated pelvic nerve ECAP responses, which were compared to recordings collected from rat pelvic nerve (Payne et al., 2020).
Animal Studies
Tissue Processing and Microscopy
Procedures were approved by the Animal Ethics Committee of the University of Melbourne, and in compliance with the Australian Code for the Care and Use of Animals for Scientific Purposes (National Health and Medical Research Council of Australia).
For anatomical studies of the pelvic nerve, five male Sprague-Dawley rats (7–8 weeks old) were sourced from the Biomedical Sciences Animal Facility (University of Melbourne) and housed under a 12-hour light-dark cycle, in a temperature-controlled room with ad libitum access to food and water. Animals were anesthetized (100 mg/kg ketamine, 10 mg xylazine i.p. [Lyppard, Keysborough, Australia]) then perfused transcardially with saline (0.9% sodium chloride containing 1% sodium nitrite and 5000 IU/ml heparin [Ellar Laboratories, Tullamarine, Australia]), followed by fixative (2% paraformaldehyde and 1.25% glutaraldehyde [EM grade, Proscitech, Thuringowa, Australia)] in 0.1M phosphate-buffered saline [PBS], pH 7.3) for 15–20 minutes (Keast and Osborne, 2019). Left pelvic ganglia with their attached pelvic nerve were then dissected, postfixed in the same fixative for 18–24h at 4C, washed in PBS (3 × 30 min), imaged under a dissecting microscope then stored in PBS for transportation. Ganglia were couriered to Drs Havton and Biscola at UCLA, for further processing and microscopy. All reagents were obtained from Merck-Millipore (Bayswater, Australia) unless otherwise stated.
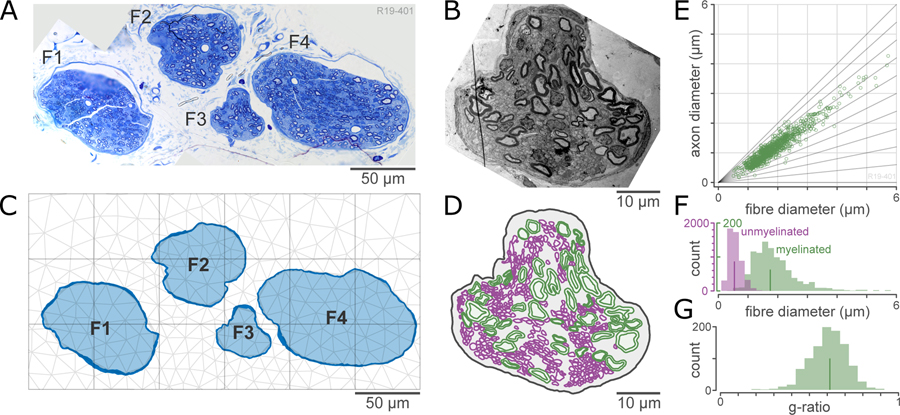
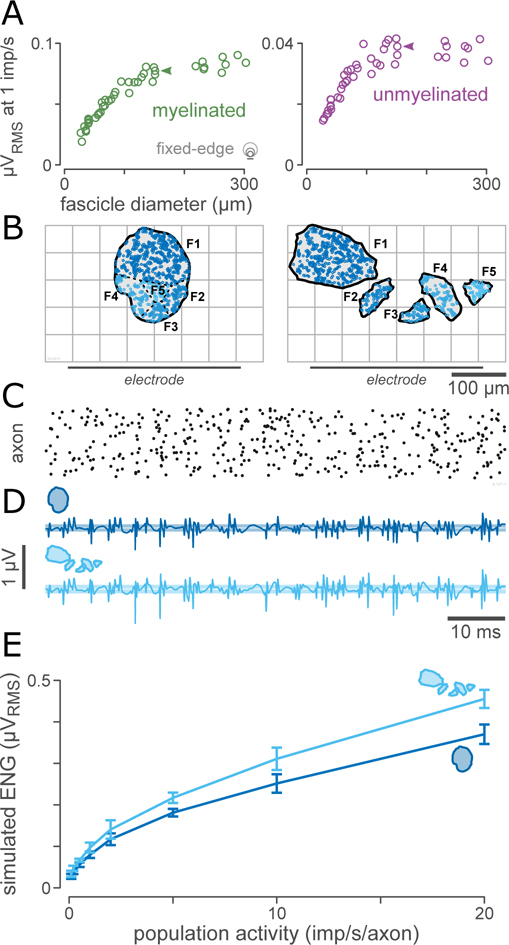
The detailed protocols for embedding and electron microscopy are available online (Biscola and Havton, 2020) In brief, pelvic ganglia with attached pelvic nerve were washed in water (3× 10 min), fixed with 1% osmium solution (1h), washed in water, dehydrated through increasing concentrations of ethanol then propylene oxide, and infiltrated with Epon resin (Ted Pella Inc., Redding, CA, USA). Samples were blocked in the orientation appropriate for obtaining transverse sections of pelvic nerve. Semi-thin sections (0.5 μm) through pelvic nerve were stained with 1% toluidine blue solution (30 seconds), washed in water, dried and cover-slipped with DPX mountant. Images were obtained using a Nikon Eclipse E600 microscope and Nikon camera DS-Fi3. Figure 2(A) shows an example of a micrograph of a pelvic nerve stained with toluidine blue.
Figure 2. Processing of anatomical inputs to ViNERS.
A: Light micrograph of an example pelvic nerve section stained with toluidine blue.
B: Electron micrograph of fascicle #3 of (A), showing myelinated and unmyelinated axon profiles.
C: Tracing of inner and outer perineurium surfaces, used to define fascicles (F1-F4). Dark blue outline shows the traced perineurium and the light blue fill shows the endoneurium. A finite element mesh is superimposed in light grey.
D: Traced axon profiles from the fascicle (F3) shown in (B). Myelinated axons are shown in green and unmyelinated axons are shown in purple.
E: Quantification of the distribution of axon diameters and g-ratios from the sample shown in (A). Scatterplot shows the joint distribution of axon diameter and fiber (axon + myelin) diameter; diagonal lines are lines of constant g-ratio (ratio of axon to fiber diameter).
F: Histogram of the distribution of fiber sizes for myelinated and unmyelinated axons. Lines indicate medians of the distributions (1.75 μm and 0.53 μm for myelinated and unmyelinated axons)
G: Histogram of the distribution of g-ratios for myelinated axons (median 0.64).
Ultrathin sections (70–90 nm) of pelvic nerve (RMC PowerTome Ultramicrotome, Boeckeler Instruments) were collected on formvar-coated single slot grids, and contrasted with uranyl acetate and lead citrate. The sections were analyzed under a transmission electron microscope operating at 80 kV (Tecnai G2 Spirit Twin, FEI, ThermoFisher Scientific). Figure 2(B) shows an example of an electron micrograph of one fascicle of a pelvic nerve.
Microscopy and Image Analysis
For the light micrographs of the pelvic nerve, each fascicle was identified and the inner and outer surfaces of the perineurium were traced in Matlab (R2019b; Mathworks), resulting in a collection of 23 fascicles from 5 animals. For compound fascicles (in which multiple endoneurial compartments are separated by perineurium and enclosed in a common bundle), each sub-fascicle was traced separately. These tracings were saved as vectors in an XML-based neuromorphological file format (Sullivan et al., 2020) to be imported into ViNERS. For the purposes of computing summary statistics, we computed equivalent fascicle diameters, calculated as the diameter of a circle with the same area as the total area of tissues (endoneurium and axons) inside the perineurium (Pelot et al., 2020b). Where a gap was present between the perineurium and endoneurium, this was considered a tissue processing artefact (e.g. due to differential shrinkage of the endoneurium) and this area was included in the measure of the fascicle interior. Perineurium thickness was determined for each fascicle by taking the mean of the distance from each vertex of the polygonal tracing of the outer surface of the perineurium to the nearest point on the inner surface of the perineurium. Figure 2(C) shows an example of a traced set of pelvic nerve fascicles. This dataset was supplemented with a publicly accessible dataset of rat vagus nerve fascicle sections (Pelot et al., 2020b; Pelot, 2021), which contained 9 traced fascicles from 9 animals measured at the cervical level and 13 fascicles from 9 animals measured at the abdominal (subdiaphragmatic) level. These rat vagus nerve sections had been traced in the same way as our pelvic nerve fascicle sections. Fascicle diameter and perineurium thickness measurements were rederived from the traced perineurium and endoneurium outlines to ensure that all samples were analyzed consistently. In total, 45 fascicles from three types of nerves derived from 15 animals were analyzed. These data, including source images, fascicle outlines, and simulation outputs, are available on the sparc.science data portal at [https://dx.doi.org/10.26275/z61u-2tcs].
A representative pelvic nerve (four fascicles) was selected to undergo electron microscopy. For the electron micrographs of the pelvic nerve, the inner and outer surfaces of the myelinated axons and the outer surfaces of the unmyelinated axons were traced in Neurolucida 360, (2019.1.1, MBF biosciences), as shown in Figure 2(D). Axon diameter and myelin thickness were measured using minimum Feret diameters (Bartmeyer et al., 2021), and the g-ratio (ratio of inner to outer axon diameter) was calculated for the myelinated axons. The resulting distributions of diameters and g-ratios are shown in Figure 2(E)–(G). In total, 979 myelinated axons and 5184 unmyelinated axons were measured. Our axon counts are in close agreement with previously published measures of the composition of the pelvic nerve (Hulsebosch and Coggeshall, 1982; Nakayama et al., 1998).
Pelvic Nerve ECAP Recordings
The ECAP data used for this study have been published previously (the ‘Acute Implant’ experimental group from Payne et al., 2020) and were re-analyzed for the present study; therefore, minimum methodological details are supplied here. All animal procedures were approved by the Animal Ethics Committee of St. Vincent’s Hospital (Melbourne), the Bionics Institute, and complied with the Australian Code for the Care and Use of Animals for Scientific Purposes (National Health and Medical Research Council of Australia).
To summarize, five male Sprague-Dawley rats (8–10 weeks old) were anesthetized (urethane 1.2 g/kg s.c., Merck (Sigma-Aldrich, St Louis, MO, United States) and implanted with a custom planar four-electrode array (inter-electrode spacing 0.75 mm, inter-pair spacing 2.85 mm) over the pelvic nerve and adjacent to the pelvic ganglion. The planar array was fixed securely to the nerve by means of four sutures to the surrounding connective tissue on the surface of the prostate (see Fallon, 2020). ECAPs were recorded by stimulating electrode pairs E1–E2 (Figure 3) using bipolar stimuli (100 μs pulse width with 50 μs interphase gap; 10 Hz) and recording with electrode pair E3–E4 (bipolar recording). Two sets of ECAP recordings (averaged from a total of 50 responses each) were made using stimulus currents ranging from 0 to 1.75 mA, and recordings were sampled at a rate of 100 kHz (filtered using high pass: 300 Hz; low pass: 5000 Hz; voltage gain 102). Neural responses were quantified by measuring the peak-to-peak amplitude of the response within each specified analysis window. Animals were euthanized at the end of the experiment (300 mg/kg i.m. Lethobarb; Virbac, Wetherill Park, NSW Australia).
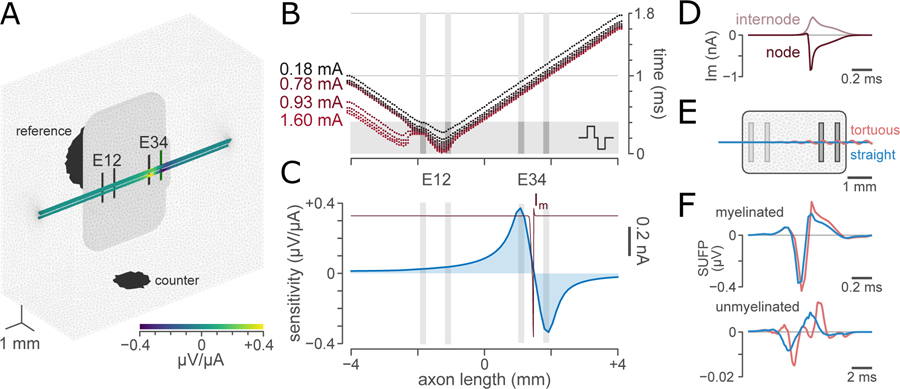
Figure 3. Demonstration of the intermediate steps of ViNERS.
A: Visual overview of a 3D nerve with the electrode array and surrounding medium, showing the computed sensitivity field for an example fascicle pattern for a bipolar recording montage (E3-E4).
B: Example computed raster of spike-time, spatial location tuples for a range of electrical stimuli in an example myelinated efferent (1.73 μm). The axon was positioned 130 μm above the array in the center of a fascicle. Each dot shows the arrival time of a stimulated action potential at a node of Ranvier driven by a single extracellular stimulus. A 0.18 mA but not a 0.15 mA stimulus evoked an action potential in this axon.
C: Computed sensitivity profiles for a bipolar recording, superimposed with a spatial membrane current profile showing the current at each node of Ranvier at the moment of maximum single unit field potential (SUFP) amplitude.
D: Temporal membrane current profiles for an example node of Ranvier (dark red) and the sum of the current across one set of internodal segments (MYSA, FLUT, and STIN; grey). This summation is for illustrative purposes only; for computation of SUFPs, each internodal segment contributes a separate current. Negative values represent inward currents.
E: Example electrode array and model with idealized straight (blue) and tortuous (pink) fascicles. The tortuous fascicle follows a helical curve defined in supplemental Table S-7
F: SUFP for a typical myelinated (1.75 μm; top) and unmyelinated (0.53 μm; bottom) axon in a straight (blue) and a tortuous (pink) fascicle.
ViNERS Overview
ViNERS (Figure 1) is an automated multi-scale, multi-physics MATLAB-based neural interface modelling pipeline. ViNERS builds detailed electro-anatomical finite element models from neural interface electrode array geometries in combination with nerve and fascicular geometries using GMSH (4.4.1; RRID:SCR_021226, (Geuzaine and Remacle, 2009)). ViNERS then simulates these finite element models to compute extracellular electrical potentials (Ve)and extracellular recording sensitivities (Tc) using EIDORS (3.9.1; RRID:SCR_019262). ViNERS then generates customized axon models incorporating distributions of axon ultrastructural and biophysical properties, which ViNERS then simulates using NEURON (7.7.2, Yale; RRID:SCR_005393). Extracellular potentials can be input to the NEURON models to predict extracellular stimulation thresholds, as in a standard hybrid neural interface model (Romeni et al., 2020), and the outputs from NEURON can be combined with the extracellular recording sensitivities to predict single-fiber and ensemble recordings of spontaneous and electrically-evoked activity.
ViNERS is provided as a MATLAB toolbox and can be downloaded from the sparc.science data portal. Each modelling step is implemented as a separate MATLAB module; different modelling workflows (e.g. modelling stimulation vs recording with ViNERS) can be implemented by calling different modules in sequence for fully automated model pipeline evaluation. Module inputs and outputs are automatically saved in a SPARC data structure (Bandrowski et al., 2021) as .mat files, and model generation and evaluation can be customized. Source code and example model input data, including a detailed programmers’ reference and example scripts demonstrating typical modelling workflows, are available on the sparc.science data portal at [https://dx.doi.org/10.26275/chfk-eugm]. In the remainder of this section, we describe the core operations of ViNERS. We then detail the model inputs used to model the influence of fascicle diameter and perineurium thickness on neural interface performance and, separately, the model inputs used to validate ViNERS against in-vivo ECAP recordings collected from rat pelvic nerve.
Three-dimensional Finite Element Modelling of Electrical Fields in EIDORS
The first stage of ViNERS is the creation of an electro-anatomical nerve finite element model (FEM) incorporating the desired nerve and electrode array. First, the user specifies the design (architecture and electrode layout) for their neural interface; this can be done programmatically within MATLAB, these parameters can be read from a json (javascript object notation) file, or a json file describing the desired electrode array can be generated using a separate graphical user interface. Next, the target nerve anatomy (fascicle cross-section and perineurium thickness) is imported from traced nerve sections, such as those described in the anatomical methods, or synthetic fascicles may be used. ViNERS is compatible with neuromorphological data saved in the neuromorphological file format (Sullivan et al., 2020); for other neuromorphological data, fascicle outlines must be converted to a MATLAB structure. If desired, the fascicle trajectory can be defined as a path; otherwise, fascicles are extruded along the z-axis. ViNERS combines the nerve anatomy with the electrode array (specified programmatically) using GMSH to generate a tetrahedral finite-element mesh (Figure 2(C)) for the computation of the electrical fields in EIDORS. The perineurium was modelled as a uniform layer of finite thickness around the inner fascicle boundary defined by the extent of the simulated endoneurium (including axons). As the bulk tissue conductivity approach for modelling electric field distributions for peripheral neural implants has been shown to be adequate to model neuromodulation (Pelot et al., 2019), each tissue or material in the FEM was assigned a (possibly anisotropic) bulk conductivity (see Table I). The surrounding space was modelled with a conductivity of interstitial fluid with Neumann (zero-current) boundary conditions except at the electrodes, which are excluded from the FEM and modelled using the complete electrode model (Cheng et al., 1989). A counter electrode (2 mm diameter) for transmembrane currents and a reference electrode (3 mm diameter) are added to the external boundaries of the mesh. Supplementary Figure S-1 shows the effects of varying mesh size and domain size on the computed sensitivity fields. By default, all electrodes were modelled with an idealized contact impedance of 1 ohm.
TABLE I.
CONDUCTIVITY OF DIFFERENT REGIONS IN THE MODEL
| Tissue or Material | Conductivity, S/m | Reference |
|---|---|---|
| Fascicle (longitudinal) | 0.570 | (Nicholson, 1965) |
| Fascicle (transverse) | 0.088 | (Nicholson, 1965) |
| Perineurium | 8.7e-4 | (Grinberg et al., 2008) |
| Epineurium | 0.083 | (Raspopovic et al., 2017) |
| Interstitial Fluid | 0.66 | (Abdalla et al., 2010) |
| Silicone | 1e-12 | (Mark, 2009) |
The platinum electrode contacts are not explicitly included in the model; instead these are represented as a boundary contact impedance of 1 ohm implemented in EIDORS as the complete electrode model (Cheng et al., 1989).
ViNERS computes forward solutions for the extracellular potential , as a function of spatial position , for electrical stimuli delivered through the electrode array using a quasi-static electrical field approximation neglecting permittivity using the EIDORS function `fwd_solve_1st_order` to solve the underlying Laplace equations. This same model was also used to compute the potential (in μV / nA, relative to a distant reference) observed by each electrode for a point monopole located at , for each mesh element which might contain part of an axon. This computation generates a map of the recording sensitivity for each channel of the recording array, as shown in Figure 3(A). We have previously validated this application of EIDORS for the calculation of extracellular potentials and sensitivity profiles (Eiber et al., 2020). Axons were positioned within the fascicles quasi-randomly: first, a surplus of random points were generated from a uniform random distribution within the bounding box of the fascicle. Next, the spacing between points was made more uniform via Lloyd relaxation (3 iterations). Points outside the fascicle were discarded, and axons were assigned to the remaining points such that each randomly located myelinated axon was further separated from its neighbors than any unmyelinated axon. This algorithm produces arrangements of axons within fascicles where myelinated axons and unmyelinated axons are more clustered together than would be expected by random chance, as is observed from electron micrographs. The details of the axon positions were not included in the mesh; instead, the resulting extracellular potentials and recording sensitivities (defined at each mesh node) were interpolated to the collocation points of the axon model using natural-neighbor interpolation.
Modelling Biophysically Realistic Axon Populations in NEURON
The second stage of ViNERS is the generation of biophysical axon models appropriate to the axon population of the nerve being modelled. To model pelvic nerve, we generated models of myelinated and unmyelinated afferent (sensory) axons as well as myelinated and unmyelinated efferent (motor) axons, all of which are present in the pelvic nerve (Hulsebosch and Coggeshall, 1982). ViNERS populates each fascicle in the finite element model with myelinated and unmyelinated axons whose diameters and g-ratios are sampled from an axon population. In our case, we used our measured population of pelvic nerve axons (Figure 2(E)). Axon diameters and g-ratios may also be derived from published distributions for other nerves (e.g. Prechtl and Powley, 1990; Soltanpour and Santer, 1996). ViNERS then uses these distributions to automatically derive customized axon models from well-established models: MRG model of myelinated axons (Gaines et al., 2018; McIntyre et al., 2002) and Sundt generic nociceptor model for unmyelinated axons (Sundt et al., 2015). Extending ViNERS to incorporate other axon models (e.g. Pelot et al., 2020a) is straightforward, as the specification of the axon biophysics is decoupled from the MATLAB-NEURON interface.
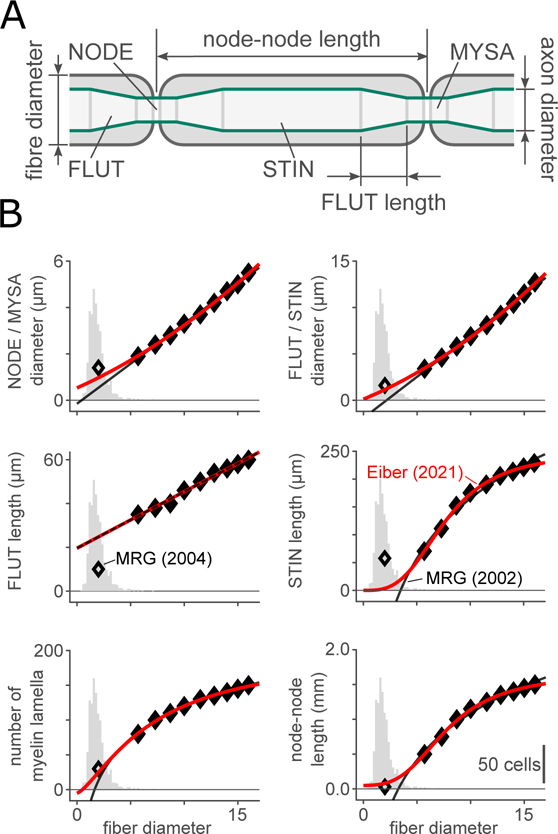
Most visceral myelinated axons are smaller in diameter than the somatic myelinated axons which are modelled in (McIntyre et al., 2002). The ultrastructural relationships used by Gaines et al. (2018) to relate fiber diameter to axon diameter, compartment length at each of the node of Ranvier (NODE), paranode (MYSA), juxtaparanode (FLUT) and stereotypical internode (STIN), and number of myelin lamellae predict negative diameters and segment lengths when extrapolated to these small axons. To correctly model distribution of fiber diameters and g-ratios measured for myelinated axons in the pelvic nerve, we re-fit the ultrastructural data from McIntyre et al. (2002) with quadratic (most parameters, following (Lubba et al., 2019)) or saturating hyperbolic (STIN length and number of myelin lamellae) equations. In our equations (supplemental Table S-2), g-ratio is treated as an independent, rather than dependent, variable by adjusting the axon diameters in each compartment. Figure 4 shows our predicted relationships between fiber diameter and the other ultrastructural parameters for axons with g-ratio 0.6. With the exception of the relative length of the FLUT within the internode, our equations closely matched the extrapolated small-diameter fibers presented in (McIntyre et al., 2004; Pelot et al., 2019). The following ultrastructural parameters were constant: the length of each node of Ranvier (1 μm), the length of each MYSA segment (3 μm), the width of the periaxonal space at the MYSA (2 nm), and the width of the periaxonal space throughout the remainder of the internode (4 nm). The unmyelinated axon model did not contain detailed representations of the axon ultrastructure and was modelled as a multi-segment single-cable model.
Figure 4. Axon ultrastructural parameters used in ViNERS.
A: Schematic of an idealized myelinated axon profile showing the node of Ranvier (NODE), paranode or myelin attachment region (MYSA), juxtaparanode or fluted region (FLUT), and stereotypical internode (STIN).
B: Comparison of the fiber-diameter-dependent ultrastructural relationships from (McIntyre et al., 2002) (filled markers, black lines), the reparametrized relationships given in Table S-1 (red lines) for g = g0, the McIntyre (2004) extrapolations (open markers), and the distribution of visceral fiber diameters observed in pelvic nerve (grey histograms, reproduced from Figure 2(E)).
The electrical properties of the axon models are presented in Table II. The biophysical parameters of the myelinated afferent and efferent models (Gaines et al., 2018) and the unmyelinated nociceptor model (Sundt et al., 2015) have been published previously, and are available at https://senselab.med.yale.edu/ModelDB/ under accession numbers 243841 and 187473, respectively (note: following (Gaines et al., 2018), our myelinated afferent and efferent axons are distinguished solely on the basis of their maximum ionic conductances). For the unmyelinated axon, the axon model was derived from the peripheral axon segment model, which did not contain KCNQ or Ca2+-dependent K+ channels. The maximum conductances for each ion channel mechanism included in each of the three models are given in supplemental Table S-3. All channel kinetics were adjusted using Q10 factors to simulate body temperature (37° C) using the Q10 values supplied in (Gaines et al., 2018; Sundt et al., 2015). Generated fiber models were verified programmatically by checking that axons did not spontaneously generate action potentials but that action potentials would propagate once generated.
TABLE II.
ELECTRICAL PARAMETERS FOR AXON MODELS
| Property (unit) | Myelinated axons | Unmyelinated Axons |
|---|---|---|
| axoplasmic resistivity 𝜌a | 7×105 Ω·μm | 1×106 Ω·μm |
| axon membrane capacitance | 2 μF/cm2 | 1 μF/cm2 |
| myelin conductance | 0.001 S/cm2/lamella | |
| myelin capacitance membrane | 0.1 μF/cm2/ lamella |
Parameters based on the published model properties (Gaines et al., 2018), (McIntyre et al., 2002), (Sundt et al., 2015)
These customized axon models were then used by ViNERS to simulate spatiotemporal transmembrane current profiles and responses to extracellular stimulation. Each compartment of the myelinated axon was modelled as one (node and paranode) or six (internode) connected segments in NEURON. The unmyelinated axon did not vary along its length and was discretized into 20 μm long segments for simulation (although our results do not depend on this choice; see supplemental Figure S-4(A–C)). To compute transmembrane current profiles and axon conduction velocities, propagating action potentials were established using a step injection of current at one end of the axon. An intracellular current injection was used to avoid any distortions to the membrane current profile or conduction velocity which could arise from an externally imposed electric field. Membrane current profiles (Figure 3(C), (D)) were recorded at one node of Ranvier, the flanking paranodal and juxtaparanodal sections and six equispaced points along the length of the internode for myelinated axons and at one point near the midpoint of the axon for unmyelinated axons. For computational tractability, these membrane currents profiles were generated using a set of 24 representative axons of each type (myelinated afferent, myelinated efferent, and unmyelinated), chosen based on nearest-neighbor clustering of axon and fiber (axon + myelin) diameters (supplemental Table S-5). Modifying this clustering has a comparable effect to changing the arrangement of axons within the nerve for ECAPs near threshold (supplemental Figure S-6).
Responses to extracellular simulation were generated by modulating the extracellular potential for each axon segment with a stimulation waveform (in this case, a symmetric biphasic rectangular pulse; ViNERS supports arbitrary waveforms, specified via MATLAB structures). The arrival times of action potentials at each node (for myelinated axons) or each segment (unmyelinated axons) were captured and saved for each axon, simulated independently and in parallel. Figure 3(B) shows an example of a set of spike-time, spike-location tuples for varying levels of extracellular stimulation for a representative axon in an example simulated pelvic nerve. All NEURON simulations were conducted using the default implicit integration method with a time-step of 10 μs, following (Gaines et al., 2018).
Output Metrics for Neural Interface Performance
ViNERS can estimate several important metrics for predicting neural interface performance. One important parameter for neuromodulation is the stimulus threshold, which can be derived by ViNERS for any electrode array design or spatiotemporal stimulus pattern for each axon in the nerve. To determine extracellular electrical stimulation thresholds, ViNERS provides the following automated procedure: for each axon we simulate an electrical stimulus. Depending on whether an action potential (Vm > −20 mV) is observed for any node in the axon within 20 ms of the stimulus onset, the amplitude of the electrical stimulus is adjusted (doubled or halved) until a 1% increase in stimulation amplitude causes that axon to transition from emitting zero to one (or more) action potentials. For myelinated axons, the maximum electrical stimulation used in the binary search was 2 mA; for unmyelinated axons, the maximum electrical stimulus was 10 mA. With these current ranges and the range of axon-electrode separations considered, purely ohmic effects on the membrane potential (i.e. those driven solely by the applied extracellular field without any recruitment of biophysical mechanisms) do not drive the membrane potential above −20 mV.
To characterize neural interface performance for recording neural activity, the equivalent metric to stimulus threshold is the amplitude of the single-unit field potential (SUFP, sometimes also referred to as the single-fiber action potential or SFAP (Struijk, 1997; Lubba et al., 2019)). To compute the SUFP, axon trajectories were formalized as where ℓ is a length parameter (e.g. Eiber et al., 2017). This formalism may describe a straight axon, an axon taking a tortuous path within a fascicle, an axon following the trajectory of a tortuous fascicle, as shown in Figure 3(E) (see supplemental Table S-7), or any combination of the above. For each axon, the SUFP computed from the sensitivity map and the computed transmembrane current profiles Im(ℓ, t) was given by the line integral
| (1) |
subject to the simplifying assumption that where ℓNN is the length between nodes of Ranvier and v is the conduction velocity in m/s. Figure 3(C) illustrates this computation, and figure 3(F) shows the resulting SUFPs for an example myelinated and unmyelinated axon embedded in the center of a straight and a tortuous fascicle (Figure 3(E); Table S-7). While ViNERS can simulate fascicles with realistic trajectories as well as cross-sections, for the remainder of this paper we focus on idealized straight fascicles while we investigate the effect of fascicle cross-section (diameter and perineurium width).
The summation of many SUFPs occurring at different times gives rise to the simulated electroneurogram (ENG), and the summation of many SUFPs from axons where the spike arrival times are determined by an extracellular stimulus yields the simulated electrically-evoked compound action potential (ECAP) (Ward et al., 2020b). To simulate ECAPs, ViNERS simulates the response of each axon in the nerve to progressively increasing stimulus current levels (from 17.5 μA to 3.95 mA). Specifically, for each stimulus level and segment ℓi of each simulated axon, action potentials were exported from NEURON each time the nodal membrane potential Vm depolarized past −20 mV. These stimulus-evoked action potentials were exported as 〈tk, ℓi〉 tuples, which were then used to modify equation (1) to predict the recorded signal Vc(t) for each recording channel in the electrode array
| (2) |
In which is the trajectory of the ath axon, spikesa is the set of spike-time, spike-location tuples 〈tk, ℓi〉 for the ath axon, and is the membrane current template corresponding to cluster of which the ath axon is a member. This relation expresses the signal as the summation over the axon population of many propagating action potentials, and can capture dynamics such as the initiation of multiple action potentials, action potential collision, stimulus-dependent action potential timing, bursting responses, activity-dependent slowing, etc. As a summary metric, we have reported the peak-peak amplitude of the ECAP following (Fallon, 2020; Payne et al., 2020).
Modelling the influence of Nerve Geometry
To quantify the influence of fascicle diameter and the thickness of the perineurium on neural interface recording and stimulating performance, we simulated thresholds and SUFPs for axons in each fascicle from our dataset of 45 fascicle cross sections from three nerves (rat pelvic, rat cervical vagus, rat subdiaphragmatic vagus). Each fascicle was simulated independently; simulations were set up as follows:
Electrode Array
We simulated a standardized planar electrode array consisting of two bipolar electrode pairs (electrode dimensions 0.2 mm × 0.75 mm, inter-electrode center-center spacing 0.75 mm, inter-pair spacing 3.25 mm), embedded in an insulating carrier (4.8 mm × 2.9 mm, thickness 0.8 mm) with a 0.1 mm recess. Simulated extracellular stimulation thresholds were based on stimulation delivered through the first electrode pair (E12) and SUFPs were recorded using the second electrode pair (E34). The electrical stimulus for this experiment was a 400 μs / phase, 20 μs inter-phase gap charge-balanced biphasic symmetric stimulus.
Nerve Geometry
In ViNERS, two sets of simulations were performed for each fascicle. In the first, each fascicle was positioned over the planar electrode array such that the closest point of the fascicle was 20 μm from the surface of the simulated electrode array (fixed-edge). In the second, each fascicle was positioned with its centroid located 455 μm from the array (fixed-center), simulating a fascicle deeper into the tissue. Each fascicle was meshed independently; mesh sizes ranging from 0.61 to 3.49 million elements with typical minimum element quality (Baker’s τ; Baker, 1989; Liu and Joe, 1994) 0.11 and mean element quality 0.63. In a mesh convergence analysis, neither axon SUFP magnitude nor myelinated axon stimulation thresholds showed a significant trend with mesh element size (supplemental Figure S-1(B–C)); unmyelinated axon thresholds had a fascicle-size-dependent trend towards higher thresholds in larger fascicles and lower thresholds in smaller fascicles as mesh element size approached 0 (this effect is in the same direction as that reported in the results). Each fascicle was simulated with a perineurium of uniform thickness based on that fascicle’s measured perineurium from the light micrographs. In a representative subset of fascicles (n=7), the effect of perineurium thickness (independent of fascicle size and location) was further investigated by simulating fascicles encapsulated by 0%, 20%, 50%, 100%, and 150% of the measured perineurium thickness. To investigate whether a simplified nerve model might be sufficient for treatment planning, we also simulated circular and elliptical approximations for this fascicle sample.
Axon Population
To isolate the effect of nerve anatomy from the effect of axon size, for the determination of SUFP magnitudes and extracellular stimulation thresholds we simulated a uniform grid of axons of constant size: 1.75 μm diameter, g-ratio 0.64 for myelinated axons (conduction velocity 3.52 m/s) and 0.53 μm diameter for unmyelinated axons (conduction velocity 0.35 m/s). These sizes correspond to the median diameter and g-ratio for myelinated and unmyelinated axons in our example pelvic nerve. For the computation of SUFP magnitude, between 130 and 650 axons of each type were used per fascicle (median: 382), based on a square grid of 31×31 axons per fascicle and excluding axons falling outside the fascicle boundary. The computation of extracellular stimulation thresholds is more computationally expensive, so to reduce computational time we simulated 12 myelinated and 12 unmyelinated axons per fascicle, uniformly spaced at varying distances from the electrode array along a line passing through the centroid of the fascicle and the location of the fascicle nearest the electrode array.
Axon Biophysics
For myelinated axon SUFPs and thresholds, we used the biophysics for the efferent (MRG) model as presented in (Gaines et al., 2018). For unmyelinated axon SUFPs and thresholds, we used the unmyelinated peripheral axon biophysics published in (Sundt et al., 2015) (i.e. no KCNQ or Ca2+ channels were included in the axon model). In both cases the ultrastructure for the model was updated to reflect the median myelinated or unmyelinated fiber for the pelvic nerve.
Electroneurogram recording
We computed the ENG for each fascicle from the simulated SUFPs by first computing the expected number of action potentials nAP in a 40-ms window as the product of the fascicle area, the rate per axon (1 imp/s), the window length (40 ms), and the axon density. The axon density was 1 axon per 15 μm2 for myelinated axons and 1 axon per 2.8 μm2 for unmyelinated axons, as measured from the pelvic nerve sample (4 fascicles) shown in Figure 2(A). We then randomly sampled nAP SUFPs (randomly selected with replacement from within the fascicle) and randomly shifted each SUFP in time following a uniform distribution over the size of the window to simulate recording of quasi-stationary Poisson population activity with a mean population activity of 1 imp/s/axon (chosen as a reference value). The magnitudes of the resulting ENG traces were quantified using the median RMS of 50 simulated 40-ms segments of ENG. SUFPs and nerve recordings were sampled at 30 kHz.
Modelling pelvic nerve stimulation ECAPs
For the simulation of pelvic nerve ENG and ECAP responses to electrical stimulation, ViNERS was configured to match the experimental set-up described in (Payne et al., 2020). The key differences between the model configuration for the ECAP simulations and the model configuration for investigating the influence of nerve geometry are the presence of multiple fascicles in the model, the use of a synthetic (simplified) fascicular geometry (see Figure 9(A)), the use of the full ultrastructural distribution of axon parameters, and the use of both afferent and efferent myelinated axon biophysics.
Figure 9. Multifasciculated nerves generate stronger signals than single-fascicle nerves.
A: Overall electroneurogram (ENG) amplitude saturates with fascicle size. ENG magnitudes for typical myelinated visceral axons (1.75 μm) across a range of fascicle sizes (n=45 fascicles from 15 animals), assuming a population spike-rate of 1 imp/s and a population density of 1 axon per 15 μm2 for myelinated axons and 1 axon per 2.8 μm2 for unmyelinated axons. The RMS of the ENG increases for small fascicles but saturates for large fascicles.
B: Paired comparison of a single-fascicle and a synthetic multifasciculated nerve. Both fascicle patterns have a cross-sectional area of 17700 μm2 and are composed of 870 myelinated and 4000 unmyelinated axons. Both patterns have the same number of axons located the same distance from the electrode with identical distributions of diameter and g-ratio; the only difference between these arrangements of axons is the lateral location of each axon and the division of axons into fascicles (indicated by the coloration of the axons across the two panels).
C: Example population firing activity (1 imp/s/axon), shown as a raster plot. Each row corresponds to one axon in the population.
D: Example ENG computed from the population activity shown in (C) for the nerve geometries shown in (B).
E: Comparison of simulated ENG magnitude for a range of levels of population activity from 0.1 to 20 imp/s/axon. The simulated ENG for the multifasciculated nerve is 1.2 times greater than the simulated ENG for the single-fascicle nerve across the full range of levels of population activity.
Electrode Array
To match the experimental configuration for ECAP responses we simulated a standardized planar electrode array consisting of two bipolar electrode pairs (electrode dimensions 0.2 mm × 0.75 mm, inter-electrode spacing 0.75 mm, inter-pair spacing 2.85 mm), embedded in an insulating carrier (4.8 mm × 2.9 mm) with a 0.1 mm recess. Simulated extracellular stimulation thresholds were based on stimulation delivered through the first electrode pair (E12) and ECAPs were recorded on the second electrode pair (E34).
Nerve Geometry
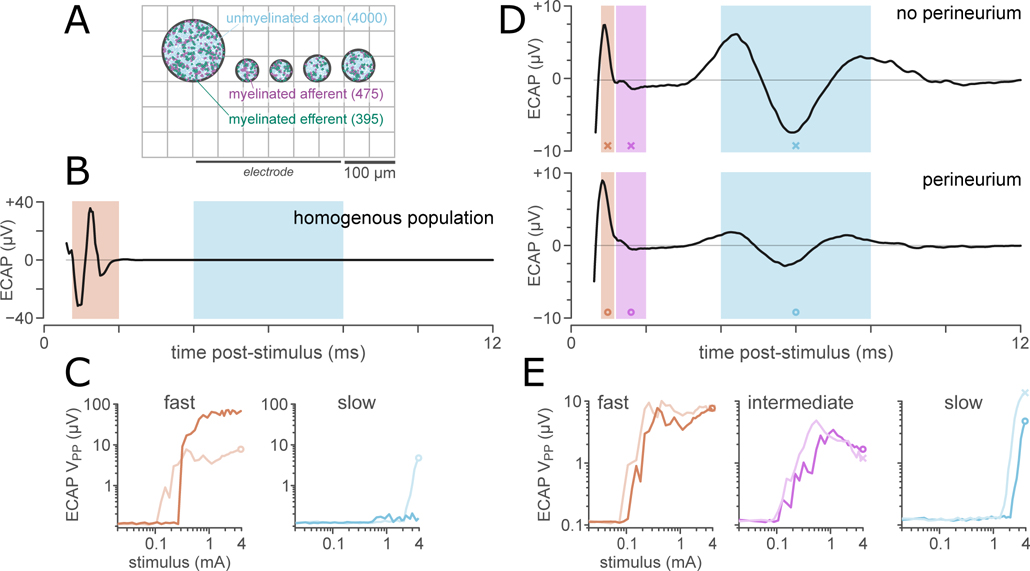
For ECAP responses, a synthetic fascicle pattern was generated with 5 circular fascicles whose diameters and sequence matched that reported for adult rat pelvic nerve (Bertrand et al., 2020). Fascicles were positioned with 25 μm between each fascicle and fascicles positioned with their closest points 150 μm from the surface of the planar electrode array, as shown in figure 10(A). No epineurium was included, as the pelvic nerve lacks a resistive epineurium.
Figure 10. Axon populations and perineurium thickness determine the shape of the ECAP.
A: Synthetic pelvic nerve cross-section consisting of 5 fascicles (diameters from Bertrand et al. (2020)), approximated as circles. Fascicles were positioned with 25 μm between each fascicle and fascicles positioned with their closest points 150 μm from the surface of the planar electrode array.
B: A simulated ECAP (3.95 mA) from a simulation in which all axons took the median diameter for a myelinated (1.75 μm) or unmyelinated (0.53 μm) axon with no inter-axon variation. For this fascicle geometry, the median unmyelinated fiber was not recruited by the maximal stimulus (3.95 mA).
C: Comparison of the ECAP stimulus-response functions for a homogenous population (dark lines) and diverse populations (light lines) of myelinated (fast) and unmyelinated (slow) axons.
D: Predicted ECAPs (3.95 mA) from simulations in which the axon population was morphologically diverse, for simulations excluding (top) and including (bottom) a perineurium. All ECAPs were filtered from 500 – 3 kHz (2nd-order bandpass filter). Shaded areas show the regions of interest for the fast (0.7–1.1 ms), intermediate (1.2–2 ms), and slow (4.3–7.3 ms) responses analyzed to produce stimulus-response functions (D).
E: Response function for the fast, intermediate, and slow components of the ECAP, comparing responses for axon populations in fascicles with (dark line) and without (light line) a simulated perineurium.
Axon Population
We simulated pelvic nerve ECAP responses for a population of 475 myelinated afferents, 395 myelinated efferents, 1200 unmyelinated afferents, and 2800 unmyelinated efferents, matching published values for the afferent and efferent fiber composition of the pelvic nerve (Hulsebosch and Coggeshall, 1982). These axons were distributed across the five fascicles proportional to fascicle area. This population comprises classes of primary afferent (sensory) axons with somas in the dorsal root ganglia corresponding to spinal segment L6/S1 as well as pre-ganglionic parasympathetic efferent axons and a small number of post-ganglionic sympathetic efferent axons (Hulsebosch and Coggeshall, 1982; Keast, 2006; Middleton and Keast, 2004; Osborne, 2017). The myelinated efferents are projections of autonomic preganglionic neurons from the sacral spinal cord (segment L6/S1); unmyelinated efferents are a mix of projections of sacral preganglionic neurons and autonomic postganglionic neurons arising from the paravertebral (sympathetic chain) ganglia.
Axon Biophysics
For the ECAP validation model, we applied the standard approach for generating axon models in ViNERS as described above. To summarize, the biophysical parameters for afferent and efferent myelinated axons differed according to the differences published by Gaines et al. (2018); the Sundt et al. (2015) model was used for both afferent and efferent unmyelinated axons. Myelinated axon ultrastructure was modified from Gaines et al. (2018) to follow the distribution observed for pelvic nerve shown in Figure 2(E). Each modelled axon was 6 mm long and contained between 45–1079 elements (median 523, depending on fiber diameter). For the myelinated axons, we simulated a range of fiber diameters between 0.68 – 6.15 μm (median: 1.75 μm), with corresponding g-ratios between 0.27 – 0.83 (median: 0.64). For the unmyelinated axons, the range of axon diameters was 0.27 – 0.98 μm (median: 0.53 μm). Each of the 870 myelinated and 4000 unmyelinated axons was simulated independently to generate stimulus-evoked spike-time, location tuples. These were then used to compute ECAPs using the sampled membrane currents profiles; supplemental Table S-5 enumerates the specific axon diameters and g-ratios used to derive the membrane current profiles to simulate pelvic nerve ECAPs.
Extracellular Stimulus
We simulated 36 charge-balanced biphasic electrical stimuli (100 μs / phase, 50 μs inter-phase gap) ranging from 17.5 μA to 3.95 mA in a 130-ms response window centered on the stimulus onset. Simulated ECAPs were sampled at 30 kHz, band-pass filtered (500 – 3 kHz, time-reversed 2nd-order IIR Butterworth filter) to match the signal processing applied to the ECAPs collected in-vivo (Payne et al., 2020). The 130-ms response window was chosen to ensure that model gating variables had reached their resting values, and to permit the first and last 15 ms of the simulation to be discarded (e.g. to eliminate filter boundary artifacts). On an x64-based PC based on an Intel Xeon Gold 6128 (12 cores) with 96 GiB RAM running Windows 10, MATLAB R2019b, and NEURON 7.7.2, computing the responses of 870 myelinated and 4000 unmyelinated axons to 36 stimulation levels took, on average, 30 hours wall clock time. For a detailed breakdown of runtime for other modules of ViNERS, see supplemental table S-8.
Statistics
Unless otherwise specified, all statistical comparisons were conducted using n-way analysis of covariance (ANCOVA) in MATLAB, preceded by model identification using sequential F tests using the MATLAB function `vartest2`. For the relationship between fascicle diameter and perineurium thickness, a one-way ANCOVA was conducted to determine if this relationship depended on the type of nerve under consideration (pelvic, subdiaphragmatic vagus, or cervical vagus). To identify the independent contributions of fascicle location, fascicle diameter and perineurium thickness on the performance of our planar electrode arrays, a multivariate ANCOVA was conducted treating fascicle diameter and perineurium thickness as continuous predictor variables and the fascicle-electrode separation (fixed-edge vs fixed-center) as a categorical covariate for each of SUFP peak-peak magnitude and extracellular stimulation thresholds. All factors were independent (between-subjects). The fitted polynomial relationships underlying the ANCOVA were then applied to a separate dataset of pelvic nerve fascicle diameters (Bertrand et al., 2020) to predict the degree of variation in neural interface performance arising from intra-subject anatomical variation in the pelvic nerve. As this dataset does not contain measurements of perineurium width, we used our fitted fascicle diameter-perineurium relationship and residual variance to predict the distribution of perineurium widths corresponding to these fascicles. Reported variance explained follows the usual definition of 1 − variance(residual)/variance(data).
Results
Perineurium thickness is proportional to fascicle diameter for small fascicles
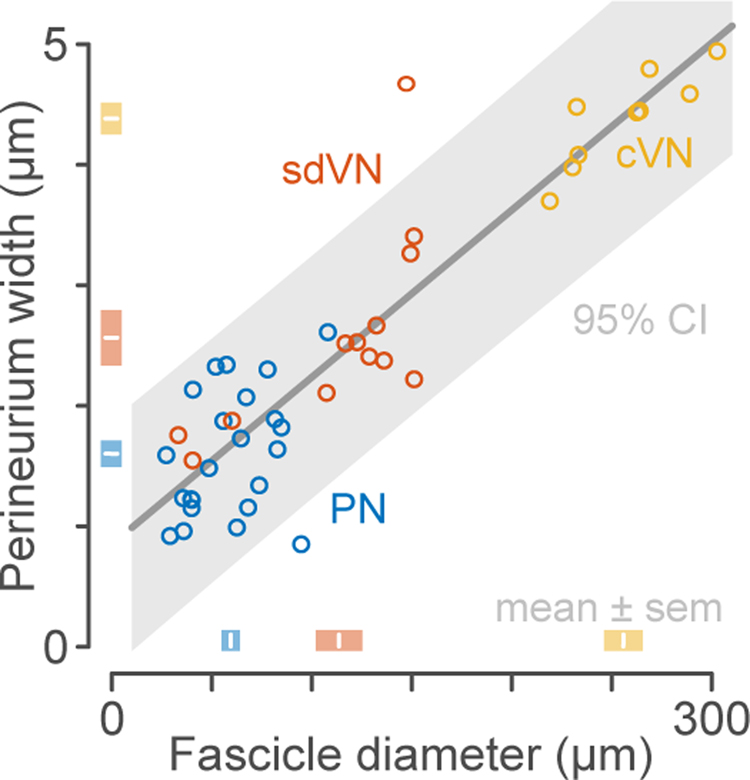
Light and electron microscopy images of rat pelvic and vagus nerve sections were used to derive morphology and parameter estimates for FEM. In rat, the pelvic nerve is a compound nerve which most commonly includes five fascicles joined by loose connective tissue without a common epineurium. Perineurium width increased by 1.77% (95% CI: 1.47% – 2.07%) for every unit increase in fascicle diameter, with an offset of 0.65 μm (95% CI: −0.04 – 1.34 μm) (Figure 5). This relationship was independent of the class (nerve type) of fascicle being measured (F2,39 = 0.33, p = 0.72, ANCOVA), indicating that the relationships derived for larger visceral nerves extrapolate to the adult rat pelvic nerve. The proportional + offset relation described the fascicle diameter-perineurium relationship significantly better than either a constant model (F44,44 = 6.30, p < 0.001) or a strictly proportional relationship (F44,44 = 1.68, p = 0.043). The absolute variation in perineurium width for small fascicles was not significantly greater than for large fascicles (p = 0.058, Bartlett test) but the ratio of the perineurium width to the fascicle diameter was significantly heteroscedastic (p < 0.001, Bartlett test), i.e. the fascicle diameter-perineurium relationship was more variable for small fascicles. For pelvic nerve fascicles, the residual variance was approximately normally distributed with a standard deviation of 0.41 μm.
Figure 5. Comparison of pelvic and vagus fascicle morphometric parameters.
Scatterplot of fascicle diameter vs perineurium thickness measured in 45 visceral nerve fascicles from 15 animals. Line and shaded area show the proportional + offset fascicle diameter-perineurium relationship and 95% confidence interval. Shaded boxes show group means ± standard error. cVN, cervical vagus nerve; sdVN, subdiaphragmatic vagus nerve; PN, pelvic nerve.
Effects of fascicle size on electrical stimulation thresholds
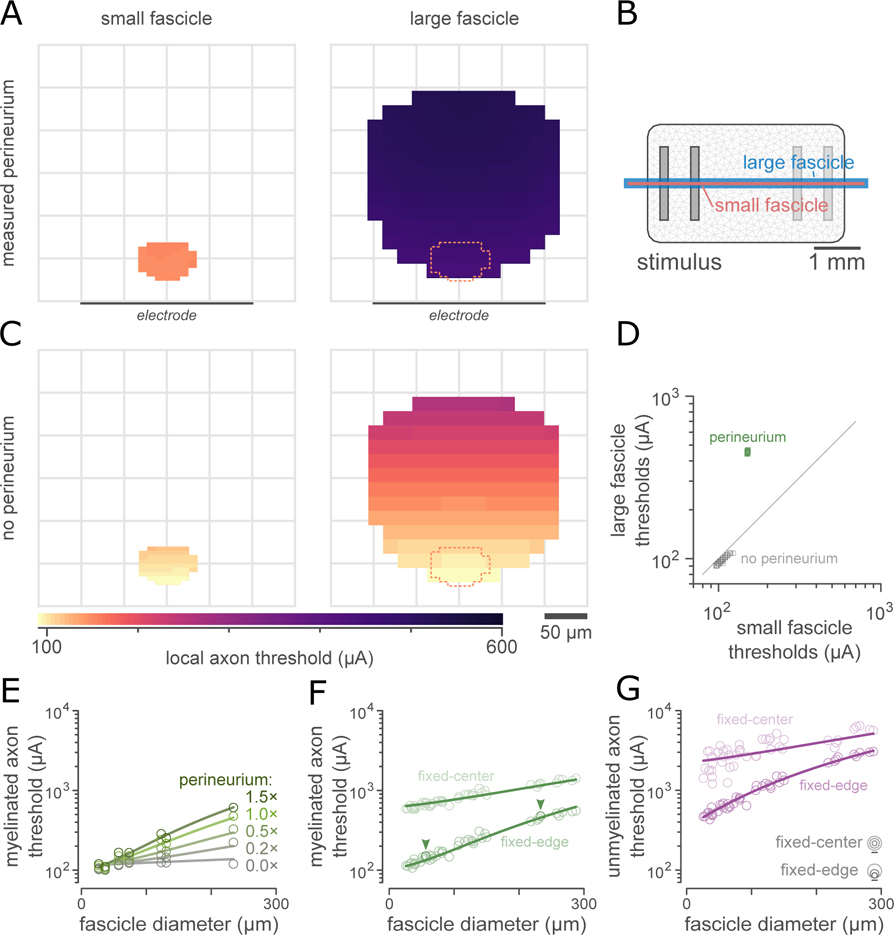
We then simulated nerve stimulation thresholds to understand how fascicle diameter and perineurium thickness influence extracellular activation in visceral nerves. Figure 6(A) shows extracellular electrical stimulation thresholds for typical myelinated axons (1.75 μm fiber diameter) within a representative small (pelvic; 2500 μm2, 2.34 μm perineurium) and large (vagus; 42,720 μm2, 4.48 μm perineurium) visceral nerve fascicle. When fascicles were positioned with the closest point of the endoneurium 20 μm from the surface of the planar electrode array (Figure 6(B)), extracellular electrical stimulation thresholds were dramatically larger in the larger fascicle with the thicker perineurium. By contrast, when the resistive perineurium was excluded from the model, (Figure 6(C)), the difference in thresholds between the two fascicles was negligible for axons equidistant from the stimulating array (Figure 6(D)). Thresholds increased with electrode-axon separation in both the large and the small fascicles.
Figure 6. Perineurium thickness affects extracellular stimulation thresholds.
A: Electrical stimulation thresholds estimated by ViNERS for 1.75 μm myelinated axons in an example small and large visceral nerve fascicle, plotted as a heatmap. Lighter colors correspond to lower electrical stimulation thresholds.
B: Electrode array used in these simulations, showing the small (pink) and the large (blue) fascicle to scale with the stimulating electrodes.
C: Removing the resistive perineurium (thickness: 2.34 μm for the small fascicle, 4.48 μm for the large fascicle) reduced stimulation thresholds in both small and large fascicles. This decrease is dramatically larger for axons in the larger fascicle with the thicker perineurium.
D: Scatterplot comparison of thresholds in panel A (green markers) and B (grey markers) at axon locations defined by the small fascicle. Diagonal is line of unity.
E: Median extracellular stimulation thresholds for typical autonomic myelinated axons across a range of fascicle diameters and perineurium thicknesses. The effect of fascicle diameter on thresholds is mediated by perineurium thickness: when perineurium thickness is zero, fascicle diameter has no effect on thresholds (p>0.51, ANCOVA).
F: Comparison of the median extracellular stimulation thresholds for typical myelinated autonomic axons across a range of fascicle sizes (n=45 fascicles from 15 animals). Each fascicle is simulated with the perineurium thickness measured from the corresponding micrograph at two different fascicle-electrode separations. Line shows the fitted extracellular stimulation threshold prediction based on fascicle diameter and diameter-dependent perineurium thickness (Fig 3G). The example fascicles in A and B are indicated with arrowheads.
G: Comparison of the extracellular stimulation thresholds for typical unmyelinated autonomic axons (0.53 μm diameter) for the same population of fascicles as (E).
As fascicle diameter and perineurium thickness were strongly correlated (Figure 5(C)), we next separated the relative contributions of these parameters by computing thresholds for myelinated and unmyelinated axons in a small subset of pelvic and vagus fascicles (n=7) with perineurium widths ranging from 0× to 1.5× the perineurium width measured for that fascicle from the segmented light micrographs. To increase the generalizability of our conclusions, this was done at two fascicle-electrode separations: fixed-edge, for which the closest point of the fascicle was 20 μm from the surface of the simulated electrode array, and fixed-center, for which each fascicle was positioned with its centroid located 455 μm from the array. Using our iterative model identification approach, we fit simplified (polynomial) statistical models to these data to predict extracellular stimulation thresholds as functions of fascicle diameter, perineurium thickness, and fascicle position. The results of this experiment for myelinated axon thresholds are shown in Figure 6(E). Adding interaction terms to the statistical relation for myelinated axons continued to significantly improve the fit up to a relation containing all first-order interactions (F69,69 > 3.0, p < 0.001); a full model did not significantly improve the approximation (F69,69 = 1.08, p = 0.382). For unmyelinated axons, a simpler relation with terms only for fascicle position and perineurium thickness was adequate to explain thresholds (F69,69 > 2.2, p < 0.001 against simpler relations, F69,69 < 1.4, p > 0.098 against more complex relations). For consistency, both myelinated and unmyelinated axons thresholds were further analyzed using an interaction ANCOVA. The main effects of fascicle position and perineurium thickness for the myelinated axon thresholds shown in Figure 6(E) were significant under ANCOVA (F1,62 = 564.4, p < 0.001 and F1,62 = 9.32, p < 0.005, respectively), while the main effect of fascicle diameter was not (F1,62 = 0.0, p > 0.95). The interactions between perineurium thickness and the other predictor variables were also significant (F1,62 > 74.6, p < 0.001). For unmyelinated axon thresholds, the main effect of fascicle position was significant (F1,62 = 68.1, p < 0.001), as was the interaction between perineurium width and fascicle diameter (F1,62 = 7.07, p < 0.01); the other main effects and interactions were not significant (F1,62 < 1.7, p > 0.20). Complete ANCOVA tables are supplied in the supplemental material (Table S-9).
The overall effect of fascicle size (including both fascicle diameter and perineurium thickness) on electrical stimulation thresholds for fascicles 27–302 μm in diameter is shown in Figure 6(F) for myelinated axons and Figure 6(G) for unmyelinated axons. Figure 6E provides a deeper look at the influence of perineurium thickness, while figure 6F provides a population overview of the overall range of thresholds given fascicle size for myelinated axons (at two fascicle-electrode separations). In our data sample, the total variation in extracellular stimulation thresholds in fascicles close to the electrode array was 139 μA (coefficient of variation 0.60) for myelinated axons and 806 μA (coefficient of variation 0.70) for unmyelinated axons. Our fitted statistical relations predict 98.8% (97.8%) of this variation for myelinated (unmyelinated) axons, respectively; presumably, the remaining 1–3% variation is due to variations in fascicle shape which were modelled but not statistically quantified. Importantly, 91.5% (89.9%) of the variation between fascicles of different nerves (pelvic, cervical vagus, subdiaphragmatic vagus) can be captured by modelling a fascicle with the median diameter and perineurium width for that nerve, and 98.1% (97.9%) of the variation between individual fascicles can be predicted by approximating the perineurium width as a function of fascicle diameter using the relation shown in figure 5.
For visceral nerves closely apposed to a planar array, the natural intra-subject variation in fascicle diameter and perineurium width in adult rat pelvic nerve (Bertrand et al., 2020) would lead to an approximately 41 μA variation in myelinated axon extracellular stimulation thresholds (standard deviation; coefficient of variation 0.178) in the largest fascicles of the pelvic nerve and 9.7 μA in the smallest fascicles of the pelvic nerve (coefficient of variation 0.078). For unmyelinated axon extracellular stimulation thresholds, the influence of fascicle geometry is greater: in the largest fascicles, the expected variation would be 245 μA (coefficient of variation 0.21) and in the smallest fascicles, the expected variation would be 57 μA (coefficient of variation 0.11). To summarize, a thicker perineurium around a fascicle results in an increase in electrical stimulation thresholds for the axons within that fascicle; this relationship is demonstrated in Figure 6. Changes in fascicle diameter primarily affect thresholds via the correlation between fascicle diameter and perineurium thickness, as opposed to determining thresholds directly.
Effects of fascicle size on nerve recording parameters
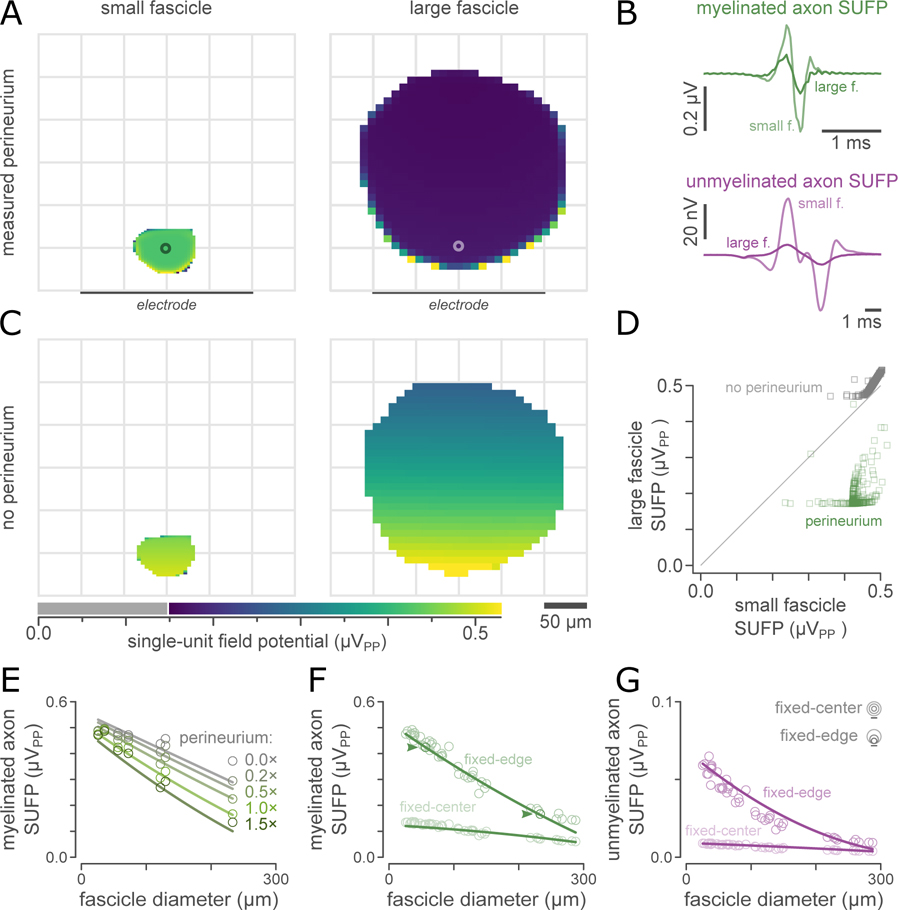
Next, we studied how fascicle diameter and perineurium thickness influence the ability of neural interfaces to record signals from axons, to compare how recording and neuromodulation were differentially affected by fascicle diameter and perineurium thickness. We characterized recording performance using the magnitude of the recorded single-unit field potentials (SUFPs). Unlike for neuromodulation, which was dominated by the effect of the perineurium, we found that the median magnitude of the recorded SUFP within a given fascicle depended on both the fascicle diameter and the perineurium thickness; this is demonstrated in Figure 7 for the same example fascicle pair as Figure 6.
Figure 7. Fascicle size affects single-unit field potential (SUFP) magnitudes.
A: SUFP magnitudes (peak-peak voltages) estimated by ViNERS for 1.75 μm myelinated axons for the same visceral nerve fascicles as figure 6, plotted as a heatmap. Lighter colors correspond to larger SUFPs.
B: SUFP waveforms, measured at the point marked with a circle in (A), for myelinated axons (1.75 μm) and unmyelinated axons (0.53 μm). The additional deflections in the modelled unmyelinated axon SUFPs arise from opposite-polarity summation of a polyphasic monopolar SUFP as it passes over each electrode in the bipolar recording montage.
C: Removing the resistive perineurium increased SUFP magnitudes for axons in both fascicles. This increase is dramatically greater for axons in the larger fascicle with the thicker perineurium
D: Scatterplot comparison of SUFP magnitudes in panel A (green markers) and B (grey markers) at axon locations defined by the small fascicle. Diagonal is line of unity. Horizontal trailing points in correspond to axons very close to the fascicle boundary.
E: Median SUFP magnitudes for typical autonomic myelinated axons across a range of fascicle diameters and perineurium thicknesses. The effect of fascicle diameter on SUFP magnitude is enhanced by the presence of a perineurium but does not depend on the presence of a perineurium.
F: Median SUFP magnitudes for typical autonomic myelinated axons across a range of fascicle sizes (n=45 fascicles from 15 animals). Each fascicle is simulated with the perineurium thickness measured from the corresponding micrograph, at two different fascicle-electrode separations. Lines show the fitted SUFP magnitude prediction based on fascicle diameter and diameter-dependent perineurium thickness (fig 3G). The example fascicles in A and B are indicated with arrowheads.
G: Comparison of the SUFP magnitudes for typical autonomic unmyelinated axons, for the same population of fascicles as (E).
Figure 7(A) shows SUFP magnitudes for bipolar recordings of typical myelinated pelvic nerve axons (1.75 μm fiber diameter), within the same representative small (pelvic) and large (vagus) visceral nerve fascicles as above. Myelinated and unmyelinated axon SUFPs had a lower magnitude within the large fascicle (Figure 7(B)) as compared to the small fascicle (Figure 7(A)); this remains true when the effects of axon-electrode separation are controlled by considering identical axon coordinates relative to the electrode array (Figure 7(D)). When the perineurium was excluded from the model (Figure 7(C)), the SUFP magnitude in the large fascicle increased significantly, but the SUFP magnitude in the small fascicle remained relatively unchanged (Figure 7(D)). In both fascicles, SUFP magnitude diminished monotonically as electrode-axon separation increased.
The multi-factor relationship between fascicle diameter, perineurium thickness, and SUFP magnitude is summarized in Figure 7(E) for myelinated axons. Using our iterative model identification approach, we found that a full polynomial ANCOVA relation (including all interaction terms) provided a significantly better statistical description of the influence of fascicle diameter and perineurium thickness than simpler models, for both myelinated and unmyelinated axons (F69,69 > 4.3, p < 0.001 for myelinated axons and F69,69 > 3.5, p < 0.001 for unmyelinated axons). The overall effect of fascicle diameter and perineurium thickness across our sample population of 45 fascicles is shown in figure 7(F) for myelinated axon SUFPs and figure 7(G) for unmyelinated axon SUFPs. Using this statistical relation for myelinated axon SUFP magnitudes (fit to the data shown in figure 7(E)), all main and interaction effects were significant in the ANCOVA (F1,62 > 4.2, p < 0.044) except for the interaction between perineurium width and fascicle diameter (F1,62 = 1.12, p = 0.29). The direct effect of fascicle diameter on myelinated axon SUFP magnitude (F1,62 = 121, p < 0.001) was greater than that of perineurium width (F1,62 = 41.2, p < 0.001). For unmyelinated axon SUFP magnitudes, all terms were significant in the ANCOVA (F1,62 > 11.5, p < 0.001). The direct effect of fascicle diameter on unmyelinated axon SUFP magnitude (F1,62 = 107, p < 0.001) was again greater than that of perineurium width (F1,62 > 51, p < 0.001). The full ANVOCA tables for the SUFP modelling are provided as supplemental Table S-10.
The overall effect of fascicle size (including both fascicle diameter and perineurium thickness) on SUFP magnitudes is shown in Figure 7(F) for myelinated axons and Figure 7(G) for unmyelinated axons, at two fascicle-electrode separations. In our data sample, the total variation in SUFP magnitudes in fascicles close to the electrode array was 0.117 μV (coefficient of variation 0.36) for myelinated axons and 0.017 μV (coefficient of variation 0.51) for unmyelinated axons. Our fitted statistical relations predict 95.6% (92.8%) of this variation for myelinated (unmyelinated) axons, respectively. 78.2% (69.3%) of the variation in SUFP amplitudes between fascicles of different nerves (pelvic, cervical vagus, subdiaphragmatic vagus) can be captured by modelling a fascicle with the median diameter and perineurium width for that nerve, and 94.5% (92.2%) of the variation between individual fascicles can be predicted by approximating the perineurium width as a function of fascicle diameter using the relation shown in figure 5.
For visceral nerves closely apposed to a planar array, the natural intra-subject variation in fascicle diameter and perineurium width in adult rat pelvic nerve (Bertrand et al., 2020) would lead to an approximately 12 nV variation in myelinated axon SUFP magnitudes (standard deviation; coefficient of variation 0.10) in the largest fascicles of the pelvic nerve and 8.7 nV in the smallest fascicles of the pelvic nerve (coefficient of variation 0.05). For unmyelinated axon SUFP magnitudes, which are less than myelinated axon SUFPs, the relative influence of fascicle geometry is greater: in the largest fascicles, the expected variation would be 5.6 nV (coefficient of variation 0.19) and in the smallest fascicles, the expected variation would be 4.9 nV (coefficient of variation 0.10). To summarize, both perineurium thickness and fascicle diameter influenced SUFP magnitudes, which decreased for axons in larger fascicles with thicker perineurium.
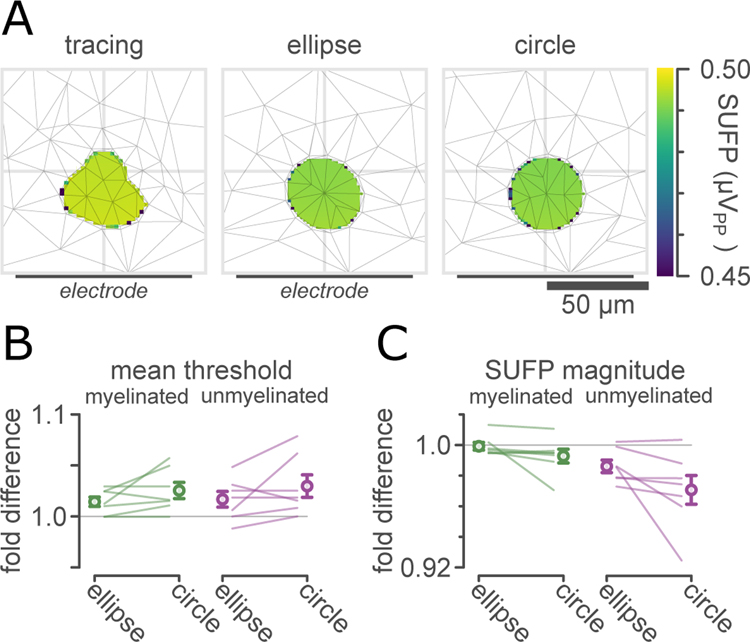
Modelling simplified vs realistic fascicles
To determine the level of anatomical detail necessary to accurately model extracellular electrical stimulation and recording, for our representative subset of 7 fascicles we simulated extracellular stimulation and recording in realistic fascicles (traced from our light micrographs) as well as equivalent circular and elliptical fascicles. Figure 8(A) shows SUFP magnitudes for bipolar recordings of typical myelinated pelvic nerve axons (1.75 μm fiber diameter) in an example traced pelvic nerve fascicle (522 μm2, 1.59 μm perineurium), along with SUFP magnitudes computed in elliptical (middle) and circular (right) approximations to this fascicle. Models of circular fascicles predicted slightly higher thresholds (Figure 8(B)) and slightly lower SUFP magnitudes (Figure 8(C)) compared to models of elliptical or traced fascicles, with mean effect sizes on the order of 1–2%. Despite this small effect size, under pairwise comparison (n=7, paired t-tests), the difference between circular and realistic fascicles was statistically significant for myelinated axon thresholds (p=0.02), unmyelinated axon thresholds (p=0.03), and unmyelinated axon SFUPs (p=0.03), but not for myelinated axon SUFPs (p=0.16).
Figure 8. Realistic and simplified fascicles.
A: Heatmap comparison of SUFP magnitudes (peak-peak voltages) estimated for 1.75 μm myelinated axons for an example traced visceral nerve fascicle (left), an elliptical approximation to that fascicle (middle), and a circular approximation to that fascicle (right). Thin grey lines show tetrahedral elements in a section of the finite-element mesh. Lighter colors correspond to larger SUFPs. This fascicle had a 1.59 μm perineurium.
B: Comparison of differences in median extracellular stimulation thresholds for typical autonomic myelinated axons (1.75 μm) and unmyelinated axons (0.53 μm), expressed as fold change from the median extracellular stimulation thresholds in the realistic fascicle. Markers show mean ±1 SEM.
C: Comparison of differences in median SUFP magnitudes for typical autonomic myelinated and unmyelinated axons, expressed as fold change from median SUFP magnitudes in the realistic fascicle.
Modelling recordings of population activity in single fascicles and multifasciculated nerves.
In practice, ENG and ECAP recordings made with planar and cuff electrode arrays are the aggregate signals from many axons, and the number of axons contained within a given fascicle increases with fascicle diameter. To investigate this, we simulated Poisson-distributed population spiking activity of 1 imp/s with a population density of 1 axon per 15 μm2 for myelinated axons and 1 axon per 2.8 μm2 for unmyelinated axons. Figure 9(A) shows how the magnitude of the ENG depended on fascicle size for myelinated and unmyelinated axons. For small fascicles, the ENG increased due to the increasing number of axons for fascicles up to approximately 135 μm in diameter. For fascicles greater than 135 μm in diameter, the decrease in SUFP sensitivity with fascicle size balanced the increase in axon count for myelinated axons, resulting in no further net increase in recorded signal. For unmyelinated axons this critical diameter was somewhat smaller (95 μm). Because of this relationship, recordings from compound nerves composed of several smaller fascicles yielded stronger signals than recordings from comparable numbers of axons arranged into a single fascicle.
Figure 9(B) shows a comparison between a simple nerve geometry (a 151 μm diameter fascicle, subdiaphragmatic vagus) and a synthetic compound nerve geometry which was contrived to maintain the overall number of axons as well as the individual electrode-axon distance for each axon. At a population activity level of 1 imp/s/axon (Figure 8(C)), the simulated activity in the multifasciculated nerve produced a signal 1.21 times greater than the signal produced in the simple nerve (Figure 9(D)), with all other variables being equal (number and type of axons, per-axon electrode-axon separation, and temporal pattern of spiking activity).This ratio was approximately constant (range 1.19 – 1.26) for a range of levels of population activity from 0.1 imp/s/axon to 20 imp/s/axon (Figure 8(E)). Repeating this experiment with a smaller 33 μm diameter initial fascicle resulted in a stronger shift (ratio 1.45 at 1 imp/s/axon, range 1.41–1.47).
Modelling pelvic nerve ECAPs recorded by implanted electrode arrays
To validate the predictions made by ViNERS regarding electrical stimulation and recording, we simulated pelvic nerve ECAP responses to electrical stimulation. To produce physiologically realistic ECAPs, it was necessary to simulate a realistic distribution of axon diameters and g-ratios in addition to accounting for the influences of fascicle diameter and perineurium thickness; this is illustrated in figure 10. Figure 10(A) shows a cross-section of the simplified pelvic nerve geometry, consisting of 5 circular fascicles. In Figure 10(B), we simulated ECAPs in an idealized pelvic nerve with no variation between axons: every myelinated axon had a diameter of 1.75 μm and a g-ratio of 0.64, and every unmyelinated axon had a diameter of 0.53 μm (as used in Figures 6 and 7). ECAPs produced from this simplified population were not physiologically realistic; ECAP amplitudes were much larger than experimentally observed ECAP amplitudes for the pelvic nerve (Payne et al., 2020) and recruitment curves (Figure 10(C)) were more abrupt than is experimentally observed. When a realistic distribution of axon diameters and g-ratios was used to populate the model, the resulting ECAPs (figure 10(D)) were more realistic; a complex early response with peaks corresponding to axons of different conduction velocities was visible, as was a robust late response. Response thresholds decreased and the maximum observed amplitudes increased when the perineurium was excluded from the model (Figure 10(E)), as expected from the single-axon results.
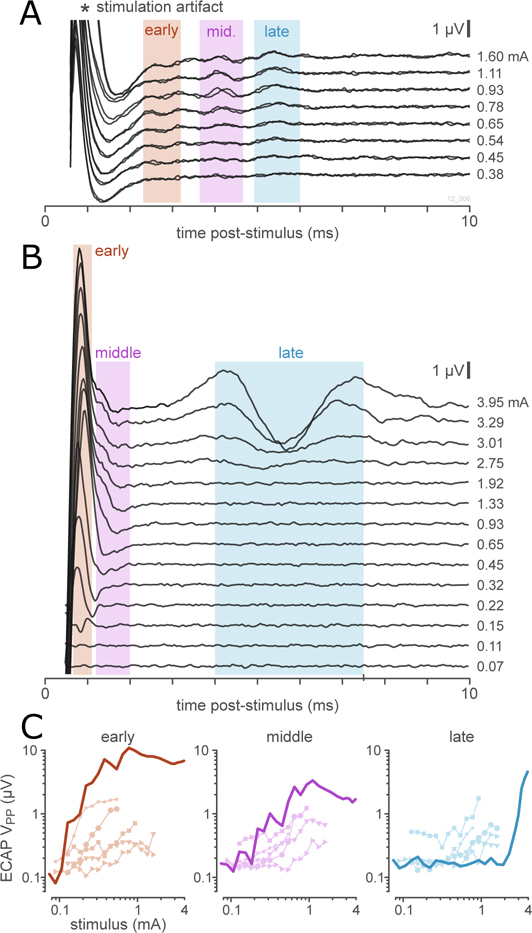
When all of the relevant influences (fascicle diameter and perineurium thickness, distributions of axon diameters and g-ratios, and biophysical distinctions between afferent and efferent axon) were taken into account, ViNERS produced simulated ECAP recordings reproduced the major components of in-vivo recordings of pelvic nerve responses to electrical stimulation, as shown in Figure 11. Figure 11(A) shows a typical set of ECAPs recorded from rat pelvic nerve in response to pelvic nerve stimulation. The electrical stimulation artifact dominated the first 2 ms post-stimulation. As we have published previously (Payne et al., 2020), three responding populations can be distinguished by their response latencies and thresholds in pelvic nerve responses. Figure 11(B) shows an example set of ECAPs generated by ViNERS for an idealized rat pelvic nerve section, and Figure 11(C) shows the response functions for the simulated and recorded data in the early, middle, and late components of the response. While ViNERS produced three distinct responses, the latency of the fastest responses predicted by ViNERS are likely obscured by the stimulation artifact in the in vivo recording. ViNERS predicted a single late component with latency 5.7 ms that corresponded with the late component of the in-vivo recordings (5.62 ms); although with a 2.2-fold higher threshold (2.74 mA vs 1.26 mA, respectively) and with a 2.9-fold larger amplitude (1.70 μV vs 0.59 μV, respectively).
Figure 11. Comparison of simulated ECAPs and ECAPs recorded in-vivo.
A: Example set of two repeats of in-vivo recorded ECAPs recorded from a single animal. Three neural responses are visible at latencies of 2.75, 3.25, and 5.33 ms (shaded regions). Electrical artifact dominates below 2 ms.
B: Example set of simulated ECAPs. Shaded areas show the regions of interest for the fast (0.7–1.1 ms), intermediate (1.2–2 ms), and slow (4.3–7.3 ms) responses analyzed to produce stimulus-response functions (C).
C. Stimulus-response functions for simulated and in-vivo recorded ECAPs. Thick lines show the simulated ECAPs (B). small lines with markers show ECAP response functions recorded in-vivo; markers identify individual animals (n=5).
Discussion
We conducted a combined neuroanatomical and computational study to measure rat pelvic nerve fascicle cross-sectional profiles and distributions of axon properties, and developed a computational pipeline, ViNERS, to simulate large-scale neural recording and electrical stimulation of peripheral visceral nerves. ViNERS is a multifunctional, up-to-date neural interface modelling pipeline which can simulate nerve recording as well as nerve stimulation for accurate neural interface geometries. To validate both the electrical stimulation and electrical recording capabilities of ViNERS, we compared simulated ECAPs with ECAPs recorded in-vivo from rat pelvic nerve using a planar electrode array.
The ViNERS Pipeline
ViNERS addresses the need for an open-source computational neural interface model which can simulate both neural stimulation and recording to predict and optimize closed-loop neural interface performance. ViNERS accurately captured the influences of the neural interface design, the anatomy of the nerve, the visceral nerve axon populations, and the biophysical properties of the individual axons, extending work which modelled only electrical stimulation (Grinberg et al., 2008; Grill, 2015; Gaines et al., 2018; Pelot et al., 2019; Gupta et al., 2020; Romeni et al., 2020; Bucksot et al., 2021) or provided only a simplified model for neural recording (Struijk, 1997; Karimi and Seydnejad, 2015; Lubba et al., 2019). ViNERS is comparable to contemporary commercial offerings for neural interface modelling such as Sim4Life; compared to these, ViNERS is a more specialized and streamlined application offering 2.5D and limited 3D modelling; experimentally derived, morphologically diverse NEURON models; and extensive experimenter extensibility with minimal code. On the other hand, Sim4Life can generate and mesh more complex nerve and electrode models including branching structures and supports interoperability with many common computer-aided design packages, high performance computing for the EM simulations, provides efficient methods to avoid discretizing the thin perineurium layers, and can consider nerve-external anatomy, e.g. to model non-invasive neural interface stimulation and recording. Another key distinction is in the language used: ViNERS is MATLAB-based, while Sim4Life and PyPNS are python-based.
ViNERS currently supports parameterized circular and rectangular cuff and planar electrode arrays; extending ViNERS to incorporate other array designs (e.g. intra-fascicular or intra-vascular electrodes) is straightforward. One limitation of the ViNERS pipeline compared to other nerve recording models (PyPNS; Lubba et al., 2019) is that simulations of neural recordings from tortuous (i.e. not following the path of the fascicle) or branching axons are not yet fully supported. We are not simulating stochastic activity of axons, which may be relevant for small-diameter fibers, nor are we simulating ephaptic coupling of axons. We have also used a quasi-static electrical fields solution, not a fully coupled electromagnetic field solution, which is valid for the stimulation pulse lengths used but not for extremely short (ns) pulses (e.g. Casciola et al., 2017).The electric fields computed very close to the electrode for the complete electrode model (Cheng et al., 1989) may differ from the fields computed for a model which explicitly simulates the current density within the electrode contact. Another limitation arises from the membrane current template approach: changes in membrane currents, e.g. due to previous spiking activity, will not be reflected in the simulated ECAP or ENG waveforms. ViNERS is built from open-source components and achieves computational efficiencies that allow large-scale simulations of entire axon populations, enabling researchers to investigate new stimulating and recording strategies in-silico.
We compared the ECAPs generated using ViNERS with ECAPs recorded in a small multifasciculated visceral nerve, the rat pelvic nerve (Bertrand et al., 2020; Payne et al., 2020). Using a simplified abstract fascicular geometry, ViNERS produced ECAPs which reproduced the major components of ECAPs recorded in-vivo, in terms of myelinated axon thresholds and overall response profiles. ViNERS did not reproduce the observed distribution of conduction velocities; this is a limitation of the axon models used (Gaines et al., 2018; McIntyre et al., 2002; Sundt et al., 2015), which are extrapolations of somatomotor and nociceptor axons, and points to a need for peripheral-visceral-neuron-specific axon models, as discussed below. Another limitation of this comparison is that we do not have images of the stimulated nerve in-situ with the electrode array; this provides another large source of predicted variance.
Modelling Peripheral visceral nerve axons
One limitation of the present study is the axon models used. While we used well-validated models for mammalian afferent and efferent myelinated axons (Gaines et al., 2018; McIntyre et al., 2002) as well as a recent, up-to-date model for mammalian unmyelinated axons (Sundt et al., 2015), these axon models are based on human somatic afferents and efferents, whereas the pelvic nerve comprises visceral afferents and autonomic pre- and post-ganglionic efferent axons (de Groat et al., 1982; Hulsebosch and Coggeshall, 1982). Furthermore, pelvic nerve afferents include both peptidergic polymodal nociceptors (which would be well-described by the Sundt et al. (2015) model) and biophysically distinct non-peptidergic C-fiber low-threshold mechanoreceptor classes (de Groat et al., 1982; Sengupta and Gebhart, 1994; Yoshimura et al., 1996; Shea et al., 2000; Yoshimura et al., 2003; Zagorodnyuk et al., 2007; Grundy et al., 2018), which we have not specifically modelled here. Pelvic nerve efferents include both preganglionic parasympathetic efferent axons and a small number of postganglionic sympathetic efferent axons (Hulsebosch and Coggeshall, 1982; Keast, 2006; Middleton and Keast, 2004; Osborne, 2017); however, as no biophysical models distinguishing these axon classes are available, no distinction was made between these classes in the model.
Given these limitations, the simulated conduction velocities for our unmyelinated axon model predicted the slowest-latency response populations quite well. The failure to reproduce response latencies of the other observed pelvic nerve response populations isnot surprising, as neither computational models of unmyelinated peptidergic non-nociceptive afferents nor of unmyelinated preganglionic visceromotor efferents were included in these simulations. Single-unit recordings of unmyelinated bladder afferents report conduction velocities for unmyelinated non-nociceptive bladder afferents range from 0.8 to 2.2 m/s (Sengupta and Gebhart, 1994; Shea et al., 2000), matching the ranges of the faster response components reported in (Payne et al., 2020) but absent from our modelled responses. The conduction velocities of the myelinated afferent and efferent models we have used match previously reported values for single-unit recordings of myelinated bladder afferents (Sengupta and Gebhart, 1994; Shea et al., 2000) if one assumes that the axon diameters are 20% larger in-vivo than the structures in nerves fixed and processed for electron microscopy(i.e. a shrinkage artifact, as discussed by Gaines et al. (2018)). These response components are likely obscured by the stimulation artifact in the in vivo recording. The single response population with a well-matched velocity we have simulated here is an improvement on previously published models: Lubba et al (2019) artificially increased the conduction velocity of their unmyelinated axons (based on Hodgkin and Huxley, 1952) to better match their rat vagus nerve recordings. While ViNERS has the capability to apply such a correction factor, no such correction has been applied here. There is an urgent need to develop biophysically detailed models for the major functional types of peripheral visceral afferent and efferent axons, as begun by (Mandge and Manchanda, 2018; Pelot et al., 2020a).
Nerve anatomy influences neural interface performance
The electro-anatomical geometry of visceral nerves played a large role in determining the performance of neural interfaces for both recording and neuromodulation. In our simulations, axons in small, multi-fasciculated visceral nerves had lower thresholds and yielded stronger neural recordings compared to equivalent numbers of axons in single larger fascicles for a simulated planar electrode array. This increase in sensitivity arising from smaller fascicles may assist in overcoming some of the challenges of stimulating and recording from small-caliber visceral axons. Our simulations revealed that single-unit field potentials diminish for visceral axons in large fascicles to such an extent that, despite the fact that large fascicles contain more axons, ensemble recordings of neural activity (ENG and ECAP signals) fail to significantly increase in amplitude per fascicle for fascicles greater than about 100 μm in diameter. As a consequence of these diminishing returns, we predict that highly multifasciculated nerves will yield stronger overall recordings. This result parallels the situation for nerve stimulation, albeit with some differences regarding the relative influences of different features of fascicular geometry. In agreement with (Grinberg et al., 2008; Koole et al., 1997; Pelot et al., 2019), we found that while larger fascicles had lower extracellular stimulation thresholds when the influence of the resistive perineurium was considered, fascicle diameter did not by itself have a strong effect on extracellular stimulation thresholds in the absence of the effect of the resistive perineurium. Our interpretation is that the apparent influence of fascicle diameter is primarily mediated by the correlation between fascicle diameter and perineurium thickness. This relationship appeared for both myelinated and unmyelinated axons; given the constraints on the mesh element size in the work presented here, we have likely underestimated the true magnitude of the effect of nerve geometry on unmyelinated axons in particular. In contrast, for nerve recording, median axon SUFP magnitude depended on both fascicle diameter and perineurium thickness, and was not dominated by either factor. We speculate that this difference may arise from the different arrangement of current sources and sinks in stimulation vs. recording; further experimentation is required to understand how ensemble recordings relate to population activity in large-scale peripheral nerve recordings. We have not investigated how the relative arrangement of fascicles with respect to the stimulating electrode may influence electrical stimulation or recording, as was done by Grinberg et al. (2008), nor have we investigated how the results we obtained apply to compound fascicles, in which multiple endoneurial compartments are separated by perineurium and enclosed in a common bundle.
Summarizing the output of ViNERS for visceral nerve stimulation with a planar electrode array using simplified statistical relationships, the effects of fascicle diameter and perineurium thickness on myelinated axon thresholds and SUFP magnitudes were more predictable than the effects on unmyelinated axons. The relationship between fascicle size and SUFP magnitudes was closer to linear (a greater fraction of the variance was explained) than for thresholds for both myelinated and unmyelinated axons. We acknowledge that the simplified polynomial relationships do not give exact predictions of thresholds or SUFP magnitudes given summary description of the fascicles, highlighting the necessity of computational pipelines such as ViNERS for making these kinds of predictions. We explored several variations of our statistical approach, including manipulations such as log-transforming our outcome variables; however, this did not improve the distribution of residuals. The conclusions we report are robust against variations in the applied statistical approach. Of note, we did not investigate the effects of axon diameter on thresholds or SUFP magnitudes, as described by Wijesinghe et al. (1991). We also did not systemically investigate the influence of higher-order shape parameters, such as fascicle eccentricity or concavity, on intra-fascicle thresholds or SUFP magnitudes. Based on the remining unexplained variance between the simulation results and the simplified statistical relations based on fascicle diameter, fascicle location, and perineurium thickness, the maximum effect size for higher-order shape parameters would be less than 10% of the effect sizes of fascicle diameter and perineurium thickness. This range is in line with the differences we observed between our simulated fascicles and circular approximations thereof.
The degree to which the precise anatomical details of fascicle orientation and arrangement need to be represented in a model depends on the desired precision of the model outputs. For predictions of “typical responses”, the approach we have used here (circular fascicles with diameters from a population average) is likely adequate, as the variance between individual subject thresholds in our recorded data is approximately 50–60% of baseline (Payne et al., 2020), greater than the 8–20% variance we derive from fascicle size and perineurium thickness. For patient-specific treatment planning, the use of dedicated MRI protocols and new neuroimaging modalities such as electrical impedance imaging to estimate fascicle location and size (Ohana et al., 2014; Chen et al., 2019; Ravagli et al., 2021) will be required for patient-specific models. For detailed analysis of data from pre-clinical animal models, it is important to collect detailed cross-sectional images of fascicle size and position to cross-reference to the in-vivo recordings for computational modelling to make meaningful predictions across spatial scales.
We found that the fascicle diameter–perineurium thickness relationship was significantly more variable for small fascicles than for larger fascicles, limiting the utility of the standard approximation that the perineurium thickness is 3% of the fascicle diameter (Grinberg et al., 2008; Pelot et al., 2019; Williams et al., 2000). For nerves composed of small fascicles, accurate perineurium thickness measurements (e.g. Pelot et al., 2020b) are critical for accurately predicting visceral neural interface performance. The work presented here is based on measurements of rat visceral nerves; further work is necessary to determine appropriate fascicle diameter-perineurium thickness relationship for human visceral nerves, as begun by Pelot et al. (Pelot et al., 2020b). Neural-implant related changes to nerves and surrounding tissue have been observed in the context of chronic nerve cuff implantation (Sahyouni et al., 2017; Payne et al., 2018). Growth of a fibrous tissue encapsulation layer around the implant likely dominates changes in threshold observed in the first 8 weeks post-implant (Grill and Mortimer, 1998; Christie et al., 2017; Payne et al., 2018). As EIDORS can compute electrical field distributions for arbitrary conductivity distributions, future work with ViNERS will use measurements of chronic tissue impedances to better understand how fibrous tissue encapsulation develops around planar electrode arrays changes over time and how these changes predict post-implant changes in thresholds and neural implant recording performance.
Conclusion
ViNERS is a powerful platform for building a stronger understanding of peripheral visceral neuroscience. ViNERS enables fundamental studies conducted at the single-axon level to be linked to clinical and pre-clinical research conducted at the whole-nerve level with aggregate stimulus and response measures such as ECAPs, improving the efficacy and translation of therapies for autonomic dysfunctions (e.g. Byku and Mann, 2016). ViNERS has the flexibility to capture a wide variety of stimulus- and activity-dependent effects such as paired-pulse inhibition, activity-dependent slowing, response phase advancement and rebound excitation, dependent only on the fidelity of the biophysical models. ViNERS supports both high-throughput simulation for the investigation of broad ranges of parameters and parameter combinations as well as high-fidelity simulation of entire axon populations in peripheral nerves.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health, Office of the Director, Stimulating Peripheral Activity to Relieve Conditions (SPARC) Program under Award Number OT2OD023872 (JK, PO, and JF) and OT2OD026585 (LH). The content of this work is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The Bionics Institute acknowledges the support it receives from the Victorian Government through its Operational Infrastructure Support Program. LH also acknowledges support from the Dr. Miriam and Sheldon G. Adelson Medical Research Foundation. We would like to acknowledge Kiyotada Naito for surgical assistance; Alex Thompson for technical assistance with electrical equipment; Ross Thomas for the manufacture and refinement of the array design; Amy Morley and Erin Smyth for assistance and support conducting electrophysiology experiments; JingYang Liu and Eric Musselman for beta-testing the modelling pipeline; and John-Paul Fuller-Jackson, Nicole Wiedmann, and Ankita George for assisting with pelvic nerve sample preparation, perfusions, and tissue washes. We would also like to acknowledge Dr. Matt Ward for intellectual input on some of the research concepts and selection of model outputs.
References
- Abdalla S, Al-ameer SS, Al-Magaishi SH, 2010. Electrical properties with relaxation through human blood. Biomicrofluidics 4. 10.1063/1.3458908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker TJ, 1989. Element quality in tetrahedral meshes. Presented at the Proc. 7th Int. Conf. on Finite Element Methods in Flow Problems, p. 1018. [Google Scholar]
- Bandrowski A, Grethe JS, Pilko A, Gillespie T, Pine G, Patel B, Surles-Zeigler M, Martone ME, 2021. SPARC Data Structure: Rationale and Design of a FAIR Standard for Biomedical Research Data. 10.1101/2021.02.10.430563 [DOI] [Google Scholar]
- Bartmeyer PM, Biscola NP, Havton LA, 2021. A shape-adjusted ellipse approach corrects for varied axonal dispersion angles and myelination in primate nerve roots. Sci Rep 11, 3150. 10.1038/s41598-021-82575-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berthold CH, Rydmark M, 1983a. Electron microscopic serial section analysis of nodes of Ranvier in lumbosacral spinal roots of the cat: ultrastructural organization of nodal compartments in fibres of different sizes. J Neurocytol 12, 475–505. 10.1007/BF01159386 [DOI] [PubMed] [Google Scholar]
- Berthold CH, Rydmark M, 1983b. Electrophysiology and morphology of myelinated nerve fibers. VI. Anatomy of the paranode-node-paranode region in the cat. Experientia 39, 964–976. 10.1007/BF01989761 [DOI] [PubMed] [Google Scholar]
- Bertrand MM, Korajkic N, Osborne PB, Keast JR, 2020. Functional segregation within the pelvic nerve of male rats: a meso- and microscopic analysis. Journal of Anatomy 237, 757–773. 10.1111/joa.13221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biscola N, Havton L, 2020. Nerve tissue processing for transmission electron microscopy (TEM) [WWW Document]. protocols.io. 10.17504/protocols.io.xpxfmpn [DOI]
- Bouton CE, Czura CJ, 2018. Chapter 131 - Sensing and Decoding Neural Signals for Closed-Loop Neuromodulation and Advanced Diagnostics in Chronic Disease and Injury, in: Krames ES, Peckham PH, Rezai AR (Eds.), Neuromodulation (Second Edition). Academic Press, pp. 1541–1549. 10.1016/B978-0-12-805353-9.00131-5 [DOI] [Google Scholar]
- Buccino AP, Einevoll GT, 2021. MEArec: A Fast and Customizable Testbench Simulator for Ground-truth Extracellular Spiking Activity. Neuroinform 19, 185–204. 10.1007/s12021-020-09467-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucksot JE, Chandler CR, Intharuck NM, Rennaker RL, Kilgard MP, Hays SA, 2021. Validation of a parameterized, open-source model of nerve stimulation. J. Neural Eng. 18, 042001. 10.1088/1741-2552/ac1983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byku M, Mann DL, 2016. Neuromodulation of the Failing Heart: Lost in Translation? JACC: Basic to Translational Science 1, 95–106. 10.1016/j.jacbts.2016.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casciola M, Xiao S, Pakhomov AG, 2017. Damage-free peripheral nerve stimulation by 12-ns pulsed electric field. Scientific Reports 7, 10453. 10.1038/s41598-017-10282-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Haacke EM, Li J, 2019. Peripheral nerve magnetic resonance imaging. F1000Res 8, F1000 Faculty Rev-1803. 10.12688/f1000research.19695.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng K-S, Isaacson D, Newell JC, Gisser DG, 1989. Electrode models for electric current computed tomography. IEEE Transactions on Biomedical Engineering 36, 918–924. 10.1109/10.35300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christie BP, Freeberg M, Memberg WD, Pinault GJC, Hoyen HA, Tyler DJ, Triolo RJ, 2017. “Long-term stability of stimulating spiral nerve cuff electrodes on human peripheral nerves.” Journal of NeuroEngineering and Rehabilitation 14, 70. 10.1186/s12984-017-0285-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Groat WC, Booth AM, Milne RJ, Roppolo JR, 1982. Parasympathetic preganglionic neurons in the sacral spinal cord. Journal of the Autonomic Nervous System 5, 23–43. https://doi.org/10/cjjg7p [DOI] [PubMed] [Google Scholar]
- DeVries L, Scheperle R, Bierer JA, 2016. Assessing the Electrode-Neuron Interface with the Electrically Evoked Compound Action Potential, Electrode Position, and Behavioral Thresholds. J Assoc Res Otolaryngol 17, 237–252. 10.1007/s10162-016-0557-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eiber CD, Dokos S, Lovell NH, Suaning GJ, 2017. A spectral element method with adaptive segmentation for accurately simulating extracellular electrical stimulation of neurons. Med Biol Eng Comput 55, 823–831. 10.1007/s11517-016-1558-x [DOI] [PubMed] [Google Scholar]
- Eiber CD, Keast JR, Osborne PB, 2020. Simulating bidirectional peripheral neural interfaces in EIDORS. Annu Int Conf IEEE Eng Med Biol Soc 2020, 2934–2937. 10.1109/EMBC44109.2020.9175921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fallon J, 2020. Electrophysiological recording of electrically-evoked compound action potentials. 10.17504/protocols.io.bfwyjpfw [DOI]
- Gaines JL, Finn KE, Slopsema JP, Heyboer LA, Polasek KH, 2018. A model of motor and sensory axon activation in the median nerve using surface electrical stimulation. J Comput Neurosci 45, 29–43. 10.1007/s10827-018-0689-5 [DOI] [PubMed] [Google Scholar]
- Geuzaine C, Remacle J-F, 2009. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering 79, 1309–1331. 10.1002/nme.2579 [DOI] [Google Scholar]
- Grill WM, 2015. Chapter 7 - Model-based analysis and design of waveforms for efficient neural stimulation, in: Bestmann S (Ed.), Progress in Brain Research, Computational Neurostimulation. Elsevier, pp. 147–162. 10.1016/bs.pbr.2015.07.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill WM, Mortimer JT, 1998. Stability of the input-output properties of chronically implanted multiple contact nerve cuff stimulating electrodes. IEEE Trans Rehabil Eng 6, 364–373. 10.1109/86.736150 [DOI] [PubMed] [Google Scholar]
- Grinberg Y, Schiefer MA, Tyler DJ, Gustafson KJ, 2008. Fascicular Perineurium Thickness, Size, and Position Affect Model Predictions of Neural Excitation. IEEE Trans Neural Syst Rehabil Eng 16, 572–581. 10.1109/TNSRE.2008.2010348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grundy L, Erickson A, Caldwell A, Garcia-Caraballo S, Rychkov G, Harrington A, Brierley SM, 2018. Tetrodotoxin-sensitive voltage-gated sodium channels regulate bladder afferent responses to distension: PAIN 159, 2573–2584. 10.1097/j.pain.0000000000001368 [DOI] [PubMed] [Google Scholar]
- Gupta I, Cassará AM, Tarotin I, Donega M, Miranda JA, Sokal DM, Ouchouche S, Dopson W, Matteucci P, Neufeld E, Schiefer MA, Rowles A, McGill P, Perkins J, Dolezalova N, Saeb-Parsy K, Kuster N, Yazicioglu RF, Witherington J, Chew DJ, 2020. Quantification of clinically applicable stimulation parameters for precision near-organ neuromodulation of human splenic nerves. Communications Biology 3, 1–11. 10.1038/s42003-020-01299-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF, 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology 117, 500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn CC, Ardell JL, Fisher LE, 2019. Electroceutical Targeting of the Autonomic Nervous System. Physiology 34, 150–162. 10.1152/physiol.00030.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hulsebosch CE, Coggeshall RE, 1982. An analysis of the axon populations in the nerves to the pelvic viscera in the rat. The Journal of Comparative Neurology 211, 1–10. 10.1002/cne.902110102 [DOI] [PubMed] [Google Scholar]
- Jabbari M, Erfanian A, 2019. Estimation of Bladder Pressure and Volume from the Neural Activity of Lumbosacral Dorsal Horn Using a Long-Short-Term-Memory-based Deep Neural Network. Sci Rep 9, 18128. 10.1038/s41598-019-54144-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaqua K, Powell CR, 2017. Where Are We Headed with Neuromodulation for Overactive Bladder? Curr Urol Rep 18, 59. 10.1007/s11934-017-0711-x [DOI] [PubMed] [Google Scholar]
- Johnson CR, Barr RC, Klein SM, 2007. A Computer Model of Electrical Stimulation of Peripheral Nerves in Regional Anesthesia. Anesthes 106, 323–330. [DOI] [PubMed] [Google Scholar]
- Karimi F, Seydnejad SR, 2015. Velocity Selective Neural Signal Recording Using a Space-Time Electrode Array. IEEE Transactions on Neural Systems and Rehabilitation Engineering 23, 837–848. 10.1109/TNSRE.2014.2379594 [DOI] [PubMed] [Google Scholar]
- Keast JR, 2006. Plasticity of pelvic autonomic ganglia and urogenital innervation. Int Rev Cytol 248, 141–208. 10.1016/S0074-7696(06)48003-7 [DOI] [PubMed] [Google Scholar]
- Keast JR, Osborne PB, 2019. Intracardiac perfusion with fixative for anatomical studies [WWW Document]. protocols.io. URL https://www.protocols.io/view/intracardiac-perfusion-with-fixative-for-anatomica-w24fggw/ (accessed 6.10.21).
- Koole P, Holsheimer J, Struijk JJ, Verloop AJ, 1997. Recruitment characteristics of nerve fascicles stimulated by a multigroove electrode. IEEE Transactions on Rehabilitation Engineering 5, 40–50. 10.1109/86.559348 [DOI] [PubMed] [Google Scholar]
- Larson CE, Meng E, 2020. A review for the peripheral nerve interface designer. Journal of Neuroscience Methods 332, 108523. 10.1016/j.jneumeth.2019.108523 [DOI] [PubMed] [Google Scholar]
- Leventhal DK, Durand DM, 2003. Subfascicle stimulation selectivity with the flat interface nerve electrode. Ann Biomed Eng 31, 643–652. [DOI] [PubMed] [Google Scholar]
- Liu A, Joe B, 1994. Relationship between tetrahedron shape measures. BIT 34, 268–287. 10.1007/BF01955874 [DOI] [Google Scholar]
- Lubba CH, Le Guen Y, Jarvis S, Jones NS, Cork SC, Eftekhar A, Schultz SR, 2019. PyPNS: Multiscale Simulation of a Peripheral Nerve in Python. Neuroinformatics 17, 63–81. 10.1007/s12021-018-9383-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandge D, Manchanda R, 2018. A biophysically detailed computational model of urinary bladder small DRG neuron soma. PLOS Computational Biology 14, e1006293. 10.1371/journal.pcbi.1006293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark, 2009. The Polymer Data Handbook, 2 edition. ed. Oxford University Press USA, Oxford; New York. [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV, 2004. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J Neurophysiol 91, 1457–1469. 10.1152/jn.00989.2003 [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM, 2002. Modeling the Excitability of Mammalian Nerve Fibers: Influence of Afterpotentials on the Recovery Cycle. Journal of Neurophysiology 87, 995–1006. 10.1152/jn.00353.2001 [DOI] [PubMed] [Google Scholar]
- Middleton JW, Keast JR, 2004. Artificial autonomic reflexes: using functional electrical stimulation to mimic bladder reflexes after injury or disease. Autonomic Neuroscience 113, 3–15. 10.1016/j.autneu.2004.04.008 [DOI] [PubMed] [Google Scholar]
- Musselman ED, Cariello JE, Grill WM, Pelot NA, 2021. ASCENT (Automated Simulations to Characterize Electrical Nerve Thresholds): A pipeline for sample-specific computational modeling of electrical stimulation of peripheral nerves. PLOS Computational Biology 17, e1009285. 10.1371/journal.pcbi.1009285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama H, Noda K, Hotta H, Ohsawa H, Hosoya Y, 1998. Effects of aging on numbers, sizes and conduction velocities of myelinated and unmyelinated fibers of the pelvic nerve in rats. Journal of the Autonomic Nervous System 69, 148–155. 10.1016/S0165-1838(98)00013-7 [DOI] [PubMed] [Google Scholar]
- Nicholson PW, 1965. Specific impedance of cerebral white matter. Experimental Neurology 13, 386–401. 10.1016/0014-4886(65)90126-3 [DOI] [PubMed] [Google Scholar]
- Ohana M, Moser T, Moussaouï A, Kremer S, Carlier RY, Liverneaux P, Dietemann J-L, 2014. Current and future imaging of the peripheral nervous system. Diagnostic and Interventional Imaging 95, 17–26. 10.1016/j.diii.2013.05.008 [DOI] [PubMed] [Google Scholar]
- Osborne PB, 2017. Stimulating bioelectronic medicine discovery for urological disorders. American Journal of Physiology-Renal Physiology 313, F1133–F1135. 10.1152/ajprenal.00372.2017 [DOI] [PubMed] [Google Scholar]
- Ouyang Z, Sperry ZJ, Barrera ND, Bruns TM, 2019. Real-Time Bladder Pressure Estimation for Closed-Loop Control in a Detrusor Overactivity Model. IEEE Transactions on Neural Systems and Rehabilitation Engineering 27, 1209–1216. 10.1109/TNSRE.2019.2912374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker JL, Shariati NH, Karantonis DM, 2017. Electrically evoked compound action potential recording in peripheral nerves. Bioelectronics in Medicine 1, 71–83. 10.2217/bem-2017-0005 [DOI] [Google Scholar]
- Payne SC, Burns O, Stebbing M, Thomas R, Silva A. de, Sedo A, Weissenborn F, Hyakumura T, Huynh M, May CN, Williams RA, Furness JB, Fallon JB, Shepherd RK, 2018. Vagus nerve stimulation to treat inflammatory bowel disease: a chronic, preclinical safety study in sheep. Bioelectronics in Medicine 1, 235–250. 10.2217/bem-2018-0011 [DOI] [Google Scholar]
- Payne SC, Wiedmann NM, Eiber CD, Wong AW, Senn P, Osborne PB, Keast JR, Fallon JB, 2020. Recording of Electrically Evoked Neural Activity and Bladder Pressure Responses in Awake Rats Chronically Implanted With a Pelvic Nerve Array. Front. Neurosci. 14. 10.3389/fnins.2020.619275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelot NA, 2021. Quantified Morphology of the Rat Vagus Nerve [WWW Document]. Quantified Morphology of the Rat Vagus Nerve. URL 10.26275/ILB9-0E2A [DOI] [Google Scholar]
- Pelot NA, Behrend CE, Grill WM, 2019. On the parameters used in finite element modeling of compound peripheral nerves. Journal of Neural Engineering 16, 016007. 10.1088/1741-2552/aaeb0c [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelot NA, Catherall DC, Thio BJ, Titus ND, Liang ED, Henriquez CS, Grill WM, 2020a. Excitation Properties of Computational Models of Unmyelinated Peripheral Axons. Journal of Neurophysiology. https://doi.org/10/ghjh9m [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelot NA, Goldhagen GB, Cariello JE, Musselman ED, Clissold KA, Ezzell JA, Grill WM, 2020b. Quantified Morphology of the Cervical and Subdiaphragmatic Vagus Nerves of Human, Pig, and Rat. Front. Neurosci. 14. 10.3389/fnins.2020.601479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prechtl JamesC., Powley TerryL., 1990. The fiber composition of the abdominal vagus of the rat. Anat Embryol 181. 10.1007/BF00198950 [DOI] [PubMed] [Google Scholar]
- Raspopovic S, Petrini FM, Zelechowski M, Valle G, 2017. Framework for the Development of Neuroprostheses: From Basic Understanding by Sciatic and Median Nerves Models to Bionic Legs and Hands. Proceedings of the IEEE 105, 34–49. 10.1109/JPROC.2016.2600560 [DOI] [Google Scholar]
- Rattay F, 1986. Analysis of models for external stimulation of axons. IEEE Trans Biomed Eng 33, 974–977. [DOI] [PubMed] [Google Scholar]
- Ravagli E, Mastitskaya S, Thompson N, Welle EJ, Chestek CA, Aristovich K, Holder D, 2021. Fascicle localisation within peripheral nerves through evoked activity recordings: A comparison between electrical impedance tomography and multi-electrode arrays. Journal of Neuroscience Methods 358, 109140. 10.1016/j.jneumeth.2021.109140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romeni S, Valle G, Mazzoni A, Micera S, 2020. Tutorial: a computational framework for the design and optimization of peripheral neural interfaces. Nature Protocols 15, 3129–3153. 10.1038/s41596-020-0377-6 [DOI] [PubMed] [Google Scholar]
- Sahyouni R, Chang DT, Moshtaghi O, Mahmoodi A, Djalilian HR, Lin HW, 2017. Functional and Histological Effects of Chronic Neural Electrode Implantation. Laryngoscope Investig Otolaryngol 2, 80–93. 10.1002/lio2.66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta JN, Gebhart GF, 1994. Mechanosensitive properties of pelvic nerve afferent fibers innervating the urinary bladder of the rat. Journal of Neurophysiology 72, 2420–2430. 10.1152/jn.1994.72.5.2420 [DOI] [PubMed] [Google Scholar]
- Shea VK, Cai R, Crepps B, Mason JL, Perl ER, 2000. Sensory Fibers of the Pelvic Nerve Innervating the Rat’s Urinary Bladder. Journal of Neurophysiology 84, 1924–1933. 10.1152/jn.2000.84.4.1924 [DOI] [PubMed] [Google Scholar]
- Smets H, Stumpp L, Julémont N, Cury J, Debelle A, Innocenti B, Vespa S, Haut B, Doguet P, Vanhoestenberghe A, Delbeke J, Tahry RE, Nonclercq A, 2021. Analysing vagus nerve spontaneous activity using finite element modelling. J. Neural Eng. 10.1088/1741-2552/abe68f [DOI] [PubMed] [Google Scholar]
- Soltanpour N, Santer RM, 1996. Preservation of the cervical vagus nerve in aged rats: morphometric and enzyme histochemical evidence. Journal of the Autonomic Nervous System 60, 93–101. 10.1016/0165-1838(96)00038-0 [DOI] [PubMed] [Google Scholar]
- Sperry ZJ, Na K, Parizi SS, Chiel HJ, Seymour J, Yoon E, Bruns TM, 2018. Flexible microelectrode array for interfacing with the surface of neural ganglia. J Neural Eng 15, 036027. 10.1088/1741-2552/aab55f [DOI] [PMC free article] [PubMed] [Google Scholar]
- Struijk JJ, 1997. The extracellular potential of a myelinated nerve fiber in an unbounded medium and in nerve cuff models. Biophys J 72, 2457–2469. 10.1016/S0006-3495(97)78890-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan AE, Tappan SJ, Angstman PJ, Rodriguez A, Thomas GC, Hoppes DM, Abdul-Karim MA, Heal ML, Glaser JR, 2020. A comprehensive, FAIR file format for neuroanatomical structure modeling. bioRxiv 2020.09.22.306670. 10.1101/2020.09.22.306670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundt D, Gamper N, Jaffe DB, 2015. Spike propagation through the dorsal root ganglia in an unmyelinated sensory neuron: a modeling study. Journal of Neurophysiology 114, 3140–3153. https://doi.org/10/f747js [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward MP, Gupta A, Wo JM, Rajwa B, Furness JB, Powley TL, Nowak TV, 2020a. An emerging method to noninvasively measure and identify vagal response markers to enable bioelectronic control of gastroparesis symptoms with gastric electrical stimulation. J Neurosci Methods 336, 108631. 10.1016/j.jneumeth.2020.108631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward MP, Pelot NA, Biscola NP, Pena E, Jaffey D, Havton LA, Grill WM, Powley TL, 2020b. SPARC: A Hybrid Computational Approach to Classify Vagal C Fiber Functions. The FASEB Journal 34, 1–1. 10.1096/fasebj.2020.34.s1.09657 [DOI] [Google Scholar]
- Ward MP, Qing KY, Otto KJ, Worth RM, John SWM, Irazoqui PP, 2015. A Flexible Platform for Biofeedback-Driven Control and Personalization of Electrical Nerve Stimulation Therapy. IEEE Transactions on Neural Systems and Rehabilitation Engineering 23, 475–484. 10.1109/TNSRE.2014.2351271 [DOI] [PubMed] [Google Scholar]
- Wenzel BJ, Boggs JW, Gustafson KJ, Grill WM, 2006. Closed Loop Electrical Control of Urinary Continence. The Journal of Urology 175, 1559–1563. 10.1016/S0022-5347(05)00657-9 [DOI] [PubMed] [Google Scholar]
- Wijesinghe RS, Gielen FLH, Wikswo JP, 1991. A model for compound action potentials and currents in a nerve bundle III: A comparison of the conduction velocity distributions calculated from compound action currents and potentials. Ann Biomed Eng 19, 97–121. 10.1007/BF02368462 [DOI] [PubMed] [Google Scholar]
- Williams PE, Lowry A, Hill R, Masson E, 2000. Relationship between fascicle size and perineurial collagen IV content in diabetic and control human peripheral nerve. Histopathology 36, 551–555. 10.1046/j.1365-2559.2000.00897.x [DOI] [PubMed] [Google Scholar]
- Yoshimura N, Seki S, Erickson KA, Erickson VL, Chancellor MB, Groat W.C. de, 2003. Histological and Electrical Properties of Rat Dorsal Root Ganglion Neurons Innervating the Lower Urinary Tract. The Journal of Neuroscience 23, 4355–4361. 10.1523/JNEUROSCI.23-10-04355.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimura N, White G, Weight FF, Groat W.C. de, 1996. Different types of Na+ and A-type K+ currents in dorsal root ganglion neurones innervating the rat urinary bladder. The Journal of Physiology 494, 1–16. 10.1113/jphysiol.1996.sp021471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagorodnyuk VP, Gibbins IL, Costa M, Brookes SJH, Gregory SJ, 2007. Properties of the major classes of mechanoreceptors in the guinea pig bladder. J Physiol 585, 147–163. 10.1113/jphysiol.2007.140244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanos S, 2018. Closed-Loop Neuromodulation in Physiological and Translational Research. Cold Spring Harb Perspect Med a034314. 10.1101/cshperspect.a034314 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.