Abstract
The cornea is a highly specialized organ that relies on its mechanical stiffness to maintain its aspheric geometry and refractive power, and corneal diseases such as keratoconus have been linked to abnormal tissue stiffness and biomechanics. Dynamic optical coherence elastography (OCE) is a clinically promising non-contact and non-destructive imaging technique that can provide measurements of corneal tissue stiffness directly in vivo. The method relies on the concepts of elastography where shear waves are generated and imaged within a tissue to obtain mechanical properties such as tissue stiffness. The accuracy of OCE-based measurements is ultimately dependent on the mathematical theories used to model wave behavior in the tissue of interest. In the cornea, elastic waves propagate as guided wave modes which are highly dispersive and can be mathematically complex to model. While recent groups have developed detailed theories for estimating corneal tissue properties from guided wave behavior, the effects of intraocular pressure (IOP)-induced prestress have not yet been considered. It is known that prestress alone can strongly influence wave behavior, in addition to the associated non-linear changes in tissue properties. This present study shows that failure to account for the effects of prestress may result in overestimations of the corneal shear moduli, particularly at high IOPs. We first examined the potential effects of IOP and IOP-induced prestress using a combination of approximate mathematical theories describing wave behavior in thin plates with observations made from data published in the OCE literature. Through wave dispersion analysis, we deduce that IOP introduces a tensile hoop stress and may also influence an elastic foundational effect that were observable in the low-frequency components of the dispersion curves. These effects were incorporated into recently developed models of wave behavior in nearly incompressible, transversely isotropic (NITI) materials. Fitting of the modified NITI model with ex vivo porcine corneal data demonstrated that incorporation of the effects of IOP resulted in reduced estimates of corneal shear moduli. We believe this demonstrates that overestimation of corneal stiffness occurs if IOP is not taken into consideration. Our work may be helpful in separating inherent corneal stiffness properties that are independent of IOP; changes in these properties and in IOP are distinct clinically relevant issues that affect the cornea health.
INTRODUCTION
Tissue stiffness is an important biomechanical property that helps the cornea maintain its aspheric geometry and therefore its refractive power and visual function (Girard et al., 2015; Hon et al., 2017; Matalia et al., 2017; Mikula et al., 2018; Whitford et al., 2015). Irregularities in the corneal shape are common causes of impaired vision, and diseases such as keratoconus have been linked to abnormal tissue stiffness and biomechanics (Andreassen et al., 1980; Nash et al., 1982; Vellara and Patel, 2015). Furthermore, tissue stiffness has been shown to play a direct role in corneal cell mechanosignaling and in the maintenance of limbal stem cells (Eberwein and Reinhard, 2015; Gouveia et al., 2019a, 2019b; Jones et al., 2012; Sun et al., 2021). Currently, there are no clinically available imaging methods that can non-invasively provide direct, quantitative measurements of corneal stiffness, and thus, our understanding of its role in corneal health and disease is limited. However, the recent development of optical coherence elastography (OCE) technology has allowed for a fully non-contact and non-destructive method of measuring tissue stiffness directly within the cornea (Ambroziński et al., 2016; Han et al., 2017; Nair et al., 2020; Pitre et al., 2020; Singh et al., 2017; Wang and Larin, 2014; Zhou et al., 2019). OCE relies on the principles of elastography where mechanical shear waves are generated and tracked as they propagate through a tissue. The shear wave behavior is dependent on the tissue mechanical properties, and therefore, information such as tissue stiffness and viscosity can be obtained through wave analysis. Several groups have already demonstrated considerable clinical potential with the first studies involving human participants recently being published (Lan et al., 2021b, 2021a; Ramier et al., 2020; Ye et al., 2021). The development of OCE may open new clinical opportunities to evaluate corneal stiffness in the context of disease progression and surgical treatments. With a means to directly image tissue stiffness in vivo, OCE may also help translate in vitro findings in the field of cellular mechanobiology and improve our understanding on the biomechanical forces present on a macroscopic scale in organ systems and biomaterials (Hadden et al., 2017; Kennedy et al., 2015).
Accurate quantitation of corneal tissue stiffness using OCE ultimately relies on the underlying mathematical theories used to model wave behavior in the cornea. It has been shown that elastic waves propagate as guided Lamb or Rayleigh-Lamb waves in the cornea where the tissue’s plate-like geometry acts as a waveguide (Han et al., 2015). Mathematically, guided wave theory is complicated even for the simplest of cases. Two groups have currently developed mathematical models to specifically describe guided wave propagation in the cornea. Han et al. incorporated a one-sided fluid loading to a plate structure which consisted of a free anterior boundary and a fluid-loaded posterior boundary representing the aqueous humor (Han et al., 2017, 2015). This model was termed the modified Rayleigh-Lamb frequency equation (mRLFE) and demonstrated that fluid loading slows the wave velocities, and an underestimation of the corneal shear modulus occurs if the fluid effect is not taken into account. A second more recent model was developed by Pitre et al. and utilized a similar approach (Pitre et al., 2020). Importantly, this group demonstrated that the layered corneal tissue is a nearly incompressible, transverse isotropic (NITI) material that requires two shear moduli, in-plane and out-of-plane. Their work provides an explanation for the order of magnitude difference in corneal moduli observed between the newer OCE and shear-based methods of mechanical measurements with those of more traditional destructive tensile and compressive testing. This is significant as it helps to integrate OCE studies with both the existing literature and clinical understanding of corneal mechanical properties.
A limitation of OCE is that corneal stiffness estimates can be strongly influenced by IOP (Ambroziński et al., 2016; Han et al., 2017; Pitre et al., 2020; Singh et al., 2017; Zhou et al., 2019). The eye can be simplified as an internally pressurized spherical structure where the IOP prestresses the walls of the ocular tissue (Chung et al., 2016; Pierscionek et al., 2007; Purslow and Karwatowski, 1996). Due to the non-linear mechanical properties of biological tissue, prestress will directly affect tissue stiffness, and therefore, IOP and corneal stiffness are inherently related. Any separation of the two properties is technologically challenging and has been argued whether possible. This problem is not only apparent in OCE but is present in nearly all methods used to measure mechanical properties of the eye in situ. For instance, in tonometry, the clinical standard for assessing IOP, abnormal corneal stiffness or geometry can introduce significant inaccuracies in IOP estimates (Colakoglu et al., 2021; Costin et al., 2014; Kwon et al., 2008; Lu et al., 2019; Vinciguerra et al., 2020). While IOP-induced prestress indeed will cause a non-linear response in the cornea, it is known that prestress alone can strongly affect elastic wave behavior (Pau and Lanza di Scalea, 2015; Peddeti and Santhanam, 2018). This is seen particularly in the fields of muscle and tendon elastography where muscle or tendon activity can induce very large changes in shear wave velocities (Bernabei et al., 2019; Martin et al., 2018; Wang et al., 2019). This effect on wave behavior has been attributed to tensile loading, rather than actual changes in tissue properties. While the tensile effects may not be as extreme in the cornea, we theorize that tensile prestress may be causing an overestimation of the non-linear response of the corneal tissue due to IOP fluctuations, particular at high pressures.
In this work, we evaluate the effects of IOP on corneal wave behavior to determine if normal levels of IOP can induce significant changes in guided wave dispersion. Our goal was to determine whether an overestimation of corneal stiffness occurs if prestress was not accounted for and if it is possible to correct for this overestimation. We first speculated that IOP and corneal stiffness will differentially affect elastic waves of different frequencies. Low frequency waves are more strongly influenced by the effects of preload and less affected by the properties of the material. In contrast, high frequency waves are more affected by the material properties due to their short wavelengths (Chen and Wilcox, 2007; Mazzotti et al., 2012; Song et al., 2013). We hypothesized that the analysis of low and high frequency regions of wave dispersion behavior may be able to discern the effects of IOP and corneal stiffness. A combination of mathematical modeling, and experimental data of ex vivo porcine corneas were used in this study. The results supported our theory that IOP can introduce a tensile prestress effect that is able to considerably increase wave velocities. Additionally, we observed a low-frequency cutoff behavior that was influenced by IOP. This phenomenon was mathematically modeled with the incorporation of an elastic spring foundation. Our findings were integrated into the NITI equations of motion modeling guided wave behavior in the cornea developed by Pitre et al. Fitting of the modified NITI model with ex vivo porcine corneal data resulted in lower shear moduli estimates that were less influenced by IOP. We believe that this method provides a more accurate estimate of the non-linear corneal tissue response to IOP.
THEORY AND CALCULATIONS
Approximate Thin-Plate Theory: Incorporation of Prestress and Foundational Effects
The approximate theory describing the dynamic motion of thin plates was first evaluated for the understanding of the effects of IOP. The thin-plate theory is an extension of the Euler-Bernoulli beam model where the assumption is made that displacements do not vary through the thickness of the material. It should be noted that this assumption is only valid for elastic waves with wavelengths substantially greater than the plate thickness; this would correspond to the lower range of frequencies of interest in the present study. The equation of motion governing the dynamic behavior of an isotropic, homogenous, and linear elastic thin plate is given as:
| (1) |
where and is the Young’s modulus, v is the Poisson’s ratio, ρ is the material density, h is the material thickness, w is the displacement field, and ẅ denotes the second-order partial derivative with respect to time. Tensile prestress was incorporated as a second-order spatial derivative by analogy to the derivation of the equations of motion for an ideal string or membrane:
| (2) |
where and is the circumferential hoop stress induced by IOP. Fully expanded, Eq. (2) takes the form:
| (3) |
where the subscripts denote partial differentials. With a plane wavefront assumption, partial derivatives with respect to y can be ignored and the equation simplifies to:
| (4) |
The general solution for Eq. (4) is given in the form:
| (5) |
where k is the angular wavenumber (), ω is the angular frequency (), and . Using the solution defined in Eq. (5), the dispersion relationship of Eq. (4) can be solved for and is given as:
| (6) |
Eq. (6) can be used to assess the effects of tensile prestress and stiffness on wave dispersion in thin-plate structures. In order to incorporate the theorized elastic foundational effect related to IOP, the spring constant term Ka was introduced which represents the “approximate theory spring constant” per unit area (). The spring constant term is capitalized to avoid confusion with the wavenumber k. Incorporation of the foundational term into Eq. (4) was done accordingly:
| (7) |
And solving for the dispersion relationship results in the equation:
| (8) |
The cutoff frequency of the dispersion curves, , can be determined by setting k = 0. is therefore defined as:
| (9) |
The cutoff frequency is only dependent on the spring constant per unit area (Ka), material density (ρ) and thickness (h). Eq. (8) can be used to assess the effects of prestress, stiffness, and the elastic foundation on wave behavior in thin plates.
Modified NITI model: Incorporation of Prestress and Foundational Effects
After examining the effects of tensile prestress and foundational loading in the approximate thin-plate model, integration of prestress and foundational loading into a more accurate theory describing wave behavior in a cornea-like structure was explored. The work of Han et al. and Pitre et al. are two of the most comprehensive theories published in the OCE literature thus far. Here, the effects of IOP were incorporated into the nearly incompressible, transverse isotropic (NITI) model of the cornea developed by Pitre et al. In this model the cornea, itself, resides in the plane of isotropy and the axis of isotropy is normal to the cornea. Addition of the tensile prestress and spring foundational terms into the equations of motion of a NITI material are highlighted in bold. The terms in blue represent the changes resulting from incorporation of tensile prestress while those in red are from the addition of the elastic foundation. Here, the foundational effect was incorporated as a boundary condition rather than directly into the governing equations of motion as in the approximate theory. The system was solved for in the dimensionless form and all variables were defined according to the work of Pitre et al. (Pitre et al., 2020). Non-dimensionalization of the equations was performed using the following scales where the subscripts denote the scaling factors:
The linearized unstressed material properties of the NITI material were defined via the stiffness tensor and the stress-strain relationship as:
| (10) |
Here the subscripts denote stress and strain directions, G is the out-of-plane shear modulus, μ is the in-plane shear modulus, and λ is the first Lamé parameter. A plane wavefront assumption is made and therefore only displacements with respect to x and z are considered. Adapting acoustoelastic analyses that can be found in the seminal text of Biot (Biot, 1965), or in more recent studies, such as Singh et al. (Singh et al., 2010), the governing equations of motion for the NITI system are derived in their dimensionless form:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Here, is defined as the dimensionless displacement field with x and z components, respectively. The parameters , , and are the dimensionless parameters with representing the additional tensile prestress term. σθ is defined as the circumferential hoop stress induced by IOP. Note, the above formulation, based inherently on a small strain assumption due to the applied stress, can be made to match predictions of phase speed in isotropic (Gennisson et al., 2007) and transverse isotropic (Remeniares et al., 2021) acoustoelastic models that allow for larger strain values by appropriate choice of third order Landau coefficients. For the isotropic case, this is achieved by setting the 3rd order coefficient in the references “A” equal to −6G, which is within the range of values reported for agar-gelatin and polyvinyl alcohol soft tissue phantom materials based on ultrasound elastography measurements under compressive stress loading. For the transverse isotropic case, three additional 3rd order Landau coefficients in the second reference are set to specific values to match the small strain assumption used in the formulation presented here in equations (11–12).
In the following we’ll assume that and . Thus, in equations (11–12), , and thus will be ignored in the last two terms for the following derivations. The general harmonic solutions are assumed in the form:
| (17) |
| (18) |
Here, k and 𝑙 are the dimensionless angular wavenumbers, ω is the dimensionless angular frequency, and 𝐴 and 𝐵 are arbitrary coefficients denoting the amplitude of the harmonic waves. The dispersion relationship is solved for in the same manner as described in Pitre’s work where substitution of the solutions (Eqs. (17 & 18)) into the governing equations (Eqs. (11 & 12)) results in the system:
| (19) |
| (20) |
| (21) |
The linear system of equations defined in Eq. (19) has non-trivial solutions if and only if the determinant of the matrix is zero. This results in a biquadratic equation for 𝑙 with four solutions, expressed as below, assuming .
| (22) |
Here
| (23) |
| (24) |
From the linear system defined in Eq. (19), B = 1 can be assumed without loss of generality and the coefficient A can be solved for in terms of each solution of l. This results in the following solutions where the inner and outer ± signs match for each of the four solutions of A and l:
| (25) |
The full solutions are defined as linear combinations of four partial waves:
| (26) |
| (27) |
The effects of the elastic foundation were incorporated into the fluid domain equations that define the boundary condition of the posterior surface of the plate. Both Han et al. and Pitre et al. incorporated a one-sided unbounded fluid loading (fluid half-space) to represent the effects of the aqueous humor of the eye (Han et al., 2017, 2015; Pitre et al., 2020). In order to account for the finite bounds of the aqueous humor and the theorized elastic restoring effect of the surrounding tissue, we incorporate the additional foundational effect to the boundary conditions defined by Pitre et al. The fluid is assumed as an acoustic material and thus the acoustic wave equations can be applied. In the dimensionless form, the fluid domain equations are defined as:
| (28) |
Eq. (28) defines an irrotational flow where is the particle velocity with x- and z-components , , respectfully, and is the corresponding velocity potential. The dimensional acoustic wave equation in pressure form is given as:
| (29) |
Here is the compressional wave speed in the fluid and p is the pressure deviation. By introducing the scaling factor , the equation can be written in a dimensionless velocity potential form given as:
| (30) |
where,
| (31) |
The dimensional fluid pressure equation is defined as:
| (32) |
where ρfis the density of the fluid. The general solution for Eq. (30) is given as:
| (33) |
| (34) |
The solutions for the coefficients C1–4 defined in Eqs. (26 & 27) and C5 defined in Eq. (33) are chosen so that they satisfy the non-dimensional boundary conditions as defined by Pitre et al. and similarly by Han et al.
| (35) |
Here, and are defined via the stress-strain relationships given by Eq. (10) and as defined in Eq. (32). Here, we incorporate the elastic foundational effect by assuming that the restoring force q of the foundation is linearly proportional to the deflection it sustains:
| (36) |
Here, Ke is foundational spring constant per unit area () and is the z-component displacement of the fluid domain, which is equal to the displacement of the solid, v, at the solid-fluid interface (z = 0). The dimensional fluid pressure equation modified from Eq. (32) to incorporate the elastic foundational effect is given by (the added foundational terms are highlighted in bold red):
| (37) |
By using the scales:
Eq. (37) can be non-dimensionalized in the form:
| (38) |
where is the dimensionless spring constant parameter defined by:
| (39) |
Substituting the general solutions into the boundary conditions results in a 5×5 homogenous system for the coefficients as defined by matrix M:
Here, the term (highlighted in red) is a result of the additional effects of the elastic foundation. All l and A terms are modified due to the effects of the tensile prestress (highlighted in blue). A non-trivial solution for this system can be achieved by setting the determinant of the matrix equal to zero (det(M) = 0). The final solution is the characteristic equation that describes the relationship between the wavenumber and frequency and is therefore the dispersive behavior of the NITI system.
METHODS
Fitting of Experimental Data with Modified NITI Model
Fitting of ex vivo porcine data was performed using a simplex optimization method (fminsearch, MATLAB, MathWorks, Natick, MA) published in the original NITI study by Pitre et al. 2020 (a detailed description can be found their Supplementary Note 7). Briefly, initial guesses for all parameters were first supplied to compute the forward model. Various physical parameters were considered fixed including the corneal density (1000 kg/m3), mean corneal thickness (taken from OCT images, ~0.6 mm), longitudinal wave speed in the cornea (1540 m/s), density of water (1000 kg/m3), and the longitudinal wave speed in water (1480 m/s). The parameters allowed to vary include the out-of-plane shear modulus G, the in-plane shear modulus μ, and the additional parameters of prestress σθ and the foundational spring constant Ke that were incorporated into the original MATLAB scripts for the current study. The dispersion relation was computed for the given parameters and the A0 mode was extracted using a mode-tracing algorithm. A 7-point Gaussian-weighted window centered on the A0 mode of the dispersion curve was then computed and applied to the normalized power spectrum of the experimental OCE surface velocity data, obtained using a 2D Fourier transform. The optimization method iterates through parameters G, μ, σθ, and Ke and seeks to maximize the spectral energy of the data within the Gaussian-weighted window. It should be noted that a unique solution to this system does not exists if all four parameters are allowed to vary, and certain assumptions were required to arrive at a unique solution.
RESULTS AND DISCUSSION
Tensile Effect of IOP in the Isotropic Thin-Plate Theory
The eye can be modeled as an internally pressurized spherical vessel where an increase in the internal pressure strains the walls of the ocular tissue and induces a tensile, circumferential hoop stress (). The range of tensile stress can be roughly estimated using Laplace’s law for a spherical pressure vessel (Eq. (40)).
| (40) |
Here, P is the internal pressure, r is the radius of the sphere, and t is the thickness of the sphere walls. Although actual quantitative values are likely inaccurate as this represents a gross simplification of the ocular structure (Chung et al., 2016), the magnitude of hoop stresses induced by normal levels IOP can be roughly approximated. By assuming a radius of 10 mm and thickness of 0.6 mm, IOP values of 5, 10, 15, and 20 mmHg were estimated to induce hoop stresses of 5.56, 11.11, 16.67, and 22.22 kPa, respectively. To compare, finite element (FE) studies have also reported hoop stresses within the range of roughly 15–25 kPa around 15–18 mmHg IOP (Shih et al., 2017; Simonini and Pandolfi, 2015).
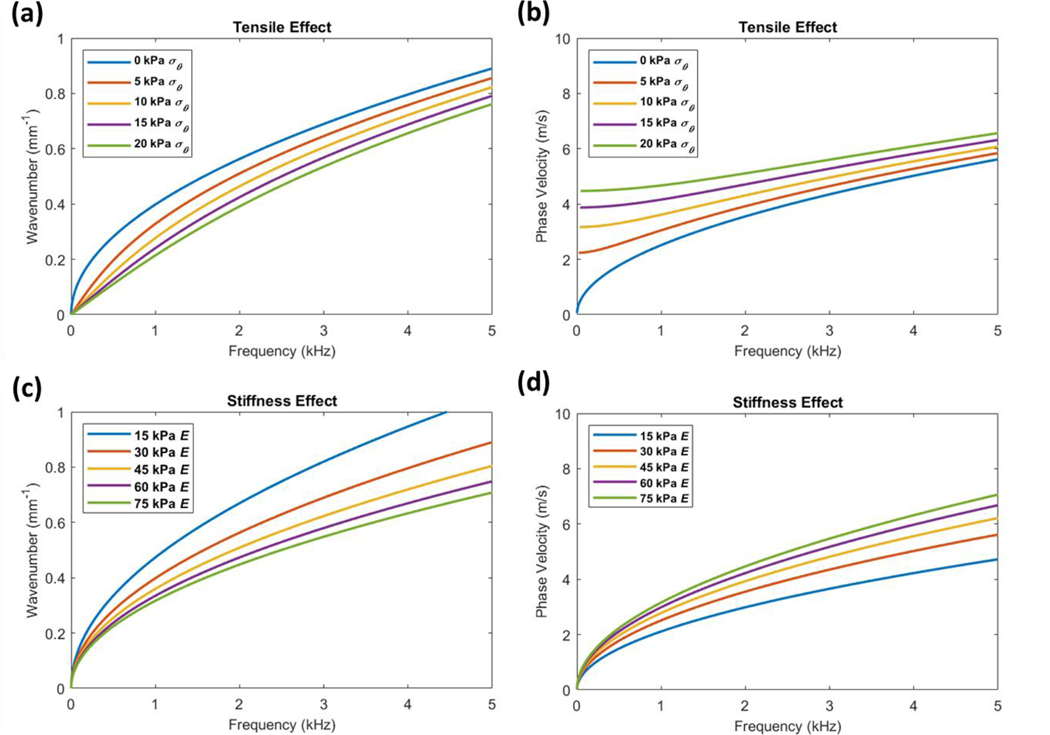
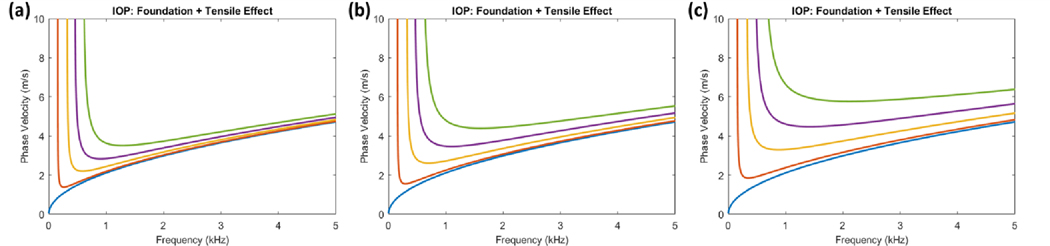
To evaluate whether tensile prestress within this range can influence wave dispersion, we first utilized the approximate mathematical theories describing wave behavior in thin-plate structures. The approximate thin-plate theories are greatly simplified from the exact theories of guided wave behavior due to the assumption that displacements do not vary through the plate thickness. This assumption is only valid for low-frequency elastic waves, and modeling of high-frequency waves which are normally used to estimate tissue stiffness may be inaccurate. We thus use the approximate thin-plate theory primarily as a qualitative assessment of the effects of IOP. Prestress was incremented between 0–20 kPa to estimate the tensile effect of IOP. For comparison to the effects of material stiffness, the Young’s modulus was also separately incremented between 15–75 kPa. Using the dispersion equation defined in Eq. (6), the linear wavenumber vs. frequency dispersion curves and their associated phase velocity curves were plotted (Figure 1).
Figure 1. Thin-plate theory for comparing the effects of tensile prestress and stiffness on wave dispersion.
(a) The linear wavenumber vs. frequency dispersion curves demonstrate that estimated prestress values σθ incremented between 0–2.0 × 104 Pa can alter wave behavior independently of material stiffness (where E = 3.0 × 104 Pa). (b) The corresponding phase velocity curves demonstrate that tension strongly influences low-frequency phase velocities while high-frequency waves are also affected. (c) Dispersion curves demonstrate that stiffness affects wave behavior similar to tension when incremented between 1.5–7.5 × 104 Pa (where σθ = 0 Pa), though its effects at high frequencies are more apparent. Additionally, when comparing (a) and (c), the low-frequency components below ~1 kHz are affected less by stiffness than tension. (d) This is reflected in the corresponding phase velocity curves where low frequency phase velocities are less influenced by stiffness. Further comparison of (b) and (d) show that both tension and stiffness can change the high-frequency phase velocities that are used to estimate corneal stiffness.
The results demonstrated that increasing both the tensile prestress and the stiffness terms can alter wave dispersion similarly. The slope of the dispersion curves decreases as both tension and material stiffness increase which corresponds to an increase in phase velocities. Importantly, this indicates that the high frequency asymptotes of the dispersion curves that are normally used to estimate corneal shear moduli can be significantly influenced by both prestress and stiffness. While both effects are similar, differences in the dispersion curves can be observed, particularly in the lower frequency regions. From the approximate thin-plate model, tensile prestress appears to strongly influence the low-frequency dispersion behavior, while the effects of stiffness are more apparent at higher frequencies. Though it still remains to be assessed whether this behavior is seen in the exact theories of guided waves, these results suggest that tensile prestress within the range predicted for normal IOP values can indeed influence wave behavior and that differential analysis of low- and high-frequency dispersion components may be able to help discern the effects of prestress and stiffness. We emphasize that if these prestress effects are not accounted for, an overestimation of corneal shear moduli may arise, particularly at high IOPs.
Foundational Effect of IOP in the Isotropic Thin-Plate Theory
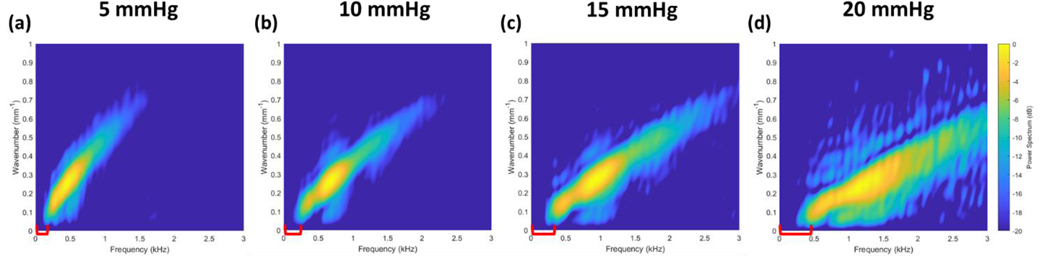
We next identify the presence of a low-frequency cutoff in the wave dispersion behavior that may be associated with IOP. We first begin with observations of existing data published by multiple groups in the OCE literature. Dispersion data acquired from ex vivo porcine corneas deviate strongly from predicted Rayleigh-Lamb wave dispersion curves at frequencies below 1–2 kHz (Ambroziński et al., 2016; Ramier et al., 2019). The phase velocity curves from these studies exhibit an asymptotic behavior where velocities increase rapidly and seemingly approach a vertical asymptote as the frequency approaches zero. Phase velocity is determined from the wavenumber-frequency relationship where . The asymptotic phase velocity behavior can arise when there is a frequency intercept in the dispersion curves where ω is positive as k approaches zero. Notably, the presence of this intercept can be observed in the experimental data recently published by the group of Pitre et al. (Pitre et al., 2020). The dataset shown in Figure 2 was kindly provided by Pitre’s group and was used throughout this work. The data consists of porcine corneas pressurized at 5, 10, 15, and 20 mmHg IOP and mechanically stimulated using a fully non-contact, acoustic micro-tapping technique (AμT).
Figure 2. Ex vivo porcine cornea dataset acquired at 5, 10, 15, and 20 mmHg IOP.
Acoustic micro-tapping method was used to generate elastic waves in whole globe porcine corneas pressurized at a) 5 mmHg b) 10 mmHg c) 15 mmHg and d) 20 mmHg (Pitre et al., 2020). The dispersion data is shown here as the linear wavenumber vs. frequency. A low-frequency intercept can be visually observed that increases with IOP (highlighted with red brackets).
We believe that a frequency intercept can be observed in this data which appears to increase with IOP (highlighted with red brackets). While we emphasize that interpretation of this low-frequency behavior is speculative and requires further validation, this observation may correspond with a shifting of the vertical asymptotes of the phase velocity curves to higher frequencies as seen in the results published by Ambroziński et al. (Ambroziński et al., 2016).
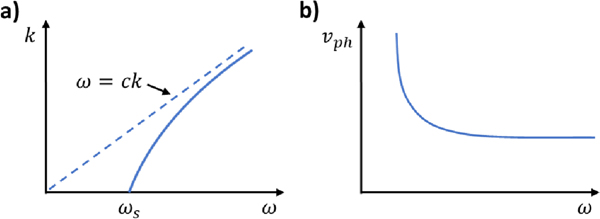
Interestingly, this asymptotic phase velocity behavior is seen when a waveguide is supported on a spring-like, elastic foundation. In this scenario, the foundational springs act as a high-pass filter where vibrational frequencies below the natural frequency of the springs () are cut off and do not propagate () (Figure 3a). This gives rise to the asymptotic phase velocity behavior as ω approaches the cutoff frequency ωS (Figure 3b).
Figure 3. Dispersion behavior of a thin plate supported by an elastic foundation.
(a) An elastic foundation introduces a cutoff frequency ωs to the dispersion relationship as seen in the k vs. ω dispersion curves. The dispersion relationship approaches that of a system without foundational effects at high frequencies. (b) An asymptotic behavior is seen in the phase velocity curves as ω approaches zero which is a result of the cutoff frequency ().
Waves below the cutoff frequency () exist as evanescent waves that decay rapidly with distance from the vibrational source. In comparison, vibrational frequencies above the natural frequency () are faster than the reaction time of the springs and will generate travelling waves. As the vibrational frequency increases, the dispersion behavior approaches that of a system without a spring foundation for . At the cutoff frequency (), the wavenumber k approaches zero, and thus the wavelength approaches infinity () which represents an oscillation of the entire bulk structure rather than a propagating wave. Here, the structure oscillates at the natural frequency of the springs which is determined by the foundational spring constant and the inertia involved. From observations of published OCE studies, we speculate that this low-frequency cutoff may be associated with the prestressed state of the eye that is induced by IOP.
Interpretation of this effect may arise from the inherent structure of the eye and represent a restoring force that is affected by the IOP. Notably, the study and applications of Winkler’s foundation may be particularly relevant for examining the origins of the foundational effect. Originally formulated in 1867, Winkler’s theory states that the restoring force q provided by an elastic foundation is linearly proportional to the deflection w it sustains by the relationship q = Kw, where K is the foundational spring constant. This theory has since been applied to a wide range of engineering problems. While more commonly applied to model the behavior of beams resting on elastic soil foundations, it has also been applied to the study of pressurized cylindrical tanks where the restoring force is not provided by a separate medium, but rather is due to the hoop stresses developed by material stretching as a result of internal pressure (Dillard et al., 2018; Hetenyi, M, 1946). We theorize that this may provide an explanation for the foundational effect seen in OCE studies which reflects the restoring force of the corneal tissue induced by IOP. This may provide a basis for assessing the IOP-induced prestressed state of the cornea, though we emphasize that care needs to be taken in the interpretation of this frequency cutoff and comprehensive studies are required before any conclusions can be made.
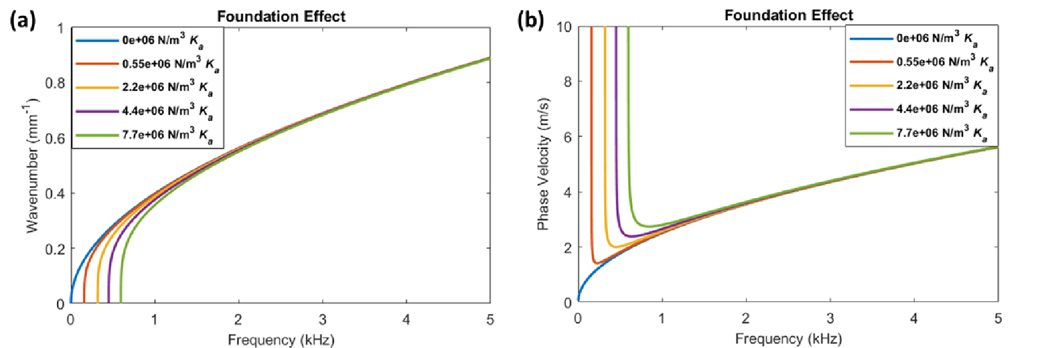
The foundational effect of IOP was mathematically incorporated into the approximate thin-plate theory by the addition of a spring constant term, which represents the “thin-plate spring constant” per unit area () as seen in Eq. (7). The resulting dispersion relationship of the system is given by Eq. (8). When the wavenumber is set to zero (k = 0), the cutoff frequency is defined by . The effects of incrementing the foundational spring constant on the dispersion curves are shown in Figure 4.
Figure 4. Thin-plate theory for modeling the effects of foundational loading on wave dispersion.
(a) The dispersion curves demonstrate a shifting of the frequency intercept as the foundational spring constant (Ka) is incremented from 0–7.7 × 104 N/m3 (where E = 3.0 × 104 Pa and σθ = 0 Pa). Only the low-frequency regions near the intercept are affected by the foundational loading and almost no change is seen at higher frequencies. (b) The corresponding phase velocity curves demonstrate an asymptotic behavior below approximately 1 kHz frequency which is a direct effect of the shifting frequency intercept. As the foundational spring constant increases, the vertical asymptote shifts to higher frequencies. This is compared to a system with no foundational loading (blue curve) where this asymptotic behavior is not seen.
The dispersion curves demonstrate a shifting of the cutoff frequency to higher values as Ka is increased (Figure 4a). While the very low-frequency components near the cutoff are affected by the foundational term, there are little to no changes in the high-frequency regions. The corresponding phase velocity curves demonstrate an asymptotic behavior below ~1 kHz, while all curves converge above ~3 kHz (Figure 4b). This suggests that the foundational effect is predominantly isolated to very low-frequency components of the dispersion curves which significantly contrasts to the effects seen with tension and stiffness (Figure 1). We hypothesize that due to the structure of the eye, IOP simultaneously introduces both a prestress on the ocular tissue walls and also a reactive or energy storage component that may be explained by the foundational effect, as discussed above. We believe these effects will occur in addition to any non-linear changes in tissue properties induced by IOP. For visualization of this concept, here we assume that the prestress σθ and foundational spring constant Ka are linearly proportional by a constant, 𝜙 (Eq. (41)). Figure 5 demonstrates the possible dispersion behavior as IOP is increased.
Figure 5. Modeling the combined tensile and foundational effects of IOP using thin-plate theory.
The tensile and foundational effects of IOP were assumed to be proportional by a constant for visualization. The foundational spring constant Ka in the thin-plate theory was incremented from 0, 5.5 × 10−7, 2.2 × 10−6, 4.4 × 10−6, and 7.7 × 10−6 N/m3 and the tensile prestress σθ was calculated based on a proportionality constant ϕ (Eq. (41)) which was set at (a) 0.5e-06, (b) 1.0e-06, and (c) 2.0e-06. E was set to 1.5 × 104 Pa for all simulations.
| (41) |
Here, the foundational spring constant was incremented, and the prestress was calculated via the proportionality constant. Figures 5a, b, and c demonstrate the effects of increasing the proportionality constant relating tension and foundation. We reiterate that this is meant as a qualitative assessment of the potential relationship between prestress and the theorized foundational effect. Whether such a relation exists remains to be evaluated. Additionally, while the foundational effect provides an explanation for the strongly deviating low-frequency regions of phase velocity curves reported by Ambroziński et al. and Ramier et al., and also the cutoff frequency observed in the work of Pitre et al., both the validity and the origin of this effect still remain to be examined.
Influence of Prestress and Foundational Effects on the Guided Wave Behavior in a Bounded NITI Medium
To reiterate, we hypothesize that the currently reported non-linear response of the corneal tissue due to IOP overestimates the change in shear moduli because IOP-induced prestress is not explicitly taken into account. We believe that accounting for both the tensile prestress and foundational effects associated with IOP can provide corneal shear moduli estimates that are less dependent on preload. While the approximate thin-plate theory provides a qualitative understanding of the effects of IOP on the dispersion behavior of the cornea, it can result in significant quantitative inaccuracies of corneal stiffness at high frequencies as the thin-plate assumption is only valid at low frequencies. We thus turn to more accurate theories of wave behavior in the cornea to estimate corneal shear moduli. Pitre et al.’s NITI model of guided wave behavior in a cornea-like plate was used as it accounts for both the posterior fluid loading of the aqueous humor and the transverse isotropy of the corneal tissue (Pitre et al., 2020). The incorporation of the tensile and foundational terms is detailed in Eqs. (11–39). Notably, the elastic foundation was added as a boundary condition (Eqs. (36–39)) rather than directly into the equations of motion as was done in the approximate thin-plate theory (Eqs. (7 & 8)). Here, we highlight that the thesis work of James Lloyd (1962) was particularly useful in examining the different effects of an elastic foundation between the approximate and the exact theories (Lloyd, 1962). The system was solved for in the non-dimensional form in the same manner as detailed in Pitre’s work.
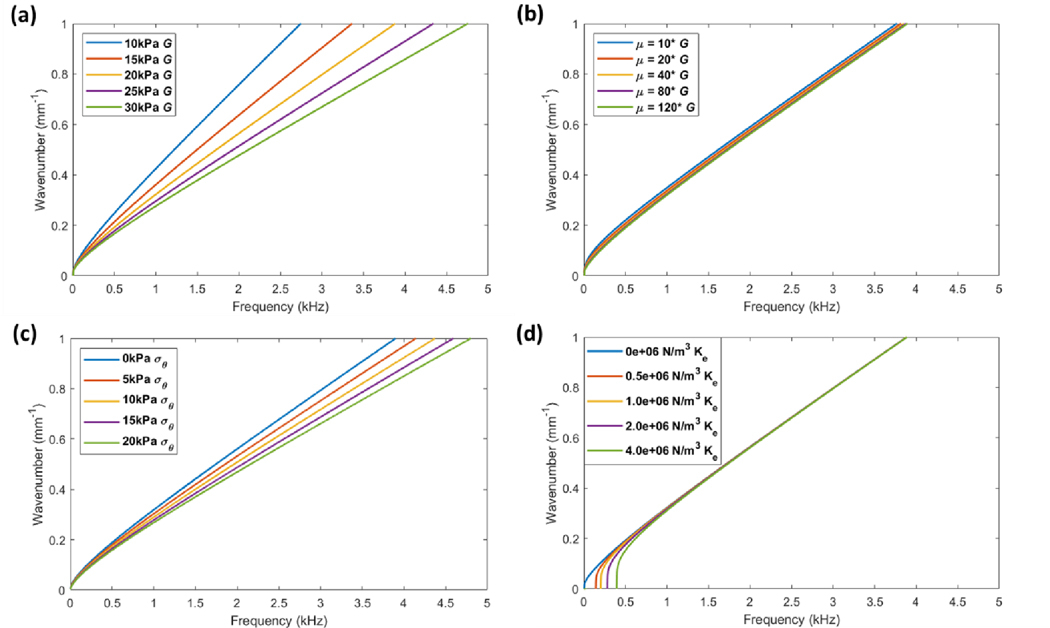
The foundational spring constant, tensile prestress, and shear moduli terms were each incremented in parametric studies to determine their effects on guided wave dispersion. The results are presented in Figure 6, where all dispersion curves represent the lowest order antisymmetric guided wave mode of the system (A0).
Figure 6. Parametric studies evaluating the effects of out-of-plane shear modulus (G), in-plane shear modulus (μ), tensile prestress (σθ), and foundational spring constant (Ke) on wave dispersion behavior.
Linear wavenumber vs. frequency relationships are plotted where all curves represent the lowest order antisymmetric mode (A0). (a) Incrementation of G between 1.0–3.0 × 104 Pa demonstrates significant changes in dispersion (where μ = 100*G, σθ= 0 Pa, Ke = 0 N/m3). (b) Incrementation of μ between 0.15–9.6 × 106 Pa demonstrates minimal effects on the A0 mode (where G = 2 × 104 Pa, σθ= 0 Pa, Ke = 0 N/m3). (c) Incrementation of prestress from 0–2.0 × 104 Pa demonstrates significant effects on the A0 mode (where G = 2 × 104 Pa, μ = 2 × 106 Pa, Ke = 0 N/m3). The effects of prestress are similar to that of G. (d) Incrementation of the foundational spring constant between 0–4.0 × 106 N/m3 demonstrates changes in the low-frequency cutoff between 0–0.5 kHz (where G = 2 × 104 Pa, μ = 2 × 106 Pa, σθ= 0 Pa). No changes in the A0 mode are observed at higher frequencies.
The results from the modified NITI theory are similar to those obtained from the approximate thin-plate theory with several notable differences. First, two uncoupled shear moduli are used to describe the transverse isotropy of the cornea in the exact theory; G represents the out-of-plane shear modulus while μ is the in-plane shear modulus. From Figures 6a–b, it can be seen that the A0 mode is predominantly affected by G (incremented between 10–30 kPa) while minimal effects are seen when μ is incremented by over an order of magnitude (0.15–9.6 MPa). This is in agreement with findings described by Pitre et al. When assessing the effect of prestress in Figure 6c, significant changes in the dispersion behavior can be seen for prestress values between 0–20 kPa. Here, the effects are more prominent when compared to the results from the approximate theory (Figure 1). This may be due to the uncoupling of G and μ and the fact that tensile prestress was only incorporated into the equation of motion describing shear wave behavior (Eq. (12)) and omitted from the compression wave equation (Eq. (11)) in this study. Nevertheless, this demonstrates that tensile prestress is able to significantly alter dispersion behavior independently of changes in material stiffness.
Further analysis demonstrates that both prestress and stiffness affect dispersion behavior similarly (Figure 6a & 6c), which differs from the results obtained in the thin-plate approximations (Figure 1). This is likely due to the fact that higher order derivatives were used in the approximate theory where the stiffness term appeared as a coefficient of a fourth-order spatial derivative (Eq. (1)) while the prestress term is a coefficient of a second-order spatial derivative (Eq. (2)). Thus, in the thin-plate model, the effects of stiffness and prestress are distinct and can be more easily separated. In comparison, the modified NITI model incorporates both prestress and the shear modulus G as coefficients of second-order spatial derivatives, though the stiffness term is coupled in two equations of motion (Eqs. (11–12)). Here, both prestress and stiffness affect all frequency components of the dispersion curves similarly and discerning the two properties is difficult, if possible. Shown in Figure 6d, the dispersion effects of incrementing the foundational spring constant between were similar to those observed in the approximate theory (Figure 4). As the spring constant is increased, the low-frequency cutoff shifts to higher frequencies. At frequencies above several kilohertz, the dispersion curves all converge to a system without foundational loading, and therefore the foundational effects are isolated to very low frequencies near the cutoff.
Fitting of Modified NITI Theory with Ex Vivo Porcine Corneal Data
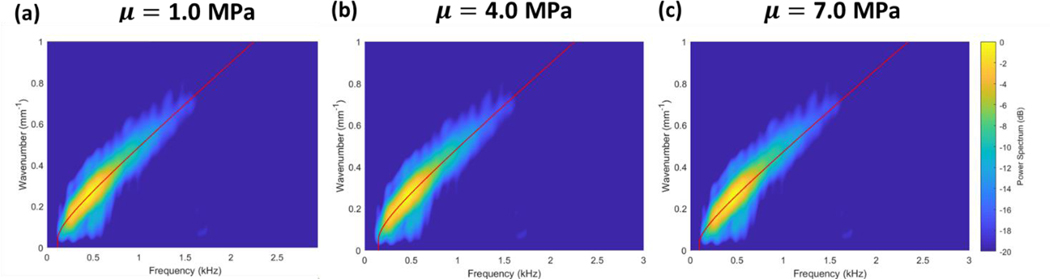
The modified NITI model was next fitted to the ex vivo porcine cornea dataset using the fitting algorithm developed by Pitre et al. 2020. Modifications were made to the algorithm to include parameters σθ and Ke. Due to the similar effects on wave dispersion of prestress and stiffness, however, this system does not result in a unique solution if G, μ, Ke and σθ are all allowed to vary (data not shown). To address this issue, we first assumed that the in-plane modulus μ does not significantly affect the modified NITI model fitting as indicated from our results in Figure 6b. In Figure 7, μ was set as 1.0, 4.0, and 7.0 MPa to determine its effects on fitting of the model to the dispersion data. The fitting parameters are listed in Table 1.
Figure 7. Ex vivo porcine cornea dataset acquired at 5, 10, 15, and 20 mmHg IOP.
Acoustic micro-tapping method was used to generate elastic waves in whole globe porcine corneas pressurized at a) 5 mmHg b) 10 mmHg c) 15 mmHg and d) 20 mmHg (Pitre et al., 2020). The dispersion data is shown here as the linear wavenumber vs. frequency. A low-frequency intercept can be visually observed that increases with IOP (highlighted with red brackets).
Table 1.
The effect of in-plane shear modulus μ in the modified NITI fitting
| IOP (mmHg) | G (kPa) | μ (MPa) | Ke (MN/m3) | σθ (kPa) |
|---|---|---|---|---|
| 5 | 4.25 ± G.61 | 1.00 | G.32 ± G.17 | 5.56 |
| 4.21 ± G.51 | 4.00 | G.31 ± G.17 | 5.56 | |
| 4.39 ± G.21 | 7.00 | G.1S ± G.G6 | 5.56 |
Table 1. The parameters G and Ke for experimental data of porcine eyes pressurized at 5 mmHg are listed above. Values for G and Ke are given as mean ± SD with n =3. The in-plane modulus μ was fixed at 1.0, 4.0, and 7.0 MPa. Tensile prestress was estimated using Eq. (40).
From these results, it can be seen that varying μ by a factor of 4 from 1.0 to 4.0 MPa has a negligible effect on the model fitting values obtained for G and Ke. Increasing μ further to 7.0 MPa still did not significantly affect G though decreased Ke. To reduce the number of variables in the fitting algorithm, μ was therefore set at 1.0 MPa for all fittings. We additionally pre-estimated the tensile hoop stress σθ induced by IOP using the approximation given in Eq. (40). While more exact estimations of the hoop stress would account for its variation through the thickness of the cornea, this approximation accurately determines the mean hoop stress values involved and illustrates the relevant concepts. By fixing μ and predetermining σθ, only G and Ke were allowed to vary during data fittings. The results of this fitting are shown in Figure 8, and all fitting parameters are listed in Table 2.
Figure 8. Fitting of the modified NITI model to the ex vivo porcine corneal dataset.
a) The modified NITI model was used to fit ex vivo corneal dispersion data pressurized at 5, 10, 15, and 20 mmHg. The in-plane modulus μ was set at 1.0 MPa while the tensile prestress was approximated via Eq. (40). b) The resulting dispersion curves are shown as linear wavenumber vs. frequency plots. c) The corresponding phase velocity curves are shown on the right. All parameters are summarized in Table 2.
Table 2.
Fitting of Ex Vivo Porcine Corneal Data with Modified NITI Theory
| IOP (mmHg) | GNITI (kPa) (Pitre et al., 2020) | G (kPa) | μ (MPa) | Ke (MN/m3) | αθ (kPa) |
|---|---|---|---|---|---|
| 5 | 7.3 ± 0.3 | 4.26 ± 0.61 | 1.00 | 0.32 ± 0.17 | 5.56 |
| 10 | 14.9 ± 1.1 | 6.82 ± 0.52 | 1.00 | 0.66 ± 0.10 | 11.11 |
| 15 | 25.6 ± 1.6 | 13.03 ± 2.07 | 1.00 | 1.95 ± 0.70 | 16.67 |
| 20 | 56.6 ± 6.0 | 39.12 ± 4.15 | 1.00 | 5.60 ± 0.90 | 22.22 |
Table 2. Parameters G and Ke obtained by fitting ex vivo porcine corneal data with the modified NITI theory are listed above. For comparison, the values obtained in the study by Pitre et al. (2020) without the inclusion of IOP prestress were included as GNITI. For values of G in the current study, the in-plane modulus μ was fixed at 1.0 MPa for all fittings. For IOPs of 5–20 mmHg, tensile prestress was estimated via Eq. (40). Values for G and Ke represent mean ± SD with n =3
Qualitatively, the modified NITI model is able to closely fit the ex vivo porcine data from 5–20 mmHg IOP and appears to capture the IOP-induced low-frequency cutoff (Figure 8a). The resulting dispersion curves demonstrate that the cutoff frequency increases with the IOP (Figure 8b), as theorized, and is associated with the shifting of the low-frequency asymptotic phase velocity behavior to higher frequencies (Figure 8c). This may indicate a greater restoring force originating from the stretching of the corneal tissue, according to Winkler’s foundation, although this interpretation requires further investigation. Additionally, the slope of the dispersion curves decreases as IOP increases, which is associated with greater phase velocities at all frequency components (Figure 8c), and again, we believe this is due to both the effects of non-linear tissue stiffness and tensile prestress.
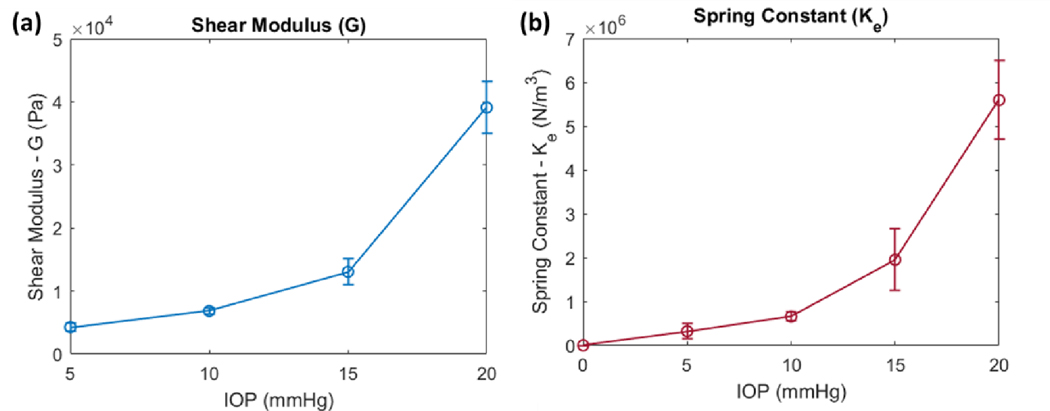
Quantitatively, the incorporation of the tensile and foundational effects into the modified NITI model results in lower estimates of the corneal shear moduli G at every IOP. The fitting results are listed in Table 2 and the values of G are compared to those reported by Pitre et al. (Pitre et al., 2020). Without accounting for the tensile and foundational effects of IOP, fitting of the original NITI model by Pitre’s group resulted in shear moduli values of 7.3 ± 0.3 kPa, 14.9 ± 1.1 kPa, 25.6 ± 1.6 kPa, and 56.6 ± 6.0 kPa (mean ± SD) for corneas pressurized at 5, 10, 15, and 20 mmHg, respectively (Pitre et al., 2020). Using the modified NITI model with predetermined values of tensile prestress, we obtained lower estimates at every IOP: 4.3 ± 0.6 kPa, 6.8 ± 0.5 kPa, 13.0 ± 2.1 kPa, and 39.1 ± 4.2 kPa (mean ± SD), respectively. Pitre’s original model estimates a ~50 kPa change in corneal stiffness from 5–20 mmHg IOP, while in comparison, a lower ~35 kPa change is estimated using our model. Additionally, with our modified NITI model, there is only a small change in the shear modulus G between 5–15 mmHg (8.7 kPa). In comparison, the change in G is roughly 2.1 times greater when predicted using the original NITI model (18.3 kPa). It is not until 20 mmHg IOP where a considerable jump in the estimated value of G is seen in the modified NITI model (Figure 9a), which may be due to the increasing effect of the cornea’s nonlinear tissue properties at higher IOPs. We speculate that between 15–20 mmHg, the collagen fibers of the corneal stroma may become fully taut and contribute to the large increase in estimated shear modulus.
Figure 9. Parameters G and Ke obtained from fitting of the modified NITI model plotted as a function of IOP.
a) A small increase in the shear modulus G is seen from IOPs of 5–15 mmHg. A large jump is seen when IOP changes from 15 to 20 mmHg and may be due to nonlinear changes in the tissue. b) A small increase between Ke and IOP is seen between 0–15 mmHg; here, Ke was assumed to equal zero at no IOP. A large jump in Ke is observed at 20 mmHg. All values represent the mean ± SD, with a sample size of n = 3.
Similarly, the foundational spring constant Ke also significantly increased between 15–20 mmHg (Figure 9b), which may indicate a greater restoring force associated with the non-linear mechanical properties of the cornea. If only the Ke values below 10 mmHg are considered, it appears that the foundational constant may be proportionally related to IOP at lower pressures (Figure 9b and Table 2); here, it was assumed that at zero IOP, Ke also equaled zero. When taken together with the estimated values of tensile prestress σθ, which are proportionally related to IOP via Eq. (40), this may suggest that Ke and σθ could also be proportionally related, but only at pressures below 10 mm Hg. While only speculative, this would be significant as Ke could be used to predict the IOP-induced tensile prestress σθ and help discern the similar effects of prestress from tissue stiffness on wave behavior.
While we believe this analysis serves as a proof of concept, several limitations should be highlighted. Most notably, no unique solution exists if all four parameters G, μ, Ke and σθ are allowed to vary. We rely on several assumptions to narrow down the number of parameters, and thus, the quantitative values obtained by this analysis are dependent on the validity of these assumptions which need to be assessed. Additionally, the fitting algorithm used here can be dependent on initial guesses for the parameters. If initial guesses differ by an order of magnitude, the system may not converge on a solution, or the solution may be a poor fit. This requires some prior knowledge of the expected range of values for corneal tissue properties and IOP.
Nevertheless, we believe that the corneal shear moduli obtained from our modified NITI model is more representative of the “true” non-linear tissue properties of the cornea. Our model aims to better separate the effects of tensile prestress and tissue stiffness on wave behavior. While several assumptions are made for simplification, we believe that our work demonstrates that the prestress effect of IOP needs to be accounted for when estimating cornea tissue stiffness from wave propagation-based methods like OCE. Prestress and tissue stiffness likely cannot be fully separated due to the inherent non-linear properties of biological tissues; the tissue will stiffen as a result of prestress. In other words, incorporation of additional third and fourth order coefficients, which cause G to be a nonlinear function of IOP and not a constant, will be needed as prestress and deformation increase (Remeniares et al., 2021). However, both in our work and in the fields of tendon and muscle elastography (Bernabei et al., 2019; Martin et al., 2018; Wang et al., 2019), prestress alone has been shown to significantly affect wave behavior. We believe that explicitly accounting for this prestress effect results in more accurate estimates of the true non-linear changes in tissue properties, particularly at higher preloads.
Limitations and Recommendations for Future Study
Further investigation is needed to rigorously assess the validity of some of the assumptions that are made and the consequent conclusions. A key outcome of the presented analysis is that previous models have led to overestimating the out-of-plane shear modulus, G, by neglecting to account for IOP-induced hoop stress. While the results reported here are comparable to values obtained by Hatami-Marbini using rheometry on excised porcine corneas (Hatami-Marbini, 2014), they reduce G anywhere from 30% to 60% as compared to the model of Pitre et al. (2020) using the same experimental OCE data. In Pitre et al.’s study, values for G were independently obtained using torsional rheometry measurements of excised corneal samples (buttons). The rheometry-based estimates of G were generally higher than the OCE-based ones. The reference identifies several reasons for why the rheometry based estimates may be higher and concludes the OCE-based estimates are more accurate for in vivo conditions. In addition to the reasons mentioned in the reference, we believe the unique collagen fiber orientation of the porcine cornea may also increase the rheometry-based estimates even more. The torsional rheometry measurement gives a location- and direction-weighted average of the value of G over the entire excised cornea button, with only shear stress and strain in the angular (torsional or twisting) direction in the plane of the cornea considered and with a strain level that is proportional to radial distance from the center of the cornea. The collagen structure of the stroma in the porcine cornea is such that the fibers are predominantly aligned circumferentially and more densely as one moves further away from the center of the cornea (Hayes et al., 2007). G is expected to increase when shearing is polarized along fiber axes. Thus, the rheometry measurement is giving the greatest “weight” to the most extreme case of shear deformation along the fiber axes, whereas OCE generally measures shear waves that propagate radially on the cornea and are polarized out of the plane of the cornea, thus both propagation and polarization directions being orthogonal to the dominant fiber axis. This also identifies a potential limitation of the NITI model, itself, which assumes isotropy within a planar slice of the cornea when in fact this may not be the case due to this organized fiber structure. A more general orthotropic model may be needed, with principal axes that vary with location. Whether the collagen structure and disconnect between polarization and propagation directions of OCE versus rheometry, or other reasons mentioned in Pitre et al. (2020), are enough to account for the discrepancy with values for G obtained in the present analysis needs further study.
It is also acknowledged that the foundational spring stiffness term added in the present analysis needs a more rigorous justification. It has been used to explain the observed cutoff frequencies that are not captured by previous models. But, other limitations of previous models, such as their neglect of the finite dimension of the cornea, and thus the influence of its finite boundaries, may also explain the lack of a cutoff frequency in previous models. As currently implemented in the literature, the NITI model (Pitre et al., 2020), as well as the modified Rayleigh-Lamb model (Han et al., 2017), treat the fluid loading from the aqueous humor as if it were an unbound (half-space) fluid, infinite in dimension below the cornea which results in only energy propagating away from the cornea (dispersal of energy). Here, the introduction of the foundational stiffness is an attempt to approximate the finite dimensions of the aqueous humor and the surrounding soft tissue structure, whose dynamics should differ from that of an infinite fluid half-space below the cornea. We hypothesize that there will be an energy storage and reactive component induced by the IOP that can be approximated with the foundation springs. However, we emphasize that rigorous studies are required to evaluate the significance and to prescribe meaning to the observed cutoff frequencies. A combination of FE analysis with experimental studies aimed at clarifying the low-frequency regions of corneal wave dispersion may be helpful. Perhaps, a more rigorous justification of the phenomenological-based foundation spring stiffness introduced here may indeed come in part from an incorporation of the finite dimension of the cornea. Further studies are needed.
As stated, our study shows that both tissue stiffness and tensile prestress affect wave behavior similarly, and therefore, their effects cannot reliably be discerned. In order to address this limitation, the prestress was precalculated using the relatively simple Laplace’s law for a uniform, thin-walled spherical pressure vessel and the known experimental IOP values. This is an approximation, as the prestress in fact will vary through the thickness of the cornea. Finite element studies using Ansys Mechanical APDL 2020 Rev 2 with the same corneal geometry, NITI properties and IOP values as in this study, resulted in prestress values that, when averaged through the corneal thickness, closely matched the Eq. (40) value and ranged from 50% to 150% of this value going from the inner to the outer edge of the cornea. While the Eq. (40) approximation is reasonable and is within the range of values reported by other studies (Shih et al., 2017; Simonini and Pandolfi, 2015), incorporating a prestress that varies through the corneal thickness would be more accurate. What effect, if any, this would have on results is left for future studies.
An additional limitation is that this method requires a prior knowledge of IOP, which can be difficult to obtain in a clinical setting. While tonometers can be relatively accurate for IOP values within reasonable levels, tonometer readings are dependent on various properties of the cornea, particularly its tissue stiffness and thickness (Colakoglu et al., 2021; Costin et al., 2014; Kwon et al., 2008; Lu et al., 2019; Vinciguerra et al., 2020). Uncertainty can thus arise in whether tonometry-based measurements of IOP are reflective of the true IOP, particularly in eyes with abnormal corneal mechanical properties, and therefore prestress can be challenging to predetermine. This again highlights the inherent coupling between IOP and corneal mechanical properties. It also suggests the importance in further evaluating the foundational effect of IOP seen in OCE which may help estimate the true IOP-induced prestress and thus begin to discern the effects of IOP from those of corneal tissue properties.
Here, observations from experimental data were used to deduce the presence of this foundational effect. Further comprehensive studies are required to assess the validity of the phenomenon, the relative influences of tissue mechanical properties, preload conditions and the finite dimension of the cornea on the low-frequency dispersion cutoff, and also to determine its relationship with the tensile prestress effect. We highlight that the theory and applications of Winkler’s foundation may be particularly useful in any related future work. It may be possible that the cutoff frequency can be used to predict both the IOP and IOP-induced prestress. Clinically, this could mean that OCE may be used as a fully noncontact method in estimating both the IOP and a true corneal stiffness in vivo. Without further studies, however, conclusions cannot be made regarding the significance of the cutoff frequency and its applications. Nevertheless, to our knowledge, this is the first study in the OCE literature attempting to account for both IOP and corneal tissue stiffness. We hope that our work may provide the basis for further studies that help improve the accuracy and clinical applicability of elastography-based measurements, particularly for tissues under preload.
CONCLUSIONS
We hypothesized that IOP-induced tensile prestress may cause an overestimation of the non-linear changes in corneal tissue stiffness due to its effects on wave behavior. This hypothesis was motivated by observations in the field of muscle and tendon elastography where it has been shown that the effects of tensile load can dominate over those of tissue properties. In the cornea, the role of prestress is likely reduced to where both prestress and tissue stiffness contribute to the resulting wave behavior. We believe that accounting for the effects of IOP-induced prestress will result in more accurate OCE estimates of corneal shear moduli, particularly at high IOPs. In this study, we determined that IOP introduces both a tensile prestress and an apparent elastic foundational effect that influences wave dispersion behavior in the cornea. Theoretical analysis was used to incorporate these findings into the existing models of guided wave behavior. Parametric studies were performed to examine the individual effects of tissue stiffness, tensile prestress, and the elastic foundation on wave dispersion. Notably, prestress within the range estimated for normal levels of IOP was shown to induce significant changes in wave velocities, thereby affecting the estimated shear moduli. While the effects of prestress and tissue shear moduli appeared to be very similar, we observed a low-frequency dispersion cutoff that was modelled with the application of an elastic spring foundation in this work. Although further comprehensive studies are required, we speculate that the low-frequency cutoff may indicate a restoring force induced by the stretching of the ocular tissues in response to IOP and related to the IOP-induced tensile prestress. Further work is needed to assess these hypotheses and the significance of the frequency cutoff and its relationship with IOP-induced prestress. Nevertheless, we believe that this work serves as a basis for understanding the effects of IOP on wave dispersion in the cornea and may be useful in improving the accuracy of OCE-based estimations of corneal stiffness.
ACKNOWLEDGEMENTS
The authors are grateful to Dr. Matthew O’Donnell, Dr. Ivan Pelivanov, Dr. John Pitre, and Mitchell Kirby from the University of Washington for providing their OCE dataset, curve fitting algorithm, and for their valuable discussions that have improved the analysis and interpretation of the presented study results. The last author, Royston, acknowledges partial support of this research from the National Science Foundation (Grant No. 1852691). This work was funded by the National Institutes of Health (Grant Nos. K12EY021475, R21EY019561, R01EY027912, and P30EY001792); the Medical Scientist Training Program Predoctoral Training Grant (Grant No. T32GM079086); the Illinois Society for the Prevention of Blindness (Grant No. 097371); the Research to Prevent Blindness Unrestricted Departmental Grant; and the Falk Medical Research Trust Catalyst Awards Program.
Footnotes
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
CITED LITERATURE
- Ambroziński Ł, Song S, Yoon SJ, Pelivanov I, Li D, Gao L, Shen TT, Wang RK, O’Donnell M, 2016. Acoustic micro-tapping for non-contact 4D imaging of tissue elasticity. Sci Rep 6. 10.1038/srep38967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreassen TT, Simonsen AH, Oxlund H, 1980. Biomechanical properties of keratoconus and normal corneas. Exp Eye Res 31, 435–441. 10.1016/s0014-4835(80)80027-3 [DOI] [PubMed] [Google Scholar]
- Bernabei M, Lee SSM, Perreault EJ, Sandercock TG, 2019. Shear wave velocity is sensitive to changes in muscle stiffness that occur independently from changes in force. Journal of Applied Physiology 128, 8–16. 10.1152/japplphysiol.00112.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biot MA, 1965. Mechanics of Incremental Deformation. John Wiley & Sons, New York. [Google Scholar]
- Chen F, Wilcox PD, 2007. The effect of load on guided wave propagation. Ultrasonics 47, 111–122. 10.1016/j.ultras.2007.08.003 [DOI] [PubMed] [Google Scholar]
- Chung CW, Girard MJA, Jan N-J, Sigal IA, 2016. Use and Misuse of Laplace’s Law in Ophthalmology. Invest Ophthalmol Vis Sci 57, 236–245. 10.1167/iovs.15-18053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colakoglu A, Colakoglu IE, Cosar CB, 2021. Correlation between corneal thickness, keratometry, age, and differential pressure difference in healthy eyes. Scientific Reports 11, 4133. 10.1038/s41598-021-83683-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costin BR, Fleming GP, Weber PA, Mahmoud AM, Roberts CJ, 2014. Corneal biomechanical properties affect Goldmann applanation tonometry in primary open-angle glaucoma. J Glaucoma 23, 69–74. 10.1097/IJG.0b013e318269804b [DOI] [PubMed] [Google Scholar]
- Dillard DA, Mukherjee B, Karnal P, Batra RC, Frechette J, 2018. A review of Winkler’s foundation and its profound influence on adhesion and soft matter applications. Soft Matter 14, 3669–3683. 10.1039/C7SM02062G [DOI] [PubMed] [Google Scholar]
- Eberwein P, Reinhard T, 2015. Concise Reviews: The Role of Biomechanics in the Limbal Stem Cell Niche: New Insights for Our Understanding of This Structure. STEM CELLS 33, 916–924. 10.1002/stem.1886 [DOI] [PubMed] [Google Scholar]
- Gennisson J-L, Renier M, Catheline S, Barriere C, Berco J, Tanter M, Fink M, 2007. Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force. J Acoust Soc Amer 122(6), 3211–3219. 10.1121/1.2793605 [DOI] [PubMed] [Google Scholar]
- Girard MJA, Dupps WJ, Baskaran M, Scarcelli G, Yun SH, Quigley HA, Sigal IA, Strouthidis NG, 2015. Translating ocular biomechanics into clinical practice: current state and future prospects. Curr Eye Res 40, 1–18. 10.3109/02713683.2014.914543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouveia RM, Lepert G, Gupta S, Mohan RR, Paterson C, Connon CJ, 2019a. Assessment of corneal substrate biomechanics and its effect on epithelial stem cell maintenance and differentiation. Nat Commun 10, 1496. 10.1038/s41467-019-09331-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouveia RM, Vajda F, Wibowo JA, Figueiredo F, Connon CJ, 2019b. YAP, ΔNp63, and β-Catenin Signaling Pathways Are Involved in the Modulation of Corneal Epithelial Stem Cell Phenotype Induced by Substrate Stiffness. Cells 8, 347. 10.3390/cells8040347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadden WJ, Young JL, Holle AW, McFetridge ML, Kim DY, Wijesinghe P, Taylor-Weiner H, Wen JH, Lee AR, Bieback K, Vo B-N, Sampson DD, Kennedy BF, Spatz JP, Engler AJ, Choi YS, 2017. Stem cell migration and mechanotransduction on linear stiffness gradient hydrogels. PNAS 114, 5647–5652. 10.1073/pnas.1618239114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Z, Aglyamov SR, Li J, Singh M, Wang S, Vantipalli S, Wu C, Liu C, Twa MD, Larin KV, 2015. Quantitative assessment of corneal viscoelasticity using optical coherence elastography and a modified Rayleigh–Lamb equation. J Biomed Opt 20. 10.1117/1.JBO.20.2.020501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Z, Li J, Singh M, Wu C, Liu C, Raghunathan R, Aglyamov SR, Vantipalli S, Twa MD, Larin KV, 2017. Optical coherence elastography assessment of corneal viscoelasticity with a modified Rayleigh-Lamb wave model. Journal of the Mechanical Behavior of Biomedical Materials 66, 87–94. 10.1016/j.jmbbm.2016.11.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatami-Marbini H, 2014. Viscoelastic shear properties of the corneal stroma. Journal of Biomechanics 47, 723–728. 10.1016/j.jbiomech.2013.11.019 [DOI] [PubMed] [Google Scholar]
- Hayes S, Boote C, Lewis J, Sheppard J, Abahussin M, Quantock AJ, Purslow C, Votruba M, Meek KM, 2007. Comparative Study of Fibrillar Collagen Arrangement in the Corneas of Primates and Other Mammals. The Anatomical Record 290, 1542–1550. 10.1002/ar.20613 [DOI] [PubMed] [Google Scholar]
- Hetenyi M, 1946. Beams on Elastic Foundations. University of Michigan Press, Ann Arbor. [Google Scholar]
- Hon Y, Chen G-Z, Lu S-H, Lam DCC, Lam AKC, 2017. High myopes have lower normalised corneal tangent moduli (less “stiff” corneas) than low myopes. Ophthalmic Physiol Opt 37, 42–50. 10.1111/opo.12335 [DOI] [PubMed] [Google Scholar]
- Jones RR, Hamley IW, Connon CJ, 2012. Ex vivo expansion of limbal stem cells is affected by substrate properties. Stem Cell Research 8, 403–409. 10.1016/j.scr.2012.01.001 [DOI] [PubMed] [Google Scholar]
- Kennedy KM, Chin L, McLaughlin RA, Latham B, Saunders CM, Sampson DD, Kennedy BF, 2015. Quantitative micro-elastography: imaging of tissue elasticity using compression optical coherence elastography. Scientific Reports 5, 15538. 10.1038/srep15538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon TH, Ghaboussi J, Pecknold DA, Hashash YMA, 2008. Effect of cornea material stiffness on measured intraocular pressure. J Biomech 41, 1707–1713. 10.1016/j.jbiomech.2008.03.004 [DOI] [PubMed] [Google Scholar]
- Lan G, Aglyamov S, Larin KV, Twa MD, 2021a. In vivo human corneal natural frequency quantification using dynamic optical coherence elastography: Repeatability and reproducibility. Journal of Biomechanics 121, 110427. 10.1016/j.jbiomech.2021.110427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan G, Aglyamov SR, Larin KV, Twa MD, 2021b. In Vivo Human Corneal Shear-wave Optical Coherence Elastography. Optom Vis Sci 98, 58–63. 10.1097/OPX.0000000000001633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd JR, 1962. Wave propagation in an elastic plate resting on an elastic foundation (PhD Thesis). California Institute of Technology, Pasadena, California. [Google Scholar]
- Lu S-H, Chong IT, Leung SYY, Lam DCC, 2019. Characterization of Corneal Biomechanical Properties and Determination of Natural Intraocular Pressure Using CID-GAT. Trans. Vis. Sci. Tech 8, 10–10. 10.1167/tvst.8.5.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin JA, Brandon SCE, Keuler EM, Hermus JR, Ehlers AC, Segalman DJ, Allen MS, Thelen DG, 2018. Gauging force by tapping tendons. Nature Communications 9, 1592. 10.1038/s41467-018-03797-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matalia J, Francis M, Gogri P, Panmand P, Matalia H, Roy AS, 2017. Correlation of Corneal Biomechanical Stiffness With Refractive Error and Ocular Biometry in a Pediatric Population. Cornea 36, 1221–1226. 10.1097/ICO.0000000000001290 [DOI] [PubMed] [Google Scholar]
- Mazzotti M, Marzani A, Bartoli I, Viola E, 2012. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method. International Journal of Solids and Structures 49, 2359–2372. 10.1016/j.ijsolstr.2012.04.041 [DOI] [Google Scholar]
- Mikula E, Winkler M, Juhasz T, Brown DJ, Shoa G, Tran S, Kenney MC, Jester JV, 2018. Axial mechanical and structural characterization of keratoconus corneas. Experimental Eye Research 175, 14–19. 10.1016/j.exer.2018.05.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair A, Singh M, Aglyamov SR, Larin KV, 2020. Heartbeat OCE: corneal biomechanical response to simulated heartbeat pulsation measured by optical coherence elastography. J Biomed Opt 25. 10.1117/1.JBO.25.5.055001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nash IS, Greene PR, Foster CS, 1982. Comparison of mechanical properties of keratoconus and normal corneas. Exp Eye Res 35, 413–424. 10.1016/0014-4835(82)90040-9 [DOI] [PubMed] [Google Scholar]
- Pau A, Lanza di Scalea F, 2015. Nonlinear guided wave propagation in prestressed plates. The Journal of the Acoustical Society of America 137, 1529–1540. 10.1121/1.4908237 [DOI] [PubMed] [Google Scholar]
- Peddeti K, Santhanam S, 2018. Dispersion curves for Lamb wave propagation in prestressed plates using a semi-analytical finite element analysis. The Journal of the Acoustical Society of America 143, 829–840. 10.1121/1.5023335 [DOI] [PubMed] [Google Scholar]
- Pierscionek BK, Asejczyk‐Widlicka M, Schachar RA, 2007. The effect of changing intraocular pressure on the corneal and scleral curvatures in the fresh porcine eye. Br J Ophthalmol 91, 801–803. 10.1136/bjo.2006.110221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitre JJ, Kirby MA, Li DS, Shen TT, Wang RK, O’Donnell M, Pelivanov I, 2020. Nearly-incompressible transverse isotropy (NITI) of cornea elasticity: model and experiments with acoustic micro-tapping OCE. Sci Rep 10. 10.1038/s41598-020-69909-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purslow PP, Karwatowski WSS, 1996. Ocular Elasticity: Is Engineering Stiffness a More Useful Characterization Parameter than Ocular Rigidity? Ophthalmology 103, 1686–1692. 10.1016/S0161-6420(96)30446-6 [DOI] [PubMed] [Google Scholar]
- Ramier A, Eltony AM, Chen Y, Clouser F, Birkenfeld JS, Watts A, Yun S-H, 2020. In vivo measurement of shear modulus of the human cornea using optical coherence elastography. Sci Rep 10. 10.1038/s41598-020-74383-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramier A, Tavakol B, Yun S-H, 2019. Measuring mechanical wave speed, dispersion, and viscoelastic modulus of the cornea using optical coherence elastography. Opt Express 27, 16635–16649. 10.1364/OE.27.016635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remeniares JP, Bulot M, Gennisson J-L, Patat F, Destrade M, Bacle G, 2021. Acousto-elasticity of Transversely Isotropic Incompressible Soft Tissues: Characterization of Skeletal Striated Muscle. Phys. Med. Biol 66, 145009 (2021). [DOI] [PubMed] [Google Scholar]
- Shih P-J, Wang I-J, Cai W-F, Yen J-Y, 2017. Biomechanical Simulation of Stress Concentration and Intraocular Pressure in Corneas Subjected to Myopic Refractive Surgical Procedures. Scientific Reports 7, 13906. 10.1038/s41598-017-14293-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonini I, Pandolfi A, 2015. Customized Finite Element Modelling of the Human Cornea. PLOS ONE 10, e0130426. 10.1371/journal.pone.0130426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh I, Madan DK, Gupta M, 2010. Propagation of Elastic Waves in Prestressed Media. Journal of Applied Mathematics 2010, e817680. 10.1155/2010/817680 [DOI] [Google Scholar]
- Singh M, Li J, Han Z, Raghunathan R, Nair A, Wu C, Liu C-H, Aglyamov S, Twa MD, Larin KV, 2017. Assessing the effects of riboflavin/UV-A crosslinking on porcine corneal mechanical anisotropy with optical coherence elastography. Biomed. Opt. Express, BOE 8, 349–366. 10.1364/BOE.8.000349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song F, Huang GL, Hu GK, 2013. Coupled piezo-elastodynamic modeling of guided wave excitation and propagation in plates with applied prestresses. Journal of Intelligent Material Systems and Structures 24, 598–611. 10.1177/1045389X12467516 [DOI] [Google Scholar]
- Sun MG, Luo Y, Teng T, Guaiquil V, Zhou Q, McGinn L, Nazzal O, Walsh M, Lee J, Rosenblatt MI, 2021. Silk Film Stiffness Modulates Corneal Epithelial Cell Mechanosignaling. Macromolecular Chemistry and Physics 222, 2100013. 10.1002/macp.202100013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vellara HR, Patel DV, 2015. Biomechanical properties of the keratoconic cornea: a review. Clinical and Experimental Optometry 98, 31–38. 10.1111/cxo.12211 [DOI] [PubMed] [Google Scholar]
- Vinciguerra R, Rehman S, Vallabh NA, Batterbury M, Czanner G, Choudhary A, Cheeseman R, Elsheikh A, Willoughby CE, 2020. Corneal biomechanics and biomechanically corrected intraocular pressure in primary open-angle glaucoma, ocular hypertension and controls. Br J Ophthalmol 104, 121–126. 10.1136/bjophthalmol-2018-313493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang AB, Perreault EJ, Royston TJ, Lee SSM, 2019. Changes in shear wave propagation within skeletal muscle during active and passive force generation. Journal of Biomechanics 94, 115–122. 10.1016/j.jbiomech.2019.07.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Larin KV, 2014. Shear wave imaging optical coherence tomography (SWI-OCT) for ocular tissue biomechanics. Opt. Lett., OL 39, 41–44. 10.1364/OL.39.000041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitford C, Studer H, Boote C, Meek KM, Elsheikh A, 2015. Biomechanical model of the human cornea: Considering shear stiffness and regional variation of collagen anisotropy and density. Journal of the Mechanical Behavior of Biomedical Materials 42, 76–87. 10.1016/j.jmbbm.2014.11.006 [DOI] [PubMed] [Google Scholar]
- Ye S, Zhou Y, Bao C, Chen Y, Lu F, Zhu D, 2021. In vivo non-contact measurement of human iris elasticity by optical coherence elastography. Journal of Biophotonics 14, e202100116. 10.1002/jbio.202100116 [DOI] [PubMed] [Google Scholar]
- Zhou Yuheng, Wang Y, Shen M, Jin Z, Chen Y, Zhou Yue, Qu J, Zhu D, 2019. In vivo evaluation of corneal biomechanical properties by optical coherence elastography at different cross-linking irradiances. J Biomed Opt 24. 10.1117/1.JBO.24.10.105001 [DOI] [PMC free article] [PubMed] [Google Scholar]