Polygenic risk modeling for prediction of epithelial ovarian cancer risk

Abstract

Polygenic risk scores (PRS) for epithelial ovarian cancer (EOC) have the potential to improve risk stratification. Joint estimation of Single Nucleotide Polymorphism (SNP) effects in models could improve predictive performance over standard approaches of PRS construction. Here, we implemented computationally efficient, penalized, logistic regression models (lasso, elastic net, stepwise) to individual level genotype data and a Bayesian framework with continuous shrinkage, “select and shrink for summary statistics” (S4), to summary level data for epithelial non-mucinous ovarian cancer risk prediction. We developed the models in a dataset consisting of 23,564 non-mucinous EOC cases and 40,138 controls participating in the Ovarian Cancer Association Consortium (OCAC) and validated the best models in three populations of different ancestries: prospective data from 198,101 women of European ancestries; 7,669 women of East Asian ancestries; 1,072 women of African ancestries, and in 18,915 BRCA1 and 12,337 BRCA2 pathogenic variant carriers of European ancestries. In the external validation data, the model with the strongest association for non-mucinous EOC risk derived from the OCAC model development data was the S4 model (27,240 SNPs) with odds ratios (OR) of 1.38 (95% CI: 1.28–1.48, AUC: 0.588) per unit standard deviation, in women of European ancestries; 1.14 (95% CI: 1.08–1.19, AUC: 0.538) in women of East Asian ancestries; 1.38 (95% CI: 1.21–1.58, AUC: 0.593) in women of African ancestries; hazard ratios of 1.36 (95% CI: 1.29–1.43, AUC: 0.592) in BRCA1 pathogenic variant carriers and 1.49 (95% CI: 1.35–1.64, AUC: 0.624) in BRCA2 pathogenic variant carriers. Incorporation of the S4 PRS in risk prediction models for ovarian cancer may have clinical utility in ovarian cancer prevention programs.

Introduction

Rare variants in known high and moderate penetrance susceptibility genes (BRCA1, BRCA2, BRIP1, PALB2, RAD51C, RAD51D and the mis-match repair genes) account for about 40% of the inherited component of EOC disease risk [1, 2]. Common susceptibility variants, reviewed in Kar et al. and Jones et al., explain about 6% of the heritability of EOC [1, 3]. Polygenic risk scores (PRS) provide an opportunity for refined risk stratification in the general population and in carriers of rare moderate or high risk alleles.

A PRS is calculated as the weighted sum of the number of risk alleles carried for a specified set of variants. The best approach to identify the variant set and their weights to optimize the predictive power of a PRS is unknown. A common approach involves selecting a set of variants that reach a threshold for association based on the p-value for each variant with or without pruning to remove highly correlated variants [4, 5]. More complex machine learning approaches that do not assume variant independence have also been used [6, 7], but these methods have produced only modest gains in predictive power for highly polygenic phenotypes [6, 8]. Penalized regression approaches such as the lasso, elastic net and the adaptive lasso have also been used with individual level data [9], but a major drawback is the computational burden required to fit the models [9, 10].

We present novel, computationally efficient PRS models using two approaches: (1) penalized regression models including the lasso, elastic net and minimax concave penalty (MCP) for use with individual genotype data; and (2) a Bayesian regression model with continuous shrinkage priors for use where only summary statistics are available—referred to as the “select and shrink with summary statistics” (S4) method. We compare these models with two commonly used methods, stepwise regression with p-value thresholding and LDPred.

Materials (subjects) and methods

Model development study population

EOC is a highly heterogeneous phenotype with five major histotypes for invasive disease—high-grade serous, low-grade serous, endometrioid, clear cell, and mucinous histotype. The mucinous histotype is the least common and its origin is the most controversial with up to 60% of diagnosed cases of mucinous ovarian cancer often being misdiagnosed metastasis from non-ovarian sites [11]. Therefore, in this study, we performed PRS modeling and association testing for all cases of invasive, non-mucinous EOC. We used genotype data from 23,564 invasive non-mucinous EOC cases and 40,138 controls with >80% European ancestries from 63 case-control studies included in the Ovarian Cancer Association Consortium (OCAC) for model development. The distribution of cases by histotype was high-grade serous (13,609), low-grade serous (2,749), endometrioid (2,877), clear cell (1,427), and others (2,902). Sample collection, genotyping, and quality control have been previously described [12]. Genotype data were imputed to the Haplotype Reference Consortium reference panel using 470,825 SNPs that passed quality control. Of the 32 million SNPs imputed, 10 million had imputation r² > 0.3 and were included in this analysis.

Model validation study populations

We validated the best-fitting PRS models developed in the OCAC data in 657 prevalent and incident cases of invasive, non-mucinous EOC and 198,101 female controls of European ancestries from the UK Biobank. Samples were genotyped using either the Affymetrix UK BiLEVE Axiom Array or Affymetrix UK Biobank Axiom Array (which share 95% marker content), and then imputed to a combination of the Haplotype Reference Consortium, the 1000 Genomes phase 3 and the UK10K reference panels [13]. We restricted analysis to genetically confirmed females of European ancestries. We excluded individuals if they were outliers for heterozygosity, had low genotyping call rate <95%, had sex chromosome aneuploidy, or if they were duplicates (cryptic or intended) [12]. All SNPs selected in the model development phase were available in the UK Biobank.

We investigated transferability of the best-fitting PRS models to populations of non-European ancestries using genotype data from females of East Asian and African ancestries genotyped as part of the OCAC OncoArray Project [14, 15]. Women of East Asian ancestries—2,841 non-mucinous invasive EOC and 4,828 controls—were identified using a criterion of >80% Asian ancestries. This included samples collected from studies in China, Japan, Korea, and Malaysia as well as samples collected from women of Asian ancestry in studies conducted in the US, Europe and Australia [14]. Similarly, women of African ancestries—368 cases of non-mucinous invasive EOC and 704 controls—mainly from studies conducted in the US, were identified using a criterion of >80% African ancestries as described previously [15].

We also assessed the performance of the best-fitting PRS models in women of European ancestries (>80% European ancestries) with the pathogenic BRCA1 and BRCA2 variants from the Consortium of Investigators of Modifiers of BRCA1/2 (CIMBA). We used genotype data from 18,915 BRCA1 (2,053 invasive EOC cases) and 12,337 BRCA2 (717 invasive EOC cases) pathogenic variant carriers from 63 studies contributing to CIMBA [16]. Genotyping, data quality control measures, intercontinental ancestries assessment and imputation to the HRC reference panel are as described for the OCAC study population.

Statistical analysis

Polygenic risk models

For all PRS models, we created scores as linear functions of the allele dosage in the general form $PR{S}_i={\sum }_j^p{x}_{ij}{\beta }_j$ where genotypes are denoted as x (taking on the minor allele dosages of 0, 1, and 2), with x_ij representing the ith individual for the jth SNP (out of p SNPs) on an additive log scale and β_j represents the weight—the log of the odds ratio—of the jth SNP. We used different approaches to select and derive the optimal weights, β_j, in models as described below.

Penalized logistic regression models

A penalized logistic regression model for a set of SNPs aims to identify a set of regression coefficients that minimize the regularized loss function given by

$$plr\left(x;\lambda ,\kappa \right)=\left\{\begin{array}{c}\hfill x-\lambda sign\left(x\right)/\left(1-\kappa \right)if∣x∣<\lambda /\kappa and∣\left(x\right)∣>\lambda \hfill \\ \hfill xif∣x∣\ge \frac{\lambda }{\kappa }\hfill \\ \hfill 0if∣\left(x\right)∣<\lambda \hfill \end{array}\right)$$

where x is the effect estimate of a SNP, λ is the tuning parameter and κ is the threshold (penalty) for different regularization paths. λ and κ are parameters that need to be chosen during model development to optimize performance. The lasso, elastic net, MCP, and p-value thresholds are instances of the function with different κ values. We minimized the winner’s curse effect on inflated effect estimates for rare SNPs by penalizing rarer SNPs more heavily than common SNPs. Details are provided in the Supplementary Methods.

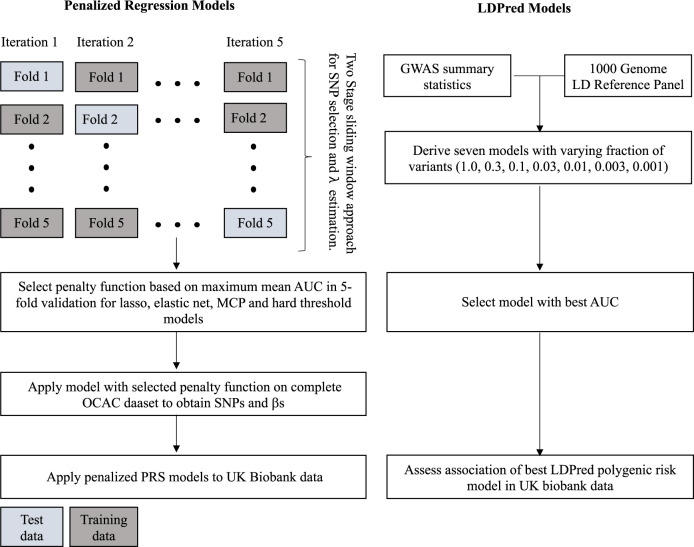
We used a two-stage approach to reduce computational burden without a corresponding loss in predictive power. The first stage was a SNP selection stage using a sliding windows approach, with 5.5 Mb data blocks and a 500 kb overlap between blocks. SNP selection was performed for each block and selected SNPs were collated. Single SNP association analyses were then run, and all SNPs with a χ² test statistic of less than 2.25 were excluded. The 2.25 cutoff was arbitrary and selected to maximize computational efficiency without loss in predictive power. Penalized regression models were applied to the remaining SNPs using λ values of 3.0 and κ values of 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0. SNPs selected in any of these models were included in subsequent analyses. In the second stage, we fit penalized regression models to the training dataset with λ values ranging from 3.0 to 5.5 in increments of 0.1 iterated over κ values from −3.0 to 1 in increments of 0.1. The lasso model (κ = 0) for each value of λ was fitted first, to obtain a unique maximum. From the fitted maximum the κ value was changed, and the model refitted.

We applied this two-stage approach with five-fold cross-validation (Fig. 1). In each iteration, the data set was split into five, with one part constituting the test data and the other four constituting the training data. The variants and their weights from the two-stage penalized logistic regression modeling in the training data were used to calculate the area under the receiver operating characteristic curve (AUC) in the test data in each iteration. AUC estimates for each combination of λ and κ were obtained. We repeated this process for each cross-validation iteration to obtain a mean AUC for each combination of λ and κ. Finally, we selected the tuning and threshold parameters from the lasso, elastic net and MCP models with the maximum mean cross-validated AUC and fitted penalized logistic regression models with these parameters to the entire OCAC dataset to obtain SNP weights for PRS scores.

Fig. 1. PRS model development using penalized regression and LDPred Bayesian approach.

Shown in the left panel is the two-stage approach with five-fold cross validation used for individual level genotype data while the right panel shows the LDPred approach used for summary level data.

Stepwise logistic regression with variable P-value threshold

This model is a general PLR model with κ = 1. As with the other PLR models, we investigated various values for λ values (corresponding to a variable P-value threshold for including a SNP in the model). However, we observed that the implementation of this model on individual level data was more difficult than for other κ values because the model would sometimes converge to a local optimum rather than the global optimum. Therefore, we applied an approximate conditional and joint association analysis using summary level statistics correcting for estimated LD between SNPs, and utilizing  a reference panel of 5,000 individual level genotype OCAC data as described in Yang et al. [17]. Details are provided in the Supplementary Methods.

LDPred

LDPred is a Bayesian approach that shrinks the posterior mean effect size of each marker based on a point-normal prior and LD information from an external reference panel. We derived seven candidate PRSs assuming the fractions of associated variants were 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, and 1.0 respectively using the default parameters as detailed in Vilhjálmsson et al. [18] and an LD reference panel of 503 samples of European ancestries from the 1000 Genomes phase 3 release with effect estimates from the OCAC model development data.

Select and shrink using summary statistics (S4)

The S4 algorithm is similar to the PRS-CS algorithm [19]—a Bayesian method that uses summary statistics and between-SNP correlation data from a reference panel to generate the PRS scores by placing a continuous shrinkage prior on effect sizes. We adapted this method with penalization of rarer SNPs by correcting for the standard deviation resulting in the selection of fewer SNPs. We varied three parameters, a, b, φ, which control the degree of shrinkage of effect estimates. Φ, the overall shrinkage parameter, is influenced by values of a which controls shrinkage of effect estimates around 0 and b which control shrinkage of larger effect estimates. We generated summary statistics for each cross-validation training set and selected the parameters that gave the best results on average from the cross-validation and applied these to the set of summary statistics for the complete OCAC data set to obtain the final set of weights.

PRS based on meta-analysis of OCAC-CIMBA summary statistics

We conducted a meta-analysis of the EOC associations in BRCA1 variant carriers, BRCA2 variant carriers and the participants participating in OCAC (see Supplementary Methods) and constructed two PRS models. An S4 PRS was generated by applying the a, b and φ parameters from the S4 model described above. A stepwise PRS was generated by selecting all SNPs that were genome-wide significant (p < 5 × 10⁻⁸) in the meta-analysis, along with any independent signals in the same region with p < 10⁻⁵ from the histotype specific analyses for low-grade serous, high-grade serous, endometrioid, clear cell ovarian cancer and non-mucinous invasive EOC.

Polygenic risk score performance

The best lasso, elastic net, stepwise and S4 models from the model development stage were validated using two independent data sources: the UK Biobank data and BRCA1/BRCA2 pathogenic variant carriers from the CIMBA. In the UK Biobank data, we evaluated discriminatory performance of the models using the AUC and examined the association between standardized PRS and risk of non-mucinous EOC using logistic regression analysis. For the CIMBA data, we assessed associations for each version of the PRS and invasive non-mucinous EOC risk using weighted Cox regression methods [20]. PRSs in the CIMBA data were scaled to the same PRS standard deviations as the OCAC data, meaning that per standard deviation hazard ratios estimated on CIMBA data are comparable to PRS associations in the OCAC and UK Biobank data. The regression models were adjusted for birth cohort (<1920, 1920–1929, 1930–1939, 1940–1949, ≥1950) and the first four ancestries informative principal components (calculated separately by iCOGS/OncoArray genotyping array) and stratified by Ashkenazi Jewish ancestries and country. Absolute risks by PRS percentiles adjusting for competing risks of mortality from other causes were calculated as described in the Supplementary Material.

Transferability of PRS scores to non-European ancestries

We implemented two straightforward approaches to disentangle the role of ancestries on polygenic risk scoring. We selected homogenous ancestral samples by using a high cut-off criterion of 80% ancestries and we standardized the PRSs by mean-centering within each population. These approaches led to a more uniform distribution of PRSs within each ancestral population. Further adjustments using principal components of ancestries did not attenuate risk estimates.

Results

Model development

The results for the models based on individual level genotype data are shown in Table 1. The elastic net model had the best predictive accuracy (AUC = 0.586). The optimal value of λ obtained from regularization paths for the MCP model was 3.3 meaning the best MCP model was equivalent to the lasso model. The best-fitting model based on summary statistics was the S4 (AUC = 0.593) and the LDPred model had the poorest performance of the methods tested (AUC = 0.552). Therefore, the LDPred model was not considered for further validation in other datasets. All SNPs selected and the associated weights for each model are provided in Supplementary Tables 1–6.

Table 1.

Performance of different PRS models in five-fold cross-validation of OCAC data.

Model	Number of SNPsa	Tuning parameter for best performance	AUC	OR per 1 SD of PRS	95% CI
(a) Models based on individual level genotype data
Lasso	1403	λ = 3.3	0.583	1.35	1.30–1.39
Elastic net	10,797	λ = 3.3, κ = −2.2	0.586	1.36	1.31–1.40
MCP	1403	λ = 3.3	0.583	1.35	1.30–1.39
(b) Models based on summary statistics
LDPred	5,291,719	ρ = 0.001	0.552	1.21	1.13–1.29
Stepwise	22	λ = 5.4	0.572	1.30	1.26–1.34
Select and Shrink (OCAC)	27,240	a = 2.75, b = 2, φ = 3e−6	0.593	1.39	1.34–1.44

AUC area under the receiver operating characteristic (ROC) curve AUC), OR odds ratio, SD standard deviation, PRS polygenic risk score, CI confidence interval, NA not applicable.

^aNumber of SNPs in PRS model run on full OCAC data set after selection of model parameters.

Model validation in women of European ancestries

Overall the PLR models performed slightly better in the UK Biobank data than the model development data (Table 2). Of the models developed using the OCAC model development data, the association was strongest with the S4 PRS. In BRCA1 and BRCA2 variant carriers, prediction accuracy was generally higher among BRCA2 carriers than BRCA1 carriers. Consistent with results from the general population in the UK Biobank, the S4 PRS model also had the strongest association and predictive accuracy for invasive EOC risk in both BRCA1 and BRCA2 carriers. Sensitivity analyses were conducted in which the unadjusted models for BRCA1 and BRCA2 carriers were progressively adjusted for birth cohort and 6 principal components. There was little difference in HR estimates and association P-values going from the unadjusted model to the model adjusting for six principal components (Supplementary Table 7). The PRS models developed using the OCAC-CIMBA meta-analysis results had better discriminative ability in the UK Biobank than the PRS models developed using only OCAC data. Compared with the S4 PRS using only OCAC data, the S4 PRS model derived from the meta-analysis had fewer SNPs, a stronger association with invasive EOC risk and better predictive accuracy. Similarly, the stepwise model from the OCAC-CIMBA meta-analysis performed better than the stepwise model from only OCAC data, but included more SNPs.

Table 2.

External validation of PRS models in European populations using data from UK Biobank and CIMBA.

Model (data set)	SNPs	UK Biobank			CIMBA BRCA1 carriersa			CIMBA BRCA2 carriersa
		AUC	OR	95% CI	AUC	HR	95% CI	AUC	HR	95% CI
(a) PRS models based on OCAC data
Lasso (OCAC)	1403	0.587	1.37	1.27–1.48	0.573	1.27	1.21–1.34	0.627	1.48	1.33–1.63
Elastic net (OCAC)	10,797	0.588	1.36	1.26–1.47	0.583	1.32	1.26–1.39	0.617	1.47	1.33–1.63
Stepwise (OCAC)	22	0.588	1.35	1.26–1.46	0.563	1.21	1.16–1.26	0.605	1.39	1.26–1.54
Select and shrink (OCAC)	27,240	0.588	1.38	1.28–1.48	0.592	1.36	1.29–1.43	0.624	1.49	1.35–1.64
(b) PRS models based on meta-analysis of OCAC and CIMBA data
Stepwise (OCAC-CIMBA)b	36	0.595	1.39	1.29–1.50	NA	NA	NA	NA	NA	NA
Select and shrink (OCAC-CIMBA)	18,007	0.596	1.42	1.32–1.54	NA	NA	NA	NA	NA	NA

AUC area under the receiver operating characteristic curve, OR odds ratio, HR hazards ratio.

^aEstimates are from unadjusted models.

^bResults in CIMBA are overfitted as the CIMBA data was used for model development.

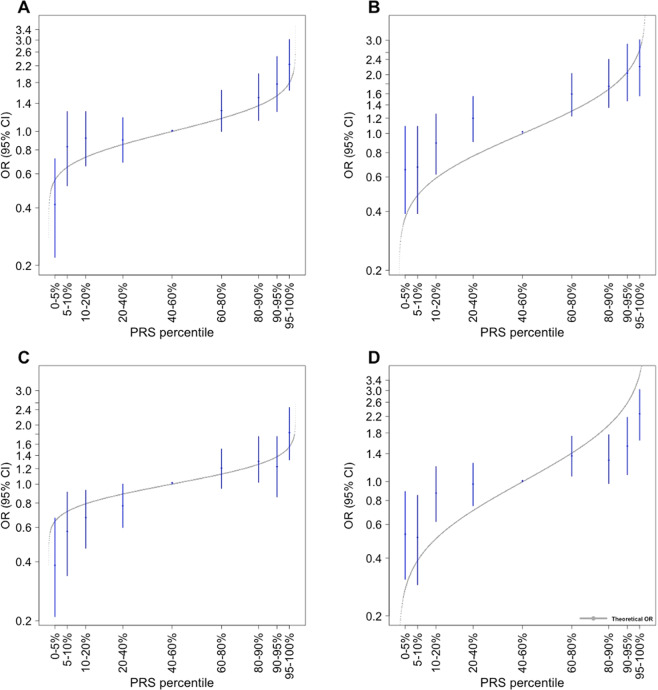
The observed distribution of the OR estimates within centiles of the PRS distribution were consistent with ORs from predicted values under the assumption that all SNPs interact multiplicatively (Fig. 2), with all 95% confidence intervals intersecting with the theoretical estimates for women of European ancestries. Compared with women in the middle quintile, women of European ancestry (UK Biobank) in the top 95th percentile of the lasso derived PRS model had a 2.23-fold increased odds of non-mucinous EOC (95% CI: 1.64 - 3.02) (Table 3).

Fig. 2. Association between the PLR PRS models and non-mucinous ovarian cancer by PRS percentiles.

Shown are estimated odds ratios (OR) and confidence intervals for women of European ancestries by percentiles of polygenic risk scores derived from lasso (A), elastic net (B), stepwise (C) and S4 (D) models relative to the middle quintile.

Table 3.

Association between polygenic risk scores and non-mucinous EOC by PRS percentiles and ancestry.

	UK Biobank			East Asian			African
Percentile	Controls (n)	Cases (n)	OR (95% CI)	Controls (n)	Cases (n)	OR (95% CI)	Controls (n)	Cases (n)	OR (95% CI)
(a) Lasso
0–5	9880	12	0.42 (0.22–0.72)	278	106	0.65 (0.51–0.83)	35	19	0.89 (0.47–1.65)
5–10	9870	24	0.83 (0.52–1.27)	271	112	0.71 (0.55–0.90)	41	13	0.52 (0.25–1.01)
10–20	19,733	53	0.92 (0.66–1.27)	487	280	0.98 (0.82–1.18)	81	26	0.53 (0.31–0.88)
20–40	39,468	104	0.90 (0.69–1.18)	993	541	0.93 (0.80–1.08)	154	60	0.64 (0.42–0.99)
40–60	39,457	115	1	967	566	1	133	81	1
60–80	39,425	147	1.28 (1.00–1.64)	941	593	1.08 (0.93–1.25)	136	78	0.94 (0.64–1.39)
80–90	19,699	87	1.52 (1.14–2.00)	466	301	1.10 (0.92–1.32)	63	44	1.15 (0.71–1.84)
90–95	9842	51	1.78 (1.27–2.46)	214	169	1.35 (1.07–1.69)	34	20	0.97 (0.51–1.78)
95–100	9830	64	2.23 (1.64–3.02)	211	173	1.40 (1.12–1.76)	27	27	1.64 (0.90–3.00)
(b) Elastic net
0–5	9876	17	0.67 (0.39–1.09)	277	107	0.72 (0.56–0.92)	35	19	0.90 (0.47–1.64)
5–10	9876	17	0.67 (0.39–1.09)	271	112	0.78 (0.61–0.99)	41	13	0.52 (0.25–1.01)
10–20	19,740	45	0.89 (0.62–1.26)	497	270	1.02 (0.85–1.22)	81	26	0.53 (0.31–0.88)
20–40	39,453	120	1.19 (0.91–1.55)	967	567	1.10 (0.95–1.28)	154	60	0.64 (0.42–0.96)
40–60	39,471	101	1	1000	533	1	133	81	1
60–80	39,413	159	1.58 (1.23–2.03)	926	608	1.23 (1.06–1.43)	136	78	0.94 (0.64–1.39)
80–90	19,695	91	1.80 (1.36–2.40)	457	310	1.27 (1.06–1.52)	63	44	1.15 (0.71–1.84)
90–95	9841	52	2.07 (1.47–2.87)	226	157	1.30 (1.04–1.64)	34	20	0.97 (0.51–1.78)
95–100	9839	55	2.18 (1.56–3.02)	207	177	1.60 (1.28–2.01)	27	27	1.64 (0.90–3.00)
(c) Stepwise
0–5	9880	13	0.39 (0.21–0.67)	254	130	0.90 (0.71–1.14)	40	14	0.75 (0.37–1.44)
5–10	9874	19	0.57 (0.34–0.91)	268	115	0.76 (0.59–0.96)	43	11	0.55 (0.26–1.10)
10–20	19,742	44	0.67 (0.47–0.93)	494	273	0.98 (0.81–1.17)	80	27	0.72 (0.42–1.21)
20–40	39,470	102	0.77 (0.60–1.00)	970	564	1.03 (0.89–1.19)	142	72	1.09 (0.73–1.63)
40–60	39,440	132	1	979	564	1	146	68	1
60–80	39,414	158	1.20 (0.95–1.51)	951	583	1.08 (0.94–1.25)	130	84	1.39 (0.93–2.07)
80–90	19,697	88	1.33 (1.02–1.75)	456	311	1.21 (1.01–1.44)	61	46	1.62 (1.00–2.61)
90–95	9853	41	1.24 (0.86–1.75)	236	147	1.10 (0.87–1.38)	35	19	1.17 (0.61–2.17)
95–100	9834	60	1.82 (1.33–2.46)	220	164	1.32 (1.04–1.65)	27	27	2.15 (1.17–3.95)
(d) Select and shrink
0–5	9957	16	0.54 (0.31–0.89)	279	105	0.63 (0.49–0.81)	38	16	0.71 (0.36–1.33)
5–10	9888	15	0.51 (0.29–0.85)	254	129	0.85 (0.67–1.08)	41	13	0.53 (0.26–1.03)
10–20	19,812	51	0.87 (0.62–1.20)	489	278	0.96 (0.80–1.14)	81	26	0.54 (0.32–0.90)
20–40	39,435	113	0.97 (0.75–1.25)	1013	521	0.86 (0.75–1.00)	156	58	0.62 (0.41–0.94)
40–60	39,512	117	1	961	572	1	134	80	1
60–80	39,316	158	1.36 (1.07–1.73)	950	584	1.03 (0.89–1.20)	137	77	0.94 (0.63–1.40)
80–90	19,718	77	1.32 (0.98–1.76)	434	333	1.29 (1.08–1.54)	61	46	1.26 (0.79–2.02)
90–95	9791	45	1.55 (1.09–2.17)	233	150	1.08 (0.86–1.36)	30	24	1.34 (0.73–2.45)
95–100	9775	65	2.25 (1.65–3.03)	215	169	1.32 (1.05–1.66)	26	28	1.80 (0.99–3.31)

OR odds ratio, CI confidence interval.

Absolute risk of developing ovarian cancer by PRS percentiles

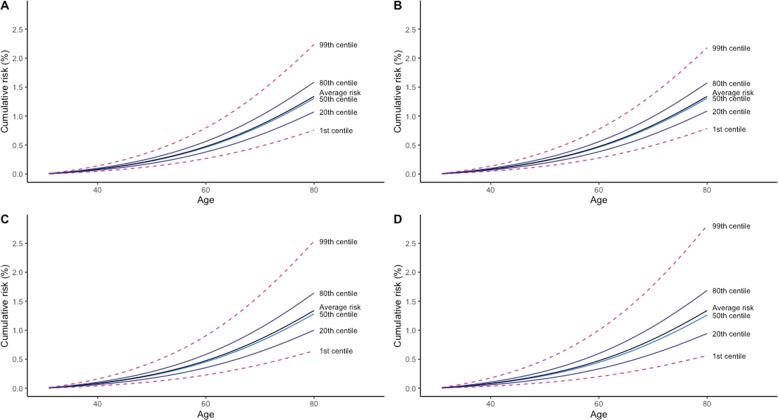
We estimated cumulative risk of EOC within PRS percentiles for women in the general population (Fig. 3), by applying the odds ratio from the PRS models to age-specific population incidence and mortality data for England in 2016. For BRCA1 and BRCA2 pathogenic variant carriers, we applied the estimated hazard ratios from PRS models to age-specific incidence rates obtained from Kuchenbaecker et al. [21]. For women in the general population, the estimated cumulative risks of EOC by age 80 for women at the 99th centile of the PRS distribution were 2.24%, 2.18%, 2.54%, and 2.81% for the lasso, elastic net, stepwise and S4 models, respectively. In comparison, the absolute risks of EOC by age 80 for women at the 1st centile were 0.76%, 0.78%, 0.64%, and 0.56% for the lasso, elastic net, stepwise and S4 models, respectively.

Fig. 3. Cumulative risk of ovarian cancer between birth and age 80 by PRS percentiles and PRS models.

Shown are the cumulative risk of ovarian cancer risk in UK women by polygenic risk score percentiles. The lasso (A) and elastic net (B) penalized regression models were applied to individual level genotype data, while the stepwise (C) and S4 (D) models were applied to summary level statistics. Note that the median and the mean risk differ because the distribution of the relative risk in the population is left-skewed (the log relative risk is a Normal distribution).

The absolute risks of developing EOC in BRCA1 and BRCA2 pathogenic variant carriers were considerably higher than for women in the general population (Figs. S1 and S2). The estimated absolute risk of developing ovarian cancer by age 80 for BRCA1 carriers at the 99th PRS centiles were 63.2%, 66.3%, 59.0%, and 68.4% for the lasso, elastic net, stepwise and S4 models, respectively. The corresponding absolute risks for women at the 1st PRS centile were 27.7%, 25.6%, 30.8%, and 24.2%. For BRCA2 carriers the absolute risks for women at the 99th centile were 36.3%, 36.3%, 33.0%, and 36.9%; and 7.10%, 7.12%, 8.24%, and 6.92% at the 1st centile for the lasso, elastic net, stepwise and S4 models, respectively.

PRS distribution and ancestries

To investigate the transferability of the PRS to other populations, we applied the scores to women of African (N = 1,072) and Asian (N = 7,669) ancestries genotyped as part of the OncoArray project. In general, the distributions of the raw PRS were dependent on both the statistical methods used in SNP selection and ancestral group. PRS models that included more variants had less dispersion, such that the elastic net models had the least between individual variation in all ancestral groups (standard deviation = 0.15, 0.19, and 0.22 for individuals of Asian, African and European ancestries respectively), while the distributions from the stepwise models were the most dispersed (standard deviation = 0.23, 0.27, and 0.30 for individuals of Asian, African and European ancestries respectively). As expected, given the variation in variant frequencies by population, the distribution of polygenic scores was significantly different across the three ancestral groups, with the least dispersion among women of Asian ancestries and the most variation in women of European ancestries. The difference in PRS distribution was minimized after correction for ancestry by standardizing the PRS to have unit standard deviation using the control subjects for each ancestral group.

High PRSs were significantly associated with risk of non-mucinous EOC in both Asian and African ancestries (Table 4), although the effects were weaker than in women of European ancestries. For example, with the lasso model, the odds ratio per unit standard deviation increment in polygenic score was 1.16 (95% CI: 1.11–1.22) in women of East Asian ancestries, 1.28 (95% CI: 1.13–1.45) in women of African ancestries and 1.37 (95% CI: 1.27–1.48) in women of European ancestries (p for heterogeneity <0.0001). Variability in effect sizes among ancestral groups was highest for the stepwise model (I² = 92%) versus 84% and 83% for elastic net and lasso derived polygenic scores respectively. The best discriminative model among women of East Asian and African ancestries were the elastic net PRS (AUC = 0.543) and the S4 PRS derived from OCAC-CIMBA meta-analysis (AUC = 0.596) respectively. Women of African ancestries in the top 5% of the PRS had about two-fold increased risk compared to women in the middle quintile (lasso OR: 1.64, 95% CI: 0.90–3.00; elastic net OR: 1.64, 95% CI: 0.90–3.00; stepwise OR: 2.15, 95% CI: 1.17–3.95; S4 OR: 1.80, 95% CI: 0.99–3.31) (Table 3). Effect estimates were smaller in women of East Asian ancestries with women in the top 5% of the PRS, having about a 1.5 fold increased risk compared to women in the middle quintile (lasso OR: 1.40, 95% CI: 1.12–1.76; elastic net OR: 1.60, 95% CI: 1.28–2.01; stepwise OR: 1.32, 95% CI: 1.04–1.65; S4 OR: 1.32, 95% CI: 1.05–1.66) (Table 3).

Table 4.

External validation of PRS models in East Asian and African Populations.

Model	East Asian ancestries			African ancestries
	AUC	OR	95% CI	AUC	OR	95% CI
Lasso	0.541	1.16	(1.11–1.22)	0.576	1.28	(1.13–1.45)
Elastic net	0.543	1.17	(1.12–1.23)	0.574	1.29	(1.14–1.47)
Stepwise (OCAC)	0.528	1.11	(1.06–1.16)	0.581	1.34	(1.18–1.52)
Select and shrink (OCAC)	0.538	1.14	(1.08–1.19)	0.593	1.38	(1.21–1.58)
Stepwise (OCAC-CIMBA)	0.542	1.17	(1.11–1.23)	0.594	1.37	(1.20–1.56)
Select and shrink (OCAC-CIMBA)	0.537	1.14	(1.08–1.19)	0.596	1.41	(1.23–1.61)

Discussion

Genetic risk profiling with PRSs has led to actionable outcomes for cancers such as breast and prostate [22, 23]. Previous PRS scores for invasive EOC risk in the general population and BRCA1/BRCA2 pathogenic variant carriers have been based on genetic variants for which an association with EOC risk had been established at nominal genome-wide significance [20, 24, 25]. Here, we explored the predictive performance of computationally efficient, penalized, regression methods in modeling joint SNP effects for EOC risk prediction in diverse populations and compared them with common approaches. By leveraging the correlation between SNPs which do not reach nominal genome-wide thresholds and including them in PRS models, the PRSs derived from penalized regression models provide stronger evidence of association with risk of non-mucinous EOC than previously published PRSs in both the general population and in BRCA1/BRCA2 pathogenic variant carriers.

Recently, Barnes et al. derived a PRS score using 22 SNPs that were significantly associated with high-grade serous EOC risk (PRS_HGS) to predict EOC risk in BRCA1/BRCA2 pathogenic variant carriers [20]. To make effect estimates obtained in this analysis comparable to the effect estimates obtained from the PRS_HGS, we standardized all PRSs using the standard deviation from unaffected BRCA1/BRCA2 carriers and provide estimates which are directly comparable to the PRS_HGS in Supplementary Table 9. All PRS models in this analysis except the Stepwise (OCAC only) had higher effect estimates [20]. The AUC estimates from the adjusted PLR methods implemented in this analysis, are higher than the corresponding PRS_HGS estimates for BRCA1 carriers (0.604). In BRCA2 carriers, the AUC estimates for the lasso and S4 models did slightly better than the PRS_HGS AUC estimate (0.667), while the stepwise did slightly worse and the elastic net estimate was comparable. The AUC estimates for women in the general population, as estimated from the UK Biobank, are slightly higher than estimates from previously published PRS models for overall EOC risk by Jia et al. (AUC = 0.57) and Yang et al. (AUC = 0.58) [25, 26].

The level of risk for women above the 95th percentile of the PRS is similar to that conferred by pathogenic variants in moderate penetrance genes such as FANCM (RR = 2.1, 95% CI = 1.1–3.9) and PALB2 (RR = 2.91 95% CI = 1.40–6.04) [27, 28]. The inclusion of other risk factors such as family history of ovarian cancer, presence of rare pathogenic variants, age at menarche, oral contraceptive use, hormone replacement therapy, parity, and endometriosis in combination with the PRS could potentially improve risk stratification as implemented in the CanRisk tool (www.canrisk.org), which currently uses a 36-SNP PRS with the potential to use other PRS models [29, 30].

We found that the discrimination of the PRS varied by ancestry with greater discrimination in women of European ancestries than in women of African and East Asian ancestries. The better performance in African than East Asian populations is in contrast to what one would expect given human demographic history, and the performance of PRS for other phenotypes in African populations. This may simply be the play of chance given the small number of samples of African ancestries. Alternatively it reflects the fact that the allele frequencies of the PRS SNPs were more similar between the African and European populations than they were with the East Asian population (Supplementary Tables 10–14).

Further optimization of the models could be achieved by varying the penalization function based on prior knowledge. For example, varying the penalty function to select more SNPs from genomic regions with known susceptibility variants given that susceptibility variants tend to cluster together. Alternatively, the penalty functions could be modified to incorporate information about functionally active regions of the genome such a promoters, enhancers, and transcription factor binding sites. However, incorporating functional annotation has resulted in limited gains in prediction accuracy for complex traits such as breast cancer, celiac disease, type 2 diabetes, and rheumatoid arthritis [31].

Machine/deep learning approaches are alternative ways to constructing PRS, but methods such as the neural net, support vector machine, and random forest have been shown to be computationally prohibitive or produce inferior results to other approaches [32, 33]. Other machine learning methods, such as those based on gradient boosting do not perform well in genomic regions where strong genetic interactions are present, for which alternative approaches such as the LDPred may perform better [18]. Our approach has several benefits over alternative machine learning methods, including its simplicity, and intrinsic robustness to minor misspecification of LD or association strength.

In conclusion, our results indicate that using the lasso model for individual level genotype data and the S4 model for summary level data in PRS construction provide an improvement in risk prediction for non-mucinous EOC over more common approaches. Our approach overcomes the computational limitations in the use of penalized methods for large-scale genetic data, particularly in the presence of highly correlated SNPs and when the use of cross-validation for parameter estimation is preferred. In practical terms, the PRS provides sufficient discrimination, particularly for women of European ancestries, to be considered for inclusion in risk prediction and prevention approaches for EOC in the future. Further studies are required to optimize these PRSs in ancestrally diverse populations and to validate their performance with the inclusion of other genetic and lifestyle risk factors.

Author contributions

EO Dareng, JP Tyrer, DR Barnes, MR Jones, X Yang, KK Aben, MA Adank, S Agata, IL Andrulis, H Anton-Culver, NN Antonenkova, G Aravantinos, BK Arun, A Augustinsson, J Balmaña, RB Barkardottir, D Barrowdale, MW Beckmann, A Beeghly-Fadiel, J Benitez, M Bermisheva, MQ Bernardini, L Bjorge, NV Bogdanova, B Bonanni, A Borg, JD Brenton, A Budzilowska, R Butzow, SS Buys, H Cai, MA Caligo, I Campbell, R Cannioto, H Cassingham, J Chang-Claude, SJ Chanock, K Chen, Y Chiew, WK Chung, KB Claes, S Colonna, LS Cook, FJ Couch, MB Daly, F Dao, E Davies, M de la Hoya, R de Putter, J Dennis, A DePersia, P Devilee, O Diez, Y Ding, JA Doherty, SM Domchek, T Dörk, A du Bois, M Dürst, DM Eccles, HA Eliassen, C Engel, D Evans, PA Fasching, JM Flanagan, RT Fortner, E Machackova, E Friedman, PA Ganz, J Garber, F Gensini, GG Giles, G Glendon, AK Godwin, MT Goodman, MH Greene, J Gronwald, E Hahnen, CA Haiman, N Håkansson, U Hamann, TV Hansen, HR Harris, M Hartman, F Heitz, MA Hildebrandt, E Høgdall, CK Høgdall, JL Hopper, R Huang, C Huff, PJ Hulick, DG Huntsman, EN Imyanitov, C Isaacs, A Jakubowska, PA James, R Janavicius, A Jensen, OT Johannsson, EM John, ME Jones, D Kang, BY Karlan, A Karnezis, LE Kelemen, E Khusnutdinova, LA Kiemeney, B Kim, SK Kjaer, I Komenaka, J Kupryjanczyk, AW Kurian, A Kwong, D Lambrechts, MC Larson, C Lazaro, ND Le, G Leslie, J Lester, F Lesueur, DA Levine, J Li, JT Loud, KH Lu, J Lubi_ski, PL Mai, S Manoukian, JR Marks, R Matsuno, K Matsuo, T May, L McGuffog, JR McLaughlin, IA McNeish, N Mebirouk, A Miller, RL Milne, A Minlikeeva, F Modugno, M Montagna, KB Moysich, E Munro, KL Nathanson, SL Neuhausen, H Nevanlinna, J Ngeow Yuen Yie, H Nielsen, L Nikitina-Zake, K Odunsi, K Offit, E Olah, S Olbrecht, OI Olopade, SH Olson, H Olsson, A Osorio, L Papi, SK Park, MT Parsons, H Pathak, I Pedersen, A Peixoto, T Pejovic, P Perez-Segura, JB Permuth, B Peshkin, P Peterlongo, A Piskorz, D Prokofyeva, P Radice, J Rantala, MJ Riggan, HA Risch, C Rodriguez-Antona, E Ross, M Rossing, I Runnebaum, DP Sandler, M Santamariña, P Soucy, RK Schmutzler, V Setiawan, K Shan, W Sieh, J Simard, CF Singer, AP Sokolenko, H Song, MC Southey, H Steed, D Stoppa-Lyonnet, R Sutphen, AJ Swerdlow, Y Tan, MR Teixeira, S Teo, KL Terry, M Terry, M Thomassen, PJ Thompson, L Thomsen, DL Thull, M Tischkowitz, L Titus, AE Toland, D Torres, B Trabert, R Travis, N Tung, SS Tworoger, E Valen, AM van Altena, AH van der Hout, E Van Nieuwenhuysen, EJ van Rensburg, A Vega, D Velez Edwards, RA Vierkant, F Wang, PM Webb, CR Weinberg, JN Weitzel, N Wentzensen, E White, SJ Winham, A Wolk, Y Woo, AH Wu, L Yan, D Yannoukakos, KM Zavaglia, W Zheng, A Ziogas, KK Zorn, K Lawrenson, TA Sellers, SJ Ramus, AN Monteiro, JM Cunningham, EL Goode, JM Schildkraut, A Berchuck, G Chenevix-Trench, SA Gayther, AC Antoniou, PD Pharoah contributed and/or designed the work that led to this submission, acquired data, played important roles in interpreting results, drafted or revised the manuscript, approved the final version and agreed to be accountable for all aspects of the work.

Data availability

OncoArray germline genotype data for the OCAC studies have been deposited at the European Genome-phenome Archive (EGA; https://ega-archive.org/), which is hosted by the EBI and the CRG, under accession EGAS00001002305. Summary statisitics for the Ovarian Cancer Association Consortium are available in the NHGRI-EBI GWAS catalogue (https://www.ebi.ac.uk/gwas/home) under the accession number GCST90016665. A subset of the OncoArray germline genotype data for the CIMBA studies are publically available through the database of Genotypes and Phenotypes (dbGaP) under accession phs001321.v1.p1. The complete data set will not be made publically available because of restraints imposed by the ethics committees of individual studies; requests for further data can be made to the Data Access Coordination Committee (http://cimba.ccge.medschl.cam.ac.uk/)

Competing interests

ADF has received a research grant from AstraZeneca, not directly related to the content of this manuscript. MWB conducts research funded by Amgen, Novartis and Pfizer. PAF conducts research funded by Amgen, Novartis and Pfizer. He received Honoraria from Roche, Novartis and Pfizer. AWK reports research funding to her institution from Myriad Genetics for an unrelated project. UM owns stocks in Abcodia Ltd. Rachel A. Murphy is a consultant for Pharmavite. The other authors declare no conflicts of interest.

Ethics statement

All study participants provided written informed consent and participated in research or clinical studies at the host institute under ethically approved protocols. The studies and their approving institutes are listed in the Supplementary Material (Ethics Statement).

Supplementary information

The online version contains supplementary material available at 10.1038/s41431-021-00987-7.