The use of machine learning to discover regulatory networks controlling biological systems

SUMMARY

Biological systems are composed of a vast web of multiscale molecular interactors and interactions. High-throughput technologies, both bulk and single cell, now allow for investigation of the properties and quantities of these interactors. Computational algorithms and machine learning methods then provide the tools to derive meaningful insights from the resulting data sets. One such approach is graphical network modeling, which provides a computational framework to explicitly model the molecular interactions within and between the cells comprising biological systems. These graphical networks aim to describe a putative chain of cause and effect between interacting molecules. This feature allows for determination of key molecules in a biological process, accelerated generation of mechanistic hypotheses, and simulation of experimental outcomes. We review the computational concepts and applications of graphical network models across molecular scales for both intracellular and intercellular regulatory biology, examples of successful applications, and the future directions needed to overcome current limitations.

INTRODUCTION

A vast web of interdependent molecular interactions governs biological systems and allows organisms to function. This network of interactions is highly complex, involving reactions at many molecular scales (e.g., from the level of genes to the level of cells) (Schaffer and Ideker, 2021). To effectively model such complex systems, it is worthwhile to examine the many molecular levels from which one might approach this challenge (Figure 1). At the molecular scale of the gene, researchers often attempt to understand the tens of thousands of different genes that drive the biological operations of complex multicellular life. Even when studied in isolation, understanding the function of each of these genes is a monumental task, and many human genes have not yet been extensively characterized (Su and Hogenesch, 2007; Stoeger et al., 2018). Moreover, genes do not act in isolation; their function is inextricably tied to the rest of the biological system. For example, transcription factors (TFs) concurrently regulate the expression of multiple genes, possibly even the gene coding for the regulating TF itself.

Figure 1. Molecular interactors in biological systems.

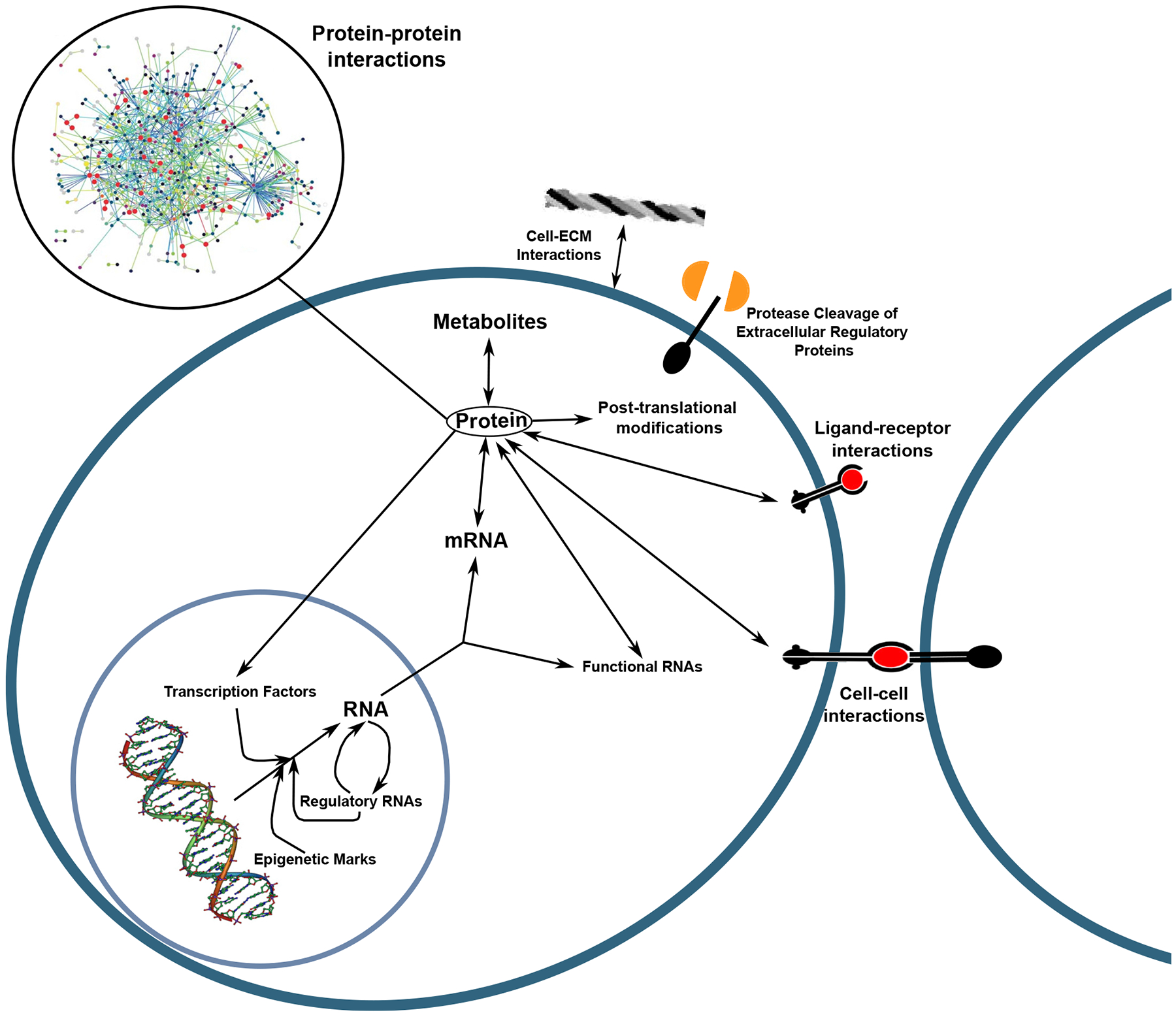
Diagram of the interactions across molecular scales that are involved in the biological processes between and within cells, including insoluble regulatory proteins and interactions with the extracellular matrix (ECM). A protein-protein interaction network is shown in the top left, demonstrating the interactive complexity that can exist within a single molecular scale. Includes as components DNA Overview 2 by Michael Ströck, licensed under Creative Commons CC BY-SA 3.0, The protein interaction network of Treponema pallidum by Titz et al., licensed under Creative Commons CC BY 1.0, a cropped version of Collagen biosynthesis by GKFK, licensed under Creative Commons CC BY-SA 3.0, and a cropped version of ligand-receptor interaction by Rit Rajarshi, licensed under Creative Commons CC BY-SA 4.0.

The expression of each gene as an RNA product is thought to be primarily controlled by its epigenetic state and the activity of regulatory proteins and functional RNAs (Harmston and Lenhard, 2013; Bhan and Mandal, 2014). However, the exact nature of this relationship is still not well characterized for most genes. The protein products of these genes likewise often cannot be well understood in isolation but must be placed in a network of other interacting proteins to accomplish a cellular task such as signal transduction, catalysis, or molecular transport. Post-transcriptional modifications and functional noncoding RNAs further impact cellular function and introduce another plethora of interactors that may be involved in a given cellular process (Cech and Steitz, 2014; Yao et al., 2019; Kuijjer et al., 2020). Each cell then interacts with other cells in the wider context of a microenvironment, a tissue, and the organism as a whole.

The regulatory complexity underlying biological processes and disease demonstrates the challenges of accurately modeling these systems. Bulk and single-cell profiling technologies are now commonly used to provide insight into the variety of molecular and cellular actors in biological processes. These technologies generate high-dimensional datasets that require specialized computational methodologies to interpret (Davis-Marcisak et al., 2021). Thus, the growth in molecular profiling technologies has been mirrored by the advancement of a wide variety of machine learning methods for high-throughput data analysis. This review describes machine learning methods for high-throughput data analysis that are designed to model the interactions between biological effectors such as genes, proteins, metabolites, and cells. We focus on methods that are predominantly based on graphical networks (Figure 2; Table 1), which explicitly model the interactions or regulatory relationships (called edges) between nodes (molecular effectors such as genes, proteins, metabolites, or cells).

Figure 2. Directed and undirected graphs and their adjacency matrices.

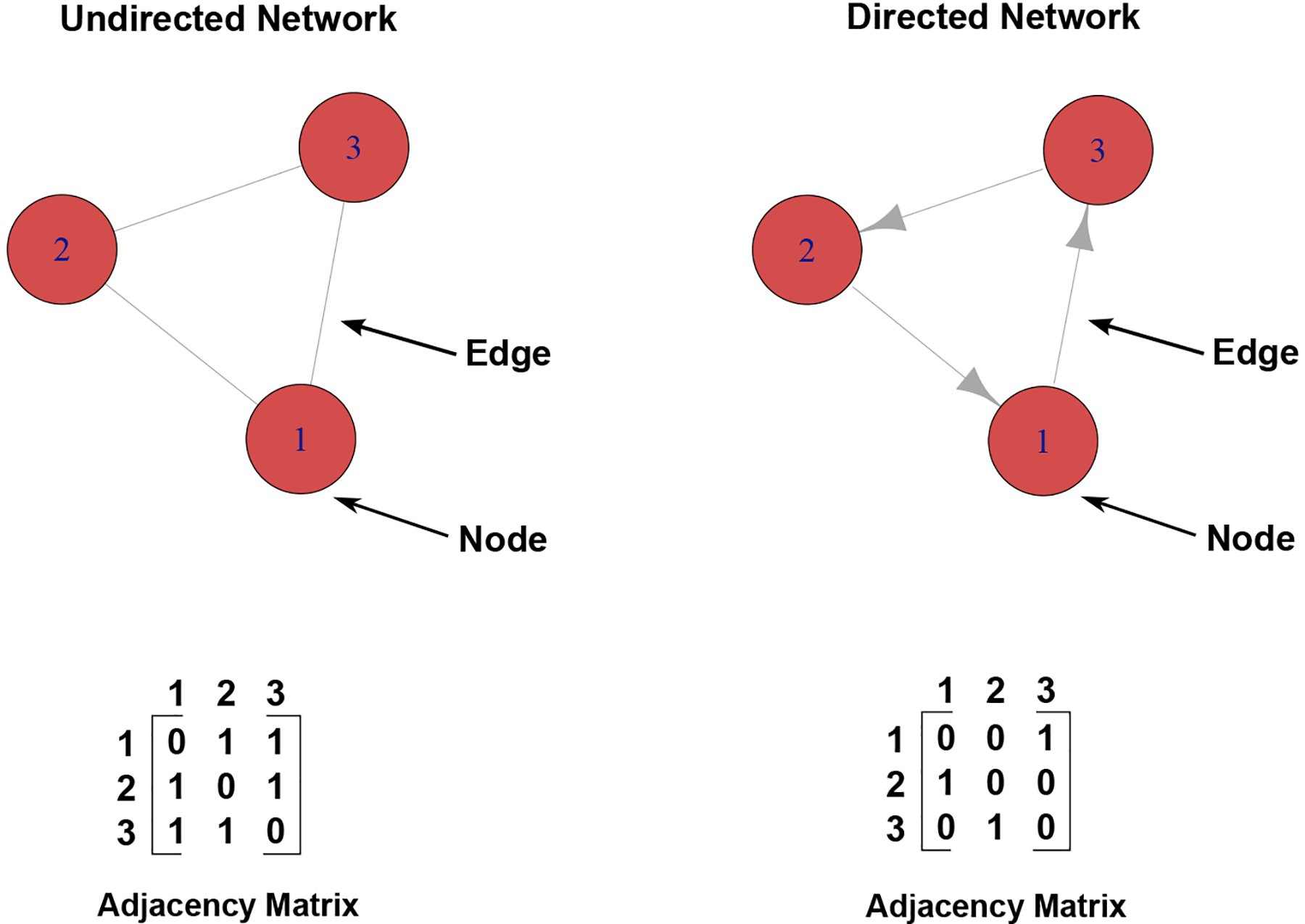
Diagram of the basic structure of an undirected and directed network graph. Each is composed of nodes (which in biological systems generally represent molecules such as genes or proteins) connected by edges (which in biological systems generally represent regulatory or direct functional relationships). Undirected networks only assert that a relationship exists among nodes, and this relationship is presented as symmetric. This feature is reflected in the symmetric adjacency matrix, a matrix representation of the network. In row 1, the given values are 0, 1, and 1, indicating that node 1 is not connected to itself but is connected to nodes 2 and 3. The columns can be read the same way for undirected networks, hence the symmetry of the matrix. Directed networks, by contrast, assert the directionality of the relationship between nodes. In biological networks, this is often intended to indicate that one node is the regulator and the other node is the target. The corresponding adjacency matrix is read slightly differently, where each row indicates the edges going out from that node, while each column represents the edges coming in. Thus, the values 0, 0, 1 in row 1 indicate that node 1 has an edge going into node 3, but not the other two nodes.

Table 1.

Basic graphical network terminology

Term	Definition
Node	An entity in the network that is capable of interacting with other entities
Edge	The interactions or relationships between nodes
Degree	The number of edges a node is connected to
Directed network	A network in which edges only can go in one direction (e.g., A > B is different from B > A)
Undirected network	A network in which edges are not directed (e.g., A-B implies that A and B are equal interactors)
Centrality	A measure of node importance, which can be determined using several different metrics, generally in some way describes the number of paths in the network that pass through a node or how many other nodes it is connected to.
Adjacency matrix	A matrix representation of a graphical network in which the values of the entries represent the interactions or relationships between nodes. The size of the matrix is n by n, where n is the total number of nodes in the network.

Table defining general terminology used to describe graphical network methods.

GENE NETWORK INFERENCE AIMS TO CAPTURE THE MECHANISTIC REGULATORY RELATIONSHIPS UNDERLYING GENE EXPRESSION

A wide variety of computational methodologies have been developed for gene regulatory network inference, a graphical network modeling approach to elucidating gene function and regulation. The ultimate goal of gene network inference is to uncover the regulatory biology of a particular system, often as it relates to a pathological phenotype. Graphical network methods have been designed to predict interactions algorithmically based on high-throughput molecular data, prior experimental knowledge, or a combination of the two. The resulting networks can be analyzed to yield humanly interpretable insights into the biological system under study from a convoluted web of molecular interactions (Figure 3). Network metrics called centrality measures (Table 1), which have been widely used for analysis of webpages and social networks, can also be applied to biological network inference. For these biological applications, network metrics can be calculated to identify key nodes (e.g., genes or proteins) in a system that may act as regulatory hubs controlling the biological process being studied, although their usefulness for this purpose in biological networks still requires thorough experimental validation. Another strategy for identifying critical parts of the network is optimization algorithms such as PCSF (Akhmedov et al., 2017) and SAMNet (Gosline et al., 2012), which have been applied in biological networks to find a smaller subsection of the network containing the nodes and edges with the largest regulatory influence in the data. Networks can also be used to generate specific mechanistic hypotheses by examining the causal predictions made by network structure. For example, if a network predicts that a specific gene regulates a set of genes that are all thought to contribute to a disease phenotype, that gene could be predicted as a molecular target to treat the said phenotype. Thus, the structure of the network implies that a node is a potentially useful target, due to its regulatory relationship with several other implicated factors. In this way, the goal of these graphical network methods is to distill relatively simple insights from the immense complexity of biological systems.

Figure 3. Building a biological network graph.

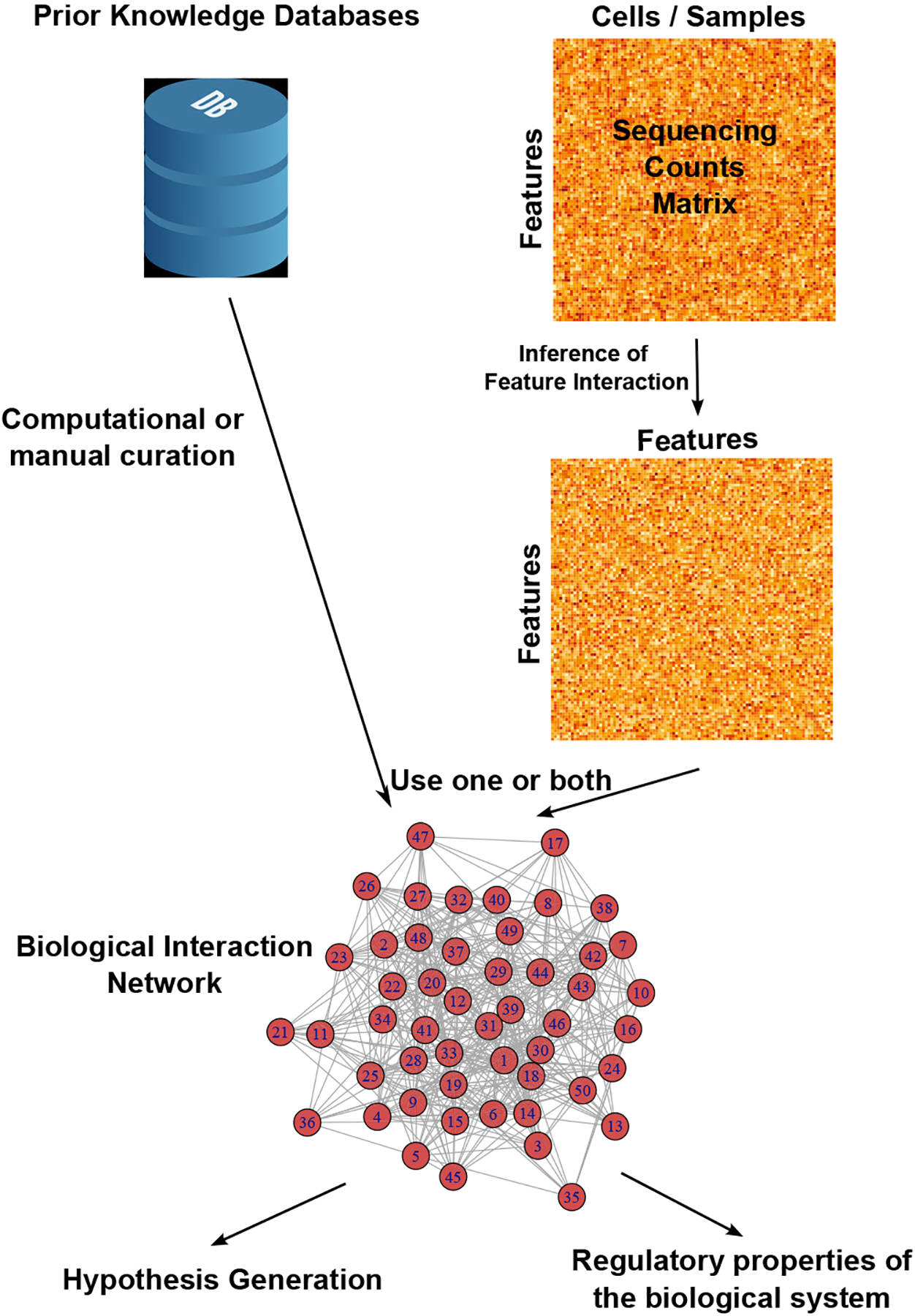
Graphical network models are generally created using prior knowledge databases, high-throughput molecular data, or some combination of both. Molecular data are usually summarized as sequencing counts or abundance matrix describing features such as genes, proteins, or sequencing peaks present in each cell or sample. An algorithm is then applied to these data to determine the likelihood that these features regulate one another. We diagram these feature correspondence predictions as a feature-by-feature matrix, with each element of the matrix giving the confidence of the algorithm in an interaction between two molecular features. These predictions can then either be used in isolation or combined with prior knowledge of feature interactions (which are generally computationally or manually curated to suit the particular application) to produce a graphical network of interactions underlying a biological system.

ACCURATELY MODELING BIOLOGICAL SYSTEMS USING GENE NETWORK INFERENCE REQUIRES THOROUGH CONSIDERATION OF EXPERIMENTAL DESIGN

Gene network inference methods have been developed to predict regulatory interactions based upon the dependencies between genes in both bulk and single-cell expression data (Nguyen et al., 2021; Mercatelli et al., 2020). The regulatory networks that can be inferred depend on the biological context and study design for the genomics data that are input to the network inference methods. The biological context is critical to consider because it is impossible to infer regulatory information about systems that are not active in the samples used to produce the data. For example, many of the regulatory processes of cell division cannot be inferred using data derived from quiescent cells. Additionally, it will be difficult to glean much regulatory information from highly stable systems—it would be impossible to determine regulatory control over genes that have expression values with no variance between conditions in a dataset.

The choice of bulk or single-cell data also impacts regulatory network inference. The main drawback of bulk data is that if it is drawn from a heterogenous mixture of cells, the expression signal from different cell types may be difficult to distinguish. The relevant regulatory interactions in different cell types may be different due to differing epigenetic landscapes, thus confounding the regulatory signal from the data. Single-cell sequencing allows individual cell types to be modeled separately, but technical dropouts (specifically genes that were expressed in the cell but zero counts were returned from sequencing due to measurement error) introduce additional challenges for predicting accurate regulatory relationships between genes because one cannot be sure if a zero occurs because of regulatory control or measurement error. In cases with known biological networks, these structures can be embedded in single-cell analysis algorithms to enhance data analysis (Elyanow et al., 2020).

COMPUTATIONAL METHODS INFER GENE INTERACTIONS THROUGH UNDIRECTED NETWORKS AND CAUSAL REGULATORY MECHANISMS VIA DIRECTED NETWORKS

After the experiment has been performed, computational methods are needed to infer regulatory networks from the resulting high-throughput datasets. The approaches for gene network inference can be generally classified into those that produce undirected networks—the interactions predicted between genes do not specify which is the regulator and which is the target— and directed networks, which attempt to make that distinction computationally (Figure 2). Additionally, a wide array of visualization tools have been developed that further support the network-based interpretation and inference of high-throughput datasets, notably the Cytoscape platform (Shannon et al., 2003; Otasek et al., 2019).

Among undirected network inference methods, the foundational approach uses Pearson correlation statistics between the expression values of pairs of genes to predict regulatory relationships between genes (Stuart et al., 2003). While this may appear to be a simplistic approach, correlation-based methods have been found to recover known regulatory interactions better than more complex methods on several datasets (Stone et al., 2021). However, they come with the caveat that genes with correlated expression are not necessarily functionally related. To overcome this limitation, another method utilizes the concept of mutual information, which measures how much one can know about the expression of gene X, given that you know the expression of gene Y. This method is popularly employed by the ARACNE algorithm (Margolin et al., 2006). Partial information decomposition (PIDC) has also been applied to refine results to functional interactions between genes (Chan et al., 2017). PIDC is used to measure statistical dependencies between three variables. These inferred dependences are applied to gene network inference by calculating the unique information between genes X and Y, divided by the information provided by every other gene Z in the dataset. The algorithm uses the relative information between genes to quantify the confidence of a regulatory link between X and Y.

The approaches described above for gene network inference all produce undirected networks: they estimate whether pairs of genes have a regulatory interaction between them but do not predict which gene is the target and which is the regulator. Therefore, these approaches require prior knowledge of gene regulation (e.g., which genes are known TFs) to distinguish the directionality of regulatory relationships. To handle cases in which prior information is unavailable or incomplete, another class of regulatory inference algorithms has been developed to infer directed networks without this reliance on prior biological knowledge. A prominent method that has performed well relative to other methods at recapitulating experimentally determined regulatory interactions, GENIE3, uses ensembles of decision trees to predict the likelihood of a regulatory link between genes based on how useful the expression of gene X is in predicting the expression of gene Y (Huynh-Thu et al., 2010; Aibar et al., 2017). Decision tree ensembles can be thought of as a model that learns many general “rules of thumb” (e.g., when gene A is above expression level X, gene B is almost always above expression level Y) about the system they are employed to predict. From those many rules, a single consensus prediction is made by a vote among all the trees (do they predict that gene A can in general be used to predict gene B?). The degree to which a gene can predict another is returned as a score of how confident the method is in the regulatory link between two genes.

The measurement noise and molecular noise in transcription introduce technical variation in gene expression datasets (Tunnacliffe and Chubb, 2020), often propagating to the inferred network. Therefore, other approaches aim to concurrently infer a directed network while reducing the noise from the input expression data. The scTenifoldNet method first produces a baseline directed network using principal components (PCs) regression (Osorio et al., 2020). PC regression performs principal components analysis (PCA), which decomposes the expression data into new variables (PCs) that describe the data’s uncorrelated sources of variance. These PCs can then be used to predict the expression of each gene in turn. Based on the value of each PC for predicting a target gene’s expression, an inference can be made about the effect of each other gene on the target gene’s expression. The resulting gene interaction network does not yet correct for technical variation in gene expression data. Therefore, this process is repeated for subsamples of the total expression data. Several networks are thus produced, the agreement between which can be used to determine which parts arise from technical variation and which correspond to regulatory biology (Osorio et al., 2020).

The methods introduced thus far are generally intended to analyze gene expression data collected from a single time point. However, datasets with measurements of gene expression over time can enhance the inference of directed networks. Expression changes in one gene that precede or follow another can better implicate a causal relationship than estimates made from a single point in time. Therefore, other approaches have been developed to model gene interactions as a system of equations with respect to time. The set of putative regulators of a gene can be determined and used to produce equations that predict how a gene’s expression values will change over time. These equations can then be solved and related to time course data through mathematical approaches such as differential equations. While using such methods with bulk RNA-seq data require explicit time course data, transitions in cellular state that occur over time can be estimated computationally from single-cell datasets using trajectory inference methods, providing a pseudo-temporal framework in which to use these methods (Trapnell et al., 2014; Saelens et al., 2019). Single-cell regulatory inference algorithms such as SCODE have been developed to perform temporal modeling using differential equations based on trajectory estimates of cell-state transitions from single-cell RNA-seq (Matsumoto et al., 2017). However, differential equations require models of the biological mechanisms through which genes interact, which may be unknown a priori and lack sufficient data to parameterize. Therefore, several other network inference methods instead perform statistical tests of whether the time series for one gene forecasts another (Granger causality), again based upon trajectory estimates from single-cell data, such as SINCERITIES (Papili Gao et al., 2018) and SINGE (Deshpande et al., 2019). The Scribe method is capable of using any time-ordered set of single-cell data as input and uses an estimation of causality from an information theory called directed information to identify direct regulatory links between genes (Qiu et al., 2020). These methods thus yield a network that is intended to account for changes in cell state over time in its regulatory predictions.

BENCHMARKING THE ACCURACY OF GENE REGULATORY NETWORKS ENABLES SELECTION OF INFERENCE METHODOLOGIES AND PRIORITIES FOR NEW ALGORITHM DEVELOPMENT

With this wide array of network inference methods (Table 2), standards for judging their relative merits are fundamental. Benchmarking computational algorithms requires applying them to datasets with a known ground truth state in order to assess performance. The two main approaches generally used for benchmarking gene network inference algorithms are based on either simulated datasets with known network structure or regulatory databases that contain experimentally determined interactions.

Table 2.

Gene network inference methods

Method	Algorithm type	Bulk or single cell	Directed or undirected	Citation	Code source
Pearson Correlation	correlation	both	undirected	Stuart et al., 2003	various
PIDC	partial information decomposition	both	undirected	Chan et al., 2017	https://github.com/Tchanders/ NetworkInference.jl
ARACNE	mutual information	both	undirected	Margolin et al., 2006	https://github.com/califano- lab/GPU-ARACNE
GENIE3	decision tree ensembles	both	directed	Huynh-Thu et al., 2010	https://arboreto.readthedocs. io/en/latest/index.html
SCODE	ordinary differential equations	single cell	directed	Matsumoto et al., 2017	https://github.com/hmatsu1226/SCODE
SINCERITIES	Granger causality	single cell	directed	Papili Gao et al., 2018	https://github.com/CABSEL/SINCERITIES
SINGE	Granger causality	single cell	directed	Deshpande et al., 2019	https://github.com/gitter-lab/SINGE
Scribe	directed information	single cell	directed	Qiu et al., 2020	https://github.com/cole-trapnell-lab/Scribe
scTenifoldKnk	principal components regression and tensor decomposition	single cell	directed	Osorio et al., 2021	https://github.com/cailab- tamu/scTenifoldKnk
CellBox	ordinary differential equations	bulk proteomics	directed	Yuan et al., 2021	https://github.com/sanderlab/CellBox

Table containing methods described in this review for or involving gene/protein network inference. These methods use transcriptomics data as input unless otherwise indicated.

Simulated benchmarks use a predefined network structure to simulate what expression profiles might look like given a known set of regulatory interactions. In some cases, gene expression datasets are simulated based upon randomized network structures. In these cases, algorithm performance is typically benchmarked in multiple simulations to test the variance of performance for a given network structure and sensitivity across a range of network parameters. However, the simulated networks may not reflect the structure of true biological networks. In other cases, the networks used in these simulated datasets are based on prior biological knowledge of gene interactions. For example, GeneNetWeaver uses a known network of regulatory interactions (such as the one that has been fully experimentally determined in Saccharomyces cerevisiae or Escherichia coli) to estimate how expression of gene products would change over time according to a system of equations that allows for both additive and multiplicative regulatory interactions (Schaffter et al., 2011). Such simulations provide a very clean way of benchmarking network inference methods because all regulatory relationships are already known, and the data only contain as much noise as is introduced purposefully by the researchers to maintain biological realism. Methods can be scored against how many of the known regulatory interactions each correctly predicts without concerns about whether this reference of interactions might be incomplete or incorrect.

However, benchmarking methods in the context they must ultimately be used in (experimental expression data) are desirable to robustly demonstrate a model’s effectiveness, especially since the assumptions necessary to simulate data may bias them in a way that does not reflect real biological systems. More complex networks of interactors with more and less predictable sources of noise will usually provide a more accurate representation of the context in which these methods will be applied. Furthermore, the performance of a method has been shown to sometimes differ substantially between simulated and experimental tests (Pratapa et al., 2020). Predictions from network inference methods are most commonly validated against ChIP-seq, ChIP-chip, and gene perturbation experiments. Often, nonspecific databases of gene interactions are used for these evaluations, and thus, the context (cell type, epigenetic state, metabolic state) in which the interaction was determined may not be the same as the dataset that the gene network inference method is applied to. Generally, this limitation can be minimized by examining only genes expressed with high variability in a dataset. Then, if a gene is not undergoing regulation or is epigenetically repressed, the method will not try to predict its regulators because that information does not exist in the data. However, there may be cases in which genes are variably expressed but are capable of acting in other, currently inactive, processes, which may lead to the appearance of the network method failing to identify a regulatory link that could have been inferred from the data. In this way, experimental benchmarking has more potential to incorrectly label a network as having generated false-negative results but provides a more realistic context than simulation-based benchmarks. These benchmarks are also expected to be incomplete descriptions of gene regulatory networks, which may additionally lead to incorrect identification of regulatory interactions as false positives. Ideally, algorithms should be tested on both types of benchmarks, as each one of them can reveal distinct properties of algorithm performance.

One of the main reasons why such a wide variety of network inference approaches have been developed is that different approaches perform better at reconstructing experimentally determined and simulated regulatory interactions in different datasets and contexts. Furthermore, no single method is currently capable of achieving a universally high prediction accuracy across simulated or experimental benchmark datasets, based on several independent assessments (Greenfield et al., 2010; Chen and Mar, 2018; Pratapa et al., 2020; Stone et al., 2021). Across these evaluations, the PIDC and GENIE3 (or methods based on GENIE3) methods have been pointed out as performing particularly well at capturing experimentally determined interactions in real expression data, although even these generally well-performing methods occasionally yield poor performances (Greenfield et al., 2010; Chen and Mar, 2018; Pratapa et al., 2020; Stone et al., 2021). The high error rates observed on some datasets could be plausibly attributed to any or all of the following factors: the need to include multiple omics datasets to improve predictions, the need for more robust algorithms to distinguish direct interactions from indirect interactions between genes and their products, molecular noise in transcription levels, measurement noise from sequencing, and methodological problems with the benchmarks used. Community-wide data science challenges, including notably the dialogue on reverse engineering assessment and methods (DREAM) challenge, have been developed to facilitate widespread validation of network inference methods from simulated and experimental datasets (Marbach et al., 2012; Hill et al., 2016). Standardizing datasets for benchmarking enables robust comparison of methods against a common ground truth and facilitates the independence of simulated datasets from the assumptions used in developing an algorithm (Camacho et al., 2018).

INFERENCE OF MULTISCALE INTRACELLULAR NETWORKS REQUIRES MULTIOMICS ANALYSIS METHODS

While building a regulatory graphical network from a high-throughput transcriptional dataset is a highly complex endeavor, it is still a considerable simplification of cellular processes. Within each cell, the DNA sequence, chromatin conformation, epigenetic modifications, gene expression, protein expression, protein modifications, and metabolites form a complex web of causal factors that produce cellular phenotypes (Figure 1). These multiscale processes are more accurately modeled from multiomics datasets that characterize these molecular scales (Table 3). In particular, elucidating the entire chain of causality by which cellular processes generate a phenotype of interest requires the following events across different molecular levels (Schaffer and Ideker, 2021) (Figure 4). Additionally, inferring networks from only a single data modality can lead to identifying interactions that appear to be only conditionally valid due to the differing epigenetic context of the cell. For example, in gene network inference, using data from one cellular context, a method may correctly identify a TF-gene regulatory link, but with data from a different context, it may fail to identify the same relationship. This could occur because the gene’s promoter in the second case was in a heterochromatic conformation and not accessible for the TF to bind or because a genetic variant altered TF binding affinity. Incorporating variant calling and epigenetic data could help resolve such problems in gene network inference, particularly as technologies to profile transcriptomics and chromatin state from the same single cell become more widely available.

Table 3.

High-throughput technologies for network modeling

Experiment	Data type	Output	Application for network modeling
RNA-seq/scRNA-seq	transcriptomics	sequences of expressed transcripts	inferring regulatory relationships between gene expression levels
ATAC-seq/scATAC-seq	chromatin conformation	sequences of DNA that are in an open conformation	identifying DNA sequences that are undergoing epigenetic regulation and which regions can express transcripts
Methyl-seq/scMethyl-seq	DNA methylation	methylated regions of DNA	identifying DNA sequences that are methylated and are thus unlikely to be able to express transcripts
ChIP-seq/scChIP-seq	protein binding to DNA	sequences of DNA with a particular protein/proteins bound	determining where particular regulatory proteins are binding in the genome
Protein mass spectrometry	proteomics	abundance of molecules with specific mass/charge ratio	estimate protein abundance and protein interaction networks
Protein microarrays	proteomics	abundance of a set of proteins	estimate protein abundance and protein interaction networks for a particular set of proteins
CyTOF	proteomics	abundance and location of a set of proteins	estimate protein abundance and protein interaction networks for a particular set of proteins, including a spatial element
CITE-seq	transcriptomics and proteomics	single-cell transcriptomics and abundance of cell surface proteins	infer relationships between gene expression and cell surface protein abundance
Metabolite mass spectrometry	metabolomics	abundance of molecules with specific mass/charge ratio	estimate the relationships between metabolite levels, to data from other experiments
NMR spectroscopy	metabolomics	abundances of organic and some inorganic molecules	estimate the relationships between metabolite levels, to data from other experiments

A list of high-throughput experiments, their outputs, and how these can be potentially applied for biological network modeling.

Figure 4. Multiscale models are necessary to capture some biological interactions.

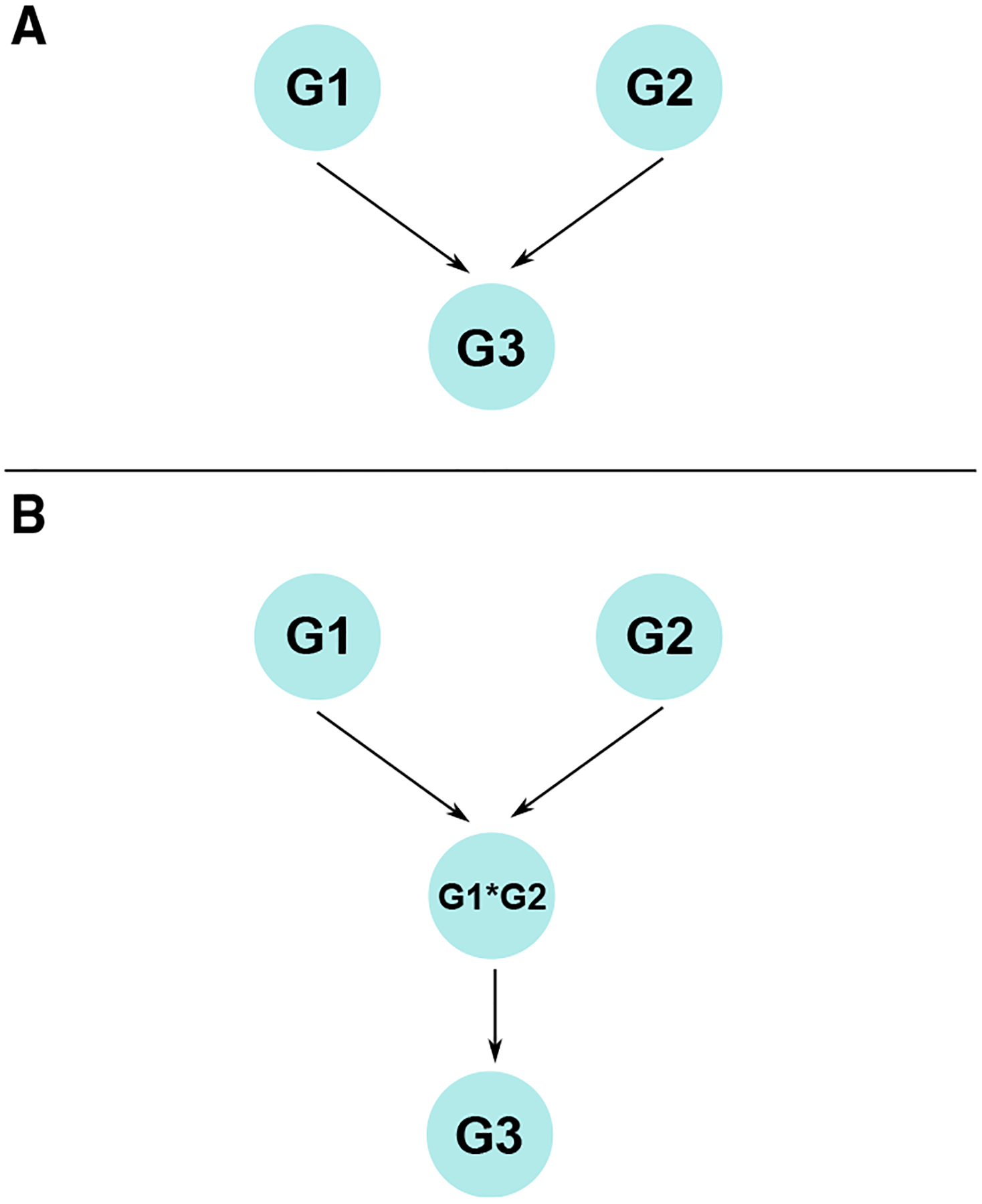
(A) A possible example of a gene regulatory structure in which two genes, G1 and G2, regulate a third gene, G3. In general, this situation poses no particular problem for gene network inference. However, if the regulation of G3 requires both G1 and G2 to be expressed for either regulatory effect to occur, (A) does not adequately describe the regulatory relationships between these three genes. If G1 is expressed and G2 is not, the regulatory link from G1 to G3 is then spurious, as is the link from G2 to G3 in the opposite situation. However, when both genes are expressed, both links appear valid.

(B) A network that can capture this possible regulatory structure, in which the products of G1 and G2 form a complex (G1*G2), which is the direct regulator of G3. Including combinations of gene products as nodes creates a multiscale network, which will exponentially increase the number of possible interactions to consider, the necessary cost of dealing with the type of regulatory behavior given in this example.

Integrating prior knowledge of TF targets, either from databases or binding assays, can be used to refine inferences of TF-gene regulation from expression data. An approach called BETA integrates ChIP-seq of TFs into expression data to infer TF-gene regulation (Wang et al., 2013). BETA predicts both whether a TF is activating or repressing gene expression and which genes are the TF’s direct targets, based on the statistical relationship between TF binding and differential gene expression. Similarly, the post-hoc statistics can be applied to matrix factorization to incorporate existing databases of TF regulation and patterns in gene expression to score the context-specific TF regulation of genes, which can be used to identify genes that are coregulated or that are regulated by multiple TFs (Fertig et al., 2013). Both these methods attempt to discover the regulatory structure of biological systems using multiple data types through transcriptional regulatory networks and serve as an important foundation as similar methods are developed for emerging single-cell datasets.

In the case of genetic variants, an approach has been developed to determine the impact of individual genetic variation on gene expression networks using EGRET (Weighill et al., 2021). The authors reason that, given the substantial proportion of functional genetic variants that appear to mediate their effects via differences in gene expression (Zhu et al., 2016), gene regulatory networks may differ between individuals in important ways. EGRET builds a general gene network based on prior knowledge, experimental TF cooperativity, and gene expression data, which it can then update based on genetic variant data to produce a different gene network for each individual. The mechanistic regulatory impact of genetic variants can be, thus, inferred, which the authors validate using cell lines with known genetic differences (Weighill et al., 2021).

While multiomics analysis can provide a more complete description of cellular processes, it also introduces several new challenges for analysis (Lê Cao et al., 2021). In the context of regulatory networks, the most immediate challenge is in combining the information across multiple data modalities into a single network. Alternatively, networks could be defined separately from each data modality, but then it would be necessary to address a similar challenge: how to model the interactions between those separate networks. One approach that has been developed to address this type of problem is the field of multilayer networks (Kivela et al., 2014), which formulates networks with distinct layers that each contain nodes of a specific type. This framework is applied by (Liu et al., 2020) using large-scale databases to produce a multilayer network containing one layer each for genes, proteins, and metabolites. The multilayer network thus produced was shown to be robust at recovering the importance of genes that are required for cellular function or have been annotated as critical cancer genes.

Predicting causal relationships between molecular effectors is also more complex when multiple levels of molecular effectors are involved, due to the need to account for possible interactions both within and between modalities. Determining the order of cause and effect is also an even larger challenge in this context, especially when processes such as gene regulation are often cyclic, making many of the best-developed causal inference frameworks, such as directed acyclic graphs (Pearl, 1995), unusable. One possible approach is to model only acyclic processes but ignoring feedback loops in biological systems will often omit substantial information. Technical variation arising from different sources of noise, variance, or batch effects across the different data modalities also must be accounted for to avoid biasing results.

The COSMOS method (Dugourd et al., 2021) attempts to navigate the many obstacles of multiomics network modeling with an approach based on prior knowledge and their previously developed method for network analysis within a single data modality (Liu et al., 2019). COSMOS finds prior knowledge networks that provide relationships between transcriptomics, phosphoproteomics, and metabolomics data using the Omni-Path protein-protein and gene regulatory interaction databases (Türei et al., 2016) and the Recon3D metabolomics database (Brunk et al., 2018). These prior knowledge networks are then refined by removing interactions that create incorrect predictions when applied to the transcriptomics, proteomics, and metabolomics datasets provided as input. It then removes interactions that lead to incoherent predictions (e.g., two molecules that should be correlated end up being anticorrelated). The network is further filtered based on the expression differences observed in the biological context of interest, which yields a set of genes, proteins, and metabolites that are differentially regulated. These molecular effectors are used to produce the final network, which only includes nodes (genes, proteins, or metabolites) a set number of regulatory steps away from the differentially regulated starting nodes. COSMOS is additionally incapable of forming loops, which is a possible limitation of the method but also allows causal analysis to be applied with much less difficulty. From this network, the regulatory effects of the perturbed molecules can be causally inferred. A statistical test for gene set analysis can then be applied to determine whether the genes identified in the network are annotated to pathways with known biological relevance (Dugourd et al., 2021). COSMOS is limited to producing a subnetwork connected to differentially regulated molecules, which appears to be a strength in that it focuses the method on relevant biological differences. However, it also creates the inability to reach relevant molecular effectors that are either more distantly regulated or not included in the prior knowledge network. COSMOS appears to be a significant step in network modeling across multiomics datasets. However, more work still needs to be done to robustly model the wide variety of regulatory interactions that control biological systems at a multiscale molecular level.

INTERCELLULAR NETWORKS MODEL SIGNALING BETWEEN CELLS, ALTERING INTRACELLULAR DYNAMICS, AND PRODUCING LARGE-SCALE PHENOTYPES

In isolation, even a highly robust model of the internal operations of a single cell would often be insufficient to characterize many phenotypes due to the importance of intercellular signaling. For example, intercellular signaling has been shown to be critical for cellular differentiation (Kirouac et al., 2010; Basson, 2012), organ homeostasis (Arneson et al., 2018; Wang et al., 2020), the cellular response to aging (Ximerakis et al., 2019), and the cellular response to disease (Fernandez et al., 2019), particularly cancer (Vaske et al., 2010; Kumar et al., 2018; Baghban et al., 2020). In general, the collective processes and interactions of many cells produce the tissue-scale and organism-scale phenotypes that are the primary focus of biomedical research. Thus, characterizing these interactions as a graphical network model provides a valuable framework to understand many phenotypes of interest in terms of the interactions of the cells that produce them.

Several methods have been developed to model cell-cell interactions, generally in the form of ligand-receptor interactions at the cell surface. Many models also include predictions of the downstream effects these interactions will have within the cells involved. Here, we will again focus on those methods that model regulatory interactions explicitly as graphical networks. Generally, these methods produce a score of cell and receptor interactions and then model the effects these interactions will have on the expression of genes regulated downstream of the receptors (Wang et al., 2019; Browaeys et al., 2020; Cherry et al., 2021). This feature allows these methods to describe the impact of intercellular interactions on intracellular processes, which seems likely to be a necessary feature to fully understand many cellular phenotypes. However, none of the methods thus developed are able to model interactions between the downstream signaling effects of multiple different receptors, which may be a significant limitation in some circumstances.

NicheNet uses prior knowledge of ligand-receptor interactions and gene regulatory networks along with bulk or single-cell transcriptomics data to predict activated receptors (Browaeys et al., 2020). These predictions are made using a personalized PageRank metric, an adaptation of the method developed by Google to score and rank web pages in their search engine (Page et al., 1998). Here, it is instead used to produce a score for ligand-receptor interactions. Another method, SoptSC, approaches the problem with a greater emphasis on cell clusters, taking single-cell expression data and a set of known receptors and their cognate ligands as input to calculate the similarity between each cell’s expression profile. This information is compiled into a matrix, from which the method creates a cell-cell interaction network and clusters the cells, ultimately allowing inferences of signaling pathways activated between cell clusters (Wang et al., 2019). DOMINO similarly emphasizes cell clusters but focuses more on TF activity as well as receptor-ligand activation (Cherry et al., 2021). DOMINO uses the results of SCENIC (Aibar et al., 2017), a method that builds on GENIE3 to score TF activity, combined with prior knowledge networks of ligand-receptor pairs to determine interactions between cell types and the activated ligands and TFs within each cell type. NATMI takes a slightly different approach (Hou et al., 2020), focusing on learning interactions between cells using bulk or single-cell expression data, not addressing the specifics of how these regulatory interactions impact downstream gene expression. NATMI uses large-scale ligand-receptor databases to create prior knowledge networks. It then calculates a weight for each interaction between genes, based on three expression-based metrics from the dataset of interest, which are used to determine cell type interactions (Hou et al., 2020).

Due to the wide array of cell-cell interactions that play roles in cancer (Kumar et al., 2018; Baghban et al., 2020), CCCExplorer was developed specifically for use with tumor data (Choi et al., 2015). CCCExplorer identifies differentially expressed ligands in cells in the tumor microenvironment as well as expressed receptors on tumor cells. It then uses expression data from tumor cells to find expressed TFs, combining prior knowledge of each TF’s regulated genes to determine the probability that the corresponding pathway is active. These data are combined to identify active signaling branches, which are further combined to generate a crosstalk network. This network is used to identify regulations between the tumor microenvironment and the tumor cellular phenotype (Choi et al., 2015).

While the methods discussed thus far all produce predictions of cell-cell interactions, an important consideration is often the question of where cells are interacting in a particular tissue, which may be highly relevant to phenotype. To account for this, SpaOTsc maps single-cell transcriptomics to spatial datasets (such as in situ hybridization) and uses the spatial element to inform the prediction of cell-cell interactions and how these impact gene regulation (Cang and Nie, 2020). This is accomplished using PIDC, which calculates the statistical dependencies between three variables (e.g., is gene A important to the relationship between genes B and C?), and ensembles of decision trees, which in effect combine many “rules of thumb” that are computationally learned from the data to produce consensus predictions (Table 4).

Table 4.

Intercellular graphical network methods

Method	Algorithm type	Data type(s)	Citation	Code source
NicheNet	PageRank	bulk or single-cell transcriptomics	Browaeys et al., 2020	https://github.com/ saeyslab/nichenetr
SoptSC	similarity matrix	single-cell transcriptomics	Wang et al., 2019	https://github.com/ WangShuxiong/SoptSC
DOMINO	decision trees and correlation	bulk or single-cell transcriptomics	Cherry et al., 2021	https://github.com/ chris-cherry/domino
SpaOTsc	partial information decomposition and decision tree ensembles	single-cell transcriptomics + spatially resolved data	Cang and Nie, 2020	https://github.com/ zcang/SpaOTsc
CCCExplorer	pathway activation probability	bulk or single-cell transcriptomics	Choi et al., 2015	https://github.com/ methodistsmab/CCCExplorer
NATMI	prior knowledge weighting	bulk or single-cell transcriptomics	Hou et al., 2020	https://github.com/asrhou/NATMI

Table containing methods for intercellular network modeling described in this review.

OVERVIEW OF VALIDATION OF NETWORK MODELS FOR BIOLOGICAL INSIGHT

In order to ensure that computational models are capable of generating robust biological insight for users, they must be thoroughly tested for accuracy and biological relevance. This is particularly essential given the complexity of network analysis for high-throughput profiling data. Several different strategies have been employed for the validation of biological network methods, each with strengths and weaknesses.

Simulated data are generally the first test a network method is subjected to and is produced by assuming a particular network structure and generating data using a mathematical model (e.g., if we know gene 1 upregulates gene 2, which downregulates gene 3, what might expression data from this system look like based on what we know about the dynamics of gene regulation?). The strengths of simulated data tests are that the correct network is known as a certainty, and it is quick and inexpensive to do large numbers of tests across different contexts. However, these simulations must rely on machine-coded assumptions to generate datasets. When the assumptions of the model do not adequately conform to the biological processes being simulated, they can produce output that lacks some characteristics of genuine datasets.

Another strategy for benchmarking uses databases of interactions that are known to occur in an organism, then scores the model against the number that it identifies correctly when tested on real biological data. While this approach has the advantage of working with the sort of data the method is intended to be used on in practice, performance assessments will be biased by the incompleteness of existing databases. Furthermore, in cases where the database was generated from data that came from a different context compared with the data input to the network model, the network may, correctly, not identify some context-dependent interactions and be penalized incorrectly.

Finally, mechanistic experiments can be performed in the same context as the data fed into the network model, providing the most reliable feedback on the usefulness of a model in identifying biologically relevant regulatory interactions. While providing a gold standard, the large number of perturbations required for high-throughput validation can make such efforts both cost and time prohibitive at a genome-wide scale. However, a limited set of experiments can greatly increase the confidence given to other predicted interactions made by the network model, if those tested are validated.

APPLICATIONS OF NETWORK METHODS ENABLE COMPUTATIONAL PREDICTION OF PERTURBATIONS AT SCALE AND PRIORITIZATION OF TARGETS FOR EXPERIMENTAL VALIDATION

Biologically, the value of gene regulatory network inference is that it can be used to discover interactions between genes. Producing this comprehensive understanding of the regulatory mechanisms of a biological system allows for the application of additional computational techniques to predict the impact of interventions on phenotypes (Sonawane et al., 2019; Belyaeva et al., 2020). These methods use the network to go beyond associating variables to predict the experimental results of an intervention to the biological system (e.g., a perturbation). Understanding the mechanistic contribution of a single gene to a particular biological process or phenotype is often the work of years or even decades using traditional experimental tools. Network methods may be able to aid in investigations about the role of genes and their products in biological systems by generating in silico hypotheses regarding the mechanistic impact of altering gene expression levels (Figure 5). This information can guide candidate prioritization and selection for more highly time-intensive experiments to accelerate mechanistic biological discovery.

Figure 5. A network model of a transcriptomic perturbation.

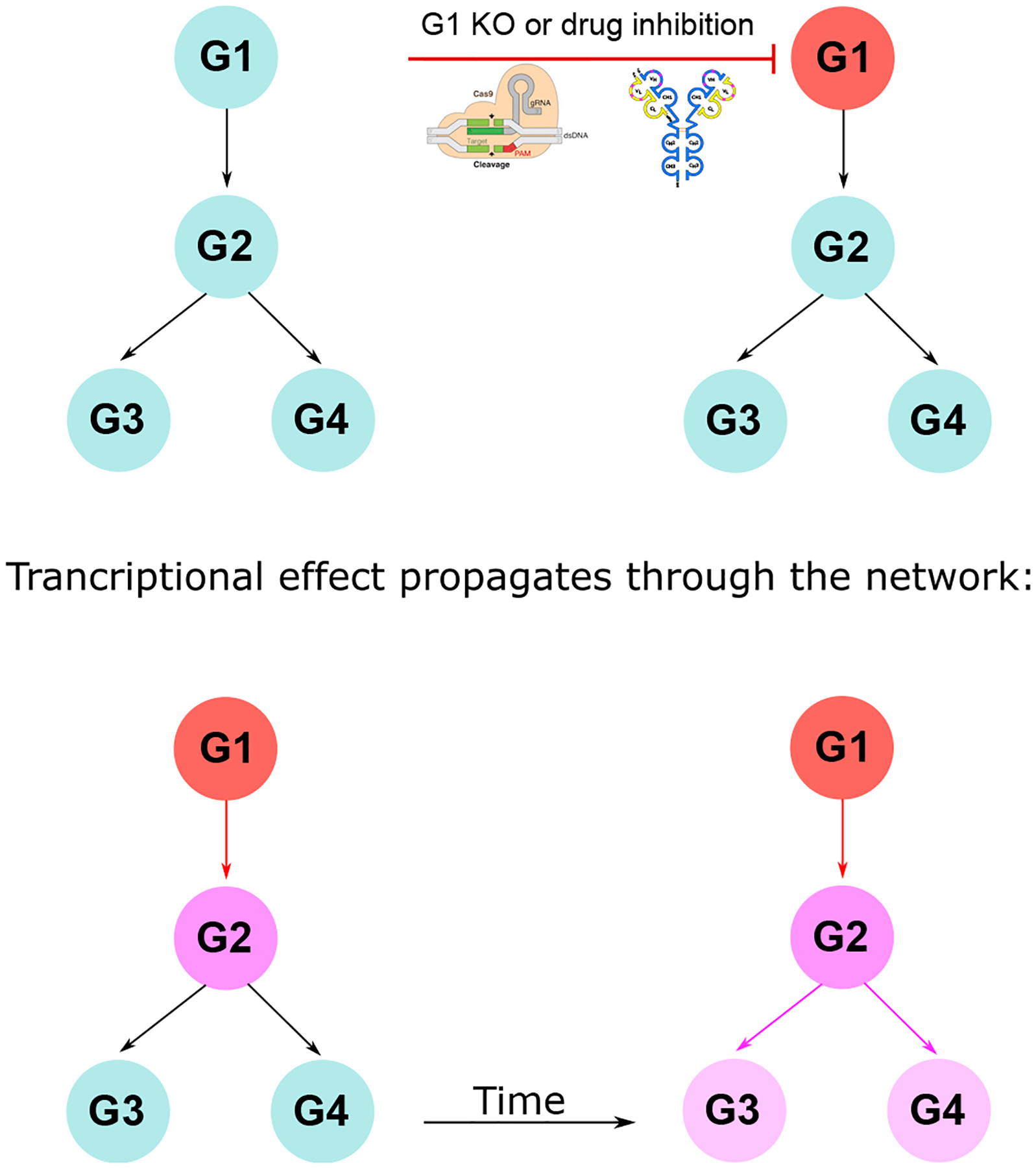
Illustration of how a genetic perturbation can be modeled using a graphical network. After a KO or inhibition by a drug, the network describes which genes will be transcriptionally affected by this perturbation and in which order. By quantifying these relationships, the transcriptional impact can be predicted along with the mechanistic steps that would produce it. This diagram can be generalized to interactions between proteins and other molecular effectors, including components like GRNA-Cas9 by Marius Walter, licensed under Creative Commons CC BY-SA 4.0, and Antibody_structureA by Michael Jeltsch, licensed under Creative Commons CC BY-NC-SA 4.0.

While some of this information can be provided by high-throughput knockout screening methods such as Perturb-seq (Dixit et al., 2016), the reasons why a particular knockout (KO) has the impact that it does may still be opaque after such experiments. The advantage of gene network analyses is that they can provide both a prediction of the end result of a perturbation and a mechanistic account of why that result was produced, which may be critical for fully understanding biological processes and rational drug design.

The scTenifoldKnk method aims to computationally predict gene KO experiments using what the authors term as virtual KO screens (Osorio et al., 2021). The method produces a directed gene regulatory network using single-cell transcriptomics data from unperturbed cells by applying their scTenifold network inference method (Osorio et al., 2020). The virtual KO is then performed using the adjacency matrix (Table 1). A gene is “knocked out” by setting the entries for the target gene to zero. This creates a version of the network in which the gene is no longer acting, simulating the results of a KO. The two networks are then compared, which can be used to evaluate which genes will be differentially expressed as a result of the gene KO. Within these putative differentially expressed genes, scTenifoldKnk searches for enrichment of known gene sets. The authors show that the gene sets found to be enriched in these virtual KO differentially expressed genes are often related to the known biology of the system being studied. For example, genes predicted to be perturbed by a CFTR gene KO are enriched for ABC transporter disorder and abnormal surfactant secretion pathways, which would be expected given the known functions of the CFTR gene. This capacity to predict differentially expressed genes enriched in pathways that would be expected based on the known function of a gene is shown across several different cellular contexts (Osorio et al., 2021). The authors additionally perform more direct experimental validation of the predicted differentially expressed genes. When they perform an experimental KO of Malat1 in mouse pancreatic cells, they predict 167 perturbations in other genes. However, only four of those predictions overlap with the 1,695 experimental differentially expressed genes they found between the wild-type (WT) and KO cells (Osorio et al., 2021). This result indicates that while the general biological significance of a KO may be recovered by the method (e.g., it predicts there will be shifts in pathways that are known to be associated with the biology of the system), the precise transcriptomic effects are not. This result suggests further development of such methods will be required to achieve the ideal of establishing a robust causal model of gene network interactions that can make accurate predictions of the transcriptomic effects of a gene KO.

CellBox is another method designed to predict experimental results computationally. However, instead of predicting the results of a gene KO, CellBox is designed to predict the results of drug perturbations on phenotypes of interest. It uses bulk proteomics data from drug perturbation experiments, in which a phenotype of interest was measured, to fit a system of ordinary differential equations. These equations can then be used to predict the phenotypic effect of unseen drug treatments and combinations of drug treatments (Yuan et al., 2021). CellBox provides the functionality of varying drug concentration as well as treatment type, which can allow many more permutations to be predicted than would normally be experimentally feasible. CellBox thus allows a small amount of drug screening data to be generalized to predict the outcome of arbitrary drug dosages and combinations at a network and phenotypic level. The authors highlight the potentially great value of CellBox for evaluating combination therapies for cancer. Oncology may be a specifically useful application of such methods due to both the potential for drug synergy as well as the logic that the more therapeutics a tumor has to evolve resistance to in order to survive, the less likely it is for resistance to develop (Bayat Mokhtari et al., 2017). If each drug requires a separate genetic or epigenetic event for a cancer cell to acquire resistance to it, it will be much less likely to undergo sufficient evolution to evade being killed by the effects of at least one of the treatments.

Given the complex regulatory relationships that exist in tumor cells and their cellular microenvironment, oncology is a field in which graphical network models may be particularly valuable. A recent study by Zhou et al. (Zhou et al., 2021) leverages both gene regulatory and cell-cell interaction models to analyze single-cell RNA-seq data from triple-negative breast cancer patients, providing an informative example of how network methods can be applied at multiple biological levels to glean insights into complex systems. The authors used the CellPhoneDB method (Efremova et al., 2020) to identify ligand-receptor pairs from their data, from which they were able to determine the dominant regulatory role of macrophages in the tumor microenvironment of the patients studied, particularly noting epithelial growth factor receptor (EGFR)-amphiregulin interactions in patients with basal-like tumors. The study further constructed TF-target-based gene regulatory networks using GENIE3 (Huynh-Thu et al., 2010), which they analyzed via centrality metrics, measures of node (in this case, gene) importance that are generally in some way based upon how many regulatory interactions a gene is involved in. Some centrality measures only account for direct interactions, while others include information about how many interactions the interactors of a node have as well. These centrality measures were used to predict critical genes, capturing known important genes such as MYC and identifying ETV6 as an activated critical gene across all subtypes. This use of centrality metrics is a simple and highly useful approach to identifying key nodes that may warrant further examination and experimental testing of their importance in the biological system of study.

Experimental validation is critical to ensure the reliability of computational methods and is particularly important when dealing with highly complex models such as network methods. An advantage of the network methods and subsequent predictions is that these analyses can prioritize candidate targets for validation experiments. Such validation can yield much greater confidence in the ability of a method to capture the underlying biology of a system or phenotype. The study describing CCCExplorer provides an excellent example of this type of validation (Choi et al., 2015). CCCExplorer predicted that the high IL6 expression in tumor-associated macrophages in their data activated the IL6 receptor on the tumor cells, activating the STAT3 pathway. They established an in vitro system of macrophages and the same type of tumor cells in which tumor-conditioned media upregulated IL6 in WT macrophages, which in turn increased phosphorylated-STAT3 levels in the tumor cells more than 10-fold. Additionally, macrophages with IL6 knocked out did not upregulate phosphorylated-STAT3 in the tumor cells. This kind of validation experiment is able to demonstrate the ability of a computational method to not only capture already known interactions but also identify novel relationships that have important effects on the biological system of study. This sort of validation is critical to establish sufficient confidence in these methods beyond computational benchmarking so that they can begin to help guide experimental planning and therapeutic development.

CONCLUSIONS AND FUTURE DIRECTIONS

Graphical network methods provide a model to understand the complexity and sheer number of interacting molecular effectors that contribute to cellular and organism-level phenotypes. Progress is ongoing, and many improvements have been made in the ability of these methods to model the relationships between molecular effectors and translate these regulatory models into meaningful insights into biological systems and the phenotypes they produce. These methods allow researchers to identify regulatory controls active within a cell, which can be used to generate hypotheses about how to manipulate a biological process to treat disease. Given the complexity of biological systems, such insights may, in some cases, be extremely difficult to achieve without a model capable of containing many of the molecular effectors at play.

Network methods are currently being used to yield insights into regulatory biology, protein and metabolic interactions, intercellular interactions, and how this molecular web translates into phenotypes. However, there are still several areas in which significant further research is warranted. One of the highest priority areas is the fact that gene network inference methods often do not perform reliably in benchmark experiments on either experimental gold standards or simulated datasets (Chen and Mar, 2018; Pratapa et al., 2020; Stone et al., 2021), as discussed in the benchmarking the accuracy of gene regulatory networks enables selection of inference methodologies and priorities for new algorithm development subsection. Predicting whether genes are causally interacting or merely correlated, dealing with transcriptional and measurement noise, and cellular heterogeneity still pose major challenges for the field. Identifying strategies for handling these issues is a crucial area of ongoing research. Another important problem in the field is that few existing network methods integrate across omics datasets. Many approaches do not include multiomics data for reasons of complexity, computational capacity, or data availability. While a challenging problem, incorporating information across molecular scales is necessary to accurately model the regulatory biology of many cellular processes and diseases. Finally, many studies also do not provide experimental validation of the novel predictions their methods make. Although such validation requires substantial investments of researchers’ time and resources, if a method is intended to generate hypotheses worthy of further investigation, such validation seems critical to providing users the confidence to plan experiments based on a computational method’s predictions.

While this review primarily focuses on more recently developed algorithms for emerging single-cell technologies, several foundational methods developed for older microarray and bulk profiling technologies have continued relevance for analyses of these emerging datasets. The solid foundation of mathematical insight into how to model biological interactions has allowed these models to continue to be useful even as network methods are updated and refined. We note that Camacho et al. and Sonawane et al. (Camacho et al., 2018; Sonawane et al., 2019) provided additional reviews of a range of computational methodologies for biological network methods, providing greater detail on the methods, while we focus more on their specific biological applications in this review. Some of the major recent developments in network modeling have been based on accounting for technical features of biological datasets, such as sources of noise and heterogeneity (Osorio et al., 2020), as well as providing tools to more easily ascertain the biological significance of network models (Aibar et al., 2017).

As algorithms and validation develop to accurately model disease and biological systems with network methods, they have the potential to become more powerful tools for therapeutic development. Much of the time required to develop new treatments or discover the main drivers of some biological process is spent on finding a relatively high-confidence target and understanding the mechanism of action. Thus, prioritizing functional candidates through network methods could significantly improve the speed of preclinical studies for therapeutic development and studies exploring pathways and complex interacting mechanisms in biological systems.