Abstract
COVID-19 is a life threatening disease which has a enormous global impact. As the cause of the disease is a novel coronavirus whose gene information is unknown, drugs and vaccines are yet to be found. For the present situation, disease spread analysis and prediction with the help of mathematical and data driven model will be of great help to initiate prevention and control action, namely lockdown and qurantine. There are various mathematical and machine-learning models proposed for analyzing the spread and prediction. Each model has its own limitations and advantages for a particluar scenario. This article reviews the state-of-the art mathematical models for COVID-19, including compartment models, statistical models and machine learning models to provide more insight, so that an appropriate model can be well adopted for the disease spread analysis. Furthermore, accurate diagnose of COVID-19 is another essential process to identify the infected person and control further spreading. As the spreading is fast, there is a need for quick auotomated diagnosis mechanism to handle large population. Deep-learning and machine-learning based diagnostic mechanism will be more appropriate for this purpose. In this aspect, a comprehensive review on the deep learning models for the diagnosis of the disease is also provided in this article.
Keywords: COVID-19 Diagnosis, deep learning, machine learning, natural language processing, SEIR, SIR, sentimental analysis
I. Introduction
During the end of December, 2019, a few cases of acute pneumonia with unknown causes were reported in the city of Wuhan, Hubei Province, China. Analysis made on the lower respiratory tract samples clearly indicated an infection caused by a novel virus, named as novel Coronavirus 2019 (COVID-19) by world health organization [1]. This virus resembles “severe acute respiratory syndrome coronavirus” (SARS-CoV) and is widespread among healthcare workers and others indicating a transmission from human-to-human. It has a 70% of genetic sequence similarity with “severe acute respiratory syndrome coronavirus”. Moreover, among the family of ribonucleic acid (RNA) coronavirus, it is a seventh member to infect humans. It originated from China and became pandemic.
As of 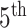 , January, 2021, there are 84 233 579 confirmed cases, among them 1 843 293 are dead across the globe . It has been declared as a pandemic of massive destruction to human lives by the world health organization. Signs of symptoms of the disease include, dry cough, high fever, sore throat and viral pneumonia [2].
, January, 2021, there are 84 233 579 confirmed cases, among them 1 843 293 are dead across the globe . It has been declared as a pandemic of massive destruction to human lives by the world health organization. Signs of symptoms of the disease include, dry cough, high fever, sore throat and viral pneumonia [2].
It is needed to model the transmission dynamics of COVID-19 mathematically to assess the impact of different intervention strategies [3], [4]. Whenever a new virus like COVID-19 outbreaks, and the process of finding the drug is on the go, its spreading nature and number of cases that will be affected can be at least predicted, so that the pandemic can be controlled [5].
Authors [6] gave an idea on how to search for a balance between analyzable, simple and unsolvable models. Though there are various resources, namely World Health Organization and repository of Johns Hopkins University [7], which provide updated research data in the form of excel sheets [8], which can be used in prediction models. There are a lot of challenges in modelling the pandemic. One of the difficulties in mathematical modeling relies on the selection of models. The selected model should be simple enough, so that the prediction or estimation of some parameters will be quite easy [9]. Another challenge in the modeling is the incorporation of preventive measure taken by the people, since it affects the change of dynamic of spreading. A few more such challenges include unableness of quantifying the quarantine and social distancing [10], [11].
When the differential equation based model is considered, SEIR is one of the best known models [2], [12]. The Suceptible, Exposed, Infectious, and Recovered (SEIR) model divides the group of people into compartments namely, susceptible (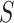 ), exposed (
), exposed (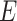 ), infectious (
), infectious (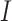 ), and removable (
), and removable (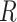 ). In [2], some additional parameters, namely, infectious but undetected
). In [2], some additional parameters, namely, infectious but undetected 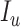 , hospitalized or quarantined at home
, hospitalized or quarantined at home 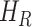 , hospitalized that will die
, hospitalized that will die 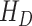 , recovered after being detected as infectious
, recovered after being detected as infectious 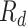 , and Recovered after being previously infectious but undetected
, and Recovered after being previously infectious but undetected 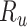 are included into the fundamental parameters of SEIR and prediction was carried out. The bayesian SEIR epidemiological model is used to perform a parametric regression on the COVID-19 outbreak data [13]. A compartmental SEIR model for epidemic in India is reported by modeling the flow of individuals using a set of differential equations [14].
are included into the fundamental parameters of SEIR and prediction was carried out. The bayesian SEIR epidemiological model is used to perform a parametric regression on the COVID-19 outbreak data [13]. A compartmental SEIR model for epidemic in India is reported by modeling the flow of individuals using a set of differential equations [14].
Considering the countries as individuals, a model describing spread between the countries and within the country is proposed in [15]. The name of this model is BeCoDis, which characterize disease initiation, epidemic strength, and spread per country. The variation of BeCoDis model was employed by authors [16] to find the international spread of the novel coronavirus outbreak. A method to estimate the parameters of epidemiological models, through multi objective problem formulation and its optimization is proposed in [17]. To solve the multi objective function, authors have used Achievement Scalarizing Function Genetic Algorithm [17]. Authors [18] have introduced a disease modeling, which is intended for researchers who are new in the development of ‘susceptible-infectious-recovered’ (SIR) type models. Authors have also highlighted a few issues to be taken care when analyzing these models.
A “Bats-Hosts-Reservoir-People transmission fractional-order” model was proposed by [19] for the simulation of the potential transmission of COVID-19. In [20], authors simplified the “Bats-Hosts-Reservoir-People transmission fractional-order” model as Reservoir-people transmission network model. To analyse the transmissibility, authors have adopted the “next generation matrix” approach to find the reproduction number. The reproduction number reflects how infectious a disease could be. This number is used to assess alternative interventions to control an outbreak [21]. The work [22] models the dynamics of COVID-19. The details about the transmission of infection among bats and people is briefly described in the work. In this work, bats are considered as the hosts, while the seafood market is assumed to be the source for which the mathematical results are presented followed by a formulation of the fractional model.
A Gaussian elimination using graph reduction method [23] based on graph theory was proposed for finding the reproduction number in epidemiological models. An explanation on how this model can be applied in the compartmental methods described by a set of differential equations is also illustrated by the authors of this work [23].
Epicurve is a model that describes the mode by which the disease can be spread. The different modes of spreading are point source, continuous common source and person-to-person spread. A spatial-hybrid model, called Be-FAST is described in [24], which relies on the composition of a stochastic individual based model. In this model, between-farm and within-farm spread for swine fever is modelled. Authors of [25] proposed 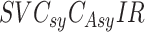 model to consider susceptible, vaccinated individual, symptomatic carrier, asymptomatic carrier, infected individual and recovered individual at time
model to consider susceptible, vaccinated individual, symptomatic carrier, asymptomatic carrier, infected individual and recovered individual at time 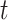 .
.
The mathematical model using predator-prey population is presented in [26], in which prey and predator are generated randomly to model the scenario. A model based on a tree with active and hidden nodes is proposed by authors in [27].
The spread rules of diseases, namely COVID-19, SARS and middle east respiratory syndrome (MERS) are developed with a propagation growth model in [10]. In another model, an estimate of infection is proposed by incorporating contact restriction into account [28]. Usage of non-pharmaceutical interventions for controlling the COVID-19 pandemic is highlighted by authors in [29] to reduce the burden on the health care system. A predictive model that can describe the idea of the fate of the virus, future projections and indicative data to forecast the future-effect caused by the disease is proposed by an Indian author [30]. An estimation of timing of presymptomatic communication of COVID-19 is proposed using the mathematical models by combining the data of the incubation period and serial interval [31].
Considering the statistical models, the impact of environmental factors which determine the spread of COVID-19 is reported in [32]. The model analyzed four most affected areas in China and five areas in Italy. Furthermore, authors [33] have used statistical models to derive the delay adjusted asymptomatic proportion of infections. They also derived the infections’ timeline with respect to the data of Japan. Authors [34] have estimated the asymptomatic ratio from the information of japanese nationals evacuated from Wuhan, china using the bayesian framework. A version of IndiaSIM is used to describe the number of hospitalised and affected cases in India [35]. IndiaSIM is widely accepted for years together, and is the best one for important decision making. Infectious disease model in [36] is used to find the relationship between the number of cases and cumulative number of cases.
A prediction work on the transmission process of the COVID-19 is developed using Gaussian distribution theory by taking the transmission characteristics of epidemic at different stages of corona [37]. The Gaussian distribution function with mean 1 and variance 1.5 is used to simulate the propagation ability of the virus. A generalized-logistic growth model (GLM) is used for short-term forecasting the trajectory of infectious disease with very good performance [38]. A prediction model for Italian Regions to get the epidemics progression using Chinese epidemiological dynamics data through machine learning is reported in [39].
A few machine learning methods are also explored for COVID-19. Machine learning methods of support vector regression (SVR) [40] and polynomial regression (PR) [41] are used for the prediction of covid-19 with the polynomial kernel of degree 6. Artificial inspired methods based on modified stacked auto-encoder are proposed for the real time forecasting of COVID-19 in China [42]. A machine learning based methods using logistic model, Bertalanffy model, Gompertz model is proposed in [43], in which differential equations characterizing these models are derived and then the parameters are estimated.
Deep learning models are an advancement of machine learning models, which are also explored in the literature for COVID-19. A deep learning framework based on long short-term memory method, the autoregressive integrated moving average method (ARIMA), and the ordinary least squares (OLS) method are proposed for the prediction of infectious disease in [44]. For the diagnosis, the following variables including, occurences, naver, twitter, tempearture and humidity are considered in [44]. These are assumed to be the input variables and using which the data matrix is formed for prediction purpose. In another work reported in [45], the logistic and exponential models are used for prediction [46]. For the SEIR model, a type of recurrent neural network, called LSTM is used to predict the number of new infections over time [12]. A short term high resolution forecasting based on Deep Learning Epidemic Forecasting with Synthetic Information (DEFSI) is proposed in [47], which is a more generalized and realizable epidemic framework. A mixed method of modelling using epidemiological equations and neural networks is proposed for reproduction number estimation [11]. This model is developed using the data from Wuhan, Italy, South Korea and the United States of America. Eventhough there are a lot of articles related to COVID-19, the following factors motivated us to write this review article:
-
1)
Eventhough the vaccines are developed for controlling COVID-19, the genomic structure of COVID-19 modify itself rapidly. Incase if any other evolution of this virus or any other virus of similar nature evolves, the mathematical and diagnostic models are essential to handle them. This has motivated us to provide a comprehensive analysis of spreading mathematical models, namely differential equation based models, statistical models and prediction based models.
-
2)
Diagnostic mathematical models are equally important for diagnosing the large volume of population through automated and systematic way. This being our second motivational factor, we provide a few diagnostic models in this article based on machine learning and deep learning for prediction and diagnosis.
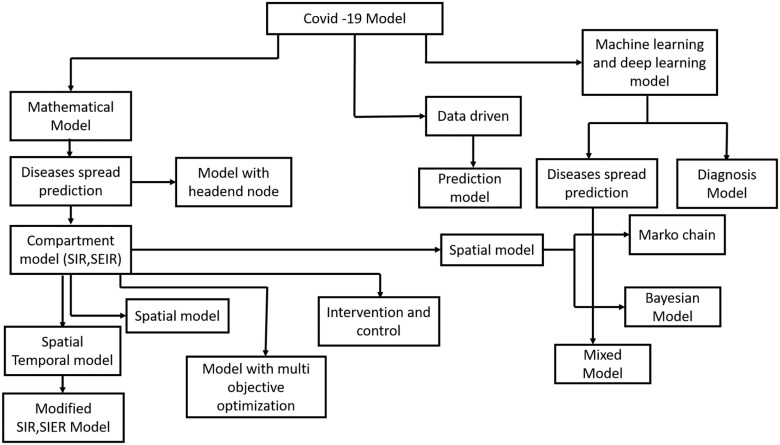
We categorize this paper by presenting a survey in different mathematical and machine learning models, the best usage of them for modeling COVID-19 pandemic. We present the survey on different model strategies, including differential equations based models, statistical analysis methods, prediction based models and machine learning based methods as shown as the tree diagram in Fig. 1.
Fig. 1.
Tree diagram representing the models described in the article.
Inorder to provide a comprehensive view of all the models, a comparision of various models interms of its meaning, objective, outcome, required mathematical assumptions, and limitations is shown in Table I.
TABLE I. Description of Models Interms of Various Factors.
| Factor | Compartment Model | Statistical Models | Data Driven Model | Machine Learning and Deep Learning Based Models | Mixed Models |
|---|---|---|---|---|---|
| Meaning | The model is named, becuase the entire population is divided into different compartents. The dynamic behavior on spreading of disease is modelled as movement of people from one compartment to another. | The model is named, because, the models are based on probabiliy theory. | Data driven models are named, because, they predict only using real time data. | The models work by learning from data. | The combination of statistical, differential equation, machine learning and deep learning models are called mixed models. |
| Objective | Capture the spreading of the disease using simple differential equation. | To derive the closed form mathematical expression for the disease spread. | To develop disease spread prediction model by learning from the data alone. | To provide generalized model which can cover wide scenario | To provide better performance by exploiting the advantages of mixed models. |
| Data Considered | Data collected from various organization like WHO can be used. | Data collected from various organization like WHO can be used. | The real time data collected from various sources, which are listed in Table I. | Data are collected from various sources as like mentioned in Table I. | As the model is mixed one, the data required for the model will be from mixed sources. |
| Mathematical Assumption | 1. Initially, fixed number of population is assued to be in susceptible compartment. 2. Movement of people is not considered and population size is assumed to be fixed one. | The model assume that the disease dynamic follows particular proability distribution for the given condition and scenario. | The model works well with the assumption that the data are correlated with some degree. The drastic change in the data will affect the performance of the model and it will take some time to correct itself. | 1. It is assumed that the data are normally distributed with 0 mean and variance 1. 2. Intraclass data are highly correlated and interclass data are less correlated. | 1. It is assumed that the data are not exactly normally distributed and has high variance. 2. Interclass and intraclass data are moderately correlated. |
| Outcome | The number of people in each compartment at the given time can be obtained from the model. | The solution can be obtained by simple substitution of parameters in the closed form expression. | The prediction of event related to disaese spreading is the major outcome, since it uses the available real time data for prediction. | Outcome includes the disease spread prediction, purely based on available data | Outcome includes high precision results in comparision with traditional models. |
| Limitations | Model is purely based on available old statistical data which fails to capture sudden changes in the spreading. Not able to handle more dynamic scenario. | The assumed probability distribution may not be valid for all scenarios. | The performance depends purely on the correctness of the data. However, the data available from the sources have some level of ucertainity. | The model need large amount of training data which consume exhaustive training time. | It is highly complex, as the model consists a mixture of many models. |
II. About COVID-19
A. Origin of COVID-19
By the end of December 2019, Chinese government has informed the world health organization (WHO) about severe acute cases of pneumonia with unfamiliar etiology [48]. This outbreak originates from the seafood market in the city of Wuhan, China and started infecting more than 50 people. The live animals, namely, frogs, snakes, marmots, rabbits and bats are usually sold at the Hunan sea market. On 12 January 2020, an order was released from the National Health Commission of China stating that there is an epidemic of viral Pneumonia. Using sequence-based analysis, the Government has identified that the cause of the disease is due to a novel coronavirus. Moreover, the Government provided the genetic sequence for the diagnosis of infection. Initially, it was thought that some infected patients would have visited the seafood market or would have used the animals sold at the market as the source of their food. However, further reported infections revealed that there are some patients who have no record of visiting the market. This indicated the community spreading capability of this virus, which became pandemic in more than 150 countries around the world. Community spread occurs due to the close contact with the infected persons and respiratory aerosols. The aerosols penetrate the body through inhalation through nose or mouth [48].
B. Characteristics of COVID-19
Coronaviruses contain particular genes in downstream areas that have proteins for viral reproduction, spikes and nucleocapsid formation [48]. The spikes at the outer areas are responsible for the attachment and entry of the virus into human cells. As the binding is loosely attached, the virus may infect multiple cells. The entry mechanism of a virus depends on human airway trypsin-like protease, cathepsins and transmembrane protease serine 2 [48].
III. Challenges of Mathematical Modeling and Data Sources on Pandemic Analysis
The mathematical models are used to provide insights on the transmission dynamics of infectious diseases and also used to assess the impact of different intervention strategies [3], [4]. Whenever a new infectious virus like COVID-19 emerges and is not likely to be characterized by a biological means and the traditional approach, the mathematical model will be able to serve handling the spread of the virus and to control it [5].
A. Difficulties in Modeling
One of the difficulties for generating an accurate model for prediction of COVID-19 is arriving to the parameter value required for the model to ensure unbiasedness and reliability. A complex model can be used with more complex data of biological and epidemiological information. However, this kind of complex model involves the estimation of more parameters. This estimation process consumes much time and results in large amounts of uncertainty in the model predictions [9] [15].
Selection of the correct model - by balancing the biological realism and reducing the uncertainty in model predictions - is an important one. The proper choice of model selection also determines its reliability. There are various model selection methods available like the Akaike Information Criteria (AIC).
The prediction models reported till date do have a large range of variations. The ocurrence of this variance is because of the nonidentifiability in model calibrations of the data of confirmed-cases. The model can be calibrated using maximum likelihood methods and the “Bayesian inference based Markov chain Monte Carlo” (MCMC) methods which deals with the uncertainties in data. Convergence and rate of convergence are the other issues associated with calibration of models. A modified method called “Affine Invariant Ensemble Markov Chain Monte Carlo Algorithm” is used for model calibration to overcome the slow convergence of Markov Chain Monte Carlo Algorithms.
Unavailability of accurate data is another issue in modelling the spread and prediction. Most of the reported data are not accurate, because of political and other reasons. So the model, which is based on this kind of erroneous data will not provide an accurate prediction.
Yet another issue in the modeling will be the change of dynamic of spread, because of the prevention measure taken by the people [10]. The prevention activities actually reduce the spreading rate, which needs to be taken into account of the model. Capturing the impact of such prevention and control measurement is really challenging, because of the involvment of many non-deterministic factors. These factors include
-
•
Change of culture from region-to-region.
-
•
Attitude changes.
-
•
Educational background of the people
-
•
How quickly the people adopt to the prevention activity.
Moreover, social distancing and quarantine are the widely used prevention measures. However, the effectiveness of those measures is very difficult to quantify [11], because of the (i) difficulty in capturing the individual’s travel patten (ii) deliberate violation of the social distance. Moreover, there is a chance that the unidentified infected people may communicate it to others. The capturing of these informations into the model will be a difficult task.
B. Data Sources for Modeling
There are various data sources available for the analysis and mathematical modelling of COVID-19. The world heath orgnaization (WHO) provides live updated research data in the form of Excel file [8], which can be used in prediction model. Moreover, the model outcome can be compared with the next update data. The data has eight columns with the labels namely, day, country code, country name, region, deaths, cumulative deaths, confirmed case and cumulative confirmed case.
The repository of Johns Hopkins University [7] provides timely data with a regular update on every day. The time-series tables in the format of comma separated file (CSV) is provided with three tables for confirmed, death and recovered cases of COVID-2019. Each of these table data has six attributes, namely, labels of province/state, country/region, last update, confirmed, death and recovered cases. There are various data sources like reported Case statistics, Genetic sequence and metadata, Twitter Dataset, health temperature, lung CT scans, Chest CT-scans, Xrays images, and Mobility statistics with textual reports are used to analyze and predict the covid 19 spread. Table – list all such kinds of data sources and the attribute of the data. Image data like x rat, ct scan can be used for Developing a model for the diagnosis of covid 19. Case statistics ac be used to model and predict the spreading of viruses and future confirmed cases.
Twitter Dataset sets are text data set which can be used for the natural language processing model which can able to classify people mental state, emotional state, and people movements. Genetic sequence and metadata can be used for drug discovery. Health temperature data collected from the smart temperature meters from houses with the health of mobile applications can track the health satus of individual persons and predict the infection for individually. Mobility statistics in the form of textual reports can be used to analyze the root cause of spread and source of spread of the COVID 19 viruses. The collection of databases for collecting the data for COVID-19 is listed in Table II.
TABLE II. Resources for Data Collection.
| Data source | Type of data | Data attribute | Links |
|---|---|---|---|
| JHU CSSE COVID-19 Data | Case statistics | Number of infections, number of cured patients, total mortality count, location | https://github.com/CSSEGISandData/COVID-19 |
| Novel Corona-virus 2019 dataset | Case statistics | Patient demographics, case reporting date, location, brief history | https://www.kaggle.com/sudalairajkumar/novel-corona-virus-2019-dataset |
| Coronavirus Source Data | Case statistics | Time series of confirmed daily COVID-19 cases | https://ourworldindata.org/coronavirus-source-data |
| CHIME | Case statistics | Daily number of susceptible, infected and recovered patient | https://github.com/CodeForPhilly/chime |
| COVID-19 Korea Dataset | Case statistics | Patient routes, age, gender, diagnosed date | https://github.com/ThisIsIsaac/Data-Science-for-COVID-19 |
| hCOV-19 | Genomic epidemiology | Genetic sequence and metadata | https://www.gisaid.org/epiflu-applications/next-hcov-19-app/ |
| New York Times dataset | USA State-wise cumulative cases | Date, state name, number of cases, death count | https://github.com/nytimes/covid-19-data |
| Public Corona-virus | Twitter Dataset | Tweet IDs Twitter ID with location | https://github.com/echen102/COVID-19-TweetIDs |
| Coronavirus COVID19 | Public Tweets on COVID-19 | UserID, location, hashtags, tweet text | www.kaggle.com/smid80/coronavirus-covid19-tweets |
| COVID-19 Open Research Challenge | dataset of a variety of cases | Date, number of cases, death count | https://www.kaggle.com/allen-institute-for-ai/CORD-19-research-challenge |
| WHO data | Case statistics | Daily number of susceptible, infected and recovered patient | https://www.who.int/emergencies/diseases/novel-coronavirus-2019/global-research-on-novel-coronavirus-2019-ncov |
| COVID-19 Community Mobility Reports | 131 Countries Mobility statistics with textual reports | Presence of people at grocery stores, pharmacies, recreational spots, parks, transit stations, workplaces, and residences | https://www.google.com/covid19/mobility/ |
| COVID-19 DATABASE | Italy Radiology data | Xrays and demographics | https: //www.sirm.org/category/senza-categoria/covid-19/ |
| RKI COVID19 | Germany Cases | data Number of infection cases | https://npgeo-corona-npgeo-de.hub.arcgis.com/datasets/dd4580c810204019a7b8eb3e0b329dd6 0/data |
| BSTI Imaging Database | CT scans | Patient CT scans | https://www.bsti.org.uk/training-and-education/covid-19-bsti-imaging-database/ |
| nCoV2019 Dataset | Epidemiological data | Patient demographics, case reporting date, location, brief history | https://github.com/beoutbreakprepared/nCoV2019 |
| COVID Chestxray | Chest X-ray scans and reports | X-Ray Image, date, patient, demographics, findings, location and survival information | https://github.com/ieee8023/covid-chestxray-dataset |
| COVID-19 CT segmentation | Lungs CT scans | JPG image scans with segmentation and label report | [48] |
| COVID-CT-Dataset | Chest CT-scans | Scans with associated labels | http://medicalsegmentation.com/covid19/ |
| Kinsa Smart Thermometer | Health Weather Map | Temperature readings from internet-connected thermometers made by Kinsa Health. | https://healthweather.us/?mode=Atypical |
IV. State-of-The Art Mathematical Models
In this section, we will describe various mathematical models, and their uses in the prediction of COVID-19 pandemic and the number of cases infected over the days.
The drawback presented in the SEIR model includes the behaviour of the human by reducing the contact and improving their immunity. The impact of the same is included in the modified SEIR model.
A. Compartment Model
Conventionally, any linear system can be modelled in terms of differential equation. COVID-19 is not an exception, for which there are many works proposed in this direction. The first differential equation based conceptual model is known as ‘Susceptible-Infectious-Removed’ (SIR). A SIR predictive model that can describe the fate of the virus, future projections based on the indicative data to forecast the future is proposed in [30]. The model can be used to manage the health care systems of the present scenario. Following this, the recommendations can be made and advisories can be prepared. The fundamental equations that the authors considered are based on SIR model, they are
 |
where 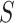 denotes susceptible,
denotes susceptible, 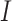 denotes infectious and
denotes infectious and 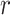 is the rate at which the infectious recover. The value of
is the rate at which the infectious recover. The value of 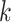 is somewhere between 1.4 and 2.5.
is somewhere between 1.4 and 2.5.
‘Susceptible-Exposed-Infectious-Removed’ (SEIR) was another conceptual model used to model the outbreak. Under the SEIR model the peoples are categorized into the compartments of Susceptible (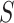 ), Exposed (
), Exposed (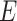 ), Infectious (
), Infectious (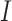 ) and Removed (
) and Removed (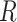 ) compartments. The movement of people dynamic among different compartments is modelled by a set of differential equations since the disease has an incubation period after that only exposed compartment people become infectious.
) compartments. The movement of people dynamic among different compartments is modelled by a set of differential equations since the disease has an incubation period after that only exposed compartment people become infectious.
Modeling of spread of the disease by considering each person in one of the compartments including, susceptible 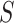 , exposed
, exposed 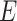 , infectious
, infectious 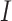 , infectious but undetected
, infectious but undetected 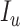 , hospitalized or quarantined at home
, hospitalized or quarantined at home 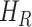 , hospitalized that will die
, hospitalized that will die 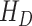 , dead by COVID-19
, dead by COVID-19 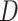 , recovered after being previously detected as infectious
, recovered after being previously detected as infectious 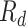 , and Recovered after being previously infectious but undetected
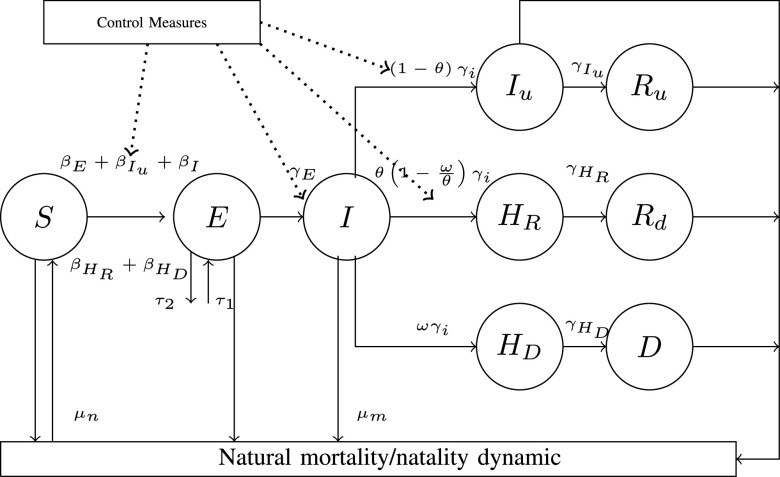
, and Recovered after being previously infectious but undetected 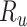 is proposed in [2]. The applicable control measures, namely, isolation, quarantine, tracing, and increase of sanitary resources are also mentioned in [2]. The diagram depicting the spread model is shown in Fig. 2. Other parameters shown in Figure 2 are
is proposed in [2]. The applicable control measures, namely, isolation, quarantine, tracing, and increase of sanitary resources are also mentioned in [2]. The diagram depicting the spread model is shown in Fig. 2. Other parameters shown in Figure 2 are 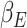 ,
, 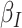 ,
, 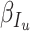 ,
, 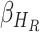 ,
, 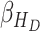 - the disease contact rates in the respective compartments of a person,
- the disease contact rates in the respective compartments of a person, 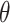 - the fraction of infected people that are detected and documented by authorities,
- the fraction of infected people that are detected and documented by authorities, 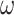 - the case fatality rate,
- the case fatality rate, 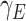 - the transition rate per day from compartment
- the transition rate per day from compartment 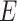 to compartment
to compartment 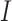 ,
, 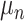 - the natality rate per day,
- the natality rate per day, 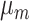 - the mortality rate per day,
- the mortality rate per day, 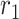 - the people infected that arrives to territory from other territories per day,
- the people infected that arrives to territory from other territories per day, 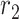 - the people infected that leaves territory per day,
- the people infected that leaves territory per day, 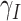 denote transition rate per day,
denote transition rate per day, 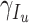 ,
, 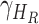 ,
, 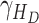 - the transition rates per day from compartments
- the transition rates per day from compartments 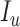 ,
, 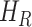 and
and 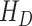 to compartments
to compartments 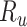 ,
, 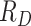 , and
, and 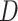 respectively.
respectively.
Fig. 2.
Modified SEIR Model with Control Measure [2].
Outputs of this model are presented in [2], which includes model cumulative number of COVID-19 cases, model cumulative number of deaths, basic reproduction number and effective reproduction number. Furthermore, the number of people who will be admitted to hospital can be calculated as
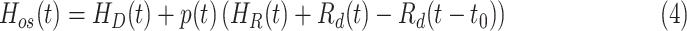 |
where 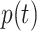 denotes the fraction of people in compartment
denotes the fraction of people in compartment 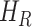 , who are hospitalized.
, who are hospitalized.
The calculation of the number of people who need the clinical bed can be obtained as
 |
People who are infected by contacting the people in the compartment 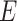 is given by
is given by
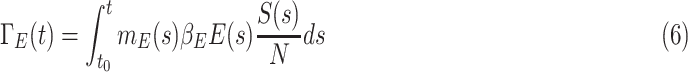 |
Similarly, the people who are infected by contacting the people with 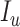 and
and 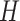 are given by
are given by
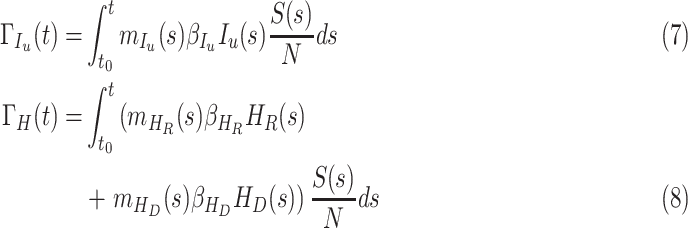 |
respectively. In equation (6), (7) and (8), 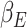 ,
, 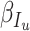 ,
, 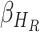 denote the disease contact rate,
denote the disease contact rate, 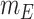 ,
, 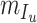 ,
, 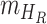 ,
, 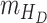 denote the functions representing the efficiency of the control measures applied to the corresponding compartment respectively.
denote the functions representing the efficiency of the control measures applied to the corresponding compartment respectively.
1). Spatial Model
Spatial model is used to predict the spread along with its location. Spread prediction on particular location is important for handling the disease effectively by imposing some preventive measure at a particular location. In this direction, a few works are reported. Classical swine fever is a viral disease transmitted from pigs. A spatial-hybrid model, called Be-FAST is described in [24], which relies on the composition of a stochastic Individual Based model. In the proposed method, “between farm” and “within farm” spread is modelled. For modeling, authors have considered the monte carlo simulation method, in which there are 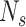 epidemic scenarios. At the beginning, except one randomly selected farm, all the other farms are assumed to be in a susceptible state. Then for a specified time duration, “within farm” and “between farm” spread routines are applied. If an epidemic disappears at the end of simulation day, then the current scenario is stopped and the next scenario will be started with the same process [24].
epidemic scenarios. At the beginning, except one randomly selected farm, all the other farms are assumed to be in a susceptible state. Then for a specified time duration, “within farm” and “between farm” spread routines are applied. If an epidemic disappears at the end of simulation day, then the current scenario is stopped and the next scenario will be started with the same process [24].
Under some assumption, authors have modelled the evolution of susceptible and infected pigs in a farm 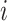 at time
at time 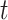 using the differential equation
using the differential equation
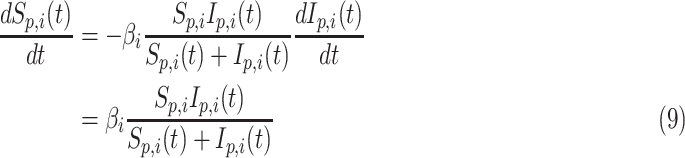 |
where 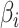 is the daily transmission parameter, which the authors have set to 0.66, 0.4 and 0.53 depending on the nature of the farm. The daily discrete version of the above system is given by [24]
is the daily transmission parameter, which the authors have set to 0.66, 0.4 and 0.53 depending on the nature of the farm. The daily discrete version of the above system is given by [24]
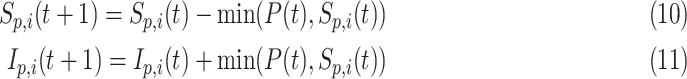 |
where 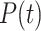 denotes poisson distribution.
denotes poisson distribution.
2).  Model
Model
A modified version of SIR model with addition of three more parameters, namely vaccinated individual 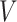 , symptomatic carrier
, symptomatic carrier 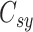 , asymptomatic carrier
, asymptomatic carrier 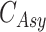 is known as
is known as 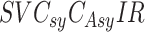 Model [25]. These parameters at time
Model [25]. These parameters at time 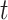 are denoted as
are denoted as 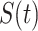 ,
, 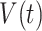 ,
, 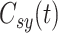 ,
, 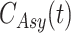 ,
, 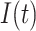 and
and 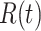 . The authors have developed a differential equation for all the parameters and solved it to get the number of infected cases as
. The authors have developed a differential equation for all the parameters and solved it to get the number of infected cases as
 |
where 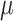 indicates the natural mortality rate,
indicates the natural mortality rate,  indicate recruitment rate,
indicate recruitment rate, 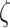 denotes disease induced death rate and
denotes disease induced death rate and 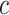 is the constant of integration in the process of deriving (12).
is the constant of integration in the process of deriving (12).
3). Predator-Prey Model
A model that describes the group of infectious being as prey and uninfectious being as predator is called predator-prey model, in which the predator population acquire an infection from the prey population, during the predation process. Authors have developed a mathematical model using predator-prey population in [26], in which preys population is assumed to be of 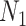 and predator population is assumed to be
and predator population is assumed to be 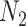 . Out of
. Out of 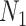 , there is a susceptible group of size
, there is a susceptible group of size 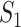 and an infected group of size
and an infected group of size 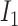 . Similarly, among
. Similarly, among 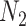 , susceptible and infected groups are of size
, susceptible and infected groups are of size 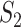 and
and 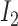 respectively. These susceptible and infected groups are described in terms of a differential equation and then the solution is obtained and plotted and verified to be matching with actual data. Even though the predator model is originally developed for other disease spread, it is also applied to COVID-19.
respectively. These susceptible and infected groups are described in terms of a differential equation and then the solution is obtained and plotted and verified to be matching with actual data. Even though the predator model is originally developed for other disease spread, it is also applied to COVID-19.
4). Spatio-Temporal Model
A model called “between countries disease spread” (BeCoDis) is proposed by authors in [15]. This model is developed on the basis of spatio-temporal epidemiological description for the study of spread of disease between and inside the countries. Considering the countries as individuals, this model works on the basis of deterministic individuals [15]. Simulation result of BeCoDis includes an outbreak characteristic, namely risk of disease initiation, epidemic strength, and spread per country. Other simulation results include inter-country interactions and disease spread. These are compared with the results obtained from the deterministic compartment model [50] and verified that the results are in close match with the value reported by WHO.
5). Application of BeCOdis
BeCoDis model was employed by authors in [16] to find the international spread of the novel coronavirus outbreak. In this work, they have tried to forecast the spread across countries from the collected data. The forecast of day wise plot of cumulative number of people who are affected and dead is obtained, compared and verified with the results reported by WHO [16].
6). Multi Objective Optimization Model
A novel idea that adjusts the parameters of compartmental epidemiological models is presented in [17]. First, the available epidemic data is posed as a a multi-objective optimization problem with the model parameters being the optimization variables. These parameters are estimated through optimization. Authors have given a few steps in the algorithm, which are (i) estimation of the model parameters identification (ii) multi-objective problem formulation, and (iii) appropriate configuration extraction from the obtained solution.
The multi objective problem can be formulated as
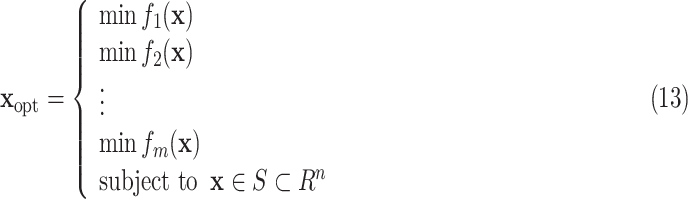 |
Where 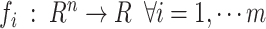 are the objective functions with the feasible region
are the objective functions with the feasible region 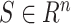 and
and 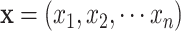 is the decision vector
is the decision vector 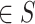 . Moreover, the vectors that satisfy the objective function are called objective vectors. The set of decision vectors that solve the multi-objective problem are also called as the pareto optimal set.
. Moreover, the vectors that satisfy the objective function are called objective vectors. The set of decision vectors that solve the multi-objective problem are also called as the pareto optimal set.
The problem in (13) can be posed alternatively for COVID-19 as below
 |
where in (14), the 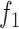 ,
, 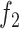 ,
, 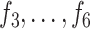 are the objective functions of Susceptible (
are the objective functions of Susceptible ( ), Exposed (
), Exposed ( ), Infectious (
), Infectious (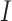 ), Hospitalised (
), Hospitalised (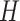 ), Recovered (
), Recovered (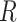 ), and Dead (
), and Dead (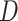 ). The constraint in (14) indicates that
). The constraint in (14) indicates that  ,
, 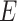 ,
, 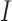 ,
, 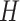 ,
, 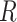 and
and 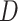 are to be a subset of real numbers in
are to be a subset of real numbers in 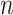 dimensional space.
dimensional space.
To solve the multiobjective optimization problem, authors [17] have used Weighting Achievement Scalarizing Function Genetic Algorithm (WASFGA), which is a population-based evolutionary algorithm that explores the feasible region to find the solution. Over the populations, it performs reproduction and replacement mechanisms as like any Genetic algorithm. In reproduction, the new offspring are created following Darwin’s principle. From the new offspring and with the current population, the population of the next generation is composed in the replacement stage. In most of the genetic algorithms, replacement happens through dominance, whereas in WASFGA, authors have used a reference point, and whichever population is closest to it, that will be chosen for the next generation.
7). Model With Hidden Nodes
All mathematical models deal with the number of identified cases. However, in practice there is a chance that the person may be infected and unidentified. Those persons are ought to be considered as hidden nodes, whose incorporation gives the realistic scenario. In this direction, a model based on active and hidden nodes is proposed by authors in [27]. In the paper, the author assumes that one corona infected patient comes in contact with other people. Assuming that it spreads to 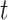 persons, among them
persons, among them 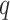 numbers are quarantined, but there are
numbers are quarantined, but there are 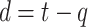 persons who break the lockdown, not showing symptoms, so behaving like hidden active nodes. These hidden nodes can spread the disease among
persons who break the lockdown, not showing symptoms, so behaving like hidden active nodes. These hidden nodes can spread the disease among 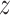 other nodes and the process goes on and on. So, hidden nodes increase by a constant
other nodes and the process goes on and on. So, hidden nodes increase by a constant 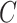 each time, and therefore the increase in hidden nodes are denoted as
each time, and therefore the increase in hidden nodes are denoted as 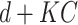 , where
, where 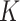 denotes unit time. Assuming this model, authors derived a formula for total number of cases as [27]
denotes unit time. Assuming this model, authors derived a formula for total number of cases as [27]
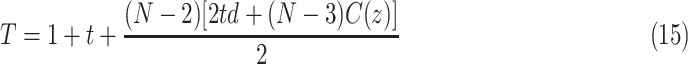 |
where 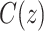 denotes the rate of infection and
denotes the rate of infection and 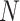 indicates the number of terms in the summation series.
indicates the number of terms in the summation series.
8). Models With Intervention and Control Information
While modelling the spreading we can consider the following additional parameters which is not addressed in conventional models.
-
1)
Population movement from one part to another part which may affect the contact percentage of infected person with others. To address this the movement of people is incorporated in spreading model in few literatures. Especially [51] is addressing the movement of the infected person on the spreading model.
-
2)
The awareness about COVID-19 spread and personal precautions is another additional factor which probably decrease the spreading rate and death rate. This factor is not addressed mostly in any spreading model because of the practical difficulty to quantify and incorporate into the model.
-
3)
The preventive measures like Lock down and Law Enforced Quarantine taken by the Government agencies will reduce the spreading rate and death rate. Those factors are addressed in a few literatures, which are discussed in detailed in this section.
As said above, analyzing the impact of prevention and control measurement is essential one. This is required because in the initial stage of spread, people may not pay attention to prevent. However, when the spread is increasing, they may pay attention and do prevention measure. This prevention measure taken by the people may decrease the spread pattern and it might decrease the growth rate monotonically.
A mathematical infection model to estimate coronavirus infection in Germany is proposed with incorporation of contact restriction into account [28]. The contact restriction parameter is adapted dynamically to model the random variation in the contact restriction. This model can provide an estimate of the number of infected people, new infections and deaths in the region of study.
The bayesian SEIR epidemiological model, which is used to perform a parametric regression on the COVID-19 outbreak data of China, America, Italy, and France was highlighted in [13]. The model estimates the impact of containment measures on the basic reproduction ratio 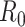 . It is also observed that the impact of these measures is detectable. Authors have also found the biases and inconsistencies present in the available data to provide an estimate for the number of cases spread in a region. Compartmental modeling like SEIR is also used for the infectious disease [52].
. It is also observed that the impact of these measures is detectable. Authors have also found the biases and inconsistencies present in the available data to provide an estimate for the number of cases spread in a region. Compartmental modeling like SEIR is also used for the infectious disease [52].
In SEIR model, the people are transferred from one compartment to another, for example susceptible to exposed, exposed to infectious, etc. The conversion rate of Exposed to Susceptible is denoted as 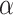 , Infectious to Exposed is referred as
, Infectious to Exposed is referred as 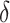 and Susceptible to Infectious is referred as
and Susceptible to Infectious is referred as 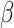 , then the exposed number of people is calculated by
, then the exposed number of people is calculated by 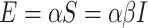 . Once
. Once 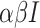 people are moved from
people are moved from 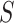 to
to 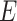 , the numbers are removed from
, the numbers are removed from 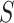 and added to
and added to 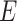 . After incubation, the actual infected from
. After incubation, the actual infected from 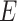 are moved to
are moved to 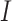 compartment with a rate
compartment with a rate 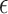 . A quarantine
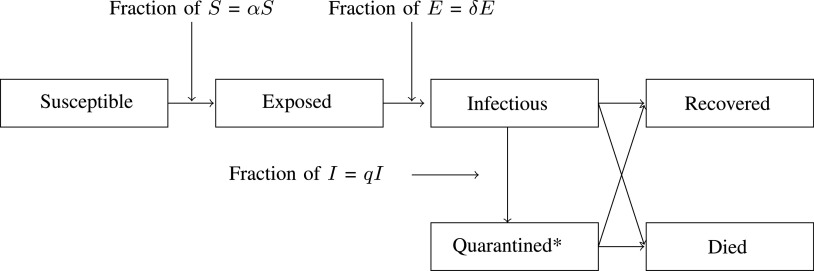
. A quarantine 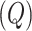 compartment can be added to model the effects of isolation as shown in Figure 3. A fraction
compartment can be added to model the effects of isolation as shown in Figure 3. A fraction 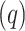 of people are moved from
of people are moved from 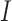 to
to  in the isolation process. It is assumed that the remaining people in the
in the isolation process. It is assumed that the remaining people in the 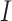 compartment may recover with a rate
compartment may recover with a rate 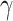 , or die with a rate
, or die with a rate 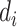 . Those who are recovered from the
. Those who are recovered from the 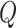 compartment are removed with a rate,
compartment are removed with a rate, 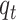 , or die at a death rate
, or die at a death rate 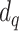 .
.
Fig. 3.
SEIR Model with quarantine and death compartment [52].
A Compartmental SEIR model for epidemic in India is reported with modelling the flow of individuals using a set of differential equations [14]. While comparing with the classical SEIR model, the model proposed in [14] included the compartment of died and quarantine. Also, it analyzed the impact of national preventive intervention as extra feature. This extra feature provides more reliabiity on disease spread prediction. Monte Carlo simulation is carried out for different scenarios with 1000 runs using MATLAB. Hospitalization, ICU requirements and deaths were modeled on SimVoi software. The impact of Non-Pharmacological Interventions (NPI) like keeping social distancing and lockdown is also incorporated. Result of the prediction model is reported in Table III. From the model the growth rate is predicted as 1.15 and the tabulated numerical values are the forecasted data for 25 May.The table shows that by ataining NPIs prevention the impact of infections can be reduced by almost 90%.
TABLE III. Performance Comparison Between “with NPI” and “without NPI” [14].
| Case | Total Infections | Hospitalization | ICU Admissions | Death Rate |
|---|---|---|---|---|
| Without NPIs | 3 Million | 125 455 (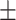 18 034) 18 034) |
26 130 (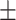 3298) 3298) |
13 447 ( 1819) 1819) |
| With immediate institution of NPIs | 241 974 ( 33 735) 33 735) |
10 214 ( 1649) 1649) |
2121 ( 334) 334) |
1081( 169) 169) |
A SEIR model for the prediction of cases in Wuhan is reported with the individual reactions and governmental actions like holiday extension, city lockdown, hospitalisation and quarantine are incorporated [53].
Usage of non-pharmaceutical interventions for controlling the COVID-19 pandemic is highlighted by authors in [29] to reduce the burden on the health care system. In this paper, authors have used an age-structured container model of transmission in the state of ontario, canada. They compared the base cases like, isolation, quarantine and social distancing. Implementation is carried out for fixed duration or it is dynamically cycled on/off. They found in results that the dynamic social distance can maintain a good health system capacity.
Another model with control and measurement is reported based on propogation growth. The spread rules of diseases of COVID-19, sever acute respiratory syndrome (SARS) and MERS are developed with a propagation growth model [10]. This model analysis shows that the growth rate of COVID-19 is twice that of the SARS and MERS. It is also reported that the COVID-19 doubles the cycle within two to three days.
If 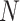 denote the number of infected people then,
denote the number of infected people then, 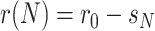 , where
, where 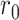 is a constant indicating the growth rate at initial state without prevention measures,
is a constant indicating the growth rate at initial state without prevention measures, 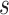 is the infection inhibition constant, which indicates the effect of prevention and control measures. The differential equation of the model is given below
is the infection inhibition constant, which indicates the effect of prevention and control measures. The differential equation of the model is given below
 |
where 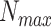 is the maximum number of infected cases. The first term
is the maximum number of infected cases. The first term 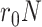 of differential equation (16) expresses the natural epidemic trend of infectious disease in the absence of any prevention and control measures, while the second term
of differential equation (16) expresses the natural epidemic trend of infectious disease in the absence of any prevention and control measures, while the second term 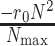 shows the effect of prevention and control measures for communicable diseases.
shows the effect of prevention and control measures for communicable diseases.
Equation (16) is the initial value problem of variable-separable differential equation, which can be solved to give number of infected people as
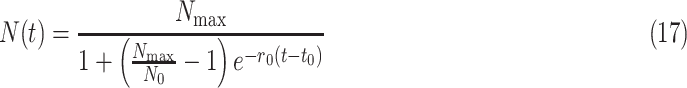 |
B. Statistical Models
Statistical model for the analysis of the impact of environmental factors that determine the spread of COVID-19 is reported [32]. The model analysed the four most affected areas in China and five areas in Italy. This model considered 1) Maximum relative Humidity 2) Maximum temperature 3) Highest wind speed as environmental factors which may affect the spreading of the virus for the analysis. The result of the investigation shows that maximum relative humidity and the highest wind have no impact, but the temperature has a moderate effect on the spread.
On 5 February 2020, a cruise ship in Japan hosting 3711 people has undergone a 14 days quarantine and afterwards was found that 634 persons onboard were tested positive. Authors [33] have used statistical models to derive the delay adjusted asymptomatic proportion of infections. They also derived the infections’ timeline. Most of the infections were found to occur before the quarantine starts.
The asymptomatic cases consist of both true asymptomatic cases and the case that became symptomatic later. For individuals 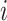 , let
, let 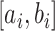 denote an interval of infection and
denote an interval of infection and 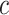 denote sensor date of being symptomatic. Denoting
denote sensor date of being symptomatic. Denoting 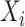 being the time at which the individual became infectious,
being the time at which the individual became infectious, 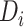 being the delay from the time of infection until they are found to be symptomatic with cumulative distribution function
being the delay from the time of infection until they are found to be symptomatic with cumulative distribution function 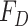 . Let
. Let 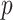 denote a probability that an individual will never develop symptoms. Then the probability that an individual who exposed to the scenario during the time
denote a probability that an individual will never develop symptoms. Then the probability that an individual who exposed to the scenario during the time 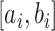 will be asymptomatic at time
will be asymptomatic at time 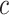 is [33]
is [33]
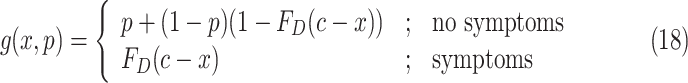 |
where 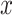 denotes the value of the random variable
denotes the value of the random variable 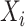 . Authors [34] have estimated the asymptomatic ratio from the information of japanese nationals evacuated from Wuhan, China. Their model uses a bayesian framework. The patients who are found to be symptomatic among
. Authors [34] have estimated the asymptomatic ratio from the information of japanese nationals evacuated from Wuhan, China. Their model uses a bayesian framework. The patients who are found to be symptomatic among 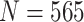 evacuated patients are denoted as
evacuated patients are denoted as 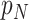 and its value is 63. The means of finding them to be symptomatic includes, temperature screening and face-to-face interview to collect information about cough, fever, and breathing problems. Using bayesian theorem, the asymptomatic ratio is defined as
and its value is 63. The means of finding them to be symptomatic includes, temperature screening and face-to-face interview to collect information about cough, fever, and breathing problems. Using bayesian theorem, the asymptomatic ratio is defined as
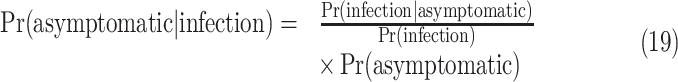 |
Authors present an infectious disease model in [36] and they have used their model to use the parameters to find the relationship between number of cases and cumulative number of cases. The cumulative number of cases in the discrete time is given by 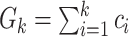 , where i denote discrete time intervals and
, where i denote discrete time intervals and 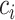 is the total number of cases. So, the number of cases at a particular time instant can be given by
is the total number of cases. So, the number of cases at a particular time instant can be given by 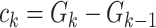 . Moreover, using
. Moreover, using 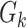 , they have used statistical approaches to infer and forecast. A function used to relate number of cumulative cases and number of case at particular time instant is given by [36]
, they have used statistical approaches to infer and forecast. A function used to relate number of cumulative cases and number of case at particular time instant is given by [36]
 |
where 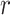 is the intensity growth and it follows normal distribution with mean 0 and variance 10,
is the intensity growth and it follows normal distribution with mean 0 and variance 10, 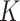 denotes total number of cases and it follows Gamma distribution with parameter 0.001. Using this relation, the number of cases is modelled as a poisson distribution as [36]
denotes total number of cases and it follows Gamma distribution with parameter 0.001. Using this relation, the number of cases is modelled as a poisson distribution as [36]
 |
An estimating of timing of presymptomatic communication of COVID-19 is proposed using the mathematical models by combining the data of the incubation period and serial interval [31]. Using the model, it is found that presymptomatic transmission takes on the average of 3.8 days and 79% of transmission is presymptomatic. The probability of being infectious is given by
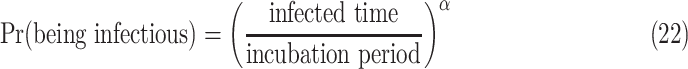 |
Where 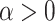 is a shaping parameter of transmission behaviour.
is a shaping parameter of transmission behaviour.
Autoregressive integrated moving average (ARIMA) is one of the statistical models for predicting non-stationary data. A forecasting ARIMA model of the COVID-19 for Italy, which analyses the impact of lockdown, is highlighted in [54]. ARIMA forecasting model is utilized for this purpose. The result of the model shows that it can make Predictions with 93.75% of accuracy of the infected cases and 84.4% of accuracy of recovered cases. The forecasting indicates that at the end of MAY, 2020, the infected case may reach around 182 757, and recovered cases could be around 81 635.
1). Markov Chain Model
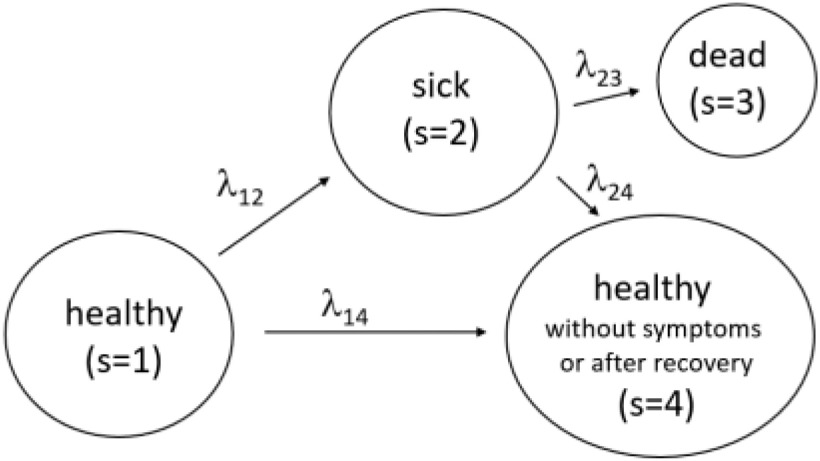
The model based on continuous time markov chain of 4 states, namely 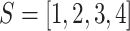 is proposed by authors in [55], in which the states represent healthy without infection, sick, dead, and healthy with infection. The same authors have talked about lifting up the contact ban in Germany in [55]. Initially state is 1 for all individuals, i.e.,
is proposed by authors in [55], in which the states represent healthy without infection, sick, dead, and healthy with infection. The same authors have talked about lifting up the contact ban in Germany in [55]. Initially state is 1 for all individuals, i.e., 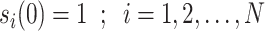 for all individuals, where
for all individuals, where 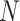 denote the population size, which is assumed to be 83 100 000 in this case . There is a transition between the states
denote the population size, which is assumed to be 83 100 000 in this case . There is a transition between the states 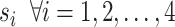 , whose rates are denoted by
, whose rates are denoted by 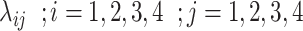 as shown in the Figure 4.
as shown in the Figure 4.
Fig. 4.
Statistical Markov Model [55].
The probability of random contacts with healthy and sick individuals will be
 |
where 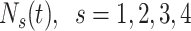 is the number of expected individuals at state
is the number of expected individuals at state 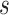 at time
at time 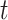 .
.
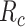 in (23) is used in obtaining the individual sickness rate as shown in the below equation.
in (23) is used in obtaining the individual sickness rate as shown in the below equation.
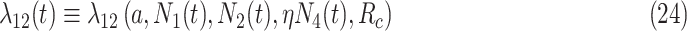 |
where 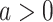 , and
, and 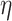 denotes the share of healthy individuals in state 4 who can infect healthy individuals from state 1.
denotes the share of healthy individuals in state 4 who can infect healthy individuals from state 1.
Equation (24) is used in further to derive the relaion between 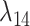 and
and  . A few transition probabilities are derived as
. A few transition probabilities are derived as
 |
Where 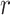 is a recovery rate or mortality rate and
is a recovery rate or mortality rate and 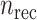 denotes the number of days it takes until recovery. Given an exponential distribution of staying duration in a state, the probability that a person gets sick in a day is given by
denotes the number of days it takes until recovery. Given an exponential distribution of staying duration in a state, the probability that a person gets sick in a day is given by
 |
In the same way, the probability of being sick for a week is given by
 |
2). Bayesian Model
An empirical time series framework is proposed to predict US cases using various countries as reference. On the basis of observed US data and the parameters from the reference countries, the forecast is implemented [56].
Let  denote the number of COVID-19 cases with
denote the number of COVID-19 cases with 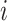 being the
being the 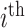 country and
country and 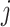 being the day on which the cases are increased to 100 or more for the first time. The likelihood (prediction) of being infected at
being the day on which the cases are increased to 100 or more for the first time. The likelihood (prediction) of being infected at 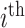 country on a
country on a 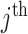 day is obtained with the help of functional mixed effects model by taking the natural logarithm of
day is obtained with the help of functional mixed effects model by taking the natural logarithm of 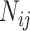 , which is given by
, which is given by
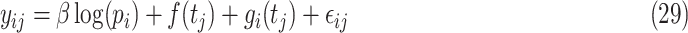 |
Where 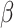 is the fixed effect slope for
is the fixed effect slope for 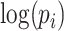 ,
, 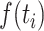 is the functional fixed effects,
is the functional fixed effects,  is the population size in millions,
is the population size in millions, 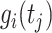 is the functional random effects, and
is the functional random effects, and 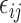 is the Gaussian error term with mean 0 and variance
is the Gaussian error term with mean 0 and variance 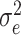 . In the above equation,
. In the above equation, 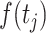 is modelled by a cubic smoothing spline using the state space representation as
is modelled by a cubic smoothing spline using the state space representation as
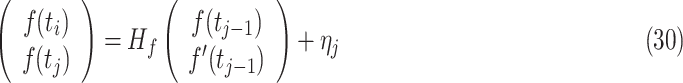 |
where 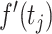 is the first derivative,
is the first derivative, 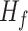 is the state transition matrix and
is the state transition matrix and 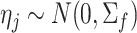 is the state innovation vector with
is the state innovation vector with 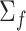 depending on the smoothing factor
depending on the smoothing factor 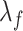 .
. 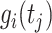 can also be modelled in a similar fashion, and it inturn depends on a smoothing factor
can also be modelled in a similar fashion, and it inturn depends on a smoothing factor 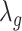 .
.
The estimate of a parameter vector 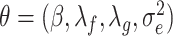 is given by [56]
is given by [56]
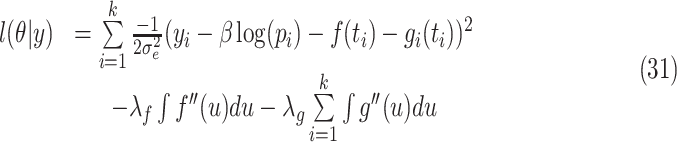 |
where 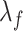 ,
,  are the smoothing parameters.
are the smoothing parameters. 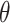 depends on fixed effect slope
depends on fixed effect slope 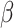 , smoothing factors,
, smoothing factors, 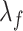 ,
, 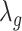 , and the variance
, and the variance 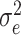 of
of 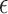 . Parameter theta in turn affects state transition matrix and the prediction
. Parameter theta in turn affects state transition matrix and the prediction 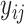 .
.
3). Generalized-Logistic Growth Model
Phenomenological models are widely used for forecasting the disease spreading. A phenomenological model captures the empirical relationship of phenomena with each other. It has provided very good performance in forecasting for the disease like SARS, Ebola, pandemic influenza, and dengue. A generalized-logistic growth model (GLM) is used for short-term forecasting the trajectory of infectious disease with very good performance [38]. Logistic growth model was employed for epidemic forecasting of Ebola, which is given by
 |
Where 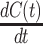 models the rate of change in the number of new cases at week
models the rate of change in the number of new cases at week 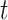 . The logistic model relies on two parameters, the intrinsic infection rate
. The logistic model relies on two parameters, the intrinsic infection rate  and the final epidemic size
and the final epidemic size 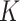 .
.
Modified version of generalized-logistic growth model is known as Generalized Richards Model (GRM) is used to capture a range of early epidemic growth profiles ranging from sub exponential to exponential growth [57]. The model is represented by a differential equation [57] as
 |
where 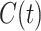 - cumulative number of cases at time
- cumulative number of cases at time 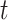 ,
, 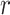 is a positive parameter denoting the growth rate which is given as (people)
is a positive parameter denoting the growth rate which is given as (people) 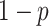 per time,
per time, 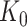 is the final epidemic size, and
is the final epidemic size, and 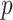 is the “scaling of growth” parameter. If
is the “scaling of growth” parameter. If 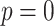 , a constant epidemic over the time, if
, a constant epidemic over the time, if  , it acts as exponential growth model. Intermediate values of
, it acts as exponential growth model. Intermediate values of 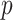 , means
, means 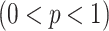 describe sub-exponential i.e., polynomial growth patterns.
describe sub-exponential i.e., polynomial growth patterns.
C. Usage of Epicurve in the Analysis
Epicurve is a statistical chart used in epidemiology to visualise the onset of a disease outbreak. It helps to identity the mode of transmission of disease. It is also used to display the magnitude and clustering nature of the disease. In general, to analyze the outcome of any mathematical model, the epicurves are plotted and the various aspects of disease spreads are analyzed. The epicurve anlysis shows that the outbreak at Wuhan is likely to follow a continuous common source pattern. Epicurve reveals a lot about an outbreak, such as
-
•
The distribution of cases over time.
-
•
Cases that stand apart from the overall pattern.
-
•
Outbreak’s magnitude
-
•
Knowledge about the pattern of spread.
Epicurve tells about the mode by which the disease can be spread. In general, the modes are,
-
•
Point source
-
•
Continuous common source
-
•
Person-to-person spread
In a point source mode, the number of cases will go to the peak and start decreasing gradually. Majority of cases can happen in one incubation period of the outbreak [58]. In a continuous common source outbreak, exposure is prolonged over a period of days, weeks, or longer. Moreover, persons will be exposed to the same resources. On the other hand, in propagated mode, spread happens from person to another person and the graph will show a peak in each incubation period.
D. Data Driven Model
In this direction, using only collected patient information, prediction of death is calcualted with the name of algorithm called as patient Information Based Algorithm (PIBA) [50]. PIBA is one of the data driven models, which calculates the death rate for the near future using the real time available data. The method does not depend on any mathematical framework, but it simply predicts using an available formula. This estimate deals with the data of Wuhan and other cities in china. The death rates prediction works for estimation of daily numbers of deaths rate from February 25, 2020. It is also proved that real death and prediction results are very close. This work was extended and its working model was proved even for the Korean people. Another finding reported that the fatality rate has an impact on climates and temperatures.
A prediction work on the transmission process of the COVID-19 is proposed in [37]. Then the prediction model is developed using Gaussian distribution theory by taking the transmission characteristics of epidemic at different stages of COVID-19. The Gaussian distribution function with mean 1 and variance 1.5 is used to simulate the propagation ability of the virus. This assumption is valid for the initial stage, in which it is assumed that one infected person infects one other person on the average. The prediction curves of the model matches exactly with an actual official data curves of Hubei, China, South Korea, Italy, and Iran. The majority factors that influence the spread of the virus include 1) basic reproduction number 2) virus incubation period 3) daily infection number, which are also captured using this model.
E. Machine Learning and Deep Learning Based Models
Machine learning and deep learning models are also used for the COVID-19 prediction across the world. To predict the cases for the 10 consequent days from the start of the disease as proposed in [59]. Machine learning methods, namely, support vector regression (SVR) [40] and polynomial regression (PR) [41] are used for the prediction of COVID-19 with the polynomial kernel of degree 6 and 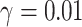 ,
, 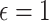 , and
, and 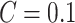 , where
, where 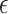 represents maximum error constraint value under support vector regression,
represents maximum error constraint value under support vector regression, 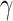 is denoted as the amount of deviation from the maximum margin and
is denoted as the amount of deviation from the maximum margin and 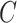 is denoted as hyper parameter, which is tuned to control the deviation value
is denoted as hyper parameter, which is tuned to control the deviation value 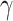 .
.
The deep learning regression models of deep neural network (DNN) and recurrent neural networks (RNN) of long short-term memory (LSTM) [60] are also employed in this work. For this purpose, the DNN architecture is designed with input layer of 128 neurons, three hidden dense layers of 256 neurons and output layer with a single neuron. The LSTM is designed with three stack layers with 64 neutrons in each with 10% dropout and an output layer with a single neuron. These prediction models are trained to predict the total number of confirmed, recovered, and death cases worldwide. The model also incorporates increasing the lockdown period, executing the sanitation procedure, providing the everyday resources in account.
The performance measure in terms of root mean squared error (RMSE) for all the methods namely SVR, DNN, LSTM and PR are discussed here interms of confirmed prediction, death prediciton and recovered predition. The corresponding values of SVR are 27 456.47, 1360.47 and 16 762.15 respectively. The same values for DNN are 163 335.65, 8554.55 and 25 415.03 respectively. The same values for LSTM goes as 15 647.64, 1076.06 and 4092.01 respectively. On the other hand, PR takes the values as 455.92, 117.94 and 809.71 respectively. These reported results confirms that the PR approach provides the best prediction in terms of RMSE.
Artificial inspired methods based on modified stacked auto-encoder are proposed for the real time forecasting of COVID-19 in China. This algorithm can estimate the size, length and ending time of COVID in China. Forecasting is based on a time series data. Training samples are taken in terms of 128 segments of time series, which correspond to the segments for 8 days. These data are stacked in to the matrix 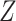 . From the matrix
. From the matrix 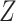 , one element is randomly chosen to indicate a starting day and the data corresponding to other days are the subsequent values of the matrix. With the chosen data, a modified auto encoder is used to forecast. The number of nodes in the first latent, second latent layer and output layer in the auto encoder was set to 8, 4 and 1 respectively.
, one element is randomly chosen to indicate a starting day and the data corresponding to other days are the subsequent values of the matrix. With the chosen data, a modified auto encoder is used to forecast. The number of nodes in the first latent, second latent layer and output layer in the auto encoder was set to 8, 4 and 1 respectively.
A machine learning based methods using logistic model, Bertalanffy model, Gompertz model is proposed in [43]. In this work, the model equation for logistic model is given by
 |
In Bertalanffy model, the equation for prediction is
 |
In Gompertz model, it is given by
 |
where 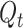 is cumulative confirmed cases,
is cumulative confirmed cases,  is maximum of confirmed cases,
is maximum of confirmed cases, 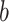 and
and 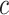 are fitting coefficients.
are fitting coefficients.
Using these equations, the plot of number of confirmed cases with respect to days is plotted and verified with the avilable data [43].
LSTM model uses equations for storing, forgetting, renewing and outputting the information in the cell through the activation functions, namely hyperbolic tangents and logistic sigmoid.
In another work reported in [45], a logistic model and exponential models are used for prediction. Authors considreed the genral expression of the logistic as
 |
where 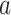 denotes infection speed,
denotes infection speed, 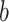 is the day with the maximum infections occurred and
is the day with the maximum infections occurred and 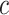 is the total number of infected people at the infection’s end. The prediction from exponential model is
is the total number of infected people at the infection’s end. The prediction from exponential model is
 |
1). DEFSI Model
A short term high resolution forecasting based on Deep Learning Epidemic Forecasting with Synthetic Information (DEFSI) is proposed in [47], which is a more generalized and physical consistency epidemic framework. A two branch network architecture is used in this framework, while considering within-season and between-season observations as features. The network is trained on high resolution synthetic data. When high resolution surveillance data is not available, the network enables detailed forecasting. The method [47] achieves better performance than any state-of-the-art methods available for forecasting.
The advantages and disadvantages of various models are listed in a Table IV for better illustration.
TABLE IV. Comparison Between Spreading Models.
| Model | Advantages | Disadvantage |
|---|---|---|
| Compartment Model | Simplest and generally used for any kind of disease spread | Model purely based on available old statistical data which fails to capture sudden changes in the spreading. Not able to handle more dynamic scenario |
| Hidden Node Model | Accuracy is more as the hidden node informations are accounted | Can not handle the situation of asymptomatic cases |
| Statistical Model | Model is based on mathematical approaches, so well reliable and opens up the way for more possible analysis | More dependent on the previous statistics |
| Mixed Model | Reliability is high, as it shares the advantages of various other models | Computational complexity is high and model design is complex. |
F. Mixed Models
A mixed method of modelling using epidemiological equations and neural network is proposed for “reproduction number estimation” [11]. This model is developed using the data from Wuhan, Italy, South Korea and the United States of America. This model addresses the issue of incorporating the impact of quarantine and isolation measures in those countries. The neural network is used as a function approximation for estimating the effect of quarantine, which is incorporated in epidemiological equations model. The results of the model show that quarantine and isolation can halt the spread of infection.
A prediction model for Italian Regions to get the progression of the epidemic, predict peaks of new daily infections through machine learning is reported in [39]. The model uses Chinese epidemiological dynamics data for this purpose. A modified autoencoder neural network model is trained using Chinese data. The prediction of epidemic curves for different Italian regions is obtained. The conventional “Susceptible Exposed Infectious Removed” (SEIR) model is also utilized to predict the spread. The reproduction number is also estimated by curve fitting on growth rate across one month, and day-by-day assessment. The prediction shows that Italy regions may reach 1,60 000 infected cases by April 30th. The model is validated by the measure of mean average precision between official Italian data and the prediction.
Another mixed model with the SEIR model and a type of recurrent neural network, called LSTM is used to predict the number of new infections over time. Authors used the 2003 SARS epidemic statistics data set for the training [46]. In addition, they have incorporated COVID-19 epidemical parameters, namely incubation rate, the probability of death & recovery and probability of transmission. In order to avoid overfitting, a simpler network was chosen. The model is optimized using adam optimizer and ran for 500 epochs.
G. Deep and Machine Learning Models for Diagnosis
Artificial Intelligence (AI) tools like machine learning and deep learning can make quick decisions for the diagnosis of the infection of COVID-19 using medical images namely, Computed tomography (CT), and Magnetic resonance imaging (MRI) [48] [61].
An automatic quantification of COVID-19 infection using deep learning for CT images of the lung is reported in [62]. The model does the automatic segmentation using “VB-Net” and quantification of infection in the chest CT scans. The training of the model is carried out using data collected from 249 COVID-19 patients and validated using 300 new COVID-19 patients. The similarity measure between manual detection of infection and automated detection using the proposed model is taken as a performance evaluation parameter. A parameter called Dice similarity coefficients is used as similarity measure, which is reported as 91.6%. The fully manual diagnosis system takes 1 to 5 hours, which is reduced to 4 minutes using this automated system.
A deep learning-based early screening model to find COVID-19 pneumonia from Influenza-viral pneumonia using a pulmonary CT image is reported [63]. A 3-dimensional deep learning model is used for infection region segmentation. A location-attention classification model is used for categorizing those segmented images into three classes of COVID-19, namely Influenza-A, viral pneumonia, and no infection. The infection type and total confidence scores are estimated through Noisy or Bayesian function. The overall accuracy of 86.7% is reported.
Convolutional Neural Network-based auto diagnosis of COVID-19 for X-ray images is reported in [64]. Transfer learning is applied to achieve an accuracy of 97.82% for the detection of COVID-19. The model uses a total of 1428 X-Ray images for training and testing purposes with 224 images of confirmed COVID-19, 700 images of common confirmed pneumonia, and 504 images without any problem.
Deep learning requires a lot of data for successful training. But in the current situation, there is a lack of datasets for COVID-19, especially the chest X-rays images. To overcome the above issue, a generative adversarial network (GAN) is used to generate more images. A GAN with a deep transfer learning model for coronavirus detection in chest X-ray images is presented in [65]. In the work, the dataset of 307 images are taken for four different classes. The GAN is used to generate 30 times larger than this real data set. This artificially created data is used to avoid the overfitting of the deep learning model. The Alexnet, Googlenet, and Resnet-18 models are used by transfer learning to detect coronavirus. This combined GAN and deep transfer models prove a more accurate result which is reported in the Table V.
TABLE V. Performance Comparison Between Deep Learning models [65].
| Number of classes | Googlenet | Alexnet | Restnet18 |
|---|---|---|---|
| 4 classes | 80.6% | 66.7% | 66.7% |
| 3 classes | 81.5% | 85.2% | 81.5% |
| 2 classes | 100% | 100% | 100% |
A deep learning-based framework to diagnose COVID-19 using Smartphone Embedded Sensors is proposed in [49].The symptom for COVID-19 like fever, fatigue, headache, nausea, dry cough, and shortness of breath are classified by the deep learning method of convolution neural network (CNN) and recurrent neural network (RNN) algorithms. The smartphone sensors like cameras, inertial sensors, microphones, and temperature sensors are used for the data collection. Temperature fingerprint sensor available under the touch-screen is used to predict the fever level. Inertial sensors and Camera images are used to detect fatigue. The COVID-19 is detected Using those detected data set.
V. Future Direction
There is a huge need for applying the mathematical, deep learning model in computational biology and medicine. There are a few works on discovering drug compounds against the virus [66], [67]. A deep and machine learning model is required for investigating the genetics and chemistry of the virus to make vaccines and treatment drugs.
Exploring and analysing the protein structures of viruses are also the vital application of the deep and machine learning model, which is one of the requirements for an efficient vaccine or drug discovery [68].
Deep learning techniques for COVID-19 diagnosis using radiology imaging data are currently on going. Yet there is no benchmarking for utilizing these models in real-world clinical practice. So, there is a need for developing a benchmark framework to evaluate the models and apply them in practice. This framework must be universal to allow anyone to upload their medical image and get the result.
Mass diagnosis is another issue in highly populated countries. This issue can be solved by mathematical and deep learning models based on smartphone applications for pre-screening. In addition, NLP can be augmented with deep learning and SIR models [69] for effective prediction. However, it needs to be further enhanced by taking the social media, other web source data and mobile phone data like travel history, etc.
VI. Conclusion
A comprehensive review of available mathematical models for the transmission of COVID-19 is presented in this article. The review was carried out on the various models namely, differential equation based, statistical based, prediction based, mixed model, machine learning and deep learning based. In addition, machine learning and deep learning based models for the diagnosis of COVID-19 using radiological images are also reviewed in this article. Furthermore, the usage of natural language processing for the analysis of mental illness and feeling of the public based on the comments posted in the social media is also reviewed in the article.
Biographies

J. Christopher Clement (Member, IEEE) received the M.E. degree in communication systems from Anna university, Chennai, India and, the Ph.D. degree in wireless communication from the Vellore Institute of Technology (VIT), Vellore, India. He is currently a certified MATLAB, Python Programmer and a Data Scientist. He has been teaching for 15 years. He has authored a book titled “Cognitive Radio” for Krishna publishers. His research interests include machine learning, deep learning, statistical signal processing, and cognitive radio communication. He was with MultiTech Software Systems as a Senior Software Programmer and developed an Internet Radio project. He was the recipient of consistent Researcher Award presented internaly and an internal Grant to complete the project “Smart communications for Smart Grid”. He is a potential Reviewer in various peer reviewed journals, including IEEE Access. He is currently with the School of Electronics Engineering, VIT University, India, as an Associate Professor.

Vijayakumar Ponnusamy (Senior Member, IEEE) received the B.E. degree in electronics and communication engineering from Madras University, Chennai, India, in 2000, the M.E. degree in engineering in applied electronics from the College of Engineering Guindy, Anna University, Chennai, India, in 2005, and the Ph.D. degree from SRM IST, Kattankulathur, Chennai, India, in 2018. He is a Certified “IoT Specialist” and “Data Scientist. He is the Co-Investigator of the BRNS grant Project titled, Real time hardware based raw data processing for dual energy X-ray baggage Inspection system XBIS. He has completed two projects sponsored by an external agency. He is currently an Associate Professor with ECE Department, SRM IST, Chennai, India. His current research interests include machine learning and applications, data analytics, IoT based intelligent system design, cognitive radio networks, and smart systems. He was the recipient of the NI India Academic award for excellence in research in 2015.

K. C. Sriharipriya received the Ph.D. degree in wireless communication engineering from IIT Madras, Chennai, India, with publications in a SCI/Thomson Reuters indexed journals. She has 15 years of teaching experience, which includes six years of research experience. She is currently an Associate Professor with the Vellore Institute of Technology, Vellore, India. She is an Active Reviewer in peer reviewed journals related to communication and signal processing. She has coauthored the book titled “Cognitive Radio” in 2019. Her research interests include signal processing, communication, deep learning, and machine learning with IoT applications. She was the 3GPP RAN 1 delegate representing IITM funded by TSDSI. He was the recipient of Postdoctrol fellowship in 5G wireless communication from IIT Madras.

R. Nandakumar received the B.E. degree in electronics and communication engineering and the M.E. degree in applied electronics from the K.S.Rangasamy College of Technology, Namakkal, India, in 2000 and 2006, respectively, and the Ph.D. degree in faculty of information and communication from Anna University, Chennai, India, in 2017. He is currently a Professor and the Head of the Department of ECE, K S R Institute for Engineering and Technology, Namakkal, India. His research interests include medical image processing, medical electronics, and machine learning.
Contributor Information
J. Christopher Clement, Email: John,christopher.clement@vit.ac.in.
VijayaKumar Ponnusamy, Email: vijaymean2win@gmail.com.
K.C. Sriharipriya, Email: sriharipriya.kc@vit.ac.in.
R. Nandakumar, Email: drrnandakumar@gmail.com.
References
- [1].Song Y. et al. , “Deep learning enables accurate diagnosis of novel coronavirus (covid-19) with Ct images,” IEEE/ACM Trans. Comput. Biol. Bioinf., Mar. 11, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Ivorra B., Ferrández M., Vela-Pérez M., and Ramos A., “Mathematical modeling of the spread of the coronavirus disease 2019 (covid-19) considering its particular characteristics. the case of china,” Tech. Rep., MOMAT, Mar. 2020. [Online]. Available: https://doi-org.usm.idm.oclc.org [DOI] [PMC free article] [PubMed]
- [3].Kucharski A. J. et al. , “Early dynamics of transmission and control of covid-19: A mathematical modelling study,” Lancet Infect. Dis., vol. 20, no. 5, pp. 553–558, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Liu T. et al. , “Transmission dynamics of 2019 novel coronavirus (2019-ncov),” bioRxiv, 2020. [Online]. Available: https://www.biorxiv.org/content/early/2020/01/26/2020.01.25.919787 [Google Scholar]
- [5].Chowell G., Sattenspiel L., Bansal S., and Viboud C., “Mathematical models to characterize early epidemic growth: A review,” Phys. Life Rev., vol. 18, pp. 66–97, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Brauer F., Castillo-Chavez C., and Castillo-Chavez C., Mathematical Models in Population Biology and Epidemiology. Berlin, Germany: Springer, 2012. [Google Scholar]
- [7].Miller M., “2019 novel coronavirus covid-19 (2019-Ncov) data repository,” Bull.-Assoc. Can. Map Libraries Arch., vol. 1, no. 164, pp. 47–51,2020. [Google Scholar]
- [8].“Who coronavirus (covid-19) dashboard,” Accessed: Jan. 5, 2021. [Online]. Available: https://covid19.who.int/
- [9].Roda W. C., Varughese M. B., Han D., and Li M. Y., “Why is it difficult to accurately predict the covid-19 epidemic?,” Infect. Dis. Model., vol. 5, pp. 271–281, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Liang K., “Mathematical model of infection kinetics and its analysis for covid-19, SARS and MERS,” Infect., Genet. Evol., vol. 82, 2020, Art. no. 104306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dandekar R. and Barbastathis G., “Neural network aided quarantine control model estimation of global covid-19 spread,” 2020. [Online]. Available: https://arxiv.org/abs/2004.02752 [DOI] [PMC free article] [PubMed]
- [12].Lekone P. E. and Finkenstädt B. F., “Statistical inference in a stochastic epidemic seir model with control intervention: Ebola as a case study,” Biometrics, vol. 62, no. 4, pp. 1170–1177, 2006. [DOI] [PubMed] [Google Scholar]
- [13].Brouwer E. De, Raimondi D., and Moreau Y., “Modeling the covid-19 outbreaks and the effectiveness of the containment measures adopted across countries,” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/19/2020.04.02.20046375 [Google Scholar]
- [14].Chatterjee K., Chatterjee K., Kumar A., and Shankar S., “Healthcare impact of covid-19 epidemic in india: A stochastic mathematical model,” Med. J. Armed Forces India, vol. 76, no. 2, pp. 147–155, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Ferrándeza M. R., Ivorrab B., Ortigosaa P. M., Ramosb A. M., and Redondoa J. L., “Application of the be-codis model to the 2018-19 ebola virus disease outbreak in the democratic republic of congo,” ResearchGate Preprint, vol. 23, pp. 1–17, 2019. [Google Scholar]
- [16].Ivorra B. and Ramos A. M., “Application of the be-codis mathematical model to forecast the international spread of the 2019-20 Wuhan coronavirus outbreak,” ResearchGate Preprint, vol. 9, pp. 1–13, 2020. [Google Scholar]
- [17].Ferrándeza M. R., Ivorrab B., Redondoa J. L., Ramosb A. M., and Ortigosaa P. M., “A multi-objective approach to estimate parameters of compartmental epidemiological models. application to Ebola virus disease epidemics,” vol. 1, pp. 1–48, 2020. [Google Scholar]
- [18].Blackwood J. C. and Childs L. M., “An introduction to compartmental modeling for the budding infectious disease modeler,” Lett. Biomat., vol. 5, no. 1, pp. 195–221, 2018. [Google Scholar]
- [19].Shaikh A. S., Shaikh I. N., and Nisar K. S., “A mathematical model of covid-19 using fractional derivative: outbreak in india with dynamics of transmission and control,” in Proc. Adv. Difference Equ., 2020, pp. 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Chen T.-M, Rui J., Wang Q.-P, Zhao Z.-Y, Cui J.-A, and Yin L., “A mathematical model for simulating the phase-based transmissibility of a novel coronavirus,” Infect. Dis. Poverty, vol. 9, no. 1, pp. 1–8, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Khailaie S. et al. , “Development of the reproduction number from coronavirus sars-cov-2 case data in germany and implications for political measures," BMC Med., vol. 19, no. 1, pp. 1–16, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Khan M. A. and Atangana A., “Modeling the dynamics of novel coronavirus (2019-ncov) with fractional derivative,” Alexandria Eng. J., vol. 59, no. 4, pp. 2379–2389, 2020. [Google Scholar]
- [23].Camino-Beck T. de, Lewis M. A., and Driessche P. van den, “A graph-theoretic method for the basic reproduction number in continuous time epidemiological models,” J. Math. Biol., vol. 59, no. 4, pp. 503–516, 2009. [DOI] [PubMed] [Google Scholar]
- [24].Ivorra B., Martínez-López B., Sánchez-Vizcaíno J. M., and Ramos Á. M., “Mathematical formulation and validation of the be-fast model for classical swine fever virus spread between and within farms,” Ann. Operations Res., vol. 219, no. 1, pp. 25–47, 2014. [Google Scholar]
- [25].Otoo D., Opoku P., Charles S., and Kingsley A. P., “Deterministic epidemic model for (svcsycasyir) pneumonia dynamics, with vaccination and temporal immunity,” Infect. Dis. Model., vol. 5, pp. 42–60, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Cojocaru M.-G, Migot T., and Jaber A., “Controlling infection in predator-prey systems with transmission dynamics,” Infect. Dis. Model., vol. 5, pp. 1–11, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Singh S. S. and Mohapatra D. K., “Predictive analysis for covid-19 spread in india by adaptive compartmental model,” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/07/09/2020.07.08.20148619 [Google Scholar]
- [28].Mimkes J. and Janssen R., “On the corona infection model with contact restriction,” MedRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/11/2020.04.08.20057588 [Google Scholar]
- [29].Tuite A. R., Fisman D. N., and Greer A. L., “Mathematical modelling of covid-19 transmission and mitigation strategies in the population of ontario, canada,” CMAJ, vol. 192, no. 19, pp. E497–E505, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Bhola J., Venkateswaran V. R., and Koul M., “Corona epidemic in indian context: predictive mathematical modelling,” MedRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/07/2020.04.03.20047175 [Google Scholar]
- [31].Zhang W., “Estimating the presymptomatic transmission of covid19 using incubation period and serial interval data,” MedRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/06/2020.04.02.20051318 [Google Scholar]
- [32].Bhattacharjee S., “Statistical investigation of relationship between spread of coronavirus disease (covid-19) and environmental factors based on study of four mostly affected places of china and five mostly affected places of italy,” 2020, arXiv:2003.11277, [Online]. Available: https://arxiv.org/abs/2003.11277
- [33].Mizumoto K., Kagaya K., Zarebski A., and Chowell G., “Estimating the asymptomatic proportion of coronavirus disease 2019 (covid-19) cases on board the diamond princess cruise ship, Yokohama, Japan, 2020,” Eurosurveillance, vol. 25, no. 10, 2020, Art. no. 2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nishiura H. et al. , “Estimation of the asymptomatic ratio of novel coronavirus infections (covid-19),” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/02/17/2020.02.03.20020248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].“Covid-19 by indian state,” Accessed: Jan. 5, 2021. [Online]. Available: https://cddep.org/covid-19/
- [36].Villela D. A., “Discrete time forecasting of epidemics,” Infect. Dis. Model., vol. 5, pp. 189–196, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Li L. et al. , “Propagation analysis and prediction of the covid-19,” Infect. Dis. Model., vol. 5, pp. 282–292, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Roosa K. et al. , “Real-time forecasts of the covid-19 epidemic in china from february 5th to february 24th, 2020,” Infect. Dis. Model., vol. 5, pp. 256–263, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Distante C., Piscitelli P., and Miani A., “Covid-19 outbreak progression in italian regions: approaching the peak by march 29th,” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/02/2020.03.30.20043612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Awad M. and Khanna R., “Support vector regression,” in Efficient Learning Machines, Berlin, Germany: Springer, 2015, pp. 67–80. [Google Scholar]
- [41].Castro Y. De et al. , “Approximate optimal designs for multivariate polynomial regression,” Ann. Statist., vol. 47, no. 1, pp. 127–155, 2019. [Google Scholar]
- [42].Hu Z., Ge Q., Jin L., and Xiong M., “Artificial intelligence forecasting of covid-19 in China,” 2020, arXiv:2002.07112, [Online]. Available: https://arxiv.org/abs/2002.07112
- [43].Jia L. et al. , “Prediction and analysis of coronavirus disease 2019,” 2020. [Online]. Available: https://arxiv.org/abs/2003.05447
- [44].Chae S., Kwon S., and Lee D., “Predicting infectious disease using deep learning and big data,” Int. J. Environ. Res. Public Health, vol. 15, no. 8, 2018, Art. no. 1596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].“Covid-19 infection in Italy,” Accessed: Jan. 5, 2021. [Online]. Available: https://towardsdatascience.com/covid-19-infection-in-italy-mathematical-models-and-predictions-7784b4d7dd8d
- [46].Yang Z. et al. , “Modified seir and ai prediction of the epidemics trend of covid-19 in china under public health interventions,” J. Thoracic Dis., vol. 12, no. 3, 2020, Art. no. 165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wang L., Chen J., and Marathe M., “Defsi: Deep learning based epidemic forecasting with synthetic information,” in Proc. AAAI Conf. Artif. Intell., 2019, pp. 9607–9612.
- [48].Shereen M. A., Khan S., Kazmi A., Bashir N., and Siddique R., “Covid-19 infection: Origin, transmission, and characteristics of human coronaviruses,” J. Adv. Res., vol. 24, pp. 91–98, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Maghdid H. S., Ghafoor K. Z., Sadiq A. S., Curran K., and Rabie K., “A novel ai-enabled framework to diagnose coronavirus covid 19 using smartphone embedded sensors: Design study,” in Proc. IEEE 21st Int. Conf. Inf. Reuse Integr. Data Sci., 2020, pp. 180–187.
- [50].Wang L. et al. , “Real-time estimation and prediction of mortality caused by covid-19 with patient information based algorithm,” Sci. Total Environ., vol. 727, 2020, Art. no. 138394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Yu Y. et al. , “Covid-19 asymptomatic infection estimation,” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/04/23/2020.04.19.20068072
- [52].Blackwood J. C. and Childs L. M., “An introduction to compartmental modeling for the budding infectious disease modeler,” Lett. Biomath., vol. 5, no. 1, pp. 195–221, 2018. [Google Scholar]
- [53].Lin Q. et al. , “A conceptual model for the coronavirus disease 2019 (covid-19) outbreak in Wuhan, China with individual reaction and governmental action,” Int. J. Infect. Dis., vol. 93, pp. 211–216, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Chintalapudi N., Battineni G., and Amenta F., “Covid-19 disease outbreak forecasting of registered and recovered cases after sixty day lockdown in italy: A data driven model approach,” J. Microbiol., Immunol. Infection, vol. 53, no. 3, pp. 396–403, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Donsimoni J. R., Glawion R., Plachter B., and Wälde K., “Projecting the Spread of covid19 for Germany,” German Econ. Rev., vol. 21, no. 2, pp. 181–216, 2020. [Google Scholar]
- [56].Liu Z. and Guo W., “Government responses matter: predicting covid-19 cases in us under an empirical bayesian time series framework,” medRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/03/30/2020.03.28.20044578 [Google Scholar]
- [57].Pell B., Kuang Y., Viboud C., and Chowell G., “Using phenomenological models for forecasting the 2015 ebola challenge,” Epidemics, vol. 22, pp. 62–70, 2018. [DOI] [PubMed] [Google Scholar]
- [58].“Centers for disease control and prevention. using an epi curve to determine mode of spread,” Accessed: Jan. 5, 2021. [Online]. Available: https://www.cdc.gov/training/QuickLearns/epimode/
- [59].Punn N. S., Sonbhadra S. K., and Agarwal S., “Covid-19 epidemic analysis using machine learning and deep learning algorithms,” MedRxiv, 2020. [Online]. Available: https://www.medrxiv.org/content/early/2020/06/01/2020.04.08.20057679 [Google Scholar]
- [60].Greff K., Srivastava R., Koutník J., Steunebrink B. R., and Schmidhuber J., “LSTM: A search space odyssey,” IEEE Trans. Neural Netw. Learn. Syst., vol. 28, no. 10, pp. 2222–2232, Oct. 2017. [DOI] [PubMed] [Google Scholar]
- [61].Haleem A., Vaishya R., Javaid M., and Khan I. H., “Artificial intelligence (ai) applications in orthopaedics: An innovative technology to embrace,” J. Clin. Orthopaedics Trauma, vol. 11, pp. S80–S81, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Shan F. et al. , “Lung infection quantification of covid-19 in CT images with deep learning,” 2020, arXiv:2003.04655, [Online]. Available: https://arxiv.org/abs/2003.04655
- [63].Xu X. et al. , “Deep learning system to screen coronavirus disease 2019 pneumonia,” 2020, arXiv:2002.09334, [Online]. Available: https://arxiv.org/abs/2002.09334
- [64].Apostolopoulos I. D. and Mpesiana T. A., “Covid-19: Automatic detection from X-Ray images utilizing transfer learning with convolutional neural networks,” Phys. Eng. Sci. Med., vol. 43, no. 2, pp. 635–640, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Loey M., Smarandache F., and Khalifa N. E. M., “Within the lack of chest covid-19 x-ray dataset: a novel detection model based on gan and deep transfer learning,” Symmetry, vol. 12, no. 4, 2020, Art. no. 651. [Google Scholar]
- [66].“Computational predictions of protein structures associated with covid-19, deepmind,” Accessed: Jan. 5, 2020. [Online]. Available: https://deepmind.com/research/opensource/computational-predictions-of-protein-structures-associated-with-COVID-19
- [67].Zhavoronkov A. et al. , “Potential covid-2019 3c-like protease inhibitors designed using generative deep learning approaches,” Insilico Med. Hong Kong Ltd A, vol. 307, 2020, Art. no. E 1. [Google Scholar]
- [68].“Ai can help scientists find a covid-19 vaccine. wired,” Accessed: Jan. 5, 2020. [Online]. Available: https://www.wired.com/story/opinion-ai-can-help-find-scientists-find-a-covid-19-vaccine/
- [69].Du S. et al. , “Predicting covid-19 using hybrid Ai model,” SSRN, 2020. [Online]. Available: https://ssrn.com/abstract=3555202orhttp://dx.doi.org/10.2139/ssrn.3555202 [DOI] [PubMed] [Google Scholar]