Abstract
Lesion detectability (LD) quantifies how easily a lesion or target can be distinguished from the background. LD is commonly used to assess the performance of new ultrasound imaging methods. The contrast-to-noise ratio (CNR) is the most popular measure of LD; however, recent work has exposed its vulnerability to manipulations of dynamic range. The generalized CNR (gCNR) has been proposed as a robust histogram-based alternative that is invariant to such manipulations. Here, we identify key shortcomings of CNR and strengths of gCNR as LD metrics for modern beamformers. Using measure theory, we pose LD as a distance between empirical probability measures (i.e. histograms) and prove that 1) gCNR is equal to the total variation distance between probability measures, and 2) gCNR is one minus the error rate of the ideal observer. We then explore several consequences of measure-theoretic LD in simulation studies. We find that histogram distances depend on bin selection, that LD must be considered in the context of spatial resolution, and that many histogram distances are invariant under measure-preserving isomorphisms of the sample space (e.g., dynamic range transformations). Finally, we provide a mathematical interpretation for why quantitative values such as contrast ratio, CNR, and signal-to-noise ratio should not be compared between images with different dynamic ranges or underlying units, and demonstrate how histogram matching can be used to re-enable such quantitative comparisons.
Index Terms—: Ultrasound, Image quality assessment, Quantification and Estimation, Evaluation and Performance
I. Introduction
Ultrasound image quality is difficult to define in an objective and rigorous manner. Image quality depends intrinsically on the specific task that the image is used for. A popular task in ultrasound imaging is to detect a low-contrast lesion or target embedded in a background, where an imaging method with greater lesion detectability (LD) is one that more easily detects the target. The most widely-used measure of LD is the contrast-to-noise ratio (CNR), which rewards increased overall contrast between the target and background while penalizing increased variance within each. Historically, the CNR has been popular for its connections to the ideal observer with statistical decision theory, a rigorous hypothesis-based framework for detecting signals in noise [1].
As early as 1983, the ideal observer for lesion detection was derived for envelope-detected speckle amplitudes and intensities [2]. The ideal observer was then derived for raw radiofrequency (RF) echo signals [3], and it was later shown that LD is degraded by the envelope detection process [4, 5]. More recently, Nguyen et al. [6, 7] have further extended the ideal observer to minimum variance and Wiener-filter beamformers. These ideal observer approaches provide rigorous upper bounds on ultrasound LD for given signal and noise models. Under appropriate conditions, lesion detection performance of the ideal observer test statistic t is captured by the CNR:
| (1) |
where f and g denote the probability distributions of t in the lesion and background, respectively, and Ef[t] and Varf[t] denote the expected value and variance of t under distribution f.
However, major inconsistencies in current practices have undermined the utility of CNR as a LD measure, as demonstrated by Rindal et al. [8]. Ultrasound images are often treated as qualitative sources of information, where the raw pixel values are less important than their relative values. Clinicians are regularly presented with images that have undergone substantial post-processing, such as dynamic range compression, speckle reduction, edge enhancement, and more. As ultrasound researchers seek clinically-relevant imaging methods, the line between traditional quantitative beamforming and qualitative image presentation has become blurred. This trend is especially apparent in the proliferation of adaptive methods wherein the delay-and-sum (DAS) beamformer output is weighted by various quantities such as coherence factor [9], generalized coherence factor [10], and phase coherence factor [11], as well as in nonlinear beamformers that replace DAS altogether, such as short-lag spatial coherence (SLSC) [12], delay-multiply-and-sum (DMAS) [13], and echogenicity estimation with neural networks [14].
CNR is currently used as the de facto measure of LD when proposing and evaluating new imaging techniques. However, recent seminal work by Rindal et al. [8] and Rodriguez-Molares et al. [15] demonstrated that arbitrarily high values for CNR can be obtained by skewing the image dynamic range. We further found that CNR is preserved only for affine dynamic range transformations and not for the more general monotonic transformations common to image post-processing [16]. As we will show, many newer methods violate core assumptions used to derive the ideal observer for traditional DAS. Amidst the recent proliferation of ultrasound image reconstruction techniques, these findings demand that we revisit the definitions and assumptions surrounding the ideal observer and CNR as an image quality metric. There is a critical need for robust LD image quality metrics that are valid across a wide range of different techniques.
To this end, Rodriguez-Molares et al. [15] recently proposed a generalized CNR (gCNR) as a robust alternative metric for LD. The gCNR compares histogram-derived probability densities of two regions in an image (e.g., lesion and background), denoted as f and g, as
| (2) |
The gCNR is reported as being resistant to dynamic range alterations, independent of signal units, and as being related to the minimum probability of error by the ideal observer [15]. Here, we provide a rigorous confirmation of these findings, and further elucidate the reasons why CNR breaks down and why gCNR is robust to transformations on the dynamic range of images. The main contributions of this article are as follows:
A review of classical LD using statistical decision theory and its often-violated assumptions.
A measure-theoretic description of LD as a distance between probability measures, with a clear identification of where classical LD metrics fail.
Mathematical proofs that gCNR is the total variation distance, and that it describes ideal observer performance.
Key considerations for measure-theoretic LD and a suggested remedy to restore the applicability of classical LD metrics.
II. Classical Lesion Detectability
A. Deriving the Ideal Observer
Statistical decision theory provides a framework for detecting lesions embedded in a background. Denote the probability density functions (PDFs) of image values a in the lesion and background as f(a) and g(a), respectively. Classical decision theory addresses the simple hypothesis testing problem, wherein f and g are fully known a priori [1]. In this framework, the LD problem can be posed as: Given a sample of N independent and identically distributed (i.i.d.) samples a = {a1, a2, …, aN}, decide if a is drawn from f or g. A useful quantity is the likelihood ratio of a:
| (3) |
The Neyman-Pearson lemma [17] states that is the most powerful test at a given significance level α, where the decision boundary is selected as for some threshold γα that depends on α [1]. The same optimal decision boundary can be obtained using monotonic transformations of (and the corresponding transformations of γα), including the more convenient log-likelihood ratio.
Consider the case of detecting a speckle lesion embedded in a speckle background. Classically, ultrasound speckle amplitudes and intensities are Rayleigh- and exponentially-distributed, respectively [18]. The PDFs of speckle amplitudes in the lesion f(a) and background g(a) are given by
| (4) |
| (5) |
where the parameters θf and θg correspond to the known lesion and background reflectivity, respectively. The log-likelihood ratio for N i.i.d. samples is
| (6) |
The log-likelihood is monotonic to the mean speckle intensity:
| (7) |
Thus t, the mean speckle intensity, is an optimal test statistic for lesion detection for two Rayleigh-distributed speckle amplitudes. The same optimal test statistic is derived when starting with speckle intensity distributions for f and g [2]. Others have derived optimal test statistics for more difficult cases, such as multivariate normally-distributed RF data [3] and for data from beamformers with matched filtering, minimium variance, and Wiener filtering [5–7].
B. Characterizing the Ideal Observer with CNR
As N increases to infinity, t in (7) converges to the expected intensity:
| (8) |
Furthermore, t itself becomes normally-distributed by the central limit theorem, allowing it to be fully characterized using only its mean and variance, which are
| (9) |
for j = f, g. For sufficiently large N, the detection performance of the optimal test statistic can be wholly captured by the CNR in (1), also referred to as the “signal-to-noise ratio” (SNR) of the optimal test statistic [2]:
| (10) |
A rule of thumb is that the approximation is valid for speckle intensities when N > 10 [2] and for multivariate-normally distributed RF data when N > 50 [19]. Nguyen et al. [19] further showed that the CNR is also equal to the square root of the Kullback-Leibler divergence and the “detectability index” under conditions of normality.
Note that this ideal observer characterization by CNR uses the expected value and variance of the statistic t, and not of the image values a themselves (i.e., not E[a] and Var[a]).
C. Quantifying Lesion Detectability with CNR
In practice, the CNR is used as a LD metric directly on image values a rather than on statistic t [20]. However, image values are not normally-distributed in general, in which case CNR does not describe ideal observer performance. Consider the CNR of speckle intensities a2, which are exponentially distributed with means and variances . As the number of samples N → ∞ (i.e. as the regions of interest grow to include more speckles), the CNR approaches
| (11) |
Thus CNR(a2) can be viewed as a N = 1 approximation of the ideal observer characterization CNR(t); however, at N = 1, the central limit theorem does not apply. The CNR of speckle amplitudes a (mean 2θj, variance ) shows even less resemblance to the ideal observer performance:
| (12) |
We can attempt to restore the ideal observer interpretation of CNR by devoting a proportion of the samples towards first estimating a test statistic t (normally-distributed by the central limit theorem), followed by measuring the CNR of t. However, the number of samples (i.e. size of the region of interest) is often a limiting factor, making this approach impractical.
Thus the CNR of a normally-distributed optimal test statistic is an excellent quantifier of LD built on rigorous hypothesis testing assuming a known signal model; however, these assumptions are commonly violated in ultrasound LD image analysis, causing CNR to lose its ideal observer interpretation.
III. Measure-Theoretic Lesion Detectability
The rising interest in imaging methods with non-traditional statistics strongly motivates a need for distribution-free tests of LD, i.e. tests that do not assume a known underlying PDF. Two examples include work by Nguyen et al. [19, 21], who first demonstrated how detection performance is related to the Kullback-Leibler divergence, an information-theoretic measure of class separability, as well as Rodriguez-Molares et al. [15], who proposed gCNR using image histograms. Below, we unify these ideas using the framework of measure theory to develop a new perspective of LD that is suitable for non-traditional ultrasound imaging methods.
A. Definitions
We begin with some definitions from measure theory [22, 23], presented for completeness and to build towards our discussion of LD as a distance between probability measures.
Consider an arbitrary set Ω. A σ-algebra of Ω is a collection of subsets of Ω that includes Ω itself, is closed under complement, and is closed under countable unions. A σ-algebra defines the set of all measurable events of interest. Examples include the trivial σ-algebra {∅, Ω}, the Borel σ-algebra (the set of all open subsets for a topological space Ω), and the discrete σ-algebra 2Ω (the set of all possible subsets for a discrete Ω, i.e. its power set). The pair (Ω, Σ) is a measurable space, comprised of a set Ω and a σ-algebra Σ defined on Ω.
A measurable function is a map ϕ : (Ω1, Σ1) → (Ω2, Σ2) from one measurable space (Ω1, Σ1) into a second measurable space (Ω2, Σ2) such that if a measurable event S is in Σ2, then ϕ−1(S) = {ω ∈ Ω1 : ϕ(ω) ∈ S} ∈ Σ1. That is, every measurable event in Σ2 must have a corresponding measurable event in Σ1 under the inverse mapping ϕ−1.
A measure on (Ω, Σ) is a function μ : Σ → [0, ∞] that gives a “size” to every measurable subset of Ω (i.e. every S ∈ Σ) while satisfying the properties of a null empty set (μ(∅) = 0) and countable additivity ( for disjoint Xi ∈ Σ). A measure provides a systematic and self-consistent way of assigning sizes to arbitrary events S ∈ Σ. Important examples are the Lebesgue measure (e.g., the length, area, or volume of an open set in , , or ) and the counting measure (which assigns measure 1 to every element in a discrete Ω). When the entire set has measure 1 (μ(Ω) = 1), μ is called a probability measure and μ(S) is the probability of event S occurring.
A density of μ with respect to a reference measure λ on (Ω, Σ) is f = dμ/dλ, defined such that for any S ∈ Σ. For the standard case of a continuous Ω with σ-algebra , the density with respect to the Lebesgue measure gives the familiar probability density function. For the standard case of a discrete Ω with σ-algebra 2Ω, the density with respect to the counting measure gives the familiar probability mass function.
B. Images, Sample Spaces, and Their Embeddings in
Denote an imaging field of view (FOV) as , where the FOV is a subset of d-dimensional Euclidean space, often a 2D or 3D rectangular or sector region of space originating at the transducer. While Ω can refer to a continuous FOV, we often work with discrete FOVs of pixels or voxels in practice. A real-valued ultrasound image maps Ω to by assigning some real number to every point in the FOV.
Here, we explicitly decompose this real-valued representation into two distinct parts: 1) the intrinsic image ϕ : Ω → A, which maps the FOV into some abstract sample space A; and 2) its extrinsic representation using real numbers , which embeds A in . The sample space A is the abstract set of values that ϕ can produce, e.g., {a1, a2, …}; these are then represented as real values (e.g., {0, 0.1, …}) via an embedding {ρ(a1), ρ(a2), …}. There are many ways to embed A in : for instance, we may wish to have an embedding ρlin that preserves linearity with respect to the inputs, or an embedding ρlog on a logarithmic scale designed to optimize contrast for human observers. Within this framework, dynamic range transformations are simply different embeddings ρ applied to the same image ϕ. Fig. 1 illustrates the composition ρ ◦ ϕ.
Fig. 1.
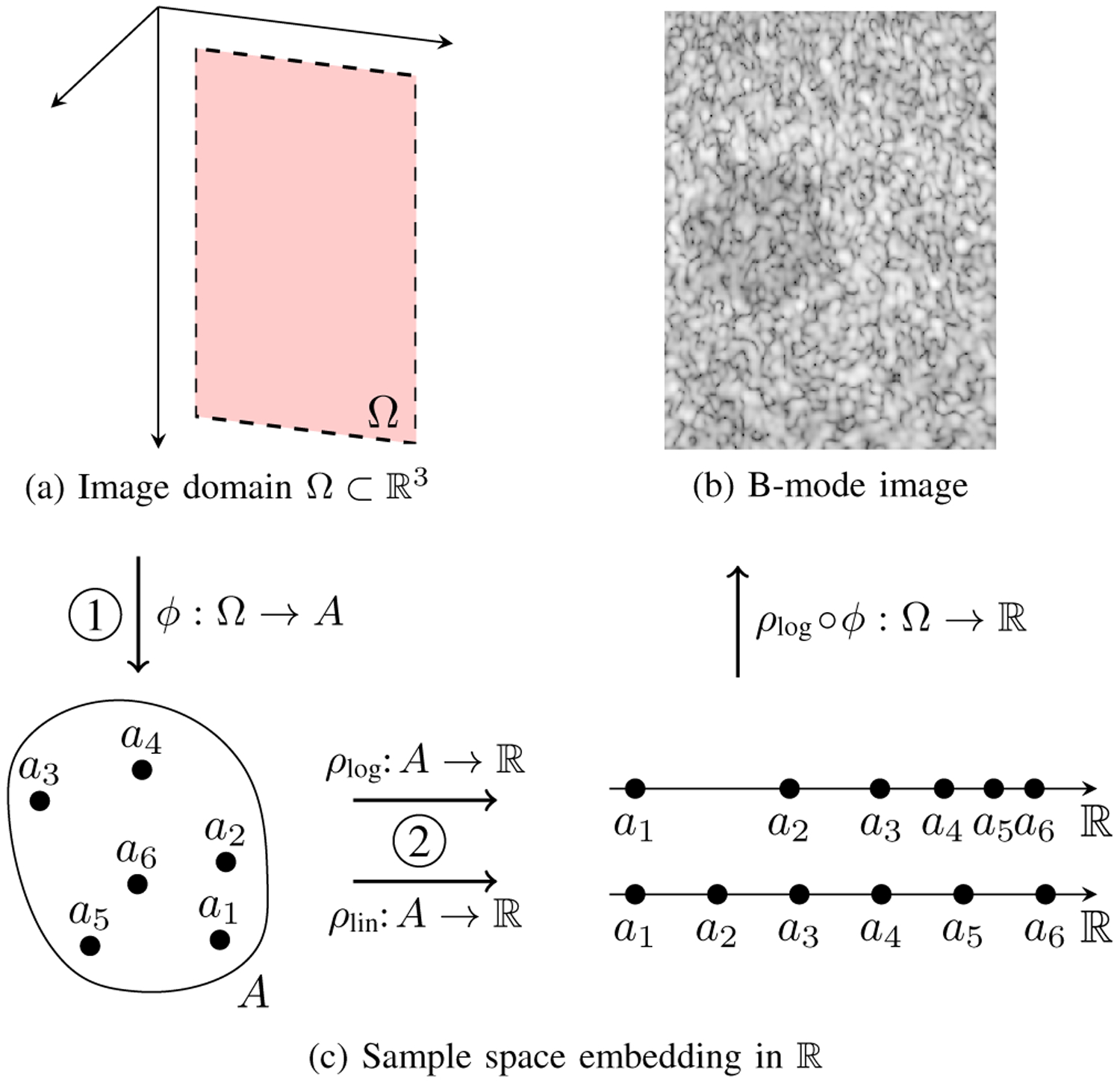
(a) A 2D FOV Ω in 3D space. (b) A log-compressed B-mode image with a −6 dB lesion. (c) Image formation is decomposed into two distinct steps: 1) mapping Ω to an abstract sample space A using ϕ, and 2) embedding A in using ρ. Examples of a linear and logarithmic embedding are shown. The final image in (b) corresponds to the composition of ϕ with ρlog.
We often work with real-valued images (i.e. ρ ◦ ϕ), treating the embedding step as implicit. However, an image ϕ carries intrinsic information in its distribution over A that is independent of its embedding in by ρ. This intrinsic information is the primary focus of this paper. For the remainder of the paper, we explicitly refer to intrinsic image values as a ∈ A and their real-valued embeddings as ρ(a). We address the special case of quantitative images (where the embedding ρ itself also conveys information, e.g., as physical units) in Sec. IV-D, where we also show that ambiguity in embedding leads to a major lapse in rigor for traditional lesion detectability with newer methods.
C. Image Histograms as Probability Measures
Images provide a natural definition of a probability measure based on the proportion of the FOV that corresponds to a given image value. Let us define an image more precisely as a measurable function ϕ : (Ω, Σ) → (A, ΣA), where Σ and ΣA are σ-algebras on each respective space. For any measurable subset of image values S ∈ ΣA, there is a corresponding subset of the FOV whose image values are in S (see Fig. 2). We refer to this as the inverse image of S, defined as the set of all FOV points with values in S:
| (13) |
By the definition of a measurable function, ϕ−1(S) is also measurable, i.e. S ∈ ΣA implies ϕ−1(S) ∈ Σ.
Fig. 2.

Illustration of how a probability measure is induced by an image ϕ. (a) Three disjoint subsets (E1, E2, E3) of the sample space A are shown in different shades of gray. (b) Each Ei corresponds to a different subset of the FOV Ω under the inverse mapping ϕ−1 (shown as the corresponding shades of gray). The fraction of the total FOV area corresponding to each ϕ−1(Ei) defines a probability measure μ (i.e. μ(Ei) is the probability of observing a value in Ei in the FOV) whose density is the histogram f = dμ/dλ.
Let m be a measure on (Ω, Σ) that describes the size of any measurable region of interest (ROI) in Ω. Specifically, let m be the Lebesgue measure for continuous Ω or the counting measure for discrete Ω. For a given set of image values S, the fraction of the FOV that takes on these values defines a probability measure μ:
| (14) |
That is, μ(S) is the proportion of Ω that has image values that lie in S. Another way to say this is that μ is the pushforward of a normalized Lebesgue or counting measure from (Ω, Σ) onto (A, ΣA). The density f of μ with respect to an appropriate (Lebesgue or counting) reference measure λ is referred to as the (continuous or discrete) histogram of the image. Note that ΣA essentially defines the histogram intervals of interest. This entire process is illustrated in Fig. 2. For real-valued images, if the embedding is a measurable function , then the composition of ϕ with ρ is also a measurable function, i.e. , in which case the real-valued image specifies a probability measure in the same way.
To summarize, an ultrasound image ϕ maps a FOV Ω into a sample space A. This image naturally defines a probability measure μ and histogram f, measured as the fraction of Ω that gets mapped into the corresponding image values.
D. Lesion Detectability as a Distance Between Measures
Consider now two regions of interest (ROIs) Ωf, Ωg ⊂ Ω corresponding to a lesion and background, as illustrated in Fig. 3a. For an image ϕ : (Ω, Σ) → (A, ΣA), we can restrict ϕ to Ωf and Ωg and form the corresponding probability measures μ and ν with histograms f and g, respectively (Fig. 3b). We further require that both μ and ν are measures on the same measurable space (A, ΣA) (e.g., both ROIs share a common set of histogram intervals). Then μ and ν constitute two points in the space of all probability measures on (A, ΣA), and LD implies the notion of a distance between μ and ν, where an easily detectable lesion corresponds to a larger distance and an undetectable lesion to a smaller distance.
Fig. 3.
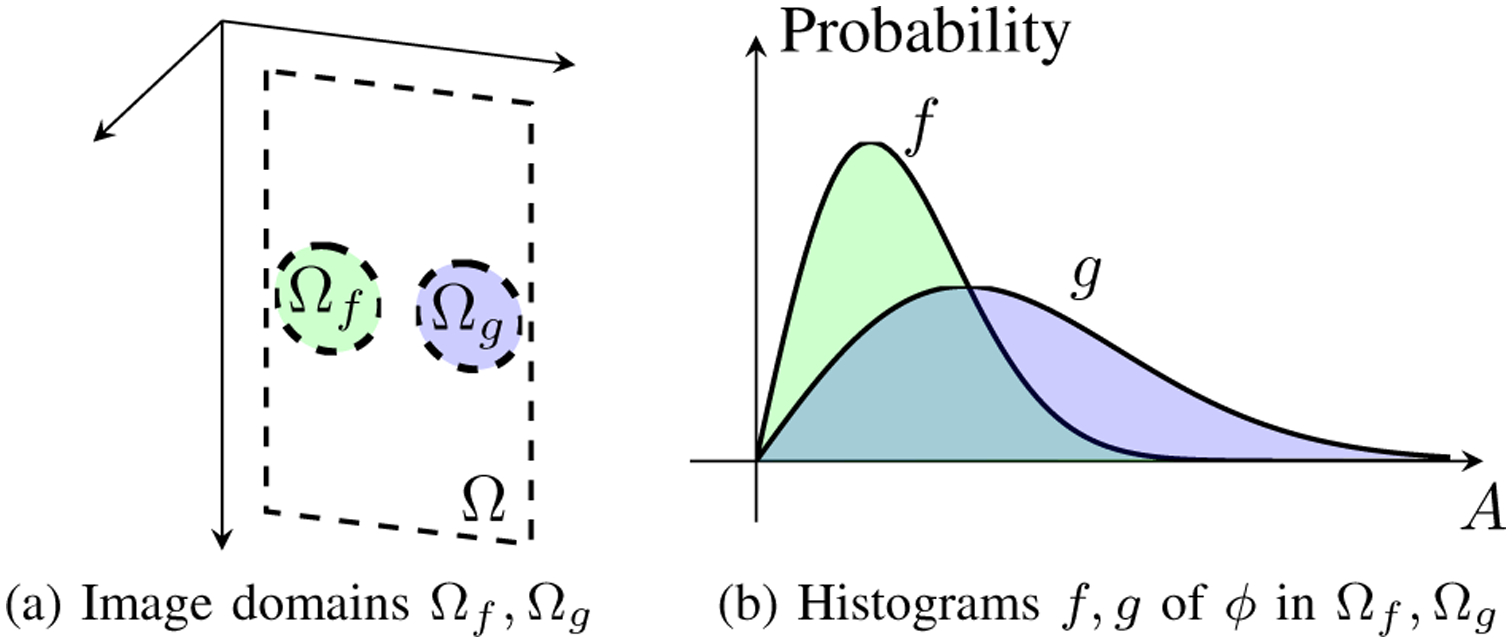
The lesion detectability problem is illustrated. (a) Given the image function ϕ from Fig. 1b, we select two image domains Ωf and Ωg (e.g. regions of interest). (b) The histograms of ϕ in Ωf and Ωg are obtained as f and g, respectively. Lesion detectability can be measured as the distance between the probability measures specified by f and g.
Traditional LD can be expressed in this framework, given some embedding . The contrast ratio (CR) between the two ROIs is defined as
| (15) |
where Eμ[ρ(a)] is the expected value of ρ(a) over μ. Observe that the expected value only makes sense in the context of a real-valued embedding. The CR is the ratio between the first moments of ρ(a) with respect to μ and ν. Similarly, CNR takes the difference of first moments normalized by the second centered moments of ρ(a):
| (16) |
These expectations are taken over A, and are equivalent to the more classical expectation over Ωf and Ωg.
Neither CR nor CNR are true “metrics” in the geometric sense because zero distance does not imply μ = ν and CNR does not satisfy the triangle inequality. Furthermore, CR and CNR depend only on the first and second moments and do not capture higher-order statistics such as skewness or kurtosis. Perhaps most importantly, CR and CNR depend explicitly on . Consequently, neither CR nor CNR are invariant under dynamic range transformations, as demonstrated by Rindal et al. [8]. We expand upon this point in Sec. IV-D.
E. Generalized CNR is the Total Variation Distance
Let μ and ν denote two probability measures on (A, ΣA), and let f = dμ/dλ and g = dν/dλ denote their respective densities. The gCNR [15] is defined as
| (17) |
The total variation distance of μ and ν is defined as [24]:
| (18) |
| (19) |
where (19) is a maximum over all functions h : A → [−1, 1]. In words, the total variation distance describes the maximum difference in the values that μ and ν can give to the same event S, for all possible S ∈ ΣA.
Theorem 1.
The gCNR is the total variation distance.
Proof.
The total variation distance can be rewritten as
| (20) |
| (21) |
where (20) is obtained by replacing dμ = f dλ and dν = g dλ in (19), and where we observe that the absolute value of the integral in (20) is maximized by a function h(a) defined as ±1 depending on the sign of f(a)−g(a), which is equivalent to bringing the absolute value inside of the integral.
The gCNR can also be rewritten. Observe that the pointwise minimum of two functions is
| (22) |
Therefore, the gCNR is
| (23) |
| (24) |
where we see in (23) that because μ and ν are probability measures. Therefore, gCNR = dTV. □
F. Total Variation Distance and the Ideal Observer
The original derivation of gCNR [15] identified a statistical relationship to the minimum probability of error Pmin for the ideal observer, defined as a decision boundary based on an optimal threshold ρ(a) = ϵ0 (see Fig. 2 and Eq. (13) in [15]). As noted by the authors, this derivation only applies to the case where densities f and g intersect at a single point, and would require multiple thresholds to extend the derivation to the more general case of multimodal f and g (or more precisely, to when f and g may intersect multiple times).
Here, we provide a formal proof to complete the derivation by restating a well-known theorem from measure theory [25]. The proof replaces sample-space thresholds (i.e. along the horizontal axis A in Fig. 3b) with probability-based thresholds (i.e. along the vertical axis in Fig. 3b), analogous to the difference between a Riemann integral and a Lebesgue integral. The proof further dispenses of the embedding ρ of A in , working directly with the abstract A.
Let μ and ν denote probability measures on (A, ΣA) for a positive and negative ground truth (i.e. lesion and background) and let f and g denote their densities with respect to reference measure λ, respectively. Let ψ : A → [0, 1] denote a detection algorithm, where a positive decision by the algorithm is denoted ψ(x) = 1. The probability of error by ψ is the sum of the false positive and false negative probabilities.
Theorem 2.
For all possible detectors ψ, the infimum (i.e. greatest lower bound) on the probability of error is 1 − dTV:
| (25) |
| (26) |
Proof.
(Adapted from [25].) Rewrite (25) using f, g, and dλ:
| (27) |
| (28) |
The optimal ψ that minimizes the integral in (28) is
| (29) |
This is equivalent to restricting A to the subset S where f > g:
| (30) |
Denoting the complement of S as Sc ≡ A \ S, the integral over all of A can be decomposed as the sum over S and Sc:
| (31) |
Furthermore, note that because μ and ν are probability measures, i.e. . Therefore,
| (32) |
Next, observe that the definition of the absolute value implies
| (33) |
i.e., the integral of f−g over S (where f > g) plus the integral of g − f over Sc (where f ≤ g).
We can use (32) and (33) together to show that
| (34) |
Finally, combining (30) and (34), we have
| (35) |
| (36) |
completing the proof. □
Therefore, dTV = 1 − Pmin, coinciding with the original interpretation of gCNR [15]. Theorem 2 implicitly handles an arbitrary number of intersections between f and g, extending the derivation to the case of arbitrary probability measures μ and ν, as illustrated in Fig. 4. Additionally, ψ★ defines the ideal observer in the Pmin sense. Observe that this ideal observer makes no assumptions on the distribution of a, unlike prior definitions of the ideal observer that assumed parametric distributions on a [2–7, 26]. Furthermore, ψ★ bases its decision only on the sign of f(a)−g(a), and is entirely independent of A’s embedding in , unlike CR, CNR, and even the ρ(a) = ϵ0 interpretation of gCNR. This decoupling of A from makes dTV invariant under isomorphisms of A, and thus dTV is an excellent metric for comparing LD between imaging methods with different units (i.e., different embeddings of A).
Fig. 4.

The advantages of the measure-theoretic ideal observer are illustrated. (a) The one-intersection case is easily handled by a threshold ρ(a) = ϵ0 [15]. (b) Multiple intersections between f and g require multiple thresholds and a complicated decision rule that depends on ρ. (c) The measure-theoretic perspective extends gCNR to arbitrary intersections of f and g with the simple decision rule f ≥ g, and is entirely independent of the embedding ρ.
G. Other Distances Between Probability Measures
The total variation is one of many well-studied distances on the space of probability measures on (A, ΣA), including integral probability metrics (IPMs) such as the Kolmogorov, Kantorovich (i.e. Wasserstein), and Hellinger metrics, as well as ϕ-divergences such as the Kullback-Leibler divergence (i.e. relative entropy) [24, 27, 28]. We list several examples in Table I. Each of these quantities can be used to quantify LD as the distance between two probability measures. The specific choice of metric depends upon the application and desired statistical properties. Metrics like dTV are excellent choices for qualitative data where distances in A are not physically meaningful, such as grayscale-transformed image data, where the actual pixel values have arbitrary units. By contrast, metrics like the Wasserstein distance may be preferred for quantitative data where the geometry of A is meaningful, such as velocity estimates. (See Sec. IV-D for further discussion.)
Table I.
Distances Between Probability Measures
| Name | Distance Between μ and v |
|---|---|
| Contrast Ratio* | |
| CNR* | |
| Total Variation (gCNR) | |
| Kolmogorov† | |
| Kullback-Leibler‡ | |
| Hellinger | |
| Lp norm | |
| Wasserstein* |
Dependent on embedding ρ;
An asymmetric divergence
F and G are cumulative distribution functions
The present exposition is intentionally abstract to illustrate the wide applicability of this framework. The sample space A can refer to image values of not only DAS B-mode but also to SLSC [12], F-DMAS [13], Power Doppler, Color Doppler, acoustic radiation force impulse (ARFI), shear-wave elastography imaging (SWEI), to vector-valued images like vector flow Doppler and channel data, and even to other medical imaging modalities altogether. As long as the probability measures μ and ν (from ROIs Ωf and Ωg, respectively) are defined on a common measurable space (A, ΣA), LD can be measured as the distance between μ and ν using not only dTV (i.e. gCNR) but also with any of the other distances mentioned above.
IV. Further Considerations and Examples
A. Methods: Ultrasound Simulations
Below, we highlight several key considerations for measure-theoretic LD using simple simulated examples of pulse-echo ultrasound. Using Field II [29, 30], an L12–3v transducer (128 elements, 8 MHz center frequency, 60% fractional bandwidth) was simulated in a full-synthetic aperture configuration with single element transmissions. A speckle phantom of size 10 mm × 3 mm × 10 mm (azimuth × elevation × depth) was centered at the elevation lens focal depth of 20 mm. Speckle was simulated using randomly placed scatterers with random amplitude at a density of 20 scatterers per resolution cell. Cylindrical lesions with a diameter of 3 mm were placed at the focus, and were simulated to have intrinsic contrasts of −20 dB, −12 dB, −6 dB, and 0 dB. A total of 8 speckle realizations were simulated per lesion contrast. Dynamic focusing was applied on transmit and receive.
B. Lesion Detectability with Empirical Densities
The histograms of image pixels within the lesion and background are empirical densities that define empirical probability measures and . These empirical measures are estimates of a true underlying μ and ν. While the goal is to measure d(μ, ν), in practice we can only measure . Therefore, care must be taken to ensure that the distance of empirical measures is an accurate reflection of the true distance [31].
For example, dTV is sensitive to the choice of histogram bins (i.e. σ-algebra Σ). Fig. 5 shows a pathological example where two histograms with zero overlap (Fig. 5a, dTV = 1) can completely overlap under a coarser bin size (Fig. 5b, dTV = 0). Fig. 6 further illustrates how dTV varies as a function of the number of histogram bins for −20 dB, −12 dB, −6 dB, and 0 dB lesions. Although lesions with greater intrinsic contrast have greater detectability as expected, all lesions can be made to have dTV → 0 by using extremely coarse bins and dTV → 1 by using extremely fine bins. Nearly identical plots were observed for lesions with positive contrast (+20 dB, +12 dB, and +6 dB; not pictured). This behavior does not reflect a true change in the underlying LD but rather an artifact due to inadequate sampling.
Fig. 5.
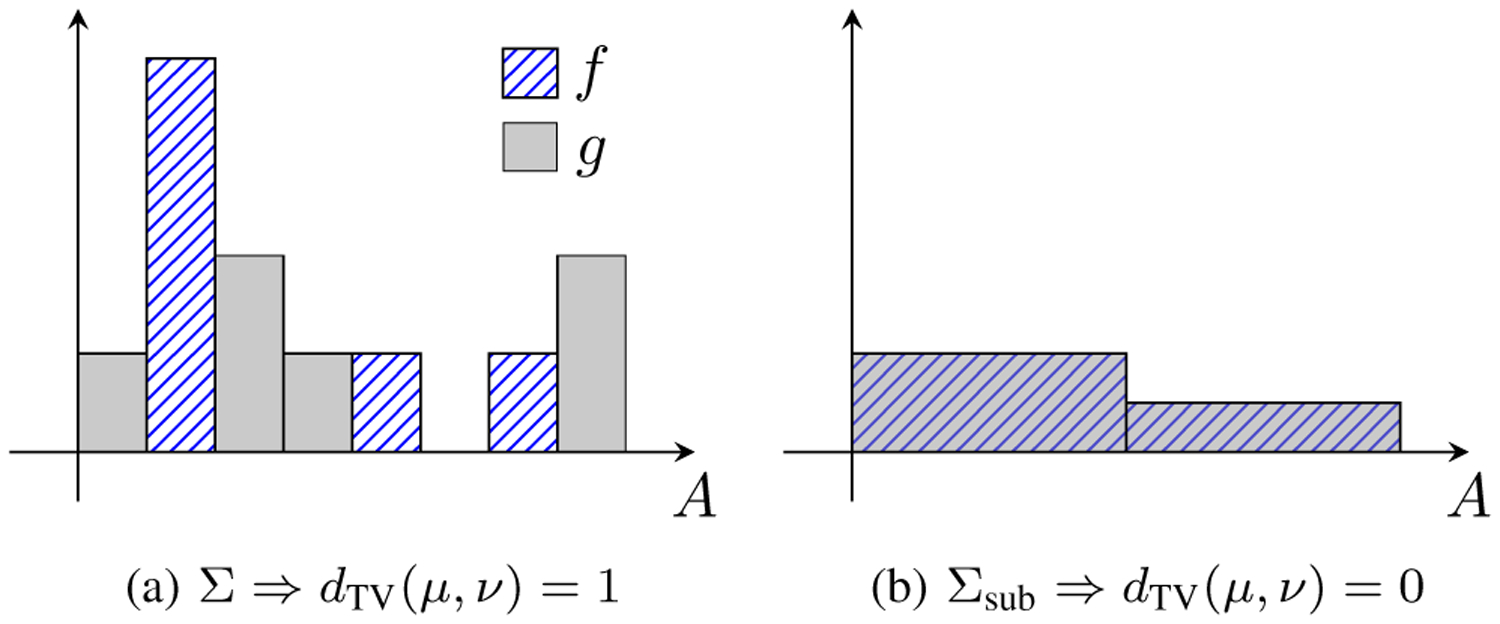
An example of how the choice of histogram bins (i.e. σ-algebra Σ) affects the distance estimate. The histograms f (hatched bars) and g (gray solid bars) show the densities of μ and ν. (a) Measures μ and ν on Σ are maximally distant (dTV = 1). (b) The exact same measures restricted to a coarser sub-σ-algebra Σsub ⊂ Σ are indistinguishable (dTV = 0). The choice of Σ has an undesirably strong influence on histogram distance measures.
Fig. 6.

The total variation distance (gCNR) is plotted as a function of number of bins for 0 dB, −6 dB, −12 dB, and −20 dB lesions. The distance is artificially low when using few coarse bins (left) and grows arbitrarily high when using many fine bins (right). The dashed line shows the number of pixels in the whole image, and the shaded area around each plot shows one standard deviation measured across 8 speckle realizations.
Therefore, histogram bins must be fine enough to capture the detailed behavior of the density, yet coarse enough to avoid bins of artificially low counts due to insufficient samples. A reasonable choice for number of bins depends on the number of available samples; popular rules of thumb include and N1/3. When comparing the LDs of two different imaging methods (e.g., with different underlying units), appropriate histograms bins should be selected for each method separately (e.g., with variable widths for heavily-skewed distributions), preferably with the same number of bins.
C. Lesion Detectability Versus Spatial Resolution
It is important to emphasize that LD is a narrow aspect of overall image quality. Although histogram distances are an excellent measure of LD, histograms ignore the spatial arrangement of the pixel values within each ROI. Consequently, these histogram-based methods ignore important spatially-dependent image quality attributes such as spatial resolution, as first observed by Rindal et al. [32].
Fig. 7 shows a clear example of the interplay between dTV and spatial resolution for a −6 dB lesion. B-mode images were formed using six image reconstruction methods: conventional DAS beamforming, coherence factor (CF)-weighted B-mode [9], SLSC [12, 33], DMAS [13], incoherent spatial compounding (4 subapertures on receive), and the beamforming deep neural network (DNN) from Hyun et al. [14] designed for speckle-reduced echogenicity estimation. The original images from each beamformer (top row) were low-pass filtered using a 2D Gaussian window with standard deviations of roughly , , and λ ≈ 193 um. Surprisingly, we were able to achieve arbitrarily high dTV using low-pass filtering with every tested method. One concerning interpretation of these results is that techniques with worse spatial resolution perform better in LD tasks. Indeed, spatial compounding (which trades resolution for speckle reduction) reported higher dTV than every other method besides the DNN (which aggressively smooths speckle while preserving edges and resulted in the maximum dTV = 1). When LD is the sole image quality metric, one can simply low-pass filter the same image to achieve better LD up to the maximum of dTV = 1. These results agree with the conclusions of Rindal et al. [32] and strongly indicate that LD must be taken in the context of spatial resolution.
Fig. 7.

LD of a −6 dB lesion is compared for several imaging methods (columns) under low-pass filtering with Gaussian windows of increasing standard deviation (rows). With low-pass filtering, the dTV (i.e. gCNR) of every tested method could be made arbitrarily high. These results demonstrate that lesion detectability cannot be considered independently of spatial resolution.
In Fig. 8, we demonstrate how LD can be combined with spatial resolution to draw more powerful conclusions. A simple low-pass filter (LPF) was compared against spatial compounding (SC) beamforming. LPF was applied to a DAS image of a −6 dB lesion, with standard deviations ranging from 0 λ to 0.7 λ. Spatial compounding (SC) was performed by dividing the receive aperture into N subapertures, where N ranged from 1 to 128. For each case, dTV was plotted against the axial and lateral resolution, measured as the speckle autocorrelation FWHM. While there were individual cases where LPF had higher dTV than SC, these plots make clear that for a fixed spatial resolution, SC was strictly superior to LPF in dTV. Spatial resolution thus provides crucial context needed to avoid making unfair comparisons between different imaging methods. However, defining spatial resolution for nonlinear methods remains a difficult and open challenge [34, 35].
Fig. 8.
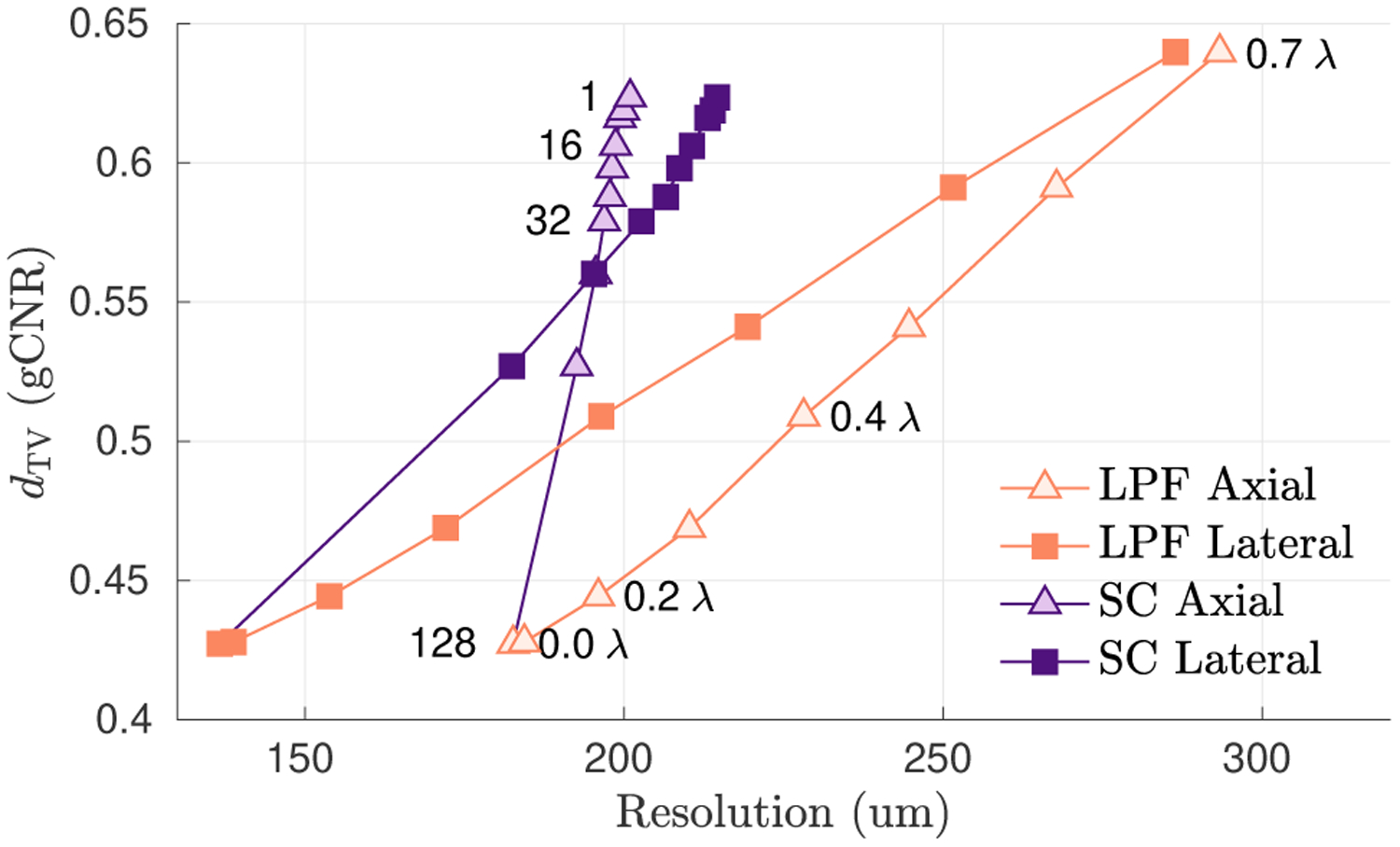
Total variation distance (gCNR) is plotted as a function of axial and lateral resolution for low-pass filtering (LPF) versus spatial compounding (SC), for different filter window sizes and different subaperture sizes, respectively, as annotated on the plots. Both LPF and SC improve dTV at the cost of resolution, but SC achieves better dTV for a given resolution. Lesion detectability is more informative when measured as a function of spatial resolution.
D. Comparing Quantitative Measurements
As described in Sec. III-B, a raw image ϕ and its sample space A are intrinsic entities independent from their extrinsic embedding in via ρ. We have shown that probability measure distances like the total variation, Kolmogorov, Hellinger, and Lp norm can be used to comparing raw images directly without reference to their embeddings. However, images are eventually embedded in for display and analysis. Therefore, it is important to be able to analyze the real-valued representations of images within the context of an embedding.
A variety of embeddings are used in practice. For instance, DAS B-mode images are commonly analyzed (e.g., CR, CNR, SNR) using a linear scale embedding , but displayed using a log-scale embedding . Many of the new beamforming methods being introduced today also use different embeddings. Hverven et al. [36] provide a comprehensive comparison of the distributions of popular ultrasound beamformers, noting that speckle statistics vary significantly. Using the images in Fig. 7 as an example, we can express this variety of embeddings as . Note that although CF and DMAS images are all considered “B-mode” images, in reality, their sample spaces are embedded in in slightly different ways, i.e., .
This use of different embeddings creates a problem. Criteria like CR, CNR, and SNR, measure statistics of the composition ρ ◦ ϕ, and thus the results are affected by changes in both ρ and ϕ. For example, a change in CNR before and after log-compression describes the effect of ρ, not ϕ. These criteria are useful when analyzing quantitative images, where ρ imparts meaningful, numerical information, such as physical units or preserving linearity. However, we encounter a critical lapse in rigor when ρ is considered to be a degree of freedom. Rindal et al. [8] showed that one can raise and lower these quantitative criteria arbitrarily with dynamic range transformations, i.e., when ρ is not held constant. Arguably, most ultrasound beamforming efforts aim to improve the intrinsic content ϕ, not the extrinsic embedding ρ. Therefore, to restore rigorous quantitative evaluations of ϕ, we must first hold ρ constant.
In certain situations, a preferential embedding may exist. For instance, we may be calibrated to a canonical embedding, e.g., lesion contrasts defined with respect to , or we might want to compare methods within the embedding used for a visual observer, e.g., under . Whatever the selected embedding, we are able to isolate the contribution of the underlying image by holding ρ constant, e.g., {ρ ◦ ϕDAS, ρ ◦ ϕCF, ρ ◦ ϕSLSC, …}. (Alternatively, one could hold the image ϕ constant and use different embeddings intentionally as {ρDAS ◦ ϕ, ρCF ◦ ϕ, …} to study the embedding’s impact on image perception, but we leave that discussion to future work.) In these cases, quantitative criteria like CR, CNR, and SNR can be used rigorously to evaluate image quality under the specified embedding.
E. Enforcing a Common Embedding with Histogram Matching
In practice, images are already embedded in when they are obtained. To place all images under a common embedding, we must first undo their respective embeddings and then apply the desired one. For example, given a real-valued image ρ1 ◦ ϕ, we can embed ϕ via ρ2 as
| (37) |
where is a measurable function that takes an image embedded by ρ1 and embeds it by ρ2 instead. The requirement of a measurable function ensures that any probability measures can be properly pushed forward from one embedding to another in a measurable way.
This process is a well-established practice in image processing better known as histogram matching [37], and has been used sporadically for comparing visually different ultrasound images [16, 38–40]. There are numerous criteria one can use to “match” two histograms. We provide a brief survey of methods for ultrasound histogram matching in Bottenus et al. [16], including matching the full FOV vs. ROIs and using affine vs. monotonic transforms .
We illustrate with an example in Fig. 9 comparing DAS and SLSC images. Each image is usually presented under its own respective embedding, e.g., vs. . These images differ significantly in their overall appearance and in the range of values observed for CR, CNR, and SNR. Some of these differences are attributable to differences in the information captured in the underlying images, whereas others are due to differences in their embeddings. Here, we isolate the effect of the images by holding the embedding constant, using for display and for quantitative values, allowing the images to be compared qualitatively and quantitatively in a fair manner. The change in embeddings is achieved using a full FOV monotonic histogram match [16].
Fig. 9.
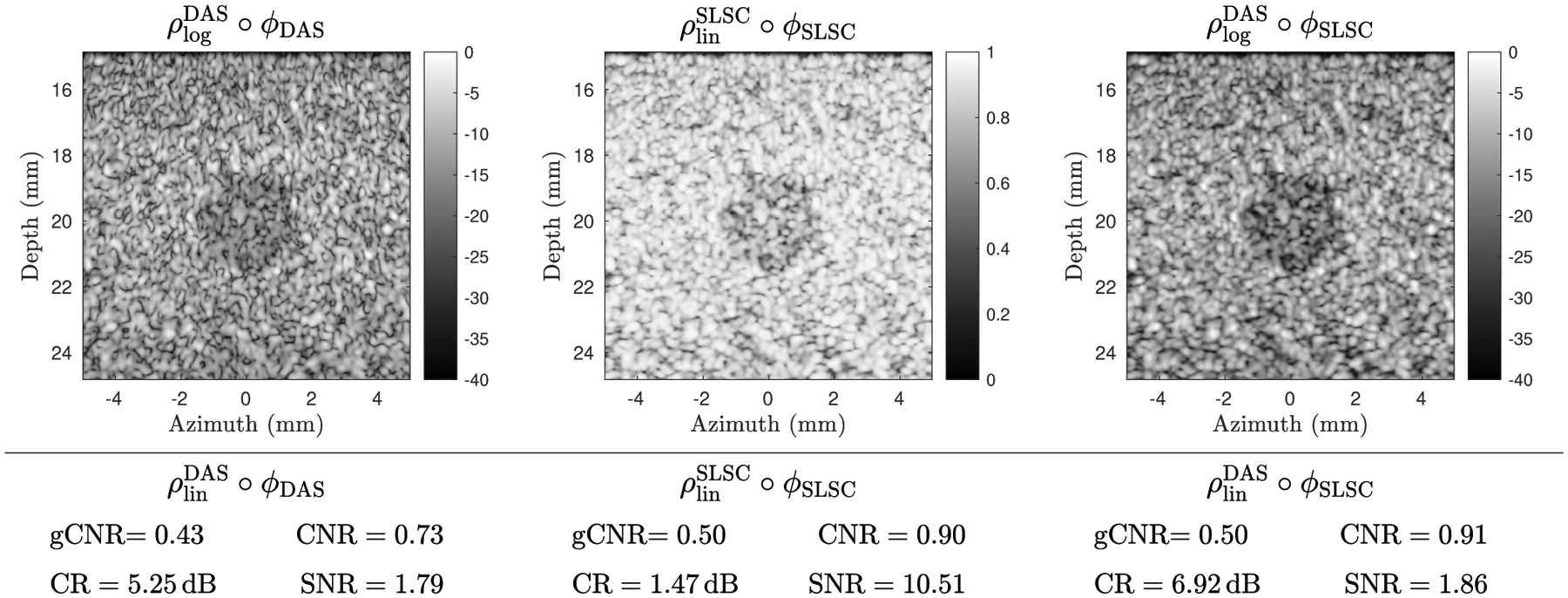
To compare the intrinsic information content of ultrasound images, the embedding should be held constant. (top left) A DAS image ϕDAS is displayed using a log-scale DAS embedding . (top middle) An SLSC image is displayed using a linear-scale SLSC embedding and has a sharply different appearance. (top right) The SLSC image is placed on the same embedding as the log-scale DAS image via histogram matching, resulting in a fairer visual comparison of the underlying information content. (bottom left) The gCNR, CR, CNR, and SNR are computed on ϕDAS using a linear scale DAS embedding . (bottom middle) The same are computed for ϕSLSC using the SLSC embedding, yielding very different CR and SNR values. (bottom right) The same values are computed for ϕSLSC using , allowing quantitative analysis of the underlying image that is not confounded by . Note that gCNR (i.e. dTV) does not depend on the embedding and is thus invariant under histogram matching.
Histogram matching is not always exact, especially in cases where the two embeddings correspond to physically different values (e.g., echogenicities vs. correlation coefficients) that have no natural one-to-one mapping. The validity of any quantitative comparisons of histogram-matched images rests on the validity of the selected histogram matching process. The methods prescribed by Bottenus et al. [16] provide an empirical way to obtain on a per-image basis. It is possible that more meaningful matching can be achieved by using a large database of paired images or even using an analytical equation. Nevertheless, even a first-order attempt to match embeddings should considerably improve the rigor with which new ultrasound methods are compared.
V. Discussion and Conclusion
Traditional LD theory relies on signal and noise models with known PDFs. However, knowledge of the PDF has become an untenable assumption in modern ultrasound beamforming and imaging research, where complex and nonlinear methods are regularly proposed and deployed under non-ideal imaging conditions. We showed in Sec. II that while the CNR has origins in rigorous ideal observer theory, many of its underlying assumptions are violated regularly in current practice. By contrast, we described in Sec. III a distribution-free histogram-based approach to LD without making assumptions on the PDFs. We decomposed real-valued images into their abstract representation ϕ and their embedding as real numbers ρ. Although not discussed here, this decomposition has information-theoretic implications, where the probability measure induced by ϕ can be used to measure quantities like the entropy of the image [35]. Finally, we showed that LD can be formulated as a distance between probability measures of image values from lesion and background ROIs.
Theorem 1 proved that the popular gCNR metric is equal to the well-known total variation distance. Theorem 2 proved that its value is equal to one minus the best achievable error rate by an ideal observer. We further showed that dTV is one among many histogram distance metrics, listed in Table I; just as the L1 and L2 errors give two measures of regression error, each histogram distance presents its own statistical properties and interpretations. Unlike traditional contrast values like CR and CNR, many histogram distances are independent of the sample space embedding in , making them invariant under monotonic transformations and well-suited for comparing information content between images that have undergone different dynamic range transformations, or that have different underlying units.
The measure-theoretic approach has several potential pitfalls. In general, distribution-free approaches sacrifice some statistical power for broader applicability. We consider this trade off necessary given the breadth of current ultrasound research. Additionally, we illustrated in Sec. IV-B how histogram-based LD is affected by the histogram estimation process. Similar to how the CNR approximates classical detection performance in the limit of N → ∞, empirical histogram distances are approximations of the true underlying distance that depend on the quality of the histograms. The histogram bins must be fine enough to capture the important shapes of the distributions but coarse enough that the given number of samples can sufficiently characterize the distribution.
We also showed in Sec. IV-C that LD describes a narrow aspect of image quality. Histogram distances discard information about the spatial arrangement of image values and hence must be presented in the context of spatial resolution. Fig. 7 showed that a simple low-pass filter sharply increased dTV for every tested beamformer, at the cost of resolution. Fig. 8 gave a basic example of how presenting dTV as a function of spatial resolution provided important context for interpreting imaging performance. However, there is a current lack of consensus on an appropriate definition of spatial resolution for nonlinear imaging methods. The rigorous development of complementary image quality metrics should be an emphasis of future work [35].
Finally, we utilized the measure-theoretic framework in Sec. IV-D to illustrate why quantitative values like CR, CNR, and SNR cannot be compared across different imaging methods unless they share the same embedding. Quantitative values are explicitly defined with respect to a particular embedding. However, modern beamforming techniques introduce changes to both the underlying image and its embedding. When the embedding is unconstrained, one can arbitrarily improve the quantitative values without qualitatively changing the image [8]. The images must thus be embedded in using a common embedding to enable rigorous cross-method comparisons. We proposed to resolve this issue via histogram matching [16], a method that specifies a new embedding for an image, allowing direct comparisons of CR, CNR, SNR, and beyond.
Through these derivations and examples, we have found that framing LD as a distance between probability measures sheds light on existing pitfalls and provides a powerful perspective to guide new developments in ultrasound imaging research.
Acknowledgment
The authors would like to thank Brett Byram, Marko Jakovljevic, and Leo You Li for insightful conversations on related topics regarding image quality metrics, as well as the anonymous referees for their helpful suggestions.
This research was supported in part by the Human Placenta Project, in part by the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the National Institutes of Health under Award R01HD086252, and in part by the National Institute of Biomedical Imaging and Bioengineering under Grants R01-EB013361, R01-EB027100, and K99-EB032230.
Biographies

Dongwoon Hyun (Member, IEEE) received the B.S.E. and Ph.D. degrees in biomedical engineering from Duke University, Durham, NC, USA, in 2010 and 2017, respectively. He is currently an Instructor in the Department of Radiology, Stanford University, Stanford, CA, USA. His research interests include ultrasound beamforming and image reconstruction with artificial intelligence, ultrasound molecular imaging, real-time software beamforming, and the measurement of image quality.

Gene B. Kim received the B.A. degree in mathematics from Rutgers University, NJ, USA in 2008, the M.A. degree in mathematics from the University of California Los Angeles, CA, USA in 2011, and the Ph.D. degree in mathematics from the University of Southern California, CA, USA in 2018. He is currently a Lecturer in the Department of Mathematics at Stanford University, Stanford, CA, USA. His research interests lie in analytic and probabilistic combinatorics.

Nick Bottenus (Member, IEEE) received the B.S.E. degree in biomedical engineering and electrical and computer engineering and the Ph.D. degree in biomedical engineering from Duke University, Durham, NC, USA, in 2011 and 2017, respectively. From 2017–2019 he was a research scientist at Duke University. He is currently an Assistant Professor in the department of Mechanical Engineering at the University of Colorado Boulder. His research interests include developing methods for performing large aperture ultrasound imaging and improving image quality through beamforming.

Jeremy J. Dahl (M’11) received the B.S. degree in electrical engineering from the University of Cincinnati (Cincinnati, OH, USA) in 1999, and the Ph.D. degree in biomedical engineering from Duke University (Durham, NC, USA) in 2004. He is currently an Associate Professor with the Department of Radiology at Stanford University, Stanford, CA, USA. His current research interests include beamforming, coherence and noise in ultrasonic imaging, speed of sound estimation, and phase aberration correction.
Contributor Information
Dongwoon Hyun, Department of Radiology, Stanford University, Stanford, CA, USA..
Gene B. Kim, Department of Mathematics, Stanford University, Stanford, CA, USA.
Nick Bottenus, Department of Mechanical Engineering, University of Colorado Boulder, Boulder CO, USA..
Jeremy J. Dahl, Department of Radiology, Stanford University, Stanford, CA, USA..
References
- [1].Kay SM, Fundamentals of statistical signal processing: detection theory. Prentice Hall PTR, 1998. [Google Scholar]
- [2].Smith SW, Wagner RF, Sandrik JM, and Lopez H, “Low contrast detectability and contrast/detail analysis in medical ultrasound,” IEEE Trans. Sonics Ultrason, vol. 30, no. 3, pp. 164–173, 1983. [Google Scholar]
- [3].Zemp RJ, Parry MD, Abbey CK, and Insana MF, “Detection performance theory for ultrasound imaging systems,” IEEE Trans. Med. Imag, vol. 24, no. 3, pp. 300–310, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Abbey CK, Zemp RJ, Liu J, Lindfors KK, and Insana MF, “Observer efficiency in discrimination tasks simulating malignant and benign breast lesions imaged with ultrasound,” IEEE Trans. Med. Imag, vol. 25, no. 2, pp. 198–209, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Abbey CK, Nguyen NQ, and Insana MF, “Optimal beamforming in ultrasound using the ideal observer,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 57, no. 8, pp. 1782–1796, 2010. [DOI] [PubMed] [Google Scholar]
- [6].Nguyen NQ, Prager RW, and Insana MF, “A task-based analytical framework for ultrasonic beamformer comparison,” The Journal of the Acoustical Society of America, vol. 140, no. 2, pp. 1048–1059, 2016. [DOI] [PubMed] [Google Scholar]
- [7].——, “Improvements to ultrasonic beamformer design and implementation derived from the task-based analytical framework,” The Journal of the Acoustical Society of America, vol. 141, no. 6, pp. 4427–4437, 2017. [DOI] [PubMed] [Google Scholar]
- [8].Rindal OMH, Austeng A, Fatemi A, and Rodriguez-Molares A, “The effect of dynamic range alterations in the estimation of contrast,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 66, no. 7, pp. 1198–1208, 2019. [DOI] [PubMed] [Google Scholar]
- [9].Mallart R and Fink M, “Adaptive focusing in scattering media through sound-speed inhomogeneities: The van cittert zernike approach and focusing criterion,” The Journal of the Acoustical Society of America, vol. 96, no. 6, pp. 3721–3732, 1994. [Google Scholar]
- [10].Li P-C and Li M-L, “Adaptive imaging using the generalized coherence factor,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 50, no. 2, pp. 128–141, 2003. [DOI] [PubMed] [Google Scholar]
- [11].Camacho J, Parrilla M, and Fritsch C, “Phase coherence imaging,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 56, no. 5, pp. 958–974, 2009. [DOI] [PubMed] [Google Scholar]
- [12].Lediju MA, Trahey GE, Byram BC, and Dahl JJ, “Short-lag spatial coherence of backscattered echoes: Imaging characteristics,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 58, no. 7, pp. 1377–1388, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Matrone G, Savoia AS, Caliano G, and Magenes G, “The delay multiply and sum beamforming algorithm in ultrasound b-mode medical imaging,” IEEE Trans. Med. Imag, vol. 34, no. 4, pp. 940–949, 2014. [DOI] [PubMed] [Google Scholar]
- [14].Hyun D, Brickson LL, Looby KT, and Dahl JJ, “Beamforming and speckle reduction using neural networks,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 66, no. 5, pp. 898–910, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Rodriguez-Molares A, Rindal OMH, D’hooge J, et al. , “The generalized contrast-to-noise ratio: A formal definition for lesion detectability,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Bottenus N, Byram B, and Hyun D, “Histogram matching for visual ultrasound image comparison.,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Neyman J and Pearson ES, “Ix. on the problem of the most efficient tests of statistical hypotheses,” Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, vol. 231, no. 694–706, pp. 289–337, 1933. [Google Scholar]
- [18].Goodman JW, Speckle phenomena in optics: theory and applications. Roberts & Company, 2007. [Google Scholar]
- [19].Nguyen NQ, Abbey C, and Insana MF, “Objective assessment of sonographic quality i: Task information,” IEEE Trans. Med. Imag, vol. 32, no. 4, pp. 683–690, 2012. [DOI] [PubMed] [Google Scholar]
- [20].Patterson M and Foster F, “The improvement and quantitative assessment of b-mode images produced by an annular array/cone hybrid,” Ultrasonic Imaging, vol. 5, no. 3, pp. 195–213, 1983. [DOI] [PubMed] [Google Scholar]
- [21].Nguyen NQ, Abbey CK, and Insana MF, “Objective assessment of sonographic: Quality ii acquisition information spectrum,” IEEE Trans. Med. Imag, vol. 32, no. 4, pp. 691–698, 2012. [DOI] [PubMed] [Google Scholar]
- [22].Folland GB, Real analysis: modern techniques and their applications. John Wiley & Sons, 1999, vol. 40. [Google Scholar]
- [23].Bogachev VI, Measure theory. Springer Science & Business Media, 2007, vol. 1. [Google Scholar]
- [24].Tsybakov AB, Introduction to nonparametric estimation. Springer Science & Business Media, 2008. [Google Scholar]
- [25].Lehmann EL and Romano JP, Testing statistical hypotheses. Springer Science & Business Media, 2006. [Google Scholar]
- [26].Insana MF and Hall TJ, “Visual detection efficiency in ultrasonic imaging: A framework for objective assessment of image quality,” The Journal of the Acoustical Society of America, vol. 95, no. 4, pp. 2081–2090, 1994. [Google Scholar]
- [27].Gibbs AL and Su FE, “On choosing and bounding probability metrics,” International Statistical Review, vol. 70, no. 3, pp. 419–435, 2002. [Google Scholar]
- [28].Sriperumbudur BK, Fukumizu K, Gretton A, Schölkopf B, Lanckriet GR, et al. , “On the empirical estimation of integral probability metrics,” Electronic Journal of Statistics, vol. 6, pp. 1550–1599, 2012. [Google Scholar]
- [29].Jensen JA and Svendsen NB, “Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 39, no. 2, pp. 262–267, 1992. [DOI] [PubMed] [Google Scholar]
- [30].Jensen JA, “Field: A Program for Simulating Ultrasound Systems,” Medical & Biological Engineering & Computing, vol. 34, no. 1, pp. 351–353, 1996.8945858 [Google Scholar]
- [31].Parzen E, “On estimation of a probability density function and mode,” The annals of mathematical statistics, vol. 33, no. 3, pp. 1065–1076, 1962. [Google Scholar]
- [32].Rindal OMH, Rodriguez-Molares A, Måsøy S-E, and Bjåstad TG, “Improved lesion detection using nonlocal means post-processing,” in 2019 IEEE International Ultrasonics Symposium (IUS), IEEE, 2019, pp. 1013–1016. [Google Scholar]
- [33].Hyun D, Crowley ALC, and Dahl JJ, “Efficient strategies for estimating the spatial coherence of backscatter,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 64, no. 3, pp. 500–513, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Rindal OMH, Austeng A, and Rodriguez-Molares A, “Resolution measured as separability compared to full width half maximum for adaptive beamformers,” in 2020 IEEE International Ultrasonics Symposium (IUS), IEEE, 2020, pp. 1–4. [Google Scholar]
- [35].Hyun D, “An information-theoretic spatial resolution criterion for qualitative images,” in 2021 IEEE International Ultrasonics Symposium (IUS), IEEE, 2021, pp. 1–4. [Google Scholar]
- [36].Hverven SM, Rindal OMH, Rodriguez-Molares A, and Austeng A, “The influence of speckle statistics on contrast metrics in ultrasound imaging,” in 2017 IEEE International Ultrasonics Symposium (IUS), 2017, pp. 1–4. [Google Scholar]
- [37].Gonzalez RC and Woods RE, Digital Image Processing (3rd Edition). USA: Prentice-Hall, Inc., 2006. [Google Scholar]
- [38].Bottenus N and Üstüner KF, “Acoustic reciprocity of spatial coherence in ultrasound imaging,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 62, no. 5, pp. 852–861, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Lee Y, Kang J, and Yoo Y, “Automatic dynamic range adjustment for ultrasound b-mode imaging,” Ultrasonics, vol. 56, pp. 435–443, 2015. [DOI] [PubMed] [Google Scholar]
- [40].Fatemi A, Måsøy S-E, and Rodriguez-Molares A, “Row–column-based coherence imaging using a 2-d array transducer: A row-based implementation,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 67, no. 11, pp. 2303–2311, 2020. [DOI] [PubMed] [Google Scholar]


