Patient-specific computational fluid dynamics analysis of transcatheter aortic root replacement with chimney coronary grafts

Abstract

OBJECTIVES

Transcatheter aortic root repair (TARR) consists of the simultaneous endovascular replacement of the aortic valve, the root and the proximal ascending aorta. The aim of the study is to set-up a computational model of TARR to explore the impact of the endovascular procedure on the coronary circulation supported by chimney grafts.

METHODS

Computed tomography of a patient with dilated ascending aorta was segmented to obtain a 3-dimensional representation of the proximal thoracic aorta, including aortic root and supra-aortic branches. Computed assisted design tools were used to modify the geometry to create the post-procedural TARR configuration featuring the main aortic endograft integrated with 2 chimney grafts for coronary circulation. Computational Fluid Dynamics simulations were run in both pre- and post-procedural configurations using a pulsatile inflow and lumped parameter models at the outflows to simulate peripheral aortic and coronary circulation. Differences in coronary flow and pressure along the cardiac cycle were evaluated.

RESULTS

After the virtual implant of the TARR device with coronary grafts, the flow became more organized and less recirculation was seen in the ascending aorta. Coronary perfusion was guaranteed with negligible flow differences between pre- and post-procedural configurations. However, despite being well perfused by chimney grafts, the procedure induces an increase of the pressure drop between the coronary ostia and the ascending aorta of 8 mmHg.

CONCLUSIONS

The proposed numerical simulations, in the specific case under investigation, suggest that the TARR technique maintains coronary perfusion through the chimney grafts. This study calls for experimental validation and further analyses of the impact of TARR on cardiac afterload, decrease of aortic compliance and local pressure drop induced by the coronary chimney grafts.

INTRODUCTION

Transcatheter aortic valve replacement (TAVR) is a consolidated alternative to surgical aortic valve replacement for high-risk patients, valve-in-valve procedures and, recently, also for low-risk patients [1], while transcatheter endovascular arch replacement, supported by the development of new devices featuring chimneys, branches, etc. [2], is performed in very few cases, mostly when surgical treatment is highly risky [3].

In many cases, such as the presence of a degenerated bicuspid aortic valve, there is a need of replacing both the native valve and the ascending aorta, which is often dilated increasing the risk of rupture or dissection [4]. As stated earlier, both alternatives are available as separate endovascular treatments, but a transcatheter device that includes a combined replacement of the aortic valve, the root and the ascending aorta has not yet been proposed. Some of the challenges of such a procedure are the high pulsatility of the ascending portion of the aorta, its angulated anatomy and the need to keep the coronary perfusion.

Recent studies showed a high level of success of ‘off-label’ use of endovascular devices in the treatment of ascending aortic diseases [5]. However, the outcome of endovascular repair can also be evaluated through virtual simulation techniques. As an example, Romarowski et al. [6] proved that tailor-made devices performed much better than off-the-shelf endoprosthesis that were adapted for their use in the ascending aorta. However, these studies remained limited to the repair of the ascending aorta and did not include the replacement of the aortic root. To the best of our knowledge, only 2 studies have analysed the simultaneous endovascular repair of ascending aorta and aortic root. Gaia et al. [7] described the endovascular management of a patient that was considered inoperable after conventional aortic valve replacement. A customized stent attached to a transcatheter valve was deployed, thus being the first-in-human case of what they called, the ‘Endo-Bentall procedure’. The patient did not have any sign of myocardial infarction at a 4-month follow-up. Previous work of our group presented a preliminary test of a transcatheter aortic root repair (TARR) [8] using computed tomography (CT) scan-derived 3-dimensional (3D) printed root model [9] (Fig. 1). In particular, the authors proposed the feasibility of using chimney grafts as a way to perfuse the coronary ostia in a very simplified haemodynamic model. Given such encouraging outcomes, the goal of the present study is to set-up a proof-of-concept computational model of TARR to explore the impact of the endovascular procedure on the coronary circulation. To this aim, a patient-specific model of an aneurysmatic ascending aorta including the coronary ostia is derived from CT angiography. Computational fluid dynamics (CFD) simulation of the preprocedural cardiovascular model is performed to define a reference for the evaluation of post-procedural configuration obtained by the simulation of the TARR procedure.

Figure 1:

In vitro deployment of a device combining an ascending aorta endograft with a temporary valve and 2 coronary chimney grafts. (A) Sketch; (B, C) deployment within a 3-dimensional printed model (patient-specific aortic root).

MATERIALS AND METHODS

Medical imaging analysis and processing

CT images of a patient with dilated aortic root and ascending aorta were used for this study and informed consent for use of anonymized data was provided. A patient-specific 3D model of the preprocedural ascending aorta was obtained by image segmentation of contrast-enhanced CT scan. The model included the aortic root, coronary ostia, aortic arch and epiaortic branches (Fig. 2A). The segmentation was performed using the open-source software ITK-Snap (http://www.itksnap.org).

Figure 2:

Three-dimensional model of the aortic root, ascending aorta and aortic arch. (A) Pre-procedural model as derived from medical image segmentation; (B) CAD elaboration to insert coronary chimney grafts; (C) CAD elaboration to insert aortic endograft; (D) final CAD post-procedural transcatheter aortic root repair model including the main endograft and the chimney grafts; (E) computational grid (mesh) for computational fluid dynamics analysis, the image depicts the mesh in the zone of the model highlighted in D). CAD: computer-aided design.

TARR procedure and post-procedural aortic model

The proposed TARR procedure described in our previous work [8] implies the transcatheter deployment of one main endograft within the aortic root (28 mm diameter) and two 6-mm-diameter 10-cm-long coronary chimney grafts. The main graft features a temporary non-biologic aortic valve at its proximal side that impedes ventricular dilatation after the deployment. After completion of the TARR procedure, a commercially available low-profile TAVR valve is inserted in the main graft at the level of the temporary aortic valve.

Given these indications, we have modified the preprocedural reconstruction of the vascular model to include these devices using computer-aided design (CAD) software (Autodesk Inventor Professional 2017). For this study, the temporary aortic valve was not included in the computational model.

The model of the root endograft was drawn on the base of the aortic centreline extracted by the VMTK library (http://www.vmtk.org). In particular, the aortic centreline was used to mimic the longitudinal axis of the endograft, while various planes normal to the centreline were used in the lofting to define the cross-sectional profile of the endograft. The first of these planes was placed at the level of the left ventricular outflow tract. The downstream planes were placed following the orientation imposed by the aortic centreline up to the end of the ascending aorta, immediately before the ostium of the brachiocephalic trunk. Using section lofting, the cylindrical solid model of the root endograft with a thickness of 1 mm was created; this model is tapered with a proximal diameter of 22 mm at the left ventricular outflow tract and a distal diameter of 36 mm at the end of the ascending aorta.

Similarly, the models of the coronary chimney grafts were drawn: (i) the intra-coronary part is sketched by inserting a flow extension (15 mm length) of the native coronary ostia to let the flow develop and avoid boundary effects from the numerical simulation [10] (Fig. 2B) and (ii) the path of each graft inside the aortic root and ascending aorta were designed based on the visual inspection of the in vitro model proposed in Ferrari et al. [8] (Fig. 2C). The 3D preoperative model of the aorta, the CAD model of the root endograft and the 2 models of the coronary chimney grafts were merged using CAD Boolean operations with Netfabb software (Autodesk, San Rafael, CA, USA) (Fig. 2D); the resulting model describes the luminal surface of the post-TARR aorta and it was used to create a computational grid suitable for CFD as shown in Fig. 2E.

Computational fluid dynamics analysis

CFD simulations were performed in both pre- and post-procedural geometries using the solver SimVascular [11] in a computing node with 2 Intel Xeon Gold 6148 processors and 192 GB di RAM totalizing 40 cores. Meshes were also created in SimVascular with an element length based on the local radius. As a result, the preoperative mesh featured 1.8M elements whereas the post-procedural mesh had 2.7M elements accounting for the radius-based meshing technique. Blood flow was considered laminar, homogeneous and Newtonian with a density of 1060 kg/m³ and a viscosity of 0.0035 Pa·s. Given the lack of patient-specific boundary flow conditions, we used a pulsatile inflow wave extracted from Xu et al. [12] at the origin of the ascending aorta featuring a duration of 1 s each heart cycle discretized into 1000 time-steps. Such a pulsatile blood flow, with a peak in systole and almost no flow in diastole, imitates the inflow behaviour right after the aortic valve.

The goal of our study requires particular attention to the modelling of the coronary circulation. For this reason, we have adopted a 3D-0D modelling approach (Fig. 3) where the 3-dimensional domain of the aorta is coupled with 0D models accounting for the peripheral circulation at the outlets of the supra-aortic branches, the descending aorta, and the coronary circulation. In the supra-aortic vessels and the descending aortic outlet, 3-element Windkessel lumped circuits were attached to mimic the downstream vasculature [12]. In the coronary outlets, a lumped parameter model was used following the work by Sankaran et al. [13]. The details of parameter estimation are described in Supplementary Material.

Figure 3:

Left: computational fluid dynamics domain including a flow extension at the ascending aorta and the transient inflow wave set in the simulations taken from Xu et al. [13]. Centre: lumped parameter model implementation of the pre-procedural geometry in the MATLAB toolbox Simulink. Right: electric circuit inside each block of the lumped parameter model shown in the middle. AA: ascending aorta; BCT: brachiocephalic trunk; DAo: descending aorta; LCA: left coronary artery; LCCA: left common carotid artery; LSA: left subclavian artery; RCA: right coronary artery.

Post-processing

Five instants of the last cardiac cycle were considered from the inflow curve: the beginning of the systole (t = 0s), maximum systolic acceleration (t = 0.06s), systolic peak (t = 0.18s), maximum systolic deceleration (t = 0.32s) and beginning of diastole (t = 0.4s). The velocity field along the aorta was analysed by inspecting the streamlines using Paraview 5.8.0 (Kitware Inc., Clifton Park, NY, rates at all the outlets were compared between the pre- and post-procedural simulations, as well as coronary flow, split to quantify the differences caused by the intervention. Qualitative and quantitative analyses of the bulk flow were treated in both pre- and post-procedural configuration. We expect that the TARR procedure to maintain the same bulk flow features of the preprocedural configuration. Qualitatively, we compute the local normalized helicity (LNH), which corresponds to the cosine of the angle formed between the vorticity vector and the velocity vector. It is a measure of the alignment/misalignment of the local velocity and vorticity vectors. It ranges from −1 to 1 and its sign is useful to understand the direction of helical structures. Quantitatively, we compute the h₂ helicity index, which is a bulk flow descriptor given by time-averaging the absolute value of the helicity [14]. The h₂ helicity index denotes the helicity intensity in the fluid domain. Recalling that the helicity is defined by the spatial integral of the scalar product of the velocity and vorticity, the h₂ index assumes major values in the fluid domain in which velocity and vorticity vectors are aligned. The h₂ index was computed by integration over 3 volumetric fluid domains, i.e. the segment of the right coronary artery, the segment of left coronary artery (LCA) and the whole fluid domain.

Finally, as an indicator of the influence of the chimney grafts in the coronary blood supply, we estimated the pressure drop from the origin of the aorta (i.e. aortic annulus) to the distal section of the coronaries.

RESULTS

Figure 4 illustrates the streamlines along the aorta during the selected 5 instants in both preprocedural and post-procedural TARR configuration. The major difference after the intervention is seen during t1 and t2 in the ascending portion of the aorta. Flow becomes more organized and less recirculation is seen at the point where the aneurysm was present.

Figure 4:

Results of computational fluid dynamics simulations. Streamlines of pre- and post-procedural transcatheter aortic root repair configurations along the selected 5 instants of cardiac cycle. The source of the streamlines is located at the aortic annulus.

There is also an acceleration during the systole as compared to the preprocedural geometry that can be attributed to the narrowing in the lumen caused by the new endoprosthesis. Table 1 also reports a jump of 4 mmHg in the ascending aorta pressure after the TARR procedure which can also be a consequence of the presence of the endograft.

Table 1:

Pressure at the selected 5 instants along the cardiac cycles in the AA and coronary outlets together with the pressure jump between points

	t0	t1	t2	t3	t4
Pre-procedural
P (mmHg)
AA	66.95	95.73	117.35	103.38	96.08
RCA	67.36	95.22	117.22	103.33	95.66
LCA	67.01	95.29	117.16	102.96	93.96
ΔP (mmHg)
RCA-AA	−0.42	0.50	0.13	0.06	0.42
LCA-AA	−0.07	0.44	0.18	0.42	2.13
Post-procedural (TARR system simulation)
P (mmHg)
AA	67.10	100.19	114.96	101.83	95.97
RCA	67.05	91.90	116.29	103.76	95.63
LCA	65.32	91.21	115.93	100.94	87.83
ΔP (mmHg)
RCA-AA	0.05	8.29	−1.33	−1.94	0.33
LCA-AA	1.78	8.98	−0.97	0.89	8.13

AA: ascending aorta; LCA: left coronary artery; RCA: right coronary artery; TARR: transcatheter aortic root repair.

Figure 5 depicts the velocity streamlines at t2 and t4 inside the coronary arteries after the procedure. We can observe that there are no recirculation zones at the connection to the body of the main graft. In Fig. 6, the superposition of the flow waves in the supra-aortic vessels as well as the coronaries is shown. Negligible differences are present in the brachiocephalic trunk, left common carotid artery, left subclavian artery and descending aorta, ensuring that the systemic circulation has not been compromised with the implantation of the TARR devices.

Figure 5:

Results of computational fluid dynamics simulations. Streamlines of post-procedural configuration at systolic peak (t2) and early diastole (t4). The source of the streamlines is located at the outflow sections of the RCA and LCA in order to highlight the pattern of the coronary flow LCA: left coronary artery; RCA: right coronary artery.

Figure 6:

Results of computational fluid dynamics simulations. The flow rate curves at the model outlets along the cardiac cycle are reported for pre- and post-procedural transcatheter aortic root repair configurations. BCT: brachiocephalic trunk; DAo: descending aorta; LCA: left coronary artery; LCCA: left common carotid artery; LSA: left subclavian artery; RCA: right coronary artery.

Differences in the output flow in the coronary arteries showed negligible differences as reported in Fig. 6. The inlet aortic flow rate was 5.43 l/min and was kept equal for both pre- and post-procedural TARR simulations. In the preprocedural configuration, the right coronary artery flow rate was 28.93 ml/min (corresponding to the 0.53% of the total aortic inflow) while the LCA flow rate was 136.94 ml/min (which correspond to the 2.52% of the total aortic inflow), totalizing a coronary supply of 3.05% of the aortic inflow. After the virtual TARR procedure, there was a very limited decrease in coronary flow circulation corresponding to RCA flow: 0.53%, LCA flow: 2.45% and a total coronary flow: 2.98% of the aortic inflow.

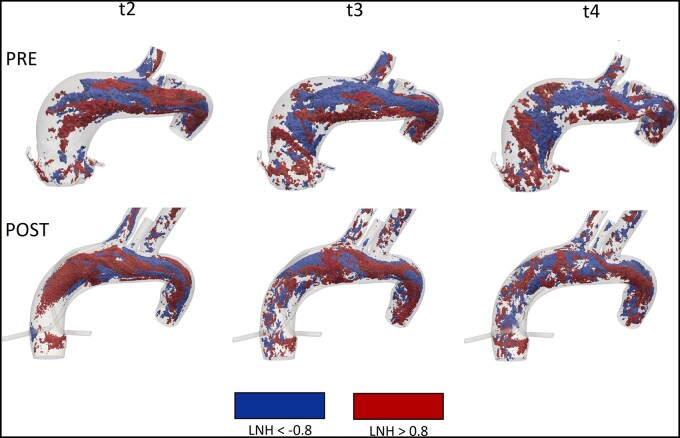
Regarding the bulk flow, Fig. 7 represents helical structures given by considering LNH values with a threshold of ±0.8. The LNH was computed at the systolic peak (t2), at maximum systolic deceleration (t3) and beginning of diastole (t4). The h₂ values computed in the total volume of both the configurations (${\mathrm{h}}_2^{\text{PRE}}$ = 5.1 m/s² and ${\mathrm{h}}_2^{\text{POST}}$ = 7.6 m/s², where ${\mathrm{h}}_2^{\text{PRE}}$ and ${\mathrm{h}}_2^{\text{POST}}$ denote the values of h₂ computed in the pre- and post-procedural configuration, respectively) are in good agreement with the values reported by Morbiducci et al. [14]. Despite the value of h₂ related to the total volume is very similar in both the pre- and post-procedural configurations, significant differences characterize the coronary arteries, in particular the h₂ values related to the LCA (${\mathrm{h}}_2^{\text{PRE},\text{RC}}$ = 1.3 m/s², ${\mathrm{h}}_2^{\text{POST},\text{RC}}$ = 0.052 m/s², ${\mathrm{h}}_2^{\text{PRE},\text{LC}}$ = 24.0 m/s², ${\mathrm{h}}_2^{\text{POST},\text{LC}}$ = 6.8 m/s², where ${\mathrm{h}}_2^{\text{PRE},\text{RC}}$ and ${\mathrm{h}}_2^{\text{POST},\text{RC}}$ denote the values of h₂ computed in the right coronary arteries in the pre- and post-procedural configuration, respectively, and ${\mathrm{h}}_2^{\text{PRE},\text{LC}}$ and ${\mathrm{h}}_2^{\text{POST},\text{LC}}$ are the values of h₂ computed in the left coronary arteries in the pre- and post-procedural configuration, respectively).

Figure 7:

Results of computational fluid dynamics simulations. Isosurfaces of high threshold values of LNH (±0.8) at systolic peak (t2), maximum deceleration (t3) and early diastole (t4), in pre- and post-procedural configurations. LNH: local normalized helicity.

In Table 1 we have reported the differences in pressure values between the coronary ostia (either the native ostia in the preprocedural geometry or the distal section of the graft in the post-procedural TARR model) and the aortic inflow section. The highest difference in the pressure jumps was found during t1 of the post-procedural configuration, where both coronaries had an 8 mmHg difference with the aortic inlet. Conversely, this jump was negligible in the preprocedural model. From Table 1, we can see that this jump was caused by the concomitant increase in the aortic input and a decrease in the coronary outflow.

DISCUSSION

The present study proposes a patient-specific computational fluid dynamic analysis of a new TARR technology, an endovascular procedure consisting of the simultaneous replacement of the aortic valve, the aortic root and the proximal part of the ascending aorta. To the best of our knowledge, this study is the first computational study in this emerging field; indeed, literature only recalls a proof-of-concept experimental test of TARR proposed by Ferrari et al. [8], who used a CT-based 3D-printed root model to deploy the TARR components (endografts). In our previous article, we proved that the deployment of the endografts is feasible and also analysed the coronary flow, although in a very simplistic in vitro setting using water and neglecting coronary circulation and coronary resistances. In the present study, the coronary perfusion is implemented by the coupling of the 3D model of the aortic root, coronary ostia, ascending aorta and supra-aortic branches with a lumped parameter model (0D) of the coronary circulation [15]. The modelling of the coronary flow is of paramount importance for the development of any new TARR technology and we need reliable bench-test models to guarantee interpretable results when tests on coronary perfusion are performed. Our simulation results show that there is a negligible difference between preprocedural and post-procedural coronary perfusion, encouraging further analysis of the proposed TARR procedure towards its clinical implementation. However, at the same time, our results indicate an increase of the pressure drop between the coronary ostia and the aortic inflow section; we can attribute such an increase to the hydraulic resistance induced by the long chimney graft used in the post-procedural TARR configuration, in concomitance with the pressure increase at the aortic inlet, due to the reshaping of the aortic root and ascending aorta determined by the presence of the main endograft. The increase in pressure can be interpreted as a downside of the intervention that has already been described as increasing post-procedural afterload in patients undergoing thoracic endovascular aortic repair [16]. Even though our simulation was performed within a rigid wall model, the native aorta becomes stiffer due to the higher rigidity of the stent graft compared to the native tissue [17]. Recent literature analysing the haemodynamics in chimney grafts associated high pressure drops to mid-term failure of the intervention in both the thoracic and the abdominal aorta [18, 19]. However, being this study he first in its type and without postoperative data of the patient, we cannot conclude whether the pressure jump that was found in the simulations is predictive of the failure of the coronary grafts.

The post-procedural reshaping of the dilated root and dilated ascending aorta produced, in our simulations, a flow that is more organized when compared with the preprocedural one. This result confirms the phenomenon, already reported in patients with an aneurysm in the ascending aorta, where the postoperative configuration features less flow recirculation, which is known to be a factor triggering aneurysmal growth [20].

It is worth noting that our model proposes an idealization of the inlet cross-sectional sections of the chimney grafts, which can be elliptical due to compression induced by the main endograft, as shown in Fig. 1 depicting the in vitro model. Moreover, we are neglecting gutters, which can be present between chimney grafts and the main endograft as long as the circumference of the main endograft is linear [21]. Nevertheless, this issue can be addressed using a pre-shaped main aortic endograft that presents the opposite incisures at the distal side that partially inglobe the chimney coronary grafts. As we mentioned earlier, the ascending aorta is a hostile environment in terms of biomechanics and future studies may require extending the distal part of the endograft to improve fixation. If that would be the case, the analysis of cerebral perfusion should be reconsidered to ensure that there are no deficits.

Regarding the study of helicity, Fig. 7 highlights positive (in red) and negative (in blue) LNH values, corresponding to left-handed and right-handed rotating fluid structures along the flow direction in both the configurations, respectively. Therefore, even if the post-TARR configuration shows more helical structures than the pre-TARR configuration, the rotating flow structure has been maintained. The good agreement of the h₂ values between the 2 configurations, when considering the total volume, denotes that the post-procedural aortic model slightly affects the bulk flow, as we expected it. However, the gap obtained in coronary arteries should be analysed and studied in the next work, in which we will investigate more cases with different sizes and lengths of the grafts. Moreover, to the best of our knowledge, a comparison of the values of h₂ with a preoperative and postoperative configuration in a patient-specific aorta is still missing in literature.

The last point to be mentioned, the model did not present a virtual aortic valve within the proximal portion of the main endograft. However, we believe that the valve does not interfere in the coronary bloodstream during TARR because the coronary inflows are displaced from the Valsalva Sinuses to the distal ascending aorta. Nevertheless, the presence of a temporary or a definitive aortic valve has to be taken into consideration in further simulations, in vitro or in vivo studies.

Limitations

Our results should be interpreted in the context of some limitations. First, the results of our simulations should be validated against an in vitro model to test whether the results are comparable to reality. A further step could be a validation against post-procedural imaging [e.g. phase-contrast magnetic resonance imaging (MRI)] [22] if the TARR procedure with chimney grafts will be executed in animals or a real patient. Furthermore, this study has been conceived as a proof-of-concept to evaluate the feasibility of TARR using computational tools and therefore cannot be extrapolated to a wider population. To this aim, at least a retrospective study using more patients would be required. Secondly, the choice of the configuration of the main body of the prosthesis and the coronary grafts was fixed to follow our previous work [8]. Further work may include variations in the design suited for every single patient as well as different materials to modulate the rigidity of the grafts. This would avoid kinking that may compromise perfusion in the long term.

Thirdly, we assumed that the wall compliance is negligible, thus imposing a rigid wall condition according to Auricchio et al. [3] and Sankaran et al. [13]. In particular, Mendez et al. [23] proved that a stiff aneurysmal wall in the ascending aorta reduces differences in the shear stress predictions between a fluid-structure interaction analysis and a CFD simulation.

In fourth place, a well-known limitation of such retrospective studies is the lack of patient-specific preoperative flow in the aorta to be used as boundary conditions. Having such data (i.e. extracted from PC-MRI) would enrich the simulation set-up and give more reliable results for each patient.

Finally, we are not accounting for long-term cardiac remodelling that can occur after endovascular aortic repair as we are using the same haemodynamic boundary conditions for pre- and post-procedural configuration; this aspect can be investigated in future developments of the present study implementing a lumped-parameter heart model calibrated with the pre- and post-TEVAR (thoracic endovascular repair) data as proposed by van Bakel et al. [24].

CONCLUSION

Endovascular repair of the aortic root is certainly a challenging technological aim and has been addressed only by few authors. The focus of the work was to quantify with various haemodynamic indicators the impact on coronary circulation. With the proposed CAD modelling embedded into a reconstruction patient-specific dilation of the ascending aorta, we can conclude that the configuration proposed in our work does not significantly affect the coronary perfusion. A validation step has yet to be addressed as well as a less idealized representation of the coronary grafts. In particular, an in vivo study should be performed to confirm our in-silico results and provide clinically relevant conclusions.

Funding

This work was supported by the Swiss Heart Foundation [FF17007].

Conflict of interest: none declared.

Author contributions

Michele Conti: Conceptualization; Data curation; Formal analysis; Methodology; Writing—original draft. Rodrigo M. Romarowski: Data curation; Formal analysis; Writing—review & editing. Anna Ferrarini: Data curation; Formal analysis; Writing—review & editing. Matteo Stochino: Data curation; Formal analysis; Writing—review & editing. Ferdinando Auricchio: Conceptualization; Data curation; Formal analysis; Supervision. Simone Morganti: Data curation; Formal analysis. Ludwig Karl von Segesser: Conceptualization; Methodology; Supervision. Enrico Ferrari: Conceptualization; Data curation; Formal analysis; Funding acquisition; Methodology; Supervision; Validation; Writing—review & editing.

Reviewer information

Interactive CardioVascular and Thoracic Surgery thanks Eric J Lehr and the other, anonymous reviewer(s) for their contribution to the peer review process of this article.

Abbreviations

CAD

Computer-aided design

CT

Computed tomography

LCA

Left coronary artery

LNH

Local normalized helicity

MRI

Magnetic resonance imaging

TARR

Transcatheter aortic root repair

3D

3-Dimensional