Save lives or save livelihoods? A cross-country analysis of COVID-19 pandemic and economic growth

Abstract

This paper studies whether containing COVID-19 pandemic by stringent strategies deteriorates or saves economic growth. Since there are country-specific factors that could affect both economic growth and deaths due to COVID-19, we first start with a cross-country analysis on identifying risk and protective factors on the COVID-19 deaths using large across-country variation. Using data on 100 countries from 3 January to 27 November 2020 and taking into account the possibility of underreporting, we find that for deaths per million population, GDP per capita, population density, and income inequality are the three most important risk factors; government effectiveness, temperature, and hospital beds are the three most important protective factors. Second, inspired by the stochastic frontier literature, we construct a measure of pandemic containment effectiveness (PCE) after controlling for country-specific factors and rank countries by their PCE scores for deaths. Finally, by linking the PCE score with GDP growth data in Quarters 2 and 3 of 2020, we find that PCE is positively associated with economic growth in major economies. Countries with average PCE scores, such as Malaysia, would gain more GDP growth by 3.47 percentage points if they could improve their PCE scores for deaths to South Korea’s level in Q2 of 2020. Therefore, there is not a trade-off between lives and livelihood facing by governments. Instead, to save economy, it is important to contain the pandemic first. Our conclusion is also mainly valid for infections due to COVID-19.

1. Introduction

On 11 March 2020 the WHO Director General characterized COVID-19 as a pandemic. Globally, by the 27 December 2020, there have been more than 80 million confirmed cases of COVID-19, including 1.7 million deaths, reported to the WHO. The increasing spread of the coronavirus across countries has prompted many governments to introduce unprecedented public policies and lockdowns to contain the pandemic for saving lives. Such stringent containment policies led to economic disruptions and thus slowed down economic growth. Viscusi (2020) argues that there will be long run economic costs associated with these disruptions. There could be a vicious trade-off facing by governments: save lives or save livelihoods. However, Eichenbaum et al. (2020) find that over the long run there exists an optimal containment strategy to reduce economic costs despite a short-term trade-off between economic activity and health outcomes. Hsu et al. (2020) study optimal containment policy for combating a pandemic in an open economy context. Hong et al. (2021) argue that the either/or trade-off misses the benefits of pandemic containment for the economy in the long run.1

Different from economists’ view, the WHO and IMF think that controlling the pandemic is a prerequisite to saving livelihoods.2 If the virus is not effectively controlled, people will not be able to consume and hence, the economic recovery will be hindered. From this perspective, pandemic containment could have positive impact on economic growth.3 Recently, Alvelda et al. (2020) argue that we should save lives first in order to save the economy, by plotting each country’s coronavirus deaths against the total economic loss each suffered using data of Quarter 2 (Q2) in 2020.4 In China’s context, Chen et al. (2020) document a strong recovery in April and May 2020 using data of truck flows and online consumption after the 76-day lockdown of Wuhan ended on April 8, 2020.

This paper aims to empirically test whether there is a trade-off between lives and livelihoods using cross-country variation. If we simply link COVID-19 deaths to economic loss using country level data, there is no clear empirical evidence showing deaths per million people are negatively associated with GDP growth, after accounting for country effects. Also, there are many country specific factors, such as GDP per capita, population density, health infrastructure, government effectiveness, etc., that could affect both economic growth and COVID-19 deaths and infections. In the existing literature, several studies have explored the cross-country data to study the economic or governments’ responses to the pandemic (Khalid, Okafor, Burzynska, 2021, Milani, 2021, Okafor, Khalid, Burzynska, 2021, Sebhatu, Wennberg, Arora-Jonsson, Lindberg, 2020, Shafiullah, Khalid, Chaudhry, 2021). However, the definition as well as measure of pandemic containment effectiveness (PCE) have not been extensively discussed. This motivates us to explore the methodology of constructing the PCE index. In other words, this paper contributes to the literature by explicitly quantifying the PCE while controlling for country specific factors. In addition, we test the trade-off between lives and livelihoods by linking our PCE score and GDP growth using cross-country data. Subsequently, a counterfactual analysis shows that a better containment of the pandemic can be translated into GDP gains. This provides policymakers cross-country evidence on designing and implementing optimal pandemic containment strategies when facing significant economic recession due to the pandemic.

In this paper, we first start with a cross-country analysis on identifying risk and protective factors on the reported deaths due to COVID-19. Second, inspired by the stochastic frontier literature, we construct a measure of pandemic containment effectiveness, after controlling for country-specific factors in the cross-country analysis, and rank countries by their PCE scores for deaths. Third, we estimate the impact of pandemic containment on GDP growth by linking the PCE score with GDP data in Q2 and Q3 of 2020.

In Section 2, we start with how the global pandemic has distributed heterogeneously across countries, by documenting the patterns and statistics for a set of normalized measures by country. This set includes cumulative and daily cases for death per million people, and the case fatality rate (CFR), from 3 January to 27 November 2020. A raw global ranking based on these measures highlights an interesting fact: best and worst countries in the ranking are vastly different in many aspects. “Everyone wants to know how well their country is tackling coronavirus, compared with others”, as pointed out in one of the recent BBC reality checks.5 The United States, for example, has more than 14.4 million of people being infected by COVID-19 on 27 No. 2020, far more than any other countries. China, on the other hand, only reported 86,601 confirmed cases so far, due to the strict lockdown policies at the beginning of the pandemic. What is underneath the huge variation of the pandemic could be the huge heterogeneity, in some important risk and protective factors of the disease, say, GDP per capita.6 This motivates our cross-country regression analyses.

Section 3 examines to what extent the substantial variations documented in Section 2 could be explained by a set of predetermined country characteristics. This includes demographic conditions, geographic conditions, economic conditions, global interdependency, healthcare conditions, and public governance. We find there does exist a set of explanatory variables that are robustly significant under different model specifications, across different subsamples, and with reasonable adjustment for the reported death numbers. All else being equal, a country with higher GDP per capita, higher population density, larger income Gini coefficient, fewer hospital beds, lower temperature, and lower government effectiveness, tends to have more deaths. For example, all else being equal, a 100% increase in GDP per capita is associated with a 94.4% increase in deaths per million people. Enhancing the government effectiveness from a level of Italy to that of South Korea, would reduce deaths by nearly 96.6%. Given all else being equal, a country with a one standard deviation higher population density than the sample average, expects 65% more reported deaths per million people. A country with 2.60 hospital beds per 1,000 people more than the sample average of 3.33, that is, an increase by one standard deviation, would reduce unit deaths by 49.3%, all else being equal. Similarly, a country with 11 ${}^{\circ }$C higher from the global average may expect 85.9% lower deaths per million population. More discussions on additional results and robustness checks are delegated to Appendix of Section 7.

Our cross-country regression model provides a useful statistical device. It shows on average how the set of predetermined country characteristics would predict the COVID-19 deaths for each country. As the actual death is the outcome of both predetermined country characteristics and the pandemic policies, if we use the global average as a benchmark, the gap between the actual and the predicted numbers is informative about how effectively each country has been dealing with the COVID-19 relative to others.7 Based on this rationale, and inspired by the stochastic frontier literature, we construct a measure of PCE and thus provide a global ranking. We find that for some countries, such as China and the US, their rankings do vary substantially over the pandemic course; and for other countries, such as Singapore, their rankings do vary by infections or by deaths. We also find some countries who have been consistently exceptionally better or worse than the global average, after controlling for a large set of predetermined country characteristics.

Based on the cross-country analysis and the PCE scores in Sections 3 and 4, Section 5 empirically examines the relationship between economic growth and pandemic containment performance in major economies using the data in Q2 and Q3 of 2020. We find that the empirical results do not reflect the trade-off between economic activities and the pandemic containment. Instead, there is a significant and positive impact of PCE on economic growth. Countries with average PCE scores, such as Malaysia, would gain more GDP growth by 3.47 percentage points if they could improve their PCE scores for infections to South Korea’s level in Q2 of 2020.

2. Data and patterns on infections and deaths

Various sources have been tracking the confirmed infections and deaths by country over time. In this paper, we use the data from the WHO, which are officially reported by the Center for Disease Control and Prevention or Ministry of Health or equivalent of each country. As reported by the WHO, the first mass vaccination started in early December 2020. On 31 December 2020, Pfizer vaccine was issued the first emergency use validation from the WHO, indicating the world-wide access to the vaccines. Besides, a new variant of COVID-19 virus, known as B.1.1.7 (or Alpha), was first found in the UK and then began to widely spread in mid-December 2020. Therefore, to avoid confounding factors of vaccination as well as new virus variants in our analysis, we collect number of reported deaths of COVID-19 from 3 January to 27 November 2020 on a daily basis for 100 countries, which have complete information on all the independent variables in our regression analyses.8 Particularly, it is worth taking note that even though there might be potential underreporting issue for both cumulative infections and cumulative deaths which in turn affect our empirical results, the magnitude of such discrepancy is vastly different. As found by Rahmandad et al. (2020), the estimated cumulative infections across 86 countries through July 2020 are 10.5 times higher than the official reports, while the estimated deaths is just 1.47 times above the reported values. In other words, data of reported deaths suffers less from underreporting compared to reported infections. Therefore, in our paper we only report the our main empirical results based on reported deaths due to COVID-19 and provide results based on infections as supplementary in the Appendix.

Since its first emergence in late 2019, COVID-19 has rapidly spread to most of the countries in the world. They started increasing rapidly around the declaration of global pandemic by WHO on 11 March. During the last month of our sample period, on average, the coronavirus has infected almost 600,000 people and killed more than 10,000 people worldwide every day, suggesting that the global transmission of the virus has not been under control. The time series plots of global cumulative and daily cases can be found in Fig. A.a1 and A.b1 in the Appendix. Here we compare the COVID-19 outbreak across countries by plotting daily deaths per million people for four representative countries, Vietnam, China, the US, and Luxembourg, in Fig. 1 . We find that the scale of the COVID-19 outbreak varies substantially among countries. Vietnam has the lightest outbreak with its highest daily deaths of 0.3 per million people, while that of China is more than 3 times higher. However, the pandemic outbreak is markedly severer in the US and Luxembourg as their maximal daily deaths are around 20 and 17 per million people, respectively. Why are the deaths so different, even after being normalized by population size?

Fig. A.a1.

Global cumulative infections and deaths in 2020.

Fig. A.b1.

Global cumulative infections and deaths in 2020.

Fig. 1.

Daily deaths of four representative countries.

To better examine the heterogeneity of COVID-19 outbreak across countries, we provide the summary statistics and a raw global ranking for cumulative infections and cumulative deaths per million population, and the CFR in Table 1 .9 Firstly, the substantial difference between minimum and maximum values of pandemic outcomes across countries suggests that most of the worst 10 countries are either developed countries or large emerging economies, while most of the best 10 countries are developing countries. Why the COVID-19 seems severer within countries that are economically more developed? One possible explanation is that economic activities are much higher in developed countries and hence, this causes greater transmission of virus. Alternatively, a lower average income is usually associated with poorer healthcare conditions and public governance, which may lead to more underreporting and hence fewer reported infections and deaths.

Table 1.

Cumulative infections and deaths: summary statistics, worst and best 10 countries.

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
Variables	Unit	Mean	Median	Std. D	Min	Max	Worst 10	Value	Best 10	Value	Form in regression
Cumulative infections	per million people	14,043	9416	13,881	6	52,800	Luxembourg	52,800	Laos	6	log
							Qatar	49,634	Vietnam	14
							Belgium	49,630	Cambodia	19
							Czechia	48,121	Thailand	57
							Armenia	44,836	China	67
							US	38,085	Burkina Faso	141
							Panama	37,955	Nigeria	342
							Israel	37,397	New Zealand	349
							Switzerland	36,734	Uganda	447
							Spain	34,561	Rwanda	476
Cumulative deaths	per million people	283	139	320	0	1419	Belgium	1419	Cambodia	0	log
							Peru	1117	Laos	0
							Spain	948	Bhutan	0
							Italy	875	Vietnam	0
							UK	858	Thailand	1
							Argentina	848	China	3
							Mexico	821	Burkina Faso	3
							Brazil	815	Rwanda	4
							Chile	813	Mozambique	4
							US	789	Uganda	4
Case fatality rate (CFR)	ratio	2.0%	1.7%	1.5%	0.0%	9.7%	Mexico	9.7%	Laos	0.0%	ratio
							Ecuador	7.1%	Cambodia	0.0%
							Bolivia	6.2%	Bhutan	0.0%
							Egypt	5.8%	Singapore	0.0%
							Iran	5.1%	Qatar	0.2%
							China	5.1%	Botswana	0.3%
							Peru	3.7%	UAE	0.3%
							UK	3.6%	Sri Lanka	0.4%
							Italy	3.5%	Iceland	0.5%
							Guatemala	3.4%	Malaysia	0.6%

Data source: The World Health Organization (as of 27 November 2020). Statistics are computed from 100 countries.

Another interesting observation is that the geographical location may also affect infections and deaths as the worst 10 countries are mainly from Europe and the Americas, while most of the best 10 countries are from Africa and South East Asia. Finally, it is also worthwhile to point out that, though there is a large overlap in the list of worst and best countries for infection and death rates, some countries with very bad infection rates may have relatively low death rates. For example, Qatar is one of the worst countries in terms of infections per million people but is among the 10 best countries for CFR.

Overall, all these comparisons and observations suggest that, it is important to control the large heterogeneity in other factors that may affect the death rate in a statistical way, in order to provide a fair global ranking on the pandemic containment effectiveness. This motivates our regression analyses in Section 3.

3. Cross-country regression

3.1. Empirical specification

Since different countries were hit by the pandemic on different time points, we put them in same phases of the pandemic by considering the following regression:

$$y_{it}={\beta }_0+{\beta }_1{X}_i+{\beta }_2{Z}_{it}+f\left(Day{s}_{it}\right)+{\epsilon }_{it}.$$ (1)

Here $y_{it}$ represents the number of cumulative reported deaths per million people, for country $i$. Different from a usual panel data regression, here $t$ represents days since the first reported death was reported in a country, instead of a calendar date.

$X_i$ denotes a set of predetermined variables that may affect how vulnerable a country is inherently to COVID-19. $Z_{it}$ refers to additional time-varying control variables that may affect the reported deaths besides $X_i$. As the outbreak of COVID-19 takes place in different countries on different dates, a common time trend, $Day{s}_{it}$, days since the first reported death in country $i$ on date $t$, is included in the regression in a nonlinear form $f(·)$ to control for the impact of different outbreak dates on deaths.10

The time-invariant coefficients ${\beta }_1$ and ${\beta }_2$ capture the average effects of $X_i$ and $Z_{it}$ on $y_{it}$ over time. However, depending on the epidemiology of the disease, the same set of variables may have different predicting power to the pandemic over time. In addition, some explanatory variables which are essential determinants in an early stage may become less relevant at a late stage, or the other way round. To allow for time-varying ${\beta }_1$ and ${\beta }_2$, we also run regression of Eq. (1) using subsamples made of different weeks over the pandemic course.

Unlike Janiak et al. (2021), who focus on the impacts of pandemic policies such as sanitary protocols on pandemic and economic outcomes, regression Eq. (1) does not explicitly include any COVID-19 pandemic policies that countries have been adopting. Although understanding the causal effect of specific policies is crucially important, it is not the goal of this paper. Instead, here we take a reduced-form approach to assess the relative effectiveness of the pandemic policies as a whole for each country. Denote such policies as $W_{it}$. The deaths in a country $y_{it}$, should be affected by $W_{it}$, on top of $X_i$ and $Z_{it}$, i.e.,

$$y_{it}={\alpha }_0+{\alpha }_1{X}_i+{\alpha }_2{Z}_{it}+{\alpha }_3{W}_{it}+g\left(Day{s}_{it}\right)+{\eta }_{it}.$$ (2)

However, such containment policies, by definition, must depend on the situation of the pandemic itself and would be endogenous if they were included in our regressions. Furthermore, as pointed out in Angeli and Montefusco (2020), the containment policies are highly dependent on initial country-specific characteristics. Similarly, Wright et al. (2020) also find that the compliance rate of pandemic containment policies such as shelter-in-place protocols is higher among residents of higher income regions in the US, implying that the effectiveness of such containment policies depends on country-specific factors. That is, $W_{it}$ itself may also depend on $X_i$ and $Z_{it}$, in addition to $y_{it}$, which implies that we could write $W_{it}$ as,

$$W_{it}={\pi }_0+{\pi }_1{X}_i+{\pi }_2{Z}_{it}+{\pi }_3{y}_{it}+h\left(Day{s}_{it}\right)+{\xi }_{it}.$$ (3)

Plugging $W_{it}$ in Eq. (2) by (3) and solving for $y_{it}$ leads to Eq. (1). Therefore, the regression Eq. (1) can be regarded as a reduced-form equation for $y_{it}$ from a system of structural Eqs. (2)and Eq. (3). As such, coefficients ${\beta }_1$ and ${\beta }_2$ in regression (1) can be interpreted as the overall effects of $X_i$ and $Z_{it}$ on $y_{it}$.

It is worth noting that to address this research question why the deaths are so different across country, a cross-country regression using a cross-sectional sample would serve this purpose. However, compared with a cross-sectional regression, our static regression model Eq. (1) using daily observations helps to improve the accuracy of estimates.11 Of course, the regression Eq. (1) above with a daily-frequency structure does not account for autocorrelations of both the dependent variable and the time-varying regressors, which could explain a significant part of variation in deaths. However, achieving a better model fit by accounting for the autocorrelation in the data is not the main target of this paper. Our approach is to adopt a static model and leave the dynamics (or autocorrelation) in the errors. The autocorrelation in the errors can be addressed by using clustered standard errors at the country level.12

3.2. Data on independent variables

Motivated by existing literature on COVID-19 and economic intuitions, we consider six categories of factors in $X_i$:

• i.Demographic conditions (total population, ratio of population 65 years and above, and population density);
• ii.Geographic conditions (average temperature and rainfall in March);
• iii.Economic conditions (GDP per capita and income Gini coefficient);
• iv.Global interdependency (international visitors and international trade);
• v.Healthcare conditions (health expenditure as a share of GDP, number of hospital beds per 1,000 people, and SARS outbreak dummy);
• vi.Public governance (government expenditure as a share of GDP and government effectiveness index constructed by the World Bank).

All these variables are fixed and taking values before 2020. In other words, they are exogenous to the outbreak of COVID-19 in our regression analyses. Since there are more than 20 variables for these predetermined factors used in regressions with various specifications, due to limited space, we include the detailed information of these variables in the Appendix, including definitions, years observed and data sources. Table 2 reports their summary statistics.

Table 2.

Summary statistics of independent variables.

	Variables	Unit	Mean	Std. D	Min	Max	Form in regression	Source
1	total population	million	66.90	196.56	0.35	1392.73	log	World bank
2	population 65+	%	11.2	6.7	1.1	27.6	%	World bank
3	population density	per square kilometer	229	809	3	7953	log	World bank
4	urban population ratio	%	64.72	21.36	17.21	100.00	%	World bank
5	temperature	${}^{\circ }$C	14.78	11.01	-15.17	31.91		Climate Change Knowledge Portal
6	rainfall	millimeter	63.65	56.66	0.00	356.37	log	Climate Change Knowledge Portal
7	GDP per capita	dollars	20,436	23,929	499	1,16,597	log	World bank
8	debt ratio	%	52	36	6	198	%	CEIC
9	employment in agriculture	%	18.77	18.71	0.06	72.45	%	World bank
10	Industrial ratio	%	26.90	8.30	11.32	56.89	%	World bank
11	Gini coefficient		37.44	8.15	24.20	63.00		World bank
12	international visitors	per million people	7,80,549	10,89,944	4552	66,44,912	log	World bank
13	international trade		0.88	1.63	0.00	10.85		United Nations Comtrade
14	health expenditure	%	6.91	2.65	2.27	17.06	%	World bank
15	GHS		49.03	13.36	25.20	83.50		https://www.ghsindex.org/
16	hospital beds	per thousand people	3.33	2.60	0.30	13.40	log	World bank
17	SARS outbreak		0.26	0.44	0	1	0 or 1	World Health Organizatio
18	government expenditure	%	16.36	4.98	4.93	30.05	%	World bank
19	political regime		1.90	1.00	0.00	3.00		Our World in Data
20	government effectiveness		0.38	0.88	-1.07	2.23		Worldwide Governance Indicators, World Bank
21	rest of world infections		1.81*107	1.7*107	0	6.05*107	log	World Health Organizatio
22	rest of region infection		2.8*106	4.6*106	0	2.51*107	log	World Health Organizatio
23	daily test ratio	per million people	13,082	45,347	0.644	4,50,019	log	Humanitarian Data Exchange
24	Economic stimulus spending	dollars	1.21*1011	4.24*1011	9*106	2.86*1012	log	Oxford COVID-19 Government Response Tracker database
25	Economic support index		62	23	12.5	100		Oxford COVID-19 Government Response Tracker database

For definitions and sources, see data appendix.

Besides $X_i$, we also include two other explanatory variables in $Z_{it}$ as additional controls. The first one is the number of cumulative infections in the rest of the world. This is to control both the potential externalities from other countries and the prevailing trend in the course of a global pandemic. The second is the test ratio for COVID-19, defined as the number of people tested for COVID-19 per million people, which is considered as exogenous in our analysis.13 This is because the testing capability of a country is highly unlikely to change in the short-run. Hence, including the test ratio into the regressions is one way to mitigate the underreporting concerns.

We consider the test ratio as an equilibrium quantity for testing demand and testing supply in a country. The demand for testing depends on both the severity of COVID-19 and the testing criteria in a country. The supply for testing is mainly determined by the capacity and the willingness to test, which largely depends on its predetermined healthcare conditions and public governance. Therefore, conditional on the healthcare conditions and public governance, if two countries have the same severity of COVID-19, the country with a lower test ratio is more likely to have underreported infection or death cases due to a stricter testing criterion.

3.3. Main findings

Tables 3 reports the regression results for Eq. (1) for deaths per million people. Column (1) reports the benchmark results with full sample. Across all these regressions, an $R^2$ around 0.65 suggests that our explanatory variables explain a substantial proportion of variations of the observed deaths across the world.

Table 3.

Risk and protective factors for deaths.

Dependent variable	log of deaths per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
sample	Full	TOP25	UHC adjusted	VA adjusted	RE	CRE	FEF
Days	0.028***	-0.001	0.034***	0.035***	0.024***	0.013***	0.029***
	(6.466)	(-0.155)	(7.115)	(7.238)	(62.532)	(28.934)	(5.368)
Days2	-0.000***	-0.000	-0.000***	-0.000***	-0.000***	-0.000***	0.000***
	(-5.802)	(-1.336)	(-7.199)	(-7.338)	(-51.169)	(-23.180)	(-4.856)
total population	0.146	0.485***	0.126	0.171	0.141	0.191	0.186
	(1.249)	(2.921)	(0.999)	(1.368)	(1.162)	(1.592)	(1.602)
population 65+	-0.006	0.151***	-0.002	-0.028	-0.013	0.005	-0.005
	(-0.170)	(2.993)	(-0.062)	(-0.779)	(-0.377)	(0.152)	(-0.159)
population density	0.184*	0.177*	0.200**	0.218**	0.187*	0.182*	0.224***
	(1.956)	(1.833)	(1.988)	(2.221)	(1.952)	(1.913)	(2.600)
temperature	-0.078***	-0.058***	-0.087***	-0.086***	-0.074***	-0.074***	-0.065***
	(-4.933)	(-4.927)	(-4.758)	(-5.014)	(-4.266)	(-4.336)	(-3.603)
rainfall	-0.027	0.365	-0.049	-0.044	-0.056	-0.065	-0.055
	(-0.219)	(1.295)	(-0.359)	(-0.331)	(-0.444)	(-0.517)	(-0.348)
GDP per capita	0.944***	1.658***	0.976***	1.060***	0.927***	1.078***	1.005***
	(5.634)	(3.201)	(5.248)	(5.700)	(4.843)	(5.678)	(6.019)
Gini coefficient	0.042**	-0.045	0.049**	0.043**	0.037*	0.044**	0.038**
	(2.350)	(-0.829)	(2.361)	(2.107)	(1.805)	(2.163)	(2.214)
international visitors	0.172	-0.163	0.167	0.223	0.133	0.144	0.065
	(1.330)	(-0.417)	(1.143)	(1.530)	(0.954)	(1.038)	(0.579)
international trade	-0.172*	-0.035	-0.173*	-0.163*	-0.158	-0.198**	-0.218***
	(-1.799)	(-0.487)	(-1.669)	(-1.750)	(-1.574)	(-1.981)	(-2.979)
health expenditure	0.216***	-0.018	0.212***	0.217***	0.223***	0.204***	0.216***
	(4.344)	(-0.229)	(3.822)	(4.092)	(3.717)	(3.434)	(4.367)
hospital beds	-0.631***	-1.162***	-0.702***	-0.576**	-0.535**	-0.583***	-0.414*
	(-2.763)	(-3.439)	(-2.819)	(-2.331)	(-2.508)	(-2.760)	(-1.688)
SARS outbreak	0.103	-0.887	0.030	0.076	0.142	0.045	-0.018
	(0.283)	(-1.581)	(0.077)	(0.201)	(0.429)	(0.138)	(-0.046)
government expenditure	-0.009	-0.064	-0.012	-0.007	-0.000	-0.006	0.003
	(-0.352)	(-1.011)	(-0.448)	(-0.271)	(-0.001)	(-0.224)	(0.113)
government effectiveness	-1.098***	-1.621***	-1.187***	-1.360***	-1.131***	-1.138***	-1.190***
	(-4.027)	(-3.821)	(-3.934)	(-4.713)	(-3.891)	(-3.949)	(-4.484)
rest of world (ROW) infections	0.118	1.017***	0.187	0.194	0.130***	-1.015***
	(0.973)	(4.948)	(1.346)	(1.416)	(13.192)	(-32.843)
ROW infections time average						1.090***	-0.009
						(21.598)	(-0.078)
daily test ratio	0.007		0.004	0.011	0.067***
	(0.265)		(0.120)	(0.367)	(22.009)
daily test ratio time average						0.327***	0.085**
						(17.337)	(2.378)
Number of observations	24,241	6442	24,241	24,241	24,241	24,241	27,724
Adjusted R2	0.647	0.745	0.643	0.651	N.A.	N.A.	N.A.

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first death case. 3. Column (2) reports results of a subsample of 25 countries with the hightest test ratio. 4. Columns (3) and (4) report results of using deaths adjusted by UHC and VA to address underreporting concern. UHC and VA refer to the universal healthcare and voice and accountablity indices, respectively, constructed by the World Bank. 5. Column (5) reports results of the random effect model based on the specification in column (1). 6. Column (6) reports results of the correlated random effect model by including the time average of the time-variant variables, based on the specification in column (1). 7. Column (7) appies the fixed-effect filtered estimates proposed by Pesaran and Zhou (2018).

These empirical exercises aim to identify the risk and protective factors for deaths. As potential data underreporting could be a serious concern for interpreting meaningful empirical results, we only report the results for deaths to uncover significant and robust patterns as our main empirical findings. Additional results for infections are discussed in the Appendix.

First, across the large set of our empirical exercises, we find that GDP per capita, population density, and Gini coefficient are the three most important risk factors, while government effectiveness, temperature, and hospital beds are the three most important protective factors for deaths. Fig. 2 visualizes our main findings by sorting the risk factors on the right and the protective factors on the left for deaths. The corresponding magnitudes measure the percentage change in deaths per million people due to one standard deviation increase in each of these factors, based on their estimated coefficients in column (1) of Table 3, together with the summary statistics in Table 2.

Fig. 2.

Impacts of risk and protective factors on deaths.

We start our discussion with the effect of GDP per capita on deaths. The coefficient 0.944 interpreted as the elasticity of infections with respect to GDP per capita, implies that a country with a 100% higher GDP per capita may expect 94.4% more reported cumulative deaths per million people, all else being equal. A unit elasticity of GDP per capita on death rate is very close to similar studies using cross-country data, such as Goldberg and Reed (2020). The importance of average income may explain a striking fact that most of the top 10 countries with the highest deaths per million people listed in Table 1, have relatively higher GDP per capita compared to the top 10 countries with least deaths. This somewhat unpleasant finding is consistent with Adda (2016) findings on incidence of several viral diseases in France over a quarter of a century. As higher GDP per capita implies more market production, consumption, as well as social activities and interactions among people, leading to more deaths. Thus, this finding may indicate that economic activity is a fundamental mechanism for the spread of the epidemic.

Population density is the second most important contributing factor of deaths, suggesting that a country with a dense population is more vulnerable to the spread of COVID-19. The elasticity of 0.184 implies that all else being equal, a country with one standard deviation higher population density than the sample average, expects 65% more reported deaths per million people. Combining the considerable impacts of both GDP per capita and population density on reported deaths, it is logical to expect large death numbers in many megacities in developed economies, such as New York City, London, and Milan.

Income inequality measured by Gini coefficient is the third most important factor that induces more reported deaths. The coefficient 0.042 suggests that on average, a country with a higher Gini coefficient than the cross-country average by one standard deviation could witness 34.2% more cumulative deaths per million people. While identifying the exact mechanisms on why inequality could spread COVID-19 is beyond the scope of this paper, our cross-country findings echo the statement of Ahmed et al. (2020) that pandemics rarely affect all people in a uniform way.14

Among the three most important protective factors, government effectiveness and hospital beds are of our key interest, as they have directly applicable policy implications. The government effectiveness index used here is provided by the Worldwide Governance Indicators, and reflects the performance of government in the quality of public services and policy implementation, and the credibility of the government’s commitment.15 By the definition of this index, the government effectiveness is expected to be closely related to the quality and implementation of pandemic containment policies in one country, e.g., mandates of wearing masks, social distancing, and lockdowns. However, its protective effect is surprisingly remarkable. In Table 3, we observe that its coefficient -1.098 suggests that an increase in government effectiveness index by one standard deviation from the sample average, a value close to Italy’s, to the value of South Korea, would reduce unit deaths by 96.6%, holding other explanatory variables constant. This finding is in line with Liang et al. (2020), who find COVID-19 mortality has negative relationships with test number and government effectiveness.

Another important protective factor comes from the number of hospital beds, a key measure of medical infrastructure. Its coefficient -0.631 suggests that a country with 2.60 hospital beds per 1000 people more than the sample average of 3.33, that is, an increase by one standard deviation, would reduce unit deaths by 49.3%, all else being equal. Our finding illustrates that adequate medical infrastructure can effectively reduce the death of infectious diseases. This is consistent with the findings by Okoi and Bwawa (2020) on the importance of access to health services in addressing the COVID-19 outbreak in Sub-Saharan Africa.

As the third robust protective factor, temperature also has a large negative impact on the COVID-19 deaths, indicating that a higher temperature is not conducive to the survival and spread of the viruses that cause deaths. The coefficient of -0.078 infers that countries with 11.01 ${}^{\circ }$C higher from the sample average (14.78 ${}^{\circ }$C) expect 85.9% lower unit deaths. This evidence may suggest why countries from Africa and South East Asia, are on average hit relatively less severely by the pandemic during the sample period. The blessing effect of high temperature is consistent with many epidemic-related researches, such as Bannister-Tyrrell et al. (2020).

In addition, we address the underreporting issue and conduct robustness checks in Table 3.16 In particular, we first adjust our dependent variable with the universal health coverage (UHC) and the voice and accountability (VA) as both indices are expected to have inverse relationship with the tendency of underreporting. Secondly, we also add results of random effects (RE), correlated effects models (CRE), and fixed effect filtered (FEF) estimates in Table 3. The results are all consistent with our benchmark results in column (1) of Table 3. Besides that, we add a series of robustness checks in Tables A.2–A.5 in the Appendix. Overall, the results are robust to different subsamples, different measure of dependent variable and additional explanatory variables.

4. Pandemic containment effectiveness: a global ranking

In Section 3, risk factors and protective factors have been identified to explain the huge cross-country variations observed in cumulative deaths, after being normalized by population size. In this section, we aim to rank countries by their PCE performance in terms of deaths, after controlling for the predetermined and time-varying observable factors. The rankings and constructed effectiveness scores can be regarded as an indirect and holistic inference on how effective the pandemic public policies have been on reducing deaths relative to other countries.

Recently, Viscusi (2020) applies the value of a statistical life (VSL) to monetize COVID-19 deaths, and estimates that the costs of the US and global mortality over 100 countries are 1.4 trillion USD and 3.5 trillion USD, respectively, in the first half of 2020. Inspired by Greene (2004) on the cross-country health care comparison, we treat regression Eq. (1) as a production process, with deaths as outputs. In light of the fact that COVID-19 deaths are associated with huge medical costs and GDP loss due to economic activity disruptions, regression Eq. (1) can be interpreted as a process similar to a cost function.

Inspired by the stochastic cost frontier literature, we decompose the error term in Eq. (1) into two parts: a one-sided inefficiency term $u_{it}\ge 0$ and a two-sided idiosyncratic error $v_{it}$: (Greene, 2007, pp.117, 137),

$${\epsilon }_{it}=u_{it}+v_{it}.$$ (4)

The inefficiency term $u_{it}\ge 0$ measures the deviation from the cost frontier. A larger value of $u_{it}$ implies higher costs associated with deaths and the corresponding country $i$ is less cost effective. The idiosyncratic error $v_{it}$ is considered as a measurement error.

Kumbhakar et al. (2015) summarize several approaches to estimate cost efficiency in stochastic frontier models with cross-sectional data and panel data, including maximum likelihood estimation, corrected ordinary least squares (COLS) and panel data methods. To be in line with coefficient estimation results in Section 3, COLS is adopted in our context. Denote $e_{it}$ the pooled OLS residual obtained from Eq. (1): $e_{it}=y_{it}-{\widehat{y}}_{it}$. As in Eq. (4.29) of Kumbhakar et al. (2015, p.109), an efficiency measure

$$\exp (mi{n}_j{e}_{jt}-e_{it})$$ (5)

can be used for cost effectiveness for country $i$ on day $t$ when ranking countries.

However, as pointed out in the literature, this approach could be vulnerable to extreme values in the data. In specific, its accuracy could be contaminated by the presence of the zero-mean random shock $v_{it}$ in the error term ${\epsilon }_{it}$. To make good use of panel data in our sample and smooth out $v_{it}$, we can split the sample into $K$ periods, i.e.,$T_1,\cdots ,T_K$, and use a time-average of $e_{it}$ over a time period from $T_{k-1}+1$ to $T_k$, say a two-week period, i.e., ${\overline{e}}_i\left(T_k\right)=\frac{1}{T/K}{\sum }_{t=T_{k-1}+1}^{T_k}{e}_{it}$.

Similar to the cross-sectional data counterpart of (5), ${\overline{e}}_i\left(T_k\right)$ can be considered as a measure of deviation from the cost frontier. A country with a smaller value of ${\overline{e}}_i\left(T_k\right)$ is more cost effective or efficient. Intuitively, its actual deaths are smaller relative to its model predictions. In specific, for a time period over which we assume that $u_{it}$ is relatively stable, i.e.,

$$u_{it}=u_i\left(T_k\right)\text{and}{\epsilon }_{it}=u_i\left(T_k\right)+v_{it}\text{,}t=T_{k-1}+1,\cdots ,T_k.$$ (6)

Given that the COLS residual $e_{it}$ is a consistent estimator of ${\epsilon }_{it}$, $v_{it}$ can be smoothed out in the time-average ${\overline{e}}_i\left(T_k\right)$ for the period $T_k$. In this case, ${\overline{e}}_i\left(T_k\right)$ can be regarded as a good estimator of the inefficiency term $u_i\left(T_k\right)$, the distance to the cost frontier for the period $T_k$ .

Recall that ${\epsilon }_{it}$ is the error in the reduced form Eq. (1). One concern is that governments’ pandemic containment policies $W_{it}$ are not included in Eq. (1) and thus, ${\epsilon }_{it}$ is a mixture of the residual impacts of the pandemic and residual policy responses to the pandemic. In specific, ${\epsilon }_{it}=({\eta }_{it}+{\alpha }_3{\xi }_{it})/(1-{\alpha }_3{\pi }_3)$, where ${\eta }_{it}$ is the residual impact of the pandemic in the structural Eq. (2) and ${\xi }_{it}$ is the residual pandemic policy response in Eq. (3). To separate the impact of residual pandemic policy responses, ideally, ${\eta }_{it}$, instead of ${\epsilon }_{it}$, should be used to construct a measure of deviation from the cost frontier. However, without sufficient information on $W_{it}$ in (2) and dealing with endogeneity in (3), ${\eta }_{it}$ cannot be identified. Under the assumption that ${\xi }_{it}$ is an idiosyncratic shock with $E{\xi }_{it}=0$, $\frac{1}{T/K}{\sum }_{t=T_{k-1}+1}^{T_k}{\xi }_{it}$ is close to zero, implying that residual pandemic policy responses can be smoothed out in the time-average ${\overline{e}}_i\left(T_k\right)$. Thus, ${\eta }_{it}$ can be identified by ${\epsilon }_{it}$ up to a scale ($1/(1-{\alpha }_3{\pi }_3)$) in this panel data model (6), and ${\overline{e}}_i\left(T_k\right)$ can be considered as a good estimate of the time-invariant part of ${\eta }_{it}$.17

We rank all 100 countries in our sample based on $-{\overline{e}}_i\left(T_k\right)$ by using their corresponding 14-day averaged residuals obtained from regression Eq. (1), in respective pandemic weeks. A country with a larger value of $-{\overline{e}}_i\left(T_k\right)$ has a higher ranking. Like the efficiency measure in (5) which lies in (0,1), a normalized pandemic containment effectiveness (PCE) score for country i the period $T_k$ is defined as:

$$PC{E}_i\left(T_k\right)=\frac{ma{x}_j{\overline{e}}_j\left(T_k\right)-{\overline{e}}_i\left(T_k\right)}{ma{x}_j{\overline{e}}_j\left(T_k\right)-mi{n}_j{\overline{e}}_j\left(T_k\right)},k=1,\cdots ,K.$$ (7)

A PCE score hence is constructed by taking all the predetermined country specific factors such as government effectiveness, geographical location, and demographic condition into account. Using $PC{E}_i$, the country which is the most pandemic containment effective or cost efficient in the sample achieves a score of 1 and the least effective one scores 0. Countries with a smaller number of ranking are more effective in constraining the pandemic in terms of deaths.18

Since Eq. (7) is a monotonically increasing function of $-{\overline{e}}_i\left(T_k\right)$, the ranking based on $PC{E}_i\left(T_k\right)$ is same as that based on $-{\overline{e}}_i\left(T_k\right)$. In the same spirit as the two-sided technical efficiency measure proposed by Feng and Horrace (2012), $PC{E}_i\left(T_k\right)$ has the advantage of having a same scale across the sample, and therefore, the differences of PCE score among different countries are comparable. In this sense, PCE scores are cardinal. A cardinal measure of PCE scores makes it possible to use its differences to explain cross-country GDP growth variation in the next section.

Fig. 3 presents PCE rankings of 10 selected countries in terms of deaths. Except China, Iran, and Philippines, the rest of countries in the sample with death cases either have their first death case in March and April or at least three weeks after their first confirmed infection case. Thus, we use the ${\overline{e}}_i$ from column (1) of Table 3, that is since the first confirmed death as a common starting point for our PCE ranking exercises. In this way, we are comparing China on 11 January with Italy on 23 February, the US on 3 March, and the UK on 7 March, and onwards. As we observe from Fig. 3, during the first 2 weeks after the first reported death, the US performs the best among the 100 countries. In comparison, China’s PCE ranking is at the very bottom among the 10 selected countries because the spread of virus in China was drastically fast during its initial stage. Thanks to the prompt responses, massive resource mobilization and strict containment policies, its PCE ranking improves steadily over time. By late June, China achieves the $21{}^{st}$ spot out of 97 countries, indicating that the COVID-19 has been effectively contained. In contrast, the PCE ranking for the US has been declining quickly since week 5 to 6, consistent with the massive outbreak in the US starting at the end of March. Nevertheless, at the end of our sample period, despite the US has the world’s highest number of deaths, its PCE ranking is $45{}^{th}$ out of 97. This suggests the importance of controlling for the risk factors and protective factors for a fair global ranking. Overall, Japan has a steady and high PCE ranking since its first two weeks. Brazil, Spain, and the UK have been performing persistently poorly, while New Zealand, South Korea and Japan, are among the most efficient group.

Fig. 3.

Ranking of pandemic containment effectiveness (PCE) for deaths in 10 representative countries.

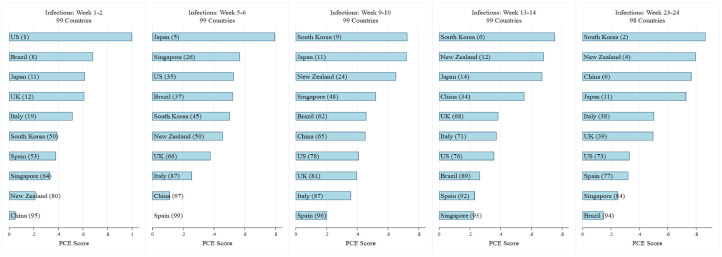
Interestingly, Singapore’s PCE ranking in terms of deaths is constantly high, which is vastly different from its PCE ranking on infections in Fig. A.5 in the Appendix.19 In other words, despite its high cumulative infections due to the massive dormitory transmission among migrant foreign workers, the number of its cumulative deaths is one of the lowest in the world. This is consistent with its advanced health infrastructure and well-known government effectiveness, two most important protective factors for death highlighted by our empirical exercises.

Fig. A.5.

Ranking of pandemic containment effectiveness (PCE) for infections in 10 representative countries.

5. Pandemic containment and economic growth

In this section, we examine whether PCE is associated with economic growth. In specific, GDP growth is regressed on the pandemic containment effectiveness measured by PCE scores obtained in Section 4. Thus, the hypothesis on the trade-off between the lives and livelihoods can be tested by looking at the effect of PCE. Due to data availability, we collect data of GDP growth in the first three quarters of 2020 for 73 and 70 major economies, respectively. The quarterly GDP growth rates are on a year-over-year (YoY) basis with seasonal adjustment. The regression model considered here is:

$${\mathrm{growth}}_i={\gamma }_0+{\gamma }_1\mathit{PC}{E}_i\left(T_k\right)+{\mathrm{controls}}_i+{ϵ}_i.$$ (8)

As in the ranking analysis of Section 4, we use the PCE score instead of a raw measure of deaths here, thus, effects of country-specific factors on deaths can be controlled. Control variables in Eq. (8) here include cumulative announced economic stimulus spending (in USD) and economic support index as fiscal measures collected from the Oxford Coronavirus Government Response Tracker (OxCGRT) database. For a better interpretation of the parameter of interest ${\gamma }_1$, a PCE score multiplied by 100 is included in regression Eq. (8).

As reported by WHO, most countries in our sample reached their first death around March 2020. Therefore, for GDP growth in Q1 of 2020 we consider the PCE scores measured in weeks 3– 4 after the first death in these countries, implying that most countries in the sample are at the end of March 2020. Similarly, for GDP growth in Q2 and Q3 of 2020, respective PCE scores measured in weeks 15–16 and weeks 27–28, corresponding to late June and late September 2020, are used in the Eq. (8).

Table 4 presents the estimated impacts of PCE for deaths on GDP growth. Column (1) reports the cross-section regression for GDP growth in Q2 of 2020 with control variables. Similarly, the regression for GDP growth in Q3 of 2020 is included in column (2) of Table 4. The positive and significant PCE score coefficients in these regressions suggest that those countries that control the pandemic more effectively achieve higher economic growth rates. The magnitudes of 0.105 and 0.074 for coefficients in columns (1) and (2) show that on average 1.05 and 0.74 percentage points of GDP would be added if a country could increase its PCE score (multiplied by 100) for deaths by 10 points in Q2 and Q3 of 2020, respectively.

Table 4.

Economic growth and pandemic containment effectiveness (PCE) for deaths.

Dependent Variable	Quarterly GDP growth rate
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
Sample period	Q2	Q3	Q2-Q3	Q1	Q2’	Q3’	Q2’-Q3’	Q2	Q3	Q2-Q3	Q1
PCE Score (X 100)	0.105***	0.074***	0.169*	-0.003	0.105***	0.070***	0.270***	0.100***	0.053**	0.236**	-0.009
	(2.820)	(3.190)	(1.963)	(-0.177)	(2.879)	(2.838)	(3.643)	(2.955)	(2.092)	(2.562)	(-0.604)
economic stimulus spending	0.522	0.310			0.532	0.339*		0.017	0.247
	(1.364)	(1.593)			(1.395)	(1.683)		(0.042)	(1.172)
economic support index	-0.030	-0.019			-0.026	-0.017		-0.034	0.004
	(-0.927)	(-1.033)			(-0.833)	(-0.900)		(-0.848)	(0.124)
Specification	OLS	OLS	FD	OLS	OLS	OLS	FD	OLS	OLS	FD	OLS
Sample countries	CEIC							OECD+G20+Singapore
Number of observations	73	70	70	70	73	70	70	48	48	48	48
R2	0.149	0.157	0.073	0.000	0.146	0.135	0.184	0.159	0.101	0.203	0.005

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. PCE scores of Quarters 2 and 3 of 2020 in columns (1)–(3) and (8)–(10) are determined by Weeks 15–16 and Weeks 27–28 after the first confirmed death, respectively. 3. PCE scores of Quarter 1 of 2020 in columns (4) and (11) are measured by Weeks 3–4 after the first confirmed death. 4. PCE scores of Quarters 2 and 3 of 2020 in columns (5)–(7) are determined by Weeks 13–14 and Weeks 23–24 after the first confirmed death, respectively. 5. Data used in columns (8)–(11) exclude more countries with smaller size in Asia, South America, and Africa. 6. For a full list of countries used in the regressions in columns (8)–(11), see footnote 22 of the text.

Equivalently, this implies that countries with average PCE scores (0.54), such as Denmark, Malaysia, and Switzerland in Q2 of 2020, would gain 3.47 more percentage points in their GDP growth if they could improve their PCE scores for deaths to South Korea’s level (0.87) in Q2 of 2020, respectively. The lost GDP growth rate of 3.47 can be translated into 11.68 billion USD in Malaysia in Q2 of 2020. This also echoes the findings in Dai et al. (2021) that firms’ resilience to the pandemic shock is largely determined by their business performance.

To address the potential concern of endogeneity due to the reverse causality between deaths and economic stimulus (and fiscal situation), and unobserved country-specific factors, a first-difference (FD) estimate using both Q2 and Q3 of 2020 data is reported in column (3) of Table 4. Since the data collected by OxCGRT on economic stimulus and fiscal situation is time-invariant during the sample period, these controls are omitted in column (3). FD estimation here also controls other country-specific factors that could potentially affect GDP growth. The result shows that the FD coefficient of PCE is still significantly positive at 10$\%$ nominal level, which is consistent with our findings in the previous two columns.

For robustness checks, first, we run the Eq. (8) using data of Q1 of 2020 in column (4). As expected, the coefficient of PCE is -0.003 and insignificant, suggesting that pandemic containment effectiveness has no significant impact on economic growth in Q1 of 2020. Second, in columns (5)–(7), we examine the lag effect of PCE scores on GDP growth by altering the subsamples of Q2 of 2020 from weeks 15–16 to weeks 13 –14, Q3 of 2020 from weeks 27–28 to weeks 23–24, respectively. In this case, the PCE scores are measured by different pandemic weeks within same quarters. Similarly, the coefficients of PCE scores are still significantly positive throughout these columns and the FD coefficient is even more significant at 1$\%$ nominal level, implying that the positive relationship between pandemic containment effectiveness and economic growth is stable within a short period of time. Third, in columns (8)–(11) we report results excluding countries with smaller size in Asia, South America and Africa.20 We observe similar patterns throughout these columns.

Additionally, one may argue that the economic growth of a country could also be affected by country-specific factors. To address this concern, we control for GDP per capita, Gini coefficient, total population, population 65+, international trade, and government expenditure. These variables are included in the regression Eq. (1), in addition to economic stimulus spending and economic support index in Eq. (8). The results are reported in columns (1)–(3) in Table 5 .

Table 5.

Economic growth and pandemic containment effectiveness (PCE) for deaths: robustness checks.

Dependent variable	Quarterly GDP growth rate			Annual GDP growth rate
	(1)	(2)	(3)	(4)	(5)	(6)
Sample period	Q2	Q3	Q1	Q2	Q3	Q1
PCE Score (X 100)	0.101***	0.064**	0.006	0.054***	0.047***	-0.013
	(2.747)	(2.437)	(0.328)	(3.189)	(2.863)	(-0.656)
economic stimulus spending	0.160	0.161		0.001	-0.062
	(0.358)	(0.724)		(0.005)	(-0.380)
economic support index	-0.005	-0.004		-0.025*	-0.033**
	(-0.154)	(-0.203)		(-1.854)	(-2.281)
GDP per capita	0.924	0.272	-0.251
	(0.831)	(0.350)	(-0.594)
Gini coefficient	-0.456***	-0.174*	-0.023
	(-2.884)	(-1.936)	(-0.541)
total population	0.275	0.095	-0.186
	(0.305)	(0.146)	(-0.606)
population 65+	-0.390**	-0.178	-0.071
	(-2.499)	(-1.477)	(-1.277)
international trade	0.558	0.353	-0.268
	(1.006)	(1.007)	(-0.869)
government expenditure	-0.031	-0.007	-0.112
	(-0.130)	(-0.040)	(-1.418)
Specification	OLS	OLS	OLS	OLS	OLS	OLS
Sample countries	CEIC			IMF
Number of observations	73	70	70	89	85	89
R2	0.316	0.215	0.199	0.150	0.117	0.004

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. PCE scores of Quarters 2 and 3 of 2020 in columns (1),(2) and (4),(5) are determined by Weeks 15–16 and Weeks 27–28 after the first confirmed death, respectively. 3. PCE scores of Quarter 1 of 2020 in columns (3) and (6) are measured by Weeks 3–4 after the first confirmed death. 4. Annual GDP growth data retrieved from the IMF database including more countries is used in columns (4)–(6). 5. The PCE scores in columns (4)–(6) are still on a quarterly basis.

By construction, the PCE score, a linear function of the averaged residuals of regression Eq. (1), is uncorrelated with these additional contry-specific variables included in regression Eq. (1). Thus, it is not surprising to see that the coefficients of PCE in columns (1)–(3) of Table 5 are similar to those in columns (1), (2), and (4) of Table 4. We still observe significantly positive coefficients associated with PCE score, suggesting its conducive impact on GDP growth, after accounting for country-specific factors. The coefficient in Q1 is insignificant which is also consistent with our previous findings in Table 4.

Besides, we also include more countries in columns (4)–(6) in Table 5 by collecting annual GDP growth from the International Monetary Fund (IMF) database. In particular, we regress the annual GDP growth on the quarterly PCE scores in Eq. (8). Similar to our findings in columns (1), (2) and (4) of Table 4, we still observe that PCE scores are positively related to economic growth, indicating a country with higher effectiveness in terms of deaths will achieve higher GDP growth subsequently.

6. Conclusion

Does battling COVID-19 pandemic bust or save economic growth? To answer this question, we first find out that the substantial variation in the cross-country deaths is indeed associated with many contributing factors. Our empirical exercises suggest that countries with a higher population density, lower temperatures, a higher average income, and more income inequality, are predicted to be more vulnerable to the global pandemic. We find the importance of some risk and protective factors does change over time. This could be useful to policy makers in those countries hit by the pandemic later than other countries to make good use of the protective factors and to best prevent or respond to risk factors. Furthermore, even though some of these factors are either impossible or undesirable to change, there are certainly other factors that countries could improve, for example, the healthcare infrastructure, and in particular, the effectiveness of a government. For instance, the number of hospital beds are not possible to expand especially for some developing countries with financial constraints. Alternatively, our findings suggest that those developing countries could switch to improve their income inequality via wealth transfer or improve their government effectiveness instead. For developed countries, on the other hand, they have the capability to improve all the protective factors as they have less constraints. In this case, all of the countries could be well prepared not only for COVID-19 but for any such crisis in the future.

The cross-country regression analyses then allow us to identify groups of countries that are exceptionally better or worse than predicted in a systematic way. As our ranking exercises can be regarded an indirect and holistic inference on the pandemic policy efficiency, it could help policymakers to think why one country might be doing better than another, and what they can learn from that. For example, Edwards (2020) claims that the relative success of New Zealand in managing the virus could provide an opportunity for countries in the Pacific region to explore the pathway of recovery from COVID-19.

Most importantly, our cross-country empirical results show a significant positive relationship between the PCE and economic growth. In particular, countries with higher PCE score are able to achieve higher GDP growth. The key policy implication of our findings is that battling COVID-19 better helps to boost the economic growth.

In addition, a counterfactual analysis also suggests that countries with average PCE scores, such as Malaysia, would gain more GDP growth by 3.47 percentage points if they could improve their PCE scores for deaths to South Korea’s level in Q2 of 2020. This provides constructive insights for policymakers when implementing the optimal containment policy. In particular, policymakers could quantify such a trade-off in terms of monetary values, which has not been extensively discussed in the existing literature.

Finally, there is still room for improvement in our paper. First, our proposed PCE score provides a measure to rank countries on their pandemic performance. Future research may improve our findings by using state or city level data instead of country level, to allow for more variations. Next, in the main analysis, we measure international interdependency by number of international tourists and international trade shares. Moreover, we incorporate a SAR model to quantify the spatial spillovers in the robustness checks. Future research could explore models such as gravity model as a good alternative to examine the connectedness between economic activities or human mobility and respective pandemic outcomes. Moreover, it would also be interesting to investigate the relationship between pandemic containment and economic growth by accounting for the impact of vaccination. Lastly, this paper uses data up to November 2020, in order to avoid confounding factors due to new COVID-19 variants and vaccination. Future research may extend the sample period to account for new variants such as Delta and Omicron.

Declaration of Competing Interest

None.

Appendix I: Additional results on risk and protective factors

To provide an overview of the global situation, we display the time series plots of global cumulative and daily cases in Figs. A.a1 and A.b1 , respectively. An exponential form of global cumulative infections and deaths is revealed in Fig. A.a1 . Specifically, the curves were relatively flat in January and February 2020. The fact that early to middle March is the global outbreak point is also revealed in Fig. A.b1 by the sharp increase of daily cases. After April, daily infections continue growing, while daily deaths show a flattening trend. Starting from June, the number of daily infections rises quickly again although daily death cases stay relatively stable. Subsequently, we observe a second wave of pandemic outbreak as daily confirmed cases increased rapidly again at the beginning of October 2020. Table A.1 reports summary statistics of additional variables used in regressions.

Table A.1.

Summary statistics of additional variables.

	Variables	Unit	Mean	Std. D	Min	Max	Form in regression	Source
1	School closing		1.81	1.22	0	3		Oxford COVID-19 Government Response Tracker database
2	Workplace closing		1.41	1.05	0	3		Oxford COVID-19 Government Response Tracker database
3	Cancel public events		1.35	0.85	0	2		Oxford COVID-19 Government Response Tracker database
4	Restrictions on gatherings		2.39	1.61	0	4		Oxford COVID-19 Government Response Tracker database
5	Close public transport		0.58	0.73	0	2		Oxford COVID-19 Government Response Tracker database
6	Stay at home requirements		0.99	0.95	0	3		Oxford COVID-19 Government Response Tracker database
7	Restrictions on internal movement		0.95	0.92	0	2		Oxford COVID-19 Government Response Tracker database
8	Fiscal policy stimulus	%	10.08	8.83	-1.19	54.90	%	Elgin et al., 2020
9	Interest rate cut	%	28.29	33.33	-76.74	100.00	%	Elgin et al., 2020
10	Macro-financial package	%	10.61	11.54	0	64.64	%	Elgin et al., 2020
11	Other monetary measures		0.35	0.48	0	1.00	0 or 1	Elgin et al., 2020
12	BoP measures	%	1.49	3.52	0	16.30	%	Elgin et al., 2020
13	Other BoP measure		0.35	0.48	0	1.00	0 or 1	Elgin et al., 2020
14	Control of corruption		0.26	1.01	-1.33	2.21		Worldwide Governance Indicators, World Bank
15	Political stability		0.07	0.84	-2.26	1.50		Worldwide Governance Indicators, World Bank
16	Rule of law		0.28	0.94	-1.15	2.05		Worldwide Governance Indicators, World Bank
17	Retail and recreation		-18.55	18.03	-65.46	30.00		Community Mobility Reports
18	Grocery and pharmacy		2.88	15.11	-26.60	76.00		Community Mobility Reports
19	Transit stations		-14.44	18.11	-61.90	49.00		Community Mobility Reports
20	Workplaces		-24.76	16.27	-56.50	31.00		Community Mobility Reports
21	Parks		-16.31	12.34	-56.09	11.00		Community Mobility Reports
22	Residential		8.58	6.12	-12.31	27.00		Community Mobility Reports
23	Quarterly economic growth rate	%	-5.39	6.95	-38	8.15	%	CEIC Database
24	Annual economic growth rate	%	-5.31	3.59	-13.94	3.80	%	World Economic Outlook database
25	International support	dollars	1.03*1010	8.94*1010	0	8.40*1011	log	Oxford COVID-19 Government Response Tracker database

For definitions and sources, see data appendix.

Table A.2.

Risk and protective factors for deaths: robustness checks 1.

Dependent variable	log of deaths per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
sample	Monthly	Jan-April	May-Nov	105th day	Density 1K-	no China	lag test ratio
Days	0.038***	0.080***	0.032***		0.028***	0.025***	0.027***
	(7.497)	(7.704)	(5.671)		(6.229)	(6.020)	(6.483)
Days2	-0.000***	-0.001***	-0.000***		-0.000***	-0.000***	-0.000***
	(-5.096)	(-3.956)	(-5.073)		(-5.696)	(-5.782)	(-5.713)
total population	0.136	-0.183**	0.174	0.188	0.120	0.105	0.147
	(1.149)	(-2.433)	(1.304)	(1.223)	(1.028)	(0.848)	(1.254)
population 65+	-0.011	0.008	-0.016	-0.025	-0.008	-0.002	-0.005
	(-0.325)	(0.289)	(-0.439)	(-0.600)	(-0.239)	(-0.067)	(-0.163)
population density	0.189**	0.184***	0.186*	0.237*	0.228**	0.165*	0.184*
	(1.987)	(3.142)	(1.770)	(1.940)	(2.165)	(1.767)	(1.958)
temperature	-0.080***	-0.051***	-0.087***	-0.099***	-0.075***	-0.078***	-0.078***
	(-5.067)	(-4.792)	(-4.996)	(-5.089)	(-4.842)	(-5.045)	(-4.927)
rainfall	-0.012	0.169**	-0.045	-0.026	-0.023	-0.020	-0.027
	(-0.095)	(2.393)	(-0.337)	(-0.172)	(-0.182)	(-0.162)	(-0.220)
GDP per capita	0.870***	0.536***	0.904***	1.039***	0.933***	0.947***	0.947***
	(5.079)	(3.841)	(4.727)	(4.687)	(5.465)	(5.262)	(5.717)
Gini coefficient	0.044**	-0.013	0.055***	0.054**	0.043**	0.041**	0.042**
	(2.440)	(-1.028)	(2.796)	(2.183)	(2.451)	(2.274)	(2.389)
international visitors	0.186	0.121	0.195	0.149	0.199	0.151	0.171
	(1.451)	(1.531)	(1.357)	(0.862)	(1.506)	(1.133)	(1.325)
international trade	-0.189*	0.051	-0.244**	-0.201	-0.166*	-0.027	-0.172*
	(-1.857)	(0.838)	(-2.001)	(-1.577)	(-1.791)	(-0.227)	(-1.797)
health expenditure	0.224***	0.080**	0.253***	0.234***	0.215***	0.181***	0.216***
	(4.583)	(2.327)	(4.572)	(3.812)	(4.304)	(3.136)	(4.342)
hospital beds	-0.632***	-0.724***	-0.621**	-0.678**	-0.622***	-0.640***	-0.632***
	(-2.801)	(-4.391)	(-2.508)	(-2.419)	(-2.674)	(-2.825)	(-2.769)
SARS outbreak	0.111	0.188	0.068	0.126	0.180	0.051	0.102
	(0.307)	(0.734)	(0.169)	(0.293)	(0.486)	(0.139)	(0.283)
government expenditure	-0.008	0.027*	-0.017	0.006	-0.010	-0.007	-0.009
	(-0.315)	(1.682)	(-0.624)	(0.198)	(-0.425)	(-0.301)	(-0.361)
government effectiveness	-1.040***	-0.659***	-1.095***	-1.078***	-1.065***	-1.120***	-1.100***
	(-3.821)	(-2.702)	(-3.783)	(-3.244)	(-3.900)	(-4.115)	(-4.019)
rest of world infection	-0.040	0.141	-0.472*	-0.377	0.124	0.204	0.120
	(-0.250)	(1.544)	(-1.797)	(-0.970)	(0.979)	(1.596)	(1.031)
daily test ratio	0.010	0.007	0.008	0.024	0.008	0.002
	(0.353)	(0.326)	(0.267)	(0.587)	(0.288)	(0.082)
30 day lag daily test ratio							0.008
							(0.294)
Number of observations	24,241	4091	20,150	97	23,502	23,919	24,241
Adjusted R2	0.662	0.694	0.600	0.503	0.649	0.653	0.647

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first death case. 3. Column (1) reports results adding monthly dummies. 4. Columns (2) and (3) report results for subsamples during Jan-April and May-No. 2020, respectively. 5. Column (4) reports results for subsamples of day 105 since first death case. 6. Column (5) reports results excluding countris with population density larger than 1000 people per square kilometer. 7. Column (6) reports results excluding China in the sample. 8. Column (7) resports results using the 30-day lag of daily test ratio.

Table A.3.

Risk and protective factors for deaths: robustness checks 2.

Dependent variable	log of deaths per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
sample	Region	Neighborhood	no Africa	Northern	OECD	Europe	Pop. 2M+	CFR
Days	0.028***	0.020***	0.027***	0.028***	-0.006	0.002	0.029***	0.039**
	(6.144)	(6.682)	(4.896)	(6.129)	(-0.780)	(0.239)	(6.608)	(2.731)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	-0.000	-0.000	-0.000***	-0.000***
	(-5.513)	(-5.065)	(-4.842)	(-5.853)	(-0.597)	(-1.284)	(-5.886)	(-4.560)
total population	0.140	0.160	0.205	0.060	0.292	0.128	0.132	1.110***
	(1.407)	(1.519)	(1.536)	(0.515)	(1.354)	(1.023)	(0.974)	(3.039)
population 65+	-0.020	-0.019	0.001	0.004	0.026	-0.002	-0.007	0.470***
	(-0.671)	(-0.634)	(0.020)	(0.101)	(0.608)	(-0.050)	(-0.209)	(2.955)
population density	0.126*	0.185**	0.157	0.177	0.456***	0.445**	0.163	0.538*
	(1.729)	(2.222)	(1.590)	(1.488)	(3.290)	(2.371)	(1.575)	(1.826)
temperature	-0.025**	-0.068***	-0.084***	-0.071***	-0.035*	-0.064	-0.076***	-0.073**
	(-2.276)	(-3.998)	(-5.311)	(-3.500)	(-2.007)	(-1.609)	(-4.624)	(-2.592)
rainfall	-0.049	-0.084	0.218	0.005	-0.692*	0.770**	-0.012	1.711**
	(-0.449)	(-0.722)	(1.546)	(0.036)	(-1.889)	(2.276)	(-0.093)	(2.304)
GDP per capita	0.527***	0.813***	1.137***	1.066***	1.125**	0.362	0.927***	2.779***
	(2.806)	(5.268)	(5.359)	(5.573)	(2.118)	(0.824)	(5.376)	(3.245)
Gini coefficient	0.043**	0.046***	0.048**	0.028	0.034	0.003	0.037*	-0.233
	(2.480)	(2.698)	(2.323)	(1.356)	(0.746)	(0.120)	(1.880)	(-1.475)
international visitors	-0.020	0.118	0.119	0.094	0.753**	0.019	0.207	-0.892
	(-0.194)	(1.072)	(0.880)	(0.744)	(2.466)	(0.082)	(1.539)	(-1.134)
international trade	-0.100*	-0.126	-0.169	-0.155	0.096	-0.099	-0.155	-0.194
	(-1.808)	(-1.482)	(-1.577)	(-1.652)	(0.843)	(-0.755)	(-1.549)	(-1.013)
health expenditure	0.147***	0.173***	0.173***	0.206***	0.069	0.042	0.226***	-0.284
	(2.847)	(3.395)	(3.597)	(4.328)	(0.450)	(0.438)	(4.113)	(-1.486)
hospital beds	-0.401**	-0.555**	-0.734***	-0.639**	-1.442***	-0.423	-0.667***	-3.818***
	(-2.608)	(-2.584)	(-2.708)	(-2.466)	(-3.684)	(-1.304)	(-2.880)	(-3.685)
SARS outbreak	0.471*	0.213	-0.159	0.313	0.178	1.098**	0.130	-0.071
	(1.943)	(0.695)	(-0.415)	(0.840)	(0.508)	(2.339)	(0.361)	(-0.044)
government expenditure	-0.007	0.004	-0.009	-0.014	-0.003	0.045	-0.007	0.019
	(-0.315)	(0.172)	(-0.326)	(-0.523)	(-0.067)	(0.938)	(-0.281)	(0.139)
government effectiveness	-0.324	-0.800***	-1.200***	-1.237***	-0.716	-0.308	-1.141***	-3.348***
	(-1.266)	(-3.238)	(-3.757)	(-4.142)	(-0.904)	(-0.689)	(-3.938)	(-3.681)
rest of world infections	0.084		0.190	0.137	1.155***	0.853***	0.112	0.407
	(0.662)		(1.221)	(1.070)	(5.516)	(4.178)	(0.905)	(0.829)
daily test ratio	0.016	-0.004	-0.007	-0.008	-0.055	0.030	0.006
	(0.685)	(-0.171)	(-0.258)	(-0.304)	(-1.608)	(1.156)	(0.192)
rest of region infections		0.322***
		(4.383)
Number of observations	24,241	24,241	20,947	20,986	9135	10,242	22,787	6,442
Adjusted R2	0.729	0.681	0.635	0.669	0.720	0.706	0.653	0.642

Notes: 1. t-values are reported in parentheses. *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first death. 3. Column (1) reports results adding continent dummies. 4. Column (2) reports results using rest of region infections to control for spillover effect. 5. Column (3) reports results excluding countris in Africa. 6. Column (4) reports results excluding countries in the Southern Hemisphere. 7. Column (5) reports results using subsample of OECD countries. 8. Column (6) reports results using subsample of European countries. 9. Column (7) reports results excluding countris with population less than 2 million. 10. Column (8) resports results using CFR as dependent variable and a subsample of 25 countries with the hightest test ratios.

A1. Addressing underreporting

There have been many media reports, based on anecdotes and some anatomies, on how individual countries may have omitted or concealed infection and death cases. The academia has tried to infer the magnitude of underreporting under various assumptions and with the auxiliary of some additional information, such as Bommer and Vollmer (2020), Hortaçsu et al. (2021), Li et al. (2020), and Stock et al. (2020). However, most of these researches focus on individual countries. The estimated magnitude also varies vastly across different researches. To address the underreporting issue in a cross-country setup, we first show evidences from our empirical analyses that are consistent with the presence of underreporting. This motivates us to adjust our dependent variables in a systematic way to address underreporting. We then examine whether our main findings are robust to such adjustment.

In column (1) of Table 3, we have reported the full sample for death regression. Interestingly, health expenditure is significantly positive for both infections and deaths, which seems to be counterintuitive. However, if we focus on the subsample of countries with top 25% COVID-19 virus test ratios reported in column (2) of Table 3, the coefficient of health expenditure changes from positive to negative. This is no longer counterintuitive. This pattern seems to be consistent with our conjecture that death data is subject to underreporting.21

Motivated by this empirical finding, we adjust the deaths data by the country-specific universal health coverage (UHC) index and the voice and accountability (VA) index. The UHC index, provided by the World Bank, measures coverage index for essential health services that people have access to without financial hardship, including services of reproductive, maternal, newborn and child health, infectious diseases, and non-communicable diseases. UHC is presented on a scale of 0 to 100, and a higher index suggests stronger medical capability and easier access to health services. The VA index is provided by the Worldwide Governance Indicators. It reflects the degree of freedom of people in a country, including participation in selecting their government, freedom of expression, freedom of association, and free media. We normalize the VA index from the original -2.5 to 2.5 into a scale of 0 to 100, too, where a higher index implies a louder voice of people and more transparent information.

Presumably, the magnitude of underreporting in a country is largely determined by its testing regimes and reporting guidelines, which should be inversely related to UHC and VA.22 Thus, we modify our dependent variables by multiplying the number of infection or death with the square root of (100-UHC) or (100-VA) in two separate robustness checks, reported in columns (3) and (4) of Table 3.23 Under this adjustment, for a country with the lowest UHC or VA, we assume its actual deaths are nine times larger than the reported numbers. For the rest of the countries, the magnitude of underreporting decreases with UHC and VA in a declining fashion. Thus, we assume that unless a country has the full score in UHC and VA, there is always some underreporting. As we obtain in Table 3, no matter whether the adjustment index is UHC or VA, the results in columns (3) and (4) are very similar to those in column (1) of Table 3. This implies that our main findings are robust to underreporting, at least to the type of adjustment we have applied.

A2. Robustness checks

To control for the country effects, we add results of random effects (RE) and correlated random effects models (CRE) in columns of (5) and (6) in Table 3 as robustness checks. In addition, fixed effect filtered (FEF) estimates proposed by Pesaran and Zhou (2018) are also reported in column (7) of Table 3. Although the coefficients of RE, CRE, and FEF are slightly different from the baseline results in column (1), the main findings remain unchanged.

A series of additional robustness checks are presented in Tables A.2–A.5 discussed in the Appendix. Particularly, in Table A.2, we include month dummies in column (1). It turns out that the results are consistent with the benchmark findings in Tables 3. Moreover, the coefficients of the dummies generally increase over time, which motivates our second robustness check. In columns (2) and (3), we divide the full sample into two subsamples, January to April and May to November. As shown, most of the risk factors in column (3) have significantly larger coefficients than those of column (2), again suggesting the massive transmission of virus at a later stage. More interestingly, the coefficients of international trade in columns (2) and (3) of Table A.2 turn from positive to negative, after changing the sample period from Jan-April to May-Nov. This is partly due to the stringent pandemic containment and border control policies imposed by many countries at later phase of COVID-19.

To address potential concern on autocorrelation in the data, in column (4) of Table A.2, cross-country regression results using one observation for each country ($105\text{th}$ day since the first death case) are reported. Though the adjusted $R^2$ slightly decreases to 0.503 in Table A.2 from 0.647 in column (1) of Table 3, the important risk and protective factors remain valid with similar coefficients. This comparison indicates that our findings mainly come from cross-country variation, instead of time series variation, and thus autocorrelation is less of a concern. Besides, as the mechanism of death rate could be different in the epicenter and in the rest of the world, it is important to know whether our findings are robust by excluding China from the sample. Also, it is possible that the relationship between death per million people and population density is mainly driven by the size of countries. In this case, we exclude small countries with population density above 1000 people per square kilometer in column (5) of the table. It turns out that the conclusion for all the protective and risk factors remains and the impact of population density on death rate become even more pronounced. Column (6) of Table A.2 shows that excluding the initial epicenter from our sample has little impact on our main findings.

Lastly, test ratio could be endogenous since it could be considered as a containment measure depending on infections and deaths. To address this concern, we reexamine the regression (1) by replacing the current value of daily test ratio with its 30-day lag in column (7) of Table A.2, as its lagged value is less likely to be affected by the current value of deaths or infections. Overall, column (7) of Table A.2 presents similar results to those in column (1) of Table 3.

A3. Results using weekly subsamples

To allow for time-varying ${\beta }_1$ and ${\beta }_2$, we also run regression Eq. (1) using weekly subsamples and plot the estimates together with their 95% confidence intervals by week in Fig. A.2 for deaths. As there could be many random factors in the first week of a pandemic and there are too few observations in the later weeks, only results from week 2 to week 30 are presented.

Fig. A.2.

Impacts of risk and protective factors on deaths over time.

Consistent with Table 3, the same set of risk and protective factors are also identified in Fig. A.2, using weekly subsamples. More interestingly, a salient pattern is that the magnitude of some risk factors and protective factors do change over time, suggesting the importance of different factors along the course of the pandemic.

Overall, we can observe that the importance of most of the protective and risk factors increases over time. In particular, GDP per capita becomes the most prominent risk factor by the end of the sample period, while that of population density remains relatively flat. From the perspective of protective factors, government effectiveness and temperature both have consistent protective power against the pandemic over time, while that of hospital beds remains constant after five pandemic weeks. This is in line with our common sense as the government plays a critical role in containing the pandemic and the number of hospital beds within a country is very unlikely to expand in the short run.

A4. Additional robustness checks

Additional robustness checks are presented in Tables A.3–A.5. In Table A.3, we first control for spillover effects from neighboring countries. In particular, we include continent dummies in column (1), while in column (2), we account for spillovers of the pandemic from neighboring countries of the same continent. The results are consistent with the findings in Table 3. Next, we exclude African countries as those countries may be outliers due to much higher average temperature and potential underreporting issues. The results in column (3) of Table A.3 indicate that there is little impact on our main findings by excluding African countries. Moreover, since the global outbreak started around March, the climate in the northern is completely different from those of southern hemispheres. Therefore, we exclude the countries in the southern hemisphere and report the results in column (4) of Table A.3. We observe that the main risk and protective factors remain unchanged.

Additionally, we also examine the robustness by dividing countries into two subgroups. Specifically, we use samples of OECD and European countries in columns (5) and (6), respectively. Since countries belong to the same economic zone usually share similar government regimes, therefore, it accounts for all country-specific characteristics. Compared with the results shown in column (1) of Table 3, most of the factors have become less significant in the two columns. One possible explanation is that the variations of GDP per capita, Gini coefficient, and number of hospital beds are small for countries in Europe.24

The next set of robustness checks investigate whether our results are sensitive to the sample of countries included. In column (7) of Table A.3, we exclude countries with population sizes less than two million. This is similar as excluding countries with population density above 1000 people per square kilometer in column (5) of Table A.2. The results are generally similar compared to the baseline results in column (1) of Table 3. This suggests that our findings are not driven by including either too small countries or too crowded countries.

Furthermore, we experiment with an alternative measure for the death rate. In our main results, the death rate is defined as the number of deaths per million people. An alternative definition is the CFR, which represents the proportion of deaths among all the infected individuals. Presumably, the data on CFR is more likely subject to measurement error problem, as it depends on two variables: infections and deaths, which are the denominator and numerator, respectively. Besides, the reporting guidelines for infections, and for deaths, could vary substantially across countries or even over time within a country. Thus, we only restrict our analyses to those countries with the highest 25% test ratios. The results in column (8) of Table A.3 are consistent with our baseline findings. Similar to column (1) of Table 3, GDP per capita is the most important risk factor, while hospital beds and government effectiveness remain to be the most important protective factors. What is more interesting is that the magnitudes of all these factors are even larger for CFR than for the number of deaths per million people. Particularly, the coefficient of population 65+ has changed from -0.006 in the benchmark to 0.470. This result is more intuitive as age is the most prominent risk factor for death (see Karlsson et al., 2014). Also, the magnitude of government effectiveness has increased by more than three times from -1.098 to -3.348.

Next, we include alternative controls to further examine the determinants of deaths in Table A.4. More specifically, we include the percentage of people living in urban areas to control for demographic factors in column (1), and the share of employment in agriculture to account for economic conditions in column (2), respectively. As shown, the coefficient of urban population ratio is positive but insignificant in column (1) of Table A.4. On the other hand, countries with higher shares of employment in the agriculture sector may expect fewer reported deaths. Overall, the results are consistent with our main findings. It also provides a reason of why developed countries have been hit harder by the pandemic.

Also, we include other measures of government effectiveness in World Governance Indictors in order to examine the impacts of lockdown or cross-border measures on the pandemic outcomes. Columns (3)–(5) of Table A.4 show the results accounting for control of corruption, political stability, and rule of law, respectively. As expected, we observe significantly negative coefficients of political stability and rule of law, suggesting important protective factors. The results emphasize the importance of government regulation and enforcement. Additionally, the importance of government effectiveness declines, compared to our main findings in Table 3. One potential reason is that the impact of government effectiveness is partly explained by these additional three measures.

In addition, we also address spatial spillovers from neighboring countries by a Spatial AutoRegressive (SAR) model (Lee, 2002). In particular, we replace the infection rate from rest of the world (ROW) with a spatial lag term in column (6) of Table A.4. The spatial lag term is defined as the sum of death rates in the rest of the countries, weighted by a weighting matrix which contains information of economic distance. The economic distance in the weighting matrix is computed by the international trade shares among the 100 countries. As shown in the table, the coefficient of spatial lag term is significantly positive, indicating that higher death rates in neighboring countries, weighted by the economic distance, lead to a higher pandemic outbreak in country $i$. Also, the results of both risk and protective factors still remain, which implies that our empirical results are robust to different measures of pandemic spillovers from the rest of the world.

Besides, we also examine the robustness by including variables of government debt, industrial production output, and population mobility in the regression Eq. (1) separately and all together. The results are reported in Tables A.5. Particularly, we collect the information of government debt ratio from CEIC, industrial production ratio from the world bank, and the Google mobility index from the community mobility report. The results show that our main findings are almost unchanged.

Finally, one may argue that the positive relationship between PCE score and economic growth found in our empirical results is simply because those countries were hit less by the pandemic and hence, incurred less economic loss. Consequently, we conduct another robustness check by replacing the PCE score with raw death measures as our explanatory variable. Table A.6 lists the regression results of economic growth over deaths.

In columns (1) and (2), we observe significantly negative coefficients of death rate in Q2 and Q3, suggesting that countries with higher death rate, achieve lower economic growth in the subsequent quarter of 2020. This is consistent with our main empirical findings. After accounting for country specific fixed effects, however, we find significantly positive coefficient of death rate in column (3), which is counterintuitive. On the other hand, the results of Q1 in column (4) is still insignificant indicating the fact that the GDP growth in Q1 is not heavily affected by the pandemic. Also, we still find similar results after controlling for other country-specific factors included in regression Eq. (1) in columns (5) and (6). In addition, similar results are obtained even though the coefficients become less significant if we exclude countries with small size in Asia, South America, and Africa in columns (7)–(10).

A5. Additional results for infections

We now supplement our results by switching to the regression Eq. (1) with infection rate as the dependent variable. Firstly, in column (1) of Table A.7, a coefficient of 1.207 for GDP per capita interpreted as the elasticity of infections with respect to GDP per capita, implies that a country with a 100% higher GDP per capita may expect 120.7% more reported cumulative infections per million people, all else being equal.

Population density is the second most important contributing factor of infections, suggesting that a country with a dense population is more vulnerable to the spread of COVID-19. The elasticity of 0.319 implies that all else being equal, a country with a one standard deviation higher population density than the sample average, expects 112.7% more reported infections per million people.

Income inequality measured by Gini coefficient is the third most important factor that induces more reported infections. The coefficient 0.039 suggests that on average, a country with a higher Gini coefficient than the cross-country average by one standard deviation could witness 31.8% more cumulative infections per million people.

Among the two most important protective factors, government effectiveness is of our key interest. Its protective effect is surprisingly remarkable. The coefficient -0.870 suggests that an increase in government effectiveness index by one standard deviation from the sample average, a value close to Italy’s, to the value of South Korea, would reduce unit infections by 76.6%, holding other explanatory variables constant.

As the second robust protective factor, temperature also has a large negative impact on the COVID-19 infections, indicating that a higher temperature is not conducive to the survival and spread of the viruses. The coefficient of -0.068 infers that countries with 11.01 ${}^{\circ }$C higher from the sample average (14.78 ${}^{\circ }$C) expect 74.9% lower unit infections. The impacts of risk and protective factors on infections are visualized in Fig. A.3 below.

Fig. A.3.

Impacts of risk and protective factors on infections.

Comparison between Figs. 2 and A.3 also reveals a few interesting findings. First, GDP per capita, population density, and Gini coefficient are also the three most important risk factors for infections with relatively larger magnitude. Second, some predetermined factors are less pronounced on infections than on deaths. In particular, the coefficients of hospital beds becomes insignificant when using infection rate as the dependent variable, suggesting that it is no longer a protective factor for infections. The coefficient of temperature in column (1) of Table 3 is -0.078, that is 1.15 times compared to their corresponding coefficients for infections reported in column (1) of Table A.7.

Next, we also allow for time-varying coefficients by using weekly subsamples for our baseline regression. Overall, these changes are consistent with our expectation and echo the time-varying patterns of parameters highlighted in Fig. A.2. The only exception is that hospital beds is no longer a protective factor for infection rate and hence, it is not reported in Fig. A.4 .

Table A.4.

Risk and protective factors for deaths: robustness checks 3.

Dependent variable	log of deaths per million population
	(1)	(2)	(3)	(4)	(5)	(6)
sample	Urban	Agriculture	Corruption	Stability	Law	Spatial
Days	0.027***	0.025***	0.027***	0.026***	0.026***	0.021***
	(6.149)	(5.169)	(5.925)	(5.611)	(5.490)	(78.034)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***
	(-5.554)	(-4.829)	(-5.460)	(-5.229)	(-5.135)	(-43.886)
total population	0.119	0.135	0.113	0.017	0.100	0.109
	(0.992)	(1.224)	(0.939)	(0.135)	(0.852)	(1.309)
population 65+	-0.002	-0.010	-0.007	0.011	0.006	-0.010
	(-0.061)	(-0.322)	(-0.227)	(0.338)	(0.174)	(-0.389)
population density	0.188*	0.175*	0.174*	0.132	0.187**	0.158**
	(1.980)	(1.904)	(1.844)	(1.396)	(2.134)	(2.376)
temperature	-0.080***	-0.083***	-0.075***	-0.069***	-0.076***	-0.044***
	(-5.211)	(-5.611)	(-4.808)	(-4.590)	(-4.818)	(-3.553)
rainfall	-0.005	0.122	-0.024	-0.013	-0.055	0.018
	(-0.043)	(0.945)	(-0.186)	(-0.101)	(-0.446)	(0.205)
GDP per capita	0.768***	0.538**	0.975***	0.955***	1.007***	0.551***
	(3.830)	(2.579)	(5.784)	(5.964)	(5.907)	(3.940)
Gini coefficient	0.038**	0.034**	0.037**	0.045**	0.040**	0.034**
	(2.115)	(2.050)	(2.013)	(2.608)	(2.251)	(2.345)
international visitors	0.156	0.115	0.142	0.172	0.108	0.038
	(1.161)	(1.016)	(1.094)	(1.402)	(0.817)	(0.401)
international trade	-0.152	-0.124	-0.166	-0.124	-0.182*	-0.123*
	(-1.536)	(-1.335)	(-1.649)	(-1.319)	(-1.838)	(-1.762)
health expenditure	0.207***	0.196***	0.231***	0.217***	0.237***	0.167***
	(4.137)	(4.263)	(4.563)	(4.572)	(4.573)	(4.066)
hospital beds	-0.666***	-0.831***	-0.706***	-0.587***	-0.722***	-0.468***
	(-2.959)	(-3.726)	(-2.968)	(-2.891)	(-3.293)	(-3.147)
SARS outbreak	0.138	-0.001	0.102	0.083	0.091	0.043
	(0.382)	(-0.004)	(0.282)	(0.237)	(0.250)	(0.182)
government expenditure	-0.012	-0.014	0.003	-0.020	-0.004	-0.004
	(-0.505)	(-0.591)	(0.108)	(-0.827)	(-0.174)	(-0.190)
government effectiveness	-1.060***	-0.934***	-0.677	-0.799***	-0.301	-0.804***
	(-3.781)	(-3.522)	(-1.570)	(-2.886)	(-0.602)	(-3.954)
rest of world infection	0.136	0.173	0.142	0.164	0.176
	(1.074)	(1.258)	(1.102)	(1.217)	(1.287)
daily test ratio	0.008	0.014	0.007	0.004	0.001	0.124**
	(0.299)	(0.534)	(0.261)	(0.145)	(0.025)	(2.130)
urban population ratio	0.012
	(1.604)
employment in agriculture		-0.038***
		(-3.534)
control of corruption			-0.419
			(-1.201)
political stability				-0.546**
				(-2.303)
rule of law					-0.829*
					(-1.929)
spatial lag						0.445***
						(90.063)
Number of observations	24,241	24,241	24,241	24,241	24,241	33,000
Adjusted R2	0.652	0.665	0.650	0.658	0.656	N.A.

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first death. 3. Column (1) reports results including urban population ratio as an additional explanatory variable. 4. Column (2) resports results including employment share in agriculture as an additional explanatory variable. 5. Column (3) resports results including control of corruption as an additional explanatory variable. 6. Column (4) resports results incluing political stability as an additional explanatory variable. 7. Column (5) resports results including rule of law as an additional explanatory variable. 8. Column (6) reports results replacing rest of world infections with a spatial lag and using the robutness standard errors.

Table A.5.

Risk and protective factors for deaths: robustness checks 4.

Dependent variable	log of deaths per million population
	(1)	(2)	(3)	(4)	(5)	(6)
sample	Mobility	Debt	Industrial	Mob+Ind+Debt	Regime	GHS
Days	0.037***	0.028***	0.028***	0.040***	0.028***	0.028***
	(7.388)	(5.235)	(6.254)	(6.424)	(6.403)	(6.600)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***
	(-6.490)	(-5.202)	(-5.634)	(-6.357)	(-5.766)	(-5.958)
total population	0.114	0.232*	0.169	0.182	0.153	0.010
	(0.930)	(1.716)	(1.563)	(1.278)	(1.334)	(0.077)
population 65+	-0.027	0.017	-0.039	-0.006	-0.042	-0.021
	(-0.693)	(0.471)	(-1.039)	(-0.146)	(-0.868)	(-0.586)
population density	0.118	0.257***	0.144	0.110	0.216**	0.213**
	(1.341)	(2.641)	(1.459)	(1.171)	(2.137)	(2.242)
temperature	-0.070***	-0.075***	-0.074***	-0.077***	-0.078***	-0.080***
	(-4.677)	(-4.771)	(-4.575)	(-4.320)	(-5.330)	(-5.136)
rainfall	0.127	0.204	-0.040	0.256**	-0.037	-0.010
	(1.076)	(1.373)	(-0.320)	(2.045)	(-0.315)	(-0.090)
GDP per capita	0.816***	1.126***	1.064***	0.984***	0.927***	0.902***
	(5.058)	(5.400)	(6.811)	(4.841)	(5.879)	(5.519)
Gini coefficient	0.019	0.047**	0.031*	0.021	0.035*	0.045***
	(0.966)	(2.412)	(1.706)	(1.169)	(1.859)	(2.638)
international visitors	0.164	0.111	0.142	0.127	0.216	0.116
	(1.282)	(0.813)	(1.205)	(1.051)	(1.633)	(0.888)
international trade	-0.007	-0.212**	-0.218***	-0.046	-0.143	-0.140
	(-0.073)	(-2.224)	(-2.658)	(-0.446)	(-1.607)	(-1.553)
health expenditure	0.188***	0.231***	0.224***	0.166***	0.197***	0.188***
	(3.384)	(4.837)	(4.700)	(2.941)	(4.270)	(3.590)
hospital beds	-0.514**	-0.678**	-0.493**	-0.572**	-0.520**	-0.562**
	(-2.206)	(-2.306)	(-2.156)	(-2.040)	(-1.994)	(-2.326)
SARS outbreak	-0.060	-0.014	0.306	-0.011	0.164	-0.052
	(-0.185)	(-0.041)	(0.905)	(-0.038)	(0.452)	(-0.157)
government expenditure	0.030	0.030	0.005	0.045*	0.005	-0.006
	(1.331)	(1.049)	(0.219)	(1.849)	(0.205)	(-0.289)
government effectiveness	-1.047***	-1.419***	-1.191***	-1.250***	-1.248***	-1.343***
	(-4.098)	(-4.676)	(-4.657)	(-4.695)	(-4.462)	(-4.411)
rest of world infections	0.150	0.154	0.100	0.206	0.107	0.109
	(1.275)	(1.053)	(0.796)	(1.524)	(0.873)	(0.896)
daily test ratio	-0.001	0.005	0.011	-0.022	0.012	0.002
	(-0.033)	(0.195)	(0.435)	(-1.017)	(0.449)	(0.069)
retail and recreation	-0.023***			-0.020***
	(-4.085)			(-4.363)
grocery and pharmacy	0.011***			0.012***
	(2.721)			(3.286)
transit stations	0.004**			0.003*
	(2.199)			(1.827)
workplaces	-0.007			-0.008
	(-0.969)			(-1.058)
parks	-0.004			-0.001
	(-0.784)			(-0.163)
residential	0.005			0.021
	(0.233)			(1.137)
debt ratio		-0.005		-0.006
		(-1.253)		(-1.650)
industrial			-0.025*	-0.015
			(-1.686)	(-1.107)
political regimes					0.279
					(1.412)
GHS						0.034**
						(1.995)
Number of observations	21,051	20,409	23,480	17,889	24,241	24,241
Adjusted R2	0.703	0.654	0.671	0.722	0.653	0.659

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Column (1) reports results including six google mobility indices as additional explanatory variables. 3. Column (2) reports results including debt ratio as an additional explanatory variable. 4. Column (3) reports results including industrial ratio as an additional explanatory variable. 5. Column (4) reports results for subsamples including political regime as an additional explanatory variable. 6. Column (5) reports results including Global Health Security as an additional explanatory variable. 7. Column (6) reports results including six google mobility indices, debt ratio, and industrial ratio as additional explanatory variables. 8. Column (7) reports results including economic stimulus spending and international support as additional explanatory variables. 9. Column (8) reports results including seven containment policy indices as additional explanatory variables.

Table A.6.

Economic growth and deaths.

Dependent Variable	Quarterly GDP growth rate
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Sample period	Q2	Q3	Q2-Q3	Q1	Q2	Q3	Q2	Q3	Q2-Q3	Q1
Deaths per million population	-1.073**	-0.831**	4.946***	-0.347	-1.160*	-0.790**	-1.065*	-0.511	4.205***	0.082
	(-2.077)	(-2.389)	(5.631)	(-1.148)	(-1.897)	(-2.020)	(-1.768)	(-1.080)	(3.028)	(0.246)
economic stimulus spending	0.517	0.352*			0.146	0.114	-0.026	0.255
	(1.299)	(1.777)			(0.287)	(0.477)	(-0.058)	(1.206)
economic support index	-0.021	-0.011			-0.008	-0.007	-0.026	0.010
	(-0.688)	(-0.600)			(-0.252)	(-0.317)	(-0.643)	(0.318)
GDP per capita					1.291	0.751
					(1.018)	(0.989)
Gini coefficient					-0.428***	-0.162*
					(-2.717)	(-1.767)
total population					0.082	0.059
					(0.086)	(0.089)
population 65+					-0.334**	-0.146
					(-2.251)	(-1.236)
international trade					0.590	0.388
					(1.050)	(1.115)
government expenditure					-0.042	-0.006
					(-0.175)	(-0.035)
Specification	OLS	OLS	FD	OLS	OLS	OLS	OLS	OLS	FD	OLS
Sample countries	CEIC						OECD+G20+Singapore
Number of observations	73	70	70	70	73	70	48	48	48	48
R2	0.093	0.115	0.312	0.020	0.269	0.196	0.092	0.053	0.227	0.001

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Deaths of Quarters 2 and 3 of 2020 in columns (1)–(3) and (5)–(9) are determined by averaged deaths of Calendar Weeks 15–16 and Weeks 27–28, respectively. 3. Deaths of Quarter 1 of 2020 in columns (4) and (10) are measured by the averaged death rate of Calendar Weeks 3–4. ”4. Data used in columns (7)–(10) exclude more countries with smaller size in Asia, South America, and Africa.

” 5. For a full list of countries used in the regressions in columns (7)–(10), see footnote 22 of the text.

Table A.7.

Risk and protective factors for infections.

Dependent variable	log of infections per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
sample	Full	TOP25	UHC adjusted	VA adjusted	RE	CRE	FEF
Days	0.029***	-0.025***	0.029***	0.029***	0.034***	0.019***	0.034***
	(3.155)	(-3.054)	(2.738)	(2.823)	(68.373)	(36.515)	(3.671)
Days2	-0.000***	0.000	-0.000***	-0.000***	-0.000***	-0.000***	0.000***
	(-3.371)	(1.631)	(-3.196)	(-3.271)	(-59.190)	(-29.572)	(-3.687)
total population	0.012	-0.082	-0.015	0.028	-0.000	0.060	0.000
	(0.118)	(-0.812)	(-0.147)	(0.276)	(-0.002)	(0.568)	(-0.003)
population 65+	-0.080**	-0.093**	-0.077**	-0.104***	-0.090***	-0.065**	-0.091***
	(-2.448)	(-2.572)	(-2.345)	(-3.166)	(-2.891)	(-2.041)	(-2.817)
population density	0.319***	0.215***	0.323***	0.341***	0.329***	0.327***	0.329***
	(3.860)	(3.763)	(3.850)	(3.908)	(3.982)	(3.878)	(4.020)
temperature	-0.068***	-0.027***	-0.069***	-0.067***	-0.066***	-0.073***	-0.066***
	(-4.605)	(-3.364)	(-4.399)	(-4.586)	(-4.411)	(-4.792)	(-4.092)
rainfall	-0.042	0.392*	-0.055	-0.047	-0.056	-0.068	-0.056
	(-0.334)	(1.935)	(-0.422)	(-0.377)	(-0.504)	(-0.598)	(-0.410)
GDP per capita	1.207***	0.260	1.138***	1.206***	1.132***	1.297***	1.131***
	(6.654)	(1.177)	(6.105)	(6.497)	(6.832)	(7.660)	(6.691)
Gini coefficient	0.039**	0.026	0.043**	0.035*	0.033*	0.052***	0.033*
	(2.072)	(0.912)	(2.175)	(1.828)	(1.888)	(2.875)	(1.699)
international visitors	0.017	0.123	0.002	0.066	0.010	0.021	0.010
	(0.119)	(0.632)	(0.013)	(0.438)	(0.085)	(0.172)	(0.074)
international trade	-0.171**	0.140***	-0.146*	-0.136*	-0.199**	-0.289***	-0.199***
	(-2.206)	(3.460)	(-1.814)	(-1.875)	(-2.301)	(-3.263)	(-2.617)
health expenditure	0.150***	0.048	0.132**	0.136**	0.174***	0.142***	0.174***
	(2.649)	(0.866)	(2.235)	(2.380)	(3.406)	(2.715)	(3.281)
hospital beds	-0.128	-0.453*	-0.146	-0.012	-0.063	-0.122	-0.062
	(-0.511)	(-1.853)	(-0.569)	(-0.047)	(-0.341)	(-0.643)	(-0.247)
SARS outbreak	-0.191	0.389	-0.253	-0.192	-0.151	-0.240	-0.150
	(-0.490)	(1.054)	(-0.632)	(-0.495)	(-0.518)	(-0.804)	(-0.380)
government expenditure	0.008	0.060	0.005	0.010	0.009	-0.005	0.009
	(0.297)	(1.589)	(0.196)	(0.370)	(0.392)	(-0.200)	(0.333)
government effectiveness	-0.870***	-0.608***	-0.847***	-1.008***	-0.908***	-0.750***	-0.909***
	(-3.298)	(-3.652)	(-3.135)	(-3.892)	(-3.585)	(-2.897)	(-3.434)
rest of world infections	0.485**	1.745***	0.641***	0.631***	0.276***	-1.507***
	(2.404)	(12.346)	(2.791)	(2.821)	(28.941)	(-40.559)
ROW infections time average						1.501***	0.274
						(34.408)	(1.415)
daily test ratio	0.087**		0.086**	0.094**	0.144***
	(2.262)		(2.155)	(2.391)	(42.814)
daily test ratio time average						0.555***	0.145***
						(43.206)	(3.298)
Number of observations	27,724	7213	27,724	27,724	27,724	27,724	27,724
Adjusted R2	0.766	0.880	0.762	0.765	N.A.	N.A.	N.A.

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first infection case. 3. Column (2) reports results of a subsample of 25 countries with the hightest test ratio. 4. Columns (3) and (4) report results of using infections adjusted by UHC and VA to address underreporting concern. UHC and VA refer to the universal healthcare and voice and accountablity indices, respectively, constructed by the World Bank. 5. Column (5) reports results of the random effect model based on the specification in column (1). 6. Column (6) reports results of the correlated random effect model by including the time average of the time-variant variables, based on the specification in column (1). 7. Column (7) appies the fixed-effect filter proposed by Pesaran and Zhou (2018).

Table A.8.

Risk and protective factors for infections: robustness checks 1.

Dependent variable	log of infections per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
sample	Monthly	Jan-April	May-Nov	day 105	Density 1K-	no China	lag test ratio
Days	0.039***	0.074***	0.021		0.029***	0.018***	0.025**
	(3.822)	(4.288)	(1.533)		(3.109)	(3.718)	(2.571)
Days2	-0.000***	-0.000***	-0.000***		-0.000***	-0.000***	-0.000***
	(-5.317)	(-3.374)	(-2.630)		(-3.291)	(-3.916)	(-2.877)
total population	0.040	-0.253**	0.097	0.120	0.030	0.021	0.018
	(0.416)	(-2.107)	(0.837)	(0.970)	(0.289)	(0.208)	(0.175)
population 65+	-0.077**	-0.030	-0.094**	-0.095**	-0.080**	-0.077**	-0.076**
	(-2.460)	(-0.935)	(-2.434)	(-2.414)	(-2.482)	(-2.439)	(-2.360)
population density	0.327***	0.196***	0.360***	0.326***	0.275***	0.319***	0.319***
	(4.007)	(3.501)	(3.606)	(2.947)	(3.014)	(3.824)	(3.833)
temperature	-0.068***	-0.028*	-0.085***	-0.068***	-0.070***	-0.068***	-0.070***
	(-4.762)	(-1.798)	(-4.866)	(-3.373)	(-4.490)	(-4.755)	(-4.807)
rainfall	-0.065	0.165*	-0.112	-0.118	-0.056	-0.057	-0.044
	(-0.550)	(1.675)	(-0.787)	(-0.738)	(-0.430)	(-0.462)	(-0.359)
GDP per capita	1.220***	0.786***	1.341***	1.468***	1.185***	1.210***	1.233***
	(6.733)	(5.629)	(6.101)	(6.227)	(6.495)	(6.714)	(6.829)
Gini coefficient	0.037*	-0.010	0.058**	0.026	0.039**	0.037**	0.042**
	(1.909)	(-0.607)	(2.501)	(0.888)	(2.078)	(1.989)	(2.217)
international visitors	0.028	0.102	-0.009	0.010	0.035	0.018	0.017
	(0.192)	(0.928)	(-0.052)	(0.052)	(0.231)	(0.123)	(0.109)
international trade	-0.175**	0.161	-0.304**	-0.099	-0.170**	-0.129	-0.166**
	(-2.053)	(1.313)	(-2.428)	(-1.032)	(-2.146)	(-1.242)	(-2.160)
health expenditure	0.150***	0.043	0.188***	0.152**	0.160***	0.143**	0.143**
	(2.647)	(0.676)	(2.694)	(2.149)	(2.778)	(2.189)	(2.576)
hospital beds	-0.136	-0.149	-0.142	-0.036	-0.129	-0.128	-0.141
	(-0.563)	(-0.763)	(-0.477)	(-0.107)	(-0.527)	(-0.528)	(-0.573)
SARS outbreak	-0.057	-0.289	-0.173	0.246	-0.226	-0.119	-0.198
	(-0.148)	(-0.786)	(-0.364)	(0.536)	(-0.574)	(-0.314)	(-0.513)
government expenditure	0.004	0.023	0.002	-0.009	0.011	0.005	0.005
	(0.159)	(0.904)	(0.081)	(-0.286)	(0.415)	(0.189)	(0.202)
government effectiveness	-0.836***	-0.494*	-0.987***	-0.861**	-0.896***	-0.848***	-0.851***
	(-3.317)	(-1.947)	(-3.361)	(-2.528)	(-3.302)	(-3.279)	(-3.184)
rest of world infection	0.264	0.454***	0.548	1.250*	0.476**	0.727***	0.577***
	(0.882)	(2.952)	(0.856)	(1.851)	(2.309)	(6.487)	(2.928)
daily test ratio	0.083**	0.096***	0.078*	0.103**	0.090**	0.086**
	(2.143)	(3.499)	(1.746)	(2.101)	(2.256)	(2.176)
30 day lag daily test ratio							0.075**
							(2.187)
Number of observations	27,724	6624	21,100	100	26,883	27,395	27,724
Adjusted R2	0.784	0.741	0.618	0.570	0.764	0.778	0.763

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first infection case except for column (8). 3. Column (1) reports results adding monthly dummies. 4. Columns (2) and (3) report results for subsamples during Jan-April and May-No. 2020, respectively. 5. Column (4) reports results for subsamples of day 105 since first infection case. 6 Column (5) reports results excluding countris with population density larger than 1000 people per square kilometer. 7. Column (6) reports results excluding China in the sample. 8. Column (7) resports results using the 30-day lag of daily test ratio.

Table A.9.

Risk and protective factors for infections: robustness checks 2.

Dependent variable	log of infections per million population
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
sample	Region	Neighborhood	no Africa	Northern	OECD	Europe	Pop. 2M+	50 Cases
Days	0.036***	0.025***	0.027**	0.027**	-0.007	-0.022***	0.031***	-0.028***
	(4.349)	(5.855)	(2.430)	(2.580)	(-0.731)	(-2.950)	(3.369)	(-3.508)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	0.000	0.000**	-0.000***	0.000**
	(-4.365)	(-4.593)	(-2.675)	(-2.813)	(0.197)	(2.143)	(-3.566)	(2.531)
total population	-0.069	0.017	0.052	-0.081	-0.027	-0.107	-0.007	-0.097
	(-0.890)	(0.175)	(0.475)	(-0.887)	(-0.168)	(-1.103)	(-0.052)	(-0.897)
population 65+	-0.086***	-0.102***	-0.093**	-0.082**	-0.040	-0.090**	-0.079**	-0.089**
	(-3.621)	(-3.639)	(-2.481)	(-2.256)	(-1.350)	(-2.031)	(-2.224)	(-2.206)
population density	0.217***	0.315***	0.290***	0.345***	0.259***	0.219*	0.323***	0.280***
	(2.739)	(4.092)	(3.221)	(3.272)	(3.574)	(1.718)	(3.420)	(5.044)
temperature	-0.013	-0.061***	-0.078***	-0.071***	-0.022*	-0.035	-0.070***	-0.034***
	(-0.975)	(-4.060)	(-5.231)	(-3.922)	(-1.767)	(-1.241)	(-4.446)	(-4.342)
rainfall	-0.022	-0.114	0.270*	-0.000	-0.539*	0.154	-0.045	0.411**
	(-0.188)	(-0.972)	(1.944)	(-0.001)	(-1.699)	(0.711)	(-0.340)	(2.260)
GDP per capita	0.649***	0.952***	1.287***	1.275***	0.860*	0.521*	1.182***	0.382*
	(3.465)	(5.665)	(5.910)	(6.091)	(1.897)	(1.696)	(6.050)	(1.869)
Gini coefficient	0.039**	0.049**	0.055***	0.041**	0.040	0.005	0.041**	0.032
	(2.156)	(2.626)	(2.782)	(2.033)	(1.292)	(0.276)	(2.017)	(1.193)
international visitors	-0.133	-0.027	-0.036	-0.071	0.507**	0.170	-0.007	0.192
	(-1.185)	(-0.217)	(-0.287)	(-0.582)	(2.364)	(0.984)	(-0.042)	(0.991)
international trade	-0.067	-0.130*	-0.171*	-0.151*	0.139*	0.056	-0.171*	0.093**
	(-1.240)	(-1.707)	(-1.944)	(-1.783)	(1.931)	(0.658)	(-1.973)	(2.773)
health expenditure	0.074	0.110**	0.116**	0.128**	0.086	0.103	0.142**	0.080
	(1.441)	(2.040)	(2.122)	(2.209)	(0.998)	(1.580)	(2.247)	(1.419)
hospital beds	0.046	-0.136	-0.089	-0.081	-0.613*	-0.102	-0.111	-0.452*
	(0.280)	(-0.586)	(-0.325)	(-0.288)	(-1.918)	(-0.358)	(-0.423)	(-1.797)
SARS outbreak	0.194	-0.086	-0.439	-0.025	-0.064	0.829*	-0.195	0.262
	(0.708)	(-0.257)	(-1.091)	(-0.063)	(-0.217)	(1.916)	(-0.485)	(0.699)
government expenditure	0.001	0.028	0.008	0.014	0.011	0.044	0.007	0.057
	(0.038)	(1.071)	(0.272)	(0.508)	(0.341)	(1.132)	(0.248)	(1.531)
government effectiveness	-0.040	-0.449*	-0.840***	-0.939***	-0.367	-0.517	-0.827***	-0.884***
	(-0.157)	(-1.817)	(-2.657)	(-3.187)	(-0.713)	(-1.593)	(-2.893)	(-4.603)
rest of world infection	0.327*		0.539**	0.543**	1.245***	1.573***	0.458**	1.473***
	(1.843)		(2.363)	(2.452)	(5.255)	(11.884)	(2.279)	(8.851)
daily test ratio	0.081***	0.070**	0.073*	0.067*	0.005	0.043	0.091**	0.088**
	(2.801)	(2.147)	(1.705)	(1.731)	(0.151)	(1.682)	(2.168)	(2.567)
rest of region infections		0.449***
		(9.115)
Number of observations	27,724	27,724	23,850	24,009	9976	11,129	25,841	6,625
Adjusted R2	0.814	0.811	0.766	0.775	0.816	0.841	0.764	0.822

Notes: 1. t-values are reported in parentheses. *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first infection. 3. Column (1) reports results adding continent dummies. 4. Column (2) reports results using rest of region infections to control for spillover effect. 5. Column (3) reports results excluding countris in Africa. 6. Column (4) reports results excluding countries in the Southern Hemisphere. 7. Column (5) reports results using subsample of OECD countries. 8. Column (6) reports results using subsample of European countries. 9. Column (7) reports results excluding countris with population less than 2 million. 10. Column (8) resports results using observations since first 50 infection cases, instead of the first case.

Table A.10.

Risk and protective factors for infections: robustness checks 3.

Dependent variable	log of infections per million population
	(1)	(2)	(3)	(4)	(5)	(6)
sample	Urban	Agriculture	Corruption	Stability	Law	Spatial
Days	0.030***	0.030***	0.029***	0.029***	0.030***	0.044***
	(3.296)	(3.221)	(3.073)	(3.141)	(3.203)	(137.702)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***
	(-3.484)	(-3.409)	(-3.296)	(-3.364)	(-3.418)	(-98.891)
total population	-0.050	-0.052	-0.039	-0.180	-0.061	-0.023
	(-0.481)	(-0.614)	(-0.373)	(-1.627)	(-0.602)	(-0.209)
population 65+	-0.074**	-0.088***	-0.083**	-0.059*	-0.068**	-0.055*
	(-2.209)	(-2.989)	(-2.561)	(-1.800)	(-2.123)	(-1.672)
population density	0.317***	0.283***	0.311***	0.238***	0.331***	0.304***
	(4.002)	(3.729)	(3.695)	(2.909)	(4.311)	(3.516)
temperature	-0.071***	-0.078***	-0.067***	-0.057***	-0.068***	-0.042***
	(-5.056)	(-5.453)	(-4.622)	(-4.301)	(-4.556)	(-2.623)
rainfall	0.006	0.227*	-0.035	-0.014	-0.070	0.031
	(0.057)	(1.894)	(-0.270)	(-0.105)	(-0.558)	(0.263)
GDP per capita	0.813***	0.452**	1.218***	1.175***	1.252***	0.756***
	(4.222)	(2.111)	(6.771)	(6.805)	(6.906)	(4.166)
Gini coefficient	0.030*	0.024	0.034*	0.040**	0.038**	0.057***
	(1.687)	(1.444)	(1.801)	(2.343)	(1.998)	(3.020)
international visitors	0.003	-0.041	-0.024	0.042	-0.073	-0.160
	(0.019)	(-0.368)	(-0.166)	(0.321)	(-0.490)	(-1.288)
international trade	-0.129*	-0.075	-0.162*	-0.102	-0.192**	-0.150*
	(-1.678)	(-1.034)	(-1.961)	(-1.399)	(-2.390)	(-1.662)
health expenditure	0.136**	0.102**	0.161***	0.151***	0.176***	0.125**
	(2.516)	(2.259)	(2.860)	(2.998)	(3.075)	(2.329)
hospital beds	-0.204	-0.522**	-0.195	-0.093	-0.230	-0.280
	(-0.877)	(-2.216)	(-0.743)	(-0.433)	(-0.952)	(-1.448)
SARS outbreak	-0.131	-0.324	-0.174	-0.195	-0.186	-0.531*
	(-0.347)	(-0.980)	(-0.453)	(-0.548)	(-0.492)	(-1.746)
government expenditure	-0.003	0.001	0.021	-0.012	0.015	0.017
	(-0.112)	(0.057)	(0.769)	(-0.490)	(0.558)	(0.685)
government effectiveness	-0.785***	-0.560**	-0.420	-0.440	0.143	-0.754***
	(-2.930)	(-2.377)	(-1.058)	(-1.503)	(0.312)	(-2.854)
rest of world infection	0.465**	0.465**	0.494**	0.496**	0.487**
	(2.359)	(2.366)	(2.428)	(2.462)	(2.438)
test ratio	0.087**	0.095***	0.090**	0.081**	0.084**	0.304***
	(2.260)	(2.956)	(2.338)	(2.309)	(2.133)	(4.038)
urban population ratio	0.025***
	(3.547)
employment in agriculture		-0.062***
		(-5.368)
control of corruption			-0.422
			(-1.529)
political stability				-0.752***
				(-2.771)
rule of law					-1.025***
					(-2.687)
spatial lag						0.413***
						(99.061)
Number of observations	27,724	27,724	27,724	27,724	27,724	33,000
Adjusted R2	0.777	0.794	0.768	0.777	0.773	N.A.

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Days stands for the number of days since first infection. 3. Column (1) reports results including urban population ratio as an additional explanatory variable. 4. Column (2) resports results including employment share in agriculture as an additional explanatory variable. 5. Column (3) resports results including control of corruption as an additional explanatory variable. 6. Column (4) resports results incluing political stability as an additional explanatory variable. 7. Column (5) resports results including rule of law as an additional explanatory variable. 8. Column (6) reports results replacing rest of world infections with a spatial lag and using the robutness standard errors.

Table A.11.

Risk and protective factors for infections: robustness checks.

Dependent variable	log of infections per million population
	(1)	(2)	(3)	(4)	(5)	(6)
sample	Mobility	Debt	Industrial	Mob+Ind+Debt	Regime	GHS
Days	0.031***	0.028**	0.031***	0.030***	0.030***	0.029***
	(4.147)	(2.478)	(3.256)	(3.678)	(3.192)	(3.147)
Days2	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***	-0.000***
	(-4.642)	(-2.819)	(-3.431)	(-4.329)	(-3.403)	(-3.361)
total population	-0.015	0.003	0.042	-0.002	0.017	0.026
	(-0.130)	(0.029)	(0.461)	(-0.015)	(0.171)	(0.210)
population 65+	-0.053	-0.077**	-0.117***	-0.034	-0.098**	-0.078**
	(-1.312)	(-2.332)	(-3.159)	(-0.798)	(-2.019)	(-2.247)
population density	0.213**	0.314***	0.271***	0.176*	0.334***	0.315***
	(2.445)	(3.614)	(3.185)	(1.992)	(3.594)	(3.698)
temperature	-0.056***	-0.066***	-0.067***	-0.066***	-0.068***	-0.068***
	(-4.034)	(-4.736)	(-4.940)	(-4.247)	(-4.718)	(-4.495)
rainfall	0.075	0.221	-0.056	0.273**	-0.046	-0.043
	(0.520)	(1.507)	(-0.451)	(2.159)	(-0.375)	(-0.340)
GDP per capita	1.085***	1.291***	1.331***	1.238***	1.201***	1.211***
	(6.581)	(5.929)	(7.289)	(6.080)	(6.623)	(6.735)
Gini coefficient	0.031	0.037*	0.029	0.021	0.035*	0.039**
	(1.463)	(1.926)	(1.595)	(1.083)	(1.787)	(2.050)
international visitors	-0.030	0.011	0.001	-0.013	0.044	0.024
	(-0.207)	(0.101)	(0.009)	(-0.122)	(0.303)	(0.168)
international trade	-0.045	-0.127	-0.218***	0.026	-0.158**	-0.174**
	(-0.412)	(-1.412)	(-3.149)	(0.260)	(-2.150)	(-2.169)
health expenditure	0.099	0.122**	0.152**	0.036	0.140**	0.153**
	(1.390)	(2.497)	(2.603)	(0.564)	(2.517)	(2.555)
hospital beds	-0.195	-0.222	0.002	-0.352	-0.079	-0.137
	(-0.766)	(-0.842)	(0.008)	(-1.391)	(-0.283)	(-0.554)
SARS outbreak	-0.359	-0.259	-0.017	-0.278	-0.165	-0.173
	(-0.960)	(-0.720)	(-0.045)	(-0.920)	(-0.417)	(-0.447)
government expenditure	0.052**	0.047*	0.018	0.071***	0.014	0.008
	(2.118)	(1.730)	(0.768)	(3.035)	(0.511)	(0.287)
government effectiveness	-0.655**	-1.125***	-0.955***	-0.953***	-0.947***	-0.842***
	(-2.494)	(-3.731)	(-3.820)	(-3.614)	(-3.429)	(-2.686)
rest of world infections	0.573***	0.554**	0.454**	0.751***	0.475**	0.485**
	(3.365)	(2.316)	(2.235)	(4.849)	(2.340)	(2.405)
daily test ratio	0.088*	0.060*	0.086**	0.033	0.089**	0.088**
	(1.953)	(1.813)	(2.343)	(1.215)	(2.323)	(2.248)
retail and recreation	-0.034***			-0.030***
	(-5.534)			(-5.817)
grocery and pharmacy	0.021***			0.021***
	(4.471)			(4.809)
transit stations	-0.001			-0.002
	(-0.398)			(-0.875)
workplaces	0.008			0.006
	(1.100)			(1.033)
parks	-0.010*			-0.000
	(-1.778)			(-0.081)
residential	0.009			0.037*
	(0.462)			(1.878)
debt ratio		-0.003		-0.006
		(-0.923)		(-1.652)
industrial			-0.028*	-0.005
			(-1.737)	(-0.388)
political regimes					0.135
					(0.703)
GHS						-0.004
						(-0.242)
Number of observations	23,513	22,778	26,883	19,657	27,724	27,724
Adjusted R2	0.815	0.779	0.778	0.843	0.766	0.766

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Column (1) reports results including six google mobility indices as additional explanatory variables. 3. Column (2) reports results including debt ratio as an additional explanatory variable. 4. Column (3) reports results including industrial ratio as an additional explanatory variable. 5. Column (4) reports results for subsamples including political regime as an additional explanatory variable. 6. Column (5) reports results including Global Health Security as an additional explanatory variable. 7. Column (6) reports results including six google mobility indices, debt ratio, and industrial ratio as additional explanatory variables. 8. Column (7) reports results including economic stimulus spending and international support as additional explanatory variables. 9. Column (8) reports results including seven containment policy indices as additional explanatory variables.

Table A.12.

Economic growth and pandemic containment effectiveness (PCE) for infections.

Dependent Variable	Quarterly GDP growth rate in 2020
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
Sample period	Q2	Q3	Q2-Q3	Q1	Q2’	Q3’	Q2’-Q3’	Q2	Q3	Q2-Q3	Q1
PCE Score (X 100)	0.158***	0.115***	-0.156**	0.043***	0.166***	0.103***	-0.139**	0.167***	0.105***	-0.083	0.023
	(3.205)	(5.258)	(-2.099)	(2.956)	(3.337)	(4.450)	(-2.071)	(3.332)	(4.659)	(-0.861)	(1.469)
economic stimulus spending	0.411	0.204			0.450	0.250		0.008	0.211
	(1.066)	(1.090)			(1.168)	(1.343)		(0.018)	(1.144)
economic support index	-0.049	-0.039**			-0.044	-0.033*		-0.046	-0.010
	(-1.499)	(-2.100)			(-1.384)	(-1.792)		(-1.206)	(-0.369)
Specification	OLS	OLS	FD	OLS	OLS	OLS	FD	OLS	OLS	FD	OLS
Sample countries	CEIC							OECD+G20+Singapore
Number of observations	73	70	70	70	73	71	71	48	48	48	48
R2	0.163	0.270	0.047	0.108	0.161	0.234	0.041	0.197	0.267	0.015	0.039

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. PCE scores of Quarters 2 and 3 of 2020 in columns (1)–(3) and (8)–(10) are determined by Weeks 15–16 and Weeks 27–28 after 50 confirmed infection cases, respectively. 3. PCE scores of Quarter 1 of 2020 in columns (4) and (11) are measured by Weeks 3–4 after 50 confirmed infection cases. 4. PCE scores of Quarters 2 and 3 of 2020 in columns (5)–(7) are determined by Weeks 13–14 and Weeks 23–24 after 50 confirmed infection cases, respectively. 5. Data used in columns (8)–(11) exclude more countries with smaller size in Asia, South America, and Africa.

6. For a full list of countries used in the regressions in columns (8)–(11), see footnote 22 of the text.

Table A.13.

Economic growth and pandemic containment effectiveness (PCE) for infections.

Dependent Variable	Quarterly GDP growth rate			Annual GDP growth rate
	(1)	(2)	(3)	(4)	(5)	(6)
Sample period	Q2	Q3	Q1	Q2	Q3	Q1
PCE Score (X 100)	0.149***	0.107***	0.041**	0.052**	0.056***	0.030
	(3.150)	(4.933)	(2.221)	(2.218)	(2.911)	(1.595)
economic stimulus spending	0.116	0.153		-0.106	-0.173
	(0.247)	(0.690)		(-0.629)	(-1.004)
economic support index	-0.019	-0.018		-0.031**	-0.041***
	(-0.603)	(-0.850)		(-2.124)	(-2.851)
GDP per capita	0.837	0.015	-0.416
	(0.728)	(0.019)	(-0.922)
Gini coefficient	-0.425***	-0.146	-0.044
	(-2.749)	(-1.426)	(-1.067)
total population	-0.097	-0.005	-0.434
	(-0.111)	(-0.008)	(-1.266)
population 65+	-0.462***	-0.185*	-0.041
	(-2.832)	(-1.710)	(-0.692)
international trade	0.805	0.358	-0.109
	(1.558)	(1.250)	(-0.427)
government expenditure	-0.075	-0.019	-0.092
	(-0.337)	(-0.127)	(-1.169)
Specification	OLS	OLS	OLS
Sample countries	CEIC			IMF
Number of observations	73	70	70	91	87	91
R2	0.327	0.316	0.260	0.105	0.137	0.030

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. PCE scores of Quarters 2 and 3 of 2020 in columns (1),(2) and (4),(5) are determined by Weeks 15–16 and Weeks 27–28 after 50 confirmed infection cases, respectively. 3. PCE scores of Quarter 1 of 2020 in columns (3) and (6) are measured by Weeks 3–4 after 50 confirmed infection cases. 4. Annual GDP growth data retrieved from the IMF database including more countries is used in columns (4)–(6). 5. The PCE scores in columns (4)–(6) are still on a quarterly basis.

Fig. A.4.

Impacts of risk and protective factors on infections over time.

In addition, we also conduct the same sets of robustness checks for infection rate and present the results in Tables A.8–A.11. The only difference is that we use the CFR as the dependent variable in Table A.3, while we use observations since the first 50 infection cases instead of the first infection case in column (8) of Table A.9. This is to address the concern that some countries, such as the US, there has been a long-time gap between the first imported case and the subsequent large-scale outbreak. The effect of government effectiveness is even more pronounced. Overall, we still obtain similar results compared to the baseline model in column (1) of Table A.7.

A6. Global ranking for infections

For infections, to rule out the substantial randomness in early days of infections, we use the ${\overline{e}}_i$ from column (8) of Table A9, after the first 50 confirmed infection cases for our PCE ranking exercises. In this way, we are comparing China on 3 January with Italy on 23 February, the US on 24 February and the UK on 3 March, and onwards. As we observe from Fig. A.5, during the first 2 weeks after the first 50 confirmed infections, the US performs the best in terms of infection among the 99 countries. Again, China’s performance in terms of infection is at the bottom ($95\text{th}$) among affected countries and then, its ranking improves after the implementation of strict containment policies. By late June, China achieves the $6\text{th}$ spot out of 98 countries, indicating that the COVID-19 has been effectively contained. In contrast, the PCE ranking for the US has been declining quickly since week 5 to 6, consistent with the massive outbreak in the US starting at the end of March. Similarly, at the end of our sample period, the PCE ranking of the US is $73\text{rd}$ out of 98 even though it has the highest number of infections in the world, again suggesting the importance of controlling for the risk factors and protective factors for a fair global ranking. Overall, Japan still has a steady and high PCE ranking in terms of infection over the whole sample period. South Korea, New Zealand, and Italy improve their rankings over time, while countries such as Brazil and Spain perform persistently below the average.

A7. Growth regression for infections

The regression results using PCE for infections are presented in Table A.12. Column (1) reports the cross-section regression for GDP growth in Q2 of 2020 with control variables. Similarly, regressions for GDP growth in Q3 of 2020 are included in column (2). The positive and significant PCE score coefficients in these regressions suggest that those countries with more effective pandemic controls achieve higher economic growth rates. The magnitudes of 0.158 and 0.115 for coefficients in columns (1) and (2) show that on average 1.58 and 1.15 percentage points of GDP would be added if a country could increase its PCE score (multiplied by 100) for infections by 10 points in Q2 and Q3 of 2020, respectively.

In other words, countries with average PCE scores (0.47), such as Australia, Finland, and Mexico in Q2 of 2020, would gain 4.58 more percentage points in their GDP growth if they could improve their PCE scores for infections to South Korea’s level (0.76) in Q2 of 2020, respectively. The lost GDP growth rate of 4.58 can be translated into 123.66 billion USD in Mexico in Q2 of 2020.

Similarly, to address the potential concern of endogeneity due to the reverse causality between infections and economic stimulus (and fiscal situation), and unobserved country-specific factors, a first-difference (FD) estimate using both Q2 and Q3 of 2020 data is reported in column (3) of Table A.12. The results show that the FD coefficient of PCE is significantly negative, while that of Table 4 is significantly positive. For other robustness checks, we replicate Table 4 by using the PCE score for infections instead of deaths throughout columns (4)–(11). Similarly, the coefficients of PCE scores are still significantly positive throughout these columns, implying that the positive relationship between pandemic containment effectiveness and economic growth is stable within a short period of time. Some counterintuitive results in columns (4) and (10) are mainly due to the underreporting in infections. In general, the robust findings in these two tables suggest that there is no a clear trade-off between lives and livelihood facing by governments and international agencies. Instead, to save economy, it is important to contain the pandemic first.

Next, we also examine the robustness by accounting for more country-specific factors in Eq. (8) for infection rate in Table A.13. As we observe from the table, we consistently obtain significantly positive impacts of the PCE scores in terms of infection rate against both annual and quarterly GDP growth rate. This also supports our findings in Table 5 using PCE scores for death rate.

Finally, we replicate the robustness checks in Table A.6 by replacing the PCE scores with raw infections per million people in Table A.14 . Overall, the results based on infection rate are mostly consistent with our main findings based on death rate, even though there are still some discrepancies due to severe underreporting of infection number.

Table A.14.

Economic growth and infections.

Dependent Variable	Quarterly GDP growth rate
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Sample period	Q2	Q3	Q2-Q3	Q1	Q2	Q3	Q2	Q3	Q2-Q3	Q1
Infections per million population	-1.105*	-1.198***	5.063***	-0.365*	-1.576**	-1.400***	-1.171	-1.155***	5.096***	-0.020
	(-1.914)	(-3.439)	(9.683)	(-1.792)	(-2.309)	(-3.937)	(-1.568)	(-2.889)	(5.978)	(-0.079)
economic stimulus spending	0.411	0.244			0.108	0.083	-0.118	0.159
	(1.036)	(1.323)			(0.210)	(0.362)	(-0.252)	(0.794)
economic support index	-0.025	-0.015			-0.017	-0.020	-0.020	0.016
	(-0.792)	(-0.814)			(-0.519)	(-0.854)	(-0.494)	(0.520)
GDP per capita					1.926	1.230
					(1.411)	(1.589)
Gini coefficient					-0.397**	-0.115
					(-2.581)	(-1.116)
total population					-0.288	-0.163
					(-0.315)	(-0.267)
population 65+					-0.483***	-0.231**
					(-2.768)	(-2.110)
international trade					0.619	0.312
					(1.188)	(1.028)
government expenditure					-0.026	0.024
					(-0.111)	(0.150)
Specification	OLS	OLS	FD	OLS	OLS	OLS	OLS	OLS	FD	OLS
Sample countries	CEIC						OECD+G20+Singapore
Number of observations	73	70	70	70	73	70	48	48	48	48
R2	0.084	0.187	0.480	0.047	0.283	0.279	0.071	0.134	0.485	0.000

Notes: 1. t-values are reported in parentheses. The stars *, ** and *** indicate the significance at 10%, 5% and 1%. 2. Infection rate of Quarters 2 and 3 of 2020 in columns (1)–(3) and (5)–(9) are determined by the averaged infection rate of Calendar Weeks 15–16 and Weeks 27–28, respectively. 3. Infection rate of Quarter 1 of 2020 in columns (4) and (10) are measured by the averaged infection rate of Calendar Weeks 3–4. 4. Data used in columns (7)–(10) exclude more countries with smaller size in Asia, South America, and Africa. 5. For a full list of countries used in the regressions in columns (7)–(10), see footnote 22 of the text.

Appendix II: Additional information on data

The data used in this study are all collected from official sources that are publicly available. Our explanatory variables include six categories: demographic conditions, geographic conditions, economic conditions, global interdependency, healthcare conditions and public governance. This data appendix provides a detailed definition and data source of these variables.

A8. Demographic conditions

A8.1. Total population

The World Bank provides us the midyear estimate of the total population in 2018, which are combined from the United Nations Population Division and Census reports of different national statistical offices. All residents, regardless of legal status or citizenship, belong to the total population of each country. We fill in any missing value of the total population in 2018 with the latest value we can obtain from the same source in an early year. The same procedure is applied to all the other explanatory variables if missing values arise to ensure the data integrity.

A8.2. Population 65+

Population65+ is calculated by taking the ratio of the population age 65 and above to the total population. The definition of the total population is discussed above, while the population age 65 and above is offered by the World Bank. The World Bank staff estimates the total population age 65 and above by using the source of age/sex distributions of the United Nations Population Division’s World Population Prospects: 2019 Revision. The latest data is for 2018, and we fill in the missing value with the latest value we can obtain.

A8.3. Population density

To reduce measurement error, we use land area instead of the territorial area to calculate population density. The World Bank provides land area (sq.km) in 2018, which excludes area under inland water bodies, national claims to continental shelf, and exclusive economic zones, collected by the Food and Agriculture Organization (FAO) of the United Nations through annual questionnaires. Population density is the total population divided by land area in square kilometers.

A8.4. Urban population ratio

The World Bank provides us with the urban population ratio updated to 2018, which is the proportion of the population living in the urban areas as defined by the National Bureau of Statistics to the total population. The data is calculated by using population estimates and urban ratios from the United Nations World Urbanization Prospects.

A9. Geographic conditions

A9.1. Temperature and rainfall

Temperature and rainfall are provided by the Climate Change Knowledge Portal, a portal under the World Bank to comprehensive country data related to climate change. We use the average temperature (${}^{\circ }$C) and average rainfall (mm) across countries in March 2016 as proxies of temperature and rainfall during the pandemic of COVID-19. The data for 2016 is the latest data available on the website, and climate change is not significant in just a few years. Besides, the COVID-19 is characterized as a pandemic by WHO in March. Thus, we believe the data of March 2016 are reasonable proxies.

A10. Economic conditions

A10.1. GDP per capita

The World Bank provides GDP across countries in 2018, which is the sum of gross value added by all resident producers in the economy plus any product taxes and minus any subsidies not included in the value of the products. Data are in current U.S. dollars. GDP per capita is GDP divided by the total population we defined above.

A10.2. Debt ratio

The CEIC data provides us with the quarterly data of debt ratio, which is the proportion of the national government debts to nominal GDP. The debt ratio is calculated by monthly government debt and rolling sum of quarterly nominal GDP. We use the average debt ratio of 2019 as proxies of government debt position and fill in the missing value with the latest value we have.

A10.3. Gini coefficient

Based on primary household survey data of the most recent year, the World Bank constructs the Gini coefficient, measuring the degree of inequality in a distribution. The Gini coefficient is the ratio of the area between the Lorenz curve and a hypothetical line of absolute equality over the total area under the hypothetical line of absolute equality. Thus, a Gini coefficient of 0 implies perfect equality, while a coefficient of 100 implies perfect inequality.

A10.4. Employment in agriculture

The World Bank provides us with an estimate of the ratio of employment in the agriculture sector to total employment. Employment refers to persons of working age who are engaged in activities to produce goods or provide services for pay or profit. Any activity in agriculture, hunting, forestry, and fishing belongs to the agriculture sector. We collected data for 2018 and fill in the missing value with the latest value we can obtain.

A10.5. Industrial ratio

The industrial ratio is the percentage of industry value added to GDP, provided by the World Bank. Industry includes mining, manufacturing, construction, and electricity, water and gas, corresponding to International Standard Industrial Classification of All Economic Activities (ISIC) divisions 05–43 and ISIC divisions 10–33. Value-added refers to net output after adding up all outputs and subtracting intermediate inputs. We collected data for 2019 from the World Bank.

A11. Global interdependency

A11.1. International visitor

We collect data from the World Tourism Organization provided by the World Bank. It reports the number of international inbound tourists in 2018. International inbound tourists refer to people who travel to a country other than their usual residence and usual environment for a period not exceeding 12 months. Also, the primary purpose of this travel is other than an activity remunerated from within the country visited. The international visitor variable in our study is normalized by taking the natural logarithm of international visitors per million people.

A11.2. International trade

Using the import and export of goods of each country in 2018 provided by United Nations Comtrade, we construct a measure of global interconnectedness. We start with a matrix where the first row is filled country1$\prime$s import from and export of goods to country 2, 3, 4, and so on, respectively. The rest rows have a similar definition. The diagonal of the matrix, which is the country’s import and export of goods to itself, is 0. Then we normalize this matrix from absolute values into shares of import and export of each country, using its total import and export to the rest of the world. For data in row $i$ and column $j$, it measures the effect on the country $i$ from each country $j$. International trade is calculated by summing up all the shares in one column, let’s say column $j$. It measures the weighted interconnectedness of country $j$ with respect to the rest of the world. Ideally, this measure should be based on by-country international passengers from a country and into a country. However, such information is not publicly available. Thus, we use the by-country import and export of goods as an alternative.

A12. Healthcare conditions

A12.1. Health expenditure

The World Bank provides us with current health expenditure expressed as a percentage of GDP in 2017, which stems from the WHO Global Health Expenditure Database. Estimates of this variable include the consumption of healthcare goods and services during each year but exclude capital health expenditures such as buildings, machinery, IT, and stocks of vaccines for emergencies or outbreaks.

A12.2. Global health security (GHS)

We collect the GHS index from its official website. The GHS index is developed by considering the following six categories: (1) disease prevention; (2) detection and reporting for epidemics; (3) rapid response to pandemic; (4) strong health systems; (5) compliance with international norms; (6) overall risk environment. The overall score of health security is from 0 (weak) to 100 (strong).

A12.3. Hospital beds

The information of hospital beds per 1000 people is offered by World Bank who supplement the WHO’s original data by country data. The latest data available is for 2015, with massive missing values. Thus, a large amount of data is supplemented by data in the previous years, such as 2013 or 2014. Hospital beds include inpatient beds that can be used in public, private, general, and specialized hospitals and rehabilitation centers. In most cases, this also includes emergency and chronic beds.

A12.4. SARS outbreak

SARS outbreak is a dummy variable, which equals to one if the country reported probable cases of SARS in 2003 and zero otherwise. The source is collected from Cumulative Number of Reported Probable Cases of Severe Acute Respiratory Syndrome (SARS), reported by WHO.

A13. Public governance

A13.1. Government expenditure

Government expenditure refers to the ratio of general government final consumption expenditure to GDP. It includes most government and security expenditures such as the purchases of goods and services, compensation of employees, and expense of national defense and security. It excludes government military expenditures that are part of government capital formation. We collect the source in 2018 from the World Bank database.

A13.2. Political regimes

The Our World in Data combines the Wimmer and Min (2006) and Center for Systemic Peace to provide the political regime worldwide. The range of this variable is from -10 (autocracy) to 10 (full democracy). We collect the data for 2015 as proxies of political regimes during the pandemic of COVID-19.

A13.3. Government effectiveness

We collect the data of government effectiveness in 2018, provided by the Worldwide Governance Indicators. Estimates of government effectiveness reflect the performance of government in the following field: (1) the quality of public services; (2) the quality of civil services and the degree of its independence from political pressures; (3) the quality of policy formulation and implementation; (4) the credibility of the government’s commitment to such policies. The range of this variable is from approximately -2.5 (weak) to 2.5 (strong).

A13.4. Control of corruption

We collect the data of control of corruption in 2018, provided by the Worldwide Governance Indicators. Estimates of control of corruption capture the extent to which public power is exercised for private gain. This behavior mainly includes two aspects: (1) petty and grand forms of corruption; (2) capture of the state by elites and private interests. The range of this variable is from approximately -2.5 (weak) to 2.5 (strong).

A13.5. Political stability

We collect the data of political stability in 2018, provided by the Worldwide Governance Indicators. Its full name is Political Stability and Absence of Violence/Terrorism, which measures the probability of political instability and politically motivated violence, including terrorism. The range of this variable is from approximately -2.5 (weak) to 2.5 (strong).

A13.6. Rule of law

We collect the data of rule of law in 2018, provided by the Worldwide Governance Indicators. It mainly captures the people’s trust and compliance with social rules in the following field: (1) contract enforcement; (2) property rights; (3) the quality of police and courts; (4) the possibility of crime and violence. The range of this variable is from approximately -2.5 (weak) to 2.5 (strong).

A14. Additional controls

A14.1. Rest of world infections

Based on the daily number of infections of COVID-19 for each country from the WHO, we construct the rest of world infection relative to a country by calculating cumulative infection cases of COVID-19 excluding the country itself.

A14.2. Rest of region infections

We construct the rest of region infection relative to a country by calculating the cumulative infection cases of COVID-19 in the same region excluding the country itself. Being in the same region is defined as being on the same continent. Based on the classification of the WHO, we divided the world into 6 continents, including Africa, Americas, Eastern Mediterranean, Europe, South-East Asia and Western Pacific.

A14.3. Daily test ratio

We download the total COVID-19 tests performed by country from the Our World in Data, that compiles sources from different government databases and only updates from time to time. At the moment of our current empirical exercises, which is 18 December, the most recent complete data for our sample is up to 15 December. We use this latest test data of each country to construct the time-variant daily test ratio. The number of daily test is filled with value of zero before the first test performed in the country, in order to construct a balanced panel dataset. The daily test ratio in our paper is normalized by taking the natural logarithm of total test per million people.

A14.4. Google mobility indices

The COVID-19 Community Mobility Reports provided by Google show the movement trends over time across different places including retail and recreation, groceries and pharmacies, parks, transit stations, workplaces, and residential. We collect these six mobility indices from 15 Feb 2020 to 27 No. 2020, which show the percentage change of the movement over time in these different places. The baseline day for comparison is the median value during the 5-week period from 3 Jan 2020 to 6 Feb 2020. The baseline day is different for any day from Monday to Sunday.

A15. Additional variables

A15.1. Quarterly economic growth rate

The economic growth rate is defined as the GDP growth rate compared to the same quarter in the previous year with seasonal adjustment. The sample period is from 2020Q2 to 2020Q3, for all the OECD countries and Singapore. The data source is OECD.Stat database and Singapore Department of Statistics. We also include more countries in our regression model Eq. (8) by switching to the CEIC database.

A15.2. Annual economic growth rate

The annual economic growth rate is defined as the annual GDP growth rate in year 2020, on a year-on-year basis. More countries are included compared to our quarterly data. The data is collected from the World Economic Outlook database.

A15.3. Economic stimulus spending

The variable records cumulative monetary value in USD of fiscal stimuli since 1 January 2020, includes any spending or tax cuts since the outbreak of COVID-19, excluding international support, emergency investment in healthcare, and investment in vaccines. We take the natural logarithm of it in our regression models Eq. (1) and Eq. (8). The data source is Oxford COVID-19 Government Response Tracker (OxCGRT) database.

A15.4. International support

The variable records cumulative monetary value in USD of international announced offers of COVID-19 related aid spending to other countries since 1 January 2020. We take the natural logarithm of it in our regression model Eq. (1). The data source is OxCGRT database.

A15.5. Economic support index

The index measures how much economic support has been made available (such as income support and debt relief since the outbreak of COVID-19. The value of the index is between 0 and 100. The data source is OxCGRT database.

A15.6. Containment and closure policies

The set of variables record containment and closure policies stringency since 1 January 2020. It includes: (1) school closing; (2) workplace closing; (3) cancel public events; (4) restrictions on gatherings; (5) close public transport; (6) stay at home requirements; (7) restrictions on internal movement, repectively. A value of zero suggests no measures for each containment and closure policy, while larger value implies more stringent policy. The data source is OxCGRT database.

A15.7. COVID-19 economic stimulus index

The set of data constructed by Elgin et al. (2020), covers 166 countries and records their corresponding: (1) fiscal policy stimulus; (2) interest rate cut; (3) macro-financial package; (4) other monetary measures; (5) balance of payment (BoP) measures; (6) other BoP measures. While other monetary measures and other BoP measures are binary dummy variables, the rest of the variables are all in percentage form.

Supplementary material

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.jebo.2022.02.027.

Appendix B. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/