Use of Machine Learning to Estimate the Per-Protocol Effect of Low-Dose Aspirin on Pregnancy Outcomes: A Secondary Analysis of a Randomized Clinical Trial

Yongqi Zhong; Maria M Brooks; Edward H Kennedy; Lisa M Bodnar; Ashley I Naimi

doi:10.1001/jamanetworkopen.2021.43414

. 2022 Mar 9;5(3):e2143414. doi: 10.1001/jamanetworkopen.2021.43414

Use of Machine Learning to Estimate the Per-Protocol Effect of Low-Dose Aspirin on Pregnancy Outcomes

A Secondary Analysis of a Randomized Clinical Trial

Yongqi Zhong ¹, Maria M Brooks ², Edward H Kennedy ³, Lisa M Bodnar ², Ashley I Naimi ^4,^✉

¹Department of Epidemiology, The Johns Hopkins University, Baltimore, Maryland

²Department of Epidemiology, University of Pittsburgh, Pittsburgh, Pennsylvania

³Department of Data Science and Statistics, Carnegie Mellon University, Pittsburgh, Pennsylvania

⁴Department of Epidemiology, Emory University, Atlanta, Georgia

Accepted for Publication: October 29, 2021.

Published: March 9, 2022. doi:10.1001/jamanetworkopen.2021.43414

^✉

Corresponding Author: Ashley I. Naimi, PhD, Department of Epidemiology, Emory University, 1518 Clifton Rd, Atlanta, GA 30322 (ashley.naimi@emory.edu).

Author Contributions: Dr Naimi had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis.

Concept and design: Brooks, Kennedy, Bodnar, Naimi.

Acquisition, analysis, or interpretation of data: Zhong, Naimi.

Drafting of the manuscript: Zhong, Kennedy, Naimi.

Critical revision of the manuscript for important intellectual content: Zhong, Brooks, Bodnar, Naimi.

Statistical analysis: Zhong, Kennedy, Naimi.

Obtained funding: Naimi.

Administrative, technical, or material support: Naimi.

Supervision: Naimi.

Conflict of Interest Disclosures: Drs Brooks, Kennedy, Bodnar, and Naimi reported receiving grants from the National Institutes of Health (NIH) during the conduct of the study. Dr Brooks reported serving on the data safety and monitoring board for Cerus Corporation. No other disclosures were reported.

Funding/Support: This study was supported by grant R01HD093602 from the NIH. The original Effects of Aspirin in Gestation and Reproduction (EAGeR) trial was supported by contracts HHSN267200603423, HHSN267200603424, and HHSN267200603426 from the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH.

Role of the Funder/Sponsor: The sponsor had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.

Data Sharing Statement: See Supplement 3.

Additional Contributions: The trial could not have been conducted without the extraordinary commitment of the EAGeR participants, the EAGeR investigators and staff, and the members of the data safety monitoring board. Enrique F. Schisterman, PhD, Neil J. Perkins, PhD, Sunni L. Mumford, PhD, and Lindsey Sjaarda, PhD, were instrumental in the construction of the data used in these analyses.

^✉

Corresponding author.

PMCID: PMC8908068 PMID: 35262718

Key Points

Question

How can machine learning be used to estimate per-protocol effects in randomized clinical trials?

Findings

In a cohort of 1227 women derived from secondary analysis of a randomized clinical trial, ensemble machine learning with augmented inverse probability weighting was used to estimate the per-protocol effect of daily low-dose aspirin on pregnancy detected using human chorionic gonadotropin (hCG) levels. Relative to placebo, adherence to the assigned treatment protocol was associated with an increase of 8.0 hCG-detected pregnancies per 100 women, approximately double the intention-to-treat estimates.

Meaning

These findings suggest that in per-protocol analysis, machine learning techniques may allow for confounder adjustment while reducing the occurrence of model misspecification.

This secondary analysis of a randomized clinical trial uses machine learning methods to estimate the per-protocol effects of a low-dose aspirin regimen on pregnancy in the Effects of Aspirin in Gestation and Reproduction trial.

Abstract

Importance

In randomized clinical trials (RCTs), per-protocol effects may be of interest in the presence of nonadherence with the randomized treatment protocol. Using machine learning in per-protocol effect estimation can help avoid model misspecification owing to strong parametric assumptions, as is common with standard methods (eg, logistic regression).

Objectives

To demonstrate the use of ensemble machine learning with augmented inverse probability weighting (AIPW) for per-protocol effect estimation in RCTs and to evaluate the per-protocol effect size of aspirin on pregnancy.

Design, Setting, and Participants

This secondary analysis used data from 1227 women in the Effects of Aspirin in Gestation and Reproduction (EAGeR) trial, a multicenter, block-randomized, double-blind, placebo-controlled clinical trial of the effect of daily low-dose aspirin on pregnancy outcomes in women at high risk of pregnancy loss. Participants were recruited at 4 university medical centers in the US from June 15, 2007, to July 15, 2012. Women were followed up for 6 menstrual cycles for attempted pregnancy and 36 weeks of gestation if pregnancy occurred. Follow-up was completed on August 17, 2012. Data analyses were performed on July 9, 2021.

Exposures

Daily low-dose (81 mg) aspirin taken at least 5 of 7 days per week for at least 80% of follow-up time relative to placebo.

Main Outcomes and Measures

Pregnancy detected using human chorionic gonadotropin (hCG) levels.

Results

Among the 1227 women included in the analysis (mean SD age, 28.74 [4.80] years), 1161 (94.6%) were non-Hispanic White and 858 (69.9%) adhered to the protocol. Five machine learning models were combined into 1 meta-algorithm, which was used to construct an AIPW estimator for the per-protocol effect. Compared with adhering to placebo, adherence to the daily low-dose aspirin protocol for at least 5 of 7 days per week was associated with an increase in the probability of hCG-detected pregnancy of 8.0 (95% CI, 2.5-13.6) more hCG-detected pregnancies per 100 women in the sample, which is substantially larger than the estimated intention-to-treat estimate of 4.3 (95% CI, −1.1 to 9.6) more hCG-detected pregnancies per 100 women in the sample.

Conclusions and Relevance

These findings suggest that a low-dose aspirin protocol is associated with increased hCG-detected pregnancy in women who adhere to treatment for at least 5 days per week. With the presence of nonadherence, per-protocol treatment effect estimates differ from intention-to-treat estimates in the EAGeR trial. The results of this secondary analysis of clinical trial data suggest that machine learning could be used to estimate per-protocol effects by adjusting for confounders related to nonadherence in a more flexible way than traditional regressions.

Trial Registration

ClinicalTrials.gov Identifier: NCT00467363

Introduction

Intention-to-treat (ITT) effects from randomized clinical trials (RCTs) are the reference standard for evaluating treatment effects. Importantly, ITT effects capture the impact of assigning treatments to individuals. The ITT approach does not provide estimates of the effects that would be observed if all individuals adhered with a desired treatment protocol^1,2,3—that is, in the presence of nonadherence, the ITT effects may differ in important ways from the effect of taking the treatment under study in a specified way (ie, a study protocol).^2,4

Several investigators^2,5 have called for a more formal approach to per-protocol effect estimation in RCTs, and several per-protocol analyses^{4,6,7,8,9,10,11,12} have demonstrated important deviations from ITT estimates when nonadherence is accounted for. Unfortunately, when per-protocol effects are targeted in RCTs, all limitations associated with observational studies must be considered, such as confounding bias.^2,4 Machine learning methods can be used with augmented inverse probability weighting (AIPW) and stacked regression models to overcome some of these limitations^13,14 and to estimate per-protocol effects when adjusting for confounding variables. However, compared with traditional regression models, machine learning methods may be better suited to avoiding problems with model misspecification.^15,16 For example, a model would be misspecified if a linear regression were used to fit 2 variables with nonlinear relations (eg, perinatal mortality and maternal hemoglobin levels).¹⁷ Many machine learning algorithms can avoid these problems,^15,16 but they have not yet been applied to scenarios in which per-protocol effects are of primary interest.

In this report, we illustrate the use of machine learning methods to estimate the per-protocol effects of low-dose aspirin on pregnancy in the Effects of Aspirin in Gestation and Reproduction (EAGeR) trial. We evaluate how machine learning methods can be used to estimate per-protocol effects and discuss the feasibility and trade-offs of using machine learning methods for adherence-adjusted analyses.

Methods

Study Design

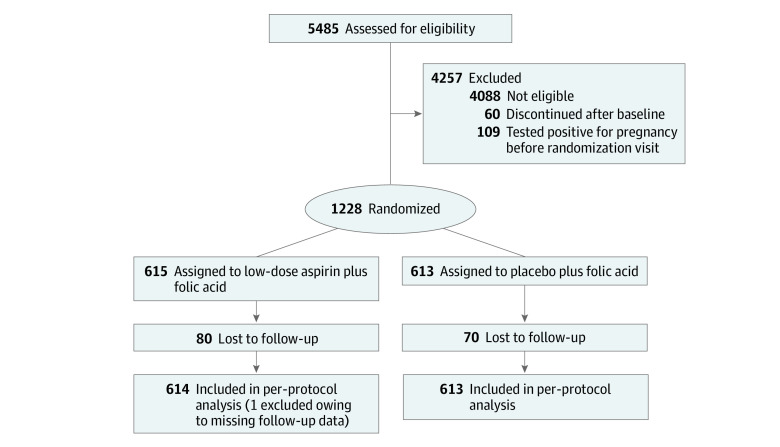
In this secondary analysis of an RCT, we used the data from the EAGeR trial—a multicenter, block randomized, double-blind, placebo-controlled clinical trial. The EAGeR trial recruited women aged 18 to 40 years who were actively trying to become pregnant and who had 1 or 2 prior pregnancy losses and no history of infertility from 4 university medical centers in the US from June 15, 2007, to July 15, 2012. Follow-up was completed on August 17, 2012. A total of 1228 women were recruited and randomized. Most of the participants (1161 [94.5%]) self-identified as non-Hispanic White race and ethnicity. For as many as 6 menstrual cycles, participants were followed up biweekly in their first 2 cycles and monthly afterward while attempting pregnancy. If a pregnancy was observed, follow-up continued throughout pregnancy for the live birth outcome (the registered primary end point of the trial). Institutional review board approvals at each clinical site and data coordinating center were obtained. A data safety and monitoring board was also formed to ensure participants’ safety and monitor the efficacy of the trial. Missing data were addressed via single imputation. Details about study design, eligibility criteria, baseline characteristics, and other relevant information has been published elsewhere,^4,18,19,20 and a complete copy of the trial protocol is available in Supplement 1. All participants provided written informed consent. The present analysis was conducted on July 9, 2021, and this study followed the Consolidated Standards of Reporting Trials (CONSORT) reporting guideline.

Treatment and Adherence

With 1:1 randomized treatment allocation, the treatment group (n = 615) received preconception-initiated daily low-dose aspirin (81 mg) plus folic acid (400 μg) and the control group (n = 613) received placebo plus folic acid (400 μg). For women who became pregnant, study treatment was to continue until week 36 of gestation. A total of 1227 women were included in the analysis of the present study (1 participant had missing follow-up data).

Adherence was assessed via bottle weight measurements in both groups during regular follow-up visits. Weekly adherence status was determined by evaluating whether a participant took their assigned pills for at least 5 of 7 days (equivalent to 70%) during a given week. A woman was deemed adherent with the study protocol if, in any given week during follow-up, she took a pill on at least 5 of 7 days. For each woman, this time-varying measure was categorized as adherent if the mean adherence during follow-up was at least 80% of their follow-up time before becoming pregnant or the entire follow-up time for those without pregnancy. Notably, this adherence status is a dichotomized, time-fixed variable, which is commonly used in a typical per-protocol analysis but differs from the previous analyses of this trial.⁴

Outcome

Pregnancy detected with human chorionic gonadotropin (hCG) levels during the defined treatment period was the primary outcome for this analysis. Pregnancies were determined by a positive result on a real-time hCG pregnancy test (QuickVue; Quidel), which was sensitive to 25 mIU/mL of hCG. The test was conducted at each study visit when expected menses were absent or by batched urine testing using daily first morning urine collected at home, stored on the last 10 days of each participant’s first cycle after randomization, and analyzed in the laboratory.

Baseline Covariates and Postrandomization Confounders

Baseline data on demographic, behavioral, and pregnancy history information were obtained via questionnaires, including age, race and ethnicity, educational level, marital status, income, frequency of exercise, alcohol and cigarette use in the past year, number of prior pregnancy losses, and number of months attempting pregnancy before randomization. Physical measurements of height and weight were used to calculate body mass index at baseline. Blood samples were also collected to measure serum high-sensitivity C-reactive protein levels using an immunoturbidimetric assay (COBAS 6000 autoanalyzer; Roche Diagnostics) with a detection limit of 0.0015 mg/dL (to convert to mg/L, multiply by 10).

Postrandomization confounders, including unusual (or excessive) bleeding and nausea and/or vomiting, were collected via questionnaire at regular intervals during follow-up. Similar to overall adherence status, we dichotomized these 2 postrandomization confounders by setting the values to 1 if a woman experienced unusual bleeding for at least 50% or nausea and/or vomiting for at least 20% of their follow-up time at least 1 of 7 days (20%) per week.

Statistical Analysis

In this study, we selected a protocol in which women would adhere to their assigned treatment for at least 5 of 7 days of a given week and for more than 80% of their follow-up time before pregnancy. This protocol allows us to evaluate whether consistently taking aspirin (vs placebo) is associated with an increased probability of experiencing an hCG-detected pregnancy. Differences in treatment, outcome, baseline characteristics, and postrandomization confounders between adherence status were tested by χ² test for categorical variables and by Kruskal-Wallis test for continuous variables. To examine the impact of different adherence thresholds on the overall findings as well as the number of individuals who were adherent and nonadherent with treatment in the samples, we explored protocols under assigned treatment for at least 4 of 7 days, 5 of 7 days, and 6 of 7 days of a given week for 60%, 70%, and 80% of person-weeks of follow-up.

Our target per-protocol effect is defined as the average per-protocol treatment effect among women who adhered to the aspirin protocol.²¹ To estimate this per-protocol effect of interest with machine learning methods, we used an AIPW estimator with an ensemble machine learner known as the Super Learner (or stacked generalization).^16,22,23,24 Per-protocol effects were quantified on both the risk difference and the risk ratio scales for the pregnancy outcome.

Stacking is a machine learning technique that combines several different algorithms into a single meta-algorithm. The benefit of using stacking as opposed to a single regression model or machine learning algorithm (eg, the least absolute shrinkage and selection operator regression or random forests) is flexibility; stacking algorithms can combine the strengths of each individual algorithm based on how they fit the data, thus avoiding the need of the potentially strong assumptions on which single algorithms rely for validity. The stacking technique first trains several machine learning models individually as the first layer. Estimates (or predictions) of the individual models from the first layer are then used as the input for the second layer, which is the meta-algorithm. Cross-validation is used to determine the importance of each first-layer algorithm in the overall meta-algorithm and to avoid potential overfitting.^16,23

In this study, we stacked 5 regression models (from traditional to flexible): a standard generalized linear model with main effects only, a standard generalized linear model with main effects and all 2-way interactions, multivariate adaptive regression splines,²⁵ random forests,²⁶ and extreme gradient boosting.²⁷ For multivariate adaptive regression splines, random forests, and extreme gradient boosting, a grid of tuning parameters was included in the stacking algorithm. All algorithms were combined into the meta-algorithm via nonnegative least squares. The predictions from these stacked models were then used to construct the AIPW estimator.

Augmented inverse probability weighting is a “doubly robust” estimator that relies on estimating the exposure model (ie, propensity score) and the outcome model separately (both modeled with the stacking algorithm) and then combining the predictions from these models into a single estimator that quantifies the average treatment effect.²² Augmented inverse probability weighting is consistent as long as at least the exposure model or the outcome model is correctly specified. Further, AIPW performs well, even when using flexible machine learning methods.^13,24 Using the aforementioned stacked machine learning algorithm, we estimated propensity scores by modeling the exposure with the aforementioned baseline covariates (exposure model) and constructed the outcome model using the exposure and those covariates. Cross-fitting, an additional layer of the fitting process on top of the stacking machine learning, is applied in the AIPW estimator to obtain valid inference (eg, low bias) and to further avoid overfitting.^13,24

Sensitivity analyses were conducted by using other thresholds of time-fixed adherence status, which is a combination of adherence to at least 4, 5, and 6 days in a given week during at least 60%, 70%, and 80% of person-weeks of follow-up. In addition, we also provided the ITT estimates obtained via g-computation,²⁸ inverse probability weighting,²⁹ targeted maximum likelihood estimation,³⁰ and AIPW and unadjusted per-protocol effects (with different thresholds) estimated by g-computation, inverse probability weighting, targeted maximum likelihood estimation, and AIPW. We constructed g-computation and inverse probability weighting with a standard generalized linear model with main effects only. Targeted maximum likelihood estimation is also a doubly robust estimator, which performs well when machine learning methods are used. We constructed the targeted maximum likelihood estimator using the same stacking machine learning algorithms for the AIPW. Further, we repeated all analyses after adjusting for postrandomization confounders (ie, unusual bleeding and nausea and/or vomiting).

All analyses were performed in R, version 3.6.2 (R Project for Statistical Computing). We conducted the implemented AIPW estimation using the AIPW package. The AIPW package supports the Super Learner package for stacking machine learning with cross-validation and provides a user-friendly interface for cross-fitting.^24,31 A prior study using the data resampled from the EAGeR trial²⁴ has shown excellent statistical performance for the AIPW package. Targeted maximum likelihood estimation was conducted with the tmle package.³² The code needed to reproduce our analyses is available in the eMethods in Supplement 1. Two-sided P < .05 indicated statistical significance.

Results

A total of 1227 women were included in the analysis (mean [SD] age, 28.74 [4.80] years]). In the EAGeR trial, most of the participants were non-Hispanic White (1161 [94.6%]), had at least a high-school education (1057 [86.1%]), and were married (1123 [91.5%]) and employed (919 [74.9%]). Table 1 shows the randomized treatment assignment, outcome, baseline characteristics, and postrandomization confounders by adherence status. The CONSORT flow diagram for the EAGeR trial is presented in Figure 1. Taking at least 5 of 7 pills in a given week during at least 80% of person-weeks of follow-up was associated with the hCG-detected pregnancy outcome (χ²₁ = 278.6; P < .001) as well as non-Hispanic White race and ethnicity (χ²₁ = 17.5; P < .001), high school education (χ²₁ = 8.2; P = .004), marital status (χ²₁ = 33.1; P < .001), annual income (χ²₁ = 20.1; P < .001), and history of smoking in the past year (χ²₁ = 22.8; P < .001) but not with the randomized treatment assignment. Figure 2 presents the number of participants who adhered to the protocol, which decreased as the adherence threshold increased. Overall, 858 (69.9%) of the 1227 trial participants adhered to their assigned study medication protocol, and 784 (63.9%) became pregnant.

Table 1. Treatment Assignment, Outcome, Baseline Covariates, and Postrandomization Confounders.

Variable	Adherence (n = 1227)^a		Statistical analysis	P value
Variable	No (n = 369 [30.1%])	Yes (n = 858 [69.9%])	Statistical analysis	P value
Treatment: daily low-dose aspirin	190 (51.5)	425 (49.5)	χ²₁ = 0.4	.53
Outcome: hCG-detected pregnancy	107 (29.0)	677 (78.9)	χ²₁ = 278.6	<.001
Baseline covariates
Non-Hispanic White race	334 (90.5)	827 (96.4)	χ²₁ = 17.5	<.001
High school educational level	302 (81.8)	755 (88.0)	χ²₁ = 8.2	.004
Married	312 (84.6)	811 (94.5)	χ²₁ = 33.1	<.001
Employed	283 (76.7)	636 (74.1)	χ²₁ = 0.9	.34
Annual income ≥$40 000	213 (57.7)	608 (70.9)	χ²₁ = 20.1	<.001
Exercise per week
Low	106 (28.7)	216 (25.2)	χ²₂ = 2.3	.32
Moderate	140 (37.9)	360 (42.0)
High	123 (33.3)	282 (32.9)
No. of previous pregnancy losses
1	125 (33.9)	278 (32.4)	χ²₁ = 0.3	.61
2	244 (66.1)	580 (67.6)	χ²₁ = 0.3	.61
No. of previous live births
0	173 (46.9)	352 (41.0)	χ²₃ = 6.0	.11
1	125 (33.9)	308 (35.9)
2	68 (18.4)	179 (20.9)
3	3 (0.8)	19 (2.2)
Alcohol ever consumed in past year	137 (37.1)	271 (31.6)	χ²₁ = 3.6	.06
Tobacco ever smoked in past year	71 (19.2)	81 (9.4)	χ²₁ = 22.8	<.001
Age, median (IQR), y	28.0 (24.6-31.8)	28.4 (25.5-31.8)	NA	.12
Time attempting pregnancy before randomization, median (IQR), mo	3.0 (1.0-7.0)	3.0 (1.0-6.8)	NA	.09
BMI, median (IQR)	25.2 (21.8-30.3)	24.4 (21.3-29.3)	NA	.05
hsCRP level, median (IQR), mg/dL	0.13 (0.06-0.36)	0.11 (0.05-0.31)	NA	.22
Postrandomization confounders
Unusual bleeding^b	67 (18.2)	166 (19.3)	0.2 (1)	.63
Nausea and/or vomiting^c	69 (18.7)	138 (16.1)	1.3 (1)	.26

Open in a new tab

Abbreviations: BMI, body mass index (calculated as weight in kilograms divided by height in meters squared); hCG, human chorionic gonadotropin; hsCRP, high-sensitivity C-reactive protein; NA, not applicable.

SI conversion factor: To convert hsCRP to mg/L, multiply by 10.

^{^a}

Adherence was measured as taking 5 of 7 pills (70%) per week for 80% of person-weeks of follow-up. Unless otherwise indicated, data are expressed as number (%) of patients.

^{^b}

Indicates bleeding ≥1 of 7 days (20%) per week for ≥50% of person-weeks of follow-up.

^{^c}

Indicates nausea and/or vomiting ≥1 of 7 days (20%) per week for ≥20% of person-weeks of follow-up.

The estimated per-protocol effect of low-dose aspirin on hCG-detected pregnancy is shown in Table 2. Relative to participants adhering to placebo, those participants who adhered to the low-dose aspirin treatment protocol experienced 8.0 (95% CI, 2.5-13.6) more hCG-detected pregnancies per 100 women in the sample, which was approximately double the ITT estimate of 4.3 (95% CI, −1.1 to 9.6) more hCG-detected pregnancies per 100 women in the sample. Risk ratios for the estimated per-protocol effects are also presented in Table 2.

Table 2. Effects of Low-Dose Aspirin on hCG-Detected Pregnancy Among Women With Adherence to the Assigned Treatment^a.

Method	Machine learning	Risk difference estimate (SE) [95% CI]	Risk ratio estimate (SE) [95% CI]
Intention-to-treat analysis	No	0.04 (0.03) [−0.01 to 0.10]	1.07 (0.04) [0.98 to 1.16]
Per-protocol analysis adjusted for baseline covariates
AIPW	Yes	0.08 (0.03) [0.03 to 0.14]	1.11 (0.04) [1.03 to 1.19]
TMLE	Yes	0.08 (0.03) [0.03 to 0.13]	1.10 (0.03) [1.04 to 1.17]
g-Computation	No	0.07 (0.03) [0.02 to 0.13]	1.10 (0.03) [1.02 to 1.17]
IPW	No	0.07 (0.03) [0.02 to 0.13]	1.10 (0.04) [1.02 to 1.18]
Unadjusted per-protocol analysis	No	0.08 (0.03) [0.03 to 0.14]	1.11 (0.04) [1.04 to 1.20]

Open in a new tab

Abbreviations: AIPW, augmented inverse probability weighting; hCG, human chorionic gonadotropin; IPW, inverse probability weighting; TMLE, targeted maximum likelihood estimation.

^{^a}

Assigned treatment was taking 5 of 7 pills (70%) per week during at least 80% of person-weeks of follow-up.

Using other estimation methods, the per-protocol estimates remained similar, including the unadjusted estimates (Table 2 and eTable and eFigure in Supplement 2). Similar per-protocol effect estimates were also observed when adjusting for unusual bleeding and nausea and/or vomiting (risk difference per 100 woment, 8.4 [95% CI, 2.8-14.0]) (eTable in Supplement 2). Using other adherence thresholds, our sensitivity analyses with AIPW and machine learning show per-protocol effect estimates increase. These per-protocol effect estimates ranged from 5.6 per 100 women (95% CI, 0.0-11.2) to 9.0 per 100 women (95% CI, 3.4-14.5) when adherence thresholds ranged from 4 of 7 days for at least 60% of person-weeks of follow-up to 6 of 7 days for at least 80% of person-weeks of follow-up (eFigure in Supplement 2).

Discussion

We demonstrate the use of stacked machine learning with AIPW in estimating the per-protocol effects in the EAGeR trial. Our time-fixed, per-protocol analysis results were consistent with previous findings of the per-protocol effect estimate of aspirin that accounted for the time-varying nature of adherence and select time-varying confounders.⁴ However, unlike previous research, we used nonparametric machine learning methods to estimate these effects. Our analyses demonstrate a novel approach for per-protocol effect estimation using advanced statistical methods. In addition, our results suggest that a preconception low-dose aspirin regimen increases hCG-detected pregnancies for women with 1 or 2 prior pregnancy losses who adhered to at least 5 of 7 days of low-dose aspirin therapy for at least 80% of the follow-up.

Supervised machine learning algorithms have been widely adopted to predict various health outcomes.^33,34,35 Although they can also be used for effect estimation, additional steps are needed.^13,14 Importantly, these steps nclude the need to adjust for relevant confounders and to use doubly robust methods such as AIPW.

The benefits of using machine learning with doubly robust methods lie primarily in the ability to avoid strong parametric modeling assumptions. Machine learning models can be more flexible and data adaptive than traditional regression models.^15,16 For example, the inclusion of an interaction term in a regression model is determined by the investigators’ domain-specific knowledge, whereas tree-based models (eg, random forests) adopt a more data-adaptive approach to interaction inclusion.^36,37 Failure to include an interaction term may result in model misspecification and lead to biased effect estimation. However, as a result of this increased data adaptiveness and extra modeling flexibility, tree-based models—and flexible machine learning in general—are more likely to overfit the data and have larger mean squared error.³⁶ To mitigate these issues, combining tree-based methods (eg, random forests) and regression-based methods (eg, generalized linear models and multivariate adaptive regression splines) is advisable.^13,16 In our study, we stacked 5 different machine learning models to create added flexibility and used cross-validation to mitigate overfitting.

The purpose of this study was to illustrate the use of machine learning as an alternative approach for per-protocol effect estimation rather than convincing the readers to use machine learning only. However, it should be recognized that if the model is correctly specified (even this is a rare scenario), parametric regression is more statistically efficient than flexible machine learning methods.¹³

We used supervised machine learning methods with doubly robust estimators to quantify the per-protocol effect of aspirin on hCG-detected pregnancy. In an RCT where all participants are fully adherent with the treatment protocol, per-protocol effect will be identical to ITT effects.³⁸ However, in the EAGeR trial, the ITT effects of low-dose aspirin on hCG-detected pregnancy differed substantially from the estimated per-protocol effect owing to nonadherence with the specified protocol during follow-up. In many settings captured by clinical trials with repeated opportunities to take the assigned treatment (eg, every day during weeks of follow-up), perfect adherence is unlikely, and a practical adherence level has to be chosen based on either clinical knowledge or the data at hand. In the EAGeR trial, the adherence rate declined over time and dropped quickly after the start of pregnancy.⁴ We defined adherence based on a protocol of taking 5 of 7 pills in a given week for at least 80% of person-weeks because some literature suggests that a biological effect of low-dose aspirin could be achieved at this adherence level⁴ and because of the relatively short half-life of aspirin.³⁹

We found that our unadjusted estimates were similar to estimates we obtained by improperly adjusting for postrandomization confounders (eg, unusual bleeding and nausea and/or vomiting) but properly adjusting for baseline confounders (eg, age, marital status, or annual income). In addition, these results aligned closely with those from a prior study⁴ that properly adjusted for postrandomization confounding, albeit with methods that were much less flexible (ie, parametric g-computation). This finding lends additional empirical support to the use of daily low-dose aspirin in increasing hCG-detected pregnancies.

Our analytic approach using time-fixed adherence can be more broadly applied in other analysis principles of RCTs as well as in observational studies, particularly those with only 1 time point. For example, our approach can be directly applied to the as-treated analysis in RCTs, such as a trial for evaluating the efficacy of emergency contraception. Modified ITT (despite not being consistently defined)^40,41 can be incorporated with our approach as well because the modification of ITT may not be free of confounding (eg, only including participants with initiation of drug therapy for a nonblinded study). Further, adjusting for covariates with machine learning in (modified) ITT analysis can improve statistical efficiency for higher precision of treatment effect estimates.⁴²

Limitations

This study has some limitations. In a well-conducted trial, an ITT approach provides unbiased estimates of the assignment effect. The ITT estimates capture the impact of the treatment assignment strategy and generally can be interpreted as the effectiveness of recommending or prescribing one treatment compared with another.¹ In contrast, an appropriately adjusted per-protocol analysis can be used to estimate the effect of taking the active treatment according to the specifications of the protocol, allowing estimation of the treatment efficacy. Similar to most per-protocol analyses, our study relied on time-fixed adherence status, which is an important limitation. Although our effect estimates of low-dose aspirin on hCG-detected pregnancy are similar to those of the prior study that accounted for time-varying adherence,⁴ limitations should be considered when conducting a time-fixed, per-protocol analysis. First, in conducting a time-fixed analysis, we had to collapse time-varying adherence status into a single time point, losing detailed information of how adherence changed during follow-up. Second, time-fixed analyses are generally unable to appropriately adjust for time-varying confounders, such as unusual bleeding and nausea. For example, at a given time point, adherence to treatment is associated with an increased likelihood of adverse effects (eg, unusual bleeding), which is further associated with a decreased likelihood of adherence at the next time point. Therefore, postrandomization confounders (eg, unusual bleeding and nausea) could simultaneously mediate and confound the effect of adherence status, requiring an analytic approach that we did not use.²⁸ In addition, other common limitations of observational studies should also be considered in the per-protocol analysis, such as unmeasured confounders. Last, we had limited information on important variables such as race and ethnicity, which limits the generalizability of our findings.

Conclusions

This secondary analysis of a randomized clinical trial suggests that machine learning methods with doubly robust estimators, such as AIPW, can be used to estimate per-protocol treatment effects. Furthermore, our empirical findings align with prior results supporting the prophylactic use of daily low-dose aspirin to improve the chances of hCG-detected pregnancy in women at high risk of pregnancy loss.

Supplement 1.

Trial Protocol

Click here for additional data file.^{(811.5KB, pdf)}

Supplement 2.

eTable. Sensitivity Analyses of the Effects of Low-Dose Aspirin on hCG-Detected Pregnancy Among Women Adhering to the Assigned Treatment: 5 of 7 Pills per Week Over at Least 80% of Person-Weeks of Follow-up Using Different Estimation Methods

eFigure. Sensitivity Analyses of the Effects of Low-Dose Aspirin on hCG Conception Using Different Adherence Levels and Estimation Methods

eMethods. R Code for Per-Protocol Effect Estimation

Click here for additional data file.^{(740.8KB, pdf)}

Supplement 3.

Data Sharing Statement

Click here for additional data file.^{(15.5KB, pdf)}

References

1.Gupta SK. Intention-to-treat concept: a review. Perspect Clin Res. 2011;2(3):109-112. doi: 10.4103/2229-3485.83221 [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Hernán MA, Hernández-Díaz S, Robins JM. Randomized trials analyzed as observational studies. Ann Intern Med. 2013;159(8):560-562. doi: 10.7326/0003-4819-159-8-201310150-00709 [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Manson JE, Shufelt CL, Robins JM. The potential for postrandomization confounding in randomized clinical trials. JAMA. 2016;315(21):2273-2274. doi: 10.1001/jama.2016.3676 [DOI] [PubMed] [Google Scholar]
4.Naimi AI, Perkins NJ, Sjaarda LA, et al. The effect of preconception-initiated low-dose aspirin on human chorionic gonadotropin-detected pregnancy, pregnancy loss, and live birth: per protocol analysis of a randomized trial. Ann Intern Med. 2021;174(5):595-601. doi: 10.7326/M20-0469 [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Hernán MA, Robins JM. Per-protocol analyses of pragmatic trials. N Engl J Med. 2017;377(14):1391-1398. doi: 10.1056/NEJMsm1605385 [DOI] [PubMed] [Google Scholar]
6.Cain LE, Cole SR. Inverse probability-of-censoring weights for the correction of time-varying noncompliance in the effect of randomized highly active antiretroviral therapy on incident AIDS or death. Stat Med. 2009;28(12):1725-1738. doi: 10.1002/sim.3585 [DOI] [PubMed] [Google Scholar]
7.Lodi S, Freiberg M, Gnatienko N, et al. Per-protocol analysis of the ZINC trial for HIV disease among alcohol users. Trials. 2021;22(1):226. doi: 10.1186/s13063-021-05178-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Lodi S, Sharma S, Lundgren JD, et al. ; INSIGHT Strategic Timing of AntiRetroviral Treatment (START) Study Group . The per-protocol effect of immediate versus deferred antiretroviral therapy initiation. AIDS. 2016;30(17):2659-2663. doi: 10.1097/QAD.0000000000001243 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Murnane PM, Brown ER, Donnell D, et al. ; Partners PrEP Study Team . Estimating efficacy in a randomized trial with product nonadherence: application of multiple methods to a trial of preexposure prophylaxis for HIV prevention. Am J Epidemiol. 2015;182(10):848-856. doi: 10.1093/aje/kwv202 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Murray EJ, Hernán MA. Improved adherence adjustment in the Coronary Drug Project. Trials. 2018;19(1):158. doi: 10.1186/s13063-018-2519-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Neumann A, Maura G, Weill A, Ricordeau P, Alla F, Allemand H. Comparative effectiveness of rosuvastatin versus simvastatin in primary prevention among new users: a cohort study in the French national health insurance database. Pharmacoepidemiol Drug Saf. 2014;23(3):240-250. doi: 10.1002/pds.3544 [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Toh S, Hernández-Díaz S, Logan R, Robins JM, Hernán MA. Estimating absolute risks in the presence of nonadherence: an application to a follow-up study with baseline randomization. Epidemiology. 2010;21(4):528-539. doi: 10.1097/EDE.0b013e3181df1b69 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Naimi AI, Mishler AE, Kennedy EH. Challenges in obtaining valid causal effect estimates with machine learning algorithms. Am J Epidemiol. Published online July 15, 2021. doi: 10.1093/aje/kwab201 [DOI] [PubMed] [Google Scholar]
14.Zivich PN, Breskin A. Machine learning for causal inference: on the use of cross-fit estimators. Epidemiology. 2021;32(3):393-401. doi: 10.1097/EDE.0000000000001332 [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Hastie T, Tibshirani R, Friedman JH. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer; 2009. [Google Scholar]
16.Naimi AI, Balzer LB. Stacked generalization: an introduction to super learning. Eur J Epidemiol. 2018;33(5):459-464. doi: 10.1007/s10654-018-0390-z [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Little MP, Brocard P, Elliott P, Steer PJ. Hemoglobin concentration in pregnancy and perinatal mortality: a London-based cohort study. Am J Obstet Gynecol. 2005;193(1):220-226. doi: 10.1016/j.ajog.2004.11.053 [DOI] [PubMed] [Google Scholar]
18.Schisterman EF, Silver RM, Perkins NJ, et al. A randomized trial to evaluate the effects of low-dose aspirin in gestation and reproduction: design and baseline characteristics. Paediatr Perinat Epidemiol. 2013;27(6):598-609. doi: 10.1111/ppe.12088 [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Schisterman EF, Silver RM, Lesher LL, et al. Preconception low-dose aspirin and pregnancy outcomes: results from the EAGeR randomized trial. Lancet. 2014;384(9937):29-36. doi: 10.1016/S0140-6736(14)60157-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Schisterman EF, Mumford SL, Schliep KC, et al. Preconception low dose aspirin and time to pregnancy: findings from the effects of aspirin in gestation and reproduction randomized trial. J Clin Endocrinol Metab. 2015;100(5):1785-1791. doi: 10.1210/jc.2014-4179 [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Rudolph JE, Naimi AI, Westreich DJ, Kennedy EH, Schisterman EF. Defining and identifying per-protocol effects in randomized trials. Epidemiology. 2020;31(5):692-694. doi: 10.1097/EDE.0000000000001234 [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Robins JM, Rotnitzky A. Semiparametric efficiency in multivariate regression models with missing data. J Am Stat Assoc. 1995;90(429):122-129. doi: 10.1080/01621459.1995.10476494 [DOI] [Google Scholar]
23.Van der Laan MJ, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol. 2007;6(1):e25. doi: 10.2202/1544-6115.1309 [DOI] [PubMed] [Google Scholar]
24.Zhong Y, Kennedy EH, Bodnar LM, Naimi AI. AIPW: an R package for augmented inverse probability weighted estimation of average causal effects. Am J Epidemiol. 2021;190(12):2690-2699. doi: 10.1093/aje/kwab207 [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Friedman JH. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67. doi: 10.1214/aos/1176347963 [DOI] [PubMed] [Google Scholar]
26.Breiman L. Random forests. Mach Learn. 2001;45(1):5-32. doi: 10.1023/A:1010933404324 [DOI] [Google Scholar]
27.Chen T, Guestrin C. XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery; 2016:785-794. [Google Scholar]
28.Naimi AI, Cole SR, Kennedy EH. An introduction to g methods. Int J Epidemiol. 2017;46(2):756-762. doi: 10.1093/ije/dyw323 [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Hernán MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578-586. doi: 10.1136/jech.2004.029496 [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Rose S, van der Laan MJ. Targeted Learning: Causal Inference for Observational and Experimental Data. Springer; 2011. [Google Scholar]
31.Polley E, LeDell E, Kennedy C, Lendle S, van der Laan M. SuperLearner: Super Learner Prediction. 2019. Accessed August 27, 2020. https://cran.r-project.org/web/packages/SuperLearner/index.html
32.Gruber S, van der Laan MJ. tmle: An R package for targeted maximum likelihood estimation. J Stat Softw. 2012;51(13):1-35. doi: 10.18637/jss.v051.i13 23504300 [DOI] [Google Scholar]
33.Carin L, Pencina MJ. On deep learning for medical image analysis. JAMA. 2018;320(11):1192-1193. doi: 10.1001/jama.2018.13316 [DOI] [PubMed] [Google Scholar]
34.Wang S, Pathak J, Zhang Y. Using electronic health records and machine learning to predict postpartum depression. Stud Health Technol Inform. 2019;264:888-892. doi: 10.3233/SHTI190351 [DOI] [PubMed] [Google Scholar]
35.Khera R, Haimovich J, Hurley NC, et al. Use of machine learning models to predict death after acute myocardial infarction. JAMA Cardiol. 2021;6(6):633-641. doi: 10.1001/jamacardio.2021.0122 [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. 2nd ed. Springer; 2009:587-604. [Google Scholar]
37.Cutler D, Lleras-Muney A.. Education and health: evaluating theories and evidence. In: House J, Schoeni R, Kaplan G, Pollack H, eds. Making Americans Healthier: Social and Economic Policy as Health Policy. Russell Sage Foundation; 2008. [Google Scholar]
38.Dunn G, Lovrić M. Complier-average causal effect (CACE) estimation. In: Lorvić M, ed. International Encyclopedia of Statistical Science. Springer Nature; 2011. [Google Scholar]
39.Awtry EH, Loscalzo J. Aspirin. Circulation. 2000;101(10):1206-1218. doi: 10.1161/01.CIR.101.10.1206 [DOI] [PubMed] [Google Scholar]
40.Abraha I, Montedori A. Modified intention to treat reporting in randomized controlled trials: systematic review. BMJ. 2010;340:c2697. doi: 10.1136/bmj.c2697 [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Montedori A, Bonacini MI, Casazza G, et al. Modified versus standard intention-to-treat reporting: are there differences in methodological quality, sponsorship, and findings in randomized trials? a cross-sectional study. Trials. 2011;12(1):58. doi: 10.1186/1745-6215-12-58 [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Benkeser D, Díaz I, Luedtke A, Segal J, Scharfstein D, Rosenblum M. Improving precision and power in randomized trials for COVID-19 treatments using covariate adjustment, for binary, ordinal, and time-to-event outcomes. Biometrics. 2021;77(4):1467-1481. doi: 10.1111/biom.13377 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement 1.

Trial Protocol

Click here for additional data file.^{(811.5KB, pdf)}

Supplement 2.

eFigure. Sensitivity Analyses of the Effects of Low-Dose Aspirin on hCG Conception Using Different Adherence Levels and Estimation Methods

eMethods. R Code for Per-Protocol Effect Estimation

Click here for additional data file.^{(740.8KB, pdf)}

Supplement 3.

Data Sharing Statement

Click here for additional data file.^{(15.5KB, pdf)}

[zoi211206r1] 1.Gupta SK. Intention-to-treat concept: a review. Perspect Clin Res. 2011;2(3):109-112. doi: 10.4103/2229-3485.83221 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r2] 2.Hernán MA, Hernández-Díaz S, Robins JM. Randomized trials analyzed as observational studies. Ann Intern Med. 2013;159(8):560-562. doi: 10.7326/0003-4819-159-8-201310150-00709 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r3] 3.Manson JE, Shufelt CL, Robins JM. The potential for postrandomization confounding in randomized clinical trials. JAMA. 2016;315(21):2273-2274. doi: 10.1001/jama.2016.3676 [DOI] [PubMed] [Google Scholar]

[zoi211206r4] 4.Naimi AI, Perkins NJ, Sjaarda LA, et al. The effect of preconception-initiated low-dose aspirin on human chorionic gonadotropin-detected pregnancy, pregnancy loss, and live birth: per protocol analysis of a randomized trial. Ann Intern Med. 2021;174(5):595-601. doi: 10.7326/M20-0469 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r5] 5.Hernán MA, Robins JM. Per-protocol analyses of pragmatic trials. N Engl J Med. 2017;377(14):1391-1398. doi: 10.1056/NEJMsm1605385 [DOI] [PubMed] [Google Scholar]

[zoi211206r6] 6.Cain LE, Cole SR. Inverse probability-of-censoring weights for the correction of time-varying noncompliance in the effect of randomized highly active antiretroviral therapy on incident AIDS or death. Stat Med. 2009;28(12):1725-1738. doi: 10.1002/sim.3585 [DOI] [PubMed] [Google Scholar]

[zoi211206r7] 7.Lodi S, Freiberg M, Gnatienko N, et al. Per-protocol analysis of the ZINC trial for HIV disease among alcohol users. Trials. 2021;22(1):226. doi: 10.1186/s13063-021-05178-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r8] 8.Lodi S, Sharma S, Lundgren JD, et al. ; INSIGHT Strategic Timing of AntiRetroviral Treatment (START) Study Group . The per-protocol effect of immediate versus deferred antiretroviral therapy initiation. AIDS. 2016;30(17):2659-2663. doi: 10.1097/QAD.0000000000001243 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r9] 9.Murnane PM, Brown ER, Donnell D, et al. ; Partners PrEP Study Team . Estimating efficacy in a randomized trial with product nonadherence: application of multiple methods to a trial of preexposure prophylaxis for HIV prevention. Am J Epidemiol. 2015;182(10):848-856. doi: 10.1093/aje/kwv202 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r10] 10.Murray EJ, Hernán MA. Improved adherence adjustment in the Coronary Drug Project. Trials. 2018;19(1):158. doi: 10.1186/s13063-018-2519-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r11] 11.Neumann A, Maura G, Weill A, Ricordeau P, Alla F, Allemand H. Comparative effectiveness of rosuvastatin versus simvastatin in primary prevention among new users: a cohort study in the French national health insurance database. Pharmacoepidemiol Drug Saf. 2014;23(3):240-250. doi: 10.1002/pds.3544 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r12] 12.Toh S, Hernández-Díaz S, Logan R, Robins JM, Hernán MA. Estimating absolute risks in the presence of nonadherence: an application to a follow-up study with baseline randomization. Epidemiology. 2010;21(4):528-539. doi: 10.1097/EDE.0b013e3181df1b69 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r13] 13.Naimi AI, Mishler AE, Kennedy EH. Challenges in obtaining valid causal effect estimates with machine learning algorithms. Am J Epidemiol. Published online July 15, 2021. doi: 10.1093/aje/kwab201 [DOI] [PubMed] [Google Scholar]

[zoi211206r14] 14.Zivich PN, Breskin A. Machine learning for causal inference: on the use of cross-fit estimators. Epidemiology. 2021;32(3):393-401. doi: 10.1097/EDE.0000000000001332 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r15] 15.Hastie T, Tibshirani R, Friedman JH. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer; 2009. [Google Scholar]

[zoi211206r16] 16.Naimi AI, Balzer LB. Stacked generalization: an introduction to super learning. Eur J Epidemiol. 2018;33(5):459-464. doi: 10.1007/s10654-018-0390-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r17] 17.Little MP, Brocard P, Elliott P, Steer PJ. Hemoglobin concentration in pregnancy and perinatal mortality: a London-based cohort study. Am J Obstet Gynecol. 2005;193(1):220-226. doi: 10.1016/j.ajog.2004.11.053 [DOI] [PubMed] [Google Scholar]

[zoi211206r18] 18.Schisterman EF, Silver RM, Perkins NJ, et al. A randomized trial to evaluate the effects of low-dose aspirin in gestation and reproduction: design and baseline characteristics. Paediatr Perinat Epidemiol. 2013;27(6):598-609. doi: 10.1111/ppe.12088 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r19] 19.Schisterman EF, Silver RM, Lesher LL, et al. Preconception low-dose aspirin and pregnancy outcomes: results from the EAGeR randomized trial. Lancet. 2014;384(9937):29-36. doi: 10.1016/S0140-6736(14)60157-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r20] 20.Schisterman EF, Mumford SL, Schliep KC, et al. Preconception low dose aspirin and time to pregnancy: findings from the effects of aspirin in gestation and reproduction randomized trial. J Clin Endocrinol Metab. 2015;100(5):1785-1791. doi: 10.1210/jc.2014-4179 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r21] 21.Rudolph JE, Naimi AI, Westreich DJ, Kennedy EH, Schisterman EF. Defining and identifying per-protocol effects in randomized trials. Epidemiology. 2020;31(5):692-694. doi: 10.1097/EDE.0000000000001234 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r22] 22.Robins JM, Rotnitzky A. Semiparametric efficiency in multivariate regression models with missing data. J Am Stat Assoc. 1995;90(429):122-129. doi: 10.1080/01621459.1995.10476494 [DOI] [Google Scholar]

[zoi211206r23] 23.Van der Laan MJ, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol. 2007;6(1):e25. doi: 10.2202/1544-6115.1309 [DOI] [PubMed] [Google Scholar]

[zoi211206r24] 24.Zhong Y, Kennedy EH, Bodnar LM, Naimi AI. AIPW: an R package for augmented inverse probability weighted estimation of average causal effects. Am J Epidemiol. 2021;190(12):2690-2699. doi: 10.1093/aje/kwab207 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r25] 25.Friedman JH. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67. doi: 10.1214/aos/1176347963 [DOI] [PubMed] [Google Scholar]

[zoi211206r26] 26.Breiman L. Random forests. Mach Learn. 2001;45(1):5-32. doi: 10.1023/A:1010933404324 [DOI] [Google Scholar]

[zoi211206r27] 27.Chen T, Guestrin C. XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery; 2016:785-794. [Google Scholar]

[zoi211206r28] 28.Naimi AI, Cole SR, Kennedy EH. An introduction to g methods. Int J Epidemiol. 2017;46(2):756-762. doi: 10.1093/ije/dyw323 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r29] 29.Hernán MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578-586. doi: 10.1136/jech.2004.029496 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r30] 30.Rose S, van der Laan MJ. Targeted Learning: Causal Inference for Observational and Experimental Data. Springer; 2011. [Google Scholar]

[zoi211206r31] 31.Polley E, LeDell E, Kennedy C, Lendle S, van der Laan M. SuperLearner: Super Learner Prediction. 2019. Accessed August 27, 2020. https://cran.r-project.org/web/packages/SuperLearner/index.html

[zoi211206r32] 32.Gruber S, van der Laan MJ. tmle: An R package for targeted maximum likelihood estimation. J Stat Softw. 2012;51(13):1-35. doi: 10.18637/jss.v051.i13 23504300 [DOI] [Google Scholar]

[zoi211206r33] 33.Carin L, Pencina MJ. On deep learning for medical image analysis. JAMA. 2018;320(11):1192-1193. doi: 10.1001/jama.2018.13316 [DOI] [PubMed] [Google Scholar]

[zoi211206r34] 34.Wang S, Pathak J, Zhang Y. Using electronic health records and machine learning to predict postpartum depression. Stud Health Technol Inform. 2019;264:888-892. doi: 10.3233/SHTI190351 [DOI] [PubMed] [Google Scholar]

[zoi211206r35] 35.Khera R, Haimovich J, Hurley NC, et al. Use of machine learning models to predict death after acute myocardial infarction. JAMA Cardiol. 2021;6(6):633-641. doi: 10.1001/jamacardio.2021.0122 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r36] 36.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. 2nd ed. Springer; 2009:587-604. [Google Scholar]

[zoi211206r37] 37.Cutler D, Lleras-Muney A.. Education and health: evaluating theories and evidence. In: House J, Schoeni R, Kaplan G, Pollack H, eds. Making Americans Healthier: Social and Economic Policy as Health Policy. Russell Sage Foundation; 2008. [Google Scholar]

[zoi211206r38] 38.Dunn G, Lovrić M. Complier-average causal effect (CACE) estimation. In: Lorvić M, ed. International Encyclopedia of Statistical Science. Springer Nature; 2011. [Google Scholar]

[zoi211206r39] 39.Awtry EH, Loscalzo J. Aspirin. Circulation. 2000;101(10):1206-1218. doi: 10.1161/01.CIR.101.10.1206 [DOI] [PubMed] [Google Scholar]

[zoi211206r40] 40.Abraha I, Montedori A. Modified intention to treat reporting in randomized controlled trials: systematic review. BMJ. 2010;340:c2697. doi: 10.1136/bmj.c2697 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r41] 41.Montedori A, Bonacini MI, Casazza G, et al. Modified versus standard intention-to-treat reporting: are there differences in methodological quality, sponsorship, and findings in randomized trials? a cross-sectional study. Trials. 2011;12(1):58. doi: 10.1186/1745-6215-12-58 [DOI] [PMC free article] [PubMed] [Google Scholar]

[zoi211206r42] 42.Benkeser D, Díaz I, Luedtke A, Segal J, Scharfstein D, Rosenblum M. Improving precision and power in randomized trials for COVID-19 treatments using covariate adjustment, for binary, ordinal, and time-to-event outcomes. Biometrics. 2021;77(4):1467-1481. doi: 10.1111/biom.13377 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Use of Machine Learning to Estimate the Per-Protocol Effect of Low-Dose Aspirin on Pregnancy Outcomes

Yongqi Zhong, PhD, MPH, MB

Maria M Brooks, PhD

Edward H Kennedy, PhD

Lisa M Bodnar, PhD, MPH, RD

Ashley I Naimi, PhD

Key Points

Question

Findings

Meaning

Abstract

Importance

Objectives

Design, Setting, and Participants

Exposures

Main Outcomes and Measures

Results

Conclusions and Relevance

Trial Registration

Introduction

Methods

Study Design

Treatment and Adherence

Outcome

Baseline Covariates and Postrandomization Confounders

Statistical Analysis

Results

Table 1. Treatment Assignment, Outcome, Baseline Covariates, and Postrandomization Confounders.

Figure 1. CONSORT Study Flow Diagram for the Effects of Aspirin in Gestation and Reproduction (EAGeR) Trial.

Figure 2. Number of Participants Who Adhered to Assigned Treatment by Different Follow-up Thresholds.

Table 2. Effects of Low-Dose Aspirin on hCG-Detected Pregnancy Among Women With Adherence to the Assigned Treatmenta.

Discussion

Limitations

Conclusions

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Table 2. Effects of Low-Dose Aspirin on hCG-Detected Pregnancy Among Women With Adherence to the Assigned Treatment^a.