Children's Long-Term Retention is Directly Constrained by their Working Memory Capacity Limitations

Abstract

We explored the causal role of individual and age-related differences in working memory (WM) capacity in long-term memory (LTM) retrieval. Our sample of 160 participants included 120 children (6 – 13-years old) and 40 young adults (18 – 24 years). Participants performed a WM task with images of unique everyday items, presented at varying set sizes. Subsequently, we tested participants' LTM for items from the WM task. Using these measures, we estimated the ratio at which items successfully held in WM were recognized in LTM. While WM and LTM generally improved with age, the ability to transfer information from WM to LTM appeared consistent between age groups. Moreover, individual differences in WM capacity appeared to predict LTM encoding. Overall, these results suggested that LTM performance was constrained by experimental, individual, and age-related WM limitations. We discuss the theoretical and practical implications of this WM-to-LTM bottleneck.

As children develop, their memory performance improves (in the visual domain, see Forsberg et al., in press). Working memory ¹ (WM), or the very limited information that is temporarily more accessible than other information (Adam et al., 2017; Cowan, 2001, 2017), shows consistent development during the school years (e.g., Cowan, 2016; Cowan et al., 2011; Gathercole et al., 2004). In contrast, long-term memory (LTM), the indefinite retention of an unlimited amount of information (e.g., Brady et al., 2008; Standing, 1973), develops in ways that are arguably more confusing. For example, although younger children are often viewed as less reliable court witnesses due to their poor memory abilities (e.g., Knutsson & Allwood, 2014), sometimes their memory report accuracy can be adult-like (e.g., Allwood et al., 2009; Jack et al., 2014). At all ages, LTM is far from perfect in terms of the information encoded into it and in terms of which information can be retrieved in a given circumstance (e.g., for the encoding and later retrieval of a school lesson).

The development of both WM and LTM has immense practical importance for children's ability to navigate both their everyday lives and formal education. Individual differences in WM capacity have consequences for children's ability to acquire new knowledge and skills (Cowan & Alloway, 2008), and may be a good predictor of academic success (Gathercole et al., 2004). Yet, it is unclear whether individual differences and general developmental trajectories of WM and LTM abilities are causally related. WM capacity and educational attainment may co-vary due to some third covariate. For instance, WM capacity differences correlate with fluid intelligence and reasoning ability (Conway et al., 2003; Unsworth et al., 2014) that may also assist LTM. Alternatively, correlations between higher WM capacity and greater educational attainment might be partially driven by more efficient transfer of information to LTM.

The present contribution is to quantify the retrievable information in LTM in terms of information previously in WM, from the early elementary school years to adulthood. It has long been understood that WM serves as a portal to LTM (e.g., Atkinson & Shiffrin, 1968; Bartsch et al., 2019; Cowan, 1988, 2019; Forsberg et al., 2020; Fukuda & Vogel, 2019; Loaiza et al., 2020), albeit to an extent that seems methods-dependent (Shimi & Logie, 2019). There are, however, alternative potential scenarios for the childhood development of that portal for LTM. We know that WM capacity increases with age, and LTM could develop only in that more WM information becomes available for transfer into LTM. Alternatively, the transfer of information from WM to LTM may change with development. In this study, we tested how children's WM capacity limitations restrict their subsequent LTM retrieval, using an adapted version of a recent procedure (Forsberg et al., 2020).

Forsberg et al. (2020) found that WM capacity limitations constrained the number of items young-adult participants recognized in a later LTM test. They manipulated – and measured – the number of items participants held in WM, and then estimated the ratio of items held in WM that were remembered in a subsequent LTM test. LTM performance was better for items presented under lower WM load up to a capacity limit (e.g., better for items presented within arrays of 2 items as opposed to 6). We explored whether (1) children's WM capacity deficits also explain their LTM deficits, (2) the ratio is the same or different across age groups, and (3) individual differences in WM capacity within an age group explain individual differences in LTM.

We used the Forsberg et al. (2020) method to distinguish between three possibilities. First, the ratio of items that can be retrieved in a subsequent LTM test – out of the number of items held in WM – may be constant with age. If we find support for this, it suggests that children are equally adept at encoding items into LTM when their WM limitations are accounted for. Second, younger children may retrieve a smaller proportion of their successfully encoded WM items in the subsequent LTM test than older children, or adult participants. This would suggest that children's LTM deficits go beyond their WM encoding deficits and may depend on other processes (e.g., difficulty transferring items to LTM, less complete consolidation of LTM items, and/or difficulty in retrieval from LTM). Third, and finally, younger children may retrieve a higher proportion of successfully remembered WM items in LTM than older children and adults. This counterintuitive finding could be plausible if children selectively focus more deeply on a small subset of WM items in a way that results in deeper LTM encoding of such items, perhaps aligned with the levels-of-processing hypothesis (Craik & Lockhart, 1972). Applied to our stimuli, a shallow level of processing would be one in which the form or structure of an object is observed, a deeper level would be one in which the semantic category of the object is recognized, and a still deeper level might be one in which a coherent scene is invented to link together items in an array (e.g., imagining a butterfly from the array landing on a nearby wheel in the array). Moreover, we were interested in individual differences in WM ability and LTM encoding of items. If high WM ability promotes better LTM encoding of items, participants with greater age-adjusted WM capacity should retrieve comparatively more items in the LTM test.

Method

The methods, and all analyses (except those labeled 'as exploratory') were pre-registered on the Open Science Framework at [ https://osf.io/uyaj4/?view_only=c74fa9ce36a246a1ab3d87757bfbc46b].

Participants

Pilot Data

At the point of pre-registration, we had collected data from 20 participants (including 19 6- or 7-year-olds and one third grader) to ensure that such young participants were able to complete the task online. We looked at each participants' average performance but had performed no analyses at the point of pre-registration.

Sample Size Rationale

Based on Bayes Factor Design Analysis (BFDA; Schönbrodt & Stefan, 2018) simulations, we used a sequential stopping procedure (see Online Supplement, Section 1 for more information). Our pre-registered first stopping point was at N = 30 per age group. At this point, we ran a pre-specified Bayesian t-test on age differences in the WM/LTM ratio in the youngest children versus the adults. The Bayes Factor (BF) for this analysis was 'inconclusive', i.e., neither providing evidence for or against an age difference (defined as a BF between 1/3 and 3). Therefore, as specified, we tested 10 more participants per age group and reanalyzed. And this point, the BF evidence against an age difference in the WM/LTM ratio was > 3, and therefore, data collected stopped at N = 160.

Recruitment

We recruited participants via social media and local schools and by inviting local college students. Participants received either course credit (some college students) or 15 USD for completing the study. If the session took longer than 45 minutes, they received additional compensation. This study was approved by the local IRB committee and all participants gave their informed consent prior to their inclusion in the study.

Exclusions and Replacements

One participant in the youngest age group was excluded and replaced per our pre-registered exclusion criteria (see Supplement, Section 2) for accuracy less than .55 at set size two in the WM task. Four participants started the study but did not complete it, three due to technical issues and one choosing to end participation after a few minutes. We performed three unanticipated online-testing-related exclusions and replacements. One participants' parent was heard whispering answers (1st and 2nd grader-group), one reported that the screen was zooming in and out, preventing them from seeing the items (3rd and 4th grader-group), one was unable to click and responded verbally instead (5th through 7th grader-group). These participants were excluded and replaced to ensure good data quality.

Final Sample

The final sample included 40 participants in each of four different age groups: 1st and 2nd graders (M = 7.9, SD = 0.72 years, 50.0% female), 3rd and 4th graders (M = 9.8, SD = 0.73 years, 47.5% female), 5th through 7th graders; M = 11.9, SD = 0.89 years², 47.5% female) and young adults; (M = 19.6, SD = 1.8 years, 47.5% female). See the Supplement, Section 3, for detailed inclusion criteria and demographic information.

Online Study Administration

We collected data online using an online communication software (Zoom) and PsyToolkit (Stoet, 2010, 2017). The experimenter explained instructions, was available for questions and encouragement, and was able to see the task as seen by the participant. The experimenter muted their webcam audio and turned off the video when the participant was doing the task, except to provide a minimum of three positive reinforcement phrases (e.g., "Hang in there!") during the WM and LTM tasks. If a participant appeared to be losing focus, the experimenter provided additional encouragement as needed. The experimenter also repeated numbers and provided positive feedback during the running span task.

On average, participants completed the main experiment (excluding the running span task) in the following timeframe: 1st and 2nd graders, M=42.2, SD=7.03, range=28–60 min; 3rd and 4th graders, M=37.7, SD=7.28, range=28–63 min; 5th through 7th graders, M=36.2, SD=6.49, range=27–51 min; and young adults, M=28.3, SD=4.8, range=17–40 min.

General Study Design

Participants completed four different tasks in a fixed order: (1) a WM probe-recognition task, (2) 4 trials of an unrelated visuospatial memory distraction task to purge the Task 1 items from WM, (3) an LTM probe-recognition test, assessing memory for items previously studied in the WM task, and finally, (4) an auditory WM running span-task (completed by 154 of the 160 participants) as a quick individual working memory assessment that correlates well with aptitudes (Broadway & Engle, 2010; Cowan et al., 2005).

WM Task

We selected memory items from the Microsoft Office Icons, consisting of various easily recognizable images (e.g., animals, fruits, and furniture). All items were presented in black on a light grey background. Participants studied a total of 288 unique memory items in the WM task at varying set sizes (2, 4, or 6 items). Items in an array were presented around a central fixation cross (+) in an imaginary circle with 8 possible locations (one at every 45-degree increment). Locations were selected at random for each trial.

Each trial started with the 250 ms central fixation cross, followed by the memory array and a 2000 ms delay, before the probe item and response options were presented (See Figure 1). The memory array was presented for 250 ms times the number of items in the array. The probe item was drawn randomly from the array on half of the trials and was a new, unseen item in the other half. Participants responded by clicking on one of the following options presented on the screen along with the probe: 'I'm sure I saw it', 'I think I saw it', 'I guess I saw it', 'I guess I didn't see it', 'I don't think I saw it', or 'I'm sure I didn't see it'.

Figure 1.

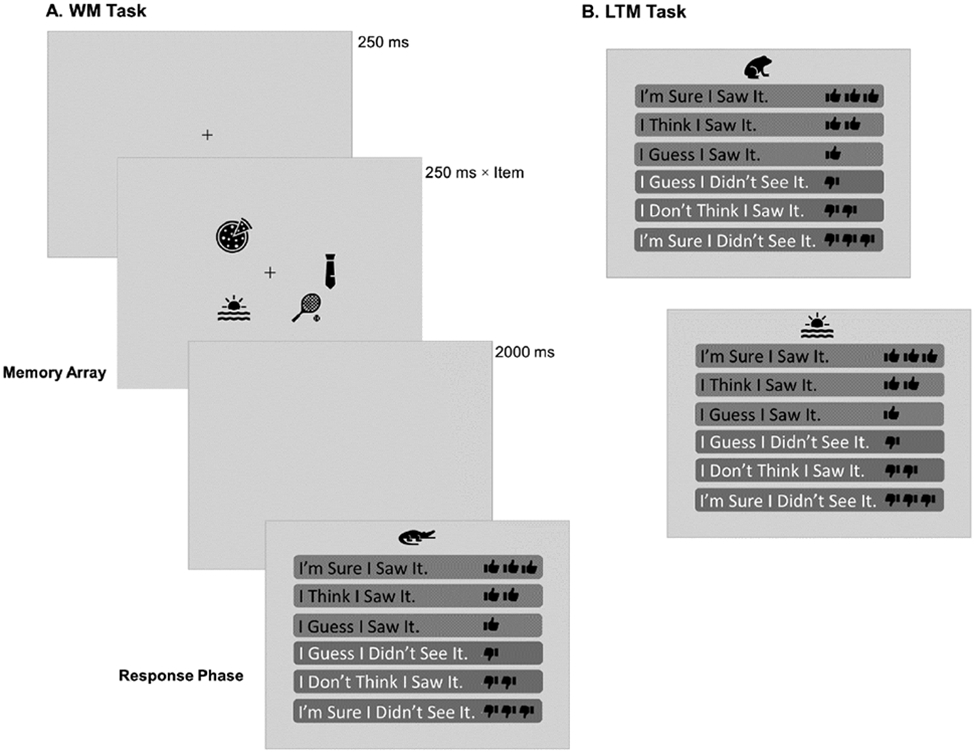
Outline of some typical trials. Panel A, Working Memory (WM) Task trial. Panel B, two trials in the Long-Term Memory (LTM) Task. The memory array set size in the WM task varied between 2, 4, or 6 items, and the presentation time was adjusted to be 250 ms per item. During the WM response phase, participants indicated whether they had seen the probe item in the Memory Array or not, and also selected their level of confidence, by clicking on the relevant option. In the LTM task, participants indicated whether they had previously seen the probe items in the WM task. This figure is presented in greyscale. In the real experiment, the response scale was green for the three response options indicating having seen the object, and red for the options indicating not having seen the objects.

Each participant completed 88 WM trials (48 trials at set size 2, 24 trials at set size 4, and 16 trials at set size 6). Hence, participants saw a total of 96 items at each set size (set size 2, 48 trials × 2 items; set size 4, 24 trials × 4 items, set size 6, 16 trials × 6 items). The order and items for each trial were randomized for each participant.

Distraction Task

Participants completed four trials of an unrelated brief visual memory task. During this task, participants saw aliens appear in a 3-by-3 grid and clicked on the locations in which they thought the aliens were previously presented. There were two trials with four aliens and two trials with five aliens.

LTM Task

We tested participants' memory for items they had previously studied in the WM task. On each trial, participants saw a probe item and had to say whether that item was studied in the WM task, or was a new item (see Figure 1). They responded by clicking on one of the following options: 'I'm sure I saw it', 'I think I saw it', 'I guess I saw it', 'I guess I didn't see it', 'I don't think I saw it', or 'I'm sure I didn't see it'. To avoid repeated exposure, items that were probed in the WM task were not probed in the LTM task. Each participant responded to a total of 168 items in the LTM task (46 new items, 36 items from set size 2, 42 items from set size 4, and 44 items from set size 6). Participants were not informed that they would be tested on the WM items again³.

Running Span Memory Task

Last, participants completed 32 trials of the running span memory task (from Cowan et al., 2005). Participants heard sequences of digitally compressed spoken digits presented at a fast rate (4 items/s). When the number list stopped, they were to remember as many of the numbers from the end of the list as possible in the order that they heard them. For example, if the last three numbers were 4, 5, 1, and they remembered the last two, they would respond "5, 1". Spoken responses were recorded by the experimenter. To score answers, we aligned the participant's response list to the end of the presented digit list (e.g.., we compared their final digit to the final digit of the presented list). Credit was given for the number of items recalled in the correct location relative to the list’s end, throughout the entire response.

Analysis Methods

Inferential Statistics

We use Bayesian statistics and a nomenclature in which BF₁₀ refers to the Bayes Factor for the presence of an effect and BF₀₁ refers to an absence of an effect, where BF₀₁=1/ BF_10.

Recognition Modeling

For each participant, we estimated the proportion of items from a given WM set that was observable in memory at the time of (1) WM testing; p(WM), and (2) LTM testing; p(LTM). With these measures, we formed a ratio of LTM to WM item production, by set size and age group (see Forsberg et al., 2020).

For these measures, we ignored the participants' certainty (sure, think, or guess) and only considered whether the correct half of the response scale was used. The p(WM) estimates were obtained by calculating the rate at which the participant correctly detected studied items (i.e., the hit rate, h) and the rate at which they incorrectly identified new items as old (i.e., the false alarm rate, f). To estimate p(WM) we used a model derived from Pashler (1988) that was applied to the present single-probe test situation by Cowan et al. (2013, the "reverse-Pashler" formula).⁴ We assume that when the probed item is in WM, participants respond correctly, and otherwise guess that the item is new with a certain rate (g). Then, the rate of correct detection of old items, h, equals the probability that the probe item is in WM plus the probability that it is not in WM but that a correct "old" guess g is given:

$$h=p(\text{WM})+[1\text{-}p(\text{WM})](g)$$

For a new item there is no match, so performance depends on the guessing rate, and an incorrect response (f) is made at the rate, f=g. Combining these formulas, it can be shown that:

$$p(\text{WM})=\left(\frac{h-f}{1-f}\right)$$

A similar formula can also be used to estimate the proportion of items in LTM, in which hits (hl) is the rate of correctly detected old items and false alarms (fl) the rate of incorrectly responding that a novel item was old:

$$p(\text{LTM})=\left(\frac{hl-fl}{1-fl}\right)$$

However, if the false alarm rate exceeds the hit rate, p(WM) or p(LTM) would be a negative value. This makes little theoretical sense and probably reflects a combination of poor memory and unlucky guessing. We had pre-registered two approaches to deal with such negative values. First, we adjust negative values to theoretically plausible values. P(WM) values equivalent to holding < 1 item in WM were adjusted to equal 1, and p(LTM) values < 0 were adjusted to 0. In the second approach, we completely excluded participants with a negative value at one or more set sizes, either for WM or LTM. We report the former, adjusted analyses in the paper, and the latter in the Supplement (Section 4), and point out discrepancies.

Results

Working Memory

First, we confirmed that our WM set size manipulation had the intended effect on WM accuracy, using a similar approach to Forsberg et al. (2020). Using Bayesian logistic regression, we found credible evidence that memory performance decreased as set size increased and that older participants outperformed younger participants. There was evidence against an age group by set size interaction. See the Supplement (Section 5), for further details. We found similar patterns in an exploratory analysis using 'generalTestBF' function⁵ in the BayesFactor package for R (Morey et al., 2015) of the pre-registered p(WM) measure, which was higher for lower-set size items, BF₁₀=1.11×10⁴⁸ , F(1, 472)=241.11, η_p²=0.338; better for older participants, BF₁₀=6.67×10⁴, F(3,472)=19.02, η_p²=108; with evidence against an interaction, BF₀₁=37.09, F(3,472)=2.022, η_p²=0.013 (see Figure 2 and Table 1).

Figure 2.

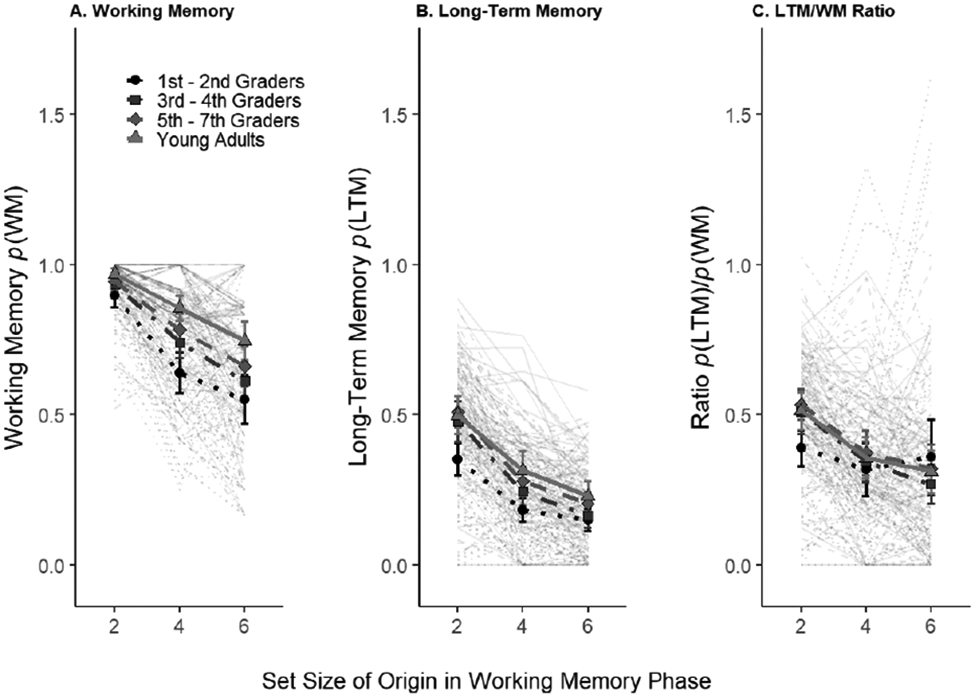
Memory accuracy by WM set size. Panel A, p(WM) (i.e., the estimated probability that items were held in WM); Panel B, p(LTM) (i.e., the estimated probability that items were held in LTM); Panel C, the p(LTM)/p(WM) ratio. Triangles and solid lines and show the college students data, diamonds and long-dashes the 5-7^th graders, squares and mixed dashes 3^rd – 4^th graders, and circles and dotted lines the 1^st – 2^nd graders. Lighter lines show individual subjects estimates. Error bars represent 95% confidence intervals.

Table 1.

Averages for transformed data by Set Size (adjusted; N = 40 per age group)

Set Size	p(WM)	p(LTM)	LTM/WM ratio	WM capacity (k)
1st and 2nd graders
2 items	.90 (.12)	.35 (.17)	0.39 (0.19)	1.8 (0.25)
4 items	.64 (.21)	.18 (.13)	0.32 (0.28)	2.6 (0.85)
6 items	.55 (.25)	.15 (.11)	0.36 (0.40)	3.3 (1.50)
3rd and 4th graders
2 items	.93 (.07)	.48 (.21)	0.51 (0.23)	1.9 (0.14)
4 items	.74 (.16)	.24 (.14)	0.34 (0.21)	3.0 (0.64)
6 items	.61 (.20)	.17 (.13)	0.27 (0.20)	3.7 (1.20)
5th through 7th graders
2 items	.94 (.09)	.51 (.16)	0.54 (0.16)	1.9 (0.18)
4 items	.78 (.17)	.28 (.15)	0.37 (0.23)	3.1 (0.69)
6 items	.66 (.21)	.20 (.13)	0.32 (0.25)	4.0 (1.30)
College students
2 items	.97 (.06)	.50 (.19)	0.51 (0.19)	1.9 (0.12)
4 items	86 (.13)	.31 (.20)	0.36 (0.22)	3.4 (0.53)
6 items	.75 (.20)	.23 (.16)	0.31 (0.22)	4.5 (1.20)

Note. Values in Parenthesis represent Standard Deviations. Values equivalent to WM k < 1 were replaced with the corresponding p(WM) for k = 1, and values of p(LTM) × Set Size ≤ 0 were replaced with zero.

Long-Term Memory

We tested whether performance in the LTM task (p(LTM)) varied as a function of WM set size and age group. We found 'decisive' evidence that p(LTM) was higher for lower-set size items, BF₁₀=1.10×10⁵⁷, F(1,472)=225.42, η_p²=0.323; and evidence of age group differences, BF₁₀=70.58, F(3,472)=12.61, η_p²=0.074; but against an interaction, BF₀₁₌14.39, F(3,472)=1.89, η_p²=0.012 (see Figure 2 and Table 1 for mean values).

Participants incorrectly responded ‘studied’ to novel items in the LTM test at the following rates: 1st and 2nd graders (M=.20, SD=0.18), 3rd and 4th graders (M=0.18, SD=0.13, 5th through 7th graders (M=0.22, SD=0.13), and young adults (M=0.29, SD=0.17).

LTM/WM Ratio: Analysis of the Average Number of Items in WM and LTM

As our key measure, we explored how many of the items encoded into WM could be retrieved on an LTM test (i.e., the LTM/WM ratio shown in the right-hand panel of Figure 2). First, we compared the average ratios of the very youngest child group with the adults and found evidence against age differences in the average LTM/WM ratio (BF₀₁=4.12; youngest children average ratio: M=0.36, SD=0.22, young adults, M=0.39, SD=0.17, d=0.19).

Then, we compared ratios across all age groups (and set sizes). We found strong evidence that the LTM/WM ratio differed by Set Size, BF₁₀=9.06×10¹¹, F(1,472)=41.78, η_p²=0.081; but evidence against an age group difference, BF₀₁=15.16, F(3,472)=1.76, η_p²=0.007; and some evidence for an age group × set size interaction, BF₁₀=3.73, F(3,472)=3.20, η_p²=0.020 (see Figure 2 and Table 1).

Exploratory Bayesian t-tests on the most extreme age comparison (the youngest children vs. adults) and found evidence for a ratio difference at set size 2 (BF₁₀=6.50, Children: M=0.39, SD=0.19; Adults: M=0.51, SD=0.19), but evidence against such a difference at set size 4 (BF₀₁=4.73, Children: M=0.32, SD=0.28; Adults: M=0.36, SD=0.22) and set size 6 (BF₀₁=4.82, Children: M=0.36, SD=0.40; Adults: M=0.31, SD=0.22). If it exists, the interaction indicates less of a set size effect on the ratio in younger participants (Figure 2), as one might expect if Set Size 2 is not below capacity for some participants.

Indeed, the average k value was lower in 25 participants whose negative p(WM) and p(LTM) values needed to be adjusted compared to other participants (in the 4 groups, respectively, 2.12 vs. 2.62; 2.62 vs. 2.88; 2.67 vs. 3.00; and 3.00 vs 3.30). When we exclude these 25 participants (remaining n=135), there is evidence against the interaction, BF₀₁=28.06; F(3,397)=1.22, η_p²=0.009. There was still evidence for the set size effect, BF₁₀=1.89×10¹², F(1,397)=49.63, η_p²=0.111; and against a main effect of age, BF₀₁=8.78, F(3,397)=1.83, η_p²=0.014. Given these discrepancies between analyses, the overall evidence for differential ratio differences across set sizes in young children and adults should be interpreted cautiously.

Correlations between Measures

WM and LTM.

We explored correlations between average WM capacity (k) and the number of items held in LTM, estimated using p(LTM) × the number of items in the original array. First, we used each participant's average across the set sizes. We observed a positive correlation between average age-standardized k-scores and p(LTM) scores, r=.31, BF₁₀=9.90×10². These relations are shown by age group in Figure 3 and appear due to comparable relations in the three older groups. We also tested separate, age-standardized k-scores and p(LTM) correlations for memory from items presented as part of Set Sizes 2, 4 and 6, respectively (Set Size 2: BF₁₀=6.43×10², r=.31; Set Size 4: BF₁₀=2.60, r=.18, and Set Size 6: BF₁₀=1.42×10², r=.28).

Figure 3.

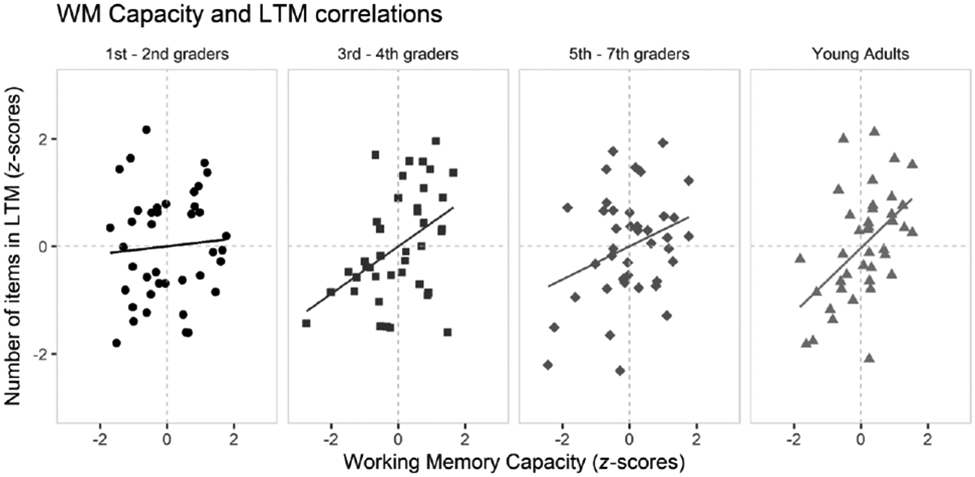
Correlations between age-adjusted z-scores of the average number of items in LTM and working memory capacity, in participants of the four age groups.

Running Span and LTM/WM Ratio

Average running span scores (i.e., the number of correctly recalled digits) increased with age from the youngest children (M=2.6, SD=0.57, N=36) to the second youngest (M=2.7, SD=0.52, N=40) to adolescents (M=2.8, SD=0.43, N=39) and adults (M=3.1, SD=0.65, N=39; BF₁₀=52.71, F(3,150)=6.26, η_p²=0.11). Six participants did not complete the running span task. We tested whether individual age-adjusted running span performance was correlated with the age-adjusted LTM/WM ratio. We observed evidence against a correlation between these age-standardized scores, r=.0073, BF₀₁= 5.35. In an exploratory analysis, we tested whether higher age-adjusted running span scores were correlated with remembering more items in the LTM test (age-standardized) and found some evidence against a correlation (r=.041, BF₀₁= 4.67). Moreover, while raw running scores were positively correlated with raw average WM capacity (r=.22, BF₁₀= 9.54), we observed inconclusive evidence against such a correlation using age-standardized values (r=.10, BF₀₁=2.32). See the supplement for a summary of exploratory correlations between all measures.

Other Measures

We present confidence ratings for each memory task, set size, and age group in the Supplement (Section 6), and as indicated above, we observed similar patterns of results regardless of participants’ confidence levels. Accuracy on the visuospatial distraction task was comparable in the youngest group (M=98.2%), second-youngest (M=99.6%), adolescents (M=99.2%) and adults (M=100.0%).

Discussion

We tested whether younger children's comparatively small WM capacity constrains their LTM ability by forming a narrower LTM encoding bottleneck. Consistent with previous research in adults (Forsberg et al., 2020), our findings suggest that having to remember more items in a WM task limits subsequent LTM retrieval of items, in children aged 6 – 13. When the array includes fewer items, attention is not spread as thin (e.g., Morey & Bieler, 2013) and a higher proportion of items might receive covert verbal labels that assist LTM retention (e.g., Gathercole et al., 1997).

Our central research question was whether the ratio of items recognized in LTM to those that had been held in WM differed between young children and adults. Overall, we found that, despite younger children's generally poorer WM and LTM performance, the LTM/WM ratio remained constant across age groups, as shown in Figure 2. This finding suggests that an individual’s WM limitations largely explain their LTM deficits, regardless of individual or developmental differences in WM itself. We do not know if this conclusion extends beyond the present study in which arrays of known objects were to be remembered and LTM testing occurred within the same session as WM testing. Differences in the WM load during encoding may explain observations of young children's memory abilities as being very good in some ways and poor in other ways (Miller, 2014). Further research could explore implications of this LTM encoding process for the optimal methods of presentation of educational material.

Individual differences within an age group also were found. Participants with higher WM capacity commensurately remembered more items in the subsequent LTM test. More efficient LTM encoding in higher-capacity participants might form part of the causal link between high WM capacity and better educational attainment (Cowan, 2016). The finding also appears aligned with suggestions that verbal short-term memory ability may predict LTM word learning in children (e.g., see Gathercole et al., 1997). However, running span task performance did not predict object LTM. We found this surprising, inasmuch as running span with a rapid presentation like ours requires attention, does not allow rehearsal, and loads with visual WM as heavily as it loads with verbal WM (Bunting et al., 2008; Cowan et al., 2005; Gray et al., 2017). Upon reconsideration of the procedure, this, though, may be the issue. More adept participants may form verbal codes that help in the LTM encoding of items, a process that running digit span does not reflect well. It remains to be seen whether our results are specific to our arrays with different real objects on every working-memory trial, a situation in which long-term representations enhance working memory (Endress & Potter, 2014). Moreover, the inconclusive evidence for a WM and running span correlation when using age-standardized values suggests that perhaps the group sizes were not large enough to detect reliable individual differences across measures beyond the large ones based on age-related maturation.

We observed some tentative evidence that the WM set size manipulation (2, 4, or 6 items) affected the WM/LTM ratio differently in young children and adults, with ratios differing only at set size 2. This result was eliminated when we excluded participants with negative ratios, who had relatively low capacities overall. If some young children's WM was close to maximum capacity at this set size, whereas most older participants had extra resources available, the older participants could carry out deeper encoding of the two items (see Craik & Lockhart, 1972; Forsberg et al., 2020). The specific mechanisms underlying the set size effect in WM – and, correspondingly, in LTM – are not yet clear. Participants may have used elaborative strategies, attentional refreshing (Camos et al., 2018), or verbal rehearsal (Forsberg et al., 2019) to keep items in WM. All of these strategies would presumably be more effective for smaller, compared to larger, set sizes. Recent work suggests these different approaches may affect working and long-term memory performance to different extents (Bartsch et al., 2018), and importantly, participants in different age groups may have used these strategies to different extents. This is a prime topic for follow-up research.

Our results are broadly consistent with theories of WM and LTM as linked, closely related systems (Cowan, 2019), which may share the same encoding bottleneck (see Brady et al., 2008). Overall, we saw commensurate improvement of WM and LTM from 6-7-years-olds, across early adolescence, into adulthood. Further work could clarify how WM and LTM may interact as they develop together. Developing ability to use LTM to detect patterns in the environment may allow better chunking of information, relieving the load on attention in WM (Forsberg et al., in press) and assisting in the acquisition of concepts (Cowan, 2016).

Research Highlights.

• Working memory load at encoding determined subsequent long-term memory performance in children (6 – 13-year-olds) and young adults (18 – 24 years).

• Young children's working memory capacity limits appeared to constrain their long-term memory.

• When accounting for their working memory limitations, young children encoded visual items into long-term memory at similar rates as adults.