Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Feb 26;7(9):7531–7540. doi: 10.1021/acsomega.1c05532

Monomolecular Cracking of Propane: Effect of Zeolite Confinement and Acidity

Zainab A Alaithan 1,*, Giuseppe Mallia 1, Nicholas M Harrison 1
PMCID: PMC8908521  PMID: 35284742

Abstract

graphic file with name ao1c05532_0006.jpg

The effect of zeolite pore geometry and intrinsic acidity on the activation energy of propane monomolecular cracking was investigated for six topologically distinct zeolites with different pore sizes. Periodic density functional theory calculations were used to calculate the activation energy, while cluster models were used to calculate deprotonation energies. The computed intrinsic activation energies showed a smaller variation with topology than the adsorption energies. No correlation was found between the computed deprotonation and ammonia adsorption energies at the acid site and the intrinsic activation energy. Detailed analysis of the computed structures and properties suggests that acid sites with different pore topologies impose geometrical constraints on the ion-pair formed by the ammonium molecule, which differs significantly from those that affect the propane reaction.

Introduction

Zeolites are microporous materials composed of corner-sharing AlO4– and SiO4 tetrahedra linked in a superlattice of cages and channels. When the negative charge on the AlO4– site is compensated by a proton, a (≡Al–OH–Si≡) Brønsted acid site is formed. For any particular zeolite cage, the specific geometric structure of the Brønsted acid sites affects their ability to accommodate guest species. Guest-site congruity imparts differences in the stability of reactive species, transition states, and intermediates, giving rise to shape selectivity.1−7 In addition to acidity and microporosity, the high thermal stability and low production cost facilitate the use of zeolites in many industrial processes. Fluid catalytic cracking is a key process in the conversion of crude oil to transportation fuels and petrochemical feedstock.8 The mechanism of cracking depends on the reaction conditions.9 The bimolecular mechanism dominates at low temperatures, high partial alkanes pressure, and high conversion. This mechanism involves a chain of reactions propagated by the carbenium ions.10 The alternative monomolecular Haag-Dessau mechanism is preferred at high temperature (T > 600 K) and low partial alkanes pressure.9 This mechanism represents the direct protonation of the alkane at the Brønsted acid site,11 creating a carbocation intermediate, which then dissociates into a shorter alkene and alkane:

graphic file with name ao1c05532_m001.jpg 1

Monomolecular cracking has been subject to numerous experimental9,12,13 and theoretical studies based on density functional theory (DFT) using periodic14−17 and cluster models.18−21 Most studies agree that the rate-limiting step of monomolecular cracking is the protonation of the alkane11,19,20,22−24 by attacking the C–C bond.19,20,22

The experimental measurement of the apparent activation energy, Eapp, inevitably also includes the contributions of both site adsorption energy and the intrinsic activation energy:

graphic file with name ao1c05532_m002.jpg 2

where Eads is the alkane adsorption energy at the reaction site and Eint is the intrinsic activation energy. The intrinsic activation energy is the energy required to cross the barrier between the adsorbed reactant state and the product state. Experimental activation enthalpies of monomolecular cracking decrease as the pore diameter of the zeolite framework decreases.13,25,26 The analysis of experimental data suggests that the decrease in the apparent activation energy with confinement is caused by the decrease in the adsorption energy and that the intrinsic activation energy is rather insensitive to framework type.12,13,27 However, the analysis that distinguishes the intrinsic activation energy from the apparent activation energies has some shortcomings. The adsorption measurements are usually conducted at temperatures well below the actual cracking temperatures and include the contribution of alkanes adsorption at non-Brønsted acid sites. Recent progress has been made both computationally and experimentally in addressing these issues. Theoretically, adsorption energies were calculated by Janda et al.28 using Monte Carlo simulations of the Brønsted acid sites and at realistic reaction temperatures. This facilitated the calculation of the intrinsic activation energies from the experimentally measured activation energies for butane cracking and dehydrogenation.28 They demonstrated that the intrinsic activation energy might be affected by confinement in 10-ring zeolites, depending on the location of the cracked bond. The intrinsic activation energy of cracking at the terminal carbon atom decreased as confinement increased. On the other hand, the intrinsic activation energy of cracking at the central bond of butane was found to be invariant with respect to the level of confinement. Experimentally, Kadam et al.13 obtained the apparent rate constants, kapp, and adsorption constants, Kads, at the same temperature using IR operando spectroscopy. They concluded that confinement mainly influences the adsorption energies and that the intrinsic activation energies in different zeolites are similar.13 More recently, Berger et al.29 calculated the intrinsic activation energy of propane cracking in MFI, FER, MVY, CHA, and FAU zeolites using a hybrid QM:QM method and confirmed that adsorption energies dominate the predicted apparent activation energies.

Since monomolecular cracking involves proton transfer from the acid site to the alkane, zeolites acidity has been the subject of extensive theoretical studies.30−33 There are two proxies commonly used to quantify the acidity of a site: the deprotonation energy or the adsorption energy of basic molecules. Deprotonation energy is defined as the energy required to release the proton from the Brønsted site. It is now accepted that the intrinsic acidity of the Brønsted sites in different zeolite frameworks is similar. Deprotonation energies were calculated using the QM-Pot method for CHA, TON, FER, MFI, MOR, and FAU and were found to lie within a range <30 kJ mol–1.34,35 This conclusion was confirmed by Jones and Iglesia32 who calculated the ensemble average deprotonation energy, ⟨DPE⟩, for the 12 distinct T sites in MFI and found them to be similar to a value of 1201 ± 11 kJ mol–1.

Ammonia, NH3, adsorption is a convenient base also commonly used to probe the acidity of zeolites. While ammonia adsorption is well suited for Brønsted acid site quantification, it has been suggested that the correlation between the intrinsic acid site strength and the adsorption energy is not unambiguous.36 For instance, Jones and Iglesia32 have shown that NH3 adsorption energies do not correlate monotonically with the DFT calculated ensemble-averaged deprotonation energies ⟨DPE⟩, suggesting that the measured adsorption energies are indicative of the confinement effect.33 Boronat and Corma33 also concluded that the adsorption energies of strong bases include the contribution of multiple interactions between the protonated base and the surrounding anionic framework O atoms. Even though ammonia adsorption energies do not correlate with deprotonation energies, Liu et al.37 reported a correlation between NH3 adsorption energy and the intrinsic activation energy of propane cracking in FAU type zeolites.

In the present study, the monomolecular cracking activation energy and the acidity will be investigated with DFT methods in 6 frameworks (FAU, AFI, MFI, MEL, CHA, AEI). The influence of confinement and acidity on the intrinsic activation energy, apparent activation energy, and adsorption energies will be investigated.

Methods

Periodic DFT Calculations

Periodic density functional theory (DFT) calculations were performed with the CRYSTAL software38 with the effects of electronic exchange and correlation described by the ωB97X-D functional,39 which has been reported to take noncovalent interactions into account and was used for similar systems.14,40 London dispersion interactions were estimated using Grimme’s dispersion correction.41 Triple valence 6-311G(d,p) Gaussian basis sets were used throughout the calculations.42 The Brillouin zone sampling was restricted to the γ point. The reaction paths and the transition states were determined with the climbing image nudged elastic band method43 as implemented in the atomic simulation environment package (ASE) package.44 Geometry optimization of the initial, final, and path images was performed with fixed cell parameters. Vibrational frequencies were computed to confirm the nature of the transition state.45,46 Unconstrained geometry optimization of all coordinates was performed to find local minima with convergence assumed to be reached when the forces on each atom are less than 0.02 eV Å–1.

Activation and Adsorption Enthalpies

The enthalpy of a system X, HX, was calculated as

graphic file with name ao1c05532_m003.jpg 3

where the zero-point vibrational energy, E0, and the vibrational contribution to the thermal energy, ET, were calculated within the quasi-harmonic approximation.47 The intrinsic activation energy was then calculated as

graphic file with name ao1c05532_m004.jpg 4

where HTs denotes the enthalpy of the transition state, and HZ–P denotes the enthalpy of the adsorbed propane. The adsorption enthalpy was calculated as

graphic file with name ao1c05532_m005.jpg 5

where HZ–M denotes the enthalpy of the adsorbed system, HZ denotes the enthalpy of the zeolite crystal, and HM denotes the enthalpy of the molecule in the gas phase. Adsorption enthalpies were then corrected for the basis set superposition error (BSSE) using the counterpoise correction method.48

Cluster DFT Calculations

Using periodic models allows for an accurate and systematic comparison of the intrinsic activation energies and the ammonia adsorption energies in different zeolites. However, unambiguous assignment of the energy reference for the potential energy in charged cells means that it is problematic to compare descriptors such as the deprotonation energy between zeolites frameworks. Here this is achieved by using cluster models of the reaction sites using the same basis set, exchange-correlation functional, and numerical tolerances as the periodic calculation. Suitably converged clusters must be defined. A widely used method is to include all atoms within N bonds from the Al atom. The clusters generated by this method are termed N-bond clusters. Jones et al.49 examined the effect of the cluster size on deprotonation energies using N-bond clusters. Their results showed that the deprotonation energy varies systematically with the cluster size. The variation in the calculated deprotonation energy converges for clusters with more than 20T atoms, where T stands for either of the tetrahedrally coordinated Si or Al atoms. Hence, Jones et al.49 deduced that the negative charge that remains upon deprotonation is localized within the second coordination sphere of the oxygen atoms from the aluminum atom. In this study selecting N = 6 generated clusters with more than 30T atoms for all of the examined frameworks and thus was used to generate the clusters to evaluate the deprotonation energy. Deprotonation energies were then calculated according to the following equation:

graphic file with name ao1c05532_m006.jpg 6

Zeolite Frameworks

Six frameworks with varying pore sizes were used to sample a wide range of confinement and acidity strengths. Those frameworks are FAU, AFI, MFI, MEL, AEI, and CHA. Details of these structures and the optimized cell parameters are listed in Table 1. AFI has a lattice constant of just 8.58 Å in the crystallographic c-direction, which may result in interactions between periodic images. AFI was therefore described with a doubled unit cell along this direction. The periodic cell models are illustrated in Figure 1. Zeolites frameworks can have several crystallographically distinct T sites, and each T atom is coordinated to four oxygen atoms. The acidic proton can hop between those oxygen atoms.32 In the present study, we are focused on the trends in activation energies with zeolite topology. We, therefore, adopt a model of the reaction site based on a single T site in each zeolite where the acidic hydrogen is bonded to a single oxygen position as indicated in Table 4. This choice facilitates the extraction of trends but prevents the direct comparison of computed data to experiment, which is best achieved with an ensemble average over all of the kinetically accessible T sites and oxygen positions. Absolute values for experimental results are quoted below for qualitative comparison with those computed.

Table 1. Optimized Cell Parameters for Studied Zeolites’ Periodic Models Used in DFT Calculations and LCD.

framework type LCDa (Å) Al position Si/Al cell cell parameters
FAU 1 11.9 T1 47 rhombohedra a = b = c = 17.37
          α = β = γ = 60°
FAU 2 11.9 T1 47 rhombohedra a = b = c = 17.37
          α = β = γ = 60°
AFI 8.1 T1 47 hexagonal a = 13.89, b = 13.89, c = 17.22
          α = β = 90°, γ = 120°
MFI 7 T12 95 orthorhombic a = 20.36, b = 19.78, c = 13.36
          α = β = γ = 90°
MEL 8.4 T6 47 rhombohedral a = b = c= 15.83
          α = β = γ = 100.63°
CHA 8 T1 35 trigonal a = b = 13.84, c = 14.45
          α = β = 90°, γ = 120°
AEI 8 T1 47 orthorhombic a = 13.79, b = 12.63, c = 18.50
          α = β = γ = 90°
Open in a new tab
a

Largest cavity diameter (LCD) calculated by First et al.50

Figure 1.

Figure 1

Open in a new tab

Unit cells of the periodic models used in the DFT calculations represent zeolites. FAU (48 T atom), AFI (48 T atom), MFI (96 T atom), MEL (48 T atom), CHA (36 T atom), AEI (48 T atoms).

Table 4. Calculated Adsorption Enthalpies and Experimental Adsorption Enthalpies in kJ mol–1 in Zeolites: FAU, AFI, MFI, MEL, CHA, AEI.

    simulation experiment
framework T[K] ΔHads Si/Al ΔHads
FAU (T1)(O4) 323 –30 2.7 –3151
FAU (T1)(O1) 323 –33 2.7 –31
AFI (T1)(O2) 323 –39    
MFI (T12)(O25) 323 –44 35 –4651
MEL (T4)(O1) 323 –47    
CHA (T1)(O1) 313 –37 14 –3852
AEI (T1)(O4) 323 –35    
Open in a new tab

Results and Discussion

Propane Adsorption Energies

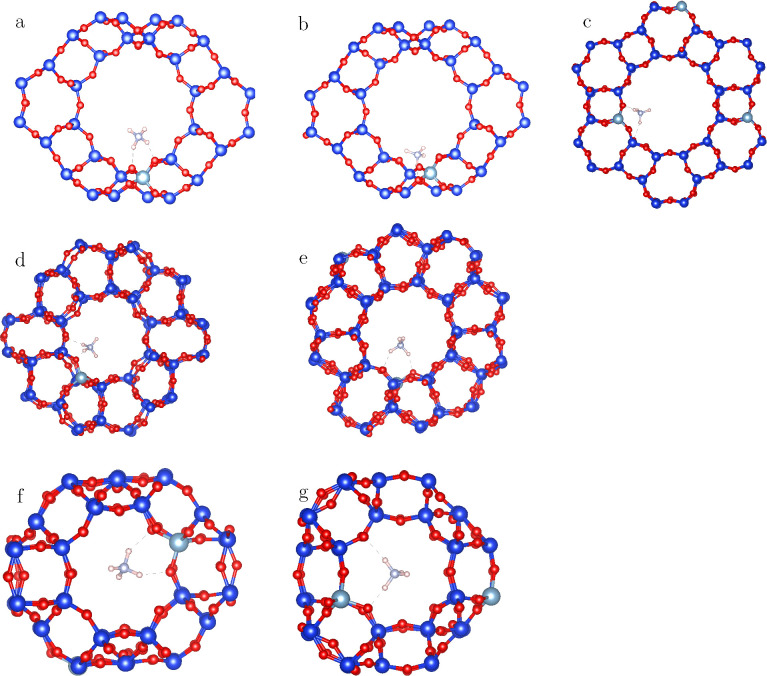
Adsorbed propane geometries are displayed in Figure 2. Propane interacts with the zeolite through multiple hydrogen bonds with the framework oxygen atoms. The main geometrical parameters have been supplied in Table 2. These parameters are the distances between the Brønsted hydrogen atom and the propane carbon atoms, and the shortest distance between the propane hydrogen atoms and the zeolite oxygen atoms, [Hpropane–Ozeolite]shortest. The reactant state geometries suggest that the oxygen atoms in the acidic site act as a Lewis base anchoring the propane molecule prior to the proton attack on the carbon–carbon bond.

Figure 2.

Figure 2

Open in a new tab

Optimized geometries of propane inside the main cages and channels of acidic zeolites; FAU (a,b), AFI (c), MFI (d), MEL (e), CHA (f), AEI (g).

Table 2. Selected Interatomic Distances (Å) of Adsorbed Propane Geometries in Zeolites: FAU, AFI, MFI, MEL, CHA, AEIa.

  HB–C1 HB–C2 HB–C3 [Hpropane–Ozeolite]shortest
FAU (T1)(O4) 2.69 2.49 3.07 2.73
FAU (T1)(O1) 2.95 3.00 3.12 2.62
AFI (T1)(O2) 3.33 2.41 2.43 2.69
MFI (T12)(O25) 3.58 2.50 2.25 2.68
MEL (T4)(O1) 3.19 2.48 2.57 2.67
CHA (T1)(O1) 3.24 3.23 3.62 2.45
AEI (T1)(O4) 4.5 3.05 3.38 2.66
Open in a new tab
a

HB denotes the Brønsted hydrogen.

The calculated adsorption energies and the BSSE corrected energies are displayed in Table 3. The results show that the BSSE correction is significant at this basis set level. The calculated adsorption enthalpies are then displayed in Table 4 along with the experimental values. The calculated adsorption enthalpies range from −33 to −47 kJ mol–1, and there is a good agreement in general between the experimental values and the calculated values. The calculated adsorption energies generally reduce (become more negative) with the decrease of the LCD of the framework channels or cages except for propane adsorption energy in MEL. This may be due to the incomplete sampling of the configuration space. Bučko et al.16 demonstrated that adsorption energies could vary by as much as 12 kJ mol–1 within a single framework.16

Table 3. Calculated Propane Adsorption Energies, ΔE(BSSE), and BSSE Corrected Energies, ΔE, in kJ mol–1 in Zeolites: FAU, AFI, MFI, MEL, CHA, AEI.

  ΔE(BSSE) ΔE
FAU (T1)(O4) –55 –33
FAU (T1)(O1) –65 –39
AFI (T1)(O2) –67 –42
MFI (T12)(O25) –81 –47
MEL (T4)(O1) –87 –50
CHA (T1)(O1) –71 –43
AEI (T1)(O4) –66 –39
Open in a new tab

Activation Energies

The transition state geometries and the main geometrical parameters are displayed in Figure 3 and Table 5. The distances of the cracked bond at the transition state range from 2.12 to 2.60 Å, indicating a late transition state. This big distance range can be attributed to the high mobility of the transition state ions, which gives rise to many local minima of intermediates, separated by small rotations and translations and connected by small energy barriers.29 Swisher et al.11 have also reported late transition states with C–C bond distances of 2.56 and 2.66 Å for propane cracking in FAU and MFI, respectively, obtained from B3LYP calculations on T5-clusters. Berger et al.,29 on the other hand, reported the distances of the cracked C–C bond in three cracking mechanisms using PBE+D2 periodic calculations. They obtained 1.8 Å for the C–C bond when cracking is initiated by the protonation of the terminal carbon atom, 1.8 Å for the protonation of the C–C bond, and 2.5 Å for the concerted path, in which no alkoxide intermediate is formed.

Figure 3.

Figure 3

Open in a new tab

Optimized geometries of the transition states inside the main cages and channels or of acidic zeolites; FAU (a,b), AFI (c), MFI (d), MEL (e), CHA (f), AEI (g).

Table 5. Selected Interatomic Distances (Å) of Transition States in Zeolites: FAU, AFI, MFI, MEL, CHA, AEIa.

  C–C HB–C HB–C [HTs–Ozeolite]shortest
FAU (T1)(O4) 2.3 1.16 1.42 2.14
FAU (T1)(O1) 2.12 1.20 1.34 2.15
AFI (T1)(O2) 2.51 1.14 1.55 2.20
MFI (T12)(O25) 2.60 1.12 1.70 2.20
MEL (T4)(O1) 2.4 1.16 1.46 1.98
CHA (T1)(O1) 2.60 1.13 1.7 1.90
AEI (T1)(O4) 2.16 1.19 1.36 2.18
Open in a new tab
a

HB denotes the Brønsted hydrogen, HTs denotes the hydrogen atom in the transition state structure.

Table 6 shows the calculated and experimental activation enthalpies. Experimental results are affected by extra-framework species, external surface acidity, and internal silanol groups. Those factors may result in differences between the calculated activation enthalpies and the experimental activation enthalpies. The range of the calculated apparent activation energies for all frameworks, <20 kJ mol–1, is smaller than the experimental range of the apparent activation energies (<52 kJ mol–1) for the FAU, MFI, and CHA frameworks, which is probably due to the wide variability of the experimental samples in terms of Si/Al ratios, extra-framework species, surface acidity, and morphologies. The calculated apparent activation enthalpies for FAU lie within the range of the reported experimental values. However, for CHA, the exact agreement between the calculated and experimental values is probably accidental, considering the differences between real crystals and our idealized model. There is an 11 kJ mol–1 difference between the calculated apparent activation enthalpy for MFI and the experimental value.

Table 6. Calculated Apparent and Intrinsic Activation Energies and Experimental Apparent and Intrinsic Activation Energies in kJ mol–1 in Zeolites: FAU, AFI, MFI, MEL, CHA, AEI.

    simulation
 experiment
framework T[K] ΔHapp ΔHint Si/Al ΔHapp ΔHint
FAU (T1)(O4) 823 181 207 2.6, 3.3, 3.6 201, 179, 169 231, 209, 19953
FAU (T1)(O1) 823 172 197 2.6, 3.3, 3.6 201, 179, 169 231, 209, 19953
AFI (T1)(O2) 773 170 206      
MFI (T12)(O25) 773 161 201 35 149 ± 10 192 ± 1054
MEL (T4)(O1) 773 164 207      
CHA (T1)(O1) 773 164 193 12 164 20055
AEI (T1)(O4) 773 165 195      
Open in a new tab

The calculated intrinsic activation energies fall between 193 and 207 kJ mol–1 with a range of 14 kJ mol–1 for the 6 frameworks. It is also interesting to note that the intrinsic activation energies calculated for FAU, at the same acidic site starting from a different propane orientation and Brønsted H position, differ by 10 kJ mol–1. Bučko et al.16 have also reported that the orientation of the propane molecule relative to the framework can cause the intrinsic activation energy of propane cracking to vary by as much as 23 kJ mol–1 in the CHA framework. The residual negative charge upon site deprotonation is localized within the second coordination sphere of O atoms from the Al atom.49 Therefore, the charge does not extend to the whole ring, and the electrostatic interactions are confined to the region that is close to the Al ion. Moreover, van der Waals forces are similar for the transition states and the reactant states. Hence, the observed differences in the intrinsic activation energies at a single site are due to the different geometrical constraints that the propane experiences at different orientations to the framework, which can either contribute to strengthening or weakening the ionic interactions between the cationic transition state and the anionic framework. This explanation also suggests that the pore diameter does not influence the intrinsic activation energies. This conclusion is supported by the results of Kadam et al.13 and Berger et al.29 who reported a narrow range of 4 kJ mol–1 and 8 kJ mol–1 for the intrinsic activation energies, respectively, in several zeolite frameworks.

Deprotonation Energies

The link between the intrinsic acidity and the intrinsic activation energy can be illustrated by the thermochemical cycle of the acid-catalyzed activation of alkanes, which is depicted in Scheme 1. The thermochemical cycle links the activation energy with the energies of the hypothetical elementary steps that lead to the transition state.27 Those steps are adsorption to the acid site Eads, deprotonation of the acid site EDPE, protonation of the reactant EPA, and finally stabilization of the transition state Estab. The calculated deprotonation energies of the studied frameworks range from 1211 kJ mol–1 to 1230 kJ mol–1, see Table 7, which is in agreement with previous cluster DFT studies.56 It is evident in Figure 5b that there is no correlation between the calculated intrinsic energy barriers and the deprotonation energies. This suggests that the strength of the ionic interaction between the protonated transition state and the anionic zeolite attenuates the differences in the deprotonation energies of any particular O–H bond.

Scheme 1. Hypothetical Elementary Steps of Acid-Catalyzed Activation of Alkanes in Zeolites Brønsted Acid Sites.

Scheme 1

Open in a new tab

Adsorption energy of the reactant Eads, deprotonation energy of the acid site EDPE, protonation energy of the reactant EPA, stabilization energy of the transition state Estab, intrinsic activation energy of the reactant, Eint.

Table 7. Deprotonation Energies (DPE) in kJ mol–1 of Zeolites: FAU, AFI, MFI, MEL, CHA, AEI.

framework DPE
FAU (T1)(O4) 1228
FAU (T1)(O1) 1215
AFI (T1)(O2) 1230
MFI (T12)(O25) 1211
MEL (T4)(O1) 1219
CHA (T1)(O1) 1223
AEI (T1)(O4) 1225
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Plots of the intrinsic activation energy ΔEint obtained by the periodic DFT calculation and the NH3 adsorption energy ΔE(DFT)ads[NH3] (a), deprotonation energy DPE (b).

Ammonia Adsorption Energies

The interaction between the ammonia molecule and the Brønsted acid site results in the formation of ammonium [NH4+], which then interacts with the negatively charged framework through several hydrogen bonds as shown in Figure 4. Table 8 lists the shortest two hydrogen bonds between the ammonium molecule and the negatively charged zeolite. According to Jones and Iglesia,32 the N–H–O bonds may contribute up to 60 kJ mol–1 to the adsorption energy depending on the bond length and angle, and it is sensitive to the local geometrical variations of the acid site.32Table 8 shows variable bond distances between the ammonium and the framework oxygen atoms.

Figure 4.

Figure 4

Open in a new tab

Optimized geometries of ammonia inside the main cages and channels or acidic zeolites; FAU (a,b), AFI (c), MFI (d), MEL (e), CHA (f), AEI (g).

Table 8. Shortest O–H Bonds Distances (Å) in Adsorbed Ammonia Geometries in Zeolites: FAU, AFI, MFI, MEL, CHA, AEI.

  H–O H–O
FAU (T1)(O4) 1.66 2.16
FAU (T1)(O1) 1.70 1.73
AFI (T1)(O2) 1.63 1.97
MFI (T12)(O25) 1.63 2.03
MEL (T4)(O1) 1.70 1.87
CHA (T1)(O1) 1.82 1.86
AEI (T1)(O4) 1.65 1.95
Open in a new tab

The calculated adsorption energies and the BSSE corrected adsorption energies are displayed in Table 9. In the case of ammonia adsorption, the discrepancy between the experimental adsorption energies and the calculated adsorption energies is worse after the BSSE correction. Because of the proton transfer, the chemical environments of the free molecule and the free zeolite change after the interaction. In this case, the counterpoise correction method may not be suitable to correct for the BSSE. Therefore, uncorrected adsorption energies will be used in the following analysis.

Table 9. Calculated Ammonia Adsorption Energies, ΔE(BSSE), and BSSE Corrected Energies, ΔE, in kJ mol–1 in Zeolites; FAU, AFI, MFI, MEL, CHA, AEI.

  ΔE(BSSE) ΔE
FAU (T1)(O4) –147 –123
FAU (T1)(O1) –166 –135
AFI (T1)(O2) –153 –115
MFI (T12)(O25) –144 –113
MEL (T4)(O1) –145 –116
CHA (T1)(O1) –169 –135
AEI (T1)(O4) –176 –145
Open in a new tab

Ammonia adsorption enthalpies are listed in Table 10 along with the experimental values. As noted above, the experimental values are a statistical average of the ammonia adsorption energies at all the T sites and possible [NH4+] orientations. For instance, ammonia adsorption enthalpy at FAU (O4) differs by 16 kJ mol–1 compared with the adsorption enthalpy at FAU (O1). To compare directly with experiments, ab initio molecular dynamics simulations may be required to sample the full configuration space of adsorbed [NH4+]. With this consideration, the calculated adsorption enthalpies lie within a reasonable range from the reported experimental values of ammonia adsorption. As discussed earlier, it has been suggested that quantification of acidity using the binding energy of a basic molecule includes contributions from both the intrinsic acidity and confinement.57 If one accepts deprotonation energies as a measure for the intrinsic acidity, it is evident that ammonia adsorption energies do not correlate with deprotonation energies due to the dominant effect of the electrostatic interactions and dispersion forces.

Table 10. NH3 Adsorption Energy Based on DFT (ΔE(DFT)ads), Dispersion Contribution (ΔE(D)ads[NH3]), Total Adsorption Enthalpy (ΔHads), and Experimental Adsorption Enthalpy (ΔHads) in kJ mol–1.

framework ΔE(DFT)ads ΔE(D)ads ΔHads experimental ΔHads
FAU (T1)(O4) –126 –21 –137 –15058
FAU (T1)(O1) –145 –21 –153 –15058
AFI (T1)(O2) –129 –24 –141  
MFI (T12)(O25) –120 –24 –133 –129,59 –15058
MEL (T4)(O1) –124 –21 –134  
CHA (T1)(O1) –143 –26 –157 –14460
AEI (T1)(O4) –149 –27 –165  
Open in a new tab

Probe molecules that integrate acidity and ion pair interaction energy were potentially suggested for predicting the intrinsic activation energy. However, the dispersion contribution to the ammonia adsorption energy is not desirable for predicting the intrinsic activation energy as the long-range dispersion forces may be expected to be similar in the reactants and transition states and thus provide poor differentiation. Recalculating the ammonia adsorption energies explicitly excluding the long-range dispersion contribution, ΔE(D)ads[NH3], produces the data displayed in Table 10. Figure 5a shows no correlation between the calculated ammonia adsorption energies and the intrinsic activation enthalpies for the zeolites topologies studied here. This indicates that the ion-pair interaction energies are specific to the molecule-site pair and that the intrinsic activation energy cannot, therefore, be approximated reliably by the adsorption of the ammonia molecule, which experiences different geometrical constraints to propane. A similar conclusion was made by Liu et al.,57 who reported that MFI and CHA did not follow the scaling relation obtained for FAU and the acid strength determined by the NH3 adsorption energies for the conversion of π-adsorbed isobutene into alkoxy species.

Conclusion

The influence of the acid site geometry on the activation energy of propane cracking was investigated using periodic DFT calculations for a number of topologically distinct zeolite frameworks. Acid sites were characterized with the LCD, ammonia adsorption energies, and deprotonation energies. The calculations were performed with the ωB97X-D functional, 6-311G(d,p) Gaussian basis set, and Grimme’s dispersion correction. Deprotonation energies were calculated using cluster models to achieve unambiguous referencing of energies in charged systems. A single reaction site in each framework was adopted to facilitate the examination of trends due to the varying confinement. The computed data suggest that the intrinsic activation energies are not significantly affected by the zeolite pore diameter. The computed intrinsic activation energies did not correlate with deprotonation energies due to the ionic interaction at the transition state, which attenuates the deprotonation energies. Intrinsic activation energies also did not correlate with the ammonia adsorption energies because the ammonia ion-pair interaction is subject to different geometrical constraints to that of the protonated propane. We, therefore, conclude that neither deprotonation energies nor ammonia adsorption energies provides a reliable proxy for intrinsic activation energies in aluminosilicate frameworks with different topologies.

Acknowledgments

Z.A. thanks Saudi Aramco for the full Ph.D. scholarship and the High-Performance Computing service of Imperial College London. Via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431, EP/T022213), this work used the ARCHER UK National Supercomputing Service.

The authors declare no competing financial interest.

References

  1. Smit B.; Maesen T. L. Molecular Simulations of Zeolites: Adsorption, Diffusion, and Shape Selectivity. Chem. Rev. 2008, 108, 4125–4184. 10.1021/cr8002642. [DOI] [PubMed] [Google Scholar]
  2. Haag W. O.; Lago R. M.; Weisz P. B. Transport and reactivity of hydrocarbon molecules in a shape-selective zeolite. Faraday Discuss. Chem. Soc. 1981, 72, 317. 10.1039/dc9817200317. [DOI] [Google Scholar]
  3. Janda A.; Vlaisavljevich B.; Smit B.; Lin L.-C.; Bell A. T. Effects of Pore and Cage Topology on the Thermodynamics of n-Alkane Adsorption at Brønsted Protons in Zeolites at High Temperature. J. Phys. Chem. C 2017, 121, 1618–1638. 10.1021/acs.jpcc.6b09703. [DOI] [Google Scholar]
  4. Weisz P. B.; Frilette V. J. Intracrystalline and Molecular Shape Selective Catalysis by Zeolites Salts. J. Phys. Chem. 1960, 64, 382. 10.1021/j100832a513. [DOI] [Google Scholar]
  5. Rozanska X.; van Santen R. A.; Demuth T.; Hutschka F.; Hafner J. A Periodic DFT Study of Isobutene Chemisorption in Proton-Exchanged Zeolites: Dependence of Reactivity on the Zeolite Framework Structure. J. Phys. Chem. B 2003, 107, 1309–1315. 10.1021/jp021646b. [DOI] [Google Scholar]
  6. Smit B.; Maesen T. L. Towards a molecular understanding of shape selectivity. Nature 2008, 451, 671–8. 10.1038/nature06552. [DOI] [PubMed] [Google Scholar]
  7. Guo Q.; Fan F.; Ligthart D. A. J. M.; Li G.; Feng Z.; Hensen E. J. M.; Li C. Effect of the Nature and Location of Copper Species on the Catalytic Nitric Oxide Selective Catalytic Reduction Performance of the Copper/SSZ-13 Zeolite. ChemCatChem. 2014, 6, 634–639. 10.1002/cctc.201300775. [DOI] [Google Scholar]
  8. Vogt E. T. C.; Weckhuysen B. M. Fluid catalytic cracking: recent developments on the grand old lady of zeolite catalysis. Chem. Soc. Rev. 2015, 44, 7342–7370. 10.1039/C5CS00376H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Krannila H.; Haag W. O.; Gates B. C. Monomolecular and bimolecular mechanisms of paraffin cracking: n-butane cracking catalyzed by HZSM-5. J. Catal. 1992, 135, 115–124. 10.1016/0021-9517(92)90273-K. [DOI] [Google Scholar]
  10. Abbot J.; Wojciechowski B. W. The mechanism of catalytic cracking of n-alkenes on ZSM-5 zeolite. Can. J. Chem. Eng. 1985, 63, 462–469. 10.1002/cjce.5450630315. [DOI] [Google Scholar]
  11. Swisher J. A.; Hansen N.; Maesen T.; Keil F. J.; Smit B.; Bell A. T. Theoretical Simulation of n-Alkane Cracking on Zeolites. J. Phys. Chem. C 2010, 114, 10229–10239. 10.1021/jp101262y. [DOI] [Google Scholar]
  12. Babitz S. M.; Williams B. A.; Miller J. T.; Snurr R. Q.; Haag W. O.; Kung H. H. Monomolecular cracking of n-hexane on Y, MOR, and ZSM-5 zeolites. Appl. Catal. A: Gen. 1999, 179, 71–86. 10.1016/S0926-860X(98)00301-9. [DOI] [Google Scholar]
  13. Kadam S. A.; Li H.; Wormsbecher R. F.; Travert A. Impact of Zeolite Structure on Entropic–Enthalpic Contributions to Alkane Monomolecular Cracking: An IR Operando Study. Chem.-Eur. J. 2018, 24, 5489–5492. 10.1002/chem.201800793. [DOI] [PubMed] [Google Scholar]
  14. Tranca D. C.; Zimmerman P. M.; Gomes J.; Lambrecht D.; Keil F. J.; Head-Gordon M.; Bell A. T. Hexane Cracking on ZSM-5 and Faujasite Zeolites: a QM/MM/QCT Study. J. Phys. Chem. C 2015, 119, 28836–28853. 10.1021/acs.jpcc.5b07457. [DOI] [Google Scholar]
  15. Mallikarjun Sharada S.; Zimmerman P. M.; Bell A. T.; Head-Gordon M. Insights into the Kinetics of Cracking and Dehydrogenation Reactions of Light Alkanes in H-MFI. J. Phys. Chem. C 2013, 117, 12600–12611. 10.1021/jp402506m. [DOI] [Google Scholar]
  16. Bučko T.; Benco L.; Hafner J.; Ángyán J. G. Monomolecular cracking of propane over acidic chabazite: An ab initio molecular dynamics and transition path sampling study. J. Catal. 2011, 279, 220–228. 10.1016/j.jcat.2011.01.022. [DOI] [Google Scholar]
  17. Mansoor E.; Van der Mynsbrugge J.; Head-Gordon M.; Bell A. T. Impact of long-range electrostatic and dispersive interactions on theoretical predictions of adsorption and catalysis in zeolites. Catal. Today 2018, 312, 51–65. 10.1016/j.cattod.2018.02.007. [DOI] [Google Scholar]
  18. Kazansky V. B.; Senchenya I. N.; Frash M.; van Santen R. A. A quantum-chemical study of adsorbed nonclassical carbonium ions as active intermediates in catalytic transformations of paraffins. I. Protolytic cracking of ethane on high silica zeolites. Catal. Lett. 1994, 27, 345–354. 10.1007/BF00813921. [DOI] [Google Scholar]
  19. Collins S. J.; Omalley P. J. A Theoretical Description for the Monomolecular Cracking of C-C Bonds over Acidic Zeolites. J. Catal. 1995, 153, 94–99. 10.1006/jcat.1995.1111. [DOI] [Google Scholar]
  20. Collins S. J.; O’Malley P. J. The mechanism of alkane activation over zeolite Brønsted acid sites. A density-functional study. Chem. Phys. Lett. 1995, 246, 555–561. 10.1016/0009-2614(95)01149-3. [DOI] [Google Scholar]
  21. Maihom T.; Pantu P.; Tachakritikul C.; Probst M.; Limtrakul J. Effect of the Zeolite Nanocavity on the Reaction Mechanism of n-Hexane Cracking: A Density Functional Theory Study. J. Phys. Chem. CC 2010, 114, 7850–7856. 10.1021/jp911732p. [DOI] [Google Scholar]
  22. Janda A.; Vlaisavljevich B.; Lin L.-C.; Mallikarjun Sharada S.; Smit B.; Head-Gordon M.; Bell A. T. Adsorption Thermodynamics and Intrinsic Activation Parameters for Monomolecular Cracking of n-Alkanes on Brønsted Acid Sites in Zeolites. J. Phys. Chem. C 2015, 119, 10427–10438. 10.1021/acs.jpcc.5b01715. [DOI] [Google Scholar]
  23. Boronat M.; Viruela P.; Corma A. Ab initio and density-functional theory study of zeolite-catalyzed hydrocarbon reactions: hydride transfer, alkylation and disproportionation. Phys. Chem. Chem. Phys. 2000, 2, 3327–3333. 10.1039/b002013n. [DOI] [Google Scholar]
  24. Tranca D. C.; Hansen N.; Swisher J. A.; Smit B.; Keil F. J. Combined Density Functional Theory and Monte Carlo Analysis of Monomolecular Cracking of Light Alkanes Over H-ZSM-5. J. Phys. Chem. C 2012, 116, 23408–23417. 10.1021/jp307558u. [DOI] [Google Scholar]
  25. van Bokhoven J. A.; Williams B. A.; Ji W.; Koningsberger D. C.; Kung H. H.; Miller J. T. Observation of a compensation relation for monomolecular alkane cracking by zeolites: the dominant role of reactant sorption. J. Catal. 2004, 224, 50–59. 10.1016/j.jcat.2004.02.003. [DOI] [Google Scholar]
  26. Babitz S. M.; Williams B. A.; Miller J. T.; Snurr R. Q.; Haag W. O.; Kung H. Monomolecular cracking of n-hexane on Y, MOR, and ZSM-5 zeolites. appl. catal. a gen 1999, 179, 71–86. 10.1016/S0926-860X(98)00301-9. [DOI] [Google Scholar]
  27. Gounder R.; Iglesia E. The catalytic diversity of zeolites: confinement and solvation effects within voids of molecular dimensions. Chem. Commun. 2013, 49, 3491. 10.1039/c3cc40731d. [DOI] [PubMed] [Google Scholar]
  28. Janda A.; Vlaisavljevich B.; Lin L. C.; Smit B.; Bell A. T. Effects of Zeolite Structural Confinement on Adsorption Thermodynamics and Reaction Kinetics for Monomolecular Cracking and Dehydrogenation of n-Butane. J. Am. Chem. Soc. 2016, 138, 4739–56. 10.1021/jacs.5b11355. [DOI] [PubMed] [Google Scholar]
  29. Berger F.; Rybicki M.; Sauer J. Adsorption and cracking of propane by zeolites of different pore size. J. Catal. 2021, 395, 117–128. 10.1016/j.jcat.2020.12.008. [DOI] [Google Scholar]
  30. Haase F.; Sauer J. Ab initio molecular dynamics simulation of methanol interacting with acidic zeolites of different framework structure. Microporous Mesoporous Mater. 2000, 35–36, 379–385. 10.1016/S1387-1811(99)00235-8. [DOI] [Google Scholar]
  31. Eichler U.; Brändle M.; Sauer J. Predicting Absolute and Site Specific Acidities for Zeolite Catalysts by a Combined Quantum Mechanics/Interatomic Potential Function Approach. J. Phys. Chem. CB 1997, 101, 10035–10050. 10.1021/jp971779a. [DOI] [Google Scholar]
  32. Jones A. J.; Iglesia E. The Strength of Brønsted Acid Sites in Microporous Aluminosilicates. ACS Catal. 2015, 5, 5741–5755. 10.1021/acscatal.5b01133. [DOI] [Google Scholar]
  33. Boronat M.; Corma A. What Is Measured When Measuring Acidity in Zeolites with Probe Molecules?. ACS Catal. 2019, 9, 1539–1548. 10.1021/acscatal.8b04317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sauer J.; Sierka M. Combining quantum mechanics and interatomic potential functions in ab initio studies of extended systems. J. Comput. Chem. 2000, 21, 1470–1493. . [DOI] [Google Scholar]
  35. Brändle M.; Sauer J. Acidity Differences between Inorganic Solids Induced by Their Framework Structure. A Combined Quantum Mechanics/Molecular Mechanics ab Initio Study on Zeolites. J. Am. Chem. Soc. 1998, 120, 1556–1570. 10.1021/ja9729037. [DOI] [Google Scholar]
  36. Lercher J. A.; Gründling C.; Eder-Mirth G. Infrared studies of the surface acidity of oxides and zeolites using adsorbed probe molecules. Catal. Today 1996, 27, 353–376. 10.1016/0920-5861(95)00248-0. [DOI] [Google Scholar]; Vibrational Spectroscopy of Adsorbed Molecules and Surface Species on Metal Oxides.
  37. Liu C.; Li G.; Hensen E. J. M.; Pidko E. A. Relationship between acidity and catalytic reactivity of faujasite zeolite: A periodic DFT study. J. Catal. 2016, 344, 570–577. 10.1016/j.jcat.2016.10.027. [DOI] [Google Scholar]
  38. Dovesi R.; Saunders V. R.; C. Roetti R. O.; Zicovich-Wilson C. M.; Pascale F.; Civalleri B.; Doll K.; Harrison N. M.; Bush I. J.; D’Arco P.. et al. CRYSTAL17 User’s Manual; University of Torino, 2017. [Google Scholar]
  39. Chai J. D.; Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–20. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  40. Van der Mynsbrugge J.; Janda A.; Mallikarjun Sharada S.; Lin L.-C.; Van Speybroeck V.; Head-Gordon M.; Bell A. T. Theoretical Analysis of the Influence of Pore Geometry on Monomolecular Cracking and Dehydrogenation ofn-Butane in Brønsted Acidic Zeolites. ACS Catal. 2017, 7, 2685–2697. 10.1021/acscatal.6b03646. [DOI] [Google Scholar]
  41. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–99. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  42. Pritchard B. P.; Altarawy D.; Didier B.; Gibson T. D.; Windus T. L. A New Basis Set Exchange. J. Chem. Inf. Model 2019, 59, 4814–4820. 10.1021/acs.jcim.9b00725. [DOI] [PubMed] [Google Scholar]
  43. Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901. 10.1063/1.1329672. [DOI] [Google Scholar]
  44. Hjorth Larsen A.; Mortensen J. J.; Blomqvist J.; Castelli I. E.; Christensen R.; Dułak M.; Friis J.; Groves M. N.; Hammer B.; Hargus C.; et al. The atomic simulation environment-a Python library for working with atoms. J. Condens. Matter Phys. 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  45. Zicovich-Wilson C. M.; Pascale F.; Roetti C.; Saunders V. R.; Orlando R.; Dovesi R. Calculation of the vibration frequencies of alpha-quartz: the effect of Hamiltonian and basis set. J. Comput. Chem. 2004, 25, 1873–81. 10.1002/jcc.20120. [DOI] [PubMed] [Google Scholar]
  46. Pascale F.; Zicovich-WIlson C. M.; Lopez Gejo F.; Civalleri B.; Orlando R.; Dovesi R. The Calculation of the Vibrational Frequencies ofCrystalline Compounds and Its Implementation in theCRYSTAL Code. J. Comput. Chem. 2004, 25, 888–897. 10.1002/jcc.20019. [DOI] [PubMed] [Google Scholar]
  47. Cramer C. J.Essentials of Computational Chemistry -Theories and Models, 2nd ed.; John Wiley & Sons ltd: Chichester, West Sussex, England, 2004. [Google Scholar]
  48. Boys S. F.; Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. 10.1080/00268977000101561. [DOI] [Google Scholar]
  49. Jones A. J.; Carr R. T.; Zones S. I.; Iglesia E. Acid strength and solvation in catalysis by MFI zeolites and effects of the identity, concentration and location of framework heteroatoms. J. Catal. 2014, 312, 58–68. 10.1016/j.jcat.2014.01.007. [DOI] [Google Scholar]
  50. First E. L.; Gounaris C. E.; Wei J.; Floudas C. A. Computational characterization of zeolite porous networks: an automated approach. Phys. Chem. Chem. Phys. 2011, 13, 17339–17358. 10.1039/c1cp21731c. [DOI] [PubMed] [Google Scholar]
  51. Eder F.; Stockenhuber M.; Lercher J. A. Brønsted Acid Site and Pore Controlled Siting of Alkane Sorption in Acidic Molecular Sieves. J. Phys. Chem. CB 1997, 101, 5414–5419. 10.1021/jp9706487. [DOI] [Google Scholar]
  52. Piccini G.; Alessio M.; Sauer J.; Zhi Y.; Liu Y.; Kolvenbach R.; Jentys A.; Lercher J. A. Accurate Adsorption Thermodynamics of Small Alkanes in Zeolites. Ab initio Theory and Experiment for H-Chabazite. J. Phys. Chem. CC 2015, 119, 6128–6137. 10.1021/acs.jpcc.5b01739. [DOI] [Google Scholar]
  53. Xu B.; Bordiga S.; Prins R.; van Bokhoven J. A. Effect of framework Si/Al ratio and extra-framework aluminum on the catalytic activity of Y zeolite. Appl. Catal. A: Gen. 2007, 333, 245–253. 10.1016/j.apcata.2007.09.018. [DOI] [Google Scholar]
  54. Narbeshuber T. F.; Vinek H.; Lercher J. A. Monomolecular Conversion of Light Alkanes over H-ZSM-5. J. Catal. 1995, 157, 388–395. 10.1006/jcat.1995.1304. [DOI] [Google Scholar]
  55. Yun J. H.; Lobo R. F. Effects of temperature pretreatment on propane cracking over H-SSZ-13 zeolites. Catal. Sci. Technol. 2015, 5, 264–273. 10.1039/C4CY00731J. [DOI] [Google Scholar]
  56. Niwa M.; Suzuki K.; Morishita N.; Sastre G.; Okumura K.; Katada N. Dependence of cracking activity on the Brønsted acidity of Y zeolite: DFT study and experimental confirmation. Catal. Sci. Technol. 2013, 3, 1919. 10.1039/c3cy00195d. [DOI] [Google Scholar]
  57. Liu C.; Tranca I.; van Santen R. A.; Hensen E. J. M.; Pidko E. A. Scaling Relations for Acidity and Reactivity of Zeolites. J. Phys. Chem. C 2017, 121, 23520–23530. 10.1021/acs.jpcc.7b08176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Parrillo D. J.; Gorte R. J. Characterization of acidity in H-ZSM-5, H-ZSM-12, H-Mordenite, and H-Y using microcalorimetry. J. Phys. Chem. 1993, 97, 8786–8792. 10.1021/j100136a023. [DOI] [Google Scholar]
  59. Rodríguez-González L.; Hermes F.; Bertmer M.; Rodríguez-Castellón E.; Jiménez-López A.; Simon U. The acid properties of H-ZSM-5 as studied by NH3-TPD and 27Al-MAS-NMR spectroscopy. Appl. Catal. A: Gen 2007, 328, 174–182. 10.1016/j.apcata.2007.06.003. [DOI] [Google Scholar]
  60. Katada N.; Nouno K.; Lee J. K.; Shin J.; Hong S. B.; Niwa M. Acidic Properties of Cage-Based, Small-Pore Zeolites with Different Framework Topologies and Their Silicoaluminophosphate Analogues. J. Phys. Chem. CC 2011, 115, 22505–22513. 10.1021/jp207894n. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES