Two-Step Registration on Multi-Modal Retinal Images via Deep Neural Networks

Abstract

Multi-modal retinal image registration plays an important role in the ophthalmological diagnosis process. The conventional methods lack robustness in aligning multi-modal images of various imaging qualities. Deep-learning methods have not been widely developed for this task, especially for the coarse-to-fine registration pipeline. To handle this task, we propose a two-step method based on deep convolutional networks, including a coarse alignment step and a fine alignment step. In the coarse alignment step, a global registration matrix is estimated by three sequentially connected networks for vessel segmentation, feature detection and description, and outlier rejection, respectively. In the fine alignment step, a deformable registration network is set up to find pixel-wise correspondence between a target image and a coarsely aligned image from the previous step to further improve the alignment accuracy. Particularly, an unsupervised learning framework is proposed to handle the difficulties of inconsistent modalities and lack of labeled training data for the fine alignment step. The proposed framework first changes multi-modal images into a same modality through modality transformers, and then adopts photometric consistency loss and smoothness loss to train the deformable registration network. The experimental results show that the proposed method achieves state-of-the-art results in Dice metrics and is more robust in challenging cases.

I. Introduction

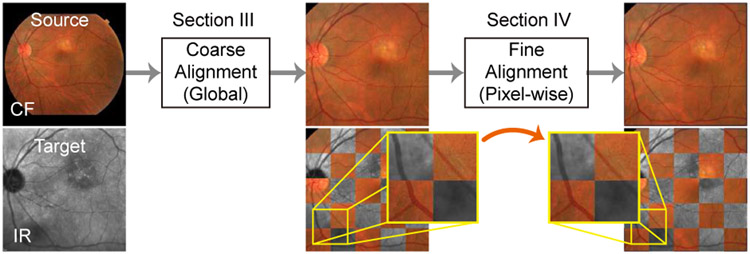
Multi-modal retinal image registration plays an important role in assisting the examination and diagnosis of retina diseases. In this task, multi-modal retinal images are captured from the same patient using various retinal imaging instruments, and then aggregated and aligned, so that complementary information of the retina can be integrated for more accurate and faster inspection. In order to accurately align retinal image pairs, a two-step coarse-to-fine pipeline has been adopted (e.g., [1], [2]) for coarse (global) alignment and fine (local) alignment, as shown in Fig. 1. In the coarse alignment step, a source (floating) image is warped towards a target (fixed) image based on an estimated global transformation model (e.g., affine transformation). In the following fine alignment step, the globally aligned source image is warped again locally based on a pixel-wise registration field in order to further reduce misalignment errors.

Fig. 1.

A two-step coarse-to-fine registration framework.

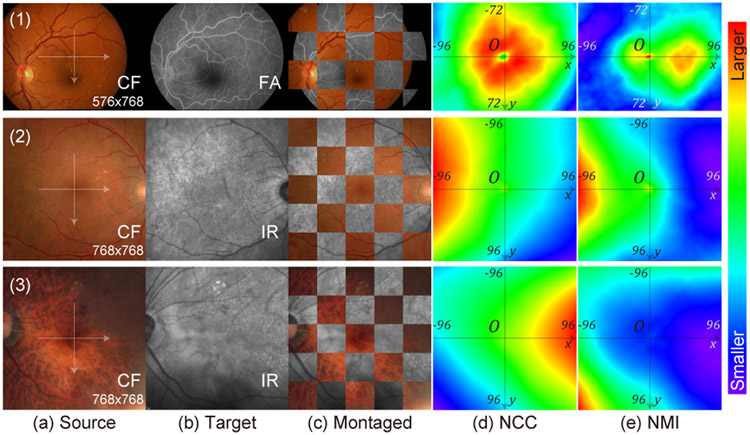
A big challenge in aligning multi-modal retinal images comes from the inconsistent appearance of anatomical and diseases patterns among modalities since each instrument has different imaging mechanisms and settings. For example, in the first row of Fig. 2, the vessels show lower intensities than the background in the Color Fundus (CF) image, but higher intensities in the Fluorescein Angiography (FA) image. In the third example, the CF images shows choroid patterns beneath the retinal vessels which are not visible in the Infrared Reflectance (IR) image. As a result, these inconsistent patterns will produce unmatched features and ourliers in image matching process which affects the registration performance. Furthermore, retinal images usually have thin and sparse vessels and lack dense anatomical structures, which yields multiple local maximas when computing commonly used similarities metrics such as Normalized Cross-Correlation (NCC) and Normalized Mutual Information (NMI), as shown in Fig. 2. This also causes difficulties for intensity-based registration methods in finding the correct alignment.

Fig. 2.

Similarity measurements on multi-modal retinal images with regard to image translation. First, we coarsely align the source images (a) with the target images (b), which are overlaid as (c). Then, we translate the source images in both x and y directions by different number of pixels. At each position, we compute Normalized Cross-Correlation (NCC) (d) and Normalized Mutual Information (NMI) (e) between the two images, and plot their heatmaps. We only use the overlapping pixels in the imaging area of both images to compute the similarity metrics. First row is from the CF-FA dataset. Second and third rows are from the JRC dataset. In these examples, both NCC and NMI should be the highest at the center (0,0) to correctly estimate alignment.

There has been extensive research on multi-modal retinal image registration. For example, many methods have used hand-designed algorithms to replace certain steps in a conventional registration pipeline, including keypoint detection (e.g., UR-SIFT [3]), hand-crafted feature description (e.g., PIIFD [4], and Step Patterns [5]), and matching and outlier rejection (e.g., [6], [7]). Meanwhile, some have also tried to utilize the mutual structures in paired images to aid registration, including vessels [2], [8]-[10], and vessel bifurcations and crossovers [2]. Nevertheless, many of these methods lack robustness in challenging scenarios like poor imaging qualities.

Recently, with the rapid development of deep learning techniques, some methods have applied Deep Neural Networks (DNNs) in this task, as summarized in Table I. However, the restrictions of each method limit its application on general multi-modal retinal datasets as follows: (1) The authors of [12]-[14] applied Convolutional Neural Networks (CNNs) for parts or additional modules of a conventional global registration pipeline, whose performance is still limited by the conventional algorithms. (2) Many methods require massive labeling works (e.g., pixel-wise alignment or segmentation) for training which is hard to achieve in large-scale datasets, e.g., [13], [15] demand explicit segmentation ground-truths, [14], [18] adopt pre-trained vessel segmentation networks which implicitly demand segmentation labels, and [11] requires accurately aligned image pairs. only a few methods [16], [17] need coarsely aligned images which are easy to obtain (i.e., requiring affine matrices by labeling the positions of three corresponding point pairs). (3) Some methods [14], [15] contain camera-specific designs which might restrict their application in general cases. (4) All the previously proposed methods only handle one step (coarse only or refinement only), i.e., [12]-[15], [18] only support the global transformation which limits their registration accuracies, and [11], [16], [17] tackle deformable registration with unsupervised training which would fail on images with large displacements. To our knowledge, there are no DNN methods to support both global and deformable alignment.

TABLE I.

Comparison of Multi-Modal Retinal Registration Algorithms Adopting Deep Learning

Method	Transformation Model	Working Modalities	Required Annotations / Inputs	Fully Network	Method Description	Major Limitations
Mahapatra et al. [11]	Deformable	No restriction	Accurately aligned images	Yes	GAN for warped image synthesis	No explicit warping process
Lee et al. [12]	Global (affine)	No restriction	Not required	No	CNN for feature selection in a conventional pipeline	Performance limited by conventional methods
Arikan et al. [13]	Global (affine)	No restriction	Vessel segmentations + keypoint locations	No	CNN for vessel segmentation and keypoint detection, plus RANSAC	Demanding massive labeling
Ding et al. [14]	Global (polynomial)	UWF CF&FA	Pre-trained vessel segmentation CNN for FA	No	CNN for vessel segmentation, plus a conventional alignment method	Requiring a pre-trained segmentation network
Luo et al. [15]	Global (affine)	ICGA + MC	Affine matrix + optic disc segmentation	Yes	CNN for optic disc segmentation and matrix estimation	Initialized by camera-specific scaling factors
Tian et al. [16]	Deformable	No restriction	Coarsely aligned images	Yes	CNN for optical flow estimation	Only for small displacements
Zhang et al. [17]	Deformable	No restriction	Affine matrix or coarsely aligned images	Yes	CNN for vessel segmentation and optical flow estimation	Only for small displacements
Wang et al. [18]	Global (perspective)	No restriction	Affine matrix + pre-trained vessel segmentation CNN	Yes	CNN for vessel segmentation, feature detection & description, and outlier rejection	Requiring pre-trained segmentation networks
Ours	Global (affine) + Deformable	No restriction	Affine matrix + a style target image	Yes	CNN for vessel segmentation, feature detection and description, outlier rejection, and optical flow estimation

To this end, we propose a two-step coarse-to-fine registration algorithm for multi-modal retinal images as shown in Fig. 1. The proposed method only requires easy-to-obtain annotations (i.e., affine matrix) for training, and is completely built upon DNN which eliminates restrictions of the conventional methods. In the coarse alignment step, vessels of source and target images are first extracted via vessel segmentation networks. Then, keypoints and features of the vessels are derived using a feature detection and description network. Afterwards, a transformation matrix is estimated by an outlier rejection network where the matrix is used to warp the source image to the target image for the global alignment. in the next fine alignment step, a deformable registration network predicts a pixel-wise registration field to warp the source image for a second time to further reduce misalignment errors. In the learning process, we also propose a high-level structure, which is named modality transformer, to handle different appearance of modalities and the lack of pixel-wise ground-truths. The modality transformers can find common structures between multi-modal images to enable unsupervised training for the deformable registration network. We set up two kinds of transformers in this paper, i.e., a non-learnable local phase signal extractor, as well as the vessel segmentation networks which are trained jointly with the deformable network using style loss [19], [20]. Meanwhile, the feature detection and description network is trained on a large-scale synthesized dataset, and the outlier rejection network is trained with ground-truth transformation matrices on the retinal datasets.

In this paper, we expand our previous works [17], [18] to support both coarse and refinement registration in the following aspects. (1) For the deformable alignment task [17], we set up an unsupervised learning framework consisting of the deformable registration network and two modality transformers. During training, the modality transformers convert multi-modal images into image signals of a common modality to compute photometric consistency loss. (2) We also propose a Local Phase Modality Transformer that extracts local phase terms in Monogenical Signals [21] for the deformable registration task. (3) We enhance the network structures and training settings from [17], and extend the experiments to show the influences on deformable registration performance from various factors, including smoothness weights, number of local phase’s channels, and the choice of style targets. (4) We also include extensive ablation studies for the global registration network comparing to our previous publication [18]. (5) We combine the coarse alignment [18] and the deformable registration [17] methods into a complete pipeline, and train and test it on a newly collected multi-modal retinal dataset.

The paper is organized as follows. Section II introduces backgrounds and related works for multi-modal retinal image registration. Sections III and IV describe algorithmic details of the proposed coarse and fine alignment networks. Section V presents experimental results and ablation studies on our methods.

II. Backgrounds and Related Works

A. 2D Image Registration

2D image registration algorithms can be categorized into feature-based and intensity-based methods. For feature-based methods, most conventional algorithms follow a fixed non-iterative routine which consists of keypoint detection (e.g., Harris corner detector [22]), feature description (e.g., SIFT [23]), feature matching, and outlier rejection (e.g., RANSAC [24]). In intensity-based methods, a correlation metric (e.g., Mutual Information) is designated to evaluate the alignment quality between an image pair, and an iterative optimization algorithm helps search for a set of warping parameters that achieves the best quality of alignment. Usually, the latter approaches are much more time-consuming, because the searching process could not be done in parallel.

There are mainly two types of transformation models that describe the warping process on the source image: global and deformable. In global transformation, the movement of all pixels are determined by a set of global parameters such as scaling, translating, rotation, and skewing of the affine transformation. In deformable transformation, the pixel-wise registration fields (optical flows) are estimated, and each pixel of a source image is warped to the target pixel using its own optical flow that describes the direction and the distance.

In this paper, the proposed two-step framework adopts an affine transformation for coarse alignment and a deformable transformation for fine alignment. Both steps are accomplished through non-iterative processes.

B. Global Registration for Natural Images

Recently, much effort has been made in adapting deep neural networks for the global registration tasks. Most methods comply with the feature-based registration pipeline explicitly or implicitly. Some have trained networks to replace certain steps in the registration pipeline, e.g., descriptors [25], [26], outlier rejection [27], [28], descriptors with matching metrics [29], detectors with descriptors [30]-[33]. Moreover, other methods (e.g., CNN-Geometric [34], [35]) proposed to replace the complete pipeline with an end-to-end network. Nevertheless, in order to achieve good registration results on crossmodality tasks, these methods require large-scale labeled data for training, or need pre-trained network-based descriptors which can extract robust features from multi-modal images.

In our proposed coarse alignment method, SuperPoint [31] is adopted as the keypoint detector and descriptor, and the outlier rejection network [28] is trained to estimate the transformation matrix. Especially, two vessel segmentation networks help translate multi-modal retinal images into single-modal vessel images as SuperPoint’s input, so that SuperPoint only needs training on synthesized single-modal data instead of labeled multi-modal data.

C. Optical Flow Estimation for Deformable Registration

Optical flow estimation computes a dense registration field between the source and target images of a same modality. It is built on the assumption of brightness consistency between the two images. Conventional algorithms (e.g., [36]) often involve an iterative searching process over a loss function which optimizes photometric consistency and smoothness constraints in deformable alignment.

Recently, multiple CNN-based methods have been proposed to learn a set of parameters on training data and to eliminate the iterative optimization process during testing. The network can be trained by a supervised scheme or an unsupervised scheme. Some methods [37]-[39] adopt the supervised training on large-scale synthesized datasets with ground-truth flows, which enables them to handle larger displacements. Meanwhile, others [40], [41] adopt the photometric consistency and smoothness loss for the unsupervised training (i.e., without ground-truth labels), which are limited to predict small displacements. Spatial Transformer Networks (STN) [42] is often used as a differentiable image warper in the unsupervised learning scheme.

In this paper, we adopt the unsupervised training method for the fine alignment step of our framework with the help of modality transformers (i.e., vessel segmentation networks or local phase signals).

D. Medical Image Registration

In contrast to aligning natural images, the intensity-based techniques form the vast majority of conventional registration methods on medical images [43]. Widely-used similarity metrics include NCC, Mutual Information (MI), and NMI [44], etc, which can be applied to both mono- and multi-modal registration.

Recently, multiple CNN-based methods [45]-[50] have also been proposed for medical image registration in one shot, i.e., non-iteratively. These methods adapts the unsupervised learning scheme in Section II-C by replacing the photometric consistency loss with other aforementioned similarity metrics. Furthermore, anatomical structures within the images can also be extracted and compared during training [48] to boost performance. Among these methods, the networks proposed in [45], [47], [48] only perform one-time registration, which are limited to predicting small displacements. Instead of using only one network, de Vos et al. [46] proposed a coarse-to-fine registration framework which concatenates an affine registration network and multiple deformable networks. Zhao et al. [49], [50] also proposed a recursive cascaded network where the floating image is warped progressively by multiple cascades, which enables predictions for large displacements.

It should be noted that, due to the nature of the similarity metrics, these methods achieved success by correlating the dense anatomical structures between images. In addition, when aligning subjects with large displacements, they rely on the subjects’ surfaces/contours to find the initial warping direction. However, they are not suitable for retinal images which have sparse and thin vessels and lack subject boundaries (e.g., [51]), because they will be trapped at local maximas in the searching space of similarity measurements during optimization. Fig. 2 shows simple examples of NCC and NMI measurements when aligning retinal images by 2D translation. In the first row, there are two local maxima areas in the NMI heatmap, in which the right one corresponds to the wrong alignment based on the imaging circles. In the second and thrid rows, the local maximas in the center (i.e., the correct alignment position) become much less obvious (the second row) or even invisible (the third row), which will mislead the algorithms into wrong warping directions. Lee et al. [52] also shared a similar observation in their work.

E. Multi-Modal Retinal Image Registration

Table I summarizes multi-modal registration methods based on deep learning, and none of them addresses the complete coarse-to-fine registration pipeline. Lee et al. [12] proposed a feature filtering CNN to detect and remove unreliable step features for multi-modal retinal image registration. Specifically, their network is trained with image patches as inputs and their corresponding step patterns [5] as outputs. During testing, unreliable patches are removed if their predicted patterns from the network deviate from any possible patterns. Arikan et al. [13] proposed to align multi-modal retinal images based on vessel segmentations and bifurcations using two CNNs. However, the networks are trained with segmentation and bifurcation ground-truths which are difficult to obtain in most cases. Luo et al. [15] proposed a CNN to estimate affine transformation matrix for IndoCyanine Green Angiography (ICGA) and Multi-Color (MC) images. However, it requires optic disc segmentations and dataset-specific scaling parameters for training, which limits its application on other datasets. Tian et al. [16] proposed a deformable retinal registration network, which adopts image gradients of two images as alignment signals for unsupervised training. Mahapatra et al. [11] proposed a deformable registration model based on unsupervised CycleGAN [53]. Instead of predicting a registration flow field, their network directly synthesizes a warped floating image, which cannot be used for diagnose purpose since the results might include non-existing patterns and lose critical lesion diseases. They also attached an additional branch to the network to predict registration fields which requires accurately aligned images for training, which is not applicable in most cases.

Particularly, Ding et al. [14] proposed to train a vessel segmentation network for Ultra-Wide Field (UWF) CF images through a joint segmentation and registration scheme, which bears similarities to the fine alignment network of our previous publication [17] and the second step of the proposed framework in section IV-B. In brief, with paired UWF CF and FA images as well as a pre-trained vessel segmentation network for FA, the vessel ground-truths for CF are obtained from the vessel predictions on FA images by aligning FA vessels with CF vessel predictions. The vessel segmentation network for CF and the alignment process are trained and optimized iteratively. However, their method mainly focuses on vessel segmentation instead of multi-modal registration, and is designed for UWF images from a same optic system which have similar scales and resolutions. It relies on a good initialization (i.e., a pre-trained segmentation network for one modality) which is hard to obtain in general cases. Besides, it adopts a global transformation model (with 12 parameters) which is insufficient for images bearing larger distortions (e.g., images from different instruments). In comparison, our proposed method does not require good initialization for segmentation and adopts a two-step coarse-to-fine structure, which is a more flexible and general solution for multi-modal retinal registration.

III. Two-Step Framework: Coarse Alignment

The proposed coarse alignment algorithm consists of three sequentially concatenated networks for vessel segmentation, feature detection and description, and outlier rejection as is shown in Fig. 3. First, the vessel segmentation network transforms multi-modal images into a common modality (i.e., grayscale vessel maps). Next, the feature detection and description network finds sparse keypoints from the vessel maps and extracts features on all keypoints. Then, features from source and target images are matched against each other based on their similarities. Finally, the outlier rejection network finds the correct matches (inliers) and removes the incorrect ones (outliers) such that an accurate affine matrix can be estimated from the inliers.

Fig. 3.

The coarse alignment step of the proposed two-step framework.

A. Vessel Segmentation

Vessel extraction has become the basis of multiple retinal registration algorithms [2], [8]-[10], [13], because vessels are usually the most prominent and useful patterns in multi-modal retinal images. Even though DNN has achieved great performance on retinal vessel segmentation with supervised training, its performance is not guaranteed on test data of other modalities unseen during training. Besides, we can hardly find any segmentation datasets on modalities other than CF, while it is labor-intensive to label the vessel segmentation for new datasets. Therefore, we propose an unsupervised scheme to train two vessel segmentation networks for each input modality without segmentation ground-truths. Specifically, the segmentation networks are trained jointly with a deformable registration network in Section IV. Style loss [19], [20] is used as a guidance for the segmentation task. Details on network structures and loss functions are presented in Section IV-B.

B. Feature Detection and Description

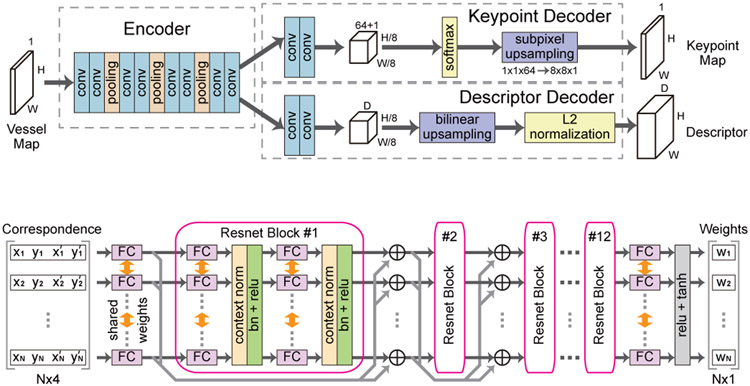
SuperPoint [31] network is adopted as our feature detector and descriptor, whose structure is shown in Fig. 4 (a). The network consists of an encoder which takes the grayscale vessel map from the previous segmentation network, and two decoders which predict a keypoint probability map and a descriptor tensor respectively. Accordingly, two loss functions are designed to train the network, including a keypoint loss and a descriptor loss. The keypoint loss penalizes missed or wrong keypoint predictions through a cross-entropy loss. Meanwhile, the descriptor loss maximizes the similarities between features of matching points or vice versa through a hinge loss. Readers could refer to [31] for more details.

Fig. 4.

The feature detection and description network and the outlier rejection network of the coarse alignment step.

(a) Feature detection and description network (SuperPoint [31])

(b) Outlier rejection network [28]

Since ground-truth keypoints for our retinal images are not available, we directly use a SuperPoint model which is pre-trained on a large-scale synthesized dataset [31]. Specifically, the training dataset consists of rendered images with grayscale shapes and their ground-truth corners, which bear much similarity with our vessel maps. Therefore, the trained model can be directly applied to extract keypoints and features from the vessel segmentation results. As a post-processing step, nonmaximum suppression thresholded at 5 pixels is applied over the keypoint probability maps, and pixels with confidence larger than 0.015 are denoted as keypoints. Afterwards, the corresponding feature vectors of the keypoints from both images are matched against each other based on minimum euclidean distances through a bi-directional search, e.g. feature A from the source should be the best match for feature B from the target, and vice versa. Finally, the corresponding coordinates of the matched keypoint pairs are forwarded to the next outlier rejection network.

C. Outlier Rejection Network

To obtain an accurate transformation matrix, we adopt and train an outlier rejection network [28] to detect and eliminate outliers from the matching pairs. First, the network takes the coordinates of the matched keypoint pairs from the feature detection and description network, and outputs their probabilities of being inliers. Then, the affine matrix is computed from the weighted coordinates. During training, in addition to the classification loss on the predicted weights and the regression loss on the estimated matrix, we also propose a Dice loss which evaluates the alignment quality based on the estimated matrix.

The structure of the network is shown in Fig. 4 (b). The network has 12 consecutive residual blocks. In each block, there are 2 fully connected layers with shared weights among N different entries, where N is the number of correspondences. Each fully connect layer is followed by a context normalization layer [28] and a batch normalization layer. Specifically, the weight-sharing design ensures that each correspondence will be processed independent of its input order. Meanwhile, the context normalization layers enable the sharing of global context among all correspondences.

In the forward process, the network takes a matrix $[{\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_N{]}^T\in {\mathbb{R}}^{N\times 4}$ as input, where ${\mathbf{q}}_i=[{\mathbf{p}}_i^T,{\mathbf{p}}_i^{\prime T}{]}^T$, and p_i = [x_i, y_i]^T and ${\mathbf{p}}_i^{\prime }=[x_i^{\prime },y_i^{\prime }{]}^T$ are the source and target keypoint coordinates respectively for the i-th correspondence. The network’s output is a vector $[o_1,o_2,\dots ,o_N{]}^T\in {\mathbb{R}}^{N\times 1}$, which is further translated into a weight vector w = [w₁, w₂, … ,w_N]^T, with each element w_i = tanh(ReLU(o_i)) ∈ [0, 1) being a weight for its input correspondence. Larger weights indicate more importance in estimating the affine matrix, and zero weights indicate outliers. Afterwards, an affine matrix $\mathbf{M}\in {\mathbb{R}}^{2\times 3}$ can be solved via weighted least square method based on the correspondences’ coordinates and their weights w, i.e., solving

$$\underset{\mathbf{M}}{\text{arg}\text{min}}{\left(\mathbf{b}-\mathbf{A}\text{Vec}(\mathbf{M})\right)}^T\mathbf{W}\left(\mathbf{b}-\mathbf{A}\text{Vec}(\mathbf{M})\right)$$ (1)

where Vec(M) is the vectorized M, $\mathbf{b}=[x_1^{\prime },y_1^{\prime },\dots ,x_N^{\prime },y_N^{\prime }{]}^T\in {\mathbb{R}}^{2N\times 1}$, $\mathbf{A}\in {\mathbb{R}}^{2N\times 6}$ is constructed as

$$\left(\begin{array}{cccccc}\hfill x_1\hfill & \hfill y_1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill x_1\hfill & \hfill y_1\hfill & \hfill 1\hfill \\ \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill \\ \hfill x_N\hfill & \hfill y_N\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill x_N\hfill & \hfill y_N\hfill & \hfill 1\hfill \end{array}\right),$$ (2)

and $\mathbf{W}=\text{diag}([w_1,w_1,\dots ,w_N,w_N])\in {\mathbb{R}}^{2N\times 2N}$ is a diagonal matrix. The solution to Eq. (1) is

$$\text{Vec}(\mathbf{M})={\left({\mathbf{A}}^T\mathbf{W}\mathbf{A}\right)}^{-1}\left({\mathbf{A}}^T\mathbf{W}\mathbf{b}\right).$$ (3)

It should be noted that we adopt the simpler affine transformation instead of the perspective transformation in [18], because the misalignment errors can be corrected by the following fine alignment step.

In order to train the network, three loss functions are combined, including a classification loss, a regression loss and a Dice loss. The classification loss is defined as

$${\mathcal{L}}_c=\frac{1}{N}\sum _{i=1}^N{\gamma }_i\text{BCE}(y_i,\sigma (o_i))$$ (4)

where BCE(·) is binary cross entropy loss, σ(·) is sigmoid function, y_i ∈ {0, 1} is the inlier ground-truth, and γ_i is a weight to balance positive and negative samples. The inlier ground-truth is obtained based on the ground-truth affine matrix M_gt as

$$y_i=\{\begin{array}{cc}1,\hfill & \Vert T({\mathbf{p}}_i,{\mathbf{M}}_{gt})-{\mathbf{p}}_i^{\prime }\Vert \le 5\text{pixels}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (5)

where T(p_i, M_gt) calculates the corresponding coordinate in target image for the source point p_i based on M_gt, i.e., a keypoint pair with distance no more than 5 pixels in the target image after warping are denoted as inliers.

In addition to the loss on the predicted weights, the regression loss penalizes the mean squared error (MSE) of the estimated affine matrix M from the ground-truth M_gt, which is defined as

$${\mathcal{L}}_r=\text{MSE}({\mathbf{M}}_{gt}-\mathbf{M}).$$ (6)

Moreover, a Dice loss is proposed to check the alignment quality of the target and source vessel map after warping based on the estimated matrix. The Dice coefficient is defined as

$$\text{DICE}(I_1,I_2)=\frac{2\mid I_1\cap I_2\mid }{\mid I_1\mid +\mid I_2\mid }$$ (7)

where I₁ and I₂ must be binary images in this function. Since our vessel maps are grayscale images, we define a Soft Dice function by relieving the binary constraint over I₁ and I₂ as

$${\text{DICE}}_s(I_1,I_2)=\frac{2\cdot \sum (\text{ele}\_\text{min}(I_1,I_2))}{\sum I_1+\sum I_2}$$ (8)

where ele_min(·, ·) takes the element-wise minimum values across the two images, and I₁, I₂ are vessel probability maps. The Dice loss is defined as

$${\mathcal{L}}_D=1-{\text{DICE}}_s(\text{STN}(I_{src}^{seg},\mathbf{M}),I_{tgt}^{seg})$$ (9)

where STN(·, ·) is the non-parametric differentiable image warping function [42], $I_{src}^{seg}$ and $I_{tgt}^{seg}$ are vessel segmentation maps of source and target images respectively, as denoted in Fig. 3. Finally, the total loss is written as

$$\mathcal{L}={\lambda }_c{\mathcal{L}}_c+{\lambda }_r{\mathcal{L}}_r+{\lambda }_D{\mathcal{L}}_D$$ (10)

where λ_c, λ_r and λ_D are weighting factors.

IV. Two-Step Framework: Fine Alignment

Due to lack of accuracy in the estimated matrices, image distortion from imaging instruments, and various field of view, there are still registration errors between the warped source image and the target image after the coarse alignment step. Many of these errors are minor and exist in local areas, which are hard to be corrected by global transformation. Since a fine alignment step using deformable transformation is necessary to further reduce these misalignment, we propose an unsupervised learning framework to train a deformable registration network and introduce modality transformers to aid the training process for multi-modal retinal images.

A. Unsupervised Learning Framework

The proposed learning framework of Fig. 5 for training consists of a deformable registration network and two modality transformers for the source image I_src-c = STN(I_src, M) and the target image I_tgt. The deformable registration network takes the multi-modal retinal image pairs as input, and predicts a pixel-wise registration field F. This is similar to optical flow networks [40] except that two input images fail to meet the brightness consistency assumption for optical flow estimation. Therefore, the photometric consistency loss cannot be directly applied on the inputs for unsupervised training. However, the proposed modality transformers change muti-modal inputs into common modality images, $I_{src\text{-}c}^t$ and $I_{tgt}^t$, t ∈ {seg, phase}, which can maintain pixel-wise correspondence as illustrated in Fig. 5. This helps to satisfy the brightness consistency constraint on input images like the optical flow estimation since the photometric consistency loss needs to be evaluated over their transformed modality during training. in this paper, two different modality transformers are proposed, i.e., vessel segmentation networks in Section IV-B, and Monogenical Phase Signal extractors in Section IV-C. The training process for the registration network does not require ground-truth flows for supervision, which is similar to the methods in [40], [41].

Fig. 5.

Training and testing phase for fine alignment framework.

Two loss functions are used to train the registration network, i.e., photometric consistency loss and smoothness loss. The photometric consistency loss is defined as

$${\mathcal{L}}_{pc}(I_{src\text{-}c}^t,I_{tgt}^t,F)=\text{MSE}(\text{STN}(I_{src\text{-}c}^t,F),I_{tgt}^t).$$ (11)

In brief, it takes the difference between the common structures extracted from the warped source image and the target image as the supervision for training. Meanwhile, the smoothness loss is defined as

$$\begin{gathered} {\mathcal{L}}_{sm}(F)=\underset{k,i,j}{\text{mean}}((F_{k,i,j}-F_{k,i+1,j}{)}^2)+ \\ \underset{k,i,j}{\text{mean}}((F_{k,i,j}-F_{k,i,j+1}{)}^2) \end{gathered}$$ (12)

where F has dimension 2 × h × w, and k, i, j are indices in F. It forces neighboring pixels in an estimated registration field to share similar warping directions and magnitudes. Therefore, displacement vectors for areas lacking details (e.g., non-vessel areas in a vessel segmentation map) can be estimated from their neighboring areas (e.g., areas containing vessels). In the case of using non-learnable modality transformers (e.g., local phase signals), the total loss of the deformable registration network is written as

$${\mathcal{L}}_{Def}={\lambda }_{pc}{\mathcal{L}}_{pc}+{\lambda }_{sm}{\mathcal{L}}_{sm}$$ (13)

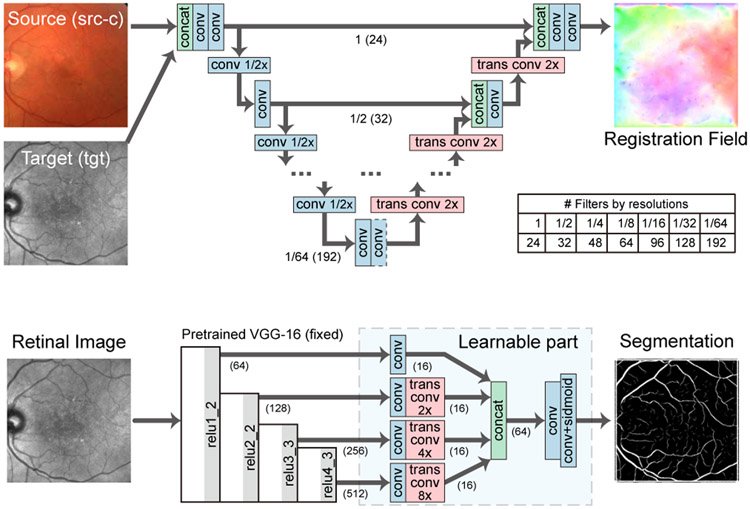
where λ_pc and λ_sm are weighting factors. In this paper, we adopt a modified U-Net [54] as our fine registration network as illustrated in Fig. 6 (a). In brief, the network first extracts multi-scale features from a concatenation of two multi-modal images, where convolutional layers with stride 2 are used as downsampling layers. Then, it gradually upsamples the features at each scale and concatenates them with features from a higher scale, where transposed convolutional layers are used for upsampling. Finally, it estimates the registration field F which has the same spatial size as the input images.

Fig. 6.

Network structures for fine alignment.

(a) Deformable registration network

(b) Modality transformer: vessel segmentation network

B. Modality Transformer: Vessel Segmentation Network

In this section, we adopt segmentation networks as the modality transformers to guide registration and propose an unsupervised learning scheme, which is based on style transfer [19], [20], to train the segmentation networks jointly with the registration network without segmentation ground-truths. Specifically, the segmentation network is trained through a style loss [20] which penalizes the style difference between the network output and a style target. First, a pre-trained VGG-16 [57] network ϕ takes an image I and computes a feature tensor from its j-th layer as ϕ_j(I) with shape c_j × h_j × w_j. Then, ϕ_j(I) is reshaped into a matrix Φ_j(I) with shape c_j × (h_jw_j). Next, the style feature of I is represented by a c_j × c_j Gram matrix G_j(I) as

$${\mathbf{G}}_j(I)=\frac{1}{c_j{h}_j{w}_j}{\Phi }_j(I){\Phi }_j^T(I)$$ (14)

where the spatial information in ϕ_j(I) is removed and only the information on global style distributions (e.g., vessel-like structures) are preserved. Finally, the style loss is derived by minimizing the difference of two style distributions as

$${\mathcal{L}}_{sty}^j(I_1,I_2)=\Vert {\mathbf{G}}_j(I_1)-{\mathbf{G}}_j(I_2){\Vert }_F^2$$ (15)

where ∥ · ∥_F computes Frobenius norm over a matrix. In our case, I₁ is a segmentation network’s prediction ($I_{src\text{-}c}^{seg}$ or $I_{tgt}^{seg}$), and I₂ is a style target I_style, i.e., one of the vessel images in Fig. 7. Therefore, the segmentation network should produce an output which also demonstrates vessel-like appearance but no pixel-wise correspondence with the style target.

Fig. 7.

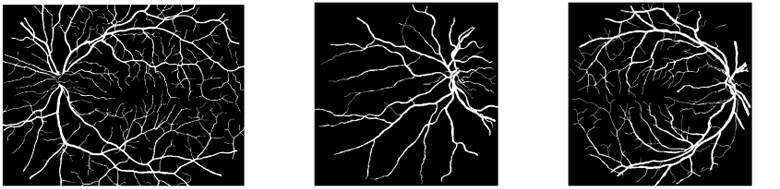
Style target images I_style taken from publicly available datasets.

(a) HRF-12h [55]

(b) DRIVE-23 [56]

(c) DRIVE-28 [56]

In addition to the style loss, we propose a self-comparison loss to enforce rotation invariance on the vessel segmentation results. Since image edge filters show directional dependency, it is necessary to enforce the learning of edge filter pairs with inverse directions when training without ground-truths such that both edges of the vessels can be extracted. Therefore, the self-comparison loss is defined as

$${\mathcal{L}}_{com}(I)=\text{MSE}\left(\text{rot}\left(\mathrm{H}\left(\text{rot}(I)\right)\right),\mathrm{H}(I)\right)$$ (16)

where H(·) is the segmentation network, and rot(I) rotates the input image by 180°. When we jointly train the segmentation networks and the registration network, we include the style loss ${\mathcal{L}}_{sty}$ and the self-comparison loss ${\mathcal{L}}_{com}$ to the total loss ${\mathcal{L}}_{Def}$. As a result, the total loss function is defined as

$$\begin{gathered} {\mathcal{L}}_{Def\text{-}Seg}={\mathcal{L}}_{Def}+{\lambda }_{com}\sum _x{\mathcal{L}}_{com}(I_x)+ \\ {\lambda }_{sty}\sum _{x,j}{\mathcal{L}}_{sty}^j(I_x^{seg},I_{style}) \end{gathered}$$ (17)

where j ∈ {relu1_2, relu2_2, relu3_3, relu4_3} are VGG-16 layers and x ∈ {src, tgt}. Through the joint training, the segmentation networks can achieve better performance, as the segmentation prediction $I_{src\text{-}c}^{seg}$ is supervised by both the style constraints ${\mathcal{L}}_{sty}^j$ and another segmentation map $I_{tgt}^{seg}$, and vice versa. We adopt a modified network structure based on DRIU [58] for the segmentation network as shown in Fig. 6 (b). The network first extracts multi-scale features using a pre-trained VGG-16 network. Then it upsamples all features via transposed convolutional layers, and concatenates them for final prediction.

Comparing with the original implementation in [17], we set up a unified parallel structure for segmentation and registration, which enables more choices of transformed modalities other than the vessel maps. Besides, we replace the ℓ1 norm in the smoothness loss ${\mathcal{L}}_{sm}$ with ℓ2 norm to generate smoother registration fields, and remove the SSIM loss since it does not help in improving the registration performance.

C. Modality Transformer: Local Phase Signals

Instead of the vessel segmentation modality, we can also use the multi-scale local phase images, which is based on Monogenic signal [21], as a common modality to improve the registration performance in non-vessel areas. Previously, Li et al. [1] have shown the effectiveness of Monogenic local phase signals in a conventional multi-modal retinal registration pipeline.

In brief, the Monogenic signal is a multi-dimensional generalization of analytic signal. It can be computed by applying Riesz transformation on an input image [21], and the local phase term of the signal can be seen as the gradients of the image [59]. In order to extract image gradients in a certain range of scales (i.e., frequencies), the input image is filtered with a 2D log-Gabor band-pass filters prior to the Riesz transformation. The log-Gabor filter is given in frequency domain as

$$G(\omega )=\text{exp}\left(-\frac{(\log (\Vert \omega \Vert ∕{\omega }_0){)}^2}{2(\log ({\sigma }_0){)}^2}\right)$$ (18)

where ω₀ and σ₀ are center frequency and width of the filter which control the range of passed frequencies. After Riesz transformer, the 2-D local phase signal of the image I can be obtained as

$$\varphi (I)=\text{arctan}\left(\frac{(f_{o1}(I{)}^2+f_{o2}(I{)}^2{)}^{1∕2}}{f_e(I)}\right)$$ (19)

where f_o1(I), f_o2(I), and f_e(I) are two odd parts and one even part of the Riesz transformation output from an filtered image.

In this paper, we use K log-Gabor filters with σ₀ = 0.55 and ω₀ = 1/(5 × 1.5^k), k = 0, 1, … , K − 1 respectively to extract local phase maps at multiple scales. Fig. 8 shows an example of extracted local phase maps from multi-modal retinal images using the above log-Gabor filter settings. Filters with higher center frequencies ω₀ help extract finer details throughout the whole images, and results from lower frequency filters tends to focus on larger-scale patterns. Moreover, patterns in non-vessel areas are also extracted which can help increase their weights in the photometric consistency loss. Therefore, the alignment quality of the deformable registration network can be improved in the non-vessel areas.

Fig. 8.

The phase signals of a multi-modal image pair are extracted with the Log-Gabor filters in Eq. (18) (k ∈ {0, 1, … , 7}).

V. Experiments

A. Settings

1). Dataset:

We use two datasets, i.e., CF-FA and JRC, for our experiments. CF-FA [60] is a public dataset captured in the modalities of CF and FA. It contains 59 pairs of retinal images of shape 720 × 576, 29 pairs of which are from healthy eyes and the rest show diseases. We take 30 pairs with odd index in the file names as the training set, and the remaining 29 for testing. The JRC dataset is collected by the Jacobs Retinal Center (JRC) at Shirley Eye Institute. It consists pairs of CF images of shape 3000 × 2672 and Infrared Reflectance (IR) images of shape 768 × 768 or 1536 × 1536. It has 530 pairs for training, 90 pairs for validation, and 253 pairs for testing. Especially, each image is graded by ophthalmologists as {high / medium / low} according to its imaging quality, and as {yes / no} based on the appearance of diseases.

Compared with the JRC dataset, the CF-FA dataset is less challenging since it shows crispy retinal patterns, and contains denser vessels and less diseases. An example of CF-FA images is shown in the first row of Fig. 2. However, the JRC dataset is more challenging, as its images often show sparser vessels, more diseases and unmatched structures. For example, in Fig. 2, the second example is considered as good quality, and the third example is graded as low quality due to the unwanted choroidal patterns and unfocused vessels in the CF image.

As an image preprocessing step, the images of the CF-FA dataset are expanded with zeros to 768 × 576, and the images of the JRC dataset are padded with zeros to the square shape and then resized to 768 × 768. To obtain the coarse alignment ground-truths for each image pair, we manually label three pairs of matching points and derive the ground-truth affine matrix M_gt based on the points’ coordinates. In this paper, we set CF as a source modality and FA/IR as a target, i.e., CF images are warped towards a target modality.

2). Training and Testing Settings:

For the outlier rejection network in the coarse alignment step, we set its input dimension as N ≤ 128. We set λ_c = 1 and λ_r = λ_D = 0.1 in the loss function Eq. (10). Adam [61] optimizer is used for training with learning rate as 1e-4. All the image coordinates are normalized into [−1, 1], and the ground-truth matrices M_gt are modified accordingly. The network is trained for 1000 epoches with batch size 32 on the JRC dataset. Due to small size of the CF-FA dataset, we take the model which is pre-trained on the JRC dataset and finetune it on the CF-FA dataset for 1000 epoches with batch size 30. The best checkpoint is selected based on the minimum Dice loss ${\mathcal{L}}_D$ on training set (CF-FA) or validation set (JRC).

For the fine alignment step, the networks are trained with Adam optimizer with learning rate as 1e-3. We set λ_pc = 1e-3, λ_sm = 5e-4, λ_com = 1e-3, and λ_sty = 1.0 in Eq. (13) and (17). During training, two images of original size without any cropping are fed into the networks due to the requirement of style transfer loss, which takes up huge amount of GPU memory. Therefore, we set batch size to 1, and apply the same setting when training with local phase signals. The deformable networks are trained with 5000 (CF-FA) or 1500 (JRC) epoches, and the checkpoints with best Dice_s value on the training set (CF-FA) or validation set (JRC) are selected for final evaluation. Two vessel segmentation images, i.e., HRF-12h [55] in Fig. 7 (a) and DRIVE-28 [56] in Fig. 7 (c) from publicly available datasets, are selected as style targets for the CF-FA and JRC datasets respectively.

In addition, we employ data augmentation to train the fine alignment networks. First, training image pairs are set up based on M_gt. For both datasets, coarsely aligned image pairs ⟨STN(I_src, M_gt), I_tgt⟩ are used for training. For the CF-FA dataset, inversely aligned pairs $\langle I_{src},\text{STN}(I_{tgt},{\mathbf{M}}_{gt}^{-1})\rangle$ are also included in the training set, which increases its size to 60. Next, the training pairs are augmented by random flipping (for both datasets) and rotation (for JRC only). Finally, random warping is applied on each image, i.e., 2 × 4 × 3 (for CF-FA) or 2 × 4 × 4 (for JRC) arrays are first sampled from a normal distribution (mean 0, standard deviation 5 pixels), then expanded to the image’s resolution, and finally used to warp the image.

For evaluation on the JRC dataset, we separate the 253 test image pairs into 4 categories based on the gradings of imaging qualities and existence of diseases. In detail, the images are first categorized into two groups as High & Medium Quality and Low Quality. Then, the High & Medium Quality group is further divided into three sub-groups based on the number of images with diseases in each pair as in Table II.

TABLE II.

Average Dice/Dice_s values of two-step registration on the JRC and CF-FA datasets where the highest scores are marked in bold.

Method				JRC Dataset (253 images)					CF-FA Dataset (29 images)
Group	Row #	Coarse Alignment	Fine Alignment	High & Medium Quality (203)			Low Quality (50)	Overall (253)
				No Disease (111)	1 Disease (42)	2 Diseases (50)
(a)	(a1)	Before registration		0.0734 / 0.2536	0.0754 / 0.2565	0.0732 / 0.2666	0.0749 / 0.2679	0.0740 / 0.2595	0.1012 / 0.2582
(b)	(b1)	[1] (Phase-HoG-RANSAC)	N/A	0.4160 / 0.4461	0.4181 / 0.4490	0.3431 / 0.4175	0.1792 / 0.3170	0.3551 / 0.4154	0.5504 / 0.5050
	(b2)		MIND [63]	0.4894 / 0.5047	0.4726 / 0.4961	0.4094 / 0.4692	0.2166 / 0.3435	0.4169 / 0.4644	0.6289 / 0.5291
(c)	(c1)	IRR-PWC [39] (input: vessel)		0.3754 / 0.4007	0.3479 / 0.3916	0.3135 / 0.3866	0.2332 / 0.3384	0.3305 / 0.3841	0.2959 / 0.3910
	(c2)	IRR-PWC [39] (input: image)		0.3505 / 0.3913	0.3369 / 0.3880	0.3178 / 0.3894	0.2590 / 0.3523	0.3237 / 0.3826	0.2251 / 0.3535
(d) Ours	(d1)	CoarseNet	N/A	0.5701 / 0.5129	0.5623 / 0.5052	0.4949 / 0.4793	0.3331 / 0.3864	0.5071 / 0.4800	0.5902 / 0.5204
	(d2)		Seg-DeformNet	0.6040 / 0.5431	0.6034 / 0.5384	0.5549 / 0.5185	0.4139 / 0.4356	0.5566 / 0.5162	0.6812 / 0.5394
	(d3)		Phase-DeformNet	0.5835 / 0.5576	0.5819 / 0.5534	0.5343 / 0.5350	0.3890 / 0.4338	0.5350 / 0.5280	0.6678 / 0.5412

All networks are implemented in PyTorch and trained on GTX 1080 Ti GPU cards. During testing, all methods are tested on a desktop with a Intel i7-7700K CPU and a GTX 1080 Ti GPU card.

3). Evaluation Metrics:

We adopt three evaluation metrics for registration quality assessment:

(a) Dice ∈ [0, 1] is defined as the Dice coefficient of Eq. (7) which takes binary vessel segmentations from B-COSFIRE [62] as its inputs. The Dice coefficient is often used to evaluate retinal alignment quality (e.g., [1]) when registration ground-truths are not available. It calculates the ratio of overlapping binary vessel areas to the sum of total vessel areas from both images. Larger Dice coefficients represent more overlapping area of vessels, which indicates better alignment quality. To extract binary vessels, we adopt B-COSFIRE [62] as the segmentation method. We keep the default settings in B-COSFIRE’s codes except its segmentation threshold which is determined as follows. For the CF-FA dataset which shows better image qualities, two global thresholds are determined for each modality which maximizes the difference of Dice before and after warping based on the Phase + MIND [63] method in Section V-C1. For the JRC dataset, global thresholds lead to worse segmentation results (i.e., too sparse or too dense vessels) due to the huge variance of image qualities, which impacts the alignment evaluation process. To ensure more reasonable segmentation results on the JRC test set, we estimate an individual threshold for each image which minimizes the style loss of Eq. (15) by comparing the thresholded result with the style target DRIVE-28.

(b) Dice_s ∈ [0, 1] is defined as the Soft Dice of Eq. (8) which takes vessel probabilities from Frangi’s [64] method as its inputs. Soft Dice is extended from the Dice coefficient and takes vessel probability maps. Similarly, it computes the ratio of vessel intersection to the sum of two vessel maps, and larger values indicate better alignment results. Frangi’s [64] algorithm is used to extract vessel probabilities from retinal images. We first enhance a retinal image with CLAHE [65], then compute its vesselness map using Frangi’s method, and finally rescale the vesselness map into [0, 1] based on its min & max values.

(c) #success is defined as the number of successfully aligned image pairs in each category. This metric is only used for the coarse alignment evaluation. The alignment success is achieved when

$$\underset{\mathbf{p}\in P}{\max }{\Vert T\left(T(\mathbf{p},{\mathbf{M}}_{gt}^{-1}),\mathbf{M}\right)\Vert }_2\le \text{Threshold}$$ (20)

where T(·, ·) warps a coordinate p based on a transformation matrix, and P is a set of 6 correspondences for each image pair which is labeled by human. We empirically set Threshold = 10 pixels, i.e., if all the source coordinates fall within the range of 10 pixels from their corresponding target coordinates after transformation, it is considered a success.

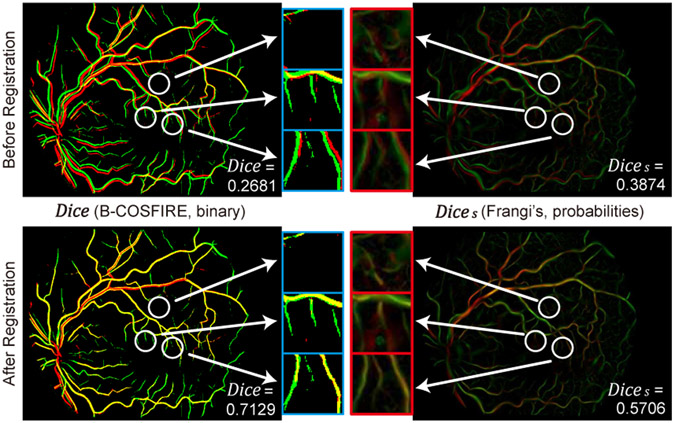
Fig. 9 shows an example of Dice and Dice_s calculation. The overlapping maps of their extracted vessel binaries or probabilities are plotted before and after registration. In the left column, some tiny vessels and non-vessel structures from the source image (red) are missed in Dice due to the binary thresholding. But those structures are preserved as probabilities in Dice_s (right column), and can be included in the registration quality evaluation. Therefore, Dice mainly assesses the alignment quality of prominent vessels, while Dice_s pays attention to both major and tiny retinal structures.

Fig. 9.

A comparison of Dice and Dice_s over a same pair of input images before and after registration. Red and green areas indicate extracted vessel binaries or probabilities from source and target image respectively, and yellow areas indicate their overlapping parts. White circles point to tiny vessels which are missed in Dice but maintained in Dice_s. Pixel intensities in red boxes are enhanced for visual inspection.

B. Results on Two-Step Coarse-to-Fine Registration

For comparison, four groups of methods/results are set up for coarse-to-fine registration evaluation for the quantitative and qualitative comparison in Table II and Fig. 10, respectively. The groups are:

Fig. 10.

Two-step registration results on three examples from the JRC dataset, where source and target images are displayed interlaced as small grids. From top to bottom lines are: (a1) Input images, (b1) Phase-HoG-RANSAC (coarse only), (b2) Phase-HoG-RANSAC + MIND (two-step), (c1) IRR-PWC (input: vessel) (c2) IRR-PWC (input: image), (d1) CoarseNet (coarse only), (d2) CoarseNet + Seg-DeformNet (two-step), (d3) CoarseNet + Phase-DeformNet (two-step). In each example, the leftmost column shows complete images, and the following three columns show magnified details in the yellow, blue and green boxes denoted by numbers. Red Arrows point to misalignment of retinal structures. Red circles show improved alignment results by the second step in a two-step registration pipeline over its global alignment results.

(a): Input images without any warping.

(b): An improved version of a conventional two-step registration pipeline [1], where the time-consuming matching algorithm is replaced by a much faster one [23]. Specifically, local phase signal is adopted to help its feature-based coarse alignment step (denoted as Phase [21] - HoG [66] - RANSAC [24]), and then MIND¹ [63] is used for fine alignment.

(c): A state-of-the-art optical flow network IRR-PWC [39] with supervised training. Since coarse-to-fine registration pipelines based on fully CNN are unavailable, a pre-trained IRR-PWC is adopted and finetuned on multi-modal retinal images. The network takes an image pair as input and estimates a registration field map which warps the source image in one step. Specifically, two types of inputs are fed into IRR-PWC, i.e., original retinal images, or predicted vessel maps from our segmentation networks which mimics the optical flow estimation process. For each type of input, two models are trained on different optical flow ground-truths, and the better one is used for evaluation. The ground-truth optical flows are generated based on either M_gt only, or a combination of M_gt and our best deformable alignment result (i.e., results in Section V-C).

(d): Our proposed pipeline, where we denote the coarse alignment network as CoarseNet, the fine alignment network with the modality transformer for the vessel segmentation as Seg-DeformNet, and the fine alignment network with the modality transformer for the local phase signals as Phase-DeformNet.

Table II shows the quantitative evaluation results for the JRC (blue columns) and CF-FA (red column) datasets. On the JRC dataset, the proposed two-step methods in group (d) achieve the best performance in both Dice and Dice_s metrics. Moreover, the conventional two-step method (b2) outperforms the single-step networks with supervised training in group (c), which shows that two-step approaches are more effective for multi-modal registration. When we compare Dice/Dice_s of the proposed two-step networks in group (d) with the conventional method (b2) for each category from left to right, the advantage of our method gradually increases as the images become more challenging. For example, the gains of row (d3) over (b2) from left to right are 0.0941/0.0529 for No Disease, 0.1093/0.0618 for 1 Disease, 0.1249/0.0658 for 2 Diseases, and 0.1724/0.0903 for Low Quality images. This result demonstrates that our two-step methods are more robust to multi-modal images with more disease lesions and lower image qualities.

The last column in Table II shows the results for the CF-FA dataset. The rankings of Dice/Dice_s values of groups remain similar with that on the JRC dataset. The advantage of our networks (d) over the conventional method (b2) (i.e., difference between row (d3) and (b2)) is reduced to 0.0389/0.0121 since the CF-FA dataset contains fewer challenge cases than the JRC dataset. Nevertheless, the single-step optical flow networks with supervised training in group (c) have the lowest performance.

In Fig. 10, we compare qualitative results on two image pairs from JRC dataset where a normal pair and a diseases pair are shown in example 1 and 2 respectively. In both examples, our methods can correctly and accurately align most vessels and disease patterns. In contrast, the other methods fail in at least one of the examples, e.g., Phase - HoG - RANSAC + MIND of (b2) fails in the example 2 to align vague vessels (box 2) and lesions (box 3) and the IRR-PWC’s results contain obvious misalignment errors in all examples, as indicated by red arrows.

Apart from the above comparison, within each group (b) and (d) in Table II, the additional fine alignment steps of (b2)/(d2)/(d3) are able to improve the registration performance over coarse alignment results of (b1)/(d1). This is also demonstrated in red circles of Fig. 10, where misalignments from CoarseNet of (d1) are corrected by fine alignment networks in (d2)/(d3). This result presents clearly that the refinement step can help to correct errors from the first step and thus increase the robustness of the registration pipeline. Therefore, two-step coarse-to-fine structures achieve better results comparing to single-step ones for multi-modal retinal registration.

C. Ablation Study on Deformable Registration Networks

In this section, we investigate the performance of the proposed fine alignment networks on both datasets by comparing it with other methods. Moreover, we further analyze several factors that influence its registration quality. Testing image pairs aligned by M_gt are adopted for evaluation. All the testing images are preprocessed by the identical augmentation procedure in fine alignment network training which is described in Section V-A2. Therefore, the size of the CF-FA test set is doubled to 58 in this section. The random warping flows applied on the input images are fixed for all methods.

1). Fine Alignment Evaluation:

Table III shows the deformable registration results for the JRC and CF-FA datasets. The proposed deformable networks outperform the conventional method Phase + MIND in all cases, showing the advantages of CNN in this task. In addition, our proposed networks achieve better performance than another unsupervised network, VoxelMorph [48], which uses local NCC as the similarity metric in training. This shows the advantages of transformed modalities (vessel maps and phase signals) over conventional image-based similarity metrics in the deformable registration task on multi-modal retinal images.

TABLE III.

Average Dice/Dice_s values for fine alignment on the JRC and CF-FA datasets where the highest scores are marked in bold.

Fine Alignment Method	JRC Dataset					CF-FA Dataset
	High & Medium Quality			Low Quality	Overall
	No Disease	1 Disease	2 Diseases
Mgt + Random Warping	0.3459 / 0.3920	0.3320 / 0.3904	0.3048 / 0.3851	0.2412 / 0.3430	0.3148 / 0.3807	0.2744 / 0.3934
MIND [63]	-	-	-	-	-	0.6019 / 0.5269
Phase [21] + MIND [63]	0.5426 / 0.5196	0.5302 / 0.5124	0.4794 / 0.4889	0.3527 / 0.4006	0.4905 / 0.4888	0.6178 / 0.5303
VoxelMorph (NCC) [48]	*	*	*	*	*	0.6408 / 0.5358
Zhang et al. [17]	-	-	-	-	-	0.6546 / 0.5398
Seg-DeformNet (Ours)	0.5970 / 0.5355	0.5910 / 0.5320	0.5426 / 0.5120	0.4173 / 0.4237	0.5497 / 0.5082	0.6692 / 0.5442
Phase-DeformNet (Ours)	0.5675 / 0.5442	0.5669 / 0.5427	0.5065 / 0.5197	0.3888 / 0.4225	0.5201 / 0.5151	0.6487 / 0.5435

^*VoxelMorph failed in multiple trials on the JRC dataset, by predicting either NaN values or extremely large displacement fields.

When comparing Phase-DeformNet and Seg-DeformNet on the JRC dataset in the blue columns, Phase-DeformNet ranks highest in Dice_s in most categories except the low quality images, while Seg-DeformNet performs best in Dice across all groups. However, on the CF-FA dataset in the red column, Seg-DeformNet achieves the best performance in both Dice_s and Dice, although its advantage in Dice_s is marginal (i.e., +0.0007). Similar relations of two methods are also observed in Table II, where the gap of Dice_s values between Seg-DeformNet and Phase-DeformNet is smaller on the CF-FA dataset (i.e., −0.0018) than that on the JRC dataset (0.0118 in the Overall column). It might result from the different supervision signals in the content loss (Eq. (11)) and different characteristics of the datasets. Specifically, Seg-DeformNet is trained by optimizing the alignment of extracted vessels, and cannot directly align non-vessel areas if their segmentation predictions are zero. Thus, it tends to get higher values in Dice (i.e., the overlapping degree of prominent vessels) but lower values in Dice_s (which puts more emphasis on non-vessel areas). Since Phase-DeformNet is trained by aligning local phase patterns which distribute over the whole images, it tends to achieve better performance in non-vessel areas, i.e., higher Dice_s. On the other hand, images in the CF-FA dataset have denser vessels and less non-vessel patterns (e.g., diseases) than those in the JRC dataset. Therefore, it is possible for Seg-DeformNet to have minor margin over Phase-DeformNet on the CF-FA dataset by only aligning vessel patterns.

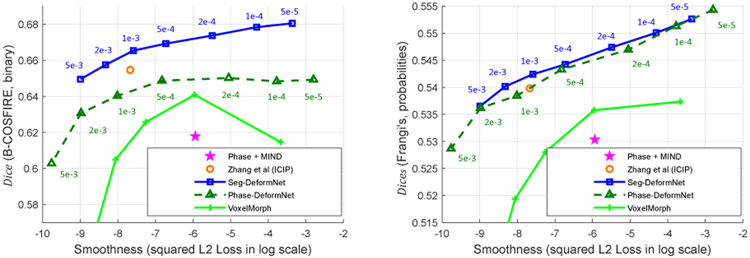
2). Smoothness Weight:

We analyze the influence of different smoothness factor λ_sm in Eq. (13) and (17) on the registration results. Theoretically, higher λ_sm makes it more difficult to correct abrupt misalignments in small areas and reduces alignment quality because of competitions between photometric consistency loss ${\mathcal{L}}_{pc}$ (Eq. (11)) and smoothness loss ${\mathcal{L}}_{sm}$ (Eq. 12). In this experiment, we set λ_sm ∈ {5e-3, 2e-3, 1e-3, 5e-4, 2e-4, 1e-4, 5e-5} for both Seg-DeformNet and Phase-DeformNet and train them on the CF-FA dataset where other settings remain unchanged. The evaluation results on the test set are displayed in Fig. 11 as the relations between Dice/Dice_s values and ${\mathcal{L}}_{sm}$ (Eq. (12)). As can be seen from Fig. 11 (b), Dice_s of two methods keep increasing as λ_sm decreases, which complies with the theoretical analysis. Moreover, from Fig. 11 (a), the trend of increase in Dice for Phase-DeformNet stops below λ_sm = 5e-4, which implies that the network cannot make improvement in aligning vessels by reducing λ_sm. Therefore, we choose λ_sm = 5e-4 as our setting in Section V-B.

Fig. 11.

Deformable registration performance on the CF-FA dataset for networks trained with various λ_sm. Each data point indicates Dice/Dice_s and ${\mathcal{L}}_{sm}$ values measured on the test set. The number besides each point indicates the corresponding λ_sm.

(a) Dice to ${\mathcal{L}}_{sm}$.

(b) Dice_s to ${\mathcal{L}}_{sm}$.

Fig. 11 also plots the results of the conventional method (i.e., Phase + MIND) and our previous network [17]. The proposed Seg-DeformNet (the blue point at λ_sm = 1e-3) has better alignment quality than our previous network [17] (the orange point) at a similar smoothness level. Besides, both the proposed Seg-DeformNet and Phase-DeformNet achieve higher Dice/Dice_s values than the conventional method (the purple star), which shows the strengths of DNN on this task.

3). Diffeomorphic Property of Deformation Fields:

Diffeomorphic registration is another research topic in medical image registration and has been incorporated in recently proposed networks [67]-[69]. It aims to obtain a topology-preserving and invertible transformation that enforces one-to-one mapping. Nevertheless, it is not a major concern or contribution in this work. Therefore, we only measure the diffeomorphic property of our predicted registration fields during testing.

The diffeomorphic property of a registration field can be analyzed by the determinant of Jacobian matrix, which is defined on each pixel (x, y) as

$$\mid J_F(x,y)\mid =\mid \begin{array}{cc}\hfill \frac{{\partial }_{F_{0,\cdot ,\cdot }}(x,y)}{\partial x}\hfill & \hfill \frac{{\partial }_{F_{0,\cdot ,\cdot }}(x,y)}{\partial y}\hfill \\ \hfill \frac{{\partial }_{F_{1,\cdot ,\cdot }}(x,y)}{\partial x}\hfill & \hfill \frac{{\partial }_{F_{1,\cdot ,\cdot }}(x,y)}{\partial y}\hfill \end{array}\mid$$ (21)

where F_0,·,· and F_1,·,· are the maps of displacement vectors in two directions. If ∣J_F (x, y)∣ < 0, the deformation at (x, y) fails to preserve the same warping orientation as its neighbors, which is unfavored. In this work, we compute ∣J_F(x, y)∣ for all predicted registration fields on the test sets, and count the number of pixels with negative determinant values. On the CF-FA dataset, the percentage of pixels with negative determinant values are 0.0002% for Seg-DeformNet and 0% for Phase-DeformNet. On the JRC dataset, the values become 0.0044% for Seg-DeformNet and 0% for Phase-DeformNet. These numbers show that only a small portion of pixels in the predicted registration fields have negative values. Therefore, the diffeomorphic property is mostly preserved by our proposed deformable networks.

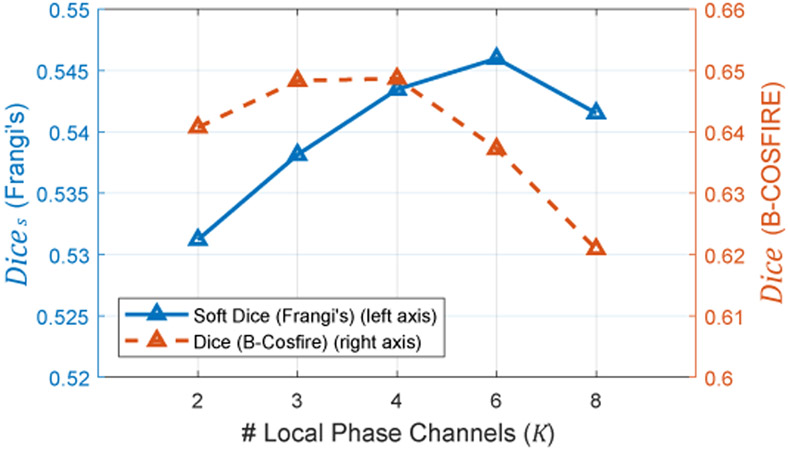
4). Number of Local Phase Image Channels:

The relation of Phase-DeformNet’s performance with regard to the number of channels K in local phase signal is shown in Fig. 12. In theory, networks trained with small K can only see detailed information (high-frequency patterns) in alignment. Increasing K includes more low-frequency information for registration. As shown in Fig. 12, Dice peaks on both K = 3 and K = 4 and start to decrease sharply from K = 6. Dice_s keeps increasing from K = 2 to K = 6 and decrease afterwards. In order to achieve a balance between Dice and Dice_s, we select K = 4 for Phase-DeformNet in our experiments.

Fig. 12.

Registration performance of Phase-DeformNet on the CF-FA dataset when trained with different number of local phase channels K.

5). Style Target Choices:

The influences over Seg-DeformNet’s performance from different style targets are demonstrated in Table IV. In details, three different segmentation maps are selected from HRF [55] and DRIVE [56] datasets, as shown in Fig. 7 where the vessel density of HRF-12h, DRIVE-23, and DRIVE-28 is dense, sparse, and in-between, respectively. On the CF-FA dataset, the network trained with HRF-12h achieves the best performance. On the JCR dataset, DRIVE-28 helps the network to obtain the highest Dice/Dice_s values. We attribute this performance’s variations of a certain style target to the similarities between the style target and the datasets’ images. Since images in the CF-FA dataset generally have good quality and dense vessel structures, a style target with denser vessels (e.g., HRF-12h) might achieve better vessel segmentation, and thus leads to better alignment results. However, the images in the JRC dataset has relatively sparse vessel densities and also show lower image quality. Therefore, the best result is achieved with the sparser vessel style image DRIVE-28 instead of HRF-12h.

TABLE IV.

Average Dice/Dice_s values of Seg-DeformNet on the JRC and CF-FA datasets trained with different style targets.

Style Target Image	JRC	CF-FA
HRF-12h [55]	0.5088 / 0.5056	0.6692 / 0.5442
DRIVE-23 [56]	0.5290 / 0.4963	0.6345 / 0.5353
DRIVE-28 [56]	0.5497 / 0.5082	0.6559 / 0.5416

D. Ablation Study on Coarse Alignment

In this section, we investigate the performance of the coarse alignment step on the JRC dataset. We set up additional groups of methods and training settings in Table V as follows:

TABLE V.

Coarse alignment performance on the JRC dataset: average Dice/Dice_s (#success).

Group	Row #	Coarse Alignment Method	High & Medium Quality (203)			Low Quality (50)	Overall (253)
			No Disease (111)	1 Disease (42)	2 Diseases (50)
(a)	(a1)	Before registration	0.0734 / 0.2536	0.0754 / 0.2565	0.0732 / 0.2666	0.0749 / 0.2679	0.0740 / 0.2595
(b)	(b1)	[1] (Phase-HoG-RANSAC)	0.4160 / 0.4461 (55)	0.4181 / 0.4490 (23)	0.3431 / 0.4175 (19)	0.1792 / 0.3170 (5)	0.3551 / 0.4154 (102)
(e)	(e1)	DRMIME [70]	0.1003 / 0.2720 (1)	0.0906 / 0.2706 (0)	0.0817 / 0.2753 (0)	0.0832 / 0.2706 (0)	0.0916 / 0.2721 (1)
	(e2)	AffineNet of DLIR [46]	0.0805 / 0.2558 (0)	0.0749 / 0.2591 (0)	0.0799 / 0.2750 (0)	0.0811 / 0.2701 (0)	0.0795 / 0.2630 (0)
(f) Input+SIFT+RANSAC	(f1)	IR (MUNIT [71])	0.2217 / 0.3227 (21)	0.1850 / 0.2914 (4)	0.1298 / 0.2591 (3)	0.1133 / 0.2520 (0)	0.1760 / 0.2910 (28)
	(f2)	B-Cosfire [62]	0.2346 / 0.3269 (30)	0.2525 / 0.3379 (13)	0.1827 / 0.3008 (9)	0.0962 / 0.2494 (2)	0.2000 / 0.3083 (54)
	(f3)	Phase [21]	0.1473 / 0.2498 (11)	0.1345 / 0.2705 (2)	0.1066 / 0.2558 (2)	0.0746 / 0.2275 (0)	0.1228 / 0.2500 (15)
	(f4)	SegNet (Ours)	0.1968 / 0.3090 (21)	0.2005 / 0.3073 (10)	0.1344 / 0.2849 (6)	0.0804 / 0.2372 (1)	0.1621 / 0.2898 (38)
(g) Input+SuperPoint+RANSAC	(g1)	IR (MUNIT [71])	0.4489 / 0.4553 (79)	0.4363 / 0.4426 (28)	0.3517 / 0.4089 (25)	0.1552 / 0.2955 (8)	0.3696 / 0.4124 (140)
	(g2)	B-Cosfire [62]	0.4310 / 0.4358 (70)	0.4000 / 0.4178 (24)	0.3324 / 0.3901 (23)	0.2259 / 0.3147 (11)	0.3659 / 0.3999 (128)
	(g3)	Phase [21]	0.5006 / 0.4808 (89)	0.4447 / 0.4532 (30)	0.3942 / 0.4194 (29)	0.1371 / 0.2853 (4)	0.3984 / 0.4254 (152)
	(g4)	SegNet (Ours)	0.5189 / 0.4859 (92)	0.5072 / 0.4769 (34)	0.3985 / 0.4162 (31)	0.2254 / 0.3062 (13)	0.4352 / 0.4351 (170)
(h)	(h1)	CoarseNet (w/o LD)	0.5693 / 0.5141 (106)	0.5623 / 0.5085 (40)	0.4942 / 0.4806 (43)	0.3370 / 0.3866 (21)	0.5074 / 0.4813 (210)
	(h2)	CoarseNet (w/o Lc)	0.5582 / 0.5058 (104)	0.5402 / 0.4934 (38)	0.4652 / 0.4649 (34)	0.2862 / 0.3653 (16)	0.4831 / 0.4679 (192)
	(h3)	CoarseNet (w/o Lr)	0.5698 / 0.5149 (107)	0.5630 / 0.5077 (41)	0.4976 / 0.4826 (41)	0.3260 / 0.3848 (23)	0.5062 / 0.4816 (212)
(d)	(d1)	CoarseNet	0.5701 / 0.5129 (107)	0.5623 / 0.5052 (41)	0.4949 / 0.4793 (46)	0.3331 / 0.3864 (24)	0.5071 / 0.4800 (218)

(e): DRMIME [70] and the AffineNet in DLIR [46] adopt image-based similarity metrics. DRMIME is an iterative optimization method for multi-modal registration based on the MI metric. Specifically, it computes approximate MI values via MIME (mutual information neural estimation) [72], and sets up input image pyramids for registration. In our experiments, we use five pyramid layers and 20% random sampling for registration, and keep the other settings unchanged. In order to remove most contours in CF and reduce initial scale differences between both modalities, we use a different image preprocessing step, i.e., a CF images is downsampled by 1/3 from its original resolution, and then its center 768 × 768 area is cropped for optimization.

DLIR is a coarse-to-fine cascade pipeline that connects an affine registration network and multiple deformable networks. The deformable networks are trained based on the outputs of previous networks. Negative NCC is used as the loss function for unsupervised training. We only implement the affine network instead of the full pipeline.

(f) and (g): We investigate the influences on the registration performance from different combinations of input image modalities and features. We set up four types of mono-modal inputs, i.e. IR images, B-Cosfire [62] vessel segmentation maps, averaged local phase maps (K = 4), and the vessel maps from our segmentation network (SegNet). Especially, we trained a MUNIT [71] model on the training set to translate all CF images into the IR modality. We do not use the opposite translation path (i.e., IR to CF) because of lower quality in the synthesized CF images. Besides, we use two feature detectors and descriptors, i.e., SIFT [23] and the pre-trained SuperPoint [31] network.

(h): We retrain the outlier rejection network in three additional settings, with each ignoring one loss term in Eq. (10). Groups (a), (b) and (d) are from Table II.

1). Coarse Alignment Evaluation:

In Table V, we compare our proposed network (d1) with three other methods, i.e., (b1) a feature based conventional registration pipeline [1], (e1) an iterative optimization method [70] based on MI, and (e2) an unsupervised affine network [46] based on NCC. As observed, our proposed network has a large advantages in Dice/Dice_s values over the compared methods. Moreover, the methods (e1) and (e2) which use image-based similarity metrics fail in most cases, i.e., only 1 and 0 successful alignment respectively, which has been implied in Fig. 2. This indicates that multi-modal retinal image registration is a very challenging task for intensity-based methods.

2). Choice of Input Modalities and Features:

When combined with SIFT features (Group (f) in Table V, the overall registration performance remains at lower levels, with B-Cosfire (f2) achieving the best performance. However, the SuperPoint network (Group (g)) boosts the registration performance over SIFT by a large margin, especially for the modalities of Phase maps (g3) and the vessel maps by our segmentation networks (g4). Finally, the overall optimal performance is achieved by (g4) SegNet + SuperPoint, which is also adopted in our coarse alignment step.

3). Loss Terms for Outlier Rejection Network:

In Table V Group (h), we investigate the influences of different loss terms in Eq. (10) on the outlier rejection performance. By comparing the various settings in (h) with (d1) which is trained with the complete loss function, it shows that the largest performance drop is triggered by removing the classification loss, while ignoring the other two terms has less impact on the alignment quality. This demonstrates the major contribution from the classification loss in training the outlier rejection network for our task.

In Table VI, we further investigate the value of the proposed Dice loss ${\mathcal{L}}_D$ in the cases of training with uncleaned ground-truths. We adjust each element in the ground-truth matrices M_gt by random percentages sampled in [−5%, 5%] or [−10%, 10%] to simulate polluted labels. Then we train the outlier rejection network on these labels under various settings. As observed, when trained with uncleaned labels, the settings using ${\mathcal{L}}_D$ show better alignment results than the ones without ${\mathcal{L}}_D$. Besides, increasing the weight λ_D for Dice loss can further improve the performance.

TABLE VI.

Coarse alignment performance of CoarseNet on the JRC dataset, trained with corrupted ground-truths: average Dice/Dice_s (#success).

Corruption Level of Ground-Truth	Training Settings	High & Medium Quality (203)			Low Quality (50)	Overall (253)
		No Disease (111)	1 Disease (42)	2 Diseases (50)
	Before registration	0.0734 / 0.2536	0.0754 / 0.2565	0.0732 / 0.2666	0.0749 / 0.2679	0.0740 / 0.2595
5% Corruption	w/o ${\mathcal{L}}_D$	0.5218 / 0.4856 (98)	0.5190 / 0.4826 (35)	0.4374 / 0.4544 (32)	0.2762 / 0.3550 (15)	0.4561 / 0.4531 (180)
	w/ ${\mathcal{L}}_D$, λD = 0.1	0.5345 / 0.4929 (102)	0.5268 / 0.4871 (37)	0.4353 / 0.4532 (34)	0.2864 / 0.3632 (15)	0.4646 / 0.4584 (188)
10% Corruption	w/o ${\mathcal{L}}_D$	0.4529 / 0.4471 (69)	0.4424 / 0.4401 (26)	0.3772 / 0.4207 (23)	0.2281 / 0.3373 (10)	0.3918 / 0.4190 (128)
	w/ ${\mathcal{L}}_D$, λD = 0.1	0.4690 / 0.4547 (78)	0.4308 / 0.4346 (24)	0.3730 / 0.4149 (25)	0.2290 / 0.3354 (7)	0.3963 / 0.4208 (134)
	w/ ${\mathcal{L}}_D$, λD = 1	0.4999 / 0.4742 (83)	0.4818 / 0.4634 (34)	0.4127 / 0.4393 (33)	0.2456 / 0.3453 (11)	0.4294 / 0.4400 (161)

E. Runtime Analysis

A disadvantage of our proposed network is that, the segmentation networks take more time and large GPU memory in training. This is mainly the result of the style loss computation, which compares style features between two complete segmentation maps, and thus requires the inputs of the complete retinal images. When training Seg-DeformNet on the JRC dataset, the network takes 7.9 GB in GPU memory and 9 days for training. In the other hand, the Phase-DeformNet takes 1.8 GB of GPU memory and 4 days for training, since it does not perform segmentation. In addition, the outlier rejection network takes 4.5 GB GPU memory and 7 hours for training.

There are 0.26M trainable parameters in each segmentation network (in addition to the pre-trained VGG-16 layers with 14.7M parameters). Besides, the networks for feature detection and description, outlier rejection, and deformable registration have 1.30M, 1.58M and 1.53M parameters respectively. Table VII shows the per-pair testing time of our network on the 768 × 768 images pairs from the JRC dataset. Our proposed two-step pipeline takes less than one second for prediction, which is much faster than the conventional methods.

TABLE VII.

Testing runtime of each method on the JRC dataset.

Method	Registration Step	Platform	Time/ Pair	GPU Memory
DRMIME (500 iters)	Coarse	PyTorch	49.5s	1.2 GB
Phase-HoG-RANSAC	Coarse	Matlab	1.51s
Phase+MIND	Fine	Matlab	41.9s
IRR-PWC	Two-Step	PyTorch	0.264s	1.3 GB
Ours	Two-Step	PyTorch	0.705s	7.8 GB
–Segmentation			0.525s
–Feature Detection & Description			0.141s
–Outlier Rejection			0.0277s
–Deformable Registration			0.0117

VI. Conclusion

In this paper, we set up a two-step coarse-to-fine CNN-based registration algorithm for multi-modal retinal images. In the coarse registration step, an accurate transformation matrix is estimated for an image pair through extracting vessels, finding features and eliminating outlier matchings with three consecutive networks. The fine alignment step further improves alignment quality by estimating a pixel-wise registration map using a deformable registration network. To train the deformable networks, we propose to transform multi-modal images into a common modality to fulfill the color consistency requirements in the unsupervised training scheme. we propose to train vessel segmentation networks via style loss, which can benefit both coarse and fine alignment steps. Experiment results show that our method achieve the state-of-the-art registration result in both quantitative and quality measurements.

In the future, we would like exploit the potential of our proposed method on aligning more challenging retinal images e.g., multi-phase images, images with large scale variations, ultra wide field images, etc. In addition, Generative Adversarial Networks (GAN) that disentangle image content and styles, e.g., [71], have shown feasibilities in aligning [73] multi-modal medical images. By incorporating GAN as modality transformers into our unsupervised joint learning scheme may further unveil the potentials of both methods.

Biography

Junkang Zhang received the B.E. degree in automation from Hohai University, Changzhou, China, in 2014 and the M.E. degree in pattern recognition and intelligent system from Southeast University, Nanjing, China, in 2017. He is currently a PhD student in electrical and computer engineering in University of California, San Diego, CA, USA. His research interests include image processing and computer vision.

Yiqian Wang is currently a Ph.D. student in the Electrical and Computer Engineering Department, University of California, San Diego. She received her B.S. degree in Electrical Engineering from Beijing Institute of Technology, Beijing, China, in 2018. Her research interests include medical image processing, signal processing, and machine learning.

Ji Dai [S’15] is currently a research scientist at Facebook. He received the B.S. degree in electrical engineering from Shanghai Jiao Tong University, Shanghai, China, in 2013, the M.S. degree in electrical engineering from Boston University, MA, USA, in 2015, and the Ph.D. degree in electrical engineering from UC San Diego, CA, USA. His research interests include computer vision, deep learning, and image processing.

Melina Cavichini is currently a Retina Fellow Research at Jacobs Retina Center in the Shilley Eye Institute, University of California, San Diego. She did her Vitreo Retinal Surgery Fellowship at Suel Abujamra Institute, São Paulo, Brazil in 2014, her Ophthalmology Residency at School of Medicine from ABC region, São Paulo, Brazil in 2011, and her MD degree is from University Gama Filho, Rio de Janeiro, Brazil in 2008. Her research interest includes retinal diseases, the use of artificial intelligence in retina and new technologies for retina.

Dirk-Uwe G. Bartsch is Associate Adjunct Professor and Co-director of the Jacobs Retina Center. Dr. Bartsch attended Technische Universitaet Darmstadt for his undergraduate degree and went on to complete his Ph.D. in bioengineering and post-doctoral fellowship at University of California, San Diego.

Dr. Bartsch’s research is focused in retinal imaging, scanning laser imaging -confocal/non-confocal, optical coherence tomography (OCT), indocyanine green and fluorescein angiography, and tomographic reconstruction of the posterior pole in patients with various retina diseases such as age-related macular degeneration, diabetes and HIV-related complications.

William R. Freeman is Distinguished Professor of Ophthalmology, Director of the UCSD Jacobs Retina Center and Vice Chair of the UCSD Department of Ophthalmology. He is a full time Retina Surgeon and also a researcher who has held NIH grants for nearly 30 years. He works closely with imaging groups in the department of Ophthalmology as well as in the UCSD School of Engineering. He has over 600 peer reviewed publications.

Truong Q. Nguyen [F’05] is currently a Professor at the ECE Dept., UC San Diego. His current research interests are 3D video processing and communications and their efficient implementation. He is the coauthor (with Prof. Gilbert Strang) of a popular textbook, Wavelets & Filter Banks, Wellesley-Cambridge Press, 1997, and the author of several matlab-based toolboxes on image compression, electrocardiogram compression and filter bank design. He has over 400 publications.

Prof. Nguyen received the IEEE Transaction in Signal Processing Paper Award (Image and Multidimensional Processing area) for the paper he co-wrote with Prof. P. P. Vaidyanathan on linear-phase perfect-reconstruction filter banks (1992). He received the NSF Career Award in 1995 and is currently the Series Editor (Digital Signal Processing) for Academic Press. He served as Associate Editor for the IEEE Transaction on Signal Processing 1994-96, for the Signal Processing Letters 2001-2003, for the IEEE Transaction on Circuits & Systems from 1996-97, 2001-2004, and for the IEEE Transaction on Image Processing from 2004-2005.

Cheolhong An is an assistant adjunct professor at the Electrical and Computer Engineering, University of California, San Diego. Earlier, he worked at Samsung Electronics, Korea and Qualcomm, USA. He received the B.S. and M.S. degrees in electrical engineering from Pusan National University, Busan, Korea, in 1996 and 1998, respectively, and Ph.D. in Electrical and Computer Engineering in 2008. His current research is focused on the medical image processing and the real-time bio image processing. His research interests are in 2D and 3D image processing with machine learning and sensor technology.