Abstract
Recent studies have demonstrated that the mathematical model used for analyzing and interpreting fMRI data in gray matter (GM) is inappropriate for detecting or describing blood-oxygenation-level-dependent (BOLD) signals in white matter (WM). In particular the hemodynamic response function (HRF) which serves as the regressor in general linear models is different in WM compared to GM. We recently reported measurements of the frequency contents of resting-state signal time courses in WM that showed distinct power spectra which depended on loca structural-vascular-functional associations. In addition, multiple studies of GM have revealed how functional connectivity between regions, as measured by the correlation between BOLD time series, varies dynamically over time. We therefore investigated whether and how BOLD signals from WM in a resting state varied over time We measured voxel-wise spectrograms, which reflect the time-varying spectral patterns of WM time courses. The results suggest that the spectral patterns are non-stationary but could be categorized into five modes that recurred over time. These modes showed distinct spatial distributions of their occurrences and durations, and the distributions were highly consistent across individuals. In addition, one of the modes exhibited a strong coupling of its occurrence between GM and WM across individuals, and two communities of WM voxels were identified according to the hierarchical structures of transitions among modes. Moreover, these modes are coupled to the shape of instantaneous HRFs. Our findings extend previous studies and reveal the non-stationary nature of spectral patterns of BOLD signals over time, providing a spatial-temporal-frequency characterization of resting-state signals in WM.
Keywords: Resting state, fMRI, White matter, Dynamic, Power spectra, Hemodynamic response function
1. Introduction
Functional magnetic resonance imaging (fMRI) has been widely exploited for mapping brain activities by measuring changes in blood-oxygenation-level-dependent (BOLD) signals that are coupled with energy consumption by neurons (Ogawa et al., 1990). Mathematical models have been developed to identify image voxels that exhibit increased signal amplitudes triggered by a task performed by a participant during a scan, thereby mapping the brain activation associated with the task (Ogawa et al., 1992). In addition, BOLD signal fluctuations measured during a resting state reflect spontaneous variations in neural activities and reveal intrinsic functional networks characterized according to the degree of temporal synchronization among brain regions (Biswal, 2012). While reports of BOLD signals in gray matter (GM) have dominated the fMRI literature, there have been far fewer descriptions of BOLD effects in white matter (WM), partly because they are weaker due to the smaller blood flow/volume compared to GM (Helenius et al., 2003). However, a growing body of evidence suggests that BOLD signals can be reliably detected in WM and reflect neural activities (Courtemanche et al., 2018; D’Arcy et al., 2006; Ding et al., 2018; Fraser et al., 2012; Gawryluk et al., 2014; Gore et al., 2019; Li et al., 2020a, 2020b; Mishra et al., 2020; Peer et al., 2017; Schilling et al., 2019; Wu et al., 2019), and such signals are altered significantly in patients with neurological or psychiatric disorders (Gao et al., 2020; Huang et al., 2020; (Lin et al., 2020); (Lin et al., 2020). Recent studies have demonstrated how the temporal profiles of WM BOLD responses to stimuli are different from GM, with reduced magnitudes and delayed peaks, reflecting differences in hemodynamic conditions between GM and WM (Fraser et al., 2012; Li et al., 2019; Tong et al., 2017, 2013; Wang et al., 2020; Yarkoni et al., 2009). These studies highlight the importance of understanding the characteristics of WM timecourses so that they can be incorporated into appropriate detection models to increase their sensitivity.
We recently showed that the power spectra of WM time courses differ in shape from those in GM in the low-frequency (0.01–0.08 Hz) band, and that they vary as a function of location and depend on the local neurovascular and anatomical configurations of WM (Li et al., 2021). Moreover, the spectral patterns at different locations predict their engagements in functional integration as well as specific human behaviors. These findings suggest the frequency contents of WM signals are hetero-geneous spatially. However, potential additional temporal variations in BOLD signal characteristics in WM have not been investigated, reflecting an assumption that BOLD signals are statistically stationary. Here we examine this assumption and demonstrate that BOLD power spectra vary during a scan and reflect an average of multiple sub-patterns that recur over time.
Our data suggest that the time-averaged spectrum (such as reported in our previous study) is, in fact, the combination of five sub-patterns, which we call spectral modes (or frequency modes (Yaesoubi et al., 2017)), that recur over time. They include four unimodal modes (each of which exhibits single spectral peaks at different frequencies, modes 1–4) and one uniform mode (with power distributed uniformly across the frequency band of interest at a relatively low level, mode 5). These modes show distinct spatial distributions of their occurrences and durations across WM voxels, and these distributions were highly consistent across individuals. One of the modes (mode 1) exhibited a strong coupling of its occurrence between GM and WM across individuals. More interestingly, two communities of WM voxels were identified according to the hierarchical structures of transitions among modes. Specifically, in community 1, the probability of transitions among modes 1, 2, and 5 are significantly higher than in community 2. By contrast, in community 2, the probability of transitions among modes 3, 4, and 5 are significantly higher than in community 1. Moreover, the instantaneous spectral patterns are associated with distinct HRFs that also vary with time. Our findings extend our previous study by looking at dynamic changes in BOLD spectra and reveal the non-stationary nature of spectral patterns as well as their physiological coupling over time, thereby providing a spatial-temporal-frequency characterization of resting-state BOLD signals in WM.
2. Methods
2.1. Ethics statement
The human studies involved in this research were approved by the Washington University Institutional Review Board. All participants provided written informed consent to participate in this study.
2.2. HCP data
Two hundred individuals were randomly selected from the HCP healthy young adult database (88 male and 112 female, whose ages ranged between 22 and 35 years) (Van Essen et al., 2012). The imaging protocols are described in detail in a previous report (Van Essen et al., 2012). Briefly, all images were acquired using a 3T Siemens Skyra scanner (Siemens AG, Erlanger, Germany). Two sessions of resting-state images were acquired using multiband gradient-echo echo-planar imaging (EPI). Each session was comprised of two runs (left- to-right and right-to-left phase encoding) of 14 min and 33 s each, repetition time (TR) = 720 ms, echo time (TE) = 33.1 ms, voxel size = 2 mm isotropic, number of volumes = 1200. Physiological data, including respiratory and cardiac fluctuations, were recorded throughout fMRI scanning. As structural references, T1 images were acquired using a 3D magnetization-prepared rapid acquisition with gradient echo (MPRAGE), TR = 2400 ms, TE = 2.14 ms, voxel size = 0.7 mm isotropic.
2.3. Preprocessing
As detailed elsewhere, the preprocessed images that were drawn from the HCP repository went through the minimal preprocessing pipelines (MPP) (Glasser et al., 2013). Briefly, T1 images were nonlin-early registered to MNI space using FNIRT (Jenkinson et al., 2012) and went through a Freesurfer pipeline producing volume/surface parcellations as well as morphometric measurements (Dale et al., 1999). For fMRI, the pipeline consisted of head motion correction, susceptibility-derived distortion correction using reversed-phase encoding directions, and nonlinear registration to MNI space. We carried out additional processing including regression of nuisance variables, including 12 head movement parameters (three translations, three rotations, along with their derivatives), and respiratory and cardiac fluctuations that were modeled by the RETROICOR method (Glover et al., 2000), followed by a correction for linear trends and temporal filtering with a band-pass filter (0.01–0.08 Hz). A group-wise WM mask was reconstructed by averaging the WM parcellations (derived from Freesurfer) across all subjects and thresholding at 0.95, which was used for restricting the calculations within WM. In a similar manner, a GM mask was also reconstructed using a lower threshold due to higher individual variabilities therein. 0.65 was specifically selected as an optimal threshold by first setting a threshold of 0.5 which then was increased gradually in steps of 0.01 until there were no overlapping voxels between WM and GM. Finally, to increase the signal-to-noise ratio, and to reduce the computational load, we downsampled the preprocessed images from 2 mm resolution to 3 mm.
2.4. Calculation of the spectral modes
The workflow for calculating the spectral modes is shown in Fig. 1. First, a spectrogram was calculated for the BOLD signal of each voxel using a short-time Fourier transform (STFT) (Sejdić et al., 2009) by first splitting the entire time course into a set of partially overlapped windows and calculating the transform for each window. Then the power spectrum of each window was calculated, showing the amplitude of BOLD fluctuations at different frequencies as they varied with time. In practice, we selected a window length of 100.4 s (140 TR) to provide a frequency resolution down to 0.01 Hz, which was considered the low cutoff of the baseline brain activity band (Yu-Feng et al., 2007) and has been suggested in several previous works (Leonardi and Van De Ville, 2015; Pedersen et al., 2018; Vergara et al., 2019). To provide sufficient temporal resolution while avoiding excessive computation load, we selected a step length of 2.88 s (4 TR). This resulted in 266 windows that overlapped by 97.52 s (136 TR) with each neighbor, evenly spanning the duration of the BOLD time course. By obtaining the spectrograms across voxels and subjects, we obtained a large number of observations (more than 490 million) of the spectral patterns across time. These observations were then grouped into a set of clusters using the K-means method. The modes stand for the centroids of the clusters. Then each window-wise spectral pattern can be assigned to a specific mode according to its Euclidean distance to the centroids. The elbow criterion (Thorndike, 1953) was used to determine the optimal value of the number of clusters. Specifically, we successively increased the number of clusters from 1 to 20 and plotted the curve of the sum of the observation-to-centroid distances against the number of clusters. The optimal value of the number of clusters was determined by the location of the elbow on the curve. In practice, to find the elbow point, we used a function that operates by walking along the curve one bisection point at a time and fitting two lines, one to all the points to the left of the bisection point and one to all the points to the right of the bisection point. The elbow is judged to be at a bisection point which minimizes the sum of errors for the two fits (Details can be found at https://www.mathworks.com/matlabcentral/fileexchange/35094-knee-point). To further certify the reliability of the number of clusters, we used a bootstrap method to randomly sample a small portion (1000 to 10,000) of the spectral features (from 490 million features in total in our current study) and applied the k-means clustering and elbow method to them. This process was repeated 1000 times and the histogram of the cluster number was calculated.
Fig. 1.
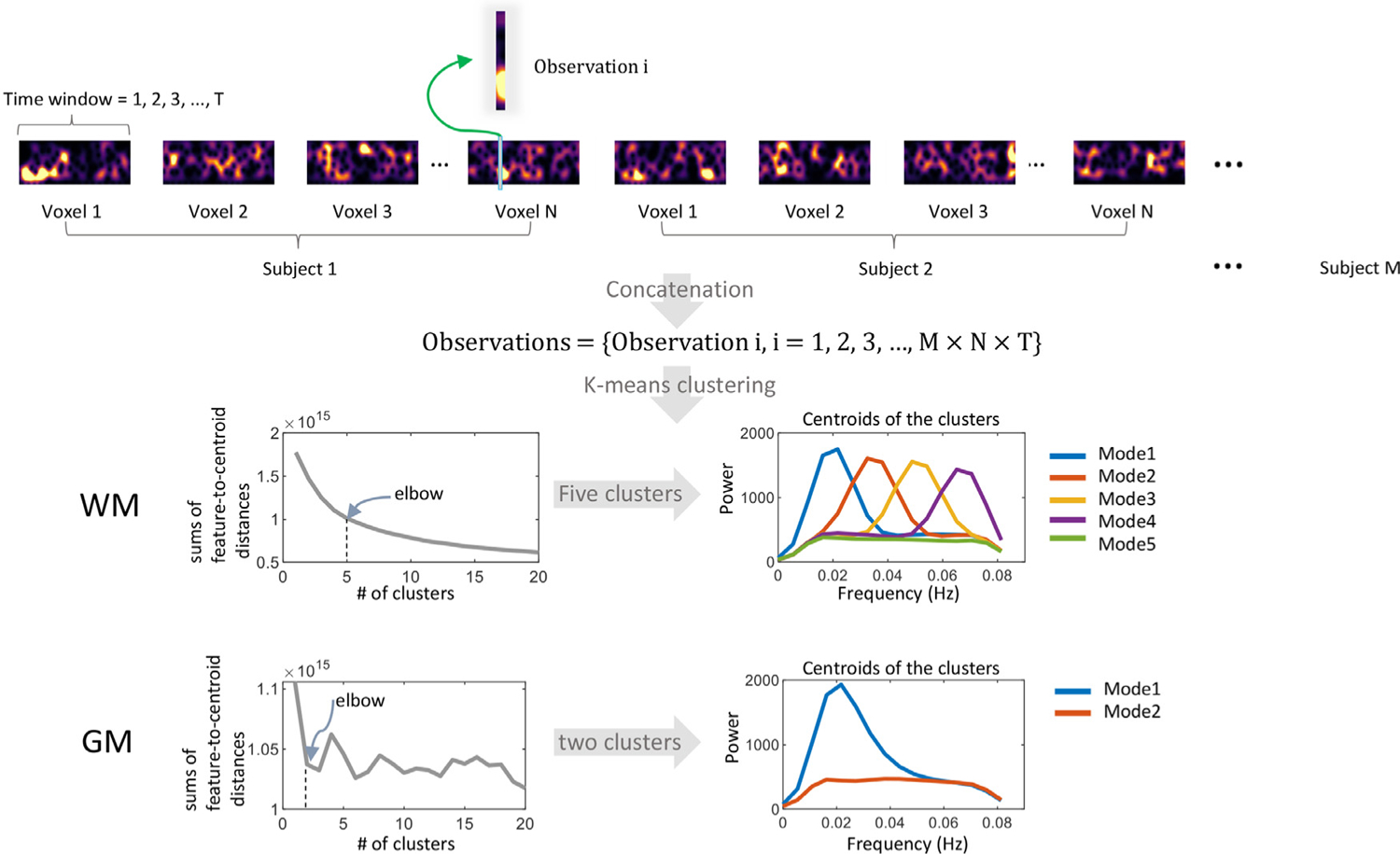
The workflow of calculating the spectral modes. A set of observations were generated by concatenating the spectrogram over voxels and subjects. Each observation is a vector, recording the spectra pattern of the signal corresponding to a specific time window. Observations were grouped into five clusters for WM and two clusters for GM using the K-means method. The elbow criterion was used to determine the optimal value of the # of clusters.
Even though we expected that the result would change (actually be less accurate) if we shorten the window length (as it can not completely cover the frequency of interest 0.01–0.08 Hz) and increased the step size, extra tests were performed using the window length of 100.4 s, 86.4 s (140 TR and 120 TR) and step sizes of 2.88 s, 17.28 s, and 31.68 s (4 TR, 24 TR, 44 TR) based on 10 subjects randomly selected from the 200 data we used in our current work. Furthermore, we tested the step size of 0.72 s (1 TR) which is the highest temporal resolution the HCP data can provide, accompanied by the window length of 100.4 s which fully covered the frequency band we studied. We applied K-means to these data separately and used the elbow criterion to determine the optimal number of modes.
2.5. Calculation and statistics of the occurrence, duration, and transitions of the modes
The original BOLD time course of each voxel can be represented by transitions between the five modes over time, including their frequency of occurrence and durations. The occurrences can be obtained by counting the numbers of each mode over the time course. The duration describes how long any mode persists before the signal switches to another mode. As each mode occurs multiple times during scanning, the duration is actually a mean time over multiple occurrences. A transition simply means a specific switch of modes from one to another. The total number of transitions is how many times we identify mode i at time point t and mode j at time t-1 where i ≠ j.
The occurrences, durations, and transition number can be measured for every voxel, resulting in maps of their distributions for each subject. Before group-level statistics, we performed Z transformations (i.e., we subtracted the global mean value and then divided by the standard deviation) to each map for each subject. The Z maps were spatially smoothed within the WM and GM masks separately with a 4 mm FWHM Gaussian kernel. Then a one-sample t-test was used to identify clusters of voxels that exhibited significantly (group-level) higher values compared to zero (Wang et al., 2011), the mean measurement across all voxels on the Z map.
2.6. Calculation of coupling between modes in GM and WM
In the case of coupling between mode A of GM and mode B of WM, for subject i, we first extract the gi, the mean occurrence of mode A over GM voxels that exhibit a significantly high occurrence of mode A. Repeating this process for all subjects, we obtain a vector {gi i = 1,2,3,…,200}. Then for a voxel in WM x, we extract the occurrence of mode B, wxi. Repeating this process for all subjects, we obtained a vector {wxi i = 1,2,3,…,200}. Then we performed a Pearson’s correlation between {gi} and {wxi} for every voxel in WM, producing a distribution of r values across all WM voxels {x}. The higher r of a WM voxel indicates that a higher occurrence of mode A in GM predicts a higher occurrence of mode B in this voxel in the same subject.
2.7. Estimation of window-wise HRFs
Window-wise HRFs were estimated from resting-state timecourses b(t) of each time window in each subject using a blind deconvolution approach (Wu et al., 2015, 2013). The approach requires no prior hypothesis about the HRF and is based on the notion that relatively large-amplitude BOLD signal peaks represent the occurrence of separable, major, spontaneous events (Liu and Duyn, 2013; Tagliazucchi et al., 2012). In our study, such events were detected as peaks beyond a specified threshold (here, greater than 1.5 standard deviations over the mean). For each event, a general linear model was fitted using a combination of sn(t), the onset of the event, and h(t), which represents a linear combination of two gamma functions as well as its temporal derivative. Here n characterizes the delay time from the onset to the impulse function s(t), where s(t) = 1 only if t corresponds to the peaks (events) we detected. The double gamma functions together with temporal derivative are capable of modeling the general HRF with an initial dip (Friston et al., 1998, 1995). By searching for an n (n∈ 0–12 s) and minimizing the covariance of the residuals cov[b(t) – conv(sn(t), h(t))], the value of n and several parameters that model h(t) can be estimated, and therefore the HRF hn (t) can be obtained.
2.8. Data/code availability statement
MRI images can be downloaded from HCP website: https://www.humanconnectome.org/
The tool we used for analyzing the data can be downloaded from:
PhysIO Toolbox: https://www.nitrc.org/projects/physio/
Circos table viewer: http://mkweb.bcgsc.ca/tableviewer/visualize/
3. Results
3.1. The spectral modes
As illustrated in Fig. 1, five spectral modes were derived using k-means clustering of windowed spectral patterns (observations) across time windows, WM voxels, and subjects. Modes 1–4, which we called unimodal modes, exhibit single sharp peaks at different frequencies, while mode 5, is a uniform mode, with spectral power relatively constant and low across the frequency band of interest. The same workflow yielded two modes in GM, including one unimodal mode whose pattern is similar to mode 1 in WM and one uniform mode, which approximates to mode 5 in WM. Fig. S1 shows examples of calculated spectrograms from selected WM voxels. We observed that the static power spectral peaks (Fig. S1 middle column) we observed in our previous study (Li et al., 2021) are primarily determined by widely separated bursts of higher powers, as shown in Fig. S1 left column.
The clustering results with respect to different window lengths and step sizes are shown in Fig. S2. We observed that even with 5% (10 out of 200 subjects) of the data we used in our current manuscript, we successfully reproduce the five modes in WM. More surprisingly, we found that even when we change the window length and step size (within a limited range), the elbow criterion still indicates 5 modes that show consistent distributions with our existing modes. The reproducibility of the number of clusters is shown in Fig. S3. We observed that, after 1000 repetitions of sampling and clustering, the elbow indicates that 5 is the optimal number for WM in 86.4% of the samples.
3.2. Occurrence and duration of the modes
The distribution of voxels that exhibit significantly high occurrence (p<0.05, FWE corrected) of each mode is shown in 3D in Fig. 2. Fig. S4 shows details of such distributions in axial slices, where the inferior frontal WM voxels exhibit significantly higher occurrences of modes 1 and 5 than other voxels. Meanwhile, the paraventricular and temporal voxels exhibit significantly higher occurrences of modes 3 and 4 than other voxels. However, the occurrences of mode 2 show little group effects, and so are not shown in Fig. 2. Note that the occurrence of mode 2 is not significantly lower than other modes as shown in Fig. 2. In each panel of Fig. 2, the boxplots represent the group-level distributions of the number of occurrences and the durations of a mode before a transition to another, measured from the area visualized in the brain maps shown to their left. We observed that mode 5 occurs most often and persists longest across all areas shown in Fig. 2. In addition, in general, mode 1 occurs more often and persists longer than modes 3 and 4 in the inferior frontal area, whereas it arises less often and lasts for shorter times in paraventricular and temporal areas, where modes 3 and 4 occur more often. Overall, the number of occurrences and durations is highly consistent across subjects, reflected by the tight interquartile range (distance between the upper bound and lower bound) of the boxes.
Fig. 2.

Voxels that exhibit significantly high occurrence of each mode across all subjects. In each of the four panels, the figure on the left visualizes the voxels that exhibit significantly higher occurrence of a certain mode than the rest of the WM voxels across all subjects (one-sample t-test, p<0.05 FWE corrected). The figure on the upper right of each panel shows the number of occurrences of the five modes within the area shown on the left figure. The figure on the lower right of each panel shows the average duration of the five modes within the area shown on the left figure. Each box visualizes the distribution of the measurements from all subjects. Note that the data for mode 2 is not shown because only a few voxels were found showing the significantly higher occurrence of mode 2 comparing to the rest of the WM voxels across subjects.
The distributions of voxels that exhibit significantly higher occurrences of the two modes in GM are shown in Fig. 3. Cortical areas that are closer to the surface of the brain exhibited significantly higher occurrences of mode 1 than the rest of GM. Meanwhile, the voxels at insular, temporal areas and cingulate gyrus exhibit significantly higher occurrences of mode 2 than other GM voxels.
Fig. 3.
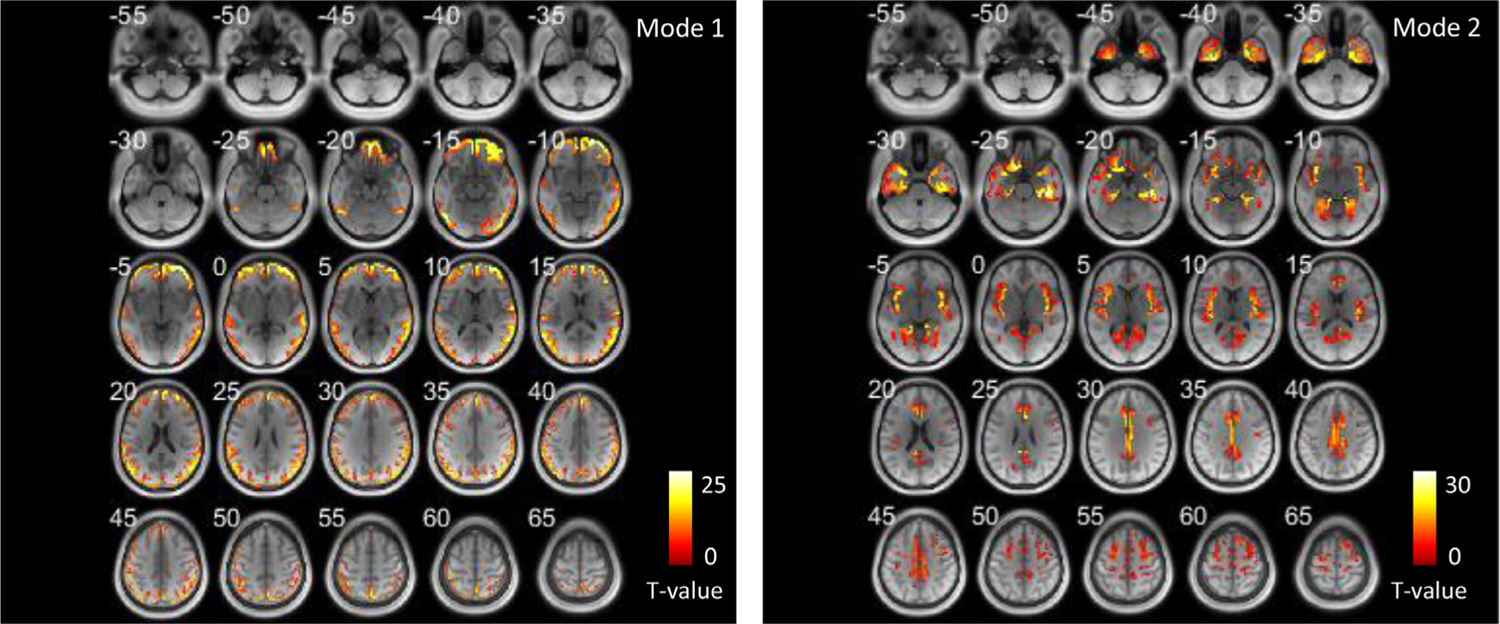
Areas that exhibit significantly high occurrence of the two modes in GM across all subjects shown in axial slices. (one-sample t-test, p < 0.05 FWE corrected).
3.3. Coupling of occurrence of modes between GM and WM
Fig. 4 maps the coupling of the patterns of occurrences of specific modes that are prevalent in specific GM and WM voxels. The intensity of a WM voxel in the left figure indicates the Pearson’s correlation coefficient (r) between the occurrence of mode 1 at the voxel and the average occurrence of mode 1 in the GM region shown in Fig. 3 (left) across subjects. It can be observed that a high occurrence of mode 1 in selected surface cortical areas reliably predicts high occurrences of mode 1 in extensive WM voxels in the same subject, and vice versa. The corresponding data that exceed a higher threshold (r>0.45) are shown in Fig. S5. For comparison, the coupling of occurrences of modes 2,3,4,5 in WM voxels to GM (mode 1) across subjects is shown in Fig. S6, where we observed that such high occurrence of mode 1 in GM also predicts low occurrences of mode 3 and 4 in similar WM area in the same subject, suggesting a suppressive relationship between these modes in WM.
Fig. 4.
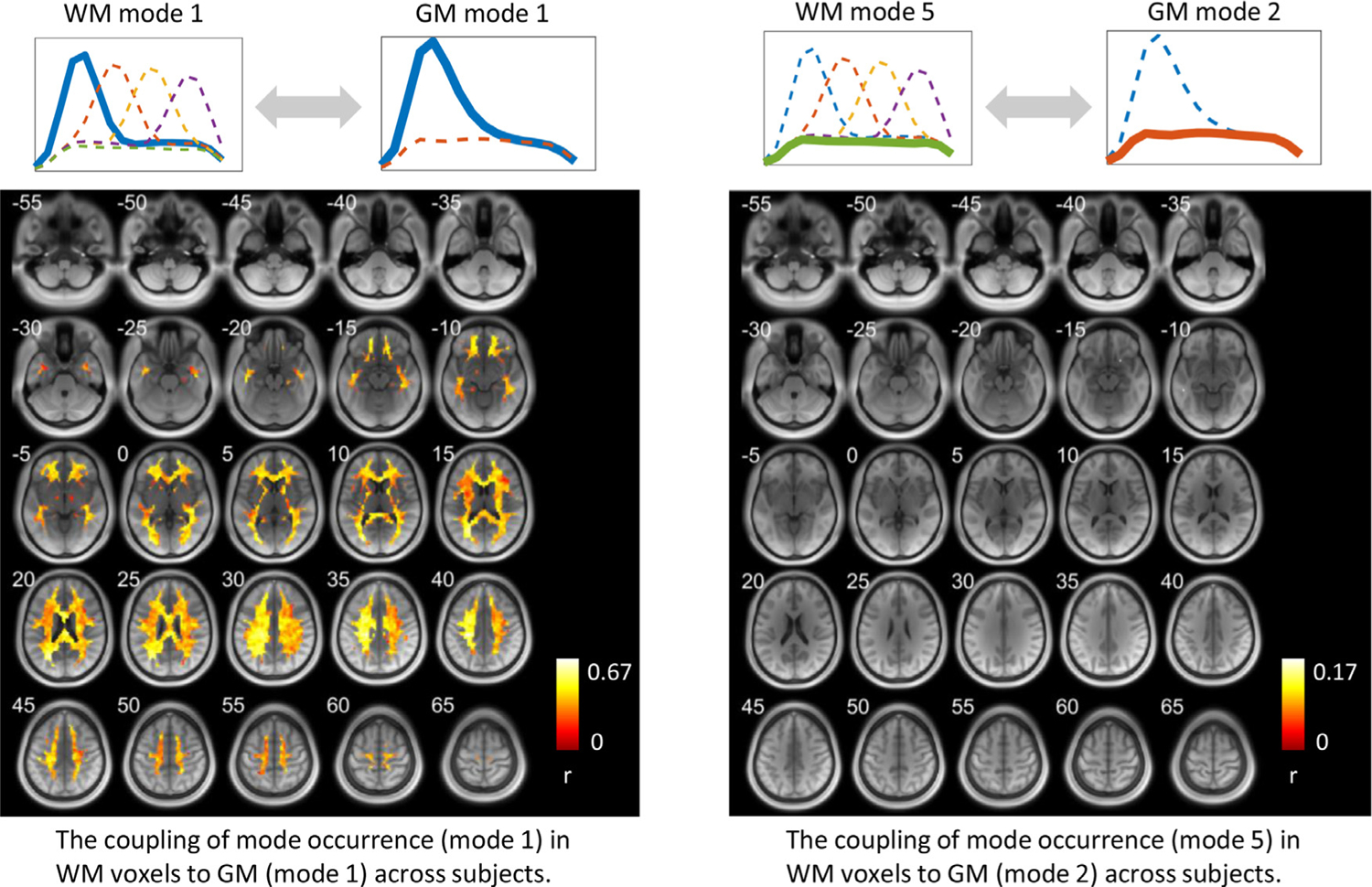
The coupling of mode occurrence in WM voxels to GM across subjects. The intensity of a voxel in the left figure indicates the Pearson’s correlation coefficient (r) between the occurrence of mode 1 at this WM voxel and the occurrence of mode 1 in the GM area shown in Fig. 3 (left) across subjects. The intensity of a voxel in the right figure indicates the Pearson’s correlation coefficient (r) between the occurrence of mode 5 at this WM voxel and the occurrence of mode 1 in the GM area shown in Fig. 3 (right) across subjects. Note that only significant (p<0.05) correlations are shown here.
The intensity of a voxel in the right figure of Fig. 4 indicates the Pearson’s correlation coefficient (r) between the occurrence of mode 5 at the voxel and the average occurrence of mode 2 in the GM region shown in Fig. 3 (right) across subjects. Only a few WM voxels show significant couplings of the occurrence of mode 5 to that of mode 2 in the GM region.
3.4. Transitions among the modes
Fig. 5 maps the number of transitions (shown as T values) among the five modes for every WM voxel. T values that are beyond a significant level (p < 0.05, FWE corrected) are visualized in Fig. S7. It can be observed that the inferior frontal area exhibits a significantly low number of transitions compared to the rest of WM.
Fig. 5.
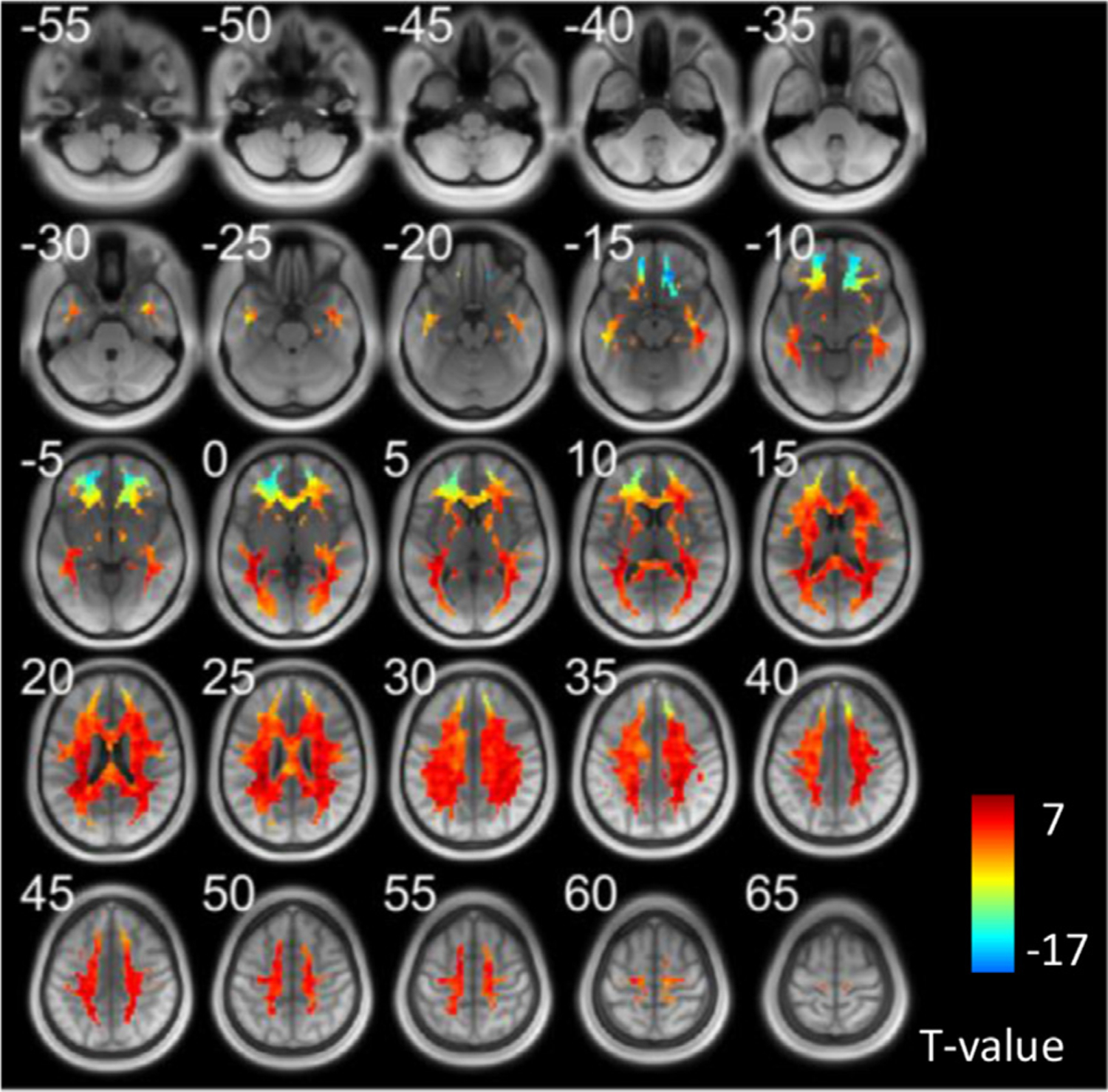
The number of transitions at each WM voxel across all subjects. T value was generated by a one-sample t-test across all subjects. Voxels that exabit significantly high/low values can be found in supplementary file.
Fig. 6 shows the voxels that exhibit a significantly higher transition from mode i to mode j than the rest of WM voxels across subjects (one-sample t-test, p < 0.05, FWE corrected). Two communities of voxels could be clearly identified and are coded by different colors. The lower left panel shows the voxels that exhibit significantly higher transitions among modes 1, 2, and 5 (community 1), along with its transition probability among the five modes shown on the right. The lower right panel shows the voxels that exhibit significantly higher transitions among modes 3, 4, and 5 (community 2), along with its transition probability among the five modes shown on the right. Note that the map with respect to each community was produced by a one-sample t-test (p<0.05, FWE corrected) on the transition maps among modes 1, 2, 5 or among modes 3, 4, 5 across all subjects. We observed that the patterns of transition probabilities are, in general, consistent between the two communities. However, a careful inspection reveals that community 1 exhibits a higher transition probability among modes 1, 2, 5, whereas a lower transition probability among modes 3, 4, 5 than community 2. Note that we have hidden the self transitions, which occupy more than 90% of the entire transitions.
Fig. 6.

The transitions among modes. The upper figure visualizes the voxels that exhibit significantly higher transitions from mode i to mode j than the rest of WM voxels across subjects (one-sample t-test, p<0.05, FWE corrected). Two communities were identified and coded by different colors. The lower left panel shows the voxels that exhibit significantly higher transitions among modes 1, 2 and 5 (community 1), along with its transition probability among five modes shown on the right. The lower right panel shows the voxels that exhibit significantly higher transitions among modes 3, 4 and 5 (community 2), along with its transition probability among the five modes shown on the right.
3.5. The relationship between instantaneous HRFs and spectral patterns
As shown in Fig. 7, the windowed HRFs vary with time as well, and their shapes are strongly coupled to the instantaneous spectral patterns, i.e., an HRF with decreased initial dip and increased time to peak is associated with an increased high-frequency component identified in power spectra. The five spectra modes correspond to distinct HRFs. The shifting peaks of modes 1–4 (shown in Fig. 1) reflect the varying magnitudes of initial dips as well as time to peaks in HRFs. As mode 5 exhibits a spectral power relatively constant across the frequency band of interest, the initial dip and time to peak of its associated HRF appear to be the average of those of modes 1–4.
Fig. 7.
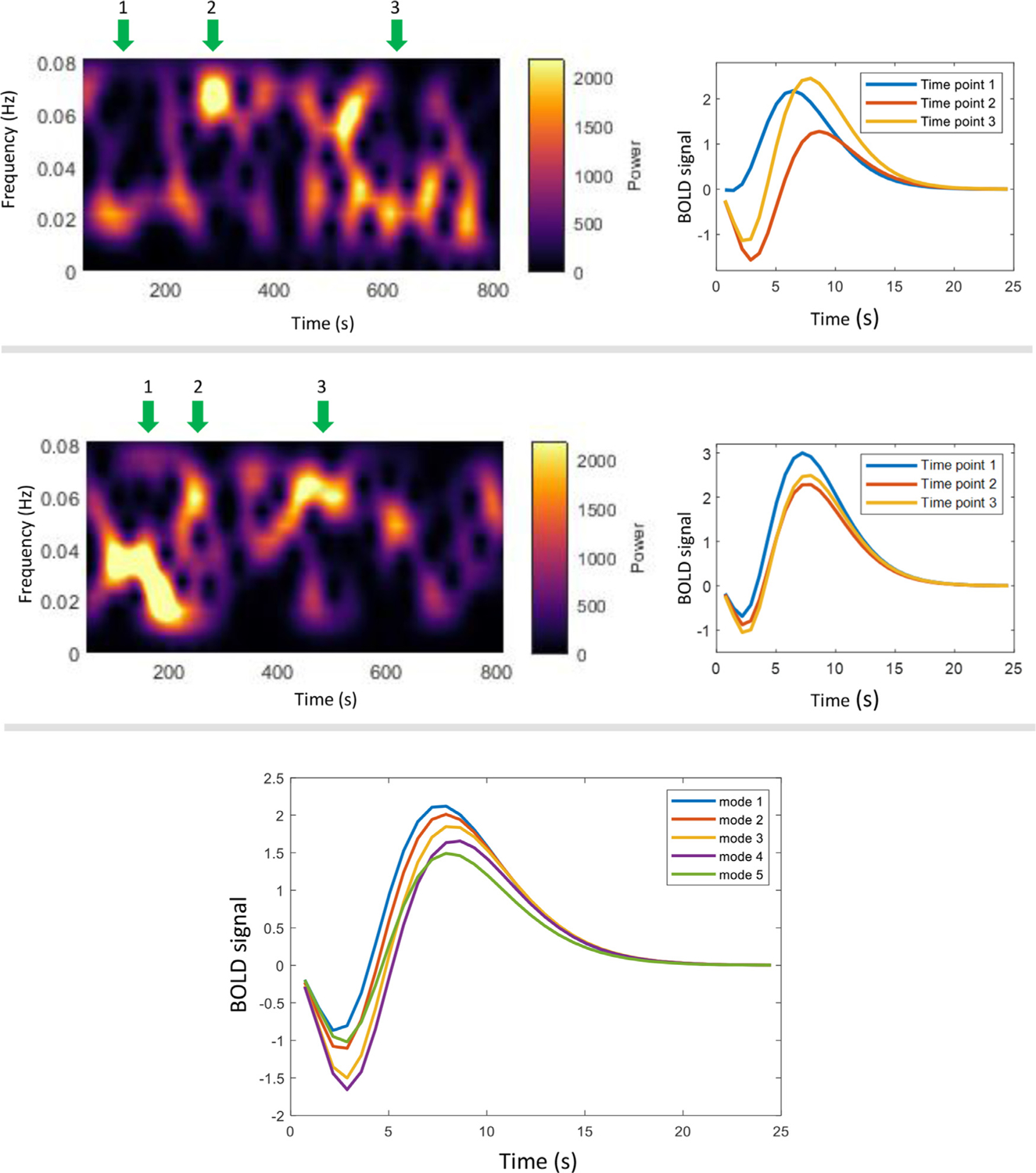
Relationship between instantaneous HRFs and spectral patterns. The upper and middle panel shows the HRFs (right) calculated in selected time windows where the spectral patterns (left) show peaks at different frequencies. Note that these two panels correspond to two voxels randomly selected from one subject. The lower panel shows the HRF corresponding to the five WM modes. Each line is the average HRF estimated from all time windows that have been assigned to a mode across time and voxels of the selected subject.
4. Discussions
This study evaluated spectrograms of BOLD signals in WM in a resting state, which reflect the temporal variations of power spectral patterns within BOLD time courses. Applying k-means clustering to a set of measurements that consisted of such patterns at different time points and from different voxels and subjects, we obtained five dominant modes, equivalent to the centroids of the clusters. Each pattern was then assigned to a mode according to its distance to the centroids. Consequently, the original time course could be represented by the five modes as they varied over time. Several parameters, including occurrence, duration, and the number of transitions, were quantified and showed strong consistency across subjects. Besides that, one of the modes showed a strong coupling of its occurrence between GM and WM across subjects. We also identified two communities of voxels, where community 1 showed a higher probability of transitions among modes 1, 2, and 5 but a lower probability of transitions among modes 3, 4, and 5 than in community 2. Last, we observed that the five modes were associated with distinct HRFs.
Time-dependent frequency analysis is a well-established method for evaluating MEG and EEG data, and provides characteristic features of signal spectrograms which are associated with specific neurological conditions (Bertrand and Tallon-Baudry, 2000; Pantazis et al., 2005). However, the frequency range of BOLD signals is much more limited so that spectrograms have rarely been applied in fMRI analyses. Recent studies have shown that the time-frequency pattern in GM is capable of describing the variabilities of functional connectivity in resting-state fMRI (Chang and Glover, 2010) and could be categorized as a set of recurring modes (Yaesoubi et al., 2017). These observations, along with our previous findings regarding the distinct power spectra identified in WM (Li et al., 2021), led us to investigate the spatial-temporal-frequency characterization of resting-state BOLD signals. The results inform us that the single/dual-peak power spectra calculated from the entire BOLD signal in our previous work (Li et al., 2021) are actually the unweighted combinations of a series of time-varying spectral patterns. These patterns can be clustered into five modes, which occurred significantly more often at specific locations and whose distributions are consistent across subjects. However, the occurrences of mode 2 show virtually no group effects. Our further examinations of individual mode distribution maps found that the spatial distributions of mode 2 are widely dispersed with no clear tendency toward particular anatomical locations. Given that mode 2 has a characteristic power spectrum centered ~0.035 Hz, it is unlikely that the lack of spatial localization of this mode is caused by random noise; a more plausible explanation is that their signal fluctuations might be driven by larger-scale neural activities (e.g., (Turchi et al., 2018)), on which more localized signal fluctuations from other modes are superimposed. This finding partially explains the dual-peak patterns in power spectra (group level) that we observed in our previous study. That is, the lack of group consistency of the spatial distribution of the occurrence of mode 2 causes the trough (around 0.035 Hz) between the two peaks at a group level (Li et al., 2021). Moreover, three “high-frequency” modes that could be identified in WM were missing from GM. This is consistent with the single-peak pattern of power spectra that we observed in GM in our previous study (Li et al., 2021). In the current study, in GM, we identified only one unimodal mode, which is very similar to WM mode 1 in shape and occurs significantly often in cortical areas that are more close to the surface. Our data also suggest that the occurrence of this mode in the cortex is positively associated with the occurrence of WM mode 1 across the entire WM. This finding suggests that the BOLD fluctuations of a specific band (centered at ≈ 0.02 Hz) reflect a global process.
The uniform mode, mode 5, exhibits substantially higher occurrence and duration than other modes, suggesting that BOLD fluctuations are maintained at a low power level across frequencies that uniformly vary between 0.01–0.08 Hz most of the time, accompanied by brief bursts (unimodal mode1 2,3,4) with higher power at more concentrated frequency ranges. A similar finding has been reported in GM in a previous study that investigated the dynamic functional connectivities among cortical areas (Liu and Duyn, 2013), suggesting that spontaneous brain activity may be dominated by brief periods of activity, possibly originating from a neuronal avalanche phenomenon. However, it must also be remembered that all BOLD phenomena reflect hemodynamic changes that are only indirect indications of neural activity. The progression of modes 1–2–3–4 corresponds to a trend of increasing negative dip and slower times to peak of the corresponding HRFs. These may reflect variations in local vasculature and metabolic demand and transitions between them may be influenced by variations in flow and oxygenation. For unimodal modes, modes 1 and 2 occur significantly often in the inferior frontal WM, whereas modes 3 and 4 occur significantly often in the paraventricular and temporal areas. Moreover, these occurrences and durations are consistent across subjects, reflecting a highly reproducible pattern of WM BOLD signal, which has not previously been identified from the original time courses. The spatial distribution of the voxels where modes 3 and 4 frequently occur is similar to the areas with higher fiber complexity identified in our previous work (Li et al., 2021). Such crossing fiber bundles connect to multiple GM areas. A possible explanation is that these bundles transduce independent neural events from multiple GM regions to which they are connected and which occur at the same time or within a short time window, which in turn evokes a BOLD response with a lower initial dip and increased time to peak in the HRF.
We identified two communities of voxels that showed distinct patterns of inter-mode transitions. Transitions between the uniform mode and unimodal modes were substantially more frequent than the transitions among unimodal modes. Particularly, direct transitions between modes 1, 2 and modes 3, 4 were rarely observed. These findings support the notion that mode 5 is a “baseline” mode from which a unimodal mode is likely to first transition before switching to other unimodal modes. Our finding also suggests that such “baseline” mode dominates the inferior frontal area, where, therefore, the time courses exhibited a significantly lower number of transitions.
A possible concern is that the observed modes in WM originate from physiological noise sources such as cardiac and respiratory variation which affect WM more due to the lower BOLD signals and different neurovascular anatomy therein. In the current study we regressed out the nuisance variables including 12 motion parameters (three translation, three rotations, along with their derivatives) and physiological regressors modeled by RETROICOR based on the respiratory/cardiac data recorded throughout the resting-state scan. Indeed, HCP provided the ICA-fixed (Salimi-Khorshidi et al., 2014) data where noise sources are removed using a more rigorous criterion. However, we can not directly use such data to interpret our findings as the white matter signals, which we are studying in this work, have also been regressed out from them. We are aware that no existing model can completely remove all noise, so residual effects might produce the observed modes. Although we believe this issue applies equally to gray matter, we performed extra analyses to verify that what we observed in our study can not (at least not completely) be explained by nuisance factors. To be specific, we created a simulated time series BOLDfake for each voxel which stands for a pure nuisance signal (including motion, respiratory and cardiac waveforms, see Fig. S8 for details). Then the BOLDfake went through the same processes, including detrending, band-pass filtering, calculation of spectrogram, as we performed to the preprocessed BOLD data in our original study. Then each window-wise spectral pattern was assigned a mode label by looking for the shortest Euclidian distance between the pattern and centroids of the existing five modes in our current paper. We make a hypothesis that the five spectral modes we observed are not from neural activity but nuisance noises alone. In this case, it is reasonable to believe that BOLDfake is capable of producing the same modes, which exhibit stronger or at least comparable group-wise effects (e.g., the spatial distribution of mode occurrence) that we observed in our current data where a small portion of noises remain. Otherwise, the hypothesis can be rejected, i.e., our findings are not from noises. In Fig. S8, we compare the group-wise distribution of mode occurrences based on BOLDfake data, data used in our current study, ICA-fixed data as well as our current data with CSF signal regressed out. Note that the results are based on 10 participants randomly selected from the 200 data in our original study and therefore the visualized voxels are based on a more relaxed threshold (p < 0.01, uncorrected). We observed that the spatial distributions of mode occurrences are consistent with our current findings when using 5% of the data (no matter with or without CSF regression) in our current work. However, the results based on BOLDfake and ICA-fixed data produce different distributions. This finding suggests that our hypothesis can be rejected. In other words, the modes we observed are not from nuisance factors. In a similar manner, we tested whether mode 5 originated from susceptibility artifacts due to the distinct location (frontal lobe). In Fig. S8, we also compared the group-wise distribution of occurrences of mode 5 based on BOLDfake data (lower-right corner) and data used in our current study. Note that the BOLDfake data here include the susceptibility waveforms extracted from the “bad ICs” identified by ICA-FIX tool. We observed that the spatial distributions of mode 5 occurrences are consistent with our current findings when using 5% of the data in our current work. However, the results based on BOLDfake produce a completely different distribution, demonstrating that mode 5 is not caused by susceptibility artifacts. Note that to further quantify the reproducibility of the 10 test data we selected, we calculate the Pearson’s correlation between the distribution maps of occurrence from test data (10 participants) and original data (200 participants). As shown in Fig. S9, the spatial distribution of occurrences between the same modes (diagonal) exhibits a high correlation, reflecting a good reproducibility of the test data. Meanwhile, the correlation between modes 1 and 5, and between 3 and 4 is relatively high, which is consistent with the spatial maps we showed in Fig. 2. In addition, Fig. S10 visualizes the mode occurrences based on BOLDfake data and our current data on the same template image for easier comparisons.
In summary, this is the first report of spatial-temporal-frequency characterization of BOLD resting-state time courses in white matter. Our results revealed the non-stationary nature of the spectral patterns of BOLD fluctuations in WM. The measurements of BOLD spectra were highly consistent and reproducible, including occurrence, duration, and transitions of modes, and reveal recurring patterns of power spectra as well as HRFs that have not been previously reported in WM BOLD signals, adding to our understanding of spatial-temporal-frequency-physiological associations in the human brain.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health (NIH) grant R01 NS093669 (J.C.G) and R01 NS113832 (J.C.G), and Vanderbilt Discovery Grant FF600670 (Gao). Imaging data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Footnotes
Declaration of Competing Interest
We declare no conflict of interest
Credit authorship contribution statement
Muwei Li: Conceptualization, Methodology, Software, Writing – original draft. Yurui Gao: Software, Investigation. Adam W. Anderson: Supervision. Zhaohua Ding: Methodology, Writing – review & editing. John C. Gore: Writing – review & editing, Supervision, Funding acquisition.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi: 10.1016/j.neuroimage.2022.118972.
References
- Bertrand O, Tallon-Baudry C, 2000. Oscillatory gamma activity in humans: a possible role for object representation. Int. J. Psychophysiol 38, 211–223. doi: 10.1016/S0167-8760(00)00166-5. [DOI] [PubMed] [Google Scholar]
- Biswal BB, 2012. Resting state fMRI: a personal history. Neuroimage 62, 938–944. doi: 10.1016/j.neuroimage.2012.01.090. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH, 2010. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50, 81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtemanche MJ, Sparrey CJ, Song X, MacKay A, D’Arcy RCN, 2018. Detecting white matter activity using conventional 3 Tesla fMRI: an evaluation of standard field strength and hemodynamic response function. Neuroimage 169, 145–150. doi: 10.1016/j.neuroimage.2017.12.008. [DOI] [PubMed] [Google Scholar]
- D’Arcy RCN, Hamilton A, Jarmasz M, Sullivan S, Stroink G, 2006. Exploratory data analysis reveals visuovisual interhemispheric transfer in functional magnetic resonance imaging. Magn. Reson. Med 55, 952–958. doi: 10.1002/mrm.20839. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 9, 179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Ding Z, Huang Y, Bailey SK, Gao Y, Cutting LE, Rogers BP, Newton AT, Gore JC, 2018. Detection of synchronous brain activity in white matter tracts at rest and under functional loading. Proc. Natl. Acad. Sci. U. S. A 115, 595 LP. doi: 10.1073/pnas.1711567115, –600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser LM, Stevens MT, Beyea SD, D’Arcy RCN, 2012. White versus gray matter: fMRI hemodynamic responses show similar characteristics, but differ in peak amplitude. BMC Neurosci. 13. doi: 10.1186/1471-2202-13-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, Turner R, 1998. Event-related fMRI: characterizing differential responses. Neuroimage 7, 30–40. doi: 10.1006/nimg.1997.0306. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Turner R, Frackowiak RSJ, 1995. Characterizing evoked hemodynamics with fMRI. Neuroimage 2, 157–165. doi: 10.1006/nimg.1995.1018. [DOI] [PubMed] [Google Scholar]
- Gao Y, Sengupta A, Li M, Zu Z, Rogers BP, Anderson AW, Ding Z, Gore JC, 2020. Functional connectivity of white matter as a biomarker of cognitive decline in Alzheimer’s disease. PLoS One 15, 1–18. doi: 10.1371/journal.pone.0240513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawryluk JR, Mazerolle EL, D’Arcy RCN, 2014. Does functional MRI detect activation in white matter? A review of emerging evidence, issues, and future directions. Front. Neurosci 8, 1–12. doi: 10.3389/fnins.2014.00239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, 2013. The minimal preprocessing pipelines for the human connectome project. Neuroimage 80, 105–124. doi: 10.1016/j.neuroimage.2013.04.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D, 2000. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn. Reson. Med 44, 162–167 . [DOI] [PubMed] [Google Scholar]
- Gore JC, Li M, Gao Y, Wu TL, Schilling KG, Huang Y, Mishra A, Newton AT, Rogers BP, Chen LM, Anderson AW, Ding Z, 2019. Functional MRI and resting state connectivity in white matter - a mini-review. Magn. Reson. Imaging doi: 10.1016/j.mri.2019.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helenius J, Perkiö J, Soinne L, Østergaard L, Carano RAD, Salonen O, Savolainen S, Kaste M, Aronen HJ, Tatlisumak T, 2003. Cerebral hemodynamics in a healthy population measured by dynamic susceptibility contrast Mr imaging. Acta Radiol. 44, 538–546. doi: 10.1034/j.1600-0455.2003.00104.x. [DOI] [PubMed] [Google Scholar]
- Huang J, Li M, Li Q, Yang Z, Xin B, Qi Z, Liu Z, Dong H, Li K, Ding Z, Lu J, 2020. Altered functional connectivity in white and gray matter in patients with multiple sclerosis. Front. Hum. Neurosci 14, 1–12. doi: 10.3389/fnhum.2020.563048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM, 2012. FSL. Neuroimage 62, 782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Leonardi N, Van De Ville D, 2015. On spurious and real fluctuations of dynamic functional connectivity during rest. Neuroimage 104, 430–436. doi: 10.1016/j.neuroimage.2014.09.007. [DOI] [PubMed] [Google Scholar]
- Li M, Ding Z, Gore JC, 2020a. Identification of white matter networks engaged in object (Face) recognition showing differential responses to modulated stimulus strength. Cereb. Cortex Commun 1. doi: 10.1093/texcom/tgaa067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Gao Y, Ding Z, Gore JC, 2021. Power spectra reveal distinct BOLD resting-state time courses in white matter. Proc. Natl. Acad. Sci. U. S. A 118. doi: 10.1073/PNAS.2103104118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Gao Y, Gao F, Anderson AW, Ding Z, Gore JC, 2020b. Functional engagement of white matter in resting-state brain networks. Neuroimage 220, 117096. doi: 10.1016/j.neuroimage.2020.117096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Newton AT, Anderson AW, Ding Z, Gore JC, 2019. Characterization of the hemodynamic response function in white matter tracts for event-related fMRI. Nat. Commun 10, 1140. doi: 10.1038/s41467-019-09076-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin H, Li M, Zhan Y, Lin L, Yang K, Hu S, Han Y, 2020a. Disrupted white matter functional connectivity in aMCI APOEϵ4 carriers: a resting-state study. Brain Imaging Behav. doi: 10.1007/s11682-020-00367-7. [DOI] [PubMed] [Google Scholar]
- Lin H, Sun Y, Li M, Zhan Y, Lin L, Ding Z, Han Y, 2020b. Sex modulates the apolipoprotein E ϵ4 effect on white matter and cortical functional connectivity in individuals with amnestic mild cognitive impairment. Eur. J. Neurol doi: 10.1111/ene.14226. [DOI] [PubMed] [Google Scholar]
- Liu X, Duyn JH, 2013. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc. Natl. Acad. Sci. U. S. A 110, 4392–4397. doi: 10.1073/pnas.1216856110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra A, Li M, Anderson AW, Newton AT, Ding Z, Gore JC, 2020. Concomitant modulation of BOLD responses in white matter pathways and cortex. Neuroimage 216, 116791. doi: 10.1016/j.neuroimage.2020.116791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Nayak AS, Glynn P, 1990. Oxygenation-sensitive contrast in magnetic resonance image of rodent brain at high magnetic fields. Magn. Reson. Med 14, 68–78. doi: 10.1002/mrm.1910140108. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K, 1992. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc. Natl. Acad. Sci. U. S. A 89, 5951 LP–5955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantazis D, Weber DL, Dale CL, Nichols TE, Simpson GV, Leahy RM, 2005. Imaging of oscillatory behavior in event-related MEG studies. In: Proceedings of the SPIE doi: 10.1117/12.600607. [DOI] [Google Scholar]
- Pedersen M, Zalesky A, Omidvarnia A, Jackson GD, 2018. Multilayer network switching rate predicts brain performance. Proc. Natl. Acad. Sci. U. S. A 115, 13376 LP. doi: 10.1073/pnas.1814785115, –13381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peer M, Nitzan M, Bick AS, Levin N, Arzy S, 2017. Evidence for functional networks within the human brain’s white matter. J. Neurosci 37, 6394–6407. doi: 10.1523/JNEUROSCI.3872-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM, 2014. Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468. doi: 10.1016/j.neuroimage.2013.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling KG, Gao Y, Li M, Wu TL, Blaber J, Landman BA, Anderson AW, Ding Z, Gore JC, 2019. Functional tractography of white matter by high angular resolution functional-correlation imaging (HARFI). Magn. Reson. Med 81, 2011–2024. doi: 10.1002/mrm.27512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sejdić E, Djurović I, Jiang J, 2009. Time–frequency feature representation using energy concentration: an overview of recent advances. Digit. Signal Process 19, 153–183. doi: 10.1016/j.dsp.2007.12.004. [DOI] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo D, 2012. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front. Physiol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorndike RL, 1953. Who belongs in the family? Psychometrika 18, 267–276. doi: 10.1007/BF02289263. [DOI] [Google Scholar]
- Tong Y, Hocke LM, Nickerson LD, Licata SC, Lindsey KP, Frederick BD, 2013. Evaluating the effects of systemic low frequency oscillations measured in the periphery on the independent component analysis results of resting state networks. Neuroimage 76, 202–215. doi: 10.1016/j.neuroimage.2013.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Lindsey KP, Hocke LM, Vitaliano G, Mintzopoulos D, Frederick BD, 2017. Perfusion information extracted from resting state functional magnetic resonance imaging. J. Cereb. Blood Flow Metab 37, 564–576. doi: 10.1177/0271678X16631755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turchi J, Chang C, Ye FQ, Russ BE, Yu DK, Cortes CR, Monosov IE, Duyn JH, Leopold DA, 2018. The basal forebrain regulates global resting-state fMRI fluctuations. Neuron 97, 940–952. doi: 10.1016/j.neuron.2018.01.032,.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TEJ, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, Della Penna S, Feinberg D, Glasser MF, Harel N, Heath AC, Larson-Prior L, Marcus D, Michalareas G, Moeller S, Oostenveld R, Petersen SE, Prior F, Schlaggar BL, Smith SM, Snyder AZ, Xu J, Yacoub E, 2012. The human connectome project: a data acquisition perspective. Neuroimage 62, 2222–2231. doi: 10.1016/j.neuroimage.2012.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergara VM, Abrol A, Calhoun VD, 2019. An average sliding window correlation method for dynamic functional connectivity. Hum. Brain Mapp 40, 2089–2103. doi: 10.1002/hbm.24509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T, Wilkes DM, Li M, Wu X, Gore JC, Ding Z, 2020. Hemodynamic response function in brain white matter in a resting state. Cereb. Cortex Commun 1, 1–13. doi: 10.1093/texcom/tgaa056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Yan C, Zhao C, Qi Z, Zhou W, Lu J, He Y, Li K, 2011. Spatial patterns of intrinsic brain activity in mild cognitive impairment and alzheimer’s disease: a resting-state functional MRI study. Hum. Brain Mapp 32, 1720–1740. doi: 10.1002/hbm.21140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu GR, Deshpande G, Laureys S, Marinazzo D, 2015. Retrieving the hemodynamic response function in resting state fMRI: methodology and application. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc 2015, 6050–6053. doi: 10.1109/EMBC.2015.7319771, IEEE Eng. Med. Biol. Soc. Annu. Int. Conf.. [DOI] [PubMed] [Google Scholar]
- Wu GR, Liao W, Stramaglia S, Ding JR, Chen H, Marinazzo D, 2013. A blind deconvolution approach to recover effective connectivity brain networks from resting state fMRI data. Med. Image Anal 17, 365–374. doi: 10.1016/j.media.2013.01.003. [DOI] [PubMed] [Google Scholar]
- Wu TL, Wang F, Li M, Schilling KG, Gao Y, Anderson AW, Chen LM, Ding Z, Gore JC, 2019. Resting-state white matter-cortical connectivity in non-human pri-mate brain. Neuroimage 184, 45–55. doi: 10.1016/j.neuroimage.2018.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaesoubi M, Miller RL, Calhoun VD, 2017. Time-varying spectral power of resting-state fMRI networks reveal cross-frequency dependence in dynamic connectivity. PLoS One 12, 1–14. doi: 10.1371/journal.pone.0171647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Barch DM, Gray JR, Conturo TE, Braver TS, 2009. BOLD correlates of trial-by-trial reaction time variability in gray and white matter: a multi-study fMRI analysis. PLoS One 4. doi: 10.1371/journal.pone.0004257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu-Feng Z, Yong H, Chao-Zhe Z, Qing-Jiu C, Man-Qiu S, Meng L, Li-Xia T, Tian-Zi J, Yu-Feng W, 2007. Altered baseline brain activity in children with ADHD revealed by resting-state functional MRI. Brain Dev. 29, 83–91. doi: 10.1016/j.braindev.2006.07.002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


