Novel-view X-ray Projection Synthesis through Geometry-integrated Deep Learning

Abstract

X-ray imaging is a widely used approach to view the internal structure of a subject for clinical diagnosis, image-guided interventions and decision-making. The X-ray projections acquired at different view angles provide complementary information of patient’s anatomy and are required for stereoscopic or volumetric imaging of the subject. In reality, obtaining multiple-view projections inevitably increases radiation dose and complicates clinical workflow. Here we investigate a strategy of obtaining the X-ray projection image at a novel view angle from a given projection image at a specific view angle to alleviate the need for actual projection measurement. Specifically, a Deep Learning-based Geometry-Integrated Projection Synthesis (DL-GIPS) framework is proposed for the generation of novel-view X-ray projections. The proposed deep learning model extracts geometry and texture features from a source-view projection, and then conducts geometry transformation on the geometry features to accommodate the change of view angle. At the final stage, the X-ray projection in the target view is synthesized from the transformed geometry and the shared texture features via an image generator. The feasibility and potential impact of the proposed DL-GIPS model are demonstrated using lung imaging cases. The proposed strategy can be generalized to a general case of multiple projections synthesis from multiple input views and potentially provides a new paradigm for various stereoscopic and volumetric imaging with substantially reduced efforts in data acquisition.

1. Main Text

Medical imaging such as X-ray imaging, computed tomography (CT), magnetic resonance imaging (MRI), and positron emission tomography (PET) presents a significant approach to view the internal structure of a patient for diagnosis, image-guided interventions and many other clinical decision-making procedures. Every year in the U.S., over hundred millions of medical imaging examinations are performed for patient care. In 2006, about 377 million diagnostic and interventional radiologic examinations were performed in the U.S. (Mettler et al., 2009). Among them, X-ray imaging and X-ray CT are widely used modalities in various applications (Xing et al., 2020; Winder et al., 2021). In X-ray imaging, an incident X-ray beam goes through the patient body, and produces a projection image of the internal anatomic structure of the body on the image plane as illustrated in Fig. 1. For image guidance of interventional procedures, projection images from different view angles are often needed to localize or recognize a structure accurately in 3D. X-ray projection data acquired at many different angles around the patient are also required in tomographic CT imaging.

Fig. 1.

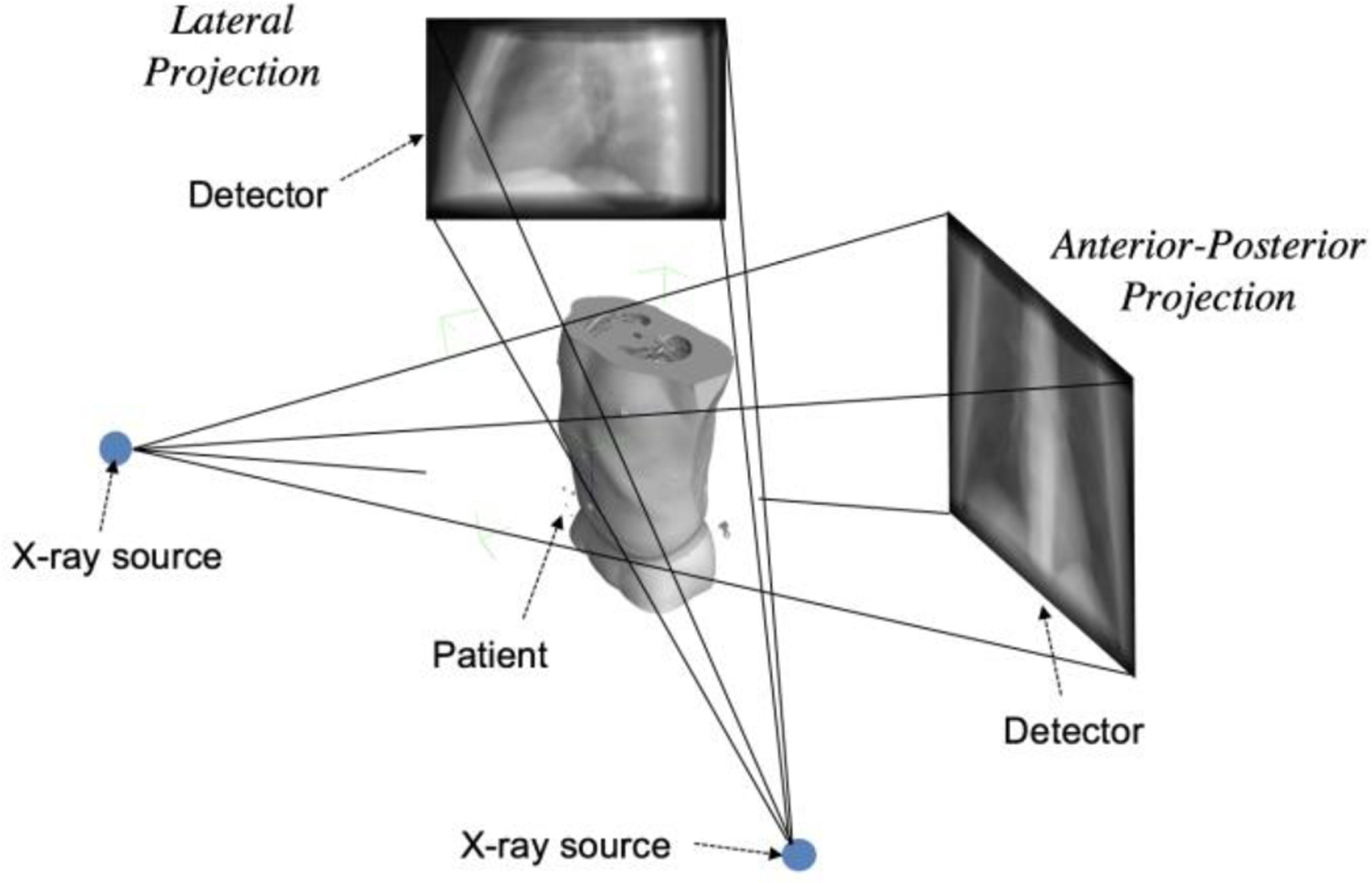
Sketch of X-ray projection imaging procedure. X-ray wave penetrates through the patient’s body and projects on the detector plane. When the X-ray source is located at different positions, different projections at different view angles are obtained. The projections in the view of anterior-posterior (AP) direction and lateral (LT) directions are shown in the figure.

Considering the practical needs for multi-view X-ray projections at different view angles and the general overhead associated with the data acquisition, it is desirable to develop alternative ways to obtain the multi-view projections with minimal cost such as computational image synthesis. Such a technique can not only reduce the cost to acquire multi-view X-ray projections, but also open new possibilities for some significant relevant challenges such as sparse-view tomographic imaging. For example, in sparse-view tomographic CT image reconstruction, synthesized X-ray projections at novel view angles could potentially help to reconstruct better CT images while reducing the needs of X-ray projection acquisition, thus, reducing the radiation dose during the imaging protocol (Shen et al., 2021). However, there is no previous work specifically discussing this interesting research topic. Toward this goal, in this work, we investigate an effective strategy of synthesizing novel-view X-ray projections by using geometry-integrated deep learning.

Recent advances in deep learning have led to impressive progress in many application fields (Xing et al., 2020), including image reconstruction (Zhu et al., 2018; Mardani et al., 2018; Shen et al., 2019) and image recognition (Krizhevsky et al., 2012; He et al., 2016; Shen et al., 2018). Moreover, in computer vision research, deep learning also brings new possibility for view synthesis task for natural images, i.e., to synthesize the novel-view images from the images at the given view angles (Eslami et al., 2018; Sitzmann et al., 2019; Mildenhall et al., 2020). Although some progress has been made in solving the view synthesis problem through volume rendering with deep learning methodology (Lombardi et al., 2019; Wiles et al., 2020), these methods cannot be directly transferred to novel-view X-ray projection synthesis because of the difference in image-forming physics between photographic and tomographic imaging. For photographic imaging, the natural lights hit the surface of objects and reflect back to the camera image plane to form an image of the object shape and the background in the RGB format. In tomographic imaging, the penetrating waves such X-ray passes through the object and project the internal structures onto image plane by ray integration. Therefore, a new formulation for the novel-view X-ray projection synthesis problem is required.

Understanding the underlying geometry changes in the physical world is important to solve this X-ray projection synthesis problem. In this case, each pixel value in the X-ray projection does not represent the RGB value at a certain point like that in the natural image, but indicates the integration along the ray line in the projection direction. Therefore, to synthesize an X-ray projection at a new view angle, it is necessary to consider the geometric changes in the physical world, which relates the projections at different angles. Specifically, we observe that the underlying subject is rotated when viewed from different angles, thus, the geometry features should also be transformed according to the rotation angle of view point when synthesizing a new-view projection. In reality, since the projections from different views depict the same imaging subject, they should share some common characteristics such as the subject texture. Therefore, in synthesizing a projection, we assume that the projections at different view angles share the common texture features while keeping the view-specific geometry features. In this way, we integrate the geometric relationship from physical world in the deep learning to construct a robust and interpretable projection synthesis model.

In this work, we introduce a Deep Learning-based Geometry-Integrated Projection Synthesis (DL-GIPS) framework for generating novel-view X-ray projections. Specifically, given the X-ray projections at certain angle(s), the model learns to extract the geometric and texture features from input projection(s) simultaneously, which are then transformed and combined to form the X-ray projection image at the target angle(s). The texture feature extracts the appearance characteristics such as the subject texture from the input projection to help to synthesize the target projection, whereas the geometry feature captures the subject geometric structure, such as the spatial distribution, contour, shape, size of bones, organs, soft tissues, and other body parts. To incorporate the geometry information into the view synthesis procedure, the extracted geometry features are transformed according to the source and target view angle changes based on the 3D cone-beam projection geometry, which relates to the subject’s geometry changes. Such a combination of geometry priors and deep learning also makes the model more robust and reliable. More details will be introduced in the subsequent sections.

Overall, the main contributions of this paper are three folds:

• We for the first time investigate the novel-view projection synthesis problem for X-ray imaging. The approach can also be generalized to a more general synthesis from multi-views to multi-views projections.

• We propose a deep learning-based geometry-integrated projection synthesis model (DL-GIPS) to generate novel-view X-ray projections through feature disentanglement and geometry transformation.

• We validate the feasibility of the proposed approach by experimenting on the one-to-one and multi-to-multi X-ray projection synthesis using lung imaging cases across various patients.

The remainders of this paper are organized as follows. We introduce the related works in Section 2 and elaborate our framework in Section 3. The experimental setting and results are presented in Section 4 and Section 5, respectively. We further discuss the key issues of our method in Section 6 and draw the conclusions in Section 7.

2. Related Work

2.1. View Synthesis

The view synthesis problem in computer graphics has been researched for many years (Eslami et al., 2018; Sitzmann et al., 2019; Mildenhall et al., 2020; Lombardi et al., 2019; Wiles et al., 2020). With the development of deep learning, the recent works are focused on solving this problem through volume rendering (Lombardi et al., 2019; Wiles et al., 2020), neural scene representation learning (Eslami et al., 2018; Sitzmann et al., 2019), neural radiance field (Mildenhall et al., 2020). These works employ deep neural networks to learn the representation of the underlying object or scene and try to find the intersection points of the lights and the object outer surface to generate the RGB values of the corresponding pixels onto the image plane. However, because of the physical difference of X-ray imaging scanning, it is difficult, if not possible, to apply these methods to X-ray projection forming. In this work, we propose an X-ray projection synthesis method with integration of X-ray imaging physics.

2.2. Image Translation

In recent years, there is a line of research for image-to-image translation (Zhu et al., 2017; Huang et al., 2018; Choi et al., 2018; Lee et al., 2019; Shen et al., 2020; Lyu et al., 2021), where a deep learning model is trained to translate or synthesize images across multiple domains or modalities, such as multi-contrast MRI (Lee et al., 2019; Shen et al., 2020), MRI to CT (Zhang et al., 2018) or facial images with different expressions (Huang et al., 2018; Choi et al., 2018; Shen et al., 2020). Some of the image translation methods generate new-domain images by disentangling the image semantics as content features and style features (Huang et al., 2018; Shen et al., 2020). In these methods, it is assumed that the content features are shared across domains, while style features are domain-specific. For the novel-view projection synthesis problem, it is possible to treat projection images at different view angles as different image domains (Shen et al., 2021). In this way, the problem is transferred to an image-to-image translation problem. However, such assumption completely ignores the specific viewpoint change and the corresponding geometric relationship between projections from different views.

2.3. Geometry-Integrated Deep Learning

Although deep learning has achieved impressive results in many image reconstruction and recognition tasks, in recent years, some concerns have been raised with regard to its robustness, generalization, and interpretability (Hutson, 2018; Heaven, 2019; Finlayson et al., 2019; Tatarchenko et al., 2019). To build a practically useful deep learning model for medical imaging, it is desirable to incorporate the geometry and/or physical prior into the learning process. In practice, how to integrate seamlessly the geometry into a deep learning model presents a daunting challenge. Previous works introduce feasible geometry-integrated deep learning models for 3D tomographic image reconstruction (Liu et al., 2017, Shen et al., 2021), object surface reconstruction (Yariv et al., 2020) and scene representations (Bear et al., 2020). In our projection synthesis here, the geometry priors are introduced naturally into the deep learning model by relating the geometries between different view angles.

3. Method

3.1. Approach Overview

As shown in Fig. 2, the input to the framework is the source-view projection image, and the output of the model is the synthesized target-view projection image. In order to generate the projection from the input view angle to the target view angle, two aspects of information are required. First, an important knowledge embedded in the input projection is the anatomic geometry structure of the scanned subject including the distribution and location of various organs and body parts. It is important to understand this patient-specific geometry information to generate the projection at a new view angle. Due to the view angle change from the source to the target views, the underlying subject should also be rotated and transformed accordingly, as shown in Fig. 1. Particularly, the geometry transformation should comply with the physical model of the X-ray imaging. Correctly conducting the geometric transformation from the source view to the target view helps the model to capture the change of the projected subject structure.

Fig. 2.

Illustration of the proposed Deep Learning-based Geometry-Integrated Projection Synthesis framework (DL-GIPS). The pipeline contains texture and geometry feature encoders, projection transformation and image generator. The projection transformation contains the geometric operation of backward projection and forward projection based on the X-ray imaging physical model, and 3D feature refinement model.

Beyond the geometry information, the texture characteristics are also critical to generate high quality target-view projection, and ensure the consistency of the texture and appearance characteristics between the source-view and target-view projections. We assume that the source-view and target-view images are X-ray projections scanned under the same imaging setting, which should share some common image characteristics such as the subject texture and image appearance. Therefore, the texture features captured from source-view projection are combined with the transformed geometry features to synthesize target-view projection simultaneously.

Based on the above assumptions, we propose a DL-GIPS framework for novel-view generation. As illustrated in Fig. 2, the proposed framework consists of three modules: the texture and geometry feature extraction encoders, the projection transformation based on geometry priors and view angles, and the image generator to synthesize projections. Specifically, the two image encoders extract the texture features and the geometry features from the input image, respectively. Then, the geometry features are transformed through the physical model of backward projection and forward projection. Finally, the transformed geometry features at the target view are combined with the shared texture features to synthesize the target-view projection via an image generator. The details of each module are described as follows.

3.2. DL-GIPS Net

3.2.1. Feature encoder

The feature encoders are built up by stacked downsampling convolutional layers and residual convolutional blocks to learn the semantic representations from the input projection. As aforementioned, two separate encoders are constructed to learn the geometry and texture features from the input projection respectively, denoted as geometry feature encoder ε^g, and texture feature ε^t. Given the source-view image as I_scr, the feature encoding process is denoted as follows:

$$f_{src}^g={\epsilon }^g\left(I_{src}\right)$$ (1)

$$f^t={\epsilon }^t\left(I_{src}\right)$$ (2)

To be specific, the encoder firstly contains a convolutional layer with kernel size 7 and channel dimension of 16. Then, the feature maps are downsampled by two 2D convolutional layer with kernel size 4 and stride 2, where the channel dimension is doubled in each layer. Each convolutional layer is followed by instance normalization (Ulyanov et al., 2016) and ReLU activation function. Next, four residual blocks are built up to further process the learned features. Each residual block contains two convolutional layers with kernel size 3 and the same channel dimension. A skip connection is added up from the output of the first convolutional layer to the second convolutional layer. Thus, the feature maps keep the same spatial size and channel dimension when getting through all the residual blocks. The geometry feature encoder and texture feature encoder have a similar architecture, except that there is an additional convolutional layer at the end of geometry feature encoder to reduce the geometry feature channel dimension to 32 for the subsequent geometry transformation module.

3.2.2. Geometry transformation

After the geometry features capture the geometric distribution of different parts from input projection, it is necessary for the model to understand the change between the source and target view angles. For projections at different view angles, the bones and organs projected on the image plane are differently distributed accordingly, which is related to the projection geometry from the physical model of X-ray imaging system. Thus, these geometry information and view angles should be incorporated together for the new view synthesis. To achieve that, as shown in Fig. 3, we firstly backward project the source-view geometry features extracted from the input projection backward to the 3D volume, which represents the semantic features of the underlying subject in 3D space. The backward projector is performed according to the 3D cone-beam geometry of the X-ray imaging scanner and the source view angle. As shown in the blue lines in Fig. 3, the pixel values in the image are put back to the intersected voxels along the corresponding X-ray line directions. Then, the 3D feature volume is forward projected to the target image plane according to the cone-beam geometry and target view angle. As demonstrated in the purple lines in Fig. 3, the projected pixel values are computed by integrating the crossed voxels along the ray direction. In this way, the geometry features extracted from source view projection is transformed to the corresponding features in the target view.

Fig. 3.

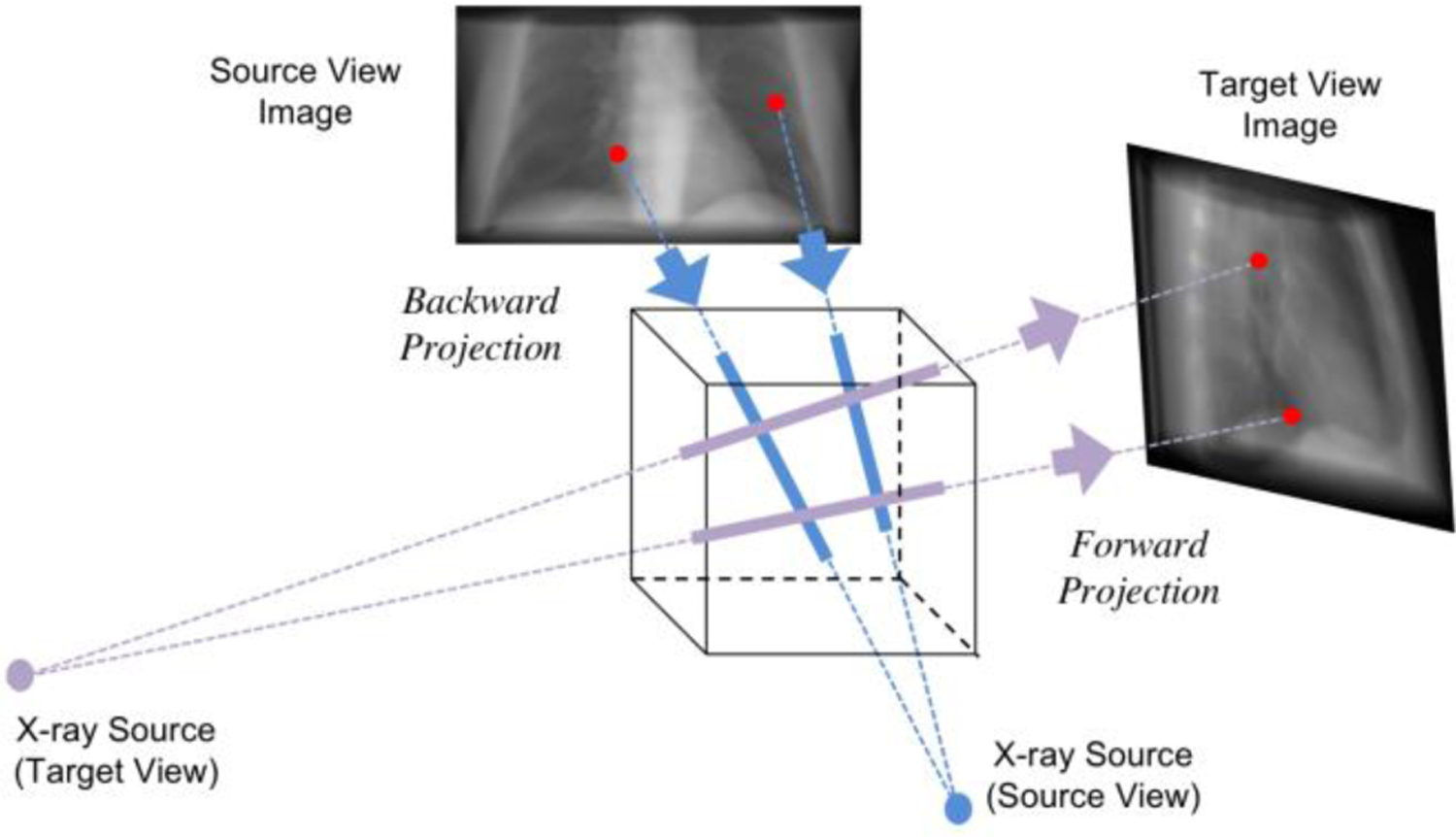
Illustration of geometry transformation with backward projection (blue) and forward projection (purple). The back projector puts the pixel intensities in the source-view image back to the corresponding voxels in the 3D volume according to the cone-beam geometry of the physical model. When the X-ray source rotates to the target view angles, the forward projection operator integrates along the projection line and projects onto the detector plane.

However, when the input projection(s) is very sparse (e.g., a single source view), the back-projected 3D feature volume is also very sparse with a lot of zero-padding voxels, which is not informative. Thus, we build up a 3D feature refinement model to inpaint the 3D feature volume after the back-projection operation. It is designed to learn a more complete 3D representation to improve the target view synthesis. With the 3D feature refinement model denoted as $\mathcal{M}$, the whole projection transformation process is denoted as follows:

$$F_{src}^g,F_{tgt}^g={\mathcal{P}}^f\circ \mathcal{M}\circ {\mathcal{P}}^b\left(f_{src}^g\right)$$ (3)

where we denote the transformed features after forward and backward projection as $F_{src}^g$, $F_{tgt}^g$. ${\mathcal{P}}^f$ and ${\mathcal{P}}^g$ represent the forward projection and backward projection operators. Note that during the forward projection, the 3D feature volume not only projects onto the target view, but also projects back to the source view to keep consistency. Therefore, the projection transformation module outputs the geometry features for target view $F_{tgt}^g$ as well as source view $F_{src}^g$.

Note that the backward projection and forward projection are deterministic operations without any learnable variables. All the transformation parameters are set up based on the geometry priors including the physical model from X-ray imaging scanner, and the source and target view angles. The 3D feature refinement network is built up by two 3D residual convolutional blocks. Each residual block contains two 3D convolutional layers with kernel size 3, followed by instance normalization and ReLU activation function. An additive path connects the outputs of the first and the second layer to enforce residual learning. Since the backward and forward projectors are differentiable, the geometry transformations are wrapped up together with network modules for end-to-end optimization.

3.2.3. Image generator

Combining the transformed geometry features and extracted texture features, image generator learns to synthesize the projection in the target view from the semantic representations of both sides. The model structure of image generator is the mirror of feature encoder, which is constructed by residual convolutional blocks and upsampling convolutional layers. The geometry features and texture features are concatenated together in the channel dimension. Denoting the generator as $\mathcal{G}$, the model outputs the target-view projection as well as the source-view projection based on the different geometry features:

$$I{\prime }_{src}=\mathcal{G}\left(F_{src}^g,f^t\right)$$ (4)

$$I{\prime }_{tgt}=\mathcal{G}\left(F_{tgt}^g,f^t\right)$$ (5)

Specifically, the generator firstly contains four residual convolutional blocks, where each block consists of two convolutional layers of kernel size 3 followed by instance normalization and ReLU activation. Similarly, the skip connection builds up in each residual block. Then, the upsampling block contains the an upsampling layer with scale factor 2 and a 2D convolutional layer with kernel size of 5. The upsampling layer interpolates the feature maps to increase the spatial size, while the convolutional layer reduces the feature channel dimension to the half. Finally, another 2D convolutional layer with kernel size 7 and tangent hyperbolic activation function transforms the feature map to the expected output channel dimension for the synthesized projection.

3.2.4. Image discriminator

In order to generate realistic projections in the target view, we build up the image discriminator deployed to the generated images for adversarial training. To be specific, the discriminator is used to distinguish between the real projections and the synthesized projections. Together training the image generator and image discriminator in an adversarial manner, the generated projections are expected to be in the same distribution as the real projections, which cannot be distinguished by the discriminator. We denote the discriminator as $\mathcal{D}$.

In our method, we build up a multi-scale image discriminator (Huang et al., 2018; Shen et al., 2020). Specifically, we use the 2D average pooling layer to downsample the image to three different scales by 2 times. Separate classifier networks are constructed for input images at different scales. The classifier contains four 2D convolutional layers with kernel size 4 and stride 2, which further downsample the spatial size of feature maps. The final layer is the 2D convolution with kernel size 1. During training, the outputs from image discriminator are used to compute the adversarial loss based on the method of least squares generative adversarial networks (Mao et al., 2017).

3.3. Training Loss

In order to train the whole model reliably, we design a training strategy that contains the image and feature consistency loss, image reconstruction loss, and adversarial loss.

3.3. 1. Consistency loss

In the whole framework, the encoder extracts geometry and texture features from image while the generator combines the features to generate images. These two processes are actually inverse operations, which should also keep consistency for the input source-view projection. That is, if we recombine the extracted features from the source-view projection, the generator can recover the same projection. The formula is denoted as:

$${\mathcal{L}}_{cyc}^{img}=\mathbb{E}\left[{\Vert \mathcal{G}\left({\epsilon }^g\left(I_{src}\right),{\epsilon }^t\left(I_{src}\right)\right)-I_{src}\Vert }_1\right]$$ (6)

where the expectation is sampled based on all the training samples. This constraint guarantee that the feature encoding and image generation keep consistency and can recover the input image.

Furthermore, in order to guarantee that the geometry features represent the correct semantic information for corresponding views, we add additional constraint on the consistency of geometry features. Suppose the generator output the synthesized projections I′_src, I′_tgt at source view and target view respectively. The geometry features extracted from the generated projections should have the same representation as the previous transformed geometry features, from which the synthesized projections are derived, as shown in Fig. 2. This also further guarantee the geometry feature encoding and image generation conduct the inverse operations. Thus, the geometry feature consistency loss is denoted as follows:

$${\mathcal{L}}_{cyc}^f=\mathbb{E}\left[{\Vert {\epsilon }^g\left(I{\prime }_{tgt}\right)-F_{tgt}^g\Vert }_1+{\Vert {\epsilon }^g\left(I{\prime }_{src}\right)-F_{src}^g\Vert }_1\right]$$ (7)

For convenience of notation, we denote the aforementioned image and feature consistency constraints as a total consistency loss. That is,

$${\mathcal{L}}_{cyc}={\mathcal{L}}_{cyc}^{img}+{\mathcal{L}}_{cyc}^f$$ (8)

3.3.2. Reconstruction loss

After applying the geometry transformation to the encoded features, the transformed geometry features are supposed to generate the projection in the novel view. We add the L1-norm loss between the synthesized projection and the ground truth projection to strengthen the anatomical-structure related generation. Moreover, the transformed geometry features in the source view should also be able to recover the source view projection through the image generator. Thus, the reconstruction loss includes the constraints on both source-view and target-view projections output from the image generator. Thus, the total image reconstruction loss is as follows:

$${\mathcal{L}}_{rec}=\mathbb{E}\left[{\Vert \mathcal{G}\left(F_{tgt}^g,f^t\right)-I_{tgt}\Vert }_1+{\Vert \mathcal{G}\left(F_{src}^g,f^t\right)-I_{src}\Vert }_1\right]$$ (9)

This constraint makes sure the backward and forward projection operators conduct the correct geometry transformation as expected. Compared with Eq. (6), the difference between the consistency loss and reconstruction loss on source-view projection is from the different geometry feature. In Eq. (6), the source-view geometry feature is directly extracted from the input source-view projection through feature encoder. In Eq. (9), the source-view geometry feature is outputted after the geometry transformation including the 3D feature refinement network. In other words, we assume the geometry feature of source view should keep consistent in these two positions. The geometry transformation module helps to derive the target-view geometry feature while it should also keep the correctness of the source-view geometry feature.

3.3.3. Adversarial Loss

The simultaneous adversarial training of the image generator and discriminator enforces the distribution of the generated projections to be close to that of the real projections. In this way, the generated projections are more realistic. The adversarial loss is as follows:

$${\mathcal{L}}_{adv}=\mathbb{E}\left[{\left(\mathcal{D}\left(\mathcal{G}\left(F_{tgt}^g,f^t\right)\right)-a\right)}^2\right]+\mathbb{E}\left[{\left(\mathcal{D}\left(I_{tgt}\right)-b\right)}^2\right]$$ (10)

Here, we adopt the objective loss function introduced by least squares generative adversarial networks (Mao et al., 2017), where a and b are the labels for synthesized and real images. The real projections and generated projections are the inputs to train the discriminator model to distinguish between the real or fake class. For the projections at different view angles, we use different discriminators for adversarial training. Thus, the loss in Eq. (10) can be also applied to the source-view projections with the corresponding real and synthesized projections.

The feature encoders, image generators, and image discriminators are jointly trained to optimize the total loss as follows:

$$\begin{gathered} \underset{{\epsilon }^g,{\epsilon }^t,\mathcal{G},\mathcal{M}}{\min }\underset{\mathcal{D}}{\max }\hspace{1em}\mathcal{L}\left({\epsilon }^g,{\epsilon }^t,\mathcal{G},\mathcal{M},\mathcal{D}\right) \\ ={\lambda }_{cyc}{\mathcal{L}}_{cyc}+{\lambda }_{rec}{\mathcal{L}}_{rec}+{\lambda }_{adv}{\mathcal{L}}_{adv} \end{gathered}$$ (11)

where λ_cyc, λ_rec, λ_adv are the hyper-parameters to balance the different parts of the total loss. The whole framework is trained end-to-end to optimize the total loss objective.

4. Experiments

To validate the feasibility of the proposed DL-GIPS model for view synthesis of X-ray projection images, we conduct experiments on lung X-ray CT images for novel-view projection synthesis. In the following sections, we will describe the dataset, experimental setting and training details.

4.1. Dataset

The experiments were conducted on a public dataset of The Lung Image Database Consortium and Image Database Resource Initiative (LIDC-IDRI) (Armato et al., 2011; Armato et al., 2015; Clark et al., 2013). This dataset contains 1018 thoracic 3D CT images from different patients. We regarded each CT image as an independent data sample for model training. In data pre-processing, all the CT images were resampled with the same resolution of 1 mm in the z-axis, and were resized to the same image size of 128 × 128 in the xy-plane.

In order to obtain the X-ray projections at different angles, we projected the 3D CT image to get the digitally reconstructed radiographs (DRRs) in different view angles. The cone-beam geometry of the projection operation was defined according to the clinical on-board cone-beam CT system for radiation therapy. Each 2D X-ray projection was of the size 180 × 300. Following the image processing of model training, the intensity values of the all the 2D X-ray projection images were normalized to the data range of [0, 1]. In experiments, we randomly selected 80% of the dataset for training and validation (815 samples) while 20% of the data were held out for testing (203 samples).

4.2. Experimental Setting

To validate the proposed model under different cases of view synthesis, we designed two experimental setting: one-to-one view synthesis and multi-to-multi view synthesis. In the experiments of one-to-one view synthesis, we focus on two typical projections: the anterior-posterior (AP) projection (0 degree) and the lateral (LT) projection (90 degree), which are commonly used in clinical practice. We experimented on two situations: to generate AP projection from LT projection, or to generate LT projection from AP projection. Given only a single projection, it is very hard to generate another novel view because the given information from the source view is very limited. We want to explore if the data-driven learning and the geometry priors can provide more additional information to make it possible.

In the experiments of multi-to-multi view synthesis, the model was trained to generate the projections at 30 and 60 degrees from the AP (0 degree) and LT (90 degree) projections. This is a more general case with multiple input sources views and more than one target views. Such multi-to-multi projection generation may further contribute to the application of sparse-view 3D CT image reconstruction for the real-time applications.

4.3. Training Details

The deep neural networks in the framework were implemented with PyTorch (Paszke et al., 2017). The backward projection and forward projection operators were implemented based on the Operator Discretization Library (ODL) in Python (Adler et al., 2017), which were wrapped up as the differentiable PyTorch module. Thus, the whole framework was built up by PyTorch layers and was trained in an end-to-end fashion. Specifically, the whole model was trained by optimizing the total loss in Eq. (11), with the loss weights λ_cyc, λ_adv as 1 and λ_rec as 10. We trained the model using the Adam optimizer (Kingma and Ba, 2015) with the beta parameters as (0.5, 0.999), the learning rate of 0.0001, and batch size 1. The model was trained for 100000 iterations in total. We will release our code publicly upon the paper acceptance.

5. Results

In the following section, we demonstrate the qualitative and quantitative results respectively for different experimental settings: one-to-one projection synthesis and multi-to-multi projection synthesis. Also, we compare the results of the proposed method with the previous methods for image translation. Finally, we conduct ablative studies to further investigate the importance of each component in the proposed DL-GIPS model.

5.1. Compared Models

UNet (Ronneberger et al., 2015): Since there is no previous method particularly designed for X-ray projection synthesis problem, we firstly compare the proposed DL-GIPS model with the baseline UNet model (Ronneberger et al., 2015), which has been widely used for image segmentation and restoration in both natural image and medical image applications. In the UNet structure, the skip connections are built up between the multi-scale features of the encoder and the decoder, but there is not feature disentanglement. To apply the UNet model for X-ray projection synthesis, the given source projections are stacked as multi-channel images for model inputs while the model outputs the stacked multi-view images altogether. The same image reconstruction loss (i.e., L1-norm loss) is applied to measure the difference between the outputs and ground truth images. The same training strategy is used to train the UNet model.

ReMIC (Shen et al., 2020): We also compare the DL-GIPS model with more advanced approach with feature disentanglement. ReMIC model (Shen et al., 2020) is a recent work proposed for multi-modality image translation such as multi-contrast MRI images. The ReMIC model generates the images across domains by feature disentanglement of content and style codes. Specifically, it assumes that multi-modality images share the same content features while also keep the domain-specific style features. Thus, the across-domain image is generated by sampling the style feature from the prior distribution. To apply the ReMIC model for the X-ray projection synthesis problem, we assume the style features are sampled from different prior distributions for different view angles. Then during the image generation process, the sampled style features are used to change the parameters of adaptive instance normalization layers in the image generator by using the same approach as described in (Shen et al., 2020). For comparison purpose, we use the same model structures for feature encoder and image generator in both ReMIC and DL-GIPS methods. The same training strategy is used for ReMIC model as well. Note that in the optimization of ReMIC model, the training losses also contain reconstruction loss, adversarial loss and feature consistency loss (Shen et al., 2020). Thus, the comparison between the ReMIC and DL-GIPS models is mainly focused on different feature learning approaches.

5.2. One-to-One Projection Synthesis

The qualitative results of synthesized projections are demonstrated in Fig. 4 and Fig. 5. Fig. 4 shows the results of synthesized LT projections from AP projections for five testing samples, while Fig. 5 shows the corresponding results of synthesized AP projections from LT projections. Each row shows the results of one testing sample. The columns present the input projection, the output projection from UNet model, the output projection from ReMIC model, the output image from DL-GIPS model, and the ground truth image. The corresponding quantitative results averaged across all the testing data are reported in Table I for both “AP → LT” and “LT → AP”. The evaluation metrics include mean absolute error (MAE), normalized root mean squared error (RMSE), structural similarity (SSIM) (Wang et al., 2004) and peak signal noise ratio (PSNR).

Fig. 4.

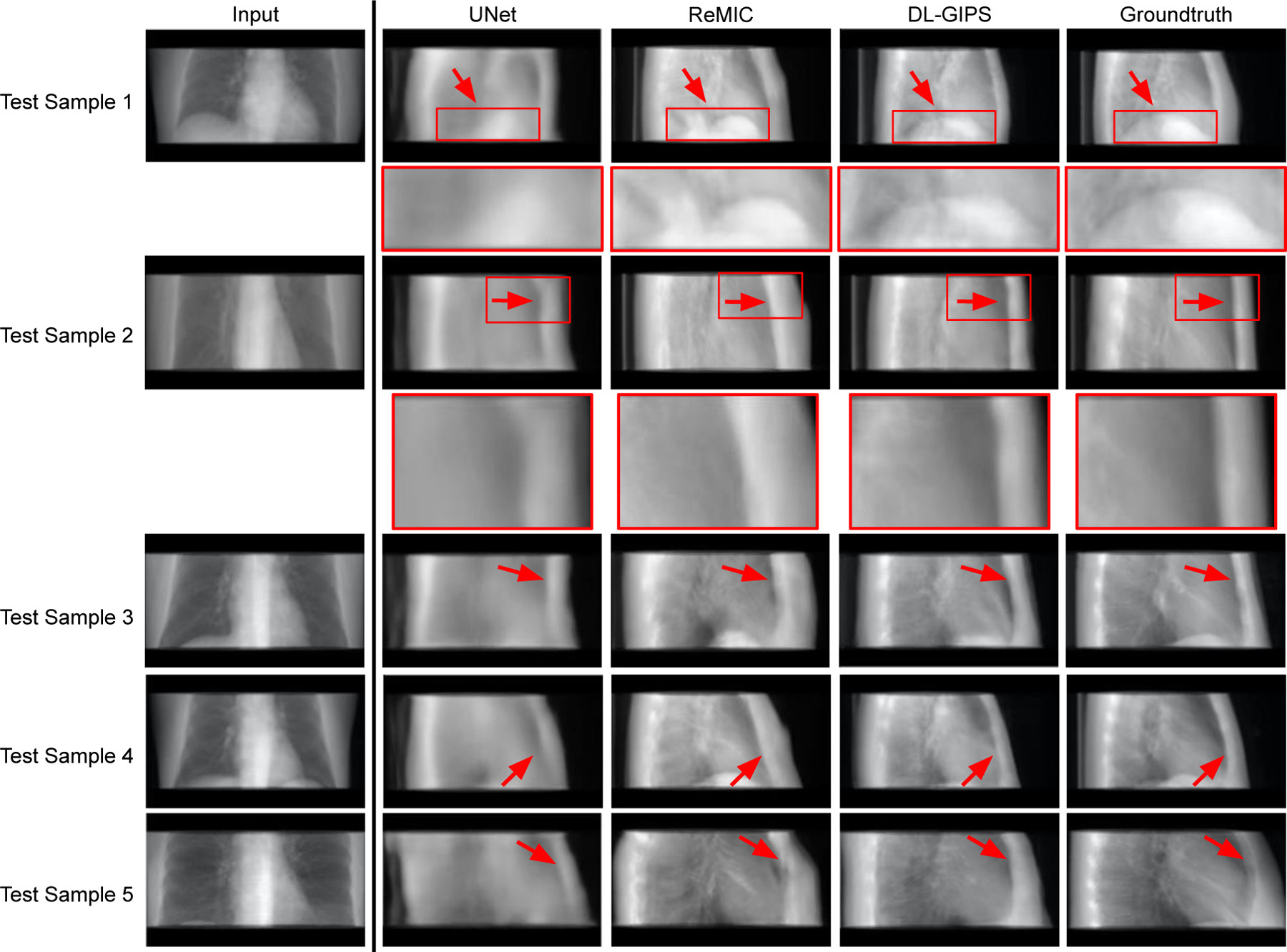
Results of synthesized lateral projection from AP projection. Each row shows the results of one testing sample. Regions of interest are zoomed in for more clear comparison in structural details. The columns are input projection, UNet synthesized projection, ReMIC synthesized projection, DL-GIPS synthesized projection, and the ground truth projection, respectively. (Red arrows highlight the compared difference among different images.)

Fig. 5.

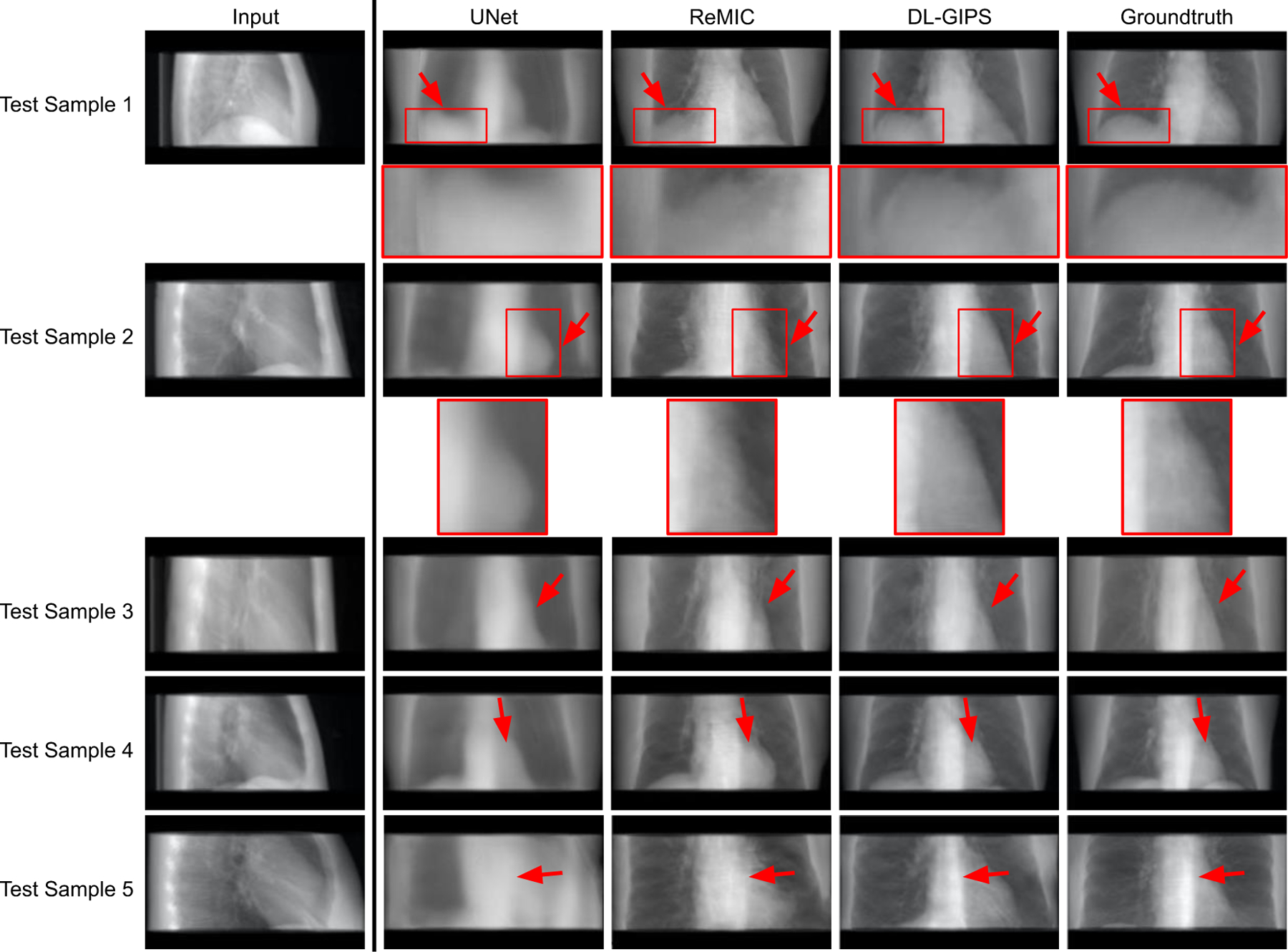
Results of synthesized AP projection from lateral projection. Each row shows the results of one testing sample. Regions of interest are zoomed in for more clear comparison in structural details. The columns are input projection, UNet synthesized projection, ReMIC synthesized projection, DL-GIPS synthesized projection, and the ground truth projection, respectively. (Red arrows highlight the compared difference among images.)

TABLE I.

Results of Novel-View Projection Synthesis

Methods	UNet (Ronneberger et al.)				ReMIC (Shen et al.)				DL-GIPS
	MAE	RMSE	SSIM	PSNR	MAE	RMSE	SSIM	PSNR	MAE	RMSE	SSIM	PSNR
AP → LT	0.069	0.296	0.838	19.312	0.058	0.239	0.854	20.305	0.045	0.185	0.880	22.646
LT → AP	0.070	0.302	0.887	20.675	0.049	0.200	0.900	22.723	0.042	0.173	0.911	23.908
Multi→Multi	0.027	0.118	0.941	27.838	0.029	0.126	0.933	27.005	0.024	0.106	0.941	28.658

From both qualitative and quantitative results, we can see that the proposed DL-GIPS model obtains more accurate synthesized projections especially about the illustration of the human body and organs in terms of the shape, contour and size. For example, the synthesized projections obtained by DL-GIPS model get more accurate human body contours, as pointed out by the red arrows in Fig. 4. Besides, as shown in the Fig. 5, the projection images synthesized by the DL-GIPS model obtain a better shape estimation of the heart and liver denoted by the red arrows. These advantages result from the proposed geometry transformation and feature disentanglement in the DL-GIPS model. In the ReMIC model, although the learned features extracted from images are also disentangled as the shared content feature and the view-specific style feature (Shen et al., 2020), there is no explicit or implicit geometry priors to guide the feature transformation across different view angles in the feature disentanglement. Therefore, in term of human body structure and internal anatomy, the proposed DL-GIPS model is able to generate more accurate results than the ReMIC model. Moreover, the synthesized images of DL-GIPS model contain more accurate details in the bone and lung region compare with the UNet model, which results from the adversarial loss in the model training. But we also notice that the adversarial loss may also introduce inaccuracy in some cases such as the unclear liver region in the testing sample 4.

5.3. Multi-to-Multi Projection Synthesis

In the experiments of multi-to-multi projection synthesis, the model is further developed to simultaneously generate multiple projections from the given multiple source views. To be specific, the model aims to synthesize the projections at the view angle of 30-degree and 60-degree when given the AP and LT projections at 0-degree and 90-degree. In Fig. 6, we show the results of five testing samples in rows respectively. The columns display the input projections, UNet results, ReMIC results, DL-GIPS results and the ground truth projections at two different output angles, respectively. We also compute the quantitative evaluation metrics averaged across all the testing samples and report in Table I as “Multi→Multi”.

Fig. 6.

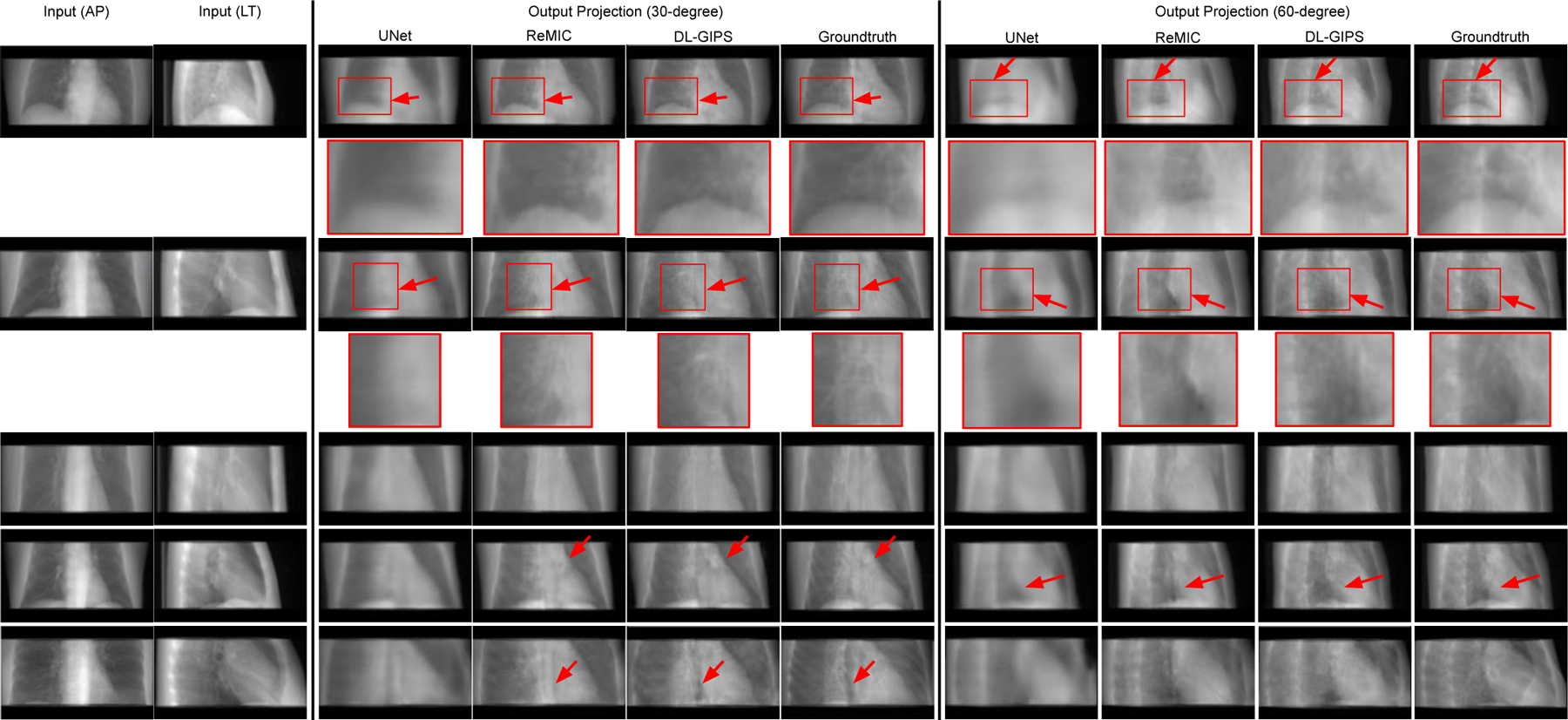
Results of synthesizing projections at the view angle of 30 degrees and 60 degrees from AP and lateral projections. Each row shows the results of one testing sample. Regions of interest are zoomed in for more clear comparison in structural details. The columns are the input projections, UNet synthesized projections, ReMIC synthesized projections, DL-GIPS synthesized projections, and the ground truth projections respectively. Please note that the model outputs the two target projections at 30 degrees and 60 degrees at one time. (Red arrows highlight the compared difference among images.)

First of all, these results show that the proposed DL-GIPS method is a general projection synthesis approach that can be generalized to accept multiple source-view projections and predict multiple target-view projections. Furthermore, we see that more input projections can provide more information for the underlying subject and synthesize more accurate novel-view projections compared with the ground truth, especially for the structure of bones, organs, and soft tissues. Thus, this indicates the source-view projections can always be increased adaptively to obtain more precise synthesized projections according to the different requirements in specific practical applications.

In comparison methods, we also observe the increased source-view projections and the increased target-view supervisions also help the UNet and ReMIC models to generate better synthesized images than the results in one-to-one projection synthesis. Due to this, UNet model can provide more reasonable structures of human body and organs in the synthesized projections despite without precise details, which even gets better quantitative results than ReMIC model in Table I. This is also because the ReMIC model synthesizes some inaccurate details due to the adversarial training loss. Similar phenomenon was also found in previous works (Ying et al., 2019) that the adversarial loss brings the trade-off between the qualitative image qualities and the quantitative evaluation scores using the metrics like MAE, SSIM, PSNR.

In the proposed DL-GIPS model, the geometry priors and integrated transformation relief such disadvantages, which not only gets correct anatomic structures with high SSIM score, but also synthesizes precise fine details with high PSNR score, as reported in Table I. Besides, as shown in Fig. 6 the synthesized projections from DL-GIPS model obtain more accurate anatomy structures pointed out by the red arrows.

5.4. Feature Visualization

Finally, we visualize the feature maps to better understand the projection synthesis procedure. Fig. 7 shows the geometry features extracted from AP and LT views and also demonstrates the texture features as introduced in the pipeline of Fig. 2. It is observed that the geometry features highlight the shape, contour and boundary of the chest including organs, bones and thoracic wall. Furthermore, the geometry features from AP and LT view angles are correlated through the geometric transformation. Unlike the geometry features, the texture features focus more on the appearance textures and the fine details of the chest with different contrasts. In this way, by combining the texture features and geometry features, the DL-GIPS model can synthesize the corresponding projections at novel-view angles.

Fig. 7.

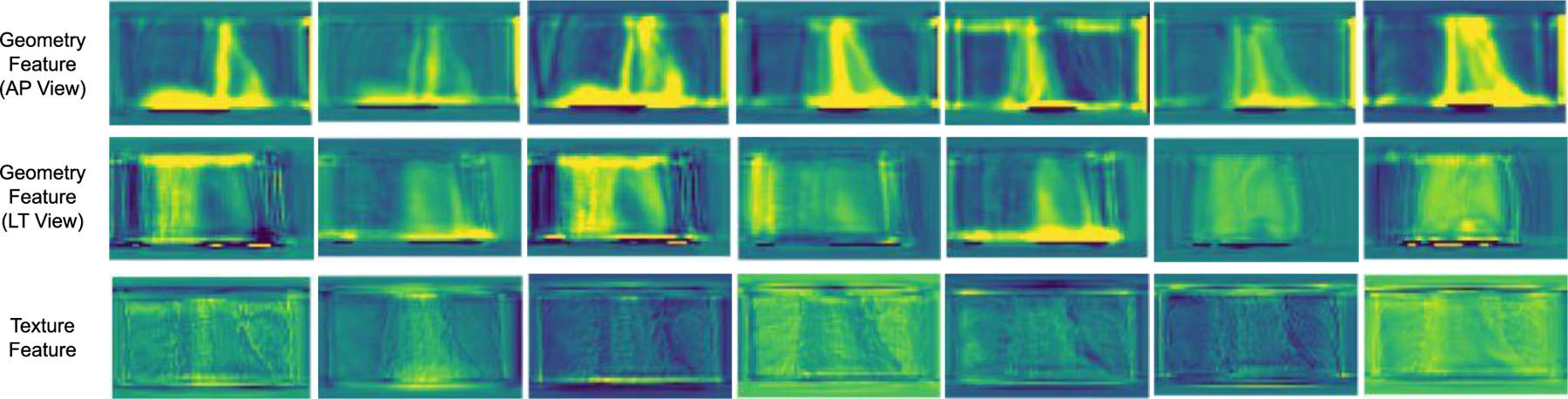
Feature map visualization. We demonstrate the different features introduced in Fig. 2. The first and the second rows show the geometry feature extracted from AP view and LT view respectively. The final row shows the texture features extracted from source view as shown in Fig. 2.

5.5. Ablative Study

In order to further analyze the proposed DL-GIPS model, we conduct the ablative study experiments for studying the necessity of different losses introduced in the total loss objective. Firstly, we train the DL-GIPS model under the same experimental settings while removing the consistency loss. In Table II, we report the results of ablative study with averaged quantitative metrics across all the testing samples, which includes MAE, RMSE, SSIM and PSNR. According to the results, the consistency loss can improve the synthesized images especially in one-to-one projection synthesis, as the feature consistency loss makes the semantic information transferred more smoothly. In the experiments of multi-to-multi projection synthesis, more given input information makes the task easier, and thus, the consistency loss does not make an obvious improvement in this case.

TABLE II.

Results of Ablative Study on Loss Function

Methods	DL-GIPS w/o Consistency Loss				DL-GIPS
	MAE	RMSE	SSIM	PSNR	MAE	RMSE	SSIM	PSNR
AP → LT	0.050	0.212	0.860	21.558	0.045	0.185	0.880	22.646
LT → AP	0.046	0.187	0.902	23.193	0.042	0.173	0.911	23.908
Multi→Multi	0.024	0.107	0.941	28.666	0.024	0.106	0.941	28.658

Then, we conduct ablative study by removing the adversarial loss. As the results shown in Fig. 8, the synthesized projections without adversarial loss are obviously blurry. Thus, adding the adversarial loss helps the model to obtain more fine details and achieve better visualized image quality, which is important to the radiologists in the practical applications.

Fig. 8.

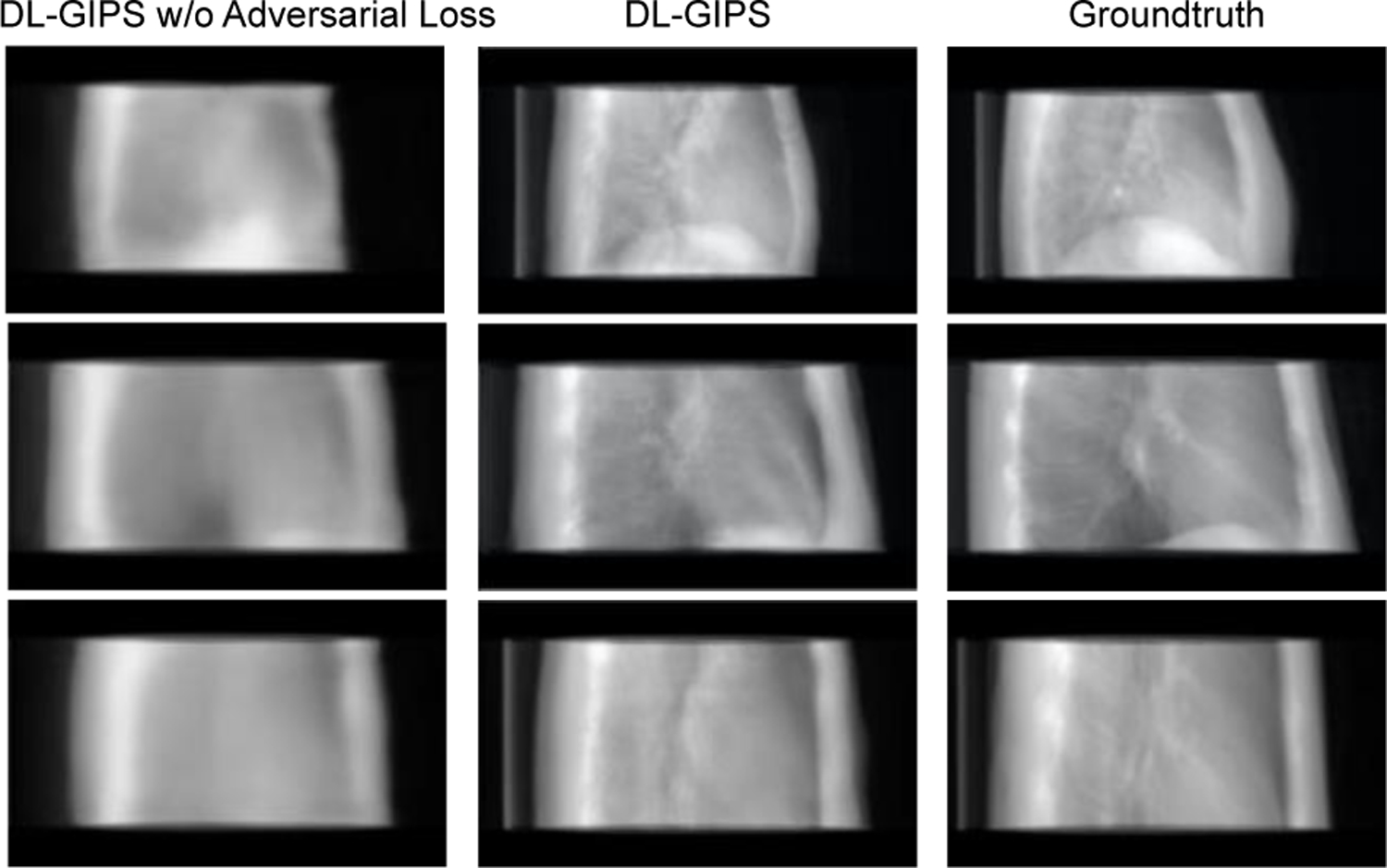
Qualitative results of ablative study for synthesizing LT projection from AP projection. Each row shows results of one testing sample. Columns are synthesized projections for DL-GIPS without adversarial loss, DL-GIPS synthesized projection, and ground truth projection.

In addition, since both ReMIC and DL-GIPS models use the same backbone model structures for feature encoder and image generator, with the same training losses, the comparison results between ReMIC and DL-GIPS models as shown in Figs. 4–6 and Table I demonstrate the superiority of geometric feature transformation in view synthesis. This indicates that the geometry priors introduced in DL-GIPS model structure help to reconstruct more reliable object structures.

Beyond the above, we also conduct the ablation study of the model structure on the learned feature dimensions. In the proposed DL-GIPS model structure, a key module is the geometry feature and texture feature encoder and decoder. Thus, we investigate how the learned feature dimensions would influence the final performance of view synthesis. The ablation experiments are conducted in the AP → LT task. The results for variant feature dimensions in the model structure are shown in Table III. For fixed geometry (texture) feature dimension, increasing texture (geometry) features lead to better performance of view synthesis, as this transfers more useful information through feature encoding and decoding for generating novel-view projection images. This also indicates that both geometry features and texture features are necessary representation learning to synthesize novel-view projections.

TABLE III.

Results of Ablative Study on Model Structure (AP → LT)

Geometry feature dimension	Texture feature dimension	Metrics
		MAE	RMSE	SSIM	PSNR
32	64	0.045	0.185	0.880	22.646
32	32	0.050	0.212	0.862	21.560
16	32	0.058	0.239	0.854	20.602

6. Discussion

In this work, we tackle the problem of novel-view synthesis for X-ray projections and propose a deep learning-based DL-GIPS network. It is shown that the proposed model is able to generate the X-ray projection at the target-view angle with the given source-view projection. The synthesized X-ray projections can be utilized for numerous practical applications, such as gaining comprehensive perspectives of the patient anatomy (Ge et al., 2019), tumor target localization and patient setup in image guided radiation therapy (Zhao et al., 2021), to ultra-sparse CT image reconstruction (Shen et al., 2021), and so forth. Specifically, for clinical usage, when the 3D tomographic image is not available for various reasons (such as limited accessible angles for imaging and restriction in imaging dose, e.g. pediatric and/or pregnant patients), synthetic projections at different view angles could help to better visualize the patient’s anatomy for tumor target localization and patient setup in image guided radiation therapy. In another example, in MRI-guided radiation therapy, for real-time guidance, current MRI-LINAC acquires only 2D images instead of 3D images. The current framework could provide an effective way to provide complementary multi-view 2D images in this case.

The proposed DL-GIPS model adopts the geometry priors of X-ray imaging model to transform the geometry features and relate the source and target view angles. Such a geometric transformation is derived from the X-ray imaging system and properly integrated with the deep learning networks in the proposed approach. Beyond the proposed approach, there may be more advanced methods to leverage the geometry priors especially in medical imaging. For example, the other image modalities of the same patients such as Magnetic Resonance Image (MRI) can also provide the prior information of anatomic structure for the same patient, which may further contribute to synthesizing the fine details in the novel-view X-ray projections.

Computational efficiency of the current method is still not ideal. The incorporation of geometry transformation increases the time consumption as compared with the standard deep learning model training process. In the experiment setting of one-to-one projection synthesis, the inference time of one data sample for different methods are around: 0.04 s, 0.05 s, 0.56 s for UNet, ReMIC, and DL-GIPS models respectively. How to speed up this process by, for examples, CUDA acceleration, parallel computing and more efficient model design, represents an interesting direction of future research.

In real CT data, there may be some specific issues that need further attention. For instance, data truncation is a common issue for most deep learning-based approaches for CT imaging and has raised a lot of attention in recent research. For example, in the recent work (Huang et al., 2021), the authors proposed a method for truncation correction in CT by extrapolating the projections. This problem is orthogonal to the view synthesis problem studied in our work and can naturally become another useful future research direction following our work.

7. Conclusion

This work investigates a strategy of the synthesis of novel-view X-ray projections and presents a robust model combining the deep learning and geometry transformation. It is shown that the generated X-ray projections reveal the internal anatomy distribution from new viewpoints, which may be utilized for numerous practical applications, such as gaining complementary perspectives of the patient anatomy, tumor target localization and patient setup in image guided radiation therapy, while reducing the overhead associated with actual projection measurements, such as reducing the extra radiation dose and speeding up the imaging process. Finally, the proposed projection synthesis has the potential to significantly simply the clinical workflow and provide a new paradigm for various stereoscopic and volumetric imaging procedures with substantially reduced efforts in data acquisition.

Highlights.

• We for the first time investigate the novel-view projection synthesis problem for X-ray imaging. The approach can also be generalized to a more general synthesis from multi-views to multi-views projections.

• We propose a deep learning-based geometry-integrated projection synthesis model (DL-GIPS) to generate novel-view X-ray projections through feature disentanglement and geometry transformation.

• We validate the feasibility of the proposed approach by experimenting on the one-to-one and multi-to-multi X-ray projection synthesis using lung imaging cases across various patients.