Performance of Molecular Mechanics Force Fields for RNA Simulations: Stability of UUCG and GNRA Hairpins

Abstract

The RNA hairpin loops represent important RNA topologies with indispensable biological functions in RNA folding and tertiary interactions. 5′-UNCG-3′ and 5′-GNRA-3′ RNA tetraloops are the most important classes of RNA hairpin loops. Both tetraloops are highly structured with characteristic signature three-dimensional features and are recurrently seen in functional RNAs and ribonucleoprotein particles. Explicit solvent molecular dynamics (MD) simulation is a computational technique which can efficiently complement the experimental data and provide unique structural dynamics information on the atomic scale. Nevertheless, the outcome of simulations is often compromised by imperfections in the parametrization of simplified pairwise additive empirical potentials referred to also as force fields. We have pointed out in several recent studies that a force field description of single-stranded hairpin segments of nucleic acids may be particularly challenging for the force fields. In this paper, we report a critical assessment of a broad set of MD simulations of UUCG, GAGA, and GAAA tetraloops using various force fields. First, we utilized the three widely used variants of Cornell et al. (AMBER) force fields known as ff94, ff99, and ff99bsc0. Some simulations were also carried out with CHARMM27. The simulations reveal several problems which show that these force fields are not able to retain all characteristic structural features (structural signature) of the studied tetraloops. Then we tested four recent reparameterizations of glycosidic torsion of the Cornell et al. force field (two of them being currently parametrized in our laboratories). We show that at least some of the new versions show an improved description of the tetraloops, mainly in the syn glycosidic torsion region of the UNCG tetraloop. The best performance is achieved in combination with the bsc0 parametrization of the α/γ angles. Another critically important region to properly describe RNA molecules is the anti/high-anti region of the glycosidic torsion, where there are significant differences among the tested force fields. The tetraloop simulations are complemented by simulations of short A-RNA stems, which are especially sensitive to an appropriate description of the anti/high-anti region. While excessive accessibility of the high-anti region converts the A-RNA into a senseless “ladder-like” geometry, excessive penalization of the high-anti region shifts the simulated structures away from typical A-RNA geometry to structures with a visibly underestimated inclination of base pairs with respect to the helical axis.

Introduction

RNA is an unbranched, linear polymer composed of four nucleotide units, A, C, G, and U. RNA molecules are usually single-stranded and fold back upon themselves. The 2′-OH group of ribose, absent in DNA, is a powerful donor and acceptor of hydrogen bonds (H-bonds) that is involved in an astonishing repertoire of non-Watson–Crick (noncanonical) interactions. The noncanonical interactions are essential features of RNA three-dimensional structure, dynamics, function, and evolution. Folded RNA molecules typically form short antiparallel double helices by aligning Watson–Crick-complementary stretches of a sequence. These canonical RNA double helices alternate with regions of nucleotides not forming canonical base pairs, i.e., formally unpaired regions. The secondary (2D) structure depicts canonical regions of the folded RNA molecule through the display of parallel lines representing canonical duplex RNA. All of the remaining nucleotides are shown as unpaired loops in such 2D plots. Although these are called loops, these nominally unpaired regions are usually precisely structured via noncanonical interactions and are of the utmost importance for RNA structure and function. The 2D structures of loops can be formally classified as hairpin loops formed by a single-strand segment folded on itself to terminate a helix, internal loops having two strand segments that occur between two helices, and multihelix junctions consisting of multiple-strand segments.^1,2

The most frequently observed and functionally important hairpin loops are tetraloops (TLs), which cap canonical helices with four loop bases, abbreviated as L1–L4 in this paper. TLs facilitate the backbone inversion required for the formation of secondary and tertiary structures.^3–7 Among all possible combinations,⁸ YNMG and GNRA (Y stands for pyrimidine, N for any nucleotide, M for adenine or cytosine, and R for purine), TL families are the most abundant.⁵ These TL families are exceptionally thermodynamically stable (namely, when the TL is closed by CG base pairs in the stem),⁹ have well-defined structures, and are involved in many biologically relevant processes. In general, TLs initiate folding of RNA structures^3,4,10 and are important interaction sites for tertiary contacts.^11–13

UNCG Tetraloop.

The UNCG TLs (a subfamily of the YNMG family) nucleate RNA global folding.³ This tetraloop displays poor binding to natural ligands except cations and is not involved in RNA/RNA interactions. Experimental structures of this loop display very limited structural variability.^14–17 The most stable of UNCG TLs (UUCG, see Figure 1) has been extensively studied by several authors. Sakata showed that the 2′-OH groups of U_L1, C_L3, and G_L4 and the amino group of G_L4 are responsible for the thermodynamic stability of the UUCG motif.¹⁸ Later Williams and Hall studied the role of 2′-OH groups of all nucleobases through ribose to 2′-deoxyribose mutations. They concluded that the most significant effect was observed for U_L1(2′-OH) deletion.^19,20

Figure 1.

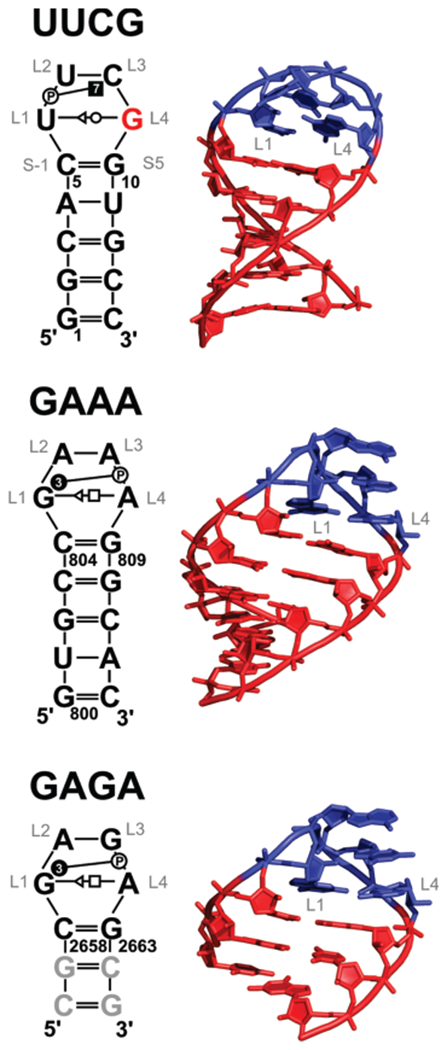
(Left) Secondary structures of the studied systems with base pairing and base–phosphate interactions annotated according to the standard classifications.^21,23 G_L4 of the UUCG tetraloop having syn orientation is highlighted in red. The modeled GC pairs in the GAGA system are shown in gray. The loop residues are labeled as L1–L4 to avoid context numbering. For instance, U6 of UUCG is labeled as U_L1. (Right) Three-dimensional structures of studied systems. The A-RNA stem part is shown in red, while the tetraloop nucleotides are in blue.

The first NMR experiments identified the trans-Watson–Crick/sugar-edge (tWS)²¹ G_L4/U_L1 base pair with the U_L1(O2′)•••G_L4(O6) H-bond as a signature interaction of the UUCG TL.²² The NMR structure further revealed extensive stacking interactions and C_L3(N4)•••U_L2(pro-R_p) base phosphate interaction type 7 (7BPh),²³ which are considered as the main source of the high thermodynamic stability.^17,22 The X-ray structures agreed well in the overall topology of the UUCG TL and unraveled two additional U_L2-(O2′)•••G_L4(N7) and C_L3(O2′)•••C_L3(O2) H-bonds.¹⁴ The latest NMR experiments of Schwalbe et al. gained an ultra-high resolution of 0.25 Å for the loop region (0.3 Å for the stem region).¹⁷ The structure confirmed the tWS G_L4/U_L1 base pair with its characteristic U_L1(02′)•••G_L4(O6) H-bond and 7BPh interaction between C_L3(N4) and U_L2(pro-R_p). Sugars of U_L2 and C_L3 adopted the C2′-endo puckering in agreement with the X-ray structure.

The stability of UUCG TL was also extensively studied by molecular dynamics (MD). Miller and Kollman²⁴ observed the destabilization of the U_L1(O2′)•••G_L4(O6) H-bond in explicit solvent MD simulations with the AMBER Cornell et al. ff94 force field and argued that the U_L1(O2′)•••G_L4(O6) interaction cannot be considered as the main source of the exceptional thermodynamic stability of the UUCG TL.²⁵ However, as we will demonstrate below, the loss of the signature U_L1(O2′)•••G_L4(O6) H-bond in simulations was in fact due to the imperfectness of the force field. The exceptional thermodynamic stability and structural features of UUCG TL were also addressed in many recent theoretical studies including replica exchange molecular dynamics and umbrella sampling PMF calculation.^26–30

GNRA Tetraloops.

Contrary to UNCG, GNRA TLs primarily mediate RNA tertiary interactions. An analysis of X-ray structures shows striking geometrical conservation also for the GNRA TLs.⁸ Structural adaptations in GNRA TL–TL receptor complexes typically includes changes of the TL receptor while the TL is stiff.³¹ Williams and co-workers identified 21 examples of standard TLs with the GNRA-like topology in the 2.4 Å resolution X-ray structure of Haloarcula marismortui (H.m.) large ribosomal subunit.⁸ Although they occur in variable contexts within the ribosomal subunit, they adopt virtually identical geometries. The study further identified many hairpin loops with nucleotide insertions, deletions, switches, or strand clips which also adopt very similar 3D structures. Nevertheless, for the GNRA TLs, other experimental methods furnish evidence supporting their conformational dynamics, although in some cases the flexibility can also reflect error margins and inaccuracies in the experiments (see below). Note that even in the lower-resolution ribosomal X-ray structure data, refinement and noise inaccuracies cannot be ruled out as sources of error. For example, this may introduce syn/anti bias^32,33 and perhaps obscure the exact hairpin loop structures in some cases.

The first information about structural features of GNRA TL came from NMR³⁴ and lower resolution (~3 Å) X-ray structures.^35,36 The high-resolution structures of the sarcin/ricin loop (SRL) domain of the large ribosomal subunit^37–40 together with a structural analysis⁸ of the large ribosomal subunit⁴¹ and NMR experiments^42,43 furnished in-depth insight into common features of the native fold of GNRA TLs. They include the trans Hoogsteen/sugar-edge (tHS) A_L4/G_L1²¹ base pair; three signature H-bonds, namely, the G_L1(N1/N2)•••A_L4(pro-R_p) 3BPh interaction, G_L1(N2)•••A_L4(N7), and G_L1(O2′)•••R_L3(N7) (Figure 2); and stacked N_L2, R_L3, and A_L4 bases. The backbone of GNRA TLs adopts classic U-turn topology. Contrary to UNCG TL, some structural variability of GNRA TLs is anticipated because, for instance, protein ribotoxin restrictocin binds an unfolded GNRA TL.⁴⁴ However, the majority of GNRA TLs (~80%) adopt the canonical structure.³⁷ The question whether ribotoxins induce the conformation change or capture a temporarily unstructured GNRA TL remains open. The dynamics of GNRA TL are the subject of intensive experimental^43,45–49 and theoretical studies.^50–52

Figure 2.

Signature H-bonds (black dashed lines) of UUCG and GAAA tetraloops on the left and right sides, respectively.

Due to their small size, TLs have been a genuine target for simulation studies.^{19,26–30,50,53,54} The simulation studies in general indicate rather substantial flexibility of the TLs, which exceeds variability that is inferred from atomic resolution experiments (see above), suggesting that simulations can be affected by the quality of force fields, typically parametrized keeping in mind the representation of regular helices, not compact irregular structures.^55–57

In the present study, we investigate the structural dynamics of three representatives (UUCG, GAGA, and GAAA) of the UNCG and GNRA TL families. The aim of the paper is two-fold: first, to get insights into the balance of forces in the TLs and, second, to better understand the performance of molecular mechanics force fields for these difficult systems. The TL simulations are supplemented by simulations of short A-RNA stems. We selected four widely used force fields for nucleic acids: three AMBER (Cornell et al.) force fields, ff94,²⁵ ff99,⁵⁸ and ff99bsc0,⁵⁹ and CHARMM27.⁶⁰ The ff99 and ff99bsc0 simulations were also performed at higher ionic strength using excess KCl salt to check the impact of ionic strength on the TL structure and dynamics.⁶¹ Besides using the above established force fields, four recent reparameterizations (two of them from our laboratories) of χ glycosidic torsion of the AMBER force field are tested. They are combined with ff99 and ff99bsc0 force fields (see the Methods for details). These χ modifications were derived recently primarily on the basis of quantum-chemical (QM) computations but were not extensively tested in real simulations. Despite centering on high-level QM calculations, results from the reparameterizations differ considerably as different models and very different levels of QM computations were applied. Thus, in total, the performances of 12 RNA force field variants and combinations were considered (CHARMM27, ff94, ff99, ff99bsc0, and the last two in combination with four χ modifications).

Methods

Starting Structures.

The starting structure of UUCG TL was taken from the high-resolution NMR structure (PDB ID: 2KOC).¹⁷ The GAAA TL was taken from the X-ray structure of a large ribosomal subunit of Haloarcula maristumortui (PDB ID, 1JJ2; mean resolution, 2.40 Å residues 800–813).⁶² The GAGA TL was derived from the high-resolution X-ray structure determined at 1.04 Å resolution of the sarcin–ricin loop (SRL; PDB ID, 1Q9A; residues 2658–2663)³⁹ and capped by two additional C/G base pairs. Short A-RNA stems were built using NAB available from the AmberTools package.⁶³

AMBER Simulation Protocol.

We performed classical MD simulations using well established simulation protocols.^57,61,64 Missing hydrogen atoms were added by the LeaP module of the AMBER package on the basis of standard residue templates. Each system was neutralized by Na⁺ counterions (radius = 1.868 Å and well depth = 0.00277 kcal/mol) and immersed for the MD simulation in a rectangular water box (TIP3P)⁶⁵ with a 10-Å-thick layer of water molecules (60 × 50 × 45 ų for UUCG and GAAA and 40 × 45 × 50 ų for GAGA systems). The RNA–solvent system was minimized prior to the AMBER simulation as follows. Minimization of the solute hydrogen atoms was followed by minimization of counterions and water molecules. Subsequently, the hairpin was frozen, and solvent molecules with counterions were allowed to move during a 10-ps-long MD run, the purpose of which is to relax the density of the system. After that, the nucleobases were allowed to relax in several minimization runs with decreasing force constants applied to the backbone phosphate atoms. After full relaxation, the system was slowly heated to 298.15 K over 100 ps using 2 fs time steps and NpT conditions using a weak-coupling scheme with a coupling time of 1 ps.⁶⁶ The simulations were carried out under periodic boundary conditions (PBC) in the NpT ensemble (298.15 K, 1 atm) with 2 fs time steps. The particle-mesh Ewald (PME) method^67,68 was used to calculate electrostatic interactions with a cubic spline interpolation and ~1 Å grid spacing, and a 10.0 Å cutoff was applied for Lennard-Jones interactions with automatic rebuilding of the buffered pair list when atoms moved more than 0.5 Å. The SHAKE algorithm was applied to fix all bonds containing hydrogen atoms. The SANDER module of AMBER 10.0⁶³ was used for simulations.

AMBER Force Fields.

Standard AMBER force fields ff94,²⁵ ff99,⁵⁸ and ff99bsc0⁵⁹ were used for simulations. In addition, simulations were performed also with four variants of alternative profiles of the glycosidic χ torsion that were suggested recently as modifications of the ff99 force field:

1. The Ode et al.⁶⁹ χ parameters are based on quantum chemical profiles obtained with high-accuracy in vacuo MP2/aug-cc-pVTZ//HF/6-31+G(d,p) energy calculations on small model compounds. The force field has been suggested to be compatible with both ff99 and ff99bsc0 basic parametrizations, and the respective simulations are henceforth labeled as ff99χ_ODE and ff99bsc0χ_ODE in the present paper. Note that this force field has not been tested in production runs so far except in our recent study on G-DNA quadruplexes, where it was shown to bring no advantage over the ff99 and ff99bsc0 force fields.

2. Reparameterization against the lower-quality in vacuo QM profile (MP2/6-31G(d)//HF/6-31G(d) level) of ribonucleosides of Yildirim et al.⁷⁰ was performed. The force field has not been tested for RNA simulations so far, but it was shown to improve the syn vs anti balance in nucleoside simulations. Although the original paper does not acknowledge the latest ff99bsc0 parametrization and considers the χ parameters exclusively in the context of ff99, we decided to test its performance with both ff99 and ff99bsc0. The respective simulations are marked as ff99χ_YIL and ff99bsc0χ_YIL.

3. Reparameterization based on a high-quality dispersion-corrected⁷¹ DFT QM profile (PBE/6-311++G(3df,3pd)/D-1.06–23//PBE/6-311++G(3df,3pd)/COSMO method) of deoxyribonucleosides in a continuum water environment (this work and Zgarbova et al., manuscript in preparation) labeled as ff99χ_OL-DFT and ff99bsc0χ_OL-DFT was performed. (The label OL stands for Olomouc, see affiliations.)

4. Reparameterization based on the high-level QM profile (MP2/CBS//PBE/6-311++G(3df,3pd)/COSMO method) in continuum water considering weighted parameters for C2′-endo deoxyribose and C3′-endo ribose was performed; this variant is labeled ff99χ_OL and ff99bsc0χ_OL (this work and Zgarbova et al., manuscript in preparation).

The OL-DFT and OL parameter files are provided in the Supporting Information, while a full account of the parametrizations including extensive testing will be given separately (Zgarbova et al., manuscript in preparation). The OL force field should be considered as the final version; nevertheless, we also provide some results obtained with the preliminary OL-DFT version, as it provides important insights into the sensitivity of the results to the parametrization.

Note that the modified χ profiles are entirely independent of the recent ff99bsc0 reparameterization of the α/γ torsional profile, and therefore the ff99bsc0 force field is to be independently cited if applied together with any of the χ terms. The ff99bsc0 is essential, particularly for DNA, in modification of the preceding versions of the AMBER Cornell et al. force fields.

To assess effect of salt concentration on the stability of TLs, reference simulations under KCl salt excess (c(K⁺) ~ 0.45 mol/L, c(Cl⁻) ~ 0.22 mol/L) conditions and using the SPC/E water model⁷² were carried out. Parameters for K⁺ (radius, 1.593 Å well depth, 0.4297 kcal/mol) and Cl⁻ (radius, 2.711 Å well depth, 0.012 kcal/mol)⁷³ were used.

CHARMM Simulations.

MD simulations of selected systems were also carried out with the CHARMM all27 force field⁶⁰ with the NAMD⁷⁴ package (ver. 2.6) using the following protocol. To avoid any differences in starting geometries, the neutralized and solvated system prepared for AMBER simulations was used as a starting structure to prepare CHARMM27 topologies and coordinates in the CHARMM⁷⁵ software package (ver. 34b2). The waters and counterions were minimized in 2500 steps and shaken by short NpT dynamics (100 ps) at 300 K and 1 atm. The system was minimized prior to simulation in 3000 steps and then slowly heated to 300 K over 100 ps using 1 fs time steps and NpT conditions using Langevin dynamics.^76,77 The simulation was produced under periodic boundary conditions in the NpT ensemble (300 K, 1 atm) with 1 fs time steps, because the 2 fs integration step produced considerably less stable trajectories for A-RNA stems. The particle-mesh Ewald method was applied to calculate electrostatic interactions (PME tolerance 10⁻⁶), and a 12.0 Å cutoff with an 8.0 Å switching distance was applied for Lennard-Jones interactions. The protocol applied performed well in test simulations on the B-DNA structure, in agreement with literature data.⁷⁸

Table 1 summarizes all simulations analyzed in this study. The simulations were initially intended to be extended to 100 ns. However, some simulations were terminated earlier because of a major degradation of the TLs, i.e., an unfolding event in UUCG_charmm and the formation of a “ladder-like” structure in GAGA_bcs0, GAGA_99χ_ODE, and GAGA_bsc0χ_ODE simulations. On the other hand, the simulations carried out with reasonably performing force fields were extended to 300 ns (ff99bsc0χ_YIL and ff99bsc0χ_OL-DFT) or to 0.8–1.0 μs (ff99bsc0χ_OL) to get better insight into the simulation behavior.

Table 1.

Overview of MD Simulations of TL Systems Carried Out

label	force field	duration (ns)	the first appearance of “ladder-like” structure80 (ns)a
UUCG_94	ff94	50	NO
UUCG_99	ff99	100	NO
UUCG_bsc0	ff99bsc0	100	NO
UUCG_99χODE	ff99χODE	100	NO
UUCG_bsc0χODE	ff99bsc0χODE	100	NO
UUCG_99χYIL	ff99χYIL	100	NO
UUCG_bsc0χYIL	ff99bsc0χYIL	300	NO
UUCG_99χOL-DFT	ff99χOL-DFT	100	NO
UUCG_bsc0χOL-DFT	ff99bsc0χOL-DFT	300	NO
UUCG_99χOL	ff99χOL	100	NO
UUCG_bsc0χOL	ff99bsc0χOL	800	NO
UUCG_charmm	CHARMM27	50	NO
UUCG_99SEb	ff99, KCl SE	100	NO
UUCG_bsc0SEb	ff99bsc0, KCl SE	100	NO
GAAA_99	ff99	50	NO
GAAA_bsc0	ff99bsc0	100	NO
GAAA_99χODE	ff99χODE	100	85
GAAA_bsc0χODE	ff99bsc0χODE	100	NO
GAAA_99χYIL	ff99χYIL	100	NO
GAAA_bsc0χYIL	ff99bsc0χYIL	300	NO
GAAA_99χOL-DFT	ff99χOL-DFT	100	NO
GAAA_bsc0χOL-DFT	ff99bsc0χOL-DFT	300	NO
GAAA_99χOL	ff99χOL	100	NO
GAAA_bsc0χOL	ff99bsc0χOL	800	NO
GAAA_charmm27	CHARMM27	100	NO
GAAA_99K+c	ff99, K+	100	95
GAAA_99SEb	ff99, KCl SE	100	NO
GAGA_99	ff99	100	36
GAGA_bcs0d	ff99bsc0	25	20
GAGA_99χODEd	ff99χODE	15	5
GAGA_bsc0χODEd	ff99bsc0χODE	25	21
GAGA_99χYIL	ff99χYIL	100	NO
GAGA_bsc0χYIL	ff99bsc0χYIL	300	NO
GAGA_99χOL-DFT	ff99χOL-DFT	100	NO
GAGA_bsc0χOL-DFT	ff99bsc0χOL-DFT	300	NO
GAGA_99χOL	ff99χOL	100	NO
GAGA_bsc0χOL	ff99bsc0χOL	1000	NO
GAGA_charmm27	CHARMM27	100	NO
GAGA_99SEb	ff99, KCl SE	100	50
GAGA_bsc0SEb	ff99bsc0, KCl SE	100	NO

^a“NO” means not observed.

^bSimulations in excess of KCl salt.

^cSimulation under minimal salt conditions with Na⁺ ions replaced by K⁺.

^dSimulations were terminated because a “ladder-like” structure was irreversibly formed.

Analyses were performed using ptraj (from AmberTools package) and X3DNA.⁷⁹ H-bonds were analyzed using in-house software H-bonds (P. Banáš, http://fch.upol.cz/en/software/) using a 3.1 Å cutoff for the H-bond distance and 40° for the hydrogen–H-bond donor•••H-bond acceptor angle.

Results

Signature Interactions in the Tetraloops.

As explained in the Introduction, the UNCG and GNRA TLs are very precisely structured recurrent RNA motifs that adopt their native structure independently of their contexts. They therefore possess several characteristic (signature) structural features. For the UUCG TL, these include a tWS G_L4/U_L1 base pair, syn conformation of G_L4, and C2′-endo sugar puckers for U_L2 and C_L3 (Figure 1). There are four UUCG signature H-bonds (Figure 2): U_L1(O2′)•••G_L4(O6), G_L4-(N1)•••U_L1(O2), C_L3(N4)•••U_L2(pro-R_p), and U_L2(O2′)•••G_L4(N7). The latter one is seen only in approximately one-third of the high-resolution NMR structurally derived ensembles.¹⁷ U_L1(O2) tends to form a bifurcated H-bond to G_L4(N1) and G_L4(N2) in some X-ray structures.^14–16 On the other hand, the distance between G_L4(N2) and U_L1(O2) is always larger than 3.3 Å in the high-resolution NMR structure¹⁷ (see also Table 2). The C_L3(N4)•••U_L2(pro-R_p) H-bond corresponds to a type 7 base–phosphate interaction (7BPh²³) between the C_L3 base and U_L2 phosphate.

Table 2.

Basic Structural Characteristics of UUCG TL and H-Bond Populations Calculated from MD Simulations^a

Structures or simulations	GL4(N1)•••UL1(O2) (Å)	CL3(N4)•••UL2(pro-Rp) (Å)	UL2(O2′)•••GL4(N7) (Å)	UL1(O2′)•••GL4(O6) (Å)	UL1 (O2′)•••UL2(O5′) (Å)	GL4 χ (deg)	tSW UL1/GL4 propeller (deg)
NMR	2.7 ± 0.1	2.9 ± 0.1	2.9 ± 0.1	2.6 ± 0.1	3.4 ± 0.1	58 ± 4	−4.3 ± 4.5
X-ray	3.0 ± 0.1	2.9 ± 0.2	4.0 ± 0.5	2.7 ± 0.3	3.8 ± 0.2	60 ± 1	−7.8 ± 7.0
UUCG_94	88%	8%	0%	68%	8%	45 ± 11	−21 ± 11
UUCG_99	87%	9%	2%	65%	8%	48 ± 13	−22 ± 11
UUCG_bsc0	55%	68%	10%	14%	41%	42 ± 18	−32 ± 32
UUCG_99χODE	90%	72%	54%	94%	4%	83 ± 13	−1 ± 13
UUCG_bsc0χODE	74%	66%	50%	70%	18%	75 ± 17	−14 ± 22
UUCG_99χYIL	95%	76%	41%	87%	6%	65 ± 15	1 ± 11
UUCG_bsc0χYIL	92%	77%	46%	89%	6%	69 ± 17	2 ± 11
UUOG_99χOL-DFT	92%	36%	28%	83%	7%	67 ± 14	−8 ± 13
UUCG_bsc0χOL-DFT	93%	70%	50%	88%	9%	76 ± 14	−1 ± 11
UUCG_99χOL	93%	68%	42%	80%	15%	64 ± 15	−5 ± 12
UUCG_bsc0χOL	92%	71%	49%	85%	10%	72 ± 17	−3 ± 12
UUCG_99SE	82%	55%	8%	15%	53%	38 ± 15	−25 ± 12
UUCG_bsc0SE	79%	59%	6%	7%	57%	34 ± 13	−29 ± 11

^aNMR values were averaged from a set of 20 structures taken from PDB 2KOC.¹⁷ X-ray values were averaged from X-ray structures 1F7Y (res. 2.8 Å),¹⁴ 1I6U (res. 2.6 Å),¹⁵ and 1FJG (res. 3.0 Å).¹⁶ Some of the values are presented as average ± standard deviation. H-bond populations are calculated from respective MD simulations of UUCG TL (see Methods).

The GNRA TLs include the tHS A_L4/G_L1 (“sheared”) base pair³⁷ complemented by three H-bonds (Figure 2): G_L1(N2)•••A_L4(pro-R_p) (3BPh interaction, which is altered with the G_L1(N1/N2)•••A_L4(pro-R_p) 4BPh interaction in MD or some X-ray structures), G_L1(N2)•••A_L4(N7), and G_L1(O2′)•••R_L3(N7).⁸ The N_L2, R_L3, and A_L4 bases form a purine triple stack.

UUCG Tetraloop Dynamics.

AMBER Simulations: χ Reparameterizations Maintain Important Signature H-Bonds and Overall Integrity of the Tetraloop.

In all UUCG TL simulations with the standard AMBER force fields (with standard χ torsion, i.e, UUCG_94, UUCG_99, UUCG_bsc0, UUCG_99SE, and UUCG_bsc0SE simulations), we observed a loss of the signature U_L1(O2′)•••G_L4(O6) H-bond immediately after the simulation started. This H-bond was replaced by the U_L1(O2′)•••U_L2(O5′) H-bond (Figure 3A). Despite the fact that the loops still stay, at first sight, locked close to the starting structure, these changes are clear signs of some force field imbalance. Considering the unambiguous structural data, this simulation development is not satisfactory.

Figure 3.

The MD snapshots (colored by atom types) compared with high-resolution NMR structure (in red) showing structural problems seen in simulations of the UUCG tetraloop (some atoms are not shown for clarity, and important parts are shown as sticks). (A) The disruption of the U_L1(O2′)•••G_L4(O6) H-bond and formation of a new U_L1(O2′)•••U_L2(O5′) H-bond observed in all MD simulations with standard χ profiles are highlighted by the blue arrow, while the simultaneous decrease of χ of G_L4 leading to a change in the U_L1/G_L4 propeller is shown by the red arrow. (B) The U_L2 phosphate α/γ flip is depicted by the black arrow. See the text for full details.

Simultaneously with the disruption of the U_L1(O2′)•••G_L4(O6) H-bond, we observed significant propeller twisting (changing from −2° to ~−25°) of the G_L4/U_L1 tWS base pair and mainly a shift of syn G_L4 χ torsion from 60° to 40° in all above-mentioned simulations (Table 2). The same shifts of χ torsion toward lower values in the syn region were also observed for syn G+1 and A38H⁺ nucleobases in ff99 MD simulations of the hairpin ribozyme (Supporting Information, Table S1).⁸⁰ This structural shift comes from the strain in G_L4 χ torsion, as the energy profile of guanosine χ torsion in AMBER ff99 (Supporting Information, Figure S1) shows that the minimum in the syn region equals 40°. On the basis of a structural analysis of the above-mentioned MD simulations, we suggest that the shift of G_L4 χ torsion is the primary source of perturbation of the signature interaction.

All simulations with reparameterized χ torsion prevented the shift of G_L4 χ torsion, and the signature U_L1-(O2′)•••G_L4(O6) H-bond was stable, except in some cases where it was disrupted due to some unrelated perturbations elsewhere in the structure (Table 2). Thus, UUCG_99χ_ODE, UUCG_99χ_OL, UUCG_99χ_YIL, UUCG_bsc0χ_OL-DFT, UUCG_bsc0χ_OL, and UUCG_bsc0χ_YIL were the most stable trajectories keeping all signature H-bonds (Table 2). In other words, stable UUCG TL was observed in all simulations with modified χ torsion parameters, except for UUCG_99χ_OL-DFT, showing an undesired α/γ flip of the U_L1 phosphate (see below) and UUCG_bsc0χ_ODE where a “ladder-like” artifact of C_S-1 and U_L1 χ torsions, described below, occurred. C_S-1 denotes stem cytosine at the 5′ side of the TL, i.e., C5 in the presented model of UUCG (Figure 1). This indicates that the modified χ torsion profiles locally improve sampling within the syn region.

The formation of the U_L1(O2′)•••U_L2(O5′) H-bond in simulations with an unmodified χ profile was likely partially facilitated by modest shifts of ε and ζ torsions of C_S-1 (ε from −126° to ~−150° and ζ from −80° to ~−60°) and U_L1 (ε from −160° to ~−175° and ζ from −100° to ~−90°). This backbone adaptation occurred in entirely all AMBER UUCG simulations in the initial minimization and was irreversible. This shift of ε and ζ torsions moved the U_L2(05′) oxygen closer to the U_L1(2′-OH) hydroxyl (from 3.4 Å in the NMR structure to ~3.0 Å in MD simulations), which supported the formation of the new U_L1(O2′)•••U_L2(05′) H-bond. However, we do not consider this backbone adaptation to be the most crucial force field problem, since in the simulations with reparametrized χ torsions the original U_L1(O2′)•••G_L4(O6) H-bond remains stable despite the ε/ζ shift.

ff99bsc0 Clearly Improves the Stability of γ Angle Distribution.

In the advanced stages of simulations (on the tens of nanoseconds time scale), we evidenced further problems due to a disruption of the C_L3(N4)•••U_L2(pro-R_p) 7BPh interaction in UUCG_94, UUCG_99, and UUCG_99χ_OL-DFT trajectories. This was caused by α/γ flip of the U_L2 phosphate (Figure 3B). The flip involved a shift of α(U_L2) from ~−160° to ~−50°, ε(U_L1 from ~−170° to ~−100°, and γ(U_L2) from ~50° to ~−170°. It further correlated with C3′-endo to C2′-endo U_L2 sugar repuckering. In all cases, the U_L2 phosphate remained distorted until the simulation ended. The γ torsion of the U_L2 phosphate sampled the gauche(+) region in all ff99bsc0 simulations except for UUCG_bsc0χ_ODE and UUCG_bsc0χ_OL, where we also observed weakly populated (population about ~5%) and fully reversible γ-trans substates. Thus, in contrast to ff99 simlations, the bsc0 correction prevents an irreversible α/γ flip of the U_L2 phosphate to γ-trans. The ff99bsc0 force field has been designed to prevent pathological γ-trans substates in B-DNA MD simulations.⁵⁹ It is worth noting that the native position of γ(G_L4) is trans due to a sharp bend of the RNA strand at the tip of UUCG TL. Interestingly, γ(G_L4) kept its native γ-trans orientation in all simulations with ff99bsc0, despite some expectations that ff99bsc0 may occasionally overcorrect the γ-trans substates.^61,64 Clearly, at least when starting simulations from the native structure, ff99bsc0 is superior to ff99 for the UUCG TL, as it prevents one undesired irreversible γ-trans flip while keeping the native γ-trans nucleotide stable.

The Occurrence of High-anti Substates in Correlation with the Force Field Artifact of Forming a “Ladder-Like” Structure.

An almost reversible disruption of the TL signature accompanied by a shift of χ torsions of C_S-1 and U_L1 from the anti to the high-anti region (from ~−150° to ~−90°) and breaking of the G_L4(N1)•••U_L1(O2) and U_L1-(O2′)•••G_L4(O6) H-bonds was observed in UUCG_bsc0 and UUCG_bsC0χ_ODE simulations (Figure 4). The shift of χ torsions to the high-anti region corresponds to a recently discovered common force field artifact named a “ladder-like” structure of RNA stems, because the most characteristic feature of the “ladder-like” structure is a transition of χ torsion to the high-anti region with a value ~−85° (the exact value slightly depends on the system and force field).⁸⁰ In a fully developed “ladder-like” structure of a duplex, besides the shift of the χ torsion, the sugar puckering, ε and ζ torsions, slide, twist, and peaks in the P–P radial distribution function are also modestly affected by the transition, which in addition is not reversible (see ref 80 for more details). In the present simulations, although the C_S-1 and U_L1 χ torsions later returned to the anti region, the signature U_L1-(O2′)•••G_L4(O6) H-bond was not fully stabilized and experienced fluctuations. As will be discussed below, the unmodified ff99 and χ_ODE⁶⁹ parametrizations support the formation of the “ladder-like” artifact, while the remaining three χ reparameterizations appear to prevent its formation. It is entirely consistent with the behavior of UUCG simulations. The independent ff99bsc0 modification of α/γ dihedrals is neutral with respect to the “ladder-like” structure formation.

Figure 4.

Structures of UUCG TL at the beginning of the UUCG_bsc0 simulation, at 50 ns and at 90 ns, showing the distortion of the UUCG tetraloop. C_L3 is not shown, for clarity.

CHARMM Simulations.

The MD simulation of UUCG TL carried out with a CHARMM27 force field showed complete melting during the first 10 ns. This is in full agreement with recently published simulation data from Deng and Cieplak.²⁸ The signature U_L1(O2′)•••G_L4(O6) and G_L4(N1)•••U_L1(O2) H-bonds were broken at ~0.5 ns, and G_L4 departed from its initial position. The C_L3 nucleobase unstacked from U_L1 at9.5ns, breaking its 7BPhC_L3(N4)•••U_L2(pro-R_p) H-bond. The ribose pucker of C_L3 switched from C2′-endo to C3′-endo at 20 ns, and G_L4 switched from a syn to an anti orientation at ~40 ns. Stem base pairs were also not stable and exhibited frequent breathing.

GNRA Tetraloop Dynamics.

In simulations of GNRA TLs with the standard χ AMBER force fields, we typically observed a transition of the A-RNA stem bearing the GNRA TL to the underwound “ladder-like” structure (Figure 5). The “ladder-like” structure is a force field artifact occurring on the tens of nanoseconds time scale, which we first described in our study on hairpin ribozymes.⁸⁰ This transition was always preceded by an irreversible disruption of the GNRA signature. The “ladder-like” structure of the stem bearing GNRA TL occurred with standard AMBER force fields as well as with the χ torsion reparameterization of Ode et al.⁶⁹ (see Table 1). On the other hand, it has been prevented by the other three χ torsion reparameterizations (χ_OL-DFT, χ_OL, and χ_YIL) and was also not observed in CHARMM simulations.

Figure 5.

Ladder-like conformer as observed in a simulation of the GNRA tetraloop with AMBER force fields, unless the χ torsion profile is appropriately modified. Initial geometry is on the left, and “ladder-like” conformer is on the right.

Although the formation of the “ladder-like” structure was shown primarily to be the force field artifact of A-RNA stems⁸⁰ (also see below), a detailed structural analysis, mainly the monitoring of χ torsions, revealed that in our present case the formation of a “ladder-like” structure in the stem was typically preceded by the structural degradation of GNRA TL. Thus, it appears that the loss of the TL integrity facilitates the “ladder-like” transition. Both issues are, however, most likely interconnected. More specifically, the loss of structural integrity of GNRA TL was mainly facilitated by a reversible flip of the β/γ torsions of the R_L3 phosphate from the trans/gauche(+) to the gauche(+)/trans conformation (Figure 6). This β/γ flip increased the buckle of the tHS A_L4/G_L1 base pair from ~5° to ~60° (Figure 6). Although the β/γ flips are reversible, we suggest that the increased A_L4/G_L1 buckle causes some steric strain of the stem–loop junction and accelerates the structural degradations of the system including a transition of the stem to a “ladder-like” structure (when the force field does not prevent this “ladder-like” artifact).

Figure 6.

Typical progression of GNRA tetraloop AMBER simulations. Left: simulations without the χ correction or with Ode et al.’s correction illustrated by a 25 ns GAGA_bsc0 simulation. Right: simulations with χ_OL-DFT, χ_OL, and χ_YIL variants illustrated by a 1 μs GAGA_bsc0χ_OL simulation. The upper graphs present a time evolution of the β(G_L3) torsion (black line), γ(G_L3) torsion (red line), and mean χ torsion averaged over either stem nucleobases (green line) or the GNRA tetraloop (blue line). The middle graph shows the G_L1/A_L4 buckle, and the lower graph presents the GNRA tetraloop signature H-bonds: G_L1(N2)•••A_L4(N7), G_L1(N2)•••A_L4(pro-R_p), and G_L1(O2′)•••G_L3(N7) in black, red, and green, respectively.

As noted above, we did not observe any formation of a “ladder-like” structure in the simulations with χ_OL-DFT, χ_OL and χ_YIL reparameterizations. However, simulations with ff99 (combining ff99 with either the χ_OL-DFT, χ_OL, or χ_YIL parametrization) exhibited serious distortion of GNRA TL caused by either the R_L3 β/γ flip or less often by a flip of the α(A_L2) torsion from trans to gauche, usually accompanied by the shift of γ(A_L2) torsion from gauche(+) to trans. Furthermore, these flips caused disruption of GNRA signatures in four of the six ff99 simulations with χ_OL-DFT, χ_OL, and χ_YIL (GAGA_99χ_YIL, GAGA_99χ_OL, GAAA_99χ_YIL, and GAAA_99χ_OL-DFT). On the other hand, the simulations combining ff99bsc0 with χ_OL-DFT, χ_OL, or χ_YIL parametrizations exhibited stable behavior of GNRA TL on the hundreds of nanoseconds time scale. It should be noted that both R_L3 β/γ and A_L2 α/γ flips were still present in simulations with the bsc0 correction; however, these flips were reversible and short-lived and thus did not result in distortion of GNRA TL.

The R_L3 β/γ flip, which seems to be the main source of GNRA TL destabilization in AMBER simulations, might be a consequence of imperfect force field parameters of β and γ torsions. Nonetheless, the R_L3 phosphate undergoing the β/γ flip is positioned in proximity to the A_L2 phosphate (P–P distance in the X-ray structure is 5.9 and 5.8 Å in GAGA and GAAA, respectively) because of sharp inversion of the sugar–phosphate backbone path. Thus, the R_L3 β/γ flip might also be alternatively caused by insufficiently compensated electrostatic repulsion between these two phosphates or some other imbalance of the intermolecular terms. This is in agreement with the fact that structural degradation is initiated by the flip of either R_L3 or A_L2 phosphate. However, the involvement of ff99bsc0 correction significantly attenuates these phosphate flips, although it is not able to completely eliminate them. Thus, it seems that both imperfect α/β/γ torsion parameters and an imbalance of the intermolecular terms can contribute to structural degradation of GNRA TL in the ff99 force field. Nevertheless, the present GNRA TL simulations are substantially improved when combining the bsc0 correction together with the χ_OL-DFT, χ_OL, or χ_YIL modification.

We extended the ff99bsc0χ_OL force field simulations of GAAA and GAGA systems to 0.8 and 1.0μs, respectively, to test the performance of this force field on the microsecond time scale. We found that the GAGA_bsc0χ_OL simulation was entirely stable on the microsecond time scale. However, we observed conformational changes of the TL region in the GAAA_bsc0χ_OL simulation after 0.56 μs. The deformation of GAAA TL is related neither to the flip of the R_L3 and A_L2 phosphates nor to the formation of a “ladder-like” structure. It may be caused by some other force field imbalances which become visible on the microsecond time scale (see Supporting Information, Figure S2).

Neither the formation of a “ladder-like” conformation nor a R_L3 β/γ flip was observed in simulations with CHARMM27. However, we observed local switches of A_L2 and R_L3 phosphates including a rapid fluctuation of α(A_L2) between native trans and gauche(+), α(R_L3) between trans and native gauche(+), and rapid switches of ε and ζ in all four TL nucleobases that were accompanied by structural distortion of the GNRA TL in both CHARMM27 simulations. Nonetheless, the most distinctive feature of CHARMM27 simulations was the instability of the stem bearing the GNRA TL that exhibited extensive terminal base pair breathing followed by the disruption of base-pairing in the stem and subsequent unfolding of the structure, similar to what has been reported, for example, for stems in simulations of kissing-loop complexes.^81,82

Simulations of A-RNA Stems.

The Supporting Information describes a set of simulations of short canonical A-RNA stems. These simulations illustrate rather visible differences between the modified χ parametrizations in the description of the canonical A-RNA structure, mainly a different inclination of base pairs with respect to the helical axis. Although not related directly to the main topic of this paper, these A-RNA simulations provide further insight into the sensitivity of A-RNA simulations to force field parameters and help understanding of the simulation behavior of the TLs.

Discussion

The 5′-UNCG-3′ and 5′-GNRA-3′ RNA tetraloops (TL) are the two most important classes of RNA hairpin loops. These thermodynamically very stable TLs belong to the most prominent RNA motifs, i.e., recurrent RNA building blocks with a precisely defined context-independent 3D structure. While the UNCG TLs play a key role in RNA folding, the GNRA TLs are involved in tertiary interactions and recognition processes.

As with each RNA motif, the UNCG and GNRA TLs are characterized by signature molecular interactions which define their native structure and, subsequently, following the isostericity principle, their consensus sequences.³³ The 3D signature of the studied UUCG TL includes the tWS G_L4/U_L1 base pair, syn conformation of G_L4, south C2′-endo pucker of U_L2 and C_L3, and four UUCG signature H-bonds: U_L1(O2′)•••G_L4(O6), G_L4(N1)•••U_L1(O2), C_L3(N4)•••U_L2(pro-R_p), and U_L2(O2′)•••G_L4(N7). The U_L1(O2′)•••G_L4(O6) and C_L3(N4)•••U_L2(pro-R_p) H-bonds are unambiguous. The U_L2(O2′)•••G_L4(N7) H-bond is seen only in approximately one-third of the high-resolution NMR structure ensemble.¹⁷ The GNRA TLs are structured with a tHS A_L4/G_L1 (“sheared”) base pair³⁷ complemented by three H-bonds: G_L1(N1/N2)•••A_L4(pro-R_p), G_L1(N2)•••A_L4(N7), and G_L1(O2′)•••R_L3(N7).⁸ The GNRA signature further includes a N_L2, R_L3, and A_L4 triple base stack.

Although it cannot be ruled out that the TLs (especially the GNRA one) exhibit some structural dynamics or can be remodeled in some structural contexts, structural biology data as well structural bioinformatics convincingly show that the above-described signature interactions define the genuine native structures of these RNA TL classes.^8,37 Therefore, correct computational methods should be capable of reproducing the characteristic structures of UNCG and GNRA RNA TLs, identifying them as global minima, and dominantly sampling them. However, as noted in the literature, a correct force field description of nucleic acid hairpin loops may be a considerable challenge for the contemporary molecular mechanical force fields.⁵⁷ Hairpin loops are characterized by a complex mixture of different molecular interactions and noncanonical backbone conformations and are substantially exposed to the solvent.

The RNA TLs, due to their small size and biochemical importance, became a favorable target for simulation studies in the past several years. These studies were primarily concentrated on the folding of the TLs, using sophisticated enhanced sampling methods and massive large-scale parallel computations.^28,29,50 These impressive studies clearly demonstrated the basic capability of the simulation technique to correctly identify the stem base pairing and subsequently fold the structure. However, less attention has been paid to the exactness of the final or most stable structures identified as the native states. Closer inspection of the published data reveals that at least in some cases the predicted topology is not fully consistent with the native topology as known from structural biology.

In the present paper, we have considered a less ambitious but perhaps no less important task. We investigate the capability of the established force fields to keep the native topology of the UNCG and GNRA TLs. We analyze typical structural rearrangements seen on the ~100+ ns time scale and their force field dependence. Simultaneously, we use the TLs as model systems to test four recent attempts (two of them from our laboratories) to adjust the χ glycosidic torsion profile of the Cornell et al. force field, in addition to the basic ff99 and ff99bsc0 force field variants. The ff99bsc0 is the only viable AMBER force field for DNA simulations, while RNA was until now considered to be almost equivalently well described by all basic Cornell et al. force field variants.^57,59 The χ modifications were derived on the basis of QM computations using different model systems, different QM levels, and different overall philosophies of parametrization (see the Introduction and Methods and the Supporting Information for parameters). There are considerable differences among the four suggested χ glycosidic torsion profiles, while they also substantially differ from the original parametrization (supplementary Figure S1B, Supporting Information). We also performed a set of simulations on short A-RNA stems (Supporting Information). Although the A-RNA simulations are not directly related to the main topic of this paper, these A-RNA simulations provide insights into the sensitivity of A-RNA simulations to force field parameters and help with understanding the simulation behavior of the TLs. The A-RNA simulations indicate that adjusting the χ torsion has a visible effect on the calculated inclination and base pair roll of A-RNA helices (see Supporting Information, Table S3). The global (helical) structure parameter inclination and local (wedge) parameter roll are mathematically interconnected. They characterize the degree to which the base pairs in the helix adopt the A-RNA geometry having the base pairs inclined with respect to the global helical axis. Due to helical twisting, the inclination then leads to base pair roll in the local base pair step coordination frames.^83,84 The χ_OL-DFT and χ_OL variants of χ adjustment modestly reduce the inclination/roll values compared with simulations using the unmodified force field (see Supporting Information, Table S3). The χ_YIL adjustment leads to a qualitative reduction (and underestimation) of inclination/roll (see Supporting Information, Table S3). The impact of these effects on RNA simulations is under further investigation. The χ_ODE parametrization destabilizes the A-RNA by promoting the “ladder-like” structure. This behavior reflects the balance of anti and high-anti regions of the respective parametrizations.

For the tetraloops, we have obtained the following results. In all UUCG TL simulations with the standard AMBER force fields (with unmodified χ torsion), we observed a loss of the signature U_L1(O2′)•••G_L4(O6) H-bond immediately after the simulation start, i.e., within few picoseconds. This H-bond is replaced by the U_L1(O2′)•••U_L2(O5′) H-bond (Figure 3A). Despite the fact that the loop subsequently remains close to the starting structure, the loss of the signature interaction is not in agreement with structural data. Simultaneously with the disruption of the U_L1(O2′)•••G_L4(O6) H-bond, we observed significant propeller twisting of the G_L4/U_L1 tWS base pair and mainly a shift of G_L4 χ syn torsion from 60° to 40°. We argued that the G_L4 χ torsion shift is the primary source of perturbation of the signature interaction. All studied modifications of χ torsions (i.e., χ_ODE, χ_YIL, χ_OL-DFT, and χ_OL) improve the behavior most likely because they provide a more realistic description of the syn region of G (Supporting Information, Figure S1B).

Further analysis indicates that the use of bsc0 correction improves the simulation behavior by stabilizing the observed distribution of the γ backbone angles, mainly by preventing the undesired and irreversible γ-trans flip of the U_L2 phosphate. Interestingly, the native γ-trans flip of G_L4 is kept. Therefore, this TL is best described when using the ff99bsc0 basic parametrization with some of the χ torsion adjustments.

The most significant feature of GNRA simulations with the standard variants of the AMBER force field is a loss of the GNRA integrity on a scale of dozens of nanoseconds followed by a subsequent “ladder-like” conversion of the whole helical stem (Figure 6). Adding the suggested χ corrections (except of χ_ODE) improves the behavior of the GNRA TL simulations and prevents larger degradations on the ~100 ns time scale, which is the typical time scale for presently published RNA simulations. The most likely reason why the three successful χ corrections improve the GNRA simulation behavior is the change of the profile in the high-anti region compared to that in the anti region (Supporting Information, Figure S1B). Compared with the basic ff99/ff99bsc0 parametrizations, χ_OL-DFT and χ_OL bring a modest penalty to the high-anti region, which however seems to be enough to prevent the forming of a “ladder-like” structure. The χ_YIL works in the same direction, but the high-anti penalty is much more vigorous. The χ_ODE rather supports the high-anti χ region, and that is why it does not prevent the ladder-like artifact. Note that despite the overall improvement the GNRA simulations exhibit some local dynamics which may indicate some more subtle imbalances. This will require further studies. We noticed reversible flips of β/γ torsions of the R_L3 phosphate from the trans/gauche(+) to the gauche(+)/trans conformation (Figure 6) which are associated with a dramatically increased buckle of the G_L1/A_L4 base pair from ~5° to ~60°. Such base pair distortion may accelerate further undesired rearrangements of the TLs. The use of ff99bsc0 correction improves the simulation behavior by stabilizing the native conformation of TLs phosphates but does not completely prevent these flips. We need to keep in mind that some of the observed dynamical effects may be related to imbalances of the intermolecular terms of the force field. In such a case, the ability of the torsion angle adjustments to improve the simulations may be limited. As noted above, we suspect that the lack of a fully balanced description of the interphosphate repulsion may contribute to the observed backbone dynamics. A balanced description of some such effects may thus require the development of polarization force fields or at least some reparameterization of the solvation terms. Taken together, the GNRA TL is best described by the ff99bsc0 basic parametrization with χ_YIL, χ_OL-DFT, or χ_OL adjustments.

In summary, our data show that three of the χ glycosidic torsion profiles, namely, χ_OL-DFT, χ_OL, and χ_YIL, improve the description of the TLs, especially when combined with the ff99bsc0 basic parametrization.⁵⁹ Mainly, they prevent the formation of the degrading “ladder-like” structures of RNA stems, which break down the simulated GNRA tetraloops. The “ladder-like” conformation is associated with an excessive high-anti shift of the χ torsion.⁸⁰ On the other hand, the χ glycosidic torsion reparameterization of Ode et al.⁶⁹ is much less suitable for RNA simulations, as it accelerates the formation of the ladder-like structures. All four χ modifications locally improve the description of the syn region, which stabilizes the UUCG TL simulations. Again, bsc0 is to be used as the basic force field for the UUCG simulation. The present results, however, should be taken as preliminary, and considerably more extensive tests on numerous different RNA and DNA systems are under way. We would like to stress that although some of the χ torsion adjustments show significant potential for improving RNA simulations, mainly by preventing the “ladder-like” structure, it cannot be ruled out that we will in the future identify also a worsening of some other properties of the simulated molecules.

When assessing the significance of the results, we have to make a few cautionary notes. First, the χ torsion reparameterizations are applicable exclusively to RNA. We have tested them (not shown) also for B-DNA and DNA quadruplex loops, and they do not improve DNA simulations. In fact, it appears that fine-tuning of the χ torsion simultaneously for DNA and RNA is not possible, unless some other parameters are modified too. This is related to the second cautionary comment. When using simple analytical force fields, the description of the simulated system is unavoidably only approximate, despite careful parametrization procedures. Thus, the force field is inescapably physically inexact and incomplete. Therefore, the impact of adjustments of the individual torsions, although potentially improving the simulation performance, should not be overrated. The physically inexact torsional potentials are used to approximate the effective overall sum of many diverse physical contributions. The QM reparameterization of torsions does not per se guarantee that the simulations are subsequently improved, as the force field performance depends on the overall balance of all of the force field terms. Therefore, before any application of a modified force field, it must be carefully tested for relevant nucleic acid systems. It is therefore a rather unusual practice that the χ_ODE and χ_YIL parametrizations were made available without any testing.^69,70 In addition, it is well-known that improving one feature of the simulated systems may have undesired side effects elsewhere. This explains why the χ torsion adjustments tested here do not improve the behavior of DNA simulations.

For the sake of completeness, we also performed limited simulations using the CHARMM27 force field. The main dynamics that we noticed in GNRA TLs are phosphate flips and fluctuations, similar to those reported above for the AMBER simulations. Nevertheless, the simulated structures were later destabilized in their stem regions (base pair fluctuations and fraying), which ultimately also affected the TLs. Note that the simulations were carried out with quite short stems. Such reduced stability of the short stems is consistent with literature data.⁸¹ The UNCG TL trajectory was unstable. This simulation result is identical to more extensive data reported and in more detail described by Deng and Cieplak.²⁸

The 100+ ns simulations are sufficient for many useful applications, such as the very basic MD characterization of existing RNA structures. Note that perturbation of the TLs may cause bias in the overall assessment of the data even when the TL is not the primary focus of a given simulation study. Therefore, stabilization of the RNA TLs on this time scale is important. Work is in progress to investigate the TLs using much longer simulations and also using substantially larger RNA systems to prevent eventual end effects.