A model of mood as integrated advantage

Abstract

Mood is an integrative and diffuse affective state that is thought to exert a pervasive effect on cognition and behavior. At the same time, mood itself is thought to fluctuate slowly as a product of feedback from interactions with the environment. Here we present a new computational theory of the valence of mood—the Integrated Advantage model—that seeks to account for this bidirectional interaction. Adopting theoretical formalisms from reinforcement learning, we propose to conceptualize the valence of mood as a leaky integral of an agent’s appraisals of the Advantage of its actions. This model generalizes and extends previous models of mood wherein affective valence was conceptualized as a moving average of reward prediction errors. We give a full theoretical derivation of the Integrated Advantage model and provide a functional explanation of how an integrated-Advantage variable could be deployed adaptively by a biological agent to accelerate learning in complex and/or stochastic environments. Specifically, drawing on stochastic optimization theory, we propose that an agent can utilize our hypothesized form of mood to approximate a momentum-based update to its behavioral policy, thereby facilitating rapid learning of optimal actions. We then show how this model of mood provides a principled and parsimonious explanation for a number of contextual effects on mood from the affective science literature, including expectation- and surprise-related effects, counterfactual effects from information about foregone alternatives, action-typicality effects, and action/inaction asymmetry.

Mood is an affective state typically defined in terms of its slow timescale, integrative properties, and contextual modulation (e.g., Lormand, 1985; Morris, 1989; Parducci, 1995; J. A. Russell, 2003). The interaction between mood and cognition is thought to be reciprocal, with complex nonlinear dynamics: on the one hand, mood is thought to evolve in response to successive cognitive appraisals of subjective experiences (Smith & Ellsworth, 1985; R. J. Larsen, 2000; J. A. Russell, 2003; Kuppens, Oravecz, & Tuerlinckx, 2010); on the other hand, there is evidence that mood itself alters a broad range of cognitive processes, and thereby influences the appraisal of future experiences (Isen & Clark, 1978; Bower, 1981; Isen & Patrick, 1983; Sanna, Turley-Ames, & Meier, 1999; Tamir & Robinson, 2007; Neville, Dayan, Gilchrist, Paul, & Mendl, 2020). At any point in time, therefore, a person’s mood is both a consequence of their recent actions and a factor that influences how they will behave in the future. The dynamics of this reciprocal interaction have significant implications for mental health and psychological wellbeing (Koval, Pe, Meers, & Kuppens, 2013; Broome, Saunders, Harrison, & Marwaha, 2015; Bonsall, Geddes, Goodwin, & Holmes, 2015). This raises an important question: why should mood and cognition be so tightly coupled? What benefit might a biological agent gain by modulating its processing of future events according to mood, if mood itself constitutes an integrated history of responses to many distinct past events?

Here, we aim to answer this question by presenting a new computational model of the valence of human mood (adopting a framework in which, along with arousal, valence constitutes one of the two core dimensions of affect; J. A. Russell, 2003). Our model seeks simultaneously to account for the cognitive antecedents of the valence of mood (i.e., to explain the types of events that produce changes in mood) and to provide a functional account of the adaptive utility of mood for a biological agent. Adopting the formal computational language of reinforcement learning (Kaelbling, Littman, & Moore, 1996; Sutton & Barto, 2018), we hypothesize that the valence of mood is a leaky integral of the Advantage (Baird, 1994) of an agent’s actions. To provide a functional justification for this hypothesized mood construct, we derive the Integrated Advantage model of mood from the principle of momentum in the field of stochastic optimization (Polyak, 1964; Nesterov, 1984). Specifically, we show that a mood variable that integrates the Advantage of recent actions can be used to approximate momentum by an actor-critic reinforcement learning algorithm, thereby substantially accelerating learning in stochastic and dynamic environments.

Our central proposal is that the valence of an agent’s mood reflects its appraisals of the Advantage of its actions, where the ‘Advantage’ of an action is defined as the difference between the value of that action and the value of the environmental state within which the action was taken. Advantage is a theoretical concept from reinforcement learning that has not seen wide usage outside the machine learning literature (although see Dayan & Balleine, 2002; O’Doherty et al., 2004), even as other concepts from reinforcement learning have profoundly influenced psychology and neuroscience (e.g., Barto, 1994; Montague, Dayan, Person, & Sejnowski, 1995; Schultz, Dayan, & Montague, 1997; Daw, Niv, & Dayan, 2005; Niv, 2009). However, within machine learning applications of reinforcement learning, agents that estimate the Advantage of their actions and use this signal to learn have recently achieved impressive performance levels across a number of domains (e.g., Schulman, Moritz, Levine, Jordan, & Abbeel, 2015; Mnih et al., 2016; Wang et al., 2016, 2017; Mirowski et al., 2017).

Overview

This article has three primary aims: first, to present the mathematical formalisms underlying the Integrated Advantage model of mood; second, to show how the Integrated Advantage model can provide a unifying explanation for a broad class of affective phenomena, including several (such as counterfactual effects) that are not easily accounted for within previous computational models of mood; and third, to provide a formal justification for the functional role of mood in learning by deriving the Integrated Advantage model from the principle of momentum in stochastic optimization. Although these three aims are mutually reinforcing, they are also somewhat separable. To this end, this article comprises distinct sections that address different components of these aims, as detailed below.

In Section 1, we provide a detailed review of mood, detailing both its general theoretical properties and the different types of contextual effects that have been shown in empirical research to influence its valence. We outline how these features represent a significant puzzle for a functional theory of mood. In Section 2, we give a mathematical description of the Integrated Advantage model, including a review of the relevant concepts from reinforcement learning for readers who are less familiar with this framework. In Section 3, we return to the empirical effects reviewed in Section 1, and describe how the Integrated Advantage model can account for each of these effects in turn. In Section 4, we turn to the functional question of mood, and give a formal derivation of the Integrated Advantage model in terms of the concept of momentum from stochastic optimization (including a review of the relevant concepts from this literature). In Section 5, we use simulations to demonstrate that mood—as conceptualized within the Integrated Advantage model—does indeed confer an adaptive benefit upon decision-making agents across three distinct computational environments, consistent with the theoretical arguments presented in Section 4. Finally, in the General Discussion we discuss the relationship between the Integrated Advantage model and its predecessors, and outline future lines of empirical research suggested by the model.

Section 1: Theoretical and empirical review of mood

The properties of mood have been discussed extensively in psychology, philosophy, and neuroscience, and we will not be able to do justice here to the entire body of extant work on the function and phenomenology of mood. Instead, we frame our theory according to three general properties of mood that we see as widely shared across theories. It is important to note that this is only one among many possible typologies of affective phenomena (see, e.g., Lazarus, 1968; Frijda, 1986; Morris, 1989) and that there are no consensus criteria across typologies for strictly delineating the construct that we refer to as mood from other related affective phenomena (e.g., emotion, subjective wellbeing).

The first, the integrative property, is that the valence of mood can be modelled as a temporal integral of the hedonic valence of moment-to-moment experience. This property, frequently noted in theories of mood across philosophy, psychology, and ethology (Edgeworth, 1881; Ruckmick, 1936; Krueger, 1937; Bollnow, 1956; Parducci, 1995; Kahneman, Diener, & Schwarz, 1999; Mendl, Burman, & Paul, 2010; Nettle & Bateson, 2012; Webb, Veenhoven, Harfeld, & Jensen, 2019), states that the valence of mood reflects a moving average of the valence of an individual’s recent experiences, rather than being the product of any single event. The integrative property captures the strong dependence between the valence of an individual’s mood and the overall valence of their recent experiences, such that an individual whose recent experiences have been generally pleasant is likely to experience a positive mood, and vice versa for generally negative recent experiences (Isen & Clark, 1978; Morris, 1989). More formally, mood can be seen as a leaky integrator of the valence of momentary experience, such that the valence of recent events influences mood more strongly than that of temporally distant events. Events are generally held to be integrated into the valence of mood over a timescale on the order of hours to days (Morris, 1989; R. J. Larsen, 2000). However, this does not preclude the possibility that older events can influence mood, since the act of recalling pleasant or unpleasant memories can itself be thought of as a psychological event with an associated valence, consistent with the utility of autobiographical memory recall as a mood induction procedure in the laboratory (e.g., Baker & Guttfreund, 1993).

Second, the non-intentional property is that mood (as distinct from other affective states, such as emotions) does not have a specific subject matter. That is, a good or bad mood is not about a specific event in the way that amusement can by about a joke or disgust can be about rotten food. Instead, moods are typically defined as unfocused and diffuse background states that do not have a specific direction or object-relatedness (Bollnow, 1956; Lormand, 1985; Frijda, 1986; Searle, 1992; R. J. Larsen, 2000; Beedie, Terry, & Lane, 2005). Since this ‘about-ness’ is known in philosophy as intentionality (e.g., Searle, 1992), moods are frequently considered to be non-intentional affective states¹.

Third, and of central importance for our theory, mood has a strong contextual property. That is, the effect of any given event on the valence of mood depends upon the event’s psychological context. Events do not affect mood in a vacuum, and therefore the same event can have dramatically different effects on mood depending upon the context in which it occurs (Feather, 1969; Parducci, 1995; Medvec, Gilovich, & Madey, 1995; Mellers, Schwartz, Ho, & Ritov, 1997). Numerous contextual effects have been documented in the literature, and these are reviewed in more detail below. Simultaneously accounting for all of these different contextual effects on mood via the same underlying psychological mechanism proves to be a challenge for existing quantitative models of mood.

Contextual effects on mood

As well as being consistent with the integrative, non-intentional, and contextual properties, a theory of mood should be able to explain known empirical phenomena. Here, we review a number of contextual effects, whereby events have a different effect on the valence of mood in context than they would have in isolation. Each contextual effect discussed can be seen as an example of the general contextual property of mood described above; as discussed further in subsequent sections, a central theoretical contribution of the Integrated Advantage model is to account parsimoniously for all of these effects within a single computational model of mood.

Expectation/surprise effects.

The expectation effect is that an event does not influence mood based on its utility, but rather according to the degree to which its actual utility differs from its expected utility (Verinis, Brandsma, & Cofer, 1968; Parrott & Sabini, 1990; Medvec & Savitsky, 1997; Mellers et al., 1997; Mellers, Schwartz, & Ritov, 1999; Mellers, 2000; Krupić & Corr, 2014; Rutledge, Skandali, Dayan, & Dolan, 2014; Eldar & Niv, 2015; Ong, Zaki, & Goodman, 2015; Otto & Eichstaedt, 2018; Bhatia, Mellers, & Walasek, 2019; Villano, Otto, Ezie, Gillis, & Heller, 2020). To illustrate this effect, consider an employee who receives $5000 from their employer in end-of-year bonus pay. This event would be likely to exert a positive effect on the valence of the employee’s mood if they had not been expecting a bonus, but a negative effect on mood if they had expected to receive a substantially larger bonus (Bell, 1985).

The expectation effect has been observed consistently inside and outside the laboratory. In computerized decision-making tasks, for example, subjects report improved mood after receiving the better of two possible gamble outcomes and worse mood after receiving the worse outcome (Mellers et al., 1997, 1999; Mellers, 2000; Rutledge et al., 2014). In naturalistic studies, it has likewise been shown that the effect of exam grades on university students’ mood depends on whether the grades exceed or fall short of expectations (Parrott & Sabini, 1990; Krupić & Corr, 2014; Villano et al., 2020). More recently, the ability to quantify affective valence on social media platforms has allowed researchers to document the expectation effect in affective responses to real-world events as diverse as political election results, sporting results, and daily weather variations (Otto & Eichstaedt, 2018; Bhatia et al., 2019).

Historically, prominent theories of the expectation effect have described these affective responses as either disappointment (for events that fall short of their expected valence) or as elation (for events that exceed their expected valence) (Bell, 1985; Loomes & Sugden, 1986). More recently, it has been noted that the expectation effect is well explained in terms of a more general effect of reward prediction errors (RPEs) on mood. Here, an RPE is defined as the difference between the valence of an outcome and its expected valence, in the mathematical sense of expectation as a probability-weighted sum of the valence of all possible outcomes. This insight has been implemented in recent computational models that conceptualize mood as a leaky integrator of RPEs (Rutledge et al., 2014; Eldar & Niv, 2015; Vinckier, Rigoux, Oudiette, & Pessiglione, 2018).²

Closely related to the expectation effect is the surprise effect, whereby an event produces an affective response whose strength is inversely proportional to the event’s prior probability (Mellers et al., 1997). Like the expectation effect, the surprise effect has been documented both in the laboratory and naturalistically. Spector (1956) observed an effect of prior probability on subjects’ satisfaction in response to a job promotion, such that outcomes that were a priori less probable (and hence more surprising when they occurred) affected mood more strongly. Likewise, in the laboratory, surprise effects have been observed in response to computerized gamble outcomes, both for gambles selected by the subject (Mellers et al., 1999) and for gambles assigned to subjects by the experimenter (Mellers et al., 1997). Like the expectation effect, the surprise effect may be explained as an instance of a broader class of RPE effects on mood: low-probability outcomes produce a larger absolute prediction error, and therefore a stronger effect on mood according to RPE models. However, it should be noted that this explanation assumes that the only aspect of an outcome that is relevant to affective responses is its reward valence. Another possibility is that surprise with respect to other aspects of outcomes (e.g., surprising outcome identity, as occurs in the unwrapping of a gift) might also influence the strength of the affective response. To date this possibility—which could not be accounted for by a RPE model—has not been investigated thoroughly in the literature on mood.

The counterfactual effect.

The counterfactual effect on mood occurs in the context of decision making. After an individual takes an action, their mood is influenced not only by the outcome of this action, but also by counterfactual information about what would have happened if they had chosen a different action instead (J. T. Johnson, 1986; Landman, 1987; Gleicher et al., 1990; Markman, Gavanski, Sherman, & McMullen, 1993; Roese, 1994; McMullen, Markman, & Gavanski, 1995; McMullen & Markman, 2002; Mandel, 2003; Coricelli & Rustichini, 2010). For example, a shopper who joins one of two grocery-store queues may experience negative affect if their chosen line moves more slowly than the unchosen line, and positive affect if their chosen line moves faster than the unchosen line.

Crucially, the direction of the counterfactual effect depends upon the direction of comparison: upward counterfactuals, in which the attained outcome is compared to a better outcome from an alternative action, generate negative affect. By contrast, downward counterfactuals—in which the attained outcome is compared to a worse outcome from an alternative action—generate positive affect (Markman et al., 1993). Moreover, the influence of counterfactual information on mood is moderated by the plausibility of counterfactual outcomes, such that more plausible counterfactuals exert a stronger influence on mood (Kahneman & Tversky, 1982b; Kahneman & Miller, 1986).

Many of the most prominent examples of this effect involve the phenomenon of regret (Bell, 1982; Loomes & Sugden, 1982; Zeelenberg & Pieters, 2007). For instance, Mellers et al. (1999) offered participants choices between pairs of two-outcome gambles (e.g., gamble A: 50% chance of winning $8 and 50% chance of losing $8; gamble B: 20% chance of winning $32 and 80% chance of losing $32) and provided simultaneous information about the outcome of the chosen gamble and of the unchosen gamble. Strong counterfactual effects were observed, such that participants experienced more negative affect if the outcome of the unchosen gamble was better than the outcome of the chosen gamble, even when the chosen gamble paid out its best possible outcome (e.g., if the subject chose gamble A in the example above and received an $8 payout, but also found out that gamble B would have paid out $32).

Unlike the expectation and surprise effects, counterfactual effects on mood cannot be explained in terms of RPEs (Coricelli & Rustichini, 2010; Miceli & Castelfranchi, 2015). This is because even when an outcome greatly exceeds expectations—and hence generates a large positive RPE—it may be inferior to the best possible outcome that could have occurred following an alternative course of action. In the grocery-store example above, the individual who joins one of two possible grocery checkout queues may proceed somewhat faster along the chosen line than expected (therefore producing a positive RPE), but still feel negative affect if the unchosen line moves even faster. The limitation of RPE models in explaining this effect stems from the fact that an RPE is defined with respect to the outcome of a particular action; by contrast, counterfactual comparisons compare outcomes across distinct actions. Consequently, some computational variable other than RPEs must be used to explain counterfactual effects on on the valence of mood.

The action-typicality effect.

The action-typicality effect is that events produce amplified affective responses when they follow actions that are in some respect unusual or exceptional (Kahneman & Tversky, 1982b; Kahneman & Miller, 1986; Miller & McFarland, 1986; Feldman & Albarracín, 2017; Kutscher & Feldman, 2019). The typicality of actions may be defined either with reference to one’s own past behavior (e.g., trying a new dish at a favourite restaurant where one typically orders the same thing each time) or with respect to implicit social standards or customs (e.g., ordering red wine with a seafood dish instead of white). The classic empirical demonstration of the action-typicality effect is given by Kahneman and Miller (1986) (replicated in Kutscher & Feldman, 2019), who presented subjects with two hypothetical scenarios involving an individual who had a car accident driving home from work. One scenario included the information that the accident occurred while the driver was following his regular route home; the other scenario reported that the accident occurred on a route that the driver took only infrequently. When asked in which scenario the driver would be more upset about the accident, a large majority of subjects chose the driver following an atypical route.

Like the counterfactual effects detailed above, the action-typicality effect is difficult to explain under an RPE model of mood. This is because RPEs are calculated without reference to the typicality of the action that produced a particular outcome; for instance, betting on the correct number at a roulette table generates an equally large RPE whether one always picks the same number or whether one picks a random number every time. As with counterfactual effects, therefore, the definition of an RPE prevents it from being able to account for the action-typicality effect on the valence of mood.

Action/inaction asymmetry.

The action/inaction asymmtery is that outcomes following an overt action typically influence affective responses more strongly than outcomes following inaction (Kahneman & Tversky, 1982a; Kahneman & Miller, 1986; Landman, 1987; Gleicher et al., 1990; Gilovich & Medvec, 1994, 1995; Zeelenberg, van den Bos, van Dijk, & Pieters, 2002; Feldman & Albarracín, 2017). For example, Kahneman and Miller (1986) presented subjects with scenarios involving two investors: the first lost $1,200 because he did not sell his stock holdings in company A to buy stock in company B when he had the chance; the second lost $1,200 because he sold his stock in company B to buy in company A. In spite of equal monetary losses, a large majority of subjects believed that the second individual, who took an explicit action, would feel greater regret than the first, who lost money through inaction.

The action/inaction asymmetry has often been explained as a variant of the action typicality effect. This argument is based upon the assumption that inaction usually represents a kind of default, status-quo policy. If this is the case, then in most cases taking an overt action would, by definition, be more exceptional than taking no action, and hence likely to generate a stronger affective response according to the action typicality effect. In support of this explanation, some researchers have observed reversals of the typical action/inaction asymmetry when action is the status quo policy, such that inaction results in amplified affective responses (N’gbala & Branscombe, 1997; Inman & Zeelenberg, 2002; Bar-Eli, Azar, Ritov, Keidar-Levin, & Schein, 2007; Feldman & Albarracín, 2017). For instance, when a soccer goalkeeper faces a penalty shot, the action of jumping is typical: goalkeepers typically jump either left or right, and only infrequently remain in place to guard the centre of the net. In line with this action-typicality interpretation, a survey suggested that professional goalkeepers would indeed feel worse when a goal was scored after they remained in place compared to a goal scored after they jumped either left or right (Bar-Eli et al., 2007). Like the counterfactual- and action-typicality effects described above, therefore, the action/inaction asymmetry is not accounted for by the RPE hypothesis of mood.

Section 2: The Integrated Advantage model of mood

Functional theories of affect seek to explain emotions and moods by describing how these phenomena serve an adaptive function for a biological agent (Darwin, 1872; Lazarus, 1968; Plutchik, 1980; Smith & Lazarus, 1990; Keltner & Gross, 1999). In this light, the five contextual effects reviewed in Section 1 can be seen as phenomena to be explained by a theory of the valence of mood, and the integrative, non-intentional and contextual properties of mood can be seen as important constraints on the hypothesized form of mood in the theory. The functional question of mood is what benefit a biological agent derives from maintaining a representation of mood that is integrative, non-intentional, and contextual, and that is contextually modulated in line with each of the effects reviewed above.

In this section we detail a theory, the Integrated Advantage model of mood, that explains each of the phenomena reviewed above in terms of the agent’s estimation of the Advantage of its actions. As described above, Advantage is a concept drawn from the formal framework of reinforcement learning. We therefore first review the fundamental concepts of reinforcement learning and introduce the concept of Advantage, before using this framework to present our model of mood. We note that since reinforcement learning incorporates elements of both learning theory and control theory, our model is in keeping with a tradition that grounds theories of affective phenomena in associative learning theory (emphasising the role played by affect in the acquisition of stimulus-stimulus and stimulus-response associations; e.g., Millenson, 1967; Gray, 1975; Rolls, 1990; Baumeister, Vohs, Nathan DeWall, & Liqing Zhang, 2007) and control theory (emphasising the role of affect in helping select courses of action that lead to the attainment of goal states; see Bowlby, 1969; Frijda, 1986; Carver & Scheier, 1990; R. J. Larsen, 2000; Carver, 2015).

Reinforcement learning in a nutshell

Reinforcement learning is a computational framework that describes how an agent can use its experience to learn to behave in a manner that maximizes its expected future reward (Kaelbling et al., 1996; Sutton & Barto, 2018). Reinforcement learning algorithms are built using the components of a Markov Decision Process: the different ‘states’ of the environment (denoted s), a set of actions (denoted a) that can be taken by the agent in each state, and scalar rewards (denoted r, and which can also be zero or negative) that are received in each state. The learning algorithms describe how an agent can update its policy (π, the probability of taking each of the possible actions in each state) based on experience with the outcomes of actions it had taken in the past.

An agent can often improve its policy by learning the value of different states of the environment, as well as the value of different actions that can be taken in each state. The state-value function is denoted V^π(s), and is defined as the expected sum of discounted future reward associated with being in state s and behaving thereafter according to policy π. According to Bellman’s equation (Bellman, 1957), this can be re-expressed as a sum of immediate reward and the discounted value of the successor state:

$$V^{\pi }(s)\equiv \mathbb{E}[r(s^{\prime })+\gamma V^{\pi }(s^{\prime })\mid s,\pi ]$$ (1)

where s′ is the successor state, r(s′) is the reward received in the transition from s to s′, and 0 < γ ≤ 1 is a discount factor. The expectation $\mathbb{E}$ is with respect to randomness in the action taken, the consequent immediate reward and the successor state the world transitions to. The superscript π on V therefore reflects the fact that, as an expectation over this randomness, the value of a state depends on the agent’s policy.

This definition of value allows for simple online (i.e., trial-and-error) learning of state values using a “temporal difference prediction error” (Sutton, 1988) – the difference between a sample of the right hand side of Equation 1 (i.e., a single experienced reward and state transition) and the left hand side of the same equation (i.e., the agent’s current estimate of the value of state s):

$$\delta \equiv r(s^{\prime })+\gamma V^{\pi }(s^{\prime })-V^{\pi }(s)$$ (2)

By updating V^π(s) in proportion to the prediction error, state values gradually approximate the true expected future rewards. The temporal difference error is therefore a useful variable for trial-and-error learning (though not an essential one, since some trial-and-error learning algorithms do not require computation of this variable; e.g., Williams (1992)). Neurally, the temporal difference error is thought to be encoded by phasic dopamine release in the primate basal ganglia (Barto, 1994; Schultz et al., 1997).

Similar to the definition of the state-value function, the action-value function is denoted Q^π(s, a), and is defined as the expected sum of discounted future reward associated with taking action a in state s and choosing actions according to π thereafter (Watkins & Dayan, 1992; Sutton & Barto, 2018):

$$Q^{\pi }(s,a)\equiv \mathbb{E}[r(s^{\prime }\mid a)+\gamma V^{\pi }(s^{\prime }\mid a)\mid s,a,\pi ]$$ (3)

Here the expectation is taken over randomness in immediate rewards and state transitions, but the initial action is set, and the immediate reward and successor state are conditioned on this action³. Analogous to the temporal difference error for learning of V-values, there exist online methods for updating Q-values according to experienced rewards and state transitions (e.g., SARSA; Sutton & Barto, 2018). For an agent that learns Q-values, the task of choosing good actions is reduced to the simpler task of choosing the action that has the highest value in each state. In the simplest case the agent deterministically chooses the action with the highest estimate action-value; alternatively, to ensure ongoing exploration of different actions the agent may use a stochastic policy such as ϵ-greedy or softmax (Sutton & Barto, 2018), although more sophisticated methods for exploration also exist, such as those based on maximising expected information gain (e.g., Houthooft et al., 2016).

Advantage.

The Advantage of taking action a in state s is denoted A^π(s, a), and defined as the value of action a above and beyond the general value of s (Baird, 1994):

$$A^{\pi }(s,a)\equiv Q^{\pi }(s,a)-V^{\pi }(s)$$ (4)

A positive Advantage indicates that, under the current policy π, the value of a exceeds the value of state s within which the action was taken; this is significant because it suggests that the agent can increase its expected reward by adjusting its policy so as to take action a more frequently in state s in the future. By contrast, negative Advantage for a suggests that the agent can increase its expected reward by adjusting its policy so as to take action a less frequently in future visits to state s. When the agent follows an optimal policy (that is, a policy that maximizes expected future reward), the Advantage associated with the optimal action in each state is 0, and the Advantage of all other actions is negative. This follows from the definition of an optimal policy: the value of a state under the optimal policy is equal to the Q-value of the best possible action in that state (Watkins & Dayan, 1992). Intuitively, this means that at convergence (i.e., for an overlearned policy) an Advantage of zero indicates that the agent took the best action that was available to it.

The definition of Advantage bears a noteworthy resemblance to the definition of a temporal difference prediction error. To see this, we can first observe that the definitions of A^π (Equation 4) and δ (Equation 2) have in common a subtraction of V^π(s), the value of the current state. We therefore turn our attention to the Q-value on the right hand side of Equation 4. As per Equation 3, the Q-value of an action is defined as the expected sum of the immediate reward and the discounted value of the successor state, conditional on that action being taken. r(s′ ∣ a) + γV^π(s′ ∣ a) can therefore be treated as a stochastic estimate of the true Q-value of action a, and be substituted into Equation 4 to produce an online estimate of the Advantage of the chosen action. Thus, as long as actions are chosen according to π, the temporal difference error is equal in expectation to the Advantage function (Bhatnagar, Sutton, Ghavamzadeh, & Lee, 2009; Schulman et al., 2015):

$$\begin{gathered} A^{\pi }(s,a)=Q^{\pi }(s,a)-V^{\pi }(s) \\ \approx r(s^{\prime }\mid a)+\gamma V^{\pi }(s^{\prime }\mid a)-V^{\pi }(s) \\ \approx \delta \end{gathered}$$ (5)

Consequently, the temporal difference error at a given timepoint can be treated as a sample of the true Advantage function for the agent’s policy at that timepoint, where variance in this sample may result from stochasticity in either the reward function or the state transition function (the two factors that determine variance in the temporal difference error). That is, the temporal difference error following a particular action is an unbiased estimate of how much better the agent could do by taking this action more frequently in future. Because the world is stochastic, however, the temporal difference error is just a sample of the true advantage function, and it is only in expectation (i.e., in with very large numbers of samples) that this estimate will converge to the true Advantage function. In this respect it is important to note that the temporal difference error is only one method for estimating the Advantage function (Mnih et al., 2016). As we discuss below, other estimators of the Advantage function also exist, and many of these have lower variance than the temporal difference error.

A final property of the Advantage function is that because it quantifies the utility of the chosen action relative to expected returns from the associated state, it helps to provide a low-variance estimate of the gradient of expected reward with respect to the chosen action (Schulman et al., 2015). That is, the advantage provides an estimate of how much and in what direction future rewards will change if this action is performed more frequently in future (positive advantage: more reward if the action is taken more frequently; negative advantage: less reward if the action is taken more frequently). This property is exploited by a family of ‘Advantage Actor-Critic’ reinforcement learning algorithms, which use the Advantage to update the parameters of the policy in the direction of increasing expected reward (e.g. Wang et al., 2016; Mnih et al., 2016).

Mood as integrated Advantage

The Integrated Advantage model proposes that mood reflects a leaky integral of the agent’s estimates of the Advantage of its actions. That is, we assume that after taking an action a in the environment state s, the agent estimates the Advantage of this action (we denote this estimate by ${\widehat{A}}^{\pi }(s,a)$). We propose that the valence of mood reflects a leaky integral (i.e., a recency-weighted average) of these estimates. In other words, positive moods will result when the agent’s estimates of the advantage of its recent actions have been generally positive, and vice versa for negative moods.

As in previous theories (Frederick & Loewenstein, 1999; Eldar & Niv, 2015), we propose to model this leaky integration process using a recursive delta-rule update:

$${\text{Mood}}_{t+1}={\text{Mood}}_t+{\eta }_{mood}\left({\widehat{A}}^{\pi }(s_t,a_t)-{\text{Mood}}_t\right)$$ (6)

This rule recursively updates mood at each timestep t according to a step-size parameter η_mood that controls the timescale of integration, such that higher values of η_mood produce a leakier integration (i.e., more recency-weighting) and lower values a less leaky integration. Note also that Equation 6 can be rearranged to show that the delta-rule formulation calculates mood as an exponential moving average of the time-series of estimated Advantages ${\widehat{A}}^{\pi }(s_t,a_t)$, ${\widehat{A}}^{\pi }(s_{t-1},a_{t-1})$, ${\widehat{A}}^{\pi }(s_{t-2},a_{t-2})$, … :

$${\text{Mood}}_{t+1}={\eta }_{mood}\sum _{\tau =0}^t\left[(1-{\eta }_{mood}{)}^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })\right].$$ (7)

Because the true Advantage function A^π is a latent construct that is not known by the agent, Equation 6 defines mood in terms of ${\widehat{A}}^{\pi }(s_t,a_t)$, which is the agent’s estimate of the Advantage of the state-action pair s_t, a_t. This Advantage estimate must be calculated on-line; that is, the estimate at time t can only be based on quantities that are available to the agent at that point in time or previously, and not based on quantities from future timesteps. In order to fully specify our model, therefore, we must describe how an agent can estimate the Advantage of its actions.

There are a number of distinct estimators of Advantage that an agent might use. Below, we review three tenable on-line estimators of Advantage, each of which can be used on-line to estimate ${\widehat{A}}^{\pi }(s,a)$. These three estimators do not exhaust the list of possible estimators⁴; however, Advantage estimation by these three estimators is sufficient to explain the contextual effects on mood reviewed in Section 1, and we therefore limit our discussion here to these estimators.

Advantage Estimator 1: Temporal difference error.

As discussed above, the temporal difference error δ is an estimator of the true Advantage of the chosen action (Schulman et al., 2015). That is, the temporal difference error following an action provides an unbiased estimate of how much better the agent could do by taking that action more frequently in future (i.e., the Advantage of the action).

One implementation note on this point concerns non-instrumental settings in which the agent’s actions do not have any effect on the subsequent reward or successor state (i.e., Pavlovian conditioning). In such cases, since actions chosen by the agent do not produce any changes in future reward, no one action is better than any other and the Advantage of all actions is 0 by definition. In this setting the temporal difference prediction error δ is still an estimator of the true Advantage function, since at convergence the expected value of δ is indeed 0. This highlights, however, that the temporal difference error may be a high-variance estimator of the advantage, since in stochastic environments the temporal difference error on any given trial may be very different from zero.

Advantage Estimator 2: Policy-weighted Q-value difference.

A second method for estimating the Advantage of an action is by comparing the learned Q-value of that action to the learned Q-values of unchosen actions, with a weighting on the different actions that depends on their probabilities under the agent’s policy. To see how this method can be used to estimate the Advantage of an action, we can first recall that the value of a state s can be rewritten as a policy-weighted sum of the Q-values of the different actions that can be taken in s (denoted $\mathcal{A}$):

$$V^{\pi }(s)=\sum _{a\in \mathcal{A}}\pi (a\mid s)Q^{\pi }(s,a)$$ (8)

This can be substituted into the definition of the Advantage function to produce a decomposition of the Advantage into a term that depends on the value of the chosen action a_t and a term that depends on the values of all unchosen actions (denoted $\tilde{a}$):

$$\begin{gathered} A^{\pi }(s_t,a_t)=Q^{\pi }(s_t,a_t)-\sum _{a\in A}\pi (a\mid s_t)Q^{\pi }(s_t,a) \\ =[1-\pi (a_t\mid s_t)]Q^{\pi }(s_t,a_t)-\sum _{\tilde{a}\ne a_t}\pi (\tilde{a}\mid s_t)Q^{\pi }(s_t,\tilde{a}) \end{gathered}$$ (9)

This formulation of the Advantage function can be estimated on-line by substituting Q-value of the chosen action with the sum of the immediate reward and the discounted value of the successor state (as in Equation 5). We term this the “policy-weighted Q-value difference” (PWQD):

$$\begin{gathered} {\text{PWQD}}_t\equiv [1-\pi (a_t\mid s_t)][r(s_t,a_t,s_{t+1})+\gamma V^{\pi }(s_{t+1})]-\sum _{\tilde{a}\ne a_t}\pi (\tilde{a}\mid s_t)Q^{\pi }(s_t,\tilde{a}) \\ ={\widehat{A}}^{\pi }(s_t,a_t) \end{gathered}$$ (10)

This method of estimating Advantage can be used on-line by agents that learn both an action-value function Q and a state-value function V (as it depends on both).

Why might an agent estimate the Advantage of an action using the PWQD rather than the temporal difference error? One reason is that the PWQD can reduce the variance of Advantage estimates by taking into account the expected outcomes of all possible actions, not just the chosen action (as in the case of the temporal difference error). In general, the PWQD formulation would be expected to reduce the variance of Advantage estimates in situations where the Q-values of actions are relatively well-learned. If these values are not well-learned, by contrast, the PWQD might introduce considerable bias into Advantage estimates (inherited from the bias of the Q-values), and the agent might be better served estimating Advantage according to the temporal difference error instead.

Advantage Estimator 3: Policy-weighted reward difference.

The previous section introduced the PWQD and described how this estimator can produce lower-variance estimates of the Advantage of an action by taking into account the expected outcomes of unchosen actions (i.e., their Q-values). In some settings, however, the agent may receive counterfactual information about the outcomes that would have resulted from unchosen actions. In such cases, it is reasonable to replace the learned Q-values of unchosen actions in Equation 9 with the immediate outcomes associated with each action (since, per Equation 5, these outcomes can be treated as stochastic estimates of the true Q-values of unchosen actions). This permits Equation 9 to be re-written as follows:

$$A^{\pi }(s_t,a_t)\approx (1-\pi (a_t\mid s_t))(r(s_t,a_t,s_{t+1})+\gamma V^{\pi }(s_{t+1}\mid a_t))-\sum _{\tilde{a}\ne a_t}\pi (\tilde{a}\mid s_t)(r(s_t,\tilde{a},s_{t+1})+\gamma V^{\pi }(s_{t+1}\mid \tilde{a}))$$ (11)

Finally, note that Equation 11 makes reference to the value of the successor states that would have followed each possible action. When all actions either result in the same successor state (or in different successor states with equal values), these successor state values can be eliminated from Equation 11 to produce a more lightweight estimator that we term the policy-weighted reward difference (PWRD) of chosen and unchosen actions:

$$\begin{gathered} {\text{PWRD}}_t\equiv [1-\pi (a_t\mid s_t)]r(s_t,a_t,s_{t+1})-\sum _{\tilde{a}\ne a_t}\pi (\tilde{a}\mid s_t)r(s_t,\tilde{a},s_{t+1}) \\ \approx A^{\pi }(s_t,a_t) \end{gathered}$$ (12)

Since the PWRD makes reference only to the immediate rewards derived from each action, this estimator can be used in situations can be used include the terminal states of a game, in iterated single-state choice environments such as a multi-armed bandit problem, or in situations where the agent cares only about immediate rewards and heavily discounts future rewards (i.e., as γ → 0).

Where such counterfactual information is available, therefore, policy-weighted reward difference can be treated by the agent as an estimate of the Advantage function (see also Li & Daw, 2011, p. 5506, for the derivation of a related expression). In fact, this estimator of the Advantage function is the most lightweight of the three estimators presented here, in that it does not require the agent to learn either a state-value function (as in the temporal difference error and the PWQD) or an action-value function (as in the PWQD); instead, it simply requires that the agent observe the outcomes of different actions and compare them. As such, Advantage can be estimated using the PWRD by any agent that observes (or infers) counterfactual information about alternative actions.

For both the PWQD and the PWRD, the magnitude of the estimated Advantage for the chosen action is inversely proportional to the probability of that action under the policy. This is because, as the probability of the chosen action approaches 1 in Equations 10 and 12, the weights on the outcomes of both the chosen action (1 − π(a_t ∣ s_t)) and all unchosen actions ($\pi (\tilde{a}\mid s_t)$) go to 0. As a result, when the probability of the chosen action is hig (as in over-learned or habitual cases), the estimated Advantage will tend to be small, and vice versa when the probability of the chosen action is low under the current policy. Intuitively, this result is a reflection of the fact that Advantage quantifies the excess value of taking an action within a state over and above the value of the state itself. When the probability of the chosen action is high, the resulting outcome will tend to be similar to the state-value, since the state-value itself is primarily a reflection of the values of probable actions. By contrast, when the probability of the chosen action is low, the resulting outcome will tend to be rather dissimilar to the state-value, and hence the estimated advantage will tend to be larger. The consequence of this feature is that the estimated Advantage of infrequent or exceptional actions will tend to have a greater absolute magnitude than the estimated Advantage of typical actions. As discussed in detail below, this is crucial in our explanation of the action-typicality effect on mood.

Combining estimates of the Advantage function.

Above, we detailed three methods by which a reinforcement learning agent can estimate the Advantage function on the basis of trial-by-trial observations. In some situations, agents will be able to estimate Advantage using more than one of these methods. For instance, an agent that receives counterfactual information might be able to estimate Advantage using both the temporal difference error (which depends only on the outcome of the chosen action, and not on counterfactual information) and the PWRD (which depends on the outcome of all actions). In these cases, the different estimation methods can be combined using a weighted average. The weights in this average may depend on the relative precision of the different estimators, such that more precisee methods are given more weight.

In our model of mood, we assume that the agent uses all information at its disposal to estimate the Advantage of its actions. When multiple estimates are available, they can be averaged, weighted by the relative precision of each estimate (to the best of the agent’s knowledge):

$${\widehat{A}}^{\pi }(s_t,a_t)=\sum _{k=1}^K{w}_k{\widehat{A}}_k^{\pi }(s_t,a_t),\text{where}\sum _{k=1}^K{w}_k=1.$$ (13)

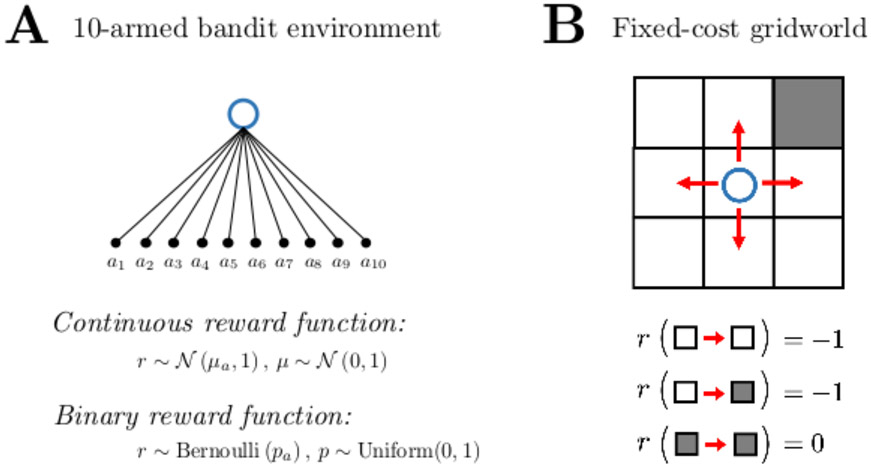
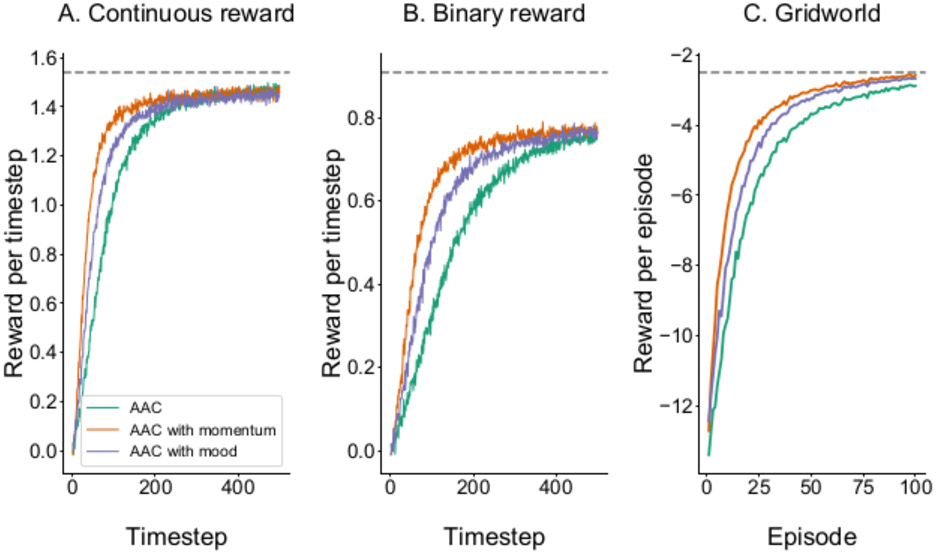
To illustrate the differences in the precision of the different estimators, we simulated the performance of a reinforcement learning algorithm on a four-armed bandit task with complete feedback (i.e., the agent observed the outcome of all four choice options, not only the chosen action). At each timestep, we estimated the Advantage of the agent’s chosen action according to each of the three estimators described above, and measured the difference between each estimate and the true Advantage of the chosen action. The results of this simulation are presented in Figure 1, and full details of the simulation can be found in Appendix A.

Figure 1.

Comparison of three estimators of the Advantage function in a simulated four-armed bandit task (200 simulations of 300 trials each; see Appendix A for further details). When an arm is chosen, it probabilistically gives a reward of 0 or 1 (probabilities in simulation were 0.2, 0.4, 0.6, and 0.8). The agent implemented a TD(0) actor-critic architecture (Kimura & Kobayashi, 1998). Presented here are distributions of estimation errors for estimation of Advantage by (A) the temporal difference prediction error δ, (B) the policy-weighted Q-value difference (PWQD), and (C) the policy-weighted reward difference (PWRD). In this setting the bias of all three estimators is low, but the temporal difference error has greater estimation variance than either the PWRD or the PWQD.

In this simulation, bias was low relative to variance for all three estimators, and both the PWRD and PWQD had substantially lower variance—and therefore lower overall error—than the temporal difference error⁵. This suggests that in this particular choice environment, the PWQD should be weighted more heavily than the other estimators in the agent’s estimates of the Advantage of its actions. However, the error of each estimator is a contingent feature of the agent’s learning and the dynamics of the environment. If the Q-values are badly misspecified, for instance, the PWQD will inherit bias from biases in the learned Q-values; in such a setting, the agent would be better-served estimating advantage using the temporal difference error or the PWRD. The weights on different estimators may therefore change over time according to a dynamic arbitration process.

Section 3: The Integrated Advantage model explains contextual effects on mood

Having introduced the Integrated Advantage model of mood, we can now detail how this model accounts for the five contextual effects reviewed in Section 1. As described in Section 2, we assume that the valence of mood is driven by an individual’s estimates of the Advantage of their actions (estimated according to one or more of the methods described above). We contend that this underlying principle of Advantage estimation provides a coherent and principled explanation for each of contextual effects on mood reviewed above.

We note that in spite of the success of recent models that assume mood is a moving average of reward prediction errors (Rutledge et al., 2014; Eldar & Niv, 2015; Eldar, Rutledge, Dolan, & Niv, 2016; Vinckier et al., 2018), these models explain only a subset of contextual effects (see Table 1). By contrast, the Integrated Advantage model, which can be seen as a generalization of reward prediction error models, provides a parsimonious account of all effects reviewed above.

Table 1.

Summary of contextual mood effects accounted for by Reward Prediction Error (RPE) models and by the Integrated Advantage model.

Effect	RPE models	Integrated Advantage model	Related estimator of Advantage
Expectation	✓	✓	TD error
Surprise	✓	✓	TD error
Counterfactual	×	✓	PWRD
Action typicality	×	✓	PWQD and PWRD
Action/inaction asymmetry	×	✓	PWQD and PWRD

TD: Temporal Difference. PWRD: Policy-weighted reward difference. PWQD: Policy-weighted Q-value difference.

Expectation and surprise effects

The expectation and surprise effects both refer to the finding that events influence mood in proportion to the degree to which they violate prior expectations (either in terms of magnitude or in terms of prior probability). We consider these effects together because they both represent cases in which the influence of an event on mood depends on the degree to which its value exceeds or falls short of its expected value. As noted in Section 1, since a reward prediction error quantifies the signed discrepancy between expected reward and actual reward, both of these effects can be explained in terms of an effect of reward prediction errors on mood (Eldar & Niv, 2015; Rutledge et al., 2014; Eldar et al., 2016; Vinckier et al., 2018). In the Integrated Advantage model, expectation and surprise effects are accounted for by the use of the temporal difference prediction error as an estimator of the Advantage function (it is in this respect that the Integrated Advantage model can be seen as a generalization of previous reward prediction error models).

Furthermore, given that we propose that changes in mood are the result of a weighted average of different Advantage estimators (Equation 13), we would also predict that expectation and surprise effects will be most strongly related to mood changes in Pavlovian settings (where there are no alternative actions to consider, and no effects of counterfactual information). By contrast, we would predict weaker expectation and surprise effects in instrumental settings, particularly when counterfactual information is presented. In such settings the temporal difference error is only one possible estimator of advantage that an individual can use; as such, expectation and surprise effects would be intermixed with other effects produced by the use of counterfactual estimators such as the PWRD or PWQD.

With respect to the surprise effect it should be noted that, as previously discussed, reward prediction errors—and therefore the Integrated Advantage model—are only capable of explaining surprise effects caused by violations of expectations regarding reward amount. This leaves open the question of how to account for hypothetical surprise effects caused by violations of expectations regarding other stimulus dimensions, such as identity. One possibility is that reward amount is only one dimension of outcomes among many that is monitored by the brain, in line with recent results showing that neural reward circuits also encode information prediction errors (i.e., violations of expectations regarding the amount of information imparted by a stimulus; Bromberg-Martin & Hikosaka, 2011; Brydevall, Bennett, Murawski, & Bode, 2018).

The counterfactual effect

The counterfactual effect is that mood is influenced not only by the outcomes of the actions that one has actually taken, but also by counterfactual information about what would have happened if a different action had been taken (J. T. Johnson, 1986; Landman, 1987; Gleicher et al., 1990; Markman et al., 1993; Roese, 1994; McMullen et al., 1995; McMullen & Markman, 2002; Mandel, 2003; Coricelli & Rustichini, 2010). The influence of counterfactual information is weighted by the plausibility of each alternative action at the time of choice, such that counterfactual information about plausible unselected actions influences mood more strongly than information about implausible unselected actions (Kahneman & Tversky, 1982b; Kahneman & Miller, 1986). Since a reward prediction error is defined as the difference between the outcome associated with the chosen action and the learned expected value of that action, it is difficult for models that assume that mood reflects an accumulation of reward prediction errors to account for counterfactual effects on mood. For the same reason, estimation of Advantage by the temporal difference error also cannot account for the counterfactual effect.

Instead, this effect can be explained in terms of the use of the PWRD (Equation 12) to estimate the Advantage of chosen actions. This estimator estimates Advantage as the policy-weighted difference between the reward associated with the chosen action and the policy-weighted sum of the rewards associated with unchosen actions. Therefore, a mood variable that partly relies on the PWRD will naturally explain the counterfactual effect.

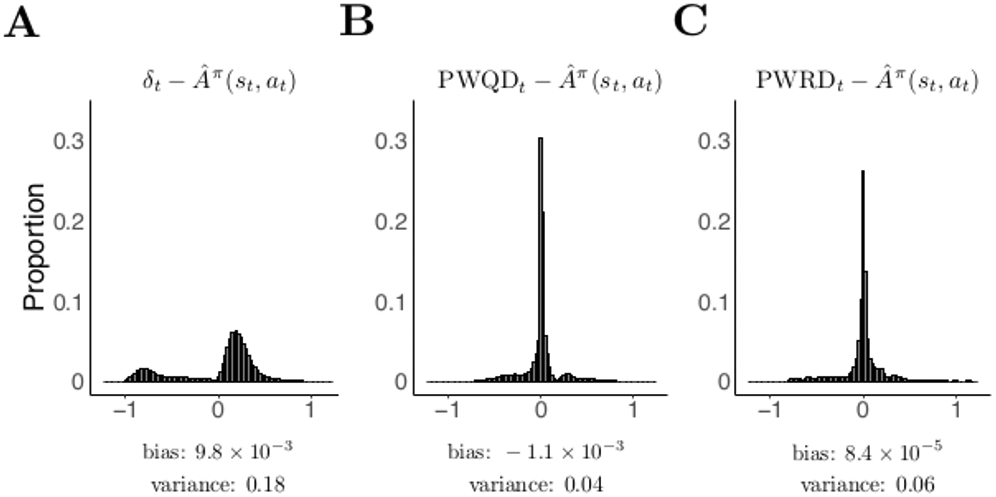
To confirm that the model can accurately predict empirical affective responses to the presentation of counterfactual information, we simulated the model’s performance on a task used by Mellers et al. (1999) (specifically, the full-information condition of their Experiment 1). In this task, participants were asked to choose repeatedly between pairs of gambles varying in outcome amount and probability. Each gamble consisted of two possible outcomes chosen from the set {+32, +8, −8, −32}, with the probability of either 0.2, 0.5, or 0.8 of the better of the two possible outcomes. An example trial, for instance, might consist of a choice between Gamble A, with 80% probability of a gain of $8 and 20% probability of a loss of $32, or Gamble B, with 50% probability of a gain of $8 and 50% probability of a loss of $8. From this space of possible gambles, participants were presented with four repetitions of each of the 36 non-dominated gamble pairs. After choosing one of the two presented gambles, participants observed the outcome of both gambles (i.e., they simultaneously learned how much they won from their chosen gamble and how much they would have won if they had chosen the other gamble instead). Participants then rated their affective response to this outcome on a continuous scale from 50 (‘extremely elated’) to −50 (‘extremely disappointed’). For each of the 36 presented gamble pairs, outcomes were rigged such that participants observed each of the four possible configurations of gamble outcomes once.

The results of this study revealed a clear effect of counterfactual outcomes on affective responses, such that participants reported more negative affective responses when the chosen gamble produced a worse outcome than the unchosen gamble, and more positive affective responses when the chosen gamble produced a better outcome than the unchosen gamble (see Figure 2). This effect was consistent across all gamble outcome configurations, regardless of whether the obtained outcome of the chosen gamble was a win or a loss, and regardless of whether this obtained outcome was better or worse than the unobtained outcome of the chosen gamble.

Figure 2.

Left: affective responses to a loss of $8 under different combinations of unobtained outcomes for the chosen gamble (x-axis) and counterfactual outcomes for the unchosen gamble (separate lines). Right: affective responses to a win of $8. Empirical means of participants’ responses are represented by black squares and solid lines; affective responses as predicted by the Integrated Advantage model are represented by white circles and broken lines. There is a close correspondence between empirical data and model predictions (root-mean-square error = 2.93). In each plot, the vertical distance between the lines represents the magnitude of the counterfactual effect (i.e., the difference in reported affective response to the same outcome paired with a gain of $32 for the unchosen gamble versus a loss of $32 for the unchosen gamble). An expectation effect is also visible in the negative slope on all lines, indicating that the affective response to the same objective outcome is more negative when the outcome is lower than the expected value of the chosen gamble. Data reproduced from Figure 4 in Mellers et al. (1999).

Because counterfactual information was presented in this task, the Integrated Advantage predicts participants’ affective responses to be a weighted average of the temporal difference prediction error and the policy-weighted reward difference (PWRD). However, because different trials in this task involved different combinations of monetary outcomes, each trial was associated with two distinct prediction errors. The first prediction error, which we denote δ_trial, occurred when the gambles were presented at the start of a trial, and depended on the configuration of monetary outcomes in each gamble (for instance, a trial with a gain-domain gamble pair of +32/+8 and +8/0 has a higher expected value than a trial with the loss-domain gamble pair −8/−32 and 0/−8, regardless of the participant’s actual choice on each trial). The second prediction error, denoted δ_outcome, occurred when the gamble outcome was presented, and is calculated as per Equation 2. For this task, therefore, the Integrated Advantage model predicts affective responses as a weighted average (per Equation 13) of the two prediction errors and the PWRD:

$$\Delta \text{Mood}\propto w_{{\delta }_{\text{trial}}}\cdot {\delta }_{\text{trial}}+w_{{\delta }_{\text{outcome}}}\cdot {\delta }_{\text{outcome}}+w_{\text{PWRD}}\cdot \text{PWRD}$$ (14)

We simulated participants’ trial-by-trial affective responses to the gambles presented by Mellers et al. (1999), treating the weights in Equation 14 as free parameters to be fit to group-mean data. To translate estimated affective responses from the latent space specified by Equation 14 onto the bounded scale (−50, 50) used in the experiment, we used a logistic link function with a slope and intercept estimated from the data⁶.

As shown in Figure 2, we found a close correspondence between the empirical group-mean data and simulated affective responses from the Integrated Advantage model. This provides strong evidence that the Integrated Advantage model can account for counterfactual effects. Moreover, the best-fitting weight parameters for this simulation were δ_outcome = 0.45, δ_trial = 0.33, and δ_PWRD = 0.22. That all three weights are non-zero suggests that, consistent with our proposed explanation of counterfactual effects, all three variables were incorporated within participants’ reported affective responses. Of the two prediction errors, we observed a larger weight on δ_outcome relative to δ_trial. Since affective responses were recorded immediately after the presentation of gamble outcomes, the greater weight on outcome-related prediction errors may suggest a recency effect in affective responses.

Action typicality effect

Recall that the action typicality effect is the tendency for outcomes of unusual or exceptional actions to produce amplified affective responses relative to the outcomes of typical actions. The Integrated Advantage model accounts for this effect by assuming that the agent can estimate the Advantage of its actions using the PWRD (when counterfactual information is provided) or the PWQD (when no counterfactual information is provided).

Specifically, for both the PWRD and the PWQD, the magnitude of the estimated Advantage is inversely proportional to the probability of the chosen action under the agent’s policy. This is because, in both estimators, the weighting on the outcomes of all actions is proportional to π(a_t ∣ s_t), the chosen action’s probability under the current policy. The net effect of this weighting scheme is that, when the chosen action is unusual under the policy, the outcome of that action (as well as the outcomes of unchosen actions, if they are observed) contributes to a larger-magnitude estimated advantage (and hence a larger change in mood).

Intuitively, the reason that the estimated Advantage is greater in magnitude when uncommon actions are chosen is because Advantage is defined (Equation 4) as the value of an action over and above the value of the state. Common actions are those that are taken with high probability in a state, and so the value of these actions will be close to the state by definition; as a consequence, these actions will tend to have small estimated Advantage when chosen. By contrast, the estimated Advantage of uncommon actions will tend to have larger absolute estimated Advantage because, being uncommon, these actions contribute less to the learned value of the state.

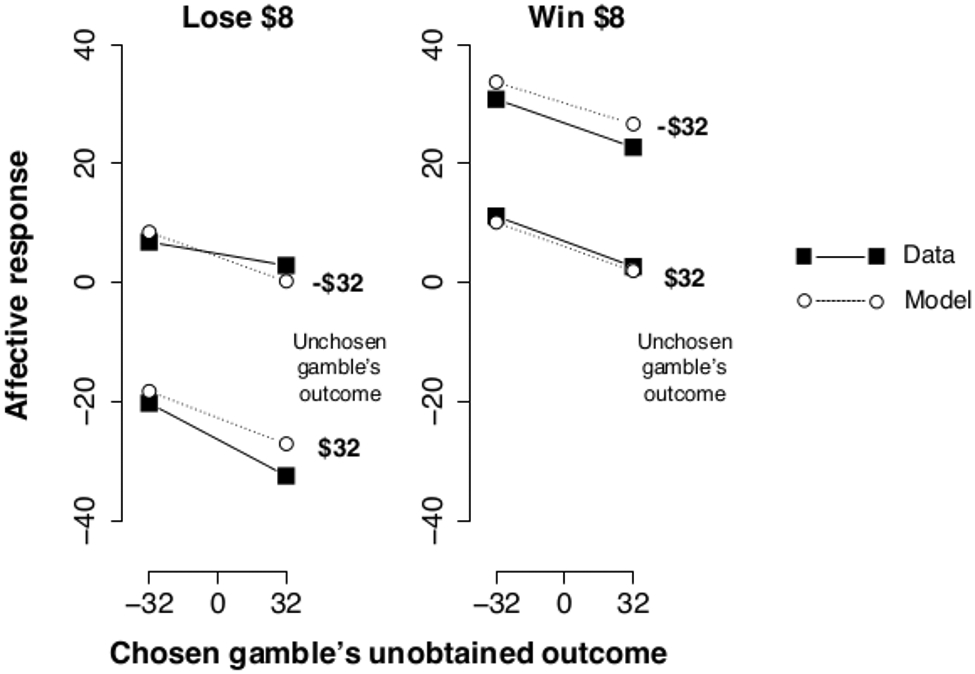
Figure 3 presents simulated Advantage estimates (from the four-armed bandit task previously described in Section 2). Consistent with the action typicality effect, both the PWQD and the PWRD estimates display a ‘funnel’ shape, such that estimates of Advantage take on larger absolute values for low-probability (i.e., atypical) actions relative to high-probablity (i.e., typical) actions.

Figure 3.

Association between estimated Advantage and the probability of the chosen action for a simulated four-armed bandit task. Both (A) the policy-weighted Q-value difference (PWQD) and (B) the policy-weighted reward difference (PWRD) take on a characteristic funnel shape, indicating greater absolute estimates of Advantage for low-probability actions than for high-probability actions.

Moreover, the Integrated Advantage model thus makes explicit the relationship between the counterfactual and action-typicality effects in terms of their mutual dependence on the probability of the chosen and unchosen actions under the policy. As a result, our model predicts that the counterfactual and action typicality effects should interact such that the influence of counterfactual information on mood also increases after atypical actions. We would also predict that individual differences in the extent to which individuals utilize counterfactual information in learning should be associated with differences in the strength of counterfactual effects on mood.

Action/inaction asymmetry

The action/inaction asymmetry, it has been suggested, is that outcomes following an explicit action influence mood more strongly than outcomes following inaction. Many accounts have explained this effect as an extension of the action typicality effect: if inaction is the default policy for many decision problems, then explicit action is more exceptional and would therefore be expected to produce stronger affective responses (Feldman, 2019).

We follow this account in explaining action/inaction asymmetries in the Integrated Advantage model. In particular, we note that the Integrated Advantage model predicts that the strength of action-inaction asymmetries should be proportional to the degree to which inaction is more likely than action under the agent’s policy in a particular choice domain. In tasks assessing the interaction between Pavlovian biases and instrumental choice behavior, for instance, it has been shown that there is a default tendency towards action for appetitive choice domains, and towards inaction for aversive choice domains (Guitart-Masip et al., 2011; Cavanagh, Eisenberg, Guitart-Masip, Huys, & Frank, 2013). Given these Pavlovian biases, the Integrated Advantage model would predict increased amplitude of affective responses following ‘no-go’ relative to ‘go’ responses in appetitive outcome domains, and following ‘go’ relative to ‘no-go’ responses in aversive outcome domains. Indeed, Swart et al. (2017) found that avoidance learning (i.e., learned inaction) was slower than approach learning in the loss domain, consistent with a reduced effect of punishment feedback on inaction than action. The Integrated Advantage model predicts that this same pattern of effects should also be observed participants’ affective responses to feedback.

Section 4: The functional role of mood in learning

In the previous section, we showed that the principle of Advantage estimation provides a parsimonious account for five contextual effects on mood. However, this in and of itself does not address functional question of mood: why should the valence of mood be a leaky integrator of the Advantage of an agent’s actions, as we propose? Of what use would such a representation be to a biological agent? Previous computational models of mood have proposed that a moving average of reward prediction errors can be used to quantify correlated changes in the value of the environment across states (Eldar et al., 2016); however, this justification no longer applies to a mood variable which, as we have proposed, integrates Advantage rather than reward prediction errors. It is incumbent on us, therefore, to explain what adaptive function might be served by mood as conceptualised in the Integrated Advantage model.

To address this question, we propose an adaptive functional basis for the Integrated Advantage model of mood. In this section we propose that mood, as set out in the Integrated Advantage model, can be used to approximate momentum, a technique from stochastic optimization theory that accelerates optimization (learning) by stochastic gradient descent. As mentioned above, a crucial role for Advantage in reinforcement learning is to appraise whether a particular action should be made more or less likely in future. Below, we set out a derivation that demonstrates how integrating Advantage over time, and using this integrated representation (i.e., mood) to guide updates to a behavioral policy, can result in improved learning performance compared to an agent that only updates its policy on the basis of single-trial information.

We note that although we provide an introduction to the relevant concepts and have endeavoured to be as clear as possible in our derivation of our model, Sections 4 and 5 include technical material that may be less accessible to readers without a grounding in machine learning. Such readers may wish to skip to the General Discussion, where the content of these sections is summarized.

Below, we first review principles of stochastic gradient descent, and outline the concept of momentum in stochastic optimization. We then explain the deep link between stochastic gradient descent and a reinforcement learning algorithm that operates on similar principles, termed policy-gradient reinforcement learning. Finally, we derive an algorithm in which a mood variable as in the Integrated Advantage model is used to help approximate momentum in a manner that accelerates learning. This demonstrates a potential adaptive basis for mood as instantiated within the Integrated Advantage model.

Gradient descent, stochastic gradient descent, and momentum

Gradient descent, a foundational method in optimization, is a method for finding the vector of parameters θ that minimize a cost function⁷ J(θ) by incrementally adjusting the parameters using the gradient of J with respect to θ (Robbins & Monro, 1951). This gradient, denoted ∇_θJ(θ), is defined as the vector of partial derivatives of J(θ) with respect to θ, and can be thought of as the slope of the cost function with respect to changes in each of its parameters.

$${\nabla }_{\theta }J(\theta )\equiv \left[\begin{array}{c}\hfill \frac{\partial J(\theta )}{\partial {\theta }_1}\hfill \\ \hfill ⋮\hfill \\ \hfill \frac{\partial J(\theta )}{\partial {\theta }_n}\hfill \end{array}\right]$$ (15)

Starting from an arbitrary initial setting of parameters θ, gradient descent iteratively improves the parameters at each timestep by adjusting them in the direction of the negative gradient:

$$\begin{gathered} u_t=\eta {\nabla }_{\theta }J(\theta ) \\ \theta \leftarrow \theta -u_t \end{gathered}$$ (16)

Here, we denote the update to parameters at time t by the vector u_t. The step-size (or learning rate) hyperparameter η determines the size of this update by controlling how far the parameters are adjusted in the direction of the gradient. A geometric intuition for this algorithm is to interpret the cost function J(θ) as describing the height of a surface at a point whose coordinates are specified by θ. The gradient descent method then moves this point down the slope some distance in the direction in which the slope is steepest.

Stochastic gradient descent is an extension of gradient descent to cases in which exact calculation of the gradient is infeasible. In stochastic gradient descent, the true gradient ∇_θJ(θ) is replaced with an approximation ${\nabla }_{\theta }\widehat{J}(\theta )$ (typically the average of a mini-batch of N samples of the true gradient, ∇_θJ_i(θ)). Stochastic gradient descent then iteratively improves θ using the estimated gradient in place of the true gradient:

$$\begin{gathered} {\nabla }_{\theta }\widehat{J}(\theta )=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }{J}_i(\theta ) \\ {u}_t=\eta {\nabla }_{\theta }\widehat{J}(\theta ) \\ \theta \leftarrow \theta -u_t \end{gathered}$$ (17)

“Momentum” is a technique for accelerating optimization by stochastic gradient descent (Polyak, 1964; Nesterov, 1984; Qian, 1999; Ruder, 2016). It involves updating parameters using both the approximate gradient of J at the current parameters and a proportion m (0 ≤ m ≤ 1) of the parameter update at the previous timestep:

$$\begin{gathered} u_t=\eta {\nabla }_{\theta }\widehat{J}(\theta )+m{u}_{t-1} \\ \theta \leftarrow \theta -u_t \end{gathered}$$ (18)

Adding momentum biases the parameter update at each timestep in the direction of the parameter update at the previous timestep, with the strength of this bias controlled⁸ by the hyperparameter m.

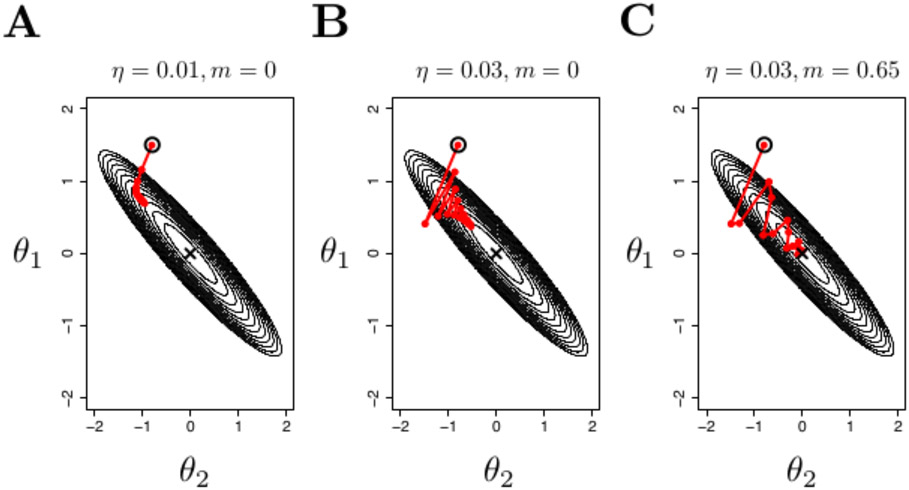
To understand why adding momentum accelerates stochastic gradient descent, we need to understand two distinct but related shortcomings of stochastic gradient descent. The first is related to the fact that stochastic gradient descent considers only the the slope of the cost function—that is, its first derivative—and not its curvature (second derivative). This slows the convergence of stochastic gradient descent procedures when the curvature of the cost function differs across different dimensions of parameter space (Sutton, 1986). Differential curvature of the cost function introduces an unavoidable trade-off in the choice of a step size hyperparameter η: while a small step size is required to smoothly descend the cost function, this small step size results in slow progress (Figure 4A). However, simply increasing the step size may not speed convergence if the gradient for some parameters is steep; instead, it can produce oscillations in parameter updates (Figure 4B).

Figure 4.

Fifteen steps of gradient descent on a two-parameter quadratic cost function under three combinations of learning rate (η) and momentum (m). Contours denote points of equal cost. Axes represent the two parameters of the cost function (θ₁ and θ₂). This function is an example of a ‘ravine’, in which the cost function has different curvature with respect to different parameters. The starting point is denoted by the black circle, and the true minimum of the quadratic function is denoted by the black cross. A: A small step size (with no momentum) results in smooth but slow progress down the cost function. B: A large step size (with no momentum) results in oscillations across the curvature of the cost function. C: Adding a momentum term allows for accelerated convergence with a large step size, because the momentum term filters out the high-frequency oscillations across the curvature of the cost function that are visible in the centre graph.

The second shortcoming of stochastic gradient descent results from the stochasticity of the gradient approximation described in Equation 17. Using the stochastic gradient approximation ${\nabla }_{\theta }\widehat{J}(\theta )$ introduces noise into the gradient descent procedure: although the approximation is equal in expectation to the true gradient, the approximation is just that: it does not represent the true gradient, and in particular, may have high variance (that is, large error around the true gradient), especially if it is computed based on relatively few samples. In practice, this means that at any single timestep, stochastic error in the approximation ${\nabla }_{\theta }\widehat{J}(\theta )$ may lead the algorithm to update its parameters in an incorrect direction.

How does momentum help overcome these two limitations? We can observe that both of the sources of error described above operate on a fast timescale (on the order of individual steps of gradient descent). When considered at a longer timescale, these error sources are effectively a kind of high-frequency noise. This explains why momentum resolves both issues: by partially incorporating the update from time t − 1 at time t, momentum averages across the errors of different timesteps (with an exponentially decreasing weight on timesteps in the far past), effectively applying a low-pass filter to parameter updates. This mitigates the impact of high-frequency noise sources while allowing overall gradient descent to proceed unimpeded (Figure 4C).

In addition, one further benefit associated with momentum in stochastic optimization is that it can accelerate convergence across areas of the cost function that are relatively flat (i.e., in which the cost function changes slowly and consistently with changes in the parameters). In this situation, an agent without momentum would take a constant step size at each timepoint (because of its constant learning rate), and would therefore traverse the objective function relatively slowly. Adding momentum would allow the agent to take successively larger steps across the objective function as long as it remains flat, hence speeding up optimization (Sutskever, Martens, Dahl, & Hinton, 2013).

For these reasons, momentum has long been widely used in optimization in machine learning applications. Classical momentum of the form described in Equation 18 was expounded by Rumelhart, Hinton, and Williams (1986) as a method for accelerating the training of neural networks and, more recently, deep learning research has developed advanced algorithms for training neural networks that incorporate momentum-style low-pass filtering of parameter updates (e.g., Kingma & Ba, 2014; Bello, Zoph, Vasudevan, & Le, 2017).

We contend that human mood may serve an adaptive function by helping to implement the principle of momentum. To illustrate this, we first review below a variant of reinforcement learning that closely corresponds to stochastic gradient descent—policy-gradient reinforcement learning—and within which a momentum-style modification can be implemented.

Policy-gradient reinforcement learning and Advantage Actor-Critic

Policy-gradient reinforcement learning refers to a family of algorithms, first introduced by Williams (1992), that operate on an equivalent principle to stochastic gradient descent. A policy-gradient reinforcement learning agent seeks to perform gradient ascent (rather than descent) on an objective function that quantifies the average expected reward per timestep:

$$J(\theta )=\sum _s{d}^{{\pi }_{\theta }}(s)\sum _a{\pi }_{\theta }(a\mid s)r(s,a)$$ (19)

Here the policy π_θ is a function⁹ (with parameters θ) that produces a probability distribution over actions a given the current state s. d^π_θ(s) is the stationary distribution over states of the environment given this policy (that is, the probability that an agent following policy π_θ will occupy the state s at an arbitrary future timepoint), and r(s, a) is the reward associated with selecting action a in state s. As such, J(θ) quantifies the expected reward by averaging over all future states, and in each state, the rewards expected for each action weighted by the probability of that action. The goal of a policy gradient algorithm is to find the parameters θ that maximize this function.

Because of the close conceptual correspondence between policy-gradient reinforcement learning and stochastic gradient descent, the advantages of momentum described above can be applied directly to policy-gradient reinforcement-learning algorithms. In this section, we first describe a state-of-the-art policy gradient algorithm; next, we augment this algorithm with momentum as defined above, and use this augmented algorithm to illustrate the practical advantages of momentum in reinforcement learning. This algorithm, Advantage Actor-Critic, incorporates recent developments in policy-gradient reinforcement learning (see Sutton, McAllester, Singh, & Mansour, 2000; Konda & Tsitsiklis, 2000; Grondman, Busoniu, Lopes, & Babuska, 2012; Bhatnagar et al., 2009; Mnih et al., 2016; Kimura & Kobayashi, 1998; Degris, Pilarski, & Sutton, 2012).

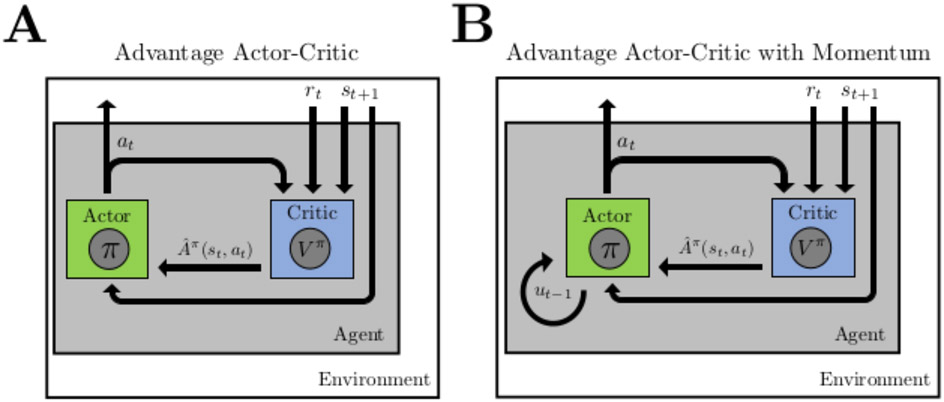
The Advantage Actor-Critic algorithm.

An Advantage Actor-Critic agent has two critical components (presented schematically in the left panel of Figure 5): a ‘Critic’ that learns estimates of the value of the different states of the environment (e.g., using an algorithm such as temporal difference learning; Sutton, 1988), and an ‘Actor,’ which maintains and updates the agent’s policy. Critically, the Actor updates its policy at each timestep using an estimate, provided by the Critic, of the Advantage of the previous action. Intuitively, the Actor chooses actions, which are then criticized by the Critic based on whether these actions were more or less advantageous (relative to the learned value of the current state under the policy). This critique helps the Actor improve its action-selection policy in the future.

Figure 5.

Schematics of two actor-critic algorithms (A: Advantage Actor-Critic; B: Advantage Actor-Critic with Momentum). At each timepoint, the agent (grey) takes an action a_t from state s_t. In response, the environment returns a reward r_t and a successor state s_t+1. The agents depicted each comprise an Actor (green), which emits actions according to the learned policy π, and a Critic (blue), which learns the value V^π of the different states of the environment under the policy. Based on the reward and successor state, the Critic calculates an estimate of the advantage of the chosen action (for instance, the temporal difference error), and provides this to the Actor. The Actor uses this gradient estimate to update the policy. The difference between Advantage Actor-Critic algorithms without (A) and with momentum (B) is that in the latter, the Actor augments its parameter updates at each timepoint according to the parameter update at the previous timepoint (u_t−1).

As discussed above, the Advantage function provides a low-variance estimate of the gradient of expected reward (i.e., of J(θ)) with respect to the chosen action (that is, how much and with what sign J(θ) would change if the chosen action were be taken more frequently). The Advantage Actor-Critic algorithm can be expressed as follows:

$$e_t=\lambda e_{t-1}+{\nabla }_{\theta }\log \pi (a_t\mid s_t)$$ (20.1: updating the eligibility trace e_t)

$$u_t=\eta {\widehat{A}}^{\pi }(s_t,a_t)e_t$$ (20.2: calculating the parameter update u_t)

$$\theta \leftarrow \theta +u_t$$ (20.3: updating the policy parameters θ)

A critical term for this algorithm is ∇_θ log π(a ∣ s), the gradient of the logarithm of the policy with respect to θ. This quantity is known as the score function, because it provides a means for assigning credit for changes in reward to the different components of the parameter vector (Williams, 1992). The exact form of the score function will depend on the form¹⁰ of the agent’s policy π; so, for instance, a softmax policy (e.g., for selecting one of several discrete actions) will have a different score function to a Gaussian policy (e.g., the angular movement of a joystick in a continuous action space). Mechanistically, the score function is used to increment an ‘eligiblity trace’ e_t, which additively accumulates score functions over time (subject to a decay factor 0 ≤ λ ≤ 1). Eligibility traces are a common feature of reinforcement learning algorithms. Accumulating an eligibility trace aids in assignment of credit for rewards received at time t to actions taken at points in the past (Sutton, 1988; Kimura & Kobayashi, 1998; Degris et al., 2012).

Adding momentum to the Advantage Actor-Critic algorithm.

Because policy-gradient reinforcement learning is an instance of stochastic gradient descent, momentum can be added to the Advantage Actor-Critic algorithm in just the same way as it was added to stochastic gradient descent in Equation 18:

$$e_t=\lambda e_{t-1}+{\nabla }_{\theta }\log \pi (a_t\mid s_t)$$ (21.1: identical to 20.1)

$$u_t=\eta A^{\pi }(s_t,a_t)e_t+m{u}_{t-1}$$ (21.2: calculating the parameter update u_t)

$$\theta \leftarrow \theta +u_t$$ (21.3: identical to 20.3)

All steps of the algorithm expressed through Equation 21 are identical to Equation 20, with the exception of the parameter update calculation. In particular, as in stochastic gradient descent with momentum, we simply augment the parameter update at time t with a proportion m of the parameter update at trial t − 1. This shows how momentum can be incorporated into a reinforcement learning algorithm (Figure 5). In the above equation, the parameter m controls the proportion (between 0 and 1) of the update at the previous timestep that is carried forward to the current timestep. When this parameter is large (e.g., m = 0.99), the momentum term is influenced by updates even far into the past; by contrast, when m is small (e.g., m = 0.01), the momentum term is dominated by the most recent updates. In this sense, the m parameter can be thought of as a “backward discounting" factor that discounts previous updates analogous to the discounting of future rewards by the γ parameter in Equation 1.

In Section 5, we present several computational simulations showing the practical utility of momentum in standard reinforcement learning problems. First, however, we show that mood—conceptualized as a leaky integral of the agent’s estimates of the Advantage of its actions—can be used to approximate the momentum update described in Equation 21.2.

Approximating momentum with mood

It appears implausible that a biological agent could implement the momentum algorithm described by Equation 21. This is because step 21.2 of the algorithm requires the agent to have exact knowledge of how the parameters of its policy were updated at the previous timepoint (the variable u_t−1). Maintaining this vector may be straightforward in silico, but it is far less straightforward in a human brain, where parameter updates may take the form of changes in synaptic plasticity at a vast number of sites across the cortex and subcortex. The question then becomes whether there is any way for an agent without access to u_t−1 to nevertheless approximate a momentum term. Here, we show that a mood variable can be used in just such an approximation.

It is possible to approximate momentum using mood because of deep resemblances between our recursive definition of mood in Equation 6 and the recursive definition of momentum in Equation 21.2. Specifically, to approximate momentum we set the learning rate for mood to one minus the desired level of momentum (i.e., η_mood = 1 − m) and incorporate mood in learning according to the following update rule (full derivation in Appendix B):

$$u_t=\eta e_t\left[{\widehat{A}}^{\pi }(s_t,a_t)+\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}{\text{Mood}}_t\right]$$ (22)

Equation 22 states that the agent (represented schematically in Figure 6 should update the parameters of its policy according to the product of three factors: first, a learning rate η; second, an eligibility trace e_t; third, the sum of the estimated advantage ${\widehat{A}}^{\pi }(s_t,a_t)$ and the agent’s current mood (the latter adjusted by a constant of proportionality $\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}$ that depends on the learning rate of the agent’s mood).

Figure 6.

Schematic of the Advantage Actor-Critic with Mood algorithm, which approximates momentum using mood. This agent is similar to those in Figure 5, except that it maintains a mood variable (red) that is recursively updates according to the critic’s estimates of the Advantage of the actor’s chosen actions. The mood variable, in turn, influences policy updates within the actor.

Intuitively, this update rule stipulates that, in determining whether the chosen action should be made more likely in future, the agent should consider both immediate feedback from its action (i.e., ${\widehat{A}}^{\pi }(s_t,a_t)$) and its current mood. This is because the effective sign of the update in Equation 22 depends on the sum of the estimated advantage of that action (i.e., feedback based on the current trial) and the agent’s current mood. If both are positive (e.g., the agent receives reinforcing feedback while in a pleasant mood), then the action will be made more likely; if both are negative (e.g., non-reinforcing feedback received while in an unpleasant mood), the action will be made less likely. If the signs of the current feedback and mood are different, however, then the effect of feedback on behavior will depend on which of the two terms is larger. This may lead to interesting phenomena where the policy update goes in the opposite direction to the feedback on the current trial. For instance, if mood is sufficiently strong, an agent in a pleasant mood may increase the probability of repeating the current action in future, even if it has received negative feedback for that action on the current trial (and vice versa for an agent that receives positive feedback on an action while in a negative mood).

It is important to note that the update rule described in Equation 22 is only an approximation of the momentum-based update rule in Equation 21.2. Briefly, this is because whereas the full recursive definition of momentum uses a decaying series of eligibility traces e_t, e_t−1, e_t−2, …, the mood-based approximation uses only the most recent eligibility trace e_t (for reasons set out in the full derivation in Appendix B). The net effect of this approximation (discussed further in the simulations of the algorithms in a subsequent section) is to introduce a slight bias in Equation 22 such that more recent actions are updated more than they would be in the full momentum update.

Section 5: Simulation of momentum- and mood-based reinforcement learning algorithms

We now build on the theoretical derivation presented in Section 4 to present three simulations designed to illustrate the utility of a mood-based approximation of momentum. These simulations employ two virtual choice environments (detailed in Figure 7) that are standard testbeds for reinforcement learning algorithms: a ten-armed bandit task and a fixed-cost gridworld (Sutton & Barto, 2018). In both environments, we simulate the performance of three distinct reinforcement learning algorithms: an Advantage Actor-Critic (AAC) agent (Figure 5A), an AAC agent with momentum (Figure 5B), and an AAC agent that maintains a mood variable and uses it to approximate momentum (Figure 6). All agents used only the temporal difference error δ to estimate Advantage. Full computational details of each simulation can be found in Appendix C, and code for reproducing all simulations is available in the online supplementary material.

Figure 7.

(A) The ten-armed bandit choice environment. At each timestep, the agent (blue circle) chooses one of ten options (‘arms’; black circles), and receives a reward that depends on which arm is chosen. The agent’s goal is to maximize its total reward. We simulated two reward functions: for continuous rewards, we used a Gaussian reward function such that a chosen arm a pays out a reward r according to a Gaussian distribution with a mean μ_a and a standard deviation of 1. The mean of each arm was initialized at the start of each simulation as a draw from a unit normal distribution. For probabilistic (binary) rewards, we used a Bernoulli function such that a chosen arm pays out either 0 or 1 according to an arm-specific probability p_a drawn from a unit uniform distribution. Each arm’s payout mean/probability was stationary over time within a simulation. (B) A fixed-cost 3x3 gridworld environment. At each step, the agent moves in one of the four cardinal directions (red arrows). The terminal state (grey square at top right) is absorbing. Once it reaches this state, the agent remains in place (self-transitions) for one timestep before the episode ends. Actions that would take the agent out of the gridworld (e.g., moving left from the leftmost states) are not permitted. The agent receives a reward of −1 for all state transitions except for self-transitions in the terminal state, which produce a reward of 0. To maximize reward, the agent must therefore learn to move in as few steps as possible from its initial state (randomized in each simulation) to the terminal state.

Across the two choice environments, simulation results supported two conclusions: first, adding momentum to an AAC agent can markedly improve the agent’s performance, across choice domains. Second, a mood-based approximation of momentum captures much (though not all) of the performance boost associated with momentum.

Ten-armed bandit task

In the ten-armed bandit task, a moderate amount of momentum (m = 0.6; orange lines in Figure 8A and 8B) provided a clear performance boost over agent without momentum (green line), both in an environment with continuous-valued rewards and in an environment with probabilistic binary rewards. Importantly for our account of mood, much of the performance boost of momentum was also captured by an agent that maintained a mood variable as a leaky integral of estimated Advantage, and used this mood variable to approximate momentum (purple lines in Figure 8). This provides empirical support for our theoretical proposal that mood as implemented in the Integrated Advantage model can be of adaptive utility for a reinforcement-learning agent.

Figure 8.

Mean reward per timestep across 5000 simulations of three different reinforcement learning problems. Green: Advantage Actor-Critic (AAC); orange: AAC with momentum; purple: AAC using mood as an approximation of momentum. Performance of agents in each environment is benchmarked relative to optimal performance (horizontal dashed line). (A) 500 timesteps of the 10-armed bandit task (Figure 7A) with continuous (Gaussian-distributed) rewards. (B) 500 timesteps of the 10-armed bandit task with binary (Bernoulli-distributed) rewards. (C) 100 episodes of the fixed-cost gridworld environment (Figure 7B). Each episode finished either after 100 steps or one self-transition in the terminal state, whichever occurred sooner.

There are several further noteworthy features of the performance of the simulated agents. The first is that, although the AAC-with-mood agent substantially outperforms the base AAC agent in both choice environments, this performance improvement is not as large as that of the AAC-with-momentum agent. This difference is because the AAC-with-mood agent represents mood as a weighted average of previous estimates of Advantage, and approximates momentum by multiplying this scalar by the eligibility trace at the current timestep. This introduces a degree of bias in the approximation of momentum, such that the most recent action effectively receives excess credit for earlier actions. This bias is small relative to the performance boost associated with momentum; nevertheless, it explains why the performance of the mood and momentum-based agents is not identical.

We note also that performance improvements for both momentum and mood were greater with a probabilistic binary environment (Figure 8B) than with a continuous reward environment (Figure 8A). One important difference between these two reward environments is that the binary reward environment has higher-variance rewards than the continuous reward environment. As the variance of rewards increases, the outcome of any single trial is less informative regarding the true value of the chosen action. This explains the performance improvement due to momentum and mood: they effectively allow the agent to marginalize over trial-by-trial stochasticity in the environment when updating its behavioral policy, with the resulting performance improvement increasing in proportion to the stochasticity of the environment (i.e., variance of rewards).

Fixed-cost gridworld

The ten-armed bandit environment lacks one important feature that is present in the broader class of reinforcement learning problems: state transitions (given that it has only one state). To test whether momentum and mood also improve performance in an environment with a more complex state-space, we simulated the same three agents in a fixed-cost gridworld environment (see Figure 7B). Here, agents traversed a 3x3 state-space, with the goal of moving as fast as possible from the (randomized) starting state to an absorbing terminal state. Rewards were deterministic: a cost of −1 for each timestep that the agent spends outside the terminal state. As a result, there were only two potential sources of stochasticity in different runs through the gridworld: randomness in the starting state and in the agent’s choices.

In spite of these differences from the 10-armed bandit environment, Figure 8C demonstrates a pattern of improvement in performance for agents that use momentum and mood that is on the same order of magnitude as that observed in Figure 8A and 8B.

These simulations both illustrate the benefits of momentum in reinforcement learning, as well as demonstrating the feasibility of mood (as defined in the Integrated Advantage model) as a tool by which a biological agent can approximate the effects of a momentum-based update to its policy. Taken together, therefore, we take the results of these simulations as support for our adaptive account of the valence of mood as a leaky integral of appraisals of Advantage. It is important to note, however, that our proposal here is that momentum can be approximated by a diffuse, integrative representation of Advantage. Although this supports the adaptive utility of mood as implemented in the Integrated Advantage, it does not imply that mood is the most accurate or efficient means by which a biological agent might implement the principle of momentum in learning.

General Discussion

In this article we have proposed the Integrated Advantage model, a computational theory of the valence of mood. The model’s central proposal is that the valence of mood is a weighted average of an individual’s appraisals of the Advantages of its previous actions. Advantage, as defined in reinforcement learning (Baird, 1994), quantifies the degree to which the outcome of a chosen action is better or worse than the value of the state within which that action was taken (this state value can also be conceptualized as the overall expected outcome in a given state under the individual’s current policy). Although related to reward prediction errors, the concept of Advantage is considerably more general. For instance, whereas a reward prediction error is defined only with reference to the chosen action, Advantage also encompasses counterfactual reasoning. The Integrated Advantage model therefore represents an extension and generalisation of previous models that conceptualize mood as a moving average of reward prediction errors (Rutledge et al., 2014; Eldar & Niv, 2015; Eldar et al., 2016; Neville et al., 2020).

This article has laid out two distinct lines of evidence in support of the Integrated Advantage model: one empirical, and one theoretical. Empirically, we have shown that the Integrated Advantage model provides a unifying explanation for a number of contextual phenomena that have not previously been explained within a single theoretical model. Our explanation for these disparate phenomena rests upon the fact that the Advantage of an action can be estimated by the agent using knowledge both of the resulting reward and of any other relevant information (e.g., knowledge of counterfactual information about rewards that would have been obtained under alternative courses of action). The standard temporal difference error is therefore one feasible estimator of the Advantage of an action. In addition, we have introduced two novel estimators (the policy-weighted reward difference and the policy-weighted Q-value difference) that may also be available to the agent and that make use of more information than does the temporal difference error. The estimation of Advantage by a combination of these estimators can account for numerous previously documented contextual effects on mood.

On the theoretical side, we have sought, via mathematical derivations and computational simulations, to demonstrate a plausible functional role for mood as instantiated in the Integrated Advantage model. We propose that mood, as a leaky integrator of Advantage, is ideally suited for approximating momentum in the context of actor-critic reinforcement learning. Momentum is a theoretical concept drawn from stochastic optimization theory, and can be thought of as a kind of low-pass filter for learning. By smoothing out high-frequency noise (e.g., that resulting from environmental stochasticity or curvature of a reward function with respect to parameters), momentum helps to accelerate learning. As an approximation of momentum, therefore, we propose that mood serves the same purpose.

In particular, we provided a mathematical derivation of the Integrated Advantage model that details exactly how a mood variable that integrates estimates of Advantage can be used to approximate momentum. Then, using simulations of two standard reinforcement learning environments, we showed that actor-critic agents with either momentum or mood substantially outperform an otherwise identical agent with neither of these features. These results constitute an in-principle demonstration that mood as instantiated in the Integrated Advantage model can improve performance for a decision making agent. More broadly, we hypothesize that one reason for the pervasive influence of mood on learning and decision making across numerous animal species (see Mendl et al., 2010; Webb et al., 2019) is that it helps to approximate the adaptive principle of momentum. We propose that this would be associated with significant adaptive benefits for biological agents, who must continually adapt their behavior to a complex, dynamic, and stochastic environment.

In the remainder of this article, we broaden our perspective and consider points of convergence and divergence between the Integrated Advantage model and some previous theories of mood. We also consider the implications of our model for understanding other affective phenomena such as hedonic adaptation and individual differences in mood dynamics.

Relation to previous RL models of mood.

The Integrated Advantage model is influenced by several earlier models that also used RL as a framework for modelling mood (Eldar & Niv, 2015; Eldar et al., 2016), but differs from these models in two important respects. The models differ with respect to, first, the cognitive appraisal that is assumed to be integrated by mood (and, consequently, the set of contextual effects that the model can explain), and, second, in the normative justification that is proposed for the hypothesised form of mood in the model (and, therefore, the functional form of the posited effect of mood on learning).

Earlier RL models of mood proposed that the core cognitive appraisal integrated by mood was reward prediction errors (action-value Rescorla-Wagner prediction errors, in the model of Eldar and Niv (2015); state-value temporal difference prediction errors, in the model of Eldar et al. (2016)). By contrast, the Integrated Advantage model posits that the cognitive appraisal integrated by mood is the agent’s estimates of the Advantage of its actions. Since temporal difference errors are one means of estimating Advantage, the reward-prediction-error model of Eldar et al. (2016) can therefore be seen as a special case of the Integrated Advantage model. This difference between models enables the Integrated Advantage model to account for a number of contextual effects on mood (the counterfactual effect, action-typicality effect, and the action-inaction asymmetry) that are not readily explained in earlier reward-prediction-error models, since it is necessary to invoke other estimators of Advantage (specifically, the PWRD and PWQD) to explain these effects.

More broadly, the proposal that mood integrates Advantage rather than reward prediction errors has implications for the implicit semantic content of mood. As demonstrated by Eldar et al. (2016), a mood variable that integrates temporal difference prediction errors effectively quantifies the overall rate of change of the value of the states an agent has recently visited. Consequently, positive mood in a reward-prediction-error model connotes that the average value of the environment is increasing (Eldar et al. (2016) give the example of seasonal changes in reward availability). By contrast, Advantage is an appraisal that centers on an agent’s own performance: it quantifies how well an agent has recently performed relative to its own expectations.

This semantic distinction between mood as computed in reward-prediction-error models and mood in the Integrated Advantage model underlies a second point of substantive difference between the models. In reward-prediction-error models, mood quantifies the rate of change of the value of the environment; consequently, in these models the mood variable is used to accelerate the learning of value by modulating the hedonic pleasantness of reward (a multiplicative change in Eldar and Niv (2015); an additive bonus in Eldar et al. (2016)). By contrast, mood in the Integrated Advantage model quantifies the performance of the agent’s recent actions relative to expectations; consequently, mood in this model is assumed to modulate the probability of recently chosen actions within the agent’s behavioral policy, such that positive (negative) mood increases (decreases) the future probability of recently chosen actions. Differences between models in interactions between mood and learning have implications for the predictions of the different models in the psychiatric domain. Eldar and Niv (2015) suggested that a positive feedback loop between mood and the hedonic pleasantness of reward might underlie mood oscillations in bipolar disorder. By contrast, since mood in the Integrated Advantage is assumed to influence learning by modifying the policy directly (rather than by modifying hedonic pleasantness of reward), the Integrated Advantage model does not predict mood oscillations of the kind proposed by Eldar and Niv (2015).

More generally, we note that a central assumption of many recent computational models of mood—including the Integrated Advantage model—is that mood can be modelled as an integrator of an agent’s cognitive appraisals of moment-by-moment events and outcomes. These models are therefore bipartite: they must specify both the cognitive appraisal that is integrated within mood (here, estimated Advantage) and the mathematical form of the integration itself (here, a simple delta-rule update). As such, compared to previous models, one primary contribution of the present theory is to elucidate a computational principle, Advantage, that might underlie cognitive appraisals of events; we have concurred with previous models in modelling the integration process itself as a delta-rule update (Frederick & Loewenstein, 1999; Eldar & Niv, 2015; Eldar et al., 2016; Vinckier et al., 2018). Notably, a separate line of contemporary affective theory focuses on the mathematical form of the integrator without specifying the cognitive appraisals themselves; for instance, the Affective Ising model of Loossens et al. (2020) posits an integrator based on statistical mechanics, but chooses to disregard the cognitive input to this integrator. Unifying these two lines of theory is an important task for future work.

Affect as information.

The model that we presented in this article is conceptually consistent with the affect-as-information principle (Schwarz & Clore, 1983; Schwarz, 1990; Clore, 1994). In its broadest form, this principle proposes that affective states provide an organism with feedback about its interactions with its environment. This feedback might concern, for instance, whether the organism is making satisfactory progress toward its goals, or whether it has sufficient resources to confront environmental challenges (Morris, 1989; R. J. Larsen, 2000).

In the Integrated Advantage model, we propose that the valence of mood serves a specific informative function: to signal whether, in sum, the outcomes of the agent’s recent actions have been better or worse than expected (relative both to state-specific expectations and to the outcomes of other actions that might have been taken). If better than expected—signalled by positive mood—this suggests that recent actions should be taken more often in future; if worse than expected—as signalled by negative mood—recent actions ought to be taken more infrequently in future. As we have discussed, the benefit of appraising recent actions as a whole (i.e., via mood), rather than separate appraisal of each individual action, is that it averages over the various different sources of randomness and noise that influence the outcomes of individual actions, and allows the agent to make a high-level appraisal of its policy.

Our proposal that mood gives high-level feedback on an organism’s actions and behavioral strategy is shared with several instantiations of the affect-as-information principle. For example, Clore et al. (2001) proposed that, when task-oriented, positive affect serves as a facilitatory go signal for one’s current strategy and inclinations, whereas negative affect serves as an inhibitory stop signal. Similarly, Clore and Palmer (2009, p. 26) proposed that positive and negative affective states respectively tune cognition by “promoting or inhibiting whatever responses happen to be dominant in a situation”. Our model presents a formal quantitative counterpart of these proposals.

The notion of an informative function for affect is also present in control-theoretic accounts of mood (e.g., Carver & Scheier, 1990; Carver, 2001, 2015). These suggest that the valence of mood is a marker of progress toward or away from some goal state, and that this signal can be used to aid in the efficient allocation of an organism’s cognitive resources (see also Simon, 1967). There are points of convergence and points of contrast between this control-theoretic perspective and the Integrated Advantage model. On the one hand, both accounts propose that affect results from a perceived discrepancy between an organism’s experiences and a reference value, and emphasize the function played by mood in promoting adaptive responses to this perceived discrepancy. On the other hand, the Integrated Advantage model differs from control-theoretic accounts both in the reference value used for comparison, and in the variable that is represented by the valence of mood. In control-theoretic models, the reference level for the comparison that drives mood is a desired behavioral or goal state; by contrast, in the Integrated Advantage model the reference level is the expected value under one’s policy of the states that one has recently visited. The Integrated Advantage model thus makes the prediction, not shared with control-theoretic models, that comparatively better outcomes are required to produce a positive mood if one is in a state known to be relatively rich than if one is in a state that has not accrued any learned value. In addition, in the Integrated Advantage model, the valence of mood represents an appraisal of the outcomes of an agent’s actions. Control-theoretic models, by contrast, propose that mood represents the rate at which progress is being made towards a goal (Carver & Scheier, 1990).

There is one other point of convergence between the Integrated Advantage model and control theory, though this aspect of control theory is not a feature of the affective theories mentioned above. A key idea in control theory is that of a proportional-integral (PI) controller (Åström & Murray, 2008). This controller adjusts the inputs of a controlled system (e.g., the motor of a refrigerator) according to both a proportional term, which quantifies the current discrepancy between the current level and the desired level of a controlled quantity (e.g., the internal temperature of the refrigerator) and an integral term, which integrates this discrepancy signal over time. The PI control model, which has also proven useful as a model of human learning (Ritz, Nassar, Frank, & Shenhav, 2018; Howlett, Thompson, & Paulus, 2019), therefore bears some interesting resemblances to the specific computational form of mood in our model (see Equation 21). One way of thinking of the algorithm implemented by the Integrated Advantage model is as a variant of PI control for policy-gradient reinforcement learning. In this context, the agent’s trial-by-trial estimates of the Advantage of its actions correspond to the proportional term, and the agent’s mood corresponds to the integral term.

Counterfactual thinking and affect.

As discussed above, the capacity of the Integrated Advantage model to account for counterfactual effects on mood represents a significant advance over previous reinforcement-learning models of mood. However, the interaction between counterfactual information and affect is also treated extensively in other previous theories, and we therefore consider it important to situate the Integrated Advantage model with respect to this work.

One influential account of the relation between counterfactual information and affect is norm theory (Kahneman & Miller, 1986). Norm theory proposes that affective responses to events are amplified when the event result from abnormal causes, and posits a critical role for counterfactual comparisons in this amplification. Abnormality in this theory is defined with respect to one’s typical experiences, whether this be typical behaviors, the typical stimuli that one is exposed to, or the typicality of a stimulus with respect to its category. Kahneman and Miller (1986) propose that, given an event, the availability of counterfactual thoughts about alternative events is proportional to the abnormality of the observed event’s causes. So, for instance, if one visits a favourite restaurant and orders an unfamiliar dish, counterfactual thoughts about the dish one usually orders would be expected to be highly available, whereas the converse is not true when ordering a familiar dish. The availability of these counterfactual alternatives following abnormal events is thought to enhance the contrast between actual and counterfactual events, and therefore to amplify affective responses.

The Integrated Advantage model shares with norm theory the prediction that outcomes of unusual actions will affect mood more strongly than the outcomes of typical actions, and also shares an emphasis on the importance of counterfactual information in this process. However, the posited psychological mechanism for the counterfactual-mood link differs between the two theories. Whereas Kahneman and Miller (1986) emphasize the role played by episodic memory in the retrieval of counterfactual information, our account proposes that the effects of action typicality on mood result from learning-related processes. In the policy-gradient reinforcement-learning framework used by the Integrated Advantage model, abnormal actions (i.e., those taken infrequently under one’s current policy) are in fact highly informative about the goodness of one’s current policy, and therefore should be integrated into a mood variable more strongly. Intuitively, this arises because taking atypical actions provides a good test of the superiority of one’s typical actions: if the outcome of an atypical action is markedly worse than the expected outcome of a typical action, this strongly confirms that the typical action is truly superior. By contrast, if the atypical action produces an outcome equal to or better in value than the typical action, this suggests that one can improve one’s policy by taking the atypical action more often in future. Of course, despite this differing emphasis on learning versus episodic memory, it is important to note that memory and learning are themselves deeply intertwined. Indeed, recent evidence suggests that events associated with higher prediction errors are both more important for learning and more strongly encoded in episodic memory (Rouhani, Norman, & Niv, 2018). This suggests a possible resolution to the different perspectives embodied within norm theory and the Integrated Advantage model.

A separate line of theorising has emphasized the role played by counterfactual thinking (including both responses to counterfactual information and the internal generation of counterfactuals when no explicit counterfactual information is present) in behavioral regulation (Roese, 1994; Epstude & Roese, 2008). In these functional theories of counterfactual thinking, counterfactuals are thought to influence behavior in two ways, termed content-specific and content-neutral. The content-specific pathway concerns the role of counterfactual information in prompting explicit causal reasoning, leading to reasoned changes in future behavior. For instance, a near-miss plane crash might prompt reasoning about the faulty processes that led to the incident, and thereby prompt a review of pilot training protocols. By contrast, the content-neutral pathway concerns the generalized effects of counterfactual thinking on behavior via other psychological factors such as motivation, affect, and mode of information processing (e.g., a poor mark on an academic test might lead to redoubled academic motivation in general, not just for the class that was tested). In this context, our model of mood can be considered a kind of content-neutral pathway between affect and behavior.

Like functional counterfactual theories, the Integrated Advantage model emphasizes the role of affect in mediating the influence of counterfactual information on behavioral change. However, whereas functional counterfactual theories discuss affect-mediated behavioral change as one among a number of other cognitive effects, the Integrated Advantage model concerns itself entirely with this aspect of counterfactual thinking, and treats other related cognitive phenomena as outside its scope. Likewise, in the Integrated Advantage model, counterfactual effects on mood are only one among a number of distinct contextual effects, for which we have proposed a unifying explanation.

Hedonic adaptation.

The Integrated Advantage model also provides a fresh perspective on the much-debated phenomenon of hedonic adaptation: the finding that repeated experience tends to produce diminishing hedonic effects over time, analogous to the adaptation of sensory systems to repeated stimulation (Brickman & Campbell, 1971; Headey & Wearing, 1989; Frederick & Loewenstein, 1999; Lyubomirsky, 2010). As a consequence, the hedonic effects of even major positive or negative life events tend to wear off over time, and mood tends to return to a baseline level termed the set point (Lykken & Tellegen, 1996), the level of which may differ across individuals. Historically, there has been some disagreement as to whether differences in hedonic set point result from inherent trait-level differences in individuals, or whether they are products of the differing environments to which different individuals are exposed. If set point were a trait, it would be expected to be relatively unaffected by the particular experiences that a person has, and therefore resistant to efforts to improve overall subjective wellbeing (Brickman & Campbell, 1971; Lykken & Tellegen, 1996). By contrast, if set point were determined by one’s experiences, it would be amenable to intervention.

The perspective of the Integrated Advantage model is intermediate between these two positions. In our model, set point is effectively defined in terms of the expectations that an individual forms about their expected future reward (expressed formally as the value of the states that the individual occupies). This means that the experiences that an individual has may substantially contribute to their set point if those experiences cause the individual to adjust their expectations about the future (i.e., to update the state-value function V^π). This is consistent with the proposal that individual differences in experience may cause changes in set point (Frederick & Loewenstein, 1999; Lyubomirsky, 2010). On the other hand, there are likely to be considerable individual differences in the way that different people form expectations about the future given an equivalent set of experiences (see, e.g., Scheier, Carver, & Bridges, 2001). The Integrated Advantage model would therefore suggest that there are indeed substantial individual differences in hedonic set point, but that these individual differences are produced by differences in the ways that different individuals form expectations about the future, rather than being a stand-alone psychological trait.

One concrete prediction from this model is that beliefs about the persistence of reward should moderate hedonic adaptation. Since the effective set point for the Integrated Advantage model is the value of the states of the environment that an individual visits, exposure to high levels of reward (or punishment) should produce adaptation only if they cause the individual to update their beliefs about the values of the states they will visit in future. Consequently, a one-off event—even a very positive or negative one—would not be predicted to lead to hedonic adaptation if it does not produce changes in the individual’s expectations of future reward (see McMullen & Markman, 2002).

The dimensionality of mood.

A long-standing debate in affective science is whether the valence of mood is better conceptualized as a bipolar or a bivalent construct. The bipolar conceptualisation (e.g. J. A. Russell, 2003) is that the valence of mood exists on a continuum between the polar opposites of unpleasant and pleasant affect, with neutral mood as an unvalenced zero point intermediate between these poles. By contrast, the bivalent conceptualisation (e.g. Watson & Tellegen, 1985) is that the valence of mood varies along two independent dimensions: a positive affect dimension that runs from neutral to pleasant, and a negative affect dimension that runs from neutral to unpleasant. In bivalent models, mood may change independently along each dimension, such that individuals can experience mixed states with high levels of both positive affect and negative affect (J. T. Larsen & McGraw, 2011).

The Integrated Advantage model adopts a bipolar conceptualisation of the valence of mood. Our rationale for this is twofold. The first reason is simply parsimony: a bipolar conceptualisation of valence is sufficient to explain each of the contextual phenomena that we have reviewed in this article; similarly, a bipolar perspective suffices for our functional explanation of the adaptiveness of mood in approximating momentum. Our second reason for using a bipolar framework is that the Integrated Advantage model is a reinforcement learning model, and as such relies upon a definition of reward as a scalar with bipolar dimensionality (Sutton & Barto, 2018). Given that the goal of a reinforcement learning agent is to maximize its cumulative expected reward, we considered it most reasonable to propose an algorithm with a mood variable that has same dimensionality as the quantity to be optimized.

However, neither of these reasons entails an absolute commitment to a bipolar conceptualisation of mood, and bivalent extensions of the Integrated Advantage model are conceivable. Some reinforcement learning models conceptualize behavior according to a bivalent perspective (drawing from a long tradition in learning theory; e.g., Konorski, 1967). Collins and Frank (2014) proposed an actor-critic reinforcement learning model that learns separate approach and avoidance tendencies. These bivalent action tendencies are updated in opposite directions according to reward prediction errors, and it is suggested that they might be reflected in separable pathways of striatal dopaminergic neurons. Analogously, one feasible bivalent extension of the Integrated Advantage model might involve two separate approximations of momentum (i.e., positive and negative affect) used separately to update the approach and avoidance portions of one’s policy. This would also be broadly in line with the bivalent control-theoretic model of mood proposed by Carver (2001), as well as bivalent conceptualisations of approach- and avoidance-related behaviors (e.g., Higgins, 1997).

Dimensions of individual variability in mood.

In the general population, the dynamics of mood vary strikingly between individuals. At its extremes, this variability manifests in mood disorders such as major depression and bipolar disorder, but there is marked variation in mood profiles even in psychiatrically healthy individuals (e.g., Penner, Shiffman, Paty, & Fritzsche, 1994; Rihmer, Akiskal, Rihmer, & Akiskal, 2010). An important question for a quantitative model of mood such as the Integrated Advantage model is how it accounts for this variation, and what it suggests as the major dimensions of interindividual variability in mood. In this way, a computational model of mood may also serve as a roadmap for investigating the information-processing dysfunctions that may give rise to psychiatric phenomena in mood disorders (Mason, Eldar, & Rutledge, 2017; Bennett, Silverstein, & Niv, 2019; Bennett & Niv, 2020).

The Integrated Advantage model suggests at least two dimensions of mood variability in the general population, each corresponding to a different component of a mood-learning algorithm. These two dimensions are mood reactivity and the strength of mood-learning interaction.

In the Integrated Advantage model, mood reactivity is controlled by η_mood, the learning rate parameter for updates to the mood variable. Formally, η_mood specifies the proportion of the estimated Advantage for any individual event that is incorporated into the mood variable. As a result, this parameter controls both the reactivity of mood and the timescale over which mood is integrated. When η_mood is close to zero, any individual event has little effect on mood, and mood has a relatively long timescale of integration (see Eldar and Niv (2015) and Chang and Chou (2018) for further discussion of this point). By contrast, a high η_mood parameter produces strong mood reactivity to individual events, but with a short timescale of integration. Extreme high values of η_mood may therefore provide a good description of affective dynamics in borderline personality disorder, which is characterized by rapid mood shifts and strong mood reactivity to individual events (J. J. Russell, Moskowitz, Zuroff, Sookman, & Paris, 2007). However, while high values of η_mood may describe mood dynamics in borderline personality, we emphasize that this is far from providing a complete account of this disorder. Indeed, affective dysregulation is often considered a non-core symptom of borderline personality disorder, secondary to other phenomena such as insecure attachment, interpersonal instability, and chronic feelings of emptiness (Gunderson & Phillips, 1991).

A second dimension of individual difference suggested by the Integrated Advantage model is the strength of the interaction between mood and learning. In our model, the strength of this effect is controlled by the momentum parameter m; values of m close to 1 produce a strong effect of mood on learning, such that policy updates are almost totally determined by current mood, and are insensitive to trial-by-trial fluctuations in outcomes. By contrast, values of m close to 0 indicate a decoupling between mood and learning, such that updates to the policy are unaffected by one’s current mood¹¹. In stochastic optimization, it has been shown that there is a ‘sweet spot’ for momentum, such that optimal performance is attained with intermediate values of momentum (Su, Boyd, & Candes, 2016): if m is too low, the learning improvement due to momentum may not be evident; if m is too high, by contrast, the learning algorithm can fail to converge to the global optimum, and may even display divergent or oscillatory behavior. Analogously, for high values of the m parameter in the Integrated Advantage model, the agent will display a specific insensitivity to feedback that is incongruent with its current mood state (since when m is high, the update in Equation 22 will tend to be dominated by the mood term and ignore the trial-wise estimated advantage). This may represent a computational analogue of several psychiatric phenomena: in positive moods, individuals with a high m parameter, when in a good mood, will tend to be insensitive to negative feedback, producing changes in behavior that resemble those associated with positive urgency and mania for positive moods (Cyders & Smith, 2007; S. L. Johnson, Tharp, Peckham, Sanchez, & Carver, 2016). By contrast, in a negative mood, high values of m render actions insensitive to positive reinforcement, as proposed in early cognitive-behavioral theories of depression (e.g., Lewinsohn, 1974).

In our derivation of the Integrated Advantage model of mood, we focused on the functional question of mood: what benefit might an agent derive from modulating its processing of future events according to its mood? This question is particularly salient in the context of mood disorders such as major depression and bipolar disorder. Though we would not claim that the behavioral benefits of mood outweigh their potential consequences for individuals with severe mood disorders, we nevertheless suggest that the advantages of mood are likely to outweigh any evolutionary selection pressures related to psychiatric phenomena when considered at a population level (see Allen and Badcock (2006) and Nettle and Bateson (2012) for related evolutionary perspectives on mood disorders). The primary function of mood in Integrated Advantage model is to accelerate learning in complex and stochastic environments, such as are confronted by most biological agents. An agent that modulates its behavior according to its mood as prescribed by the Integrated Advantage model is likely to require many fewer interactions with its environment in order to learn a good behavioral policy (i.e., mood may reduce the sample complexity of learning). Given the significant time costs associated with learning by sampling from the environment (as well as the associated risks for many animals), we propose that reciprocal interactions between mood and learning such as those proposed in the Integrated Advantage model may be associated with meaningful improvements in evolutionary fitness across species and habitats.

Conclusions

We have presented a new computational theory of mood, the Integrated Advantage model. This model provides a functional account of the valence of mood, grounded in principles from reinforcement learning, and provides a unifying explanation for numerous contextual effects on mood.

In reviewing previous theories of mood in philosophy and psychology, we identified three consensus properties of mood: that mood is integrative, that it is non-intentional, and that it is contextual. Mood as defined by the Integrated Advantage model is consistent with all three of these properties: it is integrative in the sense that it is a weighted average of past estimated Advantage, non-intentional because it is a scalar that integrates Advantage without reference to the specific actions that generated it, and contextual in the sense that the Advantage variable it integrates is an inherently contextual quantity (i.e., referenced to context-specific value expectations). Though much work remains to be done exploring the predictions of this model, our hope is that the formal quantitative framework that it provides will scaffold and stimulate future empirical and theoretical advances.

Appendix A

Details of simulated 4-armed bandit task

In order to illustrate the estimation properties of three different estimators of the Advantage function (TD error, PWQD, PWRD), Section 2 simulates the performance of a reinforcement learning agent on a 4-armed bandit task and compares each of these estimators to the true (analytic) Advantage function. We performed 200 simulations of 300 trials each; on each trial of each simulation, arms could pay out a reward of either 0 or 1 with probabilities (respectively) of 0.2, 0.4, 0.6, and 0.8. The simulated agents received full feedback (that is, they observed the payout of unchosen arms as well as chosen arms.

In each simulation, the simulated agent learned according to a TD(0) Actor-Critic algorithm (Kimura & Kobayashi, 1998); see Appendix C for further details of this algorithm, which was also implemented in the simulations for Section 5. The agent implemented a softmax policy with inverse temperature β = 1 and an actor learning rate of η = 0.3. Initial preferences for all arms were set to 0. Within the critic, Q-values for all arms were initialized at 0.5, as was the V-value of the (single) state within which the arms were situated, and the learning rate for both Q and V was set to 0.1. Note that Q-values were calculated for the purposes of Advantage estimation only and were not used in the agent’s choice rule.

Full code underlying these simulations can be found in the online supplementary material.

Appendix B

Derivation of mood update rule

Here we derive the form of the substitution of the mood variable in the momentum term (Equation 22).

First, recall the definition of momentum in the context of an Advantage Actor-Critic algorithm:

$$u_t=\eta A^{\pi }(s_t,a_t)e_t+m{u}_{t-1}$$ (23)

As a first step, we can unroll the definition of the momentum term in Equation 23 to show that u_t−1 can be expressed as a discounted sum of the products of previous timesteps’ eligibility traces and estimated Advantage:

$$\begin{gathered} u_t=\eta {\widehat{A}}^{\pi }(s_t,a_t)e_t+m{u}_{t-1} \\ =\eta {\widehat{A}}^{\pi }(s_t,a_t)e_t+m\eta {\widehat{A}}^{\pi }(s_{t-1},a_{t-1})e_{t-1} \\ +m^2\eta {\widehat{A}}^{\pi }(s_{t-2},a_{t-2})e_{t-2}+\dots +m^{t-1}\eta {\widehat{A}}^{\pi }(s_1,a_1)e_1 \\ =\eta {\widehat{A}}^{\pi }(s_t,a_t)e_t+\eta \sum _{\tau =1}^{t-1}\left[m^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })e_{t-\tau }\right] \end{gathered}$$ (24)

Next, we can observe from Equation 24 that the momentum term is proportional to an exponentially weighted average of the product of eligibility traces and estimated Advantage: ${\sum }_{\tau =1}^{t-1}\left[m^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })e_{t-\tau }\right]$. This sum strongly resembles our definition of mood as an exponential average of estimated Advantage (reproduced here from Equation 7):

$${\text{Mood}}_{t+1}={\eta }_{mood}\sum _{\tau =0}^t\left[(1-{\eta }_{mood}{)}^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })\right].$$ (25)

The difference is that the sum in Equation 24 includes an eligibility trace (e_t−τ) that is different at each past timestep. In order for a mood term to be useful in implementing momentum, therefore, it is necessary to replace the time-varying eligibility traces in Equation 24 with a term that does not depend on the index τ. One way of doing this is to approximate the time-varying eligibility trace e_t−τ with the current eligibility trace e_t, which can then be moved outside the sum:

$$\begin{gathered} u_t\approx u_t^m=\eta {\widehat{A}}^{\pi }(s_t,a_t)e_t+\eta e_t\sum _{\tau =1}^{t-1}\left[m^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })\right] \\ =\eta e_t\left[{\widehat{A}}^{\pi }(s_t,a_t)+\sum _{\tau =1}^{t-1}{m}^{\tau }{\widehat{A}}^{\pi }(s_{t-\tau },a_{t-\tau })\right] \end{gathered}$$ (26)

Here, the update u_t is approximated by a mood-based update $u_t^m$. Note that the approximation of e_t−τ with e_t introduces bias into this derivation. The similarity between successive eligibility traces is controlled by the eligibility decay parameter λ; as such, the amount of bias in this approximation will be inversely proportional to λ.

In this approximation, we can next rewrite the momentum portion of the parameter update in terms of the mood variable Mood_t−1. Specifically, to approximate an update with a momentum parameter of m, we use a mood learning rate of η_mood = (1 − m). The resulting mood variable can then be substituted into Equation 26 with a constant of proportionality of $\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}$:

$$u_t^m=\eta e_t\left[{\widehat{A}}^{\pi }(s_t,a_t)+\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}{\text{Mood}}_{t-1}\right]$$ (27)

First, recall the final part of Equation 26:

$$u_t^m=\eta e_t\left[A^{\pi }(s_t,a_t)+\sum _{\tau =1}^{t-1}{m}^{\tau }{A}^{\pi }(s_{t-\tau },a_{t-\tau })\right].$$ (28)

For a mood variable with a learning rate η_mood = 1 − m, we would like to show that

$$\sum _{\tau =1}^{t-1}{m}^{\tau }{A}^{\pi }(s_{t-\tau },a_{t-\tau })=\frac{m}{1-m}{\text{Mood}}_{t-1}.$$ (29)

(since $\frac{1-{\eta }_{\text{mood}}}{n_{\text{mood}}}=\frac{m}{1-m}$ if η_mood = 1 − m and 0 ≤ η_mood, m ≤ 1).

To do this, we can first define the left hand side of Equation 29 as a new variable μ:

$$\begin{gathered} \mu =\sum _{\tau =1}^{t-1}{m}^{\tau }{A}^{\pi }(s_{t-\tau },a_{t-\tau }) \\ =m{A}^{\pi }(s_{t-1},a_{t-1})+m^2{A}^{\pi }(s_{t-2},a_{t-2})+\dots +m^{t-1}{A}^{\pi }(s_1,a_1) \end{gathered}$$ (30)

Next, from Equation 25, we define the value at timestep t − 1 of the mood variable h with learning rate η_mood = 1 − m:

$$\begin{gathered} {\text{Mood}}_{t-1}={\eta }_{mood}\sum _{\tau =0}^{t-2}[(1-{\eta }_{mood}{)}^{\tau }{A}^{\pi }(s_{t-\tau },a_{t-\tau })] \\ =(1-m)\sum _{\tau =0}^{t-2}[m^{\tau }{A}^{\pi }(s_{t-\tau -1},a_{t-\tau -1})] \\ =(1-m)\left(A^{\pi }(s_{t-1},a_{t-1})+m{A}^{\pi }(s_{t-2},a_{t-2})+\dots +m^{t-2}{A}^{\pi }(s_1,a_1)\right) \end{gathered}$$ (31)

By dividing out the factor of 1 − m, we can express Mood_t−1 in terms of μ:

$$\begin{gathered} \frac{1}{1-m}{\text{Mood}}_{t-1}=A^{\pi }(s_{t-1},a_{t-1})+m{A}^{\pi }(s_{t-2},a_{t-2})+\dots +m^{t-2}{A}^{\pi }(s_1,a_1) \\ =\frac{\mu }{m} \end{gathered}$$ (32)

From this, we have:

$$\mu =\frac{m}{1-m}{\text{Mood}}_{t-1}$$ (33)

and we thereby obtain the update rule in Equation 27.

As a final step, we can observe that the size of the parameter update in Equation 27 is determined by the sum of the estimated Advantage ${\widehat{A}}^{\pi }(s_t,a_t)$, which depends on variables from timestep t, and a mood term $\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}$ Mood_t−1, which depends on variables from timestep t − 1. This means that the mood portion of this update is the same no matter what action is chosen or what reward is received at trial t; as such, it is feasible to increment the parameters by the mood portion of the update already at the end of trial t − 1, before any action is chosen in trial t. This leads to an algorithm (see Figure 6), that approximates momentum using a mood variable, as presented in the main text:

$$e_t=\lambda e_{t-1}+{\nabla }_{\theta }\log \pi (a_t\mid s_t)$$ (34.1: identical to 20.1 and 21.1)

$${\text{Mood}}_t={\text{Mood}}_{t-1}+{\eta }_{mood}\left({\widehat{A}}^{\pi }(s_t,a_t)-{\text{Mood}}_{t-1}\right)$$ (34.2: updating the mood variable)

$$u_t^m=\eta e_t\left[{\widehat{A}}^{\pi }(s_t,a_t)+\frac{1-{\eta }_{\text{mood}}}{{\eta }_{\text{mood}}}{\text{Mood}}_t\right]$$ (34.3: calculating the parameter update u_t)

$$\theta \leftarrow \theta +u_t^m$$ (34.4: identical to 20.3 and 21.3)

In technical terms, the difference between Equation 27 and Equation 34.3 is that Equation 22 uses mood to approximate standard momentum (Polyak, 1964), whereas Equation 34 approximates a related variant known as Nesterov momentum (Nesterov, 1984; Sutskever et al., 2013).

Appendix C

Details of momentum and mood simulations

Agents in both simulations were divided into a critic module and an actor module. Updates were performed according to the Advantage Actor-Critic algorithm described in Equation 20. Specifically, the critic estimated the value of different states of the environment using a TD(0) algorithm. The resulting temporal-difference error was propagated to the actor, which used it as an estimate of the advantage of the chosen action (Kimura & Kobayashi, 1998; Schulman et al., 2015; Mnih et al., 2016).

The actor performed policy-gradient updating of a softmax policy (with inverse temperature parameter β set to 1) parameterized by a vector θ of preferences for each possible action in each possible state (i.e., $\theta \in {\mathbb{R}}^{M\times N}$, where M is the number of states of the environment and N is the number of actions that the agent can take). When actions are chosen according to a softmax policy with β = 1, the score function of the policy (i.e., the gradient of the logarithm of the policy with respect to the parameters; Williams, 1992) has a relatively simple form that depends only on the probability of each action under the policy, and whether or not the action was chosen:

$${\nabla }_{\theta }\log \pi (a\mid s)=\varphi -\mathbb{E}[\varphi \mid \pi ,s]$$ (35)

where ϕ is a one-hot vector the length of the number of available actions in state s. ϕ indexes the chosen action: all entries are zero except for the entry corresponding to the chosen action, which is equal to one. The resulting score function is therefore also a vector equal in length to the number of available actions, with vector entries corresponding to unchosen actions equal to −π(a ∣ s) and the entry corresponding to the chosen action equal to 1 − π(a ∣ s) (Sutton & Barto, 2018, p. 329). The score function accumulated over time in an eligibility trace e_t, updated recursively subject to a decay parameter λ (see Equation 20.1). The learning rates for the actor and the critic were respectively set to η_actor = 0.1 and η_critic = 0.1 in all agents.

For the Advantage Actor-Critic with momentum agent, momentum was set to m = 0.6. To approximate an equivalent degree of momentum, the Advantage Actor-Critic with Mood agent used a mood learning rate of η_mood = 1 − m = 0.4.

For each agent, all parameters were the same across the two simulated environments, with two exceptions. In the ten-armed bandit environment, to reflect the one-step nature of learning, the discount factor for all agents was set to γ = 1 and the decay parameter for eligibility was set to λ = 0. In the fixed-cost gridworld environment, the discount factor for all agents was set to 0.9 to ensure convergence, and the decay parameter for eligibility was set to 0.6 (i.e., λ = m). State values were initialized to 0 in the the bandit environments and to $-\frac{8}{9}$ (the expected one-step reward of a random state transition) in the fixed-cost gridworld environment.

Full code underlying these simulations can be found in the online supplementary material.