Abstract
Deep learning (DL) has emerged as a powerful tool for improving the reconstruction quality of accelerated MRI. These methods usually show enhanced performance compared to conventional methods, such as compressed sensing (CS) and parallel imaging. However, in most scenarios, CS is implemented with two or three empirically-tuned hyperparameters, while a plethora of advanced data science tools are used in DL. In this work, we revisit ℓ1-wavelet CS for accelerated MRI using modern data science tools. By using tools like algorithm unrolling and end-to-end training with stochastic gradient descent over large databases that DL algorithms utilize, and combining these with conventional concepts like wavelet subband processing and reweighted ℓ1 minimization, we show that ℓ1-wavelet CS can be fine-tuned to a level comparable to DL methods. While DL uses hundreds of thousands of parameters, the proposed optimized ℓ1-wavelet CS with sub-band training and reweighting uses only 128 parameters, and employs a fully-explainable convex reconstruction model.
I. INTRODUCTION
Slow data acquisition remains a challenge for MRI, requiring accelerated imaging strategies. Conventional methods, such as parallel imaging [1], [2] and compressed sensing (CS) [3] are used clinically, but typically their acceleration rates are limited by noise amplification and residual aliasing artifacts in reconstructed images. Recently, deep learning (DL) methods for accelerated MRI [4]–[8] have emerged as a powerful tool for MRI reconstruction, with improved performance over conventional methods in many studies. Among DL methods, physics-guided DL (PG-DL) methods that unroll conventional optimization algorithms that incorporate the encoding operator have received attention [6]–[9]. While CS uses a linear transform-based representation of images for regularization, PG-DL methods utilize a non-linear representation for regularization, which is implicitly learned through neural networks.
DL reconstruction methods are trained using large databases, include a large number (usually more than hundreds of thousands or millions [6], [10], [11]) of parameters, incorporate sophisticated optimization algorithms for training [12], and utilize state-of-the-art loss functions [13], [14]. On the other hand, when CS reconstruction methods are implemented for comparison, they typically use two or three parameters, which are frequently hand-tuned using a simple grid search. Although some automatic tuning methods have been proposed [15], [16], these have not leveraged the widely-available and popular modern data science tools from the DL era.
In this work, we use these data science tools to revisit ℓ1-wavelet CS for accelerated MRI. Similar to PG-DL methods, we unroll an ADMM algorithm and train it end-to-end, while using only 4 orthogonal wavelet bases for the regularizing transforms for a total of 12 tunable parameters. Building on this naive model, we further incorporate processing of each individual wavelet subband [17], and reweighted ℓ1 minimization [18], leading to 64 and 128 tunable parameters respectively. Results show that even the naive model closes the gap in reconstruction performance to advanced PG-DL methods, while the incorporation of subband and reweighting further improves the quality of reconstruction to a level comparable to PG-DL methods. All the models proposed here enable a linear representation for interpretable and convex sparse image reconstruction at inference time.
II. MATERIALS AND METHODS
A. Inverse Problem for Accelerated MRI
The forward model for accelerated MRI is given as
| (1) |
where is the image to be reconstructed, is the undersampled k-space data from all coils, is the linear forward encoding operator containing coil sensitivity maps and partial Fourier matrix for undersampling in k-space [19], and n is the measurement noise. The inverse problem involves solving the objective function:
| (2) |
where enforces data consistency (DC) and is a regularizer.
In conventional CS MRI reconstruction, the form of is often a weighted ℓ1-norm of transform coefficients, i.e. , where Wl is a pre-specified linear (often orthogonal) transform, such as a discrete wavelet transform (DWT) [3], and L is the number of linear transforms used for regularization. The resulting convex objective function is solved via an iterative optimization algorithm [20]. These algorithms are conventionally run until a stopping criterion is met, making hyperparameter tuning difficult.
On the other hand, in PG-DL reconstruction, the inverse problem is usually solved by unrolling an iterative optimization algorithm for a fixed number of iterations [21], [22]. Typically, the solutions are decoupled to a series of regularizer and DC units. The regularizer in PG-DL is implemented implicitly via convolutional neural networks (CNNs), while the DC unit is solved by linear methods, such as gradient descent or conjugate gradient [7]. The network is trained end-to-end as:
| (3) |
where denotes the fully-sampled reference k-space of the nth subject, f(yn, En; θ) denotes network output of the unrolled network with parameters θ of the nth subject, is the fully sampled multi-coil encoding operator of the nth subject, N is the number of datasets in the training database, and is a loss function between the network output and the reference. Common choices for include ℓ2 norm, ℓ1 norm, mixed norms and perception-based loss [8], [14].
B. Proposed Learning of ℓ1-Wavelet CS Reconstruction
We optimize conventional ℓ1-Wavelet CS reconstruction by using the data science tools utilized in PG-DL techniques. First, we utilize ADMM to set
| (4a) |
| (4b) |
| (4c) |
where zl are auxiliary variables in wavelet domain, βl are dual variables, soft(·; λl/ρl) is the ℓ1 soft-thresholding operator parameterized by λl/ρl, and t denotes the iteration count. The algorithm is unrolled for T iterations, as depicted in Figure 1.
Fig. 1:
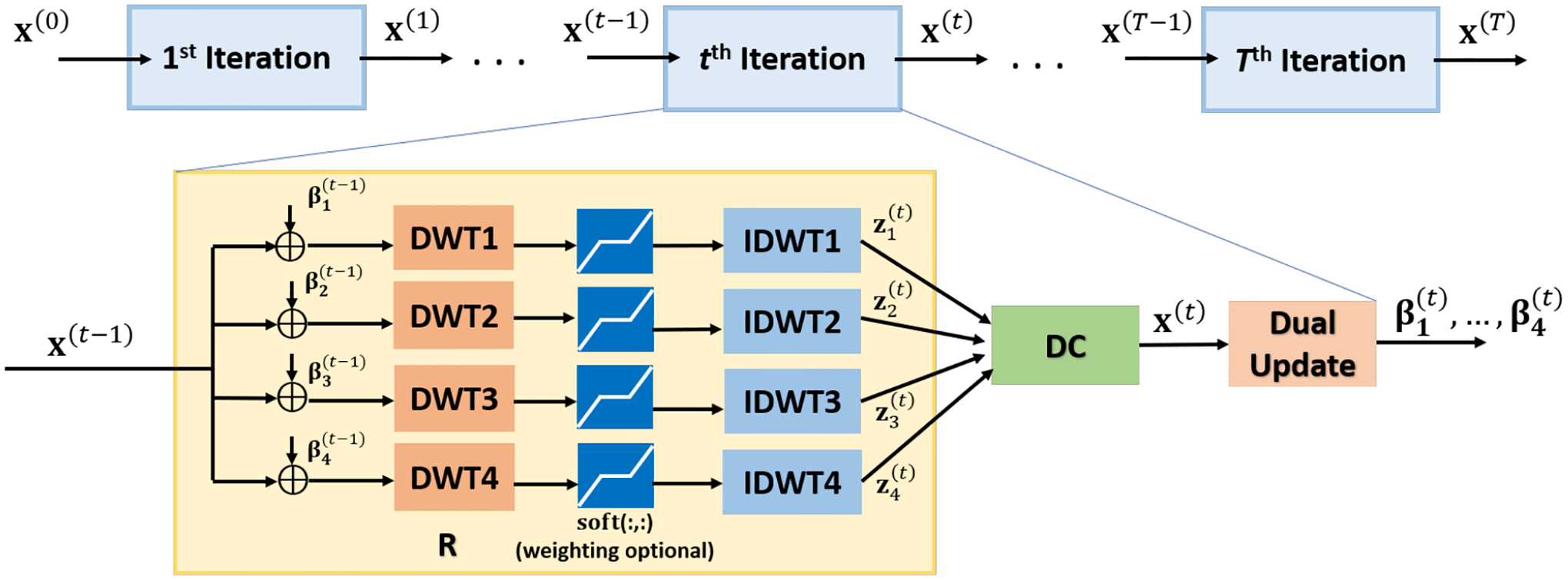
Schematic of the unrolled ADMM for ℓ1-wavelet compressed sensing (CS). One unrolled iteration of ADMM with ℓ1-wavelet regularizers consists of regularizer (R), data consistency (DC) and dual update (DWT: Discrete wavelet transform). In accordance with the ADMM framework, learnable parameters are shared across different unrolled iterations. In its simplest form, this leads to 3 trainable parameters per wavelet. Further enhancements, such as separate thresholds for wavelet subbands and reweighted ℓ1 minimization increase this number to 16 trainable parameters per wavelet.
The learnable parameters in this algorithm are ρl, λl/ρl and ηl, which correspond to parameters for augmented Lagrangian relaxation, ℓ1 soft-thresholding and the dual update per each wavelet transform. We note that these are shared across all the unrolled iterations to ensure that the objective function in (2) remains unchanged throughout the iterations, and interpretability of the algorithm can be maintained. Thus, there are 3 · L learnable parameters for the whole algorithm when using L orthogonal DWTs.
This approach serves as the foundation for all our proposed models, and is subsequently referred to as the learned naive ℓ1-Wavelet reconstruction. In all our models, the input to the network is the zerofilled image, x(0) = EHy. Furthermore, since the regularizer in (2) scales with ∥x∥∞, while the DC term in (2) scales with , λl/ρl is parametrized as , and the scaling-invariant parameter γl is learned. Overall, the learned parameters are .
C. Further Enhancements for Optimized ℓ1-Wavelet CS Reconstruction
The naive optimized ℓ1-Wavelet approach can further be enhanced using our understanding of wavelet representations [17] and of ℓ1 minimization problems [18]. In particular, we use the fact that signal scaling changes severely between different wavelet subbands for the former, and that reweighted ℓ1 minimization helps recover finer details for the latter.
Learning ℓ1-wavelet reconstruction with subband processing:
For different subbands of a wavelet transform, the soft-thresholding parameters may be different. To this end, let be an operator that select the sth subband of the lth wavelet transform. We propose to use the regularizer
| (5) |
which also lead to the following modified update in (4b).
| (6) |
for all s ∈ {1, … , S}. Thus, the learnable soft-thresholding parameters are λl,s/ρl for the sth subband of the lth wavelet transform. During end-to-end training, this parameter is again implemented in a scaling-invariant manner by defining and learning {γl,s} for l ∈ {1, … , L} and s ∈ {1, … , S}. Thus this approach leads to a total of L · (S + 2) learnable parameters when using S subbands and L orthogonal DWTs.
Learning reweighted ℓ1-wavelet reconstruction with subband processing:
A further improvement in performance, especially in the lower SNR regimes, may be achieved using reweighted ℓ1 minimization, which has been shown to improve recovery of small coefficients [18]. To this end, let denote the output of the learned subband ℓ1-wavelet reconstruction. We define a diagonal weight matrix Ul whose (k, k)th entry is given as
| (7) |
where (·)k denotes the kth coefficient of the vector (·), and ϵ is a small constant to avoid numerical issues when dividing by zero. This weight matrix is used to define the reweighted ℓ1 regularizer with subband processing as:
| (8) |
This leads to the following modified update in (4b).
| (9) |
for all s ∈ {1, … , S}. We note that the regularizer in (8) does not change if x is scaled by a constant α, while the DC term in (2) still scales with . Thus, we define a scaling-invariant thresholding factor . During end-to-end training, is learned for l ∈ {1, …, L} and s ∈ {1, …, S} in addition to .
This approach still has L · (S + 2) learnable parameters during the reweighting stage, even though signal-dependent weights are incorporated via (7). Including the learned subband reconstruction, which is used to determine the weights in (7) leads to a total of 2L · (S + 2) learnable parameters for the whole reconstruction pipeline. We also note that once these parameters are learned, they can be applied for multiple reweightings, krew, during testing, since the scaling of remains on the same order.
D. Imaging Data
Fully-sampled coronal proton density (PD), and PD with fat-suppression (PD-FS) knee data obtained from the NYU-fastMRI database [23] were used throughout the experiments. Relevant imaging parameters were: matrix size = 320×368, in-plane resolution = 0.49 × 0.44 mm2, slice thickness = 3 mm. The datasets were retrospectively under-sampled with a random mask (R = 4 with 24 ACS lines). Training was performed on 300 slices from 10 different subjects. Testing was performed on all slices from 10 different subjects. Coil sensitivity maps were generated using ESPIRiT [24].
E. Implementation Details
For all models, L = 4 wavelets were used, corresponding to Daubechies1–4 orthogonal wavelets with 14 subbands for each. Thus, the total number of learnable parameters were 12, 64 and 128 for the learned naive ℓ1-wavelet, ℓ1-wavelet with subbands, and reweighted ℓ1-wavelet with subbands reconstructions, respectively. For the last method, krew = 2 was used in testing, similar to [18].
ADMM algorithm was unrolled for T = 10 for all models. ϵ was set to 10−9 in (7). DC subproblem was solved using conjugate gradient [7] with 5 iterations and warm-start. All tunable parameters were randomly initialized. Adam optimizer with learning rate 5 × 10−3 was used for training over 100 epochs, with a batch size of 1. Supervised training was performed with a normalized ℓ1−ℓ2 loss in k-space [8], [10], using TensorFlow in Python.
For comparison, a PG-DL approach was implemented using the same ADMM unrolling except for using a ResNet-based regularizer unit. The ResNet was originally adapted from the winner of a super-resolution challenge [25], and has been used in multiple recent MRI studies successfully [9], [10]. The PG-DL approach has a total of 592,130 learnable parameters. Note this constitutes a head-to-head comparison, with the only difference being in the term, where our approaches employ ℓ1-norm of wavelets for solving a convex problem, while PG-DL uses a CNN for implicit regularization. All results were quantitatively compared using SSIM and NMSE.
III. RESULTS
Figure 2 shows a representative slice from coronal PD knee MRI, reconstructed using PG-DL and the three ℓl-wavelet CS approaches optimized with modern data science tools, respectively. For this high SNR acquisition, even the learned naive ℓ1-wavelet results in a high-quality reconstruction, while the learned ℓ1-wavelet with subbands leads to a slightly sharper reconstruction. Learned reweighted ℓ1-wavelet with subbands performs the best among the three optimized ℓl-wavelet CS approaches, resulting in a sharp reconstruction, showing comparable visual quality and quantitative metrics to PG-DL.
Fig. 2:
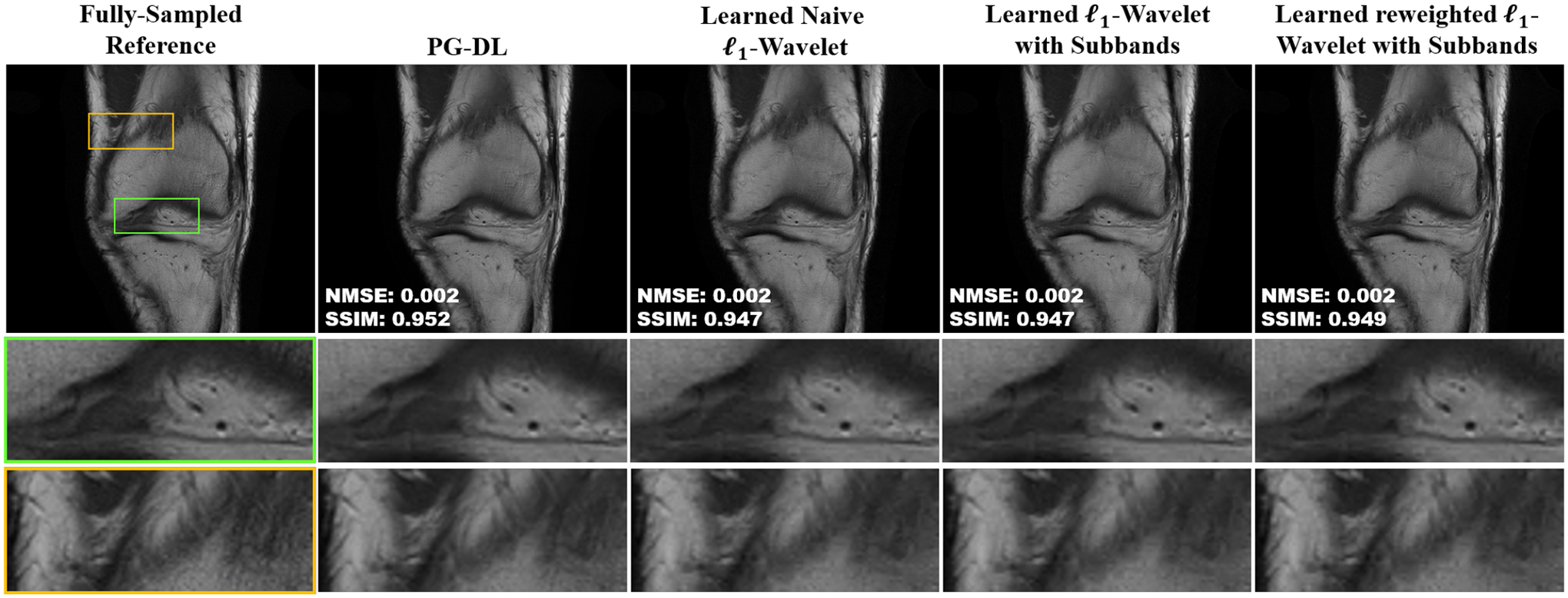
A representative slice from coronal PD knee MRI, reconstructed using PG-DL, learned naive ℓ1-wavelet, learned ℓ1-wavelet with subbands, and learned reweighted ℓ1-wavelet with subbands. The proposed optimized ℓ1-wavelet reconstructions perform closely to PG-DL. Learned reweighted ℓ1-wavelet with subbands performs the best among these ℓ1-wavelet CS variants, resulting in sharp images with similar quantitative metrics to PG-DL.
Figure 3 depicts a representative coronal PD-FS knee MRI slice, reconstructed using PG-DL and the three optimized ℓl-wavelet CS approaches. The PD-FS dataset has an inherently lower SNR compared to PD. As such, the learned naive ℓ1-wavelet results in a blurry image due to the difficulty of fine-tuning a single thresholding parameter. This is improved with subband processing, but sharpness is fully recovered only with the learned reweighted ℓ1-wavelet with subbands approach, which results in a visibly similar reconstruction to the PG-DL method.
Fig. 3:
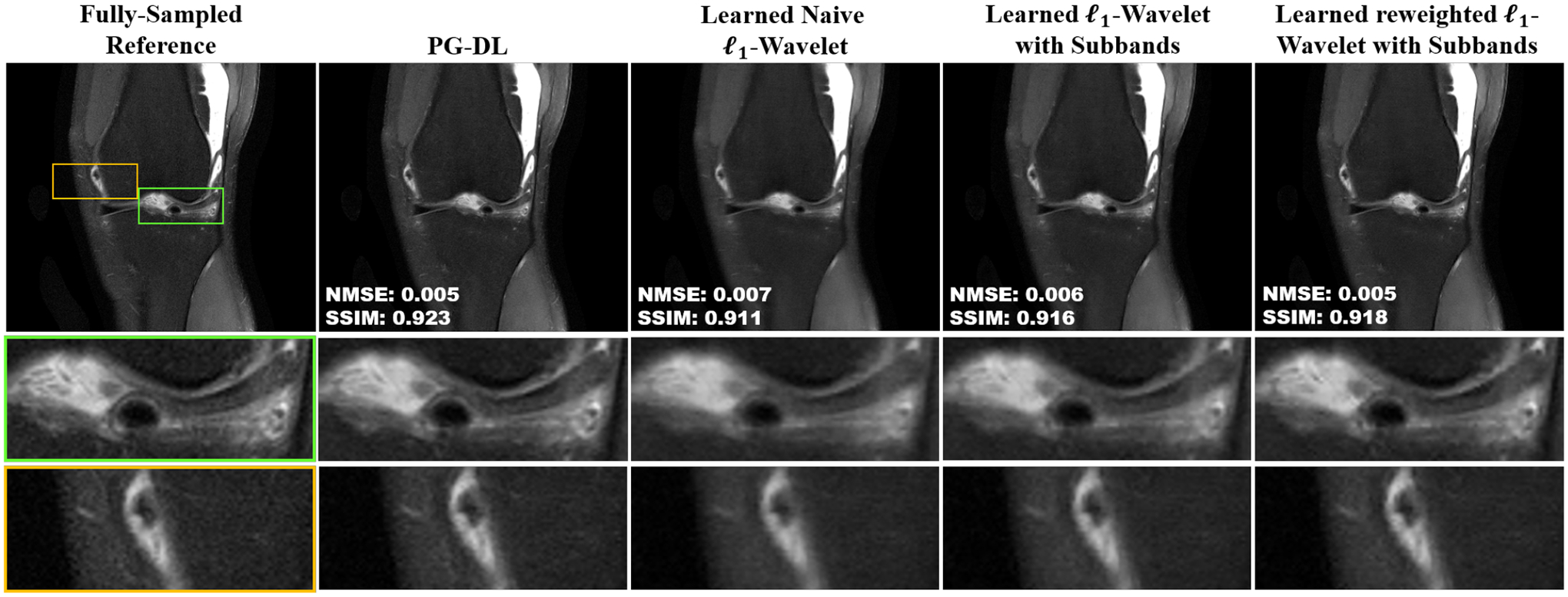
A representative slice from coronal PD–FS knee MRI, reconstructed using PG-DL, learned naive ℓ1-wavelet, learned ℓ1-wavelet with subbands, and learned reweighted ℓ1-wavelet with subbands. For this lower SNR acquisition, the learned naive ℓ1-wavelet suffers from visible blurring artifacts. These are improved using subband processing, while the sharpness is only fully recovered using the learned reweighted ℓ1-wavelet with subbands method, which leads to a visibly similar reconstruction to PG-DL.
Table I summarizes quantitative results from knee MRI. While PG-DL has the best metrics, the gap between proposed optimized ℓl-wavelet CS and PG-DL is small, with < 0.01 for SSIM and < 0.0008 for NMSE.
TABLE I:
The median and the interquartile range [25th, 75th percentile] of the NMSE and SSIM metrics on test slices from 10 subjects for coronal PD and PD-FS datasets. While PG-DL has the best metrics as expected, the gap in SSIM between PG-DL and the learned reweighted ℓ1-wavelet with subbands is < 0.01.
| Coronal PD | Coronal PD-FS | |||
|---|---|---|---|---|
| NMSE | SSIM | NMSE | SSIM | |
| PG-DL | .0013 [.0010, .0017] | 0.9673 [0.9547, 0.9775] | .0074 [.0049, 0.0107] | 0.8795 [0.8322, 0.9146] |
| Learned Naive ℓ1-wavelet | .0019 [.0014, .0024] | 0.9574 [0.9404, 0.9692] | .0090 [.0062, 0.0125] | 0.8598 [0.8121, 0.9023] |
| Learned ℓ1-wavelet with Subbands | .0019 [.0014, .0024] | 0.9588 [0.9423, 0.9699] | .0081 [.0055, .0121] | 0.8662 [0.8202, 0.9057] |
| Learned reweighted ℓ1-wavelet with Subbands | .0017 [.0013, .0022] | 0.9602 [0.9444, 0.9709] | .0082 [.0053, .0116] | 0.8694 [0.8211, 0.9068] |
IV. DISCUSSION AND CONCLUSION
In this study, we revisited ℓl-wavelet CS for accelerated MRI using modern data science tools for fine tuning. As expected, PG-DL outperformed our three optimized ℓl-wavelet CS approaches, but the performance gap was smaller than previously published literature. This is interesting for a number of reasons. First, PG-DL used a sophisticated non-linear representation for the underlying images during regularization with a large number of learnable parameters. On the other hand, the wavelet-based representations we used were linear, involved only a small number of parameters, and allowed for convex optimization. Interestingly, there was <0.01 difference in SSIM between our proposed learned reweighted ℓ1-wavelet with subbands that used 128 parameters and the PG-DL approach that used >500,000 parameters. Second, while PG-DL can be further improved with more advanced neural networks and training strategies [26], our CS approach used one of the simplest linear models described by fixed orthogonal wavelets, and did not involve learning of the representation. Our results also showed that the performance gap decreased as we proceeded from learned naive ℓ1-wavelet to learned reweighted ℓ1-wavelet with subbands, demonstrating subband training and reweighting help improve reconstruction sharpness and quantitative metrics to a level comparable to PG-DL. Further gains for CS may be possible via learning linear representations/frames [27], [28], which warrants investigation.
ACKNOWLEDGEMENTS
This work was partially supported by NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825.
References
- [1].Pruessmann KP, Weiger M, Scheidegger MB, and Boesiger P, “SENSE: Sensitivity encoding for fast MRI,” Magn Reson Med, vol. 42, pp. 952–962, 1999. [PubMed] [Google Scholar]
- [2].Griswold MA, Jakob PM, et al. , “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn Reson Med, vol. 47, pp. 1202–1210, 2002. [DOI] [PubMed] [Google Scholar]
- [3].Lustig M, Donoho D, and Pauly J, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn Reson Med, vol. 58, pp. 1182–1195, 2007. [DOI] [PubMed] [Google Scholar]
- [4].Wang S, Su Z, et al. , “Accelerating magnetic resonance imaging via deep learning,” in Proc. IEEE Int. Symp. Biomed. Imag. (ISBI). IEEE, 2016, pp. 514–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans Med Imaging, vol. 37, pp. 491–503, 2018. [DOI] [PubMed] [Google Scholar]
- [6].Hammernik K, Klatzer T, et al. , “Learning a variational network for reconstruction of accelerated MRI data,” Magn Reson Med, vol. 79, pp. 3055–3071, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Aggarwal HK, Mani MP, and Jacob M, “MoDL: Model-Based Deep Learning Architecture for Inverse Problems,” IEEE Trans Med Imaging, vol. 38, pp. 394–405, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Knoll F, Hammernik K, et al. , “Deep-learning methods for parallel magnetic resonance imaging reconstruction,” IEEE Sig Proc Mag, vol. 37, no. 1, pp. 128–140, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Hosseini SAH, Yaman B, Moeller S, Hong M, and Akçakaya M, “Dense recurrent neural networks for accelerated MRI: History-cognizant unrolling of optimization algorithms,” IEEE J. Sel. Top. Signal Process, vol. 14, no. 6, pp. 1280–1291, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Yaman B, Hosseini SAH, et al. , “Self-supervised learning of physics-guided reconstruction neural networks without fully-sampled reference data,” Magn Reson Med, vol. 84, pp. 3172–3191, Dec 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Sriram A, Zbontar J, et al. , “End-to-end variational networks for accelerated mri reconstruction,” 2020.
- [12].Zou F, Shen L, Jie Z, Zhang W, and Liu W, “A sufficient condition for convergences of adam and rmsprop,” in Proc. IEEE/CVF Conf. Comp. Vis. and Patt. Rec. (CVPR), June 2019. [Google Scholar]
- [13].Mardani M, Gong E, et al. , “Deep Generative Adversarial Neural Networks for Compressive Sensing MRI,” IEEE Trans Med Imaging, vol. 38, pp. 167–179, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Seitzer M, Yang G, et al. , “Adversarial and perceptual refinement for compressed sensing MRI reconstruction,” in Proc. MICCAI, 2018, pp. 232–240. [Google Scholar]
- [15].Shahdloo M, Ilicak E, et al. , “Projection onto epigraph sets for rapid self-tuning compressed sensing mri,” IEEE Transactions on Medical Imaging, vol. 38, no. 7, pp. 1677–1689, 2019. [DOI] [PubMed] [Google Scholar]
- [16].Ramani S, Liu Z, Rosen J, Nielsen J, and Fessler JA, “Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods,” IEEE Trans Image Proc, vol. 21, no. 8, pp. 3659–3672, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Vetterli M and Kovačevic J, Wavelets and Subband Coding, Prentice-Hall, Inc., USA, 1995. [Google Scholar]
- [18].Candès E, Wakin M, and Boyd S, “Enhancing sparsity by reweighted l1 minimization,” Journal of Fourier Analysis and Applications, vol. 14, pp. 877–905, 11 2007. [Google Scholar]
- [19].Pruessmann KP, Weiger M, Bornert P, and Boesiger P, “Advances in sensitivity encoding with arbitrary k-space trajectories,” Magn Reson Med, vol. 46, pp. 638–651, 2001. [DOI] [PubMed] [Google Scholar]
- [20].Fessler JA, “Optimization methods for magnetic resonance image reconstruction: Key models and optimization algorithms,” IEEE Sig Proc Mag, vol. 37, no. 1, pp. 33–40, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Gregor K and LeCun Y, “Learning fast approximations of sparse coding,” in Proc. Int. Conf. Mach. Learn, 2010, pp. 399–406. [Google Scholar]
- [22].Monga V, Li Y, and Eldar YC, “Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing,” IEEE Sig Proc Mag, vol. 38, no. 2, pp. 18–44, 2021. [Google Scholar]
- [23].Knoll F, Zbontar J, et al. , “fastMRI: A publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning,” Radiol AI, p. e190007, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Uecker M, Lai P, et al. , “ESPIRiT–an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA,” Magn Reson Med, vol. 71, no. 3, pp. 990–1001, Mar 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Timofte R, Agustsson E, Van Gool L, Yang MH, and Zhang L, “Ntire 2017 challenge on single image super-resolution: Methods and results,” in Proc IEEE CVPR, 2017. [Google Scholar]
- [26].Muckley MJ, Riemenschneider B, et al. , “State-of-the-art machine learning MRI reconstruction in 2020: Results of the second fastMRI challenge,” 2020.
- [27].Wen B, Ravishankar S, Pfister L, and Bresler Y, “Transform learning for magnetic resonance image reconstruction,” IEEE Sig Proc Mag, vol. 37, no. 1, pp. 41–53, 2020. [Google Scholar]
- [28].Akcakaya M and Tarokh V, “A frame construction and a universal distortion bound for sparse representations,” IEEE Trans Sig Proc, vol. 56, no. 6, pp. 2443–2450, 2008. [Google Scholar]


