A Machine Learning Compatible Method for Ordinal Propensity Score Stratification and Matching

Abstract

Although machine learning techniques that estimate propensity scores for observational studies with multi-valued treatments have advanced rapidly in recent years, the development of propensity score adjustment techniques has not kept pace. While machine learning propensity models provide numerous benefits, they do not produce a single variable balancing score that can be used for propensity score stratification and matching. This issue motivates the development of a flexible ordinal propensity scoring methodology that does not require parametric assumptions for the propensity model. The proposed method fits a one-parameter power function to the cumulative distribution function (CDF) of the generalized propensity score (GPS) vector resulting from any machine learning propensity model, and is henceforth called the GPS-CDF method. The estimated parameter from the GPS-CDF method, $\tilde{a}$ is a scalar balancing score that can be used to group similar subjects in outcome analyses. Specifically, subjects who received different levels of the treatment are stratified or matched based on their $\tilde{a}$ value to produce unbiased estimates of the average treatment effect (ATE). Simulation studies presented show remediation of covariate balance, minimal bias in ATEs, and maintain coverage probability. The proposed method is applied to the Mexican-American Tobacco use in Children (MATCh) study to determine whether ordinal exposure to smoking imagery in movies causes cigarette experimentation in Mexican-American adolescents.

1 |. INTRODUCTION

Although non-randomized observational studies with ordinal treatments are commonly encountered in public health research including mental health, substance use, and program evaluation,^1,2 propensity scoring methods for ordinal treatments remain underdeveloped. Generally, ordinal treatments refer to treatment settings with three or more treatment levels with a defined ordering (e.g. treatment dosages, levels of a environmental exposure, etc). Since binary propensity scoring methods are very well established, researchers often disregard the ordered nature of the treatment and simply dichotomize the ordinal treatment or evaluate it as a multinomial treatment.^2–5 This only enables coarse estimation of the treatment effect (e.g. high vs. low or A vs. B) rather than causal estimation which considers each level of the ordinal treatment. While dichotomization of a multi-valued variable simplifies estimation techniques and interpretation, it has also been shown to cause loss of power, residual confounding, and bias, and thus cannot be recommended in the ordinal treatment setting.⁶ The only currently well-established propensity score model for ordinal treatments uses the proportional odds (PO) model to model treatment assignment as a function of treatment-related baseline covariates.^1,7 However, the PO assumption is easily violated in real world data. One notable example is the work of Cavasos-Rehg et al. (2014), that sought to analyze the effect of ordinal smoking reduction on mood and anxiety disorders, alcohol use, and drug use.² The PO propensity model did not satisfy the proportional odds assumption - thus the authors were forced to classify the exposure as multinomial, use a multinomial specific propensity model, and ignore the natural ordering of the exposure variable. The clear limitations that result from propensity model misspecification in the ordinal treatment setting motivates the need for more robust ordinal propensity scoring methods.

1.1 |. Ordinal Treatment Propensity Scoring

Instead of decomposing ordinal treatments into binary treatment comparisons, the generalized propensity score (GPS) extends causal inference theory to the multi-valued treatment setting.^8–13 Unlike the binary treatment case where the propensity score is a scalar representing the conditional (given covariates x_i) probability a subject was treated, the GPS, ${\widehat{\mathbf{P}}}_{i,GPS}$, is a vector of length K, representing the conditional probabilities of a subject being treated under each of the K conditions, ${\widehat{\mathbf{P}}}_{i,GPS}=\left({\widehat{p}}_{i,1},\dots ,{\widehat{p}}_{i,K}|x_i\right)$.^10,14

Like binary propensity scoring techniques, multi-valued propensity scoring techniques also require the assumptions of conditional independence (no unmeasured confounding) and positivity (every individual has a non-zero probability of receiving each potential treatment).⁸ However, implementing propensity matching procedures in studies with multi-valued treatments or exposures is more complicated than matching in the binary treatment setting since there are not two distinct (bipartite) treatment and control groups. Instead all subjects are exposed to some level of treatment and disjoint treatment groups are not present (also known as non-bipartite).¹⁵ Propensity score matching with non-bipartite treatment groups require the use of complex optimal or greedy matching algorithms, thoroughly described in Lu, Zanutto, Hornik, and Rosenbaum (2001) and Lu, Greevy, Xu, and Beck (2011).^1,15 Optimal matching seeks to minimize the total distance, using an appropriate distance measure, among all possible pairings, while greedy matching iteratively creates the best available pair and then removes that pair from the pool of potential matches.^1,15 Optimal and greedy matching algorithms utilized in conjunction with propensity scoring overwhelmingly use 1:1 matching without replacement.

Recent advances in propensity methodology for multi-valued treatments (which have mostly focused on multinomial rather than ordinal treatments), typically do not construct balanced strata or matched pairs using the K − 1 elements of ${\widehat{\mathbf{P}}}_{i,GPS}$, but rather estimate average potential outcomes separately for each treatment level.^13,16 This approach only adjusts, usually through inverse probability of treatment weighting (IPTW), for the element of the GPS vector corresponding to the treatment that was actually observed rather than the full GPS vector. One notable method which utilizes information across more than one element of the GPS vector is the vector matching procedure proposed by Lopez and Gutman (2017)¹³ and extended by Scotina and Gutman (2019).¹⁷ Briefly, vector matching is performed using the following steps: after estimating a GPS vector, the vector matching procedure defines an area of common support, then utilizes K-means clustering to create K strata of subjects with similar values for K − 2 elements of their GPS vectors. Caliper matching is then performed within each stratum to create a final matched cohort.¹³ This procedure creates matches which are closely matched on one element of their GPS vector and generally similar with regard to their other elements. While vector matching does utilize information across the GPS vector, it is independent of the order of the elements of the GPS vector.¹³

As a result, ordinal propensity scoring is a special instance of multinomial propensity scoring, for which extensions from the binary treatment setting based on the GPS vector ${\widehat{\mathbf{P}}}_{i,GPS}$ have been proposed.^13,16–20 While GPS methodologies for multinomial treatments may also be applicable to the ordinal setting,^10,11 one could gain efficiency in causal estimates by leveraging the natural ordering of the treatment/covariate relationship in the propensity model. With multinomial treatments, no inherent relationship exists between treatment assignments. For instance, in a multinomial four treatment scenario, knowing information about a subject’s probability of receiving treatment A, does not necessarily give any information about their probability of receiving treatments B, C, or D. However, when treatments are ordinal, the elements of ${\widehat{\mathbf{P}}}_{i,GPS}({\widehat{p}}_{i,1},\dots ,\left({\widehat{p}}_{i,K}\right)$ have a relationship that can be leveraged. For example, with two or more ordered treatment levels, if a subject has the highest conditional probability of receiving the lowest treatment level, then the GPS vector elements typically decrease as treatment level increases. Given this ordered “dosing” structure, the full GPS vector gives a more accurate portrayal of a subject’s observed covariate profile than the GPS vector in the multinomial treatment setting.

In practice however, the full GPS vector is not typically utilized to conduct ordinal treatment propensity scoring stratification or matching. Instead, proportional odds (PO) logistic regression models are commonly used as they directly produce a scalar balancing score upon which to stratify or match, i.e., the linear predictor $\widehat{\beta }\prime \text{x}$, for a given covariate vector, x_i.^1,7 Methods that do not involve propensity score adjustment, such as marginal structural models and g-estimation, have also been proposed for causal inference in the multi-valued treatment setting.^21–23 However, while these methods have particular benefit in scenarios with time-varying treatment, they have rarely been applied in traditional studies where a multi-valued treatment is only measured once.²⁴

Flexible machine learning models, such as the well-studied generalized boosted model (GBM),^25–29 are rapidly replacing traditional logistic regression-based methods as the preferred tool for estimating propensity scores in observational studies since machine learning methods have the ability to handle high-dimensional covariate spaces, automatically select higher-order terms and interactions, and down-weight uninformative covariates in the propensity model. Additionally, they do not require a priori assumptions about the true underlying form of the propensity model, and are more robust to propensity model misspecification that logistic regression methods.^28,29 Furthermore, in the spirit of the covariate balancing propensity score (CBPS) of Imai and Ratkovic (2014), machine learning methods can automatically produce a GPS vector with optimal balancing score properties, resulting in more precise estimates of treatment effect.^14,29 Although machine learning methods have numerous benefits, they do not naturally produce a scalar balancing score. Therefore, their application has been limited within multi-valued treatment propensity score stratification and matching, instead focusing primarily on propensity adjustment using IPTW. As the popularity of multi-valued propensity score estimation using machine learning grows, stratification and matching methods for ordinal treatments need to be adapted.

1.2 |. Causal Estimands of Interest for Ordinal Propensity Scoring

When conducting a causal analysis with multi-valued treatments, it is important to first define the causal estimands of interest. Though a within subject treatment effect exists in theory, as the difference among potential outcomes, it is generally impossible to observe an individual’s outcome under each possible treatment. Thus, estimation of the treatment effect relies on summarizing individual effects across populations (or sub-populations).²⁶ The two notable estimands of interest in multi-valued treatment settings are the average treatment effect (ATE) and average treatment effect among the treated (ATT). In a setting with K treatments, let Z represent the random variable representing which of the K treatments a subject received, and z represent the observed value of Z. Then the $\left(\begin{array}{c}K\\ 2\end{array}\right)$ pairwise average treatment effects (ATEs) are defined as the differences in mean outcomes had the entire population been observed under one treatment z versus had the entire population been observed under a different treatment $z\prime \left({\text{ATE}}_{z,z\prime }\right)$.²⁶ The ATE is calculated by taking the expectation across the entire population of interest:

$${\text{ATE}}_{z,z\prime }=E\left[Y\left(z\right)-Y\left(z\prime \right)\right]=E\left[Y\left(z\right)\right]-E\left[Y\left(z\prime \right)\right].$$ (1)

Alternatively, the average treatment effect among the treated (ATT) of treatment z among those treated with $z\prime \left({\text{ATT}}_{z,z\prime }\right)$ is the expected difference between the mean outcomes of subjects treated with z^′ (their observed treatment a) and their mean outcomes had they been treated with treatment z instead.²⁶ The ATT is defined as:

$${\text{ATE}}_{z,z\prime }=E\left[Y\left(z\prime \right)|Z=z\right]=E\left[Y\left(z\right)|Z=z\right].$$ (2)

Though ATE and ATT can each be estimated within a study, which causal estimand is of the greatest interest depends on the research question. ATE is more likely to be of more interest if a treatment could be potentially offered to every member of a population.²⁶ Therefore, if the relationship between treatment and outcome in an observational study is expected to be ordinal, where all members of a random sample of an infinite super-population are exposed to at least some level of treatment or “dose”, then ATE is likely the estimand of interest. In this case, an appropriate matched or stratified outcome model estimates the treatment effect by estimating the difference in the effect size between treatment levels within a matched pair or strata, then aggregates these differences over all strata or matched pairs. Estimating ATEs are the focus of this paper since the proposed methods are specific to ordinal treatments. The examples presented in this paper assume a linear relationship between the ordinal treatment and outcome. However, the methodology presented here could be adapted to other treatment/outcome relationships.

In sum, there is room to improve current methods for ordinal propensity score analysis. Specifically, there is a need to unite the strength of machine learning methods with the ability to conduct multi-valued treatments propensity score stratification and matching. Therefore, this paper presents an innovative method, known as the GPS-CDF method, which uses the cumulative distribution function (CDF) to map an ordinal GPS vector produced by any type of propensity model (parametric or machine learning) to a single scalar balancing score. This balancing score can be used to stratify or match subjects who have similar baseline covariates, but received different treatments (or exposures). The added flexibility of using any model to estimate the GPS vector overcomes limitations inherent in being forced to use the parametric proportional odds model to calculate a balancing score. Section 2 presents the GPS-CDF method, Sections 3 and 4 test the performance of the method in simulation, Section 5 applies GPS-CDF and current ordinal propensity score methods to evaluate the effect of exposure to smoking imagery in movies to cigarette experimentation among Mexican-American teens, and Section 6 presents a discussion and outlines future work.

2 |. METHODS

The GPS vector can be conceptualized as a discrete probability distribution whose elements make up a probability mass function (PMF). If one were able to accurately describe the distribution, or “shape”, of the GPS vector using a single parameter, where subjects with similar parameter values also have similar GPS vectors, then any propensity model could be used to calculate the GPS vector. This would simplify the multi-valued treatments propensity score problem, making it similar to a binary propensity score problem, and enable propensity matching or stratification using the estimated parameter as a scalar balancing score. However, the PMF of the GPS vector is not guaranteed to be either monotonically increasing or decreasing, (for example if the maximum element of the vector does not correspond to either the highest or lowest value of treatment). One parameter functions cannot accurately model shapes which are not strictly increasing or decreasing. Therefore, the CDF of the GPS vector, ${\widehat{\mathbf{P}}}_{i,GPS-CDF}$, which is always strictly increasing, is introduced in Equation 3.

$${\widehat{\mathbf{P}}}_{i,GPS-CDF}={\widehat{\mathbf{F}}}_z\left(Z\right)=\left({\widehat{p}}_{i,1},\sum _{z=1}^2{\widehat{p}}_{i,z},\dots ,\sum _{z=1}^{K-1}{\widehat{p}}_{i,z},1|{\mathbf{X}}_i\right)$$ (3)

2.1 |. Modeling the CDF

A key backbone of propensity scoring techniques is that subjects who have similar propensity scores (or GPS vectors in the multi-valued treatments scenario) have similar baseline covariate profiles. The CDF of the GPS vector is a one-to-one function of the PMF of the GPS vector, and can thus be used to compare the similarity of two subject’s baseline covariate profiles in lieu of the GPS vector itself. Since the CDF of the GPS vector is a strictly increasing function that is bounded by [0,1], it can be accurately modeled using any flexible one parameter function. The ability to accurately describe a GPS vector with one parameter overcomes a key limitation of most propensity scoring stratification and matching methods for multi-valued treatments, the non-existence of an intuitive scalar balancing score.

The setting of this problem is similar to model-based phase I dose escalation trials for cytotoxic cancer therapies where the probability of a dose limiting toxicity increases as standardized dose, dz increases.^30–32 Standardized dose in this setting is defined as the ratio of a specific dose level z to either the maximum dose level K or the median dose level. For example, in the setting with four ordered treatments and using the maximum dose level as the reference dose (as used throughout this paper), the standardized doses d₁, d₂, d₃, d₄ equal 0.25, 0.5, 0.75, and 1 respectively. In these dose escalation trials, binary data indicating whether the patient observed a dose limiting toxicity is observed for small cohorts of patients at increasing dose levels. Then, a parametric function (often a one-parameter power function) is used to model the dose-toxicity curve of increasing doses and estimate a maximum tolerated dose. This power function can be used in a similar manner to model the CDF of the GPS vector in an ordinal propensity analysis. The proposed power function governed by the single a parameter which approximates a subject’s GPS-CDF vector is shown in Equation 4, where the left side represents the CDF for the estimated GPS vector, d₁, …, d_K are the standardized doses which lie between 0 and 1 for the K possible levels of treatment, and â is the scalar that dictates the shape of the power function fitting the CDF.

$${\widehat{\mathbf{F}}}_z\left(Z\right)\approx d_1^{exp\left(\widehat{a}\right)},\dots ,d_{K-1}^{exp\left(\widehat{a}\right)},d_K^{exp\left(\widehat{a}\right)}$$ (4)

When using the power function to model the CDF in the current setting, there are not multiple observations at each exposure or standardized dose. Instead, the probabilities of each treatment level are based on one subject’s observed covariate values. It is therefore natural to fit the power function to the data using a non-linear least squares (NLS) algorithm, given formally, for one subject i, by Equation 5.

$${\tilde{a}}_i=\underset{a}{\min }\sum _{z=1}^{K-1}{\left(d_z^{exp\left(a\right)}-{\widehat{F}}_z\left(Z\right)\right)}^2\text{for}\hspace{0.17em}z=1,\dots ,K-1$$ (5)

This NLS algorithm iteratively fits values for a, the shape parameter, until the residual distance between the estimated CDF of the GPS vector and fitted power function is minimized, thus obtaining the optimal parameter $\tilde{a}$, which is the ordinal treatments scalar balancing score. While other one parameter functions could be used to model the CDF of the GPS vector, the current method is an intuitive and computationally simple way to estimate a scalar balancing score, $\tilde{a}$. The exponential, logistic, and logarithmic functions might initially seem plausible to summarize CDFs; however they do not share the advantages of the power function. Our studies show the power function accurately fits both concave and convex CDFs. Further, using this functional form retains the desirable property, similar in spirit to the functional uniform prior proposed by Bornkamp (2012),³³ that the function’s “shape” is uniformly distributed across the parameter space. This makes the choice of d^exp(a) superior to alternatives for modeling the CDF (such as d^a) when using $\tilde{a}$ as a measure of between subject CDF similarity for matching and stratification. Under alternative parameterizations, we have observed awkward resultant CDFs, and the “jump” from a = 0 to a = 1 is large, which would result in matching or stratifying dissimilar sets of patients. The curves from a variety of parameters are shown graphically in Figure 1.

FIGURE 1.

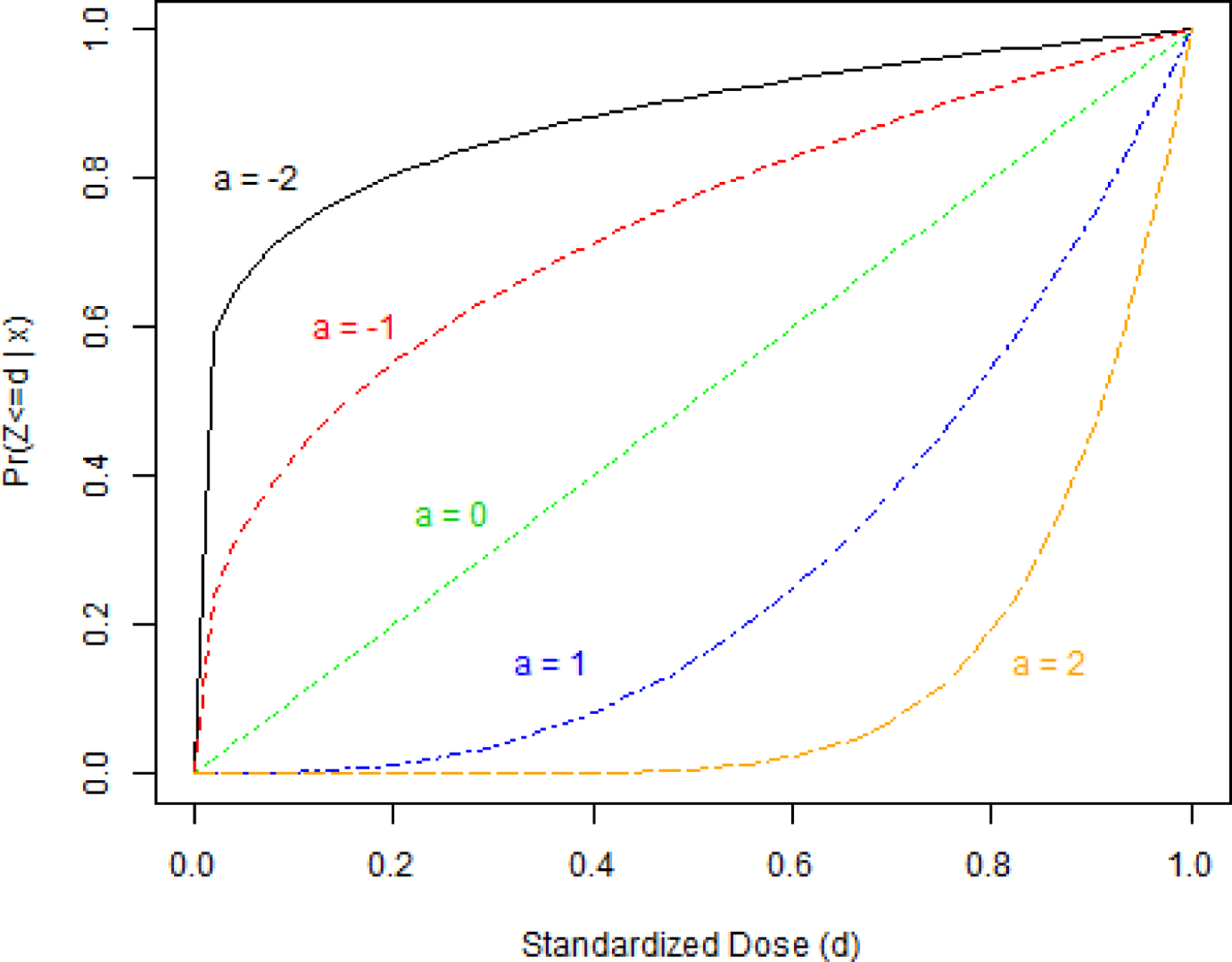
Shapes of the power model evaluated for different parameter values

The theoretical justification for the GPS-CDF method mimics that of previous work which concludes the distribution of ordered treatments only depends on a subject’s observed covariates through the balancing score. Therefore, if $\tilde{a}$ is a balancing score, then a subject’s outcome is conditionally independent of treatment assignment given $\tilde{a}$.^9,11

2.2 |. GPS-CDF Matching

After the power parameter, $\tilde{a}$, has been estimated, it can then be used in either an optimal or greedy matching algorithm to pair similar subjects who received different levels of treatment. Optimal matching seeks to minimize the total distance among all possible pairings, while greedy matching iteratively creates the best available pair and then removes that pair from the pool of potential matches.^1,15 The proposed metric for GPS-CDF matching is inspired by the equal percent bias reduction metric of Lu et al. (2001)¹ and is calculated as the ratio of the squared difference of power parameters for two subjects, ${\tilde{a}}_i$ and ${\tilde{a}}_j$, in the numerator and the squared difference in observed treatment received, z_i and z_j (or d_i and d_j in practice), in the denominator. Minimizing this metric will match subjects who have similar estimated values for $\tilde{a}$ (and thus similar CDFs, GPS vectors, and subsequent observed covariate profiles), but who received different treatments. The metric for two subjects, i and j, is shown in Equation 6 where є is a vanishingly small constant to prevent the numerator from equaling zero.

$${\mathrm{\Delta }}_p=\mathrm{\Delta }\left({\text{x}}_i,{\text{x}}_j\right)=\frac{{\left({\tilde{a}}_i-{\tilde{a}}_j\right)}^2+ϵ}{{\left(z_i-z_j\right)}^2}$$ (6)

The following steps describe the GPS-CDF matching procedure in detail:

1. Select potential confounding variables for the propensity model.

2. Estimate the GPS vector using any appropriate propensity model (ex: GBM, PO ordinal logistic regression model, etc.).

3. Calculate the cumulative distribution GPS vector for each subject.

4. Fit a one parameter power function to each GPS-CDF vector to obtain ${\tilde{a}}_i$.

5. Calculate the ∆_(i,j) matrix to determine the distance from each subject to all others based on the metric from Equation 6.

6. Establish matched pairs using an optimal or greedy matching algorithm.

7. Assess covariate balance after matching using graphical methods and standardized mean differences (SMDs).

8. Conduct an appropriate matched outcome analysis to estimate ATE.

2.3 |. CDF Stratification

The estimated power parameter ${\tilde{a}}_i$ can also be used to group similar subjects into strata. Since matching is essentially a specific case of stratification where each strata contains two subjects, the extension from GPS-CDF matching to GPS-stratification is staightforward. Within each stratum are subjects who received differing levels of treatments, but whose covariates are similar. Though any number of strata can be created, previous studies of binary treatments have shown that five equal-sized quintiles removes approximately 90% of the initial imbalance in each of the observed covariates.^7,34 The following steps describe the CDF stratification procedure in detail:

1. Follow Steps 1–4 from the GPS-CDF matching procedure.

2. Order observations by their estimated ã value and divide into quintiles.

3. Conduct an appropriate stratified outcome analysis to estimate ATE.

3 |. SIMULATION STUDY DESIGN

A simulation study was conducted to determine how the GPS-CDF matching and stratification methods perform in the presence of model misspecification. Model misspecification can occur in both the propensity model and/or the outcome model, and both must be considered.³⁵ The design of the simulation study was adapted from previous simulation studies for binary and continuous treatments, and was tailored to represent realistic scenarios.^5,36–38 Each simulated dataset assumed four ordinal exposure categories denoting treatment, nine standard normal baseline covariates, and one binary outcome. In this simulation, the treatment effect was linearly related to the log odds of the binary outcome. To produce various levels of treatment and outcome confounding, six covariates (x₁, x₂, x₄, x₅, x₇, x₈) were associated with treatment assignment probability through a specified treatment assignment model, and six covariates (x₁ – x₆) were associated with the outcome assignment probability through the outcome assignment model. As a result, four variables, x₁, x₂, x₄, and x₅ had an association with both the treatment and outcome. The associations between the baseline covariates with treatment and outcome are shown in Table 1.

TABLE 1.

Association of covariates with treatment and outcome where $x_{i,1-9}\stackrel{iid}{\sim }N\left(0,1\right)$

	Strongly Associated With Treatment	Moderately Associated With Treatment	Independent of Treatment
Strongly Associated With Outcome	x 1	x 2	x 3
Moderately Associated With Outcome	x 4	x 5	x 6
Independent of Outcome	x 7	x 8	x 9

The current simulation study considered four scenarios that are similar to those of previously conducted simulation studies and vary whether both the treatment assignment (propensity) model and outcome model are correctly specified.^5,35 In Scenario 1 both models were correctly specified. Incorrect specification was manifested by the inclusion of a non-linear, and slightly mis-measured confounding covariate, (x_i,1 + 0.5)², into the treatment assignment model (Scenario 2), outcome model (Scenario 3), or both models (Scenario 4). Further details on the simulation design, including the equations which governed treatment and outcome assignment,are shown in the Supporting Information. Since one benefit of non-parametric methods is that they do not rely on parametric assumptions such as proportional odds, in each of the four scenarios the treatment probabilities for each observation were generated from a model which violated proportional odds, that is, coefficient values quantifying the effect of a covariate on treatment assignment were not constant across treatment level. Treatment was assigned by sampling one value from a multinomial distribution with sampling weights equal to the subject’s estimated GPS vector. The logit of the binary outcome variable was assumed to be linearly related to the treatment variable and associated covariates. Each subject’s outcome variable was assigned by sampling from a Bernoulli(p_i) distribution (where p_i was calculated by applying the inverse logit transformation to the left-hand side of each subject’s outcome assignment equation). Since this study assumed a linear relationship between treatment and log odds of the outcome, after adjusting for the GPS vector (via matching or stratification) the resulting coefficient from the conditional logistic regression model provided unbiased estimation of the ATE.

For each of the four scenarios, 1000 datasets of 1000 observations were generated and analyzed using five methods of estimating ATE: unadjusted (crude odds ratio), proportional odds optimal matching on $\widehat{\beta }\prime \text{x}$, proportional odds stratification on $\widehat{\beta }\prime \text{x}$, optimal GPS-CDF matching, and GPS-CDF stratification. The proportional odds propensity model adjusted for all first order covariates associated with treatment assignment. Similarly, to test GPS-CDF matching and stratification, all covariates associated with treatment assignment were included in a non-parametric GBM propensity model to estimate the GPS vector. The GPS vector was subsequently used in conjunction with optimal GPS-CDF matching, and GPS-CDF stratification. Though GPS-CDF stratification and matching can be used with any method which can produce a GPS vector, like Griffin et al. (2017), this paper focused on using GBM to estimate the GPS vector for a few notable reasons. First, GBM is well-established in the binary and multi-valued treatment propensity research literature.^25–29 Secondly, the simulations presented in this paper considered a complex relationship between covariates and treatment (i.e. higher order unobserved confounding, and non-proportional odds violations). Setodji et al. (2017) evaluated performance of GBM versus the covariate balancing propensity score (CBPS) method¹⁴ in the binary treatment setting and found that, while both methods performed well, in some instances, when complex relationships existed between covariates and exposure (e.g. non-linearity, and interaction) GBM tended to outperform CBPS.³⁹ GBM has an associated user-friendly R package which undoubtedly increases its application across a wide range of disciplines (e.g. atrial fibrillation, trauma, and leukemia among many others).^40–42 Finally, the performance of GBM is directly related to other tree-based methods such as random forest, BART, or combination methods such as super learning.^28,29

4 |. SIMULATION RESULTS

Before propensity score adjustment, variables associated with treatment (x₁, x₂, x₄, x₅, x₇, x₈) were severely imbalanced across treatment groups. To quantify the degree of imbalance, standardized mean differences between treatment were calculated across all treatment level contrasts. Table 2 displays these results specifically for Scenario 4.

TABLE 2.

Scenario 4: Standardized mean differences between treatment levels before propensity adjustment

Variable	Average SMD	1 vs. 2	1 vs. 3	1 vs. 4	2 vs. 3	2 vs. 4	3 vs. 4
x 1	0.33	0.19	0.41	0.56	0.23	0.38	0.19
x 2	0.30	0.09	0.23	0.53	0.19	0.48	0.31
x 3	0.11	0.08	0.10	0.12	0.09	0.12	0.13
x 4	0.54	0.10	0.41	0.94	0.34	0.88	0.55
x 5	0.30	0.08	0.23	0.53	0.18	0.48	0.31
x 6	0.10	0.08	0.09	0.12	0.09	0.12	0.13
x 7	0.50	0.45	0.73	0.90	0.29	0.46	0.20
x 8	0.29	0.25	0.41	0.51	0.17	0.27	0.15
x 9	0.11	0.08	0.10	0.12	0.09	0.12	0.13

Numerous instances of SMDs indicating imbalance (>0.2) were present among those variables associated with treatment, and, as expected, as the difference in treatment level contrast increased the SMD also tended to increase. These results confirm that the simulation study design successfully created datasets which were imbalanced across treatment level and offers a reference point to assess the ability of the proposed methods to remove imbalance.

For each scenario, performance of the selected methods was compared using average bias, mean squared error (MSE), and coverage probability of the estimated ATE. Covariate balance across treatment groups was assessed using average pairwise standardized mean differences.^43–45 Box plots showing the distribution of the estimated ATE, along with the associated performance measures are shown in Figure 2.

FIGURE 2.

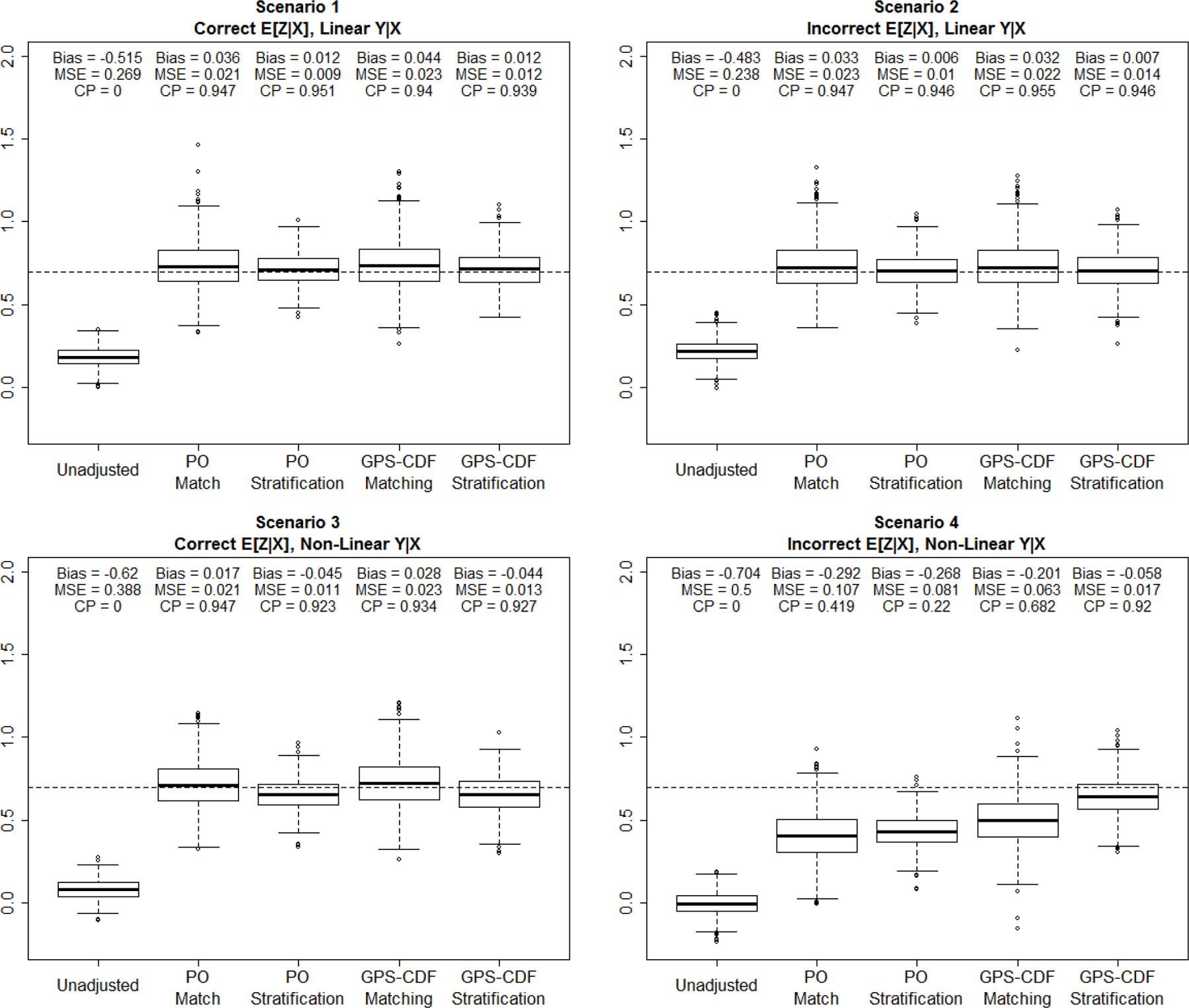
Simulation results for each method under each scenario (1000 datasets per scenario).

In Scenario 1 each method (with the exception of the unadjusted crude odds ratio), showed minimal bias and MSE, as well as coverage probabilities near 95%. This was expected since both the propensity model and outcome model were correctly specified. It is noteworthy to point out that the matching and stratification methods based on the proportional odds model performed well even though the proportional odds assumption is violated. The reason is likely due to the fact that covariate data were still ordered to some degree, with respect to the outcome and thus balance could still be achieved even though the model’s assumptions did not hold. Scenario 2, where the propensity model was misspecified, but the outcome model was correct showed comparable results to Scenario 1, indicating that the four adjustment methods chosen were robust to misspecification of the propensity model. When the outcome model was perturbed, as in Scenario 3, performance of all methods began to decline, as expected, though bias was still fairly small in the range of [−0.045, 0.028]. In this scenario, using stratification with either method (proportional odds or GPS-CDF) resulted in increased bias and decreased coverage probability compared to both matching methods. In Scenario 4, both of the GPS-CDF methods convincingly outperformed all other methods with respect to bias and coverage probability. The GPS-CDF stratification method produced small bias and coverage probability close to 95%. GPS-CDF matching did not perform at the level of GPS-CDF stratification, but still outperformed all other existing methods for ordinal treatments. Average standardized mean differences between variables, within a matched pair, after implementing GPS-CDF matching, in Scenario 4 are displayed in Table 3.

TABLE 3.

Scenario 4: Average number of matches and weighted average of standardized mean differences within matched pairs across all combinations of treatment after GPS-CDF Matching

	Weighted Average SMD	1 vs. 2	1 vs. 3	1 vs. 4	2 vs. 3	2 vs. 4	3 vs. 4
n Matches	—	238.17	25.38	45.76	138.33	16.61	35.92
x 1	0.24	0.12	0.59	1.06	0.09	0.36	0.22
x 2	0.14	0.06	0.26	0.42	0.10	0.44	0.22
x 3	0.12	0.07	0.24	0.18	0.10	0.36	0.20
x 4	0.19	0.11	0.32	0.68	0.10	0.51	0.23
x 5	0.14	0.06	0.26	0.41	0.10	0.42	0.22
x 6	0.12	0.07	0.24	0.18	0.10	0.36	0.20
x 7	0.22	0.09	0.38	0.78	0.17	0.34	0.36
x 8	0.15	0.09	0.29	0.47	0.10	0.36	0.22
x 9	0.12	0.07	0.24	0.16	0.10	0.38	0.19

Inspection of balance results the reveals that most matched pairs (82%) were constructed from individuals who had treatments only one level apart. This is not surprising since subjects who have similar treatment levels generally have more similar covariate profiles, in the simulation. Comparing Table 3 to Table 2 shows that after conducting GPS-CDF matching the weighted average SMD (weighted by number of matches created within treatment contrast) decreased for all covariates associated treatment (x₁,x₂,x₄,x₅,x₇,x₈) to near or below 0.2 indicating that observed covariate imbalance was largely removed.

4.1 |. Sensitivity to Sample Size and Number of Treatment Levels

Additional simulations were performed to assess the GPS-CDF methods’ performance across varying sample sizes (n=200, n=400, n=600, and n=800) and number of treatment levels (K = 6, K = 8, K = 10). Each of these simulations compared the same five methods as the primary simulation study (unadjusted, PO matching, PO stratification, GPS-CDF Matching, and GPS-CDF stratification). For each sample size considered, 1000 datasets with four ordinal treatment levels, were constructed under simulation Scenario 4 (incorrect specification of both the propensity and outcome model). Absolute bias, and mean squared error were the highest for each method at a sample size of 200. Both absolute bias and mean squared error decreased at a sample size of 400 and had little variation at sample sizes of 600, 800, and 1000. Coverage probability was lowest for all adjustment methods at n=200. The relationship between sample size and coverage probability had a slightly inverted-U shape for PO matching, PO stratification, and GPS-CDF matching methods. Each of these methods had their highest coverage probabilities at sample sizes of 400, 600, and 800, and slightly lower coverage probability at n=1000. While the coverage probability of GPS-CDF stratification was the lowest at n=200, it remained constantly high across all other sample sizes tested. This result was not surprising since it is more difficult to find close matches in a small pool of subjects. Across all sample sizes tested, the GPS-CDF methods outperformed existing proportional odds-based methods. Graphical representation of these results is shown in Figure 3

FIGURE 3.

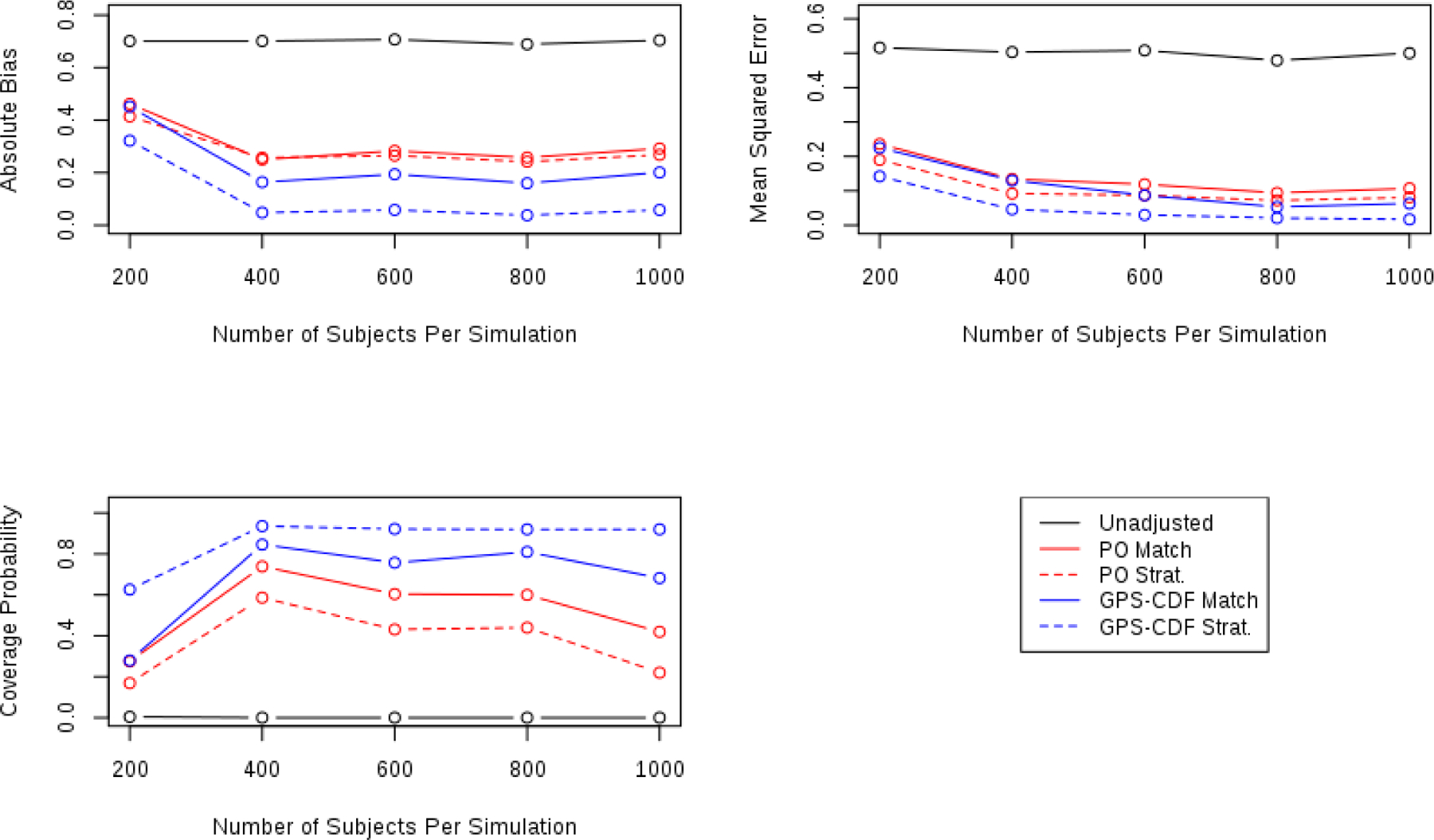
Comparing operating characteristics of each method for sample sizes of 200, 400, 600, 800, 1000

To assess the proposed methods’ performance across possible number of treatments, simulations were conducted using 6, 8, and 10 treatment levels. Simulation results are presented graphically in Figure 4.

FIGURE 4.

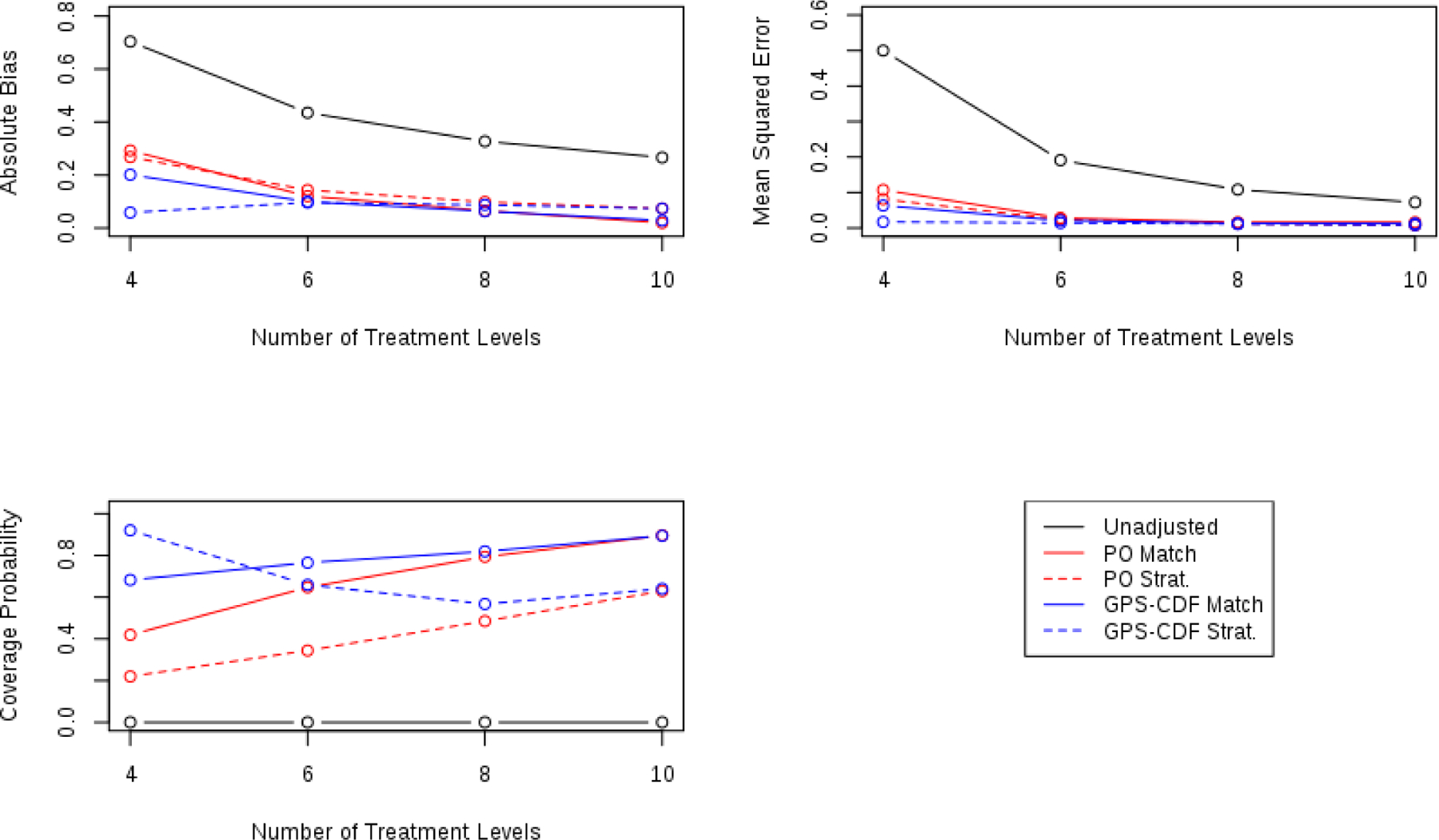
Comparing operating characteristics of each method for 4, 6, 8, and 10 possible treatment levels.

Generally, across these measures of performance, all methods tended to perform better as the number of treatments increased, except for GPS-CDF stratification (which still had generally good operating characteristics). As the number of treatments increased the absolute bias and mean squared error tended to decrease across all methods, except for GPS-CDF stratification (though bias and MSE remained small for this method). Mean squared error plateaued at 6 treatments and showed little variation up to 10 treatments. Coverage probability increased as the number of treatments increased for each method except GPS-CDF Stratification. Interestingly, as the number of treatments increased, both matching methods showed better coverage probability than each stratification method. This is likely due to increased variability around the estimate as shown in the graph of MSE and the boxplots shown in Figure 2.

5 |. THE MATCH STUDY

GPS-CDF matching and stratification procedures were applied to the Mexican-American Tobacco use in Children (MATCh) study to determine whether exposure to smoking imagery in movies influences cigarette experimentation among smoking-naive Mexican-American adolescents.⁴⁶ The MATCh study was a cohort study conducted in the Houston, Texas area to assess factors influencing an adolescent’s decision to experiment with cigarettes.⁴⁶ A primary research question assessed in the MATCh study was how exposure to smoking imagery in movies (SIM) affects a young person’s choice to experiment with cigarettes.⁴⁷ The study quantified exposure to smoking imagery in movies using the Beach method, in which a subject indicates whether or not they have viewed 50 randomly selected movies from a pool of 250 popular movies whose smoking content was analyzed by the Media Research Laboratory at Dartmouth College,^48,49 and grouped subjects into ordered quartiles based on their level of exposure. In order to facilitate comparisons between results of the MATCh study and previous research, the MATCh study calculated the odds of experimenting associated with a quartile increase in SIM exposure.^47,50,51 Prior research showed a significant positive association between increased exposure to smoking imagery in movies and experimentation with cigarettes (adjusted logistic regression OR = 1.27, 95% CI [1.10, 1.48], p = 0.002).⁴⁷ However, ordinal propensity scoring methods have never been used to analyze this endpoint. Therefore, previous results do not support causal inference. The current analysis considered a subset of 546 subjects who reported no history of cigarette experimentation and had complete information for all relevant variables. Since the MATCh study was observational and the dataset contains a non-randomized ordinal exposure of interest, it is an excellent example for ordinal propensity scoring. In fact, tobacco use and smoking are public health outcomes commonly studied using propensity scoring techniques since exposures cannot be randomized.^{2,3,11,52–54} Furthermore, the effect of media influence on substance use is a popular example of ordinal treatment exposure. Notably, Lu, Zanutto, Hornik, and Rosenbaum (2001) and Zanutto, Lu, and Hornik (2005), in their respective seminal papers on proportional odds propensity matching¹ and stratification⁷ for ordinal exposures, both evaluated the effectiveness of a national anti-drug media campaign on teens’ intentions to use drugs.

Covariate imbalance across quartile of SIM exposure prior to adjustment was expected and observed. For ease of interpretation, the averages of the pairwise SMDs between each quartile are displayed. Table 4 displays the covariate imbalance across exposure quartile for potential pre-exposure confounding variables and shows there were several average SMDs above the recommended cutoff of 0.2.^26,55 Detailed descriptions of these variables can be found in Wilkinson et al. (2009).⁴⁷ Subjects in higher SIM exposure quartiles tended to be more predominately male, be more likely to have been born in the USA, have a higher level of acculturation, have more close peers who smoke, and have higher scores for risk taking behavior, thrill and adventure seeking behaviors, drug and alcohol seeking behaviors, and social disinhibition.

TABLE 4.

Distribution of influential variables across quartile of exposure to smoking imagery in movies within the MATCh study.

	Q 1	Q 2	Q 3	Q 4	Avg. SMD
N	137	136	137	136
Age	11.5 (0.7)	11.5 (0.8)	11.7 (0.8)	11.7 (0.8)	0.171
Male (N (%))	50 (36.5)	47 (34.6)	64 (46.7)	74 (54.4)	0.238*
Born in USA (N (%))	96 (70.1)	96 (70.6)	98 (71.5)	111 (81.6)	0.140
Level of Acculturation	3.28 (0.7)	3.40 (0.7)	3.49 (0.6)	3.71 (0.7)	0.327*
Parental Educ. (N (%))					0.195
Less than HS	94 (68.6)	93 (68.4)	86 (62.8)	85 (62.5)
Completed Some HS	27 (19.7)	23 (16.9)	19 (13.9)	22 (16.2)
HS or More	16 (11.7)	20 (14.7)	32 (23.4)	29 (21.3)
Smokers in HH (N (%))					0.149
None	97 (70.8)	89 (65.4)	85 (62.0)	96 (70.6)
One	27 (19.7)	37 (27.2)	41 (29.9)	30 (22.1)
More than One	13 (9.5)	10 ( 7.4)	11 ( 8.0)	10 ( 7.4)
Close Peer Smokes (N(%))	13 (9.5)	16 (11.8)	17 (12.4)	20 (14.7)	0.084
Served Detention (N(%))	38 (27.7)	33 (24.3)	38 (27.7)	58 (42.6)	0.198
CS (N (%))	22 (16.1)	32 (23.5)	37 (27.0)	42 (30.9)	0.191
RTB	1.63 (0.8)	1.86 (0.7)	2.03 (0.8)	2.09 (0.8)	0.333*
POE	1.15 (0.3)	1.19 (0.3)	1.26 (0.4)	1.24 (0.4)	0.182
TAS	6.18 (3.1)	7.18 (3.0)	7.67 (3.0)	7.74 (3.1)	0.285*
DAA	0.41 (0.9)	0.78 (1.3)	0.91 (1.3)	0.99 (1.4)	0.270*
SD	2.97 (1.8)	3.47 (2.0)	3.91 (1.8)	4.10 (1.7)	0.353*
SSS	7.98 (1.2)	7.94 (1.6)	7.96 (1.4)	7.92 (1.3)	0.024

^*Numerous variables have average SMD > 0.2 indicating covariate imbalance.

(Note: HS = High School, HH = Household, CS = Cognitive susceptibility, RTB = Risk taking behavior score, POE = Positive outcome expectation, TAS = Thrill and adventure seeking, DAA = Drug and alcohol seeking behaviors, SD = Social disinhibition score, SSS = Subjective social status. All statistics reported as (mean (sd) unless otherwise noted).

To estimate ATE using GPS-CDF matching and stratification procedures, all variables listed in Table 4 were first entered into a GBM propensity model as independent variables to estimate the GPS vector for the probability of exposure to each quartile of smoking imagery in movies. After initial GBM propensity score estimation showed evidence of overfitting, the number of regression trees was reduced from 10,000 (default) to 4,000 and propensity scores were re-estimated. Reducing the number of trees resulted in better balance among pre-treatment covariates and eliminated concerns regarding overfitting. The two assumptions necessary for propensity scoring are positivity, which is assessed subjectively, and no unmeasured confounding, which must be assumed.^8,26 A specific rule to determine if positivity is sufficient do not exist, so it must be subjectively assessed, in conjunction with balance diagnostics (shown later in Figure 6 ), to determine if the treatment groups are sufficiently similar to support causal estimation of the treatment estimands.²⁶ Graphical evidence of positivity are shown using side-by-side boxplots in Figure 5.

FIGURE 6.

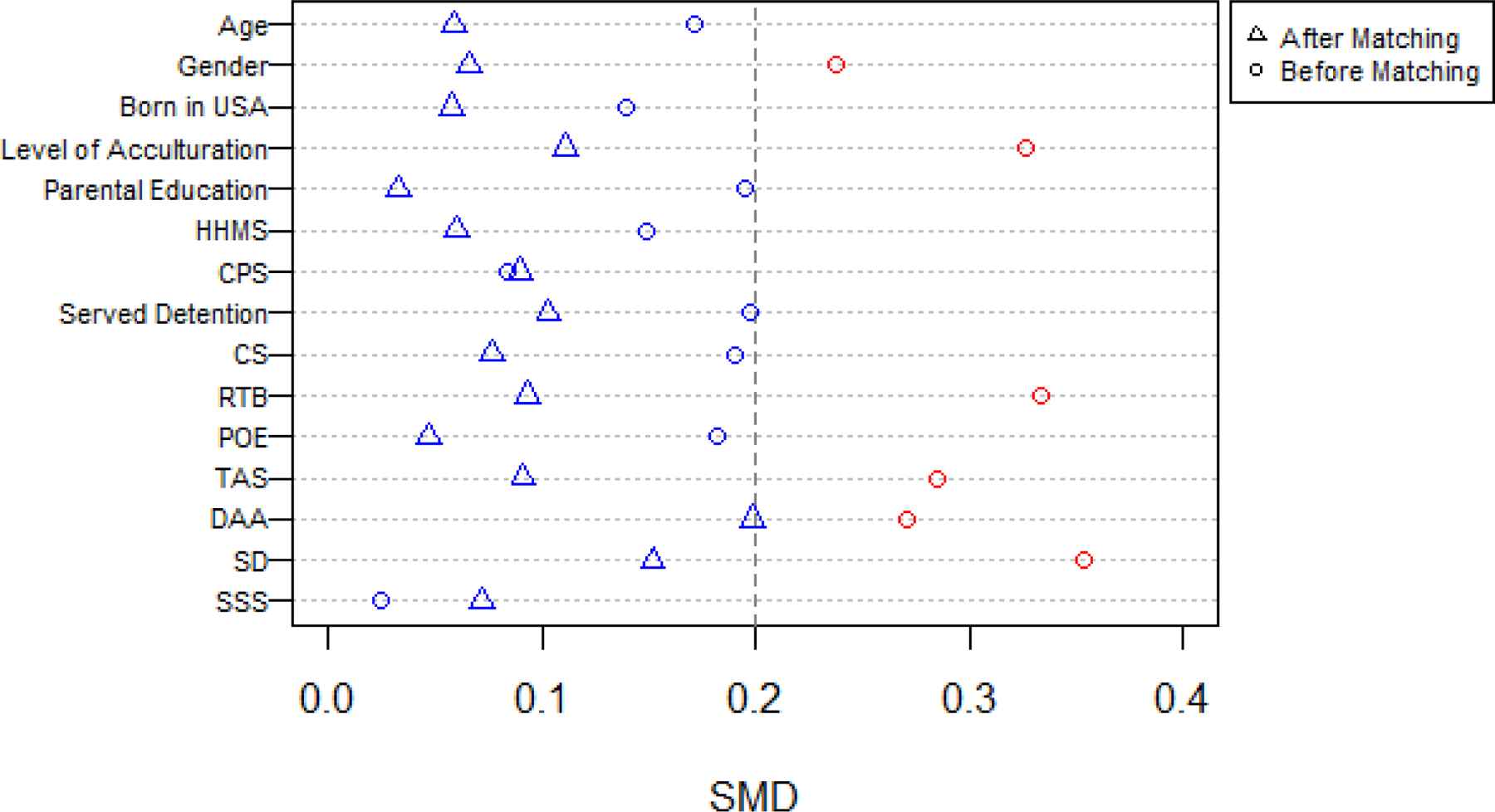
Average SMD before and after matching for influential variables from the MATCh data. A red icon indicates SMD > 0.2 and a blue icon indicates average SMD < 0.2. Note: HS = High School, HHMS = Household family member who smokes, CPS = Close Peer Smokes, CS = Cognitive Susceptibility, RTB = Risk taking behavior, POE = Positive outcome expectation, TAS = Thrill and adventure seeking, DAA = Drug and Alcohol Seeking Behaviors, SD = Social disinhibition, SSS = Subjective social status.

FIGURE 5.

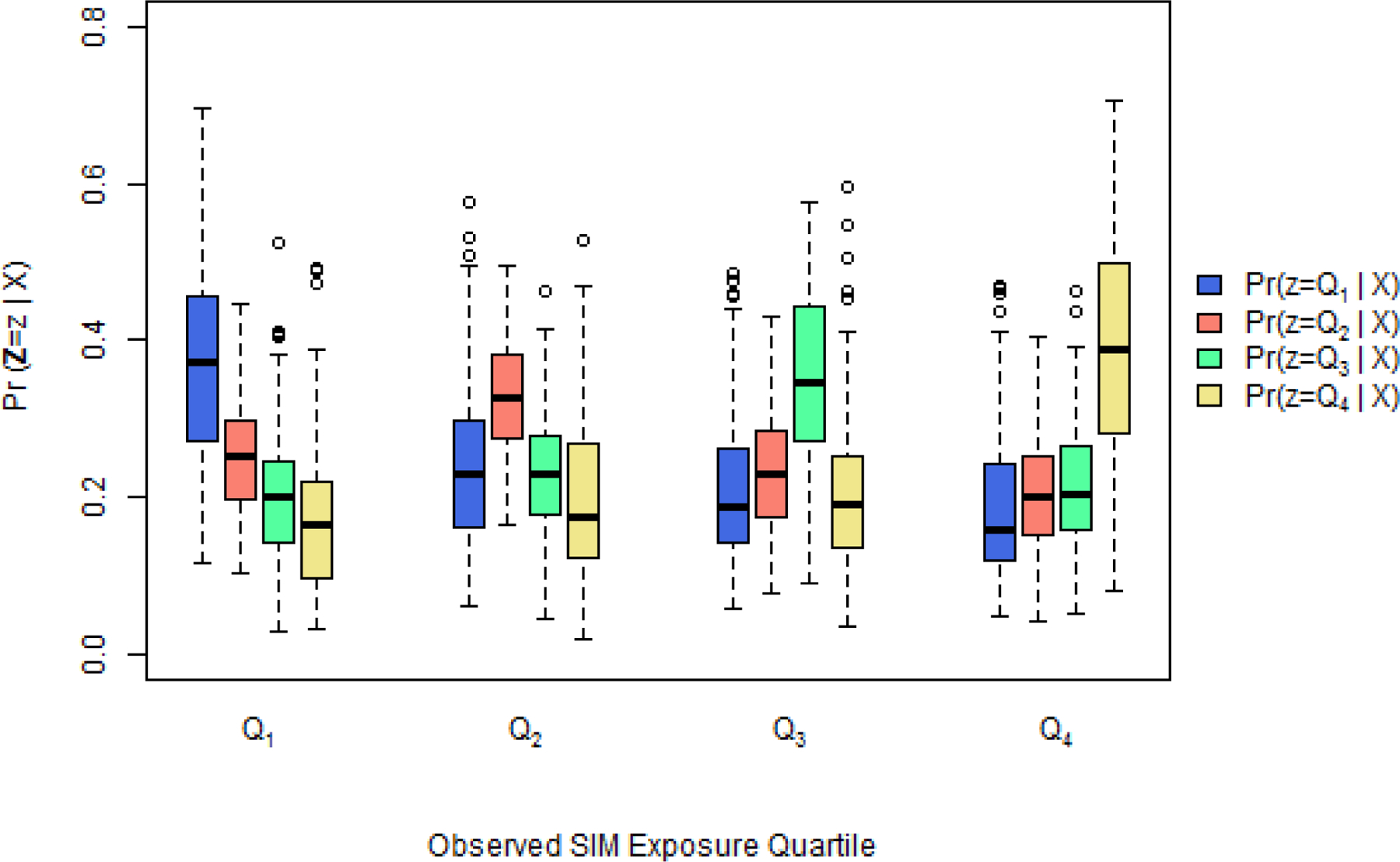
Comparing overlap of estimated generalized propensity scores from the MATCh data, that is Pr(Z = z|X_i) for z = Q₁, …, Q₄, across observed SIM exposure quartile.

As expected, the element of the GPS vector corresponding to the level of exposure which was actually observed tended to be the largest. However, there was not great separation between the boxplots representing each estimated level of exposure (to the extent seen in McCaffrey et al. (2013)), and thus, positivity and overlap assumptions were met.

5.1 |. MATCh Study Results

After applying the new GPS-CDF matching procedure it was clear that covariate imbalance was largely removed for the variables considered. This is shown graphically in Figure 6.

The average SMD value within matched pairs was below 0.2 for each potential confounder considered. This indicates balance was acheived and that subjects who were paired together had similar covariate profiles. These results, paired with the subjective assessment that the assumptions of positivity and overlap hold, support causal estimation of the ATE.

GPS-CDF stratification was also used to analyze the MATCh data, and both methods showed that odds of smoking experimentation increased as the exposure to smoking imagery in movies increased (OR_{GPS-CDF Strat}= 1.53, 95% CI [1.15, 2.03] p = 0.004, OR_{GPS-CDF Match}= 1.57, 95% CI [1.00, 2.44], p = 0.048). These results were similar to those from proportional odds matching (OR_{PO Match} = 1.61, 95% CI [1.11, 2.35], p = 0.013), and proportional odds stratification (OR_{PO Strat.} = 1.41, 95% CI [1.10, 1.80], p = 0.007). The unadjusted crude odds ratio was slightly higher than all propensity methods (OR_crude = 1.66, 95% CI [1.34, 2.06], p < 0.001). The results from all of these methods were similar and further support evidence from previous studies that adolescents’ odds of experimenting with cigarettes increases as exposure to smoking imagery in movies increases.

6 |. DISCUSSION

Despite some recent advances in methodology and application for multi-valued treatment propensity scoring, there remains a lack of propensity score literature specific to ordinal treatments, and no well-studied methods to conduct propensity score matching or stratification when strict parametric models are unable to induce covariate balance.^5,13,16,56 The methods presented here provide an easily applicable remedy when the proportional odds is violated, as encountered by Cavasos-Rehg et al. (2014) and others. Furthermore, since GPS-CDF matching and stratification have been shown via simulation to perform at least as well as matching or stratifying on $\widehat{\beta }\prime \text{x}$, they can be applied to any ordinal treatment setting, even if the proportional odds assumption holds.

Compatibility with novel non-parametric propensity score estimation is the most obvious strength of GPS-CDF matching and stratification presented in this paper. The proposed method can be implemented with any parametric or non-parametric propensity model that estimates a GPS vector. Non-parametric methods of estimating propensity scores, such as GBM, random forests, Bayesian adaptive regression trees, super learning, and high dimensional propensity score (hd-PS) methodology, have become more popular in recent years due to their ability to automatically select variables and include higher order terms while achieving excellent covariate balance.^{5,14,25,26,29,37,57–60} Using these non-parametric models decreases the amount of time researchers have to spend assessing higher order and interaction terms in the propensity score model to achieve covariate balance.

Currently generalized propensity scores estimated from non-parametric models are implemented using IPTW.^{25,26,29,37,61–63} There are several reasons to continue developing multi-valued treatments stratification and matching methods rather than solely relying on IPTW. First, IPTW utilizes the exact value of the estimated propensity score for the treatment observed rather than using the value only to group subjects with similar propensity scores (as in stratification or matching).^{10,26,63–66} When the estimated propensity score is used finely, it can be overly influential on the estimation of treatment effect.⁶⁶ This issue is amplified when estimated propensity score weights are highly variable, and thus a few observations greatly influence the estimated magnitude and precision of a treatment effect.^13,61,67,68 Large highly variable weights can be prevalent if the estimation of the propensity score is biased due to model is misspecification, incorrect model assumptions (e.g. proportional odds), or if there are a large number of predictors in the model.^28,29,61 Utilizing non-parametric machine learning procedures to estimate the propensity scores is one way to minimize the bias resulting from these scenarios.^37,69,70 Therefore, in situations likely to produce large highly variable weights, it would be preferable to estimate propensity scores using a non-parametric machine learning algorithm, then adjust for these scores using a stratification or matching procedure.

Since the CDF of the GPS is modeled using standardized doses, this novel method can accurately estimate the GPS vector even when the interval between observed doses is not constant. Furthermore, unlike other propensity matching methods for multi-valued treatments, GPS-CDF matching and stratification are not constrained by the number of possible treatments (e.g. Rassen et al. (2013)¹⁸) and its natural extension to continuous treatments is currently being developed. Assessing the performance of the proposed method with an increasing number of pre-treatment covariates is another area of future research. Griffin et al. (2017) evaluated the impact of including additional variables in the propensity model with no relation to binary treatment assignment. Their results agreed with other research, which suggests as the number of variables in the propensity model increases, SMD increases, balance degrades, and treatment effect is estimated less accurately.^29,39,71,72 Since the methods proposed in this paper can be used in conjunction with any method of estimating propensity scores which produces a GPS vector, it would be of interest to determine if there are instances where one estimation method outperforms others. Other future research topics include adapting the GPS-CDF method to non-linear treatment/outcome relationships, testing the method’s performance in high dimensional settings when paired with variable selection procedures, and comparing the performance of the GPS-CDF method with related matching and stratification methods for multinomial treatments.^13,16,17 The GPSCDF R package has been developed and is available to aid researchers in implementing the methods described in this paper.⁷³

The simulation scenarios considered in this study bring to light real-life obstacles investigators face when analyzing observational data such as severe covariate imbalance across treatment groups, parametric violations, and inability to rule out model misspecification. Overall, the simulation design and results were similar to those of previous studies that investigated continuous and binary treatments.^5,36 The proposed methods performed well across Scenarios 1–3, and were robust to the most severely perturbed Scenario 4, compared to the other methods. As it is essential to use simulation to assess the performance of novel methods to determine how robust they are to various levels of model misspecification,³⁵ we showed that GPS-CDF matching and stratification significantly outperform the currently available PO methods in the presence of this issue.

Further evidence of the usefulness and performance of the novel method was shown in the MATCh analysis. Implementing GPS-CDF matching and stratification produced an adequately balanced sample (all average SMDs < 0.2) by grouping subjects with similar covariate profiles, but who were in differing SIM quartiles. The odds ratios estimated by GPS-CDF matching and stratification indicated that the odds of experimenting with cigarettes significantly increased as exposure level of smoking imagery in movies increased. These results provide more evidence that increased exposure to smoking imagery in movies significantly influences whether or not Mexican-American adolescents decide to experiment with cigarettes. In light of these findings, targeted public health campaigns can be implemented in order to diminish the likelihood of adolescent cigarette use.

Limitations of the study exist. There may be settings where the power function is not the best for a given data set; for example, for a GPS vector near (0,0,0,1) or (1,0,0,0), the distance between the power function and vector could be large. While we expect this setting to be rare, given the necessary propensity scoring assumption of positivity requires all subjects to have a non-zero probability of receiving each potential treatment, other one parameter alternatives could be explored should this issue occur; meanwhile, the procedure outlined in the paper would remain the same, in principle. Further, guidelines on how to assess quality of causal effects specifically for the ordinal setting (e.g., necessary sample sizes, degree of balance achieved, etc.), will be important to determine in future research. Finally, regarding estimation of the standard errors of the ATE in the ordinal treatments setting, Lopez and Gutman (2017) point out that for multinomial treatments, “Like other approaches that match with multiple treatments, estimating the standard error of these point estimates is still an open research question.”¹³ Methods referred to in the multiple treatments literature include weighting and bootstrapping.^5,74 We investigated such a bootstrapping approach for a related application and the resulting standard errors were nearly identical to those from the conditional logistic regression without using bootstrapping. However, more investigation may be warranted in future research.

7 |. CONCLUSION

This paper shows the GPS-CDF method is a flexible, straightforward, and intuitive method of removing covariate imbalance in observational studies with ordinal treatments. The approach does not rely on the proportional odds model; in fact it can be used with any parametric or non parametric propensity model. The GPS-CDF method provides many opportunities for future research including extensions to continuous and multinomial treatments, applications to public health, genetics, and electronic health records datasets. Hopefully, continued development in the field of multi-valued treatments propensity scoring will encourage researchers to utilize these methods in practice.

DATA AVAILABILITY

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.