Abstract
The aims of this study were to: (a) describe and compare the volume and intensity from the workload of professional soccer players between training and MD, and (b) analyse the effect that the length of the microcycle had on the workload. A cohort study was designed for a full season in La Liga 123. Wearable tracking systems collected the distance covered in meters (m), total number of high-intensity accelerations (ACCHIGH) and decelerations (DECHIGH), total number of high-speed running actions (HSRA), high-speed running distance (HSRD), high metabolic load distance (HMLD), and player load (PL) from training days (MD+1, MD-4, MD-3, MD-2, and MD-1) and MD. Significant differences were found between training and MD workload, MD workload being the most demanding for all intensity and volume variables (F = 36.35–753.94; p < 0.01; wp2 = 0.21–0.85). The greatest training intensity and volume were found on MD-4 and MD-3 (p < 0.05). In addition, a novel finding was that the length of the microcycle had a significant effect on the workload both in volume and intensity (F = 4.84–14.19; p < 0.01; wp2 = 0.03–0.09), except for relative ACCHIGH, DECHIGH, and HMLD. Although MD-4 and MD-3 were the most suitable days for loading the players, the results showed that MD elicited a unique stimulus in terms of volume and intensity. Consequently, coaches need to include specific training drills to adapt the players for the competitive demands. Finally, special focus should be placed on MD from short and regular microcycles (5-day, 6-day, or 7-day microcycles) since declines in physical performance were observed in comparison with long microcycles (8-day or 9-day microcycles).
Keywords: Physical demands, Match analysis, Training, Tracking, Football
INTRODUCTION
Electronic performance tracking systems provide valuable information for strength and conditioning coaches, sports scientists, and researchers since a better understanding of the volume and intensity of each training session and match is possible [1, 2]. Specifically, these data allow the analysis of the workload, and therefore, programming strategies for the periodized training plan may be adopted [3]. In addition, these are objective data (e.g., distance covered, high-speed running distance, total number of accelerations) that provide further information to determine the individual profiles of each player [1, 4]. In this regard, the aim of strength and conditioning coaches from professional soccer teams is to find the right balance between loading the players for positive adaptations and reducing the injury risk [5, 6].
Although previous investigations suggested that the training sessions should promote effective transfer to the competitive environment (e.g., physical, technical, and tactical components) [7, 8], different studies showed that the workload is greater on the match days compared to the training days [8–10]. For instance, professional soccer players from an English Premier League team may cover ~4349 m in training sessions four days before the match, ~5212 m three days before the match, ~3117 m two days before the match, ~2910 m the day before the match, and ~10317 m in the match, considering a competitive week in which all starting players on match day (MD) completed all training sessions [9]. However, these data are just related to the volume of the sessions, and little is known about the intensity, which may be measured as the performance relative to time (e.g., distance covered per minute) [4, 11]. In this regard, a recent study analysed the intensity of match play through the worst-case scenarios and significant differences were found between training and match days [12]. Specifically, the results showed that the intensity of players during worst-case scenarios from training days did not meet the intensity of the match [12]. Nevertheless, the performance in the worst-case scenario is not representative of performance from a whole training session or match within a microcycle given that these scenarios are just related to specific periods of play (e.g., 1 minute or 5 minutes) [12].
In addition, the microcycles are weekly training periods, which count from the day after the match to the following match, whose length may vary depending on the competitive calendar [4, 13]. Specifically, previous studies showed that the length of the microcycle may have an impact on the workload from soccer players [4, 9, 12, 14]. For instance, the results from recent studies showed that the training load increased with longer microcycles [13, 14]. However, limited research is available to date regarding the effect of the length of the microcycle on the workload from professional soccer players in terms of volume and intensity.
In summary, few studies have analysed load dynamics within the competitive period considering both training and match days in professional soccer [15]. Therefore, since this information has vast implications for workload prescription and recovery strategies [13], the aims of this study were to: 1) describe the volume and intensity from the workload of professional soccer players and compare the workload between training and match days (MD); 2) analyse the effect that the length of the microcycle had on the workload from training and MD.
MATERIALS AND METHODS
Experimental approach to the problem
A cohort study was conducted in a professional soccer team during the 2018–2019 season in La Liga 123. Informed consent was obtained for the data collection and the study was approved by the ethics committee. The data collected by electronic performance tracking systems from match and training sessions were categorized as Match Day (MD), MD-1 (1 day prior to the match), MD-2 (2 days prior to the match), MD-3 (3 days prior to the match), MD-4 (4 days prior to the match), and MD+1 (1 day after the match). The microcycles with -5MD or MD+2 were not included since these sessions were only available for eight-day microcycles. Considering that the average length of the microcycles was 7 days, each microcycle was categorized as shorter than the average (five-day or six-day microcycles), regular microcycles (seven-day microcycles), and longer than the average (eight-day or nine-day microcycles) (Table 1).
TABLE 1.
Characteristics of short, regular, and long microcycles.
| Length | Day | Description |
|---|---|---|
| Short microcycles | MD+1 | Regeneration exercises and low-impact activities for the group of players who played more than 45 minutes in the match while the rest of the players had to compensate with rondos, possession drills, high-intensity circuits, and small-sided games. |
| MD-4 | Similar to MD+1 with an increase in intensity through positional games. | |
| MD-3 | MD-3 (for five-day microcycles) were similar to MD+1 with an increase in intensity through positional games while MD-3 (for six-day microcycles) were characterized by transition drills, positional games, and 11 vs. 11 matches. | |
| MD-2 | Light strength training, pressing tasks, and small-sided games. | |
| MD-1 | Review of tactical elements regarding the match, play small-sided games, and perform activation drills. | |
| MD | Match day. | |
|
| ||
| Regular microcycles | MD+1 | Regeneration exercises and low-impact activities for the group of players who played more than 45 minutes in the match while the rest of the players had to compensate with rondos, possession drills, high-intensity circuits, and small-sided games. |
| MD+2 | Resting days. | |
| MD-4 | Strength training, pressing tasks, and small-sided games. | |
| MD-3 | Strength training, pressing tasks, small-sided, and medium-sided games. | |
| MD-2 | Preventive strength training, rondos, control, and passing tasks, tactical drills. | |
| MD-1 | MD-1 included activation drills, small-sided games, and review of the tactical keys regarding the match. | |
| MD | Match day. | |
|
| ||
| Long microcycles | MD+1 | Regeneration exercises and low-impact activities for the group of players who played more than 45 minutes in the match while the rest of the players had to compensate with rondos, possession drills, high-intensity circuits, and small-sided games. |
| MD+2 | Resting days | |
| MD-5 | Activation drills, rondos, and 11 vs 11 games (half pitch). | |
| MD-4 | Strength training, pressing tasks, and small-sided games. | |
| MD-3 | Moderate-intensity positional games, transition drills, and 11 vs 11 matches. | |
| MD-2 | Preventive strength training, rondos, tactical drills, control and passing tasks. | |
| MD-1 | Activation drills, 6x6+6 small-sided games, and review of tactical keys regarding the match. | |
| MD | Match day. | |
MD: match day; MD-1: 1 day before the match; MD-2: 2 days before the match; MD-3: 3 days before the match; MD-4: 4 days before the match; MD-5: 5 days before the match; MD+1: 1 day after the match; MD+2: 2 days after the match.
Subjects
Data were collected from 30 professional soccer players (age: 27.2 ± 3.8 years; height: 181.8 ± 6.2 cm; weight: 75.3 ± 6.8 kg). Players from different playing positions were included in the study (forwards, n = 6; midfielders, n = 7; wide midfielders, n = 6; fullbacks, n = 6; central defenders, n = 5). Also, full-match participation was considered as an inclusion criteria for MD data collection. However, goalkeepers were not included in the study because this playing position shows a different nature of the workload profile [8, 16]. The study was approved by the ethics committee of the university (Reg. Code 2061/2018) and the club allowed the research team to access players’ data and informed consent was provided.
Procedures
WIMU Pro tracking systems (RealTrack Systems, Almeria, Spain) were used for the data collection. These tracking systems are considered as valid and reliable instruments for the analysis of workload parameters in soccer players [17]. Also, these instruments have the FIFA Quality Program approval, which eases the optimal use of this technology by coaches, researchers, etc. [18, 19]. Every tracking system was calibrated on WIMUNET (RealTrack Systems, Almeria, Spain) before the data collection according to the manufacturer’s instructions [20, 21]. Then, the devices were placed in the back pocket of a vest (Rasán, Valencia, Spain). Once the session had finished, the data were transferred to SPro (RealTrack Systems, Almeria, Spain) software in order to obtain the workload parameters.
Distance covered in meters (m), total number of high-intensity accelerations (ACCHIGH, above 3 m/s2), total number of high-intensity decelerations (DECHIGH, below -3 m/s2), total number of high-speed running actions (HSRA, above 21 km/h), high-speed running distance (HSRD, above 21 km/h), player load (PL), and high metabolic load distance (distance covered when the metabolic power was above 25.5 W/kg) were downloaded from SPro (RealTrack Systems, Almeria, Spain). These variables, which were considered as representative of the workload of professional soccer players by previous studies (e.g., using principal components analysis), represented the volume (e.g., absolute distance covered in meters) and intensity (e.g., relative distance covered in meters, which is divided by the duration of the training session or match in minutes) [4, 12, 22, 23].
Statistical analysis
Firstly, a descriptive analysis was performed to show the intensity and volume workload demands as mean (M) and standard deviations (± SD). The Kolmogorov-Smirnov test was used to confirm the normality of the data set. Data were analysed using a mixed analysis of variance to compare the intensity and volume workload demands concerning the length of the microcycle, training, and match days. The pairwise comparisons were performed using the Bonferroni method. The magnitudes of the differences for all variables were analysed using the partial omega squared (ωp 2). The ωp 2 values were qualitatively interpreted using the following thresholds: < 0.01 small; < 0.06 medium and < 0.14 large. Alpha was set at p < 0.05. The data analysis was performed using SPSS (IBM, SPSS Statistics, V 22.0 Chicago, IL, USA) and graphs were designed using GraphPad Prism (GraphPad Software, release 8, La Jolla, CA, USA).
RESULTS
Training and match days’ workload
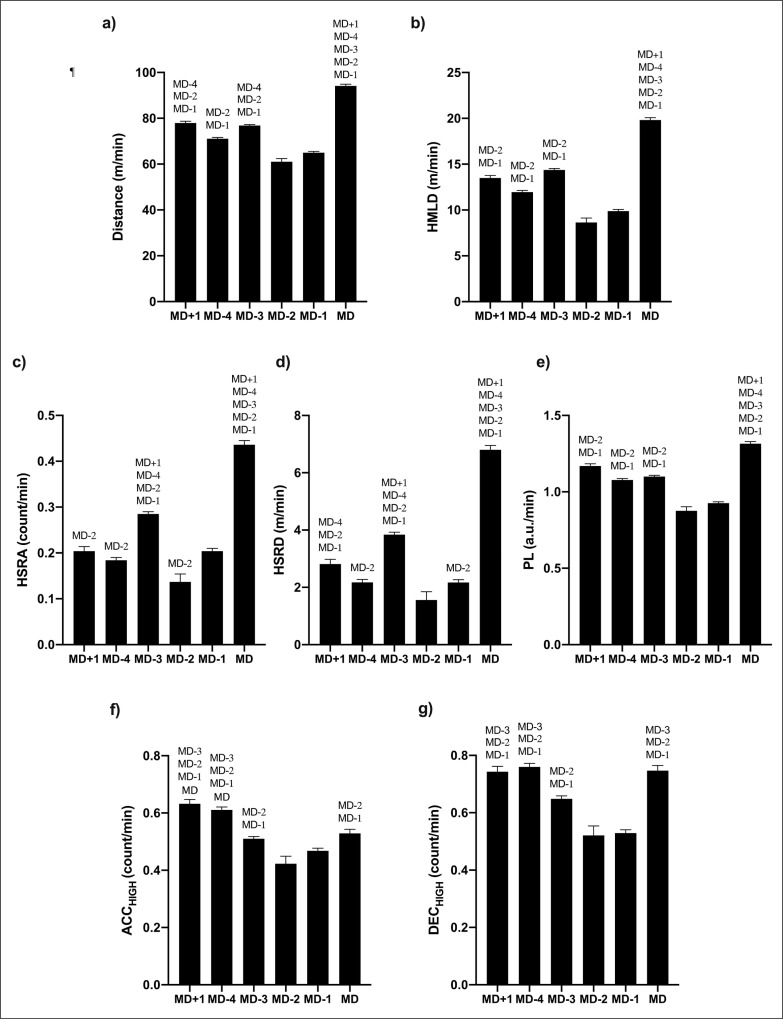
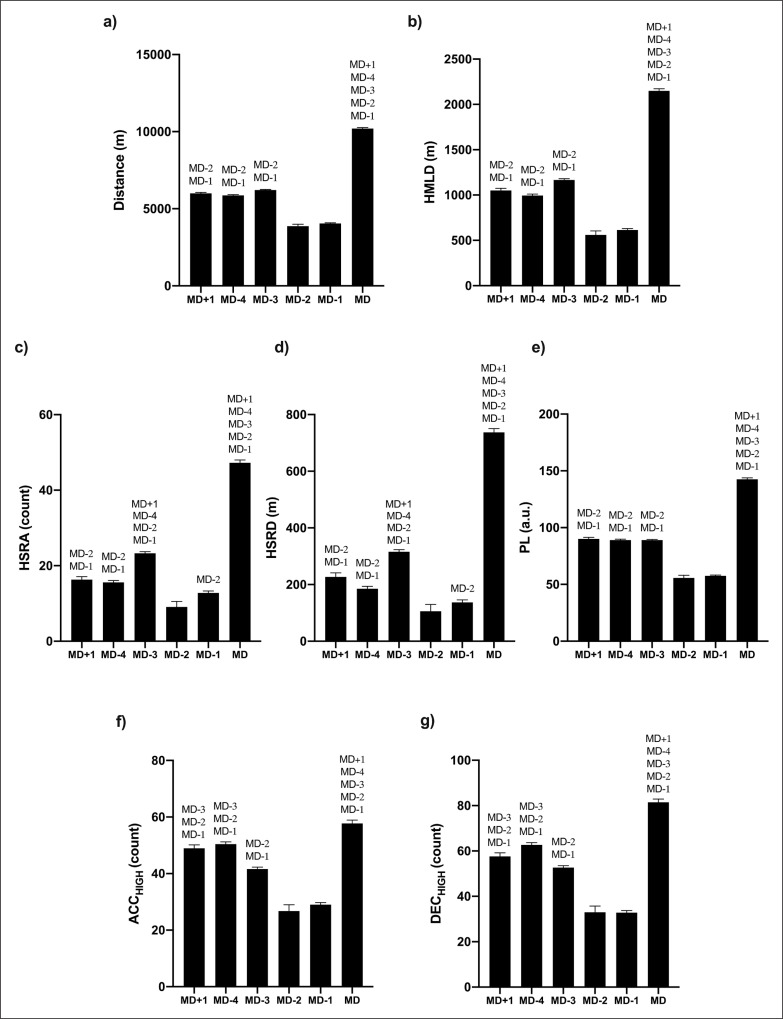
Figures 1 and 2 show the workload (volume and intensity) from training sessions and MD. Regarding training sessions, the greatest intensity and volume were found on MD-4, MD-3, and MD+1 in all variables. However, the lowest demands were found on MD-1 and MD-2. In addition, statistically significant differences (p < 0.05) between the workload from training and MD were found at all intensity and volume variables, the workload from MD being the most demanding. Specifically, the magnitude of the differences was large for all intensity and volume workload variables (F = 36.35–753.94; p < 0.01; wp2= 0.21–0.85).
FIG. 1.
Pairwise comparison between the workload from training and match days (MD) in volume of (a) distance, (b) HMLD, (c) HSRA, (d) HSRD, (e) PL, (f) ACCHIGH, and (g) DECHIGH. MD+1Significant difference compared to MD+1 (p < 0.05); MD-4significant difference compared to MD-4 (p < 0.05); MD-3significant difference compared to MD-3 (p < 0.05); MD-2significant difference compared to MD-2 (p < 0.05); MD-1significant difference compared to MD-1 (p < 0.05); MDsignificant difference compared to MD (p < 0.05).
FIG. 2.
Pairwise comparison between the workload from training and match days (MD) in intensity workload (a) distance, (b) HMLD, (c) HSRA, (d) HSRD, (e) PL, (f) ACCHIGH, and (g) DECHIGH. MD+1significant difference compared to MD+1 (p < 0.05); MD-4significant difference compared to MD-4 (p < 0.05); MD-3significant difference compared to MD-3 (p < 0.05); MD-2significant difference compared to MD-2 (p < 0.05); MD-1significant difference compared to MD-1 (p < 0.05); MDsignificant difference compared to MD (p < 0.05).
Effect of the length of the microcycle on the workload from training and match days
The length of the microcycle had a significant effect on the workload (volume and intensity variables) with a low to moderate effect size (F = 4.84–14.19; p < 0.01; w p 2 = 0.03–0.09), except in relative ACCHIGH, DECHIGH, and HMLD (F < 2.51; p > 0.08). Regarding volume-related variables, significant differences were found (Table 2) in training load when considering the length of the microcycle: (a) distance on all training days; (b) ACCHIGH on MD+1 and MD-3; (c) DECHIGH on all training days except MD-4 and MD-2; (d) HSRA on all training days except MD+1; (e) HSRD, PL and HMLD on all training days except MD+1. In addition, the workload from MD in long microcycles was always greater than regular and short microcycles even though HSRA and total distance covered were the only variables without significant differences (F = 2.29–2.95; p > 0.05).
TABLE 2.
Volume workload from training and match days and comparative analysis based on the length of the microcycle
| Short microcycles (M ± SD) | Regular microcycles (M ± SD) | Long microcycles (M ± SD) | F (p-value) | wp2 (magnitude) | Post-hoc | ||
|---|---|---|---|---|---|---|---|
| Distance (m) | MD+1 | 6153.75 ± 968.74 | 5665.65 ± 1081.67 | 5442.36 ± 1024.35 | 8.51 (< 0.01) | 0.05 (low) | a b |
| MD-4 | 4941.30 ± 1463.36 | 6065.38 ± 787.41 | 6228.05 ± 865.20 | 59.23 (< 0.01) | 0.32 (large) | a b | |
| MD-3 | 6089.56 ± 1151.19 | 6515.95 ± 926.92 | 6523.01 ± 1074.75 | 11.82 (< 0.01) | 0.08 (moderate) | a b | |
| MD-2 | 4780.22 ± 903.98 | 3190.32 ± 486.56 | 4848.41 ± 386.57 | 17.83 (< 0.01) | 0.12 (moderate) | b c | |
| MD-1 | 4091.04 ± 553.57 | 3945.54 ± 463.58 | 4376.14 ± 591.36 | 24.96 (< 0.01) | 0.16 (large) | a b c | |
| MD | 10183.93 ± 879.41 | 10183.01 ± 801.97 | 10467.40 ± 781.98 | 2.29 (0.06) | |||
|
| |||||||
| ACCHIGH (count) | MD+1 | 38.24 ± 9.56 | 56.83 ± 18.58 | 51.67 ± 17.02 | 11.20 (< 0.01) | 0.08 (moderate) | a b |
| MD-4 | 49.32 ± 15.56 | 51.12 ± 15.27 | 50.89 ± 14.36 | 0.36 (0.69) | |||
| MD-3 | 44.18 ± 15.56 | 39.46 ± 12.01 | 41.24 ± 14.99 | 4.24 (0.02) | 0.02 (low) | ||
| MD-2 | 30.63 ± 14.86 | 27.91 ± 8.88 | 29.23 ± 10.10 | 2.87 (0.09) | |||
| MD-1 | 29.09 ± 10.46 | 27.52 ± 9.39 | 30.44 ± 7.33 | 2.54 (0.08) | |||
| MD | 51.18 ± 24.62 | 60.40 ± 11.65 | 61.65 ± 12.63 | 5.44 (< 0.01) | 0.03 (low) | a b | |
|
| |||||||
| DECHIGH (count) (count) | MD+1 | 44.16 ± 9.11 | 68.54 ± 22.41 | 60.15 ± 19.31 | 14.31 (< 0.01) | 0.10 (moderate) | a b |
| MD-4 | 64.23 ± 23.16 | 60.78 ± 17.77 | 63.05 ± 17.41 | 1.06 (0.35) | |||
| MD-3 | 56.23 ± 21.05 | 51.41 ± 15.25 | 50.41 ± 15.37 | 4.30 (0.01) | 0.02 (low) | a | |
| MD-2 | 37.69 ± 18.51 | 33.27 ± 12.48 | 34.31 ± 13.33 | 2.73 (0.10) | |||
| MD-1 | 33.49 ± 14.84 | 29.76 ± 10.06 | 35.15 ± 10.19 | 5.82 (< 0.01) | 0.03 (low) | b | |
| MD | 72.23 ± 35.08 | 82.82 ± 14.78 | 89.37 ± 16.73 | 6.27 (0.02) | 0.04 (low) | a b | |
|
| |||||||
| HSRA (count) | MD+1 | 15.51 ± 10.28 | 17.48 ± 10.78 | 15.08 ± 9.96 | 1.29 (0.28) | ||
| MD-4 | 6.71 ± 5.96 | 21.37 ± 10.74 | 19.37 ± 10.36 | 71.50 (< 0.01) | 0.37 (large) | a b | |
| MD-3 | 18.74 ± 9.73 | 24.54 ± 9.17 | 23.95 ± 9.50 | 24.18 (< 0.01) | 0.16 (large) | b | |
| MD-2 | 12.96 ± 7.12 | 5.55 ± 3.24 | 10.76 ± 5.61 | 6.59 (< 0.01) | 0.05 (low) | a | |
| MD-1 | 12.42 ± 7.12 | 11.36 ± 6.19 | 14.26 ± 5.88 | 7.46 (< 0.01) | 0.05 (low) | b c | |
| MD | 45.21 ± 14.09 | 44.40 ± 13.18 | 49.29 ± 12.74 | 2.95 (0.07) | |||
|
| |||||||
| HSRD (m) | MD+1 | 224.73 ± 195.93 | 245.77 ± 214.95 | 197.82 ± 162.84 | 1.17 (0.31) | ||
| MD-4 | 63.72 ± 63.15 | 258.59 ± 167.44 | 238.19 ± 142.93 | 58.62 (< 0.01) | 0.33 (large) | a b | |
| MD-3 | 234.19 ± 157.13 | 338.50 ± 168.57 | 334.19 ± 174.65 | 25.84 (< 0.01) | 0.17 (large) | a b | |
| MD-2 | 156.91 ± 98.85 | 51.30 ± 36.89 | 127.24 ± 66.67 | 6.96 (< 0.01) | 0.05 (low) | a | |
| MD-1 | 131.04 ± 83.55 | 127.43 ± 94.74 | 162.69 ± 80.63 | 6.81 (< 0.01) | 0.05 (low) | b c | |
| MD | 696.42 ± 256.79 | 684.60 ± 251.03 | 789.16 ± 235.23 | 4.19 (0.01) | 0.02 (low) | b c | |
|
| |||||||
| PL (a.u.) | MD+1 | 88.42 ± 21.16 | 88.90 ± 18.88 | 86.77 ± 17.76 | 0.24 (0.78) | ||
| MD-4 | 75.90 ± 24.01 | 90.62 ± 14.33 | 93.14 ± 15.58 | 34.07 (< 0.01) | 0.22 (large) | a b | |
| MD-3 | 89.13 ± 19.77 | 93.10 ± 16.10 | 90.94 ± 15.91 | 3.22 (0.04) | 0.02 (low) | a | |
| MD-2 | 68.90 ± 15.23 | 45.16 ± 9.40 | 70.61 ± 8.25 | 13.97 (< 0.01) | 0.10 (moderate) | a c | |
| MD-1 | 58.06 ± 9.24 | 56.29 ± 8.24 | 62.11 ± 8.71 | 16.74 (< 0.01) | 0.12 (moderate) | b c | |
| MD | 140.73 ± 20.52 | 143.01 ± 18.42 | 150.92 ± 19.57 | 5.91 (< 0.01) | 0.04 (low) | b c | |
|
| |||||||
| HMLD (m) | MD+1 | 1039.25 ± 306.21 | 1032.75 ± 302.92 | 942.36 ± 315.45 | 2.14 (0.12) | ||
| MD-4 | 675.20 ± 383.76 | 1106.52 ± 260.09 | 1083.25 ± 299.71 | 75.03 (< 0.01) | 0.39 (large) | a b | |
| MD-3 | 1059.47 ± 336.32 | 1215.41 ± 288.72 | 1186.12 ± 287.40 | 16.24 (< 0.01) | 0.11 (moderate) | a b | |
| MD-2 | 760.38 ± 278.30 | 403.85 ± 121.38 | 713.42 ± 140.77 | 9.45 (< 0.01) | 0.07 (moderate) | a c | |
| MD-1 | 611.64 ± 161.30 | 580.97 ± 153.39 | 661.50 ± 137.85 | 10.39 (< 0.01) | 0.08 (moderate) | b c | |
| MD | 2100.77 ± 382.51 | 2103.99 ± 273.22 | 2242.09 ± 363.24 | 3.64 (0.03) | 0.02 (low) | b c | |
M: mean; SD: standard deviation; F: F-value of ANOVA; p: significance; wp2: partial omega squared.
Differences between short microcycles and regular length microcycles (p < 0.05);
differences between short microcycles and long microcycles (p < 0.05);
ifferences between long microcycles and regular length microcycles (p < 0.05).
Regarding the intensity variables (Table 3), differences in training load were found in: (a) distance on all training days except MD-2; (b) ACCHIGH on MD+1 and MD-3; (c) DECHIGH on all training days except MD-2; (d) HSRA and HMLD on MD-4, MD-3 and MD-2; (e) HSRD on all training days except MD+1 and MD-1; and (f) PL on MD-1. Furthermore, the intensity from MD in long microcycles was always greater than regular and short microcycles even though the total distance covered, HSRA, and HMLD were the only variables without significant differences (F = 1.65–2.66; p > 0.05).
TABLE 3.
Intensity workload from training and match days and comparative analysis based on the length of the microcycle
| Short microcycles (M ± SD) | Regular microcycles (M ± SD) | Long microcycles (M ± SD) | F (p-value) | wp2 (magnitude) | Post-hoc | ||
|---|---|---|---|---|---|---|---|
| Distance (m/min) | MD+1 | 78.68 ± 14.84 | 71.54 ± 7.01 | 70.77 ± 9.16 | 12.53 (< 0.01) | 0.08 (moderate) | a b |
| MD-4 | 65.38 ± 12.93 | 71.52 ± 7.69 | 72.01 ± 9.63 | 19.27 (< 0.01) | 0.12 (moderate) | a b | |
| MD-3 | 74.65 ± 10.32 | 78.10 ± 11.60 | 76.85 ± 13.24 | 4.96 (< 0.01) | 0.03 (low) | a | |
| MD-2 | 67.21 ± 12.61 | 60.12 ± 9.17 | 62.16 ± 4.96 | 2.69 (0.07) | |||
| MD-1 | 65.49 ± 8.50 | 66.20 ± 8.15 | 63.32 ± 7.56 | 4.75 (< 0.01) | 0.03 (low) | c | |
| MD | 94.04 ± 7.97 | 93.12 ± 7.48 | 95.22 ± 7.12 | 1.65 (0.19) | |||
|
| |||||||
| ACCHIGH (count/min) | MD+1 | 0.53 ± 0.14 | 0.68 ± 0.23 | 0.68 ± 0.20 | 5.26 (< 0.01) | 0.03 (low) | a b |
| MD-4 | 0.62 ± 0.20 | 0.61 ± 0.18 | 0.60 ± 0.15 | 0.47 (0.62) | |||
| MD-3 | 0.54 ± 0.17 | 0.48 ± 0.15 | 0.51 ± 0.16 | 5.38 (< 0.01) | 0.03 (low) | a | |
| MD-2 | 0.41 ± 0.19 | 0.43 ± 0.17 | 0.44 ± 0.15 | 0.09 (0.76) | |||
| MD-1 | 0.48 ± 0.18 | 0.46 ± 0.15 | 0.46 ± 0.12 | 1.03 (0.36) | |||
| MD | 0.47 ± 0.23 | 0.55 ± 0.11 | 0.56 ± 0.11 | 4.74 (0.01) | 0.02 (low) | a b | |
|
| |||||||
| DECHIGH (count/min) | MD+1 | 0.61 ± 0.12 | 0.82 ± 0.27 | 0.79 ± 0.22 | 7.44 (< 0.01) | 0.05 (low) | a b |
| MD-4 | 0.81 ± 0.28 | 0.73 ± 0.21 | 0.74 ± 0.19 | 3.59 (0.03) | 0.02 (low) | a | |
| MD-3 | 0.70 ± 0.25 | 0.62 ± 0.18 | 0.63 ± 0.18 | 5.36 (< 0.01) | 0.03 (low) | a b | |
| MD-2 | 0.51 ± 0.23 | 0.53 ± 0.24 | 0.56 ± 0.27 | 0.10 (0.75) | |||
| MD-1 | 0.56 ± 0.26 | 0.50 ± 0.16 | 0.53 ± 0.16 | 3.53 (0.03) | 0.01 (low) | a | |
| MD | 0.67 ± 0.32 | 0.76 ± 0.14 | 0.81 ± 0.15 | 5.32 (< 0.01) | 0.03 (low) | b | |
|
| |||||||
| HSRA (count/min) | MD+1 | 0.19 ± 0.13 | 0.22 ± 0.13 | 0.19 ± 0.12 | 1.42 (0.24) | ||
| MD-4 | 0.09 ± 0.07 | 0.25 ± 0.12 | 0.22 ± 0.11 | 69.81 (< 0.01) | 0.35 (large) | a b c | |
| MD-3 | 0.23 ± 0.11 | 0.29 ± 0.11 | 0.28 ± 0.11 | 23.26 (< 0.01) | 0.15 (large) | a b | |
| MD-2 | 0.18 ± 0.10 | 0.10 ± 0.06 | 0.14 ± 0.07 | 4.65 (0.01) | 0.02 (low) | a | |
| MD-1 | 0.20 ± 0.11 | 0.19 ± 0.10 | 0.21 ± 0.10 | 1.27 (0.28) | |||
| MD | 0.42 ± 0.13 | 0.41 ± 0.12 | 0.45 ± 0.12 | 2.55 (0.08) | |||
|
| |||||||
| HSRD (m/min) | MD+1 | 2.80 ± 2.42 | 3.09 ± 2.75 | 2.46 ± 1.99 | 1.28 (0.27) | ||
| MD-4 | 0.84 ± 1.80 | 3.03 ± 1.93 | 2.75 ± 1.62 | 55.67 (< 0.01) | 0.30 (large) | a b c | |
| MD-3 | 2.81 ± 1.71 | 4.05 ± 1.95 | 3.91 ± 2.06 | 26.52 (< 0.01) | 0.16 (high) | a b | |
| MD-2 | 2.19 ± 1.40 | 0.97 ± 0.70 | 1.63 ± 0.85 | 5.43 (< 0.01) | 0.03 (low) | a | |
| MD-1 | 2.05 ± 1.26 | 2.13 ± 1.56 | 2.35 ± 1.14 | 1.83 (0.16) | |||
| MD | 6.44 ± 2.38 | 6.26 ± 2.31 | 7.18 ± 2.14 | 3.59 (0.03) | 0.02 (low) | c | |
|
| |||||||
| PL (a.u./min) | MD+1 | 1.13 ± 0.28 | 1.12 ± 0.14 | 1.13 ± 0.18 | 0.56 (0.95) | ||
| MD-4 | 1.00 ± 0.22 | 1.07 ± 0.14 | 1.09 ± 0.17 | 2.51 (0.08) | a b | ||
| MD-3 | 1.09 ± 0.19 | 1.12 ± 0.20 | 1.08 ± 0.22 | 2.22 (0.10) | |||
| MD-2 | 0.97 ± 0.21 | 0.85 ± 0.18 | 0.91 ± 0.11 | 2.40 (0.09) | |||
| MD-1 | 0.93 ± 0.16 | 0.95 ± 0.15 | 0.90 ± 0.14 | 3.15 (0.04) | 0.02 (moderate) | c | |
| MD | 1.30 ± 0.19 | 1.31 ± 0.17 | 1.37 ± 0.18 | 3.96 (0.02) | 0.02 (low) | b c | |
|
| |||||||
| HMLD (m/min) | MD+1 | 13.25 ± 4.13 | 13.02 ± 3.05 | 12.10 ± 3.19 | 2.14 (0.12) | ||
| MD-4 | 8.69 ± 4.33 | 13.06 ± 2.99 | 12.58 ± 3.25 | 59.36 (< 0.01) | 0.31 (large) | a b | |
| MD-3 | 12.91 ± 3.47 | 14.58 ± 3.50 | 14.01 ± 3.70 | 12.77 (< 0.01) | 0.08 (moderate) | a b | |
| MD-2 | 10.65 ± 3.75 | 7.61 ± 2.29 | 9.15 ± 1.80 | 4.86 (< 0.01) | 0.03 (low) | a | |
| MD-1 | 9.77 ± 2.52 | 9.80 ± 2.77 | 9.67 ± 2.39 | 0.11 (0.90) | |||
| MD | 19.39 ± 3.48 | 19.24 ± 3.45 | 20.40 ± 3.32 | 2.66 (0.07) | |||
M: mean; SD: standard deviation; F: F-value of ANOVA; p: significance; wp2: partial omega squared.
Differences between short microcycles and regular length microcycles (p < 0.05);
differences between short microcycles and long microcycles (p < 0.05);
differences between long microcycles and regular length microcycles (p < 0.05).
DISCUSSION
This study aimed to describe the volume and intensity from the workload of professional soccer players, compare the workload between training and MD, and analyse the effect that the length of the microcycle had on the workload. The greatest intensity and volume from training sessions were found on MD-4, MD-3, and MD+1 in all variables. However, there were significant differences between the workload from training and MD at all intensity and volume variables, the workload from MD being the most demanding. In addition, a novel finding of this study was that the length of the microcycle had a significant effect on the workload not only in the volume but also in the intensity, except for relative ACCHIGH, DECHIGH, and HMLD.
This study showed that the training load decreased in the sessions before a competition, which is consistent with previous studies [5, 24, 25]. Specifically, these studies also showed that the workload was greater on MD-4 and MD-3 than MD-2 and MD-1 [5, 24, 25]. This confirms the tapering strategy which is adopted by strength and conditioning coaches as an attempt to decrease the stress of training and maximize performance on the competitive day [26]. In this regard, various investigations also suggested that MD-4 and MD-3 were the most suitable days for loading the players through repeated high-intensity actions, drills undertaken on larger pitch sizes or reducing the number of players in the playing area [5, 10, 24]. In addition, the results from this study indicated that another demanding training day was MD+1. However, caution should be taken with this interpretation of the results. The team was divided into two groups of players in order to compensate those players who could not participate in the match or played less than 45 minutes, and therefore these players had to complete additional tasks on MD+1 in order to replicate competition loads [5]. Moreover, various studies showed that the workload was greater on the match days in comparison with the training days [8–10]. However, this study revealed that the workload from MD was the most demanding not only in volume but also in intensity. This is one of the main findings of this study since to date, data have usually been reported in relation to the volume of the sessions. For instance, these professional soccer players covered ~5744 m at an intensity of ~70 m/min on MD-4 while they covered ~10278 m at an intensity of ~94 m/min on MD. This implies that the players may not replicate the volume of the match in training sessions, but strength and conditioning coaches may design training drills that prepare the players for the intensity of match play. Furthermore, recent investigations suggested that the players should be trained for the most intense periods of the match, which are also known as worst case scenarios or most demanding passages of play [23, 27, 28], since the players may get to cover ~191 m/min in distance covered, ~38 m/min in HSRD, ~66 m/min in HMLD, ~3 ACCHIGH/min, and ~4 DECHIGH/min during these passages of play [23].
Regarding the effect of the length of the microcycle on the workload, this study found a significant effect not only on the volume but also on the intensity, except for relative ACCHIGH, DECHIGH, and HMLD. Previous investigations also found that the length of the microcycle had a significant impact on the workload from soccer players [4, 9, 13, 14]. For example, a recent study showed that the training load increased with longer microcycles [14]. This is controversial since we did not systematically observe this tendency in our training load data, which might be explained by differences in training methodologies adopted by the coaches [29]. However, our study found that the workload from MD in long microcycles was greater than regular and short microcycles. Different investigations on professional soccer players also concluded that the length of the microcycle had an impact on some variables related to match running performance (e.g., distance covered) [4, 30], which may be a consequence of a longer recovery period or better preparation for the match. Nevertheless, there are other investigations that showed how distance covered, for instance, remained unaffected over short microcycles [31, 32]. In addition, a recent study, which investigated the intensity required during the worst-case scenarios, found that the length of the microcycle had a significant effect on the intensity from training days, but not from MD [12]. However, although there is a lack of research on the effect of the length of the microcycle on the workload from training and MD, similar periodization strategies (e.g., unloading the players on MD-2 and MD-1 as MD approaches) may be observed regardless of the length of the microcycle [24, 33, 34].
This study has some general limitations that may also guide future investigations. For example, only one professional soccer team was analysed, and it would be of interest to carry out a multi-club study. Moreover, future studies may include additional external load variables (e.g., explosive distance, and acceleration or deceleration distance) or internal load variables (e.g., mean heart rate), which were not considered in this study. Also, this study used absolute thresholds for the collected variables (e.g., 19.8 km/h for HSRD or 3 m/s2 for ACCHIGH). However, recent studies suggested the addition of individualized thresholds (e.g., considering the player’s maximal sprinting speed or acceleration) [35–37]. In addition, this study did not consider the influence that contextual variables such as MD participation had on the training load from the upcoming week (e.g., performance on MD+1).
Practical applications
This study showed significant differences between the workload from training and MD at all intensity and volume variables, the workload from MD being the most demanding. Also, the greatest intensity and volume from training sessions were found on MD-4, MD-3, and MD+1 in all variables. Specifically, data from Tables 2 and 3 may be used as a useful reference for sport scientists and strength and conditioning coaches, who are responsible for the workload periodization and make daily decisions to find the right balance between loading the players for positive adaptations and reducing the injury risk. Understanding this workload from both training and MD, coaches may include specific training drills to replicate the competition demands by considering not only the average demands but also the most demanding passages of play. Although MD-4 and MD-3 were the most suitable days for loading the players through repeated high-intensity actions, drills undertaken on larger pitch sizes or reducing the number of players in the playing area, the results showed that MD seems to elicit a unique stimulus in terms of volume and intensity. Therefore, caution should be taken on MD+1 with the recovery strategies for those who played the match while the players who could not participate in the match need to be overloaded on MD+1 considering the workload from MD. In addition, a novel finding of this study was that the length of the microcycle had a significant effect on the workload not only in the volume but also in the intensity, except for relative ACCHIGH, DECHIGH, and HMLD. Thus, special focus should be placed on MD from short and regular microcycles since declines in physical performance were observed in comparison with long microcycles.
Acknowledgments
The participants would like to thank the club for allowing the data collection from these professional soccer players during the competitive season.
Funding
The authors Carlos D. Gómez Carmona and José M. Oliva Lozano were supported by a grant from the Spanish Ministry of Innovation, Science and Universities (FPU17/00407 and FPU18/04434).
Conflict of Interest Disclosure
None of the authors has a conflict of interest to declare, and all authors were involved in the study design, data collection and interpretation, and contributed to the writing of the manuscript.
REFERENCES
- 1.Oliva-Lozano JM, Muyor JM, Fortes V, McLaren S. Decomposing the variability of match physical performance in professional soccer: implications for monitoring individuals. Eur J Sport Sci. 2020 doi: 10.1080/17461391.2020.1842513. Epub Ahead of print: 1–11. [DOI] [PubMed] [Google Scholar]
- 2.Delaney JA, Thornton HR, Rowell AE, Dascombe BJ, Aughey RJ, Duthie GM. Modelling the decrement in running intensity within professional soccer players. Sci Med Footb. 2018;2(2):86–92. [Google Scholar]
- 3.DeWeese BH, Hornsby G, Stone M, Stone MH. The training process: planning for strength–power training in track and field. Part 1: Theoretical aspects. J Sport Health Sci. 2015;4(4):308–17. [Google Scholar]
- 4.Oliva-Lozano JM, Rojas-Valverde D, Gómez-Carmona CD, Fortes V, Pino-Ortega J. Impact of contextual variables on the representative external load profile of Spanish professional soccer match-play: a full season study. Eur J Sport Sci. 2020 doi: 10.1080/17461391.2020.1751305. Epub Ahead of print 1–22. [DOI] [PubMed] [Google Scholar]
- 5.Martín-García A, Gómez Díaz A, Bradley PS, Morera F, Casamichana D. Quantification of a professional football team’s external load using a microcycle structure. J Strength Cond Res. 2018;32(12):3511–8. doi: 10.1519/JSC.0000000000002816. [DOI] [PubMed] [Google Scholar]
- 6.Drew MK, Finch CF. The relationship between training load and injury, illness and soreness: a systematic and literature review. Sports Med. 2016;46(6):861–83. doi: 10.1007/s40279-015-0459-8. [DOI] [PubMed] [Google Scholar]
- 7.Williams AM, Hodges NJ. Practice, instruction and skill acquisition in soccer: challenging tradition. J Sports Sci. 2005;23(6):637–50. doi: 10.1080/02640410400021328. [DOI] [PubMed] [Google Scholar]
- 8.Oliva-Lozano JM, Gómez-Carmona CD, Pino-Ortega J, Moreno-Pérez V, Rodríguez-Pérez MA. Match and training high intensity activity-demands profile during a competitive mesocycle in youth elite soccer players. J Hum Kinet. 2020;75:131–41. doi: 10.2478/hukin-2020-0050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Anderson L, Orme P, Di Michele R, Close GL, Morgans R, Drust B, Morton JP. Quantification of training load during one-, two- and three-game week schedules in professional soccer players from the English Premier League: implications for carbohydrate periodisation. J Sports Sci. 2016;34(13):1250–9. doi: 10.1080/02640414.2015.1106574. [DOI] [PubMed] [Google Scholar]
- 10.Kelly DM, Strudwick AJ, Atkinson G, Drust B, Gregson W. Quantification of training and match-load distribution across a season in elite English Premier League soccer players. Sci Med Footb. 2020;4(1):59–67. [Google Scholar]
- 11.Malone JJ, Di Michele R, Morgans R, Burgess D, Morton JP, Drust B. Seasonal training-load quantification in elite English Premier League soccer players. Int J Sports Physiol Perform. 2015;10(4):489–97. doi: 10.1123/ijspp.2014-0352. [DOI] [PubMed] [Google Scholar]
- 12.Oliva-Lozano JM, Gómez Carmona CD, Rojas-Valverde D, Fortes V, Pino-Ortega J. Effect of training day, match, and length of the microcycle on the worst-case scenarios in professional soccer players. Res Sports Med. 2021 doi: 10.1080/15438627.2021.1895786. Epub Ahead of print 1–14. [DOI] [PubMed] [Google Scholar]
- 13.Curtis RM, Huggins RA, Benjamin CL, Sekiguchi Y, Adams WM, Arent SM, Jain R, Miller SJ, Walker AJ, Casa DJ. Contextual factors influencing external and internal training loads in collegiate men’s soccer. J Strength Cond Res. 2020;34(2):374–381. doi: 10.1519/JSC.0000000000003361. [DOI] [PubMed] [Google Scholar]
- 14.Clemente FM, Rabbani A, Conte D, Castillo D, Afonso J, Truman Clark CC, Nikolaidis PT, Rosemann T, Knechtle B. Training/match external load ratios in professional soccer players: A full-season study. Int J Environ Res Public Health. 2019;16(17):3057. doi: 10.3390/ijerph16173057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Raya-González J, Castillo D, editors. Sports and athletics preparation, performance, and psychology: an essential guide to sports performance. Hauppauge, NY: NOVA Science publisher; 2020. Training load periodization in soccer with one official match a week: A systematic review; pp. 123–66. [Google Scholar]
- 16.White A, Hills SP, Cooke CB, Batten T, Kilduff LP, Cook CJ, Roberts C, Russell M. Match-play and performancetest responses of soccer goalkeepers: a review of current literature. Sports Med. 2018;48(11):2497–516. doi: 10.1007/s40279-018-0977-2. [DOI] [PubMed] [Google Scholar]
- 17.Bastida-Castillo A, Gómez-Carmona CD, De la Cruz E, Pino-Ortega J, Bastida Castillo A, Gómez Carmona CD, la Cruz Sánchez E, Pino Ortega J. Accuracy, intra- and inter-unit reliability, and comparison between GPS and UWB-based position-tracking systems used for time–motion analyses in soccer. Eur J Sport Sci. 2018;18(4):450–57. doi: 10.1080/17461391.2018.1427796. [DOI] [PubMed] [Google Scholar]
- 18.FIFA . FIFA Quality performance reports for EPTS [Internet] 2020. Available from: https://football-technology.fifa.com/en/media-tiles/fifa-quality-performance-reports-for-epts/ [Google Scholar]
- 19.Rico-González M, Los Arcos A, Rojas-Valverde D, Clemente FM, Pino-Ortega J. A survey to assess the quality of the data obtained by radio-frequency technologies and microelectromechanical systems to measure external workload and collective behavior. Sensors. 2020;20(8):2271. doi: 10.3390/s20082271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Oliva-Lozano JM, Maraver EF, Fortes V, Muyor JM. Effect of playing position, match half, and match day on the trunk inclination, g-forces, and locomotor efficiency experienced by elite soccer players in match play. Sensors. 2020;20(20):5814. doi: 10.3390/s20205814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Oliva-Lozano JM, Maraver EF, Fortes V, Muyor JM. Kinematic analysis of the postural demands in professional soccer match play using inertial measurement units. Sensors. 2020;20(21):5971. doi: 10.3390/s20215971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gómez-Carmona CD, Pino-Ortega J, Sánchez-Ureña B, Ibáñez SJ, Rojas-Valverde D. Accelerometry-based external load Indicators in sport: too many options, same practical outcome? Int J Environ Res Public Health. 2019;16(24):5101. doi: 10.3390/ijerph16245101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Martín-García A, Casamichana D, Gómez Díaz A, Cos F, Gabbett TJ. Positional differences in the most demanding passages of play in football competition. J Sports Sci Med. 2018;17(4):563–70. [PMC free article] [PubMed] [Google Scholar]
- 24.Stevens TGA, de Ruiter CJ, Twisk JWR, Savelsbergh GJP, Beek PJ. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci Med Footb. 2017;1(2):117–25. [Google Scholar]
- 25.Clemente FM, Owen A, Serra-Olivares J, Nikolaidis PT, van der Linden CMI, Mendes B. Characterization of the weekly external load profile of professional soccer teams from Portugal and the Netherlands. J Hum Kinet. 2019;66(1):155–64. doi: 10.2478/hukin-2018-0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fessi MS, Zarrouk N, Di Salvo V, Filetti C, Barker AR, Moalla W. Effects of tapering on physical match activities in professional soccer players. J Sports Sci. 2016;34(24):2189–94. doi: 10.1080/02640414.2016.1171891. [DOI] [PubMed] [Google Scholar]
- 27.Oliva-Lozano JM, Fortes V, Muyor JM. The first, second, and third most demanding passages of play in professional soccer: a longitudinal study. Biol Sport. 2021;38(2):165–74. doi: 10.5114/biolsport.2020.97674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Oliva-Lozano JM, Martín-Fuentes I, Fortes V, Muyor JM. Differences in worst-case scenarios calculated by fixed length and rolling average methods in professional soccer match-play. Biol Sport. 2021;38(3):325–31. doi: 10.5114/biolsport.2021.99706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Turner AN, Stewart PF. Strength and conditioning for soccer players. Strength Cond J. 2014;36(4):1–13. [Google Scholar]
- 30.Palucci-Vieira LH, Aquino R, Lago-Peñas C, Munhoz-Martins GH, Puggina EF, Barbieri FA, Palucci Vieira LH, Aquino R, Lago-Peñas C, Munhoz Martins GH, Puggina EF, Barbieri FA. Running performance in Brazilian professional football players during a congested match schedule. J Strength Cond Res. 2018;32(2):313–25. doi: 10.1519/JSC.0000000000002342. [DOI] [PubMed] [Google Scholar]
- 31.Lago-Peñas C, Rey E, Lago-Ballesteros J, Casáis L, Domínguez E. The influence of a congested calendar on physical performance in elite soccer. J Strength Cond Res. 2011;25(8):2111–7. doi: 10.1519/JSC.0b013e3181eccdd2. [DOI] [PubMed] [Google Scholar]
- 32.Carling C, Gregson W, McCall A, Moreira A, Wong DP, Bradley PS. Match running performance during fixture congestion in elite soccer: research issues and future directions. Sports Med. 2015;45(5):605–13. doi: 10.1007/s40279-015-0313-z. [DOI] [PubMed] [Google Scholar]
- 33.Los Arcos A, Méndez-Villanueva A, Martínez-Santos R. In-season training periodization of professional soccer players. Biol Sport. 2017;34(2):149–55. doi: 10.5114/biolsport.2017.64588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Castillo D, Raya-González J, Weston M, Yanci J. Distribution of external load during acquisition training sessions and match play of a professional soccer team. J Strength Cond Res. 2019 doi: 10.1519/JSC.0000000000003363. Epub Ahead of Print, 1–6. [DOI] [PubMed] [Google Scholar]
- 35.Abbott W, Brickley G, Smeeton NJ, Mills S. Individualizing acceleration in English Premier League academy soccer players. J Strength Cond Res. 2018;32(12):3503–10. doi: 10.1519/JSC.0000000000002875. [DOI] [PubMed] [Google Scholar]
- 36.Rago V, Brito J, Figueiredo P, Krustrup P, Rebelo A. Application of individualized speed zones to quantify external training load in professional soccer. J Hum Kinet. 2020;72(1):279–89. doi: 10.2478/hukin-2019-0113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sonderegger K, Tschopp M, Taube W. The challenge of evaluating the intensity of short actions in soccer: a new methodological approach using percentage acceleration. PLoS One. 2016;11(11):e0166534. doi: 10.1371/journal.pone.0166534. [DOI] [PMC free article] [PubMed] [Google Scholar]