Robust design of a green-responsive closed-loop supply chain network for the ventilator device

Abstract

This study aims to investigate the closed-loop supply chain network design problem considering the environmental and responsiveness features. For this purpose, a multi-objective mathematical model is suggested that minimizes the carbon emissions and the total costs and maximizes the responsiveness of the system. Due to the dynamic space of the business environment, uncertainty is an integral part of the supply chain problem. Therefore, this research applies the robust possibilistic programming method to cope with uncertainty. Afterwards, since the research problem has a high level of the complexity, a hybrid solution approach based on a heuristic method and the meta-goal programming method is developed to solve the research problem in a reasonable time. Then, due to the importance of the ventilator device during the recent pandemic (COVID-19), this study considers this product as a case study. The main contribution of the current study is to design a green-responsive closed-loop supply chain network under uncertainty using a multi-objective robust possibilistic programming model, for the first time in the literature, especially in the medical devices industry. On the other side, the other contribution of this study is to develop an efficient hybrid solution method. The achieved results demonstrate the efficiency of the offered model and the developed hybrid method. Eventually, by carrying out sensitivity analysis, the impact of some of the critical parameters on the model is investigated. Based on the obtained results, an increase in the demand sizes leads to increasing the environmental damages and the total costs while reducing the responsiveness level. On the other side, an increase in the rate of return leads to an increase in all of the objective functions. Also, the achieved results show that when the capacity parameter is increased, the total costs are decreased, but the responsiveness and environmental impacts are increased.

Supplementary Information

The online version contains supplementary material available at 10.1007/s11356-022-19105-1.

Introduction

Nowadays, increasing the level of competition in the market space results in increasing the importance of the supply chain (SC) management problem. In general, a supply chain consists of all the elements that act directly or indirectly in meeting the demands of the customer (Chopra and Meindl 2007; Fallahpour et al. 2018). SC management is the handling of the flow of materials and services and includes all the processes that convert raw materials into final products (Chopra and Meindl 2007). Today, managers are well aware that in order to increase the productivity of their business and gain a competitive advantage, they need to optimally design their supply chain network (SCN) (Pal et al. 2016, 2021b, a; Fallahpour et al. 2018; Nayeri et al. 2020; Diabat and Jebali 2021; Salehi-Amiri et al. 2021; Sazvar et al. 2021a). Hence, the supply chain network design (SCND) problem is known as one of the important problems in today’s competitive environment (Polat and Gungor 2021).

In the traditional approach, researchers only considered the financial aspect of the SCND problem, but in recent years the concerns about the environmental impacts of the SC are increased which has led to attracting the attention of researchers to design the environmental-friendly SCN, which so-called green supply chain (GSC) (Bhattacharya and De 2021; Chen and Ye 2021; Fallahpour et al. 2021a, b; Hong et al. 2021; Usmani et al. 2021; Waqas et al. 2021a). On the other side, increasing environmental pollutions has led to passing some regulations and rules that oblige companies to comply with environmental considerations. In general, minimizing the greenhouse gas emissions is one of the main concerns of the green view (Dogan and Seker 2016; Dogan and Turkekul 2016; Dogan and Inglesi-Lotz 2017; Alamroshan et al. 2021). Although at the first glance considering the environmental issues may lead to increasing the total costs of the SC, it can increase the profits of the SC by providing a green image from the company and retention of customers for the long term. There are some aspects to consider greenness in the SCN problem such as reducing carbon emissions, reducing energy consumption, and using environmental-friendly raw materials (Pishvaee et al. 2014; Waltho et al. 2018; Gholizadeh and Fazlollahtabar 2020; Fallahpour et al. 2021b; Nayeri et al. 2021b).

One of the concepts that has received more attention in recent years is reverse logistics (RL) (Govindan and Gholizadeh 2021). The ability of RL to utilize the end-of-use (EOU) or end-of-life (EOL) products can reduce environmental pollutions, drastically (Afra and Behnamian 2021). In general, when the forward SC and the reverse SC are integrated, the traditional SC converts to the closed-loop one (Rahimi and Fazlollahtabar 2018; Gholizadeh and Fazlollahtabar 2020). In a closed-loop supply chain network (CLSCN), the demands of customers are satisfied by the forward SC, whereas the EOU and EOL products collected from consumers are handled by RL (Gholizadeh et al. 2020b; Sazvar et al. 2021b). The efficient configuring of the CLSCN can lead to decreasing the environmental impacts of the SC by (I) utilizing the recycled components and materials to manufacturing products and (II) applying environmentally friendly transportation systems (Amin and Zhang 2013).

Since customers are the most important element of each SC, satisfying their demands is considered as the main target of the SCN. In this regard, an important criterion has been introduced in the literature named responsiveness. In general, researchers have described responsiveness as the ability of an SC to meet the demands of customers over the planning horizon (Rabbani et al. 2018; Nayeri et al. 2021b). For better understanding the importance of the responsiveness, see the following example. The market share of the Motorola company was decreased from 60% in 1994 to 16% in 2002 due to company’s inability to respond to fluctuations and change customer demand (Roh et al. 2014). This example demonstrates that ignoring the responsiveness measure can lead to irreparable financial loss. Hence, considering this criterion in the SC problem seems to be necessary. Several features such as increasing the service level, reducing the lead times, and providing various products are defined to incorporate responsiveness aspect into the SCN problem (Pishvaee and Rabbani 2011; Rabbani et al. 2018; Sabouhi et al. 2020; Nayeri et al. 2021a).

The importance of medical devices has been drastically highlighted during the recent pandemic (COVID-19). Based on World Health Organization (WHO), there are about 2,000,000 types in the market. Among them, one of the most widely used devices in the pandemic period is the ventilator. A ventilator is a device that allows air to enter the lungs and allows it to be expelled from the lungs. The ventilator performs breathing work for patients who have temporary or permanent respiratory problems. Motivated by the importance of the mentioned goods during the COVID-19 period, this research selected this product as a case study.

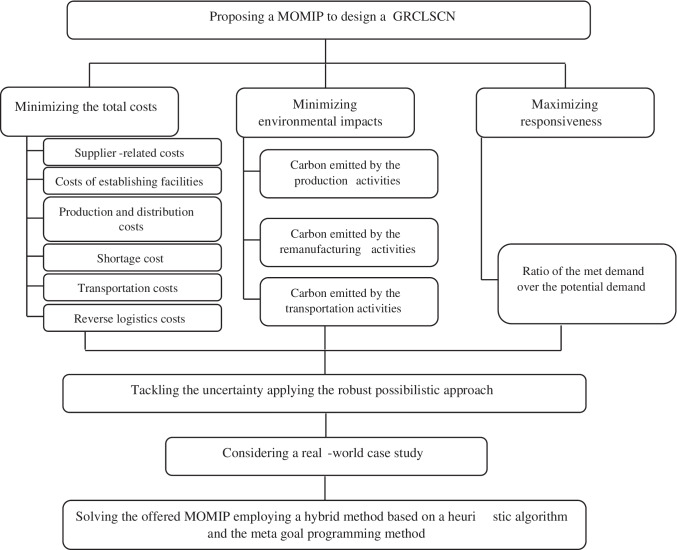
Based on the above-mentioned points, this study attempts to investigate the green-responsive CLSCN (GRCLSCN) design problem. For this purpose, a multi-objective mixed integer programming (MOMIP) model is offered to minimize the environmental damages and total costs while maximizing the responsiveness of the SCN. Since uncertainty is known as one of the major issues of the SCND problem, this study applies the robust possibilistic programming (RPP) method to tackle the uncertainty in the model’s parameters. Afterwards, considering a case study, the offered MOMIP is solved by combining the meta-goal programming (MGP) method with a heuristic method. The framework of the current research has been depicted in Fig. 1. The main advantages of the current paper comparing to the previous studies are (I) simultaneously consideration of the green and responsive features in the CLSCN design problem, (II) developing an efficient hybrid method to solve the proposed MOMIP, and (III) investigating the supply chain of the ventilator product as one of the most important medical devices in the recent pandemic (COVID-19). Therefore, improvement and novelty of the paper from the existing literature can be presented in the two aspects: (i) this is the first study that proposed a multi-objective robust possibilistic programming model to design a green-responsive supply chain network for the medical devices industry, and (ii) the current study developed an efficient hybrid solution approach based on the meta-goal programming method and a heuristic algorithm to solve the research problem. Based on the above discussions, the main innovation of the current research are as follows:

• This study simultaneously considers the greenness and responsiveness aspects in the closed-loop supply chain that never occurred in the previous research. In the green aspect, governments have paid special attention to the environmental factors that oblige the firms to comply with environmental issues (Breque et al. 2021). On the other side, considering the responsiveness aspect leads to gaining the competitive advantage for the firm that can increase the total profits (Nayeri et al. 2021b).

• Since the closed-loop supply chain network design problem is an NP-hard one, it has a high level of complexity and needs a high CPU time for solving (Tiwari et al. 2016; Çağrı et al. 2018). In this regard, to overcome this issue, this research aims at developing an efficient hybrid solution method based on the meta-goal programming, which is applied to convert the multi-objective model to a single one, and a heuristic algorithm, which is employed to tackle the complexity of the proposed model.

• Since in the recent pandemic the importance of the ventilator device has become more highlighted and the demand for this product has drastically increased, this study selects this important product as a case study.

Fig. 1.

The framework of this study

The current study aims at answering to the following research questions:

1. How to design a green and responsive closed-loop supply chain network using a multi-objective robust possibilistic programming model?

2. How to develop an efficient hybrid solution to solve the problem?

3. What is the behavior of the research problem according to a change in the crucial parameters such as demand?

4. How is the behavior of the proposed model in terms of robustness?

In the rest of this paper, the literature review is reported in “Literature review” section. “Problem definition” section presents the mathematical model. The FRO counterpart are developed in “Robust possibilistic programming counterpart” section. The hybrid solution method is explained in “Solving method” section. Case study and obtained results are provided in “Computational results” section. Finally, conclusions are presented in “Conclusions” section.

Literature review

Recently, several study papers studied the SC management problem due to the importance of it (for example, see Alizadeh et al. 2020; De and Mahata 2020, 2021; Pourmehdi et al. 2020; Bhattacharya and De 2021; Bhattacharya et al. 2021; De 2021). In this research, according to the nature of this study, this section is dedicated to reporting some of the most related previous papers.

Green closed-loop SCND

In the two last decades, regarding the importance of environmental aspects of the SC, several studies have been conducted to investigate the GSC design problem. In this field, Zohal and Soleimani (2016) developed an ant colony to configure a green CLSC (GCLSC) for the gold industry. In this regard, they proposed a MOMIP model to minimize the environmental damages and the total costs. The achieved outcomes indicated the efficiency of the offered model and the proposed method. Soleimani et al. (2017) suggested a MOMIP to design a GCLSC. Then, the authors applied fuzzy programming to tackle uncertainty in the model’s parameters. Afterwards, they employed the genetic algorithm (GA) to handle the research problem. The results indicated the validity and performance of the suggested model and the offered algorithm. Rad and Nahavandi (2018) configured a GCLSC network considering the quantity discounts by proposing a MOMIP model. Their model aimed to minimize the environmental impacts and the total costs while maximizing customer satisfaction. The authors applied the LP-metric method to solve the research problem. Su et al. (2019) examined the GCLSC problem considering third-party recycling. To do this, the authors presented a two-stage model, and then compared the impact of decentralized decision-making and centralized decision-making on the pricing and returns strategies of each participant. Zhen et al. (2019) suggested a bi-objective programming model (BOPM) for configuring a GCLSC in order to create a trade-off between CO2 emissions and operating cost. They utilized the stochastic approach to tackle the uncertainty that existed in the model’s parameters. Then, to solve the proposed model, the authors employed the Lagrangian relaxation method. Mardan et al. (2019) offered a BOPM to configure a multi-period GCLSC for the wire-and-cable industry. The authors combined the LP-metric and the Benders decomposition methods to solve their model.

Guo et al. (2020) offered a non-linear programming model to configure a GCLSC considering offline and online sales modes. Due to the complexity of the proposed model, the author employed the particle swarm optimization (PSO) and the GA algorithms to solve the research problem. Huang et al. (2020) designed a GCLSC network considering carbon emissions and cost control. They proposed a BOPM to minimize environmental damages and the total costs. Also, to deal with the uncertainty, the authors employed the stochastic programming method. Finally, the research problem was solved using the $\epsilon$-constraint method. Mohtashami et al. (2020) combined the mathematical model and queuing system to design a GCLSC considering energy consumption. They considered different types of returned products that shipped from the customers to collection centers. Also, the authors applied both exact and meta-heuristics methods to solve the research problem. Sadeghi et al. (2020) suggested a MOMIP to design a GCLSC with the location-routing problem. It should be noted that the authors selected an automotive spare parts manufacturing company as a case study. Li et al. (2021) tried to design a CLSCN with consumer preference for green design. The authors emphasize the impacts of the consumer preference for green product design and the mandated targets on the strategies of the firms. Jian et al. (2021) studied the GCLSC problem under consideration of the manufacturer’s fairness concern. Their model configures a GCLSC network with profit-sharing contract coordination fairness. The obtained results showed that the profit-sharing contract could improve the performance of the studied SC. Liu et al. (2021) offered a novel robust fuzzy model to configure a GCLSC with distribution ambiguity. The authors selected Coco-Cola Company as a case study to show the validity of their study. Mandal and Pal (2021) studied a game-theoretic method in a competitive SC considering a two-tier credit facility and imperfect production. It should be noted that the authors investigated the research problem under the environment of carbon emissions in which a manufacturer and two rival retailers compete with each other. Pal and Sarkar (2021) studied the strategies of a dual-channel GSC considering recycling under retailer promotional effort. In this regard, the authors employed the game theory approach to determine the optimal strategies. Ghomi-Avili et al. (2021) offered a bi-level mathematical model to design a multi-period and single-product SC network under the competitive environment. The authors employed the robust optimization approach to tackle uncertainty and used the Karush–Kuhn–Tucker (K-K-T) optimality conditions to solve the research problem. Sherif et al. (2021) designed a two echelon SCN by proposing a mathematical programming model for the battery manufacturing industry. The authors employed the simulated annealing algorithm to solve the research problem in the large-sized test problems.

Responsive SCND

As mentioned, responsiveness implies the capability of the SC to satisfy the demand of the customers. In recent years, several works tried to investigate the responsive SCND problem, which we report some of the most important of them in this section. Pishvaee and Rabbani (2011) proposed two MIP models to configure a responsive SCN considering direct shipment and prohibited one. They developed a graph theoretic heuristic method to handle the models. Baghalian et al. (2013) suggested a robust model to design a multi-product SC against disruptions under uncertainty in both sides of supply and demand. They used a path-based formulation to consider uncertainties in the supply side. A mathematical model is offered by Dubey et al. (2015) for designing an SCN with sustainability and responsiveness concepts. Their model aimed to minimize the total lead-time of collection and delivery activities and the total costs. They applied several types of robust optimization to tackle the uncertainty of the model’s parameters. Martí et al. (2015) offered a BOPM to design a responsive SCN considering carbon policy and transportation modes. The main goal of their study was to create a balance between the responsiveness of SC and the carbon footprint. It should be noted that the authors considered the shortage of products and the transportation time as the responsiveness level. A robust non-linear programming model was offered by Mohammaddust et al. (2017) to design a SCN with responsiveness feature under the uncertain environment. They tried to minimize the lead-time of SC as the responsiveness measures. Rabbani et al. (2018) developed a multi-layer responsive SCN. The authors considered the lateral transshipments strategy in the research problem as the responsiveness criterion. On the other hand, they tried to minimize the total delivery time in the objective function. A scenario-based programming model is offered by Sabouhi et al. (2020) to design a responsive and resilient SCN in which the service level was defined as the responsiveness measure. The authors employed a multi-cut L-shaped method to solve the research problem. Nayeri et al. (2021a, b) examined the inventory-location problem in the responsive SCN under uncertainty. They suggested a mathematical model and solved it using several metaheuristic algorithms. Also, to demonstrate the performance of the developed algorithm, the authors solved several numerical examples. Aboolian et al. (2021) investigated a responsive make-to-order SCN. The authors considered the demand and service time as uncertain parameters and applied the stochastic programming method to tackle uncertainty. Finally, they solve the proposed model employing a metaheuristic algorithm. Azaron et al. (2021) configured a responsive SCN by proposing a stochastic multi-stage mathematical model. Their model aimed to maximize the total profit and minimize the traveling time as the responsiveness measure.

Dealing with corporate social responsibility (CSR) and business environmental strategies

In recent years, due to the special attention of governments to environmental issues, managers of the firms and companies have been obliged to adopting environmental-friendly strategies for their businesses (Nayeri et al. 2020; Breque et al. 2021). In this regard, several studies have been conducted to investigate the business environmental strategies. For example, Banerjee (2001) discussed about corporate environmental strategies and actions. They studied the environmental strategies of over 250 US firms. Handfield et al. (2005) interviewed with firms from several countries to develop a framework for environmental SC strategy decision-making. They found that some goals such as recycling and using environmental-friendly raw materials were on the list of agenda of these firms. Zhulavskyi et al. (2017) studied the environmental responsibility strategies of business. They provided the main criteria to identify the strategies for environmental responsibility of companies. Pedram et al. (2017) suggested the strategy of using new and repaired products with different prices that led to using the returned product and reducing environmental damages. Rahimi and Fazlollahtabar (2018) adopted the strategy of using EOL and EOU products to control reverse flow, reduce wastes, and decrease environmental damages. Nayeri et al. (2020) considered the manufacturing and recycling technologies with lower environmental damages but higher setup costs in order to reduce the carbon emissions generated in their supply chain. Mohammed et al. (2017) studied their problem under different carbon emissions policies (e.g., tax and cap-and-trade policies) to control the carbon emission of their SCN. Homayouni et al. (2021) tried to utilize vehicles with lower carbon emission that led to reducing environmental damages of their SCN. Nayeri et al. (2021b) attempted to employ welding technology with lower emissions and also transportation modes with lower pollution to decrease the environmental impacts of their business. Waqas et al. (2018a, b) investigated the crucial barriers for implementing the reverse supply chain in the manufacturing industries. In this way, the authors developed a two-stage method based on the structural equation modeling and the Delphi method and employed SPSS and AMOS softwares. Waqas et al. (2021a, b) mapped a roadmap towards environmental performance, green innovation, and competitive advantage utilizing big data analytics. The main contribution of the mentioned work was introducing possible moderators and mediators among the relationship of big data analytics and environmental performance. Waqas et al. (2020) tried to model the reverse supply chain barriers in the manufacturing industry using interpretive structural modeling and MICMAC methods. Based on the obtained results, financial, technological, and organizational barriers were identified as dependent barriers. Waqas et al. (2018b) tried to explore the consumer willingness to select environmentally friendly options and also their attitude towards sustainable transportation in China using a norm activation model. The results demonstrated that self-enhancement and self-transcendence have negative and positive moderating impacts on the acceptability of sustainable transportation.

Cost reduction strategies

In today’s competitive market space, the majority of the firms are struggling with high operating costs. In this regard, employing cost reduction strategies can help these firms to increase their profits, dramatically. Cost reduction strategies are effective methods or principles to enhancement of efficiency of operations. Cost reduction strategies can decrease the total costs of operations while enhancing productivity and allowing reallocation of resources (Bragg 2010). One of the widely used cost reduction strategies is the supply chain management (Bragg 2010). In this regard, one of the most important goals of the supply chain management is to minimize the total costs of SC. For example, by reducing the production costs, the company can refocus budgeted resources on expanding operations. This helps companies to align the goals and also increasing market share. In this way, for example, Chen and Wang (2012) studied the SC problem considering budget constraint in which the total costs of SC could not excess a certain value (budget). Nagurney et al. (2017) adopted the limited budget strategy in order to reduce the total costs of their supply chain. (Ha et al. 2017) utilized the information sharing strategy to reduce to costs of their business. Nayeri et al. (2021a) employed Markovian-based decision-making approach to reduce the inventory and shortage costs in their business.

Research gaps and contributions

As can be seen in the literature, although many papers investigated the green or the responsive SCND problems, there is a lack of studies that simultaneously considered green and responsive features especially considering reverse logistics. Indeed, no study developed a green and responsive closed-loop supply chain network. However, as aforementioned, all of the mentioned concepts (i.e., greenness, responsiveness, and CLSC) are very important and can help the firms to gain a competitive advantage. In this regard, to cover these gaps, this study offers a MOMIP model for designing a GRCLSCN, which minimizes the environmental damages and the costs and maximizes the responsiveness of the SCN. Then, a robust possibilistic method is utilized to deal with the uncertainty. Finally, as the CLSC network design problem is considered as an NP-hard one (Tiwari et al. 2016; Çağrı et al. 2018), a heuristic method is combined with the meta-goal programming approach to solve the MOMIP. Based on the mentioned points, the main contributions of the current research are listed as below:

• To the best of our knowledge, this is the first research that proposes a multi-objective robust possibilistic programming model to design a green-responsive closed-loop supply chain network design problem.

• This research develops an efficient solution approach based on a heuristic method and the meta-goal programming method (HMGP) to solve the proposed model in a reasonable time.

• This paper investigates the ventilator device as a case study due to its importance during the recent pandemic (COVID-19).

Problem definition

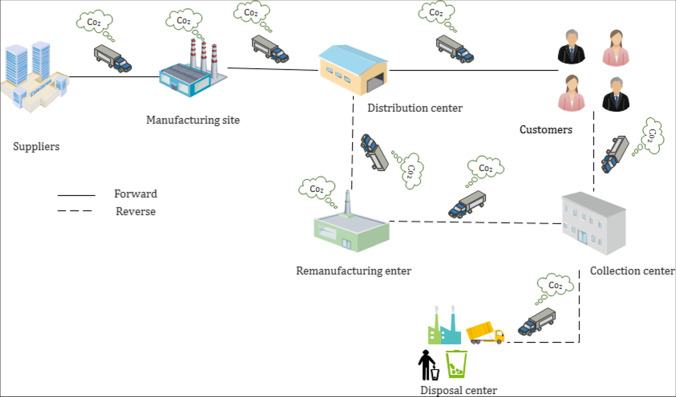
In this section, we describe the research problem and formulate the MOMIP. The CLSCN is that designed in this research includes four facilities in the forward chain involving suppliers, manufacturing sites (MSs), distribution centers (DCs), and customers. Also, it has three echelons in the reverse chain involving collection centers (CCs), remanufacturing centers (RCs), and disposal centers. The designed CLSCN is illustrated in Fig. 2. The material flows in this network are as follows. At the outset, the raw materials are purchased from the suppliers and then shipped to the MSs. Afterwards, the original goods are manufactured in the MSs and shipped to the DCs for shipping to the demand points. Then, in the reverse logistics, the EOU/EOL products are collected from customers and sent to the CCs. In the CCs, the collected products are inspected and the percentage of them that capable to repair are shipped to the RCs. The remaining of them (that cannot be repaired) are sent to the disposal center. This study considers two types of products, the first one is the original product that is produced in the MSs, and the second one is the repaired product that is sent from the RCs to the DCs and then shipped to demand points. Also, this study considers different types of manufacturing technologies and transportation modes that each of which has different costs, carbon emissions, and capacity. In this research, to incorporate the green concept in the problem, two strategies are considered: (i) considering the revers logistic that leads to re-use the EOU/EOL products and (ii) minimizing the carbon emissions due to production, remanufacturing, and transportation activities.

Fig. 2.

The proposed CLSCN

Mathematical model

This section is devoted to present the MOMIP. In the following, the necessary notations of the MOMIP are presented. There are three main reasons for proposing the MOMIP: firstly, the reason for proposing a multi-objective model is that there are some conflicting targets (i.e., minimizing total costs, minimizing environmental impacts, and maximizing responsiveness) in the research problem. In general, when we have several conflicting objective functions, we utilize multi-objective models. On the other side, since in our problem there are different types of variables (continuous, binary, and integer), we would rather propose a mixed integer programming model. Also, there are several papers that proposed MOMIP to design SCNs and obtained good results (for example, see Paydar et al. 2017; Mamashli and Javadian 2020; Nayeri et al. 2020, 2021b; Pourmehdi et al. 2020) that shows the appropriate performance of the MOMIP models in the SCN design problem.

Indices
$s$	Suppliers’ index
$i$	MSs’ index
$j$	DCs’ index
$k$	Customers’ index
$c$	CCs’ index
$t$	RCs’ index
$q$	Disposal centers’ index
$r$	Raw materials’ index
$p$	Original products’ index
$d$	Repaired products’ index
$m$	TMs’ index
$l$	Technologies’ index
Parameters
${\widetilde{\mathit{HSS}}}_s$(Rials—the local currency of Iran)	Cost of contracting with supplier s
${\widetilde{\mathit{HSM}}}_{\mathit{il}}$(Rials)	Fixed-cost (FC) of establishing MS i with technology l
${\widetilde{\mathit{HSD}}}_j$(Rials)	FC of establishing DC j
${\widetilde{\mathit{HSC}}}_c$(Rials)	FC of establishing CC c
${\widetilde{\mathit{HSR}}}_{\mathit{tl}}$(Rials)	FC of establishing RC t with technology l
${\widetilde{\mathit{HMR}}}_{\mathit{rs}}$(Rials)	The purchasing cost of raw material r from supplier s
${\widetilde{\mathit{HTM}}}_{\mathit{pil}}$(Rials)	The production cost of manufacturing the original product p in MS i using technology l
${\widetilde{\mathit{HDP}}}_j$(Rials)	The operating costs of DC j
${\widetilde{\mathit{HCC}}}_c$(Rials)	The operating costs of CC c
${\widetilde{\mathit{HTM}}}_{\mathit{tl}}$(Rials)	The cost of remanufacturing using technology l in RC t
${\widetilde{\mathit{OSH}}}_{\mathit{pk}}$(Rials)	The cost of shortage for the original product p for customer k
${\widetilde{\mathit{RSH}}}_{\mathit{dk}}$(Rials)	The cost of shortage for the repaired product d for customer k
${\widetilde{\mathit{tc}}}_m$(Rials—kg/km)	Unit of transportation cost for TM m
${\mathit{SCP}}_{\mathit{sr}}$(number)	The capacity of suppliers to provide raw material r
${\mathit{MCP}}_{\mathit{ilp}}$(number)	The capacity of MS i with technology l to produce product p
${\mathit{DCP}}_j$(number)	The capacity of DC j
${\mathit{CCP}}_c$(number)	The capacity of CC c
${\mathit{RCP}}_{\mathit{tl}}$(number)	The capacity of RC t with technology l for remanufacturing the returned products
${\widetilde{D1}}_{\mathit{pk}}$(number)	The demand of customer k for the original product p
${\widetilde{D2}}_{\mathit{dk}}$(number)	The demand of customer k for the repaired product d
${\theta }_p$	The return rate of product p
${\gamma }_{\mathit{rp}}(\text{number})$	The utilization rate of raw material r in product p
$\sigma$	Percentage of products that can be repaired
${Ds1}_{\mathit{si}}$(km)	Distance between supplier s and MS i
${Ds2}_{\mathit{ij}}$(km)	Distance between MS i and DC j
${Ds3}_{\mathit{jk}}$(km)	Distance between DC j and customer k
${Ds4}_{\mathit{kc}}$(km)	Distance between customer k and CC c
${Ds5}_{\mathit{kt}}$(km)	Distance between CC c and RC t
${Ds6}_{\mathit{cq}}$(km)	Distance between CC c and disposal center q
${Ds7}_{\mathit{tj}}$(km)	Distance between RC t and DC j
${\widetilde{\mathit{mce}}}_l$(kg)	Carbon emitted by producing product p using technology l
${\widetilde{\mathit{rce}}}_{\mathit{pl}}$(kg)	Carbon emitted by repairing process using technology l
${\widetilde{\mathit{tce}}}_m$(kg/km)	Carbon emitted by transportation activities using TM m
$\mathit{BigM}$	A large positive number
Decision variables
${\mathit{SS}}_s$	1 if supplier s is selected; 0 otherwise (ow)
${\mathit{MX}}_{\mathit{il}}$	1 if MS i is established with technology l; 0 ow
${\mathit{DX}}_j$	1 if DC j is established; 0 ow
${\mathit{CX}}_c$	1 if CC c is established; 0 ow
${\mathit{RX}}_{\mathit{tl}}$	1 if RC t is established with technology l; 0 ow
${\mathit{TSM}}_{\mathit{msi}}$	The binary variable that shows whether between nodes s and i transportation m is utilized or not
${\mathit{TMD}}_{\mathit{mij}}$	The binary variable that shows whether between nodes i and j transportation m is utilized or not
${\mathit{TDK}}_{\mathit{mjk}}$	The binary variable that shows whether between nodes j and k transportation m is utilized or not
${\mathit{TKC}}_{\mathit{mkc}}$	The binary variable that shows whether between nodes k and c transportation m is utilized or not
${\mathit{TCR}}_{\mathit{mct}}$	The binary variable that shows whether between nodes c and t transportation m is utilized or not
${\mathit{TCD}}_{\mathit{mcq}}$	The binary variable that shows whether between nodes c and q transportation m is utilized or not
${\mathit{TRD}}_{\mathit{mtj}}$	The binary variable that shows whether between nodes t and j transportation m is utilized or not
${\mathit{SMR}}_{\mathit{rsim}}$	Quantity of raw material r shipped from supplier s to MS i using TM m
${\mathit{MDQ}}_{\mathit{pijlm}}$	Quantity of the original product p produced by technology l that are shipped from MS i to DC j using TM m
${\mathit{DCQ}}_{\mathit{pjkm}}$	Quantity of the original product p shipped from DC j to customer k using TM m
${\mathit{CCQ}}_{\mathit{pkcm}}$	Quantity of the returned product p shipped from customer k to CC c using TM m
${\mathit{CRQ}}_{\mathit{pctm}}$	Quantity of the returned product p shipped from CC c to RC t using TM m
${\mathit{CDQ}}_{\mathit{pcqm}}$	Quantity of the returned product p shipped from CC c to disposal center q using TM m
${\mathit{RDQ}}_{\mathit{dtjlm}}$	Quantity of the repaired product d remanufactured by technology l that are shipped from RC t to DC j using TM m
${\mathit{RDCQ}}_{\mathit{djkm}}$	Quantity of the repaired product d shipped from DC j to customer k using TM m
${SH1}_{\mathit{pk}}$	Shortage of the original product p for customer k
${SH2}_{\mathit{dk}}$	Shortage of the repaired product d for customer k

Based on the above definitions, the proposed MOMIP can be formulated as follows. The first objective function (OF) (1) minimizes the total costs. In OF1, the first part is the fixed-cost (FC) of contracting with suppliers, the second part shows FC of opening MSs, the third part denotes the FC for DCs, part 4 represents the FC of CCs, and part 5 is the FC of RCs. On the other side, part 6 shows the purchasing costs of raw materials, part 7 denotes the manufacturing costs, part 8 is distribution costs, part 9 shows the collection costs, part 10 represents the remanufacturing costs, and parts 11 and 12 are the shortage costs. Eventually, the last part shows the transportation costs.

$$\begin{array}{c}\hfill MinZ1=\sum _s{\widetilde{\mathit{HSS}}}_s.{\mathit{SS}}_s+\sum _{l,i}{\widetilde{\mathit{HSM}}}_{\mathit{il}}.{\mathit{MX}}_{\mathit{il}}+\sum _j{\widetilde{\mathit{HSD}}}_j.{\mathit{DX}}_j+\sum _c{\widetilde{\mathit{HSC}}}_c.{\mathit{CX}}_c+\sum _{t,l}{\widetilde{\mathit{HSR}}}_{\mathit{tl}}.{\mathit{RX}}_{\mathit{tl}}\\ \hfill +\sum _{m,s,r,i}{\widetilde{\mathit{HMR}}}_{\mathit{rs}}.{\mathit{SMR}}_{\mathit{rsim}}+\sum _{t,j,p,m,i}{\widetilde{\mathit{HTM}}}_{\mathit{pil}}.{\mathit{MDQ}}_{\mathit{pijtm}}\\ \hfill +\sum _{j,p,d,k,m}{\widetilde{\mathit{HDP}}}_j.({\mathit{DCQ}}_{\mathit{pjkm}}+{\mathit{RDCQ}}_{\mathit{djkm}})+\sum _{t,m,k,p}{\widetilde{\mathit{HCC}}}_{\mathit{pc}}.{\mathit{CCQ}}_{\mathit{pkcm}}\\ \hfill +\sum _{d,l,j,m,t}{\widetilde{\mathit{HTM}}}_{\mathit{tl}}.{\mathit{RDQ}}_{\mathit{dtjlm}}+\sum _{p,k}{\widetilde{\mathit{OSH}}}_{\mathit{pk}}.{SH1}_{\mathit{pk}}+\sum _{k,d}{\widetilde{\mathit{RSH}}}_{\mathit{dk}}.{SH2}_{\mathit{dk}}\\ \hfill +\sum _m{\widetilde{\mathit{tc}}}_m.(\sum _{i,r,s}{Ds1}_{\mathit{si}}.{\mathit{SMR}}_{\mathit{rsim}}+\sum _{p,t,j}{Ds2}_{\mathit{ij}}.{\mathit{MDQ}}_{\mathit{pijtm}}+\sum _{k,j,p}{Ds3}_{\mathit{jk}}.{\mathit{DCQ}}_{\mathit{pjkm}}\\ \hfill +\sum _{j,d,k}{Ds3}_{\mathit{jk}}.{\mathit{RDCQ}}_{\mathit{djkm}}+\sum _{c,p,k}{Ds4}_{\mathit{kc}}.{\mathit{CCQ}}_{\mathit{pkcm}}+\sum _{c,p,t}{Ds5}_{\mathit{kt}}.{\mathit{CRQ}}_{\mathit{pctm}}\\ \hfill +\sum _{c,p,q}{Ds6}_{\mathit{cq}}.{\mathit{CDQ}}_{\mathit{pcqm}}+\sum _{c,p,q}{Ds7}_{\mathit{tj}}.{\mathit{RDCQ}}_{\mathit{djkm}})ts\end{array}$$ 1

The second OF minimizes the total emissions, in which the first part shows production activities emissions, the second part is remanufacturing activities emissions, and the last part is related to transportation process emissions.

$$\begin{array}{c}\hfill MinZ2=\sum _{j,p,i,m,t}{\widetilde{\mathit{mce}}}_{\mathit{pl}}.{\mathit{MDQ}}_{\mathit{pijtm}}+\sum _{d,l,j,m,t}{\widetilde{\mathit{rce}}}_l.{\mathit{RDCQ}}_{\mathit{dtjlm}}\\ \hfill +\sum _m{\widetilde{\mathit{tce}}}_m.(\sum _{r,s,i}{Ds1}_{\mathit{si}}.{\mathit{SMR}}_{\mathit{rsim}}+\sum _{j,p,i,t}{Ds2}_{\mathit{ij}}.{\mathit{MDQ}}_{\mathit{pijtm}}+\sum _{j,p,k}{Ds3}_{\mathit{jk}}.{\mathit{DCQ}}_{\mathit{pjkm}}\\ \hfill +\sum _{j,d,k}{Ds3}_{\mathit{jk}}.{\mathit{RDCQ}}_{\mathit{djkm}}+\sum _{c,p,k}{Ds4}_{\mathit{kc}}.{\mathit{CCQ}}_{\mathit{pkcm}}+\sum _{c,p,t}{Ds5}_{\mathit{kt}}.{\mathit{CRQ}}_{\mathit{pctm}}\\ \hfill +\sum _{c,p,q}{Ds6}_{\mathit{cq}}.{\mathit{CDQ}}_{\mathit{pcqm}}+\sum _{c,p,q}{Ds7}_{\mathit{tj}}.{\mathit{RDCQ}}_{\mathit{djkm}})\end{array}$$ 2

The third OF (relation (3)) maximizes the responsiveness measure. This measure has been defined based on the ratio of satisfied demand over the potential demand. In this regard, the sum of the quantity of the original and repaired products that are shipped to customers is divided by the total potential demand. This equation is inspired by Fattahi et al. (2017) and Sabouhi et al. (2020), who calculated the responsiveness level of their supply chain based on the ratio of the met demand over the total demand.

$$MaxZ3=\frac{{\sum }_{m,k,j,p}{\mathit{DCQ}}_{\mathit{pjkm}}+{\sum }_{m,k,j,d}{\mathit{RDCQ}}_{\mathit{djkm}}}{{\sum }_{k,p}{\widetilde{D1}}_{\mathit{pk}}+{\sum }_{k,d}{\widetilde{D2}}_{\mathit{dk}}}$$ 3

Constraint (4) calculates the quantity of raw materials that should be purchased from the suppliers, and relation (5) is the suppliers’ capacity constraint.

$$\begin{array}{cc}{\sum }_{m,s}{\mathit{SMR}}_{\mathit{rsim}}={\sum }_{l,j,m,p}{\gamma }_{\mathit{rp}}.{\mathit{MDQ}}_{\mathit{pijlm}}& \forall i,r\end{array}$$ 4

$$\begin{array}{cc}{\sum }_{i,m}{\mathit{SMR}}_{\mathit{rsim}}\le {\mathit{SCP}}_{\mathit{sr}}.{\mathit{SS}}_s& \forall r,s\end{array}$$ 5

Constraint (6) shows that the quantity of products shipped from MSs to DCs is equal to the quantity of products sent from DCs to demand points. Relation (7) demonstrates the limitation of the capacity of MSs. Constraint (8) demonstrates that each MS only can be opened with one technology.

$$\begin{array}{cc}{\sum }_{m,j,i}{\mathit{MDQ}}_{\mathit{pijlm}}={\sum }_{k,m}{\mathit{DCQ}}_{\mathit{pjkm}}& \forall p,j\end{array}$$ 6

$$\begin{array}{cc}{\sum }_{m,j,i}{\mathit{MDQ}}_{\mathit{pijlm}}\le {\sum }_l{\mathit{MCP}}_{\mathit{ilp}}.{\mathit{MX}}_{\mathit{il}}& \forall i,p\end{array}$$ 7

$$\begin{array}{cc}{\sum }_l{\mathit{MX}}_{\mathit{il}}\le 1& \forall i\end{array}$$ 8

Constraint (9) determines the quantity of the original product sent to customers and the quantity of the shortage for the original product. Also, constraint (10) measures the amount of repaired products shipped to the customers and the amount of the shortage for the repaired product. Relation (11) is the capacity constraint of DCs.

$$\begin{array}{cc}{\sum }_{m,j}{\mathit{DCQ}}_{\mathit{pjkm}}+{SH1}_{\mathit{pk}}\ge {\widetilde{D1}}_{\mathit{pk}}& \forall k,p\end{array}$$ 9

$$\begin{array}{cc}{\sum }_{m,j}{\mathit{RDCQ}}_{\mathit{djkm}}+{SH2}_{\mathit{dk}}\ge {\widetilde{D2}}_{\mathit{dk}}& \forall d,k\end{array}$$ 10

$$\begin{array}{cc}{\sum }_{p,d,k,m,j}({\mathit{DCQ}}_{\mathit{pjkm}}+{\mathit{RDCQ}}_{\mathit{djkm}})\le {\mathit{DCP}}_j.{\mathit{DX}}_j& \forall j\end{array}$$ 11

Constraint (12) shows the quantity of returned products shipped to CCs. On the other side, relation (13) demonstrates the capacity constraint for CCs. Equation (14) shows the quantity of products shipped from CCs to RCs. Relation (15) calculates the quantity of products sent from CCs to disposal centers.

$$\begin{array}{cc}{\sum }_{c,m}{\mathit{CCQ}}_{\mathit{pkcm}}={\sum }_{j,m}{\theta }_p.{\mathit{DCQ}}_{\mathit{pjkm}}& \forall p,k\end{array}$$ 12

$$\begin{array}{cc}{\sum }_{p,k,m}{\mathit{CCQ}}_{\mathit{pkcm}}\le {\mathit{CCP}}_c.{\mathit{CX}}_c& \forall c\end{array}$$ 13

$$\begin{array}{cc}{\sum }_{t,m}{\mathit{CRQ}}_{\mathit{pctm}}={\sum }_{k,m}\sigma .{\mathit{CCQ}}_{\mathit{pkcm}}& \forall c,p\end{array}$$ 14

$$\begin{array}{cc}{\sum }_{q,m}{\mathit{CDQ}}_{\mathit{pcqm}}={\sum }_{k,m}(1-\sigma ).{\mathit{CCQ}}_{\mathit{pkcm}}& \forall c,p\end{array}$$ 15

Equations (16) and (17) measure the quantity of repaired products shipped from RCs to DCs. Constraint (17) demonstrates the RCs’ capacity limitation. Eventually, Eq. (19) shows that an RC only can be opened by one technology.

$$\begin{array}{cc}{\sum }_{d,l,j,m}{\mathit{RDQ}}_{\mathit{dtjlm}}={\sum }_{p,c,m}{\mathit{CRQ}}_{\mathit{pctm}}& \forall t\end{array}$$ 16

$$\begin{array}{cc}{\sum }_{k,m}{\mathit{RDCQ}}_{\mathit{djkm}}={\sum }_{m,l}{\mathit{RDQ}}_{\mathit{dtjlm}}& \forall d,j,t\end{array}$$ 17

$$\begin{array}{cc}{\sum }_{m,j,i,d}{\mathit{RDQ}}_{\mathit{dtjlm}}\le {\sum }_l{\mathit{RCP}}_{\mathit{tl}}.{\mathit{RX}}_{\mathit{tl}}& \forall t\end{array}$$ 18

$$\begin{array}{cc}{\sum }_l{\mathit{RX}}_{\mathit{tl}}\le 1& \forall t\end{array}$$ 19

Relations (20)–(30) show the relationship between the location and transportation binary variables.

$$\begin{array}{cc}{\mathit{TSM}}_{\mathit{msi}}\le {\mathit{SS}}_s& \forall m,s,i\end{array}$$ 20

$$\begin{array}{cc}{\mathit{TSM}}_{\mathit{msi}}\le {\sum }_l{\mathit{MX}}_{\mathit{il}}& \forall i,m,s\end{array}$$ 21

$$\begin{array}{cc}{\mathit{TMD}}_{\mathit{mij}}\le {\sum }_l{\mathit{MX}}_{\mathit{il}}& \forall m,i,j\end{array}$$ 22

$$\begin{array}{cc}{\mathit{TMD}}_{\mathit{mij}}\le {\mathit{DX}}_j& \forall j,m,i\end{array}$$ 23

$$\begin{array}{cc}{\mathit{TDK}}_{\mathit{mjk}}\le {\mathit{DX}}_j& \forall k,m,j\end{array}$$ 24

$$\begin{array}{cc}{\mathit{TKC}}_{\mathit{mkc}}\le {\mathit{CX}}_c& \forall k,m,c\end{array}$$ 25

$$\begin{array}{cc}{\mathit{TCR}}_{\mathit{mct}}\le {\mathit{CX}}_c& \forall m,c,t\end{array}$$ 26

$$\begin{array}{cc}{\mathit{TCD}}_{\mathit{mcq}}\le {\mathit{CX}}_c& \forall m,c,q\end{array}$$ 27

$$\begin{array}{cc}{\mathit{TCR}}_{\mathit{mct}}\le {\sum }_l{\mathit{RX}}_{\mathit{tl}}& \forall m,c,t\end{array}$$ 28

$$\begin{array}{cc}{\mathit{TRD}}_{\mathit{mtj}}\le {\sum }_l{\mathit{RX}}_{\mathit{tl}}& \forall m,t,j\end{array}$$ 29

$$\begin{array}{cc}{\mathit{TRD}}_{\mathit{mtj}}\le {\mathit{DX}}_j& \forall m,t,j\end{array}$$ 30

Constraints (31)–(38) show the relationship between the flow balance variables and the transportation binary variables.

$$\begin{array}{cc}{\sum }_r{\mathit{SMR}}_{\mathit{rsim}}\le BigM.{\mathit{TSM}}_{\mathit{msi}}& \forall s,m,i\end{array}$$ 31

$$\begin{array}{cc}{\sum }_{p,l}{\mathit{MDQ}}_{\mathit{pijlm}}\le BigM.{\mathit{TMD}}_{\mathit{mij}}& \forall j,i,m\end{array}$$ 32

$$\begin{array}{cc}{\sum }_p{\mathit{DCQ}}_{\mathit{pjkm}}\le BigM.{\mathit{TDK}}_{\mathit{mjk}}& \forall k,m,m\end{array}$$ 33

$$\begin{array}{cc}{\sum }_p{\mathit{CCQ}}_{\mathit{pkcm}}\le BigM.{\mathit{TKC}}_{\mathit{mkc}}& \forall c,m,k\end{array}$$ 34

$$\begin{array}{cc}{\sum }_p{\mathit{CRQ}}_{\mathit{pctm}}\le BigM.{\mathit{TCR}}_{\mathit{mct}}& \forall m,c,t\end{array}$$ 35

$$\begin{array}{cc}{\sum }_p{\mathit{CDQ}}_{\mathit{pcqm}}\le BigM.{\mathit{TCD}}_{\mathit{mcq}}& \forall m,c,q\end{array}$$ 36

$$\begin{array}{cc}{\sum }_{l,p}{\mathit{RDQ}}_{\mathit{dtjlm}}\le BigM.{\mathit{TRD}}_{\mathit{mtj}}& \forall m,c,t\end{array}$$ 37

$$\begin{array}{cc}{\sum }_d{\mathit{RDCQ}}_{\mathit{djkm}}\le {\mathit{TDK}}_{\mathit{mjk}}& \forall m,t,j\end{array}$$ 38

Robust possibilistic programming counterpart

Since the supply chain network design problem involves different decision levels especially long-term decisions, uncertainty has been considered as a big issue in this problem. Ignoring the uncertainty in the design phase may lead to achieving unrealistic results that can result in irreparable financial losses (Gholizadeh et al. 2020a). Usually, in the SCND problem, some historical data are available but there is a lack of knowledge on input data that can be gathered from the experts (Nayeri et al. 2020). The mentioned condition is called epistemic uncertainty that known as a common type of uncertainty in the SCND problem (Bairamzadeh et al. 2018). In this regard, one of the most powerful methods to tackle epistemic uncertainty is the robust possibilistic programming (RPP) method that widely used in previous related studies and showed good performance (see Pishvaee et al. 2012b, a; Hamidieh et al. 2017; Ghaderi et al. 2018; Nayeri et al. 2020; Rabbani et al. 2020; Habib et al. 2021). Based on the mentioned reasons, we have employed the RPP approach to tackle uncertainty in this study. To provide more explanations about the RPP method, consider the following compact model.

$$\begin{array}{c}MinZ=f.y+\tilde{c}.x\hfill \\ A.x\ge \tilde{d}\hfill \\ \begin{array}{c}{A}^{\prime }.x\le {\tilde{d}}^{\prime }\hfill \\ B.x=0\hfill \\ s.x\le N.y\hfill \end{array}\hfill \end{array}$$ 39

In model (39), $\tilde{c}$, $\tilde{d}$, and ${\tilde{d}}^{{}^{\prime }}$ are the trapezoidal fuzzy numbers with four critical point (i.e., $\tilde{c}=(c_1,c_2,c_3,c_4)$); $f,A$,$A^{{}^{\prime }}$, $B,s$, and $N$ are the deterministic parameters. $y$ is the binary variable and $x$ is the continuous variable. The RPP counterpart for model (39) can be formulated as follows:

$$\begin{array}{cc}\hfill Minf.y+& \left(\frac{c_1+c_2+c_3+c_4}{4}\right).x+\eta ·\left(Z_{\mathit{max}},-,E,\left[Z\right]\right)\hfill \\ \hfill & +{\pi }_1·\left(d_4,-,\left(1,-,{\alpha }_m\right),.,d_3,+,{\alpha }_m,.,d_4\right)\hfill \\ \hfill & +{\pi }_2·\left(\left(1,-,{\alpha }_m\right),.,d_2,+,{\alpha }_m,.,d_1,-,d_1\right)\hfill \\ \hfill & A.x\ge \left(1,-,{\alpha }_m\right).{d^{\prime }}_{\left(2\right)}+{\alpha }_m.{d^{\prime }}_{\left(4\right)}\hfill \\ \hfill & \forall mA.x\le \left(1,-,{\alpha }_m\right).{d^{\prime }}_{\left(2\right)}+{\alpha }_m.{d^{\prime }}_{\left(1\right)}\hfill \\ \hfill & \forall mB.x=0\hfill \\ \hfill & s.x\le N.y0.5\le {\alpha }_m\le 1x\ge 0y\in \left\{0,,,1\right\}\hfill \end{array}$$ 40

In model (40), the first and second sections of the objective function showed the expected value (average) for of the costs ($E[Z]$). The third section shows the optimality robustness that has been incorporated by penalizing the difference between the worst case from the average. In this section, $\eta$ shows the optimality robustness penalty cost and $Z_{\mathit{max}}$ is the worst case that is calculated according to Eq. (41). The last section of the objective function demonstrates the feasibility robustness. In this regard,${\pi }_i$ represents the feasibility robustness penalty costs and ${\alpha }_m$ shows the satisfaction level.

$$Z_{\mathit{max}}=f.y+c_4.x$$ 41

Based on the above-mentioned points, the RPP counterpart model for the research problem can be formulated as follows.

$$\begin{array}{c}MinZ1={\sum }_s\frac{{\mathit{HSS}}_s^1+{\mathit{HSS}}_s^2+{\mathit{HSS}}_s^3+{\mathit{HSS}}_s^4}{4}.{\mathit{SS}}_s+{\sum }_{i,l}\frac{{\mathit{HSM}}_{\mathit{il}}^1+{\mathit{HSM}}_{\mathit{il}}^2+{\mathit{HSM}}_{\mathit{il}}^3+{\mathit{HSM}}_{\mathit{il}}^4}{4}.{\mathit{MX}}_{\mathit{il}}\\ +{\sum }_j\frac{{\mathit{HSD}}_j^1+{\mathit{HSD}}_j^2+{\mathit{HSD}}_j^3+{\mathit{HSD}}_j^4}{4}.{\mathit{DX}}_j\\ +{\sum }_c\frac{{\mathit{HSC}}_c^1+{\mathit{HSC}}_c^2+{\mathit{HSC}}_c^3+{\mathit{HSC}}_c^4}{4}.{\mathit{CX}}_c\\ +{\sum }_{t,l}\frac{{\mathit{HSR}}_{\mathit{tl}}^1+{\mathit{HSR}}_{\mathit{tl}}^2+{\mathit{HSR}}_{\mathit{tl}}^3+{\mathit{HSR}}_{\mathit{tl}}^4}{4}.{\mathit{RX}}_{\mathit{tl}}\\ +{\sum }_{r,s,i,m}\frac{{\mathit{HMR}}_{\mathit{rs}}^1+{\mathit{HMR}}_{\mathit{rs}}^2+{\mathit{HMR}}_{\mathit{rs}}^3+{\mathit{HMR}}_{\mathit{rs}}^4}{4}.{\mathit{SMR}}_{\mathit{rsim}}\\ +{\sum }_{j,p,i,m,t}\frac{{\mathit{HTM}}_{\mathit{pil}}^1+{\mathit{HTM}}_{\mathit{pil}}^2+{\mathit{HTM}}_{\mathit{pil}}^3+{\mathit{HTM}}_{\mathit{pil}}^4}{4}.{\mathit{MDQ}}_{\mathit{pijtm}}\\ +{\sum }_{j,p,m,k,d}\frac{{\mathit{HDP}}_j^1+{\mathit{HDP}}_j^2+{\mathit{HDP}}_j^3+{\mathit{HDP}}_j^4}{4}.({\mathit{DCQ}}_{\mathit{pjkm}}+{\mathit{RDCQ}}_{\mathit{djkm}})\\ +{\sum }_{p,k,m,t}\frac{{\mathit{HCC}}_{\mathit{pc}}^1+{\mathit{HCC}}_{\mathit{pc}}^2+{\mathit{HCC}}_{\mathit{pc}}^3+{\mathit{HCC}}_{\mathit{pc}}^4}{4}.{\mathit{CCQ}}_{\mathit{pkcm}}\\ +{\sum }_{d,l,j,m,t}\frac{{\mathit{HTM}}_{\mathit{tl}}^1+{\mathit{HTM}}_{\mathit{tl}}^2+{\mathit{HTM}}_{\mathit{tl}}^3+{\mathit{HTM}}_{\mathit{tl}}^4}{4}.{\mathit{RDQ}}_{\mathit{dtjlm}}\\ +{\sum }_{p,k}\frac{{\mathit{OSH}}_{\mathit{pk}}^1+{\mathit{OSH}}_{\mathit{pk}}^2+{\mathit{OSH}}_{\mathit{pk}}^3+{\mathit{OSH}}_{\mathit{pk}}^4}{4}.{SH1}_{\mathit{pk}}\\ +{\sum }_{d,k}\frac{{\mathit{RSH}}_{\mathit{pk}}^1+{\mathit{RSH}}_{\mathit{pk}}^2+{\mathit{RSH}}_{\mathit{pk}}^3+{\mathit{RSH}}_{\mathit{pk}}^4}{4}.{SH2}_{\mathit{dk}}\\ +{\sum }_m\frac{{\mathit{tc}}_m^1+{\mathit{tc}}_m^2+{\mathit{tc}}_m^3+{\mathit{tc}}_m^4}{4}.({\sum }_{r,s,i}{Ds1}_{\mathit{si}}.{\mathit{SMR}}_{\mathit{rsim}}\\ +{\sum }_{j,p,i,t}{Ds2}_{\mathit{ij}}.{\mathit{MDQ}}_{\mathit{pijtm}}+{\sum }_{j,p,k}{Ds3}_{\mathit{jk}}.{\mathit{DCQ}}_{\mathit{pjkm}}+{\sum }_{j,d,k}{Ds3}_{\mathit{jk}}.{\mathit{RDCQ}}_{\mathit{djkm}}\\ +{\sum }_{c,p,k}{Ds4}_{\mathit{kc}}.{\mathit{CCQ}}_{\mathit{pkcm}}+{\sum }_{c,p,t}{Ds5}_{\mathit{kt}}.{\mathit{CRQ}}_{\mathit{pctm}}+{\sum }_{c,p,q}{Ds6}_{\mathit{cq}}.{\mathit{CDQ}}_{\mathit{pcqm}}\\ +{\sum }_{c,p,q}{Ds7}_{\mathit{tj}}.{\mathit{RDCQ}}_{\mathit{djkm}})+\left(Z_{\mathit{max}},-,E,[Z1]\right)\\ +{\pi }_1.\left({\sum }_{p,k},{D1}_{\mathit{pk}}^4,-,\left(1,-,{\alpha }_1\right),.,{D1}_{\mathit{pk}}^3,+,{\alpha }_1,.,{D1}_{\mathit{pk}}^4\right)\\ +{\pi }_2.\left({\sum }_{d,k},{D2}_{\mathit{dk}}^4,-,\left(1,-,{\alpha }_2\right),.,{D2}_{\mathit{dk}}^3,+,{\alpha }_2,.,{D2}_{\mathit{dk}}^4\right)\end{array}$$ 42

$$\begin{array}{c}MinZ2={\sum }_{j,p,i,m,t}\frac{{\mathit{mce}}_{\mathit{pl}}^1+{\mathit{mce}}_{\mathit{pl}}^2+{\mathit{mce}}_{\mathit{pl}}^3+{\mathit{mce}}_{\mathit{pl}}^4}{4}.{\mathit{MDQ}}_{\mathit{pijtm}}\\ +{\sum }_{d,l,j,m,t}\frac{{\mathit{rce}}_m^1+{\mathit{rce}}_m^2+{\mathit{rce}}_m^3+{\mathit{rce}}_m^4}{4}.{\mathit{RDCQ}}_{\mathit{dtjlm}}\\ +{\sum }_m\frac{{\mathit{tce}}_m^1+{\mathit{tce}}_m^2+{\mathit{tce}}_m^3+{\mathit{tce}}_m^4}{4}.({\sum }_{r,s,i}{Ds1}_{\mathit{si}}.{\mathit{SMR}}_{\mathit{rsim}}\\ +{\sum }_{j,p,i,t}{Ds2}_{\mathit{ij}}.{\mathit{MDQ}}_{\mathit{pijtm}}+{\sum }_{j,p,k}{Ds3}_{\mathit{jk}}.{\mathit{DCQ}}_{\mathit{pjkm}}+{\sum }_{j,d,k}{Ds3}_{\mathit{jk}}.{\mathit{RDCQ}}_{\mathit{djkm}}\\ +{\sum }_{c,p,k}{Ds4}_{\mathit{kc}}.{\mathit{CCQ}}_{\mathit{pkcm}}+{\sum }_{c,p,t}{Ds5}_{\mathit{kt}}.{\mathit{CRQ}}_{\mathit{pctm}}+{\sum }_{c,p,q}{Ds6}_{\mathit{cq}}.{\mathit{CDQ}}_{\mathit{pcqm}}\\ +{\sum }_{c,p,q}{Ds7}_{\mathit{tj}}.{\mathit{RDCQ}}_{\mathit{djkm}})\end{array}$$ 43

$$MaxZ3=\frac{{\sum }_{m,p,j,k}{\mathit{DCQ}}_{\mathit{pjkm}}+{\sum }_{m,jd,k,j}{\mathit{RDCQ}}_{\mathit{djkm}}}{{\sum }_{p,k}\frac{{D1}_{\mathit{pk}}^1+{D1}_{\mathit{pk}}^2+{D1}_{\mathit{pk}}^3+{D1}_{\mathit{pk}}^4}{4}+{\sum }_{d,k}\frac{{D2}_{\mathit{dk}}^1+{D2}_{\mathit{dk}}^2+{D2}_{\mathit{dk}}^3+{D2}_{\mathit{dk}}^4}{4}}$$ 44

$$\begin{array}{cc}{\sum }_{j,m}{\mathit{DCQ}}_{\mathit{pjkm}}+{SH1}_{\mathit{pk}}\ge \left(1,-,{\alpha }_1\right).{D1}_{\mathit{pk}}^3+{\alpha }_1.{D1}_{\mathit{pk}}^4& \forall p,k\end{array}$$ 45

$$\begin{array}{cc}{\sum }_{j,m}{\mathit{RDCQ}}_{\mathit{djkm}}+{SH2}_{\mathit{dk}}\ge \left(1,-,{\alpha }_2\right).{D2}_{\mathit{dk}}^3+{\alpha }_2.{D2}_{\mathit{dk}}^4& \forall d,k\end{array}$$ 46

Solving method

In this section, the solution procedure of this study is presented. To solve the proposed MOMIP, we have two main challenges: (a) the proposed model is a multi-objective one and (b) the research problem is an NP-hard (Tiwari et al. 2016; Asadi-Gangraj and Nayeri 2018; Çağrı et al. 2018). In this regard, to cope with these challenges, we develop an efficient hybrid method. In this way, we combine the meta-goal programming method (to transform the MOMIP model to a single-objective model) with a heuristic method (to cope with the complexity of the problem). In the following, we briefly describe the mentioned approaches.

Meta-goal programming

One of the popular approaches to solve multi-objective problems is goal programming (GP) (Nayeri et al. 2018; Mamashli et al. 2021b; Razavi et al. 2021). In the field of the SCND problem, different variants of the goal programming method is applied and they achieved good results (see Hocine et al. 2020; Mamashli and Javadian 2020; Nayeri et al. 2020; Pourmehdi et al. 2020; Homayouni et al. 2021; Jamali et al. 2021; Mamashli et al. 2021a). In the current study, the meta-goal programming (MGP) method offered by Uría et al. (2002) is applied to solve the proposed MOMIP. The main advantages of this method are its ability to obtain more balanced solutions and its flexibility to model the preferences of the decision-makers (DMs) comparing to the other variants of GP (Benítez-Fernández and Ruiz 2019). Suppose $t_i$ is the goal value for i-th objective function that determined by the decision-maker (DM), $n_i$ shows negative deviation and $p_i$ is positive deviation. Now consider expression (47) that denoted algebraic structure of the generic i-th goal. Also, there are three types of deviations which interested readers can be refer to (Uría et al. 2002; Benítez-Fernández and Ruiz 2019) for more study.

$$f_i\left(x\right)+n_i-p_i=t_i$$ 47

Because the goals of this research are “less is better,” the unwanted deviation is positive ones (Uría et al. 2002). Uría et al. (2002) defined three types of meta-goals as follows:

• Type 1: As shown in relation (48), there is a certain bound ($Q_1$) that the sum of unwanted percentage deviation variables cannot surpass it.

  $$\sum _{i=1}^q{\delta }_i.\frac{p_i}{t_i}\le Q_1$$ 48

It should be noted that ${\delta }_i$ is a preferential weight and to normalizing the deviation variables, them dividing among their corresponding target value.

• Type 2: As shown in relation (49), there is a certain bound ($Q_2$) that the maximum percentage deviation should not be greater than it.

  $$\begin{array}{ccc}{\mathit{Max}}_{i=1,...,q}\left\{{\delta }_i,.,\frac{p}{t_i}\right\}\le Q_2& \leftrightarrow & \left\{\begin{array}{cc}{\delta }_i.\frac{p_i}{t_i}-D\le 0& i=1,\dots ,q\\ D\le Q_2\end{array}\right)\end{array}$$ 49

where $D$ shows the maximum weighted percentage deviation.

• Type 3: As shown in relation (50), there is a certain bound ($Q_3$) that the percentage of unachieved goals should not be greater than it.where $G_i$ is a binary variable and $M_i$ is a large number. Due to above definitions, the MGP is modeled as follows:

  $$\begin{array}{c}{p}_i-M_i.y_i\le 0,i=1,\dots ,q\\ \frac{{\sum }_{i=1}^q{G}_i}{q}\le Q_3\end{array}$$ 50

$$\begin{array}{c}Min({\beta }_1,{\beta }_2,{\beta }_3)\hfill \\ \begin{array}{cc}{f}_i\left(x\right)+n_i-p_i=t_i& i=1,\dots ,q\end{array}\hfill \\ \begin{array}{c}{g}_j(x)\le b_j\hfill \\ {\sum }_{i=1}^q{\delta }_i.\frac{p_i}{t_i}+{\alpha }_1-{\beta }_1=Q_1\hfill \\ \begin{array}{c}\begin{array}{cc}{\delta }_i.\frac{p_i}{t_i}-D\le 0& i=1,\dots ,q\end{array}\hfill \\ D{+\alpha }_2-{\beta }_2=Q_2\hfill \\ \begin{array}{c}\begin{array}{cc}{p}_i-M_i.G_i\le 0& i=1,\dots ,q\end{array}\hfill \\ \frac{{\sum }_{i=1}^q{G}_i}{q}{+\alpha }_3-{\beta }_3=Q_3\hfill \\ \begin{array}{cc}x,n_i,p_i,{\alpha }_j,{\beta }_j\ge 0G_i\in \{0,1\}& \begin{array}{c}i=1,\dots ,q\\ j=1,2,3\end{array}\end{array}\hfill \end{array}\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ 51

The objective function of (51) can in turn take the weighted or the MinMax form which in this paper we consider weighted form.

Heuristic method

Since the research problem is known as an NP-hard one, this study employs an efficient heuristic method that widely used in the SCND problem (see Kaur and Singh 2018; Homayouni et al. 2021; Shafiee et al. 2021) to handle the complexity of the research problem. The steps of this algorithm are listed below (Kaur and Singh 2018):

• First step: Relax the proposed model from the binary constraints (convert the binary variables to continuous ones).

• Second step: Solve the relaxed model.

• Third step: Record all non-zero quantities of $\text{relaxed variables}$ which are obtained by solving the proposed model.

• Fourth step: Equalize each non-zero quantity of $\text{relaxed variables}$ to 1, and set them as constraints to the main model.

• Fifth step: Solve the created model optimally.

The pseudo-code of the developed hybrid method is depicted in Fig. 3.

Fig. 3.

Pseudo-code of the proposed hybrid method

Computational results

Case study

The COVID-19 pandemic has led to a significant disruption in the world. This virus, which has negative effects on the human respiratory system, has led to many deaths in the past 2 years. After the recent pandemic (COVID-19), the demand for medical devices has dramatically increased. One of the most widely used medical devices during the recent pandemic is the ventilator device. On the other side, the logistics process of this product is adapted with the proposed CLSC in the current study. In this regard, in many cases when this product becomes EOU or EOL, it is collected and remanufactured for re-using. Hence, this research has selected the ventilator device as a case study. The main purpose of using a ventilator is to establish mechanical ventilation and support the lungs to supply oxygen to the patient. In fact, the ventilator does not cure the disease, but can only keep the patient alive to cure the underlying disease. Figure 4 depicts the ventilator and its application. The input data for solving the proposed MOMIP can be found in the Supplementary materials. It should be noted that the required data are gathered from the related literature (such as Hasani et al. 2015; Pedram et al. 2017; Nayeri et al. 2020and the opinion of the experts of the case study company).

Fig. 4.

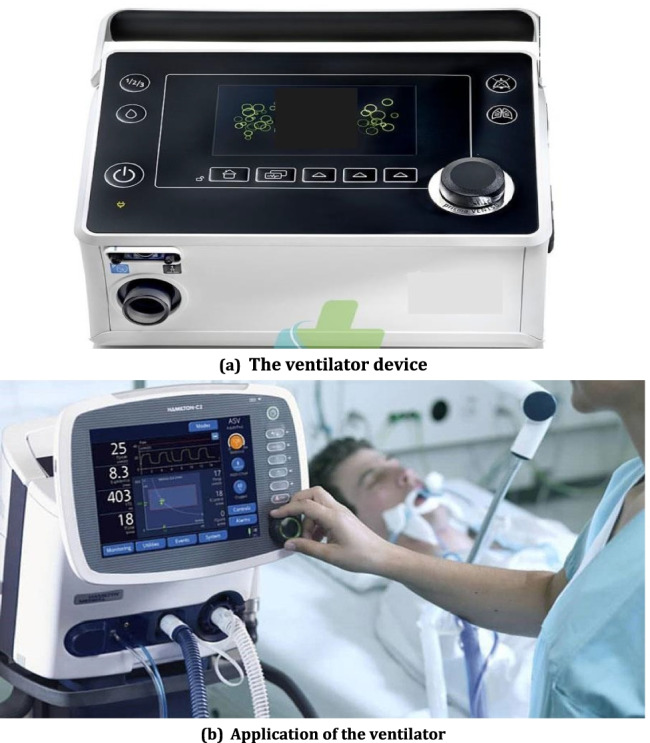
The ventilator devices and its application. a The ventilator device. b Application of the ventilator

Reporting the results

In this section, the offered MOMIP are solved and results are presented. At the outset, to show the performance of the developed solution method, the problem is solved in different sizes and the achieved results by the developed hybrid method (HMGP) are compared with the traditional MGP (TMGP). To do this, two measures are utilized: (i) GAP and (ii) CPU time, which the gap is calculated based on the following relation.

$$GAP=\frac{{\mathit{HMGP}}_{\mathit{sol}}-{\mathit{TMGP}}_{\mathit{sol}}}{{\mathit{TMGP}}_{\mathit{sol}}}\times 100$$ 52

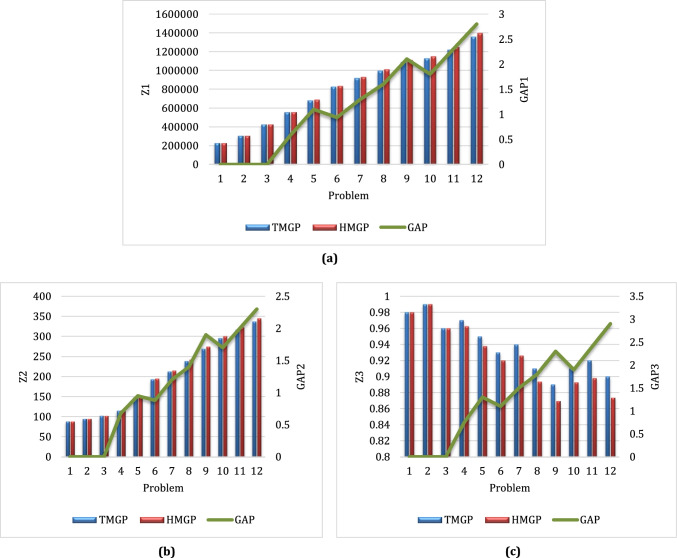
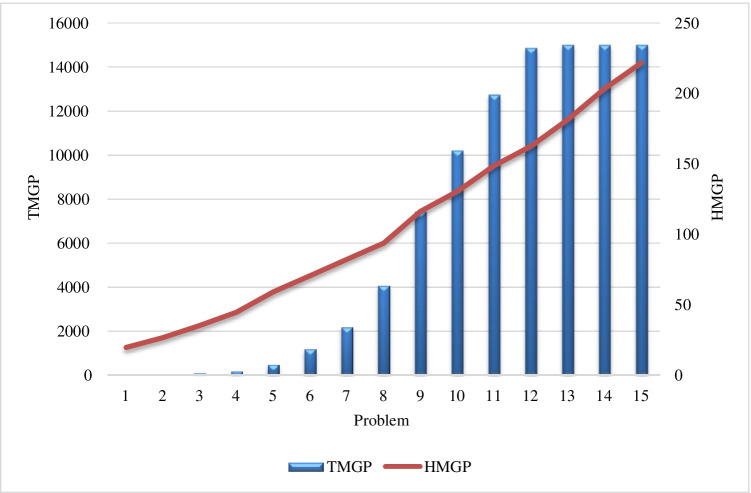
where ${\mathit{HMGP}}_{\mathit{sol}}$ is the solution obtained by the proposed hybrid method and ${\mathit{TMGP}}_{\mathit{sol}}$ represents the solution obtained by the TMGP method. Table 1 shows the results of solving the proposed MOMIP by the two mentioned methods. As shown in Table 1, the HMGP can achieve optimal/near-optimal solutions on a better time than the TMGP. In this regard, the TMGP could not solve test problems 13, 14, and 15 in less than 15,000 (s). To better understand, see Figs. 5 and 6 that compare the two methods in terms of the GAPs and CPU time, respectively. The obtained results confirm the performance and efficiency of the developed HMGP.

Table 1.

Comparing the results of TMGP and HMGP

Problem	TMGP				HMGP
	$\mathbf{Z}1\times {10}^3$	Z2	Z3	CPU time (s)	$\mathbf{Z}1\times {10}^3$	GAP1	Z2	GAP2	Z3	GAP3	CPU time (s)
1	228,846.3	88.3	0.98	13.2	228,846.3	0	88.3	0	0.98	0	19.6
2	304,753.8	94.8	0.99	28.4	304,753.8	0	94.8	0	0.99	0	26.5
3	427,039.5	102.5	0.96	96.7	427,039.5	0	102.5	0	0.96	0	35.2
4	556,816.2	115.1	0.97	175.3	560,045.7	0.58	115.9	0.68	0.96	0.75	44.7
5	680,956.5	148.6	0.95	482.5	688,447.0	1.1	150.0	0.95	0.94	1.3	59.2
6	826,428.2	192.8	0.93	1190.3	834,196.6	0.94	194.5	0.88	0.92	1.1	70.5
7	916,635.7	212.3	0.94	2182.6	928,552.0	1.3	214.8	1.2	0.93	1.5	82.1
8	994,528.1	238.5	0.91	4068.5	1,010,440.5	1.6	241.8	1.4	0.89	1.8	93.7
9	1,086,682.5	269.2	0.89	7436.8	1,109,502.8	2.1	274.3	1.9	0.87	2.3	116.3
10	1,129,325.8	295.5	0.91	10,207.1	1,149,653.7	1.8	300.5	1.7	0.89	1.9	130.5
11	1,219,534.2	316.4	0.92	12,752.5	1,247,583.5	2.3	322.7	2	0.90	2.4	148.7
12	1,358,619.6	337.2	0.9	14,863.2	1,396,660.9	2.8	345.0	2.3	0.87	2.9	162.6
13	–	–	–	> 15,000	1,459,432.1	–	361.8	–	0.89	–	181.4
14	–	–	–	> 15,000	1,601,856.8	–	372.5	–	0.92	–	203.5
15	–	–	–	> 15,000	1,724,369.5	–	390.1	–	0.90	–	221.7

Fig. 5.

Comparison of the TMGP and HMFP according to solutions’ quality. a The first objective function. b The second objective function. c The third objective function

Fig. 6.

Comparison of the TMGP and HMFP according to CPU time

Sensitivity analysis

Demand

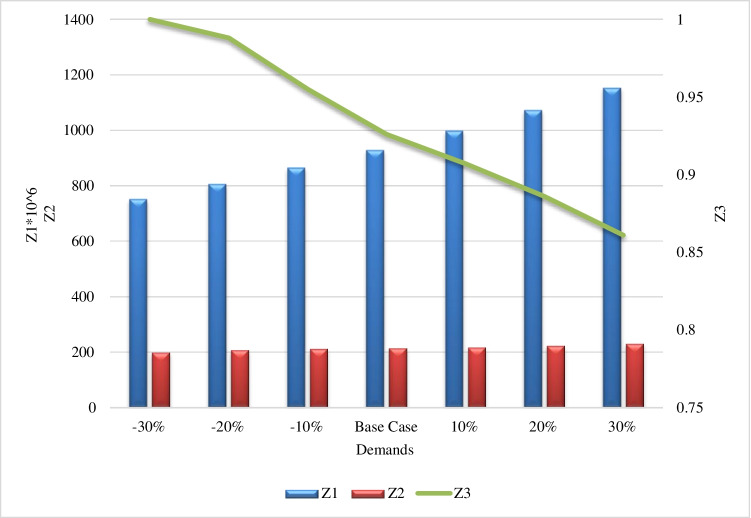
One of the most important parameters of the offered model is the demand (demand of original product and demand of repaired product). In this section, we have analyzed the behavior of the research problem according to changing the size of the demands. For this purpose, the problem has been solved with different values for the mentioned parameters and reported the achieved results in Fig. 7. According to Fig. 7 when demand is increased, the environmental impact and the total costs are increased but the responsiveness of the SC (the third objective function) is decreased. In this regard, a 30% increase in demand from its base case value leads to a 24% increase in the total costs, a 10% increase in carbon emissions, and an 8% decrease in responsiveness. In addition, by 30% decreasing the demand size from its base case, Z1 and Z2 are respectively decreased by 22% and 8%, and Z3 is increased by 7%.

Fig. 7.

The behavior of the research problem according to demands changes

Capacity

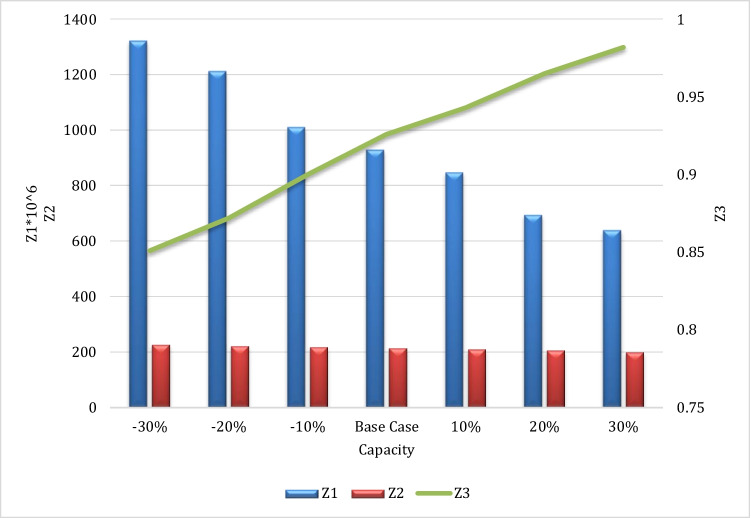
In this section, we have conducted a sensitivity analysis to examine the role of the capacity parameter. Figure 8 illustrates the behavior of the research problem according to changing the capacity parameter. As can be seen in this figure, when the capacity parameter is increased, the first objective function is decreased, but the second and third objective functions are increased. In this regard, by shifting the value of capacity from − 30 to + 30%, the total cost and environmental impacts are decreased by 52% and 12%, respectively. Also, this change leads to increasing the responsiveness of the supply chain by about 13%.

Fig. 8.

The impact of capacity on the research problem

Rate of return

This section is devoted to analyzing the behavior of the studied system according to changing the rate of return of the products parameter. In this regard, the problem is solved under different values for the mentioned parameter and the results are depicted in Fig. 9. Based on this figure, an increase in the rate of return leads to an increase in all of the objective functions. In this way, when the rate of return is increases from 0.3 to 0.7, Z1 is increased by 12%, Z2 is increased by 10%, and Z3 is increased by 8%.

Fig. 9.

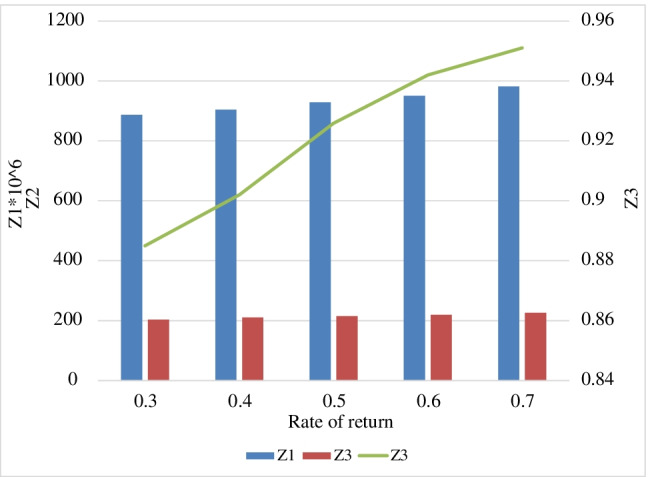
The behavior of the research problem according to changing the rate of return parameter

Feasibility robustness

Here, the effect of changing parameter $\pi$ on the offered MOMIP is analyzed. The achieved results from sensitivity analysis have been presented in Table 2. According to the results, changes in $\pi$ negligibly affect the objective functions. The minimum satisfaction level remains constant and equal to 1, as well.

Table 2.

Sensitivity analysis on $\pi$, when $\eta =0.6$

$\mathit{\pi }=1000$		$\mathit{\pi }=10000$		$\mathit{\pi }=100000000$
Z1	926,816,350.8	Z1	928,551,964.1	Z1	929,635,782.4
Z2	213.25	Z2	214.84	Z2	215.47
Z3	0.930	Z3	0.925	Z3	0.919
$\alpha$	1	$\alpha$	1	$\alpha$	1

Optimality robustness

This section is dedicated to investigating the impact of optimality robustness penalty cost on the results. Table 3 shows the result of sensitivity analysis. As can be seen in Table 3, when $\eta$ increases from 0.3 to 0.9, the model tries to get values closer than to the $Z_{\mathit{max}}$. In general, by increasing the value of $\eta$, the total cost is increased, too. This behavior is occurred due to a phenomenon, namely, “robustness price.” It should be noted that the robustness price shows the costs that entered in the problem to face the uncertainties.

Table 3.

Sensitivity analysis on $\eta$, when $\pi =10000$

$\eta =0.3$		$\eta =0.6$		$\eta =0.9$
Z1	918038142.4	Z1	928551964.1	Z1	935824833.9
Z2	208.44	Z2	214.84	Z2	221.82
Z3	0.938	Z3	0.925	Z3	0.904

Managerial implications

In this section, we try to provide some useful managerial insights obtained from this study. These implications have been listed below.

• This study has focused on the CLSCN configure problem with environmental and responsiveness features. Hence, this research can give a good view to the leaders of the SC to manage their business according to the two mentioned features. Also, this study helps the managers to see the impact of the uncertainty on the SC management problem.

• Based on Fig. 7, by increasing the demand parameter, the first objective function (costs) is increased, too. The main reasons for this behavior are that increasing the demand results in increasing the establishment, production, distribution, shortage, and transportation costs. One of the efficient strategies to cope with this condition is sub-contracting that can prevent the enhancement of the cost.

• Fig. 7 showed that an increase in demand has resulted in increasing environmental damages. In order to increase the greenness of the SC, utilizing the TMs and technologies with fewer carbon emissions can be a good action. Although these technologies and transportation modes have higher setup costs and lead to enhancement of the costs, the leaders must know that using greener facilities leads to providing a green image from the company in the eyes of customers, which results in increasing the loyalty of customers.

• Fig. 7 indicates that when the demand size is increased, the responsiveness of the SC is decreased. This point demonstrates that the shortage of products is increased by increasing the demand size. To tackle this condition, sub-contracting may be a good strategy that can manage the capacity temporarily and increase the met demand.

• According to Fig. 9, a decrease in the rate of return parameter results in decreasing the responsiveness of the SC. In this regard, considering incentive plans for customers to return the goods can be a good strategy for increasing the rate of return that leads to increasing the responsiveness of the supply chain.

Theoretical implications

The main theoretical contribution of the current research is combining the green and responsive aspects in the CLSCN that was ignored by previous studies. In this regard, we have designed a CLSC network and considered the carbon emissions as an environmental measure and the ratio of met demand over total demand as the responsiveness measure. On the other side, this paper has investigated the problem under uncertainty and employed the robust possibilistic programming method to tackle uncertainty. To the best of our knowledge, this is the first paper that has proposed a multi-objective robust possibilistic model to design a GRCLSCN. Comparing to the similar approach to tackle the epistemic uncertainty (e.g., fuzzy programming), the employed approach (robust possibilistic programming) has two main advantages as follows: (i) this method considers the risk-aversion level of output decisions that can help decision-makers (Fazli-Khalaf et al. 2017), and (ii) this method has capability to finding optimal value for the satisfaction levels (Talaei et al. 2016). On the other hand, this study has developed an efficient solution method by integrating a heuristic method and the meta-goal programming method. Comparing to the other versions of the goal programming, meta-goal programming, which has been applied in this study, has several advantages such as its ability to obtain more balanced solutions and its flexibility to model the preferences of the DMs (Nayeri et al. 2021b). Also, the heuristic method that utilized in this research is an efficient one to solve the complex problems with binary variables (Kaur and Singh 2018; Homayouni et al. 2021; Mamashli et al. 2021a; Shafiee et al. 2021). Hence, this hybrid approach can solve the multi-objective complex models, efficiently. Eventually, another theoretical contribution of this research is to investigate the supply chain of the ventilator as one of the most important medical devices during the COVID-19 pandemic.

Discussions

In this section, we attempt to compare this work with the previous studies. On the other hand, regarding the obtained results, there are some similar behaviors between this research and the previous studies, which demonstrate the validation of the offered model. In this way, for instance, the results of this research showed that when the demand increases, the environmental damages and the total cost increase, too. This behavior was also observed in the previous related studies (Sahebjamnia et al. 2018; Nayeri et al. 2020, 2021b; Pourmehdi et al. 2020; Sazvar et al. 2021a). On the other side, the achieved results demonstrated that the responsiveness of the supply chain has decreased by enhancing the demand. This behavior was also occurred in Fattahi et al. (2017), Sabouhi et al. (2020), and Nayeri et al. (2021b, a) that verifies the achieved results of this work. Also, based on results, by increasing the rate of return, the environmental impacts and the total costs have increased. Similar behavior was observed in Pedram et al. (2017) and Nayeri et al. (2020), which shows the validation of the proposed model.

Conclusions

This study addressed the GRCLSCN design problem under uncertainty. In this way, a MOMIP model is offered that minimized the environmental impacts and the total costs and also maximized the responsiveness of the supply chain. To tackle the uncertainty that existed in the nature of the supply chain problem, this research applied the robust possibilistic programming method. Then, a hybrid solution approach based on a heuristic method and the MGP method was developed to solve the proposed model. Since the demand for ventilator device is extremely increased during the COVID-19 pandemic, this study selected this product as a case study. Afterwards, the offered MOMIP was solved using the developed hybrid method and results are reported. The results demonstrated the performance and efficiency of the offered model and developed algorithm. Based on the results of the sensitivity analyses, by increasing demand the total costs and the environmental impacts were increased, but responsiveness was decreased. On the other side, an increase in the capacity of the facilities resulted in decreasing the total costs and environmental impacts while leading to increasing the responsiveness. One of the research deficiencies of this study is ignoring the global factors. However, since the top firms usually work at global scale, the future studies can add the global factors such as taxes and tariffs to the current model. Another research deficiency of the current paper is ignoring disruptions. In this regard, the future studies can add the resilience strategies such as backup suppliers to the current problem. Also, future studies can develop efficient metaheuristic algorithms to solve the suggested model.

Supplementary Information

Below is the link to the electronic supplementary material.

Author contribution

Zeinab Asadi: conceptualization, methodology, software, validation, original draft preparation, visualization.

Mohammad Valipour Khatir: supervision, investigation, investigation, validation, writing—reviewing and editing.

Mojtaba Rahimi: conceptualization, methodology, writing—original draft preparation, visualization.

Data availability

The related data have been presented in supplementary materials.

Declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication.

Not applicable.

Conflict of interest

The authors declare no competing interests.