How Sequence Context-Dependent Mutability Drives Mutation Rate Variation in the Genome

Abstract

The rate of mutations varies >100-fold across the genome, altering the rate of evolution, and susceptibility to genetic diseases. The strongest predictor of mutation rate is the sequence itself, varying 75-fold between trinucleotides. The fact that DNA sequence drives its own mutation rate raises a simple but important prediction; highly mutable sequences will mutate more frequently and eliminate themselves in favor of sequences with lower mutability, leading to a lower equilibrium mutation rate. However, purifying selection constrains changes in mutable sequences, causing higher rates of mutation. We conduct a simulation using real human mutation data to test if 1) DNA evolves to a low equilibrium mutation rate and 2) purifying selection causes a higher equilibrium mutation rate in the genome’s most important regions. We explore how this simple process affects sequence evolution in the genome, and discuss the implications for modeling evolution and susceptibility to DNA damage.

Significance

Mutation rate varies across the genome leading to differing susceptibility to both harmful and beneficial changes. One of the strongest drivers of mutation rate variation is the sequence itself, with some sequences mutating 75× more than others. This fact means that as mutation changes the DNA sequence, it will also change its own mutation rate. In this article, we use a simulation based on real mutation data to explore the novel idea that as mutations accumulate those that reduce the mutation rate will last longer resulting in a lower equilibrium rate. However, where natural selection opposes the fixation of harmful mutations this trend toward lower rates may be stopped, leading to higher mutation rates in the genome’s most critical regions.

Introduction

Mutation introduces the genetic variation that facilitates adaptive evolution but can also give rise to diseases such as cancer and age-related illnesses (Alexandrov et al. 2013; Bae et al. 2018). Although mutation is random, the relative rate of mutation at each position, or mutability, is not uniform across the genome. Variation in mutability has been demonstrated at multiple scales and the rate at which mutations occur can vary from site to site across the genome more than 100-fold (mammalian genome mutation rate variation reviewed in Ellegren et al. [2003]). Thus, individual sites and regions across the genome have the potential to participate in evolution and genetic pathologies at varying rates. Analyzing the drivers and patterns of mutability variation can help us understand the mutagenic mechanisms of human disease and the forces that generate the variation available to evolution.

Investigating how molecular processes and genomic properties predict mutation is an active area of study (Chen et al. 2017; Supek and Lehner 2019), and evidence suggests that the strongest predictor of mutation rate is the sequence itself (Michaelson et al. 2012; Sung et al. 2015). Although the mechanisms are not fully understood (Sung et al. 2015), we know that a given genomic position’s mutability is strongly influenced by not only the base itself but also the sequence at adjacent sites (Blake et al. 1992; Hess et al. 1994; Aggarwala and Voight 2016). Studies examining variation in the mutation rate among the 64 possible trinucleotide sequences have shown that the most mutable trinucleotides mutate at rates up to 75-fold higher than the least mutable (Sung et al. 2015). Therefore, if mutation rate variation among sites is influenced by sequence context, the uneven rate of mutation across the sequence should lead to changes in the underlying mutation rate variation over long periods of time.

The effect of mutation events on local mutability raises interesting questions about how sequence context and mutation rate might interact over long periods. We hypothesize that if high mutability sequences mutate more often, they are likely to persist in the genome for less time than lower mutability sequences that are more stable. Over time, this bias would lead to an enrichment of lower mutability sequences and an overall depression of mutation rate. However, in conserved sequences, we predict that purifying selection would prevent the fixation of mutations that compromise functionality. By restricting the sequence’s evolution to a lower mutability state, purifying selection may indirectly maintain some sites with higher mutability. Thus, we expect constrained sequences may evolve higher mutability than neutral regions.

In this study, we conduct a long-term simulation of DNA sequence evolution under a trinucleotide-based mutation model generated from empirical human germline mutation data. We study the influence of sequence context mutability variation on mutation rate evolution. We test our two main predictions that: 1) DNA will evolve to a low equilibrium mutation rate and 2) purifying selection will constrain the change of sequence resulting in higher equilibrium mutation rates in the genome’s most important regions. We also explore how this change in sequence composition, driven by mutability variation, manifests in the frequencies of codons in protein coding genes under purifying selection.

Results and Discussion

The Mutability Model

To simulate how sequence context influences the evolution of mutation rate variation, we generated a model of trinucleotide mutability based on ∼101k de novo SNP mutations (Jónsson et al. 2017). Each trinucleotide in our model contains the mutability, as well as the probabilities it mutates into each of the three potential descendant trinucleotides. Our model captured a large amount of mutability variation among the 32 trinucleotide sequences, with a 27-fold difference between least (GAA) and most (ACG) mutable trinucleotide. As expected, our mutability model shows that CpG trinucleotides have on average 10-fold higher mutability than non-CpG trinucleotides (Hwang and Green 2004; Hodgkinson and Eyre-Walker 2011). It is well-documented that CpG sites have the highest mutation rate in humans and many other species, primarily due to deamination mutations at methylated cytosines (Coulondre et al. 1978; Razin and Riggs 1980). However, non-CpG-bearing trinucleotides still show considerable variation, with a 3.7-fold difference between the lowest (GAA) and highest (GGT) mutability trinucleotides. Even though our model is based on human mutations, similar variation is seen in other species. In addition to the 75-fold trinucleotide mutability variation found in mismatch-repair-deficient Bacillus subtilis (Sung et al. 2015), we calculated similar trinucleotide mutability models for other organisms with sufficiently large mutation accumulation data sets and found 20-fold global mutability variation in Chlamydomonas reinhardtii (Ness et al. 2015, n = 6,843), 12-fold in Saccharomyces cerevisiae (Zhu et al. 2014, n = 867), 9–21-fold in Caenorhabditis elegans(Rajaei et al. 2021, n = 770–3,434), and 55-fold in Mus musculus (Lindsay et al. 2019, n = 764). Therefore, although the results we present here are focused on a human model, it seems reasonable that similar processes could apply across a broad range of organisms.

Does Mutability of Neutral Sequence Reduce over Time?

Our first prediction was that sequence will evolve to a lower mutability state at equilibrium because high mutability trinucleotides will mutate more often, and over time lower mutability trinucleotides will become more common. To test our prediction, we simulated the evolution of a neutral (noncoding) sequence under our mutability model. In support of our prediction, starting from random sequence, the average mutability decreased by 53% at equilibrium (from 6.13e-05 ± 2.55e-08 of initial conditions to 2.93e-05 ± 1.04e-08). We would caution that the exact magnitude of the mutability decline is arbitrary because it depends on the starting sequence, which in this case is random. It also took a large number of mutations to reach this equilibrium (mean 2 mutations per site). This long time to equilibrium likely results from the fact that the noncoding DNA was random and therefore quite far from its equilibrium. In reality, if a given genome is near its mutability equilibrium, small changes to the mutation spectrum are unlikely to require evolution to an altogether different equilibrium, and therefore would not take nearly as long. The overall reduction in mutability implies that high mutability trinucleotides were mutated more frequently, and the lower mutability trinucleotides rose in frequency. A general negative correlation between the mutability of trinucleotides and their frequency at equilibrium is evident (R² = 0.39, P ≪ 0.01). The trend is largely driven by the reduction of highly mutable CpG-bearing trinucleotides, but remains even when these are excluded (R² = 0.07, P = 0.02). The patterns of trinucleotide change through our simulations are complex, which we discuss more thoroughly below. Our results support that in the absence of other forces, the influence that sequence context has on mutability should lead DNA to settle at an equilibrium that reflects the least mutable sequences.

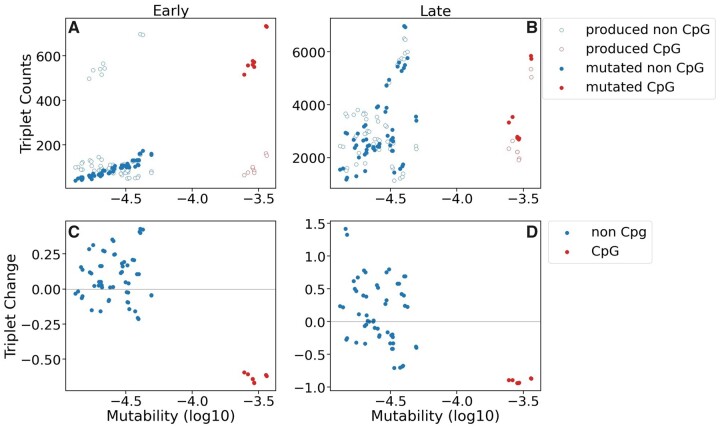
The premise of our model was that low mutability sequences will become more common because they tend to be retained for a longer time in the genome; however, the observed pattern was more complex. Early in the simulation, the number of times a trinucleotide was chosen for mutation increases with mutability (fig. 1A: filled). Counterintuitively, this does not result in a clear negative relationship between the mutability of a given trinucleotide and its change in frequency in the simulation (fig. 1C). There are a few mechanisms that we believe are obscuring this relationship. First, although the rate at which a trinucleotide is removed by mutation depends on its individual mutability, the rate at which a trinucleotide is created depends on the frequency and mutability of the trinucleotides that generate it (fig. 1A: open). For example, the points in the upper left of figure 1A are the relatively low mutability triplets that can be created by a single mutation at a high mutability CpG bearing triplet. This means that trinucleotide change over time is not a simple relationship with the probability of mutation. Second, when mutations occur, they also alter the mutability of the flanking trinucleotides. This can further obscure the relationship of mutability with equilibrium frequency when, for example, a low mutability trinucleotide is not stable because its flanks have a high mutability (e.g., GAC has mutability within the lowest 1.5% of all trinucleotides, however it decreases in frequency during the simulation, likely due to changes when it is flanked by the mutable ACG trinucleotide). These processes are further complicated over time as mutations occur on top of each other. This creates an effect where later in the simulation the number of times a trinucleotide is mutated no longer correlates to its mutability (fig. 1B: filled), the result being that it is not necessarily true that low mutability trinucleotides will be at higher frequency at equilibrium (fig. 1D). The same is not true in simulations without these effects, where triplet frequency at equilibrium correlates strongly with mutability (R² = 0.96, P ≪ 0.01, see supplementary fig. S6, Supplementary Material online), demonstrating the importance of triplets that generate and flank a given site. These interactions among sites, even with relatively small windows of sequence context (i.e., trinucleotides), highlight the complexity of this process and the importance of using simulations. Despite these intricacies, the overall pattern of a lower mutability equilibrium remains clear.

Fig. 1.

Relationship of trinucleotide mutability with trinucleotide variation in early (10% mutational coverage) and late (200% mutational coverage) stage simulations. Panels (A) and (B) display the number of times a trinucleotide is chosen to mutate in the simulation (filled) and how many times a trinucleotide is produced from a mutation event (open) in early (A) and late (B) stage simulations. Panels (C) and (D) display average trinucleotide change proportional to initial frequencies in early (C) and late (D) stage simulations. Gray horizontal line denotes the zero mark, indicating no change from the initial state. Negative values indicate decrease in frequency from the initial state, and positive values denote increases in frequency. Data for all panels was generated using ∼100 Kbp of randomly generated sequence with no purifying selection (n = 10).

Can Purifying Selection Increase Mutation Rate?

Our second prediction was that purifying selection in coding sequences stops some mutations from fixing, resulting in the retention of more mutable trinucleotides and a higher equilibrium mutability than neutral sequence. To test this prediction, we inserted random human exons in noncoding DNA to compare mutability change between these two sequence classes. To simulate purifying selection, nonsynonymous mutations were accepted or rejected in proportion to the BLOSUM90 matrix (see Materials and Methods). Exon mutability decreased to an equilibrium value 18% higher than noncoding sequence (fig. 2). Our result confirms the prediction that purifying selection generally restricts the ability of sequence to evolve to a lower mutability state. A similar pattern was simulated by Rong et al. (2020) when modeling the evolution of splice sites. The fact that coding sequence had higher mutability was not solely driven by the highly mutable CpG trinucleotides as simulations removing CpG trinucleotides produced a qualitatively similar result. Within coding sequence, the effect of purifying selection can be seen at the trinucleotide scale, as mutability has only a weak effect on the change in codon frequency through the simulation (adjusted R² = 0.16, P ≪ 0.01) as compared with the effect of mutability on trinucleotide change within non-coding sequence (adjusted R² = 0.37, P ≪ 0.01). Note that in the sliding window of mutability presented in figure 2, we observed that some exons had relatively low equilibrium mutability (e.g., first and last exon in fig. 2), which appear to be exceptions to our general finding. However, in all these cases the exons started with low mutability and experienced minimal mutability reduction during the simulation (only 33% the amount of decrease experienced by the other codons). Thus, even low-mutability exons demonstrate that coding sequences are limited in their ability to evolve toward a lower mutability state due to purifying selection.

Fig. 2.

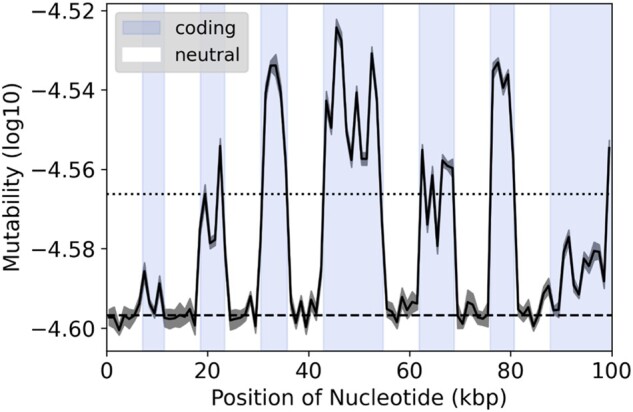
Sliding window of mutability from a simulated chromosome. The chromosome consists of ∼100 Kbp of coding (blue) and noncoding (white) regions at a ∼1:1 ratio in an alternating pattern, simulated for 200k iterations. Mutability is calculated as log10 values from the frequencies of trinucleotides in nonoverlapping windows of 1 kb. Dark gray ribbon represents standard error between replicate simulations (n = 10). The dotted and dashed lines represent the average mutability for all coding and non-coding regions, respectively.

We also used our model to explore whether mutability differences among the trinucleotides might interact with purifying selection to create codon usage bias. Previous studies have found an effect of sequence context on codon usage bias (Jia and Higgs 2008; Powdel et al. 2010). Here we simulated a modified human CDS but found no significant relationship between equilibrium codon bias in our simulation and true codon bias in the human genome (R² <0.0 1, P ∼0.5, see supplementary fig. S3, Supplementary Material online).

One might expect that coding regions would evolve lower mutability than noncoding regions to reduce the harmful consequences of mutation in functionally important regions. Our simulation shows that when purifying selection is acting the average mutability is in fact higher. In support of our findings, when we used our mutation model to estimate mutability in intergenic versus coding regions within the human genome, we found that exons had ∼40% higher mutability than intergenic regions. Furthermore, the noncoding mutability reached in our simulations was within 9% of the observed mutability in human intergenic sequence and simulated noncoding triplet frequencies are similar to triplet frequencies in genomic intergenic regions (R² = 0.76, P ≪ 0.01, see supplementary fig. S4, Supplementary Material online). These trends exist despite the fact that our noncoding simulations start from a random assortment of nucleotides. Similarly, at equilibrium, the mutability of coding exons in our simulations was within 22% of true coding sequences in the genome, despite experiencing more complex functional constraints and evolutionary forces not represented in our model. The extent to which true mutation rate variation is explained by the processes simulated here will depend on the relative role that sequence context has on mutability. We know germline mutation rates have been associated with other genomic features such as histone markers, transcription rate, and replication timing (Chen et al. 2017; Supek and Lehner 2019). Indeed, our model makes a prediction that mutation rate will be higher in genes, which is in contrast to a recent empirical study in Arabidopsis thaliana that found a lower mutation rate in coding sequence (Monroe et al. 2022). Their predictive model of mutation differs from ours in that it depends strongly on empirically estimated epigenetic factors that are not represented in our model. Additionally, their model is not fitted to single sites and therefore does not include sequence context. Michaelson et al. (2012) showed that in humans, the effect of trinucleotide sequence on mutability was five times greater than the next strongest predictor, which included numerous epigenetic features. It is possible that with larger mutation data sets, we can provide even higher resolution mutation models that account for larger sequence contexts, and specific mutability models for different genomic regions that account for mechanisms driving sequence-dependent mutation rates (e.g., variable rates of methylation, position relative to replication origins). It is also possible that with larger mutation data sets, we can provide even higher resolution mutation models that account for larger sequence contexts (7-mer, Aggarwala and Voight 2016), and specific mutability models for different genomic regions that account for mechanisms driving sequence-dependent mutation rates (e.g., variable rates of methylation, position relative to replication origins). Despite the potential with more precise models of mutability and purifying selection, the general principle that high mutability sequence will tend to destroy itself means that tension between mutation and purifying selection could prove to be fundamentally important to our models of how mutation rate variation evolves.

Materials and Methods

One of the best predictors of mutation rate at a single site is the base itself and the two bases immediately flanking it (trinucleotide). Here, we used 101k single base mutations from the human germline (Jónsson et al. 2017) and their flanking bases to estimate a mutability model of the relative mutation rate (mutability) at each trinucleotide as well as the probability of the focal site mutating into each of the three other possible nucleotides. The only mutations excluded in parent-offspring trio data are near lethal (and sterilizing, in trios where grandparents are included), thus this data produces as little bias in the mutation spectrum as possible. Trinucleotide mutability was calculated as the number of mutations of a given trinucleotide over the number of those trinucleotides present in the human reference genome (Hg38). For each trinucleotide, we also assigned the probability of each of the three possible mutations based on the frequency of each change in the observed mutation data. This mutability model therefore allows us to assign the relative probability of each mutation at any given site based on the primary sequence alone.

To simulate sequence and mutability evolution over time, we started with a hypothetical chromosome and mutated it according to the mutability model. The initial chromosome consisted of ∼100 Kbp of coding and non-coding regions at a ∼1:1 ratio in an alternating pattern. We represented the noncoding sequence in multiple ways: 1) randomly generated from equal proportions of the four nucleotides, 2) using the triplet frequencies observed in human intergenic sequence, and 3) random fragments of human intergenic sequence. Here we present only random sequence with equal proportions of bases but the results are qualitatively similar (see supplementary fig. S1, Supplementary Material online). To represent true coding sequence and the higher-order patterns of codon and amino acid usage, we randomly selected human coding exons (CDS) (see supplementary table S1, Supplementary Material online for details). To simulate purifying selection, we wanted to realistically approximate the selection constraints on amino acid change. To make our model general, and not specific to a given protein, we used the BLOSUM90 matrix (https://www.ncbi.nlm.nih.gov/IEB/ToolBox/C_DOC/lxr/source/data/BLOSUM90, last accessed February 2022); the BLOSUM90 matrix represents observed amino acid changes in sequences that are 90% identical (i.e., experienced relatively little divergence) and the frequency of these changes should broadly reflect the selective resistance to each possible amino acid change. We transformed the BLOSUM90 such that the probability of a mutation fixing was proportional to the matrix score. In the absence of invariant protein coding sites, all protein coding sites can eventually change, but extremely slowly if purifying selection is strong. However, it is known that many sites in proteins cannot change without compromising the function of the protein. We therefore included an invariant site parameter that randomly assigned sites to be immutable. We set this parameter to 50% of sites, as this is a common default setting in phylogenetic models of sequence evolution (e.g., PAUP). Higher proportions of invariant sites will result in less mutability change from the initial state, whereas lower proportions cause a larger amount of flexibility in mutability evolution. Each iteration of the simulation followed the following steps:

1. Assign mutability of each position in the chromosome based on its trinucleotide sequence.

2. Randomly sample one position weighted on all the mutability of all sites.

3. For the chosen site, assign which of the three possible mutations occurred using weighted probabilities from the mutability model.

4. To represent purifying selection, we accept or reject the proposed mutation using the following criteria:

   1. If the mutation is in a noncoding region, accept the change.

   2. If the change is in an invariant site, reject the change.

   3. If the site is in a coding region but not an invariant site, then the proposed mutation is accepted or rejected with a random probability that is proportional to the score from a BLOSUM90 matrix.

These steps were repeated, recalculating mutability after each iteration, until mean mutability reached equilibrium after 200k generations. We calculated equilibrium by averaging mutability in windows of 1k generations and determining the point at which the change in average mutability was equal to 0 to nine significant digits (see supplementary fig. S1, Supplementary Material online). Ten replicate simulations were conducted to examine consistency across runs. To further investigate particular noncoding mutational patterns, we also ran separate simulations with a 100 Kbp sequence consisting of only noncoding DNA. Simulations and analysis are conducted in Python 3 and publicly available (https://github.com/MadeleineOman/Mutation_equilibrium).

We also explored the effects of triplets that generate and flank a given site by creating simulations without these effects. We simulated a chromosome containing 1,000 distinct triplets where mutation events do not influence adjacent triplets (i.e., the flanks can never mutate). Furthermore, to eliminate the effect of differential rate at which triplets are created, a mutated triplet can change into any of the 63 other triplets with equal probability. We ran this simulation to equilibrium, and performed a quadratic regression of a triplet’s mutability and the mutability of adjacent triplets on triplet frequency.

We also explored the influence that sequence-dependent mutability would have on the relative frequencies of synonymous codons, or codon usage bias. To investigate this hypothesis, we calculated codon usage bias in the genome and used modified human CDS to understand whether sequence context mutability alone plays a role in creating codon usage bias. To this end, we used ∼100 Kbp of cumulative sequence from randomly selected exons 4–6 Kbp in length. We replaced each codon in the sequence with a random codon from the set of synonymous codons that code for the same amino acid (with replacement). The result being a sequence that still codes for the same amino acids without the bias in codon usage present in the genome. Codon usage was estimated as using relative synonymous codon usage (RSCU) where the frequency of each codon for a given amino acid is measured relative to the most common codon, therefore assigning a value between 0 (never used) and 1 (the most common codon). This sequence was mutated for 200k cycles according to the rules outlined in steps 1 through 4 above. We used a linear regression to compare the relationship between the codon usage bias (RSCU) present in the human genome and RSCU found at equilibrium in our simulation.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.