Champagne: Automated Whole-Genome Phylogenomic Character Matrix Method Using Large Genomic Indels for Homoplasy-Free Inference

Abstract

We present Champagne, a whole-genome method for generating character matrices for phylogenomic analysis using large genomic indel events. By rigorously picking orthologous genes and locating large insertion and deletion events, Champagne delivers a character matrix that considerably reduces homoplasy compared with morphological and nucleotide-based matrices, on both established phylogenies and difficult-to-resolve nodes in the mammalian tree. Champagne provides ample evidence in the form of genomic structural variation to support incomplete lineage sorting and possible introgression in Paenungulata and human–chimp–gorilla which were previously inferred primarily through matrices composed of aligned single-nucleotide characters. Champagne also offers further evidence for Myomorpha as sister to Sciuridae and Hystricomorpha in the rodent tree. Champagne harbors distinct theoretical advantages as an automated method that produces nearly homoplasy-free character matrices on the whole-genome scale.

Significance.

Character matrices form the evidential basis for any phylogenetic inference. Previous studies have often relied on morphological characters or aligned single-nucleotide characters, which are susceptible to homoplasy. Rare genomic events are less homoplasy-prone, but the search for these elements has so far been manual. We present Champagne, an automated method to identify phylogenetically informative large genomic events at the whole-genome scale for a homoplasy-free inference of phylogenetic trees.

Introduction

The “phylogenomics” approach (Eisen and Fraser 2003; Jennings 2019) promises to resolve the branching patterns in the tree of life with the enormous power of genome-scale data. Many recent phylogenomic studies have confirmed topology inferences of previous studies that mostly relied on morphological features (Prasad et al. 2008), whereas others have led to new revisions to our current understanding of the tree of life (Nikaido et al. 1999; Jarvis et al. 2014; Misof et al. 2014; Swanson et al. 2019).

Despite the proliferation of high-quality whole-genome assemblies, many topologies in the mammalian tree remain hotly contested in phylogenomic studies (Cannarozzi et al. 2007; Lunter 2007; Wu et al. 2013; Foley et al. 2016; Springer and Gatesy 2016; Liu et al. 2017). Phylogenomic methods reconstruct phylogenetic trees from a character matrix composed of molecular signals, such as DNA or protein alignments. However, a number of biological and nonbiological sources can lead to species tree incongruence. Biological sources include incomplete lineage sorting (ILS) (Hobolth et al. 2007, 2011), homoplasy (Jeffroy et al. 2006), hybridization (Sibley and Ahlquist 1987), and horizontal gene transfer (Galtier and Daubin 2008), whereas nonbiological sources include algorithmic shortcomings, such as misalignments and incorrect orthology mapping (Scornavacca and Galtier 2017). The incongruence arising from many of the above sources can be mitigated by adding more signal to the character matrix (Jeffroy et al. 2006) or by more accurately modeling a biological mechanism in the tree inference algorithm, as done in the coalescent model (Hudson 1990), statistically consistent models for ILS (Mirarab et al. 2014, 2016), and phylogenetic networks (Solís-Lemus et al. 2017; Wen et al. 2018) for ILS and hybridization. However, the incongruence resulting from homoplasy, that is, from an increased rate of parallel or convergent mutations arising through mutation rate-heterogeneity (Felsenstein and Felenstein 2004; Bergsten 2005) or similar selective pressures (Marcovitz et al. 2019), is much harder to mitigate using these strategies (Jeffroy et al. 2006; Philippe et al. 2011). Therefore, for dealing with homoplasy-induced incongruence, much of the previous work has relied on generating characters that are less susceptible to homoplasy (Rokas and Holland 2000; Churakov et al. 2010; McCormack et al. 2012; Doronina et al. 2017; Edwards 2019).

In this paper, we present Champagne—a method for generating character matrices for phylogenetic analysis using large genomic indel events. Champagne builds a character matrix using large (≥50 bp) shared insertions and deletions (indels, in short) within the intragenic regions (exons and introns) of orthologous genes among the species of interest using gene annotations in a known outgroup species. This has two major advantages over prior techniques. First, by using large shared insertions and deletions, which are extremely unlikely to occur independently, Champagne largely eliminates homoplasy that is prevalent in single-nucleotide (or amino acid) level DNA (or protein) alignments, where parallel and convergent mutations occur frequently. Second, although some prior work that focused on large shared genomic regions for inferring phylogeny have underscored the promise of homoplasy-free characters, such as transposons (Nishihara et al. 2005; Churakov et al. 2010; Doronina et al. 2019; Churakov, Zhang, et al. 2020), their techniques are typically manually curated for specific regions in the genome and discover only a handful of informative sites, which raises concerns about statistical significance and sampling bias. Similarly, ultraconserved elements have been used as characters owing to their ease-of-capture with sequencing and relatively homoplasy-free nature, making them useful even at ancient evolutionary distances (McCormack et al. 2012; Costa et al. 2016). Champagne is fully automated, works on unannotated genome sequences of target species, and typically discovers hundreds to tens of thousands of informative sites, including many in the noncoding portions of the genome. Traditionally, it has been challenging to establish orthology in noncoding portions of the genome. To address this issue, Champagne uses a strict algorithm for mapping each reference gene to at most a single orthologous query locus and uses pairwise alignments to further restrict the search to intragenic regions.

When applied to mammalian genomes, Champagne improves confidence in inferring well-established topologies by producing character matrices with significantly lower homoplasy than the matrices presented in recent morphological and nuclear sequence-based phylogenetic studies. We demonstrate that Champagne does not require elaborate inference methods and manual calibration to work correctly—it is able to produce topologies that are in agreement with those generated by the most current and thorough approaches even with the relatively simple and efficient maximum parsimony inference. Champagne reaffirms the high prevalence of ILS and potential introgression in Paenungulata and human–chimp–gorilla. Even in considering large genomic indel events, it scales easily to multiple species and provides further, homoplasy-free evidence to position Myomorpha as a sister clade to both Sciuridae and Hystricomorpha.

Results

Champagne Significantly Reduces Homoloplasy over Morphology- and Short Sequence-Based Matrices

To evaluate Champagne’s performance in producing evidence that yields the correct topology, we started with the simplest case: sets of three species. We chose six species sets for which the topologies are broadly accepted. A number of previous papers, building topologies on the basis of molecular and morphological data sets, have established the correct phylogenies for these species sets (presented in Newick format) to be: ((mouse, rat), guinea-pig); ((dog, cat), pig); ((dolphin, cow), horse); ((pig, cow), dog); ((megabat, microbat), dog); and ((human, mouse), dog) (Murphy 2001; Prasad et al. 2008; McCormack et al. 2012; Song et al. 2012; Kumar et al. 2013; Liu et al. 2017; Beck and Baillie 2018; Upham et al. 2019). We summarize these phylogenies, including the outgroups used by Champagne, in table 1. We note that of the six species sets we consider, the correct topology for human, mouse, dog is perhaps the most debated—some papers (Reyes et al. 2000; Cannarozzi et al. 2007) have proposed the alternate topology of ((human, dog), mouse), though the current consensus is still in favor of ((human, mouse), dog) (Liu et al. 2017; Upham et al. 2019). We compare the indel-based character matrices produced by Champagne with a morphological character matrix presented by O’Leary et al. (2013) and a nuclear DNA-based character matrix presented by Song et al. (2012). Retention index (RI) of the maximum parsimony tree serves as the quantitative metric to measure the level of homoplasy. Given that the species sets under consideration have widely accepted and well-supported topologies and are not believed to have undergone rapid speciation (resulting in negligible ILS) or hybridization, a phylogenetic character matrix can be expected to have a near-perfect RI (i.e., close to 1) for these sets unless it suffers from high levels of homoplasy.

Table 1.

A Comparison of the Retention Indices (RI, Ranging between 0 and 1) and the Number of Informative Sites of the Maximum-Parsimony Trees Generated Using Matrices Composed of Single-Nucleotide Characters by Song et al. (2012 ), Morphological Characters by O’Leary et al. (2013 ), and Indel-Based Characters by Champagne

	Outgroup	Retention Index (RI)			Number of Informative Sites
		O’Leary et al.	Song et al.	Champagne	O’Leary et al. (Morphological Traits)	Song et al. (Single Bases)	Champagne (Large-Shared Indels)
((mouse, rat), guinea-pig)	Rabbit	n/a	0.84	0.997	n/a	55,922	289
((dog, cat), pig)	Human	n/a	0.598	0.993	n/a	19,872	979
((dolphin, cow), horse)	Human	0.445 (incorrect)	0.657	0.990	155	29,708	491
((pig, cow), dog)	Human	0.469	0.554	0.989	350	26,331	348
((megabat, microbat), dog)	Human	0.581	0.481	0.929	296	22,942	42
((human, mouse), dog)	Elephant	n/a	0.358	0.765	n/a	28,648	17

Note.—Champagne’s high- to near-maximal RI across all six queries shows how resilient large indel-based inference is to homoplasious events, exemplifying the desirable reduction of nonphylogenetic signal in the character matrix. n/a, not available.

Because of the limited set of taxa available in O’Leary et al.’s matrices, we could not compare retention indices across all phylogenies. We found that on all six sets, Champagne, as well as Song et al.’s matrices, produced the same topologies with maximum parsimony, matching the broadly accepted topologies in previous studies. O’Leary et al.’s matrices also predicted the same topologies on two out of three topologies we could evaluate, but incorrectly predicted the ((dolphin, cow), horse) topology as ((cow, horse), dolphin). The three methods differed in their RI scores and the number of informative sites (table 1). As expected, Song et al.’s single-nucleotide substitution-based matrices had far more characters than O’Leary et al.’s morphological matrices or the Champagne matrices, which are based on rare, large indel events. Despite this, the character matrices produced by Champagne significantly outperform both Song et al.’s and O’Leary et al.’s matrices, producing a RI close to the theoretical maximum value of 1 in almost all cases (table 1). This is because large genomic events that Champagne considers rarely occur twice independently and are therefore nearly homoplasy-free, which is neither true of morphological characters nor base-pair substitutions.

Champagne Shows Considerable Effect of ILS in Cross-Species Structural Variation in Species That Underwent Rapid Radiation

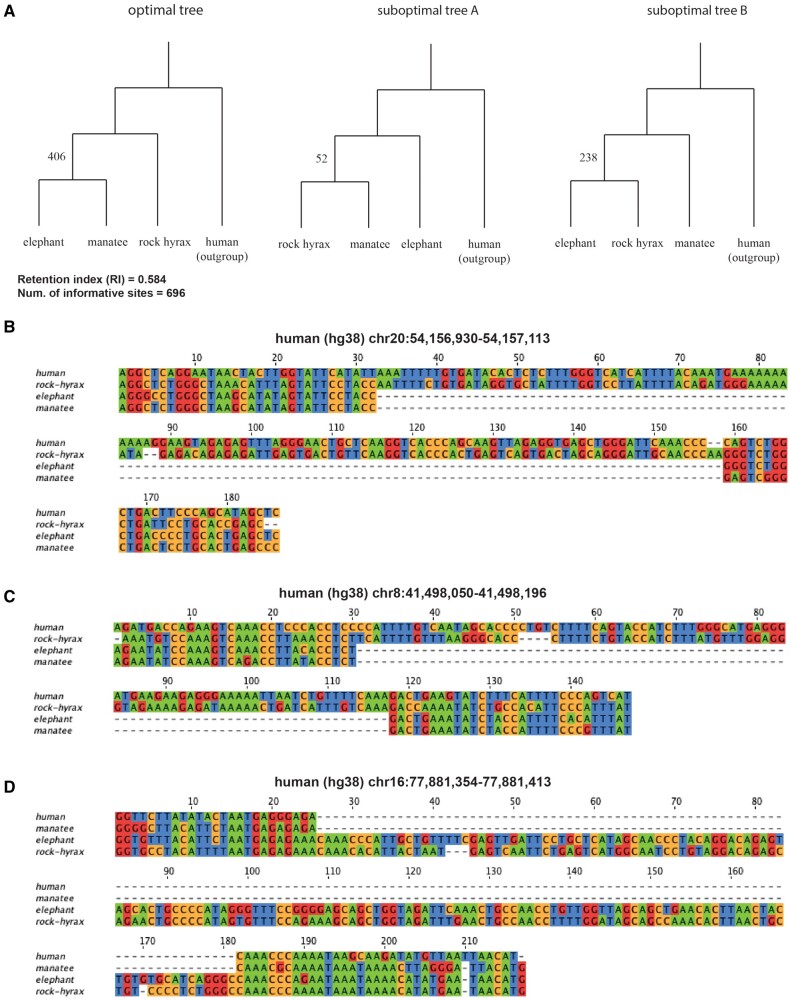
Despite a proliferation of genomic data, many topologies in particular remain unresolved to this day hindered by rapid speciation and a corresponding prevalence of ILS (Foley et al. 2016) (see supplementary fig. 1, Supplementary Material online). A classic example is the confounding branching pattern within Paenungulata (containing the clades Hyracoidea (hyraxes), Sirenia (manatees, dugongs, sea cows), and Proboscidea (elephants)). Several past papers have proposed contradictory tree topologies for Paenungulata, with some arguing that Hyracoidea is sister to Sirenia and Proboscidea (Novacek 1992; Graur 1993; Nishihara et al. 2005; Kitazoe et al. 2007; Liu et al. 2017), others arguing that Proboscidea is the sister clade (Porter et al. 1996; Murphy 2001), and a recent large survey suggesting that Sirenia is sister to the others (Upham et al. 2019). Of these, only Nishihara et al. (2005) studied this phylogeny using structural genomic changes involving retroposons but found only one informative site supporting Hyracoidea in the sister position. We sought to explore whether ILS effects resulting from the rapid radiation within Paenungulata observed by previous work on other characters could also be observed on structural genomic changes using Champagne. We selected a compact set of species to represent each tree, and used Champagne to produce corresponding evidence matrices. For Paenungulata, we consider the minimal set: {elephant, manatee, rock hyrax}, with human as outgroup. The maximum parsimonious tree produced by Champagne supports Hyracoidea as sister to Proboscidea and Sirenia (fig. 1). In particular, Champagne finds 406 indels supporting the topology: ((elephant, manatee), hyrax) (fig. 1A–C). In contrast, Champagne finds only 52 indels supporting the topology: ((hyrax, manatee), elephant), and 238 indels supporting the topology: ((elephant, hyrax), manatee).

Fig. 1.

Champagne supports Hyracoidea as the sister group in the Paenungulata tree. (A) The maximum parsimony tree generated by PAUP* using Champagne’s character matrix for Paenungulata (rock hyrax, (elephant, manatee)), as well as the other two less parsimonious alternatives. The high number of Champagne supporting indels per topology (and a moderate RI) likely reflect ILS at the root of this subtree, and the imbalance of evidence per topology could be suggestive of introgression. (B) A multiple sequence alignment for a 124-bp deletion shared by elephant and manatee, one of 406 that supports our maximum parsimony topology. (C) A multiple sequence alignment for an 87-bp deletion shared by elephant and manatee that also supports our maximum parsimony topology. (D) A multiple sequence alignment for a 152-bp insertion shared by elephant and rock hyrax, supporting the alternative topology ((elephant, rock hyrax), manatee).

Champagne’s evidence suggests a prevalence of ILS in Paenungulata as demonstrated by the relatively high proportion of identified indels that support the other possible hypotheses (fig. 1A and D). This evidence also supports prior arguments that confident resolution of this topology will remain difficult for any amount of data or approach, as the conflicting signal is likely to be phylogenetic. Moreover, Champagne observes a considerable imbalance (238 vs. 52) in the evidence supporting alternate topologies. Several evolutionary models, such as those underlying the D statistic (Green et al. 2010; Hibbins and Hahn 2019), would attribute this imbalance to introgression, and we consider this to be a strong possibility. Regardless, the number of indels identified that support the most parsimonious topology is considerably higher than the support for the alternate topologies and in this respect, we believe that the Champagne character matrix confidently supports the placement of Hyracoidea sister to Proboscidea and Sirenia. Champagne’s character matrices are in agreement with previous studies that have observed the prevalence of ILS on large, mammalian, cross-species structural variations (Springer et al. 2020; Vanderpool et al. 2020).

Champagne Scales Well to Multiple Species

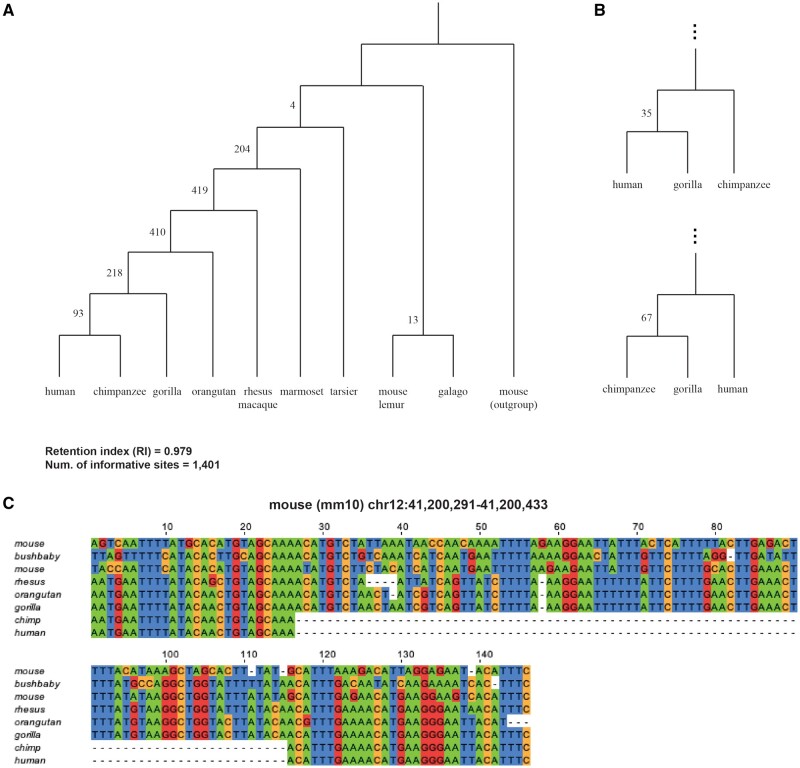
By designing the indel-search algorithm to only involve outgroup-query chains, Champagne requires only linear time and N computationally expensive chains to be produced for a phylogeny containing N species. This allows Champagne to be scaled easily around a dozen species. For primates, we build a larger Champagne matrix containing the nine primate species: {human, chimpanzee, gorilla, orangutan, macaque, marmoset, tarsier, galago, mouse lemur}, with mouse as outgroup (fig. 2). The maximum parsimony topology yielded by Champagne’s character matrix for these primates matches the topology inferred in a number of previous papers (McCormack et al. 2012; Song et al. 2012; Kumar et al. 2013) with a large number of supporting cases for most bifurcations (fig. 2A and C). Most importantly, 93 indels support grouping human and chimpanzee together before grouping either of them with gorilla or some other ingroup species, whereas 67 and 35 indels support ((chimpanzee, gorilla), human) and ((human, gorilla), chimpanzee) groupings, respectively (fig. 2B). In concordance with previous studies (Ruvolo 1997; Hobolth et al. 2011; Scally et al. 2012), Champagne also observes a high prevalence of ILS in addition to a possible introgression in human, chimpanzee, and gorilla.

Fig. 2.

Champagne correctly reconstructs primate phylogeny, finding evidence for human–chimp–gorilla ILS. (A) At each node in the tree, we depict the number of indels identified by Champagne that support the corresponding clade. (B) Champagne finds 93, 67, and 35 indels supporting gorilla, human, and chimpanzee as outgroup to the other two species, suggesting a prevalence of ILS and possible introgression at this node. (C) A multiple sequence alignment for an 87-bp deletion shared uniquely by human and chimpanzee.

Champagne Provides New and Compelling Evidence to Support Myomorpha Sister to Hystricomorpha and Sciuridae

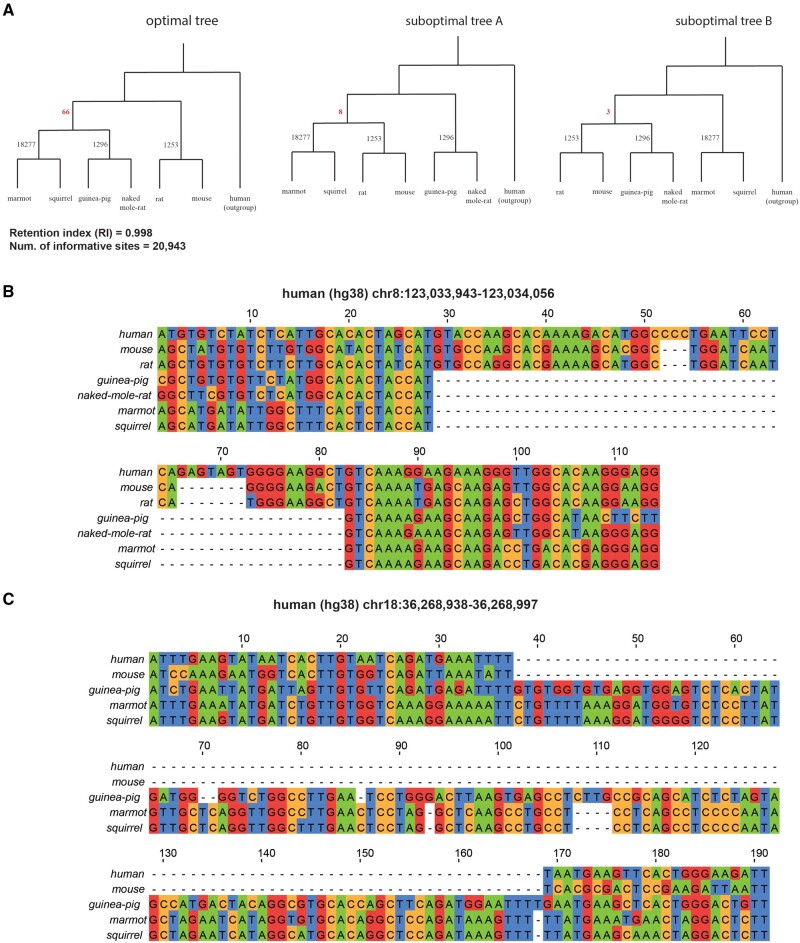
The relationship between Myomorpha (the clade that includes mouse and rat), Hystricomorpha (the clade that includes guinea-pig), and Sciuridae (the family containing squirrels) has also been much debated in prior literature, with published phylogenies alternately presenting Myomorpha as the sister group (Reyes et al. 2000; Swanson et al. 2019), Hystricomorpha as the sister group (McCormack et al. 2012), and Sciuridae as the sister group (Churakov et al. 2010; Springer and Gatesy 2016; Liu et al. 2017). To our understanding, recent consensus favors Myomorpha in the sister position (Upham et al. 2019). Using the genomes of the species {mouse, rat} for Myomorpha, {naked mole rat, guinea-pig} for Hystricomorpha, and {ground squirrel, marmot} for Sciuridae, we sought to explore this disputed topology using Champagne. We found significant evidence to place Myomorpha as the sister group, contrary to the latter recent studies, discovering 66 indels that support our phylogeny (fig. 3A–C). In contrast, we find only eight indels supporting Hystricomorpha as the sister group and only three indels supporting Sciuridae as the sister group. Although this indicates some ILS prevalence on the disputed node (fig. 3A and D), the weight of evidence favoring the placement of Myomorpha as the sister group provided by Champagne with a near-perfect RI of 0.998 is highly significant. Recently, Upham et al. (2019) also found Myomorpha sister to the other clades with their RAxML 31-gene supermatrix and Bayesian inference. However, when we tried maximum parsimony inference using their supermatrix, we found their supermatrix returned a different topology, with Sciuridae as the sister group, and with a RI of only 0.666, suggesting that the homoplasy level in their supermatrix is significantly higher than Champagne. Champagne resolves this topology unambiguously, even with maximum parsimony inference, and presents another compelling case for using homoplasy-free characters for resolving soft polytomies.

Fig. 3.

Champagne places Myomorpha sister to Sciuridae and Hystricomorpha. (A) The maximum parsimony tree generated by PAUP* using Champagne’s character matrix for a subset of rodents (left), alongside two less parsimonious trees that reflect alternate branching relationships between Sciuridae, Myomorpha, and Hystricomorpha. Sixty-six indels support Myomorpha as the sister clade, whereas only 8 and 3 support the other alternatives. (B) A multiple sequence alignment for a 54-bp deletion shared by guinea pig, naked mole rat, marmot, and squirrel. (C) A multiple sequence alignment for a 125-bp insertion shared by guinea pig, marmot, and squirrel.

Discussion

A homoplasy-free character matrix has long been sought for phylogenetic studies to overcome the limitations of the current morphological and short sequence-based approaches, that contain a large component of this nonphylogenetic signal. Previous efforts to find such a “perfect” character matrix have mostly relied on rare genomic changes caused by transposable elements (TEs) (Rokas and Holland 2000; Nishihara et al. 2005; Churakov et al. 2010; Doronina et al. 2019; Edwards 2019; Churakov, Zhang, et al. 2020). Although superior in the quality of phylogenetic signal, current rare genomic change-based phylogenomic methods suffer from multiple limitations. First, the search for TE-based orthologous events has largely been manual or has required significant manual curation. Champagne offers efficient automation at the whole-genome scale. Second, events involving TEs, even though rare, are also suspected to suffer from a small level of homoplasy resulting from known biological mechanisms (Han et al. 2011). Third, TEs often occur in bursts of activity, meaning a specific class of TEs may be informative for just a small subsection of the larger tree (Belyayev 2014). Finally, as we show, exclusively focusing on TEs misses out on a large number of informative, non-TE based rare genomic changes. For these shortcomings, the homoplasy-prone short sequence-based approaches have remained dominant in phylogenomics, for they are easy to automate and for which data are often readily available through existing resources, such as Ensembl (http://www.ensembl.org, last accessed February 23, 2022).

Our novel technique, Champagne, allows for fully automated character matrix generation for rare genomic changes. Here we use it for the purpose of deriving topologies, or cladograms, which are cornerstones of many evolutionary studies (Marcovitz et al. 2019; Turakhia et al. 2020). Using the RI (Farris 1989) on six sets of well-established topologies, we demonstrate that Champagne is largely homoplasy-free, with little or no nonphylogenetic signal, which is in sharp contrast with both short sequence-based (Song et al. 2012) and morphological (O’Leary et al. 2013) approaches. Champagne also overcomes the challenges that have long hindered previous methods using rare genome events. First, by using pairwise whole-genome alignments to conservatively predict orthology of protein-coding genes and further restricting the search to only intragenic regions (which cover >35% of the human genome), Champagne performs a genome-scale search, which typically finds hundreds to thousands of large and rare genomic events, including, in large part, in the noncoding regions of the genome, where finding orthology is considered more challenging (Armstrong et al. 2019). Second, Champagne is automated—it requires gene annotation in a single-known outgroup species and can work with unannotated genome assemblies for three or more target species. Champagne relies only on pairwise whole-genome alignments, which are much cheaper to compute than multiple-sequence alignments. In particular, for N ingroup species, Champagne requires only N pairwise alignments, one for each ingroup species paired with the outgroup. Using nine primate species, we show how Champagne can perform accurate, multispecies phylogenetic studies at a reasonable computational cost (supplementary table 2, Supplementary Material online). This indicates that Champagne can be practicably applied to resolving most hard polytomies, which typically consist of a handful of species and on which Champagne is most potent, though it may be challenging to scale it to multiple dozens of species. Unlike methods involving only TEs, Champagne is oblivious to the biological mechanism or the sequence identities involved in its genomic events. Champagne uses maximum parsimony-based tree inference because it is conceptually the simplest, and because Champagne does not suffer from a considerable long branch attraction (Felsenstein 1978) (a phenomenon common in single-nucleotide and amino acid space, whereby one or more species with a high mutation rate introduce a systematic error in phylogenetic analyses due to frequent convergent and reversal mutations), as large indel events in Champagne matrices are unlikely to occur independently or be reversed. Hence, the maximum parsimony algorithm is indeed suitable for Champagne (Mendes and Hahn 2018). We believe Champagne will allow future works to study the mutational dynamics of rare genomic changes and develop accurate evolutionary models for them (Churakov, Kuritzin, et al. 2020). This would also help perform evolutionary timescale inference using Champagne matrices and statistical frameworks in future, although for now, Champagne is designed primarily and is best suited for accurate topology inference.

It is both theoretically expected and anecdotally shown (by the lack of current consensus) that some phylogenetic nodes are more difficult to resolve than others; as previously referenced, a considerable number of phylogenies have been either left unresolved or disputed. The ability of Champagne to produce a high-signal, low-noise (i.e., low-homoplasy) character matrix is necessarily constrained by the same biological phenomena that has historically made resolving such nodes difficult. The biological process that causes incongruence between gene trees and species trees will cause incongruence, or apparent homoplasy, in the character matrix produced by Champagne. The two primary biological processes that cause such incongruence are: ILS, when rapid sequential speciation events prevent ancestral polymorphisms from being fully resolved into all resulting lineages (Hobolth et al. 2011); and introgression (Ottenburghs et al. 2017; Hibbins and Hahn 2019), when genetic information is transferred directly between different species. Indeed, in the three Paenungulata species, which are believed to have undergone rapid radiation (Gheerbrant 2009), Champagne found significant ILS involving large indels, with some evidence to suggest an additional introgression between Hyracoidea and Proboscidea. Likewise, Champagne also observes ILS to be prevalent in human–chimpanzee–gorilla, with 93 indels supporting gorilla at the sister position to human and chimpanzee and 35 and 67 indels supporting alternative topologies. With half of the observed indels (102/195) supporting alternative topologies, Champagne recovers more discordance within the human–chimpanzee–gorilla trio than the previous work of Hobolth et al. (2011) and Scally et al. (2012), who found ILS to be prevalent in 25–30% of the genome using the base-pair alignment of human, chimpanzee, and gorilla. However, this high level of discordance is in agreement with more recent work on ILS and introgression in the primate tree (Mendes et al. 2019; Vanderpool et al. 2020). To our knowledge, Champagne is the first fully automated method to observe ILS in these three primates on a genome-wide scale using rare genomic events.

In this paper, we also present a considerable set of indels that suggests that Myomorpha is sister to Hystricomorpha and Sciuridae. Some prior papers have presented alternate topologies, basing their conclusions upon a variety of evidence, including nuclear and mitochondrial DNA (Murphy 2001; dos Reis et al. 2012), morphological characters (O’Leary et al. 2013), and SINEs (Churakov et al. 2010). Churakov et al. (2010) performed a SINE/indel screen of rodent genomic information, finding eight SINEs and six indels to support an early association of the Mouse-related and Guinea pig-related clades, with the Squirrel-related clade being the sister group. The authors note that “two SINE insertions and one diagnostic indel support an association of Hystricomorpha with the Squirrel-related clade,” suggesting that these conflicts might be explained by ILS and hybridization. Champagne also searches for homoplasy-free indels but does so across 19,918 genes, resulting in a data set that finds 66 indels in support of the positioning of Myomorpha as a sister group to Sciuridae and Hystricomorpha. Champagne, too, finds evidence supporting alternative topologies—11 indels, in fact—and like Churakov et al., we believe that these could be a result of ILS and potential hybridization. Nonetheless, Champagne’s matrix has a high RI of 0.998, suggesting that the prevalence of ILS or hybridization in these rodents is fairly low. Given the lack of homoplasy inherent to its genome-wide derived characters, and five times more evidence, we argue that the Champagne character matrix is less prone to sampling bias than Churakov et al., and presents a compelling case to suggest that Myomorpha is, in fact, sister to Hystricomorpha and Sciuridae. Champagne’s rodent topology is also consistent with that of Swanson et al. (2019), who used single-nucleotide alignments derived from ultraconserved elements (Bejerano et al. 2004) for generating their character matrix. Upham et al. (2019) also supported Myomorpha as the sister group, following rigorous analysis using a combination of maximum likelihood and Bayesian inference. However, unlike Champagne’s character matrix, their supermatrix failed to recover the same topology (instead placing Sciuridae as the sister group) when using maximum parsimony inference, which is simpler and orders of magnitude faster as compared with their own methods. Furthermore, the supermatrix from Upham et al. returns a RI of 0.666, which indicates relatively high levels of homoplasy. With Champagne’s matrix returning a RI of 0.998, this challenging topology is another instance to suggest Champagne is not susceptible to homoplasy. Our results prove that Champagne not only retains the key advantage of previous rare genomic characters of being virtually homoplasy-free, and its unbiased, whole-genome scale approach consistently produces the correct tree topology as it overcomes the limitation of having to suffer from sampling bias.

Champagne is a highly general method that can easily be used on any sequenced set of species, along with an outgroup and its inferred gene set (derived even from gene-prediction or RNA-seq alone). Champagne promises to be much more homoplasy-free than morphological or single base-pair matrices. Moreover, although the ability to validate orthologous indels is expected to decay over large evolutionary distances, careful orthologous ancestral genomic region reconstruction (Blanchette et al. 2004) promises to extend its reach even further back in time. If, with hardly any manual effort, Champagne is able to consistently and correctly infer the topologies in the mammalian phylogeny that have confounded experts for decades, a world of newly and soon-to-be sequenced species awaits its analysis.

Materials and Methods

Algorithm Overview

Champagne is a fully automated, multistage computational pipeline that produces a set of phylogenetically informative evidence of large shared indels in the NEXUS format (Maddison et al. 1997), thus permitting the subsequent use of any chosen topology inference algorithm (Felsenstein 1981; Swofford 2002; Ronquist and Huelsenbeck 2003; Tamura et al. 2011; Stamatakis 2014). Champagne requires a single-known outgroup genome with an annotated gene set and unannotated, soft-masked (Kent et al. 2003) genome assemblies for the ingroup (also referred to as query) species.

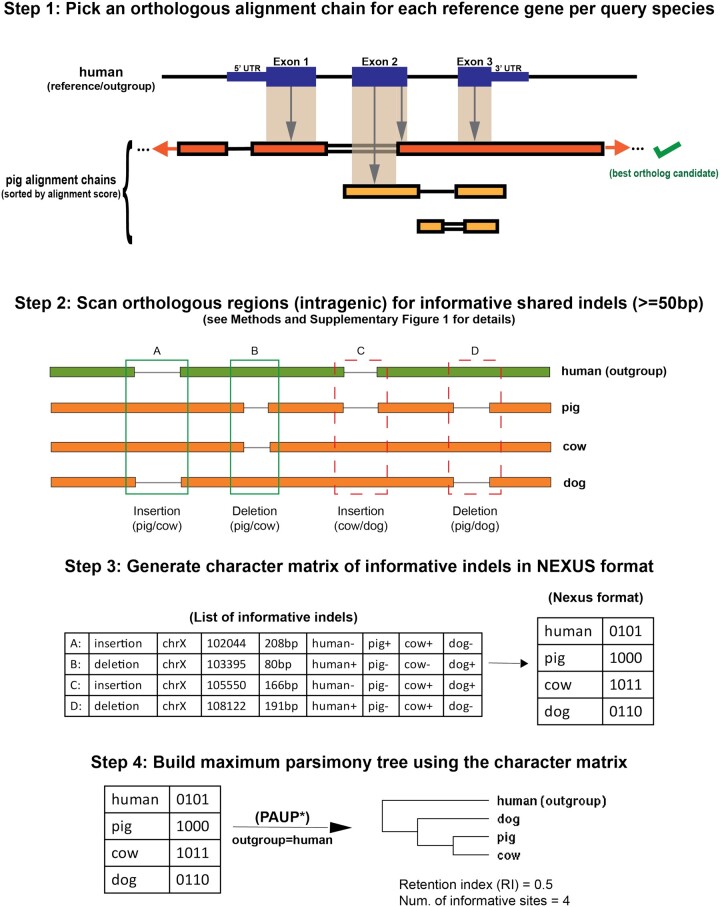
The pipeline consists of a series of discrete stages (fig. 4). Once a set of species (including an outgroup) has been selected, Champagne constructs new or uses available alignment chains (referring to the UCSC pairwise alignment chains; Kent et al. 2003) for all outgroup-query pairs, using those chains to map each outgroup gene to at most one orthologous chain in each query species (see fig. 4, step 1 for details). Ambiguous mappings are discarded. Next, for each outgroup gene that maps uniquely to more than one query species, Champagne scans the orthologous query regions corresponding to the outgroup intragenic region (exons and introns, where orthology is established with high-confidence), moving through the outgroup-query chains simultaneously and identifying large one-sided gaps in the chains (implying either an insertion in query or a deletion in outgroup, or vice versa). Upon finding this gap, Champagne determines whether this site could be phylogenetically informative, that is, at least two species could be found containing the sequence corresponding to the one-sided gap with high sequence similarity and at least two species could be found with an absence of that sequence (see fig. 5 for details). By the parsimony argument, we assume that the ancestral (common to ingroup and outgroup species) state (presence or absence of that sequence) is the same as the state of outgroup species (fig. 4, step 2): for this to be false, the indel corresponding to that sequence would have had to independently occur at least twice, once in the outgroup and once in the ingroup species sharing the outgroup state. Since it is extremely unlikely that two large indels of roughly the same sequence would independently occur at the same locus, this parsimony assumption is relatively safe to make. By the end of this step, for each informative site, all ingroup and outgroup species are assigned a character state of “+,” “−,” or “?,” depending on whether the specific indel sequence of interest is present, absent, or cannot be confidently determined in that query species, respectively. Each informative site is classified as a shared insertion or deletion between the query species differing from the ancestral and are written to an output NEXUS file (fig. 4, step 3). Finally, Champagne uses a tree inference algorithm to infer the final topology. Although Champagne is oblivious to the choice of tree inference algorithm, in this paper, we used the maximum parsimony algorithm in PAUP* (Swofford 2002), although alternative topology inference algorithms or tools (Ronquist and Huelsenbeck 2003; Tamura et al. 2011; Stamatakis 2014) could equally be used at this step (fig. 4, step 4). These stages are described in greater detail in the later sections.

Fig. 4.

An overview of the Champagne approach for speciation topology inference. In step 1, we use pairwise alignment chains between the outgroup (also used as reference) and each ingroup species (used as query) to assign at most one orthologous chain with high-confidence for each reference gene. The figure illustrates this procedure (based on Turakhia et al. [2020]) for a single outgroup–ingroup pair (human–pig) and a single reference gene. Each coding base-pair in the gene is assigned to the highest-scoring chain overlapping with the gene. If the highest-scoring overlapping chain also has the most base-pairs assigned, it is chosen as the best ortholog candidate (as shown). If gene-in-synteny and 1-to-1 mapping criteria are also satisfied (see Materials and Methods), the best candidate chain is assigned as gene ortholog. In all remaining cases, no assignment is made. In step 2, intragenic orthologous regions in all query species are scanned for each reference gene in search of phylogenetically informative, shared indels within the ingroup (see Materials and Methods and fig. 5 for details). In our illustration, four informative indels (labeled A, B, C, and D) are found. In step 3, the informative indels are printed to a NEXUS file, which is the final output of Champagne. In this example, we use this matrix in step 4, to infer the most parsimonious species tree, here ((pig, cow), dog), using PAUP* (Swofford 2002). Indels A and B in step 2 provide supporting evidence for ((pig, cow), dog), as only pig and cow share both indels. The other two indels, C and D, support ((cow, dog), pig) and ((pig, dog), cow) trees as most parsimonious, respectively. The low RI (0.5 of maximum 1) in this example reflects the relatively large fraction of nonsupporting, homoplasy-like evidence in this topology assignment.

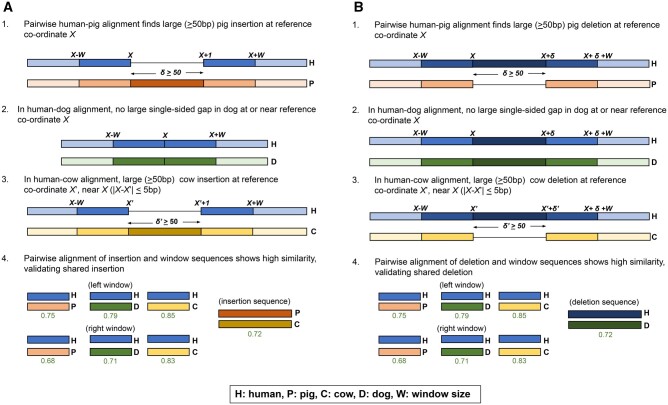
Fig. 5.

Champagne’s indel verification method. (A) Shared insertion between pig and cow detected by Champagne that is absent in dog. (1) We first identify the presence of this insertion by finding a single-sided human gap in the human–pig orthologous chains, at human coordinate X. (2) Next, we find that there is no such single-sided gap in dog chain near X, we mark the insertion as likely absent in dog. (3) Next, we navigate to coordinate X in the human–cow chains, and check for a large (similar-sized) gap at $X\prime$, within a 5-bp range of X. Finding such a gap, indicating an insertion, we mark the insertion as likely present in cow. (4) Finally, we perform a direct sequence comparison for sequence similarity. We extract a 30-bp-sized “window” sequence from either side of the insertion coordinate X in human, either side of the corresponding insertion coordinate in dog, and either side of the insertion itself in cow and pig. We also extract the sequence of the insertion itself in cow and pig. We then align the reference window sequences against each other species’ window sequences. Similarly, we align pig’s insertion sequence against cow’s insertion sequence. For each species in which we marked the indel as present, if the minimum sequence similarity for the left window, right window, and insertion (if the insertion is present) is greater than our stipulated threshold, we mark the species as definitively “+.” For each species in which we marked the indel as absent, if the sequence similarities for the left window and right window are greater than our stipulated threshold, we mark the species as definitively “−.” In either case, if a comparison fails to meet the threshold, we mark the species as “?.” (B) Symmetrical process for finding shared deletions.

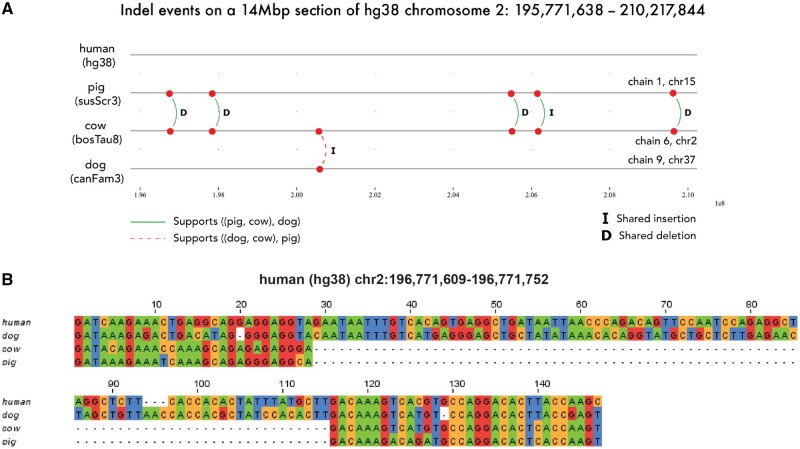
Figure 6 further illustrates a 14-Mb region in the human (outgroup) genome with real indel events annotated by Champagne for the species set {pig, cow, dog}. Even in this short segment, Champagne finds a majority of indels (5 out of 6) shared by pig and cow, not observed in dog and human (outgroup), which support the most parsimonious topology (in Newick format): ((pig, cow), dog).

Fig. 6.

A multiple-species alignment showing indels identified by Champagne in the pig, cow, and dog genomes, using human as reference species. (A) An illustration of the real pig, cow, and dog chains that align with a 14-Mb section of the human chromosome 2. Indels identified by Champagne in this section of the reference genome are shown: “I” indicates shared insertions, and “D” indicates shared deletions. On this stretch, we find five indels that are shared by pig and cow, supporting the most parsimonious topology ((pig, cow), dog), and only 1 (shown with a dashed arc) that is shared by dog and cow, possibly due to ILS. (B) A multiple sequence alignment of an 81-bp deletion shared by pig and cow, but not dog (leftmost deletion in panel A).

Species Set and Gene Set

Champagne can be used on any appropriate set of related species. Here, we used genome assemblies of 28 mammalian species (listed in supplementary table 1, Supplementary Material online), and used Ensembl 86 (http://www.ensembl.org) for our reference (outgroup) species’ gene sets.

Whole-Genome Alignments and Mapping Orthologous Genes

Once we selected a group of query (ingroup) species to study, we chose a known outgroup species for that group that also served as the reference. For each reference-query genome pair, Champagne used whole-genome pairwise alignments in the format of Jim Kent’s BlastZ-based chains (Kent et al. 2003) downloaded from the UCSC genome browser test server (https://hgdownload-test.gi.ucsc.edu/goldenPath/, last accessed February 23, 2022), or computed with the help of doBlastzChainNet utility (https://github.com/ENCODE-DCC/kentUtils, last accessed February 23, 2022) with default parameters for alignments not found on the UCSC server. Congruous to our previous work (Turakhia et al. 2020), for each reference gene, Champagne identified at most one orthologous chain in each query species when it could do so with high confidence. First, it assigned every coding base in the canonical transcript of the reference gene to the highest scoring chain (in terms of UCSC chain alignment scores) that overlaps with the base in its alignment. If the chain to which most bases were assigned was also the highest scoring chain overlapping in its alignment by one or more base-pairs with the gene, then that chain was chosen as the best ortholog candidate, C_b (fig. 4, step 1). To ensure that there was no confusing paralog to C_b, we required the UCSC alignment score of C_b to be at least 20 times higher than any other chain overlapping with the gene by one or more base-pairs. To also ensure high synteny of C_b, we required the number of bases in the aligning blocks of the chain C_b be at least 20 times greater than the number of bases in the gene itself, that is, gene-in-synteny $\ge$ 20, where gene-in-synteny $=$ length of C_b/length of gene. We also required a unique 1-to-1 mapping of coordinates between reference and query genomes, such that if two or more reference genes were mapped to the same query location, all overlapping mappings were discarded. If C_b satisfied all above conditions, it was considered as the orthologous query chain containing the reference gene. In all remaining cases, no orthologous query chain was assigned for the reference gene.

The parameters above were optimized in Turakhia et al. (2020). The parameters for the rest of Materials and Methods have been optimized via inspection of distributions and sampling for this paper. The Champagne code allows the user to adjust any parameter to their needs.

Identification and Validation of Insertions and Deletions

Next, for each outgroup gene that mapped to a unique chain in more than one query species, Champagne scanned the query regions orthologous to the reference (outgroup) intragenic regions (exons as well as introns), moving through the outgroup-query chains simultaneously and identifying large ($\ge$50 bp) indels from one-sided gaps in the chains. Specifically, a single-sided gap on the outgroup indicates either an insertion in query or a deletion in outgroup, whereas a single-sided gap on the query species indicates either a deletion in query or an insertion in outgroup (fig. 4, step 2).

As detailed in figure 2, upon finding an apparent indel in one such chain, Champagne located the corresponding coordinates in all other reference-query chains, and determined whether the indel event has occurred in the other query species by a combination of two methods: first, it confirmed the presence or absence of a similar-sized (within 10 bp) single-sided gap in the other species; and second, it extracted species’ sequences within a fixed-size window range of size 30 bp on either side of the indel and compared them directly for sequence conservation (fig. 5). For instance, if Champagne identified an insertion of size δ in query species A occurring at reference coordinate X (since a single-sided gap in the reference will start and end at the same coordinate), in order to verify the presence or absence of the insertion in another query species B, Champagne first checked that there is a single-sided gap of size $\delta \prime$, where $|\delta -\delta \prime |\le 10$, in the reference-query B chains at reference coordinate $X\prime$, within a 5-bp margin from X (i.e., $|X-X\prime |\le 5$bp). If such a gap was found, Champagne extracted the insertion sequence in both query A and B, and compared their sequence similarity. It also extracted a fixed-size “window” sequence on either side of X and $X\prime$ and compared them independently. If all of the sequence similarities exceeded our dynamically set threshold (determined as described below), Champagne assigned the indel a character state of “+” (present) for species B, indicating that the insertion should be considered present. If the sequence similarities did not all exceed the threshold, Champagne assigned the indel a character state of “?” (not confidently determinable). If no single-sided gap was found in species B near coordinate X, Champagne extracted species B’s window sequence on either side of X and compared it with species A’s window sequence; if the similarities both exceeded our threshold, the indel was assigned a state of “−.” Champagne also verified that the character state in the outgroup is actually the ancestral state (as opposed to an indel that has occurred independently in the outgroup) by requiring that at least one ingroup species aligns with high sequence similarity with the outgroup in the indel region and its surrounding windows without any large gaps. This verifies the ancestral state because we assume a very small probability of the independent occurrence of an indel at precisely the same locus in both the outgroup species and the ingroup species to which it aligns. Champagne discarded all sites where either the outgroup state could not be inferred to be the ancestral state, or where fewer than two query species had that indel.

For visual verification purposes, Champagne extracted the sequences of all species at the indel site and its surrounding windows, and used them to generate a multiple sequence alignment in the indel region using MUSCLE (Edgar 2004).

Dynamic Threshold Selection and Evidence Filtering

Recording the sequence similarity scores for each indel enabled the final step, in which Champagne tested a small range of minimum sequence similarity thresholds for insertions and deletions separately. We performed a parameter grid search over combinations of insertion and deletion thresholds in 0.025 intervals in the range $[0.6,0.7]$. For each combination, we filtered out all indels that did not meet the stated thresholds across all species. Using the resulting evidence subsets, we then generated the most parsimonious topology using PAUP*, and calculated the ratio between the number of indels in support of alternate bifurcation hypotheses on internal nodes in that topology (per our definition of support outlined later). We optimized for the ratio between the number of indels that support the most- and second-most-supported bifurcation hypotheses on the “most ambiguous” node in the tree (the node with the lowest such ratio), selecting the thresholds that maximize this ratio. Crucially, we selected these thresholds regardless of what the optimal topology actually was. It should be reiterated that all parameters used by Champagne (including minimum indel size and range of minimum sequence similarities) may be adjusted by the user as desired.

Champagne Uses the RI to Quantify Aggregate Homoplasy in Its Character Matrices

We used the RI yielded by PAUP* from the most parsimonious topology as an overall measure of the goodness-of-fit of Champagne’s character matrix to the optimal phylogeny. The RI, first proposed by Farris (1989) in 1989, expresses the degree of synapomorphy (characters shared by descendants of a common ancestor) in a character matrix; it has been interpreted as a metric for assessing the degree to which a character matrix fits a given topology and has been widely used to support phylogenies (Costa et al. 2019). Since the RI reflects a normalized value (between 0 and 1) corresponding to the number of state changes required along the branches of a given phylogenetic tree to fit the character states along the tree’s leaves while also considering the theoretical best and worst case for the same character states, it can also be interpreted as a measure of apparent homoplasy (with higher values implying lower homoplasy) in a data set. Although RI is a powerful metric to quantify the aggregate homoplasy of a character matrix to a phylogeny, it does not clearly reflect the goodness-of-fit for specific bifurcations internal to the tree, which is pertinent when more than three species are used. To overcome this, in this paper, we identified informative sites in the NEXUS file that supported each bifurcation internal to the parsimonious topology, and for contentious bifurcations, used a similar method to identify informative sites, if any, that supported alternative bifurcations. Generally, the more the supporting evidence found for a particular bifurcation relative to its alternatives, the more the confidence that could be attributed to it.

Topology Inference and Comparison Baseline

Following the threshold selection step, Champagne filtered out all evidence that failed to meet the designated thresholds, and converted the labeled indels to a character matrix in NEXUS format (fig. 4, step 3), to infer the most parsimonious tree topology using PAUP* (Swofford 2002) (fig. 4, step 4). To compare the retention indices of the topologies produced by Champagne with traditional approaches, we downloaded the single-nucleotide sequence-based and morphology-based matrices (in NEXUS format) provided by Song et al. (2012) and O’Leary et al. (2013), respectively. From these matrices we extracted the rows corresponding to the same set of ingroup and outgroup species that were used by Champagne. We used PAUP* to generate the most parsimonious topology, specifying the outgroup species and using exhaustive search on each matrix, and recorded the associated RI and the number of informative sites. Note that unlike Champagne, which is based on rare genomic events, maximum parsimony may not be the most accurate inference algorithm for the matrices in comparison (Felsenstein 1978) but has been used here primarily to compare their retention indices, and thereby their apparent homoplasy levels, with respect to Champagne.

Identifying Evidence Supporting a Particular Bifurcation

For each bifurcating branch in the tree, we also found the evidence in the Champagne matrix that supported the bifurcation. This was done as follows. For a branch which bifurcates into two sets of species, A and B, remaining ingroup species form another set C. An event was called supporting for this bifurcation if it indicated a shared insertion or deletion unique to species in A and B, not shared by any species in C. For shared insertions, we required at least one species in both A and B to be assigned a “+,” no species in either A or B to be assigned a “−,” at least one species in C to be assigned a “−,” no species in C to be assigned a “+,” and the outgroup to be assigned “−.” Similarly, for shared deletions, we required at least one species in both A and B to be assigned with a “−,” no species in either A or B to be assigned a “+,” at least one species in C to be assigned with a “+,” no species in C to be assigned a “−,” and the outgroup to be assigned “+.”

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.