Prediction of Lung Cancer Risk Based on Age and Smoking History

Abstract

Background and Objective:

The CISNET models provide predictions for dying of lung cancer in any year of life as a function of age and smoking history, but their predictions are quite variable and the models themselves can be complex to implement. Our goal was to develop a simple empirical model of the risk of dying of lung cancer that is mathematically constrained to produce biologically appropriate probability predictions as a function of current age, smoking start age, quit age, and smoking intensity.

Methods:

The six adjustable parameters of the model were evaluated by fitting its predictions of cancer death risk versus age to the mean of published predictions made by the CISNET models for the never smoker and for six different scenarios of lifetime smoking burden.

Results:

The mean RMS fitting error of the model was 6.16 × 10 −2 (% risk of dying of cancer per year of life) between 55 and 80 years of age. The model predictions increased monotonically with current age, quit age and smoking intensity, and decreased with increasing start age.

Conclusions:

Our simple model of the risk of dying of lung cancer in any given year of life as a function of smoking history is easily implemented and thus may serve as a useful tool in situations where the mortality risks of smoking need to be estimated.

Introduction

Lung cancer is a relatively common and frequently fatal disease with a strong association to smoking history. Two important initiatives designed to reduce the public health burden of lung cancer are programs to get smokers to quit and the use of low dose computed tomography (CT) imaging to screen high-risk individuals for pre-symptomatic tumors. Motivating smokers to quit and designing screening protocols are both usefully served by an ability to predict how likely a given individual is to develop lung cancer and/or eventually die from it. A suite of models known as the CISNET models, derived from US population data, have been widely used for making such predictions [1]. These models, however, vary in the assumptions they make about tumorigenesis, the unit of analysis (e.g., the cell, the tumor, the individual, or the population) and thus generate substantially different predictions that a given individual will die of lung cancer within a given year of life. They are also implemented in a variety of different operating systems [2], which complicates their use. While having a range of predictions provided by different models can be useful for gauging levels of uncertainty, there are also situation in which a single predicted value is more convenient. For example, presenting a patient with a range of predictions that they will contract or die from cancer within a certain timeframe will likely be more confusing than citing a single number as the best estimate, especially since there is no guarantee that a range of model predictions corresponds in any clear way to an interval of confidence for those predictions.

One possibility for obtaining a single prediction is obviously to apply all CISNET models to a given situation and take the average. This, however, involves much unnecessary calculation that would be avoided by having a single model provide average CISNET predictions directly. Indeed, we developed such a model in a previous study and used it in a Monte-Carlo approach to investigate screening strategies for second primary lung cancers [3]. The kernel of our model was a mathematical expression for lung cancer risk as a function of age and smoking history developed by Lubin et al [4]. This equation provides a good fit to the mean CISNET model predictions for a range of smoking scenarios [3], but can give nonsensical predictions when applied to smoking scenarios for extreme but still biological plausible situations. For example, the model predicts that an individual who consistently smokes 20 cigarettes per day beginning at age 15 years will have a 0.94% chance of dying of lung cancer in their 70_th year of life, but that this risk will be only 0.34% if they were to smoke 40 cigarettes per day. The reason for this clearly aberrant behavior of the model is that its mathematical form is not constrained to behave in an appropriate manner, such as having cancer risk increase monotonically with smoking intensity, so it extrapolates poorly.

The goal of the present study was therefore to develop a lung cancer prediction equation that is mathematically constrained to behave in a way that makes biologic and medical sense for any conceivable age and smoking history. As in our previous study [3], we calibrated the model by adjusting its free parameters so that it matches the mean predictions of the CISNET models as closely as possible.

Methods

Model Development

The probability, P, of dying from lung cancer in any given year of life exhibits a number of key characteristics. It is intuitively obvious, in fact, that P will

1. increase with age, y,

2. increase with smoking intensity, expressed as the number, n, of cigarettes smoked per day,

3. decrease with the age, s, at which a person starts smoking starts, and

4. increase with the age, q, at which a person quits smoking.

Relative to the last point, epidemiological studies indicate that P decreases toward that of the never smoker as time of quitting recedes into the past [5].

We therefore know that P is some function of the variables y, n, s, and q, and that it always has a value between 0 and 1 (in order to qualify as a valid probability). That is, P(y, n, s, q) ∈ [0, 1]. We can further think of the probability function P(y, n, s, q) as being comprised of two independent components: 1) the probability P_never(y), of dying of lung cancer purely as a function of age (i.e., for a never smoker), and 2) the probability P_smoke(y, n, s, q) of dying due to the remaining factors related to smoking, along with the ways in which they interact with age.

P_never(y) and P_smoke(y, n, s, q) must be combined in some way to produce P(y, n, s, q), but they cannot simply be multiplied together because they are both less than unity which means their product is less than either one alone, and it is obvious that the total risk of dying must be larger than either contributing component. The way forward is to consider the probabilities of not dying, since these probabilities behave in the correct manner when multiplied together. Since P(y, n, s, q) is the probability of dying from lung cancer in a given year of life, the probability of not dying from cancer within that year is (1 − P(y, n, s, q)). This is equal to the product of two independent probabilities: 1) the probability of not dying due to the baseline risk in a never smoker, (1 − P_never(y)), and 2) the probability of not dying due to the additional risk of smoking, (1 − P(y, n, s, q)), once one has reached a certain age without dying as a result of the baseline risk. That is,

$$1-P(y,n,s,q)=\left[1-P_{\mathit{\text{never}}}(y)\right]\left[1-P_{\mathit{\text{smoke}}}(y,n,s,q)\right]$$ (1)

which rearranges to give

$$P(y,n,s,q)=P_{\mathit{\text{never}}}(y)+P_{\mathit{\text{smoke}}}(y,n,s,q)-P_{\mathit{\text{never}}}(y)P_{\mathit{\text{smoke}}}(y,n,s,q).$$ (2)

P_never(y) must increase monotonically with y, since cancer in general is a disease associated with aging. This may not be due to age itself but rather to the accumulating probability of encountering additional cancer risk factors throughout life such as carcinogens other than cigarette smoke [6]. In any case, it is reasonable to postulate that P_never(y) increases with y at an accelerating rate. Indeed, the CISNET models collectively predict such behavior [1]. Accordingly, we assume the following functional form:

$$P_{\mathit{\text{never}}}(y)=A{e}^{By}$$ (3)

where A and B are constants.

We obtained an expression for P_smoke(y, n, s, q) by first determining a function f(y, n, s, q) that nominally encapsulates the effects of key lung cancer risk factors according to the following assumptions:

1. Lung cancer risk from smoking increases monotonically with smoking intensity due to the carcinogenic nature of cigarette smoke. We therefore include n as a factor in the model of risk.

2. During the smoking years, when s < y < q, the risk of death increases with the number of years smoked, reflecting the assumption that in any individual the risk is cumulative. Accordingly, f(y, n, s, q) contains the factor (y – s).

3. During the quit years, when y ≥ q, an individual’s risk ceases to increase as it did during active smoking, eventually converging toward the risk of the never smoker. Similar to previous studies [7], this is captured by including an exponentially decreasing function of time since quitting, with time-constant τ_quit, in the post-quit expression for f(y, n, s, q).

4. Lung cancer due to smoking takes time (typically many years) to develop, meaning that a given total smoking load accrued at some time in the past has an increasing chance of causing cancer with time. We incorporate this effect into f(y, n, s, q) by raising the expressions for smoking load to the power β > 1. Note that this gives f(y, n, s, q) a nonlinearly increasing dependence on both the number of cigarettes smoked per day and the number of smoking years, as has been described previously [8, 9].

5. Age is an independent risk factor for lung cancer in a smoker, over and above the age-related risk in a never smoker. We therefore let age have an exponentially increasing effect on the probability that a given smoking history will cause cancer. This is achieved by including the term $\alpha \text{exp}\left(\frac{y}{{\tau }_{\mathit{\text{age}}}}\right)$ as a factor in f(y, n, s, q), where τ_age is a time-constant defining the rate at which cancer increases with age.

Taken all together, these considerations lead to

$$\begin{gathered} f(y,n,s,q)=\alpha {[(y-s)n]}^{\beta }\text{exp}\left(\frac{y}{{\tau }_{\mathit{\text{age}}}}\right)\text{ when}s<y<q, \\ =\alpha {\left[(y-s)\text{exp}\left(\frac{q-y}{{\tau }_{\mathit{\text{quit}}}}\right)n\right]}^{\beta }\text{exp}\left(\frac{y}{{\tau }_{\mathit{\text{age}}}}\right)\text{ when}y\ge q. \end{gathered}$$ (4)

The function f(y, n, s, q) in Eq. 4 is guaranteed to be positive, but it is not guaranteed to be less than or equal to unity. It thus cannot be used directly as an expression for the probability of death from lung cancer, even though we have imbued it with reasonable dependencies on the key risk factors as explained above. In order to create the probability density function P_smoke(y, n, s, q) we therefore mapped f(y, n, s, q) onto the interval [0, 1] by incorporating it into the exponential expression

$$P_{\mathit{\text{smoke}}}(y,n,s,q)=1-\text{exp}[-f(y,n,s,q)].$$ (5)

This final step induces some distortion into the way that the five factors taken into consideration to create f(y, n, s, q) above translate into their respective effects on risk of cancer death, but their overall effects remain relatively conserved in a general sense because the function that defines P_smoke(y, n, s, q) in Eq. 5 is quasi-linear over the lower portion of its range.

Substituting Eqs. 3 and 5 into Eq. 2 gives our mathematical expression for the risk, P(y, n, s, q), of dying of lung cancer in a given year of life.

Model Fitting

With P_never(y) determined explicitly by Eq. 3, there remain six adjustable parameters −α, β, τ_quit and τ_age - requiring evaluation. First, A and B were evaluated by fitting Eq. 3 to the mean of the CISNET model predictions for a never smoker as a function of age. The remaining parameters were then determined by fitting P(y, n, s, q) simultaneously to the mean CISNET model predictions for five different scenarios up to a smoking history of 66 pack-years. This was done using a sequentially refined grid search procedure in which nominal ranges for each parameter (found by trial and error) were defined, and seven equally spaced points along each range, including the end points, were identified. These points thus defined a 3×3×3×3 grid on which the sum of squared deviation (SSD) between model prediction and data was evaluated. The grid point (set of values for α, β, τ_quit and τ_age) producing the minimum value of SSD was then used as the center point of a new grid having point spacing 67% that of the original grid. This process was repeated for a total of 20 times, at which point the parameter values producing the minimum value of SSD were taken as the best-fit values.

Results

The best-fit values of A and B in Eq. 3 were found to be 8 × 10⁻⁷ and 0.09, respectively. The fitted expression is shown in Fig 1. Although Eq. 3 is not mathematically bounded, its predictions of P_never(y) are very much less than unity over the age range 55 ≤ y ≤ 80. Indeed, it does not exceed unity until y exceeds 156 years so it qualifies as a plausible probability function for the entire conceivable lifetime of a human.

Figure 1:

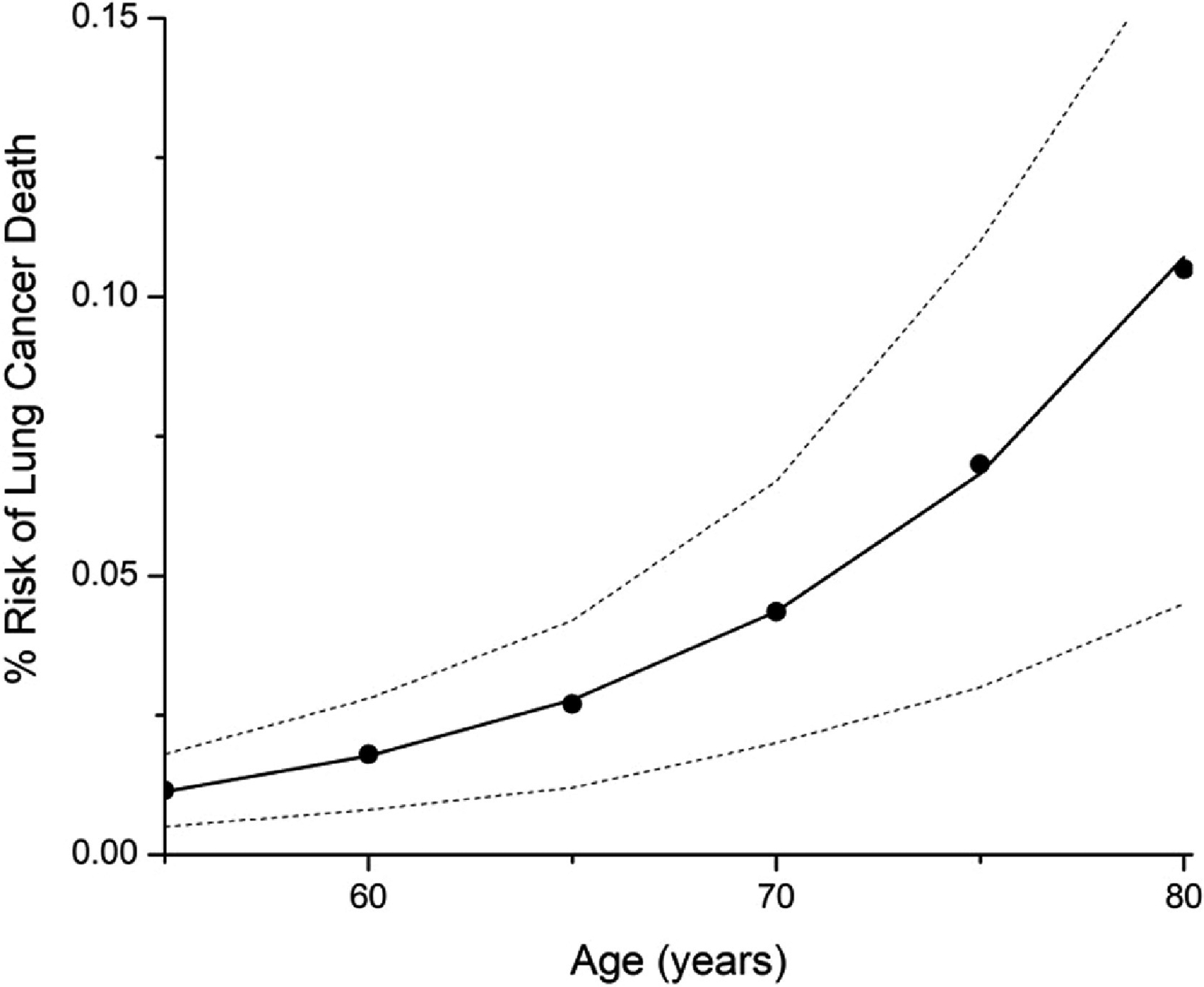
Fit of model to never smoker probability of death. The model prediction given by Eq. 3 is shown as the solid curve. The closed circles are the mean CISNET model predictions to which Eq. 3 was fit. The upper and lower bounds of the CISNET model predictions are shown by the dashed curves.

Fig 2 shows the fits of the model defined by Eqs. 1–5 to the CISNET model predictions for six different smoking and age scenarios. The predictions of the model lie, for the most part, within the bounds of the CISNET models for these six scenarios and are not far outside these bounds the rest of the time. Most importantly, the model accurately captures the major risk differences wrought by heavy versus light smoking, and by quitting early versus late. The best-fit model parameters are α = 6.27 × 10⁻⁹, β = 1.592, τ_age = 22.8 years, and τ_quit = 11.9 years. The mean squared residual for the fit is 6.6 × 10⁻³ % death risk.

Figure 2:

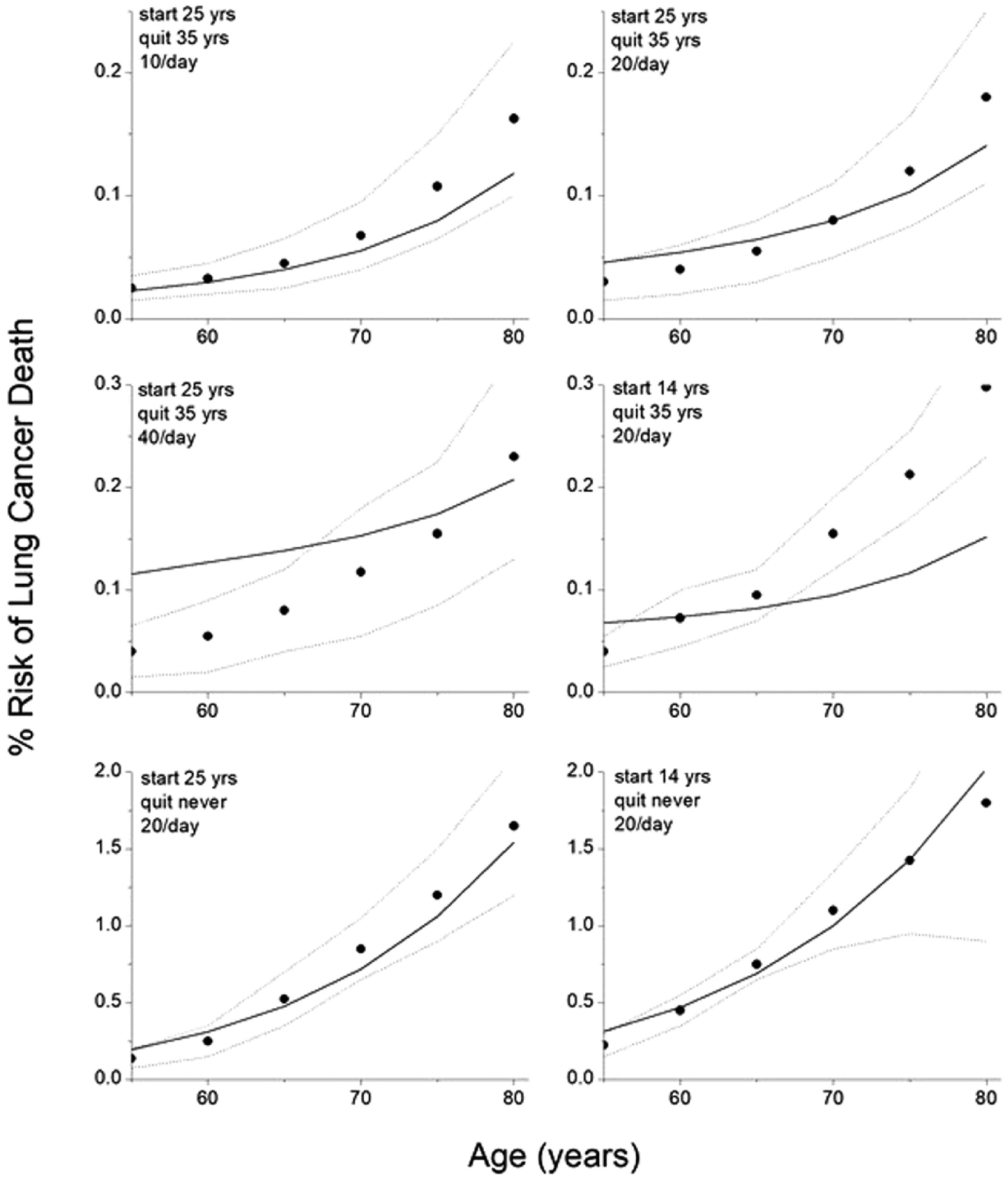
Fits of model CISNET model predictions for 6 different smoking histories to CISNET model predictions for 6 different smoking histories. The model fits provided by equation 2 combined with equations 3 and 5 are shown by the solid curves. The closed circles are the mean CISNET model predictions to which the model was fit. The upper and lower bounds of the CISNET model predictions are shown by the dashed curves.

Figure 3 shows the dependence of the model predictions on smoking start age over the range 10 to 40 years while keeping quit age and smoking intensity fixed at 85 years and 20 cigarettes per day, respectively. Figure 4 shows the dependence on quit age over the range 20 to 60 years while keeping start age fixed at 10 years and intensity fixed at 20 cigarettes per day. Figure 5 shows the dependence on smoking intensity over the range 0 to 40 cigarettes per day while keeping start age and quit age fixed at 10 and 85 years, respectively.

Figure 3:

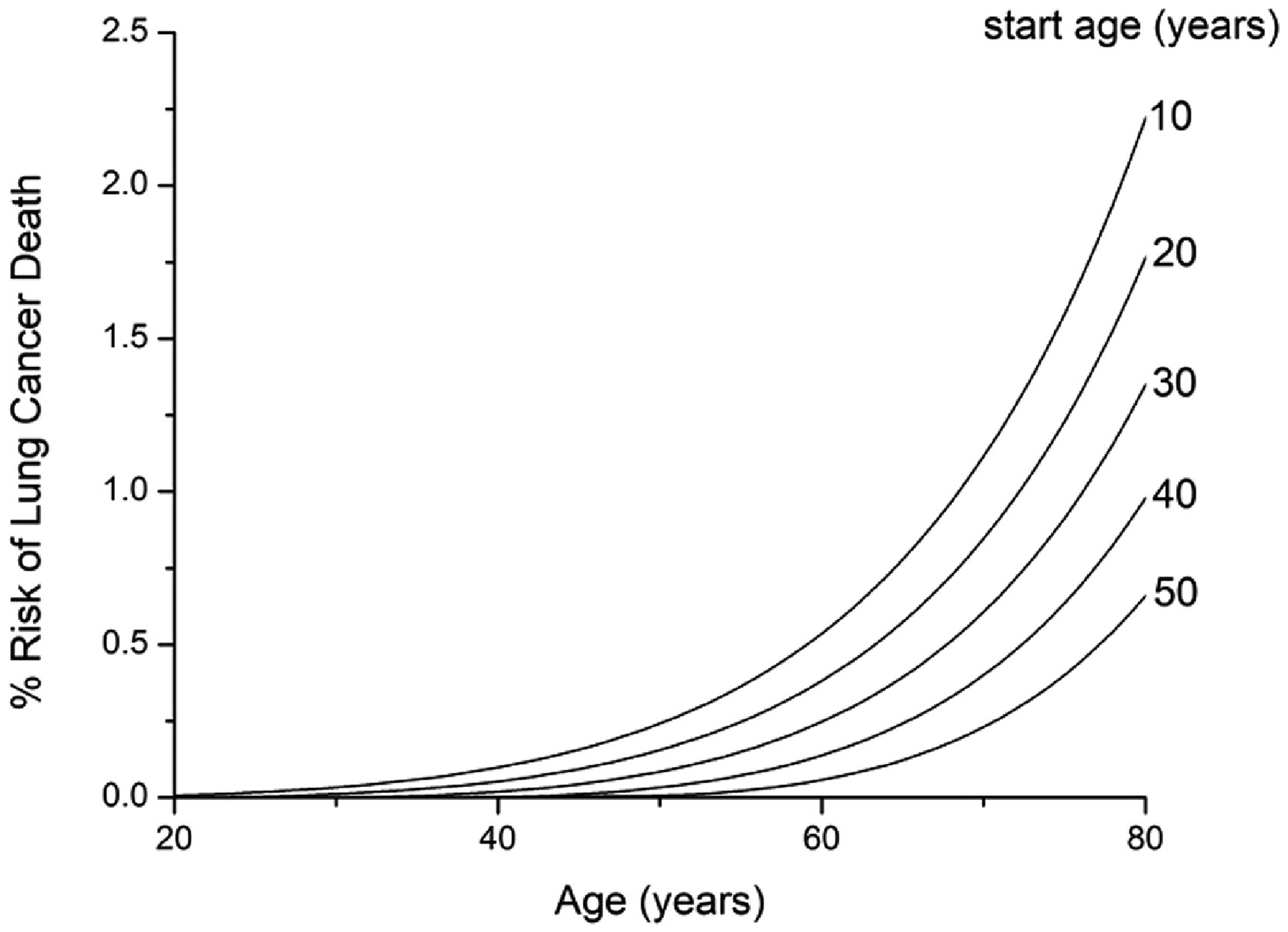
Effect of start age on prediction of % risk of dying of lung cancer within a given year of life. Smoking intensity is fixed at 20 cigarettes per day for a never quitter.

Figure 4:

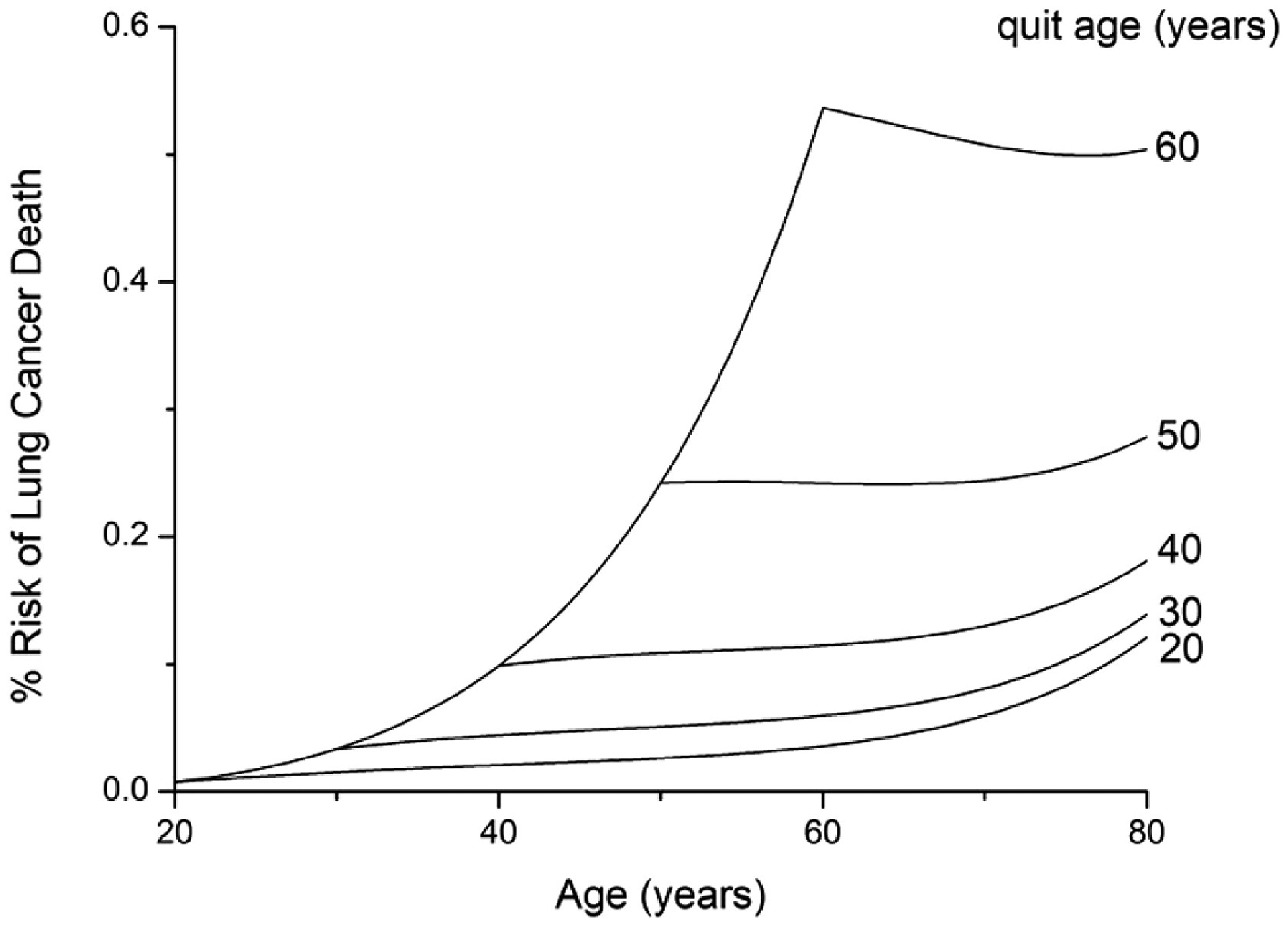
Effect of quit age on prediction of % risk of dying of lung cancer within a given year of life. Smoking starts at 10 years of age and continues with a consistent smoking intensity of 20 cigarettes per day.

Figure 5:

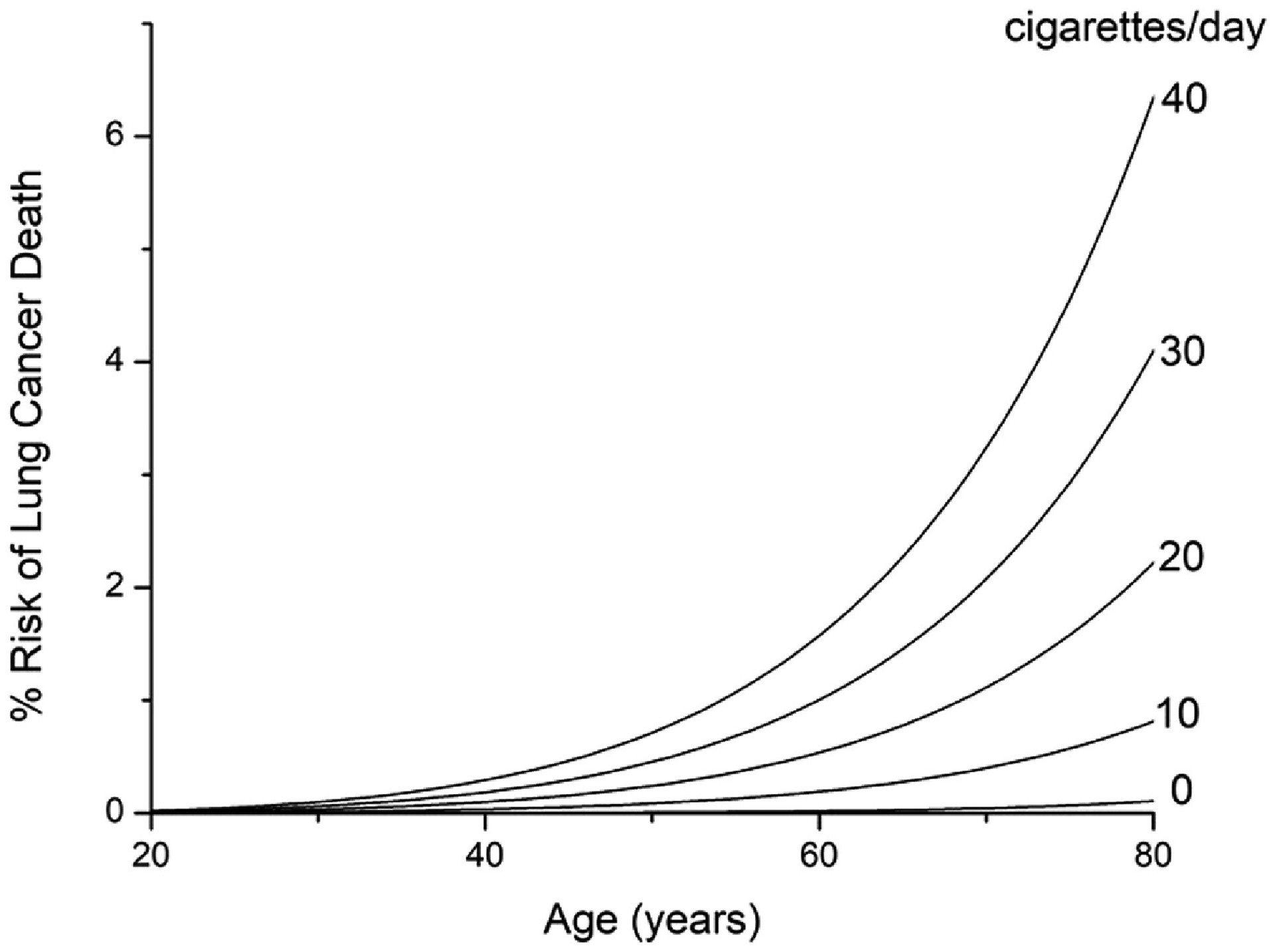
Effect of smoking intensity on prediction of % risk of dying of lung cancer within a given year of life. Smoking starts at 10 years of age and continues throughout life.

Figure 3 shows predictions of % risk of dying of lung cancer within a given year of life as a function of age for various smoking scenarios. When smoking intensity is fixed at 20 cigarettes per day for a never quitter, risk increases progressively as the age of starting smoking decreases (Fig. 3A). When smoking starts at 10 years of age with a fixed intensity of 20 cigarettes per day, quitting later leads to a progressively greater risk (Fig. 3B). Note, however, that the rate at which this risk increases with age falls dramatically after quitting. Finally, increasing smoking intensity causes a progressively increasing risk, although the rate at which this risk increases for a given age falls off with intensity (Fig. 3C).

Discussion

Lung cancer remains the preeminent example of a preventable malignancy, so understanding how mortality risk is affected by prevention measures is a public health priority. For example, it has been demonstrated that mortality is reduced by the use of low-dose CT screening to detect presymptomatic lung cancers while they are still at an early stage and may be curable [10, 11]. Mathematical models of lung cancer mortality risk, particularly the CISNET models [1, 12], have been employed to inform screening strategies, with most attention focused on who should be screened and how often [13, 14]. Optimizing these strategies relies on being able to predict the likelihood of dying from lung cancer as a function of its key risk factors, particularly smoking history and age. Screening decisions have also been informed by Katki et al. [15] who estimated the risk of an identified lung nodule being a false positive versus an actual lung cancer. Similarly, we used an empirical model based on the study of Lubin et al. [4] to predict the risk of a second primary lung cancer [3].

Smoking cessation among the general population also continues to be a major public health goal. Unfortunately, the long-term success rates of smoking cessation efforts remain disappointingly low [16], but it is conceivable that using computational models to inform patients about their cancer risks might serve as a motivational tool. For example, many people accept that smoking is bad for their health and realize that lung cancer is a potential disastrous outcome of continuing to smoke, but there are also many who do not seem to have a realistic concept of the risk smoking poses to them specifically [17]. There are others who simply lack motivation, part of which may be due to a sense that it is too late to quit; that is, they do not think it worthwhile suffering nicotine withdrawal when they presume that the damage has already been done [18]. Presenting a personalized risk assessment might help counteract this view, and thus increase motivation to quit even in those with a very heavy smoking history.

Some models of lung cancer risk, such as that of Lubin et al. [4] which we used in our previous study [3], provide accurate descriptions of risk within the range of common epidemiological conditions to which they are fit, but are not mathematically constrained to behave appropriately when extrapolated to real world smoking and age scenarios that lie outside this range. A key goal of the present study, therefore, was to derive a mathematical expression for lung cancer mortality that both mimics known risk profiles as well as extrapolating sensibly. Thus, we ensured that our predictions of probability of dying from lung cancer in a given year of life (Eqs. 3 and 5 substituted into Eq. 2) are not only mathematically constrained to lie between zero and unity, as is required for a probability, but they also exhibit a qualitative dependence on age and smoking history that must pertain. For example, it is well known that risk increases with the age of the individual and with smoking intensity, both of which are exhibited by our model (Fig. 3C). Indeed, it is biologically inconceivable that this could not be the case. Likewise, risk increases the earlier one starts to smoke (Fig. 3A) and decreases the earlier one quits (Fig. 3B), again both factors being biologic imperatives. An important goal for our model was also that it be as simple as possible. Indeed, Eqs. 4 and 5 are easily implemented to provide a rapid prediction of lung cancer death risk for any age, smoking intensity, start age, and quit age.

Having the correct qualitative behavior, however, does not guarantee that a model makes predictions that are usefully accurate, so it is necessary that the model be calibrated against data that encompass the range of scenarios likely to be encountered in is subsequent use. We decided that the most efficient way to do this was to fit out model to a set of predictions made by the CISNET models [1], since these models are themselves based on detailed epidemiological data and represent the standard upon which current screening guidelines are based [12]. Nevertheless, the CISNET models themselves exhibit substantial variation in their individual risk predictions as evidenced by the vertical spread in the ranges shown by the dashed lines in Fig 2, which is testament to the complexities involved in accounting for different data sets. In any case, by fitting our model to the mean CISNET model predictions for a wide range of smoking scenarios from the never smoker to the individual with 66 pack-years by age 80 (Fig. 2), were we able to obtain robust estimates of the four free parameters α, β, τ_quit and τ_age in Eq. 4. The fitted curves do not track exactly along the means of the CISNET predictions, but for the most part they remain within the ranges of these predictions. In those cases where the fits are outside these ranges, the differences in absolute death risk are low (Fig. 2). These findings thus show that our model captures the overall quantitative risk behavior of the data on which the CISNET models are based, making our model predictions are consistent with reported lung cancer death rates [19]. Our model also exhibits similar behavior to previous models in which the excess risk of smoking declines exponentially with time following quitting. These previous models arrived at a time-constant of risk decay ranging from 7.9 to 13.0 years [7], which encompasses the value of τ_quit = 11.9 years that we found in the present study.

Our model also has some limitations. For example, it assumes a constant rate of cigarette consumption during the smoking years and does not consider individuals who quit and then start smoking again. It is based on current data on the overall death rate for lung cancer, which has not fluctuated dramatically over the past 40 years, but could change significantly with the development of more effective therapies [19]. The model has also not been calibrated against CT screening data, does not take specific sub-sets of lung cancer into account [9, 20], and ignores other factors that may related to lung cancer incidence such as the country in which smokers reside. In addition, the model is yet to be tested outside the range of smoking scenarios predicted by the CISNET models in Fig. 2. Fitting the model directly to cancer mortality data from various sources would provide further model validation and allow it to be adapted to populations other than the US cohorts on which the CISNET models are based. Further validation of the model The predictions in Fig. 3 extend out to 140 pack-years by age 80, more than twice the maximum smoking burden considered by the CISNET models. Nevertheless, these extreme predictions are qualitatively sensible so for the time being may be useful for situations in which the risk of cancer death needs to be estimated for extremely heavy smokers.

In summary, we have developed an empirical model of the risk of dying of lung cancer in any given year of life. The model is mathematically constrained to produce probability predictions that lie between 0 and 1. The manner in which the model predictions depend on age, smoking start age, quit age, and smoking intensity make biologic sense and closely match the mean predictions of the CISNET models for a range of smoking scenarios. The model is based on an equation that is easily implemented in any conventional programming language, and thus may serve as a convenient and useful tool in such fields as lung cancer screening and smoking cessation.

Highlight.

Although a number of computational models exist for predicting the risk of dying of lung cancer in any year of life as a function of age and smoking history, their predictions are quite variable and the models themselves can be complex to implement. We have developed a simple empirical model of the risk of dying of lung cancer that is mathematically constrained to produce biologically appropriate probability predictions as a function of current age, smoking start age, quit age, and smoking intensity. This simple model is easily implemented and may serve as a useful tool in situations where the mortality risks of smoking need to be estimated.