Abstract
Feasibility assessment and planning of thoracic endovascular aortic repair (TEVAR) require computed tomography (CT)-based analysis of geometric aortic features to identify adequate landing zones (LZs) for endograft deployment. However, no consensus exists on how to take the necessary measurements from CT image data. We trained and applied a fully automated pipeline embedding a convolutional neural network (CNN), which feeds on 3D CT images to automatically segment the thoracic aorta, detects proximal landing zones (PLZs), and quantifies geometric features that are relevant for TEVAR planning. For 465 CT scans, the thoracic aorta and pulmonary arteries were manually segmented; 395 randomly selected scans with the corresponding ground truth segmentations were used to train a CNN with a 3D U-Net architecture. The remaining 70 scans were used for testing. The trained CNN was embedded within computational geometry processing pipeline which provides aortic metrics of interest for TEVAR planning. The resulting metrics included aortic arch centerline radius of curvature, proximal landing zones (PLZs) maximum diameters, angulation, and tortuosity. These parameters were statistically analyzed to compare standard arches vs. arches with a common origin of the innominate and left carotid artery (CILCA). The trained CNN yielded a mean Dice score of 0.95 and was able to generalize to 9 pathological cases of thoracic aortic aneurysm, providing accurate segmentations. CILCA arches were characterized by significantly greater angulation (p = 0.015) and tortuosity (p = 0.048) in PLZ 3 vs. standard arches. For both arch configurations, comparisons among PLZs revealed statistically significant differences in maximum zone diameters (p < 0.0001), angulation (p < 0.0001), and tortuosity (p < 0.0001). Our tool allows clinicians to obtain objective and repeatable PLZs mapping, and a range of automatically derived complex aortic metrics.
Keywords: TEVAR, Automatic segmentation, Computational geometry, Aorta, CT
Introduction
Thoracic endovascular aortic repair (TEVAR) represents the preferred approach for the treatment of pathologies of the descending thoracic aorta, including aortic aneurysm and dissection [1]. Advancements in endograft engineering and design have allowed the application of this minimally invasive technique also for the treatment of aortic disease involving the proximal tract of this vessel, namely the aortic arch. However, despite the favorable short-term outcomes with respect to surgery, TEVAR of the aortic arch still carries a significant risk of medium- and long-term complications, including endoleak, endograft migration, and collapse [2, 3], likely due to its peculiar geometric and fluid-dynamic features [4]. As of today, no standard risk assessment tool exists for arch TEVAR, but a thorough preoperative decision-making process is considered crucial for an uneventful endograft deployment, and a durable clinical success [5–7]. Feasibility of TEVAR and correct endograft sizing are based on measurements of Ishimaru’s proximal landing zones [8], i.e., the aortic wall sections corresponding to potential endograft apposition sites, during pre-procedural planning. A minimum length of 20 mm and maximum diameter of 40 mm are required for the proximal and distal landing zones to ensure adequate endograft apposition, and a variable stent graft diameter oversizing is recommended based on aortic disease [5, 6]. These criteria, however, neglect additional geometric parameters, such as angulation and tortuosity, which proved to be associated with an increased risk of endograft failure after repair, and therefore allow to identify hostile landing zones for TEVAR [3, 9, 10]. Moreover, the presence of anomalous aortic arch configurations may further complicate TEVAR planning. Of note, arches with a common origin of the innominate and left carotid arteries (CILCA) were shown to have a higher risk of developing thoracic aorta disease [11], and to be associated with dismal clinical outcome after TEVAR [12]. Interestingly, both findings are apparently related to the consistent and peculiar geometric and fluid-dynamic pattern of proximal landing zones of the CILCA arch [13, 14].
Contrast-enhanced computational tomography (CT) represents the preferred imaging modality [5, 15] to assess the pre-procedural aortic geometry, but no consensus nor detailed guidelines exist on how to extract the necessary measurements from CT image data. Such an analysis requires manual detection and definition of anatomical landmarks [15], and in some cases, measurements are manually taken directly on 2D CT image slices, thus preventing a true and accurate 3D characterization [16]. In fact, the inherent 3D nature and complexity of the anatomical data, together with the high inter-operator variability, can significantly affect the measurements, thus hindering a repeatable geometry-based pre-procedural planning for TEVAR. Nonetheless, volumetric CT-based segmentation of the thoracic aorta can provide a 3D model on which the relevant geometric parameters can be measured objectively and systematically. However, this is a time-consuming process which is rarely carried out in clinical practice.
Recent advances in deep learning algorithms for computer vision have allowed for automating complex tasks involved in medical image analysis, including fully automatic segmentation [17]. In particular, convolutional neural networks (CNNs) have achieved state-of-the-art results on a wide range of anatomical structures, including brain tumor [18], left atrium [19], liver [20] and others belonging to the Medical Segmentation Decathlon Dataset [21]. A CNN can learn to perform segmentation through a training set, i.e., by iteratively processing a large amount of sample images, comparing the automatically segmented anatomy vs. the corresponding ground truth segmentation, and refining the tuning of the parameters to minimize the observed mismatch. After training, a CNN can be validated with a test set, i.e., by processing completely new images unused during training.
In this study, we developed and applied a fully automated pipeline that feeds on 3D CT images and provides a comprehensive geometric analysis of the aortic arch, for both standard and CILCA arch configurations. Our pipeline allows clinicians to obtain automated segmentation of the thoracic aorta, automated proximal landing zones mapping, and a range of automatically derived aortic metrics. Our tool is also suitable to be used for unbiased quantitative analyses of geometric parameters in population studies.
Methods
Data Collection
We retrospectively retrieved 3D CT scans of 515 subjects, acquired between 2010 and 2020, from three Italian referral center for aortic disease. Acquisitions with artifacts due to movement, presence of metal devices, or with slice thickness greater than 1.5 mm were excluded. Accordingly, 465 subjects were eventually included in this study and, among them, 219 subjects presented a CILCA arch. Within the entire dataset, 9 cases had thoracic aortic aneurysm (TAA). For the collected CT scans, pixel spacing ranged from 0.29 × 0.29 to 0.976 × 0.976 mm2, while slice thickness ranged between 0.29 and 1.5 mm. The study was approved by the local ethics committee and informed consent was waived because of the retrospective nature of the study and the analysis of anonymized data.
Image Pre-analysis and Manual Segmentation
To standardize the dataset, images were cropped to exclude regions below the celiac trunk, when present. Subsequently, all the CT volumes were manually segmented by five independent and experienced operators, guaranteeing that each acquisition was segmented by at least one operator to reduce single operator bias and ensuring an almost even/balanced split of the dataset among them. To avoid potential bias due to the choice of a specific segmentation software, manual segmentations were performed either using ITK-snap [22], 3D Slicer [23] or Materialise Mimics Medical v.22.0 (Materialise, Leuven, Belgium), and using gold standard segmentation methods such as level-sets, region growing and thresholding.
Neural Network Training
The dataset was subsequently divided into training and test sets: 395 (85%) scans of healthy subjects with their corresponding ground truth segmentations were randomly selected and used for neural network training (training set), while the remaining 70 scans (15%), including 61 healthy subjects and 9 patients, were kept out for testing (test set). The training set included both standard and CILCA aortic arches in random amounts. To investigate the network’s generalization capability in real clinical scenarios, all the 9 pathological cases were included in the test set. Herein, the trained CNN was based on the 3D U-Net architecture proposed in [24], which is composed of a input layer of 16 filters, encoder and decoder branches of 5 resolution levels each, a bottleneck block and skip connections via concatenation. Training was accomplished through a patch/batch-based strategy, which consists in subdividing the image volume into fixed-size subvolumes (patches), and processing groups of N patches (batches) separately [25]. Patch size was set to 128 × 128 × 128 pixels, while batch size (N) was set equal to 2. A data augmentation routine was used to increase dataset diversity. The random transformations applied to the processed patches included rotation, mirroring and elastic deformation [25]. The network was implemented in Pytorch and trained in parallel on 2 NVIDIA V100 GPUs over 300 epochs, each one defined as an iteration over 300 batches. A combination of Lovsz-Softmax loss [26] and focal loss [27] was used to trained the network end-to-end to perform multi-structure segmentation of the thoracic aorta and pulmonary arteries.
Pipeline Implementation
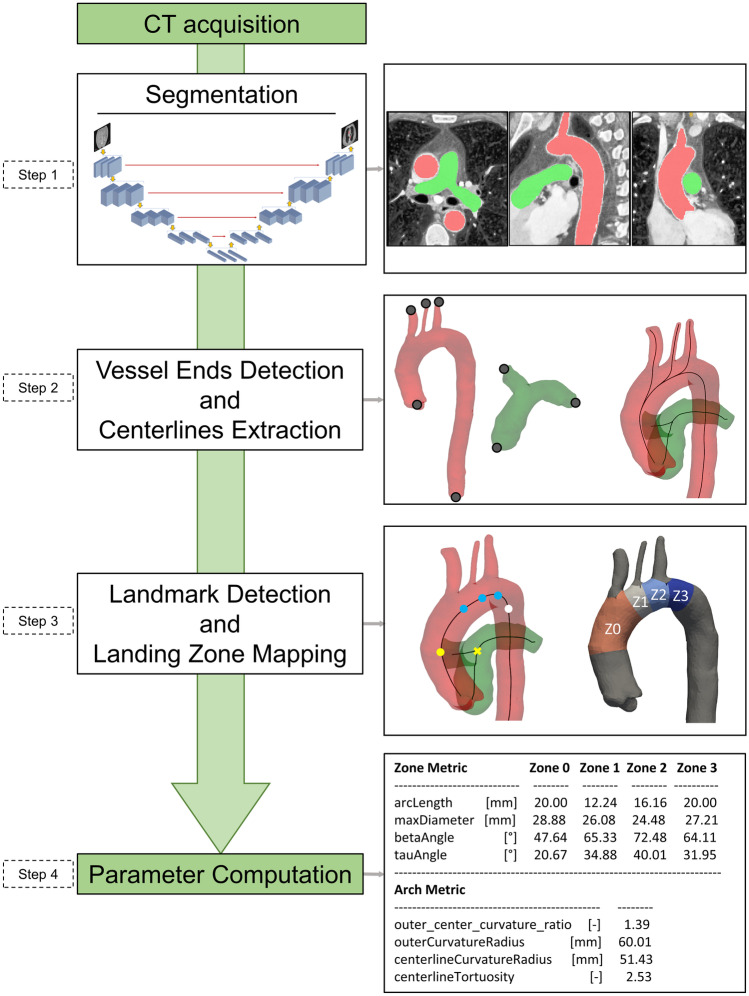
We implemented a fully automated pipeline, embedding the trained CNN, for the geometrical characterization of the aortic arch anatomy (Fig. 1). The pipeline consists of the following main processing steps: (i) segmentation, (ii) detection of vessel ends and extraction of centerlines, (iii) landing zone mapping, and (v) parameter computation.
Fig. 1.
Schematic representation of the implemented automatic pipeline. In steps 1-3, red domains and surfaces represent the thoracic aorta; green domains and surfaces represent the pulmonary artery
Segmentation (Fig. 1, step 1)
The trained CNN receives a stack of 3D CT images and automatically segments the thoracic aorta and the pulmonary trunk and arteries, yielding a multi-label mask image.
Vessel End Detection and Centerline Extraction (Fig. 1, step 2)
Triangulated surface meshes for the aorta and pulmonary vessels are obtained from the multi-label segmentation image using a marching cubes algorithm [28]. Centerlines of the aorta and of the pulmonary arteries are extracted from the corresponding surface meshes using the vascular modeling toolkit (VMTK) library [29], according to which vessel centerlines are computed as the locus of the centers of maximal inscribed spheres [30]. Centerline computation requires definition of a seed and target points on the surface of interest, which are automatically found by taking advantage of the Laplace–Beltrami (LB) operator [31]. Eigenfunctions of LB operator provide a set of bases for continuous functions defined on the surface manifold, allowing one to form a basis which is descriptive of the analyzed shape [32].
Detection of Seed and Target Points for the Aortic Centerline
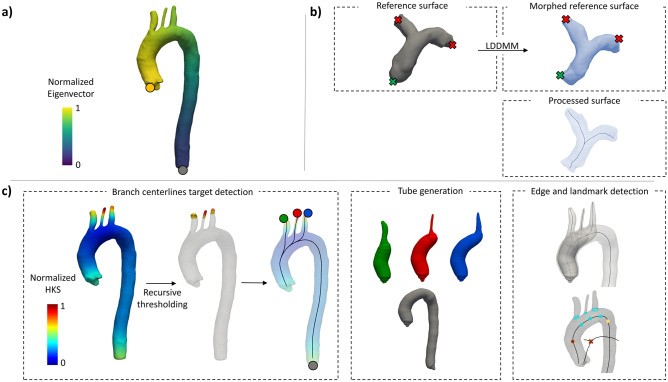
The LB operator of the triangulated aortic surface is computed. For tubular surfaces with a dominant longitudinal direction, such as the thoracic aorta, the first eigenvector of the LB operator provides for each point on the surface a scalar measure of its proximity to the left ventricle (Fig. 2a). The points on the aortic surface associated with the minimum and maximum of this shape descriptor were used as centerline seed and target.
Fig. 2.
Representation of the algorithms for automatic detection of centerlines seed and target points. a) the first normalized eigenvector of the Laplace-Beltrami operator used to find seed (yellow circle) and target (grey circle) points for the main aortic centerline. b) seed (green cross) and targets (red crosses) are manually annotated on the reference surface, which is morphed into the processed surface. From the morphed surface, left and right pulmonary arteries centerlines are computed. c) the normalized Heat Kernel Shape (HKS) is computed on the aortic surface and recursively thresholded to isolate supra-aortic branch ends; tube surfaces are generated for the aorta (grey), brachiocephalic trunk (green), left carotid artery (red) and subclavian artery (blue)
Detection of Seed and Target Points for Pulmonary Vessel Centerlines
In this case, the bifurcated nature of the pulmonary trunk and arteries does not allow for a straightforward identification of seed and target points by computing the LB eigenfunctions. The automation of this step required prior processing of a reference pulmonary artery surface that was randomly selected from the dataset. For the reference geometry, centerline seed and targets points are manually identified, and their indices stored. Then, for every processed case, the reference surface is morphed into the processed surface using a previously implemented large deformation diffeomorphic metric mapping framework (LDDMM) [33]. After registration, a soft point-to-point correspondence is achieved between the processed and the reference surfaces. The three points corresponding to seed and targets are then defined on the processed surface as the nearest to the previously stored point indices on the reference surface (Fig. 2b, Algorithm 1).
Detection of Target Points for Supra-aortic Branch Centerline Computation (Fig. 1, step 2)
The definition of the LB operator on the aortic surface is used to solve a heat equation and to compute, for every point on the processed surface, the Heat Kernel Signature (HKS) descriptor [34]. The computed HKS is normalized with respect to its maximum value. The HKS gives a scalar approximation of the local curvature of the surface by measuring the amount of heat that remains after a specified time at each point after application of a unit heat impulse. The normalized HKS can be visualized on the surface mesh (left panel of Fig. 2c). A recursive thresholding approach is used to identify supra-aortic branch extremities. Briefly, a thresholding filter is initialized to extract the surface regions with an associated normalized HKS between 1 and 1 – δ, with δ = 0.01. The value of δ is then recursively increased by a factor of 2 until the number of connected regions extracted after thresholding is equal to 3. To filter out undesired points characterized by a high curvature, candidate target regions are constrained to lie above the main aortic centerline. Finally, for each of the 3 extracted regions, the point with the highest associated normalized HKS is identified as a branch centerline target and 3 centerlines are finally computed (Fig. 2c, Algorithm 2).
Landing Zone Mapping (Fig. 1, step 3)
Once calculated, centerlines are separated according to the vessel to which they correspond and a tube surface inscribed in the vessel is generated for each centerline [29]. Herein, a tube is defined as a centerline envelope whose cross sections are circles with radius locally equal to the radius of the maximal inscribed sphere within the vessel. Intersections between tubes corresponding to supra-aortic branches and the tube of the main aortic centerline are computed (Fig. 2c, right). In this way, three bounded lines silhouetting branch origins on the arch are generated (cyan rings in Fig. 2c, right). For each edge, the landing zone landmark on the aortic centerline is identified as the projection of the most distal point in the edge onto the aortic centerline. Two additional landmarks (brown and yellow circles, Fig. 2c, right) are automatically placed on the centerline to delimit zone 0, proximally, and zone 3, distally. To automatically detect the landmark delimiting zone 0 proximally, the bifurcation point of the pulmonary vessels is identified (brown cross, Fig. 2c, bottom right) and projected onto the aortic centerline, keeping the axial coordinate fixed (brown circle, Fig. 2c, bottom right). The landmark delimiting zone 3 distally is automatically placed on the aortic centerline so as to fix the length of this zone to 20 mm, which is considered as the minimum length to identify a stable landing zone for TEVAR [15] (yellow circle, Fig. 2c, bottom right).
Parameter Computation
In this step (Fig. 1, step 4), two kinds of metrics are automatically quantified to characterize the aortic arch morphology.
Whole-Arch Metrics
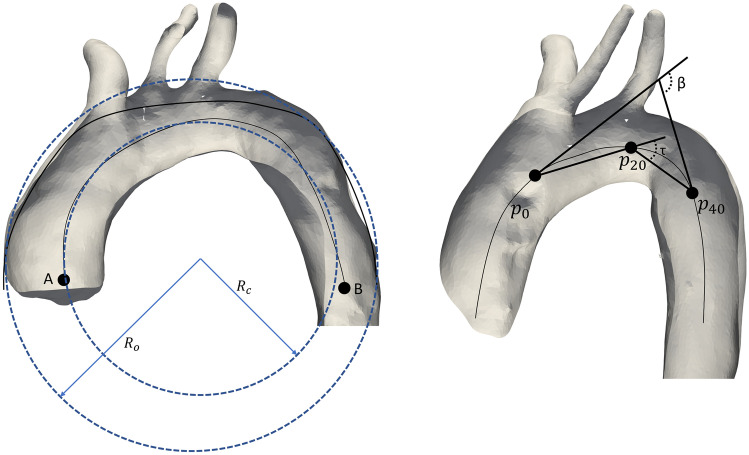
For quantitative characterization of the whole arch, two points are defined (Fig. 3). Point A is identified as the most proximal point in the vessel centerline, falling within the ascending aorta. Point B is the point of the aortic centerline that lies on the same CT image axial plane passing through point A. The portion of the centerline bounded between A and B is considered. The outer curvature path corresponding to this centerline tract is found as the diametrically opposed path to the Dijkstra path [35] with respect to the aortic centerline. For both the centerline tract and the outer curvature path, the radius of curvature is computed in two steps; first, by projecting the 3D curve onto its best-fitting plane found by singular value decomposition and, second, by finding the radius of the best-fitting circle to the curve in a least-square sense (Fig. 3, left). Additionally, arch centerline tortuosity is calculated as the ratio of the curvilinear length between A and B to their straight-line distance.
Fig. 3.
Automatic computation of geometric descriptors. A standard arch configuration (left) exemplifying centerline curvature radius (RC) and outer curvature radius (RO) (in blue). A CILCA arch (right) reporting β and tortuosity (τ) angles. N.B.: distances not to scale for display purposes
Zone-Based Metrics
Arc length along the centerline, maximum diameter, β angle, and tortuosity angle are calculated for each zone according to [15] (Fig. 3, right). Maximum zone diameters are calculated as the diameters of the largest inscribed spheres within each zone [29]. Briefly, for each zone, the most proximal point (p0) is identified together with its tangent unitary vector. Two other points, p20 and p40, located 20 mm and 40 mm distal to p0 along the centerline, respectively, are selected with their tangent unitary vectors. β is the angle formed by the tangent unitary vectors to p0 and p40. The tortuosity angle (referred to as τ in Fig. 3, right) is defined as the angle formed by the vectors connecting p0 to p20 and p20 to p40.
Statistical Analysis
Statistical analyses were performed using the Python scipy 1.5.1 statistics library. Data normality was determined using the Shapiro–Wilk test. Normally distributed variables are expressed as mean ± standard deviation; non-normally distributed variables are expressed as median [min, max]. Comparison between standard and CILCA arches was accomplished using unpaired t-tests for normally distributed variables and Mann–Whitney U tests for non-normally distributed data. Comparison among zone-based geometric parameters for standard and CILCA arches were carried out using one-way ANOVA for normally distributed data and Kruskal–Wallis tests for non-normally distributed data. A p value lower than 0.05 was considered statistically significant.
Comparison with Semi-Automated Measurements
Out of the 70 test cases, 30 were randomly selected and processed by an experienced operator using the semi-automated commercial software 3Mensio Vascular 8.0 (3Mensio Medical Imaging B.V., Bilthoven, The Netherlands). The results of the geometric analysis obtained with the proposed methodology were compared against the corresponding measurements taken through the commercial software.
Results
Test Set Results
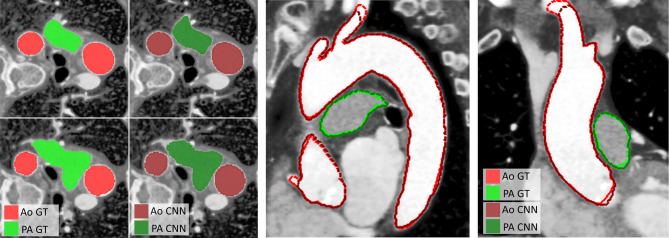
The trained CNN was employed to run inference on the test set made of 70 CT scans, 9 of which presented TAA. The automatic segmentation algorithm proved able to accurately extract the thoracic aorta and pulmonary vasculature anatomies for all the subjects of the test subjects (Fig. 4). CNN performance was quantitatively assessed, in terms of Dice coefficients and Hausdorff distances [36], with respect to manual ground truth segmentations. For the thoracic aorta, Dice score and Hausdorff distance were equal to of 0.954 [0.873, 0.999] and 11.97 [1.96, 68.83] mm, respectively. For the pulmonary trunk and arteries, mean Dice score and Hausdorff distance were equal to 0.906 [0.710, 0.999] and 11.55 [0.94, 29.86] mm. The CT acquisition phase was chosen to specifically visualize aortic structures via the injection of a contrast-enhancing agent. The reduced presence of contrast agent in the pulmonary vasculature limited the relative brightness of these vessels with respect to the background. Thus, the trained neural network was considerably better at segmenting the thoracic aorta as compared to the pulmonary arteries. Nonetheless, the worse performance in pulmonary artery segmentation did not invalidate the automated detection of the bifurcation landmark, relevant for the identification of zone 0.
Fig. 4.
Comparison of manual (ground truth, GT) segmentation in bright red (aorta, Ao) and bright green (pulmonary arteries, PA), vs. automatic segmentation obtained by the trained neural network (CNN) in dark red (aorta, Ao) and dark green (pulmonary arteries, PA) on a test case. Four axial slices with color fill are shown on the left. A sagittal and a coronal slices with dashed contours are shown on the right
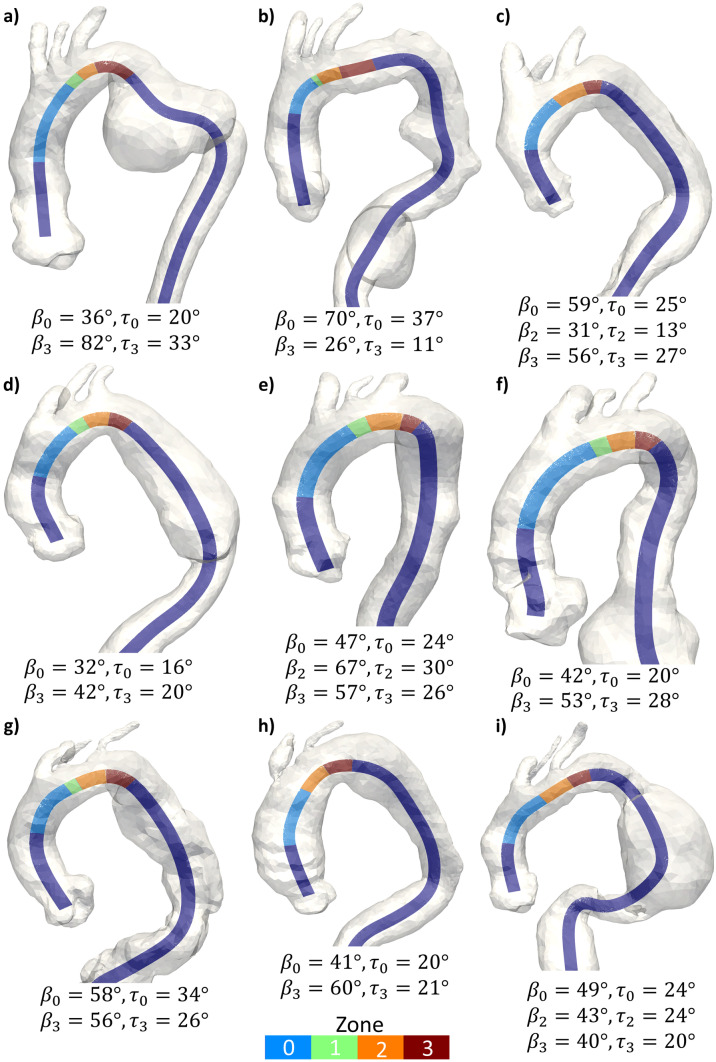
The automatic pipeline effectively identified Ishimaru’s landing zones for all the 70 test subjects, including the 9 pathological cases, as detailed in Fig. 5.
Fig. 5.
Aortic arches with thoracic aortic aneurysm from the test set with centerlines colored by landing zone. Six arches present a standard configuration with the presence of zone 1; all other arches present a CILCA arch configuration without zone 1. β and tortuosity (τ) angles for zones longer than 20 mm are reported, with subscripts indicating the zone they refer to
Geometric and Statistical Analysis
The developed automated geometric analysis (steps 2 to 4 of the pipeline) was applied to the entire dataset of manually segmented CT scans (n = 465).
Comparison of CILCA vs. Standard Arches
Statistically significant differences were observed for whole arch metrics in centerline curvature radius (p = 0.001), outer curvature radius (p = 0.004), and centerline tortuosity (p = 0.021), with CILCA arches exhibiting lower values (Table 1).
Table 1.
Whole arch-based geometric parameters calculated by the automatic tool for standard and CILCA arch cases. Median [min, max] or mean ± standard deviations are reported together with the p values obtained by the statistical analysis
| Variable | Standard | CILCA | p value |
|---|---|---|---|
| Centerline curvature radius [mm] | 50.26 [27.94, 71.31] | 48.19 [26.47, 68.45] | 0.001 |
| Outer curvature radius [mm] | 65.94 ± 8.37 | 63.68 ± 8.19 | 0.004 |
| Outer/centerline curvature ratio | 1.14 [0.97, 2.68] | 1.13 [0.95, 2.28] | 0.153 |
| Centerline tortuosity | 3.10 [1.82, 6.38] | 2.96 [1.63, 9.15] | 0.021 |
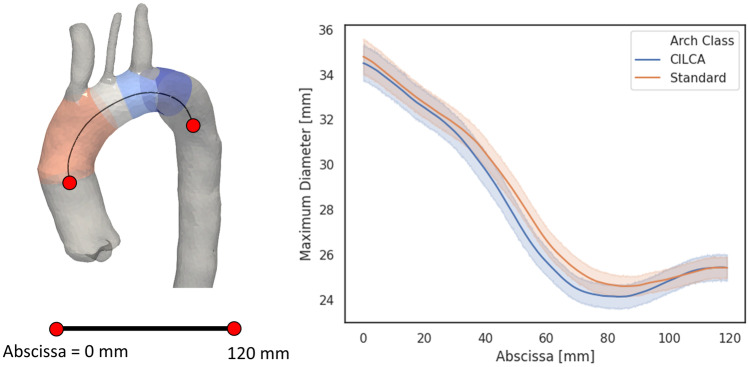
Focusing on zone-based metrics, zone 0 was found to be significantly longer in CILCA than standard arches (p < 0.001), whereas no significant difference was observed for zone 2 (Table 2). Within each landing zone, maximum diameter (Table 3) remained comparable (p > 0.089) between standard and CILCA aortic arches. However, both standard and CILCA configurations exhibited progressive maximum diameter reduction from zone 0 to zone 3 (p < 0.0001). In particular, CILCA arches showed a slightly greater variation of maximum diameter between adjacent zones (zone 0–zone 2) with respect to standard arches (zone 0–zone 1). In standard arches, the mean value of the maximum diameters ranged between 34.7 mm in zone 0 and 28.43 mm in zone 1. In CILCA arches, the mean value of the maximum diameters varied between 34.0 mm in zone 0 and 26.30 mm in zone 2. To better analyze this difference in vessel tapering, a 120 mm arch tract was extracted from every arch centerline starting from the most proximal point of zone 0 (Fig. 6), and pointwise vessel diameters were plotted as means with 95% confidence intervals (Fig. 6). In CILCA arches, a steeper curve was observed between 30 and 80 mm, indicating a more markedly tapered geometry of the vessel lumen.
Table 2.
Zone arc lengths in mm calculated by the developed automatic tool for standard and CILCA arch cases. Median [min, max] are reported together with p values obtained from the statistical analyses
| Variable | Standard | CILCA | p valuea |
|---|---|---|---|
| Arc length [mm] | |||
| Zone 0 | 48.63 [21.46, 112.15] | 53.02 [22.49, 103.67] | < 0.001 |
| Zone 1 | 8.08 [2.25, 20.82] | - | - |
| Zone 2 | 16.66 [3.36, 80.53] | 16.87 [0.64, 36.17] | 0.142 |
| p-valueb | < 0.0001 | < 0.0001 |
aStandard vs. CILCA
bANOVA among landing zones
Table 3.
Zone maximum diameters in mm calculated by the developed automatic tool for standard and CILCA arch cases. Median [min, max] are reported together with p values obtained from the statistical analyses
| Variable | Standard | CILCA | p valuea |
|---|---|---|---|
| Maximum diameter [mm] | |||
| Zone 0 | 34.70 [21.03, 52.78] | 34.00 [21.36, 53.32] | 0.247 |
| Zone 1 | 28.43 [17.09, 43.47] | - | - |
| Zone 2 | 26.49 [15.25, 42.66] | 26.30 [14.23, 52.75] | 0.089 |
| Zone 3 | 25.22 [7.13, 36.04] | 24.76 [12.19, 50.35] | 0.152 |
| p-valueb | < 0.0001 | < 0.0001 |
aStandard vs. CILCA
bANOVA among landing zones
Fig. 6.
Representation of a 60 mm centerline tract covering the landing zones (left), and maximum diameter plotted against the centerline abscissa (right). Values for standard (orange) and CILCA (blue) cases are plotted as mean (solid lines) with 95% confidence intervals (transparent bands)
Significant differences were found in β angles (Table 4) between standard and CILCA aortic arch configurations in both zone 0 (p = 0.001) and zone 3 (p = 0.015), with CILCA arches reporting larger median values. For both arches, β angles significantly differed (p < 0.0001) among the arch zones, with zone 3 reaching the highest values (Table 4). Similarly, a statistically significant difference in tortuosity angle between the two configurations was found in landing zones 0 (p = 0.001) and 3 (p = 0.048), with larger angles observed in CILCA arches (Table 5). Tortuosity angles were observed to be significantly different among landing zones for both standard and CILCA arches (p < 0.0001). In both arch types, tortuosity angle reached the highest mean values in zone 3.
Table 4.
Zone β angles in degrees calculated by the developed automatic tool for standard and CILCA arch cases. Mean ± standard deviations are reported together with p values obtained from the statistical analyses
| Variable | Standard | CILCA | p valuea | |
|---|---|---|---|---|
| β angle [°] | ||||
| Zone 0 | 50.17 [13.22, 102.66] | 54.13 [21.90, 77.38] | 0.001 | |
| Zone 1 | 46.07 [9.68, 104.49] | - | - | |
| Zone 2 | 54.55 ± 14.07 | 53.15 ± 14.92 | 0.297 | |
| Zone 3 | 57.09 [13.69, 132.41] | 59.61 [15.45, 98.88] | 0.015 | |
| p-valueb | < 0.0001 | < 0.0001 | ||
aStandard vs. CILCA
bANOVA among landing zones
Table 5.
Zone tortuosity angles in degrees calculated by the developed automatic tool for standard and CILCA arch cases. Median [min, MAX] or mean ± standard deviations are reported together with p values obtained from the statistical analyses
| Variable | Standard | CILCA | p valuea |
|---|---|---|---|
| Tortuosity angle [°] | |||
| Zone 0 | 24.81 [6.06, 53.70] | 27.18 [11.63, 39.94] | 0.001 |
| Zone 1 | 24.05 [5.58, 60.25] | - | - |
| Zone 2 | 27.14 ± 7.53 | 26.60 ± 8.14 | 0.462 |
| Zone 3 | 28.68 [6.74, 76.38] | 29.85 [10.75, 54.19] | 0.048 |
| p-valueb | < 0.0001 | < 0.0001 |
aStandard vs. CILCA
bANOVA among landing zones
Measurements on TAA Cases
In ordered to be considered suitable, the proximal landing zone for TEVAR must be at least 20 mm long [5]. For the 9 TAA cases, β and tortuosity angles of zones fulfilling this criterion are reported in Fig. 5. Among these anatomies, only 3 cases had a sufficiently long zone 2 (Fig. 5c, e, i). Severe angulation (β > 60°) was observed in zone 0 (Fig. 5b), in zone 2 (Fig. 5e), and in zone 3 of one arch (Fig. 5a). Tortuosity angles greater than 30° were observed in zone 0 for two arches (Fig. 5b, g) and in zone 3 for one arch (Fig. 5a).
Comparison vs. Semi-automated Measurements
The differences between the measurements yielded by the proposed automated tool and those obtained by an experienced operator using the semi-automated software package 3Mensio are detailed in Table 6. Notably, 3Mensio does not allow to compute a best-fitting circle to estimate curvature radii; hence, these were calculated by dividing the centerline (or outer curvature) tract by π, thus considering it equal to a semicircle. Furthermore, the commercial software now calculates the tortuosity angle using an arm length of 15 mm, rather than 20 mm (used by our tool), and it does not allow for changing this parameter. Overall, good agreement was found between the two measurement approaches, with linear measurements (lengths and diameters) differing by less than 5.4 mm, and angular measurements (β and tortuosity angles) differing by less than 6.5°
Table 6.
Comparison between geometric measurements obtained with the commercial software 3Mensio vs. our tool. Mean of differences and 95% limits of agreement are reported. Zone 1 metrics refer to standard arches only, while all other metrics refer to both standard and CILCA arches
| 3Mensio | Our tool | Bias (3Mensio—our tool) | 95% limits of agreement | |
|---|---|---|---|---|
| Centerline curvature radius [mm] | 52.31 | 52.27 | 0.05 | [−2.1, 2.19] |
| Outer curvature radius [mm] | 67.31 | 68.41 | −1.09 | [−4.03, 1.84] |
| Outer/centerline curvatures ratio | 1.29 | 1.31 | −0.02 | [−0.03, 0.0] |
| Centerline tortuosity | 1.66 | 3.05 | −1.39 | [−1.63, −1.15] |
| Arc length [mm] | ||||
| Zone 0 | 50.67 | 50.24 | 0.43 | [−2.7, 3.56] |
| Zone 1 | 10.06 | 7.52 | 2.55 | [0.89, 4.2] |
| Zone 2 | 23.28 | 17.89 | 5.39 | [−1.43, 12.22] |
| Maximum diameter [mm] | ||||
| Zone 0 | 37.82 | 36.43 | 1.39 | [0.37, 2.42] |
| Zone 1 | 30.09 | 28.73 | 1.36 | [0.22, 2.5] |
| Zone 2 | 27.41 | 26.95 | 0.47 | [−0.04, 0.97] |
| Zone 3 | 25.74 | 25.54 | 0.19 | [−0.43, 0.82] |
| Beta angle [°] | ||||
| Zone 0 | 56.4 | 49.95 | 6.46 | [2.76, 10.15] |
| Zone 1 | 45.18 | 46.82 | −1.64 | [−6.21, 2.92] |
| Zone 2 | 49.37 | 51.47 | −2.11 | [−5.85, 1.63] |
| Zone 3 | 57.07 | 56.68 | 0.39 | [−2.3, 3.08] |
| Tortuosity angle [°] | ||||
| Zone 0 | 22.4 | 24.72 | −2.31 | [−4.75, 0.12] |
| Zone 1 | 15.41 | 25.1 | −9.69 | [−13.0, −6.37] |
| Zone 2 | 17.03 | 26.2 | −9.17 | [−11.61, 6.72] |
| Zone 3 | 24.2 | 28.6 | −4.4 | [−6.46, −2.33] |
Discussion
In the present work, we developed, applied, and evaluated a fully automated pipeline for TEVAR pre-procedural planning support and aortic arch geometric analysis from CT. Our pipeline hinges on a CNN with a 3D U-Net architecture to perform automatic thoracic aorta segmentation, and on a series of geometrical computations to quantify several aortic metrics of interest for TEVAR pre-procedural planning.
The adopted 3D CNN is at the base of the developed application, providing multi-structure end-to-end segmentation that does not require any manual input nor parameter fine-tuning, thus ruling out any dependency on the operator. This proved sufficient to correctly identify supra-aortic related landmarks in all 70 test cases in our dataset. For the thoracic aorta, average Dice score, Hausdorff distance, and intersection-over-union (IoU) coefficient were 0.954, 11.97 mm, and 0.91, respectively. This level of accuracy is higher than the results reported by other studies focusing on CNNs for automatic aorta segmentation, including Noothout et al. [37] who reported Dice scores of 0.88, and [38] who obtained Dice scores and Hausdorff distances up to 0.93 and 50.0 mm, respectively. Furthermore, our IoU coefficients are greater than the scores obtained by other studies focusing on lung nodule segmentation [39]. Despite being trained only with CT scans of healthy subjects, our network was also able to perform an accurate segmentation of a small subset of diseased aortas. In fact, our training strategy, including non-rigid image deformation and scaling during data augmentation, allowed the trained U-Net to generalize to 9 pathological TAA cases, yielding an average Dice score of 0.94.
After automated segmentation, a series of algorithms for detection of anatomical landmarks were implemented through differential geometry solutions. Computation of the LB operator and its eigenvalues, was essential to achieve a robust workflow that enabled fully automated mapping of proximal landing zones for all the subjects in our cohort. To our knowledge, the developed methodologies represent a unique application of complex digital surface processing algorithms to subject-specific anatomies in a real and relevant clinical context.
From a clinical standpoint, our work addresses three relevant issues in pre-procedural TEVAR planning. First, extraction of clinically relevant geometric parameters [2, 8, 9], namely angulation and tortuosity, is technically difficult and time consuming, and may require ad hoc commercial software. Our approach does not require any specific skill from the user, as it allows quantifying automatically β and tortuosity angles of proximal landing zones, thus proving clinicians with more comprehensive information on the anatomy to treat by TEVAR. Second, current commercial solutions always require manual input, which introduces inter-operator variability. This is not the case in our tool, which delivers an objective, fully repeatable and systematic framework. Third, our solution shortens the processing time, making it compatible with the clinical routine, and applicable to large CT series for research purposes. On average, the time required by the user to process one case using commercially available software is around 30 min, whereas less than 7 min are required by our tool, i.e., about 4 and 3 min for segmentation and geometric analysis, respectively.
The reliability of our automated tool was confirmed by the comparison with geometric measurements obtained with the commercial 3Mensio Vascular 8.0 software (3Mensio Medical Imaging B.V., Bilthoven, The Netherlands). Good agreement was found between arch curvature radii, zone lengths and maximum diameters. Given the average voxel spacings of our dataset (0.75 × 0.75 × 1.25 mm3), the obtained difference biases never exceeded a length equal to twice the voxel diagonal. Larger discrepancies were observed between zone angles and centerline tortuosity. The reason behind these differences lies in the way the aortic centerlines are calculated by the two methodologies. On the one hand, in our tool, centerlines are defined as the geometric locus of the points that are centers of the maximum spheres inscribed in the vessel surface. On the other hand, 3Mensio does not require a segmented aortic surface, but allows for manual placement of centerline points on 2D views. In complex anatomies, this may lead to an oversimplified centerline characterized by remarkably lower values of tortuosity and tortuosity angles, thus requiring additional and manual correction.
Our objective analysis framework allowed investigating in a systematic fashion the differences between standard and CILCA arches in terms of metrics that are relevant for TEVAR planning. The extracted geometric parameters were compared with aortic features generally quantified using dedicated commercial software as proposed in previous works [13, 15]. With our approach, we found relevant differences in whole-arch metrics between standard and CILCA arches, with the latter showing significantly lower centerline curvature radius (p = 0.001), outer curvature radius (p = 0.004), and centerline tortuosity (p = 0.021). The average radii of curvature were 48.6 mm and 53.0 mm for standard and CILCA arches, respectively. Marrocco-Trischitta et al. [15] reported radii of curvature between 22.7 and 37.1 mm for a cohort of 60 standard arches. Such a considerable difference is due to the different methodologies adopted for the geometric analyses. In particular, in the previously referred studies, the centerline radius of curvature was approximated as half the distance between two points, on the same axial plane, one in the ascending and one in the descending aorta. Implicitly, that approach assumes that the arch centerline delimited by these two points is exactly a half circumference, which is inherently planar. Our approach improves upon this, by computing the least squares best fitting circle to approximate aortic arch curvature radius, thus accounting for the actual deviations from the idealized profile assumed in the previous work [15].
Our analysis involving zone-based metrics revealed statistically significant geometrical differences in zones 0 and 3 between standard and CILCA arches. Zone 0 of CILCA arches had greater arc length (p < 0.001), β angle (p = 0.001), and tortuosity angle (p = 0.001). Furthermore, greater β and tortuosity angles were found in zone 3 of CILCA arches. For standard arches, zone 3 β and tortuosity angles were equal to 57.09° [13.69°, 132.41°] and 28.68° [6.74°, 76.38°], respectively. Similar ranges of values were found by Marrocco-Trischitta et al. [15], who obtained β angles going from 52.3° ± 14.9° to 71.1° ± 14.1° and tortuosity angles between 25.9° ± 8.1° and 39.5° ± 8.2° on a cohort of 60 subjects. In a previous study from our group [3], zone 3 was found to be consistently associated with hostile geometric and hemodynamic features in terms of angulation, tortuosity and hemodynamic displacement forces [4]. The present analysis confirms those conclusions, highlighting the role of the β and tortuosity angles for CILCA arches. Furthermore, in the present study, the unfavorable geometric pattern displayed by CILCA arches is also suggested by the more noticeably tapered configuration followed by lumen enlargement (Fig. 6). This feature may explain the tendency of CILCA arches to develop mild aortic dilation proximal to the aortic isthmus [3, 9, 10, 40].
Limitations
Indeed, the CNN training, which requires a large number of CT scans, was performed on images of healthy subjects, and therefore our work must be conservatively regarded as a proof-of-concept study. Nevertheless, the CNN was successfully tested also for pathological CT scans, even though in a small group of aneurismatic patients. Regarding the applicability of our finding in a clinical scenario, however, previous confirmatory studies [41] showed that the aortic arch proximal landing zones present the same geometric pattern in both healthy and diseased aorta in aneurismatic patients. This is related to the fact that our analyses are based on centerline measurements, which are less likely to be affected by the modification of the aortic wall induced by the onset of pathological derangements. Notably, this applies only to patients affected with aneurysm and penetrating aortic ulcer [41], while the applicability of CNN training in aortic dissections remains to be proven, considering the peculiar anatomical features of this pathology.
Conclusions
In this work, we developed a new tool specifically tailored to automatically compute geometric parameters relevant to TEVAR planning. Our CNN successfully segmented the thoracic aorta and pulmonary vasculature of 70 CT scans unseen during training, including 9 pathological cases of TAA. Our fully automated and systematic analysis pinpointed significant differences in geometric aortic features that may explain the less satisfactory clinical results obtained by TEVAR in CILCA arches compared to standard ones. The reported tool is automated, quick and reliable, and appears to be an innovative solution to improve the decision-making process before TEVAR. Future efforts will be aimed at including more and diverse pathological anatomies in the training set, including namely aortic dissections, thus broadening the clinical scope of this methodology.
Funding
“This work was supported by “Ricerca Corrente” and 5xmille” grants from IRCCS Policlinico San Donato, a clinical research hospital partially funded by the Italian Ministry of Health.
Declarations
Ethics Approval
The study was approved by the Ethics Committee of reference (i.e., Ethics Committee of IRCCS San Raffaele (Milan, Italy). This study does not include any experiments on human participants but consists in a post hoc analysis of medical images. Patients informed consent was waived by the Ethics Committee because of the retrospective nature of the study, and the analysis of anonymized images. The study was conducted according to the principles outlined in the Declaration of Helsinki.
Consent to Participate
Patients informed consent was waived by the Ethics Committee because of the retrospective nature of the study and the analysis of anonymized images. The study was conducted according to the principles outlined in the Declaration of Helsinki.
Consent for Publication
All authors gave their consent for publication.
Conflict of Interest
The authors declare no competing interests.
Footnotes
Massimiliano M. Marrocco-Trischitta and Alberto Redaelli are equally contributing principal investigators.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Rimbau V, Böckler D, Brunkwall J. Management of descending thoracic aorta diseases. Clinical practice guidelines of the European Society for Vascular Surgery (ESVS). Eur J Vasc Endovasc Surg. 2017;53:4–52. [DOI] [PubMed]
- 2.Bellamkonda KS, Yousef S, Nassiri N, Dardik A, Guzman RJ, Geirsson A, et al. Trends and outcomes of thoracic endovascular aortic repair with open concomitant cervical debranching. Journal of Vascular Surgery. 2021;73(4):1205–12. e3. [DOI] [PubMed]
- 3.Marrocco-Trischitta MM, de Beaufort HW, Piffaretti G, Bonardelli S, Gargiulo M, Antonello M, et al. The Modified Arch Landing Areas Nomenclature predicts proximal endograft failure after thoracic endovascular aortic repair. European Journal of Cardio-Thoracic Surgery. 2020;58(2):309–318. doi: 10.1093/ejcts/ezaa115. [DOI] [PubMed] [Google Scholar]
- 4.Figueroa CA, Taylor CA, Chiou AJ, Yeh V, Zarins CK. Magnitude and direction of pulsatile displacement forces acting on thoracic aortic endografts. Journal of Endovascular Therapy. 2009;16(3):350–358. doi: 10.1583/09-2738.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.members ATF, Erbel R, Aboyans V, Boileau C, Bossone E, Bartolomeo RD, et al. 2014 ESC Guidelines on the diagnosis and treatment of aortic diseases: document covering acute and chronic aortic diseases of the thoracic and abdominal aorta of the adult The Task Force for the Diagnosis and Treatment of Aortic Diseases of the European Society of Cardiology (ESC). European heart journal. 2014;35(41):2873–926. [DOI] [PubMed]
- 6.Grabenwöger M, Alfonso F, Bachet J, Bonser R, Czerny M, Eggebrecht H, et al. Thoracic Endovascular Aortic Repair (TEVAR) for the treatment of aortic diseases: a position statement from the European Association for Cardio-Thoracic Surgery (EACTS) and the European Society of Cardiology (ESC), in collaboration with the European Association of Percutaneous Cardiovascular Interventions (EAPCI) European heart journal. 2012;33(13):1558–1563. doi: 10.1093/eurheartj/ehs074. [DOI] [PubMed] [Google Scholar]
- 7.Matsumura JS, Cambria RP, Dake MD, Moore RD, Svensson LG, Snyder S, et al. International controlled clinical trial of thoracic endovascular aneurysm repair with the Zenith TX2 endovascular graft: 1-year results. Journal of vascular surgery. 2008;47(2):247–57. e3. [DOI] [PubMed]
- 8.Ishimaru S. Endografting of the aortic arch. Journal of endovascular therapy. 2004;11(6_suppl):II-62-II-71. [DOI] [PubMed]
- 9.Altnji H-E, Bou-Saïd B, Walter-Le Berre H. Morphological and stent design risk factors to prevent migration phenomena for a thoracic aneurysm: a numerical analysis. Medical engineering & physics. 2015;37(1):23–33. doi: 10.1016/j.medengphy.2014.09.017. [DOI] [PubMed] [Google Scholar]
- 10.Ueda T, Takaoka H, Raman B, Rosenberg J, Rubin GD. Impact of quantitatively determined native thoracic aortic tortuosity on endoleak development after thoracic endovascular aortic repair. American Journal of Roentgenology. 2011;197(6):W1140–W1146. doi: 10.2214/AJR.11.6819. [DOI] [PubMed] [Google Scholar]
- 11.Marrocco-Trischitta MM, Alaidroos M, Romarowski RM, Milani V, Ambrogi F, Secchi F, et al. Aortic arch variant with a common origin of the innominate and left carotid artery as a determinant of thoracic aortic disease: a systematic review and meta-analysis. European Journal of Cardio-Thoracic Surgery. 2020;57(3):422–427. doi: 10.1093/ejcts/ezz277. [DOI] [PubMed] [Google Scholar]
- 12.Mylonas SN, Barkans A, Ante M, Wippermann J, Böckler D, Brunkwall JS. Prevalence of bovine aortic arch variant in patients with aortic dissection and its implications in the outcome of patients with acute type B aortic dissection. European Journal of Vascular and Endovascular Surgery. 2018;55(3):385–391. doi: 10.1016/j.ejvs.2017.12.005. [DOI] [PubMed] [Google Scholar]
- 13.Marrocco-Trischitta MM, Alaidroos M, Romarowski RM, Secchi F, Righini P, Glauber M, et al. Geometric pattern of proximal landing zones for thoracic endovascular aortic repair in the bovine arch variant. European Journal of Vascular and Endovascular Surgery. 2020;59(5):808–816. doi: 10.1016/j.ejvs.2019.11.019. [DOI] [PubMed] [Google Scholar]
- 14.Marrocco-Trischitta MM, Romarowski RM, Alaidroos M, Sturla F, Glauber M, Nano G. Computational Fluid Dynamics Modeling of Proximal Landing Zones for Thoracic Endovascular Aortic Repair in the Bovine Arch Variant. Annals of Vascular Surgery. 2020;69:413–417. doi: 10.1016/j.avsg.2020.05.024. [DOI] [PubMed] [Google Scholar]
- 15.Marrocco-Trischitta MM, de Beaufort HW, Secchi F, van Bakel TM, Ranucci M, Van Herwaarden JA, et al. A geometric reappraisal of proximal landing zones for thoracic endovascular aortic repair according to aortic arch types. Journal of vascular surgery. 2017;65(6):1584–1590. doi: 10.1016/j.jvs.2016.10.113. [DOI] [PubMed] [Google Scholar]
- 16.Parodi J, Berguer R, Carrascosa P, Khanafer K, Capunay C, Wizauer E. Sources of error in the measurement of aortic diameter in computed tomography scans. Journal of vascular surgery. 2014;59(1):74–79. doi: 10.1016/j.jvs.2013.07.005. [DOI] [PubMed] [Google Scholar]
- 17.Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, et al. A survey on deep learning in medical image analysis. Medical image analysis. 2017;42:60–88. doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- 18.Bakas S, Reyes M, Jakab A, Bauer S, Rempfler M, Crimi A, et al. Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge. arXiv preprint arXiv:181102629. 2018.
- 19.Tobon-Gomez C, Geers AJ, Peters J, Weese J, Pinto K, Karim R, et al. Benchmark for algorithms segmenting the left atrium from 3D CT and MRI datasets. IEEE transactions on medical imaging. 2015;34(7):1460–1473. doi: 10.1109/TMI.2015.2398818. [DOI] [PubMed] [Google Scholar]
- 20.Bilic P, Christ PF, Vorontsov E, Chlebus G, Chen H, Dou Q, et al. The liver tumor segmentation benchmark (lits). arXiv preprint arXiv:190104056. 2019.
- 21.Simpson AL, Antonelli M, Bakas S, Bilello M, Farahani K, Van Ginneken B, et al. A large annotated medical image dataset for the development and evaluation of segmentation algorithms. arXiv preprint arXiv:190209063. 2019.
- 22.Yushkevich PA, Gerig G. ITK-SNAP: an intractive medical image segmentation tool to meet the need for expert-guided segmentation of complex medical images. IEEE pulse. 2017;8(4):54–57. doi: 10.1109/MPUL.2017.2701493. [DOI] [PubMed] [Google Scholar]
- 23.Kikinis R, Pieper SD, Vosburgh KG. 3D Slicer: a platform for subject-specific image analysis, visualization, and clinical support. Intraoperative imaging and image-guided therapy: Springer; 2014. pp. 277–289. [Google Scholar]
- 24.Shen D, Liu T, Peters TM, Staib LH, Essert C, Zhou S, et al. Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, October 13–17, 2019, Proceedings, Part IV: Springer Nature; 2019.
- 25.Isensee F, Petersen J, Klein A, Zimmerer D, Jaeger PF, Kohl S, et al. nnu-net: Self-adapting framework for u-net-based medical image segmentation. arXiv preprint arXiv:180910486. 2018.
- 26.Berman M, Triki AR, Blaschko MB, editors. The lovász-softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018.
- 27.Lin T-Y, Goyal P, Girshick R, He K, Dollár P, editors. Focal loss for dense object detection. Proceedings of the IEEE international conference on computer vision; 2017. [DOI] [PubMed]
- 28.Lorensen WE, Cline HE. Marching cubes: A high resolution 3D surface construction algorithm. ACM siggraph computer graphics. 1987;21(4):163–169. doi: 10.1145/37402.37422. [DOI] [Google Scholar]
- 29.Antiga L, Steinman DA. Robust and objective decomposition and mapping of bifurcating vessels. IEEE transactions on medical imaging. 2004;23(6):704–713. doi: 10.1109/TMI.2004.826946. [DOI] [PubMed] [Google Scholar]
- 30.Izzo R, Steinman D, Manini S, Antiga L. The vascular modeling toolkit: a Python library for the analysis of tubular structures in medical images. Journal of Open Source Software. 2018;3(25):745. doi: 10.21105/joss.00745. [DOI] [Google Scholar]
- 31.Reuter M, Wolter F-E, Peinecke N. Laplace-Beltrami spectra as ‘Shape-DNA’of surfaces and solids. Computer-Aided Design. 2006;38(4):342–366. doi: 10.1016/j.cad.2005.10.011. [DOI] [Google Scholar]
- 32.Lévy B, Zhang H. Spectral mesh processing. ACM SIGGRAPH 2010 Courses2010. p. 1–312.
- 33.Bône A, Louis M, Martin B, Durrleman S, editors. Deformetrica 4: an open-source software for statistical shape analysis. International Workshop on Shape in Medical Imaging; 2018: Springer.
- 34.Sun J, Ovsjanikov M, Guibas L, editors. A concise and provably informative multi‐scale signature based on heat diffusion. Computer graphics forum; 2009: Wiley Online Library.
- 35.Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to algorithms: MIT press; 2009.
- 36.Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the Hausdorff distance. IEEE Transactions on pattern analysis and machine intelligence. 1993;15(9):850–863. doi: 10.1109/34.232073. [DOI] [Google Scholar]
- 37.Noothout JM, De Vos BD, Wolterink JM, Išgum I, editors. Automatic segmentation of thoracic aorta segments in low-dose chest CT. Medical Imaging 2018: Image Processing; 2018: International Society for Optics and Photonics.
- 38.Fantazzini A, Esposito M, Finotello A, Auricchio F, Pane B, Basso C, et al. 3D Automatic Segmentation Of Aortic Computed Tomography Angiography Combining Multi-View 2D Convolutional Neural Networks. Cardiovascular engineering and technology. 2020;11(5):576–586. doi: 10.1007/s13239-020-00481-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kumar SP, Latte MV, Siri SK. Volumetric lung nodule segmentation in thoracic CT scan using freehand sketch. IET Image Processing. 2020;14(14):3456–3462. doi: 10.1049/iet-ipr.2020.0671. [DOI] [Google Scholar]
- 40.Malone C, Urbania T, Crook S, Hope M. Bovine aortic arch: a novel association with thoracic aortic dilation. Clinical radiology. 2012;67(1):28–31. doi: 10.1016/j.crad.2011.04.004. [DOI] [PubMed] [Google Scholar]
- 41.Marrocco-Trischitta MM, Romarowski RM, De Beaufort HW, Conti M, Vitale R, Secchi F, et al. The Modified Arch Landing Areas Nomenclature identifies hostile zones for endograft deployment: a confirmatory biomechanical study in patients treated by thoracic endovascular aortic repair. European Journal of Cardio-Thoracic Surgery. 2019;55(5):990–997. doi: 10.1093/ejcts/ezy409. [DOI] [PubMed] [Google Scholar]