Abstract
Intertemporal choice requires a dynamic interaction between valuation and deliberation processes. While evidence identifying candidate brain areas for each of these processes is well established, the precise mechanistic role carried out by each brain region is still debated. In this article, we present a computational model that clarifies the unique contribution of frontoparietal cortex regions to intertemporal decision making. The model we develop samples reward and delay information stochastically on a moment-by-moment basis. As preference for the choice alternatives evolves, dynamic inhibitory processes are executed by way of asymmetric lateral inhibition. We find that it is these lateral inhibition processes that best explain the contribution of frontoparietal regions to intertemporal decision making exhibited in our data.
Keywords: frontoparietal cortex, lateral inhibition, leaky competing accumulator model, self-control
Introduction
It can be argued that many of society’s ills depend to some extent on weakness of self-control (Schroeder 2007). Obesity can be combatted by suppressing the desire to consume unhealthy but tasty foods, addiction by overcoming drug craving, and anemic savings rates by inhibiting the impulse to spend on the latest gadgets and fashion. Failures of these behaviors are commonly cited instances where the process of self-control was not used effectively (Baumeister et al. 1994; Baumeister and Heatherton 1996; Schroeder 2007; Hofmann et al. 2009; Wagner and Heatherton 2010; Heatherton 2011). In the laboratory, self-control is often studied using intertemporal choice paradigms. These tasks require participants to choose between rewards, most commonly money, of different sizes available either immediately or at some point in the future. Rates of temporal discounting estimated using this paradigm differ with obesity (Weller et al. 2008) and drug addiction (Bickel and Marsch 2001; McClure and Bickel 2014), indicating the real-world validity of derived measures for the study of self-control. Within commonly used intertemporal choice tasks, self-control may be conceptualized as the set of processes that support choosing delayed rewards, particularly in instances when immediate rewards are subjectively highly valued (Figner et al. 2010; Crockett et al. 2013; but see McGuire and Kable 2013).
Recently, intertemporal choice research has focused on understanding the neurobiological basis of temporal discounting and the mechanisms by which self-control can be exerted over impulsive decision making (McClure et al. 2004, 2007a; Kable and Glimcher 2007; Hare et al. 2009; Figner et al. 2010; Peters and Büchel 2011). It is now accepted that temporal discounting depends on neural processes in the striatum and the ventromedial prefrontal cortex (vmPFC) related to the construction of subjective value (Kable and Glimcher 2007; Peters and Büchel 2011; Bartra et al. 2013). Similarly, there is considerable agreement regarding the association of executive brain regions including the dorsolateral prefrontal cortex (dlPFC), dorsomedial frontal cortex (dmFC) and posterior parietal cortex (pPC) with self-control (McClure et al. 2004, 2007a; Hare et al. 2009; Figner et al. 2010; Peters and Büchel 2011; Essex et al. 2012). However, the mechanisms that explain how self-control is implemented are debated.
At least 2 hypotheses have been proposed to explain the neural mechanisms of self-control. One hypothesis suggests that self-control involves dlPFC modulation of temporal discounting processes in the vmPFC (Hare et al. 2009, 2011, 2014). A logical consequence of this hypothesis is the prediction that self-control should necessarily be accompanied by changes in subjective judgments of value. The second hypothesis suggests that the dlPFC influences choice behavior without altering temporal discounting processes (Figner et al. 2010). Using transcranial magnetic stimulation to disrupt neural activity, the proponents of this latter hypothesis showed that inhibiting dlPFC increases impulsive behavior without changing subjective value judgments (also see Kelley and Schmeichel 2016). Although both hypotheses have been supported empirically, they are mutually exclusive, and neither provides detailed insight into how lower-level neural processes produce self-control. Adjudicating between models is impeded by the fact that neither hypothesis has been expressed within a quantitative framework that permits explicit predictions about the relationship between neural activity and behavior. Our central aim is to generate a family of self-control models that incorporates predictions expressed in the literature, situates these predictions within process models that tie brain activity to behavior, and permits formal model comparison.
We develop a computational model of the neural basis of self-control and use it to provide an explanation for the roles played by the dlPFC, dmFC, and pPC in overcoming impulsivity in decision making. Our findings leverage evidence from previous studies implicating the dlPFC, pPC, and dmFC with action selection during intertemporal choice to show that self-control can be implemented as a biased form of action selection (Rodriguez et al. 2015a). To this end, we designed an intertemporal choice task that allowed subjects to make decisions reflecting both self-control and impulsivity. We defined a measure of self-control and used it to test for dlPFC, pPC, and dmFC involvement with self-control as observed with functional magnetic resonance imaging (fMRI). The model we develop could be used to test and evaluate different formal hypotheses about the mechanistic role that each brain region of interest plays during intertemporal choice decision making.
Experimental Procedures
Subjects
A total of 21 healthy, right handed, adults participated in this study (9 females, ages 18–45 years, mean 24.3 years). The sample size was determined on the basis of other intertemporal choice experiments we have reported (Rodriguez et al. 2014, 2015a; Turner et al. 2016). All participants gave written informed consent before completing the experiment. All procedures were approved by Stanford University’s Institutional Review Board. Two participants were excluded from the behavioral and neuroimaging analyses because their behavior did not allow us to estimate reliable temporal discounting parameters. Specifically, during the scanning session (but not the preliminary staircasing session), we obtained estimates of discount rates that suggested that they always preferred the smaller, sooner (n = 1) or larger, later (n = 1) rewards. These estimates indicated that the subjects’ behavior did not permit accurate estimates of their temporal discounting using our choice set, which made some model-based analyses of the brain activity impossible. We therefore omitted their data from several analyses, leaving a total of 19 subjects in these analyses (7 females, ages 18–45 years, mean 24.8 years). Because we did not assume a hyperbolic discounting function in the generative model, we included the data from all 21 subjects when fitting the hierarchical models to data.
Task and Stimuli
Participants completed 2 intertemporal choice tasks. The first task used a staircase procedure to measure each individual’s discount rate , assuming a hyperbolic discounting function
| (1) |
where is the subjective value of a delayed reward, is the monetary amount offered, and is the delay. The staircase procedure required participants to select between a larger delayed reward (of dollars available at delay ) and a smaller but less delayed reward of $10 or $20, available within 0 or 15 days. We will refer to the larger and more delayed reward as “larger later” (LL) and the smaller but less delayed reward as “smaller sooner” (SS). For any choice, indifference between the LL and SS options implies a discount rate of , where is the amount of the LL option, is its delay, and is the discounted value of the SS option after applying Equation (1) to it. We refer to this implied equivalence point as ; the procedure we implemented during the first task amounted to varying systematically until indifference was reached. Specifically, we began with . If the subject chose the delayed reward, decreased by a step size of 0.01 for the next trial. Otherwise, increased by the same amount. Every time the subject chose both a delayed and an immediate offer within 5 consecutive trials, the step size was reduced by 5%. Participants completed 60 trials of this procedure. We placed no limits on the response time, and presented both offers on the screen, the SS offer on the left, and the LL offer on the right. We collected fMRI data during the second experimental session (Fig. 1A). Before the second task began, we fit a softmax decision function to participants’ choices during the first task. We assumed that the likelihood of choosing the LL reward was given by the following equation:
| (2) |
where accounts for sensitivity to changes in discounted value. We simultaneously estimated the parameters and from Equations (1) and (2) for each subject using the maximum likelihood function available in MATLAB. As is common in most delay discounting models, we assumed the responses were independent and identically distributed. With the parameters describing each individual’s discounting behavior, we could evaluate the relative attractiveness of each choice. Consequently, we could examine a subject’s ability to exhibit self-control by providing offers of varying levels of attractiveness.
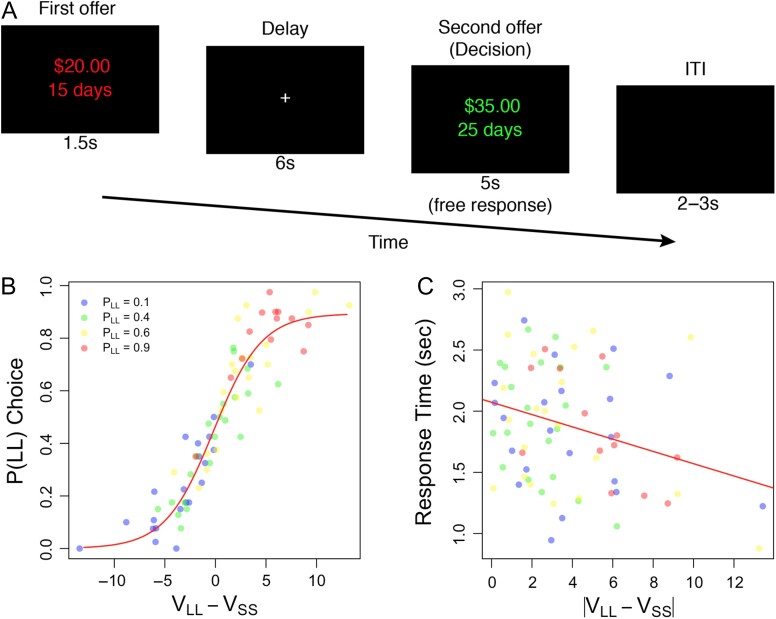
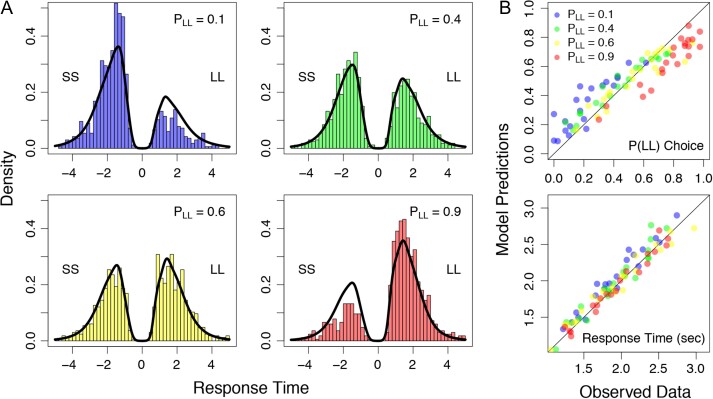
Figure 1.
Experimental design and results. (A) Offer pairs were presented sequentially. The first offer was presented in red and remained on screen for 1.5 s. After a 6 s delay, a second reward was presented in green. In half of trials the first offer presented a smaller and more immediate reward. The other half presented a larger but more delayed reward. The probability of choosing the larger reward was estimated to be 0.1, 0,4, 0.6, or 0.9, using decision parameters obtained from a staircase procedure completed outside the fMRI scanner. (B) Choice probabilities during the fMRI experiment were symmetrically distributed around indifference (i.e., ), and varied systematically with valuation. (C) Response times decrease with increases in valuation differences demonstrating that response times become faster as choice difficulty is reduced.
We develop a conceptual model of self-control for our task at the beginning of the Results section. In brief, we argue that self-control is evident when subjects choose larger, later rewards and increases as the temptation to choose the smaller, sooner options increases (captured by the estimated probability of choosing the SS reward for that trial). Mathematically, self-control exhibited on trial is therefore equal to
| (3) |
where is an unknown, monotonically increasing function, and . To approximate the shape of , we assumed was a first-order linear function of , so that
| (4) |
For convenience, we further assumed the function centered about zero by setting
| (5) |
Equations (3–5) specify a few noteworthy predictions about self-control, as measured in this article. First, self-control is maximized when a LL choice is made and is largest (i.e., , when ). Second, self-control is minimized when is the smallest (i.e., , when ). Third, when both options are equally attractive (i.e., ) and a LL choice is made, self-control obtains an intermediate value (arbitrarily equal to zero in our model). Finally, as self-control is only defined when LL alternatives are selected (see Equation (3)), trials in which a SS alternative is chosen cannot be used in our analyses below.
We also developed a measure of impulsivity to compare against the specific influence of self-control. To do this, we defined an orthogonal measure to
| (6) |
Equation (6) captures the intuition that is (1) greatest when the SS alternative is chosen and is maximized, (2) smallest when the SS alternative is chosen and is minimized, and (3) zero when .
Given these assumptions about how self-control relates to the relative subjective attractiveness of each offer, self-control can be studied parametrically by treating as the independent variable in our experiment. To maintain balance between the attractiveness of the SS and LL alternatives, we imposed the following levels of the independent variable . Each level of can then been treated as a condition in our experiment, conditions we refer to as .
Trials began with the presentation of an offer of either $20 (available at 0 or 15 days) or $40 (available at 15 or 60 days). This offer was kept on the screen for 1.5 s. A fixation cross was then shown for 6 s, followed by a second offer. When the first offer was $20, the second offer was an LL reward. Conversely, when the first offer was $40, the second offer was an SS reward. To establish the imposed conditions, we first selected a pseudorandom delay and then computed the or that satisfied Equations (1) and (2) for the intended condition. When the second offer was an LL reward, the delay was uniformly selected from a range of 16–46 days. When the second offer was an SS, the uniform delay range was 0–14 days. Subjects completed a total of 160 trials, 40 at each condition level of . Trial types were randomized and counterbalanced over 4 blocks.
Choices for the first offer were indicated by pressing a button with the right index finger, whereas choices for the second offer were indicated by pressing a button with the right middle finger. This procedure naturally counterbalanced the finger used for selecting SS and LL rewards. We measured RT relative to the presentation of the second offer. Subjects were given a maximum of 5 s to respond. We discarded any trial in which a response was made in less than 200 ms or fell outside the decision period (1.10% of trials). When subjects made choices in less than 5 s, the second offer information disappeared and an intertrial interval (ITI) was initiated. The ITI was randomly selected across trials, from a uniform distribution bounded by 2 and 3 s. In exchange for participation, subjects received a base payment of $20 cash. In addition, we randomly sampled a trial from the second task, and provided a bonus payment on the basis the choice made on that particular trial. If the bonus payment was a larger later option, we provided a post-dated check, where the date was determined by the delay information on that trial.
Imaging Procedures
We collected fMRI data using a GE Discovery MR750 Scanner. fMRI analyses were conducted on gradient echo T2*-weighted echoplanar functional images with blood-oxygenated-level-dependent (BOLD) sensitive contrast (42 transverse slices; TR, 2000 ms; TE, 30 ms; 2.9 mm isotropic voxels). Slices had no gap between them and were acquired in interleaved order. The slice plane was manually aligned to the anterior–posterior commissure line. The total number of volumes collected per subject varied depending on random ITIs. The first 10 s (5 volumes) of data contained no stimuli and were discarded to allow for T1 equilibration. In addition to functional data, we collected whole-brain, high-resolution T1-weighted anatomical structural scans (0.9 mm isotropic voxels). Image analyses were performed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/).
Behavioral Modeling
In this article, we propose a computational model—illustrated in Figure 2A,B—equipped with mechanisms for valuation and modulation of choice alternatives in intertemporal choice. Our goal was to assess the relative importance of each of these mechanisms in accounting for behavioral data. The model is most similar to the leaky competing accumulator (LCA) (Usher and McClelland 2001, 2004) model, but is also similar to the multialternative decision field theory (MDFT) (Roe et al. 2001; Hotaling et al. 2010) model in terms of its dynamics. Specifically, Usher and McClelland (2004) extended a perceptual version of the LCA model presented in Usher and McClelland (2001) by assuming a secondary stochastic process on the way in which attention is allocated to the attributes comprising a stimulus. This Bernoulli process used in the LCA model is equivalent to the process assumed by decision field theory (DFT) (Busemeyer and Townsend 1993) and its extensions (Dai and Busemeyer 2014). Where appropriate, we relate the assumptions in our model to these previously developed models.
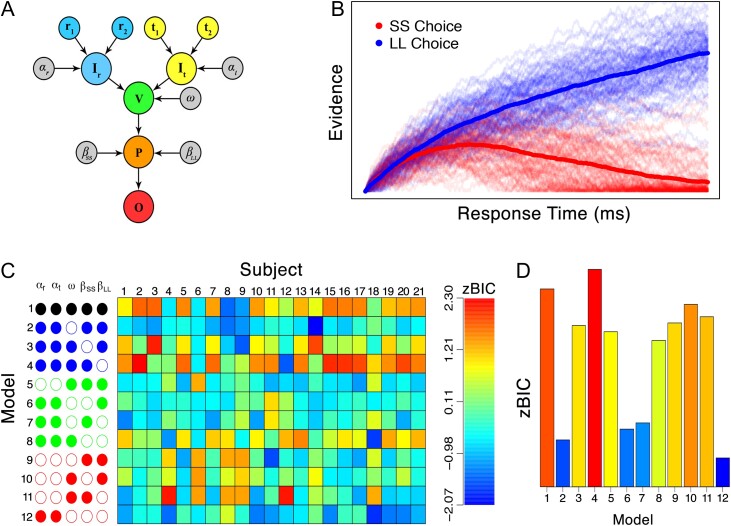
Figure 2.
Details of the model and fitting results. (A) The model takes as inputs information about the rewards (i.e., and ; blue nodes) and time delays (i.e., and ; yellow nodes), and converts these inputs to a subjective representation (i.e., and , respectively) through with parameters and . Features are selected with the parameter (i.e., the green node). Deliberation among the SS and LL alternatives is modulated by lateral inhibition parameters and (i.e., the orange node). Once an accumulator reaches a threshold amount of preference, a decision is made corresponding to the winning accumulator (i.e., the red node). (B) Example of how the model implements self-control-like behavior through lateral inhibition ( and ) and not valuation (). (C) Model fitting results in terms of a z-transformed BIC statistic separated by model constraint (rows) and subjects (columns), color coded according to the legend on the right. Empty circles indicate that a parameter was free to vary, whereas filled nodes indicate that a parameter was fixed. The model structures are grouped by the number of free parameters: black, blue, green and red indicate that a total of 3, 4, 5, and 6 free parameters were used, respectively. (D) Model fits from each model in (C), aggregated across subjects. For the zBIC, lower values (blue) indicate better model performance.
Typical intertemporal choice tasks involve the presentation of 2 alternatives, where one alternative consists of a smaller reward and smaller time delay, and the other consists of a larger reward and a longer time delay. As these features comprising the choice alternatives vary along 2 dimensions (i.e., reward and time), we can conceive of the SS choice as a vector of inputs such as , and the LL choice as . As experimenters, we have control and access to the objective measures comprising the 2 alternatives. However, as human observers are prone to computational limitations, it seems reasonable to allow for the possibility of a distortion of the objective attribute space. To build this mechanism into our model, we assumed a power transformation along both feature dimensions:
for , where the parameters and control the shape of the power functions along the reward and time dimensions, respectively. The subjective mapping function in Equation (7) is consistent with Dai and Busemeyer (2014), but inconsistent with Usher and McClelland (2004) as their model uses a loss aversion function combined with pairwise differences in the attribute space (cf. Turner, Schley, et al. 2018, forthcoming). Note that the power function used here can produce a perfectly objective representation when . While this would be the optimal representation regarding accuracy, Dai and Busemeyer (2014) have shown that allowing the power function parameters to vary freely improved model fit relative to constraining these parameters to . We explored the importance of constraining for reward and time by assessing model fits to data.
With the subjective representation constructed, the next process in the model is determining how attention should be allocated across the reward and time dimensions. In other contexts (Roe et al. 2001; Usher and McClelland 2004; Bhatia 2013), a moment-by-moment stochastic oscillation process has been assumed as a way to integrate the information from multiple features into a stable valuation of a stimulus. This process is known as a Bernoulli process, and is illustrated in Figure 2A as the green node. The Bernoulli process can be parameterized such that attention can be biased toward a particular dimension through the parameter . Letting denote the dimension to which attention is allocated at moment in the deliberation process, we can write
We can arbitrarily assume that when attention is directed toward the reward dimension, and when attention is directed toward the time dimension.
In our model, alternatives are represented as accumulators, and these accumulators receive different inputs depending on the features of the stimulus set and the manner in which attention is allocated. Letting correspond to the input term for the SS choice, and correspond to the input to the LL choice, we can write
and
| (7) |
Note that the arrangement of reward and time is flipped with respect to the input terms. The reason for this assumption centers on the framing of the features. Whereas having a larger reward is a positive feature, having to wait a longer time is considered a negative feature. Because simply flipping the sign of in Equation (7) causes some difficulties with interpretation of the accumulation dynamics, we instead chose to simply frame differences in as being “less good.” For example, as grows for the LL choice, the SS choice becomes more attractive.
Equation (7) shows how discrete values for at each moment in time can cause the valuation of a particular alternative to oscillate, giving rise to a time-varying input signal to the accumulation process described below. Having a stochastic attentional mechanism can explain interesting inconsistencies in choice behavior from one trial to the next (Dai and Busemeyer 2014; Ericson et al. 2015). For example, on one trial an observer may focus their attention on the reward dimension more than the time dimension. In this case, the input term would be larger on average than because , causing the LL choice to gain an advantage. On another trial, an observer may focus their attention on the time dimension, causing the SS choice to gain a stronger input term because .
Our model assumes that preferences for the alternatives evolve over time according to 3 dynamics: input, competition, and noise. Once the alternatives have been presented and input has been calculated, we assume that the preferences for each alternative (i.e., the accumulators) race toward a common threshold amount of preference. At the moment an accumulator reaches the threshold, a decision is made corresponding to the winning accumulator. During the race, some competitive dynamics can affect the accumulation process in ways that are different than the input terms . Conceptually, the mechanisms corresponding to this competitive dynamic are intended to mimic concepts such as self-control and impulsivity. In the model, the parameters that implement competition are denoted and , and their influence is known as “lateral inhibition.” To offset the role of lateral inhibition, another term called “leakage” is often used. These parameters represent the passive loss of information, and are denoted and . The final component in the model is valuation noise. Similar to other sequential sampling models, we incorporate valuation noise through the Weiner process, by sampling random noise from a zero-centered Gaussian distribution. Letting denote an instance of valuation noise at time , we can write
where denotes a normal distribution with mean , and standard deviation .
With the 3 dynamics in the accumulation process defined, we can specify the stochastic differential equation we used to generate predictions for preference over time. Letting and denote the preference states for the SS and LL choices, respectively, preference evolves according to the following equations:
| (8) |
The term denotes a time step in the accumulation process. In our implementation, we used the Euler method (Brown et al. 2006) to approximate the continuous process in Equation (8) by setting .
We also assume the presence of a lower bound on the accumulation process such that no accumulator can ever be negative. To implement this, we apply the following correction at every moment in time, :
| (9) |
The lower bound constraint is commonly used in the LCA model, and we retain this assumption for our analyses so that we can appreciate the roles of lateral inhibition and leakage (cf. Bogacz et al. 2006; van Ravenzwaaij et al. 2012). We also assumed that the accumulation process started at a fixed distance away from the threshold parameter . Specifically, we set the starting point to be . Adding some baseline activation is well justified from the neuroscience literature where baseline firing rates of neurons are often some proportion of their maximum firing rate (i.e., their threshold), varying from 0.20 (Schall 1991; Hanes and Schall 1996; Hanes et al. 1998; Pouget et al. 2011) to 0.33 (Ditterich 2010) to 0.50 (Roitman and Shadlen 2002; Huk and Shadlen 2005; Churchland et al. 2008), depending on the brain area. Furthermore, when a “truncation” rule is used in the LCA model (as we do in Equation (9)), an equivalence can be established between the LCA model and the “optimal” diffusion decision model (Ratcliff 1978; Ratcliff and McKoon 2008) when a baseline level of activation is assumed and the input terms are large enough (see Bogacz et al. 2006; van Ravenzwaaij et al. 2012; for details).
Figure 2B illustrates the dynamics of Equation (8) for 100 simulations of the model. The blue lines correspond to trials in which the LL alternative was chosen, and the red lines correspond to trials in which the SS alternative was chosen. The thick solid lines represent the grand average across the 100 simulations, whereas the thinner lines correspond to individual model simulations. In this simulation, we set the input terms in the model to be equivalent, meaning that both accumulators should have the same drive to the threshold. However, because we set and , the accumulation of the SS alternative gets inhibited by the LL alternative, causing the SS alternative to be chosen less frequently. This simulation effectively conceptualizes how self-control can be carried out in our model: even when the options have equal subjective value, a top-down process can reliably ensure a particular choice among the alternatives.
Finally, we assume the presence of some nondecision processes that are unimportant to the cognitive processes investigated here. We denote this parameter , and assume an additive interaction between the response time predicted by the process described in Equation (8) and .
Simulation Study: Predictions for Discounting Curves
Temporal discounting is a well-studied behavior. A standard result in the intertemporal choice literature is that the importance of reward values decrease as the delay associated with the reward increases. Despite its robustness, there is little consensus on the exact functional form of the temporal discounting curve (Frederick et al. 2002; van den Bos and McClure 2013; Cavagnaro et al. 2016). At this point, a number of functional forms have been proposed such as exponential, hyperbolic, generalized hyperbolic (Green and Myerson 2004), constant sensitivity (Ebert and Prelec 2007), double exponential (McClure et al. 2007b), and several others. At present, the hyperbolic function is the most widely accepted form of the discounting curve, perhaps due to its flexibility in fitting individual subjects and its simple parametric form (van den Bos and McClure 2013). Recently, Cavagnaro et al. (2016) have shown that there is no functional form that provides a satisfactory account of the discounting behavior across different individuals and intertemporal choice tasks. The failure of the extant forms of the temporal discounting curve to adequately generalize suggests that the precise nature of the discounting curve is highly complex, and it may be sensitive to individual differences or the particular context of the experiment.
Regardless of the precise form of the discounting curve, it is essential that any new computational model of the intertemporal choice task be able to produce some form of discounting behavior. To investigate the types of discounting curves the model could produce, we performed a simulation study of the one particular model variant (i.e., the “downstream” model discussed below). We first assumed that the intertemporal choice task involved a decision among only 2 offers—a SS offer consisting of reward and delay features and , respectively, and a LL offer with features and . To isolate the discounting behavior, we assumed that the SS offer was always fixed to a reference point of dollars and days. For the LL offer, we sampled a grid across the set of possible offers in the space . On the reward dimension, we investigated rewards ranging from $10 to $50 in increments of $0.50. On the time dimension, we investigated delays ranging from 0 to 40 days in increments of 0.5 days.
With the stimulus set constructed, we had only to specify values of the model parameters to perform the simulation. The parameters that can modulate the degree of the temporal discounting are the attention parameter , and the lateral inhibition terms for SS and LL alternatives, and , respectively. Recall that as increases, more attention is directed toward the reward information than the delay information, and when , attention is equal across the 2 feature dimensions. To investigate the effects of attention on preference for the LL alternative, we investigated a range of values for . These values of allowed us to explore biased versions of the model where the relative importance of feature dimensions changed despite a constant valuation or input from the stimulus set.
Considering lateral inhibition terms, Equation (8) shows that increases in create greater inhibition on the SS alternative, meaning that it is less capable of accumulating preference, all else being equal. Similarly, increases in create greater inhibition of the LL alternative. While our model comparison analysis suggested that freeing both lateral inhibition terms improved model performance, it was not essential to have both terms free in our simulation study. Instead, we were only interested in one lateral inhibition term relative to the other. As such, we fixed , and systematically investigated on the set . These values allowed us to investigate a range of suppressive behaviors for each SS and LL alternatives, despite constant valuation from the stimulus set.
Other parameter settings were less influential in the model’s performance. Namely, we set as in the variant examined in our model evaluation section. These settings allow the model to produce a veridical representation of the stimulus features, and this representation is fixed across the levels of the model parameters. We assumed the noise term , the threshold parameter , and the nondecision time parameter . We set . We maintained that the starting point , and a floor on activation as in Equation (9).
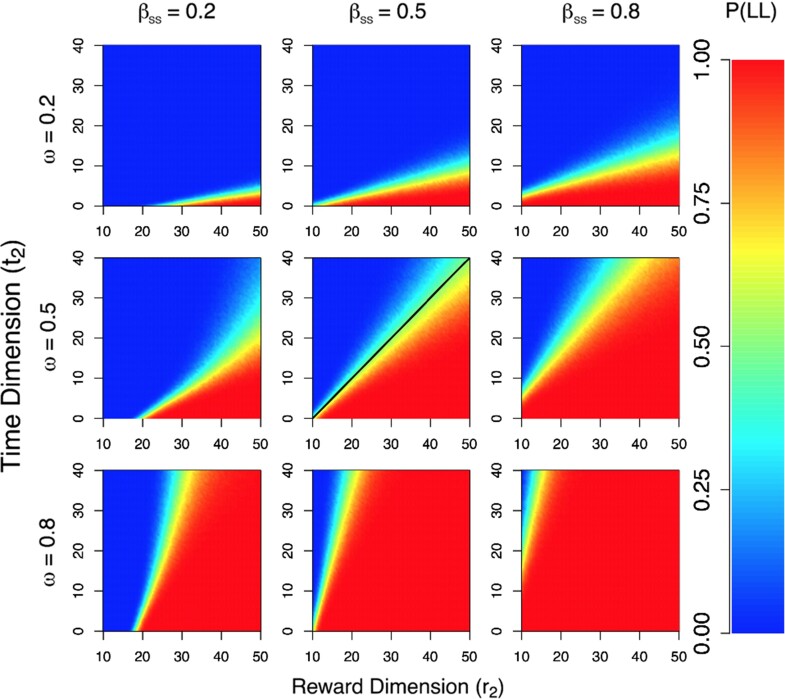
To obtain an estimate of the relative attractiveness of the LL alternative, we simulated the model 1000 times for every point in the reward-delay grid, under every pairwise model configuration for and . Following the simulation, we simply calculated the probability of choosing the LL alternative. Figure 3 shows the results of our simulation study. In each panel, the probability of choosing the LL alternative is color coded according to the key in the right panel, where red colors indicate greater preference for the LL alternative, and blue colors indicate greater preference for the SS alternative. In each panel, the set of rewards we investigated appear on the x-axis, whereas the set of delays appear on the y-axis. Each row in Figure 3 corresponds to a different level of the attention parameter , whereas each column corresponds to a different level of . Comparing across rows and columns, Figure 3 shows that both parameters have an effect on , and the parameters interact in nonlinear ways. Marginalizing across the columns, Figure 3 shows that the attention parameter has a strong effect on , where larger values of correspond to more LL choices across the reward-delay space. The dynamic that produces this effect is related to how weights the relative importance of the stimulus information. When is larger, more emphasis is placed on the reward dimension, and so the LL alternative—having more attractive properties on the reward dimension—gains an advantage in preference relative to the SS alternative. By contrast, focusing more on the time dimension gives the SS alternative an advantage, as the more immediately available option is more attractive on the time dimension.
Figure 3.
Temporal discounting behavior in a mechanistic model. Results of a simulation study showing response probability as a function of different reward amounts (; x-axis) and time delays (; y-axis) for different values of the attention parameter (i.e., rows) and the lateral inhibition term for the SS alternative (i.e., columns). In each plot, the probability of choosing the LL choice is color coded according to the key in the right panel. In all simulations, the value of the SS choice was assumed to be fixed, where dollars and days. Lateral inhibition for the LL alternative was fixed to for comparison. The black line in the middle panel represents the line of indifference from a hyperbolic discounting model (see Equations (1 and 2)) with and .
Marginalizing across the rows, Figure 3 shows that the lateral inhibition term also has an effect on . Namely, as grows, the probability of choosing the LL alternative increases. Examining Equation (8), this dynamic can be explained by increases in the amount that is subtracted off of the SS accumulator relative to that of the LL accumulator. Because was fixed to 0.5, as grows relative to , we should expect that the SS alternative becomes more inhibited, regardless of the particular reward-delay inputs comprising the LL choice. The advantage of the lateral inhibition term is that can actively suppress the SS alternative in a way that might be consistent with a goal-directed choice. In other words, despite an subject’s evaluation of a stimulus, it may not necessarily map onto a consistent choice, depending on whether or not the subject decides to invoke the goal of maximizing reward amounts in the decision-making process.
To relate the model’s predictions to conventional forms of the temporal discounting function, we also simulated choices from a hyperbolic discounting model as in Equations (1) and (2) using and . We then determined the values of and such that the probability of choosing the LL alternative was equivalent to the probability of choosing the SS alternative. These values of and comprise a line of indifference in the hyperbolic model, which is show in the middle panel of Figure 3 as the black line. The values of and were chosen to mimic the behavior of our model to illustrate that some parameter settings of the LCA model closely mimic hyperbolic discounting behavior.
Fitting the Hierarchical Model to Data
The model has many parameters, which are not all identifiable simultaneously. As discussed above, some combination of parameters must be fixed to fit the model to data, and we used patterns of fixed parameters to test the plausibility of specific mechanisms. In the presentation of the model below, we specify the structure with all parameters present, but branches of the hierarchical structure were removed when specific model parameters were fixed.
For all models, we assume the presence of a threshold parameter , a moment-to-moment noise parameter , and a nondecision time parameter , for the jth subject. We maintained that these parameters should be modeled on the log scale. The log transformation provided 2 benefits. First, it enforced that all model parameters should be positive once they were exponentiated. Second, it facilitated the development of our hierarchical models. Specifically, with appropriate choices for priors on the subject-specific parameters, we could establish a conjugate relationship between the prior and the posterior. A conjugate relationship makes posterior sampling more efficient, enabling us to gather high-quality samples at a faster rate.
Different models were comprised of different configurations of mechanistic parameters: power function mapping parameters and for reward and delay, respectively, an attention bias parameter , and lateral inhibition terms and for the SS and LL alternatives, respectively (i.e., see Equation (8)). To build the hierarchical model, we assumed
and
where denotes a normal distribution with mean and standard deviation , and denotes an indicator function on the interval . Lognormal priors were used for , , and to acknowledge the lower bound constraint of zero on these model parameters. For the rest of the model parameters, because the estimates regularly concentrated at their extremes (e.g., 0 or 1), we chose to censor their priors as a way to enforce constraint.
For the group-level mean parameters, we specified informative priors, after several simulation studies that investigated the prior predictive distribution (Vanpaemel 2010, 2011; Vanpaemel and Lee 2012):
and
For the group-level standard deviation parameters, we supplied similarly informative, but somewhat generic priors based on previous research on the spread of subject-to-subject parameters for other cognitive models (Turner, Sederberg, et al. 2013):
where denotes the Gamma distribution with shape parameter , and rate parameter , and and .
As discussed above, the model is unidentifiable when all parameters are left free to vary. Considering this, we investigated different configurations of the model structure by systematically fixing and freeing differing combinations of model parameters. When a parameter was fixed, the corresponding hierarchical structure discussed above was unnecessary, and so it was eliminated from the estimation procedure. When the shape parameters were fixed, we set for rewards, and for delays. When the attention parameter was fixed, we set . When the lateral inhibition parameters were fixed, we set for SS alternatives, and for LL alternatives. The leakage terms were never freely estimated, and were set to and .
As the stochastic process described in Equation (8) is intractable, we required an approximation technique to estimate the parameters from each hierarchical model. To this end, we used the Gibbs ABC algorithm (Turner and Van Zandt 2014) in conjunction with the probability density approximation (PDA) (Turner and Sederberg 2014) method. The details of how to use the PDA algorithm to fit models of choice response time are described in Turner and Sederberg (2014), and so we will not describe them here. Essentially, we rely on numerous simulations of the model for a candidate set of parameters to approximate the likelihood function through a kernel density estimation procedure (Silverman 1986). The degree of mismatch in the simulated data and the observed data can then be calculated, and the relative probabilities of proposed parameter values can then be evaluated (see Turner and Van Zandt 2012; for a tutorial). For a given candidate parameter value, we simulated the model 100 times for every trial for a given subject. For each simulation, we used the true values of the reward and delay information presented to the subject on a given trial. The simulated data were then collapsed to form choice response time distributions for each of the conditions.
With a suitable approximation for the likelihood in hand, we used differential evolution with Markov chain Monte Carlo (DE-MCMC) (ter Braak 2006; Turner, Sederberg, et al. 2013) to sample from the joint posterior distribution. We used 24 chains, and ran the algorithm for 4000 iterations following a burnin period of 3000 iterations, resulting in 24 000 samples of the joint posterior. A migration step was used (Turner and Sederberg 2012; Turner, Sederberg, et al. 2013) with probability 0.1 for the first 250 iterations, after which time the migration step was terminated. We also used a purification step every 10 iterations to ensure that the chains were not stuck in spuriously high regions of the approximate posterior distribution (Holmes 2015).
Estimating Single-Trial Parameters
To derive estimates of the single-trial parameters for the model, we used an empirical Bayesian procedure to isolate the contribution of the parameters , , and , using an analytic strategy similar to van Maanen et al. (2011). First, we calculated the maximum a posteriori (MAP) estimates of each subject’s threshold, within-trial variability, and nondecision time parameters (i.e., , , and , respectively), and assumed , as assumed when fitting the model hierarchically. We then fixed these parameters to their MAP value for each subject, to limit the total number of parameters that were to be freely estimated. Second, for a given subject on a given trial, we simulated the model 1000 times using the offer information for each trial, and the MAP estimates for that particular subject. Third, we adapted the probability density approximation (Turner and Sederberg 2014) method to construct an estimate of the joint probability distribution (i.e., the likelihood) for choice and response time from the simulated data. In addition to the likelihood, we added another form of constraint on the model parameters in the form of a prior. The prior was chosen on the basis of summary statistics from the posteriors of the hierarchical model. For each single-trial parameter, we used the following priors:
and
The prior, combined with the approximated likelihood, served as the posterior probability we wished to optimize. Fourth, we used the “burnin” mode of the approximate Bayesian computation with differential evolution (ABCDE) (Turner and Sederberg 2012) algorithm to obtain the values of , , and that optimized the posterior probability of observing each data point (i.e., the choice and response time) on that particular trial. To do this, we ran the algorithm for 150 iterations, following a burnin period of 50 iterations. We repeated this process for every trial and for every subject, until single-trial estimates for each of the key model parameters had been obtained.
As the parameter estimates for the model well characterized the choice response time data for each subject, our empirical Bayes procedure could not provide worse fits to the single-trial data when , , and were allowed to vary by trial, when the prior constraints were imposed. This was ensured by fixing 3 of the parameters (i.e., , , and ) to the best-fitting values obtained during the hierarchical analysis. As the fixed parameters were common to all model variants we investigated (e.g., see Fig. 2), it was assumed that these parameters did not directly produce the intended self-control behavior observed in the neural data (also see Fig. 3). By allowing the key self-control parameters to vary on each trial, we could investigate the model’s best account of the behavioral data to our ontological definition of self-control.
fMRI Preprocessing
During preprocessing, we first performed slice-timing correction and realigned functional volumes to the first volume. We then co-registered the anatomical volume to the realigned functional scans and performed a segmentation of grey and white matter on the anatomical scan. Segmented images were then used to estimate nonlinear Montreal Neurological Institute (MNI) normalization parameters for each subject’s brain. Normalization parameters estimated from segmented images were used to normalize functional images into MNI space. Finally, normalized functional images were smoothed using a Gaussian kernel of 8 mm full-width at half-maximum.
fMRI Statistical Analysis
Self-Control and Impulsivity General Linear Model Analysis
Our first goal with respect to the fMRI data was to test whether variability in self-control would be reflected by brain activity within frontoparietal regions. To this end, we built a general linear model (GLM) that predicted BOLD responses on the basis of self-control. For this and all other fMRI analyses based on self-control, we relied on parameter estimates derived from behavior observed during the fMRI part of the experiment. This allowed us to minimize any potential measurement error induced by behavioral changes between the staircase task and the second part of the experiment.
The self-control GLM specified the onset of the first offer presentation and the delay period together, modeled by a 7.5 s boxcar function. Onset regressors for the second offer and response were modeled separately as impulse gamma functions. The model also included a self-control measure (see Results) as a parametric modulator of BOLD responses during the time of the response. In addition, the model included an impulsivity measure that is orthogonal to self-control (see Results) as a second regressor of interest. Finally, the model specified 6 regressors corresponding to the motion parameters estimated during data preprocessing and 4 constants to account for the mean activity within each of the 4 sessions over which the data were collected. These additional regressors were included as control variables of no interest. Every other GLM model estimation we performed also included 6 motion regressors and 4 session constants as regressors of no interest. Every regressor in the GLM was convolved with the canonical hemodynamic response function (HRF) during model estimation.
The group-level contrast for the above specified GLM was calculated as a one-sample t-test on the beta coefficients obtained from the subject-specific self-control modulatory regressor. We used tools from AFNI to determine the minimum cluster size necessary to give a corrected significance of P < 0.05 at the cluster level. First, 3dFWHMx was used to calculate the spatial autocorrelation of the residuals using the autocorrelation function (ACF) option. Second, we ran 3dClustSim to identify a minimum cluster size of 23 voxels. All brain regions reported were significant using this criterion. For determining ROIs for subsequent analyses, we identified voxels at an uncorrected P < 0.001. We used P < 0.001, uncorrected to illustrate ROIs in the figures as well (Fig. 4).
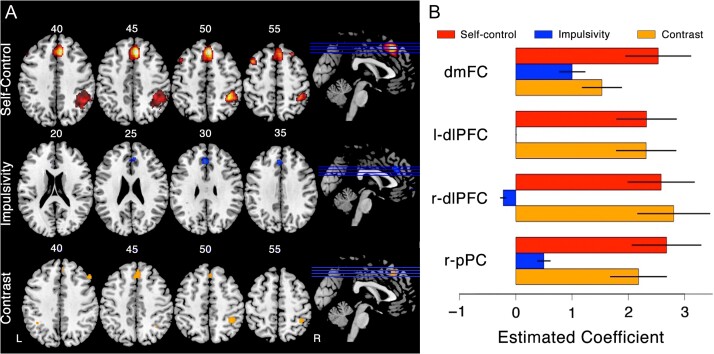
Figure 4.
Self-control and impulsivity in the brain. (A) The top row shows the results of the self-control GLM analysis, where 4 prominent regions of interest emerge: dmFC (superior frontal gyrus/supplementary motor area; [4, 28, 46]), the right pPC (inferior parietal lobule; [39, −41, 51]) and the bilateral dlPFC (middle frontal gyrus; left: [−52, 28, 24], right: [22, 38, 41]). The middle row shows the results of the impulsivity GLM analysis, and the bottom row shows the results of a contrast analysis. (B) Estimated coefficients of the GLM analysis performed in (A). For each of the 4 frontoparietal regions of interest, the red bars correspond to the self-control analysis, the blue bars correspond to the impulsivity analysis, and the orange bars correspond to the contrast between self-control and impulsivity.
To compare self-control and impulsivity effects, we performed paired sample t-tests between mean ROI coefficients from the self-control and impulsivity modulators specified in the self-control GLM. To test for RT confounds, we performed a mixed-effects GLM analysis on median RTs. This analyses specified 2 factors of interest, choice (LL or SS) and accuracy (correct or error). Trials in which subjects chose the reward associated with less discounted value were classified as errors, whereas trials in which they chose the reward associated with more discounted value were classified as correct trials. This GLM tested for the interaction between choice and accuracy as well as both simple effects.
Single-Trial Parameter GLM Analysis
Our second goal with respect to the fMRI data was to test whether variability in the single-trial parameter values would be reflected by brain activity within frontoparietal regions as we have found in testing self-control modulator. So we built a GLM that predicted BOLD responses on the basis of single-trial parameter values and their combinations. Similar with self-control and impulsivity GLM analysis, the single-trial parameter GLM specified the onset of the first offer presentation and the delay period together, modeled by a 7.5 s boxcar function. Onset regressors for the second offer and response were modeled separately as impulse gamma functions.
The model included 3 single-trial parameter values as the parametric modulator of BOLD responses during the time of the response separately. While in the self-control and impulsivity GLM analyses we used 2 parametric modulators (i.e., the self-control and impulsivity measures) within the same GLM, we included only one parametric modulator in the GLM at a time.
For the LCA analyses, in the first GLM, we included single-trial parameter estimates as the parametric modulator. In the second GLM, we included single-trial parameter estimates as the parametric modulator. In the third GLM, we created another transformed parameter by subtracting these 2 and used it as the parametric modulator. In each of the 3 models, we only included trials of LL choice.
Finally, the model specified 6 regressors corresponding to the motion parameters estimated during data preprocessing and 4 constants to account for the mean activity within each of the 4 sessions over which the data were collected. These additional regressors were included as control variables of no interest. Every other GLM model estimation we performed also included 6 motion regressors and 4 session constants as regressors of no interest. Every regressor in the GLM was convolved with the canonical HRF during model estimation.
The group-level contrast for the above specified GLM was calculated as a one-sample t-test on the beta coefficients obtained from the subject-specific single-trial parameter value modulatory regressor. We used significance level to test beta coefficients for 5 ROIs. We chose to use this liberal threshold to compensate for the random variability in the single-trial parameter estimates we obtained that is not systematically related to the variability in the brain data.
Results
Participants completed 2 intertemporal choice tasks in separate sessions. In the first session, individual rates of delay discounting were estimated using a titration task that automatically created choices to progressively converge to subjects’ indifference points (see Experimental Procedures and Rodriguez et al. 2015b; for details). Using estimated discount rates, the second experimental session was designed to offer smaller, sooner (SS) rewards and larger, later (LL) rewards so that the probability of choosing the larger, later reward () approximated a set of target values symmetrically spanning indifference (i.e., and ). The second task was completed while fMRI BOLD data were collected to assess neural processes related to self-control.
Identifying Self-Control: Behavioral Analyses
Self-control in intertemporal choice is an instance of cognitive control that supports goal-directed behaviors particularly when tempting rewards conflict with one’s goal (Miller and Cohen 2001; Figner et al. 2010). In intertemporal choice tasks, participants generally behave as though their goal is to maximize earnings. Depending on details of the experiment, maximizing total earnings can require preferentially choosing SS or LL outcomes (McGuire and Kable 2013). For most tasks, including the paradigms we employ, maximizing earnings is accomplished by selecting LL outcomes that have greater absolute value (Hare et al. 2009, 2011; Figner et al. 2010; Crockett et al. 2013; Ballard et al. 2017). Hence, self-control is associated with selecting delayed rewards in this study. It is possible that participants exert self-control in trials where the SS reward is chosen; however, for these decisions we may only conclude that the amount of control exerted was at most insufficient to select the LL outcome.
For LL choices, we can make use of the fact that control is costly to define the degree of control more precisely (Holroyd and McClure 2015). Contingent on choosing LL rewards, self-control should increase monotonically as SS rewards are more tempting. Intuitively, if the long-term benefits of an outcome drastically outweigh immediate gratification, then self-control is not required for the far sighted choice. As the value of near-term rewards increase, then self-control processes become more critical for suppressing impulsivity. The relative attractiveness of near-term rewards can be approximated by the probability that the LL outcome will be selected: . As the value of near-term rewards increases, should decrease. We can therefore perform an initial test for brain processes related to self-control by testing for regions where activity decreases with in trials where the LL outcome was selected (see Experimental Procedures for a more formal mathematical argument).
Our task manipulated behavior so that we could measure various degrees of self-control. We aimed to elicit choices of LL rewards while varying the relative value of the SS reward. The first analyses we completed tested whether our manipulation was effective. We tested whether was reliably altered in our different task conditions. Next, we note that choice difficulty should increase as choices become closer to indifference. We test for this by determining whether reaction times (RT) were greatest near indifference.
To ensure response consistency across the staircasing and fMRI tasks, we first compared discount parameters () observed during the titration procedure with the re-estimated parameters derived from the scanning session. We found that discount rates derived from the first session were highly correlated with (, ) and did not significantly differ from estimates derived from the behavior observed during the scanning session (paired t-test: , ). Next, we used the discounting parameters obtained during the scanner session to test whether choice probabilities were distributed as intended. To do this, we calculated the probability of choosing the LL alternative for each subject in each condition (i.e., ). A word about notation is in order here. We use the notation when referring to the 4 discrete conditions in the experiment, when referring to the empirical estimate of the probability of a LL response, and we use the notation when referring to the theoretical probability of a LL response, generated from the hyperbolic discounting model used to establish the conditions. Figure 1B visually shows that the choice probabilities spanned the intended range and are approximately symmetrically distributed around . As a formal test, we performed a mixed-effects logistic regression to predict choices, using the difference in subjective values () as a predictor. Differences in estimated subjective values were highly predictive of choices (, ). Thus, SS and LL alternatives were both chosen with expected frequency and the probability of making either choice depended on the subjective valuation of that choice as expected.
We next tested whether the absolute value of the difference in subjective values in a choice, , had a systematic effect on response time. Choice difficulty should decrease as the difference in subjective values increases; we therefore expected a negative correlation between the RT and . A regression analysis indicated that response times increased with decreased valuation differences (Fig. 1C; , ). Together, our behavioral results confirm that our task systematically manipulated choice probabilities and response time as intended to measure various degrees of self-control.
In addition to the relationship between the independent variable (i.e., valuation), and the behavioral variables (i.e., response probability and response time), we were also concerned with the specific shapes of the response time distributions, as they have been particularly useful in dissociating various theories about how preference states evolve over time (Ratcliff 1978; Ratcliff et al. 1999; Ratcliff and Smith 2004; Dai and Busemeyer 2014). Figure 5A shows the response time distributions for each condition in the experiment, aggregated across subjects. In each panel, the distribution of response times is shown as a histogram with response times for the SS choice shown on the negative axis, and the response times for the LL choice shown on the positive axis. By comparing the areas of the 2 responses time distributions, we can get a sense of the relative probability that a choice was made for each condition. In general, as increases, the height of the LL response time distribution increases relative to the SS distribution, a trend that is corroborated by Figure 1B.
Figure 5.
Predictions from the downstream model against the observed data. (A) Choice response time distributions as shown as histograms for each value condition: (blue; top left panel), (green; top right panel), (yellow; bottom left panel), and (red; bottom right panel). In each panel, response time distributions are separated by their choice, where shorter sooner choices appear on the negative axis, and larger later choices appear on the positive axis. Predictions from the best-fitting model (i.e., the last row of Fig. 2C) are shown as black densities overlaying the observed data. (B) Mean choice probabilities (top panel) and mean response times (bottom panel) are shown for the observed data (x-axis) against the model predictions (y-axis). The summary statistics are shown for each individual subject in each of the 4 conditions, color coded according to the legend in the top panel.
Neural Basis of Self-Control: Neuroimaging Analyses
Because our experimental manipulation showed consistent patterns with subjects’ choice probabilities, we can use the probabilities predicted from the hyperbolic discounting model (i.e., ) to investigate the neural basis of self-control (SC; defined by Equation (3)). To this end, we tested for brain areas in which activity increased with increasing attractiveness of the SS alternative, but only on trials in which the LL alternative was chosen. The top row of Figure 4A shows the results of a whole-brain GLM analysis. The GLM analysis revealed that several frontoparietal regions may be involved in self-control: the dorsal medial frontal cortex (dmFC; superior frontal gyrus/supplementary motor area; [4, 28, 46]), the right pPC; inferior parietal lobe; [39, −41, 51], and the bilateral dorsal lateral prefrontal cortex (dlPFC; middle frontal gyrus; left: [−52, 28, 24], right: [22, 38, 41]). Figure 4B shows the estimated coefficients from the GLM analysis corresponding to the 4 prominent ROIs in Figure 4A (i.e., red bars). Previously, we have found these regions to be involved in the accumulation of evidence for action selection in a different intertemporal choice task (Rodriguez et al. 2015a).
Impulsivity and Error Detection
One possible objection to our definition of self-control may be that it is confounded with error severity. When the expected probability of choosing the LL alternative (i.e., ) is low, subjects behave as expected and often choose the SS alternative. The relatively infrequent trials in which is low but the LL alternative is chosen could be due to lapses in attention or some other task failures. If the mechanism for these failures were consistent across trials, trials associated with more severe task failures would be misidentified as higher self-control in the analysis above. In fact, there is a considerable literature that associates error detection with the frontoparietal network our analysis revealed (Botvinick et al. 2004; Eichele et al. 2008; Cavanagh et al. 2009).
Our task design allows us to test whether is associated with error severity. Recall that we obtained an approximately equal probability of each choice, symmetric about the indifference point of . For example, in the condition, we should expect about 90% SS choices, and 10% LL choices, where these LL choices can be thought of as possible “errors.” Symmetric about , in the condition we should expect about 10% SS choices and 90% LL choices. On this side of the independent variable, SS choices correspond to “errors.” If the brain areas we identified in the SC analysis are purely associated with error severity, then they should be associated with both LL choice errors and SS choice errors. Hence, an equivalent but orthogonal measure of self-control, a measure we call impulsivity (), should be an equally strong predictor of dmFC, pPC and bilateral dlPFC activity as the measure (see Equation (6)).
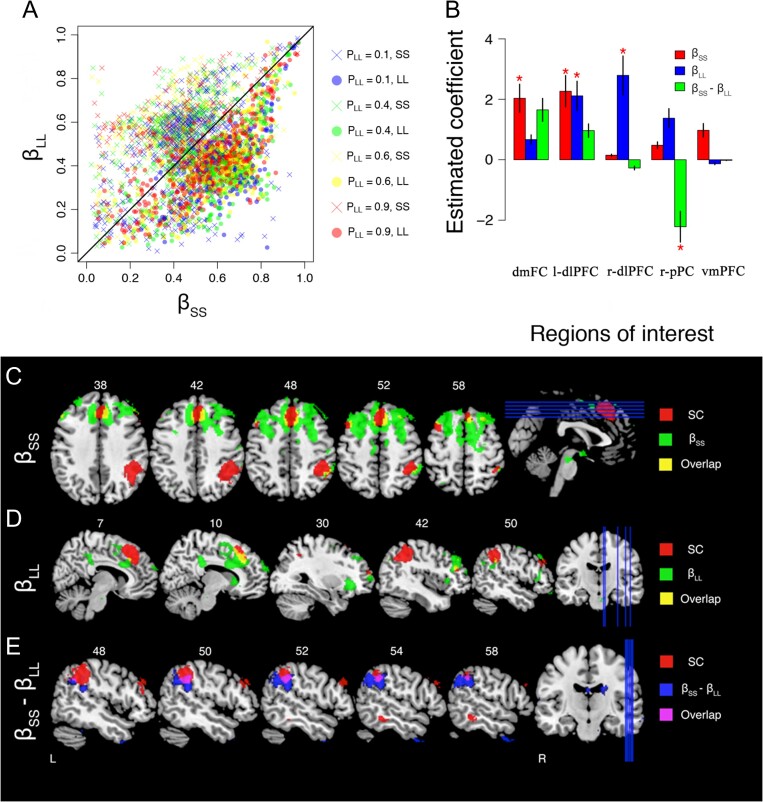
To test this possibility, we mirrored our definition of self-control and tested for brain areas where activity increased with on trials where the SS reward was selected. If measured error severity, then should predict approximately the same degree of dmFC, pPC and bilateral dlPFC activity as . To test this prediction, we performed a GLM analysis including the variables (see Equation (3)) and (see Equation (6)) as regressors. The resulting estimate of the coefficient were reported above. The middle row of Figure 4A shows the voxels associated with the coefficient in our whole-brain GLM analysis. Figure 4A shows that only voxels in the dmFC area are correlated with , but not significantly so (, ).
We then performed a contrast analysis by comparing activity associated with to , shown in the bottom panel of Figure 4A. We find that all frontoparietal regions identified in the self-control analysis are significant when directly contrasting activity related to self-control and activity related to impulsivity (i.e., ). Figure 4B shows the estimated beta coefficients for self-control (red bars), impulsivity (blue bars), and the contrast between them (orange bars) for each of the 4 prominent ROIs in Figure 4A. Our results show that the self-control measure (i.e., ) was a stronger predictor of neural activity than the impulsivity measure (i.e., ) in all 4 ROIs (dmFC: , , left-dlPFC: , , right-dlPFC: , ; right pPC , ; all paired t-tests). Moreover, the impulsivity measure was not a significant predictor of neural activity in any of the 4 regions (all ). These results confirm that activity in the dmFC, pPC, and dlPFC areas are associated with LL choices when in a way that is asymmetric about . We conclude that the activity in these brain regions cannot be interpreted as error severity.
Response Time
Another objection may be that the differences between the and measures could be explained by differences in response time. If response times for trials with high values of were slower than response times for trials with high values of , we might expect greater activity in frontoparietal regions that are associated with value accumulation (Rodriguez et al. 2015a). To test whether the difference between and effects on frontoparietal activity could be due to differences in response time, we performed multiple tests. First, we performed a mixed-effects GLM to predict median response time on the basis of choice (LL or SS), accuracy (correct or error) and their interaction. Errors were defined as trials in which the subject chose a subjectively lower valued alternative, according to their discounting behavior. This GLM showed no effect of choice (, ), and no significant interaction (, ). There was an effect of accuracy, such that errors were slower than correct choices (, ). Next, we explicitly compared median response time for LL choice errors (i.e., when self-control was executed) and SS choice errors (i.e., when impulsivity was executed). The difference in RT between the 2 errors was not significant (, ), nor was the difference between correct LL and SS choice RTs (, ).
We also performed a GLM analysis involving , , and response time as single-trial regressors to test whether or not our results from Figure 4 were affected by the additional response time regressor. The results were qualitatively identical, suggesting that response time does not explain the differences between the and measures. Together, our behavioral and neural data analyses suggest that the difference between the and effects cannot be explained by the differences in response time alone.
Mechanisms of Self-Control: Behavioral Analyses
Having identified the neural basis of self-control, we sought to determine what mechanisms might give rise to the observed pattern of behavioral data. Our approach was to develop a computational model that could explain the self-control behavior in a variety of ways, such as (1) modification of the valuation of the presented offers, (2) directed attention toward a particular feature dimension (i.e., either delay or reward information), or (3) the active inhibition of one or more choice alternatives. By having multiple mechanisms that can produce patterns of data that resemble self-control, we could directly test which mechanism(s) provide the best account of behavioral data, and subsequently use these mechanisms to explore neural correlates of self-control processes.
Figure 2A shows an illustrative path diagram of the model we developed to capture both choice and response time. The model is based on computations central to both the LCA (Usher and McClelland 2004) model, and DFT (Busemeyer and Townsend 1993; Roe et al. 2001; Hotaling et al. 2010). We assume that valuation is produced by the weighted combination of reward amount and delay, as in recent process models of delay discounting (Dai and Busemeyer 2014; Ericson et al. 2015). At the processing stage (i.e., blue and yellow nodes for reward amount and time dimensions, respectively), the model conceives of the 2 alternatives as being comprised of 2 features: the reward value and the delay length. The model contains parameters and that allow the objective values presented in the experiment to be mapped to a subjective representation that might be used by observers in the task. For these transformations, we assumed a power function where and are the exponents as in Dai and Busemeyer (2014). Hence, and are parameters that compress larger numerical values of the reward or delay information into a subjective representation (i.e., and were assumed to be larger than or equal to one). At the feature-selection stage (i.e., green node), the model possesses a feature dimension weight parameter that allows it to attend selectively to either the reward (i.e., when is large) or delay (i.e., when is small) information. For example, when selecting delay features, the SS alternative will become more attractive because delay is shorter when compared with the LL alternative. On the other hand, when reward features are selected, the LL choice will become more attractive because the LL alternative possesses a larger reward amount. Finally, at the preference accumulation stage (i.e., orange node), the SS and LL alternatives compete via a stochastic process involving lateral inhibition and leakage (see Equation (8)). Effectively, the lateral inhibition terms in the model can allow either the SS or LL alternatives to be selectively suppressed, despite the valuations arising from the processing stage.
To illustrate the behavior of the model, Figure 2B shows example trajectories of the preference accumulation process for the SS (red) and LL (blue) alternatives. In this simulation, we set the input of both accumulators to be equal (i.e., and in Equation (8)), but set the lateral inhibition terms to be asymmetric (i.e., and in Equation (8)). Under this parameter setting, the lateral inhibition terms produce an active suppression of the SS alternative, causing LL choices to be made more frequently. In this way, the model can produce behavior that resembles our definition of self-control that is not based on altering the subjective valuation of the alternatives.
To investigate the relative fidelity of the mechanisms in our model, we performed a combinatorial analysis that tested various configurations of model mechanisms. To this end, we fit hierarchical versions of our model that selectively manipulated whether sets of parameters were fixed to specific values or were free to vary across subjects. This analysis is intended to reveal the most influential set of parameters in accounting for choice behavior, while still penalizing for model complexity relative to the data. All model variants contained a threshold parameter , a within-trial variability term , and a nondecision time parameter . All models also received the objective values of the features (i.e., the reward and delay information) from every trial of the experiment as input, in the same way that subjects from the experiment did. Beyond this, each subject was allowed to have a set of freely varying parameters, and these subject-level parameters were further constrained and informed by a hierarchical structure across subjects.
Figure 2C,D shows the results of our analyses. The left-most panel of Figure 2C illustrates the particular model structure that was fit to the data. In this panel, each column corresponds to a parameter, and the circles in each column indicate whether that parameter was fixed (i.e., filled circles) or free to vary (i.e., empty circles) across subjects. The model structures are grouped by color to represent the number of free parameters. The black, blue, green, and red colors indicate families of models that contained 3, 4, 5, and 6 free parameters, respectively. The middle panel shows the model fit results in terms of a z-transformed Bayesian information criterion (BIC) (Schwarz 1978) statistic, where the measure of model fit in the BIC calculation was the largest log likelihood value obtained during the sampling process. For the BIC (and the resulting zBIC), lower values indicate better model performance, balancing model complexity relative to model fit. Each element in the matrix corresponds to a particular model fit (rows) and a particular subject (columns), and is color coded according to the legend on the right side. Figure 2D shows zBIC scores for the model fits aggregated across subjects.
Figure 2C,D shows that on average, the attention parameter has the strongest effect on model performance. For example, the 4 best-performing models are the ones allowing only (i.e., row 2), and either or (i.e., rows 6 and 7), or and both or to vary (i.e., row 12). The aggregation result in Figure 2D allows us to conclude that these 3 parameters are most important in capturing the patterns of individual differences observed in the data, as they play a larger role in determining model performance (i.e., model fit penalized for model complexity) than do the subjective valuation parameters . The best-performing model was Model 12 (i.e., row 12), which permitted variation in what could be conceptualized as “downstream” processes (i.e., postvaluation). Model 12 freely estimates the following parameters: the feature-selection parameter , the 2 lateral inhibition parameters and , the nondecision time parameter , the threshold parameter , and the within-trial noise parameter . Parameters that correspond to “valuation” processes such as the parameters corresponding to the mapping from the objective values of the offers to the subjective values used as input to the accumulators were fixed to one, indicating that no transformation occurred. Under this parameter regime, no mechanisms in the model directly affect the valuation of the features (i.e., they have no relevance in the calculation of the input to the accumulator). For example, the feature-selection weight parameter determines the strength of input only by specifying which features should be considered at a given moment in time—it does not determine the input strength of features themselves. What the model fitting results suggest is that the preliminary subjective mapping step is not as essential in predicting model performance as the manner in which the offers are contrasted during action selection. Hence, this particular model variant is closely related to the verbal model suggested by Figner et al. where dlPFC areas serve to modulate action selection rather than valuation of the stimulus values. As Model 12 relies on indirect valuations of the offers, we refer to Model 12 as the “downstream model” henceforth.
Although Figure 2 shows the relative performance of the models, it does not show how well the models fit in an absolute sense. To evaluate absolute fit, we can generate predictions from the downstream model and compare them to data. To do this, we constructed the posterior predictive distribution (PPD) by randomly sampling a parameter from the estimated joint posterior distribution for each subject, and generating 1000 choice response times. To generate predicted data for each subject, we simulated the model with the actual offers that the subject was given during the experiment. We repeated the PPD construction process for each subject individually, but then collapsed across each set of predicted data to create an aggregated PPD from the downstream model. Figure 5 shows the model fits against the observed data. Figure 5A shows the aggregated PPD (black lines) against the observed data (histograms) for each value condition in the experiment. Figure 5B shows the average model predictions (i.e., y-axis) against the observed data (i.e., x-axis) for the response probabilities (top panel) and the response times (bottom panel). In Figure 5B, the summary statistics are shown separately for each subject in each value condition, color coded according to the key in the top panel. In general, there is close agreement between the model predictions and the observed data, assuring us that the downstream model fits in both an absolute and relative (Fig. 2) sense.
Neural Correlates of the Mechanisms of Self-Control: A Model-Based Analysis
Having confirmed that the downstream model provided the best fit in the suite of models we investigated, we examined the neural basis for the mechanisms assumed by the downstream model. There are many ways to link the abstractions assumed by cognitive models to the neural responses observed in an experiment (cf. Turner, Forstmann, et al. 2017). We chose a two-stage correlation procedure to relate single-trial estimates of the model parameters to single-trial measures of the BOLD response (O’Doherty et al. 2007; van Maanen et al. 2011). We used an empirical Bayesian procedure to estimate the lateral inhibition terms for SS and LL choices (i.e., and , respectively), and the feature-selection parameter for every subject and every trial. As a method of constraint, we fixed other parameters for a given subject to the best-fitting values obtained from our hierarchical estimation procedure in the model comparison section above.
With single-trial measures of the parameters in hand, we then used the parameters as regressors in a whole-brain GLM analysis to examine the neural basis for the inhibition process used in the model. Based on our conceptual definition, self-control is greatest when a LL choice is made despite the subjective valuation of the SS alternative being larger than the LL alternative. Within the model, the lateral inhibition terms in the model are the mechanisms in which self-control is elicited. Because the downstream model allows for an asymmetric inhibition process over the 2 alternatives (i.e., ), a interesting interaction occurs between these 2 parameters that gives rise to the choice behavior elicited in the model. Figure 6A shows the joint distribution of the maximum a posteriori estimates for (i.e., x-axis) against the estimates for (i.e., y-axis) across all trials and subjects. Each estimate in Figure 6A is illustrated to represent whether a LL (circles) or SS choice (“+” symbols) was made, and color coded to reflect the specific condition according to the legend on the right. Figure 6A illustrates the tendency for the model to produce a LL choice when . In this regime, the inhibition of the SS alternative is stronger, causing the LL alternative to win the race toward threshold more often (Figure 2C). Although not visually apparent in Figure 6A, the mean differences between and when SS choices were made was also systematically related to the condition; specifically, the mean differences for the conditions 0.1, 0.4, 0.6, and 0.9 were 0.244, 0.217, 0.196, and 0.145, respectively. Undoubtedly, the decrease in the mean differences is related to the relative inputs of the SS and LL alternatives across the conditions, where larger degrees of lateral inhibition for the SS alternative are necessary to produce a LL response when the SS alternative is more attractive (e.g., in the condition). Together, these results suggest that the lateral inhibition dynamic in the downstream model can produce higher probabilities of LL choices despite larger valuation of the SS alternative—a dynamic that corresponds to our definition of self-control.
Figure 6.
Neural correlates of the model’s inhibition process. (A) The scatter plot shows joint distribution of single-trial estimates (x-axis) and (y-axis) under different choices and conditions, according to the legend on the right side. (B) Barplots of the estimated coefficient of BOLD response signal for inhibition of SS alternative (; red), inhibition of larger later (LL) alternative (; blue), and their difference (i.e., ; green) across 5 regions of interest: dmFC, right and left dlPFC, rpPC, and the ventromedial prefrontal cortex (vmPFC; frontal lobe/bottom of the cerebral hemispheres; [–3, 3, 62]). The red star indicates estimated coefficients that are significantly different from zero (i.e., ). (C, D, E) Whole-brain GLM correlation results using (C) lateral inhibition of SS alternative (i.e., ), (D) lateral inhibition of LL alternative (i.e., ), and (E) the difference between the 2 terms (i.e., ) as trial-level regressors. Red areas represent voxels found in our self-control analysis above (Fig. 4), green voxels are associated with positive correlations, blue areas are associated with negative correlations, and yellow and magenta voxels are associated with the overlap between 2 corresponding GLM analyses.
We next investigated whether or not the lateral inhibition terms in our model were related to the self-control areas identified above. Figure 6C–E shows areas of the brain that are significantly related to different combinations of the lateral inhibition terms: lateral inhibition of the SS alternative (i.e., ) in Fig. 6C, lateral inhibition of the LL alternative (i.e., ) in Fig. 6D, and the difference between the 2 terms (i.e., ) in Fig. 6E. Across all panels (i.e., Fig. 6C–E), brain areas associated with significant correlations (i.e., ) of a lateral inhibition term are shown as either green (i.e., for positive) or blue (i.e., for negative) voxels, positive correlations with our self-control measure (Fig. 4A) are shown as red voxels, and overlap across these metrics are shown as yellow (i.e., for positive correlations) or magenta (i.e., for negative correlations) voxels. Figure 6C shows that when is large and the SS alternative is actively suppressed, activation of several frontal areas is significantly higher (represented as green voxels). Less frontal activation was observed for the coefficient, with the exception of the right dlPFC area. For the difference in inhibition terms, we observed strong negative correlations with right pPC (represented as blue voxels).
To better elucidate the role that the lateral inhibition terms play, we performed an ROI analysis by correlating the 3 combinations of lateral inhibition terms to 5 key brain areas: dmFC, bilateral dlPFC, rpPC, and the vmPFC [3, 62, −3]. The first 4 regions were defined by our self-control analyses from above, and the vmPFC area was defined by the vmPFC mask identified in Bartra et al. (2013).
Figure 6B shows the estimated coefficient for inhibition of SS alternative (; red), inhibition of LL alternative (; blue), and their difference (i.e., ; green). Inhibition of the SS alternative () was significantly related to activity in the dmFC (, , Cohen’s ) and the left dlPFC (, , Cohen’s ), whereas inhibition of the LL alternative () was significantly related to activity in the left (, , Cohen’s ), and right dlPFC (, , Cohen’s ). However, the difference between the lateral inhibition terms was only significantly related to the right pPC (, , Cohen’s ). Importantly, none of our lateral inhibition regressors significantly correlated with vmPFC.
We also investigated single-trial correlations of the parameter . Although we examined linear and quadratic relations of to the neural data, we found no significant correlations in our whole-brain GLM analyses. As such, we did not perform any ROI-based analyses involving .
General Discussion
In this article, we have taken a computational approach to identify brain regions that are collectively involved in processes related to intertemporal choice and self-control. Each of our analyses associated regions of medial and lateral prefrontal cortex with self-control. These regions are commonly identified in intertemporal choice decision making, but their specific contribution to the choice process has not yet been unraveled. To dissociate the effects of self-control and impulsivity, our task design relied on presenting choice offers that were directly related to each individual’s temporal discounting behavior, assessed in a separate session. Furthermore, our task design presented subjects with multiple shorter sooner (i.e., impulsive) choice options, unlike other studies investigating intertemporal choice decisions (McClure et al. 2004, 2007a; Kable and Glimcher 2007; Ballard and Knutson 2009; Hare et al. 2014). Our first analysis established that the self-control processes engage brain areas very differently compared with impulsivity. Specifically, our analyses revealed that when LL choices are made, activity in the left and right dlPFC, right pPC, and dmFC is significantly positively correlated with the attractiveness of the SS alternative. Yet when SS choices are made, activity in these areas does not significantly correlate with the attractiveness of the LL alternative. Conceptually, our preliminary analyses revealed a clear asymmetry in the brain when we make decisions that maximize long-term rewards compared with decisions that minimize delay.
However, we argue that simply knowing that an asymmetry exists does not contribute to our understanding of the mechanisms that produce LL choices. To investigate the mechanisms of self-control, we developed a computational model of the intertemporal choice task equipped with a variety of different mechanisms that could potentially explain how self-control manifests in behavioral data. Taken together, the set of mechanisms in the model are not uniquely identifiable, so we instead investigated a factorial subset of the mechanisms by fitting several variants of the model to the data (Fig. 2C). Ultimately, we found that models that allow for feature-selection biases and lateral inhibition provided the best account of behavioral data, suggesting that a subjective mapping of objective rewards and delays (i.e., and ) were not essential to explain data from our intertemporal choice task, as has been suggested previously (Hare et al. 2009, 2011).
Finally, we obtained single-trial estimates of the feature-selection parameter and the 2 lateral inhibition parameters and . We performed whole-brain GLM analyses on different combinations of the lateral inhibition terms. Most importantly we found that the lateral inhibition of the SS alternative (i.e., ) overlapped with frontal areas (i.e., left dlPFC and dmFC) that we identified as carrying out self-control in our first analysis. These results point to a potential explanation of how self-control processes are executed in intertemporal choice tasks: self-control may be related to the ability of frontal areas to (laterally) inhibit selection of the SS alternative.
The Impetus for Self-Control
In our computational model, there are 2 mechanisms that can give rise to behavioral data that satisfy our conceptual definition of self-control. Recall that self-control was defined to scale with the relative attractiveness of the SS alternative for trials in which the LL alternative is selected. In our “downstream” model, self-control can be carried out in 1 of 2 ways. First, the valuation process can be altered by increasing the feature-sampling parameter toward the value of the reward information. Since the LL alternative always has larger reward value than the SS option, increased weighting of reward amount necessarily increased the attractiveness of the LL option. This creates a larger probability of a LL response across the space of the independent variable in our task (i.e., ; see Fig. 3). Second, the downstream action selection process can be altered by increasing the lateral inhibition term corresponding to the SS alternative (relative to the LL alternative). This alters the preference accumulation dynamics to produce a larger preference for the LL alternative (Figs 2B and 3). Given that there are 2 routes to produce higher probabilities of LL responses, one may wonder whether this feature of the model is problematic, as the model could be too flexible relative to the data.
Although the “feature-selection” regime in the downstream model can produce increases in the probability of LL responses (see our simulation study in the Experimental Procedures), in our view, this configuration of the model is inconsistent with our definition of self-control. Within the feature-selection regime, the parameter increases toward one, causing reward information to be sampled more often than the delay information. When this occurs, the input that drives the accumulators, and , changes such that the LL alternative receives more input (i.e., increases) and the SS alternative receives less input (i.e., decreases), by virtue of being larger than . When assuming that all other parameters are inconsequential (e.g., ), the most direct way the feature-selection regime generates more frequent LL responses is when . However, this inequality implies that the subjective valuation of the LL alternative is already larger than the SS alternative, and this fact is at odds with the concept of self-control. Self-control should be minimally necessary when the subjective values of the LL option dominates that of the SS option.
By contrast, as we explained in the results section, the “inhibition” regime can produce increases in the probability of a LL response regardless of how the features of the offers are combined in the valuation process. Even when the reward information is preferentially weighted over the time information, the lateral inhibition terms can be adjusted to overcome the differences in the inputs for the 2 alternatives. As we show in our simulation study, the model can produce increases in the probability of a LL response even when reward information is preferentially sampled over delay information.
Despite these arguments, we did not rule out the feature-selection regime as one possible explanation for self-control in our analyses. When fitting our model variants hierarchically to data, we allowed for the possibility of only feature-selection, only lateral inhibition, or both mechanisms to vary freely. We ultimately found that the best-fitting model variant was one that allowed all 3 terms to vary freely, suggesting that these parameters tradeoff in some way to better capture the complex patterns of choice response time in our data. In this downstream model, we found that the mean of the group-level posterior distribution for the feature-selection parameter parameter was 0.707, suggesting that most subjects preferentially weighted reward information over delay information. We also found that the mean of the group-level posterior distributions for the and parameters were 0.540 and 0.556, respectively. Taken by themselves, these means suggest that the LL alternative was suppressed more than the SS alternative. However, noting that attention was oriented toward the reward information implies that the input term was, on average, larger than . To accommodate these differences in the inputs, the lateral inhibition term needed to increase to slow the accumulation of preference so that both alternatives could be considered. Furthermore, the increase in helped the model match the spread of the response time distributions. When one feature is sampled more often than another, the input terms and become large enough to dominate the stochastic process in Equation (8), causing a lower mean and significantly lower standard deviation for the predicted response time distribution.
Perhaps more revealing was the tradeoffs that appeared when analyzing the single-trial parameter estimates. For example, Figure 6A shows that under some parameter settings, such as when , LL choices become more likely, suggesting that trial-level information may have better resolution compared with the subject-level information in answering questions about trial to trial engagement of self-control processes. We also observed strong correlations between the lateral inhibition terms and the feature-selection parameter , and these interactions were systematically related to the probability of a LL response, but they were not systematically related to the value condition . Taken together, these results suggest that while played an important role at the subject-level analyses, the lateral inhibition parameters played a more important role at the trial-level analyses.
However, when investigating the neural basis for these model parameters, we found strong relationships between the lateral inhibition parameters and key brain areas involved in our initial self-control GLM analysis. Specifically, we found interactions with dlPFC, dmFC, and even right pPC. We did not find significant correlation results for the parameter directly. Part of this failure is likely due to the complexity of the interpretation of relative to what is traditionally explained as value encoding. When increases, reward information is sampled more often, whereas when decreases, delay information is sampled more often. Although we tested different parametric forms of the brain’s relation to (e.g., quadratic), we did not find any convincing result that would elucidate its neural basis.
Given the strong relationships between lateral inhibition and feature selection in our model, it would seem to be a worthwhile endeavor to establish some link between these mechanisms. For example, Hotaling et al. (2010) used a “dominance” space to convert differences in the values of features comprising a stimulus to lateral inhibition terms in an accumulator model (Roe et al. 2001). More recently, Bhatia (2013) used the sum of the values of stimulus features to specify how attention should be allocated on a moment-by-moment basis (i.e., through a Bernoulli process). As we take inspiration from these previous efforts to commit mechanism to a particular theory, future work on the LCA model presented here could establish a theoretical link between feature selection and lateral inhibition. For now, we emphasize that there are complex tradeoffs between feature-selection and inhibition, but the mechanisms of inhibition are more directly mapped to brain activity in our study.
Joint Modeling
In our analysis above, we treated the single-trial parameters as a regressor in a GLM as a way to try and understand the neural bases for the mechanisms corresponding to the parameters. This method of linking neural and behavioral data has been referred to as a “two-stage” analysis (Turner, Forstmann, et al. 2017). The two-stage approach has limitations in that the neural data do not provide any real statistical constraint on the behavioral model; instead, the neural data only help to give us a conceptual link of where a mechanism is carried out in the brain.
Recently, new approaches have been developed for formally linking neural data to the parameters of cognitive models in a way that enforces a reciprocal relationship between these random variables (Turner, Forstmann, et al. 2013; Turner et al. 2015, 2016; Turner, Wang, et al. 2017). The benefit of using this “joint modeling” approach is that the information contained in either stream of data provides an extra layer of constraint in one formal model, and so the model’s suitability is evaluated with respect to both the behavioral and neural data, usually through model fit statistics or cross-validation tests. While we do advocate for these joint models, they require complex algorithms for estimating the model parameters, which is further complicated in the current computational model because the likelihood function is intractable. Furthermore, because we had not yet established (1) which mechanisms in the model provided the best account of the behavioral data or (2) what brain regions were likely candidates for carrying out self-control, many new models would need to be developed and fit to data. As such, we elected to first determine the best-fitting model variants as a way to ascertain the plausibility of each model mechanisms. From there, we performed a simple exploratory procedure for relating the estimates of the model parameters to the voxel-level activity for each trial by subject combination. Future research will take a more confirmatory approach by using the neural activity to directly constrain and guide the estimation of the model parameters.
Another limitation with our analyses is the way in which single-trial parameter estimates are obtained in 2 steps. Ideally, we would have devised a 3-layer hierarchical model to simultaneously infer estimates at the trial-, subject-, and group-levels. While this type of analysis is of course possible, it would require that an even more sophisticated estimation procedure be applied to each model variant we tested (Fig. 5). We chose to use our two-stage empirical Bayesian approach to limit the number of free parameters that needed to be estimated at a given stage (also see van Maanen et al. 2011). Future work will take a more confirmatory approach where the parameters corresponding to all 3 levels are estimated simultaneously.
Conclusions
In this article, we have developed a computational model that can be used to better understand the neural and mechanistic bases of self control. Our model relates to extant theories about how brain areas related to self-control modulate areas related to valuation (Hare et al. 2009, 2011, 2014), as well as theories about how self-control can be inhibited without affecting valuation (Figner et al. 2010). Although the model assumes a dynamic integration process between the valuation of the offers and the action selection process, the model has parameters designed to relate directly to valuation and self-control. As such, our model could be used as a theoretical tool to test specific assumptions about the previously stated opposing interactions between self-control and valuation, as a measurement tool to assess the degree of self-control exhibited by certain patient populations (Bickel and Marsch 2001; Weller et al. 2008; McClure and Bickel 2014), or as a prediction tool for whether certain incentive programs could be used to either focus attention toward one dimension (e.g., the attention parameter ) or impose inhibition (e.g., the lateral inhibition parameter ) of a tempting, but ultimately inferior option (Hare et al. 2009; Peters and Büchel 2010; Maier et al. 2015). Future work will further commit the mechanisms and parameters assumed by our model directly to neurophysiological information.
Supplementary Material
Notes
This research was supported by Air Force Research Lab contract FA8650-16-1-6770. The authors would like to thank Per Sederberg and Matthew Galdo for helpful discussions. Conflict of Interest: The authors declare no conflict of interest.
Contributor Information
Brandon M Turner, Department of Psychology, The Ohio State University, Columbus, OH, USA.
Christian A Rodriguez, Department of Psychology, Stanford University, Stanford, CA, USA.
Qingfang Liu, Department of Psychology, The Ohio State University, Columbus, OH, USA.
M Fiona Molloy, Department of Psychology, The Ohio State University, Columbus, OH, USA.
Marjolein Hoogendijk, Graduate School of Life and Earth Sciences, University of Amsterdam, Amsterdam, Netherlands.
Samuel M McClure, Department of Psychology, Arizona State University, Tempe, AZ, USA.
Authors’ Contributions
C.A.R., M.H., and S.M.M. designed and carried out experiment; C.A.R., Q.L., and M.F.M. analyzed the neuroimaging data; B.M.T. and Q.L. developed the models; B.M.T. and Q.L. fit the models to data; Q.L. related model parameters to neuroimaging data; B.M.T., C.A.R., Q.L., M.F.M., and S.M.M. wrote the article.
References
- Ballard I, Kim B, Liatsis A, Cohen J, McClure S. 2017. More is meaningful: the magnitude effect in intertemporal choice depends on self-control. Psychol Sci. 28:1443–1454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballard K, Knutson B. 2009. Dissociable neural representations of future reward magnitude and delay during temporal discounting. NeuroImage. 45:143–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartra O, McGuire JT, Kable JW. 2013. The valuation system: a coordinate-based meta-analysis of bold fmri experiments examining neural correlates of subjective value. NeuroImage. 76:412–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumeister RF, Heatherton TF. 1996. Self-regulation failure: an overview. Psychol Inq. 7:1–15. [Google Scholar]
- Baumeister RF, Heatherton TF, Tice DM. 1994. Losing control: how and why people fail at self-regulation. San Diego: Academic Press. [Google Scholar]
- Bhatia S. 2013. Associations and the accumulation of preference. Psychol Rev. 120:522–543. [DOI] [PubMed] [Google Scholar]
- Bickel W, Marsch L. 2001. Toward a behavioral economic understanding of drug dependence: delay discounting processes. Addiction. 96:74–86. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. 2006. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced choice tasks. Psychol Rev. 362:1655–1670. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Cohen JD, Carter CS. 2004. Conflict monitoring and anterior cingulate cortex: an update. Trends Cogn Sci. 8:539–546. [DOI] [PubMed] [Google Scholar]
- Brown S, Ratcliff R, Smith PL. 2006. Evaluating methods for approximating stochastic differential equations. J Math Psychol. 50:402–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer J, Townsend J. 1993. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev. 100:432–459. [DOI] [PubMed] [Google Scholar]
- Cavagnaro DR, Aranovich GJ, McClure SM, Pitt MA, Myung JI. 2016. Time discounting and time preference: a critical review. J Risk Uncertain. 52:233–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh JF, Cohen MX, Allen JJ. 2009. Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. J Neurosci. 29:98–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland A, Kiani R, Shadlen M. 2008. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. Nat Neurosci. 11:693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crockett MJ, Braams BR, Clark L, Tobler PN, Robbins TW, Kalenscher T. 2013. Restricting temptations: neural mechanisms of precommitment. Neuron. 79:391–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai J, Busemeyer JR. 2014. A probabilistic, dynamic, and attribute-wise model of intertemporal choice. J Exp Psychol Gen. 143:1489–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ditterich J. 2010. A comparison between mechanisms of multi-alternative perceptual decision making: ability to explain human behavior, predictions for neurophysiology, and relationship with decision theory. Front Neurosci. 4:184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebert JE, Prelec D. 2007. The fragility of time: time-insensitivity and valuation of the near and far future. Manage Sci. 53:1423–1428. [Google Scholar]
- Eichele T, Debener S, Calhoun VD, Specht K, Engel AK, Hugdahl K, Von Cramon DY, Ullsperger M. 2008. Prediction of human errors by maladaptive changes in event-related brain networks. Proc Nat Acad Sci USA. 105:6173–6178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ericson K, White J, Laibson D, Cohen J. 2015. Money earlier or later? Simple heuristics explain intertemporal choices better than delay discounting does. Psychol Sci. 26:826–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Essex BG, Clinton SA, Wonderley LR, Zald DH. 2012. The impact of the posterior parietal and dorsolateral prefrontal cortices on the optimization of long-term versus immediate value. J Neurosci. 32:15403–15413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figner B, Knoch D, Johnson EJ, Krosch AR, Lisanby SH, Fehr E, Weber EU. 2010. Lateral prefrontal cortex and self-control in intertemporal choice. Nat Neurosci. 13:538–539. [DOI] [PubMed] [Google Scholar]
- Frederick S, Loewenstein G, O’Donoghue T. 2002. Time discounting and time preference: a critical review. J Econ Lit. 40:351–401. [Google Scholar]
- Green L, Myerson J. 2004. A discounting framework for choice with delayed and probabilistic rewards. Psychol Bull. 130:769–792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanes DP, Patterson WF, Schall JD. 1998. Role of frontal eye fields in countermanding saccades: Visual, movement, and fixation activity. J Neurophysiol. 79:817–834. [DOI] [PubMed] [Google Scholar]
- Hanes DP, Schall JD. 1996. Neural control of voluntary movement initiation. Science. 274:427–430. [DOI] [PubMed] [Google Scholar]
- Hare TA, Camerer CF, Rangel A. 2009. Self-control in decision-making involves modulation of the vmpfc valuation system. Science. 324:646–648. [DOI] [PubMed] [Google Scholar]
- Hare TA, Hakimi S, Rangel A. 2014. Activity in dlPFC and its effective connectivity to vmPFC are associated with temporal discounting. Front Neurosci. 8:50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hare TA, Malmaud J, Rangel A. 2011. Focusing attention on the health aspects of foods changes value signals in vmPFC and improves dietary choice. J Neurosci. 31:11077–11087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heatherton TF. 2011. Neuroscience of self and self-regulation. Annu Rev Psychol. 62:363–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmann W, Friese M, Strack F. 2009. Impulse and self-control from a dual-systems perspective. Perspect Psychol Sci. 4:162–176. [DOI] [PubMed] [Google Scholar]
- Holmes WR. 2015. A practical guide to the probability density approximation (PDA) with improved implementation and error characterization. J Math Psychol. 68:13–24. [Google Scholar]
- Holroyd CB, McClure SM. 2015. Hierarchical control over effortful behavior by rodent medial frontal cortex: a computational model. Psychol Rev. 122:54–83. [DOI] [PubMed] [Google Scholar]
- Hotaling JM, Busemeyer J, Li J. 2010. Theoretical developments in decision field theory: comment on tsetsos, usher, and chater. Psychol Rev. 117:1294–1298. [DOI] [PubMed] [Google Scholar]
- Huk AC, Shadlen MN. 2005. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J Neurosci. 25:10420–10436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. 2007. The neural correlates of subjective value during intertemporal choice. Nat Neurosci. 10:1625–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelley N, Schmeichel B. 2016. Noninvasive stimulation over the dorsolateral prefrontal cortex facilitates the inhibition of motivated responding. J Exp Psychol Gen. 145:102–1712. [DOI] [PubMed] [Google Scholar]
- Maier SU, Makwana AB, Hare TA. 2015. Acute stress impairs self-control in goal-directed choice by altering multiple functional connections within the brain?s decision circuits. Neuron. 87:621–631. [DOI] [PubMed] [Google Scholar]
- McClure SM, Bickel WK. 2014. A dual-systems perspective on addiction: contributions from neuroimaging and cognitive training. Ann NY Acad Sci. 1327:62–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Ericson KM, Laibson DI, Loewenstein G, Cohen JD. 2007. a. Time discounting for primary rewards. J Neurosci. 27:5796–5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Ericson KM, Laibson DI, Loewenstein G, Cohen JD. 2007. b. Time discounting for primary rewards. J Neurosci. 21:5796–5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Laibson DI, Loewenstein G, Cohen JD. 2004. Separate neural systems value immediate and delayed monetary rewards. Science. 306:503–507. [DOI] [PubMed] [Google Scholar]
- McGuire J, Kable J. 2013. Rational temporal predictions can underlie apparent failures to delay gratification. Psychol Rev. 120:395–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. 2001. An integrative theory of the prefrontal cortex. Annu Rev Neurosci. 24:167–202. [DOI] [PubMed] [Google Scholar]
- O’Doherty JP, Hampton A, Kim H. 2007. Model-based fMRI and its application to reward learning and decision making. Ann NY Acad Sci. 1104:35–53. [DOI] [PubMed] [Google Scholar]
- Peters J, Büchel C. 2010. Episodic future thinking reduces reward delay discounting through an enhancement of prefrontal-mediotemporal interactions. Neuron. 66:138–148. [DOI] [PubMed] [Google Scholar]
- Peters J, Büchel C. 2011. The neural mechanisms of inter-temporal decision-making: understanding variability. Trends Cogn Sci. 15:227–239. [DOI] [PubMed] [Google Scholar]
- Pouget P, Logan GD, Palmeri TJ, Boucher L, Par M, Schall JD. 2011. Neural basis of adaptive response time adjustment during saccade countermanding. J Neurosci. 31:12604–12612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. 1978. A theory of memory retrieval. Psychol Rev. 85:59–108. [Google Scholar]
- Ratcliff R, McKoon G. 2008. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20:873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. 2004. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 111:333–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. 1999. Comparing connectionist and diffusion models of reaction time. Psychol Rev. 106:261–300. [DOI] [PubMed] [Google Scholar]
- Rodriguez CA, Turner BM, McClure SM. 2014. Intertemporal choice as discounted value accumulation. PLoS One. 9:e90138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez CA, Turner BM, van Zandt T, McClure SM. 2015. a. The neural basis of value accumulation in intertemporal choice. Eur J Neurosci. 42:2179–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez CA, Turner BM, Van Zandt T, McClure SM. 2015. b. The neural basis of value accumulation in intertemporal choice. Eur J Neurosci. 42:2179–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roe RM, Busemeyer JR, Townsend JT. 2001. Multialternative decision field theory: a dynamic connectionist model of decision making. Psychol Rev. 108:370–392. [DOI] [PubMed] [Google Scholar]
- Roitman J, Shadlen M. 2002. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 22:9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schall JD. 1991. Neuronal activity related to visually guided saccades in the frontal eye fields of rhesus monkeys: comparison with supplementary eye fields. J Neurophysiol. 66:559–579. [DOI] [PubMed] [Google Scholar]
- Schroeder S. 2007. We can do better-improving the health of the American people. N Engl J Med. 357:1221–1228. [DOI] [PubMed] [Google Scholar]
- Schwarz G. 1978. Estimating the dimension of a model. Ann Stat. 6:461–464. [Google Scholar]
- Silverman BW. 1986. Density estimation for statistics and data analysis. London: Chapman & Hall. [Google Scholar]
- ter Braak CJF. 2006. A Markov chain Monte Carlo version of the genetic algorithm differential evolution: easy Bayesian computing for real parameter spaces. Stat Comput. 16:239–249. [Google Scholar]
- Turner B, Wang T, Merkle E. 2017. Factor analysis linking functions for simultaneously modeling neural and behavioral data. NeuroImage. 153:28–48. [DOI] [PubMed] [Google Scholar]
- Turner BM, Forstmann BU, Love BU, Palmeri TJ, Van Maanen L. 2017. Approaches to analysis in model-based cognitive neuroscience. J Math Psychol. 76:65–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BM, Forstmann BU, Wagenmakers EJ, Brown SD, Sederberg PB, Steyvers M. 2013. A bayesian framework for simultaneously modeling neural and behavioral data. NeuroImage. 72:193–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BM, Rodriguez CA, Norcia T, Steyvers M, McClure SM. 2016. Why more is better: a method for simultaneously modeling EEG, fMRI, and behavior. NeuroImage. 128:96–115. [DOI] [PubMed] [Google Scholar]
- Turner BM, Schley DR, Muller C, Tsetsos K (2018). Comparing models of multi-alternative, multi-attribute choice. Psychol Rev. (forthcoming).
- Turner BM, Sederberg PB. 2012. Approximate Bayesian computation with differential evolution. J Math Psychol. 56:375–385. [Google Scholar]
- Turner BM, Sederberg PB. 2014. A generalized, likelihood-free method for parameter estimation. Psychon Bull Rev. 21:227–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BM, Sederberg PB, Brown S, Steyvers M. 2013. A method for efficiently sampling from distributions with correlated dimensions. Psychol Methods. 18:368–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BM, Van Maanen L, Forstmann BU. 2015. Combining cognitive abstractions with neurophysiology: the neural drift diffusion model. Psychol Rev. 122:312–336. [DOI] [PubMed] [Google Scholar]
- Turner BM, Van Zandt T. 2012. A tutorial on approximate Bayesian computation. J Math Psychol. 56:69–85. [Google Scholar]
- Turner BM, Van Zandt T. 2014. Hierarchical approximate Bayesian computation. Psychometrika. 79:185–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. 2001. On the time course of perceptual choice: the leaky competing accumulator model. Psychol Rev. 108:550–592. [DOI] [PubMed] [Google Scholar]
- Usher M, McClelland JL. 2004. Loss aversion and inhibition in dynamical models of multialternative choice. Psychol Rev. 111:757–769. [DOI] [PubMed] [Google Scholar]
- van den Bos W, McClure SM. 2013. Towards a general model of temporal discounting. J Exp Anal Behav. 99:58–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Maanen L, Brown SD, Eichele T, Wagenmakers EJ, Ho T, Serences J. 2011. Neural correlates of trial-to-trial fluctuations in response caution. J Neurosci. 31:17488–17495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Ravenzwaaij D, van der Maas HLJ, Wagenmakers EJ. 2012. Optimal decision making in neural inhibition models. Psychol Rev. 119:201–215. [DOI] [PubMed] [Google Scholar]
- Vanpaemel W. 2010. Prior sensitivity in theory testing: an apologia for the Bayes factor. J Math Psychol. 54:491–498. [Google Scholar]
- Vanpaemel W. 2011. Constructing informative model priors using hierarchical methods. J Math Psychol. 55:106–117. [Google Scholar]
- Vanpaemel W, Lee M. 2012. Using priors to formalize theory: optimal attention and the generalized context model. Psychon Bull Rev. 19:1047–1056. [DOI] [PubMed] [Google Scholar]
- Wagner D, Heatherton T. 2010. Giving in to temptation: the emerging cognitive neuroscience of self-regulatory failure. In: Vohs K, Baumeister R, editors. Handbook of self-regulation: research, theory, and applications. New York City, New York: The Guilford Press. p. 41–63. [Google Scholar]
- Weller RE, Cook EW, Avsar KB, Cox JE. 2008. Obese women show greater delay discounting than healthy-weight women. Appetite. 51:563–569. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.