Abstract
Biomedical data are becoming increasingly multimodal and thereby capture the underlying complex relationships among biological processes. Deep learning (DL)-based data fusion strategies are a popular approach for modeling these nonlinear relationships. Therefore, we review the current state-of-the-art of such methods and propose a detailed taxonomy that facilitates more informed choices of fusion strategies for biomedical applications, as well as research on novel methods. By doing so, we find that deep fusion strategies often outperform unimodal and shallow approaches. Additionally, the proposed subcategories of fusion strategies show different advantages and drawbacks. The review of current methods has shown that, especially for intermediate fusion strategies, joint representation learning is the preferred approach as it effectively models the complex interactions of different levels of biological organization. Finally, we note that gradual fusion, based on prior biological knowledge or on search strategies, is a promising future research path. Similarly, utilizing transfer learning might overcome sample size limitations of multimodal data sets. As these data sets become increasingly available, multimodal DL approaches present the opportunity to train holistic models that can learn the complex regulatory dynamics behind health and disease.
Keywords: fusion strategies, data integration, deep neural networks, multimodal machine learning, representation learning, multi-omics
Introduction
Individual cells and complete organisms are prototypical complex systems, as they are composed of many different parts interacting with each other and giving rise to emergent behaviors [1]. Understanding these interactions is particularly important when attempting to make predictions about complex diseases. Data modality is the result of measuring such a phenomenon with a specific sensor [2], and it therefore provides limited information on its own. With multimodal data, it is possible to gain information about the individual parts and their emergent behavior. Thanks to the rapid advances of high-throughput technologies, we now have unprecedented access to large-scale multimodal biomedical data, providing the opportunity to take advantage of this richer information.
Data fusion1 is the combination of data from different modalities that provide separate views on a common phenomenon to solve an inference problem. This holds the promise of solving such problems with fewer errors than unimodal approaches would [3]. More specifically, the advantages of data fusion can be categorized as complementary, redundant and cooperative features [4, 5], though these are not mutually exclusive.
Advantages of data fusion in the biomedical field can be illustrated with the multimodal study of a cancer patient. Genomic data from a tumor enable the identification of cancer driver genes while a whole-slide image (WSI) from a biopsy provides a view on the tumor’s morphology and microenvironment. These modalities are ‘complementary’ because they provide information about different parts of the phenomenon otherwise not observable. The fusion of transcriptomic and proteomic data are both complementary, because all mRNAs are not translated to proteins, and ‘redundant’ because the abundance of a protein confirms the translation of a specific mRNA into a protein. This redundancy is particularly important when the data are noisy or have many missing values. Data from miRNA and mRNA sequencing of the same tumor can be considered ‘cooperative’ because the combined information increases complexity. Fusion of both modalities provides a possible explanation for differential abundance of a protein of, for instance, an oncogene. This might play a vital role in the prediction of the patient’s response to a certain treatment.
The aim of fusion strategies is to effectively exploit complementary, redundant and cooperative features of different modalities. To fully take advantage of these views on the phenomenon of interest, machine learning (ML) methods have to be deployed that are able to fuse structured and unstructured data with different statistical properties, sources of non-biological variation, high-dimensionality [6] and different patterns of missing values [2].
In recent years, multimodal ML methods have been increasingly studied and applied in a variety of fields [6, 11]. Figure 1 illustrates this trend in the biomedical field. Multimodal deep learning (DL) in particular provides advantages over shallow methods for data fusion. Fully connected neural networks (FCNNs) are the conventional form of deep neural networks (DNNs) and can be viewed as a directed acyclical graph, which maps input  to label
to label  through several hidden layers of nonlinear computational operations [12]. Common DL architectures are summarized in Table 1. The goal of such algorithms is to learn high-level representations of the input data that improve the prediction by a final classifier through finding simple dependencies between underlying disentangled factors. Earlier layers learn simple abstractions of the data, whereas deeper layers combine these into more abstract representations that are informative for the learning task [13]. Crucially, multimodal DL is able to model nonlinear within- and cross-modality relationships. This has led to its application in a variety of fields [2]. However, biomedical applications face specific challenges for multimodal fusion such as small sample size compared to the combined dimensionality, missing of entire modalities and imbalance in dimensionality between modalities.
through several hidden layers of nonlinear computational operations [12]. Common DL architectures are summarized in Table 1. The goal of such algorithms is to learn high-level representations of the input data that improve the prediction by a final classifier through finding simple dependencies between underlying disentangled factors. Earlier layers learn simple abstractions of the data, whereas deeper layers combine these into more abstract representations that are informative for the learning task [13]. Crucially, multimodal DL is able to model nonlinear within- and cross-modality relationships. This has led to its application in a variety of fields [2]. However, biomedical applications face specific challenges for multimodal fusion such as small sample size compared to the combined dimensionality, missing of entire modalities and imbalance in dimensionality between modalities.
Figure 1.
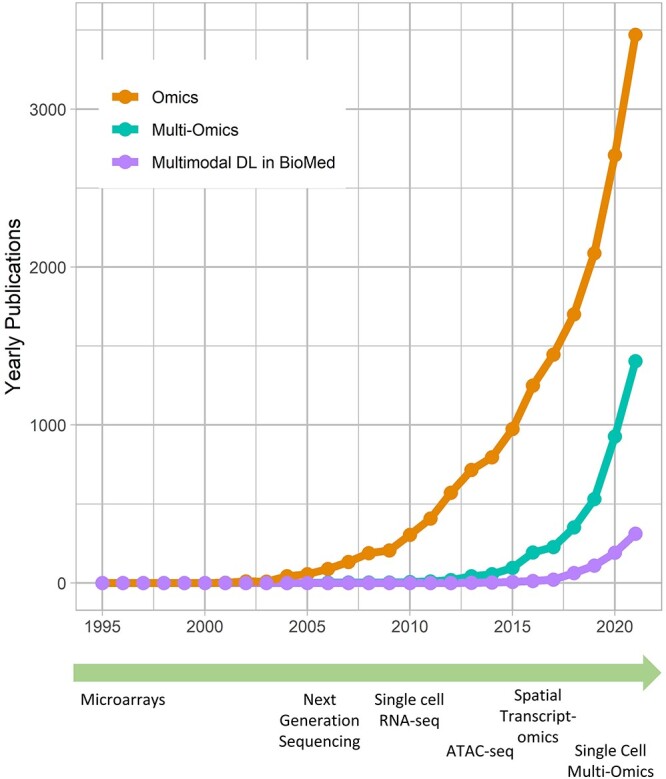
Development of technologies and multimodal deep learning (DL). ‘Omics’ and ‘multi-omics’ data become increasingly relevant in the scientific literature. To fully utilize the growing number of multimodal data sets, data fusion methods based on DL are evolving into an important approach in the biomedical field. This unprecedented generation of data has been made possible by high-throughtput technologies like microarrays and next-generation sequencing [7]. The development of bulk RNA-seq was followed by several related sequencing technologies, such as single-cell RNA-seq and ATAC-seq [8]. Currently, spatial transcriptomics [9] and single-cell multi-omics [10] are being increasingly used.
Table 1.
Common architectures of artificial neural networks. The topology of an artificial neural network has strong influence on the performance of the model. Different architectures are more appropriate for certain data types
| Architecture | Description |
|---|---|
| Fully connected neural networks | FCNNs are the most conventional deep neural networks (DNNs). |
| In a layer, each neuron is connected to all neurons in the | |
| subsequent layers [12]. | |
| Convolutional neural networks | CNNs are able to model spatial structures such as images |
| or DNA sequences. Each neuron is connected to all neurons | |
| in the subsequent layer. In convolution layers kernels are | |
| slide over the input data to model local information [12]. | |
| Recurrent neural networks | RNNs model sequential data well by maintaining a state |
| vector that encodes the information of previous time steps. | |
| This state is represented by the hidden units of the network | |
| and is updated at each time step [12]. | |
| Graph neural networks | GNNs model graphs consisting of entities and their connec- |
| tions representing e.g. molecules or nuclei of a tissue. Layers | |
| of GNNs can take on different forms such as convolutions and | |
| recurrence [14]. | |
| Autoencoders | AEs learn a lower dimensional encoding of the input data by |
| first compressing it and then reconstructing the original input | |
| data. Layers can be of different types such as fully connected | |
| or convolutional [15]. |
Although DL architectures for biomedical applications have been reviewed [16], the different DL-based fusion strategies for heterogeneous data have not. This is addressed in the present review, where we describe the state-of-the-art of DL-based fusion strategies in the biomedical domain. Additionally, we propose a taxonomy that not only outlines the standard categorization of early, intermediate and late fusion, but also describes subcategories useful for researchers and practitioners wishing to apply or enhance current approaches. Furthermore, the aim of this review is to provide guidance for under which conditions the different fusion strategies are most likely to perform well.
To do so, first, an overview of the main fusion strategies is given and a more detailed taxonomy is proposed. Next, the early, intermediate and late fusion categories and their subcategories are described in detail and extensively exemplified with applications to biomedical problems. Finally, we discuss challenges and opportunities of the described strategies in the biomedical domain and give suggestions for future research.
Fusion strategies: an overview
The ability of DNNs to learn hierarchical representations of the input data makes them especially suitable for applications to multimodal learning problems. The challenge of how to find marginal and joint representations of heterogeneous modalities in a way that enables their effective combination is central for multimodal fusion [11]. Therefore, we are taking a representation learning perspective when proposing a detailed taxonomy (see Table 2).
Table 2.
Taxonomy of data fusion methods based on multimodal DL. Early fusion strategies are subcategorized according to the applied architecture. Intermediate strategies are subcategorized according to their type of layers in the unimodal branches and whether a joint representation is learned. Late fusion strategies are subcategorized according to their type of aggregation
| Fusion strategy | Taxonomy Subcategory 1 | Taxonomy Subcategory 2 | Papers |
|---|---|---|---|
| Approach | Architecture | ||
| Early fusion | Direct modeling | Fully connected | [17–19] |
| Convolutional | [20–23] | ||
| Recurrent | [20, 24] | ||
| Autoencoder | Regular | [25–34] | |
| Denoising | [33, 35–37] | ||
| Stacked | [37–40] | ||
| Variational | [33, 40–42] | ||
| Branch | Representation | ||
| Intermediate fusion | Homogeneous design | Marginal | [43–49] |
| Joint | [21, 28, 38, 41, 50–63] | ||
| Heterogeneous designs | Marginal | [64–68] | |
| Joint | [69–81] | ||
| Aggregation | Model contribution | ||
| Late fusion | Averaging | Equal | [82–84] |
| Weighted | [85–87] | ||
| Meta-learning | Weighted | [83, 88] |
‘Marginal representation’ is defined as the result of a transformation of unimodal input data, ideally in such a way that latent useful factors are discovered. A ‘joint representation’ consists of features that represent latent factors that are based on multiple modalities, thus encoding information that might be complementary, redundant or cooperative. Baltrušaitis et al. [11] also described ‘coordinated representations’, where multimodal data are not projected into a common space. Rather marginal representations are learned that are constrained by representations of other modalities, for instance by a similarity constraint.
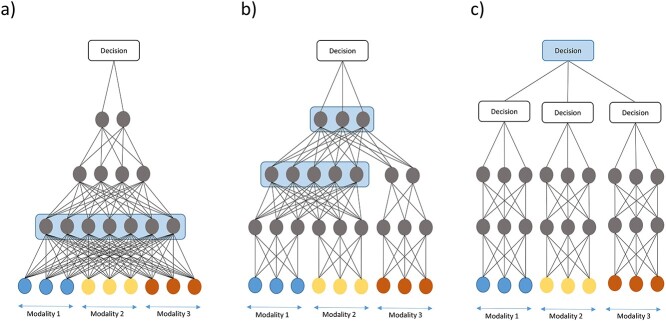
Largely, fusion strategies can be categorized according to the state of the input to the fusion layers into early, intermediate and late fusion [2] (blue layer in Figure 2). In ‘early fusion’, the original input data are concatenated, and the resulting vector is treated like unimodal input, meaning that the DL architecture does not differentiate from which modality features originates (see Figure 2a). Joint representations of the multimodal input are learned directly, and no marginal representations are explicitly learned. We further distinguish between early fusion based on ‘direct modeling’ of the input data through DNNs equivalent to their unimodal counterparts, and ‘autoencoder’ (AE) methods that first learn lower dimensional joint representations, which in turn are used for further modeling with supervised or unsupervised methods.
Figure 2.
DL-based fusion strategies. Layers marked in blue are shared between modalities and learn joint representations. (a) Early fusion strategies take as input a concatenated vector. No marginal representations are learned. (b) Intermediate fusion strategies first learn marginal representations and fuse these later inside the network. This can occur in one layer or gradually. (c) Late fusion strategies combine decisions by sub-models for each modality. Figure adapted from [2].
Early fusion has its advantages in its simplicity because no design choices about how to extract marginal representations have to be made. Despite its simplicity, early fusion strategies can learn cross-modal relationships from low-level features. However, this approach might not be able to identify relationships between the modalities when they only become apparent at higher levels of abstraction, because marginal representations are not explicitly learned. Additionally, early fusion strategies are sensitive to different sampling rates of modalities [2].
In ‘intermediate fusion’, marginal representations in the form of feature vectors are learned and fused instead of the original multimodal data (see Figure 2b). Such marginal representations can be learned through neural networks of the same type (fully connected, convolutional neural network, etc.), which we thus term ‘homogeneously’ designed networks. Alternatively, the marginal representations are learned through different types of networks, thus termed ‘heterogeneous’ design. As the naming suggests, the former is more common when the modalities are homogeneous, whereas the latter handles heterogeneity of multimodal data better.
We further distinguish between ‘marginal’ intermediate fusion, in which marginal representations are concatenated and directly input to a classifier, and ‘joint’ intermediate fusion in which more abstract joint features are learned. Marginal intermediate fusion is also sometimes termed feature late fusion or late fusion. We categorize these methods as intermediate fusion because the inputs to the fusion layers are features, whereas late fusion is defined as the fusion of decisions by sub-models. However, it is important to note that different terminology is used in the literature. In joint intermediate fusion, further multimodal disentangled factors can be found, which improve the performance of the final classifier. In this case, gradual fusion becomes an interesting possibility where highly correlated modalities are fused earlier and other modalities later in the architecture [2].
The advantages of intermediate fusion strategies lie within their flexibility of finding the right depth and sequence of fusing marginal representations. This arguably reflects more closely the true relationships between the modalities. Thus, more useful joint and marginal latent factors may be found. DL architectures are particularly suitable for intermediate fusion because they easily allow the fusion of marginal representations by connecting them to a shared layer and the correspondence of hierarchical representations to the natural world.
In ‘late fusion’, instead of combining the original data or learned features, decisions of separate unimodal sub-models are combined into a final decision [2, 11] (see Figure 2c). This allows learning good marginal representations since each model can be adapted to the specific modality. Additionally, the sub-models’ errors can be uncorrelated and thus have complementary effects [2]. However, multimodal effects on data or feature level cannot be learned by the final model. We further distinguish late fusion strategies according to how sub-models’ decisions are aggregated. These predictions can either be ‘averaged’ in an equal or weighted manner. Alternatively, ‘meta-learning’ is performed where an ML model receives the prediction probabilities as input and learns to make a final prediction.
Early fusion
Direct modeling
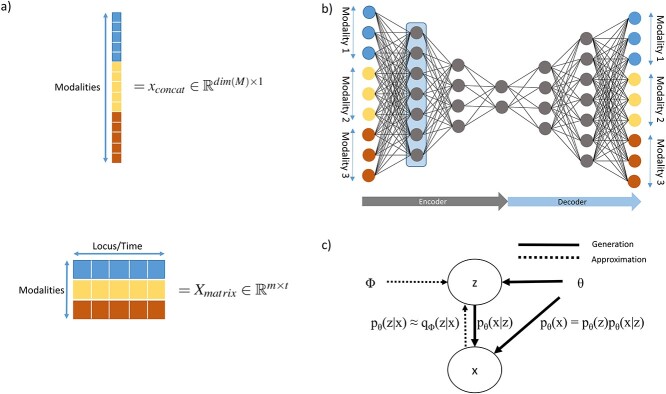
In part, the success of DL can be attributed to learning well from large data sets even when the number of features is high [89]. However, data sets within the biomedical domain often have small sample sizes, especially compared to their dimensionality. Nonetheless, one approach to early fusion is to concatenate the input features of different modalities, formally 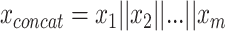 , where
, where  is the input vector of one modality (see Figure 3a). The resulting concatenated vector
is the input vector of one modality (see Figure 3a). The resulting concatenated vector 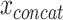 is input to the first layer of the DL architecture. The neural network does not distinguish between features from different modalities. In this approach, cross-modality and within-modality correlations are learned simultaneously at a low-level of abstraction.
is input to the first layer of the DL architecture. The neural network does not distinguish between features from different modalities. In this approach, cross-modality and within-modality correlations are learned simultaneously at a low-level of abstraction.
Figure 3.
Early fusion strategies. (a) Unimodal vector stacking alternatives. dim(M) is the combined dimensionality of the set of modalities M. m is the number of modalities and t the number of steps. (b) Architecture of a regular AE for early fusion with fusion layer marked in blue. (c) Visualization of the assumptions underlying variational AEs.
The vector 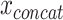 can be modeled with a fully connected input layer if the ordering of the features is irrelevant to the learning task, as done in [17, 18] and with constraints in [19]. If the ordering of the input features contains structural information, such as in the case of genomic data or time series of clinical data, recurrent layers [20, 24] or convolutional layers [20, 21, 23] can be applied to the concatenated vector. In such cases, the sequential information can also be stacked as a matrix for each sample rather than a concatenated one-dimensional vector. Each column in the matrix can, for instance, represent a location in the genome and rows represent the modalities (see Figure 3a). In the case of a convolutional layer, a kernel can then slide over the matrix to extract relevant features. In the case of a recurrent layer, each column can be seen as one-time step.
can be modeled with a fully connected input layer if the ordering of the features is irrelevant to the learning task, as done in [17, 18] and with constraints in [19]. If the ordering of the input features contains structural information, such as in the case of genomic data or time series of clinical data, recurrent layers [20, 24] or convolutional layers [20, 21, 23] can be applied to the concatenated vector. In such cases, the sequential information can also be stacked as a matrix for each sample rather than a concatenated one-dimensional vector. Each column in the matrix can, for instance, represent a location in the genome and rows represent the modalities (see Figure 3a). In the case of a convolutional layer, a kernel can then slide over the matrix to extract relevant features. In the case of a recurrent layer, each column can be seen as one-time step.
Latent representation with multimodal AEs
Autoencoders
Another commonly applied approach to learning from 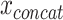 is to find a joint latent representation of lower dimension that contains the necessary information to reconstruct the original input. AEs are architectures that are able to learn such embeddings z from input x through an encoder function f(x) and a decoder function g(z) in an unsupervised manner (see Figure 3b) [15]. This is useful as some latent factors of input
is to find a joint latent representation of lower dimension that contains the necessary information to reconstruct the original input. AEs are architectures that are able to learn such embeddings z from input x through an encoder function f(x) and a decoder function g(z) in an unsupervised manner (see Figure 3b) [15]. This is useful as some latent factors of input 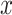 also explain the conditional probability p(y|x) [13]. The aim of the AE is to minimize the reconstruction loss function,
also explain the conditional probability p(y|x) [13]. The aim of the AE is to minimize the reconstruction loss function,
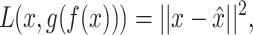 |
(1) |
where 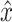 is the reconstructed input. By minimizing the reconstruction loss, the AE is aiming to approximate the original input features. If f(x) and g(z) are linear functions then z lies in the principle component subspace, making the AE similar to principal component analysis. However, if the encoder and decoder are nonlinear and nonlinearities exist in the data, they can map the input features onto a manifold in a lower dimensional space that is more informative than principle components. To extract this lower dimensional manifold, it is necessary to constrain the architecture by setting the number of neurons constituting z lower than the dimenisonality of x, also referred to undercompleteness of an AE [12]. Importantly, a single underlying factor in the embedding space might become visible in more than one modality, thus justifying the use of multimodal AEs taking
is the reconstructed input. By minimizing the reconstruction loss, the AE is aiming to approximate the original input features. If f(x) and g(z) are linear functions then z lies in the principle component subspace, making the AE similar to principal component analysis. However, if the encoder and decoder are nonlinear and nonlinearities exist in the data, they can map the input features onto a manifold in a lower dimensional space that is more informative than principle components. To extract this lower dimensional manifold, it is necessary to constrain the architecture by setting the number of neurons constituting z lower than the dimenisonality of x, also referred to undercompleteness of an AE [12]. Importantly, a single underlying factor in the embedding space might become visible in more than one modality, thus justifying the use of multimodal AEs taking 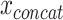 as input.
as input.
Although AEs are not exclusive to early fusion strategies, they have often been used in the biomedical literature to learn joint representations. Once learned, the joint representation z can be used for further modeling. For instance, in cancer patient survival subtyping, often the joint representation learning through an AE is followed by steps of feature selection with univariate Cox proportional hazard [90] modeling. The selected latent features are then used to infer labels for each patient corresponding to their risk subtype through unsupervised methods. A supervised model is finally trained on these labels to later predict data of unseen patients. Particularly in cancer patient survival subtyping with multi-omics modalities, this sequence of steps has become popular [25–31, 34].
For the same clinical task, a similar workflow has been adapted by researchers, but applying denoising AEs (DAEs) [91] instead [35, 36]. By adding noise to the input 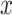 , but not to
, but not to 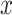 in the reconstruction loss (Equation 1), the DAE has to learn a reconstruction and also remove noise to approximate the uncorrupted vector x. This enables AEs that are overcomplete and have encoders and decoders with a large number of parameters. Overcompleteness might be desirable for the AE to have properties such as robustness to noise.
in the reconstruction loss (Equation 1), the DAE has to learn a reconstruction and also remove noise to approximate the uncorrupted vector x. This enables AEs that are overcomplete and have encoders and decoders with a large number of parameters. Overcompleteness might be desirable for the AE to have properties such as robustness to noise.
Similarly, different forms of AEs have been used to fuse biomedical data early. Islam et al. [38] and Rakshit et al. [39] used stacked AEs (SAEs) to fuse multi-omics data for classifying molecular subtypes of breast cancer. In an SAE, several AEs are stacked and sequentially trained for reconstructing the output of the preceding encoder. This architecture can then be fine-tuned for the classification task. In the case of [38], the proposed method performed similar to intermediate fusion methods. Miotto et al. [37] applied a stacked DAE to multimodal electronic health records (EHR) data, effectively representing patients in a lower dimensional space and thereby enabling a multitude of clinical predictive modeling such as the onset of disease.
Early AE fusion can also be used to initialize the first layer of another neural network as demonstrated by Jaroszewicz et al. [32] on fine-mapping of chromatin peaks. Initialization with a useful joint latent representation of the data can enhance the training procedure significantly. The joint representation layer can be further tuned, enabling the learning of more task-relevant joint representations.
Variational AEs
As mentioned previously, it is assumed that the high-dimensional data x lies on a lower-dimensional manifold. This assumption can be expressed as a directed probabilistic model where data points x are generated from a random process of the lower-dimensional variable z (see Figure 3c). Assume that z is generated by the Gaussian distribution 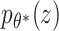 , where
, where 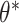 are the true generating parameters. Thus,
are the true generating parameters. Thus, 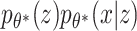 is the likelihood of seeing data x. Although z is a more direct representation of the phenomena of interest, it is useful to represent the data directly in the embedding space. However, z and
is the likelihood of seeing data x. Although z is a more direct representation of the phenomena of interest, it is useful to represent the data directly in the embedding space. However, z and 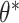 are not directly observable and estimating the true posterior
are not directly observable and estimating the true posterior 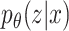 in most cases is intractable.
in most cases is intractable.
Variational AEs (VAEs) [92] are able to approximate the true posterior by learning a so-called recognition model 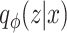 from which in turn
from which in turn 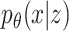 can be learned. The encoder learns a probability distribution over
can be learned. The encoder learns a probability distribution over 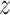 , for example assuming it to be an isotropic Gaussian distribution, with parameters
, for example assuming it to be an isotropic Gaussian distribution, with parameters 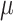 and
and 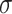 . In this example, the decoder samples
. In this example, the decoder samples 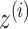 from
from 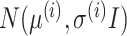 , where
, where 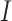 is the identity matrix, and learns
is the identity matrix, and learns 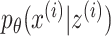 to reconstruct input x(i). An expected advantage of this method is that, due to its generative nature, the latent space
to reconstruct input x(i). An expected advantage of this method is that, due to its generative nature, the latent space 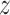 is more smooth resulting in better generalization to unseen data. Additionally, the introduction of a prior believe about the distribution of the latent space enables more flexibility for modeling the input data. These advantages are also useful when learning joint latent representations from multimodal data, as the same process described can be assumed in the multimodal case.
is more smooth resulting in better generalization to unseen data. Additionally, the introduction of a prior believe about the distribution of the latent space enables more flexibility for modeling the input data. These advantages are also useful when learning joint latent representations from multimodal data, as the same process described can be assumed in the multimodal case.
Simidjievski et al. [41] systematically investigated VAEs for the fusion of breast cancer data. While comparing different VAE fusion strategies, the early fusion VAE performed comparable to more complex VAE architectures. Furthermore, the authors found that the choice of regularization method and its weighting had strong influence on the model’s performance. Ronen et al. [40] performed survival subtyping of colorectal cancer and matched cell lines to subgroups by applying a stacked VAE based on multi-omics data. Albaradei et al. [42] replaced the fully connected layers of the VAE with convolutional layers to learn embeddings that were input to a classifier for pan-cancer metastasis prediction. Thereby, they showed that it is possible to take advantage of local patterns in multi-omics data.
Discussion of early fusion strategies
Most of early fusion models do not differ strongly from their unimodal versions. They are relatively simple to implement since no modeling of individual modalities has to be done, which might explain their popularity in the biomedical literature. The applications of early nonlinear fusion methods reviewed here have shown that these methods can outperform shallow methods on prediction tasks (e.g. [35, 36]). This demonstrates that DL methods are viable alternatives to traditional methods even when sample sizes are comparatively low, because there were as low as 96 patients in the applications reviewed above [28]. Additionally, early fusion strategies tend to outperform unimodal approaches (e.g. [39]). However, different modalities can add information to different degrees (e.g. [36, 44]).
Despite their prominent use, early fusion strategies have drawbacks. By modeling a joint representation directly, finding useful marginal representations of each modality is hindered. Relevant features of a modality might only become apparent at higher levels of abstraction. Discovering such features in a joint representation can be more difficult to achieve. Moreover, modalities can stand in different relationships to one another. Thus, fusing modalities gradually rather than all in one layer can be beneficial [2]. Finally, early fusion tends to be applied only when modalities are rather homogeneous, such as different ‘omics’ modalities. If modalities show vastly different distributions, such as image and molecular modalities, early fusion strategies are less likely to perform well.
The frequent use of AE-based fusion for biomedical applications stands out among early fusion strategies (see Table 2). The dimensionality-reducing capacity of these approaches might explain their usage primarily for high-dimensional multi-omics data. A limitation of these approaches is the task-unspecific learning. Although learning the underlying factors of 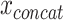 can be useful for predicting response
can be useful for predicting response 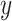 [13], AE methods learn to reconstruct the input data and not necessarily to extract relevant factors for the target. Thus, the learned joint latent representation is not guaranteed to be optimal for the final aim of the application and further target-specific learning might be beneficial if labels exist.
[13], AE methods learn to reconstruct the input data and not necessarily to extract relevant factors for the target. Thus, the learned joint latent representation is not guaranteed to be optimal for the final aim of the application and further target-specific learning might be beneficial if labels exist.
Franco et al. [33] compared several AE types for early fusion on cancer survival subtyping with multi-omics data. Though regular AE and VAE architectures seemed to outperform other AEs, the strong variation between performance on different data sets indicate the importance of choice of architecture. Despite the aforementioned drawbacks, some reviewed papers have shown that early fusion AEs can perform on par with intermediate strategies [38, 41], though other structured investigations inside [28] and outside [93] the biomedical domain have shown superiority of intermediate fusion over early fusion strategies.
Intermediate fusion
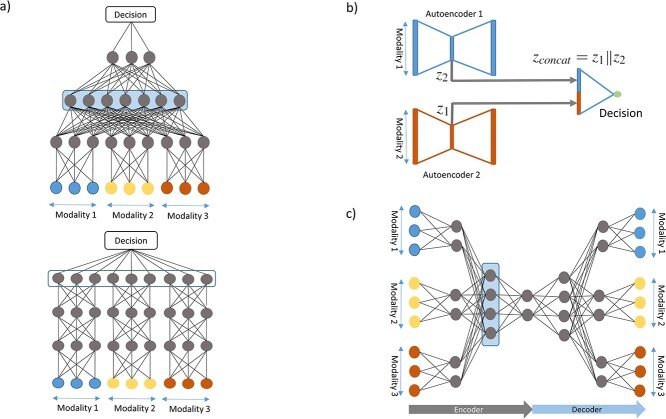
Although early fusion is ignorant toward what modality a feature originates from, intermediate fusion strategies take advantage of this prior knowledge. Marginal representations of each modality are learned to discover within-modality correlations before using these to either learn joint representations or make prediction directly (see Figure 4a). In the following, we will discuss homo- and heterogeneous intermediate fusion and their subcategories.
Figure 4.
Intermediate fusion strategies. (a) Joint intermediate fusion with shared layer in blue. Subsequent to marginal representations, joint representations are learned (top). In marginal intermediate fusion, marginal representations are directly input to the decision function (bottom). (b) Marginal AE where marginal representations are concatenated and input into a decision function. (c) Joint AE in which a joint representation is learned in the shared layer marked in blue.
Homogeneous network design
Marginal homogeneous fusion
Marginal features learned by branches with the same type of layers can be used directly as input to a decision function by concatenating these marginal representations. Although this approach is able to effectively capture within-modality correlations, cross-modality relationships are modeled less effectively, thus reducing the benefits of data fusion. However, the complexity of the model is reduced which lowers the risk of overfitting. Thus, choosing to learn only marginal representations might be beneficial if the modalities are affecting the outcome largely independently. This emphasizes the complementary and redundant nature of the multimodal data rather than the cooperative aspects.
To predict cancer patient survival, Huang et al. [43] fused mRNA and miRNA eigengene matrices through two locally fully connected branches. The marginal representations and additional clinical and demographic data were then input to a Cox proportional hazard regression model. No joint learning was performed since the authors explicitly assumed that the different modalities affect the hazard function independently.
To fuse modalities with sequential data, recurrent layers in each branch offer good performance, as temporal dependencies can be modeled effectively and input sequences can be of variable length, which is often the case in biomedical data. Recurrent layers are able to output marginal representations encoding the input sequences. Lee et al. [44] applied gated recurrent unit (GRU) networks to multimodal data of Alzheimer’s disease (AD) patients. Each branch consisting of GRU layers was first trained separately on a classification task. In a second step, marginal representations from each branch were concatenated and a logistic regression used to make a final decision.
Besides their popularity as early fusion strategies, AEs also find applications in intermediate fusion. Separate AEs can be applied unimodally, resulting in a set of encodings S = {z1, z2,..., zm}, where m is the number of modalities and zi is the latent representation of the ith modality encoded by the corresponding AE. The encodings in S can be concatenated into vector 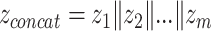 (see Figure 4b) and used as input to further modeling, such as clustering followed by a classifier for cancer subtyping [45–47], or directly as input to a classifier for multi-class classification or survival analysis [48]. In principle,
(see Figure 4b) and used as input to further modeling, such as clustering followed by a classifier for cancer subtyping [45–47], or directly as input to a classifier for multi-class classification or survival analysis [48]. In principle, 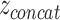 can be input to a DNN, which learns a joint representation, making it a joint fusion method.
can be input to a DNN, which learns a joint representation, making it a joint fusion method.
Joint homogeneous fusion
After concatenating the marginal representations, joint ones can be learned through multiple layers subsequent to the unimodal branches. This joint representation can then be used for making decisions and can model cross-modality interactions (see Figure 4a).
Sharifi-Noghabi et al. [50] applied separate fully connected branches to multi-omics data, followed by a multi-layer classification network for drug response prediction. This classifier thus learned a joint representation of the input modalities. Lin et al. [51] adopted this method for predicting breast cancer subtypes.
To preserve spatial information, convolutional layers can be applied in each branch if such dependencies within the modalities are to be expected. Similar to unimodal models, additional layers such as max pooling can be used within each branch to reduce the dimensionality and to avoid overfitting. Crucially, the feature maps of each branch can be connected to separate dense layers, which then are concatenated. From this vector, a joint representation can be learned in subsequent layers. Such architectures can be applied to diverse modalities such as chemical structures of drugs and genomic data [21] or to multi-omics modalities [38].
Alternatively, the unimodal branches can be made up of deep believe networks (DBNs). In multimodal DBNs, each pair of adjacent layers are restricted bolzmann machines (RBMs), which are trained to model the joint distribution of the two layers p(xl, xl+1) in an unsupervised manner. Similar to an SAE, the embedded, or hidden representation, becomes the visible input to the subsequent RBM during layer-wise training. Thus, a DBN can be considered a stacked RBM. Hierarchical representations of the input data are learned that can be used for clustering of the data. Alternatively, the representations can serve as a useful and computationally efficient initialization of a DNN, which is fine-tuned with more expensive supervised algorithms such as back propagation to learn p(y|x) [94].
DBNs have been extensively used to fuse biomedical modalities for drug repurposing [52], clustering of cancer patients [53] and predicting disease-gene pairs [54]. Suk et al. [55] applied a multimodal deep boltzmann machine (DBM) [95] to predict AD from magnetic resonance images (MRI) and positron emission tomography (PET) scans. Similarly to DBNs, DBMs consist of stacked RBMs, but in addition to a bottom-up learning step, they add a top-down feedback that enables the learning of better representations.
To take advantage of modality-specific and cross-modality correlations, marginal and joint representations can be learned in a single AE (see Figure 4c). Initially, the AE consists of branches connected to separate modalities. Further into the encoder, the marginal representations learned in these branches are fused in the embedding layer by connecting each branch to all neurons of z, as done in [28]. Alternatively, they can be fused in a hidden layer enabling potential further learning before the final encoding [57–61]. The embedding z can then be used for different prediction tasks.
Such joint representations can also be learned with VAEs. Simidjievski et al. [41] proposed and compared different versions of joint AE fusion using VAEs for fusing breast cancer multi-omics and clinical data. Hira et al. [56] also found joint multimodal VAEs useful for fusing multi-omics data and support the findings of [41] that Maximum Mean Discrepancy as a regularization term outperforms the Kullback–Leibler divergence.
Related to VAEs, Lee and van der Schaar [63] fused multi-omics data by applying the information bottleneck principle. Although VAEs effectively find latent representations of the input, they might not be optimal for the predictive task. The variational information bottleneck approach [96] finds a joint representation that preserves the information from input x relevant for predicting the target y while compressing x maximally. The objective function encourages the algorithm to find useful marginal and joint representations. Similarly, Zhang et al. [62] proposed an end-to-end VAE architecture that learns a task-specific joint representation of DNA methylation and gene expression data for pan-cancer classification. This architecture consistently outperformed a combination of VAE and support vector machine.
Heterogeneous network design
Marginal heterogeneous fusion
The main advantage of being able to model modalities with different branches is the ability to transform heterogeneous data into vectors that better represent higher level features. These new feature vectors can therefore ‘level the playing field’ with regards to data type, imbalance in dimensionality and scale between the different modalities, enabling comparison. As with homogeneous intermediate fusion strategies, such marginal representations can simply be concatenated and input to a classifier.
Xu et al. [68] concatenated lab tests, clinical data and marginal representations of computed tomography (CT) scans to predict COVID-19 infections. Zhang et al. [64] proposed a CNN- and a RNN-based fusion model that take temporal signals, sequential clinical notes as well as static demographic and admission data as input to the different branches. It embeds the former two modalities into latent feature spaces and concatenates these with the encoded static information. Thereby, a patient representation is created that is input to a classifier. Feature selection can also be used on the concatenated marginal representations, choosing latent features that most strongly influence the target variable, as done in [65] to predict prognosis of clear cell renal cell carcinoma patients. Hao et al. [67] motivated the lack of additional hidden layers with the low dimensionality of the clinical data, which is fused with high dimensional genomic data. However, the authors hypothesized that additional joint hidden layers might be necessary if more clinical features were available.
Generally, in marginal heterogeneous fusion, often for a subset of the modalities, marginal representations are found and then concatenated with the original data of the other modalities. In these cases, the nonencoded modalities are of low dimension and do not suffer from the curse of dimensionality. Thus, they might not require to be represented through disentangled latent factors.
Joint heterogeneous fusion
Often, it is reasonable to assume that the different modalities do not independently affect the target variable, but rather that cross-modality interactions exist that are informative. In joint heterogeneous intermediate fusion, such relationships are modeled by learning interactions of features from the marginal representations. These interactions can be learned by first concatenating the marginal representations and feeding this vector into fully connected layers before a task-specific output layer. For instance, MRI and clinical data can be fused for AD prediction [72] or MRI, clinical and genomic modalities can be fused for AD stage detection [69]. Also, latent representations of multiple imaging modalities and clinical data can be fused for risk assessment of liver transplantation for hepatocellular cancer [71].
Based on this general approach to joint heterogeneous intermediate fusion, other researchers have added architectural improvements to tackle specific challenges. In practice, it is often a problem that not every modality is collected for each patient. If entire modalities are missing, imputation can become challenging and training only on complete samples restricts the training set size. Thung et al. [70] proposed a multi-task network that can effectively learn from multimodal data with missing modalities by having unimodal input branches and task-specific output branches. Each task reflects the availability of a modality or combination of modalities. Thereby, only weights of the task-specific branches and the corresponding unimodal branches are updated during training. Robustness to missing modalities can also be achieved in homogeneous intermediate fusion, as shown by [63].
To tackle the challenge of making DL architectures more interpretable in a multimodal context, different methods have been proposed. Chen et al. [79] enabled modality-specific interpretability by applying Grad-CAM [97] for WSI and integrated gradient [98] for cell graph and genomic modalities using convolutional, graph convolutional [14] and fully connected branches. In another publication, Chen et al. [80] applied attention- and gradient-based interpretability to WSI and molecular modalities. Additionally, contributions to the prediction performance are attributed to the different modalities. Kang et al. [73] used an attention mechanism for multi-omics data [99] for interpreting predictions of gene expression. Generally, these gradient- and attention-based methods show that heterogeneous intermediate fusion does not impede models that allow sound biological interpretation.
A strength of intermediate fusion strategies is that an imbalance in dimensionality between modalities can be mitigated by forcing the marginal representations to be of similar size. However, if the imbalance is very large, reducing the dimensionality of the larger modality too much might result in significant loss of information. Yan et al. [76] fused high-dimensional WSIs and 29 clinical variables. In order to get a higher predictive performance, the clinical variables were duplicated 20-fold. However, Mobadersanya et al. [77] showed that imbalance does not necessarily lead to poor performance if the input features of the lower dimensional modality are chosen with prior knowledge. The authors fused histological features learned from WSIs and only two genomic features, namely isocitrate dehydrogenase mutation status and 1p/19q co-deletion, to predict survival of glioma patients and showed a statistically significant increase in performance. Similarly, though with a ‘marginal’ heterogeneous fusion strategy, Lu et al. [66] showed that concatenating biological sex of the patient as a covariate with features learned from WSIs improved the performance in predicting primary sites of cancers of unknown primary. This shows that imbalance can be effectively mitigated by carefully choosing the variables of the smaller modality.
Unsupervised learning of cross-modality interactions can help to overcome the limitations of small sample sizes. Cheerla and Gevaert [78] proposed an architecture for unsupervised fusion combining genomic, clinical and WSIs for cancer prognosis prediction. The loss function was formulated such that it encouraged marginal representations of different modalities of the same patient to be similar, and those from different patients dissimilar. Thereby, coordinated representations [11] of each modality could be learned in an unsupervised way, which resulted in encodings of patterns between modalities. This loss is combined with a Cox loss function that enables target-specific feature learning. Subsequently, a joint representation was learned from the coordinated representations.
Besides learning the joint representation from a concatenated vector of marginal representations, the feature vectors from each branch can alternatively be element-wise aggregated. This more explicitly models feature interactions. For instance, the feature representation vectors can be stacked as columns in a matrix and the row-wise maximum, sum or product can be taken, resulting in a joint vector of the same length as the marginal representations of each branch. Vale-Silva et al. [74] compared these methods, although they did not find large differences in performance for predicting long-term cancer survival. Chen et al. [79] predicted patient survival and several patient classifications by modeling WSIs, cellular interactions and genomic data. The marginal representations were fused through taking the Kronecker product. The resulting three-dimensional tensor explicitly encoded the uni-, bi- and trimodal interactions of the feature vectors. The tensor was further input to a fully connected network, which was connected to target-specific decision functions. The authors also successfully extended this fusion strategy to pan-cancer survival prediction [80]. In addition to element-wise aggregation, attention-based fusion methods can be applied in order to weight different latent features by their importance [74, 79, 81].
Discussion on intermediate fusion
DL approaches are particularly well suited for intermediate fusion. The hierarchical marginal and joint representations enable the fusion at the appropriate level of abstraction. Thereby, it is possible to capture the underlying biological relationships between the modalities in the fusion strategy. Moreover, learning joint representations from marginal ones seems to be the preferred approach as indicated by the more frequent application of joint fusion strategies (see Table 2). This contradicts the notion that modalities affect the target independently, and supports the idea of complementary and cooperative information in multimodal data.
Intermediate fusion approaches also provide solutions to other prevalent challenges of DL in biomedical field. For example, by having separate branches, interpretability-enhancing methods can be chosen according to each modality. Additionally, as described, handling feature imbalance, missing modalities and coordinated representation learning are advantages of intermediate fusion approaches. Particularly of interest for biomedical applications is the ability of intermediate fusion to close the heterogeneity gap between modalities by applying different networks and network types to each modality, enabling an effective fusion of imaging, molecular and clinical modalities. This brings the DL approach closer to clinical diagnosis and prognosis.
Although intermediate fusion strategies seem to have many theoretical advantages over other approaches, testing whether these materialize on a given problem is seldom investigated or reported. As mentioned above, early fusion can, at least on some tasks, perform similar to intermediate fusion [38, 41]. Yu et al. [28], however, showed that intermediate AE clearly outperformed their early fusion counterpart. The frequency of application seems to be balanced between early and intermediate fusion although the choice might not only be influenced by the strategies’ performance but also by the ease of use.
Late fusion
In late fusion, separate models are trained for each modality. These sub-models can be optimized so that they learn the 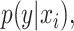 where
where 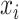 is the data from the ith modality. Because the input from each modality provides different information and the sub-models can be constructed differently, the errors made by each model are not perfectly correlated [2]. Different strategies for aggregating the predicted probabilities, and thereby taking advantage of the complementary information from each modality, are especially promising for the fusion of heterogeneous modalities.
is the data from the ith modality. Because the input from each modality provides different information and the sub-models can be constructed differently, the errors made by each model are not perfectly correlated [2]. Different strategies for aggregating the predicted probabilities, and thereby taking advantage of the complementary information from each modality, are especially promising for the fusion of heterogeneous modalities.
The simplest approach to aggregating decisions from separate sub-models is to take the average of the individual outputs. For a classification task, this could be averaging the probabilities from softmax functions for each class. This approach assumes the same contribution of each sub-model since no weighting of the outputs is performed. Deng et al. [82] fused different types of drug features by training sub-models and subsequently aggregating their predictions by averaging the probabilities of the 65 classes. Huang et al. [83] found that averaging-based late fusion with regularized DNNs as sub-models outperforms early, intermediate and other late fusion strategies on the prediction of pulmonary embolism detection utilizing CT scans and EHR data. Soto et al. [84] showed that late fusion with averaging results can outperform other late and intermediate fusion strategies.
To avoid the assumption that all sub-models hold equally relevant information to predict the target, other aggregation methods can be employed. Questioning this assumption is relevant as many methods have shown unequal contribution of different modalities to the predictive performance (see for example [36, 42]). Wang et al. [85] weighted the predicted probability of each sub-model by its uncertainty. Thereby models that were more prone to errors contributed less to the final decision. This method allows the reduction of uncertainty in the final prediction. Liu et al. [86] and Sun et al. [87] learned the weights of the predictions by their sub-models as hyperparameters on a validation set.
Alternatively, meta-learning approaches can learn complex relationships between the predictions of different sub-models. In such approaches, the output of the sub-models is input to another classifier that learns the interactions between predictions in order to make a better final prediction. Although correlations between features of different modalities can still not be learned, cross-modality (non)linear interactions can be effectively modeled. Huang et al. [83] applied an FCNN for fusing sub-model predictions, while Reda et al. [88] used a sparse SAE connected to a classifier for the final prediction.
Discussion of late fusion
Compared with early fusion, late fusion can model heterogeneous modalities and even combine DL and shallow ML methods, as done by Reda et al. [88]. Similar to intermediate fusion, imbalance in the number of input dimensions does not affect the final prediction such that high dimensional modalities would ‘drown out’ lower dimensional ones. Late fusion strategies obviously have the disadvantage of not being able to learn interactions between features of different modalities. These strategies can be advantageous when modalities are less correlated and thus this shortcoming does not come into effect.
Discussion and conclusion
In conclusion, reviewing the current literature on DL-based fusion strategies shows that multimodal approaches frequently outperform unimodal ones. It is also commonly observed that multimodal DL approaches significantly outperform shallow ML methods. While the literature is most likely skewed toward reporting positive results, it has become clear that the expected gains through DL-based fusion occur regularly.
We have outlined under which conditions early, intermediate and late fusion, and their subcategories, are likely to work best, respectively. Mainly, the choice depends on the modalities to be analyzed and willingness of the researcher to make more or less architectural choices. However, the performance of different strategies can still be very problem- and data-specific. More theoretical knowledge is needed to further specify under what conditions the different strategies excel. Thus, it is recommended to experimentally investigate and compare different fusion strategies, and evaluate their respective advantages.
Multimodal DL approaches face the same challenges that DL in the biomedical field face generally, including data volume, quality, interpretability and temporality as outlined by e.g. Miotto et al. [100]. However, multimodal-specific challenges such as missing of entire modalities must be addressed by fusion strategies. Different approaches have been proposed, such as multi-task learning [70], generative models [63] and multimodal dropout [78, 101]. To become more clinically relevant, methods need to be robust against different patterns of missing modalities and incorporate countermeasures into the learning. Additionally, as more heterogeneous data becomes available, fusion strategies need to accommodate these combinations of modalities. As mentioned above, biological processes are observable on various levels and multimodal data present the opportunity to train holistic models that can learn the complex regulatory dynamics behind health and disease. Heterogeneous intermediate fusion and late fusion are particularly suitable for this challenge.
Although these challenges are being addressed, we would like to outline some areas that are underexplored. Ramachandram and Taylor [2] outlined that a strength of DL-based fusion is the ability to gradually fuse modalities, depending on their similarity. We have not seen this being explored sufficiently in the current biomedical literature. Moreover, gradual fusion could be guided by prior biological knowledge, such as the known relationships between mRNA, miRNA and proteins. We have seen applications where prior biological knowledge has informed architectural decisions, such as separate branches according to chromosomal position [62], regularization terms in the training loss [49] or to encode pathways into the architecture [19, 67]. However, informing the gradual fusion of modalities is, to our knowledge, not comprehensively investigated.
What is further underexplored for biomedical data fusion is how to automatically find the optimal fusion strategy. Because of the choices involved in designing fusion architectures, finding the best way how to fuse different modalities becomes non-trivial. As can be seen from the comparisons between methods reviewed here, this choice can be highly problem-specific. Finding optimal fusion strategies for DL architectures is an active field of research [2] and significant improvements in performance are to be expected. Xu et al. [102] have applied search algorithms to find the optimal fusion strategy, as well as modality-specific neural architecture searches for fusing EHR data. Beyond this proposed method, we have found that such strategies are not extensively researched or applied in the biomedical field and could lead to interesting future research.
Overfitting to the training data, and therefore poor generalizability, is a major challenge for multimodal models [103]. Particularly for multimodal biomedical data sets, sample sizes are often small since generating them is costly and access to biological material is generally limited. Often the number of input variable is very large, particularly if multi-omics data is included. On the other hand, the architectures can have many parameters because several modalities have to be modeled. This can easily lead to learning of uninformative patterns in the training data.
Transfer learning (TL) is the transfer of knowledge from one task to a related one, often in form of pre-training the weights of the network. With TL the required sample size can be significantly reduced [104]. TL for multimodal biomedical data sets should therefore be explored further. Although we see some TL integrated in fusion strategies (e.g. [50]), we believe that leveraging the vast collection of public unimodal data sets for multimodal architectures with TL is a promising future path.
The importance of multimodal data fusion in the biomedical domain becomes increasingly apparent as more clinical and experimental data becomes available. DL fusion strategies constitute a promising choice for researchers and practitioners to build the best-performing models from their data. We hope this review will inspire further applications and research into these methods.
Key Points
Complex biological systems can be effectively modeled with nonlinear functions within and across modalities.
Multimodal DL provides effective and flexible architectures to fuse homo- and heterogeneous biomedical data at different levels of abstraction.
Deep fusion strategies are frequently used and regularly outperform shallow and unimodal methods.
The potential of multimodal DL in the biomedical field still has not been fully utilized because areas such as TL and gradual fusion have not been sufficiently investigated.
Funding
This work was supported by the University of Skövde, Sweden under grants from the Knowledge Foundation (20170302, 20200014).
Sören Richard Stahlschmidt is a PhD candidate at the Systems Biology Research Center, University of Skövde, Skövde, Sweden. His research interests include machine learning, multimodal deep learning, data fusion and biomarker discovery.
Benjamin Ulfenborg is Associate Senior Lecturer at the Systems Biology Research Center, University of Skövde, Skövde, Sweden. His research interests are data fusion, data mining, machine learning and statistical modeling.
Jane Synnergren is Professor at the Systems Biology Research Center, University of Skövde, Skövde, Sweden. Her research interest encompasses bioinformatics, data fusion, machine learning, deep learning and biomedical data analysis.
Footnotes
In the biomedical literature data fusion and data integration are often used interchangeably. Thus, the term data fusion is adopted in this review.
Contributor Information
Sören Richard Stahlschmidt, Systems Biology Research Center, University of Skövde, Sweden.
Benjamin Ulfenborg, Systems Biology Research Center, University of Skövde, Sweden.
Jane Synnergren, Systems Biology Research Center, University of Skövde, Sweden.
References
- 1. Maayan A. Complex systems biology. J R Soc Interface 2017;14(134):20170391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ramachandram D, Taylor GW. Deep multimodal learning: a survey on recent advances and trends. IEEE Signal Process Mag 2017;34(6):96–108. [Google Scholar]
- 3. Hall DL, Llinas J. An introduction to multisensor data fusion. Proc IEEE 1997;85(1):6–23. [Google Scholar]
- 4. Durrant-Whyte HF. Sensor models and multisensor integration. Int J Robot Res 1988;7:97–113. [Google Scholar]
- 5. Castanedo F. A review of data fusion techniques. Sci World J 2013;2013:704504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Li Y, Wu FX, Ngom A. A review on machine learning principles for multi-view biological data integration. Brief Bioinform 2018;19(2):325–40. [DOI] [PubMed] [Google Scholar]
- 7. Manzoni C, Kia DA, Vandrovcova J, et al. Genome, transcriptome and proteome: the rise of omics data and their integration in biomedical sciences. Brief Bioinform 2018;19(2):286–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Springer Nature. Milestones in Genomic Sequencing. https://www.nature.com/immersive/d42859-020-00099-0/index.html (1 December 2021, date last accessed).
- 9. Ståhl PL, Salmén F, Vickovic S, et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science 2016;353(6294):78–82. [DOI] [PubMed] [Google Scholar]
- 10. Lee J, Hyeon DY, Hwang D. Single-cell multiomics: technologies and data analysis methods. Exp Mol Med 2020;52:1428–42. 10.1038/s12276-020-0420-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Baltrusaitis T, Ahuja C, Morency LP. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans Pattern Anal Mach Intell 2019;41(2):423–43. [DOI] [PubMed] [Google Scholar]
- 12. Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge, MA: MIT Press, 2016, http://www.deeplearningbook.org. [Google Scholar]
- 13. Bengio Y, Courville A, Vincent P. Representation learning: a review and new perspectives. IEEE Trans Pattern Anal Mach Intell 2013;35(8):1798–828. [DOI] [PubMed] [Google Scholar]
- 14. Wu Z, Pan S, Chen F, et al. A comprehensive survey on graph. Neural Netw 2019; ArXiv:1901.00596v4. [DOI] [PubMed] [Google Scholar]
- 15. Ballard DH. Modular learning in neural networks. In: Proceedings of the Sixth National Conference on Artificial Intelligence, Volume 1. AAAI’87. AAAI Press; 1987. p. 279–84. [Google Scholar]
- 16. Ching T, Himmelstein DS, Beaulieu-Jones BK, et al. Opportunities and obstacles for deep learning in biology and medicine. J R Soc Interface 2018;15(141):20170387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Park C, Ha J, Park S. Prediction of Alzheimer’s disease based on deep neural network by integrating gene expression and DNA methylation dataset. Expert Syst Appl 2020;140:112873. [Google Scholar]
- 18. Xie G, Dong C, Kong Y, et al. Group lasso regularized deep learning for cancer prognosis from multi-omics and clinical features. Gen 2019;10(3):240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zhao L, Dong Q, Luo C, et al. DeepOmix: a scalable and interpretable multi-omics deep learning framework and application in cancer survival analysis. Comput Struct Biotechnol J 2021;19:2719–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Suresh H, Hunt N, Johnson A, et al. Clinical intervention prediction and understanding using deep. Networks 2017. ArXiv:1705.08498. http://arxiv.org/abs/1705.08498 (1 December 2021, date last accessed). [Google Scholar]
- 21. Chang Y, Park H, Yang HJ, et al. Cancer Drug Response Profile scan (CDRscan): a deep learning model that predicts drug effectiveness from cancer genomic signature. Sci Rep 2018;8(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Peng C, Zheng Y, Huang DS. Capsule network based modeling of multi-omics data for discovery of breast cancer-related genes. IEEE/ACM Trans Comput Biol Bioinform 2020;17(5):1605–12. [DOI] [PubMed] [Google Scholar]
- 23. Fu Y, Xu J, Tang Z, et al. A gene prioritization method based on a swine multi-omics knowledgebase and a deep learning model. Communicat Biology 2020;3:502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Bichindaritz I, Liu G, Bartlett C. Integrative survival analysis of breast cancer with gene expression and DNA methylation data. Bioinformatics 2021;37(17):2601–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Chaudhary K, Poirion OB, Lu L, et al. Deep learning-based multi-omics integration robustly predicts survival in liver cancer. Clin Cancer Res 2018;24(6):1248–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Lv J, Wang J, Shang X, et al. Survival prediction in patients with colon adenocarcinoma via multiomics data integration using a deep learning algorithm. Biosci Rep 2020;40(12):BSR20201482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Zhang L, Lv C, Jin Y, et al. Deep learning-based multi-omics data integration reveals two prognostic subtypes in high-risk neuroblastoma. Front Genet 2018;9:477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Yu J, Wu X, Lv M, et al. A model for predicting prognosis in patients with esophageal squamous cell carcinoma based on joint representation learning. Oncol Lett 2020;20(6):387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Asada K, Kobayashi K, Joutard S, et al. Uncovering prognosis-related genes and pathways by multi-omics analysis in lung cancer. Biomol Ther 2020;10(4):524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Zhang X, Wang J, Lu J, et al. Robust prognostic subtyping of muscle-invasive bladder cancer revealed by deep learning-based multi-omics data integration. Front Oncol 2021;11:689626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Lee TY, Huang KY, Chuang CH, et al. Incorporating deep learning and multi-omics autoencoding for analysis of lung adenocarcinoma prognostication. Comput Biol Chem 2020;87:107277. [DOI] [PubMed] [Google Scholar]
- 32. Jaroszewicz A, Ernst J. An integrative approach for fine-mapping chromatin interactions. Bioinformatics 2020;36(6):1704–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Franco EF, Rana P, Cruz A, et al. Performance comparison of deep learning autoencoders for cancer subtype detection using multi-omics data. Cancer 2021;13:2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Zhao Z, Li Y, Wu Y, et al. Deep learning-based model for predicting progression in patients with head and neck squamous cell carcinoma. Cancer Biomark 2020;27(1):19–28. [DOI] [PubMed] [Google Scholar]
- 35. Guo LY, Wu AH, Wang YX, et al. Deep learning-based ovarian cancer subtypes identification using multi-omics data. BioData Mining 2020;13:10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Chai H, Zhou X, Zhang Z, et al. Integrating multi-omics data through deep learning for accurate cancer prognosis prediction. Comput Biol Med 2021;134:104481. [DOI] [PubMed] [Google Scholar]
- 37. Miotto R, Li L, Kidd BA, et al. Deep patient: an unsupervised representation to predict the future of patients from the electronic health records. Sci Rep 2016;6:26094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Islam M, Huang S, Ajwad R, et al. An integrative deep learning framework for classifying molecular subtypes of breast cancer. Comput Struct Biotechnol J 2020;18:2185–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Rakshit S, Saha I, Chakraborty SS, et al. Deep learning for integrated analysis of breast cancer subtype specific multi-omics data. In: TENCON 2018–2018 IEEE Region 10 Conference. TENCON IEEE Region 10 Conference Proceedings. Jeju, Korea (South): IEEE Asia Pacific Limited, Singapore, Singapore, 2018, 1917–22. [Google Scholar]
- 40. Ronen J, Hayat S, Akalin A. Evaluation of colorectal cancer subtypes and cell lines using deep learning. Life Sci Alliance 2019;2(6):e201900517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Simidjievski N, Bodnar C, Tariq I, et al. Variational autoencoders for cancer data integration: design principles and computational practice. Front Genet 2019;10:1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Albaradei S, Napolitano F, Thafar MA, et al. Meta cancer: a deep learning-based pan-cancer metastasis prediction model developed using multi-omics data. Comput Struct Biotechnol J 2021;19:4404–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Huang Z, Zhan X, Xiang S, et al. Salmon: survival analysis learning with multi-omics neural networks on breast cancer. Front Genet 2019;10:166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Lee G, Nho K, Kang B, et al. Alzheimer’s disease neuroimaging initiative. Predicting Alzheimer’s disease progression using multi-modal deep learning approach. Sci Rep 2019;9:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Poirion OB, Chaudhary K, Garmire LX. Deep learning data integration for better risk stratification models of bladder cancer. AMIA Joint Summits on Translational Science Proceedings AMIA Joint Summits on Translational Science 2018;2017:197–206. [PMC free article] [PubMed] [Google Scholar]
- 46. Takahashi S, Asada K, Takasawa K, et al. Predicting deep learning based multi-omics parallel integration survival subtypes in lung cancer using reverse phase protein array data. Biomol Ther 2020;10(10):1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Poirion OB, Jing Z, Chaudhary K, et al. DeepProg: an ensemble of deep-learning and machine-learning models for prognosis prediction using multi-omics data. Genome Med 2021;13:112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Tong L, Mitchel J, Chatlin K, et al. Deep learning based feature-level integration of multi-omics data for breast cancer patients survival analysis. BMC Med Inform Decis Mak 2020;20:225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Ma T, Zhang A. Integrate multi-omics data with biological interaction networks using multi-view factorization Autoencoder. BMC Genomics 2019;20:944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Sharifi-Noghabi H, Zolotareva O, Collins CC, et al. MOLI: multi-omics late integration with deep neural networks for drug response prediction. Bioinformatics 2019;35:501–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Lin Y, Zhang W, Cao H, et al. Classifying breast cancer subtypes using deep neural networks based on multi-omics data. Gen 2020;11:888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Hooshmand SA, Zarei Ghobadi M, Hooshmand SE, et al. A multimodal deep learning-based drug repurposing approach for treatment of COVID-19. Mol Divers 2021;25:1717–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Liang M, Li Z, Chen T, et al. Integrative data analysis of multi-platform cancer data with a multimodal deep learning approach. IEEE/ACM Trans Comput Biol Bioinform 2015;12(4):928–37. [DOI] [PubMed] [Google Scholar]
- 54. Luo P, Li Y, Tian LP, et al. Enhancing the prediction of disease-gene associations with multimodal deep learning. Bioinformatics 2019;35(19):3735–42. [DOI] [PubMed] [Google Scholar]
- 55. Suk HI, Lee SW, Shen D. The Alzheimers disease initiative. hierarchical feature representation and multimodal fusion with deep learning for AD/MCI Diagnosis. NeuroImage 2014;101:569–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Hira MT, Razzaque MA, Angione C, et al. Integrated multi-omics analysis of ovarian cancer using variational autoencoders. Sci Rep 2021;11:6265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Xu J, Wu P, Chen Y, et al. A hierarchical integration deep flexible neural forest framework for cancer subtype classification by integrating multi-omics data. BMC Bioinfor 2019;20:1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Oh M, Park S, Lee S, et al. DRIM: a web-based system for investigating drug response at the molecular level by condition-specific multi-omics data integration. Front Genet 2020;11:564792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Zeng X, Zhu S, Liu X, et al. DeepDR: a network-based deep learning approach to in silico drug repositioning. Bioinformatics 2019;35(24):5191–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Gligorijevi V, Barot M, Bonneau R. deepNF: deep network fusion for protein function prediction. Bioinformatics 2018;34(22):3873–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Lemsara A, Ouadfel S, Froehlich H. PathME: pathway based multi-modal sparse autoencoders for clustering of patient-level multi-omics data. BMC Bioinfor 2020;21:146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Zhang X, Zhang J, Sun K, Yang X, Dai C, Guo Y. Integrated multi-omics analysis using variational autoencoders: Application to Pan-cancer Classification. In: 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM); 2019. p. 765–9. [Google Scholar]
- 63. Lee C, van der Schaar M. A variational information bottleneck approach to multi-omics data integration. Dermatol Int 2021. http://arxiv.org/abs/2102.03014 (1 December 2021, date last accessed). [Google Scholar]
- 64. Zhang D, Yin C, Zeng J, et al. Combining structured and unstructured data for predictive models: a deep learning approach. BMC Med Inform Decis Mak 2020;20:280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Ning Z, Pan W, Chen Y, et al. Integrative analysis of cross-modal features for the prognosis prediction of clear cell renal cell carcinoma. Bioinformatics 2020;36(9):2888–95. [DOI] [PubMed] [Google Scholar]
- 66. Lu MY, Chen TY, Williamson DFK, et al. AI-based pathology predicts origins for cancers of unknown primary. Nature 2021;594:106–10. [DOI] [PubMed] [Google Scholar]
- 67. Hao J, Kim Y, Mallavarapu T, et al. Interpretable deep neural network for cancer survival analysis by integrating genomic and clinical data. BMC Med Genet 2019;12:189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Xu M, Ouyang L, Han L, et al. Accurately differentiating between patients with COVID-19, patients with other viral infections, and healthy individuals: multimodal late fusion learning approach. J Med Internet Res 2021;23(1):e25535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Venugopalan J, Tong L, Hassanzadeh H, et al. Multimodal deep learning models for early detection of Alzheimer’s disease stage. Sci Rep 2021;11:3254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Thung KH, Yap PT, Shen D. Multi-stage diagnosis of Alzheimer’s disease with incomplete multimodal data via multi-task deep learning. In: Deep Learn Med Image Anal Multimodal Learn Clin Decis Support, Vol. 10553. Springer Verlag, 2017, 160–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. He T, Nolte J, Moore LW, et al. An imageomics and multi-network based deep learning model for risk assessment of liver transplantation for hepatocellular cancer. Comput Med Imaging Graph 2021;89:101894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Spasov SE, Passamonti L, Duggento A, et al. A multi-modal convolutional neural network framework for the prediction of Alzheimer ’ s disease a multi-modal convolutional neural network framework for the prediction of Alzheimer ’ s disease. Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society 2018;2018:1271–4. [DOI] [PubMed] [Google Scholar]
- 73. Kang M, Lee S, Lee D, et al. Learning cell-type-specific gene regulation mechanisms by multi-attention based deep learning with regulatory latent space. Front Genet 2020;11:869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Vale-Silva LA, Rohr K. Long-term cancer survival prediction using multimodal deep learning. Sci Rep 2021;11:13505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Liu M, Li F, Yan H, et al. A multi-model deep convolutional neural network for automatic hippocampus segmentation and classification in Alzheimer ’ s disease. NeuroImage 2020;208:116459. [DOI] [PubMed] [Google Scholar]
- 76. Yan R, Ren F, Rao X, et al. Integration of multimodal data for breast cancer classification using a hybrid deep learning method. In: Huang DS, Bevilacqua V, Premaratne P (eds). Intelligent Computing Theories and Application. Cham: Springer International Publishing, 2019, 460–9. [Google Scholar]
- 77. Mobadersany P, Yousefi S, Amgad M, et al. Predicting cancer outcomes from histology and genomics using convolutional networks. Proc Natl Acad Sci 2018;115(13). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Cheerla A, Gevaert O. Deep learning with multimodal representation for pancancer prognosis prediction. Bioinformatics 2019;35(14):i446–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Chen RJ, Lu MY, Wang J, Williamson DFK, Rodig SJ, Lindeman NI, et al. Pathomic fusion: an integrated framework for fusing histopathology and genomic features for cancer diagnosis and prognosis. 2020. ArXiv:1912.08937. https://arxiv.org/abs/1912.08937 (1 December 2021, date last accessed). [DOI] [PMC free article] [PubMed]
- 80. Chen RJ, Lu MY, Williamson DFK, et al. Pan-Cancer Integrative Histology-Genomic Analysis via interpretable multimodal deep learning 2021;1–46 ArXiv:2108.02278v1. https://arxiv.org/abs/2108.02278 (1 December 2021, date last accessed). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Wang X, Liu M, Zhang Y, et al. Deep fusion learning facilitates anatomical therapeutic chemical recognition in drug repurposing and discovery. Brief Bioinform 2021;Bbab289. [DOI] [PubMed] [Google Scholar]
- 82. Deng Y, Xu X, Qiu Y, et al. A multimodal deep learning framework for predicting drug - drug interaction events. Bioinformatics 2020;36(15):4316–22. [DOI] [PubMed] [Google Scholar]
- 83. Huang SC, Pareek A, Zamanian R, et al. Multimodal fusion with deep neural networks for leveraging CT imaging and electronic health record: a case-study in pulmonary embolism detection. Sci Rep 2020;10(22147):22147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Soto JT, Hughes JW, Sanchez PA, et al. Multimodal deep learning enhances diagnostic precision in left ventricular hypertrophy. medRxiv 2021. https://www.medrxiv.org/content/10.1101/2021.06.13.21258860v1 (1 December 2021, date last accessed). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Wang H, Subramanian V, Syeda-Mahmood T. Modeling uncertainty in multi-modal fusion for lung cancer survival analysis. In: 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), 2021, 1169–72.
- 86. Liu T, Huang J, Liao T, et al. A Hybrid Deep Learning Model for Predicting Molecular Subtypes of Human Breast Cancer Using Multimodal Data. IRBM, 2021, In Press. https://www.sciencedirect.com/science/article/abs/pii/S1959031820301858 (1 December 2021, date last accessed). [Google Scholar]
- 87. Sun D, Wang M, Li A. A multimodal deep neural network for human breast cancer prognosis prediction by integrating multi-dimensional data. IEEE/ACM Trans Comput Biol Bioinform 2019;16(3):841–50. [DOI] [PubMed] [Google Scholar]
- 88. Reda I, Khalil A, Elmogy M, et al. Deep learning role in early diagnosis of prostate cancer. Technol Cancer Res Treat 2018;17:1533034618775530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015;521:436–44. [DOI] [PubMed] [Google Scholar]
- 90. Cox DR. Regression models and life-tables. J R Stat Soc B Methodol 1972;34(2):187–220. [Google Scholar]
- 91. Vincent P, Larochelle H. Extracting and composing robust features with denoising autoencoders. In: Proceedings of the 25th International Conference on Machine Learning, 2008, 1096–103.
- 92. Kingma DP, Welling M. Auto-encoding variational bayes. In: Proceedings of the International Conference on Learning Representations (ICLR), 2014.
- 93. Karpathy A, Toderici G, Shetty S, et al. Large-scale video classification with convolutional neural networks. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2014, 1725–32.
- 94. Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Comput 2006;18:1527–54. [DOI] [PubMed] [Google Scholar]
- 95. Srivastava N, Salakhutdinov R. Multimodal learning with deep boltzmann machines. J Mach Learn Res 2014;15:2949–80. [Google Scholar]
- 96. Alemi AA, Fischer I, Dillon JV, et al. Deep variational information bottleneck. In: 5th International Conference on Learning Representations, 2017.
- 97. Selvaraju RR, Cogswell M, Das A, et al. Grad-CAM: visual explanations from deep networks via gradient-based localization. Int J Comput Vis 2020;128(2):336–59. [Google Scholar]
- 98. Sundararajan M, Taly A, Yan Q. Axiomatic attribution for deep networks. In: 34th International Conference on Machine Learning, Vol. 7. ICML; 2017, 2017, 5109–18. [Google Scholar]
- 99. Zadeh A, Vij P, Liang PP, et al. Multi-attention recurrent network for human communication comprehension. In: 32nd AAAI Conference on Artificial Intelligence, Vol. 2018. AAAI, 2018, 5642–9. [PMC free article] [PubMed] [Google Scholar]
- 100. Miotto R, Wang F, Wang S, et al. Deep learning for healthcare: review , opportunities and challenges. Brief Bioinform 2018;19:1236–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Momeni A, Thibault M, Gevaert O. Dropout-enabled ensemble learning for multi-scale biomedical data. In: Crimi A, Bakas S, Kuijf H et al. (eds). Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. Cham: Springer International Publishing, 2019, 407–15. [Google Scholar]
- 102. Xu Z, So DR, Dai AM. MUFASA: Multimodal Fusion Architecture Search for Electronic Health Records; 2021. ArXiv:2102.02340. https://arxiv.org/abs/2102.02340 (1 December 2021, date last accessed).
- 103. Wang W, Tran D, Feiszli M. What Makes Training Multi-modal Classification Networks Hard? 2020; ArXiv:1905.12681v5. https://arxiv.org/abs/1905.12681 (1 December 2021, date last accessed).
- 104. Galanti T, Wolf L, Hazan T. A theoretical framework for deep transfer learning. Informat Inference 2016;5(2):159–209. [Google Scholar]