Interpretable temporal graph neural network for prognostic prediction of Alzheimer’s disease using longitudinal neuroimaging data

Abstract

Alzheimer’s disease (AD) is a progressive neurodegenerative brain disorder characterized by memory loss and cognitive decline. Early detection and accurate prognosis of AD is an important research topic, and numerous machine learning methods have been proposed to solve this problem. However, traditional machine learning models are facing challenges in effectively integrating longitudinal neuroimaging data and biologically meaningful structure and knowledge to build accurate and interpretable prognostic predictors. To bridge this gap, we propose an interpretable graph neural network (GNN) model for AD prognostic prediction based on longitudinal neuroimaging data while embracing the valuable knowledge of structural brain connectivity. In our empirical study, we demonstrate that 1) the proposed model outperforms several competing models (i.e., DNN, SVM) in terms of prognostic prediction accuracy, and 2) our model can capture neuroanatomical contribution to the prognostic predictor and yield biologically meaningful interpretation to facilitate better mechanistic understanding of the Alzheimer’s disease. Source code is available at https://github.com/JaesikKim/temporal-GNN.

I. Introduction

Alzheimer’s disease (AD) is a progressive neurodegenerative brain disorder characterized by memory loss and cognitive decline. Today, about 5.8 million people have AD-related dementia in the United States, and it is expected to exceed 13.8 million by 2050 [1]. Despite the advances in clinical practice, it is challenging to accurately detect AD at an early stage based on their clinical symptoms or neuropathology. For example, it is important to identify biomarker detecting mild cognitive impairment (MCI, a prodromal stage of AD) since the phase of MCI increases risk of progressing to dementia. The risk of AD development increases approximately twice every five years between the ages of 65 and 85. Furthermore, AD treatments are most likely to be effective at early disease stages, even before any outward signs of dementia. Thus, early detection and accurate prognosis of AD has become an important research topic, and numerous machine learning methods have been proposed to solve this problem [2].

Recently, many researchers focused on discovering imaging biomarkers from various neuroimaging modalities for early detection and accurate prognosis of AD [3]. Although functional and structural changes have been reported as biomarkers to distinguish AD and cognitive normal (CN) subjects, the topic on capturing MCI biomarkers is still underexplored. Moreover, the main challenge in neuroimaging data with complex topological structures is how to effectively process its structural information and incorporate valuable biological knowledge in an interpretable manner. Conventional neuroimaging studies employed graph Laplacian penalization strategies to incorporate this knowledge [4]–[6].

A graph-based neural network (GNN) approach has emerged in the data science field to directly encode the graph structure and apply it to the neural network-based predictive model [7]–[10]. The GNNs have the advantage of reducing model complexity by applying spectral graph convolution compared with conventional graph-based approaches. Moreover, GNNExplainer [11], a promising interpretation method specialized in explaining GNN has been published recently. It showed better interpretation on real graph datasets than gradient- or attention-based interpretation.

In AD prognostic research, several deep learning approaches were introduced to predict AD progression using time series data [12]. Due to the characteristics of the sequential data, they applied recurrent neural networks (RNN), such as Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU), which have been shown to achieve outstanding performances in many healthcare applications with time series or sequential data [13].

With these observations, in this work, we propose an interpretable temporal graph neural network for prognostic prediction of AD from longitudinal neuroimaging data while embracing the valuable knowledge of structural brain connectivity. Our main scientific contributions are three-folds: 1) An innovative graph convolutional network (GCN) based RNN model is proposed to aggregate longitudinal neuroimaging measurements; 2) the proposed model is able to capture the neuroanatomical contribution to the classifier based on the node importance and edge importance of the graph at each time point; and 3) empirical studies demonstrate the effectiveness and benefits of our model for prognosis prediction compared with several competing models.

II. Methodology

A. Dataset

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). We downloaded the longitudinal neuroimaging data of 806 participants (i.e., 266 CN, 312 MCI, 228 AD) from the ADNI database. Table I shows the participant demographic information. Of note, from baseline to 24-month, there were 23 patients who reverted to a better condition, including 21 with MCI→CN and 2 with AD→MCI. The T1-MRI data at multiple time points, including baseline, 6-month, 12-month, and 24-month, were collected and the regional measurements (i.e., average and standard deviation of thickness, volume, and area) were extracted from 68 cortical regions based on the Desikan-Killiany atlas using Freesurfer.

TABLE I.

Demographic information

	Demographic features	Baseline	6-month	12-month	24-month
CN	Number of subjects	261	262	271	266
	Age (mean ± std.)	74.8 ± 5.6	75.2 ± 5.6	75.3 ± 6.0	76.3 ± 5.9
	Gender (M/F)	143/118	142/120	154/117	143/123
	Education (year)	15.6 ± 3.1	15.8 ± 3.2	15.9 ± 3.1	15.8 ± 3.0
MCI	Number of subjects	446	424	383	312
	Age (mean ± std.)	72.6 ± 7.4	73.1 ± 7.4	73.9 ± 7.3	74.6 ± 7.4
	Gender (M/F)	263/183	247/177	224/159	193/119
	Education (year)	15.9 ± 2.8	15.8 ± 2.9	16.0 ± 2.9	16.0 ± 2.8
AD	Number of subjects	99	120	152	228
	Age (mean ± std.)	74.8 ± 7.8	75.0 ± 7.7	75.1 ± 7.6	76.2 ± 7.4
	Gender (M/F)	59/40	72/48	91/61	126/102
	Education (year)	16.1 ± 2.7	16.0 ± 2.7	16.0 ± 2.7	15.9 ± 2.9

To incorporate relevant biological knowledge and thus avoid over-fitting, a reference structural connectivity network was computed using the diffusion magnetic resonance imaging (dMRI) data from 291 healthy participants in an independent database, the human connectome project (HCP, available at https://www.humanconnectome.org/). The FSL software was used to construct the structural connectivity networks of all the participants and the distance-dependent consensus thresholding method was applied to generate the average group-level connectivity network, and this network was used as the graph of the GNN model in our analyses [14].

B. Temporal Graph Neural Network Model for Prognosis

1). Data and Notations:

Let G = (X, A) be a graph of the brain for each subject, where $X\in {ℝ}^{p\times q}$ is the matrix containing node attribute information (i.e., node-based regional features extracted from the longitudinal neuroimaging data), $A\in {ℝ}^{p\times q}$ represents an adjacency matrix of a graph (i.e., node- or region-based brain connectivity), p is the number of nodes in the brain, and q is the number of regional imaging attributes associated with each node. For the node attributes, we use the following four neuroimaging features as initial attributes (q = 4): (1) volume and (2) area of the corresponding cortical region, and (3) average and (4) standard deviation of all the vertex-based thickness measures in the cortical region. A is defined by the average group-level structural connectivity network obtained from the HCP data, as described in Section II-A. As mentioned earlier, in this work, we focus on analyzing p = 68 cortical regions.

2). Proposed interpretable temporal graph neural network:

We propose an end-to-end interpretable temporal graph neural network for prognostic prediction. The architecture of the proposed model is shown in Figure 1. Overall, a graph at the time point passes through the two GNN encoder blocks to encode new node embedding, and then new node embeddings are fed into the LSTM to aggregate temporal information. Finally, fully connected layers with SoftMax activation function are added after for predicting multi-class diagnosis at 24-month.

Fig. 1.

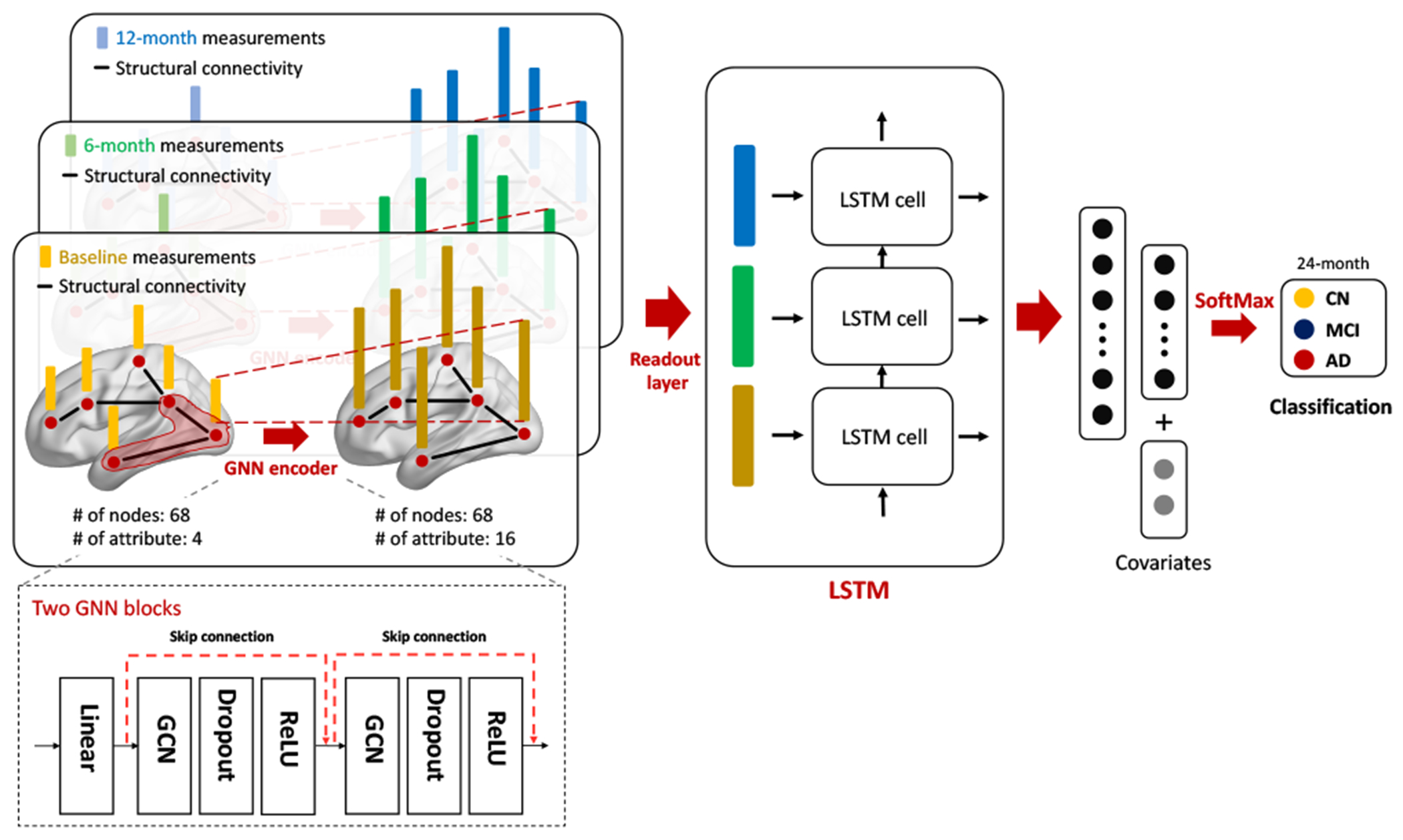
The proposed interpretable GNN model for prognosis prediction.

The the GNN encoder blocks are containing [GNN layer-Dropout-ReLU]. We carefully compare and choose GNN encoder layers among graph convolutional network (GCN) [7], GraphSAGE [8], Graph attention networks (GAT) [9], and Graph isomorphism network (GIN) [10]. To avoid over-smoothing, a pre-linear layer is added before first GNN encoder block and the skip-connection is connected between two blocks. At the last part of the GNN encoder block, the readout layer aggregates the node embeddings into the graph embedding by using the global average pooling layer.

For the LSTM layer, we explore a variety of models, including the vanilla LSTM model as well as the LSTM models with attention [15] and self-attention [16] mechanisms, to improve aggregating temporal information. These LSTM models have been broadly used in natural language processing and signal processing domains. Then, the two fully connected layers with SoftMax activation function are added after the LSTM layer for predicting multi-class diagnosis at 24-month.

In this study, we include covariates (i.e., age, gender, education, and MRI field strength) in the last fully connected layer. Finally, the sparse categorical cross-entropy loss function is applied. All the parameters in the model are optimized using the AdamW optimizer.

3). Model intepretation:

We apply GNNExplainer to identify relevant nodes that contribute to the prediction of the prognostic outcome. GNNExplainer is a state-of-the-art interpretable model that provides interpretation of GNN-based model [11]. The GNNExplainer generates a subgraph structure and a subset of node features that have a decisive role in the prediction by maximizing the mutual information between the prediction and distribution of possible subgraph structures. The resulting subgraph and node feature can be interpreted in two main perspectives: 1) node importance, 2) feature importance. Node importance can be measured by computing degree centrality (DC) in the subgraph. Feature importance can be measured by computing feature node mask.

III. Experiments and Results

A. Experimental setup

In our study, we converted weighted group-level connectivity graph into unweighted graph by thresholding it by 0.05 and used it as topology of GNN layer, since GraphSAGE and GIN do not support weighted graphs. For prediction task, we trained models (e.g., GNN, DNN, and SVM) on 60% of the data (i.e., train set), validated on 20% of data (i.e., validation set), and applied it on 20% of data (i.e., test set) to evaluate prediction accuracy. We repeated 300 times to evaluate the stability of the model and measured the performance in the form of mean ± standard deviation (std).

For benchmark algorithms, the DNN model with single hidden layer and linear SVM were used with adjusting covariates. The neural network models were trained on the NVIDIA 2080TI GPU (with cuda ver. 10.2). For DNN and GNN training, we utilized earlystopping algorithm to avoid overfitting. The proposed model was implemented as described in Section II-B. The learning rate was 5e-4, the hidden dimension size in both GNN and RNN layer was 16, dropout rate was 0.5, and the hidden dimension size in the fully connected layer was 8. Our model was implemented in pytorch (ver. 1.9.0) and pytorch-geometric (ver. 1.7.2) [17].

B. Neural network module comparisons

We conducted comparative experiments to select GNN and RNN layer types in our model. For GNN layer, we employed and compared four representative GNN layer types, including GCN, GraphSAGE, GAT, and GIN while RNN layer type was vanilla LSTM, in order to achieve the best prediction accuracy. We compared the prediction performance of four GNN layers through 300 empirical trials. Although the four models did not show significant differences, the GCN layer obtained the best accuracy of 53.5 ± 3.8 (53.4 ± 3.9 of GraphSAGE, 53.0 ± 4.0 of GAT, and 53.0 ± 4.0 of GIN).

For the RNN layer, we employed and compared four RNN layers, including Vanilla LSTM, attention LSTM, self-attention LSTM (h=1), and self-attention LSTM (h=3) while GNN layer type was GCN, in terms of their prediction accuracies. Although there was no significant performance difference, we noted that vanilla LSTM showed the best performance of 53.5 ± 3.8 (52.7 ± 3.8 of attention LSTM, 53.1 α 3.9 of self-attention LSTM(h=1), and 52.9 ± 3.8 of self-attention LSTM (h=3)). This seems different from the observation that attention and self-attention are more effective in the natural language process domain.

With this observation, we determined to implement our temporal GNN model so that its GNN layer employed GCN and its RNN layer employed the Vanila LSTM layer. Below we focus on reporting the performance of this implementation.

C. Prognostic prediction task

For prognostic prediction task, our model obtained the best performance (53.5 ± 4.5%), and outperformed the competing methods (DNN: 51.7 ± 3.6% and SVM: 51.3 ± 3.6%). Our model has the advantage to predict the AD and MCI diagnosis at 24-month, even though there is a huge alternation of diagnosis between 12 and 24 months, as shown in Table I. In addition, we also tested more complicated DNN models. However, we observed that a single layer of DNN performed more consistently than its deeper counterparts.

Of note, our prognostic prediction task is much more challenging due to classifying three diagnostic groups instead of two and predicting the diagnostic status in the future instead of the current diagnosis. It is encouraging that our model outperforms the state-of-the-art DNN and SVM models on this challenging prediction task. Given the modest performance, it warrants further study to explore additional advanced models for improving the prognostic prediction for early detection.

D. Interpretation of results

First, we measure the contribution of brain regions to prognostic prediction based on GNNExplainer. GNNExplainer extracts a subgraph that is important to predict prognosis of AD. Figure 2–A visualizes node importance maps based on degree centrality (DC) of subgraph depending on true label and predicted label, and Table II presents the top 5 overall important regions. Overall, superior frontal, precentral, insula, and superior parietal consistently contributed to the CN, MCI, and AD classification. These regions have been reported to be associated with process of AD in several studies [18], [19].

Fig. 2.

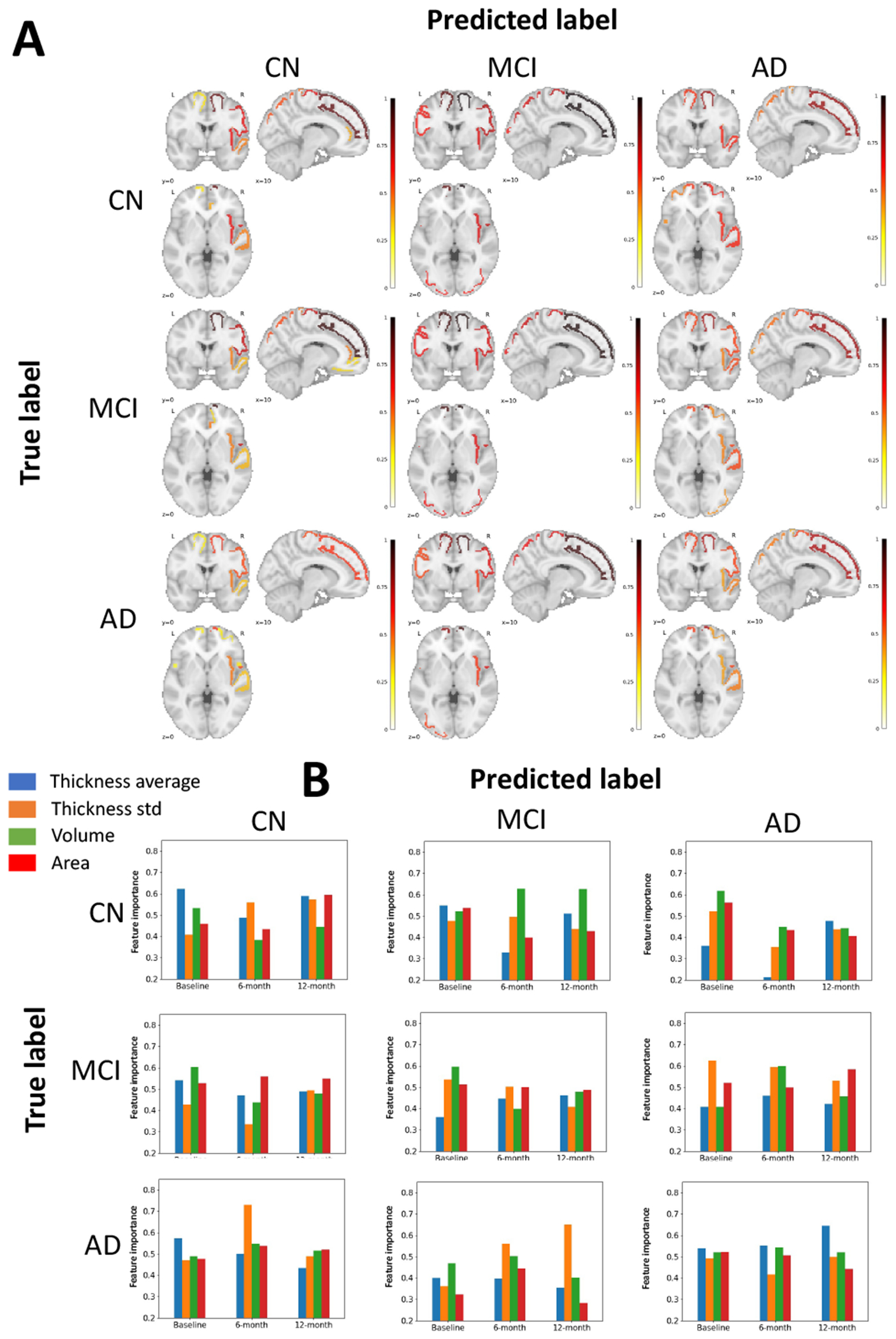
Interpretation results of the proposed model by using GNNExplainer according to true label and predicted label of CN, MCI, and AD, respectively. (A) Visualization of node importance. For each figure, the most important 10 region of interests (ROIs) are colored in red representing high contribution to the classification. (B) Visualization of feature importance. Each plot shows importance of attributes depending on the time point.

TABLE II.

Top 5 overall important ROIs in proposed model. The importance level is reported as DC of subgraph using GNNExplainer.

True Label / Predicted Label	CN / CN	CN / MCI	CN / AD	MCI / CN	MCI / MCI	MCI / AD	AD / CN	AD / MCI	AD / AD	Average DC
Right Superior Frontal	0.880	0.997	0.785	0.943	0.977	0.775	0.586	0.931	0.757	0.848
Right Precentral	0.675	0.731	0.377	0.721	0.694	0.566	0.550	0.680	0.563	0.617
Left Superior Frontal	0.290	0.889	0.583	0.287	0.930	0.562	0.276	0.810	0.571	0.578
Right Insula	0.650	0.679	0.610	0.459	0.670	0.455	0.470	0.580	0.399	0.553
Right Superior Parietal	0.541	0.697	0.493	0.550	0.713	0.491	0.189	0.653	0.466	0.533

Next, we examine which time point(s) (e.g., baseline, 6-month, and 12-month) and attribute(s) are the most important for prognostic prediction. Figure 2–B shows the importance of four attributes (average and standard deviation of thicknesses, volume, and area) for each time point, depending on true and predicted labels. We observed that there was no trend of lower or higher importance at any one time point. Likewise, four attributes have similar importance. Rather, the model is interpreted as evenly processing information at three time points for the prognostic prediction. We note that the prediction is not based on strong information at a single time point, but rather on detecting the pattern of change across three time points.

IV. Conclusion

In this study, we have proposed an interpretable GNN model for prognostic prediction of Alzheimer’s disease and mild cognitive impairment. Our model yielded promising interpretable results and improved prognostic prediction performance. We tested and compared our model with several competing models on the ADNI dataset. We demonstrated that our model not only outperforms the competing models on prognostic prediction accuracy, but also can capture neuro-anatomical contribution to the prognostic predictor and yield biologically meaningful interpretation to facilitate better mechanistic understanding of the Alzheimer’s disease.