Scaling analysis reveals the mechanism and rates of prion replication in vivo

Abstract

Prions consist of pathological assemblies of normal cellular prion protein and cause infectious neurodegenerative diseases, a phenomenon mirrored in many other prion-like neurodegenerative diseases. However, despite their key importance in disease, the individual processes governing this formation of pathogenic aggregates, as well as their rates, have remained challenging to elucidate in vivo. Here we bring together a mathematical framework with kinetics of the accumulation of prions in mice and microfluidic measurements of aggregate size to dissect the overall aggregation reaction into its constituent processes and quantify the reaction rates in mice. Taken together, the data show that multiplication of prions in vivo is slower than in in vitro experiments, but efficient when compared to other amyloid systems, and displays scaling behaviour characteristic of aggregate fragmentation. These results provide a framework for the determination of the mechanisms of disease-associated aggregation processes within living organisms.

Prions contain no conventional genetic information, yet, prions are infectious in a manner reminiscent of viruses (1, 2). To cause this behaviour, a small number of prions introduced upon infection have to be able to induce the formation of more prions, and this replication of infectious entities is thus the central process in prion diseases. This ability to replicate allows the disease to be initiated by a small number of particles, enabling prions to propagate from host to host and cause a rapidly progressing disorder. Although effects detrimental to the organism occur late in the development of the disease, and the detailed mechanism of toxicity is not yet fully established, the infection by and replication of prions is the crucial prerequisite for disease and thus understanding prion replication is central to understanding prion diseases (3–5). Prion disease is the archetypal aggregation-associated disease and in other neurodegenerative diseases the formed aggregates of proteins such as tau and α-synuclein are often termed prion-like for similarities in their mechanism of propagation (6–8). Given this analogy with prion disease, the insights gained and framework developed here is likely to be of relevance to a wide range of disorders.

To avoid any confusion arising from the use of terminology from both the fields of prion diseases and of protein aggregation, we define here explicitly the terms used: Infectious units are species capable of inducing the disease when introduced into a host (their relation to the species causing pathology is not required for this definition), infectivity is a measure of their concentration. In practice, infectivity is usually determined in dilution experiments, for example within mice (9) or in cell culture, through the Standard Scrapie Cell Assay (SSCA) (10). Aggregates are structures of several proteins in the PrP^Sc state, the process that increases the size of a given aggregate is referred to as growth. Multiplication is the specific process that increases the number of aggregates, such as fragmentation of an existing aggregate. Replication is the overall process that converts a population of molecules in the PrP^C state to aggregated molecules in the PrP^Sc state. Thus, the rates of growth, multiplication and replication denote the rate of increase of size of a given aggregate, the rate at which a given aggregate produces new ones and the overall rate at which PrP^C is converted to PrP^Sc, respectively.

It has been established that the conversion of monomeric cellular PrP^C (here also referred to simply as monomer) to PrP^Sc is at the core of the ability of prions to replicate (11). However, the molecular mechanisms, including the individual processes and their rates, by which existing infectious units can interact with PrP^C and produce new infectious units have not been established in vivo. Numerous models have been proposed, including a direct conversion mechanism, whereby each protein in the PrP^Sc state can catalyse the conversion of soluble PrP^C molecules into PrP^Sc via a hetero-dimer (12) and a fragmentation mechanism, whereby a large prion may break apart into two new prions (13). However, it has remained challenging to verify either of these models in vivo. The majority of mechanistic studies have therefore to date focused instead on the kinetics of the aggregation of purified recombinant PrP in vitro (11, 14, 15) and found the half time of aggregation to scale inversely with the square root of monomer concentration, which, as we and others have shown in the past (16), is consistent with a multiplication of aggregates by fragmentation. The relevance of these findings for the proliferation of prions in vivo remains, however, unclear, in particular as samples of aggregated, recombinant PrP^Sc produced in vitro display considerably lower infectivity when injected into mice than the types of aggregates found in the brains of diseased organisms (17), suggesting a significant difference in structure, composition or mechanism. Overall, therefore, the mechanisms of prion replication on a molecular level remain to be established in vivo.

In order to address this challenge, we present a general framework for obtaining robust, representative parameters from in vivo data and relating them to fundamental mechanisms of multiplication and growth of protein aggregates. This approach is general enough to yield a continuous spectrum of behaviour, linking the previously proposed mechanisms (13, 18–24). Here, we show its power in analysing mechanisms in living systems by determining the rates for prion growth and multiplication in vivo.

Results

Mechanistic analysis of prion multiplication.

Chemical kinetics is the gold standard tool for discovering and verifying reaction mechanisms in molecular sciences, and this framework has recently been extended to protein aggregation where it fundamentally aids the mechanistic characterisation of complex reaction networks. In the present work, we apply this approach to aggregation taking place in a living system (Fig. 1a). To obtain in vivo data amenable to mechanistic analysis within the framework of chemical kinetics, we studied the kinetics of PrP^Sc formation in a total of 78 mice from four different lines; they include wild type (WT, also referred to as Prnp^+/+) mice and genetically modified mice that express approximately half (heterozygous WTxPrnp^0/0, also referred to as Prnp^0/+), twice (heterozygous tga20xPrnp^0/0, also referred to as tga20Prnp^0/+) and three to four times (tga20, also referred to as tga20Prnp^+/+) the level of PrP^C found in the WT mice. Crucially, studying the aggregation at different concentrations of PrP^C allows the determination of the dependence of the aggregation rate on the PrP^C concentration, which in turn can be linked to the nature of the replication mechanism. To initiate aggregation, the mice were inoculated intra-cerebrally with a well-characterized prion inoculum (RML5). We collected brain samples from each mouse line at multiple time-points after inoculation until the onset of terminal disease, and measured levels of proteinase-K (PK) resistant and total PrP^Sc (i.e. the sum of PK sensitive and PK resistant) as well as the levels of PrP^C in the brains of inoculated mice. Additionally, we performed separate experiments to determine the time course of infectivity, using a standard scrapie cell assay, for a separate cohort of wild type mice (details in Online methods). To further increase the robustness of our analysis, we combine our data with similar datasets from previous works. Finally, we used measurements of the molecular diffusivity of the aggregates to determine the average size of prions directly in brain homogenate.

Figure 1: Principle of mechanistic analysis and increase of infectivity over time.

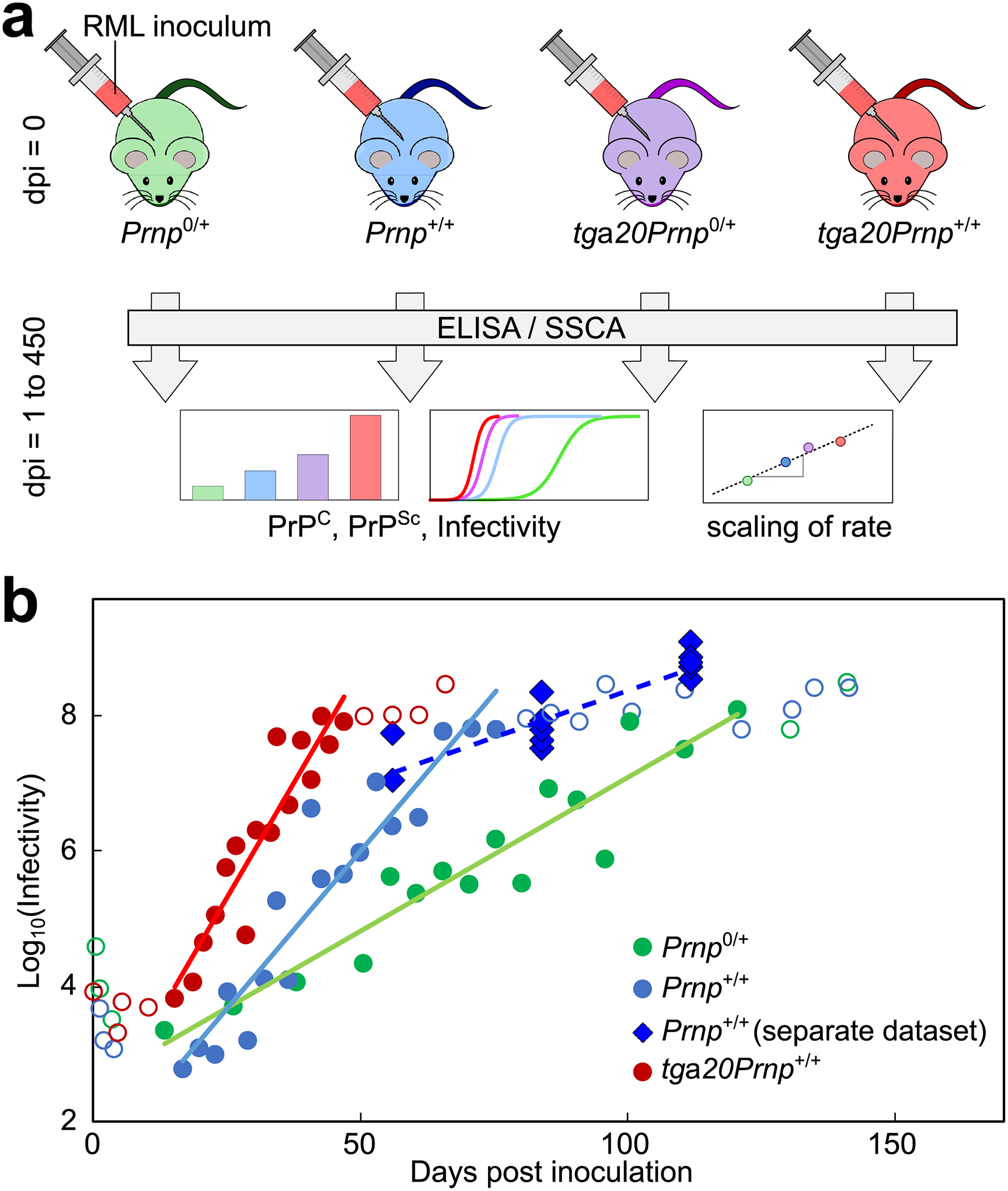
(a) Mice of four different lines are inoculated with RML prions. At several time-points throughout disease, from inoculation up to 450 days post inoculation (dpi), the levels of PrP^Sc and PrP^C in mouse brains, as well as the infectivity of brain homogenate, were determined. The scaling of the rate of accumulation with PrP^C amount serves as a guide to the mechanisms of multiplication. (b) Infectivity increases exponentially over the majority of the time-course, except the first few weeks after inoculation and close to terminal disease. Circles are data from Sandberg et al. (27), and solid lines are straight line fits in logarithmic space to the filled circles, showing that the rate of increase is faster in mice with a higher PrP^C; open circles are data excluded from this fit. Diamonds are data measured by SSCA here, in a cohort of wild type mice (n=3 at 56 dpi, n=6 at 84 and 112 dpi, each data point corresponds to one animal) separate to that for the PrP^Sc measurements (28). Data behind graphs are available online as Source Data.

Infectivity and PrP^Sc increase exponentially.

An initially exponential increase in the number of aggregates is the hallmark of all aggregation mechanisms that include a multiplication and a growth process and emerges as a natural result of the auto-catalytic nature of self-replication, as we outline later and discuss in more detail in Supplementary Note 1 and Meisl et al. (25). Indeed, the results from our kinetic assay were consistent with an exponential increase in PrP^Sc for the majority of the time-course, although PrP^Sc amounts plateau late in the disease, as observed in previous studies (26, 27). To further verify the exponential increase, given that the initial measurements lie below the sensitivity of the ELISA measurements, we also measured infectivity by SSCA as a function of time in wild type mice of a separate cohort to that used for the PrP^Sc measurements (28). The infectivity is found it to increase exponentially, by several orders of magnitude, consistent with previously published data by Sandberg et al. (Fig. 1b) (27). Our interpretation of their data differ slightly from those presented by Sandberg et al. as we show that both the PrP^Sc concentrations and the infectivity are consistent with an initially exponential increase and there is no evidence of one lagging behind the other (see Extended Data Fig. 1).

No PrP^Sc was observed in age-matched uninfected controls, indicating that exposure to the RML isolate was essential for inducing PrP^Sc formation. The average levels of PrP^C were found to be slightly lower at the terminal disease stage with the most pronounced relative decrease (by 35%) observed for WT (Prnp^+/+) mice (Fig. 2a). This finding is also in agreement with the observations of previous studies (26).

Figure 2: PrP^C and PrP^Sc concentrations over time for different mouse lines.

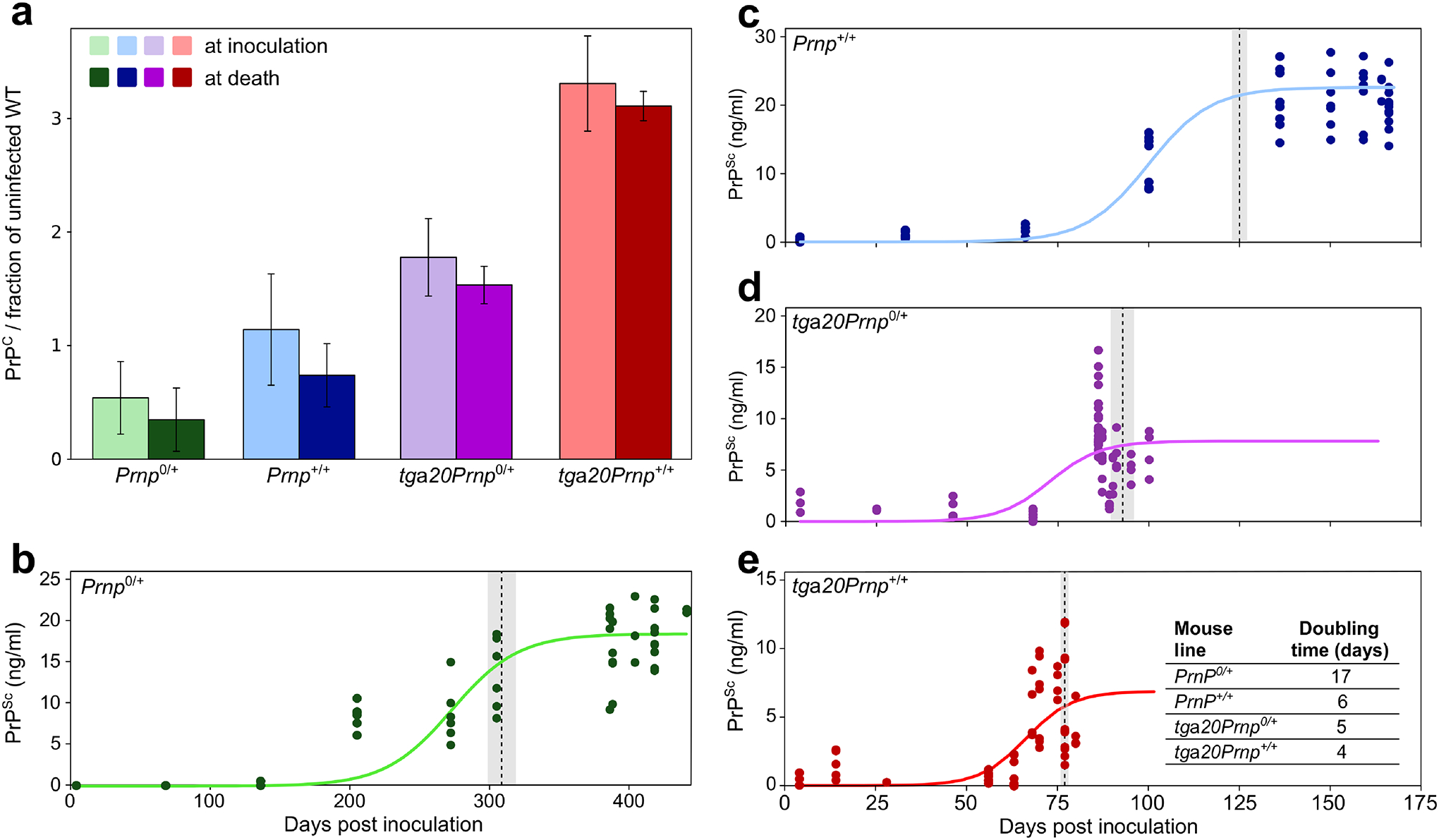
(a) PrP^C concentrations just after inoculation and shortly before terminal disease, for the each of the four different mouse lines. The concentrations are normalised to the PrP^C concentration in an uninfected wild type mouse. Data are mean and s.d. for n = 3 animals. (b-e) PK resistant PrP^Sc concentration as a function of time, for each mouse line (the analogous plot for total PrP^Sc concentration is given in the Extended Data Fig. 2). Solid lines are fits of equation (1) to all data-points. At each time-point, samples from one or more mice were analysed, 3–4 technical repeats of the ELISA assay of the same sample were performed; all technical and biological repeats are shown (all details in Extended Data Fig. 2 source data). In total, 78 mice were used (for detailed mouse numbers in each line, see Supplementary Table 1). Dotted lines denote the approximate time of onset of symptoms, grey regions are standard deviation over the mice remaining at this stage. Note the different time axis in b; the plots in c-e, share the same time axis. Data behind graphs are available online as Source Data.

The reduction in PrP^C concentration correlates with the appearance of pathological symptoms and may be the effect of higher order feedback processes, such as the organism’s response to the accumulation of aggregates (26). In the context of an analysis of the kinetics of aggregate accumulation, the data provide the most robust constraint on the mechanistic details if the direct effect of the variation in a single parameter (in this case the PrP^C concentration) can be measured. Given the complexity of any aggregate-induced response by the organism and the lack of knowledge of the exact nature and extent of the effects that a high concentration of aggregates has on the biochemical processes taking place in the organism, a kinetic analysis is thus most readily interpreted prior to the build-up of high levels of PrP^Sc and the appearance of pathology.

We have therefore focused our analysis on the exponential stages of the PrP^Sc accumulation, before its concentration plateaus and pathological symptoms of the mice become apparent. Infectivity increases by several orders of magnitude during this time period, making it the most important stage of the disease process to study in the context of prion replication. In practice, to show the robustness of our findings, we have employed 3 different methods to extract the rates of replication from these data: (1) a model free approach in which we determine the times at which a threshold concentration of PrP^Sc is exceeded for each mouse line, (2) fits of a simple exponential to the pre-plateau phase, and (3) fits of a sigmoidal function that extends the initial exponential behaviour to produce a plateau at late times. The results of the last, most sophisticated method are shown here (Fig. 2). The other methods yield essentially unchanged results, which are shown in Extended Data Fig. 2, Supplementary Table 2 and Supplementary Note 2.

The function fitted in Fig. 2 is given by

$$\left[Pr{P}^{Sc}\right]=P_{max}{\left(\left(\frac{P_{max}}{P_0}-1\right)e^{-\kappa t}+1\right)}^{-1}$$ (1)

where κ is the exponential growth rate, P₀ the initial PrP^Sc concentration and P_max the PrP^Sc concentration at the plateau. This function approaches an exponential growth curve, P₀e^κt, at early stages and allows for plateauing at late stages and in fact it emerges as the solution to the logistic differential equation, the simplest description of auto-catalytic growth with a carrying capacity. Further details on its importance in describing aggregation reactions can be found in Meisl et al. (25). Setting P₀ and allowing κ and P_max to vary reproduces the data well as shown in Fig. 2 (in Supplementary Note 2 we rationalise the choice of P₀ and show that the results are not sensitive to its specific value). The time to double the number of PrP^Sc aggregates in the exponential phase, t₂ = ln(2)/κ, is approximately 4 days in the mice with the highest PrP^C concentration (tga20) and 17 days in the mice with the lowest PrP^C concentration (Prnp^0/+).

Exponential rate depends on PrP^C concentration.

A key characteristic of each mechanism of protein aggregation is the dependence of κ on the concentration of soluble precursor protein (29), which is quantified by the scaling exponent γ as

$$\kappa \propto {\left[Pr{P}^C\right]}^{\gamma }$$ (2)

The fact that only the relative variation in the exponential rates and monomer concentrations is required to determine this scaling gives it the necessary robustness to apply to in vivo experiments. Indeed, decades of work on the kinetic analysis of protein aggregation (16, 29, 30) have shown that the two key characteristics of experimental data that is rich in mechanistic information are the nature of the time dependence (exponential or polynomial) and the concentration dependence given by γ. The level of infectivity of the inoculum or the absolute quantification of PrP^Sc do not affect these quantities, making this approach uniquely suitable as a measure of the mechanism of aggregation in complex systems.

A graph of κ versus the initial PrP^C concentration on a double logarithmic plot allows the scaling exponent to be visualised (Eq. 2), see Fig. 3. Through this analysis of the rates of accumulation of PK resistant and total PrP^Sc for the four mouse lines we find that the rates scale approximately with the square root of the PrP^C concentration, i.e. γ ≈ 1/2. As outlined above, we verified that our findings are not dependent on the specifics of the data analysis by extensively investigating the effect of changes in the fitting approaches (see Supplementary Note 2).

Figure 3: Scaling exponents of the rate of infectivity and of PrP^Sc increase.

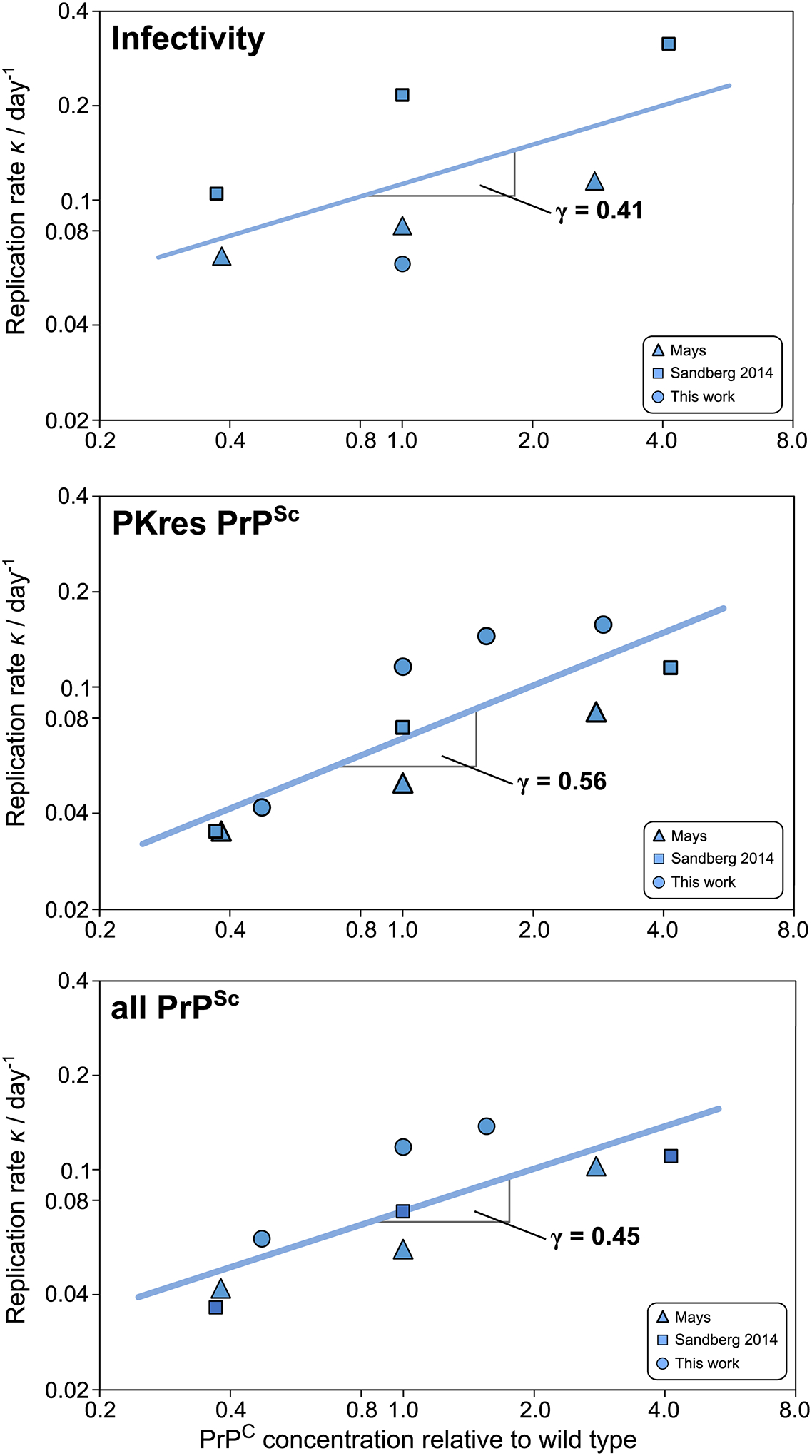
Double logarithmic plots of the rate of accumulation, κ, of infectivity, PK resistant PrP^Sc and all PrP^Sc. Data shown are from this work (circles), Mays et al. (26) (triangles) and Sandberg 2014 et al. (27)(squares). Data behind graphs are available online as Source Data. See Figs. 1b and 2, as well as Extended Data Fig. 2, 3 and 4 for primary data fits, and Supplementary Note 3 for monomer concentrations and analysis details.

Rates and its PrP^C dependence are consistent across datasets.

Similar sets of data to those recorded here have been reported independently by Mays et al. (26) and by Sandberg et al. (27), for three mouse lines in each case. We analysed these data in the same manner as the data reported in the present study (see Supplementary Note 3 and Extended Data Figs. 3 and 4). Three quantities were measured in these studies: the concentration of PK resistant PrP^Sc, the concentration of total PrP^Sc (PK resistant and other species) and the infectivity. These studies all display an exponential increase in the measured quantity and determining the exponential rates to calculate the scaling for each of the quantities yields very similar results: The rate, κ, scales approximately as the square root of the PrP^C concentration. Remarkably, this is true for both the PrP^Sc concentration and the infectivity, although on average the rates of accumulation of infectivity are slightly higher than those of the accumulation of PrP^Sc and the scaling is slightly lower. These differences may be a result of the differing sensitivities to small prion concentrations of the assays used to measure PrP^Sc and infectivity.

The doubling times for PK resistant PrP^Sc obtained in these other datasets are approximately 3 weeks and 1 week for the Prnp^0/+ and tga20, respectively, comparable to our data. We combine all data in Fig. 3 to obtain overall scaling exponents for the total and PK resistant PrP^Sc concentrations, as well as the infectivity, which are all approximately 1/2. Values of scaling exponents and errors for the different methods are summarised in Supplementary Table 2.

Scaling exponent informs on replication mechanism.

We now set out to link the experimental observations of the scaling behaviour to the underlying mechanism through a general framework for describing replication of aggregates in vivo. The general model is obtained by considering the fundamental classes of different processes that form the reaction network describing the conversion of monomeric proteins to aggregates. Generally speaking, two distinct types of processes are required to achieve replication of aggregated structures: (1) growth processes, which are responsible for the conversion of soluble PrP^C into its aggregated form through addition to existing aggregates and (2) multiplication processes, which increase the number of aggregates. New aggregates in turn are able to grow through addition of soluble protein again, closing the positive feedback loop between growth and multiplication that is responsible for the overall exponential increase in aggregate mass (Fig. 4a). It is worth noting that the hetero-dimer mechanism whereby each molecule in the PrP^Sc state can convert more PrP^C (2), here referred to as direct monomer conversion, does not involve aggregation and hence does not distinguish between growth and multiplication processes. However, it can be obtained as a mathematical limit of the more general model used here and its predictions are shown to be inconsistent with the data (Fig. 4b).

Figure 4: Reaction network and consistent mechanisms.

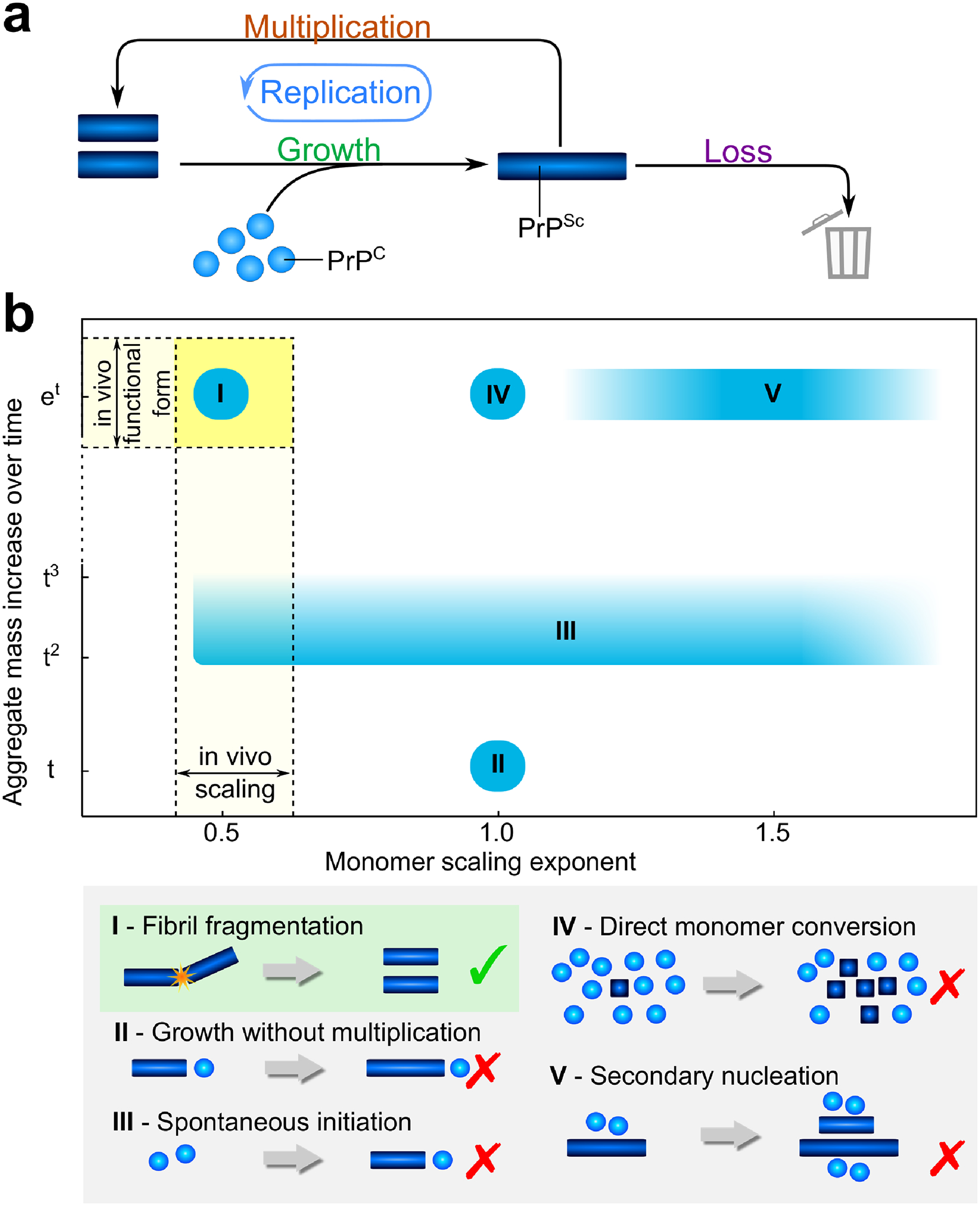
(a) Monomeric PrP^C is represented by blue spheres and PrP^Sc aggregates are represented by blue bars. Aggregates can grow by incorporating more PrP^C and can multiply for example by fragmentation. Growth and multiplication couple together in an auto-catalytic manner, the whole cycle is referred to as replication. Finally, the loss of aggregates by degradation and sequestration into plaques both have the effect of preventing the removed aggregates from further participating in the aggregation reaction (b) The scaling exponent, γ, is plotted against the functional form of the increase of aggregate mass with time, from linear to exponential. For the formation of linear aggregates without multiplication, the mass increase is linear in the absence of any spontaneous aggregate formation from monomer alone (II), or low-order polynomial if spontaneous formation of aggregates occurs (III). If aggregates are able to multiply, the mass increase is exponential (I, IV, V). Fragmentation of aggregates results in a scaling of approximately 0.5 (I), direct monomer conversion leads to a scaling of 1 (IV), and secondary nucleation gives a scaling of 1 or above (V).

Growth processes reflect the addition of soluble protein to existing PrP^Sc aggregates so are easily described by one general mechanism. However, several different processes may be responsible for the formation of new aggregates. Under the conditions studied, the de-novo formation of aggregates from soluble PrP^C alone, primary nucleation, was found to be negligible, as no PrP^Sc accumulation was observed in mice inoculated with prion-free samples (this extremely slow rate of formation of aggregates directly from PrP^C also explains the rarity of spontaneous prion disease). Thus, any production of new aggregates requires the presence of existing aggregates and is therefore a multiplication process. We can distinguish between two fundamental cases: the formation of new aggregates can depend on the concentration of aggregates alone, for example through the fragmentation of existing aggregates, or it can depend on both the concentration of existing aggregates and the concentration of monomers, for example in the case where the accessible surface of aggregates acts as a catalyst for the formation of new aggregates from soluble monomers in a secondary nucleation process (31–34). As the multiplication step is responsible for producing new aggregates, it also has to maintain the specific strain conformation. Differences of the kinetics between strains would, in this framework, be evident in differing rates of growth and multiplication (35, 36). Finally, we also consider processes that result in the removal of aggregated species from the system (37, 38), for example autophagy or engulfment by microglia, or processes that prevent them from participating in the aggregation reaction, e.g. by incorporation into plaques, to complete the in vivo model. The detailed assumptions and limitations of this models are discussed in Supplementary Note 1. A more in depth treatment of the different classes of processes, explicitly considering variations of their rates with aggregate size, are considered in Meisl et al. (25). Briefly, the population of aggregates will generally consist of a range of species of different sizes, so to develop a general description one has to consider how the rates of both growth and multiplication depend on the size of the aggregate. This can be achieved by defining one continuous parameter each for growth and multiplication, which yields a continuous spectrum of behaviour that connects the limiting physical cases of self-replication and also applies to aggregates that are not linear in geometry. In essence, all mechanisms that include a multiplication step predict an exponential increase in aggregate mass, PrP^Sc ≈ e^κt where κ is the replication rate. However, the dependence of this rate on the PrP^C concentration can differ and is determined by the reaction orders with respect to PrP^C of both the growth process and the multiplication process.

More specifically, the replication rate is the geometric mean of the growth and the multiplication rates κ = (k_multk_growth)^1/2. This conclusion does not require the precise molecular mechanisms of growth and multiplication to be specified but applies to all mechanisms that fall into the respective classes. In Fig. 4b the scaling and the functional form of the increase of PrP^Sc with time for a selection of common models are compared.

Using the data from the four independent experimental studies, we determined that the increase in PrP^Sc concentration was exponential and that the scaling exponent was approximately 0.5 (see Fig. 3). Based on these observations several general classes of mechanisms can be discarded as inconsistent with the experimental data. The exponential increase excludes mechanisms that (i) lack multiplication and only involve the growth of inoculated aggregates (Fig. 4b II) or (ii) of spontaneously formed aggregates (Fig. 4b III). Such an aggregation mechanism is observed for example in the formation of actin filaments (39), but can be ruled out in these data of prions in mice.

The low value of the scaling exponent excludes the possibility of (iii) direct monomer conversion whereby each protein in the PrP^Sc state may convert more PrP^C, also referred to as the hetero-dimer mechanism, which predicts a scaling of 1 (Fig. 4b IV), (iv) an aggregation mechanism that proceeds independently of the monomer concentration, which predicts a scaling of 0, (v) a mechanism of growth where oligomeric PrP^C species, present at low concentrations and in equilibrium with monomer, are added to growing aggregates, which predicts a scaling of > 1 (Fig. 4b V, scheme not shown) and (vi) a monomer concentration-dependent secondary nucleation process as is observed in vitro in the aggregation of the Aβ peptides associated with Alzheimer’s disease (40), which also predicts a scaling of 1 or above (Fig. 4b V), depending on the number of monomeric species that take part in the nucleation reaction and the degree of saturation (41). Our findings are however in agreement with PrP^Sc forming linear aggregates that multiply via fragmentation, γ = 0.5 (Fig. 4b I). They are also consistent with PrP^Sc forming higher dimensional aggregates, such as bundles of aggregates that thicken as they grow, that are less likely to fragment the larger they become (25). It is interesting to compare this result with data obtained from in vitro studies (16,42) which are indicative of fragmentation being the dominant mode of multiplication in the formation of linear fibrils of PrP^Sc. Therefore, although the formed structures and the rates of replication differ significantly, remarkably, the mechanism of replication in vivo is consistent with the mechanism in vitro.

Prion size in brain homogenate by microfluidic sizing.

A further experimentally accessible quantity, which allows deconvolution of the growth and multiplication rates from the overall effective rate of replication of PrP^Sc, is the average size of the aggregates formed. We used microfluidic diffusional sizing to determine the size of PK resistant PrP^Sc aggregates in the brain homogenate of tga20 mice. A schematic of the platform is shown in Fig. 5. The technique is based on the fact that no turbulent mixing takes place under the conditions of laminar flow in the microfluidic device, and thus the movement of particles lateral to the flow direction is governed purely by diffusion and hence by their size. Having allowed the sample time to diffuse, the concentrations are measured by antibody FRET using FRET-labelled POM antibodies (43). Particle-based simulations of the diffusion of different sized species in the device (see Extended Data Fig. 5) allow us to relate the measured amounts of signal in each channel to the diffusion coefficient and thus the size of the detected particle (44). As expected, we found that the diffusion coefficient of PK resistant PrP^Sc aggregates from the brains of prion-infected tga20 mice at terminal disease was over one order of magnitude lower than that of PrP^C measured by the same method. To obtain the physical dimensions of the measured species, assumptions about their shape have to be made, which is discussed in more detail below. However, the hydrodynamic radius related to a given diffusion coefficient, which is defined as the radius of a spherical particle that would diffuse at the same rate, can be calculated to assign a more easily interpretable quantity. It should not be confused with an actual size, if the particles are non-spherical.

Figure 5: Sizing prions in brain homogenate.

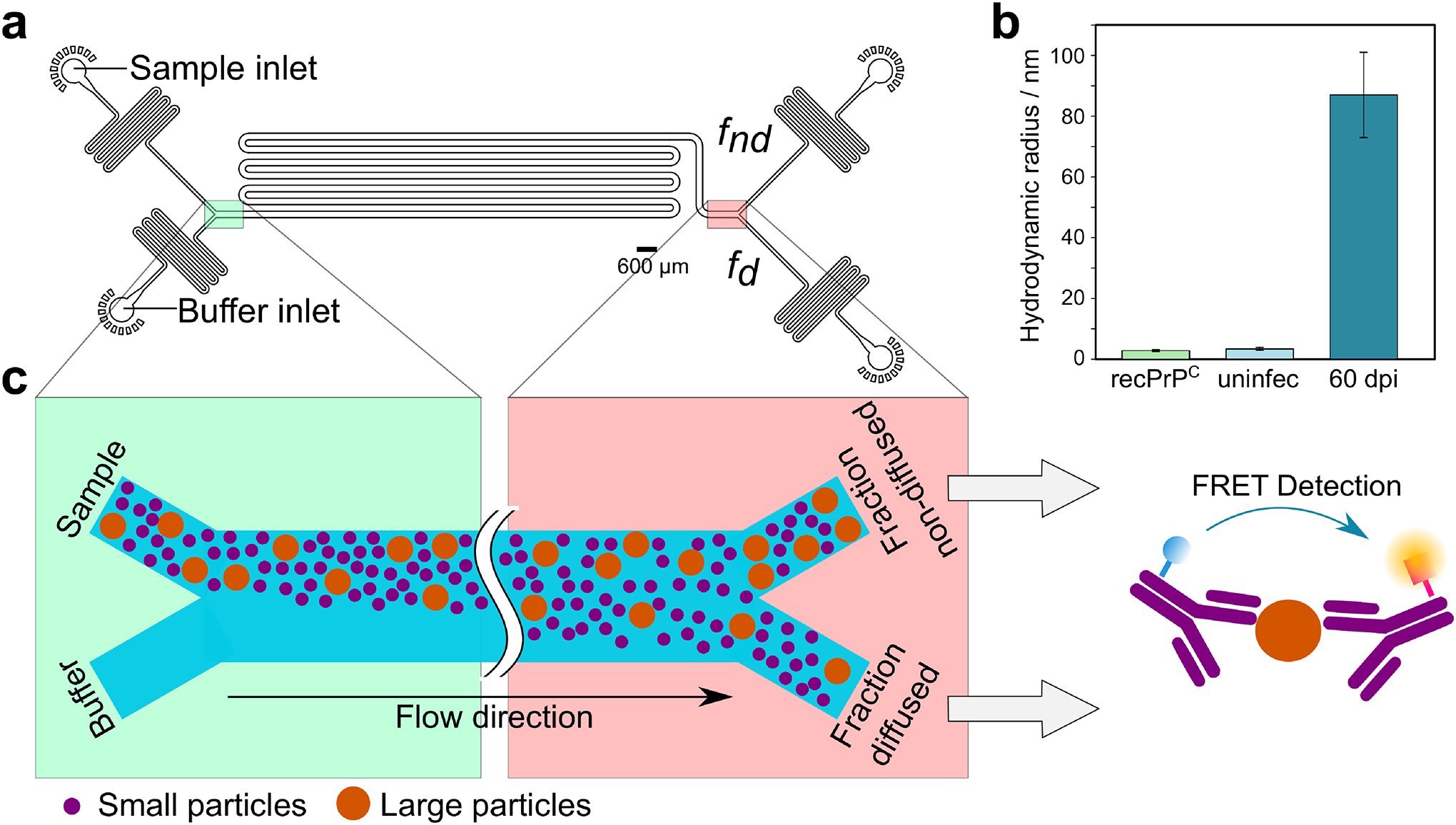
(a) Layout of the microfluidic device used to size prions in brain homogenate. The highlighted regions are shown schematically in c. (b) Measured hydrodynamic radii of recombinant PrP (”recPrPC”, 2.5 ± 0.3 nm), brain homogenates from one uninfected tga20 mouse (”uninfec”, 2.8 ± 0.8 nm) and one tga20 mouse 60 days post inoculation (”60 dpi”, 87 ± 10 nm). Data are mean and s.d. from 2 or 3 technical repeats for recPrPC and uninfec; for the 60dpi measurements, the error bar represents the measurement error expected in the diffusional measurement of large particles (40). Note that for prions, which are unlikely to be spherical, the hydrodynamic radius is likely an underestimation of their actual size. Conversion of hydrodynamic radii to numbers of PrP subunits is discussed below. (c) Schematic showing how sample is injected along with buffer into the left side of the device. Particles diffuse laterally into the buffer stream; smaller particles diffuse further than larger ones. The microfluidic channel is eventually split into 2 parts, a diffused and a non-diffused fraction. The concentration of PrP^Sc in each fraction is then determined using an antibody FRET assay. Data behind graphs are available online as Source Data.

Comparison with other disease-associated proteins in vitro.

To further probe the origin of the differences and similarities and compare the observed data in mice to the aggregation of other disease-associated proteins in vitro, we set out to obtain values for the rates of the key processes of growth and multiplication. Growth and multiplication are connected in a positive feedback loop, Fig. 4a, and thus both contribute to overall prion replication, which is reflected in the fact that their rates only occur as a product in the rate of replication, κ = (k_multk_growth)^1/2. In order to dissect the contribution from the two processes, we require an additional measurement of an orthogonal property, such as the average number of PrP subunits in an aggregate. Such a measurement of the average aggregate size under in vivo conditions represents a major challenge. However, microfluidic diffusional sizing coupled to immunochemcial detection allows the determination of the size of PK resistant PrP^Sc aggregates directly in brain homogenate from mice as detailed above (see Fig. 5). Given the measured hydrodynamic radius of 87 ± 10 nm and accounting for the range of possible shapes of the aggregates and the possible presence of molecules other than PrP^Sc in the aggregate, we obtain conservative bounds of between 100 and 100000 molecules of PrP^C per aggregate on average (details in Supplementary Note 4). A number of previous studies have investigated the size of prions by a variety of methods, from electron microscopy imaging of brain homogenate with various levels of purification (45, 46), to live cell imaging (47). While they suffer from different individual drawbacks, they generally find species hundreds of nm in length, with relatively low aspect ratios, consistent with aggregates composed of several hundreds or thousands of PrP molecules. A study by Silveira et al. (48) that measured the infectivity as a function of size, found that particles consisting only of tens of PrP molecules may already be infectious. However, even given the harsh treatment of their brain samples by sonication, the majority of species displayed a hydrodynamic radius between 30 and 60 nm. Our results are therefore consistent with previous measurements and, as the method we present here involves one of the mildest sample preparations, are likely to be a good representation of the in vivo prion size.

The average number of subunits per aggregate, μ, is related to the rates of multiplication, k_mult, and growth, k_growth, by k_mult = κ/μ. This decomposition into growth and multiplication rates is valid for any general growth-multiplication type mechanism, as we outline in Supplementary Note 1 and Meisl et al. (25). For reference, we estimate the rate of multiplication in the brain of tga20 mice for an intermediate average prion size of 3000 monomers per aggregate to be 5·10⁻¹⁰ s−1 and the rate of growth to be 5·10⁻³ s−1, from the average of the rates from all tga20 datasets. To compare these results to the aggregation of other proteins which has been measured in vitro, we use previously published values for the rate constants and extrapolate these to obtain the rates of growth, multiplication and replication at a protein concentration of 135 nM (see Supplementary Note 5), which corresponds to the concentration measured in tga20 mice (26), see Fig. 6. There are clear differences between prion replication in mice and the aggregation of purified PrP in vitro. Most notably, the multiplication rate of prions is orders of magnitude lower than that of purified PrP. These differences in rates quantify the effect of various cellular mechanisms, such as chaperones, whose function is to prevent protein aggregation. In light of this significant decrease of PrP replication in vivo compared to in vitro, it is quite remarkable that the rate of replication of prions is still significantly higher than the in vitro rates of both α-synuclein and tau, proteins whose aggregation plays a central role in Parkinson’s and Alzheimer’s diseases. The high rate associated with prion replication may lie at the core of the reason why prion diseases are generally significantly more infectious and progress more rapidly than these other aggregation-related disorders.

Figure 6: Individual rates in vivo and in vitro.

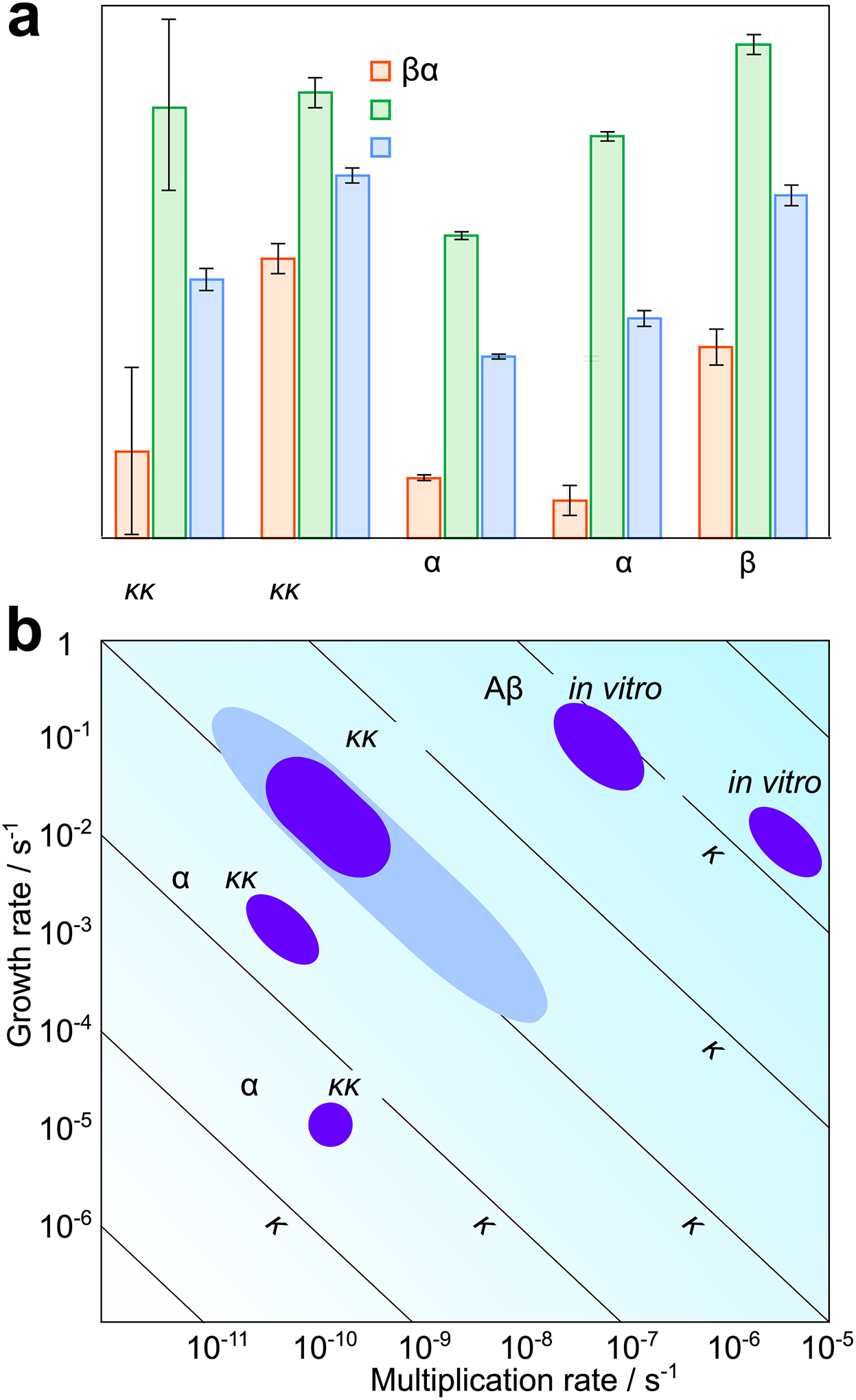
(a) Rates of growth, multiplication and overall replication for prions in tga20 mice and a range of other in vitro systems. (b) A two-dimensional visualization of the values obtained in (a). The growth rate is plotted against the multiplication rate, lines of constant replication rate are shown as diagonals. For prions in vivo, the rates obtained assuming prions are elongated structures and consist between 3000 and 30000 PrP monomers are shown in dark blue, the bounds obtained without these assumptions are shown in light blue. For both panels, the rate constants and error bars were obtained: for in vitro PrP and α-synuclein from Sang et al. (42), for tau from Kundel et al. (49), and for Aβ42 from Meisl et al. (50). The growth and replication rates for the in vitro systems were then calculated at a monomer concentration of 135 nM, which is the concentration of PrP^C in tga20 mice. The error bars for the replication rate of in vivo prions are the range of rates obtained from the different analysis methods and different datasets, the error bars for multiplication and growth are the upper and lower bounds on the average aggregate size (see Supplementary Notes 4 and 5). The height of the bars in (a) is chosen to lie halfway between these bounds. Data behind graphs are available online as Source Data.

Discussion

We have established a general framework for describing aggregation in vivo by using a robust measure, the scaling exponent. The rates and scaling exponents obtained in this manner can be linked to the underlying molecular processes, thus giving insights into the mechanisms of self-replication. Rates of the processes in this mechanism can be estimated and our results reveal that the rate of multiplication of prions in vivo is orders of magnitude slower than that of aggregates of pure PrP^Sc in vitro, but faster than that of α-synuclein and tau in vitro. We designed the application of this method for the case of mammalian prions, but the approach presented here is general and we envisage that it will be widely applicable in identifying the mechanism and rates of self-replication for a range of other aggregating systems in vivo.

Online methods

Mice used.

For PrP^Sc measurements: WT (C57BL/6), WT × Prnp^0/0, tga20 and tga20 × Prnp^0/0 transgenic mice. Both male and female mice were utilized in this study. The mice were inoculated at approximately 2 months of age (62 days +/− 3 days). For SSCA measurements & size determination: six-week old C57BL/6J male mice purchased from Charles River (Germany) were inoculated. Mice were maintained on a 12 h:12 h light/dark cycle at an ambient temperature (21 – 23 °C) and 50–60% humidity.

Inoculation of mice for PrP^Sc and PrP^C measurements.

WT (C57BL/6), WT × Prnp^0/0, tga20 or tga20 × Prnp^0/0 transgenic mice (groups of n=10–12 mice) of either sex were intracerebrally inoculated into the left parietal cortex with 30 μl of 0.01% brain homogenate containing RML5 (passage 5 of Rocky Mountain Laboratory strain mouse scrapie prions). The titer of the RML5 inoculum was 8.9 log(LD₅₀) g−1 of brain tissue. tga20 and Prnp^0/0 mice have been previously described (51, 52), and were maintained under specific pathogen-free conditions. Mice were monitored three times weekly, and prion disease was diagnosed according to clinical criteria including ataxia, kyphosis, stiff tail, hind leg clasp, and hind leg paresis. The mice were sacrificed at time-points throughout the disease incubation period or at the onset of terminal disease when showing signs including weight loss, tremors, slow movements, and kyphosis. All animal studies were performed following procedures to minimize suffering and were approved by the Institutional Animal Care and Use Committee at UC San Diego. Protocols were performed in strict accordance with good animal practices, as described in the Guide for the Use and Care of Laboratory Animals published by the National Institutes of Health.

Inoculation of mice for infectivity measurements.

C57BL/6J male mice were purchased from Charles River (Germany) and allowed at least one week of habituation before inoculations. Experimental manipulations were performed in compliance with the Swiss Animal Protection Law, and approved by the Veterinary office of the Canton Zurich (animal permits 41/2012, 90/2013, ZH040–15). Six-week old C57BL/6J male mice were injected under isoflurane anesthesia in the right hemisphere with 30 μl of RML6 (passage 6 of Rocky Mountain Laboratory strain mouse-adapted scrapie prions, available upon request) at a 10−2 dilution of a 10% homogenate (10% w/v in 0.32M Sucrose, 10^9.02 LD₅₀ units per mL) (55).

At selected time points after prion inoculation, mice were deeply anesthetized and transcardially perfused with cold PBS before brain collection. Animal experiments were performed in compliance with the Swiss Animal Protection Law, under the approval of the Veterinary office of the Canton Zurich (animal permits 41/2012, 90/2013, ZH040–15). Intracerebral injections were performed under isoflurane anesthesia. All efforts were made to prevent or minimize animal discomfort and suffering.

Sample preparation for PrP^C measurements.

10% brain homogenates from RML-infected mice shortly after inoculation and at the terminal stage were measured by the BCA assay. 200 μg of each brain sample was diluted to 60 μl total volume using phosphate buffered saline (PBS). Samples were digested using BenzonaseTM (Millipore) with gentle shaking for 20 min at 37°C, then mixed with 20 μl 4% sarkosyl with shaking for 20 min at 37°C. Samples were then centrifuged at 16,000 g for 30 min at 4°C. The supernatants were carefully collected and stored at −80°C. 50 μl of each sample was injected onto a Fast Performance Liquid Chromatography (FPLC) column (Superose 6, 3.2/30) using running buffer (50 mM NH₄OAc, 0.1% sarkosyl, pH 8.5) at a flow rate of 60 μl/min to collect 24 × 60 μl fractions (see Fig. S8A-C). Fractions 16–19 were pooled and 50 μl/well aliquots were loaded into the ELISA plate (Extended Data Fig. 6). Samples from tga20 mice were diluted 1:2 due to the higher PrP^C levels of this mouse line, and ELISA measurements from these samples were corrected for this dilution factor.

Sample preparation for PK-resistant PrP^Sc measurements.

Protein concentrations in 10% brain homogenates in PBS were measured by bicinchoninic assay (BCA) and samples were normalized using PBS. 27 μl aliquots of each sample were mixed with 1.5 μl 20% sarcosyl at 37°C for 15 min before addition of 1.5 μl PK (Roche) to a final concentration of 100 μg/mL and incubation at 37°C for 30 min. To facilitate PK digestion samples from tga20 mice only were brought to a final concentration of 0.375% sodium dodecyl sulphate (SDS) and were digested at 37°C for 30 min followed by 10 min at 45°C. Protease-digestion was stopped by addition of 1.5 μl 100 mM phenylmethanesulfonyl fluoride (PMSF) and mixed with 11 μl 8 M Gdn-HCl prior to incubation for 5 min at 80°C. Samples were then diluted by addition of 362 μl tris buffered saline containing 0.1% Tween-20 (0.1% TBST) for analysis by an enzyme-linked immunosorbent assay (ELISA).

Sample preparation for total PrP^Sc measurements.

The precipitation of PK-resistant and PK-sensitive PrP^Sc was performed as described previously (53) with minor modifications. Samples were incubated with peptide-coated magnetic beads (M-280; Invitrogen) for 2 h at 37°C with constant shaking. The beads were washed five times with buffer before denaturation with 0.1 M NaOH and neutralization with 0.3 M NaH₂PO₄. The levels of now disaggregated PrP were then measured by ELISA.

ELISA measurements.

PrP was measured by a standard ELISA assay using 96-well plates precoated with 2.5 μg/ml POM-2 antibody (54). Bound PrP was detected using a biotinylated POM-1 antibody (54) (50 ng/ml), followed by streptavidin-HRP (25 ng/ml) and a 1-Step Ultra TMB-ELISA substrate (Thermo Fisher Scientific) (see Fig. S8D,E). POM-1 was biotinylated using the EZ-Link^™ Sulfo-NHS-LC-Biotinylation Kit (ThermoFisher Scientific). The reaction was stopped by addition of an equal volume of 2 M sulfuric acid, and the plate was read at 450 nm using an iMark microplate reader (Bio Rad, Hercules CA). RML prion-infected and uninfected control brain samples were included in every experiment. Samples were run in triplicate within each ELISA plate and PrP concentrations interpolated from a standard curve generated using recombinant PrP where possible. Independent ELISAs were performed 3 times.

Immunoblotting.

Samples were digested with 20 μg/mL PK, or left undigested, for 30 min at 37°C, then mixed with an equal volume of 2x LDS loading buffer (Invitrogen) and heated to 95°C prior to electrophoresis through a 10% Bis-Tris gel (Invitrogen). Samples were transferred to a nitrocellulose membrane by wet blotting. For dot-blotting, 10 μl of undigested samples were made up to 50 μl with 2x LDS and transferred to a nitrocellulose membrane using the 96-well Bio-Dot apparatus (BioRad) under vacuum. The membrane was then removed for incubation in the presence of antibodies. Proteins were detected with anti-PrP antibody POM19 (67 ng/ml) followed by an HRP-conjugated anti-mouse IgG antibody (1:15,000; approximately 53 ng/ml)(Jackson Immunolabs, 115-035-003, polyclonal). Signals were visualized using a chemiluminescent substrate (Supersignal West DuraR, ThermoScientific) and an LAS-4000 imager (Fujifilm).

Standard Scrapie Cell Assay (SSCA) for determination of infectivity.

CAD5 cells were grown with standard OFBS Medium (Opti-MEM containing 10% FBS, 1% streptomycin and penicillin, 1%Glutamax; Gibco) in a T150 cell culturing flask. Standard scrapie cell assay was performed according to published protocols (56), with minor modifications. One day prior to infection, 10000 CAD5 and CAD5 KO cells lacking PrP^C expression were plated with 100 μL OFBS in 96-well cell culture plates (TPP) and incubated at 37°C with 5% CO₂. On the following day, 100 μL of brain homogenate diluted in OFBS mixed with 0.01% brain homogenate from C57BL/6J-PrnpZH3/ZH3 mice (57) to provide a complex matrix was added to the cells for the infection. To establish a standard curve for infection, a 1:5 serial dilution of RML6 brain homogenate (20% w/v in 0.32M sucrose, 109.2 LD50 units per mL) was used with a range from 10⁻³ to 6.4·10⁻⁸. For each sample, three different dilutions were performed ranging from 10⁻³ to 10⁻⁵. To control for residual inoculum, CAD5 KO cells were incubated with RML brain homogenate corresponding to the highest concentration of the standard (0.01%). CAD5 cells were incubated with (0.01%) non-infectious brain homogenate (10% w/v in 0.32M sucrose) to control for efficient PK (Roche) digestion and for computing the background of the assay. Three days following infection, cells were split 1:8 into new 96 well plates containing fresh OFBS. After reaching confluence, two additional 1:8 splitting steps were performed, corresponding to days 7 and 10 post infection. On day 14 post infection, ELISPOT membranes (Millipore) were activated by adding 50 μL of filtered ethanol/well, washed twice with 160 μL PBS and nearly 40000 cells per well transferred onto the membrane and dried with a plate thermomixer (Eppendorf) at 50°C. After drying, plates were stored at 4°C until lysis and digestion. 50 μL of 0.5 μg/mL PK in lysis buffer (50 mM Tris-HCl pH8, 150 mM NaCl, 0.5% w/v sodium deoxycholate, 0.5% w/v Triton-X-100) was added to each well and incubated for 90 minutes at 37°C. Following incubation, vacuum was applied to discard the contents and wells were washed twice with 160 μL PBS. To stop digestion, 160 μL of 2 mM PMSF (Sigma Aldrich) diluted in PBS was applied to the membrane and incubated at room temperature for 10 min. Tris guanidinium thiocyanate was prepared by diluting 3 M guanidinium thiocyanate in 10 mM Tris HCl pH8, and added subsequently with a total volume of 160 μL/well and incubated for 10 min. Supernatant was discarded into 2M NaOH and membrane was washed seven times with each 160 μL PBS and blocked 1 h with 160 μL Superblock (Thermo Scientific) prepared in MilliQ. Remaining blocking solution was removed under vacuum and 50 μL POM1 antibody (54) was applied at a concentration of 1:5000 diluted in TBST (10 mM Tris HCl, pH 8, 150 mM NaCl, 0.1% (v/v) Tween 20) containing 1% (w/v) non-fat dry milk for 1 h. Supernatant was discarded and wells were subsequently washed seven times with TBST under vacuum. 50 μL of anti- IgG1-AP (Southern Biotechnology Associates) was used with a 1:4500 dilution in TBST-1% (w/v) non-fat dry milk and incubated for 1 h. Discarding of the supernatant and washing was performed in the same way as for the POM1 antibody. 50 μL of AP dye (Bio-rad) for the reaction was applied and incubated for 16 minutes. Membrane was washed twice with water, dried and stored at −20°C in dark. Quantifications of the membranes were done using ImageJ (open source) with optical density, allowing to distinguish between spots (representing cells that contain PK-resistant PrP) and clear areas.

Measurement of average size of PK resistant PrP^Sc aggregates in brain homogenates by Immuno-Diffusional Sizing.

Sample preparation:

The mouse brains were washed with ethanol (2x, 70%) and sterile PBS (4x). Then they were homogenised in an eight-fold amount of PBS to prepare a 10% wt. solution with the Ribolyzer tube (speed 6.5, 4× 35s). After the first homogenisation step the tubes were cooled down on ice and the step was repeated 2 more times. The homogenates were centrifuged (700 g, 3 min). The supernatant was collected for further use and the pellet was discarded. Before injection into the microfluidic device, the brain homogenate (BH) samples were diluted to 1% on tris buffer (50 mM, pH 7.4, 1% wt. BSA). PK-digestion: tga20-RML infected 10% BH were diluted to 2% in PBS. 10 μl of PK (1000 μg/ml, Cf = 50 μg/ml) was added to 190 μl of 2% BH. The mixture was incubated for 2 hours at 37°C under continuous shaking at 650 rpm. The digestion was stopped by addition of PMSF to a final concentration of 3 mM and incubation for 15 min at 25°C with continuous shaking at 750 rpm. The samples were analysed in parallel with Western Blot. For better results, the sample were injected fresh after PK-digestion directly into the microfluidic device.

Diffusional Sizing in Microfluidic Devices:

The samples were loaded in 1 ml plastic syringes and injected into a microfluidic device with an H-filter geometry (58), using positive flow control with Nemesys syringe pumps. For the non-infected tga20 sample the flow rates for BH and buffer were 95 and 105 μl/h respectively, giving a total flow rate of 200 μl/h with a channel width of 200 μm. For the prion-infected tga20 the flow rates for BH and auxiliary buffer were 38 and 42 μl/h respectively, giving a total flow rate of 80 μl/h with a channel width of 80 μm. Wider channels were required for the non-infected samples, as the diffusion the small particles detected in those conditions would fully diffuse in a 80 μm wide channel (see Supplementary Note 4).

Immunodetection via TR-FRET (PrP^C of non-infectious brain homogenate):

Concentrations in the diffused and non-diffused fractions were determined using a FRET antibody pair consisting of Eu-POM19 antibody and APC-POM1 antibody, as detailed previously (43). Each aliquot extracted from the outlets (25 μl/well, in triplicates) was mixed with the antibody pair, Eu-labelled POM1 and APC-labelled POM19 (5 μl each) in a white 384 Opti-well® plate (Perkin Elmer). A standard curve of PrP^C from 9.4 nM to 0.05 nM diluted in Tris buffer (50 mM, pH 7, 0.1% BSA) was included for every experiment. After shaking (10 min, RT, 300 rpm), the plate was incubated overnight at 4°C before measuring it. The FRET signal was measured using the time-resolved fluorescence mode (emission at 615 nm, second emission at 665 nm), with the Envision® Platereader (Perkin Elmer).

Immunodetection via ELISA (PrP^Sc after PK-digestion):

PK-digested brain homogenate was injected into a microfluidic device. In order to disassemble the fibrils for detection with sandwich ELISA, aliquots of the samples extracted from each of the diffused and non-diffused outlets (162 μl) were mixed with NaOH (21 μl, 0.5 M) and incubated for 10 min at RT under continuous shaking (700 rpm). 24 μl of neutralising buffer, NaH2PO4 was then added to the mix and incubated for 10 min at RT under continuous shaking (700 rpm). PrP concentrations in the diffused and non-diffused fractions were determined using sandwich ELISA. The selected wells of a transparent 384-well high-binding plate were coated overnight at 4°C with 50 μl of the capture antibody POM1 (400 ng/ml) in coating buffer (0.1 M Na2CO3/NaHCO3). The plate was aspirated four times in washing buffer (PBS, 1% Tween) before the addition of 100 μl/well of blocking buffer (5% TopBlock in PBS-T) and incubated for 2h at RT. The plate was washed 4 times four times in washing buffer before addition of the samples. A standard curve of recombinant mPrP was included, from serial dilutions 1:2 starting from 0.217 nM to 53 fM. Recombinant and brain samples were loaded into the plate (50 μl per well) and incubated for 1.5 h at RT. The plate was then washed four times with PBS-T buffer. The detection antibody, biotin-labeled POM19 (50 μl, 400 ng/ml) was added in sample buffer (1% Top-Block in PBS-T) and incubated for 1h at RT. The plate was then washed for times with washing buffer. Avidin-HRP (50 μl, 2.5 μg/ml) diluted in sample buffer was added and incubated for for 1 h at RT. The plate was once again washed four times with washing buffer, before adding 50 μl/ well of stabilised TMB. After 15 min incubation, the reaction was stopped by addition of H₂SO₄ (0.5 M, 50 μl/well) and the absorbance read at a wavelength of 450 nm using the Envision® Platereader (Perkin Elmer).

Calculation of hydrodynamic radius:

To convert the measured ratio of diffused to non-diffused signal to a hydrodynamic radius, particle-based simulations were performed in Matlab (44). The general method was developed and validated in Arosio et al. (59) and we here performed additional validation using the same device design and a FRET detection on well-characterised insulin aggregates (see Extended Data Fig. 5 for simulation results and validation).

Fitting of PrP^Sc concentrations to obtain replication rates.

The fits of the data to a logistic function, equation (1), was performed by simple least squares assuming homoscedastic noise using the Amylofit platform (30), which uses python’s scipy package. The noise in the measurement itself (ELISA) is expected to be largely independent of the signal strength. The slight increase in noise at later times thus likely reflects the animal-to-animal variation. To minimise the complexity of the model and the danger of over-fitting we do not attempt to model this variation explicitly and instead assume homoscedastic noise. Allowing for heteroscedasticity is unlikely to change the results, given that our conclusions are robust even with respect to fitting the data with a different model (see Supplementary Note 2).

Extended Data

Extended Data Fig. 1. Comparison of infectivity and PrP^Sc amounts from Sandberg et al.

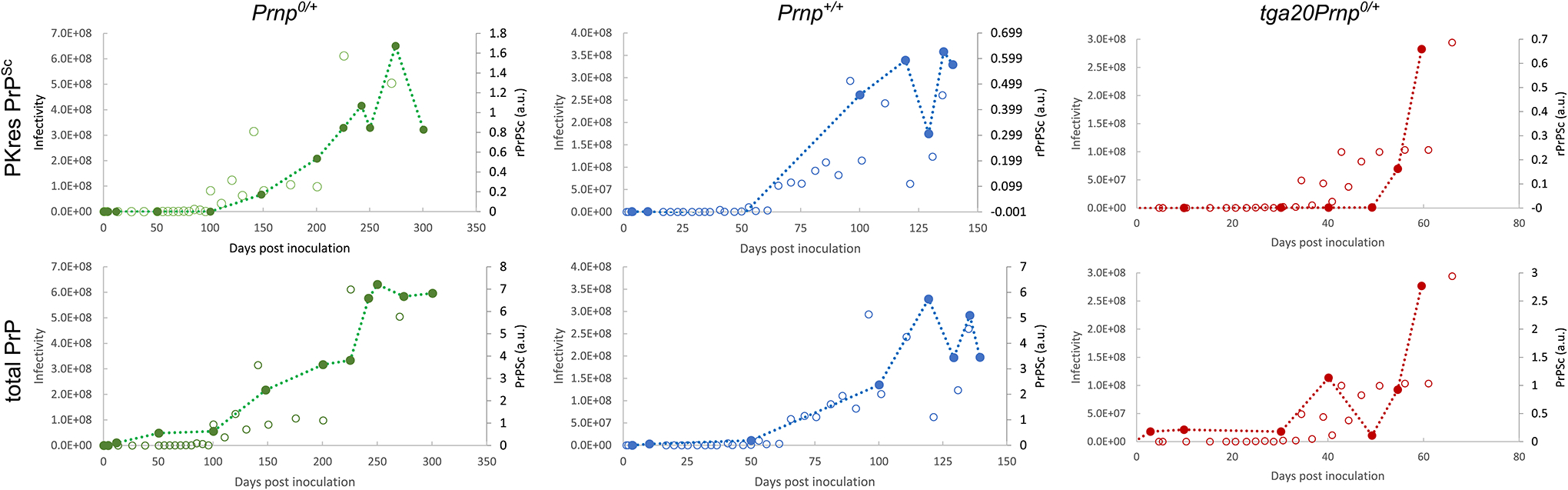
The data (open and filled circles) were obtained from Sandberg et al.[27] Fig. 1 (PrP measurements, filled circles) and Fig. 2 (infectivity measurement, open circles).

The infectivity data are given on a logarithmic scale but are here plotted on a linear scale, with the corresponding values given on the left axis. The PrP^Sc measurements are plotted on the right axis. Dotted lines connect the PrP^Sc measurements and are a guide to the eye. There is no clear systematic difference between PrP^Sc and infectivity when they are rescaled and both plotted in linear space. Data behind graphs are available as Source Data.

Extended Data Fig. 2. Sigmoidal and exponential fits of PrP^Sc measurements obtained here.

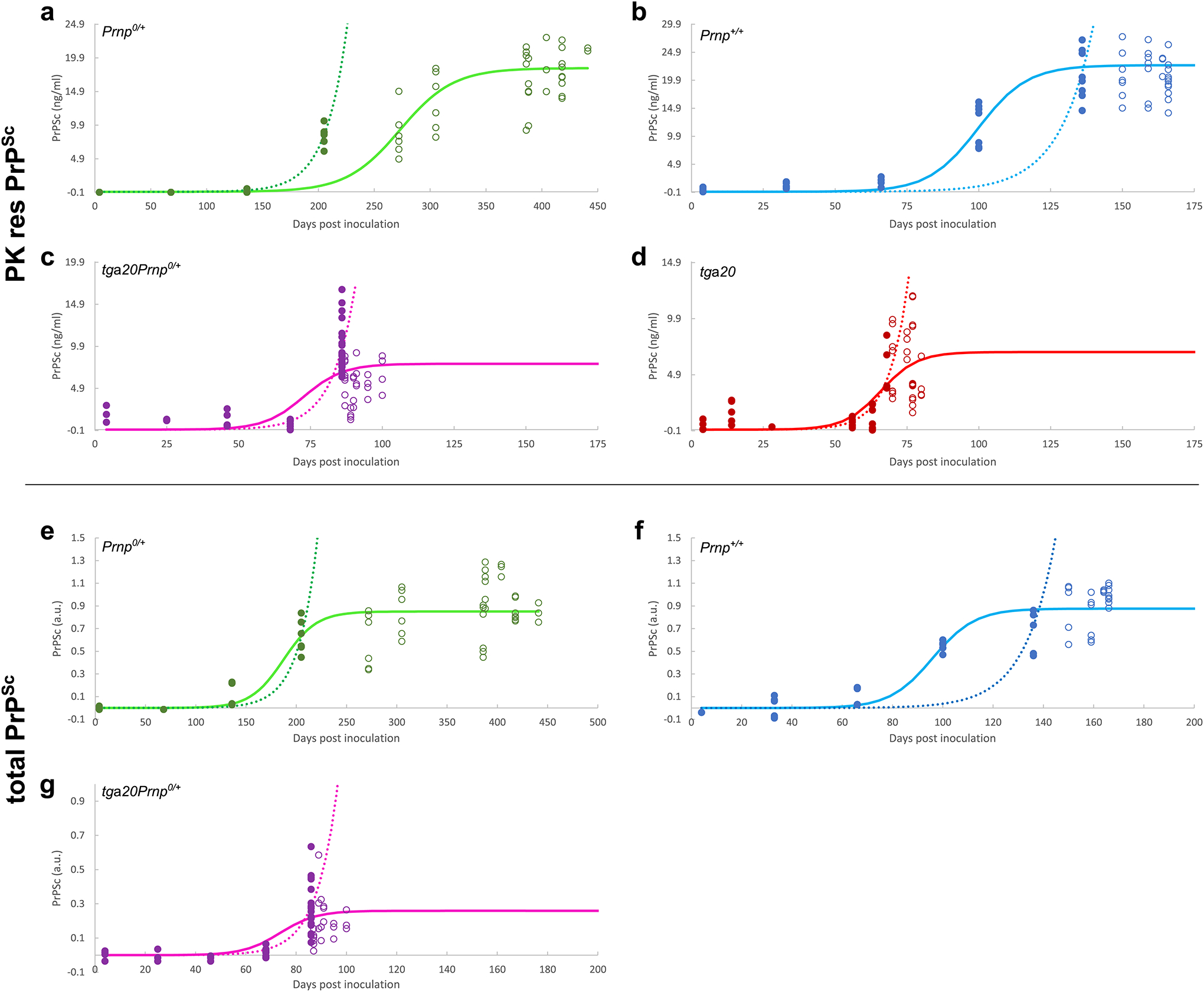
Data as shown in the main text (a-d), as well as the data obtained without PK digestion (e-g), fitted to both a sigmoidal function (solid line) and a simple exponential (dotted line). All data points (filled and open circles) are used in the sigmoidal fits, only pre-plateau data points (filled circles) are used in the exponential fits. The data include samples from different mice as well as technical repeats of the ELISA measurements (3–4 at each timepoint). Data behind graphs are available as Source Data.

Extended Data Fig. 3. Sigmoidal and exponential fits of data from Mays et al.

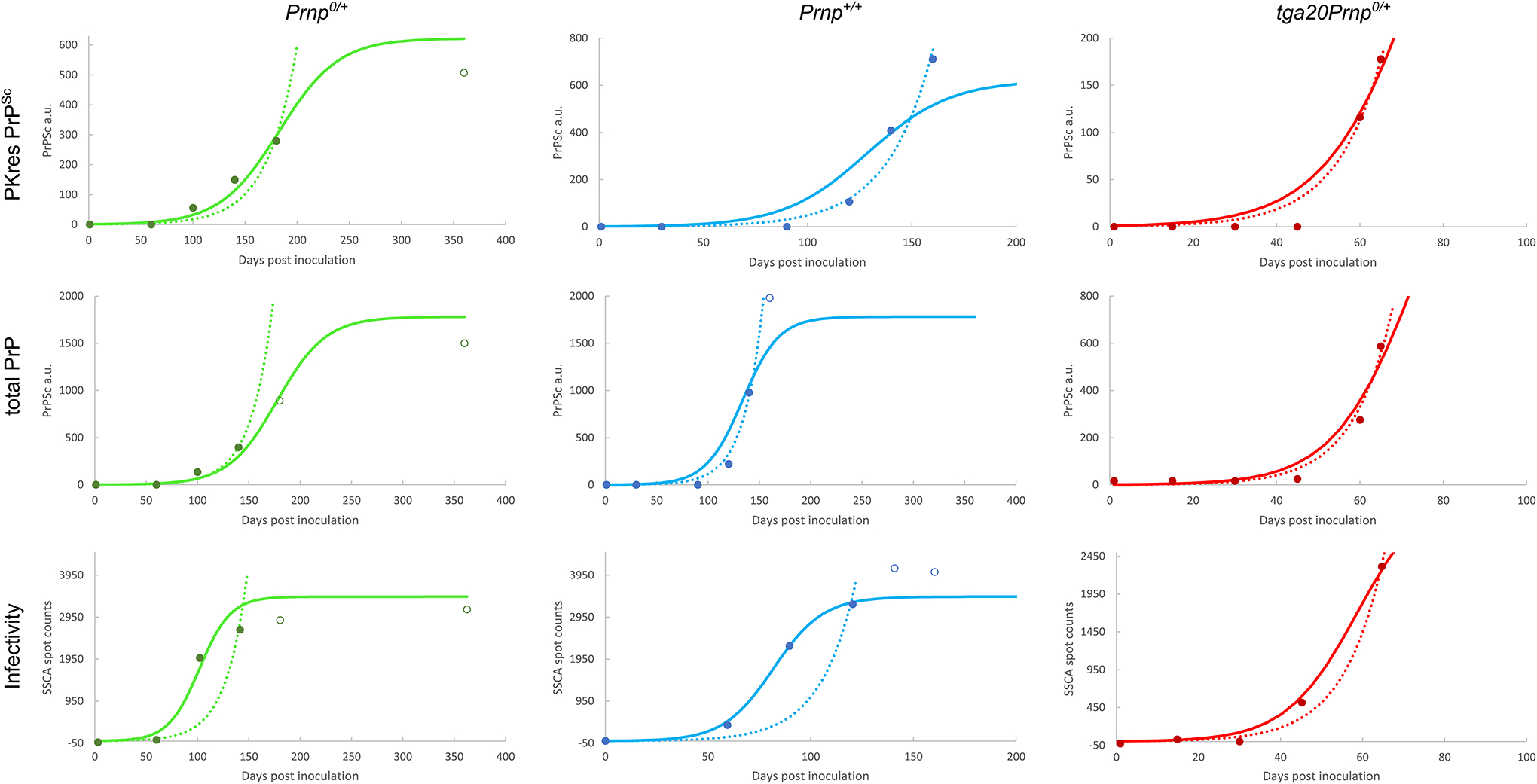
The data (open and filled circles) were obtained from Mays et al. [26] Fig. 2 (PrP measurements) and Fig. 4 (infectivity measurement). In the original paper the data are given for 10 different size fractions, the data here are a sum of all fractions. Fits to both a sigmoidal function (solid line) and a simple exponential (dotted line) are shown. All data points (filled and open circles) are used in the sigmoidal fits, only pre-plateau data points (filled circles) are used in the exponential fits. Data behind graphs are available as Source Data online.

Extended Data Fig. 4. Sigmoidal and exponential fits of data from Sand-berg et al.

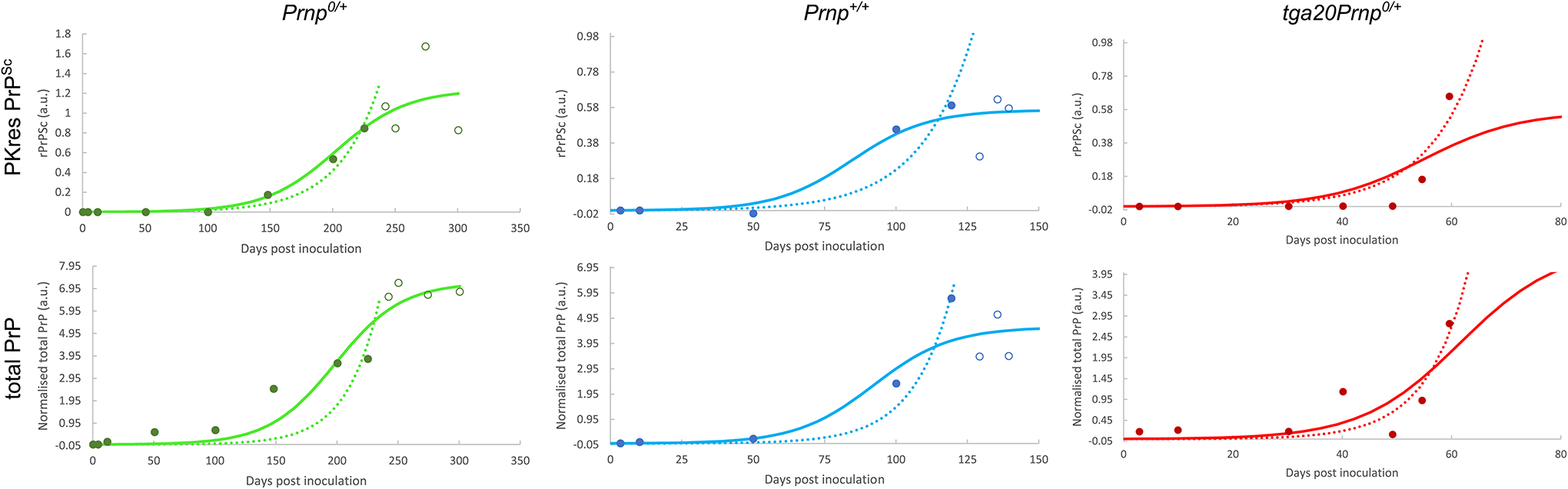
The data (open and filled circles) were obtained from Sandberg et al.[27] Fig. 1. The infectivity data are given on a logarithmic scale and are analysed separately in Figure 1 of the main text. Fits to both a sigmoidal function (solid line) and a simple exponential (dotted line) are shown. All data points (filled and open circles) are used in the sigmoidal fits, only pre-plateau data points (filled circles) are used in the exponential fits. Data behind graphs are available as Source Data.

Extended Data Fig. 5. Simulation and validation of microfluidic sizing.

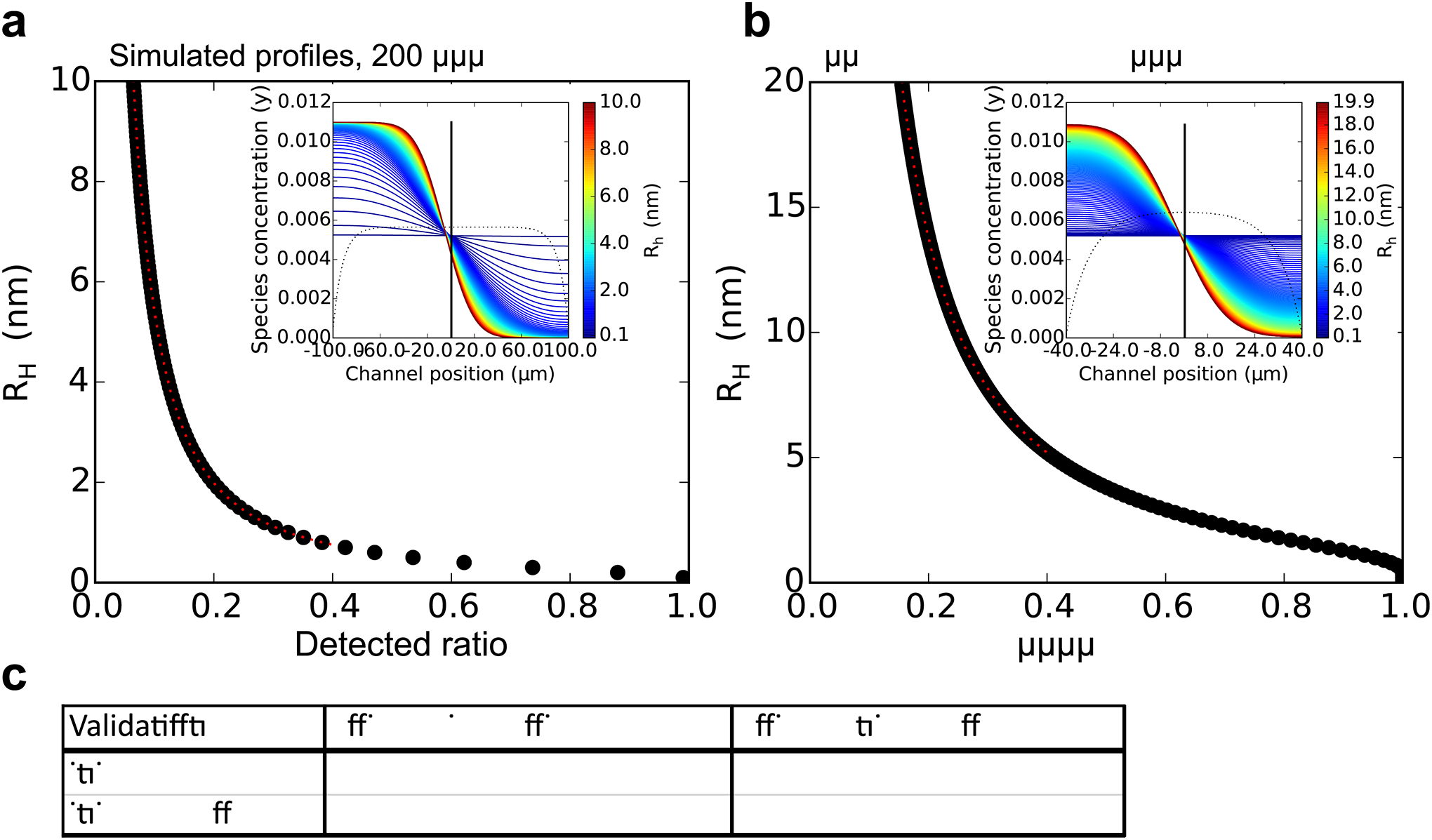
(a,b) Linking the ratio of concentrations in the diffused and the non-diffused halves of the channel to the hydrodynamic radius was accomplished by solving the diffusion equation for the relevant device geometry using finite element integration software. Shown are the results of simulations of the diffusion profiles (inset) and ratio of intensities from the non-diffused channel and the diffused channel, f_nd/f_d, for species with a range of hydrodynamic radii, for the device with 200 μm and 80 μm channel width, respectively. (c) Validation was performed using lyophilised human insulin (Sigma-Aldrich UK). An insulin stock of 10 mg/ml was prepared in 50 mM HCl, filtered through a 22 μm filter. The concentration was measured in the NanoDrop 2000c (ThermoFisher Scientific) by UV absorbance at 276 nm, using an extinction coeffcient value of 1 for 1 mg/ml[60]. Insulin hexamer was prepared as described previously[61]. Monomeric or hexameric samples were injected into the microuidic device at a total flow rate of 400 μl/h, using a flow ratio of 19:21 protein to auxiliary buffer. For detection, the commercial HTRF immunoassay kit was used (Cisbio Bioassays, Codolet, France). Samples after diffusion (2μl per well) were mixed with the antibody-pair (18 μl per well) and incubated for 30 min at room temperature. The TR-FRET readings were performed in Clariostar (BMG Labtech) in the time-resolved fluorescence mode, simultaneously with a standard curve made of 1:2 serial dilutions starting from 2 nM insulin. Quoted values are hydrodynamic radii, errors are standard deviations from 3 repeats, literature values from Oliva et al.[62].

Extended Data Fig. 6. Separation and quantification of PrP^C and PrP^Sc from prion-infected animals by centrifugation and size exclusion chromatography.

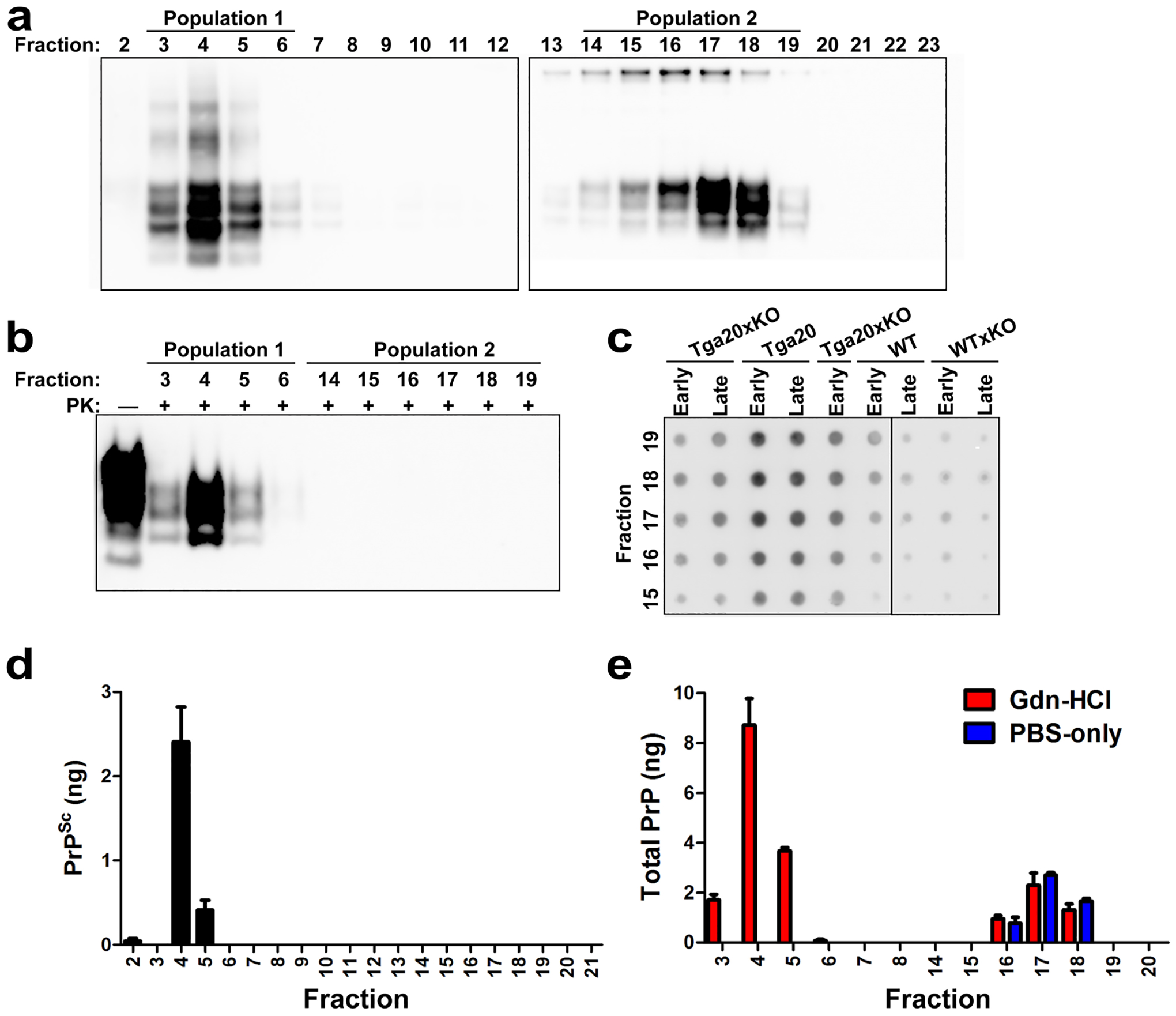
(a) Brain homogenate from a WT mouse at the terminal stage of disease was subjected to centrifugation followed by FPLC. Aliquots (10 μl each) from fractions 2–12 and 13–23 were analysed by SDS-PAGE and western blotting without PK digestion was used to monitor PrP elution from the column, and revealed two distinct populations (indicated at top of panel a). (b) PK digestion (20 μg/mL) of aliquots from fractions 3–6 (PrP^Sc) and 14–19 (PrP^C) in (A) was used to reveal proteinase-resistant PrP^Sc. (c) Aliquots (10 μl total) from fractions 15–19 of mice (genotype indicated) from shortly after inoculation and at the terminal stage of disease, labelled “early” and “late” respectively, were assessed by semi-quantitative dot blotting. PrP^C was found primarily in fractions 16–19. (d) Levels of PrP^Sc in aliquots (10 μl total) from (a) as assessed by peptide ELISA. Values were interpolated from a standard curve (R² = 0.96) generated using recombinant mouse PrP. (e) Aliquots (10 μl total) from (a) were mixed with an equal volume of 8 M Gdn-HCl or PBS and heated for 5 min at 80°C prior to ELISA. Gdn-HCl denaturation increases the signal intensity of PrP^Sc by its disaggregation but does not alter the PrP^C signals[63,64]. Samples were run in triplicate and the values were interpolated from a standard curve (R² = 0.98) generated using recombinant mouse PrP.

Data availability

All data generated or analysed during this study are included in this published article (and its supplementary information files).