Evaluation framework for systems models

Abstract

As decisions in drug development increasingly rely on predictions from mechanistic systems models, assessing the predictive capability of such models is becoming more important. Several frameworks for the development of quantitative systems pharmacology (QSP) models have been proposed. In this paper, we add to this body of work with a framework that focuses on the appropriate use of qualitative and quantitative model evaluation methods. We provide details and references for those wishing to apply these methods, which include sensitivity and identifiability analyses, as well as concepts such as validation and uncertainty quantification. Many of these methods have been used successfully in other fields, but are not as common in QSP modeling. We illustrate how to apply these methods to evaluate QSP models, and propose methods to use in two case studies. We also share examples of misleading results when inappropriate analyses are used.

INTRODUCTION

Although quantitative systems pharmacology (QSP) models have been used to save substantial time and money in drug development, their use is not as widespread as might be expected from these benefits. Lack of buy‐in from stakeholders is a major hurdle to adoption and can, in part, be attributed to lack of confidence in QSP models and their predictions. In this work, we make the case that standardization of model evaluation methods within the biotechnology/pharmaceutical (biopharma) community would support more extensive use of QSP models. For context, we position our proposed framework for model evaluation within the broader process of model development. However, we primarily focus on methods for model evaluation.

We begin by laying out the case for why model evaluation is key for expanded use of QSP models, and how it fits into other aspects of QSP modeling, such as model planning and model building. We also review prior work related to model evaluation. We then go into detail about methods that can be used for model evaluation. We conclude with comments about documentation, software, and infrastructure to support model evaluation.

What is a QSP model?

By definition, QSP models incorporate mechanistic details. ¹ For our purposes, we will define a QSP model as a mathematical model that incorporates some mechanism and examines some pharmacological effect, but may consist of even a single equation (cf. Aksenov et al. ² ). In contrast, Sorger et al. ¹ require multiple equations in their definition of a QSP model, however, they do not state how many are required. We allow a QSP model to have only one equation as this provides logical consistency, just as a 1 × 1 matrix is still a matrix. Similarly, we also allow that a mechanistic QSP model may span only a single spatial or time scale (cf. Hartmann et al., ³ Nazari et al. ⁴ ). Although many QSP models consist of ordinary differential equations (ODEs), other types of equations can be used, ⁵ and our remarks apply more broadly. Physiologically‐based pharmacokinetic (PBPK) models generally do not include pharmacological effects, but can be coupled to a pharmacological effect model to make a QSP model.

In summary, our minimal requirements that define a QSP model are as follows:

1. a mathematical model, with at least one equation; that

2. incorporates some level of mechanistic detail (could be semimechanistic); and

3. can be used to quantitatively explore the effects of an existing or hypothetical therapy.

Two notable features of QSP models set them apart from empirical models, such as many compartmental pharmacokinetic (PK)/pharmacodynamic (PD) models. The first is their mechanistic basis. Incorporating relevant biological mechanisms in the model enables predictions into realms that are not feasible with empirical models. For example, DILIsym (Simulations Plus) incorporates metabolic pathways in the liver to predict toxicities before a drug is ever tested in humans. ⁶ , ⁷ The second notable feature is the ability to encompass disparate types of information, including mechanistic understanding and parameter estimates based on data. This ability to combine all relevant information into a single, predictive model provides the strongest possible foundation for rational drug design and decision making.

QSP models can benefit drug development

Successful drug research and development (R&D) requires tremendous time and financial resources. Achieving one approved drug in the United States can take over a decade ⁸ and can cost more than $1.8 billion. ⁹ Mechanistic QSP models can substantially reduce time and cost. An early example of a QSP model for type 2 diabetes reduced an estimated 40% of the time and 66% of the cost of a phase I trial. ¹⁰ QSP models also have the potential to substantially improve efficacy and safety. ¹¹ QSP and other mechanistic systems models are thus increasingly used to support decisions in R&D, including regulatory decisions. A recent publication by authors at the US Food and Drug Administration (FDA) acknowledges the value of QSP models, stating “published QSP models have demonstrated the utility of QSP modeling in pharmaceutical research and development.” ¹²

Problem: QSP models are not getting used as much as they could

Despite their demonstrated value in R&D and regulatory decision making, QSP models are not as widely adopted as they could be. ¹³ While some pharmaceutical companies have embraced QSP modeling as an integral part of their R&D decision making, others remain reluctant to adopt QSP modeling. Similarly, although regulatory submissions with the FDA increasingly include QSP models, ¹⁴ these models have largely been in the discovery space and have mostly been used as supporting evidence in a larger evidentiary package. ¹⁵ What prevents QSP models from being more widely adopted?

Reasons include model complexity, lack of consensus on evaluation, short timelines

A 2019 survey of over 100 QSP modelers ⁵ identified several major impediments to greater adoption of QSP modeling, in particular: lack of scientists with appropriate training, budgetary and infrastructure constraints, and lack of management interest and/or support. Of these impediments, budgetary and infrastructure constraints can be a result of lack of management interest and/or support. In our experience, a major obstacle to management or stakeholder buy‐in is lack of confidence in a model and its predictions. In order to rely on a mathematical model for decision making, the model needs to be evaluated to understand the uncertainty in its predictions. This is especially important when QSP model predictions are applied in the absence of opportunities for comparison with experimental data, such as in target identification or feasibility assessment settings.

Evaluation standards exist for population PK/PD models (PopPK/PD), which include diagnostic visual predictive checks and shrinkage plots, ¹⁶ and for the use of PBPK models, which include analyzing the effect of perturbation of uncertain parameters on model results. ¹⁷ , ¹⁸ However, the QSP modeling community is still in the process of establishing standards for QSP model evaluation. For small QSP models in data‐rich settings (e.g., Aksenov et al. ² ), evaluation methods such as those used for PopPK/PD models can be applied. However, QSP models are often so complex and data are so sparse that model evaluation is challenging. ¹⁵ , ¹⁹ Because there are no standards for QSP model evaluation, evaluation approaches are tailored to specific models. The complexity of the models and the lack of standard analyses make reviews of QSP models significantly more time‐consuming than that of PopPK/PD models.

A consensus on feasible standards for QSP model evaluation is needed

A framework of feasible evaluation standards that is agreed upon and applied by the wider modeling community could increase the adoption of QSP models. ¹² , ¹⁵ The FDA employees recently wrote specifically about this need: “Quantitative and statistical criteria needed to assess model quality and assess model uncertainty are lacking.” ¹² As more QSP models are used to make business decisions, submitted to journals, or included in regulatory submissions, there is a need for a rigorous framework to evaluate QSP models and their predictive capability. It is our view that establishing such a framework is a central challenge that needs to be addressed to achieve greater adoption of QSP models in drug development.

We propose a framework for the evaluation of QSP models to contribute to such a set of standards

The purpose of this work is therefore to propose a framework of methods for the evaluation of QSP models, and recommendations for how and when these methods should be applied. This includes consideration of the underlying assumptions of various analysis methods and their appropriate applications, along with examples and some computational information. In order to avoid QSP model evaluation being too complex and time‐consuming to fit within short timelines, we propose that this framework is applied and executed by the model development team to produce a standardized document with the outcomes of the evaluation process. This document can then be reviewed by internal or independent external reviewers, to minimize the workload that the framework imposes on the reviewers.

We make our recommendations in the context of prior work in other fields

An additional goal of this work is to introduce the QSP community to methods that are already widely used in other research fields. Since World War II, researchers in applied mathematics and engineering have been developing model evaluation methods and credibility frameworks for the evaluation of quantitative models. ²⁰ We present our ideas for the evaluation of QSP models within this broader context. Although we refer to QSP models throughout this work, the methods we review apply to mathematical systems models more generally, even those that are not created based on mechanisms.

BACKGROUND: EXISTING FRAMEWORKS IN QSP AND OTHER FIELDS

Right question, right model, and right analysis

The work involved in model development can be summarized by three general categories, which we refer to as the “right question, right model, and right analysis.” ²¹ We describe these categories below:

• Right Question: Mathematical modeling, like many other endeavors, should start with a goal in mind. Determining the purpose of the work prior to commencing model building is necessary to ensure that results will be maximally useful. In drug development settings, the question to be addressed is typically decided by the modeler and project team or a subgroup with the appropriate domain‐area experts, and requires buy‐in from managers and other stakeholders. The question and purpose determined here will impact decisions for the right model and the right analysis, see below.

• Right Model: Once the “right question” has been agreed upon, decisions about an appropriate model need to be made. Decisions of scope, scale, and functional form of the equations of the model depend on the question being addressed and the resources available, including project timelines, access to prior models and code, modeler availability and expertise, software, computing power, access to domain‐area experts, and quality and quantity of different available data types.

• Right Analysis: When using a model to make predictions, we need to determine an appropriate level of confidence in those predictions. The context of use (COU) and risk assessment of the model use should help drive decisions about the types of analysis that should be included. ²² These analyses might include verification of code, unit and system testing, comparison of the model with any available data, and uncertainty quantification (see discussion below).

The planned work for each of these categories is important to establish prior to the modeling, to reduce bias in the results. Additionally, to aid in acceptance of model predictions, it is important to obtain stakeholder alignment for each of these prior to beginning the model development.

Frameworks exist for QSP modeling, but most provide limited details on model evaluation

Multiple groups have proposed QSP modeling frameworks in recent years, and many of these at least touch on all three of the categories listed above. With some exceptions that are detailed below, most previous QSP modeling frameworks provide few recommendations on specific analyses or results that would be most appropriate for the evaluation of QSP models (“right analysis”).

How other QSP frameworks touch on analysis

Even though the focus of many existing frameworks is on addressing the “right question” and “right model,” there are some frameworks that provide general discussion of activities that we consider to be part of the “right analysis.” Model structure uncertainty (“right model”) is often addressed primarily through best practices in model building. ²¹ , ²³ , ²⁴ , ²⁵ , ²⁶ For example, including domain‐area experts in the discussions is considered a best practice for model building.

Uncertainty in model parameters, however, is different, in that there are well‐established methods to quantitatively assess model parameter uncertainty. Friedrich ²³ and Gadkar et al. ²⁴ recommend sensitivity analysis to explore uncertainty. Ribba et al. ²⁷ cite the need for more identifiability analysis to be performed. Allen and Moore ²¹ and Bai et al. ¹² recommend both sensitivity analysis and identifiability analysis for parameters. Cucurull‐Sanchez et al. ²⁵ include recommendations such as “run a sensitivity analysis to identify which parameters have the most effect on model responses and how significant is that effect” and state that “a certain level of structural identifiability analysis of QSP models should be performed and reported as a prerequisite to parameter estimation and as a component of experiment design.” Zhang et al. ²⁸ note that “The more complex these models are, the greater the challenge of reliably identifying and estimating respective model parameters. Global sensitivity analysis provides an innovative tool that can meet this challenge.”

We agree that sensitivity and identifiability analyses are essential in model evaluation, as they inform us whether we can estimate parameters in a model, and how much confidence to have in model predictions. In this work, we make detailed recommendations for these analyses and others. The paper of Cucurull‐Sanchez et al. ²⁵ mentions many of the analyses that we consider; our aim here is to organize these analyses into a framework, and include concepts such as COU and credibility assessment. In addition, we provide additional detail, context, strategies, and resources for these and other types of analyses.

Ideas from other fields: credibility assessment and verification, validation, and uncertainty quantification

In order to end up with the “right analysis,” we introduce some key concepts from other computational fields. In this section, we discuss credibility assessment and verification, validation, and uncertainty quantification (VVUQ). These concepts capture many considerations in assessing appropriate analysis and use of a systems model. ²⁹ A recent publication emphasized these concepts broadly applied to drug development modeling. ³⁰

Credibility assessment of computational models is a general framework that has been developed and applied in engineering and operations research settings for decades. ²⁰ , ³¹ , ³² It has been a major focus of the medical device community in recent years. Because medical device development originated from engineering research, the devices community has drawn heavily from methods and best practices in engineering domains where modeling and simulation is well‐established. These efforts culminated in the publication of the American Society of Mechanical Engineers (ASME) verification and validation (V&V)40‐2018, ²² the first consensus standard on the topic of credibility of computational models for medical device applications.

ASME published V&V40‐2018 to provide guidance for V&V in the medical devices industry. It is based on previous ASME standards for other industries, which in turn drew from the National Aeronautics and Space Administration (NASA) standards (cf. NASA‐STD‐7009 ³³ ). The ASME V&V40‐2018 identifies three key assessments that should be made before model evaluation begins. First, the question of interest is defined as the specific question or decision that the model will be used to address. For example, the model may be intended to inform a prediction of the first‐in‐human dose for a compound to be used in clinical trials.

Second, the COU is the role of the computational model in addressing the question of interest. This includes a description of the key features modeled, the simulations to be performed, the model outputs to be analyzed, and how those results will be used with other (noncomputational) evidence in addressing the question of interest. The COU helps to determine the appropriate level of assessment needed for a model’s intended use. Requiring that credibility assessment be performed in the framework of the COU is a key feature of credibility assessment in the VVUQ literature/ASME V&V40‐2018, and is arguably a major difference from the type of evaluation regularly performed for QSP models. For instance, QSP models are often developed for multiple potential applications (i.e., multiple potential COUs) and are commonly evaluated by comparing model predictions with experimental results under a range of conditions. According to the ASME V&V40‐2018 standard, although such activities are important, it would not be appropriate to refer to the model as generically validated, even with strong validation results in certain settings; the assessment of whether the agreement between the model and experiment is sufficient requires consideration of the COU.

The third stage in ASME V&V40‐2018, after specification of the question of interest and the COU, is assessment of the risk associated with inaccurate predictions from the model. This informs the scope of the model validation process: high‐risk decisions that are based solely on evidence from model predictions require the highest level of assessment as compared to low‐risk decisions where model predictions are used in conjunction with other evidence. The risk is defined as a combination of two factors: (i) the consequence of a bad decision being made (e.g., “major” if there is a possibility of patient death); and (ii) the level of influence of the model on the decision being made (e.g., “moderate” if other information, such as data from animal experiments, will be used in making the decision). Overall, the framework proposed in ASME V&V40‐2018, while developed for medical device applications, is general and can be applied and can add value to a wide range of domains including QSP modeling. Once the question of interest, the COU, and the risk assessment have been determined, the model evaluation analysis in credibility assessment can be described in the broad categories of VVUQ. ³⁴

• Verification checks that the computational implementation correctly encodes the intended mathematical model. Verification is often performed by having the modeler perform some basic checks and/or an independent modeler perform a quality control assessment of the model code.

• Validation assesses how accurately the model captures the behavior of the biological or physical system.

• Uncertainty quantification focuses on estimating the uncertainty due to model structure, data measurements, and parameter estimates. ³⁵ Note that when we say “uncertainty,” we are including both variability and error as sources that contribute to uncertainty in the model response.

MODEL EVALUATION FRAMEWORK

Our framework consists of multiple steps in model evaluation, as shown in Figure 1. We begin by describing the major stages of these activities.

1. Planning the work: In this stage, the model aims, scope, and risk are used to plan the model building and model evaluation (“right question, right model, right analysis”).

2. Building the model: In this stage, the initial model is built. Although this often represents a large part of the time spent on a project, we will not go into detail about this. Instead, we refer the reader to previously‐published frameworks focused on QSP model building for guidance on best practices in building the initial model. ²¹ , ²³ , ²⁴ , ²⁵ , ²⁶

3. Performing the analysis: In this stage, the evaluation plan is carried out. The evaluation framework in Figure 1 shows a workflow and order in which these evaluation activities can be carried out. The inputs to the analysis and evaluation are a detailed plan, an initial model with parameter distributions, and any data that will be used for calibration or model evaluation. The evaluation activities laid out in the workflow are explained in detail in the next section. We recommend that all steps of the planning, model building, and evaluation process are documented for internal and/or external audit purposes.

FIGURE 1.

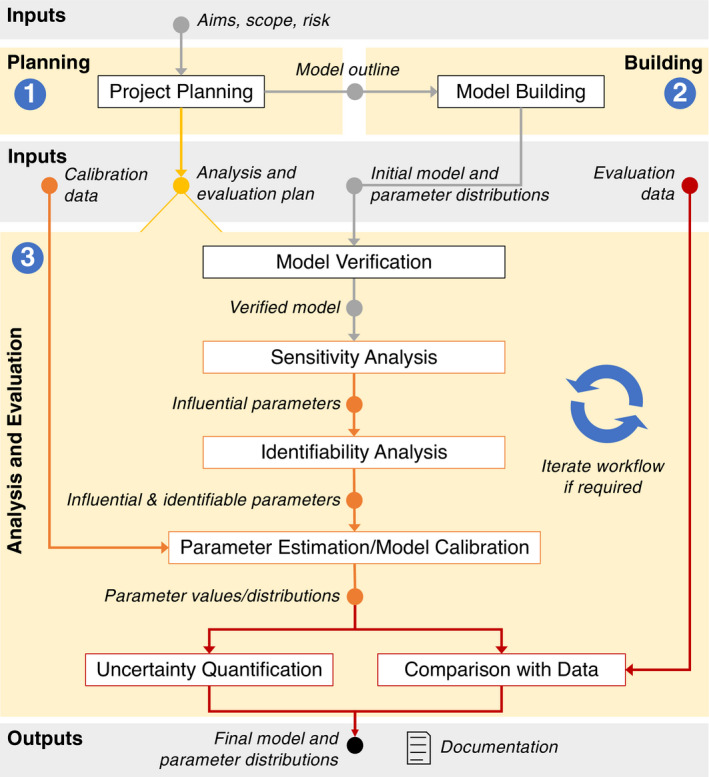
The planning stage of a modeling project includes assessing the context of use of the model and using that knowledge to develop a plan that defines which modeling and model evaluation activities will be performed. Once the initial model has been built, the initial model with parameter distributions, and any available data (for calibration and/or comparison to model predictions) are inputs to the analysis and evaluation. The workflow shows suggested analyses and how they are related to one another. Rectangular boxes represent activities, whereas the inputs and outputs for activities are represented as circles. The final output is a calibrated model with parameter estimates and/or distributions, as well as documentation of the planning, modeling, and evaluation activities that were performed and the results obtained. Analysis and evaluation steps may suggest desired changes in the model. In that case, this new model can undergo the same analysis steps, starting with model verification. See Table 2 for specific documentation recommendations for model evaluation activities

In this paper, we will consider “model evaluation” to include any of the full span of activities that can be performed to evaluate and understand a model and its predictions. We will use “credibility assessment” to mean a formal assessment of model credibility (for example, an assessment that uses the ASME V&V40‐2018 standards), which is primarily applied to models in high‐risk and/or highly‐regulated settings.

Planning the model building and analysis

Defining the aims, scope, and risk in advance of the model building helps to give clear purpose and direction to the project. Depending on the setting, the planning stage may be brief (e.g., for a small model in the discovery stage) or extensive (e.g., for a model used in a regulatory submission). In this section, we describe all steps of the planning stage in nomenclature familiar to the QSP community, but we also include reference to the ASME V&V40‐2018 framework where appropriate.

Model aims and scope

The model aims describe the primary questions that the model is intended to address (cf. ASME V&V40‐2018, ²² question of interest). Typically, there is a decision to be made, and the model will help answer questions to inform this decision.

The model scope includes the model scale and size, which components and pathways will be included, and the level of detail to be used for the modeling (e.g., semimechanistic, or mechanistic but fit‐for‐purpose). As mentioned above, at this point, it is also important to consider constraints such as time, and available resources including data, modeler expertise, and computing power. ²¹ , ²³ , ²⁴ In addition to modelers, domain‐area experts in the disease and relevant biology should be included when defining the model aims and scope, as well as during the model building process. Alignment with these experts should ensure that all parties can have some level of confidence that the science has been appropriately represented in a model. Choices such as model scale, model size, and model assumptions should be made clear, and decisions and assumptions documented.

The COU as outlined in ASME V&V40‐2018 is another important consideration in defining the model scope. This includes what will be modeled and how the model outputs will be used to address the model aims.

Data

Before the analysis can be performed, any calibration and evaluation data should be specified. In addition to evaluating the full model, it can be important to evaluate subcomponents of the model, especially for large models.

• Calibration data: Calibration data are those used to estimate the values of specified parameters in the model. QSP models often use multiple data sources to calibrate different parts of the model, integrating them into a unified model. These data sources can come from a variety of experimental settings: e.g., in vitro or in vivo, preclinical or clinical studies, and patients or healthy subjects.

• Evaluation data: Evaluation (or “validation”) data are used to compare with the model predictions. Although we sometimes use the terminology of model validation in this setting, we prefer the term evaluation, which suggests a spectrum of model prediction quality, rather than a “yes/no” threshold. The COU and risk assessment will determine whether and which data are required to evaluate the model outcomes. For example, in data‐sparse settings, such as discovery or early development phases, preclinical PK/PD data may be used for model evaluation rather than clinical data. On the other hand, in high‐consequence settings with decisions based solely on model predictions, high‐quality and relevant data are necessary to ensure that the model’s predictions are evaluated appropriately.

Model evaluation plan

QSP models can vary significantly in complexity, scope, and application. This makes it difficult to converge on a single set of analyses that is suitable for evaluating all QSP models. What we propose in this work is a systematic framework for selecting the appropriate analyses for a given model and setting.

Plans for model evaluation should be made in advance of performing the model evaluation. It is also important to decide on criteria for certain activities before performing them. Examples include which goodness‐of‐fit criterion to use (e.g., corrected Akaike Information Criterion), or which scenarios and outcomes the model should be able to predict to ensure the model and its implementation perform as intended.

Evaluation plans should be informed by the risk associated with using the model’s predictions. Two major factors determine this risk: the consequence of the decision to be made, and the relative contribution of the model predictions on that decision. In high‐risk settings, a formal assessment may be needed. Note that for small models in data‐rich settings, traditional evaluation methods for (population) PK/PD models may be sufficient. ³⁶

Credibility assessment

When a more formal model evaluation or qualification is needed, we can turn to the approach proposed in ASME V&V40‐2018. The ASME V&V40‐2018 standards base all recommendations of model evaluation on the risk involved in model use. Users can themselves define the level of model evaluation (referred to as a “credibility assessment”) appropriate for the level of risk. Determination of risk is made by considering the question of interest, COU of the model, how much the model will be relied on for a decision, and the seriousness of the consequences resulting from the decision.

Based on these considerations, ASME V&V40‐2018 defines various “credibility factors,” which are specific aspects of the verification and validation activities, and asks the practitioner to set goals for each of the credibility factors based on the overall risk assessment; higher‐risk settings require stricter goals and more model evaluation activities. Kuemmel et al. ³⁷ provide detailed guidance and examples for applying the ASME V&V40‐2018 standards to PBPK models. A similar approach can be used for other types of systems models.

Here, we provide two scenarios with examples of model evaluation choices to illustrate the use of the model evaluation framework. We emphasize that such choices should be aligned with stakeholders before implementation.

Example 1: Potential pathway target

Model Aim: Predict whether targeting a newly‐identified pathway can achieve meaningful therapeutic effect.

Model Scope: The model will be used to support a “go/no‐go” development decision by modeling the level of therapeutic effect possible to achieve with a potential pathway. If the model predicts that the maximum possible effect size is not clinically relevant, then this supports a “no‐go” decision to not develop compounds that target that pathway. The COU is that only the model results will be relied upon for making this decision. There are limited resources, data, and time available for this project. Parameter information will primarily be based on the literature.

The model will be fit‐for‐purpose and mechanistic, based on a first‐principles understanding of the underlying pathophysiology, and will include the potential therapy and its effect on the clinically‐relevant outcome.

Model Risk: Model influence is high because model predictions are the key evidence for go/no‐go decision. Decision consequence is low/medium as the outcome impacts only company decisions but not patient lives. This results in a medium‐level model risk.

Model Evaluation Plan: Verify model implementation and code. Perform a Morris method global sensitivity analysis to prioritize which parameters should be carefully estimated or sourced from literature. Consider including confidence intervals on parameter estimates and predictions. A virtual population approach can be used for exploration of possible effect sizes.

Example 2: Individualized patient dosing

Model Aim: Provide physicians with individualized dosing strategies for combination therapy for a specific disease in renally‐impaired patients who have specific biomarkers.

Model Scope: The COU is that the model will be used to support determination of safe and efficacious individualized dose regimens for renally‐impaired patients. Clinical data at standard dosing regimens are available for patients who are and patients who are not renally impaired.

The model will be a small, semimechanistic QSP model. The model includes compartmental PK models for the therapies, coupled with a semimechanistic model of kidney function that incorporates the effects of the drug therapies.

Model Risk: Model influence is moderately high, because patients will be treated with the predicted dosing strategies, without further clinical data for safety or efficacy beyond the standard‐dose data. Decision consequence is high because the drug combination has significant and irreversible adverse effects at higher doses. This results in a high model risk.

Model Evaluation Plan: Perform all possible VVUQ activities with a focus on using hold‐out data from specific renal‐impairment conditions to qualify whether the model is able to predict outcomes for these patient populations. Because the aim of this work is to provide individualized dose regimens, individual parameter estimation (using nonlinear mixed‐effects modeling) will be performed. For this reason, correct determination of which parameters can or cannot be estimated will be critical for success, and rigorous sensitivity and identifiability analyses will be needed.

Building the model

Building an initial model often represents the majority of time invested in a modeling project. However, in this work, we focus on the model evaluation analysis that is performed once the initial model has been developed. When a model is reused for multiple purposes or is developed as a platform, it is important to ensure that subsequent uses are all within the COU of the model. A good record of the model‐building process can provide the necessary information to decide if such purposes are appropriate.

For guidance and examples on building the initial QSP model based on the model aims and scope, we refer to frameworks such as those by Friedrich ²³ and Gadkar et al., ²⁴ which provide recommendations for best practices. We additionally recommend that specification of initial parameter values and distributions be considered part of the initial model specification. This parameter information is needed in model analyses such as calibration and sensitivity. In the subsequent sections, we assume an initial model has been computationally implemented and initial parameter distributions have been specified.

Performing the analysis and model evaluation

In this section, we discuss model evaluation activities in detail and provide recommendations on when to use a particular method. An overview of a wide range of possible evaluation activities is provided later, in the Documentation section. If at any stage it is decided that a model should be modified or that a different model will be considered, the process can be started from the beginning for the new model.

Verification: basic model and code testing

Verification is an essential step to ensure consistency between the implementation and the mathematical description of the model. In this section, we will focus on model and code verification, rather than verification of the underlying software, such as ODE solvers and optimization algorithms. We do this because most QSP models are developed in standardized environments and simulated using validated ODE solvers (e.g., the SUNDIALS suite by Hindmarsh et al., ³⁸ MATLAB’s ode15s in MATLAB (MathWorks) by Shampine and Reichelt ³⁹ ) with extensive testing performed by the developers. Pathmanathan and Gray ⁴⁰ provide a more‐detailed description of verification methods for ODE models and nonstandard ODE solvers.

Below we list a number of best practices for the verification of models and code:

• Equations: Starting from a mathematical model, we want to make sure that the model implementation matches the original equations. Discrepancies to look for include missing terms and the signs (±) of terms in the right‐hand sides of the equations.

• Initial values and parameter values: An initial value should be provided for each state in the model. Similarly, for every parameter in the model, a nominal (initial) value and distribution should be provided. As a best practice, the source of these values (e.g., a literature reference or a dataset that was used for calibration) should be documented to understand the origin and reliability of each of the values. If any initial or parameter value is undefined, the model cannot be verified and its simulations cannot be reproduced.

• Units: In order to avoid order‐of‐magnitude mistakes, each parameter and state should have units defined. When a parameter or state is dimensionless this should be explicitly indicated. The units should be consistent throughout the model (e.g., all time in hours, all amounts in moles, and all volumes in liters). Using a modeling environment that can automatically check and convert units (e.g., SimBiology) can help enforce a correctly defined and consistent unit system in a model.

• System‐level tests: Basic model simulations should be run to determine if they qualitatively agree with known biology. Additionally, “what‐if” scenarios can be used to investigate a QSP model and its implementation. When model simulations of the scenario agree with anticipated outcomes, this builds confidence in the model and implementation. Conversely, discrepancies can help identify problems with the model definition or implementation. Examples include:

  • ○With increasing dose, does the concentration increase?
  • ○If all clearance routes are blocked, does drug accumulate?
  • ○Do the concentrations ever become negative?
  • ○Do the concentrations remain at zero if no dose is administered?
  • ○If a therapy achieves its effect by modulating the glomerular filtration rate (GFR), is the effect of the therapy enhanced with increasing GFR?

    Each of these scenarios can be evaluated by running a simulation under the specified conditions. Different models can have different tests, so the responsibility of designing these tests lies with the model developer or reviewer. They can be considered “system tests” as they test the full QSP model, in contrast to unit tests, which are commonly used to verify individual aspects of model implementation during development.

• Mass balance: Ensuring mass balance is common practice in PBPK models where it can be used to keep track of the total mass of a drug as it is absorbed, distributed, metabolized, and excreted, and also to ensure that the blood flow through each of the tissues is consistent with the total blood flow. ⁴¹ Similar techniques can be applied to QSP models for PK, but also, for example, in hematological models to track different types of blood cells and ensure they are all accounted for. For disease areas such as metabolic diseases, energy balance can also be applied. ⁴² Lastly, setting up balance equations can also be a way to monitor numerical drift/error that results from numerical integration of the differential equations in a QSP model.

• Reproducibility: A basic principle of scientific methods is the reproducibility of experiments. In mathematical modeling, this translates to being able to reproduce the simulation results from a publication. To facilitate this, published models should include all parameter values and units, as well as the full code that was used to run associated simulations. If any random numbers were generated (e.g., when sampling from a distribution), the method and the random seed should be reported. In addition, using software that is compatible with a common mark‐up language, such as SBML, allows the model to be run in different modeling environments. Sharing the experimental data that were used to estimate parameters would enable review of the model calibration process. Someone implementing a published model should be able to re‐create key figures or predictions just from the information in the publication. ⁴³

Sensitivity analysis

A model output is said to be sensitive to one or more parameters if certain changes in those parameters result in substantial changes in the model output of interest. The parameters that cause substantial changes in model output are called influential parameters. A sensitivity analysis can be used to quantify the extent to which changes in various parameters affect the model output. The more influential a parameter is on a model output, the more important it is that the parameter is well‐estimated, to increase confidence in model output predictions. Chapters 14 and 15 of Smith ³⁵ provide a detailed foundation on the theory of local and global sensitivity analysis.

Sensitivity analysis can be valuable for the planning and prioritizing of experiments to obtain better estimates of influential parameters, in order to improve confidence in model predictions. Sensitivity analysis also provides a method for reducing the number of free parameters in a model. Noninfluential parameters can be fixed (or “frozen”) to nominal values without substantially impacting model output predictions. This reduction in the number of free parameters enables more‐thorough exploration of the subspace of influential parameters, providing greater confidence in model output predictions, and can provide a basis for model reduction. ³⁵ The relative influence of input parameters can also be used to prioritize potential therapeutic targets in drug discovery. ⁴⁴

Local sensitivity analysis

Local sensitivity analysis (LSA) is performed at a single point in parameter space. With a one‐at‐a‐time (OAT) method, a single parameter is varied, and the size of the change in a response output is noted. This technique is informative for model outputs that are linear or additive in the input parameters. LSA can also be informative for models with parameters that have been well‐estimated, as, for example, in the work of Schoeberl et al. ⁴⁵ If we have high certainty in the nominal parameter values, then we can be assured that we are in an appropriate location in parameter space while performing the analysis.

LSA may not be considered an appropriate sensitivity analysis method for models that are not linear or additive, for settings in which some of the input parameters are uncertain, or for models that may have interactions between input parameters. In these cases, which are common for QSP models, global sensitivity analysis is recommended. Numerous examples in the literature document that misleading results can be obtained when LSA is used in an inappropriate setting (cf. Thogmartin ⁴⁶ ). Figure 2 shows a simple example of how the results from an LSA are affected by the point in the parameter space at which the analysis is performed.

FIGURE 2.

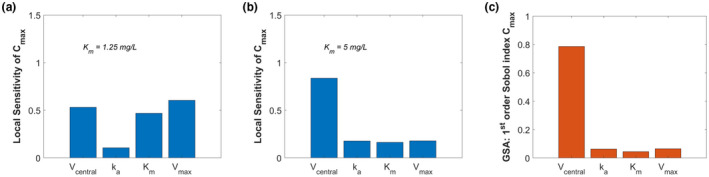
For this analysis, a one‐compartment pharmacokinetic model for phenytoin was used with k _a = 0.8 1/h, V _central = 42 L, V _max = 18.75 mg/h, K _m = 2.5 mg/L, and the model was simulated for 24 h after a single p.o. dose of 30 mg. ⁹² , ⁹³ Panels (a) and (b) represent the results from local sensitivity analyses (LSA) of C_max (maximum drug concentration in the central compartment) to the parameters in a one‐compartment PK model for phenytoin as described below. For panel (a), K _m = 1.25 mg/L; for panel (b), K _m = 5 mg/L. As the results show, the ranking of the sensitivities is different when performing LSA based at different points in the parameter space. A Sobol global sensitivity analysis (GSA, panel (c)) was also performed for C_max with the same model, for 1000 uniformly distributed samples across all parameters within a range of 50% and 200% of their nominal values (namely, K _m = 2.5 mg/L and the other parameters as listed above). The GSA results give similar rankings as the LSA in panel (b), but not in panel (a). GSA is recommended if there is substantial uncertainty in the estimated parameters, if the model contains nonlinearities or is non‐additive, or if there are interactions between input parameters. For the LSA, the scalar values represent the normalized absolute value of the sensitivity at the time of C_max. For the GSA, the scalar value represents the first‐order Sobol sensitivities of C_max. Analyses performed using MATLAB and SimBiology R2020b; code is included in supplemental information. GSA, global sensitivity analysis; LSA, local sensitivity analyses

Why use global sensitivity analysis?

In larger models, the results from LSA can be even more dependent on the calibration point than the simple model used for the example in Figure 2. Whereas an LSA is performed at one location in the parameter space, a global sensitivity analysis (GSA) is performed across a domain within the parameter space that is defined by the modeler.

The results of a GSA represent the sensitivity of the model outcomes to the input parameters across this predefined domain, typically as a weighted average. In this way, GSA results depend on the distributions of the input parameters, in addition to the model structure. In this way, the input parameter distributions are inputs for the sensitivity analysis, because the outcome depends on them. Because of this direct dependence, it is important to carefully select parameter distributions and ranges, just as we carefully select the model structure.

However, the results of GSA do not depend on a specific choice of parameter values (a specific model calibration) and can thus provide better information for decision making (e.g., which parameters to calibrate and which to fix) in settings with uncertainty in parameters. We therefore recommend the use of GSA for sensitivity analysis for most QSP model analyses, rather than LSA.

GSA analyses are currently not widely used in the QSP modeling community. In fact, Saltelli et al. ⁴⁷ systematically reviewed the literature of 19 scientific disciplines that use sensitivity analysis (including chemistry, economy and finance, engineering, environmental sciences, and medicine), and found that publications in pharmacology and toxicology have the lowest percentage use of GSA for sensitivity analysis among all 19 disciplines. For a more complete mathematical explanation of the limitations of LSA and how GSA can address these limitations, we refer to Saltelli and Annoni. ⁴⁸

Global sensitivity analysis methods

Many GSA methods can be classified as derivative‐based, correlation‐based, or variance‐based. Derivative‐based methods include the Morris method, which calculates an OAT “elementary effect” measure of sensitivity at a given point in parameter space, and looks at a type of average over all the sampled points in parameter space. This method is easy to implement and relatively fast to compute. In addition, it can be applied to models with nonlinear, nonmonotonic outputs and can also be applied when parameters have interactions. ⁴⁹

Partial rank correlation coefficient (PRCC) is similarly easy to implement, and can be applied to nonlinear, monotonic model outputs even when parameters are correlated. ⁵⁰ For PRCC, the sampling of inputs needs to match the structure of the input distributions, including any correlations, in order for the sensitivity metric generated from the samples to be accurate. ⁵¹ , ⁵²

The variance‐based GSA methods include Fourier amplitude sensitivity test (FAST), Sobol, and the extended FAST (eFAST). ⁵³ , ⁵⁴ , ⁵⁵ These methods are applicable to a wide range of model settings. They can be applied to nonlinear, non‐monotonic model outputs, even when the input parameters have interactions. These methods apportion variability in the model output to each of the model inputs. ⁵⁶

Variance‐based GSA methods, such as Sobol and eFAST, result in first‐order and higher‐order indices. The first‐order indices indicate the variance that can be attributed to a given single parameter. The total‐effect index for a given parameter indicates the variance that can be attributed to that particular parameter, plus all of the interactions of that parameter with other parameters. For example, for three parameters, the total‐effect index for parameter 1 is S_T,1 = S₁ + S_1,2 + S_1,3 + S_1,2,3 but does not include S₂, S₃, or S_2,3. Note that if a first‐order index is large, then the corresponding parameter is influential on the output. In addition, if a total‐order index is small, then the corresponding parameter is noninfluential, and could be frozen during subsequent analysis. ³⁵

Liu et al. ⁵⁷ published an example of a complex model that had similar results for both the Morris and Sobol GSA methods. In Table 1, we compare several types of sensitivity analysis.

TABLE 1.

Comparison of sensitivity analysis methods

Category	Methods	Assumptions	Advantages	Disadvantages	Approximate computational expense
LSA	Derivative‐based; analytic calculations, automatic differentiation, finite differences, or complex‐step approximation	Model is smooth; also, model is either linear or additive, or is well‐calibrated with no interactions between parameters	Computationally inexpensive, easy to implement	Due to its local nature, results may not be representative of sensitivities in other parts of parameter space when assumptions do not hold	P+1 model evaluations, where P is the number of parameters under investigation e.g., 11 evaluations for P = 10
GSA	Derivative‐based: Morris method and others (cf. Kucherenko and Iooss 61 )	Generally applicable	Least computationally‐expensive GSA method; easy to implement; Morris method is applicable to nonlinear and non‐monotonic model outputs, and when parameters have interactions 56 , 59	Although these methods globally sample parameter space, the calculations at each point are still one‐at‐a‐time; thus variance of sensitivities can be either due to interactions or nonlinearity in model parameters (see Saltelli et al., 56 p. 111)	> N*(P+1) model evaluations, where N is number of samples, with N often 10 to 100 e.g., ~500 evaluations for P = 10, N = 50
	Correlation‐based: PRCC	Output is monotonic in each of the input parameters	Easy to implement; robust for nonlinear models, and for parameters with correlations	Computationally expensive even if only 2 values sampled per parameter	> 2^P (Base number of 2 explores only the corners of parameter space) e.g., >1024 evaluations for P = 10
	Variance‐based: Sobol indices, FAST, eFAST	Variance is a good statistic to represent model output distribution (cf. Pianosi and Wagener 94 for a GSA method for non‐normal output distributions); some methods work even when parameters are correlated or otherwise dependent 60	Few assumptions; generally suitable for QSP models; applicable to nonlinear and non‐monotonic outputs, and when parameters have interactions (see Saltelli et al., 95 p. 384); quantify the relative influence of parameters	Very computationally expensive; most methods do not perform well on models with correlated parameters 95	The larger of: >(2^P)*(P+2) or > N*(P+2) model evaluations e.g., > max (12000, 12288) evaluations for P = 10, N = 1000 (Base = 2 only explores the corners of parameter space)

Abbreviations: eFAST, extended Fourier amplitude sensitivity test, FAST, Fourier amplitude sensitivity test; GSA, global sensitivity analysis; LSA, local sensitivity analysis; PRCC, partial rank correlation coefficient; QSP, quantitative systems pharmacology.

GSA can provide information on interactions between parameters

Interactions between parameters can be detected when changes in two or more parameters result in no change in response. When calculating sensitivity scores for an LSA, each derivative‐based score is calculated with respect to only one parameter, which makes it an OAT method. As a result, an LSA cannot identify interactions between parameters.

The Morris method GSA relies on multiple derivative‐based LSA evaluations and is therefore still an OAT method. ⁴⁸ , ⁵⁸ A mean and standard deviation can be calculated from the individual “elementary effects” evaluations to represent the final outcome of a Morris method GSA. Because the sensitivities are calculated one‐at‐a‐time, it is not possible to distinguish results that may reflect interactions between parameters or nonlinearity of the output. ⁵⁹ A high standard deviation from a Morris method GSA can be interpreted in two ways: either the model response is highly nonlinear in that parameter or there may be interactions with other parameters. Because of this ambiguity in interpretation, other GSA methods are needed to better understand interactions between parameters.

Note that interaction between parameters (such as for parameters x ₁ and x ₂ when the output is y = x ₁*x ₂) is different than dependence of parameters (such as when parameter x ₂ is a function of parameter x ₁). Although variance‐based GSA methods can be applied when there are interactions between parameters, most are not appropriate when parameters are not independent. However, Kucherenko et al. ⁶⁰ , ⁶¹ have developed GSA methods that can be used when parameters have dependencies.

Strategy for performing GSA

Global sensitivity analysis methods tend to be computationally expensive. The right column in Table 1 gives an indication of how the computational expense scales with the number of parameters (P) under investigation. Clearly, the variance‐based GSA methods are the most computationally expensive and do not scale as well with increasing P. For example, for P = 20, a variance‐based algorithm would require ~23 million evaluations just to sample the corners of the 20‐dimensional parameter space and to evaluate both first‐order and total‐order sensitivity indices.

To mitigate this, a screening with the Morris method can be performed first with all the input parameters that are of interest (Saltelli and Annoni 2010). The sensitivity indices from a Morris method GSA can be good proxies for those of variance‐based sensitivity analyses. ⁴⁹ The parameters that are identified as noninfluential can be fixed (or frozen) to nominal values without substantial impact on the model output. A variance‐based (Sobol/eFAST) and/or a PRCC sensitivity analysis can then be performed for the most influential parameters determined by the Morris method. ⁵⁹ The number of parameters selected for this second GSA may be on the order of 10, but will depend on computational capacity. Some researchers advocate performing both a PRCC and a variance‐based sensitivity analysis because each approach results in different insights. ⁶²

Choosing the model response/output or quantity of interest

There are several considerations when choosing which model response or quantity of interest (QOI) to use for a sensitivity analysis (SA):

• What is the QOI or response variable of interest? This can be guided by the model aims and question at hand. Examples include plasma concentration, tumor size, and blood pressure.

• One or multiple responses? You may have both an efficacy and toxicity response of interest. Performing SA on all quantities of interest is important, because responses can be sensitive to very different sets of parameters.

• Scalar or time‐varying? SA methods can use time‐dependent responses as the model output of interest, which can reveal whether a parameter is more influential at the start of a simulation or toward the end. Note that using a time‐varying QOI can make it difficult to rank‐order the sensitivities. However, a time‐dependent response can be turned into a scalar by using metrics, such as a mean or final value.

• Which metric? Using a scalar as the model output of interest requires the choice of metric to reduce a time‐dependent response (e.g., drug concentration) to a scalar. Examples of such choices include the maximum concentration or effect, the area under the curve (AUC) of concentration during a specified time interval, or a final concentration or effect.

The choice of model response can significantly affect SA outcomes. Here, we give an example of the effect of using an AUC or maximum concentration (C_max) function as the metric to reduce the drug concentration to a scalar model output. We consider the same one‐compartment model with first‐order absorption and enzymatic clearance that was shown in Figure 2. A Sobol GSA shows entirely different results in Figure 3 between using AUC or C_max as model outputs. Interestingly, absorption rate constant (k _a) does not appear to be an influential parameter, especially when using AUC as the model output. This can be explained because the AUC is independent of k _a in this model, as long as the simulation is sufficiently long to allow the concentration to return to zero and the PK is linear.

FIGURE 3.

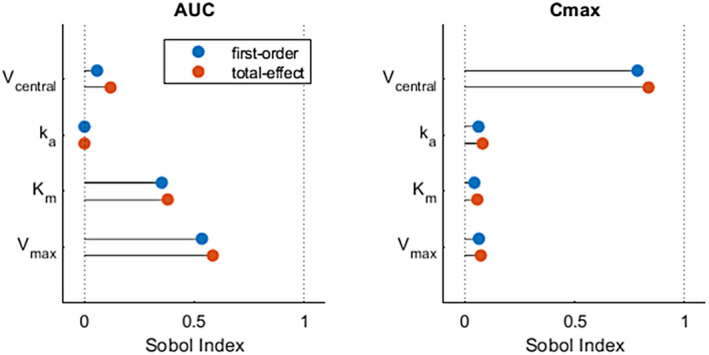
This figure shows how the choice of quantity of interest (QOI) can impact the outcome of a sensitivity analysis. Both panels show results from the same Sobol GSA as in Figure 2, with AUC and C_max calculated for the 24 h after a single dose. Each panel uses a different QOI to assess the sensitivity of the QOI to various input parameters. In the left panel, the AUC of the drug concentration is used as the QOI and is shown to be highly sensitive to V_max but not k _a. However, when the maximum drug concentration (C_max) is used as the QOI, it shows that C_max is much less sensitive to V_max and marginally sensitive to k _a. Analyses performed using MATLAB and SimBiology R2020b; code available in the supplementary information. AUC, area under the curve; k _a, absorption rate constant; K_m, Michaelis constant; V_max, maximal elimination rate

Reproducibility and random seed

Most GSA methods include some form of random sampling of the parameter space. Fixing the random seed used for sampling ensures complete reproducibility, but should only be done after determining a sufficiently large sample size. This can be quickly explored by re‐calculating the sensitivity indices from subsets of the original sampled points. Because using subsets of the original samples can give an underestimate of appropriate sample size, it is a good idea to then change the random seed to refine the estimate of sample size.

Identifiability analysis

A parameter is said to be identifiable if there is enough information to uniquely estimate a value for it. Identifiability analysis is an essential task to perform before finalizing parameter estimates. In addition to determining which parameters can be estimated, identifiability analysis can also be used to decide how to simplify a model structure, decide if additional data should be collected, and to optimize the type of data and sampling sites to be used experimentally. ⁶³

Once we have determined which parameters the model output is most sensitive to, we can use identifiability analysis to determine whether it will be possible to estimate these parameters. This is important, because computational software uses numerical approximations, and therefore parameter estimates may be supplied for these nonlinear systems even in cases where the parameters are not identifiable. This can have the very serious consequence of obtaining misleading model predictions.

The paper of Kao and Eisenberg ⁶⁴ examines a widely‐used simple model and determines that the model parameters are practically unidentifiable: two different sets of parameter values give indistinguishable fits to data. With one of the parameter sets, a specific intervention appears highly effective. However, with the other parameter set, the same intervention appears ineffective. The broad usage of this model before this identifiability analysis was performed, and the policy implications of its predictions, make this a compelling case for the importance of identifiability analysis in the interpretation of model predictions.

The two types of identifiability, structural and practical (both mentioned above), will be discussed in detail in the next sections. Broadly, structural identifiability depends only on the model structure and assumes the outputs of interest can be measured at all times with arbitrary precision. Practical identifiability depends on the data actually available, rather than assuming all possible measurements are available. Structural identifiability can be considered to be a “low bar” that must be passed: if parameters are not structurally identifiable (when all data are assumed available), then it is impossible for them to be practically identifiable (when only limited data are actually available). We recommend applying structural identifiability to narrow down the set of parameters. If appropriate data are available, then practical identifiability can also be applied, and can potentially narrow down the set of identifiable parameters even further.

Structural identifiability

Structural identifiability determines which parameters can be uniquely estimated, based only on information about the structure of the model and which types of outputs are planned to be measured.

We explain the concept of structural identifiability using the simple example of a system of linear equations. Consider a model given by the system of equations below, where x and y are unknown:

$$\begin{array}{c}3x+y=6\\ 2x‐y=‐1\end{array}$$

For this system of linear equations, we can calculate the determinant of the matrix M, where

$$M=\left(\begin{array}{cc}3& 1\\ 2& ‐1\end{array}\right)$$

If the determinant Det(M) is nonzero, then the equations are independent. If Det(M) = 0, the equations are not independent. For linear systems, if there are two independent equations and two unknowns, then we can solve for them. In this example, Det(M) = (3)(−1) – (1)(2) = −5 ≠ 0, so the equations in this system are independent, and the values of x and y (the unknown parameters in this system) can be uniquely determined. As illustrated in Figure 4, this system of equations can be represented graphically as two lines that intersect in a single point (because the equations are independent).

FIGURE 4.

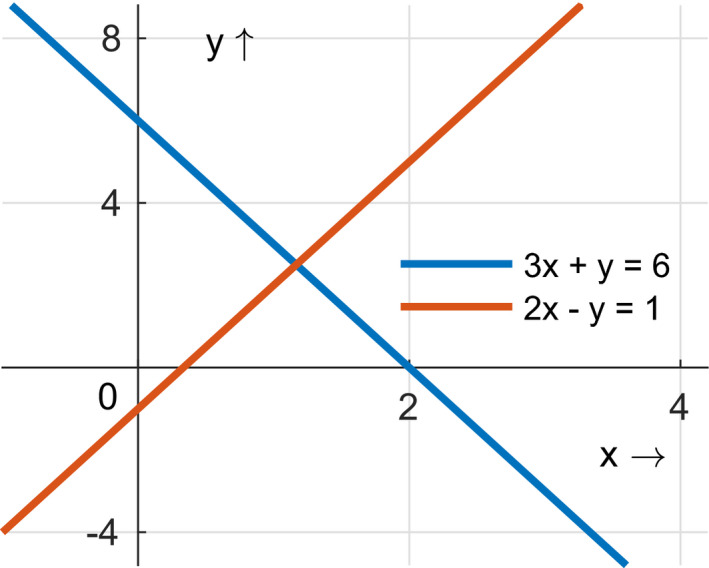
The concept of identifiability of parameters can be explained using the analogy of a system of linear equations. For the two equations represented as lines in this graph, a unique solution for x and y exists where the lines cross. If the linear equations were not independent, then the lines would be parallel, and there would be either an infinite number of possible values of x and y (if the lines overlapped) or no possible values (if the lines were not overlapping). Figure created using MATLAB R2020b

Although QSP models are usually nonlinear, and are often larger and more complex than the example above, we can use a similar approach. When a model is given by a set of equations, there are calculations we can make to determine whether we can uniquely solve for the unknown parameters, given the model structure and the location of the parameters within the model. Several free software packages are available for performing structural identifiability analysis. The methods they use differ in the types of models they are able to analyze.

• COMBOS ⁶⁵ is a web application that allows users to type in model equations and find subsets of parameters that are identifiable. It relies on Gröbner bases to compute identifiability. This is a theoretically sound method to determine which parameters or combinations of parameters can be estimated, given the model structure. However, the method can be computationally intractable, and thus is limited in its practical use when models are complex.

• Differential Algebra for Identifiability of Systems (DAISY ⁶³ , ⁶⁶ ) is a stand‐alone software package that can be used to perform structural identifiability analysis. As its name implies, it uses differential algebraic techniques to compute structural identifiability. This method only works for functions defined in polynomial or rational form.

• Generating Series for testing Structural Identifiability (GenSSI ⁶⁷ ) is a package that runs in MATLAB and can handle any nonlinearity that can be defined by analytic functions. The generating series method starts with the fact that every analytic function has a unique Taylor series expansion. Taking derivatives of both sides of this equation provides additional equations in the same variables. Generating series use Lie derivatives, a generalization of usual derivatives. Lie derivatives allow for judicious directions to be used for taking derivatives, which makes the calculations more efficient. If the equations obtained from taking derivatives yield enough equations that are independent, we can determine whether certain parameters are identifiable. A challenge when using this method is that there is no way to know in advance how many derivatives need to be computed to determine whether a given set of parameters is identifiable. If the number of derivatives to calculate is set too low, the result may be inconclusive, and an additional run with more derivatives may be needed. On the other hand, due to the significant computational time needed to compute the derivatives, it is best to not set an excessively high number of derivatives to be computed. Even with these challenges, it is one of the better methods available.

Practical identifiability

Once we have determined a set of parameters that are structurally identifiable, we can test whether those parameters are still identifiable once we look at the available data. This practical identifiability can only hold for parameters that are structurally identifiable, and thus will yield the same or a smaller set of parameters as structural identifiability analysis. Parameters with narrow likely distributions are considered practically identifiable. Here, we list three methods for performing practical identifiability:

• Markov chain Monte Carlo (MCMC) sampling: To perform practical identifiability analysis, we can use MCMC with Metropolis‐Hastings sampling of the parameter space. We compute the model output at various locations in parameter space and compare it to the data by computing a likelihood ratio. For a given model output at a given point in parameter space, a high enough likelihood ratio means we keep that point, and a low one means we discard that point. We end up with a distribution of likely points in our parameter space. If a specific parameter has only a narrow range of values remaining, then we say that point is practically identifiable. If a parameter does not have substantial restrictions on its range, then the parameter is not practically identifiable. Although the conclusion is made qualitatively, the computations are well‐defined and quantitative. Even when individual parameters are not practically identifiable, the likely distribution in parameter space may indicate parameter relationships, which can help narrow the parameter sets to be considered. Examples of this are shown in Gallaher et al. ⁶⁸

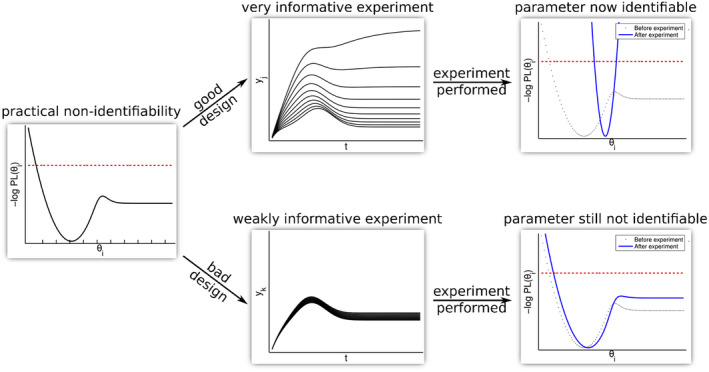
• Profile likelihood: A profile likelihood plot ⁶⁹ , ⁷⁰ represents the shape of the likelihood function for a range of values of the parameter of interest. The observed peak (when the vertical axis represents log likelihood) gives the most likely value of the parameter of interest given the observed data, and is used as the parameter estimate. The shape of the curve can inform how the estimate is bounded, and whether the parameter is practically identifiable, given the data that are available for the parameter estimation. For example, a flat shoulder on one side of the estimated parameter value means that the parameter is poorly constrained in that direction (see Figure 5, from Steiert et al. ⁷¹ ). Conversely, a narrow, paraboloid shape indicates that the parameter is practically identifiable with approximately symmetric confidence intervals. In addition to assessing practical identifiability, profile likelihood plots can also be used to communicate with experimentalists the need for additional experiments to address the identifiability issue.

  • ○Profile likelihood plots can be computationally expensive to generate because for every change in the parameter value, the optimization process has to be repeated. The calculation of profile likelihood paths can be accelerated by using integration‐based rather than optimization‐based methods, ⁷² , ⁷³ with implementations in R and SimBiology. Note that the profile likelihood paths obtained using integration are approximations of those obtained by optimization.

• Aliasing Score: Another approach to investigating identifiability uses an “aliasing score.” ⁷⁴ When a pair of parameters is not identifiable (i.e., when multiple pairs of values of these parameters lead to the same model response), the two parameters can be said to be aliasing or shadowing each other. If a time‐dependent model outcome of interest is sensitive to two parameters in similar ways over time, the shape of their respective time‐dependent local sensitivity profiles will be similar. The aliasing score quantifies this pairwise similarity of local sensitivity profiles. The score is calculated by normalizing the absolute values of time‐dependent local sensitivity profiles and calculating the differences of the time‐courses for each parameter pair. The maximum value of the differences is taken as a scalar measure of aliasing and is converted to a percentage, where 0% represents no aliasing and 100% represents maximum aliasing. Although the aliasing score cannot determine if parameters will be identifiable, the score can quickly indicate potential non‐identifiability. Due to the limitations of local sensitivity analysis on which the aliasing score is based, this analysis is best performed after parameter values have been estimated. Note that, instead of using the time profiles from a simulation, the score can also be calculated using the timepoints from experimental data as a form of practical identifiability and/or to design experimental strategies to reduce the risk of non‐identifiability of specific parameters.

FIGURE 5.

The shape of the profile likelihood can inform experimental design to maximize the value gained from an experiment. Figure from Steiert et al., ⁷¹ licensed under Creative Commons Attribution License

Parameter estimation

Once we have identified the influential and identifiable parameters, we can perform parameter estimation. As a verification step, we should check that the units in the dataset are consistent with those in the model. During parameter estimation, the aim is to find parameter values that bring the model predictions as close as possible to the observed data, which is achieved by minimizing the value of an objective function. Most software packages will construct the objective function automatically from the data and model. The definition of the objective function is dependent on the type of residual error model, so we recommend considering which residual error model is most appropriate for the problem at hand. For example, because PK concentration measurements often span multiple orders of magnitude, an error model that is proportional to the magnitude of the measurement is often used. On the other hand, for a PD effect, such as a percent change, it may be most appropriate to use a constant (additive) error model. Instead of an error model, it is also possible to assign weights to each observation in the objective function.

QSP models often have many parameters to be estimated, whereas the data being used to estimate these parameters are often sparse. This combination of sparse data and a large number of parameters, along with nonlinearities and feedback loops in the models, can result in the optimization algorithm converging to a local minimum of the objective function, yielding misleading parameter estimates. Unless we have a very good idea of the initial estimates, it is therefore advisable to use a global optimization algorithm, in order to reduce the likelihood of ending up in a local minimum. For large, complex systems, particle swarm or scatter search algorithms can be feasible global optimization options. After minimizing the objective function, we can assess the fit qualitatively by generating diagnostic plots, such as residual distribution plots, observation versus prediction plots, and QQ‐plots, and by checking that the estimated parameters are within physiological ranges.

Model selection

In data‐rich settings, goodness‐of‐fit criteria are commonly used to select between competing models according to how well they fit the data. Criteria such as the Akaike information criterion (AIC), corrected AIC (AICc), and Bayesian information criterion (BIC; also known as the Schwarz‐Bayesian Criterion) provide parsimonious model selection by rewarding a good fit to a given dataset, while simultaneously penalizing for additional parameters needed to achieve the fit. ⁷⁵ If a model selected using one of these criteria has not already been analyzed and evaluated as described above, it is recommended to do so, starting with the model verification step.

We note that the AICc is preferred over AIC as it can also be applied even in settings where the number of data points available is less than 40 per parameter. ⁷⁵ In complex QSP model settings, BIC may be preferred over AIC and AICc. BIC has a larger penalty for extra parameters once the total number of data points is greater than seven, and thus may be best for selecting the most likely and parsimonious model. All three of these criteria tend to select overfitted models, so the criterion with the strictest selection process may be preferred.

In data‐sparse settings, there can be inadequate data to perform model selection based on such fitting criteria. In such cases, following a set of best practices for model building may take the place of a quantitative model selection step. If multiple models are retained to handle model uncertainty, they can each undergo the analysis starting with the model verification step.

When a model has high complexity compared to computational resources, we might consider alternative models, such as reduced versions of the original model. Reduced models can be achieved through techniques such as the method of averaging ⁷⁶ to remove faster time scales from the model, or projection‐based model reduction. ⁷⁷ Other options include creating a surrogate model ⁷⁸ or a Gaussian process emulator ⁷⁹ of the original model in order to perform model evaluation analyses. The model evaluation methods we have recommended in this work can be performed on an alternative to the original model when that is preferable.

Model calibration using virtual populations

When there is not enough data available to estimate parameters, virtual populations or other sampling methods can be used to determine ranges and distributions for parameters. We refer to this as a model calibration, as we are still restricting the parameter values, even though we are not obtaining point estimates for the parameters. Throughout this work, we sometimes use the term model calibration to refer to methods that can only determine parameter ranges/distributions; other times we use model calibration as a more general term, to refer to these methods and/or also direct parameter estimation.

Virtual population methods use sampling to explore parameter space. In a virtual population approach, random samples are drawn from the permissible parameter input space, the model is simulated for each sample, and the simulated output is compared to observed data. A parameter sample (also called a virtual patient) is accepted if the associated simulated output falls inside the range of observed output variable data, and otherwise is rejected. If the model output is smooth (i.e., differentiable) in the input parameters (as for most QSP models), then there is some neighborhood of each rejected point in parameter space that is also not valid. The resulting allowed parts of parameter space, with the neighborhood (i.e., sphere) removed around each rejected point in parameter space, could be said to resemble a high‐dimensional block of “Swiss cheese.”

These approaches can be used to narrow the permissible ranges for parameters and to construct parameter distributions such that, when all samples are simulated, the collection of model outputs approximates the distribution of the observed data. Virtual populations usually sample a large number of parameters (e.g., >15). Similar to sampling‐based sensitivity analyses, a large number of samples is required to sufficiently explore such a large parameter space. Creating representative virtual populations is therefore generally computationally expensive, and steps should be included to ensure that the parameter space is sufficiently sampled.

Even though the basic concept of model calibration using virtual populations has been in use for several years, the QSP community has not yet converged on a standardized approach. Multiple groups have introduced their own methods that vary on details such as the sampling method and the use of resampling or prevalence weighting of virtual patients to better match the distributions of the observations. ⁸⁰ , ⁸¹ , ⁸² Several groups have also shared the code to perform these calibrations, such as QSP Toolbox, ⁸¹ VQM Tools, ⁸³ and gQSPSim, ⁸² which are all based on SimBiology. Further work and comparisons of virtual population methods with optimization‐based parameter estimation methods may be necessary to increase adoption of this approach and to standardize on a common methodology for virtual populations.

Using a calibrated virtual population, a model can predict outcomes, as well as provide an indication of the uncertainty in those outcomes for the ensemble of virtual patients. Virtual patients and populations are also used to characterize differences between healthy subjects and patients, for example, so that the model can predict how each subpopulation would respond to interventions.

Using data to evaluate models

After the parameters in a model have been estimated, we can evaluate the model’s predictive capability by comparing to data. We discuss three common ways to use data for model evaluation. We will use “validation” in place of “evaluation” in this section, as this is a more‐common terminology in some communities when discussing comparison of model predictions to data.

• External validation: When we have an independent dataset that has not been used to calibrate the model, we can compare model predictions to it, for what is called validation with an external dataset, or external validation. In high‐risk settings, comparison to external data may be necessary to attain model acceptance. A new dataset can be acquired specifically for external validation, or a historical dataset can be repurposed for this. When using external validation data, it is important to assess whether the experimental setting for that dataset is appropriate for the COU of the model. For example, if a psoriasis therapy is being modeled, the most appropriate validation dataset would be from patients with psoriasis in a clinical trial that tests a therapeutic mechanism of action that is captured in the model. In addition, we recommend verifying the quality of the data when using historical datasets. Quality checks can include confirming that the C_max order of magnitude makes sense for the dose level (e.g., assuming a V _central of around 50 ml/kg for large molecules), or checking that the lower limit of quantitation is consistent with the assay method (ligand binding assay vs. mass spectroscopy), or reviewing the methods section to verify whether reported concentrations are free or total antibody concentrations.

• Hold‐out validation: In hold‐out validation, available data are partitioned into a training set and a test set. The training set usually represents the majority of the data (e.g., 80% of the data) and is used to calibrate the model. The test set is the remainder of the data and is used to determine the predictive performance of the model by comparing the test set to the simulation results from the model calibrated using the training set.

• Cross‐validation: Ethical and/or financial limitations often mean that limited data are available for calibrating systems models. In such cases, modelers may decide to use all available data to calibrate a model. In k‐fold cross‐validation, the process described above for hold‐out validation is repeated k times, each time with 1/k of the data held out. Using k‐fold cross‐validation and an average measure of predictive performance of the model, helps guard against effects due to overfitting to specific data.

Because comparison to data is one of the few methods available to modelers to evaluate model predictions, we recommend including this in the evaluation plan prior to using data for model calibration, whenever the COU and available data permits. Note that there is no objective statistic (e.g., analogous to a p value) to provide a pass/fail threshold when comparing model predictions to data. Instead, the modeling team will need to define criteria that are appropriate for the problem at hand. An example could be that the model predictions for a safety end point are within two‐fold of the observations, which could be acceptable if a two‐fold increase would still be below a known safety threshold. Or model simulations generated from specified parameter distributions can be compared to data with a visual predictive check. ⁸⁴ , ⁸⁵ If comparison to data leads to a decision that the model should be modified, the new version of the model can have all of the analysis and evaluation steps applied to it as well, starting with model verification.

Uncertainty quantification

There are multiple sources of uncertainty in model predictions. Major sources of uncertainty include model structure and parameter value uncertainties. For model structure uncertainty, we can use information criteria to choose between alternative model structures when adequate data are available for the number of parameters that need to be estimated. If data are not available for model structure selection (which is common for QSP models), then we recommend following the model‐building best practices discussed earlier, ²¹ , ²³ , ²⁴ , ²⁵ , ²⁶ which can be used also in the case when data are available. An alternative approach to handling model structure uncertainty is the use of model averaging with a choice of weighting scheme. ⁸⁶

There are several approaches to quantifying the uncertainty in parameters. When appropriate data are available, then the values of influential and identifiable parameters (once they are determined using sensitivity and identifiability analyses) can be estimated using a maximum likelihood approach. When appropriate data are not available to use for parameter estimation, and parameter values are obtained from the literature, it is important to also record any standard deviation, variance, or confidence interval information reported in the literature for these parameters. A residual error structure (e.g., proportional, constant, combined, or exponential error model) can be used to model the unexplained individual variability in addition to measurement error. Confidence intervals for the parameter estimates themselves can be calculated (e.g., from the standard error by assuming normally distributed parameter values, or else by using bootstrapping, or by using profile likelihood methods). Using a Bayesian approach, credible intervals can be calculated for parameters. ³⁵

Once the uncertainty has been estimated for parameters, it can be propagated through the model, which depends on the model structure as well as the scale of the model. ⁸⁷ See chapter 9 in Smith ³⁵ for details and examples demonstrating various uncertainty propagation methods. These include estimating credible intervals and prediction intervals for the model predictions.

DOCUMENTATION AND INFRASTRUCTURE STANDARDS

Documentation

Documentation is an important aspect of every QSP model, for reproducibility purposes, review purposes, and to maximize the re‐use of a QSP model within an organization. Friedrich ²³ and Cucurull‐Sanchez et al. ²⁵ provide guidance on how to document a QSP model. Here, we give our own recommendations for documentation, aligned with the three stages shown in Figure 1.

Planning

For the project‐planning stage, it is important to document the planned activities for the project and the evaluation, as well as the rationale for these activities. This documentation can keep the project focused, and can reduce potential bias by prespecifying the basis for choices (e.g., which model selection criterion will be used). An additional benefit is that stakeholders can review a written document to ensure common understanding and alignment of plans before they are implemented. Documentation should include:

• The aims, scope, and risk assessment and how they inform the model evaluation plan.

• Data that will be available, and the strategy for how they will be used for parameter estimation and model evaluation.

• The model evaluation plan, including the rationale for including or excluding various model evaluation activities.

Building

The documentation of the model‐building stage is used to aid understanding and reproducibility of the model. It can also provide a record of uncertainty in specific model structures, which can be referred to if structural changes are desired. Documentation should include:

• The equations that define the model.

• A graphical representation of the model structure to aid in understanding and communicating the model. This should include all states in the model, as well as the reactions that take place between these states.

• The parameters and states (ODE state variables) and their physiological meaning, along with units, initial values, and parameter values, ranges, and any information about their distributions. This information should be accompanied by sources such as experimental or trial data used for calibration, or literature references, or a statement of assumptions that were made.

• Detailed information about the relationships between the model states and parameters, to justify the structure of the model and equations.

• The assumptions that were made during model development and any limitations related to the use of the model, to make sure that the model and its predictions are not inadvertently used outside of the intended context (cf. Friedrich ²³ ).

• The original code to run the model, or a representation of the model in a universal markup language, such as SBML ⁸⁸ or CellML. ⁸⁹ The exact software environment (version, required toolboxes/packages, and operating system) that was used to simulate the model should also be specified. Another solution is to provide a web‐based application that allows end‐users of the model (including internal and external reviewers) to view and run the model (e.g., R Shiny or MATLAB Web Apps) or to host the code in a self‐contained computational environment. ⁹⁰

Analysis and evaluation

The model analysis and evaluation activities themselves should be documented, as well as the outcomes of each analysis that was performed, and the conclusions drawn from those outcomes. Table 2 contains detailed recommendations; here, we summarize and include some additional comments:

• A record that model/code verification was performed

• Sensitivity analysis

• Identifiability analysis

• Estimation of parameters (i.e., model calibration) and their confidence intervals or their distributions

• Model selection

• Comparison of the model predictions and prediction intervals with data

• Additional parameter restrictions obtained using methods for sampling and comparing to data, such as virtual populations

• Interactive documents that include code, results, and rich‐text documentation, such as Jupyter notebooks, MATLAB Live Scripts, or R Markdown, can also be used to describe model evaluation activities in detail. This can include the exact analyses, their results and a description of the methodology, outcomes, and rationale for drawing conclusions, as well as decisions made during the model evaluation process. These “live documents” will allow end‐users to re‐run each analysis or to make changes to an analysis to gain further insights. In order to manage these documents, it is advisable to use a version‐control system such as Git or SVN.

• Visualizations of the results of model evaluation activities will help end‐users interpret and assess the model evaluation. Ideally, these visualizations are standardized within the QSP community. An example of such a proposed visualization introduced by the QSP community is the reliability‐sensitivity plot, ⁹¹ which plots reliability of parameter values, assessed by how appropriate the source is for the COU of the model, versus the sensitivity of the relevant model outcome to that parameter. The reliability‐sensitivity plot allows reviewers to quickly identify sensitive parameters that originate from a less reliable source (e.g., preclinical data, when the model is being used in a clinical setting).

TABLE 2.

Documentation for model evaluation activities

Activity	Recommended documentation
Equations and model description	All model equations with initial conditions, dosing regimens, parameter values and distributions, rationale for included mechanisms, derivations, sources for parameter values and mechanisms
QC and QA	Results of code verification and record of any changes needed
Units	Units for all model components as well as all data
Mass balance	Results of mass balance analysis
Unit tests	Commented, executable code for each unit test with anticipated and actual results (quantitative or qualitative)
Reproducibility	Software and version (e.g., MATLAB R2020b, R 4.0.2), ODE solver, tolerances, operating system details; share all necessary executable code to allow key figures or predictions to be reproduced, including a fixed random seed
Sensitivity analysis
LSA	Information on input parameters and model outputs used, method details (e.g., normalization, solver type), LSA results and interpretation
Morris method – GSA	Information on input parameters and model outputs used, method details (e.g., normalization, solver type), results and interpretation; reliability/sensitivity analysis plot
PRCC – GSA	Information on input parameters and model outputs used, method details, results and interpretation
Sobol – GSA	Information on input parameters and model outputs used, method details, results and interpretation
Identifiability analysis
Structural identifiability (using software such as DAISY, COMBOS, or GenSSI)	Choice and rationale for choosing the method used; list of identifiable parameters and/or combinations of identifiable parameters
MCMC – practical identifiability	Two‐dimensional heat maps of MCMC simulation outputs for two parameters at a time; interpretation of results (identifiable parameters or relationships between parameters)
Profile likelihood – practical identifiability	Profile likelihood plots and interpretation of results
Aliasing score – practical and structural identifiability	Inputs and outputs to analysis, similar to LSA; aliasing score heat map and time‐dependent aliasing score results; interpretation of results
Parameter estimation and model selection
Local optimization	List of parameters to be estimated, optimization algorithm and settings, error model; parameter estimates with confidence intervals, diagnostic plots; if optimization is a multistep process, documentation of the sequence
Global optimization
vPop generation	List of parameters to be included and their distributions, constraints, sampling method, prevalence weighting method, objective function; resulting parameter ranges and distributions, virtual population statistics, and comparison to data
Quantitative model selection (using a criterion such as AIC, AICc, or BIC)	Model selection criterion, list of models considered during the selection and their results
Uncertainty quantification
Parameter confidence intervals	Parameter confidence intervals, preferably from bootstrap or profile likelihood methods, or by plotting virtual population parameter distributions
Prediction intervals	Prediction interval plots, preferably with confidence intervals for the simulation percentiles
vPop simulation (sampling)	The spread in model output by plotting percentiles (e.g., 5%, 50%, and 95%) and plotting these together with data
Comparison with data
External validation	Plot of model predictions overlaid with external data; comparison of external data and data used for model calibration; may include, e.g., 2‐fold and 5‐fold discrepancy curves around the model prediction curve
Hold‐out validation	Plots of model predictions overlaid with hold‐out data; plots of predictions vs observations for hold‐out data; may include, e.g., 2‐fold and 5‐fold discrepancy curves around the model prediction curves
K‐fold cross‐validation	Values of k, mean, and variance of the mean square errors from each cross‐validation; comparison to error from parameter estimation with whole dataset

The first column of this table lists examples of model evaluation activities discussed in this work. The second column contains a description of each activity, by detailing its recommended documentation.

Abbreviations: AIC, Akaike information criterion; AICc, corrected Akaike information criterion; BIC, Bayesian information criterion; GSA, global sensitivity analysis; LSA, local sensitivity analysis; MCMC, Markov chain Monte Carlo; ODE, ordinary differential equation; PRCC, partial rank correlation coefficient; QA, quality assurance; QC, quality control; vPop, virtual population.

Once the model evaluation process is complete, the documentation should provide a complete overview of the entire model development and evaluation work to help end‐users of the model to understand and assess the quality of the model. Additionally, documenting any decisions or actions taken based on the model will be helpful in assessing the impact of the modeling, which can support future decisions about when and how modeling should be performed on various projects.

Publication

Publishing a model and its analysis and evaluation provides an additional opportunity for documentation. As we have described above, and as described previously in the literature, ²³ , ²⁵ there are guidelines for what to include when documenting a model, whether for internal purposes or for publication. An additional point we wish to make is that the first time a mathematical model is published, it should be published in a quantitative journal, with editors experienced at handling quantitative papers. This may sound obvious, but we know of examples of mathematical models that first appeared in therapeutic journals with no editors with quantitative training. Therapeutically‐relevant results should appear in therapeutic journals only after the peer‐review process has quantitatively vetted the detailed mathematical model. Peer review of a paper submitted to a quantitative journal should be considered part of best practices for modeling analyses. It should also be considered a valuable model evaluation resource, and a priority especially for high‐risk settings.

Software

Software plays a pivotal role in enabling efficient and standardized model evaluation practices. Currently, a wide variety of software platforms are being used in QSP modeling, complicating such standardization. In addition, the software to perform these evaluation methods can be hard to use for all but the most experienced modelers. Incomplete documentation, lack of a large user group, the need to use different software platforms for different analyses in the same project, and/or lack of a user‐friendly interface can all contribute to the steepness of the learning curve to use a different software platform. A common, well‐validated, documented, and easy‐to‐use software platform could therefore support more rapid adoption of model evaluation standards in the broader QSP community.

If the QSP modeling community is unable to align on a common software platform, an alternative solution could be to standardize the code used to perform the analyses described in this work, such that, for example, a Sobol GSA performed in software A will yield results similar to those from the same analysis performed in software B. In addition, by using a common language, such as SBML, ⁸⁸ models can be interchangeably used between software packages to aid in reproducibility of results and re‐use of models.

Training

Model evaluation is a topic that would benefit from more attention in graduate student coursework, as well as in the training of new employees who specialize in QSP modeling. By making students and new employees aware of these evaluation methods and when it is appropriate to apply them, these techniques can become an integral part of the QSP modeling best practices. Students who do their graduate training in departments such as mathematics, statistics, and engineering, may have the chance to learn from faculty formally trained in these methods. Students with these backgrounds can benefit the QSP field by bringing their knowledge into the biopharma modeling community. Faculty doing this type of research have been contributing to biopharma modeling in the form of conference presentations and participation in focused working groups. We hope these efforts and connections to these researchers will continue to grow.

Regarding training for computational aspects of model evaluation, the use of standardized software and/or methods, as described above, enables companies to hire people who have worked at other companies or trained at different schools more easily. Not having to completely retrain on software or methods greatly reduces the start‐up time needed for those who move into new positions.

DISCUSSION

Despite examples showing the value of QSP models, they are not used as much as they could be in decision making, including in regulatory settings. This is often because QSP models are complex and hard to qualify, leaving decision makers wondering how much confidence to have in a model and its predictions when making their decisions. Systematically performing and documenting the evaluation of a QSP model supports confidence in the model’s predictions and can help the adoption, use, and re‐use of QSP models.

Currently, the QSP community lacks a framework for the evaluation process of QSP models. Within the larger paradigm of “right question, right model, right analysis” for systems modeling work, we have therefore focused here on planning and performing the “right analysis,” building on the work of Cucurull‐Sanchez et al., ²⁵ in particular, with respect to verification, validation, and the documentation of these activities. However, we present a different perspective, focused on quantitative evaluation methods, with more detail on the evaluation methods themselves, when and how they can be applied, as well as further recommendations for the documentation.

In this work, we do not propose model acceptability criteria, analogous to the p value used in a statistical analysis. Instead, we propose a sequence of analyses that, taken together, represent a complete framework in which to perform model evaluation, with our goal being to contribute to a larger body of standards within the QSP community. We have presented a framework to perform model evaluation, as well as detailed descriptions of the methods used. This framework consists of three stages. In the first stage, a modeling and evaluation plan is defined based on the model aims, scope, and risk considerations. In the second stage, the model building takes place. In the third stage, the analyses outlined in the model evaluation plan are performed and documented to form a coherent body of evidence that builds confidence in a model and its predictions. We recommend using this framework and analyses to support QSP model development and to maximize impact of QSP models.

In most cases, when a model will be used to make predictions and decisions in drug discovery or development, we recommend the following key basic analyses be performed, when appropriate for the COU and project resources, to ensure adequate confidence in model predictions: (1) global sensitivity analysis on a full or partial set of parameters (depending on model size, prior knowledge, and goals) to determine those that are most influential; (2) structural and practical identifiability to determine which of the most‐influential parameters can actually be estimated; (3) estimation, using available data, of the most‐influential parameters that are also identifiable; and (4) comparison of model predictions to available data.

Our work summarizes and builds on the work of many others, both within the QSP community and the wider computational modeling research community. One of our goals in mentioning this prior work, describing methods, and providing extensive references is to help those who are interested in learning more. These resources can support QSP modelers interested in learning and developing techniques and software to better serve QSP modeling and model evaluation needs.

Unlike evaluation methods for empirical PK/PD models in data‐rich settings, we emphasize that there is no one‐size‐fits‐all solution for evaluation of QSP models, because the evaluation plan should take into account the model aims and scope, risk, and other factors, which can vary significantly from one QSP model/application setting to another. In addition, these model evaluations often involve a trade‐off of resources, such as the available time, personnel, data, and computational capabilities.

It is our hope that this framework will help in the efforts of the QSP community to align and standardize on evaluation methods and their documentation. We included examples to show how inappropriate analysis or a lack of analysis (e.g., LSA vs. GSA, and estimation of unidentifiable parameters) can yield misleading results, even for simple models. More‐complex models, such as many QSP models, are even more susceptible to these types of fallacies. This highlights the importance of appropriate analysis, as determined by model aims, model scope, risk, and other assessments.

There are multiple challenges regarding model evaluation analyses that would benefit from further investigation and discussion within the QSP modeling community. These include: (1) standardized, validated, easy‐to‐use software and workflow infrastructures to perform model evaluation; (2) issues related to large computational expense; and (3) appropriate curricula and content for training of graduate students and early career professionals in model evaluation methods.

DISCLAIMER

The mention of commercial products, their sources, or their use in connection with the material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.

CONFLICT OF INTEREST STATEMENT

S.B. was employed by MathWorks during the writing of this paper, and may hold stock or stock options in AbbVie. P.P. was employed by the FDA during the writing of this paper. H.M. was employed by AstraZeneca and Applied BioMath during the writing of this paper, and holds stock in Bristol‐Myers Squibb.

AUTHOR CONTRIBUTIONS

S.B. and H.M. designed the research; S.B., P.P., and H.M. wrote and edited the paper; S.B. wrote the code to generate Figures 2, 3, 4.

Supporting information

Supplementary Material

Braakman S, Pathmanathan P, Moore H. Evaluation framework for systems models. CPT Pharmacometrics Syst Pharmacol. 2022;11:264‐289. doi: 10.1002/psp4.12755