Abstract
Estimating the time lag between a pair of time series is of significance in many practical applications. In this article, we introduce a method to quantify such lags by adapting the visibility graph algorithm, which converts time series into a mathematical graph. Currently widely used method to detect such lags is based on cross-correlations, which has certain limitations. We present simulated examples where the new method identifies the lag correctly and unambiguously while as the cross-correlation method does not. The article includes results from an extensive simulation study conducted to better understand the scenarios where the new method performed better or worse than the existing approach. We also present a likelihood based parametric modeling framework and consider frameworks for quantifying uncertainty and hypothesis testing for the new approach. We apply the current and new methods to two case studies, one from neuroscience and the other from environmental epidemiology, to illustrate the methods further.
Keywords: Time series, time lag, visibility graph algorithm, cross correlation, correlogram, transfer function, local field potentials, neuroscience, ozone levels, environmental epidemiology
1. Introduction
Examples of pairs of time series, with one affecting the other, abound in various scientific disciplines. Rainfall affecting water levels in a lake or aquifer, advertising expenditures affecting sales, outdoor temperature or weather affecting electricity consumption are a few examples of pairs of related time series. In such examples, a statistical modeler is often interested in assessing the time lag or time delay between the two time series. In the case of such pairs of time series seen in epidemiology literature (e.g., air pollution levels affecting daily number of deaths in a city) precise estimation of time delay will have policy implications as well.
The classical textbook based method to detect the lag between two time series is using cross-correlograms (Wei 2006; Box, Jenkins, and Reinsel 2008). There are two approaches to using cross-correlograms for this problem. The widely used method is based on the cross-correlogram for the original pair of time series, in which the lag is identified as the point on the x-axis corresponding to the maximum correlational value. However, this method can sometimes give ambiguous or even incorrect results. A more technically sound approach is based on the transfer function framework. The second approach typically requires some careful pre-processing of the data and diagnostic checking before applying the cross-correlogram method; these preliminary steps are often ignored in practice, often leading to erroneous conclusions.
In this article, we propose a new method based on adapting visibility graph algorithm (VGA), which converts a time series into a mathematical graph (Lacasa et al. 2008; Lacasa and Luque 2010). We introduce a modeling framework for our adaptation to quantify the uncertainty related to the method. One of the advantages of the new method is that a pre-processing step is not necessary to use it. We illustrate the new method and the above concepts via simulated examples. We also illustrate the new method by applying it to two case studies.
The article is organized as follows. Sec. 2 presents the old and new methods, and illustrative examples; this section also includes a brief review of the transfer function framework for cross-correlograms. Sec. 3 presents the results from an extensive simulations study. In Sec. 4, we provide a theoretical framework for modeling the adjacency matrices in VGA, which helps with developing a statistical approach useful for hypothesis testing. We also provide a bootstrap based approach to quantify the uncertainty related to our method. In Sec. 5, we explore certain directions that could rectify some limitations of the new approach. In Sec. 6, we utilize our method to assess the relationships of two pairs of time series: (1) from neuroscience (local field potential based time series from the hippocampus) and (2) from environmental epidemiology (ozone levels affecting number of deaths). Finally we draw conclusions in Sec. 7.
2. Methods
In this section, we first present our new approach based on VGA. Later in the section we present the traditional approaches based on cross-correlograms.
2.1. Detecting lags using VGA
Consider two time series {xt} and {yt} and assume that {yt} is related to a lagged version, , of . To find the time lag (Δ) between the two time series, as a first step we fix one of the series, say {yt}, and obtain time-shifted copies of the other series, . The key step in our methodology is the conversion of all the above time series into graphs based on the VGA (Lacasa et al. 2008; Lacasa and Luque 2010; Núñez, Lacasa, and Luque 2012). For a given time series, VGA based graph has the same number of nodes as the number of time points. VGA is easy to explain if the time series is represented using vertical bars, where the height of the vertical bar at each time point corresponds to the value of the series at that particular time point. For the VGA based graph, an edge between two nodes is drawn if and only if there is visibility between the top points of the corresponding vertical bars; that is, if the straight line between the corresponding top points is not intersected by any of the vertical bars at the intermediate time points. Figure 1 top panel illustrates how the visibility algorithm works. The time series plotted in the upper panel is an approximate sine series; specifically, a sine series with Gaussian white noise added.
Figure 1.
A time series and the corresponding visibility graph. t1, t2, etc. denote the time points as well as the corresponding nodes in the visibility graph.
More formally, the following visibility criteria can be established: two arbitrary data values (tq, yq) and (ts, ys) will have visibility, and consequently will become two connected nodes of the associated graph, if any other data (tr, yr) placed between them fulfills:
In mathematical notation any graph with n nodes could be represented by its n×n adjacency matrix A which consists of 0’s and 1’s. The (i, j)th element of A is 1 if there is an edge connecting the ith and the jth node, 0 otherwise. Two graphs, G1 and G2, can be compared by the metric “distance,” between their corresponding adjacency matrices, AG1 and AG1 Here, ||·||2, called the Frobenius norm of a matrix, is the square root of the sum of the squares of the elements of the matrix; that is, the square root of the trace of the product of the matrix with itself.
Our proposed method to assess the time lag between xt and yt using the VGA is as follows. Convert the yt time series into a visibility graph and obtain its corresponding adjacency matrix, Ay. Convert also the time-shifted copies of xt into their visibility graphs and obtain the corresponding adjacency matrices . We determine the copy for which the Frobenius norm is minimized. The time lag between the two original series is then taken as τs.
We further illustrate our method using the plots in Fig. 2. ts.a, the time series given in the top panel, is an approximate sine series. The time series in the middle panel ts.b is derived by shifting ts.a to the left by two units, by reducing the amplitude to one-half that of ts.a, and adding some Gaussian noise. In other words, ts.a and ts.b have roughly the same shape although their amplitudes are different and one is shifted by two time units relative to the other as seen in the figure. We considered time-shifted copies of ts.b with time-shifts from the following set: {0, 1, 2, ... , 20}. VGA was applied and adjacency matrices for the corresponding graphs were obtained. Distance-measure based on the Frobenius norm for the time-shifted copies of ts.b compared to the reference ts.a, are plotted in the bottom panel of Fig. 2. The distance-measure is minimized at 2, which was the lag that we set a priori. Thus, in this illustrative example, the lag was correctly identified by the method that we proposed.
Figure 2.
Illustration of our method. Top two panels show time series, one shifted by a lag of two from the other. Bottom panel shows the distance-measure based on Frobenius norm for different time lags; minimum is achieved for the time lag 2.
2.2. Detecting lags via cross-correlograms
The widely used, currently existing method to detect lag between two time series is based on cross-correlograms. There are two approaches to utilize the cross-correlograms. The first approach is simply based on applying the cross-correlogram and identifying the lag corresponding to the highest peak; this approach could lead to ambiguous or incorrect results, at times. The second approach based on cross-correlograms could be understood within the transfer function modeling framework. We give a short introduction to transfer function modeling framework and illustrate via examples how the assumption of stationarity is strictly necessary within this framework. If non-stationarity is detected, transformations to make the time series stationary have to be performed before utilizing transfer function models. Furthermore, to utilize cross-correlograms within this framework, a pre-whitening step is also necessary. Our examples will illustrate all the above points. That is, how cross-correlograms will fail to detect the lag correctly if this pre-whitening step is skipped. In all the examples, we also apply our method, which require neither the assumption of stationarity nor the prewhitening step. The fact that these steps are not necessary for our method makes it easier for the practitioner.
2.2.1. Transfer function models and cross-correlations
We begin with assuming that xt and yt are properly transformed series so that they are both stationary, and yt is related to xt via the model
Here Bj is the back-shift operator , and et the noise series is assumed to be independent of xt. In practice, we typically only consider a causal, stable model for which , and the coefficients satisfy . Estimation of infinite number of coefficients is impossible with finite number of xt and yt, and hence we simplify by assuming a rational form for ν(B):
| (1) |
and b is a delay parameter representing the actual time lag before x-series produces an effect on the y-series. Our main interest within this framework is to estimate b. Rewriting Eq. (1) as
and expanding, we will see that the weights ν0, ν1, ... , νb−1 are zero, νb is non-zero, and are not necessarily zero. Thus, within the transfer function modeling framework, time lag is determined as that value of b for which νj = 0 for j < b and .
In practice, all the above analysis is done via the cross-correlogram which plots the cross-correlation function (CCF) against lag k, where
The relationship between CCF and the transfer function coefficients are given by the following equation
| (2) |
where represents the autocorrelation of the x-series at lag l. If the x-series is white noise, then and for l > 0, which reduces Eq. (2) to
| (3) |
Note that if we transform the x-series to make it white noise, then we will have to apply the same transform to the y-series as well. In summary, Eq. (3) states that the coefficient νk is a scaled version of the CCF value at lag k, assuming that xt and yt are stationary and have been pre-whitened before being fed in as inputs to the CCF. In this case, the lag between the two series may be determined as the first k for which is different from zero at a statistically significant level. Derivations and more details may be found in Wei (2006, Chapter 14) and Box, Jenkins, and Reinsel (2008).
We give three simulated examples to illustrate our point. In each example, we will see how the cross-correlogram method without the transfer function framework could lead to ambiguous results. The degree of ambiguity increases as we move from examples 1–3.
2.2.2. Example 1: an ARMA model
In the first example, we consider an ARMA model for xt and yt,
where αt and et are independent white noise series. Note that the lag is set a priori as 3. The length of both time series equals 100.
Since the roots of the quadratic equation 1 − 0.8897z + 0.4858z2 = 0 are outside the unit circle, xt and yt are stationary. However, neither series are white noise. The plot in the left panel in Fig. 3 shows the CCF without pre-whitening either series. The highest peak is at lag 3; thus, if we just pick the point on the x-axis corresponding to the highest peak, we correctly identify the lag as 3. However, the cross-correlations at lags 2 and 4 are also prominent and significantly above zero, which may lead to ambiguity. A better approach is based on the transfer function framework. We fit an ARMA model with 2 AR and 2 MA coefficients separately for x-series and y-series and the CCF based on the residuals are plotted in the right panel of Fig. 3. In this case, we see that the correlogram based method correctly identifies the lag correctly. For comparison, the Frobenius norm for the VGA method and the scores from a test statistic W that we develop in a later section are plotted in Fig. 4. Briefly, W is a statistic to test for differences between one time series and the time-shifted copy of the other corresponding to each lag. Based on Fig. 4 we note that the proposed new method detects the lag correctly.
Figure 3.
Cross correlation function without pre-whitening (left panel) and with pre-whitening (right panel) for the pair of time series in example 1.
Figure 4.
Frobenius norm (left panel) and W test statistic for the pair of time series in example 1. A horizontal line through −1.96 is plotted in the right panel.
2.2.3. Example 2: random walk model
The second example is a random walk model
The sample size for both series was set to 100. In this case, both series are non-stationary, but a simple differencing (xt − xt−1, yt − yt−1) will make them stationary and white noise.
The CCF for the original x and y series are plotted on the left panel in Fig. 5, and the CCF after differencing both series are plotted on the right panel. The highest peak in the left panel correspond to the correct lag; however, the values at the nearby lags are very close to the highest peak. Thus the degree of uncertainty about the number of lags is much more dramatic in this example, if we use the cross-correlogram based on the raw series. Making the series stationary and pre-whitening leads to eliminating this ambiguity and detecting the lag correctly, as seen in the right panel. Frobenius norm and W test-statistic scores for our proposed method are plotted in Fig. 6; we note that the W score is below −1.96 only for the correct lag (i.e. lag 3).
Figure 5.
Cross correlation function without pre-whitening (left panel) and with pre-whitening (right panel) for the pair of time series in example 2.
Figure 6.
Frobenius norm and W test-statistic scores for the pair of time series in example 2. A horizontal line through −1.96 is plotted in the right panel.
2.2.4. Example 3: an ARIMA model
For the third example we generate xt from an ARIMA(1,1,0) model with AR coefficient 0.7. The sample size was set to 75, and yt series were generated as
Note that there are three a priori set lags (i.e. lags at 3, 4 and 5) for this example. Pre-whitening was done for both series by fitting an ARIMA (1,1,0) model and obtaining the residuals.
Cross-correlogram based on the original series is shown in the left panel in Fig. 7, and that based on fitting an ARIMA (1,1,0) model is shown in the right panel. In the left panel, the highest peak is at lag 3 (0.963), followed by lag 4 (0.954) and then lag 2 (0.955). The correlation value (0.934) at lag 5 comes next. First of all, the top correlational values are so close to each other that there is ambiguity about the number of lags to pick. If we decide to pick the top three lags, we will incorrectly pick lag 2 and not pick lag 5. The results from the second approach shown in the right panel are not ideal either; only lags at 3 and 4 are picked. Thus, this example illustrates limitations of the second approach as well: there could be more than one candidate for the best model for the given series, which could lead to different results.
Figure 7.
Cross correlation function without pre-whitening (left panel) and with pre-whitening (right panel) for the pair of time series in example 3.
Figure 8 shows the Frobenius norm and values of the test-statistic W. Test statistics U that we develop in a later section are also plotted in Fig. 8; briefly, U is a statistic to test whether a given candidate-lag between the time series pair is significantly different from zero. For both test statistics, only the values at lags 3, 4, and 5 were below −1.96, and magnitude of the values in these cases are proportional to the magnitude of the effects of each model in the model that generated the time series. That is, in the generative model, the highest effect was set at lag 4, then at lag 3 and the least effect at lag 5. We see same order for the magnitude of the test statistic scores at the three lags. Thus, for this example, only the newly proposed method identified the lags correctly.
Figure 8.
Frobenius norm and test statistics for the pair of time series in example 3.
3. Simulations study
To better understand the performance of the proposed method compared to the traditional approaches, we conducted a simulation study. At each simulation iteration, within each simulation scenario, a pair of time series was generated as a bivariate ARMA(1,1) process using varma function in the “multiwave” R package (Achard and Gannaz 2016, 2019a, 2019b). Various scenarios were considered based on the underlying true time lags (3, 7, and 12), the correlation between the time series pair (ρ = 0.3, 0.6) and different ARMA(1,1) models. 1,000 iterations were done for each scenario. Table 1 presents % of iterations for which the true lags were correctly identified by each method for each scenario; the % of times the true lag ±1 was identified, is also listed. The methods considered were VGA and cross-correlation applied to the original time series (VG-O and CC-O, respectively) and VGA and cross-correlation applied to the residuals after fitting ARMA(1,1) model (VG-R and CC-R, respectively); arima function in R was used for fitting the ARMA(1,1) model at each iteration. Sample size of 200 was used for each time series generated for the results presented in Table 1. The coefficients of the ARMA(1,1) pairs considered are listed in the first column in Table 1. The coefficients lie on a range where on one end of the spectrum both ARMA(1,1) time series in a given pair have the same AR and MA coefficients: specifically, 1 and 1. As we move down the table either the MA coefficient or the AR coefficient is changed by a value of 0.5, until we reach the other end of the spectrum where either the MA coefficient or the AR coefficient has a value equal to −1. Intercept value was set to zero for all the simulations.
Table 1.
Results from simulation study with bivariate ARMA(1,1) models; % of lags correctly identified.
| Coefficients of ARMA(1,1) pair | Methods | True lag = 3 |
True lag = 7 |
True lag = 12 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
P = 0.3 |
P = 0.6 |
P = 0.3 |
P = 0.6 |
P = 0.3 |
P = 0.6 |
||||||||
| % c* | ±1** | % c | ±1 | % c | ±1 | % c | ±1 | % c | ±1 | % c | ±1 | ||
|
| |||||||||||||
| (1,1) | VG-O | 80.9 | 7.0 | 99.6 | 0.4 | 79.3 | 7.0 | 100 | 0.0 | 69.9 | 6.7 | 100 | 0.0 |
| vs. | VG-R | 68.2 | 19.4 | 89.7 | 10.3 | 69.0 | 16.1 | 90.3 | 9.2 | 59.8 | 12.1 | 89.9 | 9.7 |
| (1,1) | CC-O | 26.8 | 7.4 | 50.2 | 15.0 | 28.1 | 10.7 | 53.8 | 15.5 | 25.1 | 7.5 | 47.3 | 15.5 |
| CC-R | 71.1 | 22.3 | 87.1 | 12.9 | 63.6 | 15.3 | 84.5 | 13.4 | 55.2 | 15.1 | 82.7 | 13.5 | |
|
| |||||||||||||
| (1,1) | VG-O | 70.8 | 11.3 | 100 | 0.0 | 74.6 | 12.7 | 98.3 | 1.3 | 66.8 | 11.5 | 99.2 | 0.4 |
| vs. | VG-R | 84.2 | 4.2 | 100 | 0.0 | 88.6 | 2.1 | 99.6 | 0.4 | 80.3 | 3.7 | 99.6 | 0.4 |
| (1,0.5) | CC-O | 30.0 | 7.1 | 53.3 | 18.8 | 22.5 | 8.5 | 56.3 | 17.9 | 30.3 | 8.6 | 54.3 | 15.1 |
| CC-R | 84.2 | 10.0 | 99.2 | 0.4 | 84.7 | 4.7 | 99.6 | 0.4 | 78.3 | 7.0 | 97.1 | 2.0 | |
|
| |||||||||||||
| (1,1) | VG-O | 41.5 | 35.5 | 59.7 | 39.5 | 47.4 | 36.5 | 56.3 | 41.3 | 40.9 | 30.8 | 58.0 | 38.7 |
| vs. | VG-R | 86.8 | 3.8 | 99.6 | 0.4 | 84.3 | 5.2 | 97.9 | 2.1 | 78.9 | 8.6 | 96.6 | 3.4 |
| (1,0) | CC-O | 22.2 | 8.1 | 47.6 | 21.0 | 29.6 | 7.8 | 54.6 | 17.5 | 25.3 | 8.4 | 45.8 | 23.9 |
| CC-R | 94.9 | 2.1 | 100 | 0.0 | 90.9 | 2.6 | 99.6 | 0.4 | 88.6 | 3.0 | 98.3 | 1.7 | |
|
| |||||||||||||
| (1,1) | VG-O | 13.0 | 54.6 | 3.8 | 92.5 | 9.7 | 61.4 | 3.3 | 92.7 | 11.2 | 40.7 | 3.4 | 86.8 |
| vs. | VG-R | 86.1 | 2.1 | 95.8 | 4.2 | 80.1 | 3.0 | 96.7 | 3.3 | 78.0 | 3.7 | 94.9 | 5.1 |
| (1,−0.5) | CC-O | 21.4 | 18.5 | 27.5 | 52.9 | 19.9 | 21.6 | 18.4 | 51.8 | 22.0 | 17.0 | 21.8 | 50.0 |
| CC-R | 96.6 | 2.1 | 97.1 | 2.9 | 94.5 | 2.5 | 97.6 | 2.4 | 92.1 | 2.5 | 96.6 | 3.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 0.0 | 43.4 | 0.0 | 73.6 | 2.5 | 43.9 | 0.0 | 75.3 | 0.9 | 36.2 | 0.0 | 67.6 |
| vs. | VG-R | 84.7 | 2.5 | 99.2 | 0.8 | 83.7 | 5.0 | 98.7 | 1.3 | 79.7 | 5.2 | 99.6 | 0.4 |
| (1,−1) | CC-O | 0.4 | 18.2 | 0.0 | 24.7 | 0.0 | 20.9 | 0.0 | 24.7 | 0.4 | 16.4 | 0.4 | 30.3 |
| CC-R | 95.5 | 1.7 | 99.6 | 0.4 | 96.2 | 2.1 | 99.2 | 0.8 | 94.0 | 2.6 | 99.6 | 0.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 44.1 | 20.8 | 84.2 | 11.6 | 42.7 | 24.8 | 77.2 | 14.3 | 36.1 | 13.0 | 69.8 | 15.3 |
| vs. | VG-R | 84.7 | 4.2 | 99.6 | 0.4 | 84.2 | 2.9 | 98.3 | 1.7 | 81.1 | 1.3 | 98.3 | 1.7 |
| (0.5,1) | CC-O | 6.8 | 20.8 | 1.7 | 29.9 | 5.4 | 18.3 | 1.7 | 32.9 | 9.7 | 21.0 | 3.4 | 38.3 |
| CC-R | 98.7 | 0.4 | 99.2 | 0.8 | 95.0 | 2.5 | 98.7 | 1.2 | 95.4 | 1.3 | 99.6 | 0.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 20.5 | 29.7 | 21.1 | 62.9 | 20.5 | 29.5 | 18.4 | 63.2 | 14.9 | 22.8 | 21.8 | 47.9 |
| vs. | VG-R | 83.7 | 2.1 | 100 | 0.0 | 84.6 | 2.1 | 99.6 | 0.4 | 80.9 | 8.3 | 99.2 | 0.8 |
| (0,1) | CC-O | 0.8 | 15.1 | 0.4 | 23.2 | 3.8 | 17.5 | 0.4 | 24.4 | 4.1 | 16.6 | 0.8 | 33.2 |
| CC-R | 98.7 | 1.3 | 100 | 0.0 | 97.4 | 1.7 | 99.0 | 8.5 | 93.8 | 2.5 | 99.6 | 0.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 3.0 | 36.7 | 0.4 | 76.3 | 6.4 | 42.8 | 1.7 | 78.3 | 5.8 | 29.6 | 1.3 | 72.3 |
| vs. | VG-R | 85.7 | 3.4 | 99.6 | 0.4 | 85.6 | 2.1 | 97.9 | 2.1 | 80.7 | 1.6 | 98.3 | 1.7 |
| (−0.5,1) | CC-O | 0.8 | 19.4 | 0.0 | 19.1 | 0.4 | 19.1 | 0.0 | 21.7 | 1.6 | 21.4 | 0.4 | 28.1 |
| CC-R | 95.4 | 2.1 | 99.2 | 0.8 | 95.8 | 2.5 | 99.6 | 0.4 | 95.9 | 1.2 | 99.6 | 0.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 0.4 | 40.3 | 0.0 | 78.6 | 0.8 | 52.0 | 0.0 | 78.2 | 0.9 | 29.8 | 0.0 | 67.0 |
| vs. | VG-R | 88.6 | 2.5 | 98.4 | 1.6 | 83.2 | 3.3 | 97.4 | 2.6 | 77.9 | 1.3 | 97.4 | 2.6 |
| (−1,1) | CC-O | 0.0 | 16.1 | 0.0 | 23.0 | 0.8 | 18.4 | 0.0 | 24.4 | 0.0 | 19.6 | 0.0 | 26.2 |
| CC-R | 95.3 | 2.5 | 98.8 | 1.2 | 94.7 | 3.7 | 99.1 | 0.9 | 94.0 | 2.1 | 98.7 | 1.3 | |
: %c = percent correct;
: percent for which ±1 true lag detected.
VG-O, VG-R, CC-O, and CC-R: VGA and cross-correlation applied to original and residual series, respectively.
Based on the results in the first 4 rows in Table 1 corresponding to ARMA(1,1) pairs with the same coefficients, we see that the newly proposed method is not perfect (e.g. only 80.9% of the times are the true lag correctly identified when the true lag was set as 3, and the correlation used for bivariate data generation was 0.3). However, for that particular ARMA(1,1) pair, the new method outperforms all other methods for all lags and correlations considered. Even when the VGA and cross-correlation methods are applied on the residuals after fitting ARMA(1,1) model, the performance is considerably worse than that based on VGA applied to the original time series. The performance of the cross-correlation method applied on the original time series is substantially worse compared to all other methods. In the next four rows, corresponding to ARMA(1,1) coefficient pair (1,1) and (1,0.5), the high performance of VGO seen previously is maintained only in the scenarios with ρ = 0.6, while the performance of VG-R and CC-R gets better across all scenarios. As the magnitude of the difference between coefficients increases further down the table, the performance of VG-O weakens considerably compared to that of VGR and CC-R; however VG-O still outperforms CC-O in all scenarios.
In general, all methods performed substantially better when the underlying correlation between the time series was 0.6. Also, in general, the performance was more or less consistent across lags for all methods. We also note here that the methods based on residuals may not perform this well in practice. In our simulations, we know a priori the model to fit, viz. ARMA(1,1). A statistical modeler, in a real-world scenario though, may not fit the right model by utilizing diagnostic checking and other modeling tools at his or her disposal. In that sense, the good performance seen here for methods based on residuals may be a bit unrealistic. The overall conclusion to be drawn from the simulation results presented in Table 1 is that VG-O can be safely used only in the cases where the coefficients of the time series are exactly or very nearly the same. In the next section we presented a likelihood based modeling strategy which could be used to determine whether VG-O can be applied for a given time series pair.
We also did extensive simulations study with both time series in the pair as AR(1) and with both series as MA(1). For brevity of presentation, we show only some relevant results in Table 2; we present results only for the time series pairs generated using ρ = 0.6 and only results for underlying lag = 7 are presented. The conclusions to be drawn from Table 2 are the same as for Table 1: the performance of VG-O is high only when the coefficients across the time series pair are the same. Unlike in Table 1 though, the performance of VG-R and CC-R are also perfect when the coefficients are the same.
Table 2.
Results from simulation study with bivariate AR(1) and bivariate MA(1) models.
| Coefficients of AR(1)pair | Methods | Lag = 3 |
Lag = 7 |
Lag = 12 |
|||
|---|---|---|---|---|---|---|---|
| % c | ±1 | % c | ±1 | % c | ±1 | ||
|
| |||||||
| 1 | VG-O | 99.6 | 0.0 | 100 | 0.0 | 99.2 | 0.0 |
| vs. | VG-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| 1 | CC-O | 70.3 | 3.2 | 66.9 | 2.4 | 68.1 | 4.9 |
| CC-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 | |
|
| |||||||
| 1 | VG-O | 4.4 | 22.6 | 6.0 | 30.1 | 5.8 | 20.2 |
| vs. | VG-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| −1 | CC-O | 6.0 | 18.5 | 5.6 | 16.9 | 3.7 | 18.5 |
| CC-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 | |
|
| |||||||
| Coefficients of MA(1)pair | Methods | Lag = 3 |
Lag = 7 |
Lag = 12 |
|||
| % c | ±1 | % c | ±1 | % c | ±1 | ||
|
| |||||||
| 1 | VG-O | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| vs. | VG-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| 1 | CC-O | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| CC-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 | |
|
| |||||||
| 1 | VG-O | 0.0 | 97.2 | 0.0 | 96.8 | 0.4 | 96.4 |
| vs. | VG-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 |
| −1 | CC-O | 0.0 | 100 | 0.0 | 100 | 0.0 | 100 |
| CC-R | 100 | 0.0 | 100 | 0.0 | 100 | 0.0 | |
p = 0.6 was used in generating each bivariate series.
We also conducted simulations to study the performance of the methods as the sample size (T) of each time series increased. Table 3 presents the results for T = 200, 500, and 800. We present only the ARMA(1,1) pairs for which VG-O had the worst performance based on results in Table 1; also, only results for underlying lag = 7 are presented. The performance of VG-O is still far from desirable even when T = 800. However, it is also easy to note from Table 3 that the performance of VG-O increases with sample size while as that of CC-O does not.
Table 3.
Performance of methods as sample size increases.
| Coefficients of ARMA(1,1) pair | Methods |
T = 200 |
T = 500 |
T = 800 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
P = 0.3 |
P = 0.6 |
P = 0.3 |
P = 0.6 |
P = 0.3 |
P = 0.6 |
||||||||
| % c | ±1 | % c | ±1 | % c | ±1 | % c | ±1 | % c | ±1 | % c | ±1 | ||
|
| |||||||||||||
| (1,1) | VG-O | 2.5 | 43.9 | 0.0 | 75.3 | 0.4 | 71.9 | 0.0 | 86.7 | 0.0 | 72.0 | 0.0 | 88.6 |
| vs. | VG-R | 83.7 | 5.0 | 98.7 | 1.3 | 95.7 | 3.9 | 97.4 | 2.6 | 94.4 | 5.2 | 99.6 | 0.4 |
| (1,−1) | CC-O | 0.0 | 20.9 | 0.0 | 24.7 | 0.0 | 21.2 | 0.0 | 21.0 | 0.0 | 15.9 | 0.0 | 15.7 |
| CC-R | 96.2 | 2.1 | 99.2 | 0.8 | 96.5 | 3.5 | 99.1 | 0.9 | 95.7 | 4.3 | 99.6 | 0.4 | |
|
| |||||||||||||
| (1,1) | VG-O | 0.8 | 52.0 | 0.0 | 78.2 | 0.4 | 66.7 | 0.0 | 84.5 | 0.0 | 70.2 | 0.0 | 87.1 |
| vs. | VG-R | 83.2 | 3.3 | 97.4 | 2.6 | 93.6 | 5.1 | 98.3 | 1.7 | 93.3 | 6.7 | 96.7 | 3.3 |
| (−1,1) | CC-O | 0.8 | 18.4 | 0.0 | 24.4 | 0.0 | 19.7 | 0.0 | 22.8 | 0.0 | 17.8 | 0.0 | 14.6 |
| CC-R | 94.7 | 3.7 | 99.1 | 0.9 | 95.3 | 4.7 | 97.8 | 2.2 | 94.7 | 5.3 | 98.3 | 1.7 | |
True underlying lag = 7 was used in all scenarios.
4. Theoretical considerations
In this section, we consider a modeling strategy, an approach for quantifying uncertainty and an approach for testing hypothesis.
4.1. Modeling the adjacency matrices
In this subsection, we consider modeling the adjacency matrices under some simplifying assumptions with an eye toward developing a hypothesis framework later. If we denote as the (u, v)th element in the adjacency matrix for the y-series, then
where I denotes the indicator function. Here we assumed for convenience that the events within the intersection sign are independent, when in reality they may not be. This gives
One way to model the adjacency matrix is by assuming
Then
Similarly, if we assume
we have
It is reasonable to make the above assumption of constant probability for all and we justify it as follows. Because of autocorrelation, the generative process of yr is very similar to that of a neighboring point . Hence the probability of having an edge between yr and yv is roughly the same as that between and yv - we simplify the modeling by assuming that they are exactly the same (i.e. p). We may estimate p and q using maximum likelihood estimation. The log-likelihood in the y-series case may be written as
and for the x-series as
Note that we used only the upper triangular elements in each adjacency matrix because of symmetry, and excluded all the diagonal elements since they are all zero with probability 1.
For example, consider the two time series
| (4) |
Note that Δ is the time lag between the two series set a priori. For illustration, we generated an instance of this pair of series with T = 90 and Δ = 5. The adjacency matrices Ay and Ax based on VGA were computed and the loglikelihoods L(Ay; p) and L(Ax; q) were calculated and plotted (see Fig. 9) for each value on a grid from 0 to 1 with spacing 0.001. The maximum of the respective likelihoods were achieved at = 0.733 and = 0.732. Note that VGA is scale invariant; however, is slightly different from because of the noise term e2 in {xt}.
Figure 9.
Log-likelihood of the adjacency matrices corresponding to y-series (left panel) and x-series (right panel) for a grid of p and q values. A vertical line is drawn in each panel corresponding to the point where maximum is reached. The y-series and x-series are based on Eq. (4).
One utility of the modeling approach is to determine, in an automated or semi-automated way, the scenarios in which the new methodology can be applied. If a statistical analyst or modeler is present, he or she can determine the best fit for each time series. If both fits are of the same type and with similar coefficients, then the analyst will apply VGA to the original time series, and if the type or coefficients differ, then the analyst will apply VGA or CCF methods to the residuals from the best fitted models. However, this model fitting process cannot be automated because of the various, sometimes subjective, diagnostic checking steps involved. We show below how the likelihood based approach yields an alternate process which could help to determine which method to use for a given pair of time series.
Consider Table 4 where we have presented the absolute value of the differences between maximum-likelihood estimates of p and q for the various ARMA (1,1) pairs that we considered in Table 1. Putting the results presented in Tables 1 and 4 together, it is clearly seen for the scenarios considered that if is less than 0.025, then VG-O should be the preferred approach. Thus the semiautomated process could be that if is less than a threshold (like 0.025), apply VG-O automatically; if not, fit the best models and use the residuals for determining the lag.
Table 4.
Absolute value of difference of p and q estimates.
| Coefficients of the second ARMA(1,1 ) series |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Correlation | (1,1) | (1,0.5) | (1,0) | (1,−0.5) | (1,−1) | (0.5,1) | (0,1) | (−0.5,1) | (−1,1) |
|
| |||||||||
| p = 0.3 | 0.0236 | 0.0262 | 0.0324 | 0.0661 | 0.1537 | 0.0895 | 0.1235 | 0.1372 | 0.1491 |
| p = 0.6 | 0.0190 | 0.0200 | 0.0275 | 0.0675 | 0.1520 | 0.0935 | 0.1192 | 0.1447 | 0.1525 |
4.2. Quantifying uncertainty
We propose a bootstrap based method to quantify the uncertainty related to the Frobenius distance (plotted for example in Fig. 2) at different lags between the corresponding adjacency matrices. Our method is based on adapting slightly the “multivariate linear process bootstrap” (MLPB) method developed and presented in Jentsch and Politis 2015. The core idea behind our adaptation is same as in “DCBootCB” algorithm presented in Kudela, Harezlak, and Lindquist (2017), in the context of estimating uncertainty in dynamic functional connectivity for neuro-imaging time series. In the first step, each time series of length T is divided into K adjacent blocks of length w (T = wK). Within each of the K blocks, we generate MLPB bootstrap samples. Subsequently, adjacent blocks of bootstrap samples are combined into a single time series of length T, forming a bootstrap sample of the original time series. We do this for each time series in the original pair to get a pair of bootstrapped time series. This process is repeated 100 times to get 100 bootstrap pairs. For each bootstrap pair we may calculate the Frobenius distance between adjacency matrices at each lag, and these 100 values may be used to calculate the bootstrap based standard error and 95% confidence intervals at each lag.
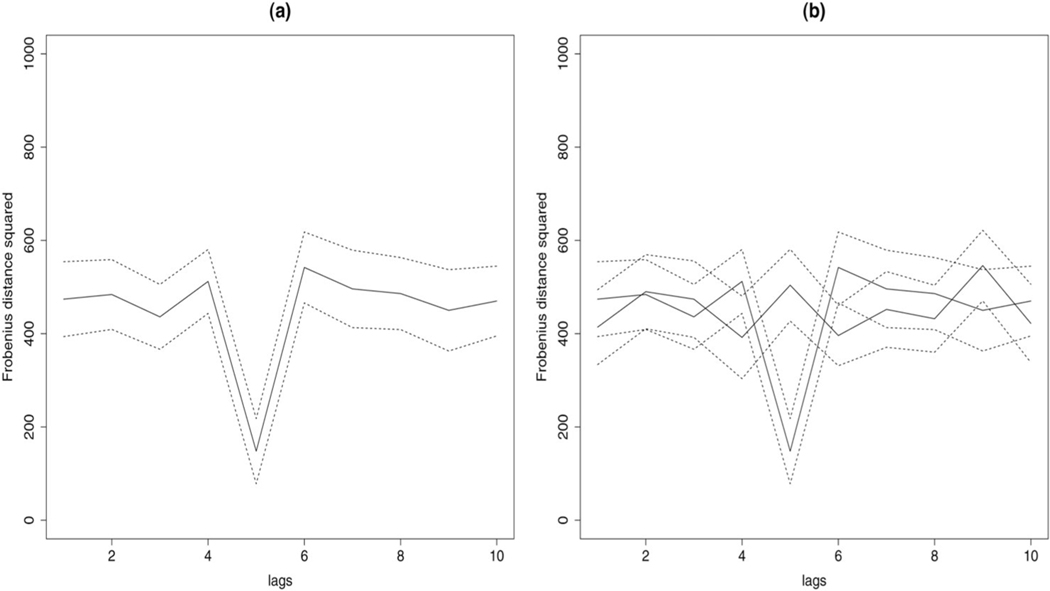
We show the results for the {yt} and {xt} series example presented above in Fig. 10a. We divided each series into 3 segments of length 30 each. MLPB algorithm was applied to each segment to generate corresponding bootstrap sample for the segment, and the further steps detailed above were completed. The confidence intervals for the square of the Frobenius distance at each time lag are plotted as dotted lines in Fig. 10a.
Figure 10.
Left panel: Square of the Frobenius distance at different lags based on the new method for the pair of time series generated via Eq. (4). 95% confidence intervals based on the bootstrap method are also plotted. Right panel: In addition to the same plot as in the left panel, Frobenius norm squared and 95% confidence intervals for permuted data are also plotted in this panel. The only lag at which the confidence intervals do not overlap is lag 5.
We may also use the confidence intervals to determine the statistical significance of the lag corresponding to the minimum value of the Frobenius norm. For this, we randomly permute both the y series and the time-shifted copy of x series (corresponding to the lag under consideration) and then calculate the Frobenius norm for the permuted pair. The corresponding bootstrap based 95% confidence intervals may also be obtained as above. The Frobenius norm values and the confidence intervals for the permuted time series corresponding to the above illustrative example is plotted in Fig. 10b. It is easy to note that the only lag where the two confidence intervals do not overlap is at lag 5, which was the lag a priori set between the two series in this example (see Eq. (4)).
4.3. Testing hypothesis
We may also identify the correct lag in a statistical testing framework. First we introduce some notation. With a slight abuse of notation let us denote the adjacency matrix of the time-shifted copy of x series at a particular time-lag under consideration, also by Ax. Then the square of the Frobenius norm may be denoted by
where the subscript ij denotes the ijth entry of the corresponding matrix, and 1 denotes the vector of 1’s. Our goal is to come up with a test statistic of the form
to reject or accept the null hypothesis
H0 : no difference between y and time shifted copy of x.
Since and are indicator functions, we have and . Using this,
so that, assuming independence between and we may write
Using the fact that the matrix (Dij) is symmetric, its diagonal elements zero, we get
which may be estimated by plugging in the ML estimates and . Again using the fact that the matrix (Dij) is symmetric, and that the variance of its diagonal, super-diagonal and sub-diagonal elements are zero we get the total variance as
where the terms in the second sum correspond to covariances between elements within each row, and the third sum for covariances of elements across rows. Covariances can be calculated as
Observing that Dij is an indicator function (so that ), we get
In practice, the covariances in the formula above are negligible, so we also consider an approximate variance term for computational ease:
The test statistic that we would like to consider ideally is
| (5) |
However, when eij is very small (e.g. below 0.001), the corresponding variance term in the denominator will also be very small, which in turn will inflate the test statistic significantly to have any meaningful performance in practical situations. Hence, we consider a modified version of the test statistic in Eq. (5) which includes only terms for which eij > τ, where τ is a pre-specified threshold:
| (6) |
The threshold τ that we chose for all practical numerical situations in this article, was 0.001. Note that and so that if we ignore the covariance terms, then and . Hence T and T1 are the corresponding standard deviations, which in turn implies that and . We will show that Z is approximately distributed standard normal using Stein’s method for sums of random variables with local dependence. Note that we will not be able to use Stein’s method for independent variables because Dij’s are not independent. The specific theorem that we will employ is Theorem 3.6 from Ross (2011), some version of which could also be read from the main result of Baldi, Rinott, and Stein (1989). For completeness, we state Theorem 3.6 from Ross (2011). We need the following definition before stating the theorem.
Definition (Dependency neighborhoods).
We say that a collection of random variables has dependency neighborhoods , i = 1, ... , n, if i ∈ Ni and Xi is independent of .
Theorem (Stein’s method).
Let X1, ... , Xn be random variables such that , , , and define . Then for Z a standard normal variable,
| (7) |
where dW(W, Z) denotes the Wasserstein metric between the probability measures of W and Z. In our case, the random variables are Eijs. We take the dependency neighborhood for Eij as the ith row and the jth column (i.e. and hence Eq. (7) will read as
| (8) |
since ignoring the covariance terms we have σ = T1. We also have .
Using binomial expansion and properties of indicator functions, it is easy to see that
| (9) |
| (10) |
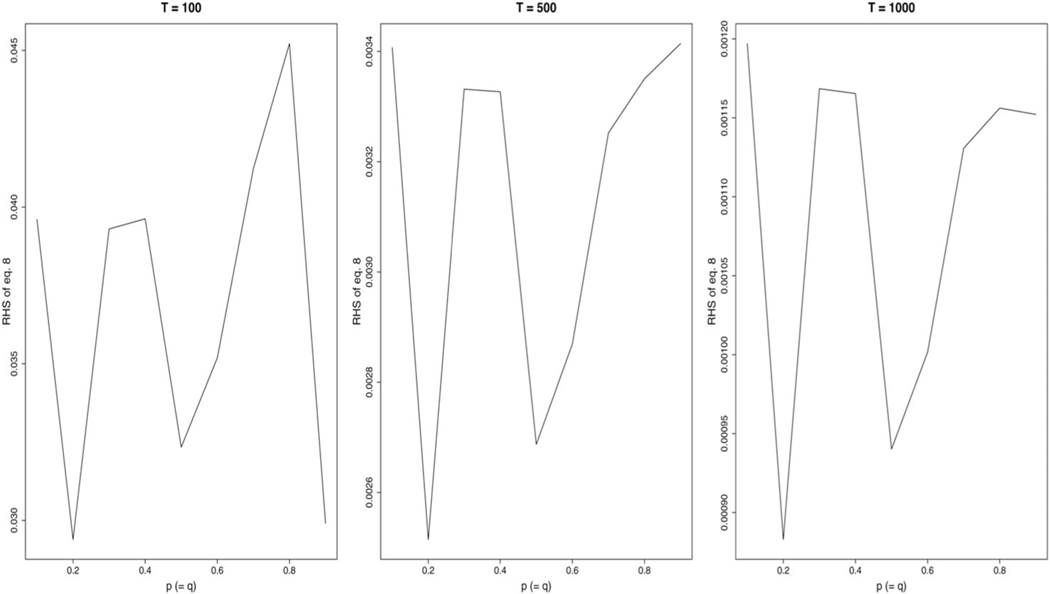
Figure 11 plots the upper bound in Eq. (8) using Eqs. (9) and (10) for values of p in the grid {0.1, ... , 0.9}, and q assumed to be equal to p. From the plot, it is seen that when T = 100, the values of the right-hand side of Eq. (8) is approximately 0.045 or less. It is also seen that as T increases, the RHS of Eq. (8) gets smaller and smaller, justifying our assumption of normality for the test statistic in Eq. (6).
Figure 11.
Right-hand side in Eq. (8) plotted against p for three sample sizes: T = 200, T = 500 and T = 1,000. q was assumed equal to p for this plot.
Note that under the null hypothesis of no difference between (time-shifted copy of) x and y, W will have a negative value and when there are differences the values of W will be large positive. Thus, a one-sided test, checking whether the test statistic is less than a critical threshold, is appropriate in this context rather than a two-sided test. Also, instead of the usual two-sided thresholds such as −1.64 (for α = 0.05) or −1.96 (for α = 0.025), much larger thresholds (e.g. −5.61 corresponding to α = 10−8) may be necessary. One way to justify such a stringent α conceptually, will be to think that we are testing for a very large (almost infinite) number of lags and thus using a very stringent α will prevent inflation of overall type-I error rate.
If the time-shifted copy of x is shifted by a lag of δ, then W depends on δ, and we may use the notation Wδ to acknowledge this dependence. If our goal is test the hypothesis
| (11) |
then we may use the test-statistic
Note that √2 is the standard deviation of the numerator assuming that the two terms in the numerator are distributed as standard normal.
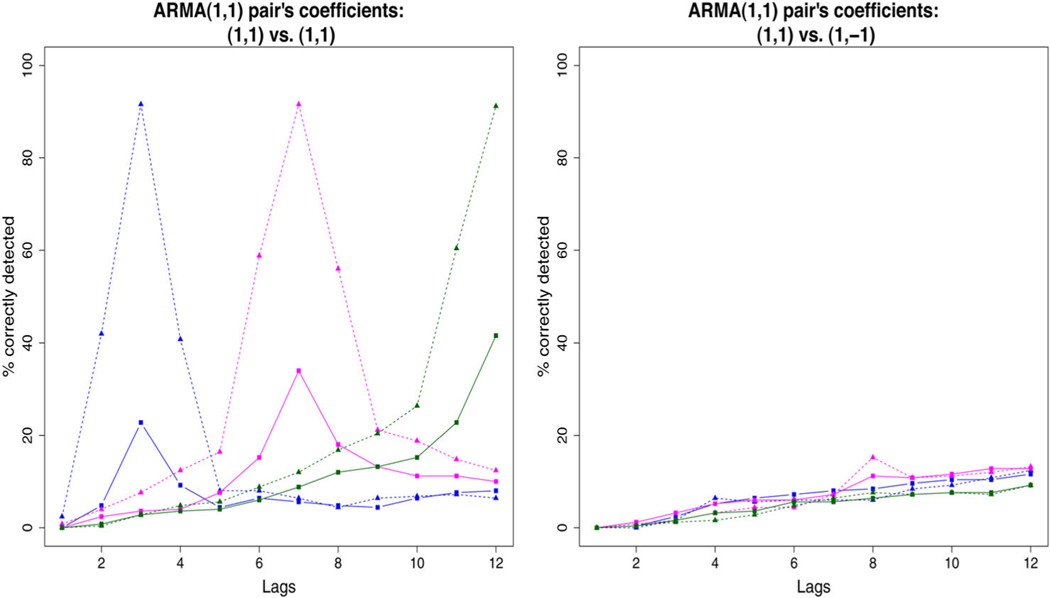
To assess the performance of the test statistic U empirically, we conducted a brief simulation study, the results of which are plotted in Fig. 12. We considered only two pairs of ARMA(1,1) time series (first pair with both coefficients (1,1) and the second pair with coefficients (1,1) and (1,−1)). The correlation coefficients that we considered for generation of bivariate time series, were 0.3 and 0.6. The true underlying lags considered were 3, 7 and 12. The one-sided critical threshold used was −5.61. Only in the case where ρ was 0.6 and the coefficients of the time series pair were exactly the same (see left panel in Fig. 12), was the performance of the test statistic good. In this scenario, the test statistic rejected the null hypothesis in Eq. (11) approximately 90% of the times when the time-shift δ corresponded with the true value of the underlying lag and rejected approximately 10% of the times for all other δ (in other words, good “sensitivity” and “specificity”). In all other scenarios (ρ = 0.3 in the left panel and all cases in the right panel), the test statistic performed poorly. Thus, we do not recommend this test-statistic at this stage of development. Nevertheless, we presented the test-statistic with the hope that it will help with future work (our own and others’) for developing a better test statistic. We also note here that the test statistics worked well for the three illustrative examples in Sec. 2.2, because each time series pair was highly correlated.
Figure 12.
Empirical performance of the U test-statistic for various lags when the true underlying lags were 3 (blue lines), 7 (magenta lines), and 12 (green lines). The scenarios in which the time series pair was generated using a correlation 0.3 is marked by squares and solid lines and with correlation 0.6 marked by triangles and dotted lines.
5. Jentsch-and-Politis type automated approaches to obtain residuals
The bottom line from the work so far presented, is that except when the underlying models for the two time series are the same and the coefficients very similar, it is more suitable to apply the methods (CCF or VGA) on a residual time series. In this regard, it is of interest to seek whether there could be an automated process (that is, without an analyst’s help) to get the appropriate residuals. A thorough exploration will be for future work, but here we explore one direction adapting an existing method available in the literature. The approach that we consider is based on Jenstch and Politis’ MLPB method for generating bootstrap samples of a multivariate time series, which we already presented in a previous section. Although the MLPB method was developed primarily for generating bootstrap samples, the key steps involved includes estimating the correlation structure of the time series pair and decorrelating it to obtain white noise series and then bootstrap resampling the white noise series, and eventually incorporating back the correlation structure to get a bootstrap sample of the original time series pair. It is the first two steps of the MLPB method—estimating correlation and decorrelating part—that we focus on adapting for our purposes. Essentially, we apply the VGA method to the white noise pair (that is, “residuals” time series pair) obtained midway of the MLPB algorithm. A detailed exposition of MLPB with more technical details may be found not only in the original article by Jentsch and Politis, but also in Kudela, Harezlak, and Lindquist (2017), and to a lesser extend in John et al. (2020).
Table 5 shows the performance of VGA and CCF applied to the white noise generated midway of Jenstch and Politis’ approach (we call the methods VGJP and CC-JP, respectively). We consider two ARMA(1,1) pairs from Table 1: one with coefficients (1,1) and (1,−1) and the other with coefficients (1,1) and (−1,1). Note that these are two pairs of models were the results presented in Table 1 looked the worst for VG-O. We consider sample sizes of 200, 500, and 800, but we restrict ourselves to the scenario with true underlying lag equals 7 and the underlying correlation equals 0.6, for brevity of the presentation. It is easily seen that the performance in this case is a vast improvement compared to what was seen for VG-O in Table 1. In Table 1, for the same scenarios considered in Table 5, the percent of lags correctly detected was zero for both VG-O and CC-O, compared to which it is a big improvement for VG-JP (18.1% and 22.8% for T = 200). The performance of the cross-correlation based approach (i.e. CC-JP) is still poor though. We also note based on Table 5 that there is no improvement for either VG-JP or CC-JP with increase in sample size. Although the performance of VG-JP improves considerably compared to VG-O, it still lags substantially behind VG-R or CC-R. Further work is warranted for improving the performance of VGA based approach in scenarios such as the ones considered in Table 5. Certain directions that could be considered for future work are discussed below.
Table 5.
Performance of VG-JP and CC-JP.
| ARMA(1,1) coefficients | Mehods | T = 200 |
T = 500 |
T = 800 |
|||
|---|---|---|---|---|---|---|---|
| %c | ±1 | %c | ±1 | %c | ±1 | ||
|
| |||||||
| (1,1) vs. | VG-JP | 18.1 | 0.0 | 12.4 | 0.0 | 12.8 | 0.0 |
| (1,−1) | CC-JP | 0.0 | 29.8 | 0.0 | 24.7 | 0.0 | 20.2 |
|
| |||||||
| (1,1) vs. | VG-JP | 22.8 | 0.0 | 20.3 | 0.0 | 9.5 | 0.0 |
| (−1,1) | CC-JP | 0.0 | 26.1 | 0.0 | 12.8 | 0.0 | 17.9 |
MLPB was developed for multivariate time series. However, an earlier work (McMurry and Politis 2010) had considered a similar approach for univariate time series. Obtaining residuals separately for univariate time series could be one direction to explore. A key component in the covariance estimation part of MLPB is a tapering function. We used only one type of tapering function (viz. trapezoid function). Variations in tapering function could also be considered when studying the empirical performance of the above-mentioned multivariate as well as univariate approaches. Ideas from other bootstrap resampling schemes for time series could also be considered. For example, Bühlmann (1997) employed a method-of-sieves based strategy to obtain the residuals, where sieves were based on autoregressive approximations. The key idea in Bühlmann’s article is to fit a series of AR(p) models for p ranging from 1 to 10log10(T), and pick the best model based on some model-selection criteria (e.g. AIC) and then obtain residuals based on this best fitted AR(p) model.
6. Case studies
In this section, we present two case studies, one from neurophysiology and another from environmental epidemiology, to illustrate some of the key points made regarding the methods.
6.1. Case study 1
Our first case study is based on local field potential (LFP) times series that is utilized in neuroscience, specifically neurophysiology, to study brain activity (Legatt, Arezzo, and Vaughan 1980; Gray et al. 1995). The three LFP time series that is used in our analysis were obtained using three different tetrodes implanted in the brain of a rat. Specifically, all three recordings were obtained from the CA1 field of the hippocampus of the rat. To make the results of our analysis accessible, we did not apply any pre-processing to the recorded LFPs except downsampling from 2 kHz to 1 kHz. More technical details about the LFP data collection is mentioned toward the end of this subsection.
Time series from each tetrode at 200 consecutive points are shown in the top panels of Fig. 13. Since the tetrodes were placed in close proximity inside the hippocampus, we do not anticipate any lag between any time series pair, from a neurophysiological perspective. ARMA(1,1) models fitted well for all three time series as seen in the ACF plots of the residual series after the fit, shown in the lower panels of Fig. 13. Visually, for the LFP series from the 3rd tetrode, although ARMA(1,1) is not a perfect fit, it is still areas on able fit. The AR and MA coefficients with standard errors in parenthesis for the three fits are as follows. Tetrode-1: AR-coeff. = 0.975 (0.015), MA-coeff. = −0.175 (0.081), Tetrode-2: AR-coeff. = 0.972 (0.016), MA-coeff. = −0.197 (0.084), Tetrode-3: AR-coeff. = 0.980 (0.014), MA-coeff. = 0.124 (0.067). The AR coefficients for all three fits are fairly close to each other. The MA coefficients for the first two tetrodes are also similar; however, the MA coefficient for the third tetrode is quite different from the other two. The absolute value of difference between the likelihood based p-estimates for tetrodes 1 vs. 2 is 0.02 and for tetrodes 2 vs. 3 is 0.03. Thus, based on conclusions from our simulation study, we can safely apply VGA based method to the original time series when assessing the lag between LFP series for tetrodes 1 and 2; VGA based method may not give the correct result when comparing tetrodes 2 and 3, unless the underlying correlation for the generative process for the time series pair is very high.
Figure 13.
The three LFP time series used in the first case study are plotted in the top panels. ACF of residuals after fitting ARMA(1,1) model to each time series are plotted directly below the corresponding series.
The top panels in Fig. 14 show, for tetrodes 1 vs. 2 comparison, the Frobenius norm of the VGA method applied to the original series, CCF applied to original and residual series, respectively. Clearly, all methods detect a lag equal to zero. The bottom panels in Fig. 14 show the corresponding plots for tetrodes 2 vs. 3 comparison; here also the lag detected by all methods is zero. In the latter case, although there was some anticipation that VG-O may yield a different result (incorrectly), it did not. Our guess is that it is due to the underlying correlation for the bivariate pair being high. There is no method to directly estimate the underlying correlation. However, a simple calculation based on Pearson correlation between the two time series yielded 0.82, which is indeed a high value, corroborating our guess. For the record, we also mention that the Pearson correlation between the LFP series for tetrodes 1 and 2 was 0.97.
Figure 14.
Frobenius norm of VGA on original series (left panels), CCF on original series (middle panels), and CCF on residual series (right panels), corresponding to LFP series pair from tetrodes 1 and 2 (top panels) and tetrodes 2 and 3 (bottom panels) mentioned in case study 1.
Technical details pertaining to LFP recordings:
The local field potential (LFP) data were recorded from an awake rat placed on a small platform. Previous to the recording, the animal had been implanted with a 16 tetrode hyperdrive assembly intended for recording in the CA1 field of the hippocampus. The tetrodes were gradually lowered in the CA1 layer across 8 to 10 days after recovery from surgery, and their tip was positioned based on the configurations of sharp waves and ripples. The 16 tetrodes were connected through a PCB to a group of four head stages with a total of 64 unity gain channels and 2 color LEDs for position tracking. The LFP signals were sampled at 2 kHz, amplified (1,000×), band-pass filtered (1–1,000 Hz), digitized (30 kHz), and stored together with LED positions on hard disk (Cheetah Data Acquisition System, Neuralynx, Inc.). Subsequently the signal was downsampled to 1K Hz, in which form it was used for the current analysis.
6.2. Case study 2
The second dataset that we use for illustration is a time series dataset from the city of London, UK. The dataset consists of mean ozone levels and total number of deaths in London, measured daily from January 1st, 2002 to December 31st, 2002. One of the environmental epidemiological questions of interest is to check whether there is a delayed or lagged association between exposure (ozone levels) and outcome (number of deaths). This dataset is part of a larger dataset that was analyzed previously by Bhaskaran et al. 2013, using time series regression methods and they determined that there is evidence of an association between ozone and mortality when the lag time is between 1 and 5 days. The above result was based on an analysis where different lag effects were not adjusted for each other. In a distributed lag model which included variables for 0 to 7 day lags, evidence of ozone-mortality associations only at lag days 1 and 2 remained. Note that Bhaskaran et al. used a dataset which included the years 2002, 2003, 2004, 2005, and 2006, while we use only time points from year 2002 because our focus is primarily illustration of the concepts discussed in this article.
The time series pair that we analyzed are plotted in the top panels in Fig. 15. ACF of residuals plotted in the bottom panels show that AR(7) and ARMA(1,1) models, respectively, are reasonable fits to ozone levels and number of deaths. Alternate models that we considered for the ozone level series were ARMA(1,1), AR(1), AR(2); however, none of these alternate models were good fits based on the ACF plots of the residuals. Also, Akaike’s information criteria was lowest for the AR(7) among the models that were considered for ozone levels. VGA based method applied on the original series showed that the lag between the two series pair was equal to 5. The absolute value of the difference between p and q estimates was 0.04, indicating that VG-O may not be the most suitable approach. CCF applied on the original series showed that the lag was at zero. The only lag where CCF applied to the residual series was significant was lag 16. VGA applied to the residual series showed again the lag to be 5. Thus, for this data the results are ambiguous, but based on the conclusions from our simulations study, the results that can be most trusted are the ones based on VGA and CCF applied to the residuals; in this case, even they diverge. However, since VG-O and VG-R both showed the lag to be 5, we may have reasons to think that the true lag is 5. The main take home point from this case study is perhaps that all results from all four methods may have to be weighed in before drawing conclusions.
Figure 15.
Time series for ozone levels and number of deaths are plotted topleft and topright, respectively. ACF of the residuals after fitting AR(7) model to ozone levels and ARMA(1,1) model to number of deaths are plotted bottomleft and bottomright, respectively.
7. Conclusions
We presented a VGA based method for detection of lag between a pair of time series as an alternate to the cross correlation function based methods. We also developed a framework for quantifying uncertainty and testing hypothesis. Further, we illustrated the new approach on two case studies.
It is known that cross-correlation function based approach yields unambiguous results only when the data is pre-whitened. The new approach identified the lags correctly, without pre-whitening, in simulated examples where the two time series were similar to each other (i.e. highly correlated, with same type of models and similar coefficients). However, extensive simulation study showed that for bivariate pairs with underlying correlations low or coefficients differing substantially, the performance of the new approach was poor compared to the traditional approaches. We explored one direction which overcame this limitation to a certain extent. Considerations for future work for further improving the new method will include a weighted version of visibility graph (e.g. as in Supriya et. al. (2016)) or just a weighted graph obtained from a time series without applying the “visibility” criterion (e.g. as in John et. al. (2020)).
Acknowledgments
We are very grateful to both anonymous reviewers, especially to one reviewer whose comments led to substantial improvement of the manuscript. We thank the Editor for his patience.
Funding
Majnu John’s work was supported in part by the following National Institute of Mental Health (NIMH) grants to PI, John M Kane: R34MH103835; PI, Anil K Malhotra: R01MH109508 and R01MH108654; PI, Todd Lencz: R01MH117646; PI, Kristina Deligiannidis: R01 MH120313; and PI, Anita Barber: R21MH122886. Janina Ferbinteanu’s research was supported by NIMH grant R21MH106708.
References
- Achard S, and Gannaz I. 2016. “Multivariate Wavelet Whittle Estimation in Long-Range Dependence.” Journal of Time Series Analysis 37 (4):476–512. [Google Scholar]
- Achard S, and Gannaz I. 2019a. “Wavelet-Based and Fourier-Based MultivariateWhittle Estimation: Multiwave.” Journal of Statistical Software 89 (6):1–31. [Google Scholar]
- Achard S, and Gannaz I. 2019b. “multiwave: Estimation of Multivariate Long-Memory Models Parameters.” R Package Version 1.4. https://CRAN.R-project.org/package=multiwave.
- Baldi P, Rinott Y, and Stein C. 1989. “A Normal Approximation for the Number of Local Maxima of a Random Function on a Graph.” In Probability, Statistics, and Mathematics, 59–81. Boston, MA: Academic Press. [Google Scholar]
- Bhaskaran K, Gasparrini A, Hajat S, Smeeth L, and Armstrong B. 2013. “Time Series Regression Studies in Environmental Epidemiology.” International Journal of Epidemiology 42 (4):1187–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box GEP, Jenkins GM, and Reinsel GC. 2008. Time Series Analysis: Forecasting and Control, 4th ed. New York: Wiley. [Google Scholar]
- Bühlmann P 1997. “Sieve Bootstrap for Time Series.” Bernoulli 3 (2):123–48. [Google Scholar]
- Gray CM,Maldonado PE,Wilson M,and McNaughton B.1995.“TetrodesMarkedlyImprove the Reliability and Yield of Multiple Single-Unit Isolation from Multi-Unit Recordings in Cat Striate Cortex.” Journal of Neuroscience Methods 63:43–54. [DOI] [PubMed] [Google Scholar]
- Jentsch C, and Politis DN. 2015. “Covariance Matrix Estimation and Linear Process Bootstrap for Multivariate Time Series of Possibly Increasing Dimension.” The Annals of Statistics 43 (3):1117–40. [Google Scholar]
- John M, Wu Y, Narayan M, John A, Ikuta T, and Ferbinteanu J. 2020. “Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm.” Entropy 22:617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudela M, Harezlak J., and Lindquist MA. 2017. “Assessing Uncertainty in Dynamic Functional Connectivity.” Neuroimage 149:165–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacasa L, Luque B, Ballesteros F, Luque J, and Nuno JC. 2008. “From Time Series to Complex Networks: The Visibility Graph.” Proceedings of the National Academy of Sciences of the United States of America 105 (13):4972–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacasa L, and Luque B. 2010. “Mapping Time Series to Networks: A Brief Overview of Visibility Algorithms.” In Computer Science Research and Technology, edited by Bauer JP, vol. 3. New York: Nova Publisher. [Google Scholar]
- Legatt AD, Arezzo J, and Vaughan HG Jr. 1980. “Averaged Multiple Unit Activity as an Estimate of Phasic Changes in Local Neuronal Activity: Effects of Volume-Conducted Potentials.” Journal of Neuroscience Methods 2:203–17. [DOI] [PubMed] [Google Scholar]
- McMurry TL, and Politis DN. 2010. “High-Dimensional Autocovariance Matrices and Optimal Linear Prediction.” Electronic Journal of Statistics 9 (1):753–88. [Google Scholar]
- Núñez A, Lacasa L, and Luque B. 2012. “Visibility Algorithms: A Short Review.” In Graph Theory, edited by Zhang Y, Intech. [Google Scholar]
- Ross N 2011. “Fundamentals of Stein’s Method.” Probability Surveys 8:210–93. [Google Scholar]
- Supriya S, Siuly S, Wang H, Cao J, and Zhang Y. 2016. “Weighted Visibility Graph with Complex Network Features in the Detection of Epilepsy.” IEEE Access 4:6554–66. [Google Scholar]
- Wei WWS 2006. Time Series Analysis: Univariate and Multivariate Methods, 2nd ed. Boston, MA: Pearson. [Google Scholar]