Abstract
The single-station microtremor horizontal-to-vertical spectral ratio (MHVSR) method was initially proposed to retrieve the site amplification function and its resonance frequencies produced by unconsolidated sediments overlying high-velocity bedrock. Presently, MHVSR measurements are predominantly conducted to obtain an estimate of the fundamental site frequency at sites where a strong subsurface impedance contrast exists. Of the earthquake site characterization methods presented in this special issue, the MHVSR method is the furthest behind in terms of consensus towards standardized guidelines and commercial use. The greatest challenges to an international standardization of MHVSR acquisition and analysis are (1) the what — the underlying composition of the microtremor wavefield is site-dependent, and thus, the appropriate theoretical (forward) model for inversion is still debated; and (2) the how — many factors and options are involved in the data acquisition, processing, and interpretation stages. This paper reviews briefly a historical development of the MHVSR technique and the physical basis of an MHVSR (the what). We then summarize recommendations for MHVSR acquisition and analysis (the how). Specific sections address MHVSR interpretation and uncertainty assessment.
Keywords: COSMOS Guidelines, Best practices, Earthquake site effects, Site amplification, Microtremor, Spectral ratio, HVSR, MHVSR, Nakamura method
Introduction
The single-station microtremor horizontal-to-vertical spectral ratio (MHVSR) method involves recording seismic ambient noise, also referred to as microtremors or ambient vibrations, with a single three-component seismometer at a location of interest and calculating the (average) ratio of the horizontal-to-vertical Fourier amplitude spectra (FAS). Earthquake site effects are commonly quantified in terms of the vertically propagating, horizontally polarized shear-wave (SH wave) transfer function. For the simple case of a uniform sedimentary viscoelastic layer of thickness, h, with shear-wave velocity, Vs, overlying viscoelastic bedrock, resonance frequencies (fn) of the SH wave transfer function occur at
Empirical evidence from sites with measured VS profiles down to bedrock and from small-strain earthquake recordings has shown that the lowest frequency MHVSR peak occurs at the fundamental mode resonance frequency (f0) of a soil layer over an elastic half-space from SH wave motion (e.g., Field and Jacob 1993; Lermo and Chavez-Garcia 1994a; Bonilla et al. 1997; Bour et al. 1998; Bard 1999; Fäh et al. 2001; Wollery and Street 2002; Molnar and Cassidy 2006; Haghshenas et al. 2008). To determine varying velocities in the soil layering, the formulae by Dobry et al. (1976) and completed in the review of Urzúa et al. (2017) can be useful.
These observations were the essence of the rapid rise in popularity of the MHVSR method where a single tri-axial seismometer, placed on the ground and left to record microtremors for tens of minutes to an hour, can provide a reliable estimate of the site’s fundamental frequency, i.e., f0HV is a measure of f0. Although the use of the MHVSR method has proliferated, standardization of the technique remains unaddressed outside of the Site Effects Assessment Using Ambient Excitations’ (SESAME) project (Bard et al. 2008) and its MHVSR guidelines (SESAME 2004). Notable paper compilations documenting advances and applications of the MHVSR method for soil and building characterization appear in Mucciarelli et al. (2009) and seismic microzonation in Roca and Olivera (2001). The MHVSR method is documented in Vs measurement guidelines for Canadian seismic site characterization in soil and rock (Perret 2015). The current status towards international guidelines of the MHVSR method as part of the COSMOS International Guidelines on Applying Non-Invasive Geophysical Methods for Characterizing Seismic Site Conditions initiative was summarized in Molnar et al. (2018). This paper supersedes Molnar et al. (2018).
The greatest challenges to an international standardization of MHVSR acquisition and analysis are (1) the what — the underlying composition of the microtremor wavefield is site-dependent, and the appropriate interpretation of the MHVSR curve and/or theoretical (forward) model for inversion are therefore still debated; and (2) the how — many factors and options are involved in the data acquisition, processing, and interpretation stages. This paper briefly reviews the historical development of the MHVSR technique and the physical basis of an MHVSR (the what). We then summarize recommendations for MHVSR acquisition and analysis (the how). Specific sections address MHVSR interpretation and uncertainty assessment.
Principles of technique
Seismic ambient vibration methods measure background seismic noise to assess the elastic properties of the earth’s subsurface, in particular, shear-wave seismic velocities, which are directly related to shear moduli. Seismic noise is defined as the ambient vibration of the earth’s surface, generated by the combination of low frequency (< ~ 1 Hz) natural microseisms and higher frequency (> ~ 1 Hz) anthropogenic microtremors (e.g., Bonnefoy-Claudet et al. 2006; Landès et al. 2010). Notable opportunities to better differentiate natural and anthropogenic seismic noise include increasing growth worldwide of wind turbine facilities (e.g., Edwards 2015; Marcillo and Carmichael 2018) and lockdown measures related to the recent COVID-19 global pandemic (e.g., Lecocq et al. 2020). This background noise is a mixture of various seismic wave phases, which contains information on the sources and transmission paths of the waves, and subsurface structure (Okada and Suto 2003). Most anthropogenic seismic noise sources and some natural sources (e.g., wind and ocean waves) are located close to the surface of the earth, which leads to energy mostly released as surface waves. Even for subsurface sources, if the source is located at large distances, surface waves are the dominant component of the microtremor wavefield (below 1 Hz) because their geometric attenuation is much lower than that of body waves (Socco and Strobbia 2004). A common assumption is that, at a distance of more than one wavelength from the source, the microtremor wavefield (generally above 1 Hz) is dominated by surface waves (Arai and Tokimatsu 2005). It is not possible to isolate every wave from microtremor recording at a single station, although it is possible to separate Love waves from Rayleigh waves (Hobiger et al. 2009).
The use of microtremors was pioneered by Bertelli (1872) in Italy and then by Omori (1909) in Japan. Aki (1957) proposed to analyze microtremors as a temporal and spatial stochastic process with reference to the nature of wave propagation. The result was a breakthrough, i.e., the well-known spatial autocorrelation (SPAC) method (see Asten and Hayashi, this issue), aimed to retrieve phase velocities of Rayleigh and Love waves. Engineering applications were introduced by Gutenberg (1958) and Kanai and Tanaka (1961). Based on the developments of these individuals, the single-station microtremor approach was adopted by Nogoshi and Igarashi (1970, 1971) in an attempt to understand the characteristics of microtremors and MHVSRs with respect to the site predominant frequency. Nakamura (1989) interpreted that the MHVSR would be the same or similar to the 1D shear-wave transfer function and was the first MHVSR publication in English; see Bonnefoy-Claudet et al. (2006) for a review of early MHVSR literature. Additional pioneering comparisons of MHVSR with spectral ratios calculated from the 1985 Mexico City earthquake recordings were accomplished by Lermo and Chávez-García (1993; 1994a, b). The MHVSR method is an analysis technique (illustrated in Fig. 1) that calculates the ratio of the horizontal-to-vertical FAS derived from microtremor recordings with a three-component seismometer at a specific location. In the previous two decades, Japanese researchers continued to advance and use the MHVSR method (e.g., Horike et al. 2001; Satoh et al. 2001; Arai and Tokimatsu 2004), while it gained popularity and use throughout Europe (SESAME project: Bard et al. 2008), Canada (Molnar and Cassidy 2006; Hunter et al. 2010), New Zealand (Wotherspoon et al. 2015; Vantassel et al. 2018), and South America (Guéguen et al. 1998; Pilz et al. 2009; Leyton et al. 2012). Its use in the USA occurred later but is increasing (Yong et al. 2013; Teague et al. 2018; Stephenson et al. 2019).
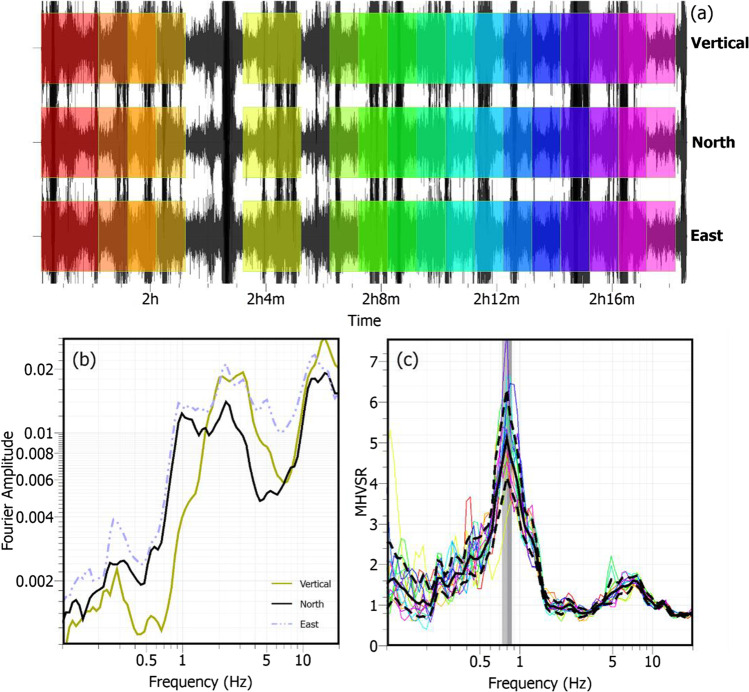
Fig. 1.
Illustrative example of the MHVSR method. a Windowing of microtremor time series. b Time window-averaged Fourier amplitude spectra (FAS) for each of the three components. c Average horizontal-to-vertical spectral ratio curve (solid black line with standard deviation shown by dashed lines) statistically calculated from each time window’s HVSR (colored lines). The peak frequency of the average HVSR curve and the standard deviation associated with the variability of the peak frequency values from the individual curves is indicated by the vertical gray shading. This example in Metro Vancouver, British Columbia, Canada, is calculated using the Geopsy software package (Wathelet et al. 2020)
Interpretation of the MHVSR curve is complicated by a lack of understanding regarding the precise composition of the microtremor wavefield. Empirical evidence suggests that the MHVSR f0HV occurs at, or close to, f0 if there is a sufficiently strong impedance contrast (e.g., Field and Jacob 1993; Lermo and Chávez-García 1994a, b). Whether the wavefield composition is primarily body waves, surface waves, and/or highly scattered (diffuse) combinations thereof (total wavefield) is still largely debated (e.g., Lachet and Bard 1994; Fäh et al. 2001; Malischewsky and Scherbaum 2004; Bonnefoy-Claudet et al. 2008; Sánchez-Sesma et al. 2011; Lontsi et al. 2015). Studies of microtremors have shown that the contribution of different wave types varies with frequency, from site to site, and that Love waves are often a dominant part of the surface wave component of the microtremor wavefield (e.g., Arai and Tokimatsu 1998; Yamamoto 2000; Köhler et al. 2007; Endrun 2011). Therefore, no single analytical expression exists for all real-world conditions.
Theoretical background: state of knowledge and ongoing debates
The ambiguity regarding the composition of the microtremor wavefield has made it challenging to theoretically model the MHVSR to infer 1D shear-wave velocity (Vs) profiles. The wavefield itself is subject to meteorological, diurnal, and seasonal variations (e.g., Volant et al. 1998; Mucciarelli and Monachesi 1998; Bour et al. 1998; Mucciarelli et al. 2003; Guillier et al. 2007). Over the years, different authors have attempted to explain the MHVSR phenomenology in terms of SH waves (Herak 2008; Nakamura 1989, 1996, 2019) and Rayleigh waves (Lermo and Chavez-Garcia 1994a, b; Fäh et al. 2001; Malischewsky and Scherbaum 2004; Tuan et al. 2011) and by adding the effects of Love waves (Arai and Tokimatsu 2004; van Der Baan 2009). Recent studies consider the role of all waves, the so-called total wavefield approach (Bonnefoy-Claudet et al. 2008; Lunedei and Albarello 2010; Sánchez-Sesma et al. 2011; Lunedei and Malichewsky 2015; García-Jerez et al. 2016; Piña-Flores et al. 2017; Spica et al. 2018).
Body wave interpretation
Nakamura (1989), in his innovative proposal of the MHVSR, assumed that the microtremor wavefield is primarily composed of S and Rayleigh waves. He proposed that the effects of Rayleigh waves are “eliminated” by considering the spectral ratio. By assuming that the MHVSR at the sediment–bedrock interface is unity, and vertical component motions do not undergo amplification within the near-surface sediments, the MHVSR at the surface can be treated as a “quasitransfer function” from which f0 and its corresponding amplification factor may be estimated. Nakamura updated his theory by including the contribution of surface waves but claiming their effects are negligible around the fundamental frequency (Nakamura, 1996) and then updated again to include the effects of P waves (Nakamura 2000). Herak (2008) developed an MHVSR modelling algorithm based on this conceptualization of the MHVSR (i.e., the ratio of the S wave to P wave transfer function). Kawase et al. (2011) obtained a similar formula under the diffuse concept for earthquakes with an amplitude correction (scaling) factor between horizontal and vertical components at the seismological bedrock. Nakamura (1989, 1996, 2000, 2008, 2014, 2019) has repeatedly asserted the correspondence between both the peak frequency and amplification factor of the MHVSR and that of the S wave transfer function. Oubaiche et al. (2016) provide an experimental study of the relationship between MHVSR peaks and both the SH wave transfer function and Rayleigh wave ellipticity. They found that the MHVSR f0HV matches the peak frequency of the SH wave transfer function but not Rayleigh wave ellipticity. While Nakamura has championed the use of MHVSR for f0 measurement, claiming that the wavefield composition at f0HV is dominated by S waves, the frequency dependence of the wavefield composition implies that the MHVSR cannot be used as a direct proxy for a site’s S wave transfer function. In other words, the shape of the MHVSR is not controlled by S waves alone.
Given the lack of correspondence between not only the shape of the MHVSR curve and the S wave transfer function, but also the amplification factor determined from the two, a method to link the two is desirable. Empirical measurement of “true” earthquake site response (amplification) is accomplished by standard (soil base-to-surface or rock-to-soil) spectral ratios (SSR) of multiple earthquakes from various azimuths (Borcherdt 1970). In practice, SSRs are sometimes challenging to calculate due to a lack of suitable bedrock reference sites and/or earthquakes. As an alternative, the single-station horizontal-to-vertical spectral ratio of earthquake motions (EHVSR) is often used. Due to differences in wavefield composition, strength of ground motions and excitation of higher modes, the frequency-dependent amplification, and spectral shape, as well as estimated resonance frequencies, may vary between earthquake and microtremor spectral ratios. Satoh et al. (2001) performed a comprehensive comparison of SSRs and HVSRs from earthquake P wave, S wave, and coda portions as well as the MHVSR from a separate microtremor recording. They showed that the MHVSR does not coincide with the earthquake SSR and HVSR calculated from the S wave portion, although there was rough agreement in f0 when it is lower than 1 Hz with an amplitude greater than 3. Horike et al. (2001) also compared earthquake SSRs and HVSRs with the MHVSR at multiple sites and concluded MHVSRs partly reflect but do not agree with S wave SSR amplification. The latest developments in empirical corrections of MHVSR to obtain the site amplification function are presented in Sect. 5.1.
Surface wave interpretation
As noted previously, many anthropogenic and natural seismic noise sources initiate energy at the ground surface, leading to a common assumption that the microtremor wavefield is composed primarily of surface waves. Nogoshi and Igarashi (1971) compared MHVSR curves with fundamental mode Rayleigh wave ellipticity and concluded that the fundamental mode Rayleigh wave provides the main contribution to the long-period microtremor wavefield. Under the Rayleigh wave ellipticity assumption, the peaks of the MHVSR are related to vanishing of the vertical component amplitude of Rayleigh wave motion near the fundamental site frequency, which occurs when the sense of motion switches from retrograde to prograde or vice versa, in the presence of a large impedance contrast. Malischewsky and Scherbaum (2004) presented an analytical formula to calculate Rayleigh wave ellipticity for a 2-layer model of compressible media. Malischewsky et al. (2008) used this analytical expression to explore Rayleigh wave particle motion as a function of material properties. These studies provide the basis to study two special features of the ellipticity function: the singularity (i.e., maximum) and the zero (i.e., minimum). It has generally been observed that the singularity occurs close to f0 but only if the impedance contrast is greater than 4 (see Bonnefoy-Claudet et al. 2008). For lower impedance contrasts or low Poisson ratios, the singularity occurs at frequencies between 0.5*f0 and 1.5*f0, and the minimum is not readily observed.
Many studies have used the relationship between MHVSR and Rayleigh wave ellipticity to invert for layered earth models (e.g., Fäh et al., 2001; Scherbaum et al. 2003; Arai and Tokimatsu 2004; Wathelet et al. 2004; Parolai et al. 2005). Cipta et al. (2018) presented a trans-dimensional Bayesian framework to invert MHVSR curves for 1D profiles, modelling the MHVSR as the fundamental mode Rayleigh wave ellipticity. Studies have shown success inverting MHVSRs for layered earth models only considering the fundamental mode Rayleigh wave (Yamanaka et al. 1994); however, other studies have shown that higher modes make contributions, particularly when low velocity zones are present (Arai and Tokimatsu 2004; Parolai et al. 2005; Rivet et al. 2015; Savage et al. 2013). To improve the results of inversion, Rayleigh wave ellipticity can be extracted from microtremors by using seismic arrays ( Maranò et al. 2017; Poggi and Fäh 2010; Poggi et al. 2012; Wathelet et al. 2018) or single-station methods (Hobiger et al. 2009, 2013).
Studies based on simulating the microtremor wavefield have shown that for impedance contrasts greater than four, MHVSR peaks can be explained by horizontal polarization of the fundamental mode Rayleigh wave coupled with the contribution of the Airy phase of fundamental mode Love wave (e.g., Bonnefoy-Claudet et al. 2008; Konno and Ohmachi 1998; Lunedei and Albarello 2010). The prominence of Love waves in the microtremor wavefield has been asserted by many authors (e.g., Endrun 2011; Köhler et al. 2007; Yamamoto 2000). Konno and Ohmachi (1998) found that if the proportion of Rayleigh waves in the microtremor wavefield is 0.4, the amplitude of the MHVSR peak is close to the S wave amplification factor. Although the peak of the MHVSR is close to the S wave resonance frequency, the MHVSR curve shape is closely related to the fundamental mode Rayleigh wave ellipticity (Arai and Tokimatsu 2000; Konno and Ohmachi 1998). This has been shown to be true not only when Rayleigh waves are dominant in the microtremor wavefield (e.g., Scherbaum et al. 2003), but also in numerical studies that use full wavefield modelling of the microtremor wavefield (Field and Jacob 1993; Lachet and Bard 1994; Lunedei and Albarello 2010).
Total wavefield interpretation
Lachet and Bard (1994) carried out a numerical simulation of the microtremor wavefield for 15 soil profiles by arranging random amplitude sources uniformly within a given radius from a receiver. The results of their theoretical study indicate that the peak of the MHVSR corresponds well with both the S wave resonance frequency, and the ellipticity peak of the fundamental mode Rayleigh wave. They suggested that the overall MHVSR curve shape is determined by all seismic phases. Field and Jacob (1993) proposed a theoretical formulation to relate the microtremor displacement power spectrum to the Green’s function of the earth’s surface. Lunedei and Albarello (2010) extended this model to include all seismic phases.
By using surface sources and several simple stratigraphic profiles in a numerical study, Bonnefoy-Claudet et al. (2008) checked the correspondence between f0HV and f0. They concluded that depending on the impedance contrast, the MHVSR peak could be explained by Rayleigh wave ellipticity, Love Airy phase, S wave resonance, or some combination thereof. Considering these theoretical and numerical investigations, it is evident that the precise composition of the microtremor wavefield is a complex function of many variables. The most appropriate explanation of the MHVSR phenomena should therefore account for all seismic phases.
Sánchez-Sesma et al. (2011) proposed that microtremors form a diffuse field containing all types of body (P and S) and surface waves (Love and Rayleigh) for which their associated illumination strengths stabilize in fixed proportions. Within this diffuse field assumption (DFA), multiple scattering and its equilibrating effects play a prominent role. The relative power of each seismic state that composes the illumination emerges from the principle of equipartition of energy. Theory asserts that within a diffuse elastic wavefield, the autocorrelation in the frequency domain (the power spectrum), at any point of the medium, is proportional to the imaginary part of the Green’s function for source and receiver at the same point. As average autocorrelations are proportional to average directional energy densities (DED) then, by following Arai and Tokimatsu (2004), one way to assess the MHVSR is the square root of the ratio of the DEDs:
where E# are the DEDs for the horizontal (E1 and E2) and vertical (E3) components. Therefore, DEDs are calculated as the averaged autocorrelation of the three recorded components at a receiver. The DFA allows linking measurements with physical properties of the medium. The MHVSR is modeled in terms of Green’s functions:
where ImGii is the imaginary part of the Green’s function for the ith component for a unit harmonic excitation in the ith direction when both source and receiver coincide. For a horizontally layered medium, this approach is straightforward for surface recordings (Sánchez-Sesma et al. 2011; Kawase et al. 2015) and at depth (Lontsi et al. 2015) and even under a water layer in offshore settings (Lontsi et al. 2019). Considering the microtremor wavefield as not systematically diffuse and equipartitioned, Tchawe et al. (2020) proposed to compute MHVSR on the coda part of the microtremor correlations. Sánchez-Sesma (2017) addresses non-uniqueness arising from inverting only MHVSR or by jointly inverting the MHVSR (under the DFA) with fundamental or higher mode surface wave dispersion curves. Wu et al. (2017) propose a simplified full wavefield approach to invert 1D velocity structure directly from the MHVSR on the basis of locked mode approximation. Lateral heterogeneity can be dealt with similarly, but computing Green’s functions becomes computationally expensive (Matsushima et al. 2014, 2017). Some encouraging results are due to Spica et al. (2015, 2017, 2018) and Perton et al. (2017).
The search for indicators of field diffusivity is ongoing. Using empirical recordings from a dense 72 station array, Pilz and Parolai (2014) employed multifractal detrended fluctuation analysis to assess wavefield character ranging from ballistic to diffusive considering varying timescales and seismic intensities. They found the character of motion varies from nearly ballistic to diffusive on frequency-dependent timescales for all materials. A time windowing scheme has been proposed to enhance diffuse properties of the field (Weaver and Yoritomo 2018). Therefore, the corresponding processing must be the same to fully exploit the diffuse field nature. Under certain circumstances, the P and S energy equilibrates, and this process anticipates the emergence of a diffuse regime (not necessarily isotropic), which justifies the interpretation of MHVSR under the DFA (Piña-Flores et al. 2021).
Microtremor recording
Microtremor data acquisition is relatively simple, requiring a single tri-axial seismometer to record for tens of minutes to hours (i.e., very little equipment and personnel required). Poor choices made by the practitioner during data acquisition have the potential to impact the MHVSR by introducing artificial resonance frequencies (MHVSR peaks) and altering the MHVSR amplitude. The natural site-related resonance frequencies are relatively robust and likely to be obtained even if the data acquisition is not ideal. This latter point combined with the minimal required equipment is the appeal of the MHVSR method. The greatest difficulty is at the interpretation stage; the practitioner should therefore seek to minimize errors during the data acquisition and analysis stages.
There is no international standard related to documenting the metadata associated with each microtremor recording. An example metadata field sheet was generated in MHVSR guidelines of SESAME (2004) and Canada (Perret 2015). The recommended minimum metadata includes equipment serial number(s), acquisition file identifier, material type the sensor is placed on/in, a site photo, and notes of only “anomalous” recording conditions, i.e., the default assumptions that “good” sensor coupling is achieved and observed seismic noise sources (environmental and anthropogenic) will not impact or degrade the MHVSR need not be documented. Any deviation from these default assumptions should be documented. Documenting the equipment used (e.g., seismometer-digitizer pair, if applicable) by their serial number or identifier is beneficial when multiple equipment is available and used over many years or in different campaigns. Field notes and site photos provide direct benefit to MHVSR calculation and interpretation. Documentation of metadata becomes cumbersome as the quantity of microtremor measurements increases into hundreds and thousands of sites. Large quantity microtremor campaigns performed for seismic microzonation mapping, site characterization of a seismic network’s stations, or post-earthquake reconnaissance purposes (e.g., Puglia et al. 2011; Albarello 2011; Molnar et al. 2020; Ladak et al. 2021) may include multiple equipment, practitioners, and/or span multiple years. In such cases, the importance of minimal standardized yet robust metadata of the microtremor measurements and their processing and interpretation increases.
Recommendations on suitable equipment and deployment and acquisition selections provided in the next two sections are based on outcomes of the SESAME project and updated when applicable. The SESAME (2004) guidelines and Koller et al. (2004) provide summaries on their equipment and experimental testing conditions which are each documented fully in SESAME WP02 deliverables D01.02 and D08.02, respectively (http://sesame.geopsy.org/SES_TechnicalDoc.htm, last accessed July 2021). Relevant figures available in those deliverables, and their appendices are not repeated here but are a valuable resource for the beginner.
Equipment
The most suitable recording instrument is a three-component seismometer (velocimeter) with a noise floor lower than the seismic noise level over the frequency band of interest (i.e., 0.1–25 Hz). Ensuring that the internal noise of the entire acquisition system is much lower than the measured microtremors is the most important factor in selecting appropriate equipment. The natural frequency of the instrument or sensor should be considered with the estimated site conditions. For sites with deeper impedance contrasts, broadband or low-frequency seismometers are recommended, whereas for shallower impedance contrast sites, higher natural frequency seismometers are suitable even if some authors claim that low-frequency peaks can be identified by short-period seismometers (Castellaro and Mulargia 2009a; Chatelain and Guillier 2013; Molnar et al. 2020). In comparison to short-period seismometers, broadband seismometers have a flat instrument response to much lower frequencies but are more difficult to deploy for short-term experiments due to a longer stabilization time and sensitivity to climatic conditions (Guillier et al. 2008). Additional published comparisons between broadband and short-period seismometers and/or between various sensor–digitizer pairs can be found in Castellaro and Mulargia (2009b) and Strollo et al. (2008). Accelerometers with a relatively high intrinsic noise level should generally be avoided (Guillier et al. 2008); use of accelerometers for free-field microtremor measurement is no longer prevalent (e.g., Theodulidis and Bard 1998).
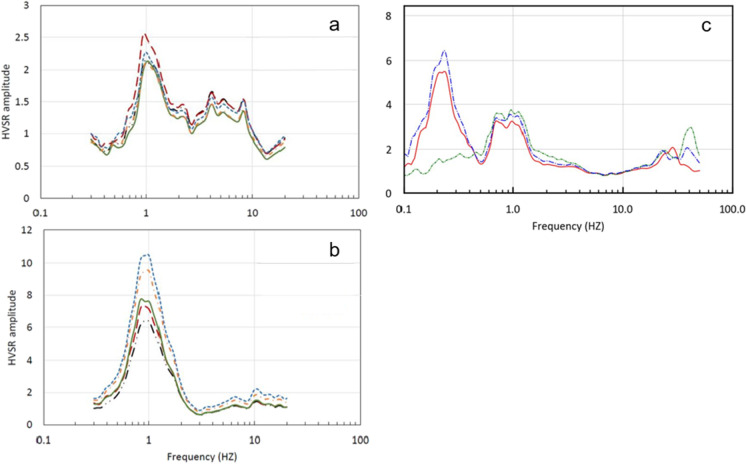
Figure 2 shows examples where the mean MHVSR obtained from simultaneous recordings using short-period and broadband seismometers immediately beside each other have nearly identical peak frequency values. However, Fig. 2 shows that a very low f0HV (0.2–0.3 Hz) can be missed within the equipment noise level when using a lower sensitivity short-period seismometer at a low seismic noise site regardless of recording duration. In terms of MHVSR amplitude, cases of consistency (Fig. 2, 2) and inconsistency (Fig. 2) between equipment types occur even when care in equipment deployment is accomplished (not a sensor coupling issue). Variability in the measured MHVSR amplitude between equipment types at a site is one facet of the caution towards direct inversion of MHVSR curves (discussed further in Sects. 5.2 and 6.2). One can certainly find MHVSR comparison demonstrations like Fig. 2 obtained using 2–3 different sensor–digitizer pairings in single publications from the last two decades, but overall, there has not been a comprehensive or international benchmark testing of equipment since the SESAME project (Guillier et al. 2008) which was focused more on reliable peak frequencies and less on the MHVSR amplitude and its entire spectrum shape. The quantity of seismic equipment developed for MHVSR measurement has also increased significantly since the SESAME project.
Fig. 2.
Variability in average MHVSRs depending on equipment. a, b For a site in Texas, USA, comparison of average MHVSRs from co-located broadband seismometers (red, green lines) and short-period 2 Hz or 5 Hz seismometers (other color lines). c For a site on the Fraser River delta, Canada, comparison of average MHVSRs from co-located broadband (red line) and two generations of a short-period seismometer (green line corresponds to older generation compared to blue line)
It is important to check the noise spectrum at a site to determine the frequency range for which results are valid. If there is not sufficient energy at certain frequencies, this may result in spurious peaks (Albarello 2001) or lack of resolution of peaks. The noise spectrum should also be cross-referenced with the theoretical instrument response spectrum to ensure the correct operation of the instrument. It is most often assumed that the instrument response for all three components is identical; this is not necessarily the case (Guillier et al. 2008). If the instrument response differs for each component and is not removed from the measured motions, this can degrade the resulting MHVSR.
Deployment and acquisition
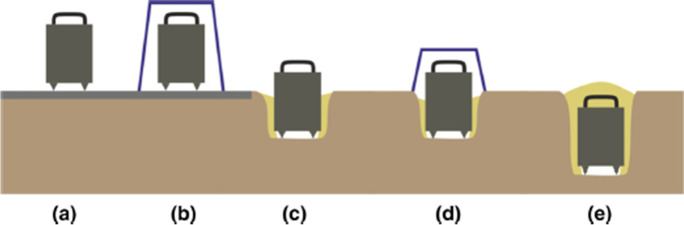
Foti et al. (2018) provides an excellent graphic (Fig. 3) that depicts the increasing preference of options for seismometer deployment. The ideal field deployment involves levelling the sensor on/just below the earth’s surface at a location of interest where the surface conditions should be representative of natural free-field ground conditions. Coupling of the sensor to the earth’s surface is crucial. Vegetation should be removed and sensor base or feet inserted firmly into the ground surface with protection from other natural phenomena including temperature fluctuation and wind (cable vibration issues, Mucciarelli et al. 2005) or rain vibrations (Chatelain et al. 2008). Measurements should be avoided during wind and heavy rain. Figure 3 depicts seismometer deployments that can mitigate against climatic factors. For example, coverage of the sensor (e.g., a bucket) is depicted in Fig. 3. A cover can help shade and keep the seismometer cool but can also lead to transmitting wind or rain droplet vibration into the ground due to its surface area. Waiting for a less windy day or use of an umbrella with fewer contact points is often better solutions towards mitigating recording wind and rain vibration. Ideally, a huddle test is accomplished to verify the interoperability of the equipment (i.e., several digitizer–seismometer pairs) but also to verify high-to-low noise sites to assess the dynamics of the digitizer–seismometer pair.
Fig. 3.
Different possible seismometer deployments for microtremor measurements, ranging from a least desirable to e most desirable for high-quality data acquisition. Due to the relatively short recording duration, deployments with infill (c, e) are rare; most deployments are performed according to a, b or d without infill.
Adapted from Foti et al. (2018)
Human-constructed surfaces or pavements should be removed prior to sensor-ground coupling. However, in urbanized settings, this is almost never possible, and most recordings will be collected on human-constructed pavements, e.g., asphalt, concrete, and stone. Measurements on stiff pavements over softer soils creates a velocity inversion in the subsurface which leads to reduction in the MHVSR below unity (deamplification) at frequencies above f0HV (Castellaro and Mulargia 2009b; Piña-Flores et al. 2020) but does not impact f0HV (Chatelain et al. 2008). When MHVSR deamplification is observed from recordings on natural ground, it is indicative of natural velocity inversions or low velocity zones (Di Giacomo et al. 2005; Castellaro and Mulargia 2009b; Piña-Flores et al. 2020).
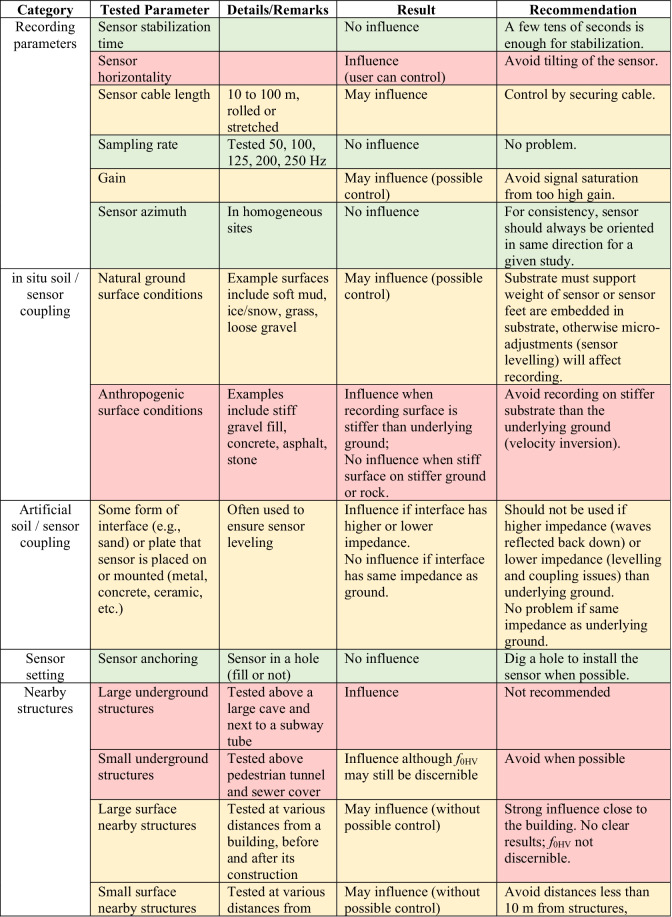
In general, any other factor that degrades the sensor-ground coupling or violates the free-field ground condition requirement should be avoided (i.e., synthetic interfaces) (Chatelain et al. 2008), if possible, or minimized. Recording over subsurface cavities or other buried human-constructed materials (e.g., electrical power lines or vents) will alter the MHVSR curve (Chatelain et al. 2008) and are recommended to be avoided; cavities that are shallow and wide violate the free-field requirement. For proximity to urban infrastructure, a general criterion is to offset the recording location by a distance equivalent to the height of the structure (Chatelain et al. 2008; Castellaro and Mulargia 2010); however, this is not always possible. If this criterion must be violated, caution should be exercised when interpreting the results, as the resonant frequency of the structure may show up in the MHVSR recording, notably when recording on the foundation of any built structure and near tall structures or long bridges. In these cases, testing the damping of the f#HV is then mandatory and should be strongly less than 1.00 (as in the natural condition). A table of acquisition parameters and their influence on the processed MHVSR is included in Appendix 1 (Fig. 9), adapted from Koller et al. (2004).
Fig. 9.
Acquisition parameters and their influence on the MHVSR. Green shading refers to parameters that have no influence, yellow shading refers to parameters that may influence (should be minimized), and red shading refers to parameters that will influence the MHVSR (should be avoided)
The microtremor recording duration must be long enough to show that a statistically stable MHVSR is achieved. The recommended recording duration is inversely proportional to the site’s fundamental frequency and should, with a general criterion, be at least 20(10/f0HV) (see Sect. 4.1). In addition, the noise wavefield at a site (nearby transient sources), climatic conditions (wind, rain, etc.), and sensitivity of the seismometer used will impact the stability of the MHVSR in time (and standard deviation of the entire curve) and therefore the recording duration. Of these, the controlling factor is the seismometer sensitivity; the less sensitive the seismometer, the less attention required towards climatic and nearby noise sources, but more attention is required towards ability of the sensor to provide reliable recordings of the ambient vibrations rather than instrumental electronic noise. In general, less sensitive sensors will perform better in urbanized environments, as the measurement quality is not degraded by the increased nearby noise sources (traffic, people walking, etc.). In general, climatic and nearby noise sources will impact the contribution of transients to the MHVSR.
During acquisition, the user should exercise judgment to compensate for periods of suspected poor microtremor recording by increasing the measurement duration. In an urban environment, it is recommended to find a location to deploy the seismometer with a buffer zone free from nearby noise sources (busy traffic, people walking, etc.) of 5 m or larger. Traffic is a common concern in highly urbanized environments; however, the MHVSR is not adversely affected even if the sensor is located on natural ground a few meters from a highway (Taniguchi and Sawada 1979; Chatelain et al. 2008). Castellaro and Mulargia (2009b) showed that the low-frequency branch of the MHVSR has increased uncertainty in the presence of a high noise level from a nearby source, while Lunedei and Albarello (2010) confirmed that the presence of nearby sources affects lower and higher frequencies on either side of f0HV. It is possible that seismic waves from sources closer to the measurement site may only propagate in shallower layers, thus obscuring peaks due to deeper structure (Mihaylov et al. 2016). Overall, to reduce MHVSR variability (standard deviation) at lower or higher frequencies, the user should mitigate climatic factors (improve seismometer deployment (Fig. 3), repeat measurement another day) or nearby noise sources (buffer zone, increased recording duration, tall buildings, and trees), respectively.
Generally, a single microtremor recording per site and its MHVSR calculation are enough to obtain an estimate of f0, especially if it can be combined with previous earthquake and MHVSR analyses at the same site. At a previously unexplored site, or where artifacts of human origin (e.g., buildings, pavements) are expected, it is recommended to take multiple recordings on different measurement surfaces, at different times of the day or night or on different dates to establish the stability of the MHVSR curve. For regional microzonation studies (e.g., Roca and Oliveira 2001; Moscatelli et al. 2020), measurements should be obtained first at a coarse or large spacing and reduced to a finer scale where rapid variations of f0HV are observed.
MHVSR calculation
The stability and reliability of the calculated MHVSR depend on the processing and interpretation steps as much as on the equipment (acquisition system) and the quality of the in situ acquisition. The general processing steps involved in computing an MHVSR are first outlined below. Then important parameters that are highlighted in the general processing using bold, italicized, and underlined text are discussed in further detail.
The entire microtremor three-component time series is split into several time windows of equal or varying length. Window length is inversely proportional to minimum frequency; longer time windows should be used for sites with expected low fundamental frequencies (i.e., long fundamental periods; T0 = 1/f0). Fourier spectra are computed for each individual tapered time window and smoothed. Each time window should be at least 10 times longer than the estimated fundamental site period, as advised by the SESAME (2004) MHVSR guidelines. After smoothing, the ratio between horizontal and vertical spectra is then performed. Similar individual HVSRs confirm underlying soil homogeneity, while variable HVSRs between individual components may indicate spatially complex, spatially variable subsurface conditions (Guillier et al. 2006; Matsushima et al. 2014, 2017; Vantassel et al. 2018; Cheng et al. 2020). The azimuth dependence of MHVSRs should be checked (e.g., Matsushima et al. 2014, 2017; Cheng et al. 2020) to find indications of two-dimensional (2D) and three-dimensional (3D) site effects including sedimentary basins and surface topography. With additional processing, MHVSR measurements have the potential to provide information on lateral variation of the subsurface, as well as 3D variations (e.g., Hinzen et al. 2004; Grippa et al. 2011; Hallal and Cox 2021), discussed further in Sects. 4.4 and 5.1. The average horizontal spectrum is valid for use once no azimuthal dependence of the MHVSR is confirmed, i.e., assumptions of 1D site effects can be reasonably accepted. The final average MHVSR for a testing location was historically calculated as the average of all MHVSRs from the spectra of the combined horizontal components of each time window (Nogoshi and Igarashi 1971; Nakamura 1989; Lermo and Chavez-Garcia 1994a, b; Fäh et al. 2001) but is increasingly determined from the averaged spectra from all time windows of each component (Arai and Tokimatsu 2004; Sánchez-Sesma et al. 2011; Lunedei and Albarello 2015; Piña-Flores et al. 2017). Averaging of MHVSRs from all selected time windows reduces variability in the mean MHVSR curve, whereas averaging of each component spectra with time is more appropriate given the diffuse wavefield assumption. The practitioner may manually perform window selection of the calculated time-averaged MHVSR by removing or “editing out” spurious time windows from the recording. Anti-triggering algorithms can be used to automatically remove time windows based on amplitude (e.g., Wathelet et al. 2020) or frequency content (Cox et al. 2020). Ultimately, it is the practitioner’s choice to limit periods of “bad” seismic noise either during data acquisition (e.g., optimizing the recording of only “good” noise) or during data processing (e.g., remove parts of the time series with “bad” noise).
Window length
The chosen window length involves a trade-off between spectral resolution and statistically meaningful results. As mentioned, each time window should be at least 10 times longer than the estimated fundamental site period, as advised by the SESAME (2004) MHVSR guidelines. A stable MHVSR will result with 20 time windows or more (Picozzi et al. 2005) with 15–20 windows required to achieve Gaussian statistics. It is common for the authors of this paper to use 30- to 60-s time windows with a minimum of 20 to 50 windows to ensure statistical stability. As such, one should expect to collect a minimum of 15 min of microtremor data. Sites with lower fundamental frequencies (longer fundamental periods) may require a total recording length up to an hour or more to ensure enough time windows are available for reliable processing.
Window selection
Spurious time windows are identified by the practitioner as statistically inconsistent, often determined by very high amplitudes at the lowest frequencies (e.g., wind effects), low amplitudes (e.g., equipment issues), a wide frequency band of high amplitude noise (e.g., saturated signal from nearby noise source), or knowledge of the source wavefield (e.g., when someone walked past the seismometer). Most software platforms for calculation of MHVSRs have built-in anti-triggering algorithms to remove transient windows based on an STA/LTA algorithm. Mihaylov et al. (2016) developed a routine to separate windows with high- and low-level ambient noise. They observed that the ratios computed with windows of high- vs. low-level ambient noise may deviate, especially in the case where a low-frequency peak is present. Transient removal using wavelet transforms has also been implemented (Vallianatos and Hloupis, 2009). There is debate regarding the impact of including/removing transient time signal. Several authors believe that transients in microtremor records carry information that is highly dependent on the source (Horike 2001; Bard et al. 2008). However, others (e.g., Mucciarelli and Gallipoli 2004) suggest that the non-stationary noise windows should not be removed because they carry information that improves agreement between MHVSR and EHVSR, through introducing more body wave content (e.g., Satoh et al. 2001). Overall, the use of an anti-triggering algorithm, wavelet transform-based removal of transients, or manual selection of windows is best determined on a site-by-site basis. It is worth noting that with a large enough number of windows, transients may have only slight influence on the average calculated MHVSR (Parolai and Galiana-Merino 2006). Considering the lack of agreement regarding how transients affect the calculated MHVSR, frequency-domain window-rejection has been proposed as an alternative. As opposed to considering the time series data, such an approach iteratively rejects time windows corresponding to MHVSR curves that deviate significantly from a statistically defined representative curve (i.e., mean/median). This has the benefit of not only decreasing variance, but also improving data quality when the transient signal is within the same bandwidth as MHVSR peak frequencies (Cox et. al 2020). Automatic window selection has also been accomplished through cluster analysis (D’Alessandro et al. 2016). The cluster analysis extracts self-consistent clusters of MHVSR curves.
Spectral smoothing
To reduce variance, some smoothing procedures are applied to the individual spectra. Konno and Ohmachi (1998) developed a logarithmic frequency sampled smoothing function to avoid bias in the peak amplitude regardless of frequency. They considered two smoothing functions: a Parzen window with a fixed bandwidth of 0.5 Hz and their proposed logarithmic one. Because the Parzen window has a fixed bandwidth, and due to the commonly employed log-scale of the x-axis, as the frequency decreases, the width (number of points) of the Parzen window increases. However, the logarithmic function considers the same number of points, regardless of the frequency (relative bandwidth). The impact of this on the actual MHVSR is that the Parzen window will affect the height of the peak differently depending on the frequency at which it occurs, whereas the logarithmic function does not.
It is recommended to use relative bandwidth filters to smooth MHVSR spectra (Konno and Ohmachi 1998; Parolai et al. 2009). The Konno–Ohmachi smoothing function is most used, with a filter coefficient b value of 40. A low b value results in very smooth spectra, while a high b value results in more erratic spectra. For example, Konno and Omachi (1998) used b = 20 in their original work; however, results in their paper clearly show that using a b value less than 30 tends to distort the HVSR peaks. Cox et al. (2020) reported achieving stable statistics on the MHVSR peak frequency when using b = 40 or 50. Mihaylov et al. (2016) proposed the use of bandpass filters to smooth spectra.
Combination of horizontal components
The MHVSR is the spectral ratio of horizontal-to-vertical component ground motions. While the vertical component is unambiguously defined, a single “horizontal” component must be defined from the two measured orthogonal components of horizontal motion. As a preliminary assessment of applicability of 1D site effects, MHVSRs of the two orthogonal horizontal components can be calculated (north–south/vertical and east–west/vertical), considering each component of horizontal motion separately. If the two ratios are similar, preliminary confidence is obtained in meeting the assumption of 1D site conditions. It is worth noting similarity of the MHVSR curve in the two measured orthogonal directions does not preclude its variation at other azimuths. MHVSR calculations performed across all azimuths (e.g., Cheng et al. 2020) is a more robust procedure to determine the site’s representative horizontal spectrum, if applicable. Cheng et al. (2020) calculate MHVSRs across all azimuths and combine them statistically to quantify the degree of azimuthal variability in the f0HV values. We note that most of the available software (discussed in Appendix 2) may automatically skip confirming azimuthal variability in the MHVSR, displaying only the horizontal average MHVSR but have the option of computing azimuthal MHVSR curves.
The average horizontal spectrum can be defined by considering the arithmetic mean, geometric mean, vector mean, vector summation, quadratic mean, or maximum horizontal value (Albarello and Lunedei 2013). Albarello and Lunedei (2013) concluded that all averaging procedures produce bias; however, by increasing the number of time windows considered, the biases associated with each procedure monotonically decrease rapidly. This is with the exception of the “maximum horizontal value” procedure. Use of the geometric mean is recommended (SESAME 2004; Cox et al. 2020).
MHVSR interpretation
The SESAME (2004) MHVSR guidelines provide three criteria to identify reliable MHVSR curves (see Appendix 3). If these criteria are not met, adjustment of processing parameters may improve the reliability of the MHVSR curve, as per the first two criteria. Albarello et al. (2011) developed a reliability classification scheme for consistent MHVSR processing that is more conservative than the SESAME guidelines to reduce variability in the extensive processed MHVSR dataset amongst multiple practitioners following the 2009 L’Aquila, Italy, earthquake. Six criteria for trustworthy and interpretable MHVSRs (class A) are based on the Fourier spectra (peaks relate to reduced vertical component amplitude) and sufficient duration leading to robust statistics and ability to evaluate MHVSR consistency with time and azimuth. Albarello et al. (2011) also further subdivides lesser quality MHVSRs; class B corresponds to ambiguous MHVSR curves that are used with caution and interpreted based on nearby MHVSR curves, and class C corresponds to poor quality (uninterpretable) curves that are to be discarded. The described MHVSR reliability classification scheme of Albarello (2011) was also used in determining 193 useable MHVSR curves of 223 Italian strong motion stations (Puglia et al. 2011).
Selection of MHVSR peak(s)
The primary or most reliable “output” from MHVSR calculation is the lowest frequency peak (f0HV) which is interpreted to be the site fundamental frequency (f0). The f0HV amplitude, often termed A0, is also typically extracted. Higher frequency peaks would be consecutively numbered (f1HV and A1, etc.). We introduce f#HV as the most generic term representing a MHVSR peak. A#HV is most often used in a relative sense between MHVSR measurement locations (higher peak amplitudes indicate larger impedance contrasts) and/or as a proxy for strength of impedance contrast(s) but is not a direct measure of soil-to-rock site amplification (discussed further in Sects. 5.2 and 5.3).
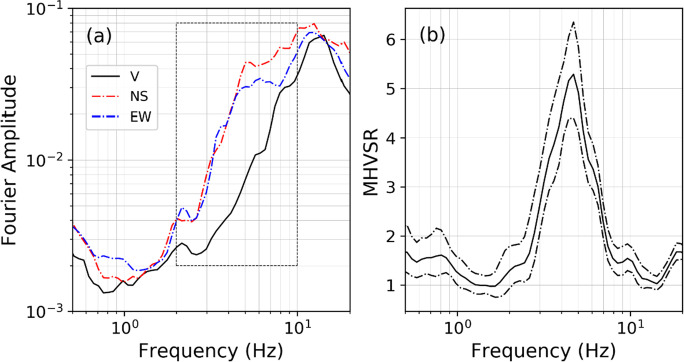
Prior to interpretation, the practitioner must ensure that every peak frequency (f#HV) has a natural stratigraphic origin. A more qualitative approach is to interpret the calculated MHVSR curve in conjunction with the individual Fourier spectral curves from all three components. A local maximum is expected in the horizontal spectra if the dominant wave type is SH waves. Love waves are indicated by the same feature. MHVSR peaks result from the amplified horizontal component amplitudes. If Rayleigh waves dominate the wavefield, this will result in a trough in the vertical spectral component at the resonant frequency and a peak at 2f0. In this case, MHVSR peaks exhibit an “eye-shape” in the Fourier spectra (Castellaro and Mulargia 2009b), in which the vertical spectrum amplitude is reduced over a limited bandwidth relative to the horizontal spectra amplitudes. Figure 4 illustrates the “eye-shape” characteristic of a peak caused by Rayleigh waves and stratigraphic origin. Another check involves reprocessing the MHVSR with reduced smoothing. If the peak is of anthropogenic origin, it should become sharper, while this would not be the case for a stratigraphic peak (SESAME 2004). A method to identify anthropogenic origin of a particular frequency in the microtremor time series is the random decrement method (Dunand et al. 2002) which allows the user to know if a specific frequency is damped (natural origin) or sustained (anthropogenic origin). Any peak at a non-damped (< < 1%) frequency will therefore be rejected for interpretation (Dunand et al. 2002; Wathelet et al. 2020). Industrial signals can travel far from their source and can influence the microtremor data even at distances of up to several kilometers from the source particularly at low frequencies (long wavelengths) (Bokelmann and Baisch 1999; Cornou et al. 2004). When the frequency of the anthropogenic signal is approximately the same as that of stratigraphic origin, it is particularly problematic.
Fig. 4.
a Individual time-averaged Fourier spectrum of each component with typical “eye-shape” (within gray box). b Corresponding average MHVSR (solid line) and one standard deviation (dot-dashed lines)
The identification of MHVSR peaks is only a straightforward process, either automated or user-selected, when clear peaks are present. The six SESAME criteria for a clear MHVSR peak (Appendix 3, Fig. 10) are well suited for measurements with clear peaks, and each peak is evaluated independently. These six criteria determine whether the peak under consideration clearly “stands out” from the background amplitude level and whether the peak is stable (low standard deviation in amplitude). The greater a MHVSR peak frequency is, the more stringent are the stability conditions for establishing a peak as clear. For all other natural cases (e.g., broad, asymmetrical, or multiple peaks; MHVSR near unity or “flat”), measurements should be assessed on a site-by-site basis. An automated peak-selection process may fail when data is complicated, requiring expert review. Wang (2020) observed that using the SESAME criteria resulted in too many measurements classified as not having clear peaks, which had identifiable peaks based on visual inspection. Wang (2020) modified the SESAME criteria to be more consistent with the subjective assessment of two analysts (Table 1).
Table 1.
Criteria for picking of clear HVSR peaks (adapted from Wang 2020). Values of Wang (2020) are shown in bold when updated from the SESAME values
| Criteria | SESAME | Wang (2020) |
|---|---|---|
| Clear 1: f ∈ [0.25f#HV,f#HV] | AHVave(f) < 0.5A#HV | AHVave(f) < 0.6A#HV |
| Clear 2: f ∈ [f#HV, 4f#HV] | AHVave(f) < 0.5A#HV | AHVave(f) < 0.6A#HV |
| Clear 3 | A#HV ≥ 2 | A#HV ≥ 1.6 |
| Clear 4: peak of f#HV [AHVave(f)-σA(f)] | within [f#HV /1.05, 1.05f#HV] | within [f#HV /1.15, 1.15f#HV] |
| Clear 4: peak of f#HV [AHVave(f) + σA(f)] | within [f#HV /1.05, 1.05f#HV] | within [f#HV /1.12, 1.12f#HV] |
| Clear 5: f#HV < 0.2 Hz | σf < 0.25f#HV | Recommends removal of Clear 5 criteria (barely satisfied) |
| Clear 5: f#HV ∈ [0.2, 0.5] Hz | σf < 0.20f#HV | |
| Clear 5: f#HV ∈ [0.5, 1.0] Hz | σf < 0.15f#HV | |
| Clear 5: f#HV ∈ [1.0, 2.0] Hz | σf < 0.10f#HV | |
| Clear 5: f#HV > 2.0 Hz | σf < 0.05f#HV | |
| Clear 6: f#HV < 0.2 Hz | σA < 3 | No change from SESAME |
| Clear 6: f#HV ∈ [0.2, 0.5] Hz | σA < 2.5 | No change from SESAME |
| Clear 6: f#HV ∈ [0.5, 1.0] Hz | σA < 2 | No change from SESAME |
| Clear 6: f#HV ∈ [1.0, 2.0] Hz | σA < 1.78 | No change from SESAME |
| Clear 6: f#HV > 2.0 Hz | σA < 1.58 | No change from SESAME |
Rows labeled Clear # represent the #-th condition for a clear peak. f#HV is the variable of interest (there could be multiple f#HV values in a single curve), A#HV is the amplitude at f#HV; AHVave(f) is the amplitude of HVSR mean curve at frequency f; σ(f) is standard deviation of f#HV, and σA(f) is standard deviation of AHVave(f)
It is not uncommon to observe double peaks in an MHVSR, sometimes multiple peaks, and the practitioner should review which peaks are of stratigraphic origin (discussed earlier in this section). Secondary peaks are more likely related to a secondary strong impedance contrast, and so forth, and less likely to be higher modes of the fundamental resonant frequency. The lowest frequency peak is caused by the deepest resonator (e.g., overburden/bedrock boundary), and higher frequency peaks are related to contrasts between soil layers within the overburden (Guéguen et al. 2000; Mihaylov et al. 2016). Hunter et al. (2020) observed two significant (A > 2) peaks in MHVSR curves which were commonly associated with large velocity contrasts within overburden, either as velocity inversions or as high-velocity inclusion layers. When large velocity variations occurred within the overburden, f0HV often appeared to be somewhat attenuated or broadened. However, in other cases, only moderate shape modification was observed. Higher modes are not commonly observed in MHVSR curves (Lermo and Chávez-García 1993), noting the prominent use of the Konno and Ohmachi (1998) filter in MHVSR calculation which was designed to suppress infinite peak amplitudes particularly at higher frequencies (discussed in Sect. 4.3).
Theoretically, rock sites are expected to have HVSR amplification of unity (or 1.414 according to equations in Sect. 2.3), but broadband or high-frequency amplification is often observed (e.g., Ladak et al. 2021). A relatively flat MHVSR can also result from the lack of a strong impedance contrast, even at a deep sediment site, e.g., coarse-grained soils over volcanic ash or heavily weathered (non-glaciated) rock common in Chile (Bonnefoy-Claudet et al. 2009; Leyton et al. 2013; Molnar et al. 2015) or from complex site effects (e.g., Uebayashi 2003; Di Giulio et al. 2010; Le Roux et al. 2012).
As mentioned in Sect. 4, a quick check to test the hypothesis of subsurface homogeneity is to process individual horizontal component HVSRs or directional HVSRs. If the directional HVSRs differ, it may be indicative of subsurface lateral heterogeneity. Matsushima et al. (2014) showed that over a 2D bedrock valley, the MHVSRs in two orthogonal directions are different in comparison to a 1D scenario with the same seismic parameters, MHVSR peak amplitude decreases, and f0HV increases. Broad or plateaued peaks are often indicative of laterally variable subsurface conditions (Uebayashi 2003; Bonnefoy-Claudet et al. 2006; Ozalaybey et al. 2011; Uebayashi et al. 2012; Le Roux et al. 2012). Even in the case of very simple two-layer geology, peak frequencies can broaden over dipping resonators (Dietiker et al. 2018, 2020). Peak shapes may be asymmetrical, and shoulders may develop where resonators curve. It is not recommended to select f0HV from plateaued curves, and a standardized procedure to select f0HV does not exist for broad peaks. A 2D resonance pattern (when observing interpolated f0HV on a spatial map) is common in steep-sided valleys with relatively thick sediment (Roten et al. 2006) or from edge diffracted waves due to a sloping interface. Dietiker et al. (2018) suggest that using the scaled difference of the two orthogonal spectral ratios might be a good indicator of 2D subsurface structure. They also suggest that by performing directional HVSR analysis, the orientation of subsurface structural trends can be inferred from the orientation of maximum polarization. In general, irregularly shaped peaks and large differences between orthogonal HVSRs are indicative of lateral heterogeneity.
Understanding whether observed MHVSR f0HV variations are due to 1D or 2D/3D site effects is crucial to avoid incorrect stratigraphic interpretations. When the subsurface geology does not meet the conditions of lateral homogeneity, the spectra of the individual components contain information on the geometry and mechanical properties of the subsurface that are confused if the two components are merged (Sgattoni and Castellaro 2020). For the specific case of 2D resonance in deeply embanked valleys, the geological structure vibrates as a unique structure with a transverse (ftrav) and longitudinal (flong) resonant frequency of motion. This makes 2D resonance easy to differentiate from 1D resonance because it gives two distinct peaks in the horizontal spectral components and the frequencies do not vary with space. The ratio of flong/ftrav depends on the aspect ratio of the valley; if the width is known, the depth may be determined for homogeneous valleys without any velocity gradient (Bard and Bouchon 1985). A specific combined inversion algorithm has also been proposed to account for 2D resonance frequencies (Roten and Fäh, 2007).
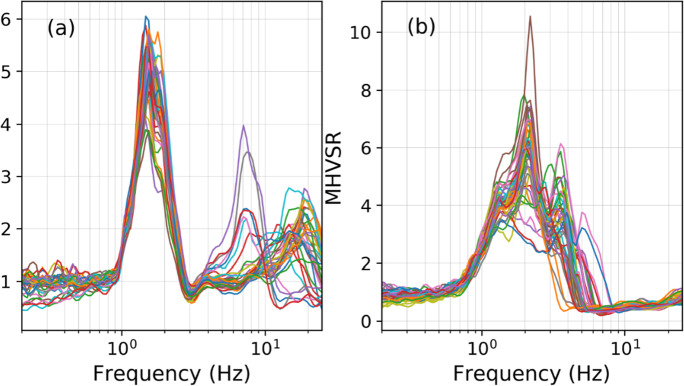
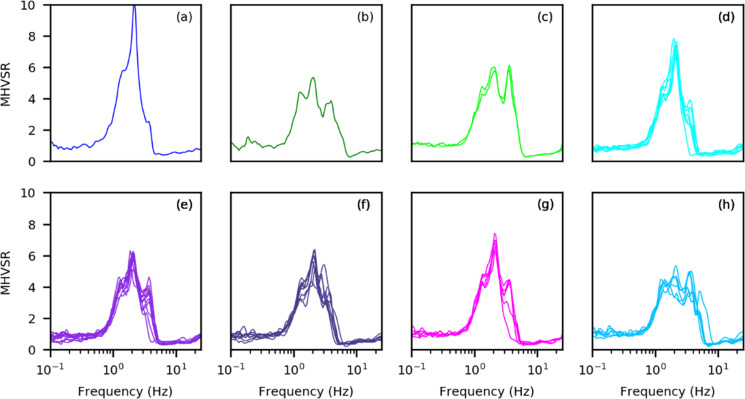
Figure 5 is provided as a summarized demonstration of MHVSR variability for 1D (Fig. 5) and 2D/3D (Fig. 5 and corresponding Fig. 6) site conditions. Figure 5 displays 42 MHVSRs obtained at a single passive seismic array site on flat ground in Vancouver, Canada; 7 seismometers were placed in a circular array of 6 different array radii of 5 to 30 m at the site. f0HV is consistent amongst all 42 tested locations (~ 1.5 Hz), indicating homogeneous 1D site conditions. Figure 5 also displays 42 MHVSRs obtained in the same way at a different array site on sloping ground in Port Coquitlam, Canada. The MHVSRs are more variable with broadened peaks (multiple narrow resonance frequencies), indicating 2D/3D effects. Interpretation of the spatial variability of f0HV can act as a proxy for geological site variability. A cluster analysis performed using the 42 variable MHVSRs from Fig. 5 determines up to eight subsets of the average MHVSRs (Fig. 6) confirming a highly variable spatial dependence of the MHVSR across the site. Further analysis of directional MHVSRs is required to decipher the 2D/3D effects at this site, i.e., f0HV should not be determined from the MHVSRs in Figs. 5 and 6.
Fig. 5.
Example MHVSRs obtained during microtremor array acquisition at multiple locations (various array radius) from each array’s sensor. a On flat ground in Vancouver, the MHVSR peak is consistent (1.5 Hz) amongst all tested locations and indicates laterally homogeneous site geology (depth to significant impedance or resonator is consistent). A second higher frequency peak shifts in frequency (5–20 Hz) and broadness indicating variable depth and possibly geometry of near-surface resonator. b On sloping ground in Port Coquitlam, multiple narrow peak resonances are observed (broad to flat peak occurs when these narrow resonances have similar amplification) amongst all tested locations and indicates rapidly changing depth to significant impedance contrast (resonator) or a laterally heterogeneous site geology
Fig. 6.
Example of eight consistent MHVSR subsets (a–h) determined by cluster analysis for the 42 MHVSRs shown in Fig. 5b
Additional MHVSR interpretations
With 1D interpretation of the MHVSR f0HV as f0 (= VSave/4 h) and the assumption of flat layering in the subsurface, a common “secondary” output from MHVSR calculation is to convert f0HV to sediment thickness or depth (z) (e.g., Ibs-von Seht and Wohlenberg 1999; Delgado et al. 2000; D’Amico et al. 2008; Gosar and Lenart 2010; Motazedian et al. 2011; Smith et al. 2013; Scheib et al. 2016; Tün et al. 2016; Jakica 2018; Pratt 2018; Moon et al. 2019). MHVSR results should be calibrated using detailed information about the local subsurface structure to provide reliable depth estimates. Figure 7 shows a selection of relations (Table 2) that determine sediment depth from f0HV
calibrated considering the local geology (z known from boreholes) in each of the seven countries. It should be noted that such a calibration and subsequent depth estimation are only accurate in flat-layered areas without a strong velocity gradient in the sediment layer (Motazedian et al. 2011). The assumption of flat-layered geology is not always correct and can negatively impact the estimation of resonator depth (e.g., Cornou et al. 2007; Guéguen et al. 2007). Where a survey objective is identification of the bedrock surface, supporting evidence is required to validate that the resonance stems from bedrock and not a sedimentary layer overlying bedrock that could give rise to similar resonance (e.g., gravel, glacial diamicton, or till). If a resonance peak resulting from a shallower resonator is misattributed to bedrock, depth to bedrock will be underestimated. Additionally, if incorrect velocities are used, or in the presence of 2D structure, estimates of depth to bedrock may be inaccurate (Roten et al. 2006; Guéguen et al. 2007).
Fig. 7.
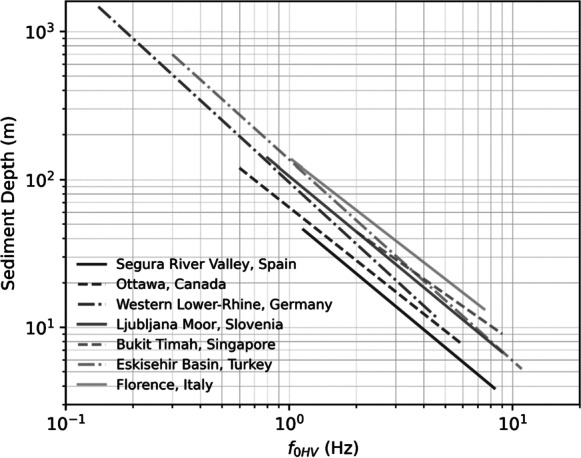
Selection of calibrated sediment depth from f0HV relations from seven countries
Table 2.
Details of selected sediment depth (z) from f0HV relations shown in Fig. 7
| Reference | Region | a | b | R2 | N | f0HV (Hz) | z (m) | Sediment type |
|---|---|---|---|---|---|---|---|---|
| Ibs-von Seht and Wohlenberg 1999 | Western Lower Rhine, Germany | 96 | 1.388 | 0.98 | 34 | 0.14–4.64 | 15–1600 | Quaternary–Tertiary |
| Delgado et al. 2000 | Segura River Valley, Spain | 55.11 | 1.256 | 0.97 | 27 | 1.16–8.3 | 4.1–44.7 | Holocene–Late Pleistocene |
| D’Amico et al. 2008 | Florence, Italy | 140 | 1.172 | 0.9 | 23 | 1.03–7.47 | 9–115 | Quaternary–Pliocene |
| Gosar and Lenart 2010 | Ljubljana Moor, Slovenia | 105.53 | 1.25 | 0.58 | 53 | 0.8–9.0 | 5–168 | Quaternary, lacustrine, and fluvial |
| Tun et al. 2016 | Eskisehir Basin, Turkey | 136 | 1.36 | 0.98 | 30 | ~ 0.3–11 | ~ 0–500 | Quaternary–Tertiary (Vs < 800 m/s) |
| Motazedian et al. 2011 | Ottawa, Canada | 64.98 | 1.198 | 0.95 | 89 | ~ 0.6–6.0 | ~ 5–130 | Soft glaciomarine sediments |
| Moon et al. 2019 | Bukit Timah, Singapore | 92.5 | 1.06 | 0.94 | 14 | ~ 2.0–9.0 | 10–45.5 | Quaternary and sedimentary (Jurong) rocks |
The tertiary “output” from MHVSR calculation, proposed originally but increasingly now in use, is direct use of the MHVSR curve to derive a site amplification function via inversion for a 1D earth model including elastic media properties of compressional velocity, VS, and density. However, the physical basis of the MHVSR (forward model) is still debated (Sect. 2), and there is no worldwide standard of MHVSR curve inversion. Wen et al. (2018) review several studies that have quantitatively interpreted the MHVSR for subsurface velocity models.
Empirical correction of MHVSR to earthquake site amplification
Hassani et al. (2019) derived a relationship to predict EHVSR predominant frequency (fd) values, the frequency of maximum peak amplitude (not the lowest frequency peak, f0HV), from fd values of the MHVSR calculated using response spectra. A regression analysis was conducted between fd values obtained from earthquake and microtremor HVSRs for 70 strong motion sites in California to derive the relation:
They suggested that the discrepancies between the two estimates of fd, from earthquake and microtremor HVRSs, may be related to the hypothesis that most microtremor energy comes from Rayleigh waves, whereas S waves contribute the most to earthquake data. While this is an effective method to overcome discrepancies between microtremor and earthquake HVSR peak frequency values, it does not account for differences in the shape of the curve.
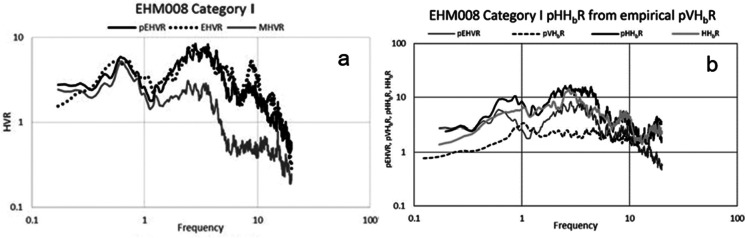
Kawase et al. (2018) developed an empirical method to correct the MHVSR shape such that it more closely approximates the EHVSR. For sites in Japan with co-located earthquake and microtremor data, the authors calculated EHVSRs and MHVSRs. They observed good agreement between the EHVSR and MHVSR up to the first peak; however, after the first peak, the EHVSR amplitude is generally greater, and higher frequency peaks (i.e., corresponding to higher modes) may be present, which are absent from the MHVSR. To correct for this, they proposed to calculate an earthquake-microtremor ratio (EMR) by taking the ratio between EHVSR and MHVSR. Before calculating the ratio, the frequency values were normalized (f/f0), and measurements were categorized based on f0HV. EMRs were calculated for each category by averaging the individual EMR estimates from each site within their respective category. By multiplying the MHVSR by the appropriate EMR, a closer approximation to EHVSR may be attained (Fig. 8). A recent development along the same line is due to Ito et al. (2021) in which they extend the method to apply to the Grenoble, France, basin in a different tectonic setting.
Fig. 8.
a Comparison of EHVR of S wave, MHVR (termed MHVSR in this paper), and pseudo-EHVSR (pEHVR) transformed from MHVSR by using empirical EMR for site EHM008 (adapted from Kawase et al. 2019; Fig. 10). The EMR correction results in a significant shift of the MHVSR amplitude towards the EHVR. b Comparison of pEHVR (MHVSR corrected by EMR), pHHbR (pEHVR corrected by pVHbR), and actual HHbR (SSR in this paper) for site EHM008 (adapted from Kawase et al. 2019; Fig. 13). pVHbR is the spectrum used to correct for vertical component amplification of EHVSR
The EHVSR is a step closer to the “true” SSR answer; however, the EHVSR is still affected by amplification of vertical component motions (e.g., Lermo and Chávez-García 1993; Theodoulidis et al. 1996; Bonilla et al. 1997; Raptakis et al. 1998; 2000; Parolai et al. 2000; Rong et al. 2019; Zhu et al. 2020). Kawase et al. (2019) proposed an additional empirical correction to translate the EHVSR to SSR (Fig. 8); similar empirical corrections were suggested by Ito et al. (2020). The methodology of Kawase et al. (2019) is based on the generalized inversion technique (Andrews 1986), whereby ground motion spectra may be decomposed into source, path, and site effects. Then, utilizing a reference spectrum (i.e., free of site effects), they calculated the spectral ratio of vertical component motions to that of reference motions to determine a frequency-dependent correction. Frequency values were not normalized by f0HV, but correction spectra were calculated for the same frequency categories as EMR. The methodology was tested on sites with both earthquake and microtremor measurements, as well as suitable reference sites to calculate SSRs. The authors report an 80% success rate with regard to obtaining good correlation with SSR. Under these empirical corrections, the MHVSR can be treated as a suitable proxy for the site amplification spectrum (S wave transfer function).
MHVSR uncertainty
Uncertainty of f0HV
Quantifying the uncertainty inherent to f0HV determined from microtremor (and earthquake) recordings is important as its use in ground motion prediction models and code-based seismic site classification is increasing (e.g., Zhao et al. 2006; Luzi et al. 2011; Cadet et al. 2012; Pitilakis et al. 2013; Hassani and Atkinson 2018; Harmon et al. 2019). This can be extended to estimates of f0 obtained through empirical approaches. Most often f0HV is estimated deterministically from the mean/median MHVSR curve, which does not provide any information regarding its variability. The MHVSR curve itself is calculated in a statistical manner through the consideration of individual time windows to define a single representative mean or median curve. Given the random nature of the microtremor wavefield, variability in individual windows is expected due to unevenly distributed sources, amongst other factors.
The lowest frequency peak of the MHVSR curve (f0HV) may not be the global maximum. All peak picking algorithms search for the global maximum; thus, it is more appropriate to refer to the auto-picked peak as fgm, the frequency corresponding to the global maximum. The automated peak picking algorithm implemented in Geopsy (Wathelet et al. 2020) works by defining a restrictive search range [fgm,mc / Rf, fgm,mc * Rf], where fgm,mc is fgm of the median curve (mc) and Rf is expressed as
within which fgm,i values are obtained from individual windows, where i denotes the individual window under consideration (Cox et al. 2020). The user defines fmin and fmax as the interval over which to calculate the MHVSR. The logic surrounding this restrictive search window is that if any window has a global peak, fgm,i, that is far from fgm,mc, then that window is likely contaminated. As opposed to removing this window from the statistical calculation of fgm,i, the algorithm searches for the local maximum within the restricted frequency range. This inclusion of contaminated windows has the potential to bias both the statistics for fgm,ave, which is the average calculated from the individual fgm,i values, as well as the median curve from which fgm,mc is obtained.
Cox et al. (2020) propose a frequency-domain window-rejection algorithm (FWA) that effectively removes contaminated windows from the computation of both fgm,ave and the median curve. The algorithm iteratively rejects windows based on consideration of fgm,ave and its corresponding standard deviation. At each iteration, these statistics are computed considering the set of windows accepted from the previous iteration. Any windows for which fgm,i deviates more than n standard deviations from the fgm,ave value determined from individual windows are rejected. The n value is the only user-defined parameter needed to run the FWA. Cox et al. (2020) recommended using n = 2.0 (i.e., two standard deviations) for most calculations. However, the exact value used for a given application should be carefully considered by the analyst to ensure reasonable time windows are not being rejected. The FWA stopping criteria involves comparison of fgm,ave computed from individual windows and fgm,mc; once these values are within a certain tolerance of each other, the algorithm stops. At each iteration, the median curve and the value of fgm,mc are updated. In this manner, contaminated windows are removed utilizing a statistically robust procedure and an unbiased estimate of fgm, and its associated standard deviation can be provided. Several methods use a log-normal distribution of MHVSR curves to determine statistics (e.g., Cox et al. 2020; Wathelet et al. 2020). Not only does this more realistically reflect the true nature of the data, but it also allows seamless transition of statistics from frequency to period.
Accounting for azimuthal variability in f#HV is not a common procedure in spite of the fact that differences in f0HV and its corresponding amplitude have frequently been observed in the individual horizontal components of MHVSR measurements (e.g., Guillier et al. 2006; Uebayashi et al. 2012; Matsushima et al. 2014; 2017; Ktenidou et al. 2016; Theodoulidis et al. 2018; Vantassel et al. 2018). As an extension of the FWA and statistical interpretation of MHVSR data developed by Cox et al. (2020), Cheng et al. (2020) proposed to more rigorously study MHVSR curves as a function of azimuth and statistically account for this variability in f0HV. Through the use of the FWA, a set of accepted windows is determined for each azimuth under consideration. It is also possible that for each azimuth, the number of accepted windows will differ. Thus, to avoid biasing the statistics, a weight (w) is applied to each f0,i value prior to calculating statistics:
where N is the number of azimuths under consideration and I is the number of accepted windows at the azimuth under consideration.
The peak picking algorithm utilized in each of the MHVSR processing platforms discussed is restricted to identifying a single dominant peak. However, MHVSR results with several peaks (resonances), f#HV, have been observed. Accounting for the variability in these additional peaks has not been the subject of significant investigation, although there have been some observational indication of MHVRs showing different directional dependency for different peaks according to the different soil layer depths (Matsushima et al. 2019).
Uncertainty of MHVSR curves
As described in Sect. 4, an average MHVSR curve is calculated for the recording site by averaging with time and the two horizontal components (i.e., source azimuth) derived from Aki’s (1957) proposal that microtremors are a stochastic process in time and space. It was noted that averaging of MHVSRs from all selected time windows reduces variability in the mean MHVSR curve compared to averaging of each component’s spectra with time and that the latter is considered more appropriate for use if the assumption is a diffuse wavefield. At 2D/3D sites, azimuthal variability in f#HV occurs, and techniques are being developed to properly capture this variability (Matsushima et al. 2017; Cheng 2020).
As mentioned in Sects. 2 and 5, some advanced uses of MHVSR curves includes prediction (modelling) of the 1D VS profile and/or site amplification. In addition to ongoing and vivid debates about such uses, the practitioner is reminded that (a) such uses should account for the uncertainty of MHVSR curves and the processing details (for instance, the amount of smoothing) by investigating the sensitivity of the inversion process on the MHVSR uncertainty and (b) that some parameters are not constrained at all by the inversion process. For example, the damping profile, needed for deriving the forward amplification function from the velocity profile, cannot presently be obtained from the MHVSR curve. Another example is the derivation of ellipticity from special processing of the MHVSR curve and its inversion in terms of the velocity profile, which requires some anchoring VS value at some depth: as shown in Scherbaum et al. (2003) and illustrated in Fig. 1 of Hobiger et al. (2013), Rayleigh wave ellipticity curves remain unchanged when velocity and depth are scaled by the same factor k (i.e., VS(z) and k.VS(k.z), and their inversion should be constrained by an independent estimate of VS at some depth, for instance, at surface (the same is true for the inversion of the S wave transfer function).
Conclusions
This paper began with splitting the greatest challenges to an international standardization of the MHVSR method into the physical basis of the MHVSR and its underlying wavefield composition (the what) and recommendations of MHVSR acquisition and analysis including its interpretation and uncertainty assessment (the how). In conclusion, we split summary of aspects of these two great challenges to MHVSR method standardization into those that are known or undebated from those that are still debated or ongoing research.
The potential and therefore use of the MHVSR method to provide a reliable estimate (proxy) of the site fundamental frequency or period have been known for approximately 3 decades with debate tapering off about 2 decades ago. The act of retrieving f0HV and secondary peaks (f#HV) is therefore not debated, but how it is accomplished still is. This paper summarized a selection of literature documenting the increasing automation and innovation of quantitative criteria towards retrieval of f#HV which continues to be an area of active research. Early on, f0HV was directly used to determine engineering bedrock depth (first instance of geologic rock under soils) but later literature reported: (1) that this is a resonator depth and (2) development of local calibrations for converting f0HV to sediment depth. The determination of f0HV at a particular location, or the mapping of its spatial variability around a site or area (regional microzonation), and its conversion to sediment thickness have always been and still are the predominant uses of the MHVSR method.
In the 2000s, the first consortium effort in recommendations for MHVSR field measurements, processing, and interpretation occurred (the SESAME project; Bard et al. 2008). In a general sense, it is no longer debated how to perform MHVSR acquisition and analysis; many practitioners have been doing so and training others for decades. The increasing commercial production in seismic equipment and associated software for MHVSR acquisition and analysis (and passive seismology in general) is a form of attestation to this undebated knowledge. However, details of how MHVSR acquisition and analysis are accomplished are still debated. The most debated aspects amongst this paper’s authors included equipment recommendations (various seismic systems are available to us and selected depending first on the site conditions and then on the suitability of operation given the project or environment; the latter is worth conveying to the untrained but can also convey unintended preference of particular brand names which is avoided here without a recent and comprehensive blind test or benchmark experiment), field acquisition recommendations (difficulties due to unlimited worldwide conditions or “exceptions to the rule”), and the rapid outdatedness of discussing particular analysis techniques and software (areas of current research).
There have been significant and important advancements into the physical basis of the MHVSR curve (the what) and its underlying microtremor wavefield composition (the appropriate forward model) throughout the past two decades. A total/diffuse wavefield approach is well suited towards a worldwide standardization, allowing the data itself to determine wavefield contributions rather than our assumptions. Hence, the current most controversial aspect of the MHVSR method is our ability to model (invert) the MHVSR curve for 1D layered earth models (simplified to VS depth profiles) and whether we should even be doing so without some form of correction/calibration particularly at frequencies above f0HV. A comprehensive and/or international benchmark test of the multitude of available equipment types and their ability to provide consistently “the same” MHVSR curve is necessary towards the inversion of MHVSR curves for subsurface models.
Acknowledgements
The Consortium of Organizations for Strong Motion Observation Systems (COSMOS) consisting of the US Geological Survey (USGS), the Geological Survey of Canada, and a group of North American power utility companies (Southern California Edison and Pacific Gas and Electric) identified the need for blind trials and provided funding and encouragement to facilitate this project. Other than for the USGS, any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the authors’ organizations or their governments. Our manuscript was improved from reviews by Guest Editor Stefano Parolai and Dario Albarello and an anonymous reviewer and internal USGS reviews by Oliver Boyd and Jamison Steidl. Thanks are given to C. Mortera (Univ. Western Ontario) and J. E. Plata and M. G. Sánchez (USI-IINGEN UNAM) for locating useful references. Open access publication fees supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) grant (RGPIN-2016-04634) held by S. Molnar. F. J. Sánchez-Sesma appreciates partial support by UNAM-DGAPA PAPIIT project IN107720.
Appendix 1
A table of acquisition parameters and their influence on the MHVSR is provided in Fig. 9, updated from Koller et al. (2004). These types of metadata associated with each microtremor recording are important to include in field notes and refer to during MHVSR calculation and interpretation.
Appendix 2
Many software packages are available now to process and analyze MHVSR measurements. Examples include Grilla, Geopsy, ModelHVSR, OpenHVSR, and HVSRPy. Most of these software suites provide the user with the ability to pre-condition (filter) time series data, if necessary. Time window selection may be accomplished manually, directly from the screen, or through the use of a time-domain anti-trigger algorithm. Once the time windows have been transformed to the frequency domain, the user has the option to smooth the spectra and decide how to combine the horizontal components to define a representative horizontal spectrum or opt to calculate two separate ratios and treat each component independently. Below is a review of currently available MHVSR processing software. Although with advancements ongoing, improvements to these software platforms may make some of the descriptions obsolete; this Appendix section is meant to provide readers with a snapshot of the current state of available MHVSR processing.
Grilla is a proprietary software to analyze Tromino® recordings (http://moho.world/en/) (Castellaro and Mulargia 2009a, b) and accepts several other non-proprietary input formats. It has the capability to perform spectral analyses, as well as time-dependent and direction-dependent MHVSR analyses.
Geopsy (Wathelet et al. 2020) is an open-source software developed from the SESAME project. It accepts a variety of different input file formats. Both single measurement and batch processing of MHVSRs are supported. Geopsy automatically provides a value of f0 from the mean MHVSR curve (deterministically), as well as from the individual windows (statistically) that can be adjusted by the user such as to delete spurious individual MHVSR curves. Geopsy provides tools to compute the MHVSR as a function of azimuth (rotate) and complete time frequency analysis, which can aid in wave composition analyses (Fäh et al. 2009). Geopsy has modules to forward model the ellipticity curve and the SH-transfer function for layered earth models.
ModelHVSR (Herak 2008) consists of several MATLAB-based modules and algorithms. It does not have the capability to deal with raw time series data, so the input data must already be transformed to the frequency domain. AVG_HVSR calculates the average MHVSR from any number of observed MHVSRs. The input to this module is the spectral data, and an option is available to apply spectral smoothing or alternatively to use Landweber filtering on the unsmoothed spectra. ModelHVSR can forward model the theoretical S wave transfer function of a layered viscoelastic model for vertically incident S waves (horizontal response) and the theoretical P wave amplification spectrum for vertically incident P waves and calculates the MHVSR as the ratio between these two quantities.
OpenHVSR (Bignardi et al. 2018) is a MATLAB-based program capable of generating and displaying MHVSR curves from raw field data. One of its strengths is the ability to handle large volumes of data and spatially correlate different forms of informative data content. All data are loaded into the same environment, which facilitates batch processing of MHVSRs, allowing easy implementation of sensitivity analyses to test the choice of a specific set of processing parameters on the output MHVSRs. An interesting feature of this software is the implementation of directional analysis of spectral ratios to check whether the data contain non-isotropic components. Spatial map products can be produced of resonance frequency values, amplitude at resonance peaks, and preferential direction of f0. OpenHVSR utilizes the same forward modelling strategy as ModelHVSR; however, it also provides the ability to simulate the surface wave contribution using the modelling routine of Lunedei and Albarello (2010).
HVSRPy is an open-source Python package for HVSR processing that was developed recently by Vantassel (2020) to implement new statistical MHVSR processing techniques proposed by Cox et al. (2020) and Cheng et al. (2020; 2021). Several features of HVSRPy make it unique from other available software. These novel functionalities include a frequency-domain window-rejection algorithm (FWA), which allows for the automatic rejection of contaminated time windows in the frequency domain, the ability to incorporate azimuthal variability into the statistical representation of f0, and the use of log-normal statistics, which allow for consistent representation of uncertainty, regardless of whether f0HV or its reciprocal T0 is the desired parameter of interest. Additionally, HVSRPy allows for calculating an unbiased, statistical representation of f0 or T0 from numerous, spatially distributed MHVSR measurements using Voronoi tessellations for spatial de-clustering. Batch-style processing is simple and easy to implement using HVSRPy. For those who wish to quickly process a single MHVSR record without the need to deal with Python code, a web-based application called HVSRweb has also been developed (Vantassel et al. 2018). HVSRweb currently has all of the functionality of HVSRPy except for the ability to calculate statistics from spatially distributed MHVSR measurements. HVSRweb can be accessed at https://hvsrweb.designsafe-ci.org/.
The HVSR IRIS station toolbox (Bahavar et al. 2020) corresponds to the Incorporated Research Institutions for Seismology (IRIS) Data Management Center’s (DMC’s) openly available HVSR station toolbox. The platform includes a variety of ways to compute the spectral ratio for ambient seismic noise by providing different averaging routines. The options range from the simple average of spectral ratios to the ratio of spectral averages. Computations take advantage of the available power spectral density estimates of ambient noise for the seismic stations, and they can be used to estimate the predominant frequency of the many three-component seismic stations available from the IRIS DMC.
Appendix 3
Fig. 10.
From the SESAME (2004) MHVSR guidelines, the three criteria for a reliable H/V (MHVSR) curve and six criteria for a clear H/V peak are presented
Author contribution
Sheri Molnar and Alan Yong contributed to the conception and outline of this review article. Literature review (post-2010) was performed by Aamna Sirohey. Aamna Sirohey and Sheri Molnar drafted the original manuscript with initial review by Alan Yong. All figures were generated by Aamna Sirohey and Sheri Molnar with contributions from Brady Cox (Fig. 2); Jamal Assaf generated Fig. 7. All co-authors reviewed and contributed to the editing of the manuscript. Co-authors that contributed significantly to the writing of the edited manuscript include Pierre-Yves Bard, Cecile Cornou, Brady Cox, Bertrand Guillier, Hiroshi Kawase, and Francisco J. Sánchez-Sesma. All authors read and approved the final manuscript.
Funding
The Consortium of Organizations for Strong Motion Observation Systems (COSMOS) and a group of North American power utility companies, consisting of Southern California Edison and Pacific Gas and Electric, identified the need for these guidelines for best-practices and provided funding and encouragement to facilitate the project. This material is also based upon work supported by the U.S. Geological Survey under Cooperative Agreement No. G17AC00058. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the opinions or policies of the U.S. Geological Survey. Mention of trade names or commercial products does not constitute their endorsement by the U.S. Geological Survey. Open access publication fees were supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (RGPIN-2016–04634).
Data availability
Not applicable.
Code availability
Not applicable.
Declarations
Conflict of interest
The authors have no financial or proprietary interests in any material discussed in this article. The Consortium of Organizations for Strong Motion Observation Systems (COSMOS) consisting of the US Geological Survey, the Geological Survey of Canada, and a group of North American power utility companies (Southern California Edison and Pacific Gas and Electric) identified the need for blind trials and provided funding and encouragement to facilitate the project. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the US Government.
Footnotes
Highlights
• The current understanding of the microtremor wavefield is summarized.
• Updated recommendations for MHVSR acquisition and calculation using available software are provided.
• Recommendations of MHVSR interpretation and uncertainty assessment are provided.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
S. Molnar, Email: smolnar8@uwo.ca
A. Sirohey, Email: asirohey@uwo.ca
J. Assaf, Email: jassaf2@uwo.ca
P.-Y. Bard, Email: pierre-yves.bard@univ-grenoble-alpes.fr
S. Castellaro, Email: silvia.castellaro@unibo.it
C. Cornou, Email: cecile.cornou@univ-grenoble-alpes.fr
B. Cox, Email: brady.cox@usu.edu
B. Guillier, Email: bertrand.guillier@ird.fr
B. Hassani, Email: behzad.hassani@bchydro.com
H. Kawase, Email: kawase@sere.dpri.kyoto-u.ac.jp
S. Matsushima, Email: matsushima@sds.dpri.kyoto-u.ac.jp
F. J. Sánchez-Sesma, Email: sesma@unam.mx
A. Yong, Email: yong@usgs.gov
References
- Aki K. Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull Earthq Res Inst. 1957;35:415–456. [Google Scholar]
- Abarello D. Detection of spurious maxima in the site amplification characteristics estimated by the HVSR technique. Bull Seis Soc Am. 2001;91(4):718–724. doi: 10.1785/0119990172. [DOI] [Google Scholar]
- Albarello D, Cesi C, Eulilli E, Guerrini F, Lunedei E, Paolucci E, Pileggi D, Puzzilli LM. The contribution of the ambient vibration prospecting in seismic microzoning: an example from the area damaged by the April 6, 2009 L’Aquila (Italy) earthquake. Bolletino Di Geofisica Teorica Ed Applicata. 2011;52(3):513–538. [Google Scholar]
- Albarello D, Lunedei E. Combining horizontal ambient vibration components for H/V spectral ratio estimates. Geophys J Int. 2013;194(2):936–951. doi: 10.1093/gji/ggt130. [DOI] [Google Scholar]
- Andrews DJ. Objective determination of source parameters and similarity of earthquakes of different size, in Earthquake Source Mechanics, S. Das (Editor) American Geophysical Monograph. 1986;37:259–267. [Google Scholar]
- Arai H, Tokimatsu K (1998). Evaluation of local site effects based on microtremor H/V spectra. In Proceedings of the 2nd international symposium on the effects of surface geology on seismic motion (Vol. 2, pp. 673-680). Japan: Yokohama.
- Arai H, Tokimatsu K (2000, January). Effects of Rayleigh and Love waves on microtremor H/V spectra. In Proceedings of the 12th World Conference on Earthquake Engineering (Vol. 2232, pp. 1-8). Auckland, New Zealand: New Zealand Society for Earthquake Engineering Inc..
- Arai H, Tokimatsu K (2004) S-wave velocity profiling by inversion of microtremor H/V spectrum. Bull Seis Soc Am 94(1):53–63
- Arai H, Tokimatsu K. S-wave velocity profiling by joint inversion of microtremor dispersion curve and horizontal-to-vertical (H/V) spectrum. Bull Seis Soc Am. 2005;95(5):1766–1778. doi: 10.1785/0120040243. [DOI] [Google Scholar]
- Asten, M., and K. Hayashi, (2021). SPAC method. Journal of Seismology (this issue)
- Bahavar M, Spica ZJ, Sánchez-Sesma FJ, Trabant C, Zandieh A, Toro G. Horizontal-to-vertical spectral ratio (HVSR) IRIS station toolbox. Seis Res Lett. 2020;91:3539–3549. doi: 10.1785/0220200047. [DOI] [Google Scholar]
- Bard PY. Microtremor measurements: a tool for site effect estimation. In Proceedings the Effects of Surface Geology on Seismic Motion. 1999;3:1251–1279. [Google Scholar]
- Bard PY, Bouchon M. The two-dimensional resonance of sediment-filled valleys. Bull Seis Soc Am. 1985;75(2):519–541. doi: 10.1785/BSSA0750020519. [DOI] [Google Scholar]
- Bard PY, Acerra C, Aguacil G, Anastasiadis A, Atakan K, Azzara R, Basili R, Bertrand E, Bettig B, Blarel F, Bonnefoy-Claudet S, Paola B, Borges A, Sørensen M, Bourjot L, Cadet H, Cara F, Caserta A, Chatelain JL, Zacharopoulos S. Guidelines for the implementation of the H/V spectral ratio technique on ambient vibrations measurements, processing and interpretation. Bull Earthq Eng. 2008;6(1):1–2. doi: 10.1007/s10518-008-9059-4. [DOI] [Google Scholar]
- Bertelli T. Osservazioni sui piccoli movimenti dei pendoli in relazione ad alcuni fenomeni meteorologici del pd Timoteo Bertelli barnabita. 1872. [Google Scholar]
- Bignardi S, Yezzi AJ, Fiussello S, Comelli A. OpenHVSR-Processing toolkit: enhanced HVSR processing of distributed microtremor measurements and spatial variation of their informative content. Comput Geosci. 2018;120:10–20. doi: 10.1016/j.cageo.2018.07.006. [DOI] [Google Scholar]
- Bokelmann GHR, Baisch S. Nature of narrow-band signals at 2.083 Hz. Bull Seis Soc Am. 1999;89(1):156–164. [Google Scholar]
- Bonilla LF, Steidl JH, Lindley GT, Tumarkin AG, Archuleta RJ. Site amplification in the San Fernando Valley, California: variability of site-effect estimation using the S-wave, coda, and H/V methods. Bull Seis Soc Am. 1997;87(3):710–730. doi: 10.1785/BSSA0870030710. [DOI] [Google Scholar]
- Bonnefoy-Claudet S, Cotton F, Bard P. The nature of noise wavefield and its applications for site effects studies: a literature review. Earth-Sci Rev. 2006;79(3–4):205–227. doi: 10.1016/j.earscirev.2006.07.004. [DOI] [Google Scholar]
- Bonnefoy-Claudet S, Köhler A, Cornou C, Wathelet M, Bard PY. Effects of love waves on microtremor H/V ratio. Bull Seis Soc Am. 2008;98(1):288–300. doi: 10.1785/0120070063. [DOI] [Google Scholar]
- Bonnefoy-Claudet S, Baize S, Bonilla LF, Berge-Thierry C, Pasten C, Campos J, Volant P, Verdugo R. Site effect evaluation in the basin of Santiago de Chile using ambient noise measurements. Geophys J Int. 2009;176(3):925–937. doi: 10.1111/j.1365-246X.2008.04020.x. [DOI] [Google Scholar]
- Borcherdt RD. Effects of local geology on ground motion near San Francisco Bay. Bull Seis Soc Am. 1970;60(1):29–61. [Google Scholar]
- Bour M, Fouissac D, Dominique P, Martin C. On the use of microtremor recordings in seismic microzonation. Soil Dyn and Earthquake Eng. 1998;17:465–474. doi: 10.1016/S0267-7261(98)00014-1. [DOI] [Google Scholar]
- Cadet H, Bard P-Y, Duval A-M, Bertrand E. Site effect assessment using KiK-net data: part 2 – site amplification prediction equation based on f0 and VSZ. Bull Earthquake Eng. 2012;10:451–489. doi: 10.1007/s10518-011-9298-7. [DOI] [Google Scholar]
- Castellaro S, Mulargia F. VS30 estimates using constrained H/V measurements. Bull Seis Soc Am. 2009;99(2A):761–773. doi: 10.1785/0120080179. [DOI] [Google Scholar]
- Castellaro S, Mulargia F. The effect of velocity inversions on H/V. Pure Appl Geophys. 2009;166(4):567–592. doi: 10.1007/s00024-009-0474-5. [DOI] [Google Scholar]
- Castellaro S, Mulargia F. How far from a building does the ground-motion free-field start? The cases of three famous towers and a modern building. Bull Seis Soc Am. 2010;100(5A):2080–2094. doi: 10.1785/0120090188. [DOI] [Google Scholar]
- Chatelain J-L, Guillier B. Reliable fundamental frequencies of soils and buildings down to 0.1 Hz obtained from ambient vibrations recordings with a 4.5-Hz sensor. Seism Res Lett. 2013;84(2):199–209. doi: 10.1785/0220120003. [DOI] [Google Scholar]
- Chatelain JL, Guillier B, Cara F, et al. Evaluation of the influence of experimental conditions on H/V results from ambient noise recordings. Bull Earthq Eng. 2008;6(1):33–74. doi: 10.1007/s10518-007-9040-7. [DOI] [Google Scholar]
- Cheng T, Hallal MM, Vantassel JP, Cox BR (2021). Estimating Unbiased Statistics for Fundamental Site Frequency Using Spatially Distributed HVSR Measurements and Voronoi Tessellation. J Geotech Geoenviron, 147(8), 04021068.
- Cheng T, Cox BR, Vantassel JP, Manuel L (2020) A statistical approach to account for azimuthal variability in single-station HVSR measurements. Geophys J Int 223(2):1040–1053
- Cipta A, Cummins P, Dettmer J, Saygin E, Irsyam M, Rudyanto A, Murjaya J (2018) Seismic velocity structure of the Jakarta Basin, Indonesia, using trans-dimensional Bayesian inversion of horizontal-to-vertical spectral ratios. Geophys J Int 215(1):431–449
- Cornou C, Guéguen P, Bard P-Y, Hagshenas E (2004) Ambient noise energy bursts observation and modeling : trapping of structure-soil harmonic induced-waves in a topmost sedimentary layer. J Seismolog 8(4):507–524
- Cornou C, Guillier B, Boussoura K, Selmi K, Renalier F (2007). Limite de la technique H/V comme outil d’exploration géophysique pour les structures 2D et 3D. In Proceedings of the 7ème colloque de l’Association Francaise de Génie Parasismique, Paris (France)
- Cornou, C., Guillier, B., Boussoura, K., Selmi, K., and Renalier, F. (2007). Limite de la technique H/V comme outil d’exploration géophysique pour les structures 2D et 3D. 7ème colloque de l’Association Francaise de Génie Parasismique, Paris (France)
- Cox BR, Cheng T, Vantassel JP, Manuel L. A statistical representation and frequency-domain window-rejection algorithm for single-station HVSR measurements. Geophys J Int. 2020;221(3):2170–2183. doi: 10.1093/gji/ggaa119. [DOI] [Google Scholar]
- D’Alessandro A, Luzio D, Martorana R, Capizzi P. Selection of time windows in the horizontal-to-vertical noise spectral ratio by means of cluster analysis. Bull Seis Soc Am. 2016;106(2):560–574. doi: 10.1785/0120150017. [DOI] [Google Scholar]
- D’Amico V, Picozzi M, Baliva F, Albarello D (2008) Ambient noise measurements for preliminary site-effects characterization in the Urban area of Florence, Italy. Bull Seis Soc Am 98:1373–1388
- Delgado J, López Casado C, Estévez A, Giner J, Cuenca A, Molina S. Mapping soft soils in the Segura river valley (SE Spain): a case study of microtremors as an exploration tool. J Appl Geophys. 2000;45:19–32. doi: 10.1016/S0926-9851(00)00016-1. [DOI] [Google Scholar]
- Di Giacomo D, Gallipoli MR, Mucciarelli M, Parolai S, Richwalski S. Analysis and modeling of HVSR in the presence of a velocity inversion: The case of Venosa. Italy Bull Seis Soc Am. 2005;95(6):2364–2372. doi: 10.1785/0120040242. [DOI] [Google Scholar]
- Di Giulio G, Savvaidis A, Theodoulidis N, et al (2010). Inversion of surface wave dispersion at European strong motion sites using a multi-model parameterization and an information-theoretic approach. In Proceedings of the 14th European Conference on Earthquake Engineering, 4595, Ohrid, Macedonia.
- Dietiker B, Pugin AJM, Crow HL, Mallozzi S, Brewer KD, Cartwright TJ, Hunter JA. HVSR measurements in complex sedimentary environment and highly structured resonator topography-Comparisons with seismic reflection profiles and geophysical borehole logs. Society of Exploration Geophysicists and Environment and Engineering Geophysical Society. 2018 doi: 10.4133/sageep.31-025. [DOI] [Google Scholar]
- Dietiker B, Hunter JA, Pugin AJ. Improved analysis of horizontal-to-vertical spectral ratio measurements for groundwater investigations. Geological Survey of Canada, Open File. 2020;8536:159–170. [Google Scholar]
- Dobry R, Oweis I, Urzúa A. Simplified procedures for estimating the fundamental period of a soil profile. Bull Seis Soc Am. 1976;66(4):1293–1321. [Google Scholar]
- Dunand F, Bard PY, Chatelain JL, et al (2002) Damping and frequency from Randomdec method applied to in situ measurements of ambient vibrations. Evidence for effective soil structure interaction. In Proceedings of the 12th European Conference on Earthquake Engineering, London. Paper (Vol. 869)
- Edwards WN. Analysis of measured wind turbine seismic noise generated from the Summerside Wind Farm. Prince Edward Island, Geological Survey of Canada, Open File Report. 2015;7763:1–66. [Google Scholar]
- Endrun B (2011) Love wave contribution to the ambient vibration H/V amplitude peak observed with array measurements. J Seismolog 15(3):443–472
- Fäh D, Wathelet M, Kristekova M, et al (2009) Using ellipticity information for site characterisation. NERIES JRA4 “Geotechnical Site Characterisation”. task B, 2
- Field E, Jacob K (1993) The theoretical response of sedimentary layers to ambient seismic noise. Geophys Res Lett 20(24):2925–2928
- Field E, Jacob K. The theoretical response of sedimentary layers to ambient seismic noise. Geophys Res Lett. 1993;20(24):2925–2928. doi: 10.1029/93GL03054. [DOI] [Google Scholar]
- Foti S, Hollender F, Garofalo F et al (2018) Guidelines for the good practice of surface wave analysis: a product of the InterPACIFIC project. Bull Earthq Eng 16(6):2367–2420
- Fukushima Y, Bonilla L, Scotti O, Douglas J. Site classification using horizontal-to-vertical response spectral ratios and its impact when deriving empirical ground-motion prediction equations. J Earthquake Eng. 2007;11:712–724. doi: 10.1080/13632460701457116. [DOI] [Google Scholar]
- García-Jerez A, Piña-Flores J, Sanchez-Sesma F, Luzon F, Perton M. A computer code for forward calculation and inversion of the H/V spectral ratio under the diffuse field assumption. Comput Geosci. 2016;97:67–78. doi: 10.1016/j.cageo.2016.06.016. [DOI] [Google Scholar]
- Gosar A, Lenart A (2010) Mapping the thickness of sediments in the Ljubljana Moor basin (Slovenia) using microtremors. Bull Earthq Eng 8:501–518
- Grippa, A., Bianca, M., Tropeano, M., et al (2011). Use of the HVSR method to detect buried paleomorphologies (filled incised-valleys) below a coastal plain: the case of the Metaponto plain (Basilicata, southern Italy). Bollettino di Geofisica TeoricaedApplicata, 52(2)
- Guéguen P, Chatelain JL, Guillier B, Yepes H, Egred J (1998) Site effect and damage distribution in Pujili (Ecuador) after the 28 March 1996 earthquake. Soil Dyn and Earthquake Eng 17:329–334
- Guéguen P, Chatelain JL, Guillier B, Yepes H. An indication of the soil topmost layer response in Quito (Ecuador) using noise H/V spectral ratio. Soil Dyn and Earthquake Eng. 2000;19(2):127–133. doi: 10.1016/S0267-7261(99)00035-4. [DOI] [Google Scholar]
- Guéguen P, Cornou C, Garambois S, Banton J. On the limitation of the H/V spectral ratio using seismic noise as an exploration tool: application to the Grenoble valley (France), a small apex ratio basin. Pure Appl Geophys. 2007;164(1):115–134. doi: 10.1007/s00024-006-0151-x. [DOI] [Google Scholar]
- Guillier, B., Cornou, C., Kristek, J., Moczo, P., Bonnefoy-Claudet, S., Bard, P. Y., Fäh, D. (2006). Simulation of seismic ambient vibrations: does the H/V provide quantitative information in 2D-3D structures. In Proceedings of the 3rd international symposium on the effects of surface geology on seismic motion, Grenoble, France, 30
- Grippa A, Bianca M, Tropeano M, et al (2011) Use of the HVSR method to detect buried paleomorphologies (filled incised-valleys) below a coastal plain: the case of the Metaponto plain (Basilicata, southern Italy). Bollettino di Geofisica Teorica ed Applicata, 52(2)
- Guillier B, Chatelain JL, Bonnefoy-Claudet S, Haghshenas E. Use of ambient noise: from spectral amplitude variability to H/V stability. J Earthquake Eng. 2007;11(6):925–942. doi: 10.1080/13632460701457249. [DOI] [Google Scholar]
- Guillier B, Cornou C, Kristek J, et al (2006). Simulation of seismic ambient vibrations: does the H/V provide quantitative information in 2D-3D structures. In Proceedings of the 3rd international symposium on the effects of surface geology on seismic motion, Grenoble, France (Vol. 30).
- Guillier B, Atakan K, Chatelain JL et al (2008) Influence of instruments on the H/V spectral ratios of ambient vibrations. Bull Earthq Eng 6(1):3–31
- Guillier B, Chatelain J-L, Tavera H, Perfettini H, Zamalloa A, Herrera B (2014) Establishing empirical period formula for RC buildings in Lima, Peru: evidence for the impact of both the 1974 Lima earthquake and the application of the Peruvian seismic code on high-rise buildings. Seis Res Lett 85:1308–1315
- Gutenberg B. Microseisms. In Advances in Geophysics, Elsevier. 1958;5:53–92. doi: 10.1016/S0065-2687(08)60075-8. [DOI] [Google Scholar]
- Haghshenas E, Bard PY, Theodulidis N, et al. Empirical evaluation of microtremor H/V spectral ratio. Bull Earthq Eng. 2008;6(1):75–108. doi: 10.1007/s10518-007-9058-x. [DOI] [Google Scholar]
- Hallal MM, Cox B. An H/V geostatistical approach for building pseudo-3D Vs models to account for spatial variability in ground response analyses I: model development. Earthq Spectra. 2021;37(3):2013–2040. doi: 10.1177/8755293020981989. [DOI] [Google Scholar]
- Harmon J, Hashash YM, Stewart JP, Rathje EM, Campbell KW, Silva WJ, Ilhan O (2019) Site amplification functions for central and eastern North America–part II: modular simulation-based models. Earthq Spectra 35(2):815–847
- Hassani B, Atkinson GM. Site-effects model for Central and Eastern North America based on peak frequency and average shear-wave velocity. Bull Seis Soc Am. 2018;108:338–350. doi: 10.1785/0120170061. [DOI] [Google Scholar]
- Hassani B, Yong A, Atkinson GM, Feng T, Meng L. Comparison of site dominant frequency from earthquake and microseismic data in California. Bull Seis Soc Am. 2019;109(3):1034–1040. doi: 10.1785/0120180267. [DOI] [Google Scholar]
- Herak M. ModelHVSR—a Matlab® tool to model horizontal-to-vertical spectral ratio of ambient noise. Comput Geosci. 2008;34:1514–1526. doi: 10.1016/j.cageo.2007.07.009. [DOI] [Google Scholar]
- Hinzen K-G, Weber B, Scherbaum F. On the resolution of H/V measurements to determine sediment thickness, a case study across a normal fault in the Lower Rhine embayment. Germany J Earthquake Eng. 2004;8(6):909–926. [Google Scholar]
- Hobiger, M., Bard, P. Y., Cornou, C., Le Bihan, N. (2009). Single station determination of Rayleigh wave ellipticity by using the random decrement technique (RayDec). Geophs Res Lett, 36(14)
- Hobiger M, Cornou C, Wathelet M, et al. Ground structure imaging by inversions of Rayleigh wave ellipticity: sensitivity analysis and application to European strong-motion sites. Geophys J Int. 2013;192(1):207–229. doi: 10.1093/gji/ggs005. [DOI] [Google Scholar]
- Horike M, Zhao B, Kawase H. Comparison of site response characteristics inferred from microtremors and earthquake shear waves. Bull Seis Soc Am. 2001;91:1526–1536. doi: 10.1785/0120000065. [DOI] [Google Scholar]
- Hunter JA, Crow HL, Brooks GR, et al. Seismic site classification and site period mapping in the Ottawa area using geophysical methods. Geological Survey of Canada, Open File. 2010;6273:1–80. [Google Scholar]
- Hunter JA, Crow HL, Dietiker B, Pugin A, Brewer K, Cartwright T. A compilation of microtremor horizontal-to-vertical spectral ratios (HVSRs) and borehole shear-wave velocities of unconsolidated sediments in south-central Ontario. Geological Survey of Canada, Open File. 2020;8725:1–12. [Google Scholar]
- Ibs-von Seht M, Wohlenberg J. Microtremor measurements used to map thickness of soft sediments. Bull Seis Soc Am. 1999;89(1):250–259. doi: 10.1785/BSSA0890010250. [DOI] [Google Scholar]
- Ito E, Nakano K, Nagashima F, Kawase H. A method to directly estimate S-wave site amplification factor from horizontal-to-vertical spectral ratio of earthquakes (eHVSRs) Bull Seis Soc Am. 2020;110:2892–2911. doi: 10.1785/0120190315. [DOI] [Google Scholar]
- Ito, E., Cornou, C., Nagashima, F., Kawase, H. (2021). Estimation of velocity structures in the Grenoble Basin using pseudo earthquake horizontal-to-vertical spectral ratio from microtremors, Bull Seis Soc Am, 111, 10.1785/0120200211
- Jakica, S. (2018). Using passive seismic to estimate the thickness of the Lenora Breakaways, Western Australia. In Proceedings of the5thAustralian Regolith Geoscientists Association Conference, Wallaroo, South Australia, 17–20
- Kanai K, Tanaka T. On microtremors VIII. Bull Earthq Res Inst. 1961;39:97–114. [Google Scholar]
- Kawase H, Sánchez-Sesma FJ, Matsushima S. The optimal use of horizontal-to-vertical spectral ratios of earthquake motions for velocity inversions based on diffuse-field theory for plane waves. Bull Seis Soc Am. 2011;101(5):2001–2014. doi: 10.1785/0120100263. [DOI] [Google Scholar]
- Kawase H, Matsushima S, Satoh T, Sánchez-Sesma FJ. Applicability of theoretical horizontal-to-vertical ratio of microtremors based on the diffuse field concept to previously observed data. Bull Seis Soc Am. 2015;105(6):3092–3103. doi: 10.1785/0120150134. [DOI] [Google Scholar]
- Kawase H, Mori Y, Nagashima F. Difference of horizontal-to-vertical spectral ratios of observed earthquakes and microtremors and its application to S-wave velocity inversion based on the diffuse field concept. Earth, Planets and Space. 2018;70(1):1. doi: 10.1186/s40623-017-0766-4. [DOI] [Google Scholar]
- Kawase Hiroshi, Nagashima F, Nakano K, Mori Y. Direct evaluation of S-wave amplification factors from microtremor H/V ratios: double empirical corrections to “Nakamura” method. Soil Dynamics and Earthquake Engineering. 2019;126:105067. doi: 10.1016/j.soildyn.2018.01.049. [DOI] [Google Scholar]
- Köhler A, Ohrnberger M, Scherbaum F. Assessing the reliability of the modified three-component spatial autocorrelation technique. Geophys J Int. 2007;168:779–796. doi: 10.1111/j.1365-246X.2006.03253.x. [DOI] [Google Scholar]
- Koller, M. G., Chatelain, J. L., Guillier, B., Duval, A. M., Atakan, K., Lacave, C., Bard, P. Y. (2004, August). Practical user guidelines and software for the implementation of the H/V ratio technique: measuring conditions, processing method and results interpretation. In Proceedings of the 13thWorld Conference on Earthquake Engineering, Vancouver, Canada
- Konno K, Ohmachi T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull Seis Soc Am. 1998;88(1):228–241. doi: 10.1785/BSSA0880010228. [DOI] [Google Scholar]
- Ktenidou OJ, Chávez-García FJ, Raptakis D, Pitilakis KD. Directional dependence of site effects observed near a basin edge at Aegion. Greece Bulletin of Earthquake Engineering. 2016;14(3):623–645. doi: 10.1007/s10518-015-9843-x. [DOI] [Google Scholar]
- Lachet C, Bard PY. Numerical and theoretical investigations on the possibilities and limitations of Nakamura’s technique. J Phys Earth. 1994;42(5):377–397. doi: 10.4294/jpe1952.42.377. [DOI] [Google Scholar]
- Ladak S, Molnar S, Palmer S. Multi-method site characterization to verify the hard rock (site class A) assumption at 25 seismograph stations across Eastern Canada. Earthq Spectra. 2021;37(S1):1487–1515. doi: 10.1177/87552930211001076. [DOI] [Google Scholar]
- Landès M, Hubans F, Shapiro NM, Paul A, Campillo M. Origin of deep ocean microseisms by using teleseismic body waves. J Geophys Res. 2010;115:B05302. [Google Scholar]
- Lecocq T, 75 other authors, (2020) Global quieting of high-frequency seismic noise due to COVID-19 pandemic lockdown measures. Science 369:1338–1343 [DOI] [PubMed]
- Lermo J, Chávez-García FJ. Site effect evaluation using spectral ratios with only one station. Bull Seis Soc Am. 1993;83(5):1574–1594. doi: 10.1785/BSSA0830051574. [DOI] [Google Scholar]
- Lermo J, Chávez-García FJ. Are microtremors useful in site response evaluation? Bull Seis Soc Am. 1994;84(5):1350–1364. [Google Scholar]
- Lermo J, Chávez-García FJ. Site effect evaluation at Mexico City: dominant period and relative amplification from strong motion and microtremor records. Soil Dyn Earthq Eng. 1994;13(6):413–423. doi: 10.1016/0267-7261(94)90012-4. [DOI] [Google Scholar]
- Leyton F, Montalva G, Ramírez P. A preliminary study of seismic microzonation of Concepción based on microtremors, geology and damages patterns. Obras y Proyectos. 2012;11:40–46. doi: 10.4067/S0718-28132012000100004. [DOI] [Google Scholar]
- Leyton F, Ruiz S, Sepúlveda SA, Contreras JP, Rebolledo S, Astroza M. Micro-tremors’ HVSR and its correlation with surface geology and damage observed after the 2010 Maule earthquake (MW 8.8) at Talca and Curicó. Central Chile Eng Geol. 2013;161:26–33. [Google Scholar]
- Lontsi AM, Sánchez-Sesma FJ, Molina-Villegas JC, Ohrnberger M, Krüger F. Full microtremor H/V (z, f) inversion for shallow subsurface characterization. Geophys J Int. 2015;202(1):298–312. doi: 10.1093/gji/ggv132. [DOI] [Google Scholar]
- Lontsi AM, García-Jerez A, Molina-Villegas JC, et al. A generalized theory for full microtremor horizontal-to-vertical [H/V(z, f)] spectral ratio interpretation in offshore and onshore environments. Geophys J Int. 2019;218(2):1276–1297. doi: 10.1093/gji/ggz223. [DOI] [Google Scholar]
- Lunedei E, Albarello D. Theoretical HVSR curves from full wavefield modelling of ambient vibrations in a weakly dissipative layered Earth. Geophys J Int. 2010;181(2):1093–1108. [Google Scholar]
- Le Roux Olivier, Cornou Cécile, Jongmans Denis, Schwartz Stéphane. 1-D and 2-D resonances in an Alpine valley identified from ambient noise measurements and 3-D modelling. Geophysical Journal International. 2012;191(2):579–590. doi: 10.1111/j.1365-246X.2012.05635.x. [DOI] [Google Scholar]
- Lunedei E, Albarello D. Horizontal-to-vertical spectral ratios from a full-wavefield model of ambient vibrations generated by a distribution of spatially correlated surface sources. Geophys J Itn. 2015;201(2):1142–1155. doi: 10.1093/gji/ggv046. [DOI] [Google Scholar]
- Lunedei E, Malischewsky P. A review and some new issues on the theory of the H/V technique for ambient vibrations. Geotechnical, Geological and Earthquake Engineering. 2015;39:371–394. doi: 10.1007/978-3-319-16964-4_15. [DOI] [Google Scholar]
- Luzi L, Puglia R, Pacor F, Gallipoli MR, Bindi D, Mucciarelli M. Proposal for a soil classification based on parameters alternative or complementary to VS30. Bull Earthq Eng. 2011;9:1877–1898. doi: 10.1007/s10518-011-9274-2. [DOI] [Google Scholar]
- Malischewsky PG, Scherbaum F. Love’s formula and H/V-ratio (ellipticity) of Rayleigh waves. Wave Motion. 2004;40(1):57–67. doi: 10.1016/j.wavemoti.2003.12.015. [DOI] [Google Scholar]
- Malischewsky PG, Scherbaum F, Lomnitz C, Tuan TT, Wuttke F, Shamir G. The domain of existence of prograde Rayleigh-wave particle motion for simple models. Wave Motion. 2008;45(4):556–564. doi: 10.1016/j.wavemoti.2007.11.004. [DOI] [Google Scholar]
- Maranò S, Hobiger M, Fäh D. Retrieval of Rayleigh wave ellipticity from ambient vibration recordings. Geophys J Int. 2017;209(1):334–352. [Google Scholar]
- Marcillo OE, Carmichael J. The detection of wind-turbine noise in seismic records. Seis Res Lett. 2018;89(5):1826–1837. doi: 10.1785/0220170271. [DOI] [Google Scholar]
- Matsushima S, Hirokawa T, De Martin F, Kawase H, Sánchez-Sesma FJ. The effect of lateral heterogeneity on horizontal-to-vertical spectral ratio of microtremors inferred from observation and synthetics. Bull Seis Soc Am. 2014;104(1):381–393. doi: 10.1785/0120120321. [DOI] [Google Scholar]
- Matsushima S, Kosaka H, Kawase H. Directionally dependent horizontal-to-vertical spectral ratios of microtremors at Onahama, Fukushima, Japan. Earth, Planets and Space. 2017;69(1):96. doi: 10.1186/s40623-017-0680-9. [DOI] [Google Scholar]
- Matsushima, S., Sawa, S., Matsushita, H., Sato, K., Nagashima, F., Masuda, S., Ikeguchi, H. (2019). Subsurface structure of Yatsushiro Plain, Japan inferred from the observed H/V spectral ratio of microtremors. 2019 Seis Soc Am Annual Meeting, 142
- Meza-Fajardo KC, Papageorgiou AS, Semblat J-F. Identification and extraction of surface waves from three-component seismograms based on the normalized inner product. Bull Seis Soc Am. 2015;105(1):210–229. doi: 10.1785/0120140012. [DOI] [Google Scholar]
- Mihaylov D, El Naggar MH, Dineva S. Separation of high-and low-level ambient noise for HVSR: application in city conditions for Greater Toronto area. Bull Seis Soc Am. 2016;106(5):2177–2184. doi: 10.1785/0120150389. [DOI] [Google Scholar]
- Molnar S, Cassidy JF. A comparison of site response techniques using weak-motion earthquakes and microtremors. Earthq Spectra. 2006;22(1):169–188. doi: 10.1193/1.2160525. [DOI] [Google Scholar]
- Molnar S, Ventura CE, Boroschek R, Archila M. Site characterization at Chilean strong-motion stations: comparison of downhole and microtremor shear-wave velocity methods. Soil Dyn Earthq Eng. 2015;79:22–35. doi: 10.1016/j.soildyn.2015.08.010. [DOI] [Google Scholar]
- Molnar S, Cassidy JF, Castellaro S, et al. Application of microtremor horizontal-to-vertical spectral ratio (MHVSR) analysis for site characterization: State of the art. Surv Geophys. 2018;39(4):613–631. doi: 10.1007/s10712-018-9464-4. [DOI] [Google Scholar]
- Molnar S, Assaf J, Sirohey A, Adhikari S. Overview of local site effects and seismic microzonation mapping in Metropolitan Vancouver, British Columbia. Canada Eng Geol. 2020;270:105568. doi: 10.1016/j.enggeo.2020.105568. [DOI] [Google Scholar]
- Moon SW, Subramaniam P, Zhang Y, Vinoth G, Ku T. Bedrock depth evaluation using microtremor measurement: empirical guidelines at weathered granite formation in Singapore. Journal of Applied Geophysics. 2019;171:103866. doi: 10.1016/j.jappgeo.2019.103866. [DOI] [Google Scholar]
- Moscatelli M, Albarello D, Scarascia Mugnozza G, Dolce M. The Italian approach to seismic microzonation. Bull Earthq Eng. 2020;18:5425–5440. doi: 10.1007/s10518-020-00856-6. [DOI] [Google Scholar]
- Motazedian D, Khaheshi Banab K, Hunter JA, Sivathavalan S, Crow H, Brooks G. Comparison of site periods derived from different evaluation methods. Bull Seis Soc Am. 2011;101(6):2942–2954. doi: 10.1785/0120100344. [DOI] [Google Scholar]
- Mucciarelli M, Monachesi G. A quick survey of local amplifications and their correlation with damage observed during the Umbro-Marchesan (Italy) earthquake of September 26, 1997. J Earthquake Eng. 1998;2(2):325–337. [Google Scholar]
- Mucciarelli M, Gallipoli MR, Arcieri M. The stability of the horizontal-to-vertical spectral ratio of triggered noise and earthquake recordings. Bull Seis Soc Am. 2003;93(3):1407–1412. doi: 10.1785/0120020213. [DOI] [Google Scholar]
- Matsushima S, Sawa S, Matsushita H, et al (2019). Subsurface structure of Yatsushiro Plain, Japan inferred from the observed H/V spectral ratio of microtremors. 2019 Seis Soc Am Annual Meeting, 142.
- Mucciarelli, M., Gallipoli, M. R. (2004). The HVSR technique from microtremor to strong motion: empirical and statistical considerations. In Proceedings of 13th World Conference of Earthquake Engineering, Vancouver, Canada
- Mucciarelli M, Gallipoli MR, Di Giacomo D, Di Nota F, Nino E (2005) The influence of wind on measurements of seismic noise. Geophys J Int 161(2):303–308
- Mucciarelli M, Gallipoli MR (2004, August). The HVSR technique from microtremor to strong motion: empirical and statistical considerations. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, Paper (Vol. 45).
- Mucciarelli M, Herak M, Cassidy JF (2009) Increasing seismic safety by combining engineering technologies and seismological data. Springer, Dordrecht
- Nakamura Y (1989) A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Quarterly Report of Railway Technical Research 30(1):25–33
- Nakamura Y (1996) Real-time information systems for seismic hazard mitigation UrEDAS, HERAS and PIC, Q.R. of RTRI, 37–3, 112-127
- Nakamura, Y. (2000) Clear identification of fundamental idea of Nakamura’s technique and its applications. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand
- Nakamura, Y. (2008) On the H/V spectrum. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China
- Nakamura, Y. (2014). A modified estimation method for amplification factor of ground and structures using the H/V spectral ratio. In Proceedings of the 2ndWorkshop on Dynamic Interaction of Soil and Structure’12, 273–284
- Nogoshi M, Igarashi T (1970) On the amplitude characteristics of ambient noise (part 1). J Atmos Oceanic Technol 23:281–303
- Özalaybey S, Zor E, Ergintav S, Tapırdamaz MC (2011) Investigation of 3-D basin structures in the İzmit Bay area (Turkey) by single-station microtremor and gravimetric methods. Geophys J Int 186(2):883–894
- Nakamura Y (1996) Real-time information systems for seismic hazards mitigation UrEDAS, HERAS and PIC. Quarterly Report-Rtri, 37(3), 112–127
- Nakamura Y (2008) On the H/V spectrum. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China
- Nakamura Y (2000, January). Clear identification of fundamental idea of Nakamura’s technique and its applications. In In Proceedings of the 12th World Conference on Earthquake Engineering (Vol. 2656). New Zealand: Auckland
- Nogoshi M, Igarashi T (1971) On the amplitude characteristics of ambient noise (part 2). J Atmos Oceanic Technol 24:26–40
- Okada H, Suto K (2003) The microtremor survey method. Society of Exploration Geophysicists DOI 10(1190/1):9781560801740
- Oliveira CS, Navarro M (2010) Fundamental periods of vibration of RC buildings in Portugal from in-situ experimental and numerical techniques. Bull Earthq Eng 8(3):609–642
- Omori, F. (1909). Report on the observation of pulsatory oscillations in Japan, Bulletin of the Imperial Earthquake Investigation Committee, The University of Tokyo 1909–09–14, 3(1), 1–35
- Oubaiche EH, Chatelain J-L, Hellel M, Wathelet M, Machane D, Bensalem R, Bouguern A (2016) The relationship between ambient vibration H/V and SH transfer function: Some experimental results. Seis Res Lett 87:1112–1119
- Özalaybey S, Zor E, Ergintav S, Tapırdamaz MC (2011) Investigation of 3-D basin structures in the İzmit Bay area (Turkey) by single-station microtremor and gravimetric methods. Geophys J Int 186(2):883–894
- Parolai S, Galiana-Merino JJ (2006) Effect of transient seismic noise on estimates of H/V spectral ratios. Bull Seis Soc Am 96(1):228–236
- Parolai S, Bindi D, Augliera P (2000) Application of the generalized inversion technique (GIT) to a microzonation study: numerical simulations and comparison with different site-estimation techniques. Bull Seis Soc Am 90(2):286–297
- Parolai, S., Picozzi, M., Richwalski, S. M., Milkereit, C. (2005). Joint inversion of phase velocity dispersion and H/V ratio curves from seismic noise recordings using a genetic algorithm, considering higher modes. Geophys Res Lett, 32(1)
- Parolai S, Picozzi M, Strollo A, Pilz M, Di Giacomo D, Liss B, Bindi D (2009) Are transients carrying useful information for estimating H/V spectral ratios? Increasing Seismic Safety by Combining Engineering Technologies and Seismological Data. Springer, Dordrecht, pp 17–31
- Pastén C, Sáez M, Ruiz S, Leyton F, Salomón J, Poli P (2016) Deep characterization of the Santiago Basin using HVSR and cross-correlation of ambient seismic noise. Eng Geol 201:57–66
- Perret, D. (2015). Single station H/V technique. In Shear wave velocity measurement guidelines for Canadian seismic site characterization in soil and rock, (ed.) J.A. Hunter and H.L. Crow; Natural Resources Canada, Earth Sciences Sector, Information Product 110 (English and French), 78–84; 90–93
- Perton M, Spica Z, Caudron C (2017) Inversion of the horizontal to vertical spectral ratio in presence of strong lateral heterogeneity. Geophys J Int 212(2):930–941
- Picozzi M, Parolai S, Albarello D (2005) Statistical analysis of noise horizontal-to-vertical spectral ratios (HVSR). Bull Seis Soc Am 95(5):1779–1786
- Pilz M, Parolai S, Leyton F, Campos J, Zschau J (2009) A comparison of site response techniques using earthquake data and ambient seismic noise analysis in the large urban areas of Santiago de Chile. Geophys J Int 178(2):713–728
- Pilz M, Parolai S (2014) Statistical properties of the seismic noise field: influence of soil heterogeneities. Geophys J Int 199(1):430–440
- Piña-Flores J, Perton M, García-Jerez A et al (2017) The inversion of spectral ratio H/V in a layered system using the diffuse field assumption (DFA). Geophys J Int 208(1):577–588
- Piña-Flores J, Cárdenas-Soto M, García-Jerez A, et al (2020). Use of peaks and troughs in the horizontal-to-vertical spectral ratio of ambient noise for Rayleigh-wave dispersion curve picking. J Appl Geophy, 177, 104024.
- Piña-Flores J, Cárdenas-Soto M, García-Jerez A, Campillo M, Sánchez-Sesma FJ (2021) The search of diffusive properties in ambient seismic noise. Bull Seis Soc Am 111(3):1650–1660
- Pitilakis K, Riga E, Anastasiadis A (2013) New code site classification, amplification factors and normalized response spectra based on a worldwide ground-motion database. Bull Earthq Eng, 11(4):925–966
- Pinnegar CR (2006) Polarization analysis and polarization filtering of three-component signals with the time—Frequency S transform. Geophys J Int 165(2):596–606
- Poggi V, Fäh D (2010) Estimating Rayleigh wave particle motion from three-component array analysis of ambient vibrations. Geophys J Int 180(1):251–267
- Poggi V, Fäh D, Burjanek J, Giardini D (2012) The use of Rayleigh-wave ellipticity for site-specific hazard assessment and microzonation: application to the city of Lucerne. Switzerland Geophys J Int 188(3):1154–1172
- Pratt TL (2018) Characterizing and imaging sedimentary strata using depth-converted spectral ratios: an example from the Atlantic Coastal Plain of the eastern United States. Bull Seis Soc Am 108(5A):2801–2815
- Puglia R, Albarello D, Gorini A, Luzi L, Marcucci S, Pacor F (2011) Extensive characterization of Italian accelerometric stations from single-station ambient-vibration measurements. Bulletin Earthquake Engineering 9:1821–1838
- Raptakis D, Theodulidis N, Pitilakis K (1998) Data analysis of the Euroseistest strong motion array in Volvi (Greece): standard and horizontal-to-vertical spectral ratio techniques. Earthq Spectra 14:203–224
- Raptakis D, Chávez-García, F. J., Makra, K., Pitilakis, K. (2000) Site effects at Euroseistest: 1. Determination of the valley structure and confrontation of observations with 1D analysis. Soil Dyn Earthq Eng 19:1–22
- Rivet D, Campillo M, Sanchez-Sesma F, Shapiro NM, Singh SK (2015) Identification of surface wave higher modes using a methodology based on seismic noise and coda waves. Geophys J Int 203(2):856–868
- Roca A, Oliveira C (2001). Introduction. Pure Appl Geophys. 158(12), 2291–2294. 10.1007/PL00001170
- Rong M, Li H, Yu Y (2019) The difference between horizontal-to-vertical spectra ratio and empirical transfer function as revealed by vertical arrays. PLoS One 14(1):e0210852 [DOI] [PMC free article] [PubMed]
- Roten D, Fäh D (2007) A combined inversion of Rayleigh wave dispersion and 2-D resonance frequencies. Geophys J Int 168(3):1261–1275
- Roten D, Fäh D, Cornou C, Giardini D (2006) Two-dimensional resonances in Alpine valleys identified from ambient vibration wavefields. Geophys J Int 165(3):889–905
- Sánchez-Sesma FJ (2017) Modeling and inversion of the microtremor H/V spectral ratio: physical basis behind the diffuse field approach. Earth, Planets and Space 69(1):92
- Sánchez-Sesma FJ, Rodríguez M, Iturrarán-Viveros U et al (2011) A theory for microtremor H/V spectral ratio: application for a layered medium. Geophys J Int 186(1):221–225
- Satoh T, Kawase H, Matsushima S (2001) Estimation of S-wave velocity structures in and around the Sendai basin, Japan, using array records of microtremors. Bull Seism Soc Am 91:206–218
- SESAME Project (2004) Guidelines for the implementation of the H/V spectral ratio technique on ambient vibrations measurements, processing and interpretation. http://sesame-fp5.obs.ujf-grenoble.fr/Papers/HV_User_Guidelines.pdf
- Savage MK, Lin F-C, Townend J (2013) Ambient noise cross-correlation observations of fundamental and higher-mode Rayleigh wave propagation governed by basement resonance. Geophys Res Lett 40(14):3556–3561
- Scheib A, Morris P, Murdie R, Piane CD (2016) A passive seismic approach to estimating the thickness of sedimentary cover on the Nullarbor Plain. Western Australia Australian J Earth Sci 63(5):583–598
- Strollo A, Parolai S, Jäckel KH, Marzorati S, Bindi D (2008) Suitability of short-period sensors for retrieving reliable H/V peaks for frequencies less than 1 Hz. Bull Seis Soc Am 98(2):671–681
- Scherbaum F, Hinzen K-G, Ohrnberger M (2003) Determination of shallow shear wave velocity profiles in the Cologne, Germany area using ambient vibrations. Geophys J Int 152(3):597–612
- Sgattoni G, Castellaro S (2020) Detecting 1-D and 2-D ground resonances with a single-station approach. Geophys J Int 223(1):471–487
- Smith N, Reading A, Asten M, Funk C (2013) Constraining depth to basement for mineral exploration using microtremor: a demonstration study from remote inland Australia. Geophysics 78:B227–B242
- Socco LV, Strobbia C (2004) Surface-wave method for near-surface characterization: a tutorial. Near Surface Geophysics 2(4):165–185
- Spica Z, Caudron C, Perton M et al (2015) Velocity models and site effects at Kawah Ijen volcano and Ijen caldera (Indonesia) determined from ambient noise crosscorrelations and directional energy density spectral ratios. Journal of Vulcanology and Geothermal Research 302:173–189
- Spica ZJ, Perton M, Nakata N, Liu X, Beroza GC (2017) Site characterization at Groningen gas field area through joint surface borehole H/V analysis. Geophys J Int 212(1):412–421
- Spica ZJ, Perton M, Nakata N, Liu X, Beroza GC (2018) Shallow vs imaging of the Groningen area from joint inversion of multi-mode surface waves and H/V spectral ratios. Seis Res Lett 89:1720–1729
- Stephenson W, Asten MW, Odum JK, Frankel AD (2019) Shear-wave velocity in the Seattle basin to 2 km depth characterized with the krSPAC microtremor array method: insights for urban basin-scale imaging. Seis Res Lett 90:1230–1242
- Taniguchi E, Sawada K (1979) Attenuation with distance of traffic-induced vibrations. Soils Found 19(2):16–28
- Tchawe FN, Froment B, Campillo M, Margerin L (2020) On the use of the coda of seismic noise autocorrelations to compute H/V spectral ratios. Geophys J Int 220(3):1956–1964
- Teague DP, Cox BR, Rathje ER (2018) Measured vs. predicted site response at the Garner Valley downhole array considering shear wave velocity uncertainty from borehole and surface wave methods. Soil Dyn and Earthquake Eng 113(10):339–355
- Theodoulidis N, Bard P-Y, Archuleta R, Bouchon M (1996) Horizontal-to-vertical spectral ratio and geological conditions: the case of Garner Valley Downhole Array in southern California. Bull Seis Soc Am 86:306–319
- Theodoulidis N, Cultrera G, Cornou C et al (2018) Basin effects on ground motion: the case of a high-resolution experiment in Cephalonia (Greece). Bull Earthq Eng 16(2):529–560
- Theodoulidis N, Bard PY (1998). Dependence of fmax on site geology: a preliminary study of Greek strong-motion data. In Proceedings of the 11th European Conference on Earthquake Engineering.
- Tsai NC, Housner GW (1970) Calculation of surface motions of a layered half-space. Bull Seis Soc Am 60(5):1625–1651
- Tuan TT, Scherbaum F, Malischewsky PG (2011) On the relationship of peaks and troughs of the ellipticity (H/V) of Rayleigh waves and the transmission response of single layer over half-space models. Geophys J Int 184(2):793–800
- Tün M, Pekkan E, Özel O, Guney Y (2016) An investigation into the bedrock depth in the Eskisehir Quaternary Basin (Turkey) using the microtremor method. Geophys J Int 207:589–607
- Uebayashi H (2003) Extrapolation of irregular subsurface structures using the horizontal-to-vertical spectral ratio of long-period microtremors. Bull Seis Soc Am 93(2):570–582
- Uebayashi H, Kawabe H, Kamae K (2012) Reproduction of microseism H/V spectral features using a three-dimensional complex topographical model of the sediment-bedrock interface in the Osaka sedimentary basin. Geophys J Int 189(2):1060–1074
- Urzúa A, Dobry R, Christian JT (2017) Is harmonic averaging of shear wave velocity or the simplified Rayleigh method appropriate to estimate the period of a soil profile ? Earthq Spectra 33(3):895–915
- Vallianatos F, Hloupis G (2009) HVSR technique improvement using redundant wavelet transform. Increasing Seismic Safety by Combining Engineering Technologies and Seismological Data. Springer, Dordrecht, pp 117–137
- van Der Baan M (2009) The origin of SH-wave resonance frequencies in sedimentary layers. Geophys J Int 178:1587–1596
- Vantassel J (2020). jpvantassel/hvsrpy: latest (Concept). Zenodo. 10.5281/zenodo.3666956
- Vantassel J, Cox B, Wotherspoon L, Stolte A (2018) Mapping depth to bedrock, shear stiffness, and fundamental site period at Centre Port, Wellington, using surface-wave methods: implications for local seismic site amplification. Bull Seis Soc Am 108(3B):1709–1721
- Volant P, Cotton F, Gabriel JC (1998). Estimation of site response using the H/V method. Applicability and limits of this technique on Garner Valley downhole array dataset (California). In Proceedings of the 11th European Conference on Earthquake Engineering.
- Volant P, Cotton F, Gabriel JC (1998). Estimation of site response using the H/V method. Applicability and limits of this technique on Garner Valley downhole array dataset (California). In Proceedings of the 11th European Conference on Earthquake Engineering.
- Wang, P. (2020). Predictability and repeatability of non-ergodic site response for diverse geological conditions, PhD Thesis, UCLA, Dept. Civil Engineering, 210 p
- Wathelet M, Jongmans D, Ohrnberger M (2004) Surface-wave inversion using a direct search algorithm and its application to ambient vibration measurements. Near Surface Geophysics 2(4):211–221
- Wathelet M, Guillier B, Roux P, Cornou C, Ohrnberger M (2018) Rayleigh wave three-component beamforming: signed ellipticity assessment from high-resolution frequency-wavenumber processing of ambient vibration arrays. Geophys J Int 215(1):507–523
- Wathelet M, Chatelain JL, Cornou C, Giulio GD, Guillier B, Ohrnberger M, Savvaidis A (2020) A user-friendly open-source tool set for ambient vibration processing. Seis Res Lett 91(3):1878–1889
- Weaver RL, Yoritomo JY (2018) Temporally weighting a time varying noise field to improve Green function retrieval. J Acous Soc Am 143(6):3706–3719. 10.1121/1.5043406 [DOI] [PubMed]
- Wen KL, Bard PY, Sánchez-Sesma FJ, Higashi S, Iwata T, Maeda T (2018) Special issue “Effect of surface geology on seismic motion: challenges of applying ground motion simulation to seismology and earthquake engineering.” Earth, Planets and Space 70(1):178
- Wollery WW, Street R (2002) 3D near-surface soil response from H/V ambient-noise ratios. Soil Dyn and Earthquake Eng 22(9–12):865–876
- Wotherspoon LM, Orense RP, Bradley BA, Cox BR, Wood CM, Green RA (2015) Soil profile characterisation of Christchurch central business district strong motion stations. Bull New Zealand Soc Earthquake Eng 48(3):147–157
- Wu H, Masaki K, Irikura K, Sánchez-Sesma FJ (2017) Application of a simplified calculation for full waves microtremor H/V based on the diffuse field approximation to identify underground velocity structures, Earth. Planets and Space 69:162
- Yamamoto, H. (2000). Estimation of shallow S-wave velocity structures from phase velocities of Love-and Rayleigh-waves in microtremors. In Proceedings of the 12th World Conference on Earthquake Engineering. Auckland, New Zealand
- Yamanaka H, Takemura M, Ishida H, Niwa M (1994) Characteristics of long-period microtremors and their applicability in exploration of deep sedimentary layers. Bull Seis Soc Am 84(6):1831–1841
- Yong A, Martin A, Stokoe K, Diehl J (2013) ARRA-funded VS30 measurements using multi-technique approach at strong-motion stations in California and Central-Eastern United States. U.S. Geological Survey, Open File Report 2013–1102:1–60
- Zhao JX, Irikura K, Zhang J et al (2006) An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio. Bull Seis Soc Am 96(3):914–925
- Zhu C, Pilz M, Cotton F (2020) Evaluation of a novel application of earthquake HVSR in site-specific amplification estimation. Soil Dyn and Earthquake Eng 139:106301
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable.
Not applicable.