Abstract

Metformin hydrochloride (MET·HCl) is one of the most widely used oral hypoglycemic drugs in the world. In addition to hypoglycemic effects, MET·HCl also has anti-inflammatory, anti-tumor, anti-aging, and other effects, showing good efficacy and safety of single and combined treatment. The solubility of MET·HCl in water, water + N,N-dimethylformamide, water + acetonitrile, and water + n-propanol was measured by the gravimetric method under atmospheric pressure at temperatures ranging from 283.15 to 323.15 K. The solubility of MET·HCl has a positive correlation with temperature and water content. The experimental solubility data in binary solvents was correlated by the modified Apelblat model, CNIBS/R-K model, Apelblat–Jouyban–Acree model, and λh model. By comparing the average ARD % values of the four models, it is found that the modified Apelblat model (ARD % = 1.26) provides better correlation. Hansen solubility parameters and apparent thermodynamic parameters were calculated to analyze the solubility behavior, indicating that the dissolution process is endothermic and entropically favorable.
1. Introduction
Metformin hydrochloride (MET·HCl, C4H11N5) is a first-line drug for the treatment of type 2 diabetes (non-insulin-dependent diabetes), and it is also one of the most widely used oral hypoglycemic drugs in the world.1−3 The chemical structure is shown in Figure 1. Compared with metformin, MET·HCl is more stable and easier to be absorbed by the body. It can reduce the absorption of glucose in the intestine and increase the uptake of glucose from the blood to the tissues. Meanwhile, it can reduce the production of glucose in the liver and increase insulin sensitivity.
Figure 1.

Molecular structure of MET·HCl.
Crystallization refers to the process of precipitation of solids from solution and is a commonly used separation method. In industrial production, the crystallization process is the key operation to purify MET·HCl. Solubility data is the basis for designing the crystallization process. At present, there are some reports on the solubility of MET·HCl. Benmessaoud et al.4 roughly measured the solubility of MET·HCl in 13 pure solvents (water, dichloromethane, 1-pentanol, 1-propanol, acetone, dimethyl sulfoxide, ethanol, ethylene glycol, formamide, methanol, tetrahydrofuran, toluene, and 1-octanol). Our previous work measured the solubility of MET·HCl (form A)5 in four binary solvents (water + acetone, water + methanol, water + ethanol, and water + isopropanol) by the gravimetric method.6 To extend the solubility database, we explored the solid–liquid equilibrium of MET·HCl in other mixed solvents.
In this work, we determined the solubility of MET·HCl in water, water + N,N-dimethylformamide (DMF), water + acetonitrile, and water + propanol at the temperature ranging from 283.15 to 323.15 K by the gravimetric method. In order to verify the reliability of the data and expand the application, the data were correlated by the modified Apelblat model,7,8 CNIBS/R-K model,8,9 Apelblat–Jouyban–Acree model,10−12 and λh model.13−15
2. Thermodynamic Models
2.1. Modified Apelblat Model
The modified Apelblat model16 is an accurate semiempirical equation which expresses the relationship between solubility and temperature. It is expressed by eq 1
| 1 |
where x1 is the mole fraction solubility of MET·HCl, T is the absolute temperature, and A, B, and C are the empirical constants.
2.2. CNIBS/R-K Model
The CNIBS/R-K model was proposed by Acree et al.17 which expressed the relationship between isothermal mole fraction solubility of binary solvent mixture and solvent composition. It is calculated by eq 2
| 2 |
where x1 is the mole fraction solubility of the solute; x20 and x30 are the initial mole fraction of the solvent mixture; XA and XB refer to the saturated mole solubility of the solute in the corresponding pure solvent. Si and n are the model parameters.
For binary solvents with n = 2, eq 2 can be simplified to eq 3
| 3 |
The b1–b5 were used to replace the constant parameters, and eq 3 can be simplified to eq 4(18)
| 4 |
2.3. Apelblat–Jouyban–Acree Model
The relationship between the solubility of solute, temperature, and initial component in binary mixed solvents was represented by the Apelblat–Jouyban–Acree model which was proposed by Jouyban Gharamaleki and his co-workers in 1988. The model is calculated by eq 5(19)
| 5 |
where x20 and x30 represent the initial molecular fraction composition of the binary solvent mixture without the solute. XA and XB are the mole fraction solubility of solute in the pure solvent, and Ji is the model constant.
For binary solvents with n = 2, eq 5 can be simplified to eq 6
 |
6 |
The A0–A8 were used to replace the constant parameters, and eq 6 can be simplified to eq 7(20)
 |
7 |
2.4. λh Model
The λh model was proposed to describe the solubility behavior of solute in solution. It can be calculated as follows21
| 8 |
where λ and h are two equation parameters and Tm is the melting temperature of the solute. The x1 is the mole fraction solubility of solute, and T is the test temperature.
2.5. Hansen Solubility Parameter
The Hansen solubility parameter (HSP)22−25 is made up of three parts: dispersion solubility parameter (δd), polar solubility parameter (δp), and hydrogen bond solubility parameter (δh). The total HSP can be calculated by eq 9
| 9 |
In binary solvent, the δmix was obtained from eq 10
| 10 |
2.6. Apparent Thermodynamics
Dissolution behavior of MET·HCl in the three binary solvents is determined by thermodynamic parameters. The parameters can be calculated by the Gibbs and van’t Hoff equations, and the modified van’t Hoff equation is shown as follows26
 |
11 |
where x1 is the mole fraction solubility of MET·HCl; R is the ideal gas constant; and T is the absolute temperature (K). Thm is the mean harmonic temperature which can calculated by eq 12(27)
| 12 |
where n is the number of temperatures studied. By plotting lnx1 against 1/T – 1/Thm, the ΔG and ΔS values are calculated as follows28
| 13 |
| 14 |
For binary solvents, the enthalpy (%ζH) and entropy (%ζTS) can compare the relative contributions and they are given as follows28
| 15 |
| 16 |
2.7. Data Correlation
The average relative deviation (ARD %) and root-mean-square deviation (rmsd) can evaluate the accuracy of thermodynamic model. They are shown as follows
| 17 |
| 18 |
3. Results and Discussion
3.1. Characterization of MET·HCl
The residual solids in different solvent mixtures and raw material of MET·HCl were determined by X-ray powder diffraction (XRPD) and are shown in Figure 2. The main peaks are mainly at 12.13, 17.42, 24.51, and 37.05° which are consistent with the crystal form A previously reported in the literature.29,30 The positions of main peaks have no change, demonstrating that no polymorphic transformation or solvate formation occurred during the whole experiment.31,32 The same XRPD patterns of all solid samples also indicate that HCl did not lost during the entire experiments. The properties of liquid such as pH values were also analyzed, and the results verified that the excess solid could not release HCl into the solution.6
Figure 2.

XRPD patterns of raw MET·HCl and excess MET·HCl in different solvents.
The thermogravimetry (TGA) and differential scanning calorimetry (DSC) curves of MET·HCl obtained in this study are presented in Figure 3. It can be seen from Figure 3 that the values of the onset melting temperature are 498.15 K, and the fusion happened before the weightless decomposition. Hence, the material could remain stable during the whole experiment.
Figure 3.
Results of TGA and DSC analysis of MET·HCl.
3.2. Solubility Results of MET·HCl
In order to verify the accuracy of our experiment, we compared the solubility in pure water at 293.15 and 313.15 K with the data of published articles.4,6 The result is shown in Table S5. As shown in Table S5, our solubility data is credible. The solubility data of MET·HCl in three binary (water + DMF, water + acetonitrile, and water + n-propanol) solvents and water are listed in Tables 1–3. The solubility of MET·HCl in three pure solvents, including DMF, acetonitrile, and n-propanol, is very small. When the content of these three organic solvents in the binary mixed solvent is high, the solubility data is still very small, which is easy to cause errors. In order to maintian the accuracy, we only determined the data that the mole fraction of water is higher than 0.3. Figures 4–6 can display intuitively the relationship between the solubility and temperature as well as water content.
Table 1. Experimental and Fitted Solubility Data of MET·HCl in Water + DMF (P = 0.1 MPa)a,b.
| 103 x1exp | 103x1apelblat | 103x1CNIBS | 103x1AJA | 103x1λh | ||
|---|---|---|---|---|---|---|
| 283.15 K | ||||||
| 0.30 | 5.572 | 5.932 | 5.556 | 5.674 | 5.540 | |
| 0.40 | 8.019 | 8.100 | 8.076 | 8.158 | 7.938 | |
| 0.50 | 10.79 | 10.83 | 10.77 | 11.03 | 10.45 | |
| 0.60 | 13.91 | 13.82 | 13.85 | 14.31 | 13.61 | |
| 0.70 | 17.92 | 17.84 | 17.61 | 18.02 | 17.70 | |
| 0.80 | 21.32 | 21.07 | 22.18 | 22.09 | 20.96 | |
| 0.90 | 27.87 | 27.71 | 27.08 | 26.25 | 27.75 | |
| 1.00 | 30.45 | 30.27 | 30.66 | 29.83 | 30.92 | |
| 288.15 K | ||||||
| 0.30 | 6.557 | 6.208 | 6.532 | 6.059 | 6.070 | |
| 0.40 | 8.860 | 8.795 | 8.949 | 8.774 | 8.719 | |
| 0.50 | 11.81 | 11.78 | 11.79 | 11.96 | 11.63 | |
| 0.60 | 15.36 | 15.33 | 15.23 | 15.66 | 15.25 | |
| 0.70 | 19.71 | 19.88 | 19.42 | 19.91 | 19.82 | |
| 0.80 | 23.32 | 23.51 | 24.37 | 24.65 | 23.48 | |
| 0.90 | 30.68 | 30.94 | 29.67 | 29.59 | 30.97 | |
| 1.00 | 33.85 | 34.32 | 34.14 | 34.02 | 34.62 | |
| 293.15 K | ||||||
| 0.30 | 7.052 | 6.571 | 7.015 | 6.518 | 6.637 | |
| 0.40 | 9.470 | 9.560 | 9.634 | 9.488 | 9.557 | |
| 0.50 | 13.05 | 12.87 | 12.83 | 13.02 | 12.90 | |
| 0.60 | 16.57 | 17.01 | 16.73 | 17.16 | 17.04 | |
| 0.70 | 22.07 | 22.13 | 21.46 | 21.98 | 22.14 | |
| 0.80 | 25.70 | 26.19 | 27.02 | 27.43 | 26.22 | |
| 0.90 | 34.35 | 34.43 | 33.15 | 33.20 | 34.44 | |
| 1.00 | 38.75 | 38.66 | 39.09 | 38.52 | 38.63 | |
| 298.15 K | ||||||
| 0.30 | 7.284 | 7.030 | 7.302 | 7.061 | 7.245 | |
| 0.40 | 10.59 | 10.40 | 10.44 | 10.31 | 10.46 | |
| 0.50 | 13.83 | 14.11 | 14.23 | 14.21 | 14.28 | |
| 0.60 | 19.11 | 18.87 | 18.80 | 18.83 | 18.98 | |
| 0.70 | 24.79 | 24.59 | 24.26 | 24.25 | 24.65 | |
| 0.80 | 29.41 | 29.11 | 30.61 | 30.44 | 29.19 | |
| 0.90 | 38.36 | 38.21 | 37.46 | 37.09 | 38.20 | |
| 1.00 | 43.60 | 43.25 | 43.82 | 43.34 | 42.97 | |
| 303.15 K | ||||||
| 0.30 | 7.469 | 7.5957 | 7.480 | 7.698 | 7.896 | |
| 0.40 | 11.62 | 11.331 | 11.51 | 11.26 | 11.42 | |
| 0.50 | 15.70 | 15.52 | 16.03 | 15.56 | 15.77 | |
| 0.60 | 21.33 | 20.93 | 21.08 | 20.68 | 21.09 | |
| 0.70 | 27.49 | 27.28 | 26.93 | 26.73 | 27.37 | |
| 0.80 | 32.52 | 32.30 | 33.79 | 33.70 | 32.40 | |
| 0.90 | 42.40 | 42.27 | 41.42 | 41.26 | 42.25 | |
| 1.00 | 48.33 | 48.09 | 48.58 | 48.46 | 47.66 | |
| 308.15 K | ||||||
| 0.30 | 7.790 | 8.283 | 7.752 | 8.443 | 8.593 | |
| 0.40 | 11.71 | 12.35 | 11.90 | 12.35 | 12.45 | |
| 0.50 | 17.17 | 17.12 | 16.95 | 17.08 | 17.37 | |
| 0.60 | 22.87 | 23.21 | 22.85 | 22.75 | 23.37 | |
| 0.70 | 29.89 | 30.22 | 29.58 | 29.46 | 30.31 | |
| 0.80 | 35.87 | 35.78 | 37.10 | 37.22 | 35.87 | |
| 0.90 | 46.52 | 46.64 | 45.27 | 45.71 | 46.60 | |
| 1.00 | 53.25 | 53.17 | 53.63 | 53.88 | 52.71 | |
| 313.15 K | ||||||
| 0.30 | 8.600 | 9.111 | 8.619 | 9.311 | 9.339 | |
| 0.40 | 13.74 | 13.47 | 13.56 | 13.60 | 13.56 | |
| 0.50 | 18.71 | 18.93 | 19.21 | 18.80 | 19.11 | |
| 0.60 | 25.95 | 25.74 | 25.57 | 25.03 | 25.84 | |
| 0.70 | 33.57 | 33.43 | 32.87 | 32.44 | 33.49 | |
| 0.80 | 39.70 | 39.57 | 41.25 | 41.03 | 39.62 | |
| 0.90 | 51.38 | 51.32 | 50.23 | 50.44 | 51.29 | |
| 1.00 | 57.72 | 58.46 | 58.00 | 59.58 | 58.15 | |
| 318.15 K | ||||||
| 0.30 | 10.61 | 10.10 | 10.53 | 10.32 | 10.14 | |
| 0.40 | 14.44 | 14.71 | 14.79 | 15.03 | 14.74 | |
| 0.50 | 21.13 | 20.99 | 20.74 | 20.74 | 20.97 | |
| 0.60 | 28.40 | 28.53 | 28.18 | 27.58 | 28.51 | |
| 0.70 | 36.77 | 36.93 | 36.59 | 35.69 | 36.92 | |
| 0.80 | 43.50 | 43.68 | 45.34 | 45.12 | 43.66 | |
| 0.90 | 56.38 | 56.33 | 54.33 | 55.46 | 56.32 | |
| 1.00 | 63.98 | 63.94 | 64.63 | 65.55 | 63.98 | |
| 323.15 K | ||||||
| 0.30 | 11.56 | 11.28 | 11.52 | 11.50 | 10.99 | |
| 0.40 | 16.41 | 16.07 | 16.58 | 16.67 | 16.01 | |
| 0.50 | 23.31 | 23.32 | 23.25 | 22.93 | 22.98 | |
| 0.60 | 31.61 | 31.61 | 31.34 | 30.40 | 31.40 | |
| 0.70 | 40.85 | 40.74 | 40.41 | 39.25 | 40.62 | |
| 0.80 | 48.08 | 48.15 | 49.95 | 49.52 | 48.01 | |
| 0.90 | 61.57 | 61.67 | 59.76 | 60.77 | 61.71 | |
| 1.00 | 69.87 | 69.59 | 70.41 | 71.76 | 70.25 | |
x1 is
the experimental solubility; the x1apelblat, x1CNIBSx1λh, and x1AJA are the calculated mole solubilities according
to the modified Apelblat model, CNIBS/R-K model, λh model, and Apelblat–Jouyban–Acree model, respectively. 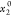 represents the initial mole fraction of
water in the binary aqueous solvent.
represents the initial mole fraction of
water in the binary aqueous solvent.
The standard uncertainty is u(T) = 0.1 K; the relative standard uncertainties ur are ur(P) = 0.01, ur(x1) = 0.05, and ur(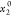 ) = 0.001.
) = 0.001.
Table 3. Experimental and Fitted Solubility Data of MET·HCl in Water + n-propanol (P = 0.1 MPa)a,b.
| 103x1exp | 103x1apelblat | 103x1CNIBS | 103x1AJA | 103x1λh | ||
|---|---|---|---|---|---|---|
| 283.15 K | ||||||
| 0.30 | 3.039 | 2.923 | 3.042 | 2.945 | 3.137 | |
| 0.40 | 5.573 | 5.504 | 5.543 | 5.428 | 5.558 | |
| 0.50 | 8.772 | 8.747 | 8.839 | 8.732 | 8.673 | |
| 0.60 | 12.65 | 12.54 | 12.75 | 12.71 | 12.90 | |
| 0.70 | 17.69 | 17.58 | 17.08 | 17.18 | 17.81 | |
| 0.80 | 20.74 | 20.69 | 21.63 | 21.88 | 20.92 | |
| 0.90 | 26.82 | 26.82 | 26.23 | 26.36 | 27.60 | |
| 1.00 | 30.45 | 30.27 | 30.59 | 29.83 | 30.92 | |
| 288.15 K | ||||||
| 0.30 | 3.337 | 3.589 | 3.339 | 3.571 | 3.721 | |
| 0.40 | 6.406 | 6.513 | 6.372 | 6.491 | 6.547 | |
| 0.50 | 10.07 | 10.25 | 10.18 | 10.32 | 10.21 | |
| 0.60 | 14.52 | 14.79 | 14.53 | 14.89 | 14.98 | |
| 0.70 | 19.96 | 20.36 | 19.37 | 19.96 | 20.48 | |
| 0.80 | 23.61 | 23.87 | 24.63 | 25.23 | 23.98 | |
| 0.90 | 30.66 | 30.97 | 29.93 | 30.19 | 31.34 | |
| 1.00 | 33.85 | 34.32 | 34.03 | 33.99 | 34.62 | |
| 293.15 K | ||||||
| 0.30 | 4.546 | 4.345 | 4.524 | 4.290 | 4.391 | |
| 0.40 | 7.647 | 7.659 | 7.759 | 7.696 | 7.672 | |
| 0.50 | 12.25 | 11.96 | 12.14 | 12.11 | 11.95 | |
| 0.60 | 17.52 | 17.29 | 17.49 | 17.30 | 17.32 | |
| 0.70 | 23.89 | 23.43 | 23.35 | 23.00 | 23.44 | |
| 0.80 | 27.70 | 27.37 | 29.21 | 28.88 | 27.37 | |
| 0.90 | 35.95 | 35.46 | 34.57 | 34.35 | 35.45 | |
| 1.00 | 38.75 | 38.66 | 39.13 | 38.48 | 38.63 | |
| 298.15 K | ||||||
| 0.30 | 5.192 | 5.189 | 5.177 | 5.108 | 5.154 | |
| 0.40 | 8.884 | 8.953 | 8.936 | 9.050 | 8.946 | |
| 0.50 | 13.77 | 13.91 | 13.83 | 14.09 | 13.92 | |
| 0.60 | 19.84 | 20.04 | 19.65 | 19.96 | 19.93 | |
| 0.70 | 26.63 | 26.79 | 26.07 | 26.33 | 26.71 | |
| 0.80 | 31.04 | 31.20 | 32.69 | 32.84 | 31.11 | |
| 0.90 | 40.39 | 40.27 | 38.93 | 38.84 | 39.94 | |
| 1.00 | 43.60 | 43.25 | 43.99 | 43.31 | 42.97 | |
| 303.15 K | ||||||
| 0.30 | 6.205 | 6.121 | 6.185 | 6.033 | 6.021 | |
| 0.40 | 10.58 | 10.41 | 10.66 | 10.56 | 10.38 | |
| 0.50 | 16.32 | 16.11 | 16.37 | 16.28 | 16.14 | |
| 0.60 | 23.30 | 23.05 | 23.01 | 22.86 | 22.83 | |
| 0.70 | 30.63 | 30.47 | 30.17 | 29.95 | 30.33 | |
| 0.80 | 35.62 | 35.37 | 37.34 | 37.11 | 35.22 | |
| 0.90 | 45.43 | 45.37 | 43.85 | 43.66 | 44.83 | |
| 1.00 | 48.33 | 48.09 | 48.76 | 48.46 | 47.66 | |
| 308.15 K | ||||||
| 0.30 | 6.961 | 7.133 | 6.946 | 7.069 | 7.003 | |
| 0.40 | 12.15 | 12.03 | 12.19 | 12.23 | 12.00 | |
| 0.50 | 18.57 | 18.58 | 18.70 | 18.67 | 18.63 | |
| 0.60 | 26.36 | 26.31 | 26.07 | 26.01 | 26.06 | |
| 0.70 | 34.59 | 34.47 | 33.94 | 33.85 | 34.30 | |
| 0.80 | 39.92 | 39.90 | 41.84 | 41.69 | 39.73 | |
| 0.90 | 50.60 | 50.73 | 48.93 | 48.79 | 50.16 | |
| 1.00 | 53.25 | 53.17 | 53.69 | 53.92 | 52.71 | |
| 313.15 K | ||||||
| 0.30 | 8.420 | 8.221 | 8.372 | 8.222 | 8.109 | |
| 0.40 | 13.71 | 13.84 | 13.93 | 14.07 | 13.81 | |
| 0.50 | 21.16 | 21.37 | 21.03 | 21.28 | 21.41 | |
| 0.60 | 29.66 | 29.82 | 29.25 | 29.42 | 29.62 | |
| 0.70 | 38.30 | 38.78 | 38.00 | 38.02 | 38.66 | |
| 0.80 | 44.40 | 44.78 | 46.44 | 46.57 | 44.66 | |
| 0.90 | 55.64 | 56.34 | 53.58 | 54.23 | 55.94 | |
| 1.00 | 57.72 | 58.46 | 58.30 | 59.70 | 58.15 | |
| 318.15 K | ||||||
| 0.30 | 9.323 | 9.375 | 9.286 | 9.496 | 9.354 | |
| 0.40 | 15.81 | 15.84 | 15.98 | 16.07 | 15.83 | |
| 0.50 | 24.20 | 24.49 | 24.13 | 24.10 | 24.52 | |
| 0.60 | 33.53 | 33.57 | 33.26 | 33.08 | 33.56 | |
| 0.70 | 43.57 | 43.43 | 42.88 | 42.48 | 43.44 | |
| 0.80 | 49.98 | 50.02 | 52.32 | 51.74 | 50.03 | |
| 0.90 | 62.41 | 62.16 | 60.28 | 59.98 | 62.20 | |
| 1.00 | 63.98 | 63.94 | 64.54 | 65.77 | 63.98 | |
| 323.15 K | ||||||
| 0.30 | 10.54 | 10.59 | 10.48 | 10.89 | 10.75 | |
| 0.40 | 18.07 | 18.05 | 18.45 | 18.25 | 18.09 | |
| 0.50 | 28.34 | 27.98 | 27.77 | 27.14 | 27.97 | |
| 0.60 | 37.62 | 37.56 | 37.72 | 36.98 | 37.89 | |
| 0.70 | 48.52 | 48.41 | 47.94 | 47.21 | 48.64 | |
| 0.80 | 55.85 | 55.63 | 57.94 | 57.20 | 55.89 | |
| 0.90 | 68.41 | 68.15 | 66.37 | 66.01 | 68.96 | |
| 1.00 | 69.87 | 69.59 | 70.44 | 72.13 | 70.25 | |
x1 is
the experimental solubility; the x1apelblat, x1CNIBSx1λh, and x1AJA are the calculated mole solubilities
according to the modified Apelblat model, CNIBS/R-K model, λh model, and Apelblat–Jouyban–Acree model,
respectively. 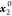 represents the initial mole fraction of
water in the binary aqueous solvent.
represents the initial mole fraction of
water in the binary aqueous solvent.
The standard uncertainty is u(T) = 0.1 K; the relative standard uncertainties ur are ur(P) = 0.01, ur(x1) = 0.05, and ur(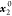 ) = 0.001.
) = 0.001.
Figure 4.

Experimental and correlated solubility of MET·HCl in water + DMF at 283.15 to 323.15 K: the points are experimental data, and the solid lines are correlative with the CNIBS/R-K model.
Figure 6.

Experimental and correlated solubility of MET·HCl in water + n-propanol at 283.15 to 323.15 K: the points are experimental data, and the solid lines are correlative with the CNIBS/R-K model.
Figure 5.

Experimental and correlated solubility of MET·HCl in water + acetonitrile at 283.15 to 323.15 K: the points are experimental data, and the solid lines are correlative with the CNIBS/R-K model.
Table 2. Experimental and Fitted Solubility Data of MET·HCl in Water + Acetonitrile (P = 0.1 MPa)a,b.
| 103x1exp | 103x1apelblat | 103x1CNIBS | 103x1AJA | 103x1λh | ||
|---|---|---|---|---|---|---|
| 283.15 K | ||||||
| 0.30 | 3.730 | 3.656 | 3.825 | 3.394 | 3.648 | |
| 0.40 | 7.404 | 7.356 | 6.648 | 7.137 | 7.154 | |
| 0.50 | 9.214 | 9.898 | 10.84 | 11.94 | 11.07 | |
| 0.60 | 17.61 | 17.43 | 16.26 | 17.09 | 17.16 | |
| 0.70 | 22.86 | 22.85 | 22.14 | 21.99 | 23.05 | |
| 0.80 | 26.14 | 25.62 | 27.20 | 26.20 | 25.76 | |
| 0.90 | 30.29 | 29.75 | 30.16 | 29.15 | 30.92 | |
| 1.00 | 30.45 | 30.27 | 30.36 | 29.89 | 31.26 | |
| 288.15 K | ||||||
| 0.30 | 3.861 | 4.016 | 3.872 | 3.823 | 4.019 | |
| 0.40 | 8.137 | 8.103 | 8.035 | 7.995 | 8.019 | |
| 0.50 | 13.15 | 11.94 | 13.38 | 13.36 | 12.54 | |
| 0.60 | 18.93 | 19.27 | 19.06 | 19.14 | 19.16 | |
| 0.70 | 25.49 | 25.49 | 24.40 | 24.70 | 25.58 | |
| 0.80 | 27.56 | 28.58 | 28.96 | 29.56 | 28.67 | |
| 0.90 | 33.17 | 34.04 | 32.37 | 33.07 | 34.72 | |
| 1.00 | 33.85 | 34.32 | 34.01 | 34.15 | 34.62 | |
| 293.15 K | ||||||
| 0.30 | 4.530 | 4.407 | 4.504 | 4.292 | 4.418 | |
| 0.40 | 8.710 | 8.945 | 8.875 | 8.922 | 8.963 | |
| 0.50 | 14.95 | 14.11 | 14.73 | 14.88 | 14.15 | |
| 0.60 | 21.39 | 21.30 | 21.35 | 21.32 | 21.33 | |
| 0.70 | 28.21 | 28.31 | 27.85 | 27.58 | 28.30 | |
| 0.80 | 32.03 | 31.78 | 33.39 | 33.13 | 31.81 | |
| 0.90 | 38.59 | 38.50 | 37.31 | 37.24 | 38.45 | |
| 1.00 | 38.75 | 38.66 | 39.09 | 38.69 | 38.63 | |
| 298.15 K | ||||||
| 0.30 | 4.688 | 4.831 | 4.687 | 4.802 | 4.847 | |
| 0.40 | 9.941 | 9.894 | 9.920 | 9.919 | 9.989 | |
| 0.50 | 16.43 | 16.34 | 16.55 | 16.50 | 15.91 | |
| 0.60 | 23.62 | 23.54 | 23.65 | 23.64 | 23.67 | |
| 0.70 | 31.50 | 31.33 | 30.64 | 30.63 | 31.24 | |
| 0.80 | 35.61 | 35.21 | 37.09 | 36.89 | 35.19 | |
| 0.90 | 43.16 | 43.10 | 42.12 | 41.63 | 42.46 | |
| 1.00 | 43.60 | 43.25 | 43.83 | 43.49 | 42.97 | |
| 303.15 K | ||||||
| 0.30 | 5.517 | 5.290 | 5.510 | 5.355 | 5.308 | |
| 0.40 | 11.11 | 10.96 | 11.11 | 10.99 | 11.10 | |
| 0.50 | 18.07 | 18.57 | 18.18 | 18.22 | 17.84 | |
| 0.60 | 25.98 | 26.02 | 25.88 | 26.09 | 26.21 | |
| 0.70 | 34.43 | 34.53 | 33.60 | 33.84 | 34.40 | |
| 0.80 | 39.06 | 38.89 | 40.81 | 40.85 | 38.84 | |
| 0.90 | 47.83 | 47.76 | 46.48 | 46.25 | 46.77 | |
| 1.00 | 48.33 | 48.09 | 48.65 | 48.53 | 47.66 | |
| 308.15 K | ||||||
| 0.30 | 5.834 | 5.787 | 5.833 | 5.956 | 5.804 | |
| 0.40 | 12.28 | 12.17 | 12.24 | 12.13 | 12.31 | |
| 0.50 | 19.97 | 20.73 | 20.23 | 20.05 | 19.95 | |
| 0.60 | 28.88 | 28.76 | 28.66 | 28.67 | 28.95 | |
| 0.70 | 37.81 | 37.94 | 36.93 | 37.20 | 37.79 | |
| 0.80 | 42.75 | 42.83 | 44.66 | 44.97 | 42.76 | |
| 0.90 | 52.37 | 52.43 | 50.93 | 51.04 | 51.39 | |
| 1.00 | 53.25 | 53.17 | 53.59 | 53.77 | 52.71 | |
| 313.15 K | ||||||
| 0.30 | 6.261 | 6.324 | 6.257 | 6.604 | 6.336 | |
| 0.40 | 13.43 | 13.53 | 13.42 | 13.36 | 13.62 | |
| 0.50 | 22.10 | 22.77 | 22.30 | 21.97 | 22.24 | |
| 0.60 | 31.74 | 31.78 | 31.60 | 31.38 | 31.90 | |
| 0.70 | 41.75 | 41.54 | 40.73 | 40.70 | 41.44 | |
| 0.80 | 47.20 | 47.03 | 49.31 | 49.25 | 46.97 | |
| 0.90 | 57.67 | 57.05 | 56.09 | 56.01 | 56.35 | |
| 1.00 | 57.72 | 58.46 | 58.09 | 59.18 | 58.15 | |
| 318.15 K | ||||||
| 0.30 | 6.739 | 6.90 | 6.742 | 7.303 | 6.908 | |
| 0.40 | 15.03 | 15.06 | 14.96 | 14.66 | 15.05 | |
| 0.50 | 24.68 | 24.62 | 24.99 | 24.01 | 24.73 | |
| 0.60 | 35.20 | 35.11 | 35.00 | 34.20 | 35.09 | |
| 0.70 | 45.31 | 45.33 | 44.31 | 44.33 | 45.34 | |
| 0.80 | 51.00 | 51.50 | 52.94 | 53.66 | 51.49 | |
| 0.90 | 61.76 | 61.56 | 60.36 | 61.11 | 61.65 | |
| 1.00 | 63.98 | 63.94 | 64.31 | 64.73 | 63.98 | |
| 323.15 K | ||||||
| 0.30 | 7.65 | 7.531 | 7.669 | 8.056 | 7.522 | |
| 0.40 | 16.77 | 16.78 | 16.60 | 16.04 | 16.58 | |
| 0.50 | 27.20 | 26.23 | 27.60 | 26.14 | 27.44 | |
| 0.60 | 38.67 | 38.78 | 38.59 | 37.14 | 38.51 | |
| 0.70 | 49.28 | 49.33 | 48.55 | 48.08 | 49.53 | |
| 0.80 | 56.44 | 56.24 | 57.37 | 58.19 | 56.34 | |
| 0.90 | 65.34 | 65.90 | 64.90 | 66.32 | 67.32 | |
| 1.00 | 69.87 | 69.59 | 69.95 | 70.39 | 70.25 | |
x1 is
the experimental solubility; the x1apelblat, x1CNIBSx1λh, and x1AJA are the calculated mole solubilities
according to the modified Apelblat model, CNIBS/R-K model, λh model, and Apelblat–Jouyban–Acree model,
respectively. 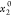 represents the initial mole fraction of
water in the binary aqueous solvent.
represents the initial mole fraction of
water in the binary aqueous solvent.
The standard uncertainty is u(T) = 0.1 K; the relative standard uncertainties ur are ur(P) = 0.01, ur(x1) = 0.05, and ur(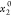 ) = 0.001.
) = 0.001.
As shown in Figures 4–6, it is obvious that the solubility of MET·HCl has a positive correlation with temperature and water content at the fixed solvent composition. Figures S1–S4 listing the parameters of the four models are demonstrated in Supporting Information. The order of the solubility is water + DMF > water + acetonitrile > water + n-propanol. When the water content is low, the difference of solubility between the water + acetonitrile and water + n-propanol is very small, but as the water content increases, the solubility differs significantly. Furthermore, the solubility is mainly determined by the interaction between solvent and solute molecules.33,34 The main physicochemical properties of the solvents are listed in Table 4. It can be seen that the polarity order of the solvent is water > DMF > acetonitrile > n-propanol, which is consistent with the order of solubility in these solvents, following the “like dissolve like” rule. However, the summation of the hydrogen bond donor propensities of the solvent (∑αb) and the summation of the hydrogen bond accept propensities of the solvent (∑βc) have no obvious correlation with solubility. Moreover, the HSP which can explain the solubility capability is listed in Table 5. It shows that in water + DMF and water + n-propanol system, the δp, δh, and δmix have a positive correlation with the water content and the δd has a negative correlation. However, in water + acetonitrile, the δd, δh, and δmix have a positive correlation with the water content and the δp has a negative correlation.
Table 4. Main Physicochemical Properties of the Four Pure Solventsa.
| solvent | πa | ∑αb | ∑βc |
|---|---|---|---|
| water | 1.09 | 1.17 | 0.47 |
| DMF | 0.88 | 0.00 | 0.74 |
| acetonitrile | 0.75 | 0.07 | 0.32 |
| n-propanol | 0.52 | 0.37 | 0.48 |
πa Polarity of the solvent. ∑αb is the summation of the hydrogen bond donor propensities of the solvent. ∑βc is the summation of the hydrogen bond accept propensities of the solvent.
Table 5. Values of HSPs of MET·HCl and the Selected Solventsa.
| δd (Mpa)0.5 | δp (Mpa)0.5 | δh (Mpa)0.5 | δmix (Mpa)0.5 | ||
|---|---|---|---|---|---|
| Water + DMF | |||||
| 0.30 | 17.24 | 13.91 | 14.11 | 26.26 | |
| 0.40 | 17.16 | 14.01 | 15.46 | 27.01 | |
| 0.50 | 17.06 | 14.13 | 17.15 | 28.02 | |
| 0.60 | 16.93 | 14.30 | 19.32 | 29.40 | |
| 0.70 | 16.77 | 14.51 | 22.21 | 31.38 | |
| 0.80 | 16.53 | 14.81 | 26.25 | 34.37 | |
| 0.90 | 16.18 | 15.26 | 32.28 | 39.20 | |
| 1.00 | 15.60 | 16.00 | 42.30 | 47.84 | |
| Water + Acetonitrile | |||||
| 0.30 | 15.34 | 17.74 | 10.76 | 25.80 | |
| 0.40 | 15.36 | 17.63 | 12.86 | 26.68 | |
| 0.50 | 15.38 | 17.49 | 15.37 | 27.90 | |
| 0.60 | 15.40 | 17.32 | 18.43 | 29.61 | |
| 0.70 | 15.43 | 17.11 | 22.23 | 32.02 | |
| 0.80 | 15.47 | 16.84 | 27.08 | 35.44 | |
| 0.90 | 15.53 | 16.49 | 33.47 | 40.41 | |
| 1.00 | 15.60 | 16.00 | 42.30 | 47.84 | |
| Water + n-Propanol | |||||
| 0.30 | 15.96 | 7.660 | 19.73 | 26.51 | |
| 0.40 | 15.94 | 8.070 | 20.84 | 27.46 | |
| 0.50 | 15.92 | 8.590 | 22.23 | 28.66 | |
| 0.60 | 15.89 | 9.240 | 24.01 | 30.24 | |
| 0.70 | 15.86 | 10.11 | 26.36 | 32.38 | |
| 0.80 | 15.80 | 11.31 | 29.62 | 35.42 | |
| 0.90 | 15.73 | 13.10 | 34.44 | 40.06 | |
| 1.00 | 15.60 | 16.00 | 42.30 | 47.84 | |
| Solute and Pure Solvents | |||||
| water | 15.60 | 16.00 | 42.30 | 47.84 | |
| acetonitrile | 15.30 | 18.00 | 6.100 | 24.40 | |
| n-propanol | 16.00 | 6.800 | 17.40 | 24.60 | |
| DMF | 17.40 | 13.70 | 11.30 | 24.86 | |
δd: dispersion solubility parameter. δp: polar solubility parameter. δh: hydrogen bond solubility parameter. δmix: the total Hansen solubility parameter.
3.3. Data Correlation
In this work, we used the 1stopt for the modeling. The solubility of MET·HCl in three binary solvents was correlated by the modified Apelblat model, CNIBS/R-K model, Apelblat–Jouyban–Acree model, and λh model. The acquired results are listed in Tables 1–3, and the model parameters, ARD %, and rmsd are listed in Tables S1–S4. As shown in the tables, all the ARD % values are less than 6%, indicating that these models can fit the solubility data well. The maximum ARD % values for the correlation models are 5.75% in the water + acetonitrile system correlated by the CNIBS/R-K model. The maximum rmsd values for the correlation models is 1.1673 × 10–2 in the water + n-propanol system correlated by the CNIBS/R-K model. In water + DMF, the order of the ARD % is the Apelblat–Jouyban–Acree model (ARD = 0.0270)>CNIBS/R-K model (ARD = 0.0168)>λh model (ARD = 0.0163)>Apelblat model (ARD = 0.0146). In water + acetonitrile and water + n-propanol, the order of the ARD % values are same as that in the water + DMF system. All in all, the modified Apelblat model provided better correlation results than the others.
3.4. Thermodynamic Properties of Solution
The apparent thermodynamic parameters including Gibbs energy (ΔG), enthalpy (ΔH), and entropy (ΔS) are calculated and shown in Table 6. The values of ΔG, ΔH, and ΔS are all positive in the three binary solvents indicating that the dissolution process is endothermic and entropically favorable. Comparing the relative contributions of enthalpy and entropy, the % ζH is more than 60% in all binary solvents while the % ζTS is more than 7%. The main contributor to standard free energy of the solution process of MET·HCl is the enthalpy.
Table 6. Apparent Thermodynamic Parameters for Dissolution Behavior of MET·HCl in Three Binary Solvents at Thm.
| ΔG (kJ·mol–1) | ΔH (kJ·mol–1) | ΔS (J·K–1·mol–1) | TΔS (kJ·mol–1) | % ζH | % ζTS | ||
|---|---|---|---|---|---|---|---|
| Water + DMF | |||||||
| 0.30 | 12.19 | 13.56 | 4.508 | 1.364 | 90.86 | 9.143 | |
| 0.40 | 11.27 | 13.71 | 8.065 | 2.440 | 84.89 | 15.11 | |
| 0.50 | 10.46 | 15.05 | 15.19 | 4.598 | 76.60 | 23.40 | |
| 0.60 | 9.730 | 16.09 | 21.02 | 6.361 | 71.67 | 28.33 | |
| 0.70 | 9.075 | 15.90 | 22.57 | 6.830 | 69.96 | 30.04 | |
| 0.80 | 8.652 | 15.94 | 24.09 | 7.289 | 68.62 | 31.38 | |
| 0.90 | 7.984 | 15.31 | 24.21 | 7.327 | 67.63 | 32.37 | |
| 1.00 | 7.685 | 16.06 | 27.68 | 8.375 | 65.73 | 34.27 | |
| Water + Acetonitrile | |||||||
| 0.30 | 13.19 | 14.33 | 3.739 | 1.131 | 92.68 | 7.319 | |
| 0.40 | 11.34 | 16.09 | 15.71 | 4.753 | 77.20 | 22.80 | |
| 0.50 | 10.17 | 19.74 | 31.64 | 9.575 | 67.34 | 32.66 | |
| 0.60 | 9.182 | 15.47 | 20.78 | 6.288 | 71.10 | 28.90 | |
| 0.70 | 8.499 | 14.71 | 20.53 | 6.212 | 70.31 | 29.69 | |
| 0.80 | 8.195 | 15.27 | 23.38 | 7.076 | 68.34 | 31.66 | |
| 0.90 | 7.732 | 15.59 | 25.96 | 7.856 | 66.49 | 33.51 | |
| 1.00 | 7.685 | 16.06 | 27.68 | 8.375 | 65.73 | 34.27 | |
| Water + n-Propanol | |||||||
| 0.30 | 12.92 | 25.24 | 40.71 | 12.32 | 67.20 | 32.80 | |
| 0.40 | 11.53 | 22.82 | 37.29 | 11.28 | 66.91 | 33.09 | |
| 0.50 | 10.42 | 22.42 | 39.65 | 12.00 | 65.14 | 34.86 | |
| 0.60 | 9.550 | 21.14 | 38.32 | 11.59 | 64.58 | 35.42 | |
| 0.70 | 8.829 | 19.51 | 35.30 | 10.68 | 64.62 | 35.38 | |
| 0.80 | 8.453 | 18.98 | 34.79 | 10.53 | 64.32 | 35.68 | |
| 0.90 | 7.845 | 18.02 | 33.63 | 10.18 | 63.91 | 36.09 | |
| 1.00 | 7.685 | 16.06 | 27.68 | 8.375 | 65.73 | 34.27 | |
4. Conclusions
The mole fraction solubility of MET·HCl (form A) in water, water + DMF, water + acetonitrile, and water + n-propanol in the temperature ranging from 283.15 to 323.15 K was determined by the gravimetric method. The crystal form is stable in the whole experiment which was verified by the XRPD and thermal analysis. The solubility of MET·HCl has a positive correlation with temperature and water content in the three binary solvents. The order of the solubility is water > water + DMF > water + acetonitrile > water + n-propanol, and it is consistent with the polar order. All the selected models give low ARD % values less than 6%. The modified Apelblat model provides better correlation results. Comparing the values of apparent thermodynamic properties, we find the dissolution process is endothermic and entropically favorable. The solubility data would be helpful for separation and purification process of MET·HCl.
5. Experimental Section
5.1. Materials
MET·HCl was obtained from Shandong Fukang Pharmaceutical Co., Ltd., China. The organic solvents (DMF, acetonitrile, and n-propanol) used in this experiment were purchased from Tianjin Fuyu Fine Chemical Co., Ltd. The deionized water was made in the laboratory (arium mini plus, Germany). These solvents have not been further purified, and the detailed sources are listed in Table 7.
Table 7. Detailed Sources and Information of Materials.
| chemcials | CAS | molar mass (g·mol–1) | source | mass fraction purity (%) | analysis method |
|---|---|---|---|---|---|
| MET·HCl | 1115-70-4 | 165.62 | Fukang Pharmaceutical Co., Ltd., China | ≥98.0 | HPLCa |
| DMF | 68-12-2 | 73.09 | Tianjin Fuyu Fine Chemical Co., Ltd. | ≥99.7 | GCb |
| acetonitrile | 75-05-8 | 41.05 | Tianjin Fuyu Fine Chemical Co., Ltd. | ≥99.7 | GCb |
| n-propanol | 71-23-8 | 60.10 | Tianjin Fuyu Fine Chemical Co., Ltd. | ≥99.7 | GCb |
High performance liquid chromatography.
Gas chromatography.
5.2. X-ray Powder Diffraction
The XRPD33,34 was used to detect the crystal form of MET·HCl during the whole experiment. An X’pert3 Powder (PANalytical B.V., Netherlands) instrument was used with the 40 kV tube voltage and 30 mA current during the measurement. The patterns were collected by the EMPYREAN (PANalytical, the Netherlands) with the Cu Kα radiation (0.15405 nm) in the 2θ range (5–45°) at room temperature. The step size was 0.02°, and the scanning speed was 8°/min.
5.3. Thermal Analysis
In order to verify the stability of MET·HCl during the entire experiment, we performed the DSC and TGA.35−38 The melting temperature Tm of MET·HCl was determined by the TGA and DSC (DSC-STA449 F3, NETZSH, Germany). Approximately, 3–5 mg of MET·HCl was added in an aluminum crucible. The sample was heated from 298.15 to 573.15 K at a heating rate of 10 K•min–1 under the protection of nitrogen atmosphere.
5.4. Solubility Measurements
The solubility of MET·HCl in water, water + DMF, water + acetonitrile, and water + n-propanol from 283.15 to 323.15 K was measured by the gravimetric method. Approximately, 25–30 mL of the solvent was added in the 100 mL custom test tube; after that, we added the excess solute to the test tubes. The test tubes were added in the constant temperature water bath which was controlled by the thermostat (CF41, Julabo, Germany) with an accuracy of ±0.01 K. The solution was stirred at a speed of 500 rpm for at least 12 h to reach the solid–liquid equilibrium. Then, we stopped the stirring and the solution system was kept still for more than 2 h to precipitate undissolved particles. Finally, we used the preheated/cooled 5 mL needle injector to extract the supernatant through the preheated/cooled 0.45 μm filter membrane and injected it into the Petri dish weighted in advance with the analytical balances (Mettler-toledo, Switzerland, the precision is ±0.0001 g). The total weight of the liquid sample and the Petri dish was measured immediately. The Petri dish containing the liquid sample was placed into the vacuum drying oven (type DZF-6000, Shanghai Yiheng Scientific Instrument Co., Ltd., China) at 318.15 K for 12 h. The experiment was repeated three times, and the mole fraction solubility (x1) of MET·HCl in pure solvents was calculated by eq 19
| 19 |
where m1 is the mass of solute and m2 is the mass of pure solvent, and M1, and M2 are the corresponding molar mass, respectively.
The content ratio of water (x20) in the initial binary solvent and the mole fraction solubility (x1) of MET·HCl in binary solvents were calculated by eqs 20 and 21
| 20 |
| 21 |
where m1 is the mass of the solvent and m2 and m3 are the mass of water and organic solvent, respectively. M1, M2, and M3 are molecular mass of the solvent, water, and organic solvent, respectively.
Acknowledgments
The authors are grateful for the financial support of the Shandong Keypoint Research & Development Plan (2021CXGC010811, 2021CXGC010514, and 2020CXGC010506), Jinan Introducing Innovation Team Project (2020GXRC034), and Science, Education and Industry Integration Technology Innovation Project (2020KJC-ZD09).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c06468.
Solubility and correlation with the modified Apelblat model and λh model in water + DMF, water + acetonitrile, and water + n-propanol at 283.15–323.15 K, model parameters, ARD %, rmsd of water + DMF, water + acetonitrile, water + n-propanol calculated by the modified Apelblat model, CNIBS/R-K model, Apelblat–Jouyban–Acree model, and λh model, and experimental solubility of MET·HCl in pure solvents (PDF)
Author Contributions
∥ C.Y. and X.S. contribute equally to this work and should be regarded as co-first authors.
The authors declare no competing financial interest.
Supplementary Material
References
- Xiong W.; Qi L.; Jiang N.; Zhao Q.; Chen L.; Jiang X.; Li Y.; Zhou Z.; Shen J. Metformin Liposome-Mediated PD-L1 Downregulation for Amplifying the Photodynamic Immunotherapy Efficacy. ACS Appl. Mater. Interfaces 2021, 13, 8026–8041. 10.1021/acsami.0c21743. [DOI] [PubMed] [Google Scholar]
- Kinsky O. R.; Hargraves T. L.; Anumol T.; Jacobsen N. E.; Dai J.; Snyder S. A.; Monks T. J.; Lau S. S. Metformin Scavenges Methylglyoxal To Form a Novel Imidazolinone Metabolite in Humans. Chem. Res. 2016, 29, 227–234. 10.1021/acs.chemrestox.5b00497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szekalska M.; Sosnowska K.; Zakrzeska A.; Kasacka I.; Lewandowska A.; Winnicka K. The Influence of Chitosan Cross-linking on theProperties of Alginate Microparticles with Metformin Hydrochloride—In Vitro and In Vivo Evaluation. Mole 2017, 22, 182. 10.3390/molecules22010182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benmessaoud I.; Koutchoukali O.; Bouhelassa M.; Nouar A.; Veesler S. Solvent screening and crystal habit of metformin hydrochloride. J. Cryst. Growth 2016, 451, 42–51. 10.1016/j.jcrysgro.2016.07.001. [DOI] [Google Scholar]
- Childs S. L.; Chyall L. J.; Dunlap J. T.; Coates D. A.; Stahly B. C.; Stahly G. P. A Metastable Polymorph of Metformin Hydrochloride:Isolation and Characterization Using Capillary Crystallization and Thermal Microscopy Techniques. Cryst. Growth Des. 2004, 4, 441–449. 10.1021/cg034243p. [DOI] [Google Scholar]
- Sun X.; Du S.; Sun Y.; Li H.; Yu C.; Guo J.; Wang Y.; Yu S.; Cheng Y.; Xue F. Solubility Measurement and Data Correlation of Metformin Hydrochloride in Four Aqueous Binary Solvents and Three PureSolvents from 283.15 to 323.15 K. J. Chem. Eng. Data 2021, 66, 3282–3292. 10.1021/acs.jced.1c00338. [DOI] [Google Scholar]
- Zhou Y.; Wang J.; Wang T.; Gao J.; Huang X.; Hao H. Solubility and dissolution thermodynamic properties of L-carnosine in binary solvent mixtures. J. Chem. Therm. 2020, 149, 106167. 10.1016/j.jct.2020.106167. [DOI] [Google Scholar]
- Li X.; Han D.; Wang Y.; Du S.; Liu Y.; Zhang J.; Yu B.; Hou B.; Gong J. Measurement of Solubility of Thiamine Hydrochloride Hemihydrate in Three Binary Solvents and Mixing Properties of Solutions. J. Chem. Eng. Data 2016, 61, 3665–3678. 10.1021/acs.jced.6b00613. [DOI] [Google Scholar]
- Yu S.; Xing W.; Xue F.; Cheng Y.; Li B. Solubility and thermodynamic properties of nimodipine in pure and binary solvents at a series of temperatures. J. Chem. Thermodyn. 2021, 152, 106259. 10.1016/j.jct.2020.106259. [DOI] [Google Scholar]
- Wang L.; Sun J.; Zhang H.; Shen Z.; Xu L.; Liu G. Solubility and thermodynamic analysis of methyleneaminoacetonitrile in binary solvents from T = (278.15 to 323.15) K. J. Mol. Liq. 2019, 283, 462–471. 10.1016/j.molliq.2019.03.069. [DOI] [Google Scholar]
- Liu Y.; Wang Y.; Liu Y.; Xu S.; Chen M.; Du S.; Gong J. Solubility of L-histidine in different aqueous binary solvent mixtures from 283.15 K to 318.15 K with experimental measurement and thermodynamic modelling. J. Chem. Therm. 2017, 105, 1–14. 10.1016/j.jct.2016.09.039. [DOI] [Google Scholar]
- Han D.; Li X.; Wang H.; Wang Y.; Du S.; Yu B.; Liu Y.; Xu S.; Gong J. Determination and correlation of pyridoxine hydrochloride solubility in different binary mixtures at temperatures from (278.15 to 313.15) K. J. Chem. Therm. 2016, 94, 138–151. 10.1016/j.jct.2015.09.026. [DOI] [Google Scholar]
- Gao Y.; Wang J.; Hao H.; Xiao Y.; Huang X.; Xia M. Solution thermodynamics of ceftiofur hydrochloride in pure and binary solvents. J. Mol. Liq. 2021, 338, 116782. 10.1016/j.molliq.2021.116782. [DOI] [Google Scholar]
- Sun R.; He H.; Yuan L.; Wan Y.; Sha J.; Li L.; Jiang G.; Li Y.; Li T.; Ren B. Thermodynamic analysis and molecular simulation of solid–liquid phase equilibrium of isoprenaline hydrochloride in eleven pure solvents at saturation. J. Chem. Therm. 2021, 160, 106411. 10.1016/j.jct.2021.106411. [DOI] [Google Scholar]
- Yang Z.; Shao D.; Zhou G. Cosolvent action of promethazine hydrochloride in (ethylacetate+alcohols) and thermodynamic property analysis. J. Chem. Therm. 2020, 143, 106030. 10.1016/j.jct.2019.106030. [DOI] [Google Scholar]
- Qi R.; Wang J.; Ye J.; Hao H.; Bao Y. The solubility of cefquinome sulfate in pure and mixed solvents. Front. Chem. Sci. Eng. 2016, 10, 245–254. 10.1007/s11705-016-1569-z. [DOI] [Google Scholar]
- Yang P.; Du S.; Qin Y.; Zhao K.; Li K.; Hou B.; Gong J. Determination and correlation of solubility and thermodynamic properties of pyraclostrobin in pure and binary solvents. J. Chem. Therm. 2016, 101, 84–91. 10.1016/j.jct.2016.05.005. [DOI] [Google Scholar]
- Barzegar-Jalali M.; Jouyban-Gharamaleki A. A general model from theoretical cosolvency models. Int. J. Pharm. 1997, 152, 247–250. 10.1016/s0378-5173(97)04922-3. [DOI] [Google Scholar]
- Jouyban A.; Acree W. E. Mathematical derivation of the Jouyban-Acree model to represent solute solubility data in mixed solvents at various temperatures. J. Mol. Liq. 2018, 256, 541–547. 10.1016/j.molliq.2018.01.171. [DOI] [Google Scholar]
- Song L.; Zhao D.; Zhang S.; Zhang X.; Wang G.; Zhu C.; Tian Y.; Yang C. Solubility of Diflufenican in Pure and Binary Solvent Systems. J. Chem. Eng. Data 2018, 63, 4176–4184. 10.1021/acs.jced.8b00632. [DOI] [Google Scholar]
- Huang Z. B.; Sha J.; Chang Y. G.; Gao Z. D.; Hu X. R.; Li Y.; Li T.; Ren B. Z. Solubility measurement, model evaluation and Hansen solubility parameter of ipriflavone in three binary solvents. J. Chem. Therm. 2020, 152, 106285. 10.1016/j.jct.2020.106285. [DOI] [Google Scholar]
- Yu S.; Yuan J.; Cheng Y.; Du S.; Wang Y.; Xue F.; Xing W. Solid-liquid phase equilibrium of clozapine in aqueous binary solvent mixtures. J. Mol. Liq. 2021, 329, 115371. 10.1016/j.molliq.2021.115371. [DOI] [Google Scholar]
- Jain A.; Yang G.; Yalkowsky S. H. Estimation of Total Entropy of Melting of Organic Compounds. Ind. Eng. Chem. Res. 2004, 43, 4376–4379. 10.1021/ie0497745. [DOI] [Google Scholar]
- Hansen C. M.; Smith A. L. Using Hansen solubility parameters to correlate solubility of C60 fullerene in organic solvents and in polymers. Carbon 2004, 42, 1591–1597. 10.1016/j.carbon.2004.02.011. [DOI] [Google Scholar]
- Zhao L.; Yalkowsky S. H. A Combined Group Contribution and Molecular Geometry Approach for Predicting Melting Points of Aliphatic Compounds. Ind. Eng. Chem. Res. 1999, 38, 3581–3584. 10.1021/ie990281n. [DOI] [Google Scholar]
- Vakili K.; Rezaei H.; Poturcu K.; Jouyban A.; Hanaee J.; Martinez F.; Rahimpour E. Solubility study of sildenafifil citrate in (2-propanol+water) binary mixtures at different temperatures. J. Mol. Liq. 2021, 344, 117915. 10.1016/j.molliq.2021.117915. [DOI] [Google Scholar]
- Panahi-Azar V.; Shayanfar A.; Martínez F.; Acree Jr W. E.; Jouyban A. Thermodynamic studies of fluphenazine decanoate solubility in propylene glycol+water mixtures and correlation with the Jouyban–Acree model. Fluid Phase Equilib. 2011, 308, 72–77. 10.1016/j.fluid.2011.06.008. [DOI] [Google Scholar]
- Pacheco D. P.; Manrique Y. J.; Martínez F. Thermodynamic study of the solubility of ibuprofen and naproxen in some ethanol + propylene glycol mixtures. Fluid Phase Equilib. 2007, 262, 23–31. 10.1016/j.fluid.2007.07.076. [DOI] [Google Scholar]
- Childs S. L.; Chyall L. J.; Dunlap J. T.; Coates D. A.; Stahly B. C.; Stahly G. P. A Metastable Polymorph of Metformin Hydrochloride: Isolation and Characterization Using Capillary Crystallization and Thermal Microscopy Techniques. Cryst. Growth Des. 2004, 4, 441–449. 10.1021/cg034243p. [DOI] [Google Scholar]
- Hansen J.; Kleinebudde P. Enabling the direct compression of metformin hydrochloride through QESD crystallization. Int. J. Pharm. 2021, 605, 120796. 10.1016/j.ijpharm.2021.120796. [DOI] [PubMed] [Google Scholar]
- Shokouhi M.; Jalili A. H.; Babakhani E. G. Hydrogen Sulfide Solubility in Aqueous N-Methylpyrrolidone Solution. J. Chem. Eng. Data 2021, 66, 1900–1913. 10.1021/acs.jced.0c00923. [DOI] [Google Scholar]
- Hnedkovsky L.; Hefter G. Densities and Apparent Molar Volumes of Aqueous Solutions of Sodium and Potassium Triflates up to High Concentrations at Temperatures 293.15–343.15 K. J. Chem. Eng. Data 2021, 66, 1802–1812. 10.1021/acs.jced.1c00009. [DOI] [Google Scholar]
- Li R.; Yin X.; Jin Y.; Chen X.; Zhao B.; Wang W.; Zhong S.; Han D. The solubility profile and dissolution thermodynamic properties of minocycline hydrochloride in some pure and mixed solvents at several temperatures. J. Chem. Therm. 2021, 157, 106399. 10.1016/j.jct.2021.106399. [DOI] [Google Scholar]
- Maher A.; Croker D.; Rasmuson Å. C.; Hodnett B. K. Solubility of Form III Piracetam in a Range of Solvents. J. Chem. Eng. Data 2010, 55, 5314–5318. 10.1021/je1003934. [DOI] [Google Scholar]
- Ouyang J.; Chen J.; Zhou L.; Liu Z.; Zhang C. Solubility Measurement, Modeling, and Dissolution Thermodynamics of Propylparaben in 12 Pure Solvents. J. Chem. Eng. Data 2020, 65, 4725–4734. 10.1021/acs.jced.0c00584. [DOI] [Google Scholar]
- Chen J.; Farajtabar A.; Jouyban A.; Acree W. E.; Zhao H. Solubility, Three-Dimensional Hansen Solubility Parameters, and Solution Thermodynamics of 3,3′-Diaminodiphenyl Sulfone in 14 Neat Solvents from 283.15 to 328.15 K. J. Chem. Eng. Data 2021, 66, 2167–2176. 10.1021/acs.jced.1c00062. [DOI] [Google Scholar]
- Ye J.; Cui Z.; Wang Z.; Yang W.; Tang H.; Chen Y.; Hu Y. Solubility of 2- Amino-5-chloro-3-methylbenzoic Acid in Ten Pure Solvents and Three Groups of Binary Mixed Solvents at T = 278.15–323.15 K. J. Chem. Eng. Data 2021, 66, 2412–2424. 10.1021/acs.jced.1c00047. [DOI] [Google Scholar]
- Liu W.; Shen Y.; Zeng F.; Lu S.; Li J.; Yang J.; Zhang K. Solubility Measurement and Model Correlating of 6- Propyl-2- Thiouracil in Four Binary Solvents at 278.15–323.15 K. J. Chem. Eng. Data 2021, 66, 2436–2448. 10.1021/acs.jced.1c00071. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



