Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2022 Mar 2;7(10):8498–8505. doi: 10.1021/acsomega.1c06144

Study of the Chain Condensation Process from a Dilute to a Concentrated Solution and the Transformation of the Chain Conformation from a Solution to a Film for the Conjugated Polymer PFO

Dong Lei 1, Yanan Guo 1, Dan Lu 1,*
PMCID: PMC8928514  PMID: 35309444

Abstract

graphic file with name ao1c06144_0007.jpg

The chain behavior in a precursor solution and its condensation process are still key issues that have been paid close attention to but have not been solved yet for semirigid conjugated polymers. In this research, the chain condensation process from a dilute to a concentrated solution and the transformation of the chain conformation from a solution to a film for the conjugated polymer poly(9,9′-dioctylfluorene) (PFO) were investigated by a scaling law method obtained from rheological measurements. By establishing a scaling relationship between specific viscosity and concentration, it was found that the motion of molecular chains conformed to the Zimm model in dilute solution, and the motion of molecular chains conformed to the Rouse model in semidilute unentangled solution as well as conformed to the Edwards tube model in semidilute entangled solution. Furthermore, it was also found that toluene is a θ solvent for PFO at 25 °C. Some important physical parameters in connection with PFO intrinsic properties were also obtained here, such as intrinsic viscosity [η] = 136.84 mL g–1, root-mean-square end-to-end distance R = 41.4 nm, and Kuhn segment length b = 6.28 nm. In particular, this was the first time that the effect of the film-forming process of spin coating on the transformation proces of the PFO chain conformation from the precursor solution to a film was studied, and the spin-coating time (t) was found to be several orders of magnitude longer than the PFO chain relaxation time (τZ(τR)). This research enriches knowledge and understanding of the chain behavior in the precursor solution for semirigid conjugated polymers and reveals the correlation of chain behaviors in solution with the film’s condensed state structure in the process of chain dynamic evolution from a solution to a film.

1. Introduction

Conjugated polymers have been widely used in photoelectronic devices, such as organic light-emitting diodes (OLEDs), solar cells (OPVs), solid-state plastic lasers, and field effect transistors (FETs)1−10 because of their excellent photoelectronic performance. As a class of conjugated polymers, polyfluorenes (PFs) have attracted great attention due to their unique emission of blue light, high photoluminescence efficiency, wide range of stimulated emission,11,12 etc. In particular, unlike many π-conjugated polymers, PFs exhibit a more complex phase structure in the crystal state, which makes them obviously different from similar benzene-based polymers in structure and properties, thus showing enormously developed potential in basic research and application. Especially, the β conformation of PFs is of higher planarity and orderliness than the other PF conformations; once it is formed, not only is the chain orderliness obviously enhanced but also the excited state level is lowered, which is very beneficial to the enhancement of the carrier mobility and efficiency of photoelectronic devices. Moreover, PFs are also a model of hairy rod polymers; thus, the research on PFs is of great theoretical and practical significance to fully understand the physics essence of the photoelectronic performance of conjugated polymers and guide their better application.

The β conformation of poly(9,9′-dioctylfluorene) (PFO) was first reported by Bradley et al. in 1997.13 They found a new UV absorption band with a narrow absorption peak at 473 nm in PFO solution, and it was also confirmed simultaneously in PFO films. Köhler et al.14 found that the β conformation has a strong effect on the photoelectronic performance of its films. Then, Chen et al.15 studied the electroluminescent properties of the β conformation and found that thin-film devices of PFO with or without the β conformation have great differences in efficiency. Bazan et al.16 used a high-boiling-point additive to induce the β conformation up to 50% in PFO solution and also investigated the luminous efficiency of thin-film devices with different contents of the β conformation. Monkman and Bradley et al.17−19 also found that PFO films with the β conformation could obtain the efficiency of the photoluminescent quantum of more than 60% with a wide excited cross section at room temperature. However, the above-mentioned research studies on PFO were mainly focused on solid thin films. Although there were a few basic research studies on chain behavior in solution, they focused merely on studying the structure of PFO chains in solution20−23 and the formative mechanism of the PFO β conformation.24,25 Research on the condensed dynamic process of PFO chains from a dilute to a concentrated solution and the transformation of the chain conformation from a solution to a film for conjugated polymers is scarce. Although close attention has been paid to this issue, it remains unsolved in academic circles until now. Hence, exploring the dynamic behavior of PFO chains in solution is very important to understand the condensed process of PFO chains from a dilute to a concentrated solution in depth so as to manipulate the condensed state structure of the PFO film to fabricate photoelectronic devices with high carrier mobility and efficiency based on conjugated polymer physics.

Rheology is mainly concerned with the relationship between material’s deformation, flow, and its intrinsic structure, which is highly fit for exploring the chain’s dynamic behavior in a conjugated polymer solution. However, the research on the rheology of conjugated polymers has been seldom reported so far. In this work, PFO solutions with different concentrations from dilute to concentrated solutions were prepared; the rheological behavior of PFO solution was systemically investigated. The scaling relationship between viscosity and concentration was revealed, and the transformation of the chain conformation from a solution to a film was explored. The consequences enrich the understanding of both chain behavior in solution and the dynamic evolution process to semirigid conjugated polymers and provide a new method for studying the chain behavior in solution based on polymer physics. More details will be discussed below.

2. Results and Discussion

2.1. Flow Curves of PFO Solution with Different Concentrations

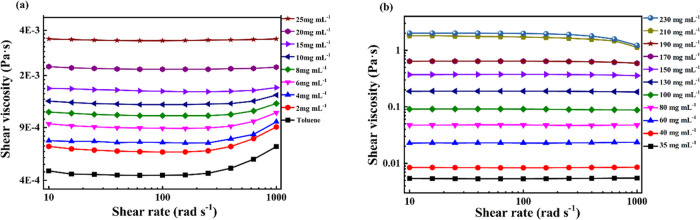
To explore the flow characteristics of PFO solution, steady flow curves of PFO solution were measured, and the results are shown in Figure 1. The shear viscosity of PFO solutions was determined by the steady shearing mode in a concentration range from 0 to 230 mg mL–1 with a shear rate range from 10 to 1000 rad s–1. As shown in Figure 1a, in a dilute solution, the shear viscosity was independent of the shear rate at a shear rate of less than 100 rad s–1 (called a Newtonian plateau). When the shear rate increases to over 100 rad s–1, the viscosity increases as the velocity gradient increases. The main cause of this phenomenon was the influence of the inertial effect of the stress-controlled rheometer used in the study.26,27 As the concentration was further increased to the semidilute unentangled range, the shear viscosity became independent of the shear rate in the entire shear rate range of 10–1000 rad s–1. When the concentration was increased to a certain extent, the viscosity of PFO solutions increased sufficiently so as to overcome the influence of the inertial effect. Interestingly, when the concentration was further increased, it was found that the viscosity decreased with the increase of velocity gradient, and this phenomenon became more and more obvious with the increase of concentration. The phenomenon that the viscosity decreases with the increase of velocity gradient might be induced by the rearrangement and orientation of macromolecular chains along the shear direction.28

Figure 1.

Figure 1

Open in a new tab

Shear viscosity versus shear rate for different concentrations of PFO solutions at 25 °C: (a) 0–25 mg mL–1 and (b) 35–230 mg mL–1.

2.2. Scaling Relationship between Viscosity and Concentration

The research on the solution behavior of semirigid conjugated polymers has been rarely reported to date because of the limitations of effective observation and research methods applied to the study of conjugated polymer solutions. Nevertheless, the scaling law with simplicity and effectiveness is just a novel and unique theoretical method for studying complex and nonlinear systems. Since de Gennes proposed the concept of the scaling law,29 its influence has been gradually surpassing polymer academia.30,31 As we know, a polymer has the characteristic of self-similarity, which is a unique scaling property. The characteristic of self-similarity can be described by the scaling law equation. From a mathematical point of view, the scaling law is expressed by a simple power law equation, y = kxa. Here, precoefficient k is generally related to the chemical properties of the monomer, and power exponent a is called the scaling exponent, which is related to the physical properties of polymeric long chains. Generally, when using the scaling law to discuss the physical phenomena and properties of polymers, researchers often tend to take only the scaling exponents into account. Therefore, the scaling law equation is rewritten as y ∝ xa.

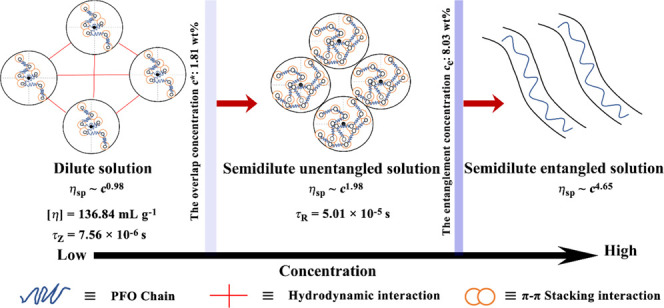
In this research, the relationship between specific viscosity and concentration was established for PFO by the equation ηsp∝ ca. Owing to different relationships between specific viscosity and concentration, the polymer solution can be divided into different concentration regions: dilute solution, semidilute unentangled solution, and semidilute entangled solution. In these different concentration regimes, the polymer chain motion pattern can be described by the Zimm, Rouse, and Edwards tube models.

In the dilute solution regime, the Zimm model can be used for describing polymer single-chain motion. The Zimm model can be assumed as a bead–spring model. The main assumption of the bead–spring model is that the shape of a molecular chain is similar to a bead chain, but it consists of N fully flexible Hook springs and N + 1 small beads, and the springs are freely connected to the beads. Hydrodynamic interactions are considered in the Zimm model, so the relationship between viscosity and concentration can be described as32

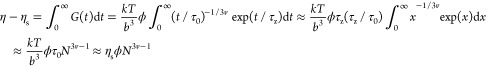2.2. 1

where η is the viscosity, ηs is the solvent viscosity, G(t) is the stress relaxation modulus, t is the time, τ0 is the Kuhn monomer relaxation time, v is the scaling exponent, τZ is the Zimm relaxation time, k is the Boltzmann constant, T is the absolute temperature, b is the Kuhn length, ϕ is the volume fraction, x is the fraction of labeled chains, and N is the degree of polymerization. In the semidilute unentangled solution regime, the Rouse model proposed a hydrodynamic screen length. When the distance of the polymer segment is greater than this length, the hydrodynamic interaction is shielded by the surrounding chain. The dynamic behaviors of macromolecule chains are considered to be in accordance with the Rouse model. Here, the scaling relationship between viscosity and concentration is as follows32

2.2. 2

Here, τchain is the relaxation time of a chain. In the semidilute entangled solution regime, the Edwards tube model proposed a tube diameter length, which is much greater than the hydrodynamic screen length.32 When the distance of the polymer segment is smaller than the hydrodynamic screen length, the relaxation mode of the polymer chain conforms to the Zimm model. When the distance of the polymer segment is larger than the hydrodynamic screen length and smaller than the diameter of the tube, the hydrodynamic interaction is shielded, the topological constraint becomes unimportant, and the motion of macromolecular chains can be described by the Rouse model. When the scale is larger than the tube diameter, the motion of macromolecular chains can be described by the Edwards tube model. The final scaling relationship between viscosity and concentration is as follows

2.2. 3

Here, τrep is the reptation time and Ne is the number of monomers in an entanglement strand. According to the data shown in Figure 1, in the dilute solution and semidilute unentangled solution regimes, the zero shear viscosity was acquired from the Newton plateau of the steady flow curves. In the semidilute entangled solution regime, the zero shear viscosity was obtained by the following Carreau model

2.2. 4

Here, η* is the complex viscosity, η0 is the zero shear viscosity (solution viscosity), ω is the shear rate, and n is the power exponent. In addition, specific viscosity ηsp= (η0 – ηs)/ηs was defined as a solute’s contribution to the viscosity of a solution.32,33 From Figure 2, it could be obviously found that the apparent viscosity (i.e., zero shear viscosity) and the specific viscosity increased gradually with the increase of concentration, but as the concentration was increased to 100 mg mL–1, the specific viscosity was enhanced rapidly with the concentration. In fact, specific viscosity eliminated the contribution of solvent to solution viscosity, and it only reflected the solute’s contribution to solution. Therefore, the nonlinear rapid increase of specific viscosity shows that the physical structure of polymer chains in solution changed with the increase of concentration.

Figure 2.

Figure 2

Open in a new tab

Dependence of zero shear viscosity and specific viscosity on the PFO solution concentration at 25 °C.

According to the logarithmic relationship of ηsp with concentration c, the scaling exponent a, the overlap concentration (c*), and the entanglement concentration (ce) could be obtained, as shown in Figure 3. Notably, the node of two lines in Figure 3 was the critical point of two concentration regimes, which is also called the overlap concentration c*. It could be calculated as c* = 1.81 wt %; similarly, the entanglement concentration could be calculated as ce = 8.03 wt % from Figure 3. As mentioned above, the dynamic behavior of the PFO chain in the dilute toluene solution conformed to the Zimm model. According to the Zimm model, there should be hydrodynamic interaction in dilute PFO/toluene solutions. In fact, the toluene solvent was hydrodynamically coupled to the PFO chains within the expanding volume. In semidilute unentangled solution, the dynamic behavior of the PFO chain was consistent with the Rouse model.32 The Rouse model proposes a hydrodynamic screen length. When the segment size of the PFO chain was bigger than the hydrodynamic screen length, the molecular chain motion was not affected by the surrounding environment.32,34 In semidilute entangled solution, the dynamic behavior of the PFO chains conformed to the Edwards tube model in which the topological constraints of the surrounding chains limited the motion of the molecular chains to the tubular region. Though the polymer chain motion along the contour of the tube was not hindered by the topological impact, the polymer chain motion perpendicular to the direction of the tube contour would be hindered.32 According to Figure 1 and eqs 1–4, the specific viscosity in dilute solution, ηsp ∼ c0.98±0.06, and in semidilute unentangled solution, ηsp ∼ c1.98±0.12, as well in semidilute entangled solution, ηsp ∼ c4.65±0.24, could be calculated. Interestingly, the theoretical scaling prediction gave the power law index a in a θ solvent as 1, 2, and 4.7 in dilute, semidilute unentangled, and semidilute entangled solution regimes, respectively, as well as 1, 1.3, and 3.9 in a good solvent for neutral polymer solutions in dilute, semidilute unentangled, and semidilute entangled solution regimes, respectively.35 According to the experimental results (Table 1), the power law index values a are 0.98, 1.98, and 4.65 in dilute, semidilute unentangled, and semidilute entangled solution regimes, respectively, for PFO/toluene at 25 °C, which suggests that PFO/toluene solutions display very similar concentration dependence of ηsp to the predictions for neutral polymer solutions in a θ solvent. In addition, the second virial coefficient A2 = 2.44 × 10–6 mol·dm3·g–2 is close to zero (Figure S2). Therefore, it is concluded that toluene is a θ solvent for PFO at 25 °C.

Figure 3.

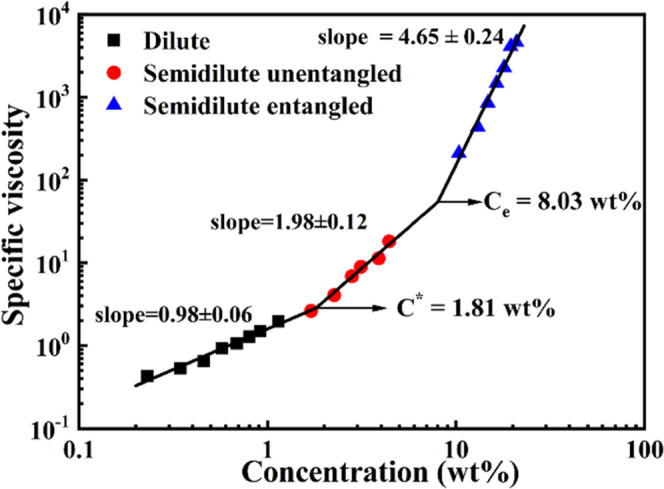
Figure 3

Open in a new tab

Scaling relationship between specific viscosity and concentration at 25 °C.

Table 1. Comparison of the Experimental Scaling Exponents a (ηsp ∼ ca) with Those of Theory.

concentrated regimes theoretical scaling exponents (θ (good) solvent)35 experimental scaling exponents (25 °C)
dilute solution 1.0 (1.0) 0.98 ± 0.06
semidilute unentangled solution 2.0 (1.3) 1.98 ± 0.12
semidilute entangled solution 4.67 (3.93) 4.65 ± 0.24
Open in a new tab

2.3. Intrinsic Viscosity and Chain Size

The reduced viscosity ηsp/c was defined as the ratio of specific viscosity to solution concentration. When the concentration is very low (close to zero), it is called the intrinsic viscosity [η]. According to the definition, the intrinsic viscosity is independent of the solution concentration. The intrinsic viscosity is a very important parameter of a material that reflects its nature. Therefore, a study on intrinsic viscosity is highly necessary not only to explore the material intrinsic properties of a material but also to find its application in different fields. Intrinsic viscosity can be usually calculated by the following Huggins and Kraemer equations36−38

2.3. 5
2.3. 6

Here, Kh is the Huggins coefficient, Kk is the Kraemer coefficient, and ηr = η0/ηs is the relative viscosity. Both plots of ηsp/c versus c and ln (ηr)/c versus c give two straight lines with an identical intercept at c = 0, and the intercept just corresponds to the intrinsic viscosity [η]. Its unit is the reciprocal of the unit of concentration (g mL–1). According to eqs 5 and 6, the intrinsic viscosity values were calculated as 135.74 and 137.94 mL g–1, respectively, in the PFO dilute solution range (Figure 4). It was found that the intrinsic viscosities calculated by the above two equations were almost consistent, so the average value was taken as 136.84 mL g–1, and all of the following discussion would take this average value unless otherwise noted. A quantitative description of the interaction between molecule chains can be done by the Huggins coefficient, and the Huggins coefficient is usually in the range of 0.25–0.5, which indicates good solubility. In this research, the Huggins coefficient Kh of the PFO/toluene solution was 0.33 at 25 °C, which showed that the PFO molecular chain was better dispersed in the toluene solvent in the range of dilute solution, and no complicated association was formed with other chains.

Figure 4.

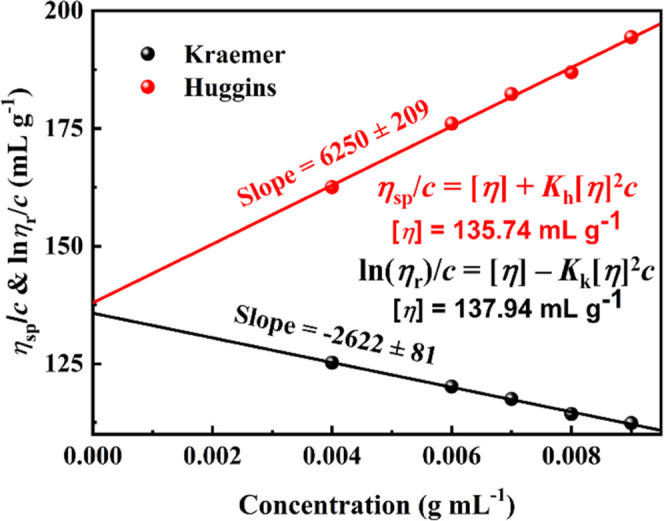
Figure 4

Open in a new tab

Intrinsic viscosity of PFO solution in the dilute regime calculated by the Kraemer and Huggins equations at 25 °C.

According to the famous Flory–Fox equation, the relationship among intrinsic viscosity, coil size, and molar mass can be established as follows

2.3. 7

Here, Φ = 0.425NAv = 2.5 × 1023 mol–1 is a universal constant for all polymer–solvent systems,32R is the root-mean-square end-to-end distance,28,39 and M is the molar mass of the polymer. From the Flory–Fox equation, root-mean-square end-to-end distance R = 41.4 nm.

As we know, the most effective way to study the intrinsic physical properties of polymer chains is describing the actual polymer chains by some ideal models. The most common model is the equivalent freely jointed chain model, in which we can artificially combine several adjacent single bonds with a polymer chain and treat them as relatively independent chain segments. As long as the number of single bonds is sufficient in the chain segment, to a certain extent, the connections between chain segments can be considered as free joints. Such a chain segment is called a Kuhn segment. Therefore, the mean square end-to-end distance of the equivalent freely jointed chain R02 is determined as

2.3. 8

Here, b is the length of the Kuhn segment and N is the number of Kuhn segments. As we know from the above result, toluene is a θ solvent of PFO at 25 °C and thus satisfies R0 = R = bN1/2. So, it is convenient to determine the number of segments (N) and the Kuhn segment length (b) of the polymer

2.3. 9
2.3. 10

Here, Rmax is the contour length of the PFO chain and R is the Kuhn chain length. According to a previous report, the length of the monomer unit was l = 0.838 nm in the PFO chain and the molar mass of the monomer was M0 = 390 g mol–1,40 so the contour length of the PFO chain Rmax = 273 nm could be obtained. Finally, we could acquire the Kuhn segment length b = 6.28 nm, and the number of segments N = 44 by eqs 9 and 10 (the detailed information of the calculation process is given in the Supporting Information).

2.4. Transformation of the Chain Conformation from a Solution to a Film

As we know, the application of conjugated polymers is generally in the form of devices made of photoelectronic thin films fabricated by spin-coating the precursor solution or spray-coating or inkjet printing, so the condensed state structure of the film arises from the arrangement and stacking of the molecular chains in the precursor solution, which is a dynamic evolution process of the chain conformation change from a solution to a film. Actually, in the process of dynamic evolution, the macromolecular chain conformation in a solution is directly related to the photoelectronic performance in a film. Therefore, rationally manipulating the macromolecular chain conformation in the precursor solution is very important to control the dynamic evolution of the film’s condensed state structure to enhance the efficiency of the photoelectronic device fundamentally. A key link of joining the precursor solution and the film is spin coating, which is an important process of film formation. In this section, therefore, whether the spin-coating process could influence the molecular chain conformation of the precursor solution was explored. Previous research has demonstrated that the aggregation state structure of the PFO precursor solution could be quantitatively inherited into the film,41 which indicated that the spin-coating process does not have an impact on the aggregation state structure in the spin-coating process. However, whether the spin-coating process has an impact on the chain conformation in the process of spin-coating the film is still not clearly investigated until now. To probe the issue, a rheometer was used, and polymer chain relaxation time τ was obtained by the rheological test to compare it with spin-coating time t in the spin-coating process. As mentioned above (Section 2.2), the PFO toluene dilute solution conformed to the Zimm model and the semidilute unentangled solution conformed to the Rouse model, but the semidilute entangled solution is not discussed here because the precursor solution used for device fabrication is usually not at a high concentration. In the Zimm model, the time at which the molecular chain diffuses the distance of its own size is called the Zimm relaxation time τZ(32)

2.4. 11

In the Rouse model, the time at which the molecular chain of the polymer diffuses the distance of its own size is called as the Rouse relaxation time τR(32)

2.4. 12

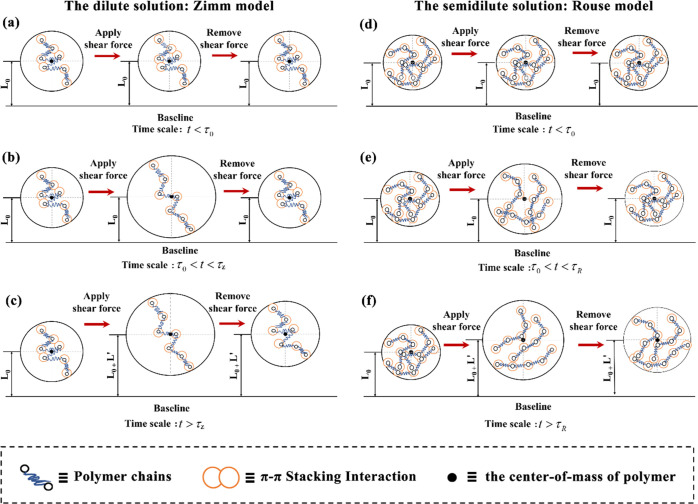
Here, τ0 ≈ ηsb3/kT is the Kuhn unit relaxation time, k = 1.38 × 10–23 J K–1 is the Boltzmann constant, and T is the temperature. As mentioned above, toluene is the θ solvent of PFO at 25 °C, so v = 0.5 can be obtained, and it is the reciprocal of the fractal dimension of the polymer. The calculated results of the relaxation time are shown in Table 2 (the detailed information of the calculation process is given in the Supporting Information). As we know, polymers are a class of soft matter that have viscoelastic properties. In fact, when the spin-coating time t was less than the Kuhn unit relaxation time τ0, the PFO chain could not move even if it was subjected to an external force and showed an elastic response, as shown in Figure 5a,d. But when this time scale of spin coating was greater than the Zimm relaxation time τZ or Rouse relaxation time τR, the PFO chains could move in a diffuse manner as if they were subjected to an external force, thereby presenting a liquid response, as shown in Figure 5c,f. And when PFO was subjected to an external force, the classical viscoelastic effect emerged at a time period τ0 < t < τZ/τR, as shown in Figure 5b,e. Generally, the spin-coating time t is about 4 ∼ 10 s, and obviously, it is several orders of magnitude longer than the results shown in Table 2. Actually, the spin-coating time is much longer than the relaxation time of chain movement of PFO; thus, chain conformations in the whole solution are changed during the spin-coating process. This indicated that the shear force in the spin-coating process had an essential influence on the dynamic evolution process of the transformation of the chain conformation from the precursor solution to the film. The chain conformation could not be transferred from the solution to the film in the spin-coating process because it was just the chain’s conformation rather than chain’s aggregation (as the PFO β conformation is a kind of ordered aggregation).41 Therefore, the relationship between chain conformations while transforming from a solution to a film is found for the first time. It is significant to understand the solution behaviors of conjugated polymers and the essential relationship between the solution and the film in depth. This research provided a new way to study the dynamic evolution process of the macromolecular chains from precursor solutions to films and proved their physical essential correlation.

Table 2. PFO Chain Relaxation Time.

concentration regimes Kuhn unit relaxation time τ0 (s) polymer chain relaxation time τZ (τR) (s)
dilute solution 2.43 × 10–8 7.56 × 10–6
semidilute unentangled solution 2.43 × 10–8 5.01 × 10–5
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Diagrams of molecular chain motion of PFO in dilute solutions with different time scales: (a) t < τ0, (b) τ0 < t < τZ, and (c) t > τZ, and in semidilute unentangled solutions: (d) t < τ0, (e) τ0 < t < τR, and (f) t > τR after applying or removing the shear force.

3. Conclusions

Using a rheometer and by applying the Zimm model (for the dilute solution), the Rouse model (for the semidilute unentangled solution), and the Doi–Edwards model (for the semidilute entangled solution), critical concentrations (c* and ce) and scaling exponents of PFO/toluene solutions are obtained. According to ηsp ∝ ca, the scaling exponent values of the PFO/toluene solution in the dilute, semidilute unentangled, and semidilute entangled solutions are 0.98, 1.98, and 4.65, respectively, which are nearly consistent with theoretical values of 1, 2, and 4.7 in the θ solvent, respectively. This result indicates that toluene is a θ solvent for PFO at 25 °C. Moreover, in the research, some important parameters in connection with PFO intrinsic properties were also obtained by calculations, such as the intrinsic viscosity of the PFO chain [η] = 136.84 mL g–1, the root-mean-square end-to-end distance R = 41.4 nm, and the Kuhn segment length b = 6.28 nm. Finally, the effect of the spin-coating process from the precursor solution to the film on the transformation of the chain conformation revealed that the spin-coating time of film formation was much longer than the PFO chain relaxation time (t ≫τZ(τR)), indicating that the spin-coating process has an essential influence on the transformation of the chain conformation from the solution to the film. The research proves that the transformation of chain conformation happened in the spin-coating process. The research is of great significance not only to understand the solution behaviors of conjugated polymers in depth but also to reveal the relationship between the solution behaviors of chains and the film’s condensed state structure in the process of dynamic evolution from the solution to the film to manipulate the condensed state structure of semirigid conjugated polymers to fabricate photoelectronic devices of high efficiency.

4. Experimental Section

4.1. Materials and Sample Preparation

PFO was purchased from American Dye Source, ADS329BE. The weight-average molecular weight (Mw) was 127192 g mol–1, and the polydispersity index was 1.12 (Figure S1). Chromatographically pure toluene was chosen as the solvent and was obtained from Beijing Chemical Co., China. Solutions of PFO with different concentrations were all prepared by dissolving different amounts of PFO in toluene with stirring at 75 °C in the dark for 24 h first and then cooling at room temperature for 3 h.

4.2. Measurements

All rheological measurements were carried out with a TA instruments DHR-2 stress-controlled rheometer. A temperature-controlled Peltier plate was used for controlling the temperature. Dynamic oscillatory experiments were performed with a frequency range from 10 to 1000 rad s–1. To prevent solvent evaporation, two 60 mm iron plates with semicircles were covered around the plate geometry, and silicone grease was filled around the gap of the iron plates. The weight-average molecular weight (Mw) and the polydispersity index (PDI) of PFO were measured by means of gel permeation chromatography (GPC) equipped with a Shimadzu RID-10A refractive index detector, using polystyrene as a standard and THF as the eluent at a flow rate of 1.0 mL min–1. Light scattering (LS) measurements were carried out with an LV-CGS3 dynamic/static combined light scattering instrument made in Germany. All solutions used need to be prepared into a dust-free solution by filtering the different solvents with a 220 nm filter membrane three to five times. The shape of the single chain and the second virial coefficient (A2) of the solutions were obtained by a static light scattering (SLS) test. The scattering angle test range was changed from 50 to 150° (measured step size was 10°, measured three times for each angle, and the error range of the three measurements was controlled within 10%).

Acknowledgments

This work was supported by grants from the National Natural Science Foundation of China (91333103 and 21574053).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c06144.

  • Calculation of the Kuhn length (b) and Kuhn segments (N) (Appendix 1.1); calculation of the Kuhn unit relaxation time (τ0) and polymer chain relaxation time (τZ(τR)) (Appendix 1.2); GPC result (Appendix 1.3 Figure S1); and LS result (Appendix 1.4 Figure S2) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c06144_si_001.pdf (221.8KB, pdf)

References

  1. Scherf U.; Emil J. W. Semiconducting polyfluorenes—towards reliable structure–property relationships. Adv. Mater. 2002, 14, 477–487. . [DOI] [Google Scholar]
  2. Friend R. H.; Gymer R. W.; Holmes A. B.; Burroughes J. H.; Marks R. N.; Taliani C.; Bradley D. D. C.; Dos Santos D. A.; Bredas J. L.; Logdlund M.; Salaneck W. R. Electroluminescence in conjugated polymers. Nature 1999, 397, 121–128. 10.1038/16393. [DOI] [Google Scholar]
  3. Dimitrakopoulos C. D.; Malenfant P. R. L. Organic thin film transistors for large area electronics. Adv. Mater. 2002, 14, 99.. [DOI] [Google Scholar]
  4. Huynh W. U.; Dittmer J. J.; Alivisatos A. P. Hybrid nanorod-polymer solar cells. Science 2002, 295, 2425–2427. 10.1126/science.1069156. [DOI] [PubMed] [Google Scholar]
  5. Brabec C. J.; Sariciftci N. S.; Hummelen J. C. Plastic solar cells. Adv. Funct. Mater. 2001, 11, 15–26. . [DOI] [Google Scholar]
  6. Sariciftci N. S.; Smilowitz L.; Heeger A. J.; Wudl F. Photoinduced electron transfer from a conducting polymer to buckminsterfullerene. Science 1992, 258, 1474–1476. 10.1126/science.258.5087.1474. [DOI] [PubMed] [Google Scholar]
  7. Günes S.; Neugebauer H.; Sariciftci N. S. Conjugated polymer-based organic solar cells. Chem. Rev. 2007, 107, 1324–1338. 10.1021/cr050149z. [DOI] [PubMed] [Google Scholar]
  8. Sirringhaus H.; Brown P. J.; Friend R. H.; Nielsen M. M.; Bechgaard K.; Langeveld-Voss B. M. W.; Spiering A. J. H.; Janssen R. A. J.; Meijer E. W.; Herwig P.; de Leeuw D. M. Two-dimensional charge transport in self-organized, high-mobility conjugated polymers. Nature 1999, 401, 685–688. 10.1038/44359. [DOI] [Google Scholar]
  9. McQuade D. T.; Pullen A. E.; Swager T. M. Conjugated polymer-based chemical sensors. Chem. Rev. 2000, 100, 2537–2574. 10.1021/cr9801014. [DOI] [PubMed] [Google Scholar]
  10. Thompson B. C.; Frechet J. M. J. Polymer-fullerene composite solar cells. Angew. Chem., Int. Ed. 2008, 47, 58–77. 10.1002/anie.200702506. [DOI] [PubMed] [Google Scholar]
  11. Bright D. W.; Galbrecht F.; Scherf U.; Monkman A. P. β phase formation in poly(9,9-di-n-decylfluorene) thin films. Macromolecules 2010, 43, 7860–7863. 10.1021/ma101570u. [DOI] [Google Scholar]
  12. Hayer A.; Khan A. L. T.; Friend R. H.; Köhler A. Morphology dependence of the triplet excited state formation and absorption in polyfluorene. Phys. Rev. B 2005, 71, 241302 10.1103/PhysRevB.71.241302. [DOI] [Google Scholar]
  13. Bradley D. D. C.; Grell M.; Xiao L.; Mellor H.; Grice A.; Inbasekaran M.; Woo E. P. Influence of aggregation on the optical properties of a polyfluorene. Proc. SPIE 1997, 3145, 254–259. [Google Scholar]
  14. Khan A. L. T.; Sreearunothai P.; Herz L. M.; Banach M. J.; Köhler A. Morphology-dependent energy transfer within polyfluorene thin films. Phys. Rev. B 2004, 69, 085201 10.1103/PhysRevB.69.085201. [DOI] [Google Scholar]
  15. Lu H. H.; Liu C. Y.; Chang C. H.; Chen S. A. Self-dopant formation in poly(9,9-di-n-octylfluorene) via a dipping method for efficient and stable pure-blue electroluminescence. Adv. Mater. 2007, 19, 2574–2579. 10.1002/adma.200602632. [DOI] [Google Scholar]
  16. Peet J.; Brocker E.; Xu Y.; Bazan G. C. Controlled β-phase formation in poly(9,9-di-n-octylfluorene) by processing with alkyl additives. Adv. Mater. 2008, 20, 1882–1885. 10.1002/adma.200702515. [DOI] [Google Scholar]
  17. Xia R.; Heliotis G.; Hou Y.; Bradley D. D. C. Fluorene-based conjugated polymer optical gain media. Org. Electron. 2003, 4, 165–177. 10.1016/j.orgel.2003.08.009. [DOI] [Google Scholar]
  18. O’Carroll D.; Lieberwirth I.; Redmond G. Microcavity effects and optically pumped lasing in single conjugated polymer nanowires. Nat. Nanotechnol. 2007, 2, 180–184. 10.1038/nnano.2007.35. [DOI] [PubMed] [Google Scholar]
  19. Rothe C.; Galbrecht F.; Scherf U.; Monkman A. The β-phase of poly(9,9-dioctylfluorene) as a potential system for electrically pumped organic lasing. Adv. Mater. 2006, 18, 2137–2140. 10.1002/adma.200600901. [DOI] [Google Scholar]
  20. Rahman M. H.; Chen C. Y.; Liao S. C.; Chen H. L.; Tsao C. S.; Chen J. H.; Liao J. L.; Ivanov V. A.; Chen S. A. Segmental alignment in the aggregate domains of poly(9,9-dioctylfluorene) in semidilute solution. Macromolecules 2007, 40, 6572–6578. 10.1021/ma071036f. [DOI] [Google Scholar]
  21. Justino L. L. G.; Ramos M. L.; Knaapila M.; Marques A. T.; Kudla C. J.; Scherf U.; Almásy L.; Schweins R.; Burrows H. D.; Monkman A. P. Gel formation and interpolymer alkyl chain interactions with poly(9,9-dioctylfluorene-2,7-diyl) (PFO) in toluene solution: results from NMR, SANS, DFT, and semiempirical calculations and their implications for PFO β-phase formation. Macromolecules 2011, 44, 334–343. 10.1021/ma102235r. [DOI] [Google Scholar]
  22. Huang L.; Zhang L. L.; Huang X. N.; Li T.; Liu B.; Lu D. Study of the α-conformation of the conjugated polymer poly(9,9-dioctylfluorene) in dilute solution. J. Phys. Chem. B 2014, 118, 791–799. 10.1021/jp406598x. [DOI] [PubMed] [Google Scholar]
  23. Huang L.; Li T.; Liu B.; Zhang L. L.; Bai Z. M.; Li X. N.; Huang X. N.; Lu D. A transformation process and mechanism between the α-conformation and β-conformation of conjugated polymer PFO in precursor solution. Soft Matter 2015, 11, 2627–2638. 10.1039/C5SM00074B. [DOI] [PubMed] [Google Scholar]
  24. Li T.; Huang L.; Bai Z. M.; Li X. N.; Liu B.; Lu D. Study on the forming condition and mechanism of the β conformation in poly (9,9-dioctylfluorene) solution. Polymer 2016, 88, 71–78. 10.1016/j.polymer.2016.02.015. [DOI] [Google Scholar]
  25. Li T.; Liu B.; Zhang H.; Ren J. X.; Bai Z. M.; Li X. N.; Ma T. N.; Lu D. Effect of conjugated polymer poly (9,9-dioctylfluorene) (PFO) molecular weight change on the single chains, aggregation and β phase. Polymer 2016, 103, 299–306. 10.1016/j.polymer.2016.09.072. [DOI] [Google Scholar]
  26. Franck A. J.Understanding Instrument Inertia Corrections in Oscillation. TA Instruments.
  27. Zhang E.; Dai X.; Dong Z.; Qiu X.; Ji X. Critical concentration and scaling exponents of one soluble polyimide—from dilute to semidilute entangled solutions. Polymer 2016, 84, 275–285. 10.1016/j.polymer.2016.01.001. [DOI] [Google Scholar]
  28. Lu F.; Wang L.; Zhang C.; Cheng B.; Liu R.; Huang Y. Influence of temperature on the solution rheology of cellulose in 1-ethyl-3-methylimidazolium chloride/dimethyl sulfoxide. Cellulose 2015, 22, 3077–3087. 10.1007/s10570-015-0740-x. [DOI] [Google Scholar]
  29. De Gennes P. G.; Witten T. A. Scaling concepts in polymer physics. Phys. Today 1980, 33, 51–54. 10.1063/1.2914118. [DOI] [Google Scholar]
  30. Stauffer D.; Coniglio A.; Adam M. Gelation and critical phenomena. Adv. Polym. Sci. 1982, 44, 103–158. [Google Scholar]
  31. Muthukumar M. Dynamics of polymeric fractals. J. Chem. Phys. 1985, 83, 3161–3168. 10.1063/1.449222. [DOI] [Google Scholar]
  32. Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press: NewYork, 2003; pp 311–373. [Google Scholar]
  33. Colby R. H. Structure and linear viscoelasticity of flexible polymer solutions: comparison of polyelectrolyte and neutral polymer solutions. Rheol. Acta 2010, 49, 425–442. 10.1007/s00397-009-0413-5. [DOI] [Google Scholar]
  34. Liu Y.; Li Y.; Xiong H. Dielectric chain dynamics of side-chain liquid crystalline polymer. ACS Macro Lett. 2013, 2, 45–48. 10.1021/mz3005988. [DOI] [PubMed] [Google Scholar]
  35. Zhu X.; Chen X.; Saba H.; Zhang Y.; Wang H. Linear viscoelasticity of poly(acrylonitrile-co-itaconic acid)/1-butyl-3-methylimidazolium chloride extended from dilute to concentrated solutions. Eur. Polym. J. 2012, 48, 597–603. 10.1016/j.eurpolymj.2011.12.014. [DOI] [Google Scholar]
  36. Huggins M. L. The viscosity of dilute solutions of long-chain molecules. IV. dependence on concentration. J. Am. Chem. Soc. 1942, 64, 2716–2718. 10.1021/ja01263a056. [DOI] [Google Scholar]
  37. Kraemer E. O. Molecular weights of celluloses and cellulose derivates. Ind. Eng. Chem. 1938, 30, 1200–1203. 10.1021/ie50346a023. [DOI] [Google Scholar]
  38. Gardas R. L.; Dagade D. H.; Coutinho J. A. P.; Patil K. J. Thermodynamic studies of ionic interactions in aqueous solutions of imidazolium-based ionic liquids [Emim][Br] and [Bmim][Cl]. J. Phys. Chem. B 2008, 112, 3380–3389. 10.1021/jp710351q. [DOI] [PubMed] [Google Scholar]
  39. Lu F.; Song J.; Cheng B. W.; Ji X. J.; Wang L. J. Viscoelasticity and rheology in the regimes from dilute to concentrated in cellulose 1-ethyl-3-methylimidazolium acetate solutions. Cellulose 2013, 20, 1343–1352. 10.1007/s10570-013-9885-7. [DOI] [Google Scholar]
  40. Bright D. W.Photophysical Studies of Beta Phase Formation in Poly(9,9-di-n-alkylfluorenes); Durham University, 2011. [Google Scholar]
  41. Bai Z.; Liu Y.; Li T.; Li X.; Liu B.; Liu B.; Lu D. Quantitative study on β-phase heredity based on poly(9,9-dioctylfluorene) from solutions to films and the effect on hole mobility. J. Phys. Chem. C 2016, 120, 27820–27828. 10.1021/acs.jpcc.6b08941. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c06144_si_001.pdf (221.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES