Mini-Review on Structure–Reactivity Relationship for Aromatic Molecules: Recent Advances

Abstract

Recent advances in quantifying nucleophilic reactivities in chemical reactions and intermolecular interactions of aromatic molecules are reviewed. This survey covers experimental (IR frequency shifts induced by hydrogen bonding) and theoretical (modeling of potential energy surfaces, atomic charges, molecular electrostatic potential) approaches in characterizing chemical reactivity. Recent advances in software developments assisting the evaluation of the reactive sites for electrophilic aromatic substitution are briefly discussed.

Introduction

Characterizing reactivities of molecular systems is a major theme of chemical research. Various methods have been employed in establishing relationships between chemical structure and reactivity. Possibilities to predict properties of complex molecules with the aid of theoretical or derived from experiment relationships are of critical importance in synthetic chemistry, the developments of new drugs for medical use, the synthesis of materials with specific functionalities, the synthesis of novel components for energy conversion systems, and many other applications. In organic chemistry, the seminal studies of Hammett¹ were the most significant step forward in transforming the field into a quantitative science. The insights on the dependencies between specific structural characteristics and reactivity provided by the Hammett equation have enabled the establishment of major concepts in organic chemistry, such as inductive, mesomeric, and steric effects. The applications of the Hammett approach have also contributed to understanding the mechanisms of a number of organic reactions, especially when combined with kinetic measurements and spectroscopic observations. Besides numerous applications,^2,3 more recent studies have focused on the theoretical concepts associated with the substituent constants, as well as the development of novel approaches for their evaluation.³⁻⁷

The impressive progress in the development of quantum mechanical methods and computational technologies during the past half-century has offered new opportunities for advances in the field of chemical reactivity. Even earlier, the frontier orbital methodology of Fukui⁸ provided key insights into the electronic factors governing chemical reactivity. The development of reactivity theory within the formalism of density functional theory^9,10 has opened new opportunities for the quantitative description of the overall reactivity of chemical systems. Domingo et al.¹¹ underlined the importance of the electron density distribution as a critical factor determining the ability of molecules to interact with other chemical systems. A significant breakthrough in the field was achieved by the application of the molecular electrostatic potential to the study of molecular structure and the energetics of intermolecular interactions and chemical reactions.¹²⁻¹⁴

Since the pioneering investigations of Hammett,¹ aromatic systems have been the focus in the development of reactivity concepts, methodologies, and applications.¹⁻⁸ The present Mini-Review covers some recent approaches in quantifying the reactivity of aromatic compounds using both experimental and theoretical approaches.

Results and Discussion

Modeling of Potential Energy Surfaces for Reactions of Aromatic Compounds

Numerous studies have investigated the potential energy surfaces for reactions involving aromatic compounds. In this section, we will only illustrate the potential of theoretical methods in characterizing aromatic reactivity by the recent studies of Brinck and co-workers¹⁵ and Liu¹⁶ on the potential energy surfaces for electrophilic aromatic substitution (EAS) reactions. Brinck and co-workers¹⁵ investigated the potential energy surfaces for 18 reactions of electrophilic halogenation of benzene derivatives with Cl₂ in water medium. The strength of these studies is underlined by the excellent correspondence between the theoretically evaluated barrier heights and the experimental kinetic data. Table 1 presents the results of these authors. The experimental barrier heights are from literature sources (see ref (15) and references therein). The energies of critical structures along the reaction paths are evaluated using the M06-2X/6-311G(d,p) method. The effect of solvent is simulated with the IEF-PCM method. Both overall reactivity and positional selectivity are reliably predicted by these transition state theory computations. The results of Brinck et al.¹⁵ illustrate the power of contemporary theoretical methods in evaluating reaction mechanisms and characterizing reactivities of organic molecules

Table 1. Theoretically Evaluated Free Energy Differences (ΔG, in kcal·mol^–1) for Critical Structures along the Reaction Paths–the First Transition State (TS1) and the σ-Complex Intermediate—for Chlorination of Monosubstituted Benzenes with Cl₂ in Water Solvent with Comparison to Experimental Data^a.

X	isomer	TS1	σ-complex	exp.b
OCH3	o-	0.1	3.1	0.8
	m-	9.1	19.8	-
	p-	0.0	0.0	0.0
CH3	o-	0.6	0.6	0.0
	m-	3.2	4.8	2.8
	p-	0.0	0.0	0.2
F	o-	1.2	2.7	1.3
	m-	5.5	8.4	-
	p-	0.0	0.0	0.0
Cl	o-	0.1	2.0	0.4
	m-	3.7	5.7	-
	p-	0.0	0.0	0.0
CF3	o-	1.5	2.0	1.4
	m-	0.0	0.0	0.0
	p-	2.3	2.4	1.8
CN	o-	0.1	0.4	0.4
	m-	0.0	0.0	0.0
	p-	1.4	1.6	1.0

^aThe theoretical estimates are from M06-2X/6-311G(d,p) computations with IEF-PCM solvation. The experimental kinetic data are from literature sources

^bFor the sources of the experimental kinetic data see ref (15) and references therein. Adapted from ref (15) with permission from the authors.

In a valuable theoretical work, Liu¹⁶ investigated the identity exchange reactions of a series of substituted benzenes with hydrogen fluoride, using boron trifluoride as catalyst in the gas phase (Scheme 1). The barrier heights for 37 reactions modeling substitutions at the meta and para positions of 18 monosubstituted benzenes derivatives as well as the unsubstituted benzene were theoretically evaluated with the M06-2X/aug-cc-pVDZ method by applying transition state theory computations (Table 2). In addition, Liu used theoretical Hirshfeld charges in rationalizing the reactivity of the benzene derivatives in the electrophilic substitutions investigated. Very good correlations between barrier heights and Hirshfeld charges at the ring carbons were obtained. The plot of ΔE vs q_C(Hirsh) is shown in Figure 1.

Scheme 1. Identity EAS Exchange Reactions of Benzene Derivatives with Hydrogen Fluoride Studied in the Work of Liu.¹⁶ Adapted with Permission from Ref (16). Copyright 2015 American Chemical Society.

Table 2. Barrier Heights (in kcal·mol^–1) for the Identity Exchange EAS Reaction of Monosubstituted Benzenes with Hydrogen Fluoride and Hirshfeld Charges (in Electrons) Are Given for meta and para Carbons from M06-2X/aug-cc-pVDZ Computations^a.

R	isomer	q(Hirsh)	barrier height	R	isomer	q(Hirsh)	barrier height
H		–0.0498	28.41	tBu	m-	–0.0514	27.63
Cl	m-	–0.0414	31.57		p-	–0.0554	25.34
	p-	–0.0488	27.35	CCl3	m-	–0.0417	31.10
Et	m-	–0.0506	27.79		p-	–0.0387	31.89
	p-	–0.0554	25.23	CF3	m-	–0.0399	32.23
F	m-	–0.0419	31.64		p-	–0.0368	33.16
	p-	–0.0560	25.38	CHO	m-	–0.0449	31.16
Me	m-	–0.0506	28.45		p-	–0.0337	32.96
	p-	–0.0558	24.59	CN	m-	–0.0380	33.47
NH2	m-	–0.0501	30.29		p-	–0.0326	33.94
	p-	–0.0717	11.09	COF	m-	–0.0408	33.00
NMe2	m-	–0.0525	29.83		p-	–0.0292	34.90
	p-	–0.0748	12.18	NH3+	m-	–0.0082	53.02
OH	m-	–0.0474	29.56		p-	–0.0048	54.92
	p-	–0.0658	16.69	NO2	m-	–0.0365	34.29
Pr	m-	–0.0508	28.49		p-	–0.0296	35.37
	p-	–0.0554	24.69	NO	m-	–0.0420	31.85
					p-	–0.0298	34.08
				SO3H	m-	–0.0356	33.68
					p-	–0.0296	35.33

^aAdapted from ref (16), with permission from the author.

Figure 1.

Strong correlation for 38 electrophilic aromatic substitution reactions between the computed barrier heights and the Hirshfeld charges on the regioselective carbon atoms in Scheme 1.

The theoretical research of Liu¹⁶ illustrates very well the effects of aromatic substituents on the reaction barriers for a considerable number of EAS reactions but also proposes a suitable theoretical quantity—Hirshfeld charge on the regiospecific carbon atom—as a nucleophilic reactivity descriptor. The investigation of Liu¹⁶ underlines the usefulness of theoretically evaluated quantities in describing the reactivity of aromatic molecules. The application of several differently defined atomic charges in quantifying aromatic reactivity is discussed later in the present survey.

Applications of O–H Stretching Frequency Shifts upon Hydrogen Bonding in Quantifying Aromatic Reactivity

The measurements of kinetic constants for a series of compounds provide a direct assessment of reactivity as well as insights concerning the structural factors determining the reaction rates. Kinetic studies involve, nonetheless, considerable experimental effort and the necessity of special equipment. For many systems, the investigator needs a more efficient approach in characterizing reactivity and positional selectivity. Quantum chemistry computations and various theoretical reactivity parameters provide appropriate solutions in this respect. In spite of the success of the theoretical procedures developed, it has always been important to employ suitable experimental quantities that would provide sufficiently reliable advance information on reactivity and positional selectivity. Basicity scales for molecules in the gas phase and in solution have found wide application in this respect. Laurence et al.¹⁷ defined the basicity of an extensive number of organic molecules belonging to different classes on the basis of measured infrared frequency shifts resulting from hydrogen bonding with proton donating species, containing an O–H group. In recent studies,¹⁸ we explored the possibility of applying the shifts of O–H stretching frequencies [Δν(OH)_exp] for selected proton donor molecules upon hydrogen bonding as experimental measures of reactivity for series of aromatic molecules. We investigated the relationships between the Δν(OH)_exp shifts induced by π-hydrogen bonding with the aromatic π-electron system and kinetic constants for electrophilic aromatic nitration reactions, as well as the quaternization of pyridine derivatives with methyl iodide.

Nitration of Aromatic Derivatives by Methyl Nitrate

The mechanisms of electrophilic aromatic substitution (EAS) reactions involve an initial interaction of the attaching electrophile with the π-electrons of the aromatic species.² Considering the nature of this initial step, we investigated the correlations between phenol Δν(OH)_exp shifts induced by π-hydrogen bonding with aromatic substrates. The experimentally recorded phenol Δν(OH)_exp shifts are juxtaposed to the relative rate constants (log k_rel) for the nitration of a series of aromatic derivatives (methylbenzenes, monoalkylbenzenes, halobenzenes, and anisole) by methyl nitrate in the presence of BF₃ in nitromethane solvent (literature kinetic data, see footnotes to Table 1 in ref (18)). The reaction is illustrated in Scheme 2.

Scheme 2. Schematic Representation for CH₃ONO₂–BF₃ Rrene Nitration.

The rate constants reported in Table 3 reflect the overall reactivity of the aromatic derivatives in the studied reactions, which may involve substitutions at different ring positions of the same compound. Therefore, no perfect correlation between the Δν(OH)_exp shifts and log k_rel can be expected. It should be emphasized that measuring the shifts of the phenol O–H stretching frequency, as induced by π-hydrogen bonding with the aromatic ring, is a very simple experiment that only requires the recording of a single IR spectrum for the complex formed. Therefore, the established relationship (Figure 2) offers a straightforward experimental approach in characterizing the nucleophilic reactivity of aromatic molecules. Limitations to the proposed approach may arise from the necessity that the initial interaction between the aromatic substrate and the attacking electrophile controls the reaction rate. As is well-known, nonetheless, aromatic rings richer in electron density participate more readily in EAS reactions.²

Table 3. Relative Overall Rate Constants (log k_rel)^a for the Nitration of Benzene, Alkylbenzenes, Halobenzenes, and Anisole. Also Reported Are Shifts of the Molecular Electrostatic Potential at 1.5 Å over the Centroid of the Aromatic Ring; and Shifts of Phenol ν(OH) Stretching Frequencies (in cm^–1) upon π-Hydrogen Bonding in CCl₄ Solvent^a.

species	log krela	Δν(OH)exp [cm–1]	ΔV (1.5) (a.u.) B3LYP/6-311++G(3df,2pd)b
benzene	0.00	48	0.0000
toluene	1.41	58	–0.0029
ethylbenzene	1.36	59	–0.0033
isopropylbenzene	1.32	55	–0.0030
tert-butylbenzene	1.29	60	–0.0033
1,2-dimethylbenzene	2.28	68	–0.0048
1,3-dimethylbenzene	2.46	69	–0.0051
1,4-dimethylbenzene	2.47	71	–0.0050
1,2,3-trimethylbenzene	2.96	75	–0.0073
1,2,4-trimethylbenzene	3.03	78	–0.0072
1,3,5-trimethylbenzene	2.98	77	–0.0075
1,2,3,4-tetramethylbenzene	3.33	87	–0.0095
1,2,3,5-tetramethylbenzene	3.27	88	–0.0098
1,2,4,5-tetramethylbenzene	3.34	85	–0.0091
pentamethylbenzene	3.41	93	–0.0117
fluorobenzene	–0.92	38	0.0114
chlorobenzene	–1.52	33	0.0134
bromobenzene	–1.52	37	0.0140
iodobenzene	–1.00	38
anisole	2.27	60	–0.0020
rc		0.991	0.969

^aRelative rate with respect to benzene (k_benzene = 1). See ref (18) and references therein for the sources of experimental kinetic data and Δν(OH)_exp shifts.

^bTheoretical computations for modeled nitromethane solvent.

^cThe correlation coefficients (absolute values are shown) refer to the linear regressions between the experimental log k_rel values and the predicted values according the 2nd order polynomial expressions.

Figure 2.

Plot (2nd order polynomial) of relative rate constants (log k_rel) for the nitration of benzene, alkylbenzenes, halobenzenes, and anisole vs shifts of phenol ν(OH) stretching frequency shifts upon π-hydrogen bonding.

An alternative theoretical approach in rationalizing reactivities was also tested for the nitration reaction considered. It was established that the change of the molecular electrostatic potential (MESP) over the centroid of the aromatic ring (at 1.5 Å over the ring) may also be employed in quantifying reactivity. The MESP is defined by the relation:¹²

1

In this expression, Z_A and R_A are the charge and position vector of nucleus A, ρ(r) is the electron density function, and r′ is an integration variable. The last column in Table 3 lists the shifts of MESP values [ΔV(1.5)], relative to benzene] for the compounds of the series investigated. The B3LYP/6-311++G(3df,2pd) and MP2/6-311++G(3df,2pd) computations were applied in estimating ΔV(1.5).¹⁸ The integral equation formalism of the polarizable continuum model (IEF-PCM) method was applied in modeling the nitromethane solvent. Table 3 shows the results from B3LYP computations. A quite satisfactory correlation (r = 0.969) between log k_rel and ΔV(1.5) was found. As discussed, for a number of compounds from the series, monosubstitutions at different positions in the ring are possible. Thus, the reported rate constants reflect the overall reactivity of the aromatic species. If the analysis is restricted to aromatic substrates with identical positions for monosubstitution (Table 4), an excellent correlation between log k_rel and ΔV(1.5) is obtained (r = 0.998).

Table 4. Relative Rate Constants (log k_rel)^a for the Nitration of Alkylbenzenes with Identical Position for Substitution, Computed Values of Molecular Electrostatic Potentials at 1.5 Å over the Ring Centroid (in a.u., Relative to Benzene) from MP2/6-311++G(3df,2pd) Computations.

species	log krela	ΔV(1.5)
benzene	0.00	0.0000
1,4-dimethylbenzene	2.47	–0.0050
1,3,5-trimethylbenzene	2.98	–0.0076
1,2,3,4-tetramethylbenzene	3.33	–0.0094
1,2,3,5-tetramethylbenzene	3.27	–0.0098
1,2,4,5-tetramethylbenzene	3.34	–0.0090
pentamethylbenzene	3.41	–0.0116
r		0.998

^aFrom ref (18) and references therein.

Quaternization of Substituted Pyridines with Ethyl Iodide

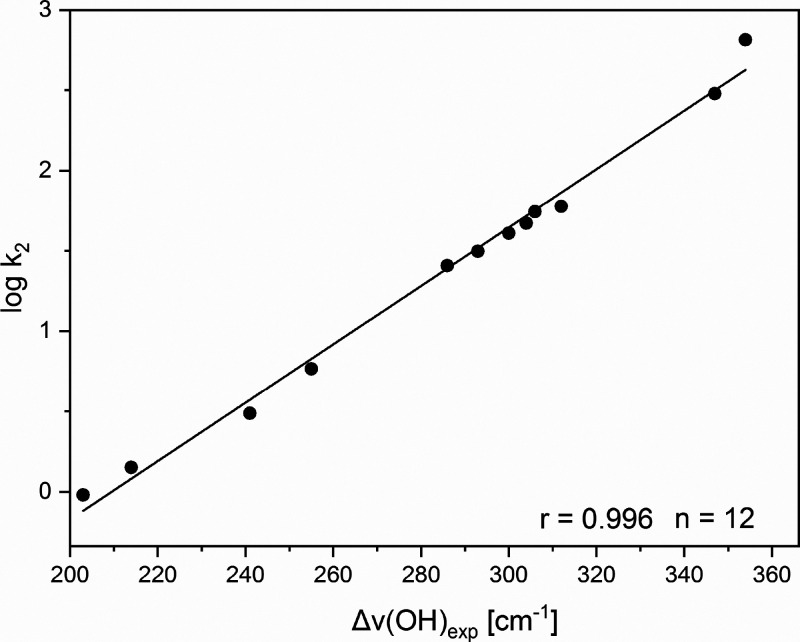
In a recent study,¹⁹ the relationships between electronic structure parameters and shifts of O–H stretching frequency upon hydrogen bonding for series of substituted pyridines were analyzed. Johnson et al.²⁰ reported the rates of quaternization of 3- and 4-substituted pyridines with ethyl iodide in different solvents. As already discussed, Laurence et al.¹⁷ have characterized the basicity of organic molecules belonging to different classes by studying the IR frequency shifts resulting from hydrogen bonding with O–H group containing proton donors. These investigations included a series of six-membered aromatic N-heterocycles.²¹Table 5 illustrates the dependence between the measured rate constants for the quaternization reaction and the shifts of O–H stretching frequencies of 4-fluorophenole (in CCl₄ solvent) induced by hydrogen bonding with substituted pyridines. A very high correlation coefficient (r = 0.996) characterizes the relationship between these two quantities. Table 5 includes derivatives, for which both rate constants and Δν(OH)_exp shifts are available. The plot between log k₂ and Δν(OH)_exp is shown in Figure 3.

Table 5. Rate Constants for the Quaternization of 3- and 4-Substituted Pyridines with Ethyl Iodide^a Compared to Δν(OH)_exp Shifts of 4-Fluorophenol upon Hydrogen Bonding.

species	log k2a	Δν(OH)expb
pyridine	1.408	286
3-bromopyridine	0.487	241
3-cyano	–0.020	203
3-methyl	1.609	300
4-methyl	1.672	304
4-ethyl	1.743	306
4-methoxy	1.776	312
4-acetyl	0.765	255
4-cyano	0.152	214
4-phenyl	1.497	293
4-amino	2.477	347
4-methylamino	2.812	354
r, cor. coef. (linear)		0.996

^aIn nitromethane solvent, from ref (20).

^bFrom ref (21).

Figure 3.

Rates of quaternization of substituted pyridines by ethyl iodide vs Δν(OH)_exp shifts of 4-fluorophenole induced by hydrogen bonding with the pyridine derivatives. Reprinted with permission from ref (19). Copyright 2022 Elsevier.

Hydrogen Bonding Probes Electron Density Variations at the Basic Center in Series of Aromatic Molecules

In this section, we cover recent research that focuses on the possibilities of gaining insights into the trend of electron density variations at a reaction center within a series of structurally related aromatic molecules. The shifts of O–H stretching frequency of a selected proton-donating molecule upon hydrogen bonding is employed as an experimental probe. In the general case, the frequency shifts induced by hydrogen bonding have been shown to characterize the overall basicity of molecules.¹⁷ In addition to the electron density at the proton-accepting basic center, other factors may also influence the reactivity of molecules in hydrogen bonding within a series of related molecules. These factors include steric hindrance, effects of molecular strain, as well as the presence strongly polarizing substituents in close proximity of the basic center. These additional factors may obscure the potential good correspondence between electron density variations and experimental spectroscopic shifts. It is, therefore, of interest to explore the correlations between Δν(OH)_exp shifts induced by hydrogen bonding and theoretical electronic structure parameters for structurally related aromatic molecules. Two series of aromatic derivatives were investigated: substituted alkyl benzoates and substituted pyridines.

Substituted Alkyl Benzoates

The relationships between the shifts of methanol O–H stretching frequencies upon hydrogen bonding with the carbonyl basic center for a series of substituted methyl and ethyl benzoates and theoretical quantities characterizing the electron densities at the proton accepting atom were examined in recent research.²² Four different types of atomic charges for the monomeric aromatic molecules were evaluated from ωB97X-D/6-311++G(3df,2pd) and MP2/6-311++G(3df,2pd) computations. The conductor-like polarized continuum model (CPCM) was employed in simulating the CCl₄ solvent used in recording the experimental IR spectra. Table 6 presents the results from the ωB97X-D method. Strong correlations were found between the Δν(OH)_exp shifts and atomic charges (Hirshfeld, CM5, NPA) for the carbonyl oxygen (q_O) in the monomeric benzoates. Because of the different assumptions in evaluating atomic charges, relationships involving these theoretical quantities are not expected to be characterized by very high correlation coefficients. For the series of meta- and para-substituted alkyl benzoates, however, excellent correlations between q_O and Δν(OH)_exp shifts were established. As discussed, the Δν(OH)_exp shifts characterize the overall basicity of molecules.¹⁷ This investigation²² goes a step further by considering the relationship between electron densities and spectroscopic shifts. The strong correlations established between the Δν(OH)_exp and q_O for the series of molecules considered shows that the approach adopted provides an experimental approach to assessing in a quantitative way the trend of variation of the electron density at the proton-accepting atom. Contributions from atom-centered basis function to the molecular electron density are employed in defining the NPA charges. The Hirshfeld and CM5 charges are obtained from procedures involving partitioning of the electron density into atomic domains. The absolute magnitude of charges is quite different for the three methods tested. Nonetheless, the correlations of with the Δν(OH)_exp shifts are quite coherent. The results obtained suggest that the variation of charges provides physical insights, while their magnitude as obtained from the different methods is of lesser significance. The magnitude of charge densities, associated with a given atom in a molecule, is certainly outside the scope of the above spectroscopic experiments.

Table 6. Experimental Hydrogen Bond Induced Δν(OH)_exp shifts (cm^–1) vs Atomic Charges at the Carbonyl Oxygen of the Monomer Esters (in Electrons)^a,^b for a Series of Substituted Alkyl Benzoates.

molecule	qO(Hirsh)	qO(CM5)	qNPAOqO(NPA)	Δν(OH)exp
ethyl benzoate	–0.2919	–0.3420	–0.6368	81
ethyl 4-methylbenzoate	–0.2949	–0.3450	–0.6402	85
ethyl 3-methylbenzoate	–0.2928	–0.3431	–0.6384	83
ethyl 4-methoxybenzoate	–0.2982	–0.3482	–0.6446	88
ethyl 4-(dimethylamino)benzoate	–0.3065	–0.3562	–0.6546	106
ethyl 4-fluorobenzoate	–0.2920	–0.3422	–0.6374	76
ethyl 3-fluorobenzoate	–0.2876	–0.3377	–0.6310	74
ethyl 4-(trifluoromethyl)benzoate	–0.2851	–0.3353	–0.6285	67
ethyl 4-bromobenzoate	–0.2890	–0.3392	–0.6333	72
ethyl 4-cyanobenzoate	–0.2827	–0.3329	–0.6254	60
diethyl terephthalate	–0.2872	–0.3374	–0.6306	69
ethyl 4-nitrobenzoate	–0.2809	–0.3312	–0.6232	57
methyl benzoate	–0.2901	–0.3402	–0.6351	76
methyl 4-methylbenzoate	–0.2933	–0.3432	–0.6386	80
methyl 4-methoxybenzoate	–0.2976	–0.3475	–0.6444	90
methyl 4-(dimethylamino)benzoate	–0.3051	–0.3548	–0.6532	107
methyl 4-fluorobenzoate	–0.2903	–0.3403	–0.6358	78
methyl 4-chlorobenzoate	–0.2878	–0.3378	–0.6323	74
methyl 4-bromobenzoate	–0.2873	–0.3373	–0.6316	74
methyl 4-cyanobenzoate	–0.2808	–0.3309	–0.6235	60
methyl 4-nitrobenzoate	–0.2792	–0.3294	–0.6214	58
correlation coefficient, rb	0.988	0.987	0.989

^aAtomic charges evaluated using the Hirshfeld, CM5 and NPA methods from ωB97X-D/6-311++G(3df,2pd) density functional theory computations (for references to the theoretical methods employed and the experimental Δν(OH)_exp shifts in CCl₄ solvent see ref (22)).

^bAbsolute values of correlation coefficients.

Substituted Pyridines

Comparing experimental Δν(OH)_exp shifts with theoretically evaluated charges in the series of pyridine derivatives offers another excellent platform for testing the application of spectroscopic quantities in following electron density variations. This possibility was explored recently¹⁹ by analyzing the relationships between theoretical charge density parameters and Δν(OH)_exp shifts for the series of meta- and para-substituted pyridines. Atomic charges from the Hirshfeld population analysis and electrostatic potential at nuclei for the pyridine nitrogen (V_N) were evaluated using ωB97X-D/6-311++G(3df,2pd) and MP2/6-311++G(3df,2pd) computations. The CPCM method was applied in modeling the tetrachloromethane solvent. This solvent was applied in the experimental measurement of the Δν(OH)_exp shifts. As already discussed, the Hirschfeld charges describe quite well the reactivity of substituted benzenes (Table 2, Figure 1).¹⁶ An alternative theoretical quantity was also tested. The electrostatic potential at a nucleus (EPN) is a rigorously defined quantum mechanical quantity. It has been shown previously²³ that the electrostatic potential at nuclei provides an accurate description of the ability of molecules to participate in hydrogen bonding. The electrostatic potential at atom Y is defined according to the equation:¹²

2

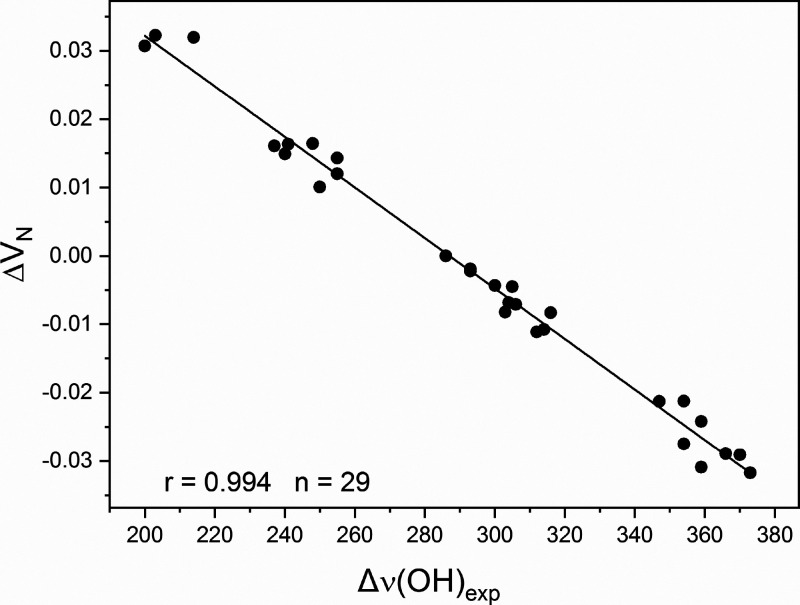
In eq 2, Z_A is the charge on nucleus A positioned at R_A, and ρ(r) is the electron density function. The singular term for R_A = R_Y is excluded. V_Y is determined by the electrostatic potential induced at point R_Y by the positive charges of all nuclei, except for atom Y, and the entire electron density of the molecules. Notably, because of the inverse relationship to R_A and r, in series of molecules with substituents positioned at a distance from the atom Y, the electron density in close proximity of the atomic center Y is expected to be a strong factor in determining V_Y. This is excellently illustrated by the established strong correlation (r = 0.994) between Δν(OH)_exp and ΔV_N (Table 7, Figure 4). The ΔV_N values are the shifts of V_N with respect to the unsubstituted pyridine. Politzer, Murrey, and Clark¹³ argued that electrostatic forces dominate the formation of hydrogen bonds.

Table 7. Experimental Hydrogen Bond Induced Δν(OH)_exp shifts^a (cm^–1), Hirshfeld, CM5 and NPA Atomic Charges (in electrons),^b and Shifts of the Electrostatic Potential at the Nitrogen Atom (ΔV_N, a.u.)^b,c of Monomer Pyridine Derivatives.

	qN(Hirsh)	qN(CM5)	qN(NPA)	ΔVN	Δν(OH)exp
pyridine	–0.1825	–0.3776	–0.4790	0.0000	286
3-fluoropyridine	–0.1700	–0.3653	–0.4563	–0.0149	240
3-chloropyridine	–0.1691	–0.3648	–0.4588	–0.0161	237
3-bromopyridine	–0.1687	–0.3645	–0.4587	–0.0163	241
3-benzoylpyridine	–0.1709	–0.3666	–0.4697	–0.0164	248
3-cyanopyridine	–0.1635	–0.3595	–0.4632	–0.0323	203
3-ethylpyridine	–0.1845	–0.3799	–0.4743	0.0045	305
3-methylpyridine	–0.1842	–0.3797	–0.4742	0.0043	300
4-methylpyridine	–0.1904	–0.3854	–0.4892	0.0069	304
4-ethylpyridine	–0.1902	–0.3852	–0.4883	0.0071	306
4-methoxypyridine	–0.2014	–0.3960	–0.5098	0.0112	312
4-vinylpyridine	–0.1850	–0.3799	–0.4806	0.0019	293
4-acetylpyridine	–0.1697	–0.3651	–0.4573	–0.0143	255
4-cyanopyridine	–0.1607	–0.3563	–0.4506	–0.0320	214
4-N,N-dimethylaminopyridine	–0.2184	–0.4121	–0.5331	0.0289	366
4-phenylpyridine	–0.1854	–0.3804	–0.4812	0.0022	293
4-piperidinopyridine	–0.2200	–0.4137	–0.5347	0.0309	359
4-aminopyridine	–0.2122	–0.4060	–0.5260	0.0213	347
4-chloropyridine	–0.1786	–0.3740	–0.4770	–0.0120	255
4-methylaminopyridine	–0.2182	–0.4117	–0.5344	0.0275	354
4-pyrrolidinopyridine	–0.2209	–0.4144	–0.5373	0.0317	373
4-tert-butylpyridine	–0.1906	–0.3859	–0.4864	0.0083	303
3,4-dimethylpyridine	–0.1918	–0.3872	–0.4839	0.0108	314
3,5-dimethylpyridine	–0.1859	–0.3816	–0.4698	0.0083	316
3,5-dichloropyridine	–0.1566	–0.3529	–0.4396	–0.0307	200
N-methyl-N-pyridin-4-ylhydrazine	–0.2138	–0.4077	–0.5271	0.0212	354
4-(4-methylpiperidino)pyridine	–0.2118	–0.4060	–0.5216	0.0242	359
4-N,N-diethylaminopyridine	–0.2199	–0.4137	–0.5344	0.0302	370
methyl nicotinate	–0.1740	–0.3693	–0.4751	–0.0101	250
r (cor. coeff.)d	0.973	0.974	0.921	0.994

^aIn cm^–1, from ref (21).

^bFrom ωB97X-D/6-311++G(3df,2pd) computations.

^cShifts with respect the V_N for unsubstituted pyridine.

^dAbsolute values of correlation coefficients.

Figure 4.

Plot of ΔV_N vs Δν(OH)_exp shifts in substituted pyridines. Reprinted with permission from ref (19). Copyright 2022 Elsevier.

The Hirshfeld charges at the carbonyl oxygen are shown in the second column of Table 6. The relationship between Δν(OH)_exp shifts and q_N(Hirsh) is characterized by a correlation coefficient r = 0.973. The results obtained show that, as in the case of alkyl benzoates (Table 6), the Δν(OH)_exp shifts characterize quite satisfactorily the trend of variations of the electron density at the basic center within the series investigated. As already discussed, the Δν(OH)_exp shifts may be taken to represent a measure of the overall basicity of molecules.¹⁷ The results obtained reveal that the O–H stretching frequency shifts upon hydrogen bonding may be employed also as a probe of the variations of electron density at a particular basic center in series of structurally related molecules.

The approach outlined is only applicable for cases where the proton accepting site is at a distance from the structural variations, as well as in the absence of significant steric effects. These results underline the importance of hydrogen bonding as a sensitive probe of molecular properties.

Atomic Charges and Aromatic Reactivity

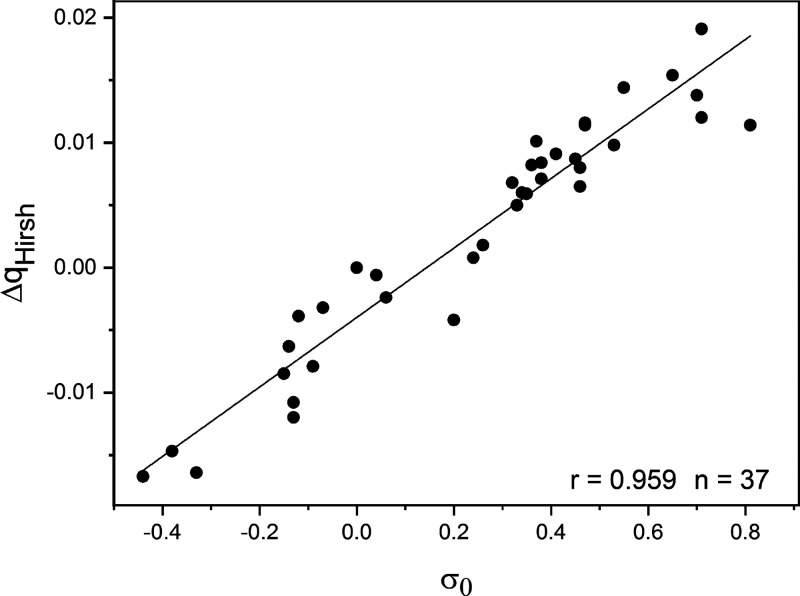
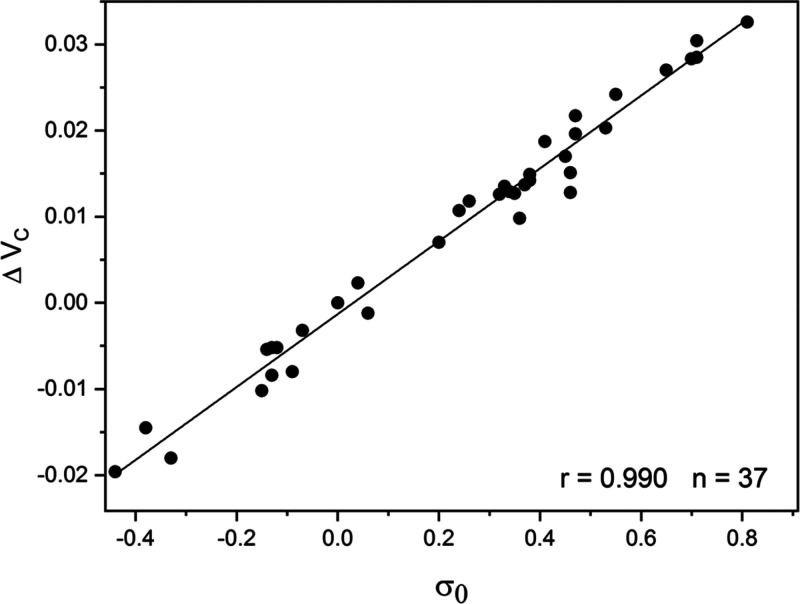
In a recent research study,²⁴ the applicability of several frequently employed methods for atomic charges evaluation in characterizing properties of aromatic molecules was examined. Atomic charges for the ring carbon atoms of monosubstituted benzenes, derived using Mulliken, Hirshfeld, natural population analysis and QTAIM (for references to these theoretical methods, see ref (24)), were correlated with substituent constants for meta and para positions with respect the substituents. The B3LYP and ωB97X-D density functional and MP2 methods combined with the 6-311++G(3df,2pd) basis set were applied in deriving the theoretical quantities. The set of σ⁰ constants for monosubstituted benzenes, evaluated from experimental kinetic data, were correlated with the theoretical atomic charges (q_C). Since the kinetic data are obtained for reactions in different solvents, the theoretical computations refer to molecules in isolation (gas phase). Among the methods tested, the Hirshfeld charges for the meta and para ring carbons provided the most significant correlation with the σ⁰ constants. The best results are obtained from MP2/6-311++G(3df,2pd) method, with a correlation coefficient r = 0.959. This plot between Δq_Hirsh and σ⁰ constants is illustrated in Figure 5 (for table data, see ref (24)). Δq_Hirsh is the difference in carbon charge between the substituted derivative and benzene. The electrostatic potential at the respective carbon atoms (ΔV_C) provides superior correlations with the σ⁰ constants: r = 0.990 for the two DFT methods applied and r = 0.980 for the MP2 results. The correlation between V_C and σ⁰ is shown in Figure 6 (for table data, see ref (24)).

Figure 5.

Correlation between shifts of Hirshfeld charges (Δq_Hirsh) for carbon atoms at meta and para positions in monosubstituted benzenes [calculated with the MP2/6-311++G(3df,2pd) method] and σ_m⁰ and σ_p⁰ substituent constants.

Figure 6.

Plot between σ⁰ constants and ΔV_C (in a.u.) from ωB97X-D/6-311++G(3df,2pd) computations. ΔV_C is the difference in V_C values for the monosubstituted derivative and benzene.

As already discussed, in an earlier study, Liu¹⁶ showed that Hirshfeld charges for the ring carbons are reliable descriptors of reactivity and regioselectivity for the identity exchange reactions of substituted benzenes with hydrogen fluoride.

Molecular Electrostatic Potential and Aromatic Reactivity

Novel studies of chemical reactivity often employ theoretically estimated molecular electrostatic potential values. An excellent review on the subject was recently published by Gadre et al.¹⁴ The authors provide a historical overview of theoretical concepts associated with the molecular electrostatic potential as well as recent advances in its applications in characterizing molecular properties and reactivity. In an early investigation Politzer et al.²⁵ employed minima of the surface electrostatic potential (V_min) in interpreting the effects of amino and nitro substituents on properties of the aromatic ring. Later Gadre and Suresh⁴ applied V_min estimates in analyzing the positional reactivity of substituted benzenes.

As already discussed in the present survey, MESP values at selected points in the molecular space may be employed in rationalizing and predicting chemical reactivity trends for reactions of aromatic compounds. It was also shown in earlier studies that the electrostatic potential at nuclei (eq 2) may be employed as a reactivity descriptor of the reactivity of molecules in hydrogen bonding.²³ The theoretically evaluated V_C values for the meta and para carbon atoms of an extended series of monosubstituted benzenes characterize quantitatively both overall reactivity and positional selectivity.⁷ On the basis of these results, an efficient computational approach for evaluation of aromatic substituent constants was proposed.⁷ The power of EPN in rationalizing and predicting the experimental O–H frequency shifts induced by hydrogen bonding for the N-heteroaromatic pyridine derivatives was already discussed in the present survey (as illustrated in Figure 4).

Software Developments and Machine Learning

The search for fast and efficient approaches to molecular design has led to the development of specialized software and machine learning methods in achieving these goals. Aromatic and heteroaromatic molecules are basic structures employed in the developments of novel drugs and various derivatives, finding application in material science as well as energy conversion and conservation devices. These developments are based on established correlations between structural characteristics and regiospecific reactivities.

Kromann et al.²⁶ designed software for prediction of the regiospecific reactivity of electrophilic aromatic substitution reactions. The RegioSQM software, developed by these authors, is based on the well-known dependence between site-specific reactivities and proton affinities at the ring carbons for aromatic molecules. Semiempirical methods (PM6-DH+, PM6, PM7, PM3, or AM1) are applied for the efficient evaluation of proton affinities. The method was tested for 525 literature examples of EAS reactions and is established to predict correctly the site of substitution in over 96% of cases. The input is simplified and requires the SMILES string of the molecule analyzed.

With the aim of facilitating the search for molecules with suitable pharmacokinetic properties, Tomberg et al.²⁷ proposed a machine learning model for predicting the most reactive site for electrophilic aromatic substitution. Six quantum mechanical descriptors are employed in defining the structure–reactivity relationship. These include partial charges, C–H bond orders, sum of bond orders around a carbon atom, condensed Fukui coefficients for electrophilic attack, atomic solvent accessible surface, and reduced-RegioSQM energies, employing the RegioSQM software.²⁶ Based on a considerable number of literature experimental data for EAS reactions, mostly halogenations, the procedure provided 93% accuracy of predictions.

The present Mini-Review covers selected developments in describing the reactivity of aromatic compounds from the past few years. A comprehensive survey of the literature on the topic published prior to 2016 is provided in the review of Brinck and Liljenberg.²⁸

Conclusions

Recent studies reveal novel approaches in describing the reactivity of aromatic systems in chemical reactions and intermolecular interactions. A simple experimental methodology utilizing the shifts of O–H stretching frequency in the IR spectra of selected proton donor molecules upon hydrogen bonding predicts with good accuracy the nucleophilic reactivity for several series of aromatic and heteroaromatic molecules. Theoretical quantities obtained from quantum mechanical computations for the aromatic reactants in the ground state also reveal an excellent potential in rationalizing and predicting the regiospecific aromatic reactivities. Strong correlations of molecular electrostatic potential values at selected points of the molecular space (above the centroid of the aromatic ring, at the positions of the ring carbons, and at the minima of the surface electrostatic potential) for the aromatic reactants and experimental kinetic data are obtained. Atomic charges from the Hirshfeld population analysis offer a good basis for interpretation and prediction of both overall reactivity and positional selectivity for reactions of aromatic compounds. Theoretically evaluated potential energy surfaces for electrophilic aromatic substitution reactions via applications of transition state theory were shown to provide comprehensive information on both reaction mechanisms and reactivity trends. Specialized software products, based on quantum reactivity descriptors, have been designed aiming at automated determination of the most reactive sites for electrophilic aromatic substitutions.

Biographies

Boris Galabov – Prof. Boris Galabov received his Ph.D. in 1975 from the University of Sofia. His current research interests include studies on the application of computational and spectroscopic methods in studies of organic reaction mechanisms, including electrophilic aromatic substitutions, ester aminolysis, amide hydrolysis, carbamate aminolysis, as well as in hydrogen bonding and describing chemical reactivity.

Henry F. Schaefer III – Before moving to Georgia, Henry F. Schaefer III was for 18 years a Professor of Chemistry at the University of California, Berkeley. At the University of Georgia, Schaefer is Graham Perdue Professor of Chemistry and Director of the Center for Computational Quantum Chemistry.

Sonia Ilieva – Prof. DSc Sonia Ilieva, is head of the Department of Pharmaceutical and Applied Organic Chemistry, Faculty of Chemistry and Pharmacy, Sofia University. Her scientific interests are in the fields of computational chemistry and biochemistry, solving organic reaction mechanisms with quantum chemistry methods and molecular spectroscopy, and in QSAR studies.

Diana Cheshmedzhieva – Associate professor Diana Cheshmedzhieva received her Ph.D. in 2009 from the University of Sofia. Her research interests are focused on modeling the mechanisms of organic reactions and quantitative description of the reactivity of organic molecules.

Valya Nikolova – Associate professor Valya Nikolova received her Ph.D. degree in 2008 from the University of Sofia. Her research interests include studies of hydrogen bonding, characterizing chemical reactivity of molecules and host–guest interactions of biomolecules.

Vassil A. Popov – A student with strong interests in the application of computational methods in research.

Boriana Hadjieva – Associate professor Boriana Hadjieva received her Ph.D. in 1990 from the University of Sofia. Her research interests are in synthetic organic chemistry, spectroscopic studies of organic reactions, including electrophilic aromatic substitutions, amide hydrolysis, ester aminolysis, as well as spectroscopic characterization of the conformation of amides and thioamides.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.