A tiered approach to population-based in vitro testing for cardiotoxicity: Balancing estimates of potency and variability

Abstract

Population-wide in vitro studies for characterization of cardiotoxicity hazard, risk, and population variability show that human induced pluripotent stem cell-derived cardiomyocytes (hiPSC-CM) are a powerful and high-throughput testing platform for drugs and environmental chemicals alike. However, studies in multiple donor-derived hiPSC-CMs, across large libraries of chemicals tested in concentration-response are technically complex, and study design optimization is needed to determine sufficient and fit-for-purpose population size considerations. Therefore, we tested a hypothesis that a computational down-sampling analysis based on the data from hiPSC-CM screening of 136 diverse compounds in a population of 43 non-diseased donors, including multiple replicates of the “standard” donor hiPSC-CMs, will inform optimal study designs depending on the decision context (hazard, risk and/or inter-individual variability in cardiotoxicity). Through 50 independent random subsamples of 5, 10, or 20 donors, we estimated accuracy and precision for quantifying potency, inter-individual variability, and QT prolongation risk; the results were compared to the full 43-donor cohort. We found that for potency and clinical risk of QT prolongation, a cohort of 5 randomly-selected unique donors provides accurate and precise estimates. Larger cohort sizes afforded marginal improvements, and 5 replicates of a single donor performed worse. For estimating inter-individual variability, cohorts of at least 20 donors are needed, with smaller populations on average showing bias towards underestimation in population variance. Collectively, this study shows that a variable-size hiPSC-CM-based population-wide in vitro model can be used in a number of decision scenarios for identifying cardiotoxic hazards of drugs and environmental chemicals in the population context.

1. Introduction

Human induced pluripotent stem cells (hiPSC) represent a unique and powerful platform in testing of drug and chemical safety as they can be used for characterization of hazard, risk and inter-individual variability (Burnett et al., 2021). Even from adult donors, a number of self-renewing cell types can be derived, bypassing the ethical issues of the use of embryonic stem cells (Huang et al., 2019). Among different types of hiPSC-derived cells, cardiomyocytes in particular have a high degree of utility for in vitro drug and chemical safety studies; these cells are among the most well-developed, characterized, and have been used in a number of decision contexts (Pang, 2020). Many studies have established hiPSC-derived cardiomyocytes (hiPSC-CMs) as a reproducible and qualitatively and quantitively human-relevant model for cardiotoxicity testing (Burridge et al., 2016; Grimm et al., 2018; Kilpinen et al., 2017).

The ability to derive hiPSC-CMs from different individuals, and the ability to reproduce in vivo phenotypes in cell culture (Mercola et al., 2013), has led to a number of studies that used them to characterize inter-individual differences in sensitivity to drug-induced cardiotoxicity (Burridge et al., 2016). A population-based hiPSC-CM model has been applied to much success for deriving chemical-specific estimates of hazard, population variability, and risk; as a platform for personalized drug safety evaluation; and as a “clinical-trial-in-a-dish” in drug development (Blanchette et al., 2020; Blanchette et al., 2019; Burnett et al., 2019; Laverty et al., 2011; Stillitano et al., 2017). Moreover, there is evidence that population-wide hiPSC-CM models afford greater precision for cardiotoxicity testing as compared to studies of a single donor (Blanchette et al., 2019; Blinova et al., 2017), even though the need for additional research and better characterization of in vitro to in vivo extrapolations has been expressed (Blinova et al., 2019; Vargas, 2019). However, the accuracy of assessments of cardiotoxicity hazard and risk in a genetically-diverse population may also depend on the size and diversity of the donor pool utilized by each study (Fermini et al., 2018). To date, most studies that used multiple hiPSC-CMs have been limited by the availability of cells from multiple donors. As a consequence, study designs have been largely driven by the cell/donor availability rather than considerations of statistical power or estimates of precision that would have been “fit for purpose” in each study. There is no previous published work which established a benchmark for a balance between the number of hiPSC-CM donors needed to be accurately estimate cardiotoxicity hazard, risk, and population variability in a drug and/or chemical safety evaluation context, and practical feasibility in terms of cost, complexity, and availability of cells.

Therefore, we tested a hypothesis that a computational down-sampling analysis based on the data from hiPSC-CM screening of 136 diverse compounds in a population of 43 non-diseased donors (Burnett et al., 2019), including multiple replicates of the “standard” donor (Grimm et al., 2018), will inform optimal in vitro cardiotoxicity study designs depending on the decision context (hazard, risk and/or inter-individual variability in cardiotoxicity). We have taken advantage of a previously reported drug and chemical testing data on hiPSC-CMs from a population of non-diseased individuals (Burnett et al., 2019) or multiple replicates of one “standard” donor-derived hiPSC-CM (Grimm et al., 2018), and a hierarchical Bayesian concentration-response data analysis workflow adopted from Blanchette et al. (2020). We generated random subsamples under four different study designs: 5 replicates of a single (“standard”) donor, 5 random donors, 10 random donors, and 20 random donors. For each subsample, we analyzed both functional and viability phenotype concentration-response data on 136 chemicals, and quantified potency in the form of a point of departure (POD) and population variability in the form of toxicodynamic variability factor (TDVF) (Blanchette et al., 2020). The results were compared in terms of accuracy and precision to those derived from the full donor cohort of 43 individuals. We further assessed the accuracy of the model using subsamples through examining the concordance of in vitro estimates of hazard to in vivo clinical data on QT prolongation.

2. Methods

2.1. In vitro experimental data and chemical treatments

The detailed description of the methods utilized to generate the in vitro experimental data is discussed in detail elsewhere (Blanchette et al., 2020; Burnett et al., 2019; Grimm et al., 2018). Data from a total of 136 compounds, comprising of a wide range of environmental compounds, pharmaceuticals, and drugs included in the CiPA initiative were included in this analysis [Supplemental Table S1 and (Burnett et al., 2019)]. These chemicals were chosen in consultation with various U.S. government agencies (Environmental Protection Agency, National Institute of Environmental Health Sciences, Food and Drug Administration), and reflect balancing multiple criteria, including known positives and negatives, the availability of reverse toxicokinetic data for in vitro to in vivo extrapolation, and previous testing in hiPSC-CM cell lines to evaluate reproducibility. De-identified hiPSC-CM cell lines from a diverse set of 43 individuals (Supplemental Table S2) with no known cardiovascular disease or familial history of cardiovascular disease [see details on donor demographics in (Burnett et al., 2019)] were obtained from Fujifilm Cellular Dynamics (Madison, WI). The hiPSC-CMs were exposed to compounds in concentration-response with inter- and intra-plate controls in a 90-minute treatment and subsequently assessed in a Ca²⁺ flux assay and high content imaging to evaluate functional performance and viability. Ca²⁺ flux data was processed in R (version 4.0.2) to extract relevant data on relevant phenotypes using previously reported data processing methods (Blanchette et al., 2019).

2.2. Computational workflow

2.2.1. Full cohort subsampling and Bayesian concentration-response modeling

A graphical representation of the computational workflow is presented in Figure 1. A total of 50 unique permutations of the 42 (out of 43 total) donors were generated such that each iteration of subsampling draws n_indiv = 5, 10, or 20 individuals from a predetermined random permutation. The “standard” hiPSC-CM donor (individual #1434) was excluded from the downsampling pipeline due to the high number of replicates (8) in relation to other donors (1–2) and was instead analyzed in a separate experiment within this study as described below. For each of the 50 sub-sampling iterations, in vitro data for five phenotypes (functional phenotypes: positive and negative chronotropy, QT prolongation; viability phenotypes: asystole, and cytotoxicity) were used to derive PODs as detailed in Blanchette et al. (2020). The PODs for these five phenotypes were based on the EC₀₅ (positive and negative chronotropy, QT prolongation), the EC₉₅ (asystole), and the EC₁₀ (cytotoxicity), as was rationalized previously (Blanchette et al., 2020).

Figure 1.

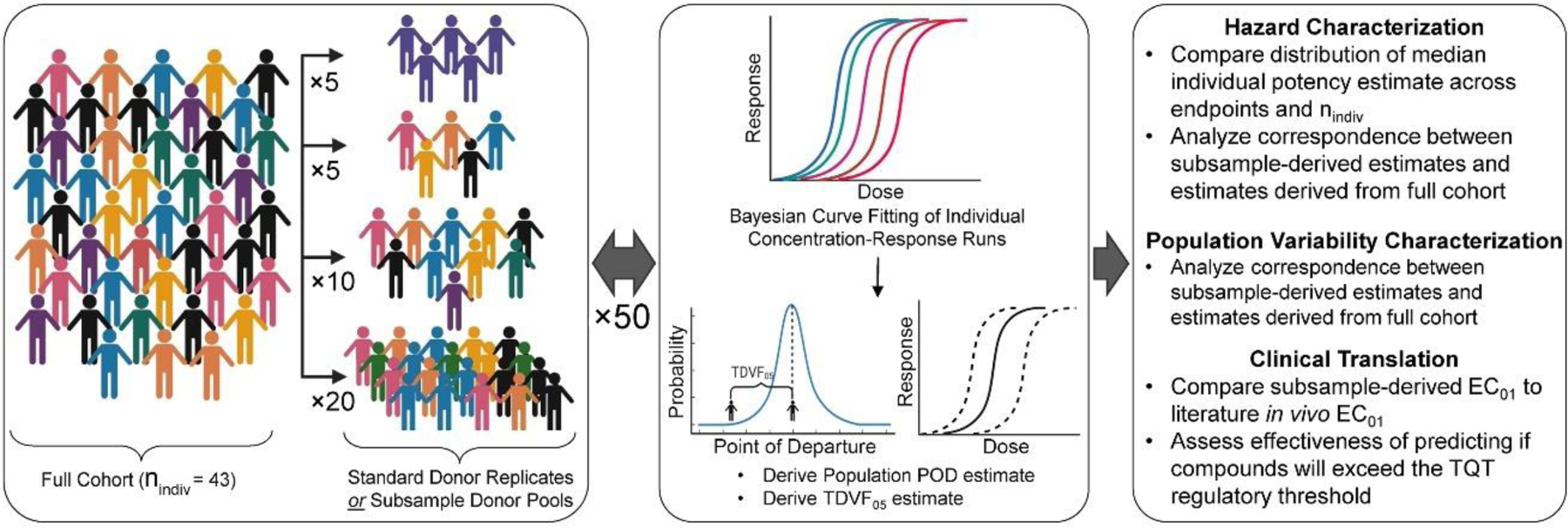
Subsampling and Data Analysis workflow.

The sub-sampled data set from each iteration and each value of n_indiv was used in conjunction with Bayesian hierarchical random-effects Hill modeling following previously described methods (Blanchette et al., 2020; Chiu et al., 2017) to fit concentration-response curves for each of the 5 phenotypes and 136 compounds. Briefly, for phenotypes that indicate the increase in a phenotypic response (positive chronotropy, QT prolongation), an “upward” Hill model was used that was reparametrized at the donor level as:

$$y=y_0\left(1+\frac{{\left(\frac{x}{x_0}\right)}^n}{1+{\left(\frac{x}{x_0}\right)}^n\frac{1}{Emax}}\right)+ϵ$$

Here, the calculated response is represented by the variable y, the nominal concentration is represented by x, and y₀, x₀, E_max, and n are model parameters representing the baseline value, the concentration at half the maximal response, the maximum fractional change from baseline, and the Hill coefficient. The “downward” version of the Hill model (negative chronotropy) was reparametrized as:

$$y=y_0\left(1-\frac{{\left(\frac{x}{x_0}\right)}^n}{1+{\left(\frac{x}{x_0}\right)}^n\frac{1}{Emax}}\right)+ϵ.$$

To avoid outsized parameter values, the model hyperparameters for the natural-log transformed population mean of E_max (m_Emax) and n (m_n) were restricted to be >−3 and between −2 and 2, respectively. For the remaining two phenotypes, asystole and cytotoxicity, a modified version of the downward Hill model was utilized which did not contain the E_max parameter under the assumption the maximal response will be at 0:

$$y=y_0\left(1-\frac{{\left(\frac{x}{x_0}\right)}^n}{1+{\left(\frac{x}{x_0}\right)}^n}\right)+ϵ$$

The restriction of the m_n hyperparameter used in the “downward” model was similarly used in this “zero” model.

For all models, the parameters and hyperparameters were natural-log transformed to ensure the values remain positive and the error ϵ was assumed to follow a scaled Student’s t distribution with scale parameter σ and five degrees of freedom in order to be robust for detection of the outliers (Chiu et al., 2017). Additionally, the hyperparameters, reflecting the population mean and standard deviation of each model parameter, were normal and half-normal, respectively, under the assumption that individuals in the population were distributed normally. See Supplemental Table S3 for details on model parameter prior distributions.

Posterior distribution sampling was conducted using the Markov Chain Monte-Carlo (MCMC) algorithm as described previously in Blanchette et al. (2020). Briefly, simulations for each compound consisted of 4 chains with a minimum of 4,000 iterations and a maximum of 36,000 iterations, the first half of which being “warm-up” iterations which are subsequently discarded. Tuning parameters for the “upward” and “downward” models were adjusted from their default values to improve modeling efficiency and reduce the occurrence of divergent transitions. Inter- and intra-chain variability were assessed for each parameter to determine if convergence has been reached, indicated by the potential scale reduction factor R̂ ≤ 1.2 (Gelman & Rubin, 1992). If convergence could not be reached for a given compound at the minimum number of iterations, the concentration-response was remodeled with an increasing number of iterations until the maximum was reached. If convergence could not be reached for a given compound and phenotype, it was not used in further data analysis. For each chain, 250 random samples were saved for further analysis, a total of 1,000 samples. These 1,000 posterior samples for each compound and phenotype were ultimately combined with those of each of the other 50 subsampling iterations for subsequent data analysis. To further improve wall-clock time required for the extensive amount of modeling conducted in this study, each of the 50 iterations of subsampling for each compound was conducted in parallel utilizing the foreach package (version 1.5.1) in R. Bayesian concentrationresponse analysis within the subsampling pipeline and subsequent posterior sampling was carried out using an R (version 4.0.3) module on the Texas A&M High Performance Research Computing Core integrated with Stan using the rstan package (version 2.12.2).

2.2.2. “Standard” donor subsampling

A similar workflow for Bayesian concentration-response modeling and posterior distribution sampling was carried out for the subsampling of the sample replicates from the “standard” donor. A total of 50 subsampling iterations of 5 (out of 8) replicates each were conducted per endpoint and chemical in utilizing a fixed effects version of the Bayesian concentration-response model, assuming no random effects (all replicates are treated as from the same individual).

2.3. Hazard assessment

2.3.1. Coverage of chemical space

In order to determine whether this study’s conclusions regarding the number of donors needed in a population-based hiPSC-CM model may apply to testing of over chemicals (i.e. the “applicability domain”), an assessment of the coverage of chemical space was conducted similar to that reported in Chiu et al. (2017). Specifically, the 136 compounds used in this study were compared to those (n = 32,464) of the Collaborative Estrogen Receptor Activity Prediction Project (CERAPP) prediction data set (Mansouri et al., 2016) that has been extensively quality-controlled for use in QSAR modeling. Over 200 molecular descriptors were calculated for compounds in both data sets utilizing the open-source Chemistry Development Kit (CDK) package “rcdk”, as implemented in R and were compared to one another in a principal components analysis. The toxicologically relevant physical-chemical properties octanol:water partition coefficient (logP), molecular weight (MW), and topological polar surface area (TPSA) were singled out for further comparison between the two chemical sets.

2.3.2. Comparison of subsample-derived potency estimates

For each phenotype, compound, and study design (subsamples using 5 standard donor replicates or using random donor subpopulations with different n_indiv), the population median POD estimate was derived from the uncertainty distribution that was the result of the combination of all 50 iterations of subsampling, as well as from each iteration for comparison against those of the full cohort. The log₁₀-transformed central estimate of the POD from the combined uncertainty distribution for each compound and endpoint was compared with that from the full cohort to calculate a deviation ΔPOD:

$$\mathrm{\Delta }POD=log10\left(PO{D}_{sub}\right)-log10\left(PO{D}_{full}\right).$$

These values served as a measurement of concordance between the subsampled measurement and the data from the full cohort. Accuracy and precision were determined for each endpoint for each study design through deriving the median ΔPOD (negative = underestimation, positive = overestimation; closer to 0 = more accurate) as the median error value, and deriving the median absolute deviation (MAD; closer to 0 = more precise).

2.3.3. Comparison of subsample-derived population variability estimates

A similar workflow was utilized in the assessment of each value of n_indiv in its accuracy and precision in estimating population variability. As before, for each phenotype, a toxicodynamic variability factor at 5% (TDVF₀₅) was calculated as the ratio of the POD for the median individual to the POD for the most sensitive 5^th percentile individual. For each phenotype and compound, the log₁₀-transformed median estimate of the TDVF₀₅ for study design was compared against that derived from the full cohort to generate a deviation ΔTDVF₀₅:

$$\mathrm{\Delta }TDV{F}_{05}=log10\left(TDV{F}_{05,sub}\right)-log10\left(TDV{F}_{05,full}\right).$$

Accuracy and precision measurements were derived similarly to ΔPOD using the median and MAD.

2.3.4. Clinical translation

To evaluate accuracy and precision of the subsamples in their capability to make clinical decisions, the common metrics used in Blanchette et al. (2019) were similarly used here. Firstly, in vivo predictions of the effective concentration (EC) at the 1% clinically relevant change in the QT interval (EC₀₁) from published PK-PD studies were compared to those derived from subsamples for each study design for the QT prolongation phenotype. As described in Blanchette et al. (2019), the selection of EC₀₁ as a benchmark was based on the “clinically significant” change of 5 msec prolongation with a baseline QTc of 421.5 msec [mean of NHANES III as previously reported (Benoit et al., 2005)], corresponding to a 1.2% change, which is then rounded to 1%. Secondly, the effectiveness of a clinical translation to a TQT study (ICH, 2015) was assessed as it was in Blanchette et al. (2019). Specifically, each subsample for each study design was evaluated as to whether it satisfied the TQT regulatory threshold of <10 ms at 95% confidence at the reported clinical maximum plasma concentration C_max [values previously used by Blanchette et al. (2019), updated based on the database of human clinical studies of TQT reported by Wiśniowska et al. (2020)].

3. Results

3.1. Coverage of chemical space

The overlap between the CERAPP compounds (Mansouri et al., 2016) and the 136 compounds used in this study is visualized in Figure 2 based on chemical descriptors. Using the first three principal components (that account for over 45% of the total variance), we found substantial overlap between the chemical space coverage of the compounds within this study and the CERAPP compounds (Figure 2A). Additionally, when examining three toxicologically relevant physical-chemical properties across the compounds of the two sets, a similarly high level of overlap was found (Figure 2B). Therefore, the 136 compounds utilized in this study are representative of the broader set of drugs and compounds of interest to environmental health, making up a sufficiently large and diverse applicability domain.

Figure 2.

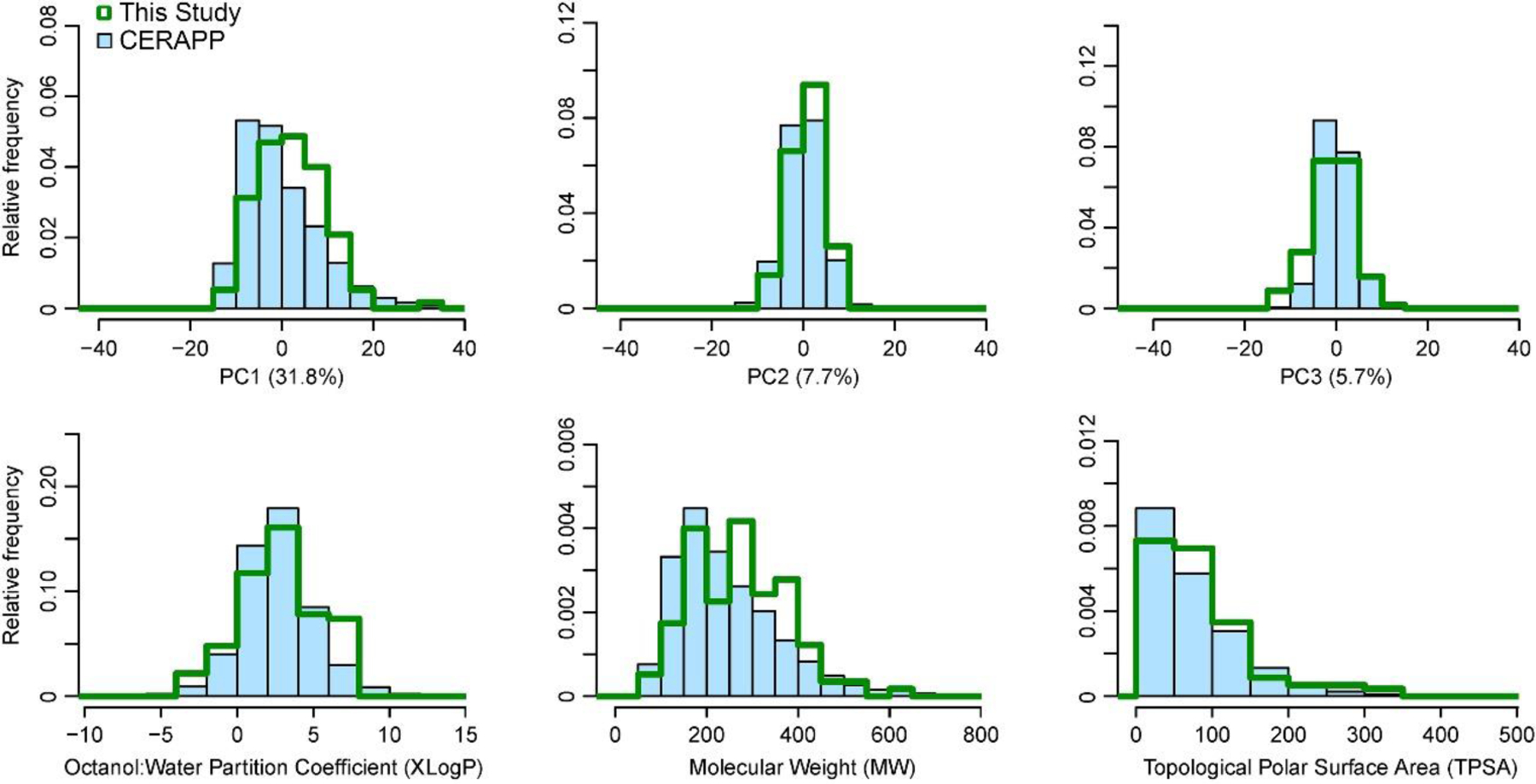
Chemical space coverage and overlap of the first three principles components and interpretable toxicologically-relevant physical-chemical properties between the 136-compound screen and the CERAPP prediction set.

3.2. Comparison of population subsample-derived potency estimates

The accuracy of the chemical and phenotype-specific population central estimations of potency were compared for each study design (subsamples using 5 random standard donor replicates and using random donor subpopulations with different n_indiv) to those derived from the full 43 donor cohort. Figure 3 shows a visual representation of the comparison between random subsample dose-response relationships and that for the full cohort for five representative compounds representing each phenotype (positive chronotrope: pyrene, negative chronotrope: mexiletine hyrdrochloride, QT prolongation: citalopram hyrdobromide, asystole: quinidine sulfate, cytotoxicity: propafenone). Concentration-response curves for the population median using subsamples of unique individuals were within the confidence band of that for the full cohort, while those for the standard donor were generally outside the confidence band, suggesting that a pooled diverse donor population was more accurate or precise than using replicates of a single donor.

Figure 3. Dose Response Comparison across study designs.

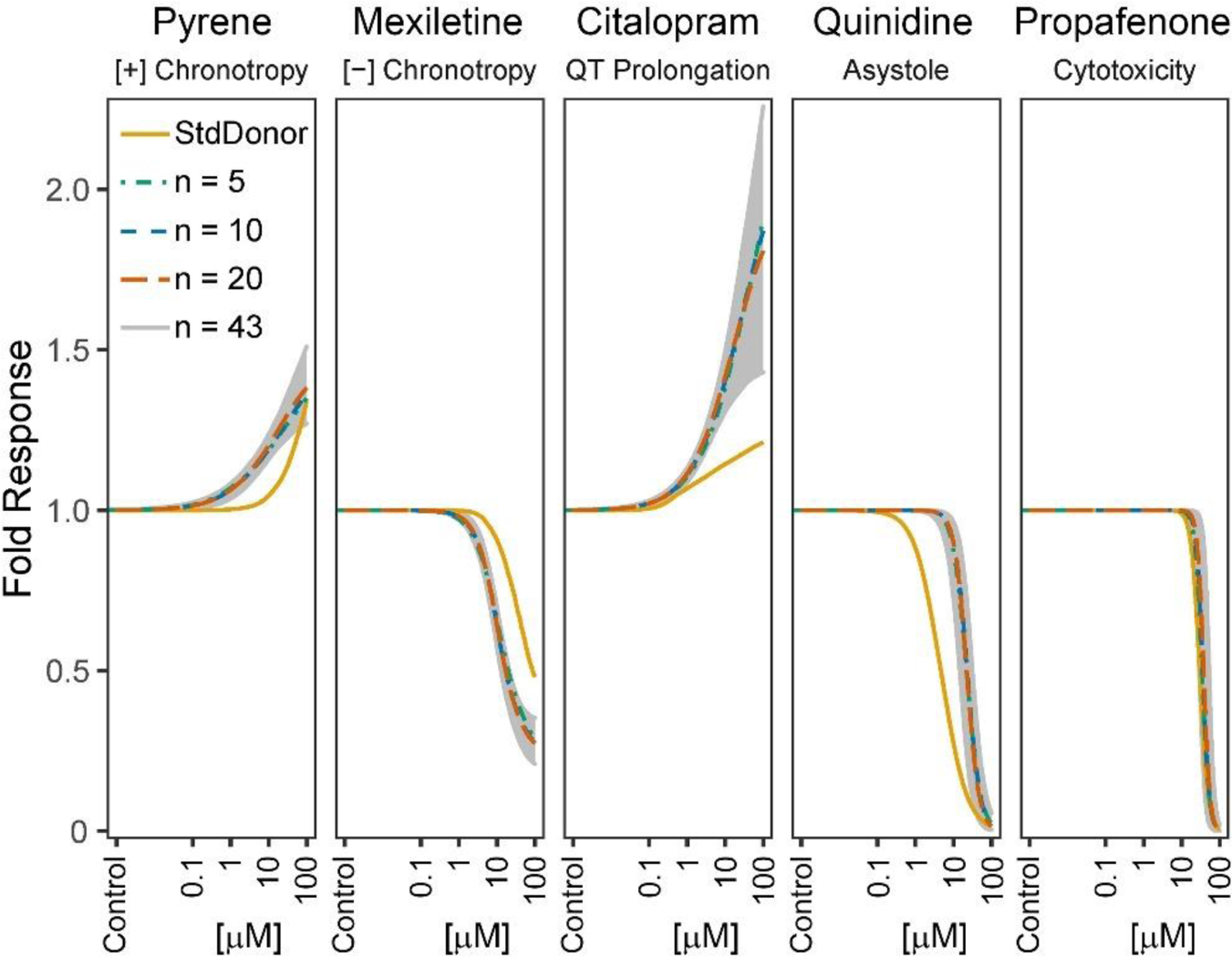
Curve fits shown are for the predicted population median for each study design, using a single random subsample, for representative compounds for each phenotype (positive chronotrope: pyrene, negative chronotrope: mexiletine hydrochloride, QT prolongation: citalopram hydrobromide, asystole: quinidine sulfate, cytotoxicity: propafenone). The confidence interval band shows the corresponding 95% CI based on the full cohort (n=43).

Figure 4A shows the resulting cumulative distribution of the compound-specific POD population central estimates across all 50 iterations of subsampling and the 90% CI of those estimates. Across all endpoints and study designs, the central estimates of the cumulative distribution corresponded well with those derived from the full (n=43 donors) cohort, with the 90% CI narrowing when replacing standard donor replicates with random unique donors, and as the number of individual donors increased. The correspondence between the median individual POD predictions from the full cohort and the subsamples were strong regardless of endpoint and study design, though the viability phenotypes (asystole and cytotoxicity) had an even narrower uncertainty interval as compared to the functional phenotypes (positive and negative chronotropy, QT prolongation). The correspondence between the subsampled estimates was further explored in Figure 4B in which the deviation ΔPOD is shown across different phenotypes and study designs. The distribution of ΔPOD becomes noticeably more centered at 0 (which corresponds to a ratio of PODs of 10⁰=1) when replacing standard donor replicates with unique donors, and as the number of unique donors increases. Specifically, using hiPSC-CMs from 5 unique donors resulted in lower bias and greater precision as compared to a study design utilizing 5 replicates of the standard donor. Summary of the accuracy and precision estimates for this analysis is reported in Table 1. Accuracy was much improved when cells from 5 unique donors were used, with more modest improvements seen as n increased further. Precision increased similarly, with greater improvements as n increased compared to accuracy improvements.

Figure 4. Hazard characterization subsampling analysis.

Hazard characterization subsample analysis. A) Cumulative distribution of PODs for each study design and phenotype. Black solid line and outer dotted lines correspond to the median individual POD for each compound across all 50 iterations, and its 90% CI. The green line indicates the cumulative distribution of the PODs for all compounds as derived from the full 43 individual cohort. B) Boxplots visualizing the distribution of the ΔPOD for each study design and phenotype.

Table 1. Accuracy and precision in potency estimates across study designs.

Accuracy is represented by the median ΔPOD (Med), and precision is represented by the median absolute deviation ΔPOD (Zou et al.), where ΔPOD is the log10-transformed deviation as compared to the full cohort.

Study design	[+] Chronotrope		[−] Chronotrope		QT Prolongation		Asystole		Cytotoxicity
	Med	MAD	Med	MAD	Med	MAD	Med	MAD	Med	MAD
Std. Donor	0.69	0.71	−0.12	0.76	0.16	0.55	−0.03	0.35	−0.39	0.36
n = 5	−0.09	0.43	−0.12	0.38	−0.08	0.38	0.04	0.13	−0.10	0.16
n = 10	−0.05	0.30	−0.08	0.29	0.03	0.10	0.03	0.10	−0.05	0.09
n = 20	−0.03	0.18	−0.06	0.15	−0.01	0.18	0.01	0.06	−0.02	0.05

Std. Donor: 5 random replicates of the standard donor

3.3. Comparison of population subsample-derived population variability estimates

A similar analysis to determine the correspondence of chemical- and phenotype-specific TDVF₀₅ was conducted through the generation of ΔTDVF₀₅ values comparing the subsampled estimate to the full cohort estimate and visualized in Figure 5. Here, only study designs with multiple unique donors were considered, because replicates of the standard donor cannot be used to estimate inter-individual variability. The cumulative distributions of the central estimates and 90% CI subsample-derived TDVF₀₅ estimates were compared to those of the full-cohort derived estimate in Figure 5A, with the distribution of deviations shown in Figure 5B. Across all phenotypes, the improvement in accuracy and precision in TDVF₀₅ estimates with the increase in the number of subsampled donors was more apparent than for the derivation of potency estimates. The cumulative distributions derived from subsamples of 5 and 10 donors were shifted left in comparison to that of the full-cohort, indicating that the TDVF₀₅ values were being routinely underestimated with small sample sizes. The sample of 20 unique donors, however, resulted in the estimations of the TDVF₀₅ across all phenotypes that were relatively concordant with those derived using all 43 donors.

Figure 5. Population variability subsampling analysis.

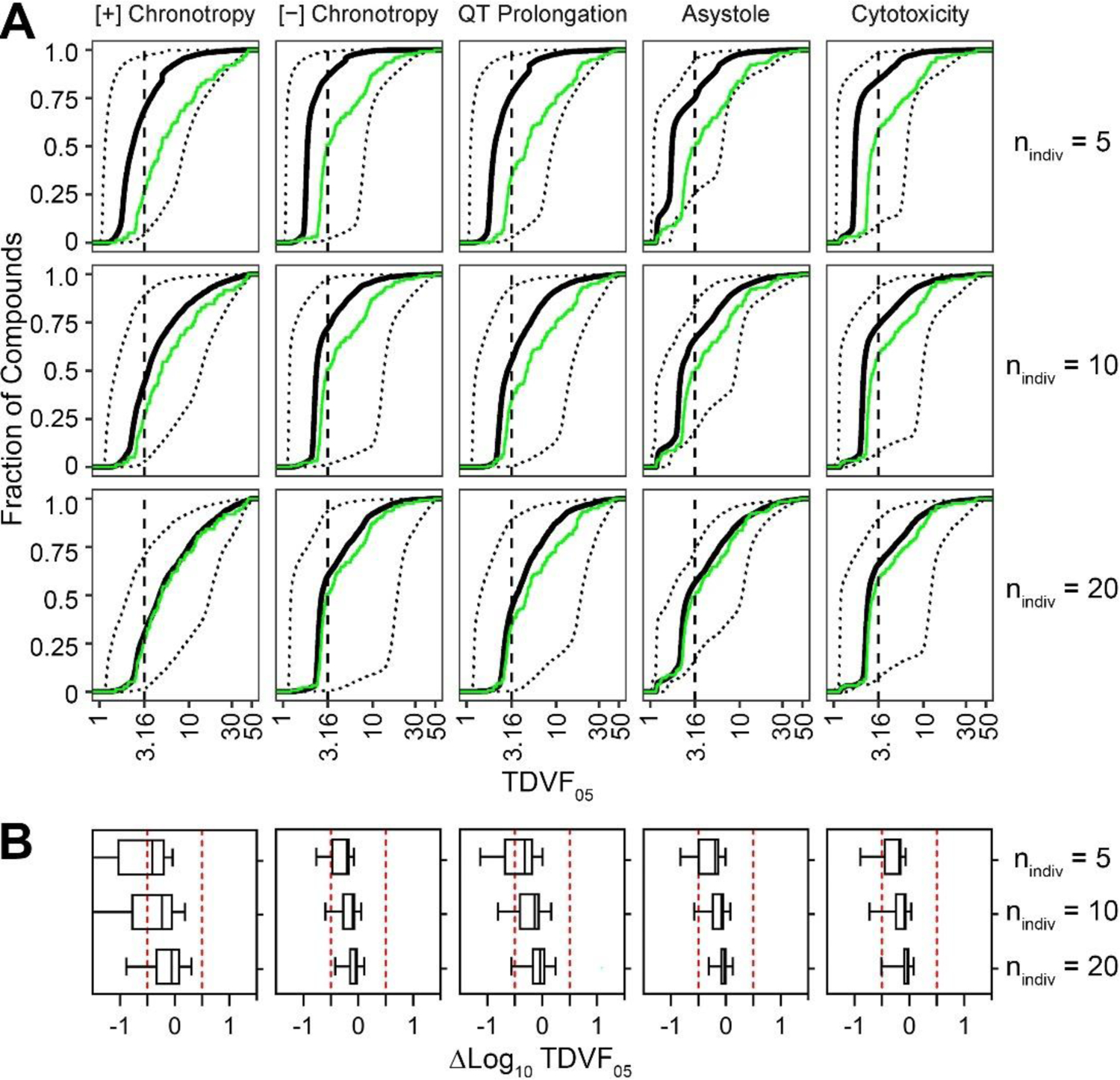
Population variability subsample analysis. A) Cumulative distribution of TDVF05s for each study design and phenotype. The black solid line and outer dotted lines correspond to the estimated TDVF05 for each compound across all 50 iterations, and its 90% CI. The green line indicates the cumulative distribution of the TDVF05 values for all compounds as derived from the full 43 individual cohort. B) Boxplots visualizing the distribution of the ΔTDVF05 for each study design and phenotype.

Additionally, at lower values of n_indiv, especially at n_indiv = 5, the functional endpoints exhibited greater uncertainty in the median TDVF₀₅ estimate than the viability phenotypes. This contrasted with n_indiv = 20 in which the distribution was narrower and centered more closely at a ΔTDVF₀₅ of 0. The functional phenotypes, especially at n_indiv = 5, had a greater degree of uncertainty in the TDVF₀₅ estimation than the viability phenotypes. Table 2 indicates significant accuracy improvements as n increased while precision also increased, although more incrementally.

Table 2. Accuracy and precision in population variability estimates across study designs.

Accuracy is represented by the median (Med) ΔTDVF₀₅, and precision is represented by the median absolute deviation ΔTDVF₀₅ (Zou et al.), where ΔTDVF₀₅ is the log-transformed deviation as compared to the full cohort.

Study design	[+] Chronotrope		[−] Chronotrope		QT Prolongation		Asystole		Cytotoxicity
	Med	MAD	Med	MAD	Med	MAD	Med	MAD	Med	MAD
n = 5	−0.41	0.44	−0.20	0.15	−0.32	0.31	−0.19	0.21	−0.18	0.13
n = 10	−0.23	0.45	−0.09	0.12	−0.14	0.26	−0.07	0.13	−0.08	0.11
n = 20	−0.06	0.31	−0.04	0.09	−0.04	0.18	−0.02	0.08	−0.03	0.07

3.4. Evaluation of clinical translation

Figure 6 shows the correspondence of clinical data-derived in vivo EC₀₁ POD values for QT prolongation to in vitro model-derived EC₀₁ using common concentration and response metrics for 10 compounds with known clinical effects. When using sub-samples of the standard donor and three choices for n_indiv, our model was able to predict human in vivo EC₀₁ with a high degree of accuracy. Pearson and Spearman correlation coefficients, as well as mean square error (MSE) values are shown. Correlation was high when utilizing replicates of the standard donor, with both values being over 0.8. Correlation was further increased when using population subsamples, with correlation coefficients above 0.9 for all sample sizes. Precision increased substantially (i.e., MSE decreased) when replacing 5 replicates of the standard donor with at least 5 unique donors, and more modestly with further increasing n_indiv.

Figure 6. Comparison of in vivo PODs to in vitro-derived PODs.

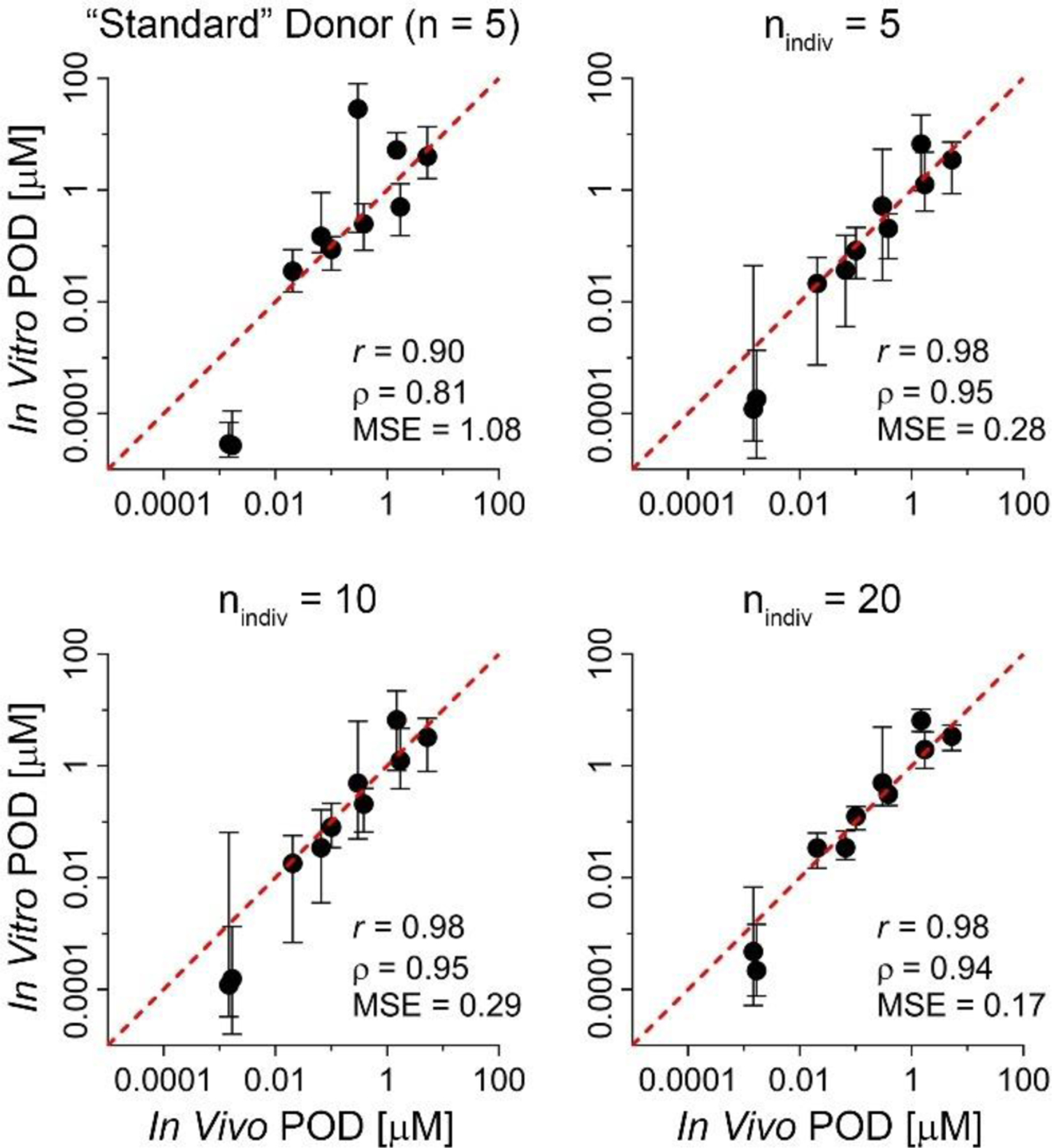
For each study design, scatterplot shows the in vivo EC₀₁ (X-axis) versus the model-predicted EC₀₁ values (median and 90% CI, y-axis) for the 10 positive controls for QT prolongation. Line displayed is the unit line (y = x). EC₀₁ values are log₁₀-transformed for correlation (r=Pearson, p=Spearman) and mean standard error (MSE) calculations; p-values for correlations were all significant (p < 0.01).

We previously demonstrated, using 10 compounds with reported clinical effects on QT and 3 drugs with no such effects, the ability of a population hiPSC-CM model with n_indiv=27 to accurately predict the probability that a compound-induced change in the QT interval at C_max will exceed 10 ms and correctly identify those compounds that will not exceed this threshold at 95% confidence (Blanchette et al., 2019). Here we repeated this analysis with the larger donor cohort of n=43, as well as with smaller subsampled cohorts, calculating the probability that the QTc was prolonged more than 10 ms at C_max, P(ΔQT_Cmax > 10ms). Those subsamples with a probability >5% were classified as positive, and those <5% were classified as negative predictions. The results of this analysis are shown in Table 3 and further visualized in Supplemental Figures S1-2.

Table 3.

Performance of different study designs in identifying regulatory QT prolongation risk at C_max. Shown for each chemical and study design is the percentage of subsampling iterations that resulted in a positive classification of QT prolongation risk at C_max of 10 msec prolongation at 95% confidence. For comparison, the reference clinical classification based on in vivo human data and the classification based on the full cohort (n = 43) are also shown. Parenthesis around a clinical classification indicates that the classification is ambiguous (some studies above and some below the regulatory threshold).

	Percent subsamples “+”
Chemical: clinical classification	Std. Donor	n = 5	n = 10	n = 20	n = 43
Cisapride: +	100	100	100	100	+
Citalopram: +	100	100	100	100	+
N-acetylprocainamide: +	100	100	100	100	+
Quinidine: +	100	100	100	100	+
Sematilide: +	100	100	100	100	+
Vernacalant: +	100	100	100	100	+
Sotalol: +	98	100	100	100	+
Disopyramide: +	84	100	100	100	+
Dofetilide: +	98	92	100	100	+
Moxifloxacin: (+)	100	94	91	96	+
Cabazitaxel: –	12	6	0	0	–
Mifepristone: –	2	16	3	0	–
Lamotrigine: (–)	100	76	31	8	–

+: Positive for QTc prolongation; –: Negative for QTc prolongation; (+) or (–): mixed or ambiguous clinical results in terms of 10 msec regulatory threshold at 95% confidence.

When data from 5 replicates of the standard donor or when subsamples of n_indiv = 5 random individuals were used, we correctly identified all positive compounds, with at least 84% of iterations resulting in a correct regulatory classification, and 2 of 3 negative compounds. The misclassification was for the “negative” compound lamotrigine (Dixon et al., 2008), for at least 76% of iterations identified it as positive instead of negative. At n_indiv = 10 and 20, the model correctly identified all positive and negative compounds. At these larger values of n_indiv, lamotrigine was correctly identified to be a negative compound, suggesting that although donors may be more sensitive and thus a larger population is needed to correctly estimate the population level effects at C_max.

4. Discussion

In a commentary on Blanchette et al. (2019), Vargas (2019) stated the need to better define the population size that shall be used to ensure that estimates derived from the in vitro studies in hiPSC-CMs accurately reflect population central estimates, and thereby to reduce the uncertainty surrounding the use of an arbitrary number of donors. A gap in our knowledge exists on how hiPSC-CM-based in vitro model shall be designed to best fit the purpose of drug and/or chemical safety testing. Additional insights are needed into effectively utilizing in vitro population models to achieve different ends, whether that be a characterization of hazard or population variability, and further increase the scientific community’s confidence in using alternatives to animal or human tests (Chiu & Rusyn, 2018). In this study, we addressed these gaps by conducting a computational downsampling analysis of both individual donors from a 43-donor cohort (Blanchette et al., 2020; Burnett et al., 2019) and replicates of the standard donor. Specifically, by subsampling 50 unique cohorts of n = 5, 10 or 20 individuals and 50 replicate combinations of 5 standard donor replicates, we were able to derive metrics of accuracy and precision of potency, population variability, and QT risk as compared to past estimates from a 43-donor cohort.

We found that potency estimates derived using a 5 standard donor replicates design were on average less accurate than those derived using cohorts of cells from 5 different individuals. This conclusion reinforces our observation made previously with a 27 donor cohort (Blanchette et al., 2019), which found that the standard donor was more sensitive to QT prolongation effects as compared to the population median, and therefore would result in the over prediction of chemical-induced risk at the population level. While this study did not find that the standard donor uniformly overpredicted risk across all compounds, phenotypes, and replicate combinations, our statistical analysis indicated a loss of accuracy and precision in hazard and risk predictions when compared against other similarly sized or larger cohort designs with genetically diverse individuals. Similarly, studies of optimal experimental designs for hiPSC-based methods caution against utilizing multiple clones of a single donor in place of a single clone per donor. For instance, Germain and Testa (2017) found that utilizing multiple replicates of a single donor in a case-control study results in the increase of spurious differences of gene expression between groups in a transcriptomic analysis. Accordingly, Volpato and Webber (2020) in iPSC-disease model guidelines state that an increase in the number of cell lines used provides far greater experimental power to detect non-spurious effects than in models that increase the number of lines derived from a single donor.

Through our down sampling approach, we have additionally identified a cohort size of 5 individual donors to be highly effective in estimating population median measurements of both hazard and risk, with relatively low bias and imprecision of less than half order of magnitude (half the dose-spacing in our experiments). Estimations of population median PODs across all 5 endpoints for cohorts of five individuals were sufficiently strong and did not vary significantly from those made in larger-size donor cohorts. Germain and Testa (2017) similarly found that utilizing iPSC lines from a minimum of 4 donors to 6 donors total yielded sufficient precision and accuracy in identifying effects in a differential expression analysis. Our findings differed from Germain and Testa (2017) in that we found that precision increased as the number of individuals increased with the most significant increase coming from replacing the standard donor replicate-derived values and those derived from the 5 donor subsampled cohorts. However, this difference in findings may be a result of the divergence of the endpoints evaluated in both studies. The ability to accurately predict population median carried over to predictions of risk, as we similarly found that cohort sizes of n_indiv = 5 performed nearly as well as larger cohorts in the clinical translation, only misclassifying one additional compound, lamotrigine (which is acknowledged to have some ambiguity as to its clinical classification), compared to the larger cohorts.

While the smaller cohorts were sufficient for hazard characterization; they were not sufficient for characterization of population toxicodynamic variability. Smaller cohort sizes of n = 5 and n = 10 tended to underpredict the extent of the toxicodynamic variability for functional phenotypes, with the smaller cohort sizes underestimating to a greater extent. Intermediate cohort sizes of n = 20, however, predicted the chemical-specific TDVF₀₅ accurately compared to that predicted by the full cohort (n = 43). Modest improvements in precision as cohort size increased were similarly observed for population variability analysis; however, precision remained relatively low for the positive chronotropy phenotype, which was noted for its high degree of variability (Blanchette et al., 2020). Our finding that a cohort size of n = 20 was sufficient in deriving TDVF₀₅ that closely resembled those derived from a cohort over double its size, indicated that population median toxicodynamic variability predictions stabilize and are not significantly affected by additional donors. These results are consistent with previous computational down sampling experiments performed with lymphoblastoid cells, which found that a cohort of 20 individuals is required to achieve a high level of sensitivity and specificity that is not significantly improved by larger sample sizes (Chiu et al., 2017). This finding is especially important in that it alleviates some burden of conducting large-scale in vitro population variability studies, many of which feature inherently large donor pools. While the source of the lymphoblastoid cell data, Abdo et al. (2015), was one of the largest of its kind, other lymphoblastoid studies have utilized 80 or more cell lines (Choy et al., 2008; Lock et al., 2012; O’Shea et al., 2011). Other studies utilizing different cell types include similarly large donor pools. For instance, 51 individual donors were used to collect primary B cells for use in a study on low dose responses of TCDD (Dornbos et al., 2016), and 45 were used in a QTL mapping study in hiPSC-CM (Knowles et al., 2018). Establishing a 20-donor population model as sufficient to accurately and precisely quantify population variability increases the feasibility of conducting efficient and high-throughput toxicodynamic variability studies in vitro.

Another important consideration for selecting sample size for future studies is the choice of the metric for deciding when the data may indicate human health hazard concern, such as changes in QTc. Specifically, human clinical data on TQT show substantial variability in both C_max and the change in QTc [see the database by Wiśniowska et al. (2020) and Supplemental Figure S3 for moxifloxacin and lamotrigine data]. We found that in vitro data from different individuals is equally variable and a distinction shall be made between detecting a significant change in QTc as opposed to exceeding the regulatory thresholds for the QTc elongation of concern. For example, the more variable in vitro model results for both moxifloxacin and lamotrigine appear to reflect the fact that the effects on QTc at the clinical C_max appear to be close to the regulatory threshold, so small changes in C_max can change the regulatory classification from “positive” to “negative” (data not shown). For instance, across over 100 clinical studies of moxifloxacin reviewed by (Wiśniowska et al., 2020), changes in QTc range from a decrease of 6.6 msec to increase of 22.3 msec, with an inter-quartile range of 10–13 msec increase. Similarly, with respect to lamotrigine, although it appears negative in healthy adult volunteers at typical therapeutic doses, QTc prolongation has been reported as a result of overdoses (Chavez et al., 2015; Dixon et al., 2008; Moore et al., 2013).

This study, while addressing a former limitation of population-based in vitro models, itself is not free from its own limitations. The full cohort used as a benchmark, while being among the largest of its kind for hiPSC-CM, is still relatively small at 43 individuals. Additionally, while similar conclusions were previously reached for a few other cell types (Chiu et al., 2017; Germain & Testa, 2017), the generalizability of our analyses could be improved with data from additional iPSC-derived cells, such as hepatocytes, which are particularly of interest in toxicology. Furthermore, the data in this study consisted solely of “normal” individuals who do not have a personal or familial history of cardiovascular, so may not apply to study design considerations for population models incorporating pre-existing disease.

In addition, a natural future direction is the application of this hiPSC-CM population-based model in high-throughput testing of additional chemicals. The hazard characterization of a large set of compounds using 5 donors would be considerably more tractable to accomplish than using the full cohort of 43 donors that is currently commercially available. Data from 5 different donors will be substantially more accurate than using only the single standard donor, making confident evaluation of a much larger and diverse chemical set highly feasible. Additionally, given that only 13 compounds were available for testing positive and negative performance (Blanchette et al., 2019; Burnett et al., 2019), further validation of the predictive performance of the model would be beneficial (Vargas, 2019); to this end, the recent database developed by (Wiśniowska et al., 2020) of clinical TQT studies would be highly informative as a benchmark for evaluation.

In conclusion, we have advanced our in vitro – in silico population-based hiPSC-CM model by better defining the study design parameters required to derive accurate and precise measurements of hazard, risk, and population variability. Overall, our results suggest that a sensible high-throughput screening approach for characterizing hazard and potency of drugs and chemicals should consist of a population-based model utilizing 5 or more unique donors, while donor populations of around 20 are required to draw conclusions about the degree of inter-individual variability. These design parameters will therefore support the development of tiered testing approaches for risk assessments of both pharmaceuticals and environmental chemicals using population-based in vitro models.