Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2021 Nov 7;240(4):678–687. doi: 10.1111/joa.13589

Comparing and combining sliding semilandmarks and weighted spherical harmonics for shape analysis

Christine M Harper 1,2,✉, Deanna M Goldstein 2, Adam D Sylvester 2
PMCID: PMC8930823  PMID: 34747020

Abstract

Quantifying morphological variation is critical for conducting anatomical research. Three‐dimensional geometric morphometric (3D GM) landmark analyses quantify shape using homologous Cartesian coordinates (landmarks). Setting up a high‐density landmark set and placing it on all specimens, however, can be a time‐consuming task. Weighted spherical harmonics (SPHARM) provides an alternative method for analyzing the shape of such objects. Here we compare sliding semilandmark and SPHARM analyses of the calcaneus of Gorilla gorilla gorilla (n = 20), Pan troglodytes troglodytes (n = 20), and Homo sapiens (n = 20) to determine whether the SPHARM and sliding semilandmark analyses capture comparable levels of shape variation. We also compare both the sliding semilandmark and SPHARM analyses to a novel combination of the two methods, here termed SPHARM–sliding. In SPHARM–sliding, the vertices of the surface models produced from the SPHARM analysis (that are the same in number and relative location) are used as the starting landmark positions for a sliding semilandmark analysis. Calcaneal shape variation quantified by all three analyses was summarized using separate principal components analyses. Results were compared using the root mean square (RMS) and maximum distance between surface models of species averages scaled (up) to centroid size created from each analysis. The average RMS was 0.23 mm between sliding semilandmark and SPHARM average surface models, 0.19 mm between SPHARM and SPHARM sliding average surface models, and 0.22 mm between sliding semilandmark and SPHARM sliding average surface models. Although results indicate that all three analyses are comparable methods for 3D shape analysis, there are advantages and disadvantages to each. While the SPHARM analysis is less time‐intensive, it is unable to capture the same level of detail around the sharp edges of articular facets on average surface models as the sliding semilandmark analysis. The SPHARM analysis also does not allow for individual articular facets to be analyzed in isolation. SPHARM–sliding, however, captures the same level of detail as the sliding semilandmark analysis, and (as in the sliding semilandmark analysis) allows for the evaluation of individual portions of bone. SPHARM is a comparable method to a 3D GM analysis for small, irregularly shaped bones, such as the calcaneus, and SPHARM–sliding allows for an expedited set up process for a sliding semilandmark analysis.

Keywords: sliding semilandmarks, three‐dimensional geometric morphometrics, weighted spherical harmonics

We tested both the comparability of three‐dimensional geometric morphometric sliding semilandmark analyses and weighted spherical harmonic (SPHARM) analyses for 3D shape quantification and the use of vertices from SPHARM‐generated surface models as the landmark starting positions for a sliding semilandmark analysis (termed SPHARM‐sliding). All three methods produce comparable results and capture the same general patterns of shape variation, although the SPHARM analysis does not capture sharp edges of the bone as well as the sliding semilandmark analysis. SPHARM–sliding does capture these details and allows for an expediated set‐up for a sliding semilandmark analysis.

graphic file with name JOA-240-678-g003.jpg

1. INTRODUCTION

Quantifying morphological shape variation is integral to biological research. Geometric morphometrics (GM), or the statistical analysis of shape, captures the geometric variation among objects, and can be carried out using many different methods, such as elliptical Fourier analysis and landmark analysis (e.g., Zelditch et al., 2012). Landmark analysis uses homologous 2D or 3D landmarks (or semilandmarks, discussed below) to describe shape variation (Adams et al., 2013; Gunz et al., 2005; Rohlf & Marcus, 1993; Zelditch et al., 2012). Fixed landmark analysis utilizes three types of landmarks (Type I, Type II, and Type III) that are characterized by the type of data they represent (Bookstein, 1991). While fixed landmark geometric morphometric analyses have expanded our understanding of morphological variation (e.g., Àlvarez et al., 2013; de Oliveira & Santos, 2018; Jasinski & Wallace, 2014; Klingenberg & McIntyre, 1998; Tallman, 2013; Turley & Frost, 2013), they capture limited aspects of morphology (e.g., Bardua et al., 2019). With the advent of sliding semilandmarks in 3D (Bookstein, 1991; Gunz et al., 2005), it is possible to quantify morphologies that lack discrete anatomical locations. This method utilizes a sliding algorithm that allows semilandmarks to achieve geometric homology on specimens with complex morphologies and is a powerful tool for detecting subtle differences in morphology (e.g., Cooney et al., 2017; Cucchi et al., 2011; Fabre et al., 2018; Gunz et al., 2012; Gunz & Mitteroecker, 2013; Harcourt‐Smith et al., 2008; Harper et al., 2021; Kieser et al., 2007; Segall et al., 2016; Sylvester, 2013).

Determining the starting positions for semilandmarks and placing them on all specimens in a consistent order and relative position, however, can represent a substantial challenge. This is particularly true of surface semilandmarks, as their initial placement has been noted to be less intuitive than curve semilandmarks (Bardua et al., 2019; Gunz & Mitteroecker, 2013; Mitteroecker & Gunz, 2009). Surface semilandmarks can be placed manually on each specimen individually or placed on a single template specimen that is then warped to all other specimens in the sample; either of which can be a time‐consuming process (Bardua et al., 2019; Gunz & Mitteroecker, 2013). Ascertaining the optimal number of semilandmarks for an analysis can also be difficult, as it is dependent on the complexity of the bony curves or surfaces (Mitteroecker & Gunz, 2009). These issues are exacerbated for complex morphologies that lack obvious homologous features for landmark placement (e.g., carpals or tarsals). Weighted spherical harmonics (SPHARM) offers an alternative method of shape analysis that sidesteps many of the difficulties associated with setting up a sliding semilandmark analysis (e.g., Bardua et al., 2019; Shen et al., 2009).

1.1. Spherical harmonics

SPHARM extends the techniques of an elliptical Fourier analysis to 3D objects. It has been used previously by neuroscientists to quantify and compare brain shapes (Gerig et al., 2001; Goldberg‐Zimring et al., 2005), as well as by biologists to study complex morphologies such as insect genitalia (Shen et al., 2009). Elliptical Fourier analyses can be used to describe the outline of a 2D object as a function (based on an angle in polar coordinates) that maps the distance from an origin to each point along the outline of the object (Rohlf & Archie, 1984). This function, expressed in terms of sine and cosine (harmonic) functions, contains Fourier coefficients (Shen et al., 2009). The more coefficients that a Fourier series contains, the more accurate and detailed the reconstruction of the contour will be. A SPHARM analysis is a Fourier‐based technique that can be used to quantify the shape of 3D objects.

The 3D shapes used in a SPHARM analysis must be closed, genus‐zero surfaces (objects without holes; Shen et al., 2009). During the SPHARM analysis, the vertices of the triangular meshes are mapped onto the surface of a unit sphere (Shen et al., 2009). The mapping is bijective (meaning each vertex point is paired with exactly one point on the surface of the sphere) and equiareal (area‐preserving) which minimizes area and topology distortion (Shen et al., 2009). Once vertices have been optimally mapped onto the surface of a sphere, their original Cartesian coordinates can be expressed as a function of their polar coordinates on the surface of the sphere. These functions (one for each coordinate direction) represent the total spherical harmonic model and contain coefficients that are determined through least squares estimation (Shen et al., 2009). Coefficients from the SPHARM functions are used to represent and reconstruct the original object's 3D surface. The number of coefficients in a SPHARM model is determined by the number of degrees to which SPHARM models are calculated, and specifies the level of detail that the model captures (Shen et al., 2009; Figure 1). The more coefficients that a model contains, the more accurate its reconstruction will be (Shen et al., 2009). To compare the shape of the 3D objects, the SPHARM models and their coefficients must be registered to a template specimen, at which point the SPHARM harmonics provide an orthogonal basis for the comparison of models in high‐dimensional shape space (Shen et al., 2009). The SPHARM coefficients thus serve as the shape descriptors for the objects being compared (Shen et al., 2009).

FIGURE 1.

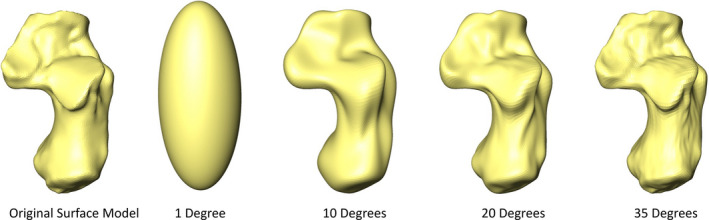
FIGURE 1

Open in a new tab

Surface models created from spherical harmonic models of a Gorilla gorilla gorilla calcaneus using coefficients for degrees 1, 10, 20, and 35

1.2. Study objectives

While SPHARM analyses have been used to evaluate the shape of different morphologies (e.g., Melinska et al., 2017; Shen et al., 2009; Styner et al., 2006), their comparability to sliding semilandmark analyses for skeletal elements has not been established. Here, we carry out a SPHARM analysis on the calcaneus of modern humans and nonhuman African apes, and compare the results to those of a sliding semilandmark analysis carried out on the same specimens. The calcaneus is an ideal bone to use for the comparison of these two methods because sliding semilandmark analyses have been successfully carried out on the bone (Harper et al., 2021a, 2021b; Polly, 2008) and because the calcaneus is a genus‐zero shape and thus appropriate for a SPHARM analysis. As a product of the SPHARM analysis, surface models are produced for each specimen that is represented by the same number of vertices. Vertices across specimens occupy the same relative position on the bone. We therefore also examine the use of these vertices as the initial starting position for a sliding semilandmark analysis (referred to as “SPHARM–sliding” throughout the manuscript) to determine if this alternative method for determining and placing semilandmarks is methodologically advantageous in terms of time.

2. MATERIALS AND METHODS

2.1. Sample and data collection

The sample consists of 60 calcanei from Gorilla gorilla gorilla (n = 20), Pan troglodytes troglodytes (n = 20), and modern Homo sapiens (n = 20) (Supporting Information Table S1), and is sex‐balanced. P. t. troglodytes and G. g. gorilla specimens are from collections curated by the Cleveland Museum of Natural History (CMNH; Cleveland, OH) and the National Museum of Natural History (NMNH; Washington, D.C.), and modern humans are from the Terry Collection curated by the NMNH. All specimens are skeletally adult, wild‐shot (nonhuman primates), and free from obvious skeletal pathology. Right calcanei were preferentially selected, but left elements were used if right elements were unavailable or damaged. Calcanei were surface scanned using a NextEngine laser scanner (0.1 mm resolution; NextEngine, Inc.). Surface models were cleaned (e.g., small holes removed) in Geomagic Wrap (3D Systems Inc., 2015).

2.2. Three‐dimensional geometric morphometric analysis

A three‐dimensional geometric morphometric (3D GM) sliding semilandmark analysis with 1007 sliding semilandmarks (Figure 2) was carried out for quantifying external calcaneus shape following Harper et al. (2021a, 2021b) to compare with the SPHARM results. The borders of the articular facets were represented by 91 curve semilandmarks that were hand placed on each specimen (31 posterior talar facet border semilandmarks; 30 anterior/middle talar facet border semilandmarks; 30 cuboid facet border semilandmarks). The remaining 916 semilandmarks were hand placed on a single template specimen in Avizo Lite 9.0.1 (FEI Visualization Sciences Group, 2015). The template specimen semilandmarks were then warped to all other specimens using the thin plate spline (TPS) interpolation function (Bookstein, 1991; Yang, 2012). The TPS function was established using the articular border semilandmarks and 15 (unanalyzed) landmarks (landmark locations described in Table S1 and Figure S1). The 15 unanalyzed landmarks were manually placed on all specimens (including the template) to ensure that the semilandmarks were in a good starting position for sliding. The warped semilandmarks were then projected on the surface of the specimen and used in the sliding semilandmark analysis.

FIGURE 2.

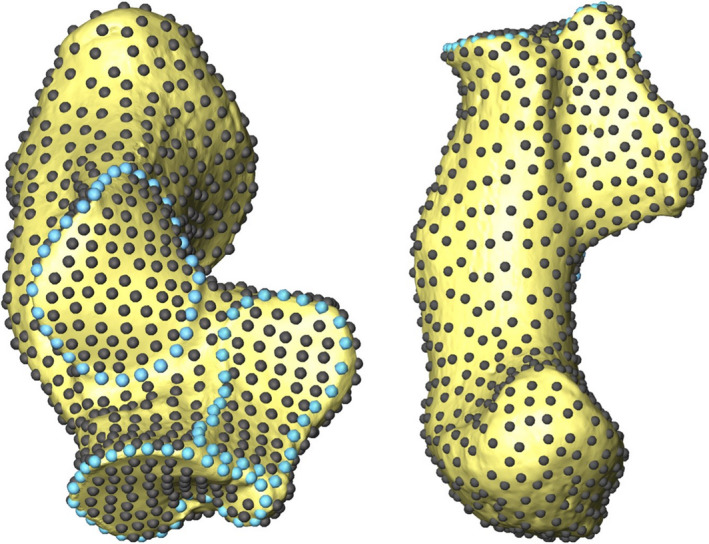
FIGURE 2

Open in a new tab

Fully landmarked right G. g. gorilla calcaneus represented by 1007 sliding semilandmarks. Curve sliding semilandmarks are in light blue and surface semilandmarks are in grey. Adapted from Harper et al. (2021a, 2021b)

Final landmark configurations were created by allowing surface semilandmarks to slide along tangent planes and curve semilandmarks along tangent vectors to minimize the bending energy of the TPS interpolation function relative to a reference specimen (Gunz et al., 2005). Because semilandmarks can slide off of the surface of the bone during this process, semilandmarks were projected back onto the bone surface following each round of sliding. These semilandmark configurations then underwent a Generalized Procrustes Analysis (GPA) to remove the effects of size, location, and orientation (Gower, 1975; Rohlf & Slice, 1990; Zelditch et al., 2012). The average Procrustes landmark configuration was then used as the reference specimen in the next round of sliding. This process of sliding, projecting, and GPA was repeated until landmark configurations no longer move during sliding and the Procrustes average ceases to change (Gunz et al., 2005).

2.3. SPHARM analysis

The SPHARM analysis was carried out in MATLAB R2019a (Mathworks, Inc., 2019) using the SPHARM software application developed by Shen et al. (2009). Surface models were uniformly downsampled to 5,002 vertices using Avizo Lite 9.0.1 (FEI Visualization Sciences Group, 2015). Objects must have the same number of uniformly distributed vertices so that they can be standardized by centroid size in preparation for the spherical harmonic analysis (Shen et al., 2009). Seven homologous landmarks (unanalyzed) were placed on surface models (Shen et al., 2009). Both the triangular mesh and landmark data were size standardized by centroid size, which was calculated based on the triangular mesh. Just as in a landmark analysis, the effect of size (as well as the effects of location and orientation; see below) must be removed in order to analyze morphological shape.

The Control for Area and Length Distortions (CALD) parameterization algorithm (Shen & Makedon, 2006) was applied to a single, size‐standardized template specimen. This algorithm maps the triangular mesh onto the surface of a sphere, minimizing distortion by applying local and global smoothing (for a detailed description see Shen & Makedon, 2006). The spherical harmonic model (calculated to 35 degrees) and associated shape‐describing coefficients are then calculated using standard least‐squares estimation (Shen et al., 2009). When a model is calculated to 35 degrees, each spatial direction in the model is represented by a function containing 1,296 coefficients ((number of degrees + 1)2) (Shen et al., 2009). As there are three coordinate directions, each object is represented by a total of 3,888 coefficients (Shen et al., 2009).

Spherical harmonic models of all other specimens in the sample were calculated using the method described above and registered to the template specimen. This registration step is guided by the unanalyzed landmarks placed prior to the analysis (see above; Shen et al., 2009). Once the objects have been roughly aligned using landmarks, surface homology is further optimized by rotating the spherical parameterizations to the template specimen until the root mean squared distance (RMSD) between the coefficients of the two models is minimized (Shen et al., 2009). Once all objects have been registered to the template, their coefficients are directly comparable with one another as shape descriptors.

2.4. Geometric morphometric analysis using spherical harmonics coordinates (SPHARM–Sliding)

An additional sliding semilandmark analysis was performed to determine if the vertices of registered spherical harmonic models could be used as starting positions of landmarks in a sliding semilandmark analysis. Using the spherical harmonic models from the SPHARM analysis (described above), surface models made up of 2,562 vertices were generated for each specimen. These semilandmarks are in the same location across specimens because each spherical harmonic model was registered to the same template specimen during the SPHARM analysis. The number of semilandmarks was chosen because of the necessary computational power to run the sliding analysis and timing per specimen. On a computer with 64 GB of RAM and a 4.4 GHz processor, it took approximately seven minutes for each specimen to go through four rounds of sliding and projection. As a result of the SPHARM software application, the next (more detailed) surface model that could be created consisted of 10,242 vertices. When a sliding semilandmark analysis was run using 10,242 semilandmarks it took approximately six and half hours per specimen. It would be possible to take a subsample of the 10,242 vertices to have greater control over the number of semilandmarks in the analysis; however, this was not explored here. No curve semilandmarks were included in this analysis.

2.5. Statistical analyses

Calcaneal shape variation for all three analyses was summarized using (separate) principal components analyses (PCA). For the sliding semilandmark and SPHARM–sliding analysis, the PCA was run on Procrustes coordinates, while for the SPHARM analysis the PCA was run on the SPHARM coefficients. Species average surface models were created from the output of each analysis (i.e., the average gorilla from the sliding semilandmark analysis, the SPHARM analysis, and the SPHARM–sliding analysis) and scaled (up) to centroid size. The root mean square (RMS) and maximum distance (MD) between these species average surface models was then calculated in Avizo Lite 9.0.1 (FEI Visualization Sciences Group, 2015) to compare the results of the three shape analyses.

As another means of comparing the three methods, pairwise distances between all objects measured in each analysis were calculated and presented relative to each other in a series of bivariate plots. For the sliding semilandmark and SPHARM–sliding analysis pairwise Procrustes distances were calculated. For the SPHARM analysis, the RMS distance between the sets of coefficients for each object was calculated instead, as this is the distance metric used in the SPHARM software to minimize the distances between the coefficients of the template and the specimen of interest during the registration step (Shen et al., 2009). In addition, Spearman's correlations between the respective sets of pairwise distances were calculated.

3. RESULTS

All three shape analyses separate species along the first two PCs (Figure 3). For all three analyses, modern humans separate from the African apes along PC1. There are minor differences in the PC plots produced by each analysis. The pattern of species separation in the sliding semilandmark PC plot (Figure 3a) is largely similar to that of the SPHARM analysis, (Figure 3b) but is slightly rotated. The sliding semilandmark PC plot and the SPHARM–sliding PC plot (Figure 3c) are also similar.

FIGURE 3.

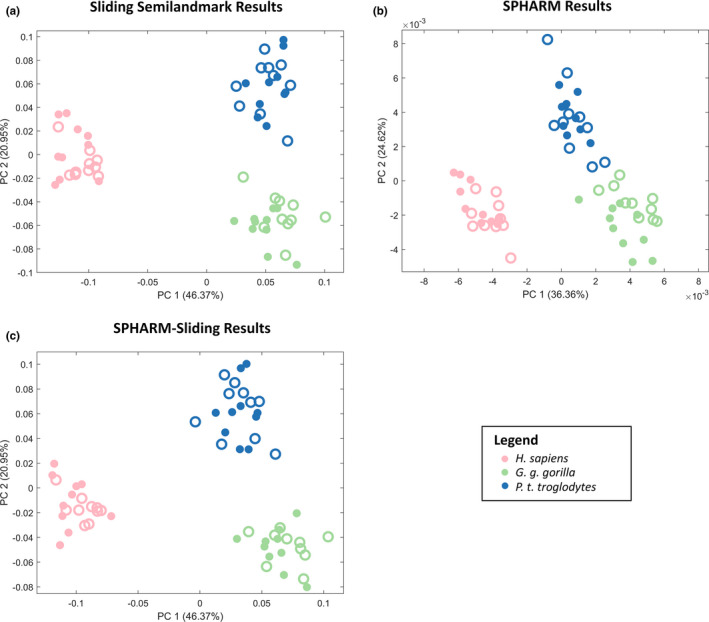
FIGURE 3

Open in a new tab

PC plots of PCs 1 and 2 for sliding semilandmarks (a), SPHARM (b), and SPHARM–sliding (c) analyses. Females are represented by open circles and males by closed circles

Despite the differences in PC plots, all three analyses capture the same general morphological distinctions among the species. Root mean square (RMS) and maximum distance values for comparison of species averages created from each analysis are presented in Table 1. The average RMS between species average surface models generated from the SPHARM and the sliding semilandmark analysis is 0.23 mm. Average RMS between the SPHARM analysis and the SPHARM–sliding analysis is 0.19 mm, and is 0.22 mm between the sliding semilandmark analysis and the SPHARM–sliding analysis.

TABLE 1.

Root mean square, mean distance, and maximum distance between species averages created from GM sliding semilandmark, SPHARM, and SPHARM–Sliding (SS) analyses

Model 1 Model 2 RMS (mm) Mean distance (mm) Max. distance (mm)
GM Avg. Gorilla SHARM Avg. Gorilla 0.26 0.19 1.14
GM Avg. Homo SHARM Avg. Homo 0.26 0.18 1.86
GM Avg. Pan SPHARM Avg. Pan 0.18 0.14 0.69
GM Avg. Gorilla SS Avg. Gorilla 0.23 0.17 1.26
GM Avg. Homo SS Avg. Homo 0.26 0.18 1.99
GM Avg. Pan SS Avg. Pan 0.17 0.13 0.78
SPHARM Avg. Gorilla SS Avg. Gorilla 0.27 0.20 1.29
SPHARM Avg. Homo SS Avg. Homo 0.25 0.18 1.42
SPHARM Avg. Pan SS Avg. Pan 0.21 0.16 0.68
Open in a new tab

Abbreviations: GM, geometric morphometric sliding semilandmark analysis; RMS, root mean square; SPHARM, spherical harmonic analysis; SS, SPHARM–sliding analysis.

The pairwise distances of the sliding semilandmark and the SPHARM analysis are significantly positively correlated with one another (r = 0.790, p < 0.001; Figure 4). The pairwise distances between the SPHARM analysis and SPHARM–sliding analysis exhibit a similar relationship to that of the sliding semilandmark and SPHARM analysis, but they are more strongly correlated with one another (r = 0.820, p < 0.001; Figure 4). The pairwise Procrustes distances of the sliding semilandmark analysis and the SPHARM sliding analysis exhibit the strongest positive correlation (r = 0.973, p < 0.001; Figure 4).

FIGURE 4.

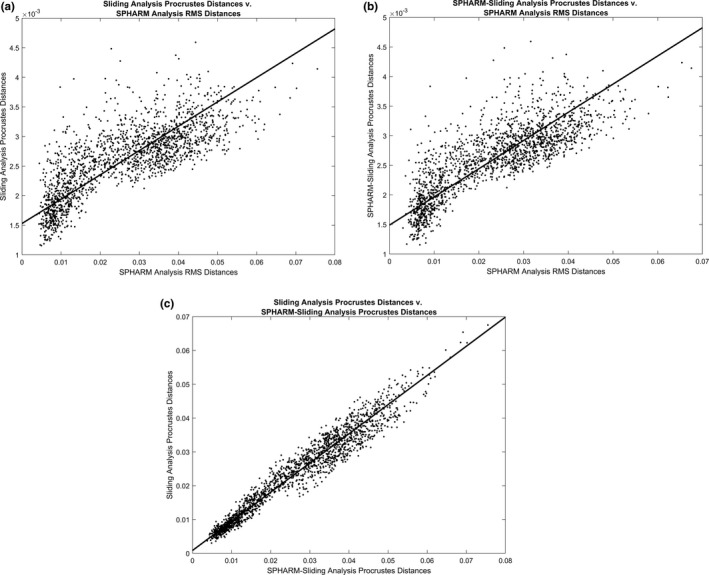
FIGURE 4

Open in a new tab

Bivariate plots of pairwise distances of specimens included in each analysis relative to each other. (a) Sliding semilandmark analysis pairwise Procrustes distances relative to SPHARM analysis pairwise RMS distances. (b) SPHARM–sliding analysis pairwise Procrustes distances relative to SPHARM analysis pairwise RMS distances. (c) Sliding semilandmark pairwise Procrustes distances relative to SPHARM–sliding analysis pairwise Procrustes distances

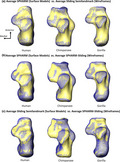
The species average surface models generated from all three shape analyses represent the same overall morphological shapes (Figure 5). The primary shape differences between surface models generated from the SPHARM analysis and surface models generated from the two sliding analyses occur around the sharp edges of the bone, such as the edge of an articular facet (Figure 5). These edges are less defined in SPHARM average surface models and appear to be rounded off compared with the average surface models from the two sliding analyses; however, these differences are relatively minor (Figure 5).

FIGURE 5.

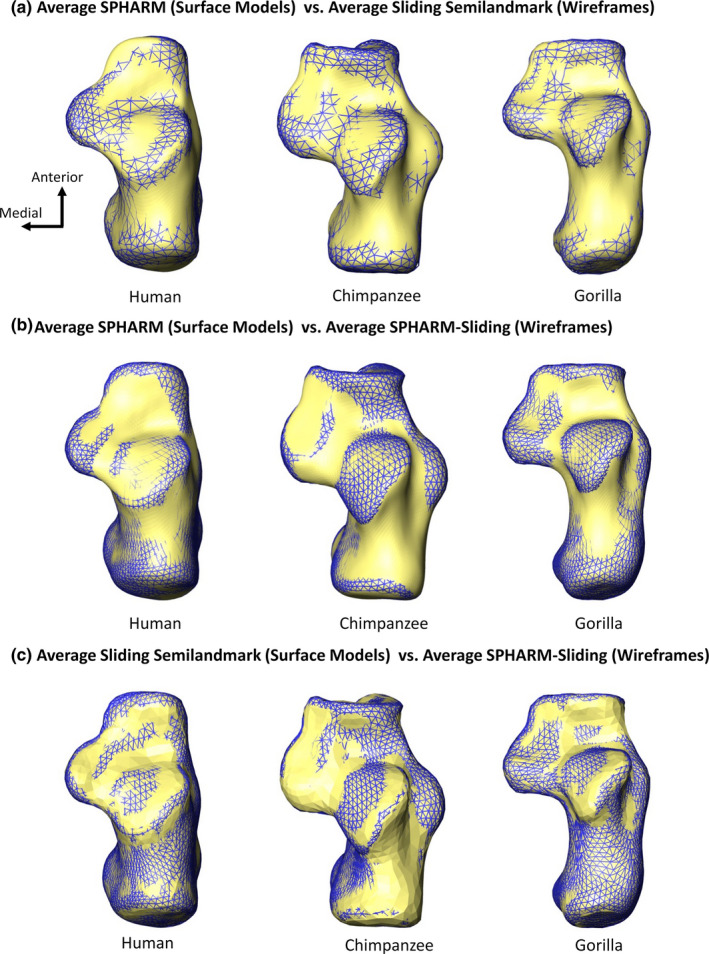
FIGURE 5

Open in a new tab

Superior view of morphological differences between the centroid scaled average of each species created from each analysis. (a) Average SPHARM surface models (surface model) relative to average sliding semilandmark surface models (wireframe). (b) Average SPHARM surface models (surface model) relative to average SPHARM–sliding surface models (wireframe). (c) Average sliding semilandmark surface models (surface model) relative to average SPHARM–sliding surface models (wireframe)

4. DISCUSSION

All three methods of shape analysis presented in this study separate the three taxa included in the sample and capture the same general patterns of shape variation. The species average surface models all exhibit the same overall morphologies with only some minor differences (discussed below). This suggests that the three approaches represent comparable methods of shape analysis. In addition, the pairwise distances among the analyses all exhibit significant positive correlations. The pairwise distances among the specimens are most strongly correlated in the sliding semilandmark analysis and SPHARM–sliding analysis. The pairwise distances are less well correlated (although still significantly positively correlated) in the SPHARM analysis relative to the two sliding analyses. The SPHARM analysis, however, required a different distance metric to be used to calculate pairwise distances, which could be driving this difference. Another possibility for this distinction is that the two types of analyses use different types of shape descriptors (i.e., coefficients in the SPHARM analysis and Procrustes coordinates in the sliding analyses). Although the differences between the three analyses are relatively small, there are advantages and disadvantages to each method.

Compared with the sliding semilandmark analysis, the SPHARM analysis is advantageous in that it does not require the process of determining and initially placing semilandmarks for sliding. As a result, the analysis is less labor intensive than a sliding semilandmark analysis because it minimally requires the placement of six initial landmarks for object registration. It is important to note, however, that algorithms do exist to place semilandmarks automatically on objects (e.g., Boyer et al., 2015; Maga et al., 2017). In addition, the SPHARM analysis itself takes less computational time to complete.

An advantage of the sliding semilandmark analysis is that it is able to capture the sharp edges of the articular facets for the species averages in greater detail than the SPHARM analysis. While spherical harmonic models for each specimen do produce crisp edges, the loss of these in surface models of species or overall averages is problematic for making shape comparisons across taxa. Spherical harmonics models are produced through a process of fitting spherical harmonics to the object based on the number of degrees, which leads to some degree of rounded edges (although not significant) with each individual model (Shen et al., 2009). This rounding becomes exacerbated when the specimens are averaged together, which likely explains why the species average surface models do not exhibit the crisp edges seen in the sliding semilandmark analysis (Shen et al., 2009). The sliding semilandmark analysis also allows for individual articular facets, or other aspects of bony morphology, to be analyzed separately from the rest of the bony morphology, which is not possible due to the nature of the SPHARM analysis.

A novel method using spherical harmonic vertices as the starting position for sliding semilandmarks in a 3D GM analysis (SPHARM–sliding) was explored in order to combat some of the disadvantages of both the SPHARM and sliding semilandmark analyses. The SPHARM analysis produces surface models with vertices that can be used as the starting landmark positions in a sliding semilandmark analysis. Using vertices from the SPHARM surface models combats the time‐consuming process of setting up a high‐density homologous landmark configuration for each specimen for a sliding semilandmark analysis. The pairwise Procrustes distances between the specimens also show strong agreement with those of the sliding semilandmark analysis, indicating that no information is being lost by using this set‐up technique. This methodology also maintains the sharp edges of the bone in species averages that are lost in the SPHARM analysis. In addition, this methodology allows for the analysis of individual articular facets and other aspects of morphology to be analyzed (as with the sliding semilandmark analysis).

While the SPHARM–sliding analysis holds promise as a method for analyzing complex shapes, there are some situations in which the analysis would not be appropriate. As the method utilizes an initial SPHARM analysis to determine the landmark set included in the sliding semilandmark analysis, this methodology can only be applied to genus‐zero shapes. SPHARM‐sliding is well‐suited for small, complex bones.

In summary, results indicate that SPHARM, sliding semilandmark, and SPHARM‐sliding analyses are comparable methods of 3D shape analysis. While all three methods quantified similar levels of shape variation between human, chimpanzee, and gorilla calcanei, the sliding semilandmark and SPHARM‐sliding analyses were able to capture the sharp edges of articular facets more precisely than the SPHARM analysis. This study suggests that SPHARM–sliding is an efficient and effective method for quantifying and comparing the shape of objects that lack features for the obvious placement of homologous landmarks.

CONFLICT OF INTEREST

We declare that we have no conflict of interest.

AUTHOR CONTRIBUTIONS

A.D.S., C.M.H., and D.M.G. contributed to concept and design; C.M.H. acquired the data; C.M.H. and D.M.G. analyzed data; A.D.S., C.M.H., and D.M.G. interpreted data; A.D.S., C.M.H., and D.M.G. writing, editing, and final approval of manuscript.

Supporting information

Supplementary Material

Click here for additional data file. (1MB, docx)

ACKNOWLEDGMENTS

The authors thank Lyman Jellema at the Cleveland Museum of Natural History (Cleveland, OH) and Darrin Lunde at the National Museum of Natural History (Washington, D.C.) for access to the nonhuman primate sample. They thank Dave Hunt at the National Museum of Natural History for access to the human sample. They are also grateful to Kaya G. Zelazny for assistance in the development of the full bone sliding code. They thank Dr. P. David Polly and the anonymous reviewer for their helpful comments, which greatly improved the manuscript.

This project was supported by NSF grant # BCS ‐ 1824630.

Harper, C.M. , Goldstein, D.M. & Sylvester, A.D. (2022) Comparing and combining sliding semilandmarks and weighted spherical harmonics for shape analysis. Journal of Anatomy, 240, 678–687. 10.1111/joa.13589

Christine M. Harper and Deanna M. Goldstein denotes equal contribution from both authors

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

REFERENCES

  1. 3D Systems Inc . (2015) Geomagic Wrap. Rock Hill: 3D Systems Inc. [Google Scholar]
  2. Adams, D.C. , Rohlf, F.J. & Slice, D.E. (2013) A field comes of age: Geometric morphometrics in the 21st century. Hystrix, the Italian Journal of Morphology, 24, 7–14. [Google Scholar]
  3. Àlvarez, A. , Ercoli, A.D. & Prevosti, F.J. (2013) Locomotion in some small to medium‐sized mammals: A geometric morphometric analysis of the penultimate lumbar vertebra, pelvis and hindlimbs. Zoology, 116, 356–371. [DOI] [PubMed] [Google Scholar]
  4. Bardua, C. , Felice, R.N. , Watanabe, A. , Fabre, A.‐C. & Goswami, A. (2019) A practical guide to sliding and surface semilandmarks in morphometric analyses. Integrative Organismal Biology, 1(1), 1–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bookstein, F.L. (1991) Morphometric tools for landmark data: Geometry and biology. Cambridge University Press. [Google Scholar]
  6. Boyer, D.M. , Puente, J. , Gladman, J.T. , Glynn, C. , Mukherjee, S. & Yapuncich, G.S. et al. (2015) A new fully automated approach for aligning and comparing shapes. The Anatomical Record, 298, 249–276. [DOI] [PubMed] [Google Scholar]
  7. Cooney, C.R. , Bright, J.A. , Capp, E.J.R. , Chira, A.M. , Hughes, E.C. , Moody, C.J.A. et al. (2017) Mega‐evolutionary dynamics of the adaptive radiation of birds. Nature, 542, 344–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cucchi, T. , Hulme‐Beaman, A. , Yuan, J. & Dobney, K. (2011) Early Neolithic pig domestication at Jiahu, Henan Province, China: clues from molar shape analyses using geometric morphometric approaches. Journal of Archaeological Science, 38, 11–22. [Google Scholar]
  9. de Oliveira, A.M. & Santos, C.M.D. (2017) Functional morphology and paleoecology of Pilosa (Xenarthra, Mammalia) based on a two‐dimensional geometric morphometrics study of the humerus. Journal of Morphology, 279, 1455–1467. [DOI] [PubMed] [Google Scholar]
  10. Fabre, A.‐C. , Granatosky, M.C. , Hanna, J.B. & Schmitt, D. (2018) Do forelimb shape and peak forces co‐vary in strepsirrhines? American Journal of Physical Anthropology, 167, 602–614. [DOI] [PubMed] [Google Scholar]
  11. FEI Visualization Sciences Group . (2015) Avizo Lite 9.0.1. Hillsboro: FEI Company. [Google Scholar]
  12. Gerig, G. , Styner, M. , Jones, D. , Weinberger, D. & Lieberman, J. (2001) Shape analysis of brain ventricles using SPHARM. Proceedings IEEE Workshop on Mathematical Methods in Biomedical Image Analysis, 2001, 171–178. [Google Scholar]
  13. Goldberg‐Zimring, D. , Talos, I.F. , Bhagwat, J.G. , Haker, S.J. , Black, P.M. & Zou, K.H. (2005) Statistical validation of brain tumor shape approximation via spherical harmonics for image‐guided neurosurgery. Academic Radiology, 12, 459–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gower, J.C. (1975) Generalized procrustes analysis. Psychometrika, 40, 33–51. [Google Scholar]
  15. Gunz, P. & Mitteroecker, P. (2013) Semilandmarks: a method for quantifying curves and surfaces. Hystrix, the Italian Journal of Mammalogy, 1–7. [Google Scholar]
  16. Gunz, P. , Mitteroecker, P. & Bookstein, F.L. (2005) Semilandmarks in three dimensions. In: Slice, D.E. (Ed.) Modern morphometrics in physical anthropology. Cambridge, MA: Springer, pp. 73–98. [Google Scholar]
  17. Gunz, P. , Ramsier, M. , Kuhrig, M. , Hublin, J.‐J. & Spoor, F. (2012) The mammalian bony labyrinth reconsidered, introducing a comprehensive geometric morphometric approach. Journal of Anatomy, 220, 529–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Harcourt‐Smith, W.E.H. , Tallman, M. , Frost, S.R. , Wiley, D.F. , James Rohlf, F. & Delson, E. (2008) Analysis of selected hominoid joint surfaces using laser scanning and geometric morphometrics: a preliminary report. In: Mammalian evolutionary morphology: a tribute to Frederick S. Szalay. New York: Springer, pp. 373–383. [Google Scholar]
  19. Harper, C.M. , Ruff, C.B. & Sylvester, A.D. (2021a) Calcaneal shape variation in humans, nonhuman primates and early hominins. Journal of Human Evolution, 159, 103050. [DOI] [PubMed] [Google Scholar]
  20. Harper, C.M. , Ruff, C.B. & Sylvester, A.D. (2021b) Gorilla calcaneal morphological variation and ecological divergence. American Journal of Physical Anthropology, 174, 49–65. [DOI] [PubMed] [Google Scholar]
  21. Jasinski, S.E. & Wallace, S.C. (2014) Investigation into the paleobiology of Dasypus bellus using geometric morphometrics and variation of the calcaneus. Journal of Mammalian Evolution, 21, 285–298. [Google Scholar]
  22. Kieser, J.A. , Bernal, V. , Neil Waddell, J. & Raju, S. (2007) The uniqueness of the human anterior dentition: a geometric morphometric analysis. Journal of Forensic Sciences, 52, 671–677. [DOI] [PubMed] [Google Scholar]
  23. Klingenberg, C.P. & McIntyre, G.S. (1998) Geometric morphometrics of developmental instability: analyzing patterns of fluctuating asymmetry with procrustes methods. Evolution, 52, 1363–1375. [DOI] [PubMed] [Google Scholar]
  24. Maga, A.M. , Tustison, N.J. & Avants, B.B. (2017) A population level atlas of Mus musculus craniofacial skeleton and automated image‐based shape analysis. Journal of Anatomy, 231, 433–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Melinska, A.U. , Romaszkiewicz, P. , Wagel, J. , Antosik, B. , Sasiadek, M. & Iskander, D.R. (2017) Statistical shape models of cuboid, navicular and talus bones. Journal of Foot and Ankle Research, 10, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Mitteroecker, P. & Gunz, P. (2009) Advances in geometric morphometrics. Evolutionary Biology, 36, 235–247. [Google Scholar]
  27. Polly, P.D. (2008) Adaptive zones and the pinniped ankle: a 3D quantitative analysis of carnivoran tarsal evolution. In: Sargis, E. & Dagosto, M. (Eds.) Mammalian evolutionary morphology. Dordrecht: Springer, pp. 165–194. [Google Scholar]
  28. Rohlf, F.J. & Archie, J.W. (1984) A comparison of Fourier methods for the description of wing shape in mosquitoes (Diptera: Culicidae). Systematic Zoology, 33, 302–317. [Google Scholar]
  29. Rohlf, F. & Marcus, L.F. (1993) A revolution morphometrics. Trends in Ecology & Evolution, 8, 129–132. [DOI] [PubMed] [Google Scholar]
  30. Rohlf, F.J. & Slice, D. (1990) Extensions of the Procrustes method for the optimal superimposition of landmarks. Systematic Biology, 39, 40–59. [Google Scholar]
  31. Segall, M. , Cornette, R. , Fabre, A.‐C. , Godoy‐Diana, R. & Herrel, A. (2016) Does aquatic foraging impact head shape evolution in snakes? Proceedings of the Royal Society B: Biological Sciences, 283, 20161645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Shen, L. , Farid, H. & McPeek, M.A. (2009) Modeling three‐dimensional morphological structures using spherical harmonics. Evolution, 63, 1003–1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shen, L. & Makedon, F. (2006) Spherical mapping for processing of 3D closed surfaces. Image and Vision Computing, 24, 743–761. [Google Scholar]
  34. Styner, M. , Oguz, I. , Xu, S. , Brechbühler, C. , Pantazis, D. & Levitt, J.J. et al. (2006) Framework for the Statistical shape analysis of brain structures using SPHARM‐PDM. Insight Journal, 1071, 242–250. [PMC free article] [PubMed] [Google Scholar]
  35. Sylvester, A.D. (2013) A geometric morphometric analysis of the medial tibial condyle of african hominids. The Anatomical Record, 296, 1518–1525. [DOI] [PubMed] [Google Scholar]
  36. Tallman, M. (2013) Forelimb to hindlimb shape covariance in extant hominoids and fossil hominins. The Anatomical Record, 296, 290–304. [DOI] [PubMed] [Google Scholar]
  37. Turley, K. & Frost, S.R. (2013) The shape and presentation of the catarrhine talus: a geometric morphometric analysis. The Anatomical Record, 296, 877–890. [DOI] [PubMed] [Google Scholar]
  38. Yang, Y. (2012) 3D thin plate spline warping function. MATLAB central file exchange.
  39. Zelditch, M.L. , Swiderski, D.L. & Sheets, H.D. (2012) Geometric morphometrics for biologists: A PRIMER. Cambridge, MA: Academic Press. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material

Click here for additional data file. (1MB, docx)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES