Significance
In this work, we explore the hypothesis that biological neural networks optimize their architecture, through evolution, for learning. We study early olfactory circuits of mammals and insects, which have relatively similar structure but a huge diversity in size. We approximate these circuits as three-layer networks and estimate, analytically, the scaling of the optimal hidden-layer size with input-layer size. We find that both longevity and information in the genome constrain the hidden-layer size, so a range of allometric scalings is possible. However, the experimentally observed allometric scalings in mammals and insects are consistent with biologically plausible values. This analysis should pave the way for a deeper understanding of both biological and artificial networks.
Keywords: olfaction, neural circuit, model selection, statistical learning theory
Abstract
Across species, neural circuits show remarkable regularity, suggesting that their structure has been driven by underlying optimality principles. Here we ask whether we can predict the neural circuitry of diverse species by optimizing the neural architecture to make learning as efficient as possible. We focus on the olfactory system, primarily because it has a relatively simple evolutionarily conserved structure and because its input- and intermediate-layer sizes exhibit a tight allometric scaling. In mammals, it has been shown that the number of neurons in layer 2 of piriform cortex scales as the number of glomeruli (the input units) to the 3/2 power; in invertebrates, we show that the number of mushroom body Kenyon cells scales as the number of glomeruli to the 7/2 power. To understand these scaling laws, we model the olfactory system as a three-layer nonlinear neural network and analytically optimize the intermediate-layer size for efficient learning from limited samples. We find, as observed, a power-law scaling, with the exponent depending strongly on the number of samples and thus on longevity. The 3/2 scaling seen in mammals is consistent with observed longevity, but the 7/2 scaling in invertebrates is not. However, when a fraction of the olfactory circuit is genetically specified, not learned, scaling becomes steeper for species with a small number of glomeruli and recovers consistency with the invertebrate scaling. This study provides analytic insight into the principles underlying both allometric scaling across species and optimal architectures in artificial networks.
Brains exhibit a large range of cell types, connectivity patterns, and organizational structures, at both micro- and macroscales. There is a rich history in neuroscience of explaining these structures from a normative point of view (1–3). Most of that work focused on computation, in the sense that it asked what circuit, and connection strengths, leads to optimal performance on a particular task. However, the connection strengths have to be learned, and model selection theory tells us that the efficiency of learning depends crucially on architecture, especially when a limited number of trials are available (4–8). This is also true for deep networks, where the choice of neural architecture plays a critical role in both learning speed and performance (9). Here we attempt to understand the organizational structure of the brain from a model selection perspective, hypothesizing that evolution optimized the brain for efficient learning.
We build a model inspired by the olfactory circuitry and study its allometric scaling analytically. We focus on the olfactory system primarily because it has a relatively simple, evolutionarily conserved, predominantly feedforward structure (10–12). In particular, odorants are first detected by olfactory sensory neurons; from there, olfactory information is transmitted to glomeruli. The number of glomeruli, however, varies widely across species, from between 10 and 100 in insects to ∼1,000 in mammals. The question we address is, How does the number of glomeruli affect downstream circuitry? And in particular, what downstream circuitry would best help the animal survive? The tradeoffs that go into answering this question are in principle straightforward: More complicated circuitry (i.e., more parameters) can do a better job accurately predicting reward and punishment, but, because there are more parameters, there is a danger of overfitting (4, 7, 8). And even if learning is performed with sample-by-sample updates to avoid overfitting, learning tends to be slower in complicated circuitry, as typically more samples are required (13, 14). Navigating these tradeoffs requires that we choose an architecture, which must come from biology. For that we take inspiration from the olfactory system of both mammals and invertebrates.
In the mammalian olfactory system, information from the glomeruli is transmitted to mitral/tufted cells, then to layer 2 of piriform cortex among others, and then mainly to layer 3; after that, information is passed on to higher-order cortical areas (10, 12). Thus, although many studies suggest that reciprocal interactions between mitral/tufted cells and granule cells (15, 16), as well as feedback from the cortex (17, 18), are also important for olfactory processing, as a first-order approximation the olfactory system can be modeled as a feedforward neural network. Moreover, because sister mitral cells receiving input from the same glomeruli are highly correlated, both with each other and with the glomeruli from which they receive input (19), the olfactory network essentially has three layers: an input layer corresponding to glomeruli, a hidden layer corresponding to layer 2 of piriform cortex, and an output layer corresponding to layer 3.
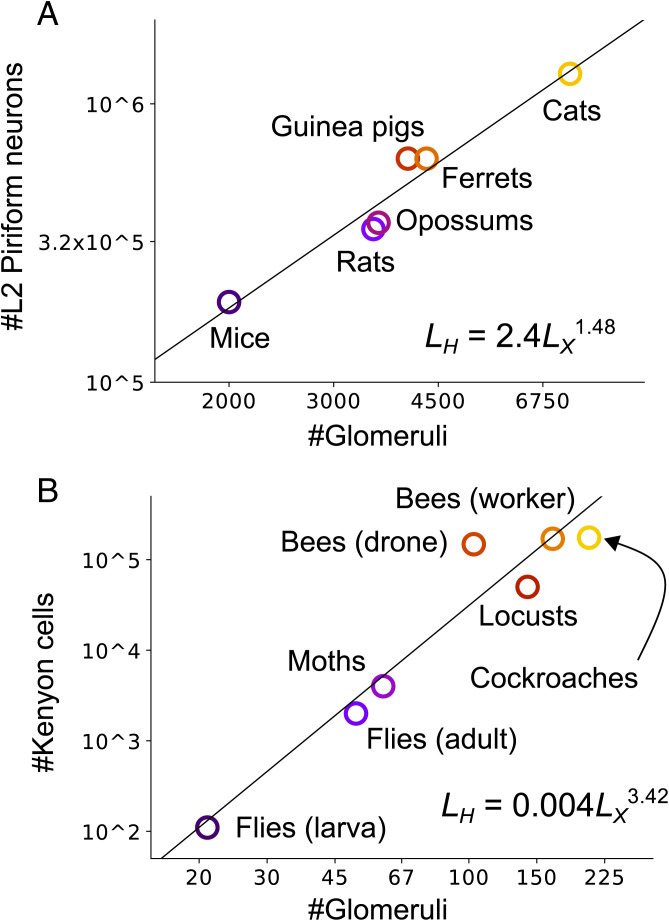
Based on this picture, in our analysis we use an architecture corresponding to a three-layer feedforward network. The size of the input layer is the number of glomeruli, and we assume that each unit of the output layer is extracting a different feature of the olfactory input, such as expected reward or punishment, or a behaviorally relevant concept. Consequently, we focus on the hidden layer. For that we ask, How many units should the hidden layer have? That question was chosen partly because its answer provides insight into learning principles in general and partly because it was recently addressed experimentally: Srinivasan and Stevens (20) found, based on six mammalian species, a very tight relationship between the number of glomeruli and the number of neurons in layer 2 of piriform cortex (Fig. 1A; data taken from ref. 20). More precisely, using Lx to denote the input-layer size (the number of glomeruli) and Lh to denote the hidden-layer size (the number of neurons in layer 2 of piriform cortex), they found the approximate scaling law .
Fig. 1.
(A) Scaling law in mammalian olfactory circuits. Data points were taken from supplementary tables S2 and S3 of Srinivasan and Stevens (20). (B) Scaling law in invertebrate olfactory circuits. See SI Appendix, section 1.1 for details.
Motivated by this result, we asked whether a similar scaling law holds for the invertebrate olfactory system. Like their mammalian counterparts, odors detected by olfactory sensory neurons converge to glomeruli. After that, though, the circuitry differs. Glomeruli send information to the projection neurons (12), which mainly extend synapses onto mushroom body Kenyon cells and lateral horn neurons (21). The latter is mostly related to innate olfactory processing (22), so we focus on the mushroom body, which transmits information to higher-order regions through mushroom body output neurons and is considered to be the learning center of the insect brain (23, 24). Insect olfactory circuits also contain various nonfeedfoward connections, such as lateral inhibition between the projection neurons (12). But, as with the mammalian olfactory system, as a first-order approximation we omit them from the model. Thus, the invertebrate olfactory system can also be modeled as a three-layer neural network: an input layer corresponding to glomeruli, a hidden layer corresponding to Kenyon cells, and an output layer corresponding to mushroom body output neurons (3, 25).
A literature survey of the number of glomeruli and Kenyon cells of various insects (23, 24, 26–35) (see SI Appendix, section 1.1 for details) yielded a scaling law, as in the mammalian olfactory system, but with an exponent of about 7/2 rather than 3/2 (, as shown in Fig. 1B). Drone (male) bees are the clear outlier. That might be because the caste system of honey bees puts the drones under unique ecological pressure; for instance, the drones are the only ones among the seven insects listed that do not engage in foraging. It should be noted that the data were not properly controlled, as they were collected from different sources and in some cases in different eras. Moreover, for the locust, we used the number of olfactory receptor genes instead of the number of glomeruli; that is because their microglomeruli structure makes direct comparison with other species difficult (36). In addition, the mushroom body also takes part in visual processing in bees and cockroaches (37).
Several normative hypotheses have been offered to explain the population size of sensory circuits. One line of theoretical work showed that expansion in the hidden layer is beneficial for sensory coding (3, 38, 39), but it remains elusive how much expansion is optimal, because in these studies, more expansion was in principle always better. Other studies estimated the optimal population size in multiple layers from a width–depth tradeoff, assuming that the total number of neurons is fixed (40, 41) by external factors such as a constraint on energy (42). However, this energy constraint should be violated if increasing the number of neurons improves foraging ability, resulting in a better energy budget (43). Evaluation of the optimal population size was also attempted from other biological constraints, such as synaptic (44) and neuronal (45) noise. While these models provided insight into circuit structure, none were able to provide a quantitative explanation for the population sizes of circuits across different species. Srinivasan and Stevens (20), on the other hand, offered a quantitative derivation of the 3/2 power law observed in mammals. Their derivation was based on the hypothesis that not much information is lost between areas. While this is a reasonable hypothesis, their derivation relied on several implicit assumptions; in particular, they assumed that the noise between different neurons is uncorrelated, and the olfactory signals are not mixed as they propagate across layers. However, both correlations and mixing are likely to exist, and that will affect the number of neurons required in downstream areas (46). In addition, their theory does not explain the 7/2 scaling seen in invertebrates.
Here we develop a mechanistic explanation of the scaling laws, focusing on the fact that the transformation from glomeruli to piriform cortex (for mammals), or from glomeruli to mushroom body output neurons (for invertebrates), has to be learned from a limited number of samples. That explanation draws on model selection theory, in which the primary constraint is the poverty of teaching signals and resultant overfitting (4, 7, 8). Because the olfactory circuit has to tune its numerous synaptic weights from very sporadic, low-dimensional reward signals in the natural environment (47, 48), this constraint should be highly relevant. Therefore, we formulate the problem of olfactory circuit design as a model selection problem and then derive the optimal hidden-layer size under various learning rules and nonlinearities.
Our derivation proceeds in two steps: First, we expand the covariance matrix in the hidden layer in powers of the average hidden-layer correlation coefficient; then we use random matrix theory to compute the generalization error. That enabled us to determine, analytically, the factors that control the optimal hidden-layer size, thus bypassing the intensive numerical optimization typically used in deep-learning settings (9, 40, 49). Our analysis shows that the optimal hidden-layer size follows an allometric scaling with the input-layer size and reveals the factors that control the scaling exponent. Not surprisingly (because learning takes time) we find that the optimal hidden-layer size, and thus the scaling exponent, depends on the lifetime of the organism. The 3/2 scaling found in mammals is, though, largely consistent with observed lifetimes. This scaling relationship is robust against the choice of nonlinearity, activity sparseness, and the noise level and also against the optimization method: It holds under both maximum-likelihood estimation and stochastic gradient descent with cumulative error minimization.
Our theory was not, however, able to capture the 7/2 power law found in invertebrates. That is because traditional model selection theory fails to take into account the fact that neural circuits are at least partially genetically specified. In particular, rich innate connectivity structure is known to exist in the invertebrate olfactory systems (22, 50). Thus, we extend the framework to the case where a fixed genetic budget can be used to specify connections and consider how that affects scaling. The budget we used—about 2,000 bits—had little effect on the scaling of the mammalian circuit, primarily because mammals have a large number of glomeruli, for which a complicated downstream circuit is needed to achieve good performance—far more complicated than could be constructed by 2,000 bits. However, it had a large effect on invertebrates, which contain far fewer glomeruli. In particular, the scaling became steeper, making it possible to replicate the observed 7/2 power law without disrupting the 3/2 power law in mammals. These results shed light on potential constraints on the development and evolution of neural circuitry.
Results
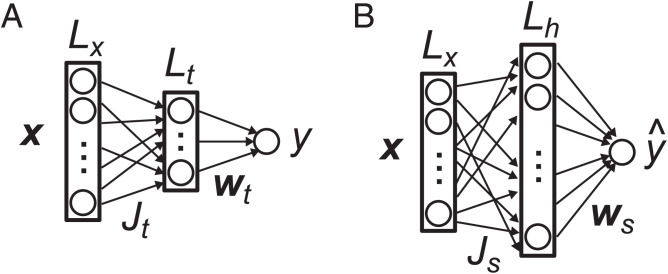
To determine scaling in the olfactory system, we use a teacher–student framework (14, 51, 52): We postulate a teacher network, which reflects the true mapping from odors to reward or punishment in the environment, and model the olfactory network using the same overall architecture, but with different nonlinearities and a different number of neurons in the hidden layer (Fig. 2). We determine the optimal hidden-layer size under several scenarios: batch learning and stochastic gradient learning and with and without information about the weights supplied by the genome.
Fig. 2.
Network models. (A) Olfactory environment (teacher). (B) Olfactory circuit that models the environment (student).
The Model.
Let us denote the olfactory input at the level of glomeruli as and the corresponding reward, or punishment, as y. We define the true relationship between x and y in the environment by a three-layer “teacher” network (Fig. 2A),
| [1] |
where gt is a pointwise nonlinear activation function and ζ is Gaussian noise, added because the relationship between input and reward is stochastic in real-world situations. Throughout the text we use uppercase letters in boldface type to denote matrices and lowercase letters in boldface type for vectors. Vectors are defined as column vectors, a superscript T denotes transpose (indicating a row vector), and for readability we use a dot product to denote the inner product between two vectors. We sampled , and x from independent Gaussian distributions for analytical tractability. Note that we used a continuous, rather than binary, valence y because odor-driven animal behavior is sensitive to both the sign and the value of valence (53).
As discussed above, we model the olfactory circuits of both vertebrates and invertebrates as a three-layer neural network (Fig. 2B),
| [2] |
where is an matrix connecting the input neurons to the neurons in the hidden layer, and is an Lh -dimensional vector connecting the hidden-layer neurons to the output neuron. For simplicity, we assume that is fixed and random, with elements drawn from an independent Gaussian distribution. Only the readout weights, , are learned from data. This is a good approximation for the invertebrate olfactory system, as the connection from the projection neurons to Kenyon cells is indeed mostly random (23) and fixed (54). In the mammalian system, the connection from mitral/tufted cells to piriform cortex, which corresponds to , is suggested to be plastic (55). However, it is thought that those connections are mainly shaped by unsupervised learning, but are seldom modulated by reward, as odor representation in layer 2 of piriform cortex is relatively stable under reward-based learning (56, 57).
The objective of learning is to predict the true reward signal, y, given the input, x. Using the mean-squared error as the loss, the generalization error is written
| [3] |
where angle brackets indicate an average over the input, x, and the teacher noise, ζ. Under this problem setting, we ask what hidden-layer size, Lh, minimizes the generalization error when is learned from N training samples. In particular, we investigate how the optimal hidden-layer size scales with the input-layer size, Lx. Intuitively, when the hidden-layer size is small, the neural network is not expressive enough, so the generalization error tends to be large even after an infinite number of training samples. On the other hand, if the hidden layer is large relative to the number of training samples, the network becomes prone to overfitting, again resulting in poor generalization. Below we address this tradeoff quantitatively.
Generalization Error.
When the learning rule is unbiased, the generalization error consists of two components: the approximation error, which arises because we do not have a perfect model (we use rather than the true weight, , to model the output, y, and we may have a different nonlinearity and hidden-layer size), and the estimation error, which arises because we use a finite number of training samples (6–8). Inserting Eqs. 1 and 2 into 3, we can write the generalization error in terms of these two components,
| [4] |
where the approximation error, ϵapr (the error under the optimal weight ), is
| [5] |
and the estimation error, ϵest (the error induced by using the learned weight, , rather than the optimal one, ), is
| [6] |
Note that under an appropriate learning rule, ϵest converges to zero in the limit of an infinite number of training samples .
We focus first on the approximation error, ϵapr, which depends on the optimal weight, . That weight is found by minimizing with respect to , with y and given in Eqs. 1 and 2, respectively. This is a linear regression problem, and so is given by the usual expression,
| [7] |
To compute , we need to invert a matrix. That is nontrivial because is a nonlinear function and the components of are correlated,
| [8] |
Because the are independent random variables, the off-diagonal elements are smaller than the diagonal elements by a factor of Lx. We can, therefore, compute as an expansion in powers of , multiplied by Lh (because there are factors of Lh more off-diagonal than diagonal elements). Working to second order in , we show in SI Appendix, section 3 that
| [9] |
where
| [10] |
is a monotonically decreasing function of z: and when . All constants are ; their values depend only on the nonlinearities and . Note that our expression for ϵapr does not explicitly depend on the teacher network size Lt. That holds as long as (SI Appendix, Eqs. S38–S41).
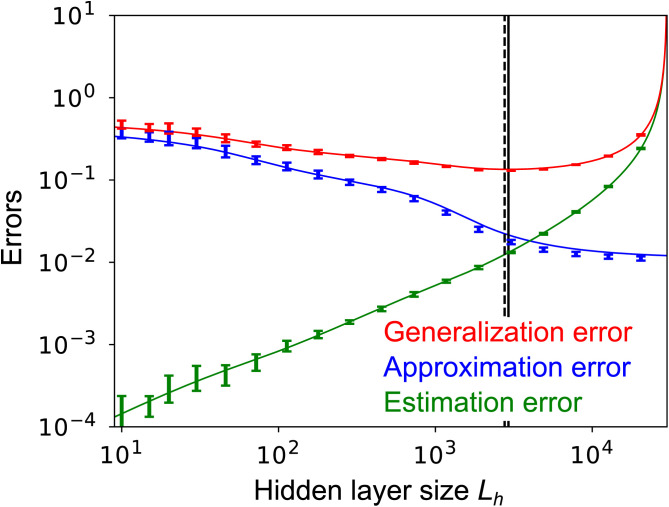
As shown in Fig. 3 (blue line), ϵapr is a monotonically decreasing function of Lh. That function derives its shape from the three Lh -dependent terms in Eq. 9: The second term, , decays to zero when Lh is large compared to 1, the third decays to zero when Lh is large compared to Lx, and the last decays to zero when Lh is large compared to . Essentially, as Lh increases, the effects of the off-diagonal elements of the covariance matrix in Eq. 7 increase, and the model becomes more expressive (and thus lowers the approximation error). Although a number of approximations were made in deriving Eq. 9, the theoretical prediction (blue line in Fig. 3) matches well the numerical simulations (points) for a wide range of Lh.
Fig. 3.
Generalization error (red; Eq. 12), approximation error (blue; Eq. 9), and estimation error (green; Eq. 11) at Lx = 50, , for various hidden-layer sizes Lh. Lines are analytical results; points are from numerical simulations (see SI Appendix, section 7.4 for details). Solid and dashed vertical lines are the minima of the generalization error from theory and simulations, respectively. Here, and in all figures except Fig. 4 D and E, both gt and gs are rectified linear functions []. In all figures except Fig. 6 we use for the noise in the teacher circuit, and in all figures the hidden-layer size of the teacher network is fixed at . Error bars represent the SD over 10 simulations.
To complete the picture of the generalization error, we need the estimation error—the error associated with finite training data. For that it matters how we learn . There are two main choices: maximum-likelihood estimation (MLE) and stochastic gradient descent (SGD). We start with MLE. Although it is not biologically plausible (it requires the learner to compute, and invert, a covariance matrix after seeing all the data), we consider it first because it is reasonably straightforward. After that, we consider the more realistic case of SGD. Both exhibit the 3/2 scaling found in the mammalian olfactory circuit.
MLE Learning.
In SI Appendix, section 4.1, we extend the analysis in ref. 58 to our maximum-likelihood setting and find that the estimation error from N samples is given by
| [11] |
This expression is intuitively sensible: In the limit of infinite data, , the estimation error vanishes, and in the opposite limit, , the estimation error blows up due to overfitting.
If is not too small, ϵest is a monotonically increasing function of Lh, as shown in Fig. 3 (green line). In particular, when Lh is significantly smaller than the number of training samples, N, ϵest is a linearly increasing function of Lh, which is consistent with classical model selection theory (4, 13). Note that when , the estimation error is small. That is because there are very few parameters, and so the network learns them almost perfectly. As Lh approaches N, the estimation error increases, and at Lh = N it goes to infinity. The divergence at Lh = N arises because the matrix on the right-hand side of Eq. 7 becomes singular.
Inserting ϵest from Eq. 11 into Eq. 4, the generalization error under MLE is
| [12] |
The first term on the right-hand side is a decreasing function of Lh; the second term is an increasing function. Together, they produce a generalization error (red line in Fig. 3) that typically has a unique global minimum as a function of Lh. Moreover, the analytically estimated optimal hidden-layer size, , closely matches its estimation from numerical simulations (solid vertical line vs. dashed vertical line in Fig. 3).
The generalization error has a concrete interpretation in terms of discriminability of valence: It tells us the resolution with which valence can be inferred and in particular how far apart odors need to be before we can confidently assign different valence to them. Because our learned network has low generalization error at the optimal hidden-layer size, its resolution at that point is relatively high. For instance, if odors are parallel to the learned direction, they can have a correlation coefficient of 0.99 and still be assigned distinct valences (blue line in SI Appendix, Fig. S1). If, on the other hand, the odors are randomly selected, the correlation coefficient must be below 0.85 (still relatively high) for the circuit to assign distinct valences (orange line in SI Appendix, Fig. S1).
Optimal Hidden-Layer Size.
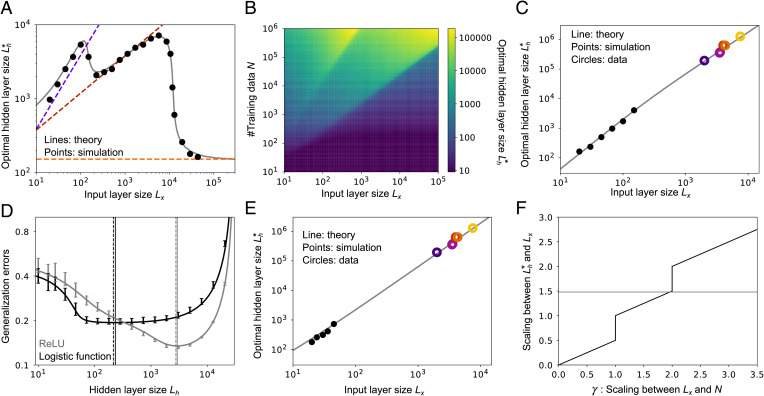
By minimizing the generalization error, Eq. 12, with respect to Lh (with the approximation error given by Eq. 9), we can find the optimal hidden-layer size, , as a function of the input-layer size, Lx. As shown in Fig. 4A, has three different scalings. That is because only one term at a time in Eq. 9 is sensitive to Lh: the second term if , the third term if , and the fourth term if . However, even considering one term at a time, minimizing Eq. 12 with respect to Lh is nontrivial, in large part because of the dependence on N. Details of the minimization are, therefore, left to SI Appendix, section 5.1; here we simply summarize the results.
Fig. 4.
Model behavior under maximum-likelihood estimation. (A) Relationship between the input-layer size, Lx, and the optimal hidden-layer size, , at a fixed sample size (). Gray lines are found by optimizing Eq. 12 with respect to Lh; dashed lines are the asymptotic expression derived in SI Appendix, section 5.1. (B) Optimal hidden-layer size, , as a function of the input-layer size, Lx, and the sample size, N, from Eq. 12. (C) Scaling at . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. Simulations were done only for low Lx, due to the computational cost of the simulations when Lx is large. (D) Relationship between the hidden-layer size, Lh, and the generalization error, ϵgen, under the logistic activation function (black), and ReLU (gray), at Lx = 50 and . Lines are theory; bars are from simulations. Vertical lines mark the minima (solid, theory; dashed, simulations). Error bars are the SD over 10 simulations. (E) Scaling for the logistic activation function with . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. As in C, simulations were done only for low Lx, due to the computational cost of the simulations when Lx is large. (F) Analytical estimation of the - Lx scaling versus the Lx-N scaling (y axis, coefficient β in the scaling ; x axis, coefficient γ in the scaling ; see SI Appendix, section 5.1 for details). The gray horizontal line is the 3/2 scaling from Fig. 1A. As in Fig. 3, the teacher network had a hidden-layer size of 500, with a ReLU nonlinearity, and the noise was set to .
The optimal hidden-layer size, , roughly follows one of the three dashed lines in Fig. 4A, depending on the value of Lx relative to N. When the input layer size, Lx, is small compared to N, is linear in Lx (purple dashed line in Fig. 4A); when Lx is comparable to N, Lh scales as the square root of Lx (red dashed line); and when Lx is larger than N, Lh stays constant as Lx changes (orange dashed line). This last scaling is reasonable because when the input layer is wide enough, expansion in the hidden layer is unnecessary. To further illustrate the dependence of on Lx and N, in Fig. 4B we plot the optimal hidden-layer size versus these two quantities. This indeed shows three distinct phases separated by the lines and . This three-phase structure is robust to the choice of N and (SI Appendix, Fig. S2A), although these parameters introduce an overall scale factor in the optimal hidden-layer size, .
While shows a relatively nontrivial dependence on Lx, its dependence on N (with Lx fixed) is simple: . That is because the effective approximation and estimation errors scale as and , respectively (SI Appendix, section 5.1). Thus, to minimize the generalization error, which is the sum of these two terms, needs to satisfy . This simple scaling is consistent with previous work, which suggests that the scaling of the MSE approximation error (59) and the dependence of the estimation error (13) are robust to model settings.
In our analysis, we assumed that the activity of the glomeruli, x, follows an independent Gaussian distribution. However, because the intrinsic dimensionality of the activity is bounded by the number of olfactory receptor genes, the glomeruli activity is not necessarily independent. This is especially relevant for mammalian olfactory circuits, where the number of glomeruli is typically larger than the number of olfactory receptor genes (20). To investigate this issue, we computed numerically the optimal hidden-layer size when the number of olfactory receptor genes was fixed. We found that if the activity at the glomeruli is whitened via a nonlinearity and lateral inhibition, the optimal hidden-layer size shows the same scaling with the number of glomeruli as it does when the number of glomeruli is equal to the number of olfactory receptor genes (SI Appendix, Fig. S3 and section 7.6). Thus, even though the intrinsic dimensionality of the activity is smaller than the number of glomeruli, because of the nonlinearities and whitening the effective dimensionality scales with the number of glomeruli.
Fig. 4B shows that the scaling relationship between and Lx depends on N. Thus, to determine scaling across species, we need to know how N scales with Lx across species. We cannot directly measure N, which is the total number of rewards/teaching signals an animal experiences in its lifetime. However, we expect that N scales linearly with the duration of learning, so we use that as a proxy. Among the six mammalian species, maximum longevity scales approximately as (SI Appendix, Fig. S4A; longevity data from AnAge database) (60). Alternatively, if we assume that learning happens mostly during the developmental period, here defined as the period from weaning to sexual maturation, a similar trend is observed, but with a slightly different exponent: Duration from the time of weaning to sexual maturation scales approximately as (SI Appendix, Fig. S4B).
Given these observations, we assumed with γ between 1.6 and 2. When we did that, we found a clear scaling law between Lx and that spans more than three orders of magnitude. That is because, unlike Fig. 4A where an increase in Lx causes a phase transition, when N also increases with Lx the system stays in one of the phases (here, the second one). When we set N to , the model reproduced the 3/2 scaling observed in the mammalian olfactory system (Fig. 4C). The coefficient, 1.65, and the exponent, , were selected to match the data in Fig. 1A (SI Appendix, Fig. S5A); notably, though, the exponent fell into the expected range from SI Appendix, Fig. S4 (1.6 to 2.0). Other values of γ gave slightly different scaling (SI Appendix, Fig. S5B).
In the above examples, we used rectified linear units (ReLU) for both teacher (gt) and student (gs), but this matching (gt = gs) might be a strong assumption. To check the robustness of our results with respect to the choice of activation function, we used a logistic function for the student (gs) while keeping a ReLU for the teacher (gt). With this choice, the generalization error is minimized at a smaller hidden-layer size compared to the ReLU student networks (black line vs. gray line in Fig. 4D; see SI Appendix, section 7.2 for details), primarily because large expansion is less helpful when the activation functions of the teacher and student networks are different. Nevertheless, assuming, as above, , we obtain the experimentally observed 3/2 scaling law between and Lx (Fig. 4E and SI Appendix, Fig. S5C). To achieve this scaling, however, the coefficient needs to be larger than when the teacher and student nonlinearity matched ( versus for the matching case).
So far, we have used parameters for which the activity in the intermediate layer is dense, meaning roughly half of the units are active for each odor. However, both Kenyon cells and layer 2 piriform neurons show sparse selectivity for olfactory stimuli (21, 61). To study the effect of sparse selectivity, we introduce a bias to the ReLU nonlinearity, , with b sufficiently large that only a small fraction of neurons in the hidden layer show nonzero activity for each odor (SI Appendix, section 7.3). In this regime, the model prefers larger expansion in the hidden layer (SI Appendix, Fig. S6A), but we still observed a 3/2 scaling law between and Lx (SI Appendix, Fig. S6B), indicating that the scaling law is robust with respect to the sparseness of activity.
Finally, in the large Lx limit the results simplify: The scaling, γ, of the hidden-layer size with the number of glomeruli follows the simple relationship shown in Fig. 4F (see SI Appendix, section 5 and Fig. S7A for details). The three lines in Fig. 4F correspond to the three phases we saw in Fig. 4 A and B. In particular, when γ is between 1.6 and 2.0—the range we found from our analysis of learning times (SI Appendix, Fig. S4)—the optimal hidden-layer size scales as . Thus, our results are robust to the observed scaling of learning time with number of glomeruli.
SGD Learning.
So far, we have considered learning by MLE. However, that is not the best choice when the hidden-layer size, Lh, is similar to the sample size N, as discussed above. In addition, batch learning is not particularly biologically plausible. Therefore, we consider online learning using stochastic gradient descent,
| [13] |
where is the readout weight after trial n and η is the learning rate. For online learning we consider minimization of the generalization error averaged over the lifetime of the organism, not the final error; that is because the fitness of an animal is much better characterized by the average proficiency during its lifetime than the proficiency at the end of its life.
Consistent with previous results (14), the learning rate that enables the fastest decay of the error is (see SI Appendix, section 4.2 for details)
| [14] |
For this learning rate, the lifetime average estimation error after N training samples, denoted , is given approximately by (see SI Appendix, section 4.2, especially SI Appendix, Eq. S91)
| [15] |
where
| [16a] |
| [16b] |
with , the rectified linear function (Fig. 5A). The coefficients , and b3 depend on Lh, but not on N, and α (which appears in the exponent of the last term) is the same constant that appeared in Eq. 9.
Fig. 5.
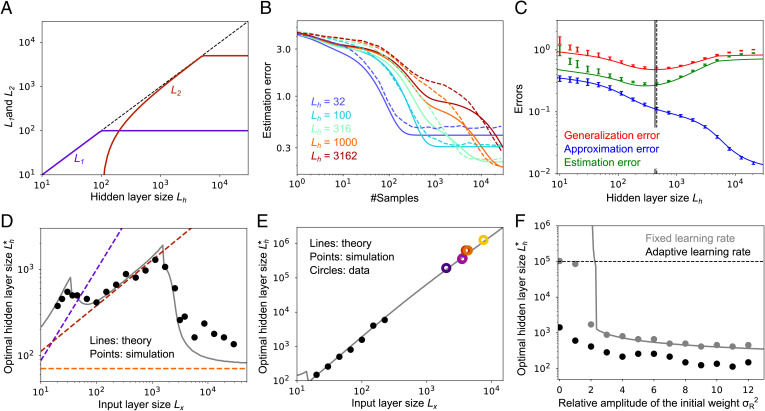
Model behavior under stochastic gradient descent. (A) Hidden-layer size dependence of the decay time constant L1 and L2, with Lx = 100. (B) Dynamics of the estimation error under various hidden-layer sizes, Lh. Dashed lines, simulations; solid lines, theory. (C) The lifetime average generalization error, approximation error, and lifetime average estimation error under various hidden-layer sizes, Lh, at . (D) Optimal hidden-layer size, , with . Dashed lines are asymptotic scaling (SI Appendix, section 5.2). See SI Appendix, Fig. S2B for curves with a range of N and . (E) Optimal hidden-layer size, , with . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. As in Fig. 4, simulations were done only for low Lx, due to the computational cost of the simulations when Lx is large. The discontinuity around is originated from approximations that do not match perfectly around (SI Appendix, sections 4.2 and 8). (F) Optimal hidden-layer size, , for various initial weight amplitudes, , and . Gray, fixed learning rate; black, adaptive learning rate. Lines are theory and dots are simulations. The initial readout weights were sampled from . The horizontal dashed line represents the cutoff of in the numerical simulations. When , under a fixed learning rate, is larger than 105. In A–C and F we set the input-layer size to . As in Fig. 3, the teacher network had a hidden-layer size of 500 and used a ReLU nonlinearity, and the noise was set to .
The behavior of the estimation error under SGD is different from that under MLE, Eq. 11, in two ways. First, for MLE, the estimation error goes to 0 as ; for SGD, it asymptotes to a constant. That is because we used a fixed learning rate for the SGD update rule rather than letting it decay, as would be necessary to reduce the estimation error to zero (62). Second, for MLE the estimation error diverges as Lh approaches N, whereas for SGD it remains finite. That is because of the online nature of SGD, which guards against overfitting.
As can be seen in Eq. 15, the lifetime average estimation error as a function of the number of training samples, N, exhibits three components, all decaying with different timescales (Fig. 5B). The timescales of these, L1, L2, and Lh, are nondecreasing functions of Lh (Fig. 5A). Thus, larger Lh means slower decay with N, as can be seen in Fig. 5B. If the coefficients bq were constant, this would imply that larger Lh would lead to larger lifetime average error. And this is indeed what we see when Lh is larger than about 300 (green line in Fig. 5C). However, for smaller Lh, the dependence of the bq on Lh becomes important, and the lifetime average error decreases with Lh. Because the approximation error decreases monotonically (blue line in Fig. 5C), the lifetime average generalization error (red line in Fig. 5C) typically has a global minimum at a finite hidden-layer size Lh.
As with MLE learning, under a fixed sample size N the optimal hidden-layer size, , shows three different scalings (gray line and dashed lines in Fig. 5D and SI Appendix, Fig. S2B). That is because the approximation error decreases with three distinct phases (Eq. 9). As a result, we observe effectively the same structure in SGD that we saw in MLE (Fig. 5D vs. Fig. 4A), although the theoretical prediction at large Lx under SGD does not match quite as well as under MLE. However, using the scaling with the same γ as before (), and fitting the coefficient in front of Lx, the experimentally observed scaling law in Fig. 1A is again reproduced (Fig. 5E). The effect of γ under SGD learning is about the same as it is under MLE (compare SI Appendix, Fig. S7B to SI Appendix, Fig. S7A, both of which are very similar to Fig. 4F), so the scaling of the optimal hidden-layer size versus that of the input-layer size can be read off Fig. 4F. Thus, as with MLE, the 3/2 scaling is relatively robust to decreases in γ, but less robust to increases.
In our model we initialized the readout weights to relatively large values, . If, however, the weights are instead initialized to small values, the optimal hidden-layer size diverges to infinity (gray line and points in Fig. 5F). This is partially because the fixed learning rate (Eq. 14), employed for analytical tractability, causes poor convergence at small Lh. If an adaptive learning rate, , is used instead (16), the cumulative generalization error is optimal at a finite hidden-layer size even when the initial readout weights are zero (black points in Fig. 5F). Although the optimal hidden-layer size, , goes up as the initial weight amplitude becomes smaller (Fig. 5F), the cumulative error becomes smaller under both fixed and adaptive learning rates (SI Appendix, Fig. S9), due to smaller initial error.
Evolutionary Constraints.
The results so far indicate that developmental constraints explain the scaling law observed in the mammalian olfactory system. However, our analysis also revealed that developmental constraints alone do not explain the 7/2 power-law scaling observed in the invertebrate olfactory circuit, suggesting the presence of additional principles. The primary candidate is a constraint on the genetic budget an animal can use to specify the olfactory circuit. We refer to this as an evolutionary constraint. Because both the number of protein-encoding genes and the total size of the genome tend to be similar across species (63), we assume that the genetic budget for the specification of olfactory circuitry is similar among the insects listed in Fig. 1B.
Inspired by the insect olfactory circuitry, we consider a two-pathway model, in which projection neurons extend connections to both lateral horn neurons and Kenyon cells (Fig. 6A), and the output is
| [17] |
where is the pathway through lateral horn neurons. Although lateral horn neurons do not directly project to mushroom body output neurons, the two pathways eventually converge in the premotor area (24), where the output could be represented. Because connections between projection neurons and lateral horn neurons tend to be stereotyped (22, 50), we assumed they were tuned over evolutionary timescales. The degree of tuning has a strong effect on the Kenyon cell pathway: If they are well tuned, the number of neurons in the hidden layer of the Kenyon cell pathway can be small; if they are poorly tuned, the number of neurons needs to be large. The lateral horn pathway cannot predict rewards and punishments in all environments, so we assumed this pathway has a limited tuning precision. Consequently, we set the weights and with low precision (SI Appendix, section 6). This is in contrast to , which was initialized randomly and fixed, and , which was learned with adaptive SGD. Using Lp to denote the number of lateral horn neurons, under a genetic information budget G, the amount of information encoded in and is bounded by
| [18] |
Fig. 6.
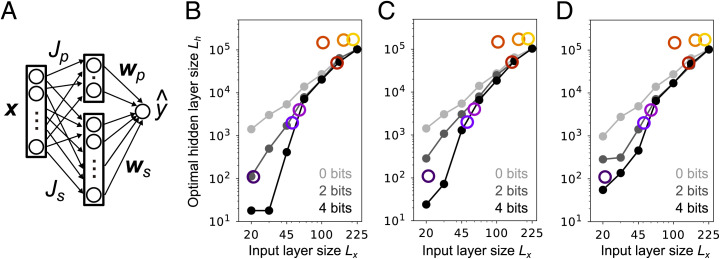
Olfactory circuit augmented with a genetically specified pathway. (A) Schematic of the two-pathway model. For the top part of the circuit, the weights and are hard wired; for the bottom part, the weights are randomly connected and are learned with adaptive SGD. (B–D) Optimal layer size of the projection neurons-to-Kenyon cells pathway under different model settings. (B) Low-bit synapses were achieved by adding Gaussian noise to and . (C) Low-bit synapses were achieved by discretizing and . (D) Low-bit synapses were achieved by adding noise to and as in B, but was additionally learned from training samples using SGD (SI Appendix, Eq. S145). In B–D, the teacher network had a hidden-layer size of 500 and a ReLU nonlinearity, and we used and trials. For sb = 2 bits we used , while for sb = 4 bits we used . For sb = 0 bits, we simply removed the hard-wired pathway. The width of the hard-wired intermediate layer, Lp, was found from Eq. 18: , rounded up to an integer. See SI Appendix, sections 6 and 7.5 for details.
where sb is the number of bits per synapse. The first term is the number of bits needed to specify ; the second term is the number needed to specify (see SI Appendix, section 6.1 for details).
The genetic budget, G, quantifies the accuracy with which the weights and can be encoded in the genome, with larger G corresponding to higher accuracy. Although we measured G using Shannon information (assuming that synapses are uncorrelated), that may not accurately characterize the minimum genome size required for hard wiring. In fact, the lower bound on the genetic complexity of the weight specification is given by the Kolmogorov complexity, which measures the minimum length of a computer program that generates the network (64). Here we make the assumption that the weights are not massively compressible. In this regime, the Shannon information provides a good estimate of the minimum genome size (SI Appendix, section 6). In our simulations we let sb vary between 0 and 4 bits per synapse, which is broadly consistent in the variability seen in the fly connectome (65). We then keep the genetic budget fixed while we vary Lx; we do that by letting (from Eq. 18) .
Under a fixed budget, G, the number of bits per glomerulus, is bounded by , suggesting that as the input-layer size, Lx, increases, tuning of and has to be more coarse grained. In particular, in the mammalian olfactory system where , the hard-wired pathway should play a minor role unless . Indeed, except for encoding of pheromone signals, evidence of hard-wired connections in the mammalian olfactory circuits is limited (66). For invertebrates, which have far fewer glomeruli, hard-wired pathways should be far more important. As the effect of the genetic budget, G, is difficult to characterize analytically, we numerically investigate its effect.
When we allowed information about the weights to be transmitted genetically, subject to the constraint given in Eq. 18, the genetically specified pathway did a good job predicting the valence when Lx was small, but not when it was large. As a result, the optimal Kenyon cell population size, Lh, was much smaller than the circuit without the projection neuron-to-lateral horn neuron pathway (compare 0-bit lines to 2- and 4-bit lines in Fig. 6 B–D), leading to steeper scaling. In particular, we found that by setting sb = 2, the 7/2 scaling observed among insects is approximately reproduced (dark gray line in Fig. 6B). The predicted curve saturates at quadratic scaling around , resulting in underestimation of the Kenyon cell population in bees and cockroaches. This saturation also indicates that in the mammalian system, for which , the genetically specified pathway is unlikely to play much of a role. This trend was observed under a different implementation of low-bit synapses (Fig. 6C and SI Appendix, Fig. S10A), under sparse implementation of the lateral horn pathway (SI Appendix, Fig. S10B and section 6.2), and even when was additionally trained with SGD from finely tuned initial weights (Fig. 6D). For additional details, see SI Appendix, section 6.3.
Discussion
In this work, we modeled the olfactory circuit of both mammals and insects as a three-layer feedforward network and asked how the number of neurons in the hidden layer scales with the number of neurons in the glomerular (i.e., input) layer. We hypothesized that the scarcity of labeled signals (reward and punishment) provides a crucial constraint on the hidden-layer size. This was indeed the case: We showed analytically, and confirmed with simulations, that the optimal hidden-layer size has a strong, nonmonotonic, dependence on the number of labeled signals. Assuming that the number of labeled signals an animal experiences is proportional to its lifetime, and using lifetimes in the range of those reported experimentally, we were able to recover the observed 3/2 scaling (the number of neurons in the hidden layer is proportional to the number of glomeruli to the 3/2 power) observed in mammals. This held under both maximum-likelihood (Fig. 4) and stochastic gradient descent (Fig. 5) learning and was robust to the choice of nonlinearity (Fig. 4 D and E), activity sparseness (SI Appendix, Fig. S6), and the noise level (SI Appendix, Fig. S2). Scarcity of labels alone does not, however, explain the 7/2 scaling found in the olfactory circuit of insects. But by considering the fact that genetic information is available for constructing hard-wired olfactory connections, and that it is limited, we recovered the 7/2 scaling law (Fig. 6), without disrupting the 3/2 scaling law in mammals. Note, though, that a certain amount of fine-tuning was required to recover this scaling: The genetic budget (for which we used 2,000 bits) had to be specified to within ∼20% (SI Appendix, Fig. S10).
To derive these results, we assumed that the input is white, the connectivity in the hidden layer is fixed and random, and the teacher network is random. If the activity is not whitened at the glomeruli, it is likely that the size of the input layer would be replaced by its effective linear dimensionality. In addition, the actual olfactory environment might have hidden structure that the genetically specified pathway can exploit, even with a low genetic budget. If that is the case, genetic encoding could play a significant role even in the mammalian system. We leave these cases for future work.
The 3/2 power in the scaling law we derived for mammals comes from two factors. First, when the number of training samples is fixed, the optimal population size of the piriform cortex increases as the number of glomeruli increases, unless the number of glomeruli is very large (Figs. 4A and 5D). Second, the optimal population size of the piriform cortex also increases with the number of training samples (Fig. 4B). Because species with more glomeruli tend to live longer and experience more samples (SI Appendix, Fig. S4), this sample size dependence causes an additional scaling between the number of glomeruli and the piriform population size. From these two factors, the optimal intermediate-layer size scales supralinearly on the number of glomeruli (Figs. 4 C and E and 5E). Because of the dependence on the number of training samples, N, the power in the scaling law is not fixed at 3/2. In fact, depending on how N scales with the input-layer size, Lx, theoretically a wide range of scaling is possible (Fig. 4F and SI Appendix, section 5). The 3/2 scaling we found was because in mammals, lifetime scales approximately quadratically with the number of glomeruli (SI Appendix, section 1.2 and Table 2).
Our analysis predicts that under both MLE and SGD learning. Assuming that this relationship holds at microscopic level as well, we predict that the number of presynaptic connections received by a neuron in the output layer should scale with the square root of the frequency of feedback signals it receives. It might be possible to test this prediction in the mushroom body output neurons of flies, where compartmentalized units receive diverse neuromodulatory inputs (24), and its detailed connectivity structure is known (28). Although we also need to estimate the frequency of the feedback signal at each compartment in the natural environment, in the near future it should be technically feasible to test this prediction.
The three-layer feedforward neural network with random fixed hidden weights is a class of neural networks that is widely studied from both biological (3, 38, 39, 67) and engineering (68, 69) perspectives. Under batch learning, the upper bound on the approximation error for this network structure is known for a large class of the target functions (59, 70), but these bounds are often too loose to be practical. Here, we instead focused on the average approximation error (SI Appendix, section 3). This allowed us to derive, analytically, accurate estimates of the optimal hidden-layer size. We found a nontrivial three-phase structure, which has not been reported before in the context of model selection (but see ref. 71). The behavior of the estimation error is also well characterized in the large sample size limit ( while ) (13, 72), but this limit is not a good approximation of an overparameterized neural network. On the other hand, the characteristics of the error in the large parameter limit (number of synapses proportional to N as ) remain mainly elusive, except for linear regression (58) (SI Appendix, section 4.1). Similarly, model selection in neural networks has been studied mostly in the large sample size limit (7, 73). The upper bound on the network size was also studied from Vapnik–Chervonenkis theory (5) and the minimum description length principle (6).
Learning dynamics in neural networks under SGD has also been widely studied (14, 52, 74). In particular, recent results suggest that overparameterization of a neural network does not harm the generalization error under both full-batch and stochastic gradient descent learning (71, 74–76). Here, though, we focused on the cumulative error, not the error at the end of training, as the former is more relevant to the fitness of the species. Under this objective function, overparameterization does tend to harm performance, because learning becomes slower (Fig. 5B), even under an adaptive learning rate (Fig. 5F).
Slow learning is consistent with previous observations that deep reinforcement learning, in which the model often needs to be trained online, requires a large number of iterations for successful learning (77). Neural architecture optimization for the minimization of cumulative loss may help build efficient and generalizable deep reinforcement learning. However, we also found that if the learning rate is fixed and the initial weights are set to very small values, having infinitely many neurons in the hidden layer minimizes the cumulative error (Fig. 5F), suggesting that overparameterization is not always harmful, even when the cumulative error is the relevant cost function. Our analysis of neural architecture selection may provide insight into scaling laws observed in artificial neural networks, although those models face different constraints than their biological counterparts (49).
Scaling laws are also observed in other regions of the brain. For instance, the number of neurons in the primary visual cortex scales with the 3/2 power relative to the population size of the lateral geniculate nucleus (78), and the number of neurons in the cerebral cortex is linear in the total number of neurons in the cerebellum (79). Given the anatomical similarity between the olfactory circuit and cerebellum (3), our methodology should be directly applicable to understanding the latter scaling. But it is not limited to olfactory-like structures; it could be applied, possibly with some modifications, anywhere in the brain and has the potential to provide insight into circuit structure in general.
Supplementary Material
Acknowledgments
This work was supported by the Gatsby Charitable Foundation and the Wellcome Trust (110114/Z/15/Z). N.H. was partially supported by the Swartz Foundation.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data Availability
The source codes of the simulations and the data analysis are deposited in GitHub (https://github.com/nhiratani/olfactory_design) (80).
References
- 1.Mathis A., Herz A. V., Stemmler M., Optimal population codes for space: Grid cells outperform place cells. Neural Comput. 24, 2280–2317 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Gjorgjieva J., Sompolinsky H., Meister M., Benefits of pathway splitting in sensory coding. J. Neurosci. 34, 12127–12144 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Litwin-Kumar A., Harris K. D., Axel R., Sompolinsky H., Abbott L. F., Optimal degrees of synaptic connectivity. Neuron 93, 1153–1164.e7 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Akaike H., A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974). [Google Scholar]
- 5.Baum E. B., Haussler D., “What size net gives valid generalization?” in Advances in Neural Information Processing Systems, Touretzky D., Ed. (NIPS, 1988), vol. 1, pp. 81–90. [Google Scholar]
- 6.Barron A. R., Approximation and estimation bounds for artificial neural networks. Mach. Learn. 14, 115–133 (1994). [Google Scholar]
- 7.Murata N., Yoshizawa S., Amari S., Network information criterion-determining the number of hidden units for an artificial neural network model. IEEE Trans. Neural Netw. 5, 865–872 (1994). [DOI] [PubMed] [Google Scholar]
- 8.Mohri M., Rostamizadeh A., Talwalkar A., Foundations of Machine Learning (MIT Press, 2018). [Google Scholar]
- 9.Elsken T., Metzen J. H., Hutter F., Neural architecture search: A survey. J. Mach. Learn. Res. 20, 1997–2017 (2019). [Google Scholar]
- 10.Davis R. L., Olfactory learning. Neuron 44, 31–48 (2004). [DOI] [PubMed] [Google Scholar]
- 11.Ache B. W., Young J. M., Olfaction: Diverse species, conserved principles. Neuron 48, 417–430 (2005). [DOI] [PubMed] [Google Scholar]
- 12.Wilson R. I., Mainen Z. F., Early events in olfactory processing. Annu. Rev. Neurosci. 29, 163–201 (2006). [DOI] [PubMed] [Google Scholar]
- 13.Amari S. I., Murata N., Statistical theory of learning curves under entropic loss criterion. Neural Comput. 5, 140–153 (1993). [Google Scholar]
- 14.Werfel J., Xie X., Seung H. S., “Learning curves for stochastic gradient descent in linear feedforward networks” in Advances in Neural Information Processing Systems, Thrun S., et al., Eds. (NIPS, 2003), vol. 16, pp. 1197–1204. [DOI] [PubMed] [Google Scholar]
- 15.Gschwend O., et al., Neuronal pattern separation in the olfactory bulb improves odor discrimination learning. Nat. Neurosci. 18, 1474–1482 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hiratani N., Latham P. E., Rapid Bayesian learning in the mammalian olfactory system. Nat. Commun. 11, 3845 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Otazu G. H., Chae H., Davis M. B., Albeanu D. F., Cortical feedback decorrelates olfactory bulb output in awake mice. Neuron 86, 1461–1477 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Grabska-Barwińska A., et al., A probabilistic approach to demixing odors. Nat. Neurosci. 20, 98–106 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Dhawale A. K., Hagiwara A., Bhalla U. S., Murthy V. N., Albeanu D. F., Non-redundant odor coding by sister mitral cells revealed by light addressable glomeruli in the mouse. Nat. Neurosci. 13, 1404–1412 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Srinivasan S., Stevens C. F., Scaling principles of distributed circuits. Curr. Biol. 29, 2533–2540.e7 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Martin J. P., et al., The neurobiology of insect olfaction: Sensory processing in a comparative context. Prog. Neurobiol. 95, 427–447 (2011). [DOI] [PubMed] [Google Scholar]
- 22.Fişek M., Wilson R. I., Stereotyped connectivity and computations in higher-order olfactory neurons. Nat. Neurosci. 17, 280–288 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Caron S. J., Ruta V., Abbott L. F., Axel R., Random convergence of olfactory inputs in the Drosophila mushroom body. Nature 497, 113–117 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aso Y., et al., The neuronal architecture of the mushroom body provides a logic for associative learning. eLife 3, e04577 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Huerta R., Nowotny T., García-Sanchez M., Abarbanel H. D., Rabinovich M. I., Learning classification in the olfactory system of insects. Neural Comput. 16, 1601–1640 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Ramaekers A., et al., Glomerular maps without cellular redundancy at successive levels of the Drosophila larval olfactory circuit. Curr. Biol. 15, 982–992 (2005). [DOI] [PubMed] [Google Scholar]
- 27.Masuda-Nakagawa L. M., Gendre N., O’Kane C. J., Stocker R. F., Localized olfactory representation in mushroom bodies of Drosophila larvae. Proc. Natl. Acad. Sci. U.S.A. 106, 10314–10319 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Eichler K., et al., The complete connectome of a learning and memory centre in an insect brain. Nature 548, 175–182 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Anton S., Hansson B. S., Central processing of sex pheromone, host odour, and oviposition deterrent information by interneurons in the antennal lobe of female Spodoptera littoralis (Lepidoptera: Noctuidae). J. Comp. Neurol. 350, 199–214 (1994). [DOI] [PubMed] [Google Scholar]
- 30.Sjöholm M., Sinakevitch I., Ignell R., Strausfeld N. J., Hansson B. S., Organization of Kenyon cells in subdivisions of the mushroom bodies of a lepidopteran insect. J. Comp. Neurol. 491, 290–304 (2005). [DOI] [PubMed] [Google Scholar]
- 31.Wang Z., et al., Identification and functional analysis of olfactory receptor family reveal unusual characteristics of the olfactory system in the migratory locust. Cell. Mol. Life Sci. 72, 4429–4443 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Leitch B., Laurent G., GABAergic synapses in the antennal lobe and mushroom body of the locust olfactory system. J. Comp. Neurol. 372, 487–514 (1996). [DOI] [PubMed] [Google Scholar]
- 33.Arnold G., Masson C., Budharugsa S., Comparative study of the antennal lobes and their afferent pathway in the worker bee and the drone (Apis mellifera). Cell Tissue Res. 242, 593–605 (1985). [Google Scholar]
- 34.Watanabe H., Nishino H., Nishikawa M., Mizunami M., Yokohari F., Complete mapping of glomeruli based on sensory nerve branching pattern in the primary olfactory center of the cockroach Periplaneta americana. J. Comp. Neurol. 518, 3907–3930 (2010). [DOI] [PubMed] [Google Scholar]
- 35.Farris S. M., Strausfeld N. J., Development of laminar organization in the mushroom bodies of the cockroach: Kenyon cell proliferation, outgrowth, and maturation. J. Comp. Neurol. 439, 331–351 (2001). [DOI] [PubMed] [Google Scholar]
- 36.Ernst K. D., Boeckh J., Boeckh V., A neuroanatomical study on the organization of the central antennal pathways in insects. Cell Tissue Res. 176, 285–306 (1977). [DOI] [PubMed] [Google Scholar]
- 37.Capaldi E. A., Robinson G. E., Fahrback S. E., Neuroethology of spatial learning: The birds and the bees. Annu. Rev. Psychol. 50, 651–682 (1999). [DOI] [PubMed] [Google Scholar]
- 38.Barak O., Rigotti M., Fusi S., The sparseness of mixed selectivity neurons controls the generalization-discrimination trade-off. J. Neurosci. 33, 3844–3856 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Babadi B., Sompolinsky H., Sparseness and expansion in sensory representations. Neuron 83, 1213–1226 (2014). [DOI] [PubMed] [Google Scholar]
- 40.Hermundstad A. M., Brown K. S., Bassett D. S., Carlson J. M., Learning, memory, and the role of neural network architecture. PLOS Comput. Biol. 7, e1002063 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kadmon J., Sompolinsky H., “Optimal architectures in a solvable model of deep networks” in Advances in Neural Information Processing Systems, Lee D., et al., Eds. (NIPS, 2016), vol. 29, pp. 4781–4789. [Google Scholar]
- 42.Aiello L. C., Wheeler P., The expensive-tissue hypothesis: The brain and the digestive system in human and primate evolution. Curr. Anthropol. 36, 199–221 (1995). [Google Scholar]
- 43.Navarrete A., van Schaik C. P., Isler K., Energetics and the evolution of human brain size. Nature 480, 91–93 (2011). [DOI] [PubMed] [Google Scholar]
- 44.Raman D. V., Rotondo A. P., O’Leary T., Fundamental bounds on learning performance in neural circuits. Proc. Natl. Acad. Sci. U.S.A. 116, 10537–10546 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yu L., Zhang C., Liu L., Yu Y., Energy-efficient population coding constrains network size of a neuronal array system. Sci. Rep. 6, 19369 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zylberberg J., Pouget A., Latham P. E., Shea-Brown E., Robust information propagation through noisy neural circuits. PLOS Comput. Biol. 13, e1005497 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lake B. M., Ullman T. D., Tenenbaum J. B., Gershman S. J., Building machines that learn and think like people. Behav. Brain Sci. 40, e253 (2017). [DOI] [PubMed] [Google Scholar]
- 48.Raine N. E., Chittka L., The correlation of learning speed and natural foraging success in bumble-bees. Proc. Biol. Sci. 275, 803–808 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bahri Y., Dyer E., Kaplan J., Lee J., Sharma U., Explaining neural scaling laws. arXiv [Preprint] (2021). https://arxiv.org/abs/2102.06701 (Accessed 18 February 2022).
- 50.Frechter S., et al., Functional and anatomical specificity in a higher olfactory centre. eLife 8, e44590 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sompolinsky H., Tishby N., Seung H. S., Learning from examples in large neural networks. Phys. Rev. Lett. 65, 1683–1686 (1990). [DOI] [PubMed] [Google Scholar]
- 52.Saxe A. M., McClelland J. L., Ganguli S., Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv [Preprint] (2013). https://arxiv.org/abs/1312.6120 (Accessed 18 February 2022).
- 53.Badel L., Ohta K., Tsuchimoto Y., Kazama H., Decoding of context-dependent olfactory behavior in Drosophila. Neuron 91, 155–167 (2016). [DOI] [PubMed] [Google Scholar]
- 54.Hige T., Aso Y., Modi M. N., Rubin G. M., Turner G. C., Heterosynaptic plasticity underlies aversive olfactory learning in Drosophila. Neuron 88, 985–998 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chapuis J., Wilson D. A., Bidirectional plasticity of cortical pattern recognition and behavioral sensory acuity. Nat. Neurosci. 15, 155–161 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Millman D. J., Murthy V. N., Rapid learning of odor–value association in the olfactory striatum. J. Neurosci. 40, 4335–4347 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wang P. Y., et al., Transient and persistent representations of odor value in prefrontal cortex. Neuron 108, 209–224.e6 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Advani M., Ganguli S., Statistical mechanics of optimal convex inference in high dimensions. Phys. Rev. X 6, 031034 (2016). [Google Scholar]
- 59.Rahimi A., Recht B., “Weighted sums of random kitchen sinks: Replacing minimization with randomization in learning” in Advances in Neural Information Processing Systems, Koller D., et al., Eds. (NIPS, 2008), vol. 21, pp. 1313–1320. [Google Scholar]
- 60.Tacutu R., et al., Human ageing genomic resources: Integrated databases and tools for the biology and genetics of ageing. Nucleic Acids Res. 41, D1027–D1033 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Pashkovski S. L., et al., Structure and flexibility in cortical representations of odour space. Nature 583, 253–258 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bottou L., “Online learning and stochastic approximations” in On-Line Learning in Neural Networks, Saad D., Ed. (Cambridge University Press, Cambridge, UK, 1998), pp. 142–177. [Google Scholar]
- 63.Pray L., Eukaryotic genome complexity. Nature Education 1, 96 (2008). [Google Scholar]
- 64.Grunwald P., Vitányi P., Shannon information and kolmogorov complexity. arXiv [Preprint] (2004). https://arxiv.org/abs/cs/0410002 (Accessed 18 February 2022).
- 65.Takemura S. Y., et al., Synaptic circuits and their variations within different columns in the visual system of Drosophila. Proc. Natl. Acad. Sci. U.S.A. 112, 13711–13716 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ishii K. K., et al., A labeled-line neural circuit for pheromone-mediated sexual behaviors in mice. Neuron 95, 123–137.e8 (2017). [DOI] [PubMed] [Google Scholar]
- 67.Ganguli S., Sompolinsky H., Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Annu. Rev. Neurosci. 35, 485–508 (2012). [DOI] [PubMed] [Google Scholar]
- 68.Huang G. B., Zhu Q. Y., Siew C. K., Extreme learning machine: Theory and applications. Neurocomputing 70, 489–501 (2006). [Google Scholar]
- 69.Dasgupta S., Stevens C. F., Navlakha S., A neural algorithm for a fundamental computing problem. Science 358, 793–796 (2017). [DOI] [PubMed] [Google Scholar]
- 70.Liu X., Lin S., Fang J., Xu Z., Is extreme learning machine feasible? A theoretical assessment (part I). IEEE Trans. Neural Netw. Learn. Syst. 26, 7–20 (2015). [DOI] [PubMed] [Google Scholar]
- 71.d’Ascoli S., Sagun L., Biroli G., “Triple descent and the two kinds of overfitting: Where & why do they appear?” in Advances in Neural Information Processing Systems, Larochelle H., et al., Eds. (NeurIPS, 2020), vol. 33, pp. 3058–3069. [Google Scholar]
- 72.Van der Vaart A. W., Asymptotic Statistics (Cambridge University Press, 2000), vol. 3. [Google Scholar]
- 73.Barkai N., Seung H. S., Sompolinsky H., Scaling laws in learning of classification tasks. Phys. Rev. Lett. 70, 3167–3170 (1993). [DOI] [PubMed] [Google Scholar]
- 74.Goldt S., Advani M., Saxe A. M., Krzakala F., Zdeborová L., “Dynamics of stochastic gradient descent for two-layer neural networks in the teacher-student setup” in Advances in Neural Information Processing Systems, Wallach H., et al., Eds. (NeurIPS, 2019), vol. 32, pp. 6981–6991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Advani M. S., Saxe A. M., Sompolinsky H., High-dimensional dynamics of generalization error in neural networks. Neural Netw. 132, 428–446 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Belkin M., Hsu D., Ma S., Mandal S., Reconciling modern machine-learning practice and the classical bias-variance trade-off. Proc. Natl. Acad. Sci. U.S.A. 116, 15849–15854 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Botvinick M., et al., Reinforcement learning, fast and slow. Trends Cogn. Sci. 23, 408–422 (2019). [DOI] [PubMed] [Google Scholar]
- 78.Stevens C. F., An evolutionary scaling law for the primate visual system and its basis in cortical function. Nature 411, 193–195 (2001). [DOI] [PubMed] [Google Scholar]
- 79.Herculano-Houzel S., Coordinated scaling of cortical and cerebellar numbers of neurons. Front. Neuroanat. 4, 12 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Hiratani N., Simulation and analysis code. GitHub. https://github.com/nhiratani/olfactory_design. Deposited 9 July 2021.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The source codes of the simulations and the data analysis are deposited in GitHub (https://github.com/nhiratani/olfactory_design) (80).