Planar Chirality and Optical Spin–Orbit Coupling for Chiral Fabry–Perot Cavities

Abstract

We design, in a most simple way, Fabry–Perot cavities with longitudinal chiral modes by sandwiching between two smooth metallic silver mirrors a layer of polystyrene made planar chiral by torsional shear stress. We demonstrate that the helicity-preserving features of our cavities stem from a spin–orbit coupling mechanism seeded inside the cavities by the specific chiroptical features of planar chirality. Planar chirality gives rise to an extrinsic source of three-dimensional chirality under oblique illumination that endows the cavities with enantiomorphic signatures measured experimentally and simulated with excellent agreement. The simplicity of our scheme is particularly promising in the context of chiral cavity QED and polaritonic asymmetric chemistry.

The design of chiral cavities with modes preserving optical helicity has recently become a major goal in the field of light–matter interactions. Coupling matter to chiral optical modes indeed enriches the field with symmetry-breaking effects that have great potential, which is well recognized in the context of high-resolution chiroptical sensing,²⁻⁴ polaritonic physics,^5,6 chiral quantum optics,^7,8 and quantum materials.⁸ In the specific context of light–matter strong coupling studies, such chiral cavities are expected to give rise to chiral polaritonic states that open uncharted paths for driving new, asymmetric, chemical syntheses and material properties.^9,10

Such cavities, however, are challenging to design because optical helicity changes sign at each mirror reflection, so that helicity densities are eventually brought to zero through the multiple paths that determine the modal structure of the cavity. Fundamentally, the difficulty stems from the pseudoscalar nature of the optical helicity, itself rooted in the pseudovector nature of the optical spin.¹¹ Therefore, filling a Fabry–Perot cavity with an optically active medium cannot yield a chiroptical response in transmission larger than the intrinsic optical activity outside the cavity. To amplify the chiroptical response, one needs to couple optical spin to the propagation direction of the light, a mechanism known as optical spin–orbit coupling.¹² Setting up such a coupling is however not a trivial task. At the cost of complexity, therefore, various schemes have been proposed for realizing helicity-preserving optical cavities, involving, for instance, intracavity polarization optics^13,14 or elaborate designs ranging from Bragg resonant twisted sculptured thin films¹⁵ to optical metamaterial metasurfaces,^16,17 which are difficult to scale down to the visible range.

In this Article, we take another route, simple yet general, by exploiting a deep connection between chirality and optical spin–orbit interactions. We show indeed that optical spin orientations can be locked to intracavity propagation directions when a seed of planar (2D) chirality is present inside the cavity. This seed is given by inserting between the two metallic mirrors of a Fabry–Perot cavity a layer of polystyrene made 2D chiral under torsional shear stress. By taking advantage of the extrinsic properties associated with planar chirality under oblique illumination, we demonstrate how the Fabry–Perot cavity can be endowed with an helicity-preserving modal response. This is a clear asset of our chiral cavities that, combined with the simplicity of our approach, immediately makes our systems particularly relevant for applications involving polaritons built on chiral light–matter states hybridized throughout the cavity mode volume.

Results

The dispersive chiroptical features of our cavities are analyzed in the framework of the Jones–Mueller formalism. We start by noting that, unlike three-dimensional (3D) chirality associated with optical activity, planar (2D) chirality in its most general expression (without point symmetry like rotational invariance¹) is characterized by polarization transfers from left- to right-handed circular polarization, that is, from positive to negative helicities, that are flipped when exchanging the enantiomeric form of the 2D chiral structure through which light is transmitted.^1,18,19

These peculiar features are most clearly described within the Jones formalism, starting in the circular basis of polarization |R⟩, |L⟩ with the Jones matrix of a birefringent (linear LB and circular CB) and dichroic (linear LD and circular CD) optical system (we define by J̅ Jones matrices expressed in the basis of the circularly polarized states, and J Jones matrices written in the linear polarization basis):

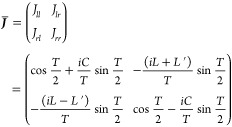1

where 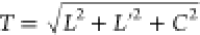for C = CB – iCD, L = LB – iLD measured along the linear |x⟩, |y⟩ polarization axes, and L′ = LB′ – iLD′ along π/4-tilted (|x⟩ ± |y⟩)/√2 linear polarization axes.^20,21 The difference χ between diagonal elements of the Jones matrix is a measure of the optical activity of the system, with a real part proportional to circular dichroism (CD) and an imaginary part associated with circular birefringence (CB) according to

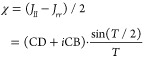2

For 2D chirality, reciprocity imposes J_ll = J_rr, that is, χ = 0, from the interconversion of the planar enantiomeric forms of the 2D chiral system when the propagation of the probing light beam is reversed.²²⁻²⁴ But, in the absence of any point symmetry, the square norm difference ρ = |J_rl|² – |J_lr|² of off-diagonal elements is nonzero and characterizes 2D chirality through what is known as the circular conversion dichroism (CCD):^1,25,26

3

that stems from the misalignment between LB and LD.

One key point for this work is that CCD associated with 2D chirality couples an optical spin with the propagation direction of the light beam, in the sense that reversing the direction of propagation and the helicity as it happens after reflection on one cavity’s end-mirror makes the light beam transmitted through the enantiomorphic Jones matrix for which J_rl and J_lr are exchanged. In striking contrast with 3D chirality, this implies that after one round-trip inside the cavity, this spin–orbit coupling leads to a different left- vs right-handed circular polarization balance that depends on the initial choice of helicity, as illustrated in Figure 1a,b.

Figure 1.

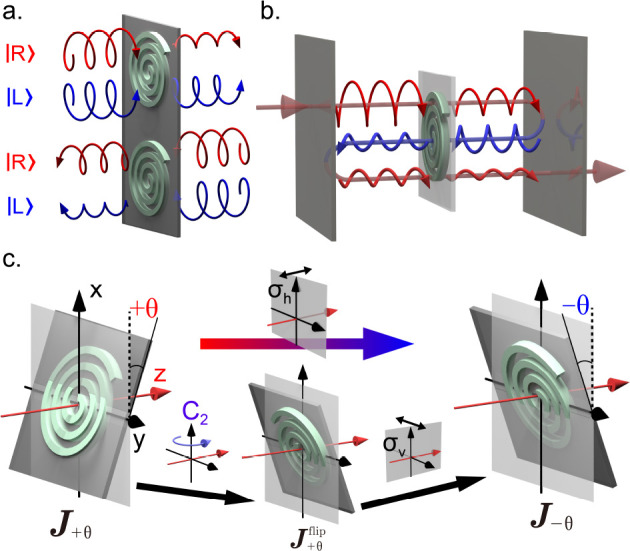
Panel (a) schematizes the spin–orbit coupling mechanism at play through a planar chiral polymer system, here conceptually represented by a 2D spiral. Planar (2D) chirality (in its most general form, that is without any rotational invariance, see ref (1)) is characterized by circular polarization conversions that depend on the direction of the probe beam transmitted through the spiral. Panel (b) illustrates the breaking of left- vs right-handed polarization in a Fabry–Perot cavity composed of two usual metallic mirrors but enclosing a 2D chiral medium. Panel (c) describes how a planar chiral system viewed under oblique illumination yields signatures of 3D chirality (i.e., circular dichroism). Two opposite ± θ oblique illumination angles are connected by a simple mirror symmetry in the (x, y) plane and this corresponds to the sequence of transformations detailed as the succession of a flip (a C₂ rotation along the y-axis) and of a mirror reflection with respect to the (x, z) plane. The result of this sequence is to show, as detailed in the main text, that the optical activity associated with this extrinsic 3D chirality induced on the planar chiral system at oblique illumination is reversed for opposite incidence angles ± θ.

There is a second key aspect associated with a planar chiral system that, viewed at an oblique angle of incidence, yields optical signatures that engage both 2D and 3D chirality. These chiroptical features can be understood by a point group symmetry analysis. A planar chiral system is noninvariant through any mirror reflection symmetry parallel to the optical axis but has one mirror symmetry plane perpendicular to the optical axis. To be truly planar chiral, the system in addition should not have any rotational invariance other than π rotations along the optical axis.²³ Thus, a truly planar chiral system is of C_2h symmetry. This contrasts with a pure 3D chiral system that corresponds to D₂ symmetry, with the optical axis as the principal rotation axis. But when observed under oblique incidence + θ, the σ_h symmetry element of the C_2h point group is lost for the planar chiral object described with the Jones matrix J_+θ, as clearly seen on the left-hand side of Figure 1c. As a consequence of the tilt, therefore, a flip of the system described by the operation Π_xJ_+θ^TΠ_x performed on the Jones matrix written in the linear polarization basis with Π_x the (x, z)-plane mirror reflection, does neither transform it into its initial configuration by any rotation along the optical z-axis (3D chirality) nor into its (x, y)-plane mirror symmetrical 2D enantiomer (2D chirality). This means that the system under oblique incidence must be described by a combination of both chiralities with different signatures viewed from both ±θ incidence angles.

The connection between opposite incidence angles ± θ can be made most straightforwardly through a (x, y)-plane mirror symmetry noted σ_h on Figure 1c. This simple operation, however, cannot be directly expressed within the Jones formalism. To do so, we decompose σ_h into two successive transformations: one C₂ rotation along the x-axis (flipping operation) followed by a (x, z)-plane mirror reflection, yielding J_+θ = J_–θ^T, where T is the matrix transpose. Within the circular basis of polarization, this relation becomes J®_+θ = σ₁J®_–θσ₁^–1, with σ₁ being the first Pauli matrix.

The most important consequence of this analysis is that the optical signatures associated with 3D chirality will be reversed under opposite oblique incidence angle and will vanish at normal incidence, while those associated with 2D chirality will be preserved. This enforces the angular relations for optical activity (χ) and CCD (ρ) as

4

following the definitions of eqs 2 and 3. As seen, the manifestation of 3D chirality is angle-dependent and as such, is totally different from intrinsic 3D chirality generally rotationnaly invariant. This illustrates how extrinsic are these 3D chiral features that emerge from 2D chirality at oblique incidence.^19,27 Below, we exploit these relations (eq 4) as a way to characterize the 2D chirality of a system, particularly relevant when the source of planar chirality remains weak.

Our approach to induce 2D chirality inside a Fabry–Perot cavity is to use atactic polymers such as polystyrene.²⁸ When a torsional shear stress is applied to such an atactic polymer, chiroptical features arise in the polymer matrix that are induced by a macroscopic chiral conformation of the chains. We generated the stress inside the polymer matrix by spin-coating clockwise or anticlockwise a thin layer (ca. 150 nm) of dissolved polystyrene solution (molecular weight of 195 K, diluted 4% in weight in toluene) on a 30–60 nm thick silver mirror; details are provided in the Supporting Information, Section 1. Friction forces the polymer chains to take a macroscopic chiral arrangement close to the surface of the mirror via in-plane spinning of the chains, adopting a macroscopic C_2h symmetry of 2D chirality. Far from the surface, the conformation of the polymer chain is not hindered by friction and the chains are simply randomly distributed within the volume (despite the fact that the conformation of each chain is chiral, intermolecular chain compensation of chirality prevents any chiroptical signal to be observed macroscopically, a property known as cryptochirality^29,30).

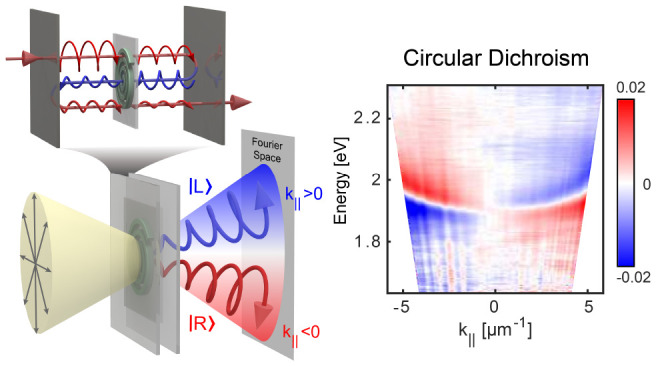
Within it, these structural changes correspond to the specific chiroptical features that we analyzed above. Experimentally, the CD signal is measured as the (0, 3) coefficient of the cumulated differential Mueller matrix, as explained in the Supporting Information, Section 3. The Mueller matrix (MM) itself is acquired on a home-built optical setup that yields calibrated, angle-resolved (Fourier space) MM described in detail in the Supporting Information, Section 2. Remarkably, the MM gives the possibility to separate linear birefringences and dichroisms from circular ones and thus to measure true planar chiroptical features and artifact free CD.^21,31

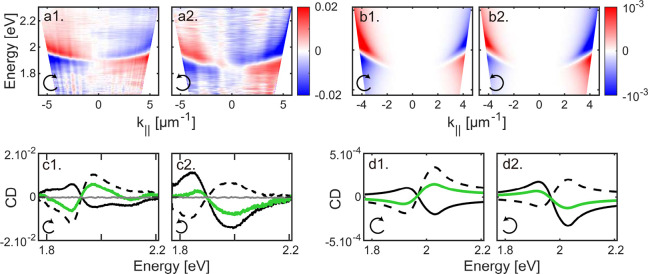
The first feature observed for a polymer layer spin-coated on a glass substrate is the absence of CD, as seen in Figure 2c1,c2 in solid gray, a trait expected from the cryptochiral nature of the polymer layer,^29,30 which shows no observable CD signal. We then form a Fabry–Perot cavity by sandwiching the polymer layer between two Ag mirrors of the same thickness (as explained in the Supporting Information, Section 1) and measure its CD in transmission. This time, as seen in Figure 2a1,a2, bisignated CD signals are observed under oblique illumination. These signatures are remarkable in that they correspond to optically active modes of the Fabry–Perot cavity probed using as the incident light the usual TE (transverse electric) and TM (transverse magnetic) polarizations with opposite contributions to the CD signal. In the following and throughout this paper, TE and TM polarizations are always associated with the incident field used to measure the transmission of the cavity. At normal incidence the opposite helicity between TE and TM modes is a direct consequence of 2D chirality, as explained in Supporting Information, Section 4. At fixed illumination angles where the degeneracy between TE and TM modes is lifted, this yields the bisignated signatures observed experimentally through the cavity at fixed illumination angles and displayed in Figure 2c1,c2. Remarkably, as seen in particular in Figure 2c1,c2 and d1,d2, the CD dispersions are not symmetric with respect to normal incidence for both enantiomeric cavities. Their enantiomorphic feature can be seen by the nonzero CD signal averaged over the entire angular (k_∥) space, which is reversed between opposite enantiomeric cavities.

Figure 2.

(a1, a2) Measured CD dispersions for both enantiomorphic cavities: clockwise shear stress, left panel, and anticlockwise shear stress, right panel. (b1, b2) Simulated CD dispersions for both enantiomorphic cavities for the same clockwise and anticlockwise shear stresses. (c1, c2) Averaged CD signals associated with (a1) and (a2) over −k_∥ (dashed line) and +k_∥ (solid line) angular subspace. Once converted in mdeg, the peak-to-peak CD values reported correspond to ca. 600 mdeg. The total CD measured in the real space averaged over all k_∥ shown in (a1) and (a2) is displayed by green curves in the cavity and compared to the real space CD of the same polymer film deposited on a glass substrate without cavity mirrors displayed by the gray curves. (d1, d2) With the same color and line coding, simulated traces averaged from the angular simulations shown in (b1) and (b2) over both ±k_∥ angular subspaces.

It is also clear from the data that reveal CD signs exchanged from both sides of the normal incidence that the spin-coated polymer thin film yields a zero CD at normal incidence inside the cavity. As discussed further below, we interpret the tilt of the whole chiral landscape as an effect of intertwined 2D chirality and extrinsic 3D chirality. This results in the more intense CD signals observed in Figure 2c1,c2 in one angular sector in relation with the enantiomorphism of the cavity.

The properties of our cavities can be simulated using the transfer matrix approach presented in the Supporting Information, Section 5. In this approach, a first approximation describes our polymer film under shear stress as a Pasteur medium, that is, as a chiral isotropic medium,^32,33 with the constitutive relations

5

6

where the permittivity (ϵ = ϵ₀ϵ_r), the permeability (μ = μ₀μ_r) are the usual isotropic parameters (c² = 1/ϵ₀μ₀) of the polymer medium and κ the (complex) parameter associated with its chiral response. This model captures well the experimental features observed in Figure 2a1,a2 and c1,c2 when describing the chiral response of our material with a (θ, λ), dispersive chiral parameter

7

In this effective model, the wavelength-dependent complex parameter κ(λ) is taken to be only weakly dispersive in the visible range, in agreement with the cryptochirality of the polymer itself, see Supporting Information, Section 5. Then the tilt of the 2D chiral material is described by involving the two signatures given in eq 4. The constant (hence, parity-even) response in θ is associated with an intrinsic 3D chirality and gauged by the a parameter. This intrinsic 3D chirality is observed experimentally in the CD traces displayed in Figure 2c1,c2. The extrinsic 3D chirality emerging from 2D chirality under oblique illumination drives the parity-odd response in θ gauged by the b parameter. By choosing a b/a ≃ 10 ratio based on our experimental results, the model reproduces well the (θ, λ) dispersion of the MM measured experimentally in strict relation with the enantiomorphism of the cavity, as shown in Figure 2b1,b2. There is a very good agreement between theory and experiment in the angular evolution of the chiroptical properties of the TE and TM modes, with the bisignation and the asymmetry in the CD signal measured between the two positive and negative ± θ angular sectors observed in Figure 2d1,d2. These features, both measured and simulated, illustrate the role of planar chiral system implanted inside a Fabry–Perot cavity for amplifying a chiral signal.

As we now show, the unique chiroptical properties that planar chirality yields under oblique illumination lead to the possibility to have a modes of a preferred helicity in one cavity round-trip, meaning that the helicity of the light field will be the same between the back and the forth propagation directions inside the cavity, as sketched in Figure 1b. To demonstrate this, we quantify the chirality of a cavity mode using the metric (used, for instance, in^2,34,35) δG(r) = (|G₊(r)|² – |G_–(r)|²)/√2, where G_±(r) = E(r) ± iηH(r) are the Riemann-Silberstein vectors and η is the usual impedance of the field. As explained in the Supporting Information, Section 5, this impedance within a chiral medium can be simplified to the local difference between left and right electric field intensities.³⁶ We chose this metric because it is directly linked to the optical chiral density and thus directly measures the predominance of one spin-polarized field over the other.³⁷ Integrating δG(r) along the z-propagation direction inside the chiral film gives the global helicity of the cavity mode i = TE, TM within a h = z₂ – z₁ thick layer

8

Those quantity are displayed in panels (a) and (b) in Figure 3, where α_i(λ) has been normalized by the field maximum intensity inside the cavity. They demonstrate that the cavity modes defined in our designer Fabry–Perot cavity are characterized by finite helicity densities, whose handedness is opposite in each ±θ angular sector. We use the linearly polarized TE and TM modes as descriptors of the modal properties of the cavity. These TE and TM modes are not polarization eigenmodes of the system, but they remain good descriptors due to the small elipticities of the true polarization eigenmodes of the chiral cavity. Here too, the combination of 2D and 3D chiralities contributes to the tilt of the chiral landscape and the change of helicity that we expect for the extrinsic 3D chirality is shifted to nonzero incidence angles. The fact that α_i(λ) is nonzero along the i = TE, TM modes at normal incidence is a central result of the Article, with the sign of the helicity of the resonator at normal incidence that depends on the clock/anticlockwise spin-coating direction. This gives our cavities a real potential for exploring resonant strong coupling signatures in chiral polaritonic chemistry and material science.

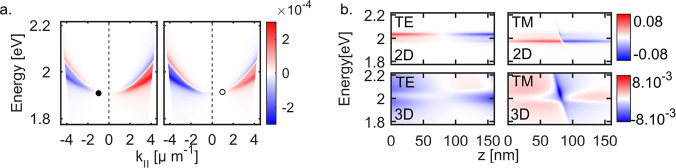
Figure 3.

(a) Global helicity α_i(λ) normalized to the maximum intensity of the intracavity electric field for the i = TE cavity mode calculated for enantiomorphic cavities with clockwise, left panel, and anticlockwise, right panel, shear stresses. For both forms, the in-plane wavevector k_∥ values for zero helicity of the mode are marked with a filled and empty circle, respectively. (b) Intracavity δG_i(z) calculated at a chosen k_∥ = +4 μm^–1 by placing inside the cavity a 2D chiral medium described by eq 7 (top row or bottom row) with the cavity uniformly filled with 3D chiral medium described by a corresponding, constant, κ_eff (4 μm^–1, θ; see main text) for both i = TE (left side) and i = TM (right side) illumination modes. Note that the contrast of the bottom row is adjusted for clarity but with values 1 order of magnitude smaller than those of the top row. In both panel the value of α_i(λ) and δG_i(z) were computed using a plane wave illumination linearly polarized along the y-axis for the TE mode and the x-axis for the TM mode.

The angular evolution of α_i(λ) is related to the profile of δG_i inside the cavity as shown in Figure 3b. The δG_i profiles, shown in Figure 3b, reveal that when the cavity is modeled with a 2D chiral layer of the polymer film, chosen here to correspond to a 20% volume fraction of the cavity, the local helicity of the cavity modes can be enhanced by ca. 1 order of magnitude in comparison with an intrinsically 3D chiral cavity. (The κ_3D parameter modeling the intrinsically 3D chiral medium is fixed in such a way that for a chosen angle θ₀, it is equal to κ_eff(θ₀, λ) with the same parameter value used for modeling the 2D chiral response. We stress that our modelization based on a Pasteur medium approach is perfectly appropriate for computing CD dispersions. However, our effective treatment of planar chirality within this approach necessarily underestimates the actual strength of δG_i inside the cavity.)

Conclusion

In conclusion, we demonstrated that a polymer film on which a chiral stress is imposed can seed planar chirality within a Fabry–Perot cavity. This seed enables a spin–orbit coupling mechanism that shapes, for each round-trip inside the cavity, transverse electric and transverse magnetic modes with a preferred helicity density. Analyzed using the Jones–Mueller formalism, the proposed mechanism for shaping such chiral modes results from the combination between 2D and 3D chiralities under oblique illumination and, as such, is a universal mechanism that can be involved in a great variety of systems, in particular, soft, polymeric media, and over large optical bandwidths. This universality, combined with the simplicity in the implementation, paves the way to exploit such chiral modes in the context of chiral cavity QED^4,8 and polaritonic chemistry.⁹ There, the chiral nature of the polaritonic states that can be created within our cavities yields the core ingredient needed for inducing a new type of selectivity for asymmetric syntheses performed in the regime of strong coupling. This will yield original strategies that we are currently exploring in the endeavor to draw a new landscape for asymmetric chemistry driven by chiral polaritonic states.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.1c00780.

• Detailed descriptions of the sample preparation method and of the experimental setup, of the data filtering procedures, of the bisignated CD and of the chiral transfer matrix approach, and refs S1–S9 (PDF)

This work of the Interdisciplinary Thematic Institute QMat, as part of the ITI 2021 2028 program of the University of Strasbourg, CNRS and Inserm, was supported by IdEx Unistra (ANR 10 IDEX 0002), by SFRI STRAT’US Project (ANR 20 SFRI 0012), by the Labex NIE (ANR-11-LABX-0058 NIE) and the Labex CSC (ANR-10-LABX-0026 CSC) Projects, the ANR Equipex Union (ANR-10-EQPX-52-01), and by the University of Strasbourg Institute for Advanced Study (USIAS; ANR-10-IDEX-0002-02) under the framework of the French Investments for the Future Program. It was also supported by the European Research Council (ERC Project No. 788482 MOLUSC).

The authors declare no competing financial interest.