Peristaltic pumping in thin non-axisymmetric annular tubes

Abstract

The two-dimensional laminar flow of a viscous fluid induced by peristalsis due to a moving wall wave has been studied previously for a rectangular channel, a circular tube and a concentric circular annulus. Here, we study peristaltic flow in a non-axisymmetric annular tube: in this case, the flow is three-dimensional, with motions in the azimuthal direction. This type of geometry is motivated by experimental observations of the pulsatile flow of cerebrospinal fluid along perivascular spaces surrounding arteries in the brain, which is at least partially driven by peristaltic pumping due to pulsations of the artery. These annular perivascular spaces are often eccentric and the outer boundary is seldom circular: their cross-sections can be well matched by a simple, adjustable model consisting of an inner circle (the outer wall of the artery) and an outer ellipse (the outer edge of the perivascular space), not necessarily concentric. We use this geometric model as a basis for numerical simulations of peristaltic flow: the adjustability of the model makes it suitable for other applications. We concentrate on the general effects of the non-axisymmetric configuration on the flow and do not attempt to specifically model perivascular pumping. We use a finite-element scheme to compute the flow in the annulus driven by a propagating sinusoidal radial displacement of the inner wall. Unlike the peristaltic flow in a concentric circular annulus, the flow is fully three-dimensional: azimuthal pressure variations drive an oscillatory flow in and out of the narrower gaps, inducing an azimuthal wiggle in the streamlines. We examine the dependence of the flow on the elongation of the outer elliptical wall and the eccentricity of the configuration. We find that the time-averaged volumetric flow is always in the same direction as the peristaltic wave and decreases with increasing ellipticity or eccentricity. The additional shearing motion in the azimuthal direction will increase mixing and enhance Taylor dispersion in these flows, effects that might have practical applications.

1. Introduction

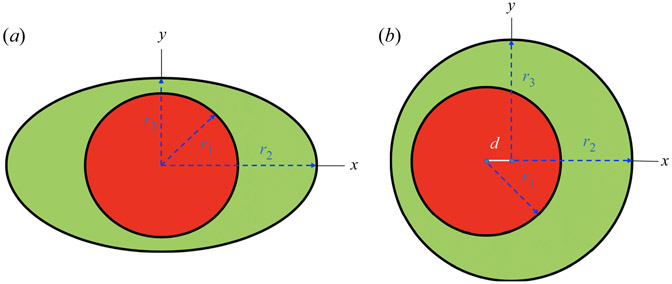
Peristaltic pumping occurs when a wave of area contraction and expansion propagates along the length of a flexible channel or tube filled with a liquid (Jaffrin & Shapiro 1971). This mechanism is the basis for roller and finger pumps, used in cases where it is necessary to keep the transported liquid from coming into contact with the pump itself. The mechanism also occurs in the perivascular spaces (PVS) surrounding arteries in the brain, in which cerebrospinal fluid is pumped by radial pulsations of the artery wall induced by the heartbeat (Bedussi et al. 2017; Mestre et al. 2018), a mechanism aptly named ‘perivascular pumping’ by Hadaczek et al. (2006). Although we take a more general approach here, our study was motivated by the observed flows in perivascular spaces. These flow channels are seldom axisymmetric. Tithof et al. (2019) have shown that the various shapes of the cross-sections of perivascular spaces around surface and penetrating arteries in the mouse brain, observed in vivo, can be fit quite well with a simple geometric model, consisting of a circular inner boundary (the artery) and an elliptical outer boundary (the outer wall of the PVS), allowing the circle to be eccentric with respect to the ellipse. We adopt the same adjustable geometric model in our present study of peristaltic pumping (see figure 1). Tithof et al. (2019) computed the hydraulic resistance for annular channels with this model cross-section, varying the ellipticity and eccentricity. We also compute the velocity profile and hydraulic resistances for steady Poiseuille flow for several cases and compare them with the results of Tithof et al. (2019), as a convenient test of our finite-element code.

Figure 1.

Cross-sections of the annular tube for the concentric elliptical annulus model (a) and the eccentric circular annulus model (b).

A number of studies have considered peristaltic pumping in annular geometries, motivated by flow and transport in the PVSs. Recently there have been attempts to model pumping in more complex geometries (Daversin-Catty et al. 2020; Kedarasetti, Drew & Costanzo 2020); however, the basic mechanism of perivascular pumping remains controversial (Thomas 2019; Ladrón-de-Guevara et al. 2020). The most relevant study for our purposes is that of Wang & Olbricht (2011): they model the system as a concentric circular annulus filled with a porous medium (instead of an open channel, as we assume in this paper), with flow driven by a sinusoidal wall wave propagating along the inner boundary. By making the long wavelength, low Reynolds number approximation (Shapiro, Jaffrin & Weinberg 1969; Jaffrin & Shapiro 1971), they are able to obtain an analytical solution.

Here, we present (in Appendix A) an analytical solution to the same problem, except with an open rather than porous annulus, and we use this solution as a check on our numerical simulations. Motivation for an open channel solution is derived from recent in vivo measurements showing the pial (surface) PVSs are open (unobstructed) (Mestre et al. 2018; Min-Rivas et al. 2020).

The analytical solution demonstrates that the volume flow rate Q produced by the pumping scales as (b/l)², where b is the amplitude of the wall wave and l is the width of the gap between the inner and outer boundaries. We can think of the magnitude of Q as being a measure of ‘pumping effectiveness’. This result forms a basis for imagining what the peristaltic flow is like, qualitatively, in our elliptical, non-concentric model. For a concentric circular annulus and an axisymmetric wall wave, the flow is axisymmetric, there are only axial and radial components of velocity, and the instantaneous streamlines lie in planes through the central axis and have wiggles in the radial direction due to the radial velocity. With an elliptical outer boundary, or an eccentric circular annulus, we can expect the flow to be three-dimensional, with secondary motions in the azimuthal direction. We can imagine a local pumping effectiveness that scales as (b/l)², as for the concentric circular annulus, but where gap width l varies in the azimuthal direction. For a concentric circular annulus, the gap width l and hence the local pumping effectiveness are axisymmetric, with the resulting flow also being axisymmetric, with only axial and radial velocity components. The instantaneous streamlines lie in planes through the central axis and wiggle only in the radial direction, due to the radial component of velocity. For an elliptical outer boundary, or an eccentric circular annulus, the gap width l, and hence the local pumping effectiveness, vary in the azimuthal direction. This causes pressure variations in the azimuthal direction (with higher pressure where the gap is narrower) that drive a secondary, oscillatory flow in the azimuthal direction; causing the instantaneous streamlines to wiggle in both the radial and azimuthal directions.

To our knowledge, this is the first study of peristaltic pumping in elliptical and eccentric annuli: hence, our results may be of interest in contexts other than perivascular pumping.

2. Computational methodology

2.1. The computational model and its scaling

We consider the flow of a Newtonian viscous fluid in an annular tube, driven by a radial displacement of the inner wall in the form of a sinusoidal wave propagating in the axial direction. The annular space between the inner and outer walls of the tube is assumed to be open (i.e. unobstructed), not porous. The annular tube is uniform in the axial direction. Its cross-section consists of a circular inner wall and an elliptical outer wall, and we allow the circle to be eccentric with respect to the ellipse (see figure 1). The inner wall is deformable, and peristaltic pumping is driven by a radial displacement of the form (in cylindrical coordinates)

$$r(z,t)=r_1+b\sin \left(\frac{2\pi }{\lambda }(z-ct)\right),$$ (2.1)

where r₁ is the undisturbed radius of the inner wall, b is the wave amplitude, c is the wave speed and λ is the wavelength.

We non-dimensionalize the geometric quantities using scalings similar to those of Tithof et al. (2019). The radii r₂ and r₃ of the ellipse, the eccentricity d (for the circular annulus) and the wave amplitude b are scaled as

$$\alpha =\frac{r_2}{r_1},\beta =\frac{r_3}{r_1},ϵ=\frac{d}{r_1},b^{\ast }=\frac{b}{r_1}.$$ (2.2a-d)

For the elliptical annuli, it is useful to use α/β as a measure of the elongation of the outer ellipse.

In our simulations, the ratio of the area A_pvs of the annular region enclosed by the two boundaries (the perivascular space) and the area A_art of the inner circle (the artery) was held constant at 1.4, an average value measured in vivo (Mestre et al. 2018). Then α and β are related, allowing all models to be defined by a single parameter. The flow velocity v = (v_r, v_θ, v_z), volume flow rate Q and pressure are non-dimensionalized using the wave speed c, as follows:

$${\mathit{v}}^{\ast }=\frac{\mathit{v}}{c},Q^{\ast }=\frac{Q}{c{A}_{pvs}},p^{\ast }=\frac{\lambda }{\mu c}p,$$ (2.3a-c)

where μ is the viscosity.

2.2. Geometric models

Three-dimensional models of the channels were created using OnShape (Cambridge, MA), a computer-aided design software package. The cross-sections shown in figure 1 were sketched in a two-dimensional (2-D) plane. The dimensions for each model were prescribed using the dimensionless lengths earlier stated. Each sketch was then extruded such that the annulus length included two full wavelengths of the peristaltic wave.

Five models were created for the elliptical annulus simulations with α/β equal to 1.0 (concentric circular), 1.067, 1.224, 1.420 and 1.667. For the eccentric simulations, the concentric circular annulus model from above was used as the base model. The outer boundary was then offset from the centre of the inner circle. Five eccentric circular models were made by setting ϵ to 0.075, 0.150, 0.225, 0.300 or 0.349. The most eccentric model was chosen to have the the same minimum distance between the inner and outer boundaries as in the most elliptic model.

2.3. Simulations

The geometric models were exported in the PARASOLID format from OnShape and imported into SimVascular (http://www.simvascular.org, Updegrove et al. 2017) and meshed with MeshSim (Simmetrix, Inc., Troy, NY). Regions near the inner and outer walls of the perivascular space were refined with a boundary layer (BL) mesh. Mesh parameters (global edge size, BL height, BL edge size) were determined with a convergence study (see Appendix B),

We carried out numerical simulations that solve the Navier–Stokes equation for an incompressible, homogeneous, Newtonian fluid. All the simulations were performed using Multi-Physics Finite Element Solver (MUPFES, Esmaily-Moghadam, Bazilevs & Marsden 2013, 2015) assuming non-porous walls and using the properties of water at 37 °C (dynamic viscosity 0.693 mPa s and density 994 kg m⁻³). On average, arterial displacements are measured to be 1% of arterial diameter in vivo (Mestre et al. 2018): we replicated this in our simulations by prescribing an inner wall wave of amplitude b* = 0.02. In our simulations we assume the frequency to be that of a typical mouse heartbeat (5 Hz), a wave speed of 1000 μm s⁻¹ and wavelength of 200 μm. A traction-free (Neumann) boundary condition was prescribed at the inlet and outlet, such that there was no imposed pressure gradient and flow was solely driven by the peristaltic wave. The local hydrodynamics was then solved by MUPFES using the fully coupled time-dependent Navier–Stokes equation. Mean flows essentially converged by the third cycle of the peristaltic wave, but all simulations were run for five cycles to ensure complete cyclic convergence was reached. All simulations employed 200 time steps per period of the peristaltic wave.

2.3.1. Validation for steady flow

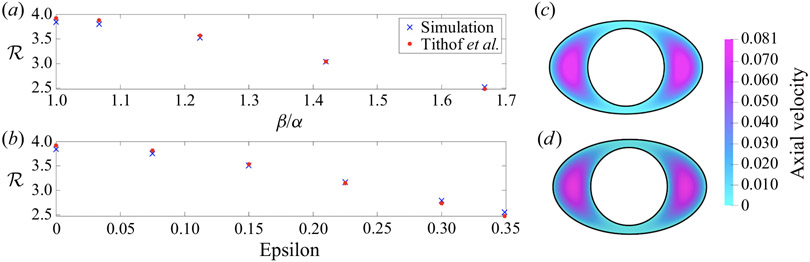
As one test of our 3-D code, we simulated steady, pressure-driven flow (Poiseuille flow), without a wall wave, in several models and compared the results with the 2-D calculations of Tithof et al. (2019) for infinitely long channels with the same cross-sections. We calculated velocity profile and the hydraulic resistance $\mathcal{R}=(-\mathrm{d}p∕\mathrm{d}z)∕Q$ (where dp/dz is the axial pressure gradient and Q is volume flow rate) for several flattened and eccentric cross-sections, keeping the cross-sectional area fixed, and compared the resulting values with the corresponding values given by Tithof et al. (2019). Figure 3 shows the results of these comparisons. All the hydraulic resistance values calculated with our 3-D code agree with the values of Tithof et al. (2019) to within 3%. The computed velocity profiles agreed within 1% in all cases.

Figure 3.

Hydraulic resistances (dimensionless) for steady Poiseuille flow calculated using our 3-D code and compared with the corresponding values calculated by Tithof et al. (2019). The cross-sectional area of the annulus is kept fixed. (a) Hydraulic resistances of concentric elliptical annuli of different ellipticity α/β. (b) hydraulic resistances of eccentric circular annuli of different eccentricity ϵ. Axial velocity profiles for the same elliptic annulus, computed by Tithof et al. (2019) (c) and our 3-D code (d). The maximum axial velocities agree within 1 %.

2.3.2. Validation for unsteady, peristaltic flow

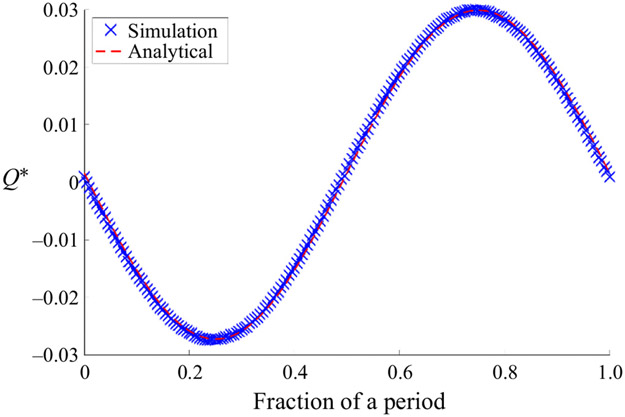
We ran convergence tests to determine the appropriate mesh size for our simulations of unsteady flows: these tests are described in Appendix B. In order to further a test our 3-D code for unsteady flows, we simulated peristaltic pumping in a concentric circular annulus and compared the results with the analytical solution for an open concentric circular annulus presented here in Appendix A. In this test, a peristaltic wave of wave speed 1000 μm s⁻¹, frequency 5 Hz, wavelength 200 μm and amplitude b* = 0.02 was propagated along the inner boundary of the concentric circular annulus model with area ratio of 1.4, $\alpha =\sqrt{2.4}$ and length equal to two wavelengths of the travelling wave. The instantaneous volumetric flow rates Q* for the simulation and the corresponding analytical solution are plotted in figure 4. The time-averaged volumetric flow rates agree to within approximately 1 %.

Figure 4.

Comparison of the instantaneous volumetric flow rate Q* given by the test simulation of peristaltic pumping in a concentric circular annulus with that of the analytical solution (in Appendix A), both plotted for one period of the peristaltic wave. (Parameter values for this simulation are given in the text.)

3. Results

3.1. The concentric elliptical annulus

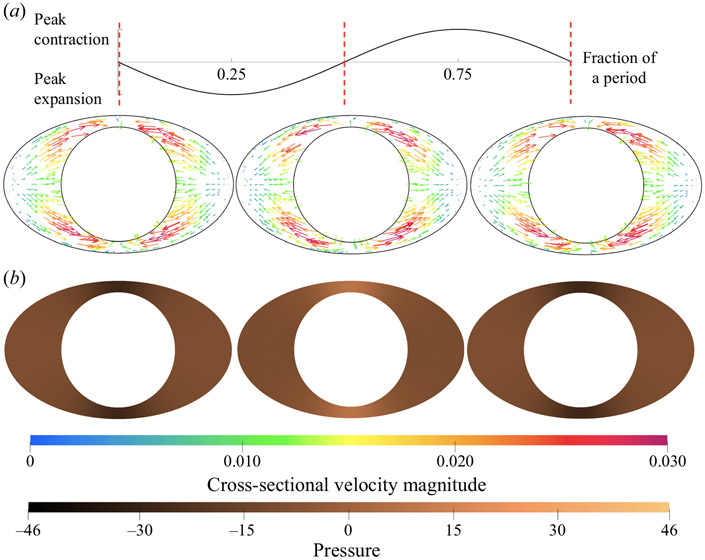
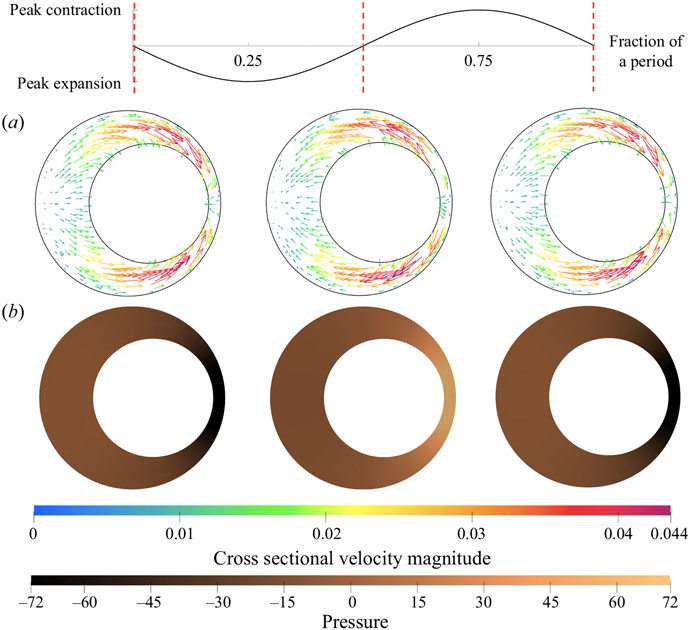
First, we examine the results for concentric annuli with an elliptical outer boundary. Introducing this ellipticity induces an azimuthal pressure gradient in each axial cross-section along the length of the tube, which drives an azimuthal velocity component. In the elliptical models, the flow oscillates in a ‘four lobe’ pattern in the quadrants created by the major and minor axes of the ellipse. The narrowest regions of each axial cross-section are at the ends of minor axis of the ellipse: henceforth, we refer to these as the ‘narrow gaps’. The widest regions of each cross-section occur at the ends of the major axis of the ellipse: we call these the ‘wide gaps’. In figure 5, we show the cross-sectional velocity and pressure distribution at three times during a cycle of the peristaltic wave: beginning, middle and end of a single wave period. These times are marked with the red vertical dashed lines along the plot of the peristaltic wave (top). In order to plot the cross-sectional pressure distribution, we subtract the mean pressure over each slice in order to remove the axial pressure variation. The resulting pressure is then non-dimensionalized as

$$p_{dist}^{\ast }=(p-p_{mean})\frac{\lambda }{\mu c}.$$ (3.1)

Figure 5.

Cross-sectional pressure distribution and velocity fields at the middle cross-section (one wavelength from either end) of the concentric elliptical annulus model with ellipticity α/β = 1.667. Values are plotted at three different phases of the peristaltic wave: beginning, middle and end (left to right). The displacement of the wall wave is plotted above at the top, with red vertical dashed lines marking the three times of the corresponding cross-sections. The colour scale indicates the magnitude of the dimensionless velocity magnitude, and the copper scale indicates the dimensionless pressure.

At the beginning of the cycle, the inner boundary is contracting from its mean position. This results in low pressure in the narrow gaps and high pressure in the wide gaps, thus driving fluid toward the narrow gaps. When the inner boundary reaches its peak contraction, the azimuthal pressure gradient and velocity both go to zero. Then, as the inner boundary expands, high pressure develops in the narrow gaps and low pressure in the wide gaps, driving fluid out of the narrow gap and into the wide gap. When the inner boundary reaches its peak expansion, the azimuthal pressure gradient and velocity again go to zero. This cycle then repeats during each period of the wall wave.

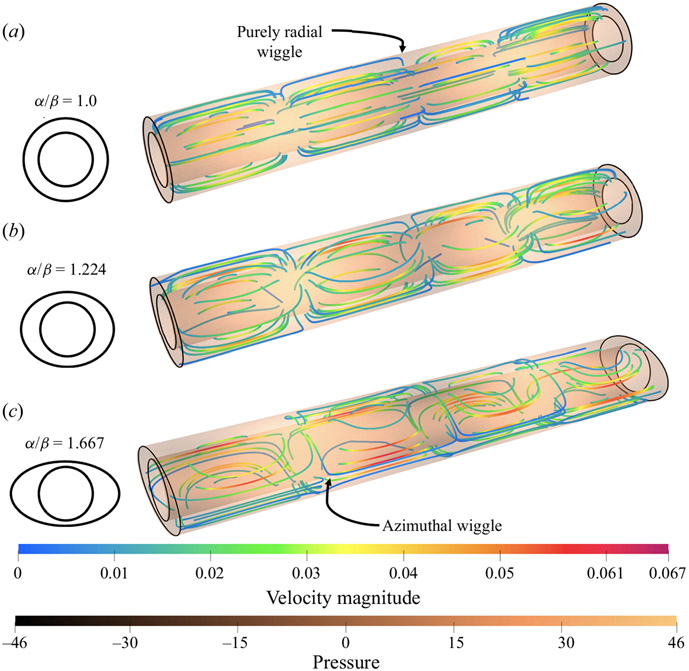
The resulting azimuthal flow causes the velocity field to be fully three-dimensional, with components in the radial, azimuthal and axial directions, and the instantaneous streamlines wiggle in the azimuthal as well as the radial direction. Figure 6 shows instantaneous streamlines for a concentric circular annulus (α/β = 1) and two of the elliptical annuli (α/β = 1.224 and 1.667). In the concentric circular annulus (left in figure 6), with no azimuthal velocity, the streamlines are axisymmetric, lie in planes through the central axis and wiggle only in the radial direction. As the outer boundary becomes elliptical, the streamlines develop an azimuthal wiggle due to the azimuthal velocity component. In the moderately elliptical annulus (central in figure 6), a slight azimuthal wiggle can be seen along each streamline. In the more elliptic model (right in figure 6), the streamlines are show significant azimuthal wiggles due to a stronger azimuthal velocity component. In table 1, we quantify the radial (v_r) and azimuthal (v_θ ) velocities and the ratio between the two for all of the elliptical annuli simulations. As the streamline plots suggest, the azimuthal velocity increases with increasing ellipticity and becomes approximately equal in magnitude to the radial component at α/β = 1.420.

Figure 6.

Instantaneous streamlines for pumping in concentric annuli with ellipticity α/β equal to 1.00 (circular), 1.224 and 1.667. For the concentric circular annulus (a) the flow is axisymmetric and the streamlines wiggle only in the radial direction. When the outer wall of the annulus is slightly flattened into an ellipse (b), the flow becomes three-dimensional, with an oscillating azimuthal velocity component, and the streamlines also wiggle in the azimuthal direction. For substantial flattening (c), the azimuthal velocity is significant, as are the azimuthal wiggles in the streamlines. The colour and copper scales indicate values of the dimensionless velocity magnitude and pressure.

Table 1.

Comparison of the magnitudes of the radial (v_r) and azimuthal (v_θ) velocities (dimensionless) for each of the elliptical models. Each component was averaged over a cross-section for each point in time during the peristaltic wave ($\overline{v_r}$, $\overline{v_{\theta }}$), and the maximum values of these averages during the period (${\overline{v_r}}_{max}$, ${\overline{v_{\theta }}}_{max}$) and their ratio, are listed in the table.

α/β	${\overline{v_r}}_{max}$	${\overline{v_{\theta }}}_{max}$	${\overline{v_{\theta }}}_{max}∕{\overline{v_r}}_{max}$
1.000	5.00 × 10−3	0	0
1.067	4.93 × 10−3	1.39 × 10−3	0.28
1.224	5.54 × 10−3	4.18 × 10−3	0.78
1.420	6.09 × 10−3	6.75 × 10−3	1.11
1.667	7.03 × 10−3	8.95 × 10−3	1.27

3.2. The eccentric circular annulus

Next we turn to the results for the circular annuli with increasing eccentricity. Figure 7 shows cross-sectional pressure distributions (3.1) and velocity when the inner boundary is offset. The flow oscillates in a ‘two lobe’ shape, separated by a line of symmetry in the same direction as the eccentricity of the inner boundary. By offsetting the inner boundary, a narrow gap and a wide gap are formed at the ends of this line of symmetry. As in the elliptical annulus, the pressure is initially low in the narrow gap as the inner boundary contracts from its mean position. When the inner boundary reaches peak contraction, the azimuthal pressure gradient and velocity go to zero. The inner boundary then begins to expand, causing higher pressure to form in the narrow gap and lower pressure to form in the wide gap, driving an azimuthal velocity toward the wide gap. Once the inner boundary reaches peak expansion, the azimuthal pressure gradient and flow go to zero. and then reverse as the inner boundary begins to contract again. This cycle then repeats for each period of the travelling wall wave.

Figure 7.

As in figure 5, but for an eccentric circular annulus model with eccentricity ϵ = 0.349.

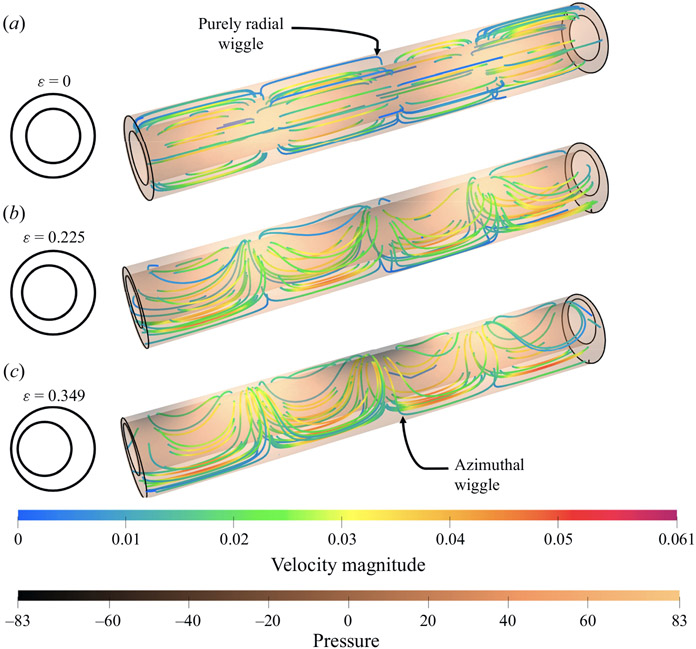
As in the elliptical case, the instantaneous streamlines wiggle in both the radial and azimuthal directions. Figure 8 shows instantaneous streamlines for the concentric circular annulus and two eccentric cases (ϵ = 0.225 and 0.349) plotted at the same phase of the peristaltic wall wave. When eccentricity is introduced, the streamlines begin to wiggle in the azimuthal direction, as an azimuthal motion is driven by the pressure distribution, as illustrated in figure 7. As the eccentricity is increased, the streamlines wiggle more in the azimuthal direction and the ratio of azimuthal to radial velocities increases. The radial and azimuthal velocities are approximately equal in magnitude at ellipticity ϵ = 0.150 (table 2).

Figure 8.

As in figure 6, but for circular annuli with eccentricity ϵ equal to 0, 0.225 and 0.349. The instantaneous streamlines wiggle only in the radial direction in the concentric annulus (a), but also wiggle increasingly in the azimuthal direction with increasing eccentricity (b,c).

Table 2.

Comparison of the magnitudes of the radial (v_r) and azimuthal (v_θ) velocities (dimensionless), as in table 1. but for the eccentric circular annulus models of different eccentricity ϵ.

ϵ	${\overline{v_r}}_{max}$	${\overline{v_{\theta }}}_{max}$	${\overline{v_{\theta }}}_{max}∕{\overline{v_r}}_{max}$
0	5.70 × 10−3	0	0
0.075	5.84 × 10−3	2.54 × 10−3	0.43
0.150	6.01 × 10−3	5.00 × 10−3	0.83
0.225	6.28 × 10−3	7.70 × 10−3	1.23
0.300	6.61 × 10−3	1.02 × 10−2	1.54
0.349	6.93 × 10−3	1.22 × 10−2	1.76

3.3. The mean volumetric flow rate

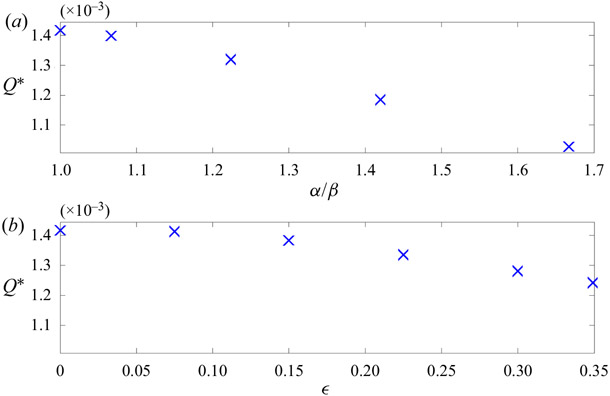
The mean (time-averaged) volumetric flow rate Q* was calculated for each of the elliptical and eccentric models (figure 9) by averaging over a full wave period. In all cases, Q* is in the direction of propagation of the wall wave. For the elliptic models, Q* decreases monotonically with increasing ellipticity. For the eccentric circular models, Q* decreases monotonically with increasing eccentricity.

Figure 9.

Time-averaged volumetric flow rate (dimensionless) plotted as a function of the ellipticity of the elliptic annulus model (a), and as a function of eccentricity of the eccentric circular annulus model (b).

As discussed in the Introduction, for a concentric circular annulus, the pumping effectiveness scales as (b/l)². When either ellipticity or eccentricity is introduced, the gap width l varies azimuthally, and this scaling suggests a local pumping effectiveness that varies azimuthally, being greater where the gap width l is smaller. Based solely on this scaling, it is not immediately obvious whether the net effect of introducing a small amount of ellipticity or eccentricity is to increase or decrease the total pumping effectiveness. The results of our simulations show that, for fixed cross-sectional area of the annulus, the pumping effectiveness always decreases when either ellipticity of eccentricity is introduced, and hence the concentric circular annulus provides the most efficient configuration for pumping.

We know that for steady, pressure-driven flow in an annular tube of fixed cross-sectional area, the hydraulic resistance decreases with increasing ellipticity or eccentricity. Tithof et al. (2019) speculated that this decrease in viscous resistance might offset to some extent the accompanying decrease in peristaltic pumping effectiveness, such that optimal pumping occurs in annular cross-sections that are not concentric circles. Here we have shown that this is not the case: apparently the decrease in pumping effectiveness dominates the reduction in viscous resistance when any amount of ellipticity or eccentricity is introduced.

4. Discussion

Here, with our simple model, we have focused on the effect of non-axisymmetry of the cross-section in producing 3-D peristaltic flow in an annular tube. The asymmetry of the cross-section causes azimuthal pressure gradients which drive an oscillatory azimuthal component of flow that is not present in the case of a concentric circular annulus. In a non-axisymmetric annulus, the azimuthal variation of the gap width, and hence of the pumping effectiveness, produces the azimuthal flow: in the narrowest part of the gap, the squeezing by the peristaltic wall wave tends to drive a flow in a direction that offers the least resistance, which in this case is not the axial direction, but instead is offset in the azimuthal direction.

As shown by Tithof et al. (2019), and here in figure 3, if we start with a concentric circular annulus, keeping the cross-sectional area of the annulus fixed, then flattening the outer boundary into an ellipse or making the annulus eccentric will lower the hydraulic resistance. (For a broader study of hydraulic resistance in elliptical annuli, see Williams et al. (2020).) This suggests the possibility that there might by a non-axisymmetric cross-section that is optimal in allowing the greatest volume flow rate for a given peristaltic wave. This is not the case, however, as we have shown here: the volume flow rate decreases monotonically for increasing ellipticity or increasing eccentricity (figure 9). Apparently the loss of effectiveness of the peristaltic driving is greater than the gain to be had from decreased viscous resistance.

Although this study was suggested by experiments showing peristaltic-like flow of cerebrospinal fluid in perivascular spaces in the brain, the model presented here is not directly applicable to that case. The wavelength of the arterial wall wave is longer than the length of the perivascular spaces, whereas here we have taken then to be comparable. As in several other studies, we have imposed the condition of zero pressure drop between the ends of the tube, in order to produce purely peristaltic flow without the addition of a flow driven by an overall steady pressure gradient. In the resulting flow the amplitude of the oscillatory flow is very much greater than that of the mean (bulk) flow, which is not what is observed in the in vivo mouse experiments (Mestre et al. 2018). However, in the actual perivascular system such a simple pressure condition does not apply: the peristaltic pump is embedded in a larger network of channels that add resistance and compliance to the system. Recently, Ladrón-de-Guevara et al. (2020) showed that coupling realistic boundary conditions, including resistance and compliance, to open-tube models of perivascular pumping produces flows that agree well with those observed in the mouse experiments (Mestre et al. 2018). The realistic time-dependent boundary conditions must reflect the presence of the compliance of arteries and other tissue that act as elastic-energy reservoirs that reduce the oscillatory amplitude of the flow downstream of the model tube and shield the peripheral circulation from high oscillatory shear stress.

One of the interesting effects of the 3-D nature of the flows we consider here is their contribution to Taylor dispersion (Taylor 1953; Aris 1956) of a solute. Asgari, de Zélicourt & Kurtcuoglu (2016) have shown how a purely oscillatory shear flow (with no net mean flow) enhances dispersion in the axial direction, compared to pure diffusion in the absence of a flow. (This enhancement is weak, however, compared to the classical Taylor dispersion due to even a slow net axial flow driven by pumping or a pressure gradient: see the discussion in Thomas (2019) and the simulations in Troyetsky et al. (2021).) Here, we point out that, for peristaltic flows in non-axisymmetric annuli, the oscillating shear flow in the azimuthal direction will enhance dispersion in that direction, in cases where the solute concentration is not initially axisymmetric. For example, consider an annulus in which a solute is injected through a small port in the outer wall. The solute enters locally at one particular azimuthal position, and if the annulus is axisymmetric, the solute will spread azimuthally only by ordinary diffusion. If, however, the annulus is non-axisymmetric, then the oscillating shear flow in the azimuthal direction will enhance the dispersion in that direction, establishing more quickly a uniform solute distribution around the annulus. This enhancement of mixing might have useful industrial or biomedical applications.

Appendix A. Analytical solution for a concentric circular annulus

We present here an analytical solution of the problem of peristaltic pumping in a thin, open tube with cross-section in the form of a concentric circular annulus. Wang & Olbricht (2011) considered the related problem of peristaltic pumping a concentric circular annulus filled with a porous medium, with flow driven by a sinusoidal wall wave propagating along the inner boundary. They use the long wavelength, low Reynolds number approximation (Shapiro et al. 1969; Jaffrin & Shapiro 1971) and are able to obtain an analytical solution. Their solution for the time-averaged volume flow rate Q is the following:

$$\begin{gathered} Q=\pi r_2^2\gamma c\left(\frac{2{\alpha }^2}{1-{\alpha }^2}\right){\left(\frac{b}{r_2}\right)}^2+\pi r_2^2(1-{\alpha }^2)\left(-\frac{\kappa \Delta p_{\lambda }}{\lambda \mu }\right) \\ -\pi r_2^2\left(\frac{1+3{\alpha }^2}{2(1-{\alpha }^2)}\right)\left(-\frac{\kappa \Delta p_{\lambda }}{\lambda \mu }\right){\left(\frac{b}{r_2}\right)}^2, \end{gathered}$$ (A1)

where α = r₁/r₂ is the ratio of the inner and outer radii of the circular annulus, μ is the dynamic viscosity, γ is the porosity of the PVS, κ is the Darcy permeability, Δp_λ is the pressure drop over one wavelength λ, b is the amplitude of the wall wave and c is the propagation speed of the wall wave. The net volume flow rate Q is hence the sum of the three terms on the right-hand side of this equation. The first term represents the net flow due to peristaltic pumping by a small-amplitude wall wave in the absence of an overall pressure gradient (Δp_λ = 0). The second term represents the net flow driven by an overall pressure gradient in the undisturbed channel (with no wall wave). The third term represents a correction accounting for the fact that the pressure-driven flow moves through the annulus whose shape is distorted by the wall wave. (For small wave amplitudes (b/r₂ ≪ 1) and a moderate imposed pressure gradient, the third term is negligibly small.) The first term on the right, representing peristaltic pumping, is a purely geometric term representing the squeezing effect of the wall wave. This term, with ϵ = 1, is the same as one would obtain for flow in an open (non-porous) space. This term does not involve the viscosity: the viscosity does come into play in determining (based on the second term) what pressure gradient would be necessary to cancel the net peristaltic flow.

Here we adopt an approach similar to that of Wang & Olbricht (2011), but consider the annular space to be open rather porous medium, and hence use the Navier–Stokes equation rather than the Darcy law. We use the same notation as in § 2: for the concentric circular annulus, r₂ = r₃ and d_x = 0. The ratio of the wavelength λ to the width of the PVS channel r₂ − r₁ is assumed to be large, the lubrication approximation (very low Reynolds number) is applied. As is usual in peristalsis-related problems, a coordinate transformation is adopted: instead of considering a travelling peristaltic wave in the laboratory frame, we use the wave frame in which the peristaltic wave is stationary. The transformation between the two frames is given by

$$r^{\prime }=r,z^{\prime }=z-ct,v_r^{\prime }=v_r,v_z^{\prime }=v_z-c,$$ (A2a-d)

where quantities in the wave frame are denoted by primes. Considering the long wavelength and the low Reynolds number, the governing Navier–Stokes equation in the wave frame is reduced to the following components:

$$\frac{\partial p^{\prime }}{\partial r^{\prime }}=0,\frac{\partial p^{\prime }}{\partial z^{\prime }}=\mu \frac{1}{r}\frac{\partial }{\partial r^{\prime }}\left(r^{\prime }\frac{\partial v_z^{\prime }}{\partial r^{\prime }}\right).$$ (A3a,b)

The boundary conditions are

$$v_r^{\prime }(h^{\prime },z^{\prime })=v_r^{\prime }(r_2,z^{\prime })=0;v_z^{\prime }(h^{\prime },z^{\prime })=v_z^{\prime }(r_2,z^{\prime })=-c.$$ (A4a,b)

From (A3) and (A4), the velocity in z direction is obtained

$$v_z^{\prime }=\frac{\mathrm{d}{p}^{\prime }}{\mathrm{d}{z}^{\prime }}\frac{r^{\prime 2}}{4\mu }+\frac{\frac{\mathrm{d}{p}^{\prime }}{\mathrm{d}{z}^{\prime }}}{4\mu \text{ln}\left(\frac{h^{\prime }}{r_2}\right)}\left[h^{\prime 2}\text{ln}\left(\frac{r^{\prime }}{r_2}\right)-r_2^2\text{ln}\left(\frac{r^{\prime }}{h^{\prime }}\right)\right]-c.$$ (A5)

The volumetric flow rate Q′ is constant, independent of z′, which gives

$$Q^{\prime }=2\pi {\int }_{h^{\prime }}^{r_2}{v}_z^{\prime }{r}^{\prime }\mathrm{d}{r}^{\prime }.$$ (A6)

Substituting v_z′ from (A5) into (A6), the pressure gradient can be found in terms of Q′. Since h′(z′) is a periodic function with period λ, the pressure gradient dp′/dz′ is also periodic with period λ, and the pressure drop over a distance λ,

$$\Delta p_{\lambda }^{\prime }={\int }_0^{\lambda }\frac{\mathrm{d}{p}^{\prime }}{\mathrm{d}{z}^{\prime }}\mathrm{d}{z}^{\prime }.$$ (A7)

is constant, independent of the starting point of the interval. Inserting the value of dp′/dz′ given by (A5) and (A6), the relationship between $\Delta p_{\lambda }^{\prime }$ and Q′ is given as

$$\Delta p_{\lambda }^{\prime }={\int }_0^{\lambda }-\frac{8\mu \text{ln}\left(\frac{h^{\prime }}{r_2}\right)[Q^{\prime }+\pi c(r_2^2-h^{\prime 2})]}{\pi \left[\text{ln}\left(\frac{h^{\prime }}{r_2}\right)(r_2^4-h^{\prime 4})+(r_2^2-h^{\prime 2}{)}^2\right]}\mathrm{d}{z}^{\prime }.$$ (A8)

Substituting h′(z′) with the sinusoidal waveform into (A8), then $\Delta p_{\lambda }^{\prime }$ in terms of given Q′ can be calculated. Since the integration is too complex to evaluate analytically, it is computed numerically instead.

Generally, the quantity of practical interest is the time-averaged volumetric flow rate (net flow rate) at each cross-section. In the laboratory frame $\Delta p_{\lambda }=\Delta p_{\lambda }^{\prime }$ and the volumetric flow rate at time t across a cross section at z is

$$Q=2\pi {\int }_h^{r_2}{v}_{z}r\mathrm{d}r=Q^{\prime }+\pi c(r_2^2-h^2).$$ (A9)

The time-averaged flow rate then is given by

$$\overline{Q}=\frac{1}{T}{\int }_0^{T}Q\mathrm{d}t=Q^{\prime }+\pi c\left(r_2^2-r_1^2-\frac{1}{2}{b}^2\right).$$ (A10)

Appendix B. Convergence study of the numerical scheme

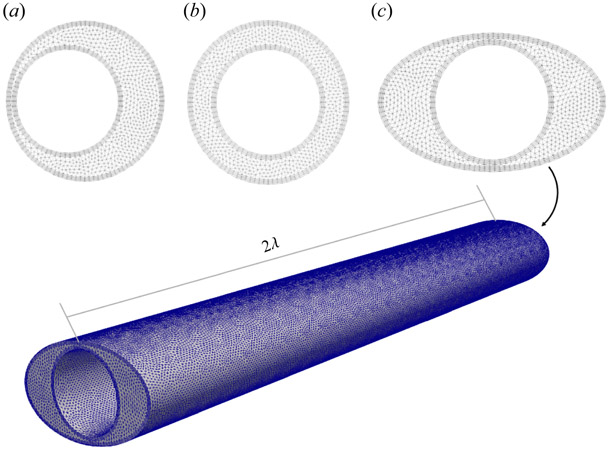
In order to determine an appropriate mesh size, a convergence study was performed using the eccentric model with (ϵ = 0.349). Each simulation was run with an amplitude of 1 % of the inner diameter and a wavelength of 16 μm at two peristaltic wave frequencies: 1 Hz and 5 Hz. The results are shown in table 3. The global edge size, BL height, and BL size of the ‘Finer, Fine BF’ simulation was selected because mean flow was within 1 % of the finest model and computational time was 10 h faster for a single period than the ‘Finest’ simulation for both peristaltic wave frequencies. A similar mesh scheme was applied to the remaining elliptical and eccentric models (figure 2).

Table 3.

Convergence study to determine the number of elements required to accurately simulate the flow in the model with the narrowest gap width, the eccentric circular annulus model with eccentricity ϵ = 0.349. Wave speeds of 16 μm s⁻¹ and 80 μm s⁻¹ were used for the 1 Hz and 5 Hz cases, respectively. All lengths have been non-dimensionalized using the inner radius, e.g. L*_dge = L_edge/r₁, and each model length is equal to two complete wavelengths of the peristaltic wave.

Frequency	Simulation name	Number of elements (NElems)	Global edge size (L*global	BL height (H*BL)	BL edge size (L*BL)	Net Q*
1 Hz
	Coarse, No BL	510 000	0.15	0	0	1.89 × 10−2
	Coarse, Coarse BL	76000	0.15	0.05	0.05	1.96 × 10−2
	Coarse, Fine BL	1200000	0.15	0.075	0.025	1.99 × 10−2
	Medium, No BL	136000	0.10	0	0	1.98 × 10−2
	Medium, Coarse BL	2 000000	0.10	0.05	0.05	2.02 × 10−2
	Medium, Fine BL	2 300000	0.10	0.1	0.05	2.03 × 10−2
	Averaged, Coarse BL	1200000	0.12	0.05	0.05	2.00 × 10−2
	Averaged, medium BL	2 000000	0.12	0.075	0.025	2.02 × 10−2
	Finer, Fine BL	2 100000	0.10	0.10	0.03	2.03 × 10−2
	Finest, No BL	3 000000	0.07	0	0	2.04 × 10−2
5 Hz
	Coarse, No BL	510 000	0.15	0	0	0.241 × 10−3
	Medium, No BL	136000	0.10	0	0	0.254 × 10−3
	Finer, Fine BL	2 100000	0.10	0.10	0.03	0.259 × 10−3
	Finest, No BL	3 000000	0.07	0	0	0.262 × 10−3

Figure 2.

The ‘Finer, Fine BL’ meshing scheme (bold in table 3) applied to the cross-sections of the most eccentric circular annulus (a), the concentric circular annulus (b) and the most elliptical concentric annulus (c).