Abstract
Spontaneous electrical activity, or automaticity, in the heart is required for normal physiological function. However, irregular automaticity, in particular, originating from the ventricles, can trigger life-threatening cardiac arrhythmias. Thus, understanding mechanisms of automaticity and synchronization is critical. Recent work has proposed that excitable cells coupled via a shared narrow extracellular cleft can mediate coupling, i.e., ephaptic coupling, that promotes automaticity in cell pairs. However, the dynamics of these coupled cells incorporating both ephaptic and gap junction coupling has not been explored. Here, we show that automaticity and synchronization robustly emerges via a Hopf bifurcation from either (i) increasing the fraction of inward rectifying potassium channels (carrying the current) at the junctional membrane or (ii) by decreasing the cleft volume. Furthermore, we explore how heterogeneity in the fraction of potassium channels between coupled cells can produce automaticity of both cells or neither cell, or more rarely in only one cell (i.e., automaticity without synchronization). Interestingly, gap junction coupling generally has minor effects, with only slight changes in regions of parameter space of automaticity. This work provides insight into potentially new mechanisms that promote spontaneous activity and, thus, triggers for arrhythmias in ventricular tissue.
We expand a well-known biophysical ventricular cell model (Luo–Rudy 911) to represent two adjacent coupled cells, including a shared intercellular cleft compartment, and derive the corresponding voltage equations for the three compartments (one for each cell, one cleft). We perform a thorough and systematic analysis of the combined effects of ephaptic and gap junction coupling on automaticity in the cell pair. We detail key properties governing automaticity—in particular, automaticity robustly occurs via the stable resting state losing stability via an Andronov–Hopf bifurcation. We describe conditions for which automaticity occurs, varying the fraction of inward rectifying potassium channels ( current) at the junctional membrane, the cleft volume, and gap junction coupling strength in both identical and heterogeneous cell pairs. Further, we find that the two cells trigger action potentials (APs) nearly synchronously for conditions for which automaticity occurs and report how parameters impact the period of spontaneous electrical activity.
I. INTRODUCTION
Automaticity, i.e., spontaneous electrical activity, is critical for robust functioning of the heart. In normal conditions, this spontaneous activity is generated within the sinoatrial node, also known as the pacemaker.2–5 Spontaneous action potentials (APs) originate in this region of the heart and propagate to the atria and then via an electrical conduction system, to the ventricles, coordinating efficient mechanical contraction and pumping of the blood. However, in pathological settings, APs can be initiated from regions outside the pacemaker that are normally quiescent, and these triggered ectopic beats in the ventricles can initiate life-threatening arrhythmias.6 Thus, it is imperative that we better understand the mechanisms that can promote or enhance automaticity in ventricular tissue.
Studies have shown that at the cellular level, there are many possible mechanisms for triggered activity, including excessive inward current due to defective ion channel gating and enhanced subcellular calcium release-mediated sodium–calcium exchanger current.7,8 However, in cardiac tissue coupled via gap junctions, the propagation of triggered activity acts as a “source” and the surrounding recovered tissue as a “sink,” such that triggered activity requires the synchronization of many myocytes, i.e., multiple cells firing at the same rate, in order to propagate in tissue, a consequence of the so-called source-sink mismatch. Xie and colleagues9 demonstrated that in a one-dimensional cardiac tissue, only tens of synchronized myocytes were required for propagation; however, in two- and three-dimensions, these numbers increase from thousands to hundreds of thousands. Reduced gap junctional coupling and other structural defects, which can occur in cardiac disease, can reduce these numbers; yet, the requirements for synchronized triggered myocytes are still quite large.
Significantly, a high prevalence of the clinical manifestation of ventricular triggered activity, i.e., premature ventricular contractions (PVCs), is associated with increased risk of cardiac dysfunction and cardiac death.10 At the same, PVCs regularly occur in healthy patients, on a daily basis,11 suggesting that there are alternative mechanisms by which ventricular automaticity can occur in healthy, well coupled tissue. In a recent study, we showed that an ephaptic coupling-mediated mechanism could promote automaticity in excitable cells (namely, the Hodgkin–Huxley12 and dynamic Luo–Rudy13 models) that in the absence of an additional stimulus do not spontaneously trigger APs.14 While coupling between cardiac cells is conventionally considered through direct electrical coupling via gap junctions, ephaptic coupling refers to the effects of electrical field and ion concentration changes that occur in a shared intercellular cleft (i.e., the narrow extracellular space between coupled cells at the cell–cell junctions). To briefly elaborate, the ephaptic coupling is governed by ionic fluxes across the membrane at the cell–cell junction (i.e., the junctional membrane) next to the cleft space in one cell (e.g., cell 1 in Fig. 1, fluxes denoted by ), which drive changes in the potential and ionic concentrations in the shared cleft space, that in turn impact the ionic fluxes of the adjacent cell (e.g., cell 2 in Fig. 1, fluxes denoted by ). That is, ionic currents at the cell–cell junction (also referred to as the intercalated disk) are interdependent, as they both govern and depend on the shared cleft ionic concentrations and voltage. Critically, this coupling does not depend on the direct electrical connection between the two intracellular spaces of the adjacent cells via gap junctions.
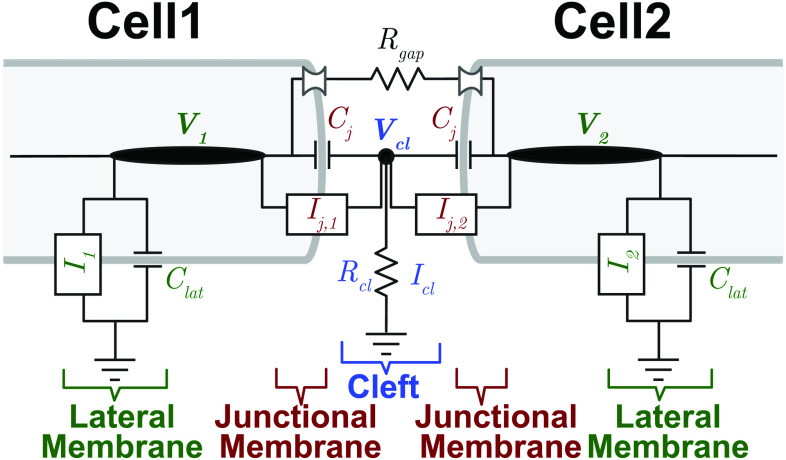
FIG. 1.
Electrical circuit representation of two cells with ephaptic and gap junction coupling. Intracellular nodes along lateral segments (with voltages and ) are coupled via gap junction resistance ( ). Extracellular cleft potential is governed by the two disk junctions and cleft resistance . Junctional and lateral membranes are governed by both capacitances ( and , respectively) and ionic currents ( and , respectively, for ).
Interestingly, most prior work, including our own, on ephaptic coupling has focused on the role of sodium channels at the cell–cell junction,15–18 as simulations predict that the large sodium influx during the action potential upstroke can drive large voltage and sodium concentration changes in the cleft. However, in our recent work,14 the ephaptic coupling-mediated mechanism promoting automaticity and synchronization (i.e., firing of electrical activity throughout the tissue at the same rate) occurred through accumulated potassium in the shared cleft space. In brief, cleft potassium accumulation elevates the resting potential of the coupled cells, which activated both inward sodium and calcium currents that drive automaticity. The mechanism required both preferentially localization of potassium channels on the junctional membrane adjacent to this cleft space and that the cleft space is sufficiently narrow. Importantly, both criteria have recently been demonstrated in ventricular myocytes, specifically the inward rectifying potassium current ( ), carried by the Kir2.1 channel.19–21 Notably, while this study demonstrated a potential mechanism for automaticity, it did not consider how gap junction coupling between neighboring cells affects their results, nor broadly how changes in ion channel and cleft properties impact automaticity characteristics in ventricular myocytes. Prior studies have shown that gap junctions can promote synchronization in spontaneously firing pacemaker myocytes;22,23 thus, it is of interest how both ventricular automaticity and synchronization depend on both ephaptic and gap junction coupling.
Here, for the first time, we consider how two ventricular cells with the combined physiological attributes of ephaptic and gap junction coupling could result in synchronized automaticity. We focus on varying the fraction of inward rectifying potassium current ( ) at the junctional membrane (denoted by ) and main lateral segment to model the dynamics of potassium accumulation (and depletion) at the cleft, considering both identical and heterogeneous current distributions between the two cells. Note that this fraction is directly related to the subcellular localization of the Kir2.1 channel. Our systematic investigation starts first with only ephaptic coupling between the two cells initially assumed to be identical. We establish parameter regions for which the cells trigger action potentials (APs) and for which they are quiescent (no APs). We then incorporate heterogeneity via different fractions of current at the junctional membranes of the coupled cells to determine when an active cell with APs can (or fail to) propagate APs to a cell via ephaptic coupling that would otherwise not emit APs. Finally, we include gap junction coupling to analyze the behavior of the two cell model. Throughout all of these analyses, we vary the cleft volume, which impacts the overall cleft potassium concentration dynamics and cleft electrical resistance.
We find APs occur via a stable resting state losing stability via a Hopf bifurcation in all cases. Detailed bifurcation diagrams show that the critical fraction of current at the junctional membrane that results in APs increases with cleft volume. Further, for conditions in which one cell is triggering APs, ephaptic and gap junction coupling can entrain a neighboring cell to similarly trigger APs that would not occur without coupling. When both cells emit APs, they are synchronous. Interestingly, we find that including gap junction coupling negligibly alters the overall dynamics.
II. MATERIALS AND METHODS
Let denote the voltage in the lateral segment, the voltage at the cell–cell junction, and the voltage in the cleft (extracellular) space.
A. Model equations
With two coupled ventricular cells, there are two voltage values at the lateral segment and (assuming the extracellular potential across the lateral segments is electrical ground), a single voltage at the cleft , and two transmembrane voltages at the cleft junction determined from the lateral segment and cleft voltages, and .
Let denote the lateral segment capacitance, where is the membrane capacitance and is the lateral membrane area assuming cylindrical geometry; is the junctional membrane capacitance at the junction with cross-sectional area . These entities are assumed to be the same in both cells. The cleft volume is a cylinder: ; the volume varies by changing the cleft width ( is fixed throughout).
The equations are derived by current balance (refer to Fig. 1),
| (1) |
| (2) |
| (3) |
where and are the sum of the lateral segment ionic currents for cell-1 and 2, respectively, and are the sum of the junctional membrane ionic currents for cell-1 and 2, respectively, is the cleft current (defined below), is the gap junctional current, and is the gap junctional conductance.
Here, we combine all ionic currents of the Luo–Rudy 19911 model to avoid cumbersome notation: on the lateral segment membrane, , and on the junctional membrane, . Using the relationship , we can derive an equivalent system for each of the three voltage compartments such that they appear on the left-hand side alone,
| (4) |
| (5) |
| (6) |
The slow-inward current is strictly localized on the lateral segment membrane. The remaining ionic currents in the model (see five other currents besides , in Table I) have a fixed nominal fraction of channels at the cleft (5% throughout), unless stated otherwise. See Table I for description of currents.
TABLE I.
Description of model parameters.
| Membrane and cleft | |
|---|---|
| Variable | Description |
| A m | Lateral segment membrane area |
| A j | Junctional membrane area |
| C m | Membrane capacitance |
| C lat | Capacitance of lateral segment membrane |
| C j | Capacitance of junctional membrane |
| C tot | Total capacitance |
| vcl | Cleft volume |
| Ionic currents (μA) | |
| Variable | Description |
| I Na | Voltage-gated sodium current |
| I K | Time-dependent potassium current |
| I b | Background leakage current |
| I Kp | Plateau potassium current |
| I K1 | Inward rectifying potassium current |
| I si | Slow-inward current |
| I cl | Cleft current |
For cell , the fraction of inward rectifying potassium currents at the junctional membranes ( ) and lateral segment ( ) are key entities that define the currents on these two membranes,
| (7) |
| (8) |
where . (Note that the factor of in the junctional membrane current arises from the currents localized on the 2 cell ends.) Conductances (per unit capacitance) on the lateral segment and junction membrane ( and , respectively) are dynamic variables that depend on other state (gating) variables, as described in the Luo–Rudy model.1 Note that the junctional membrane potassium reversal potential is also dynamic, through dependence on the cleft potassium concentration (described below), , where intracellular potassium concentration is fixed, mM. Similar definitions define the other lateral segment and junctional membrane ionic currents. See Luo and Rudy1 for a full description of the ionic current dynamics, gating variables, and additional parameters.
The cleft currents are given by the following:
| (9) |
| (10) |
| (11) |
where cleft conductance depends on the cleft width ,14,15,24 and extracellular resistivity . For fixed , we can write . The extracellular ionic concentrations are fixed: mM, mM; and constants C/mM (Faraday’s constant), J/K (gas constant), K. See Table II for other fixed parameter values.
TABLE II.
Parameter values.
| Parameter | Value (units) |
|---|---|
| r | 11 (μm) |
| L | 100 (μm) |
| A m | 2πr L (μm2) |
| A j | πr2 (μm2) |
| C m | 1 × 10−8 (μF/μm2) |
| C lat | Cm Am (μF) |
| C j | Cm Aj (μF) |
| C tot | Cm (Am + 2Aj) (μF) |
| [Na+]o | 140 (mM) |
| [K+]o | 5.4 (mM) |
| F | 96.5 (C/mM) |
| R | 8.314 (J/K) |
| T | 310 (K) |
The dynamics of the sodium and potassium concentrations at the cleft is driven by the differences in ionic currents at both junctions minus the cleft current,
| (12) |
| (13) |
III. RESULTS
A. Two identical ventricular cells with ephaptic coupling only
Our modeling study uses the well-known Luo–Rudy 91 model1 as the base model of a single ventricular myocyte. This model strikes an ideal balance in biophysical detail between minimal models, such as the aforementioned Hodgkin–Huxley model or FitzHugh–Nagumo model, and more detailed ventricular myocyte models with additional ionic currents and intracellular calcium signaling; yet the model is simple enough to enable robust bifurcation analysis (see Table I). A key feature of the expanded cell pair model is the inclusion of dynamic cleft potassium and sodium concentrations known to alter excitability (ability to trigger APs) mediated by ephaptic coupling.14,17,18,25–28 Importantly, the single or isolated ventricular myocyte model is normally quiescent in the absence of external stimuli or direct electrical coupling (via gap junctions), such that APs observed in the ventricular cell pairs can be directly attributed to the shared cleft dynamics. Figure 1 shows the main electrical network representing the two coupled cell model that we study in this paper.
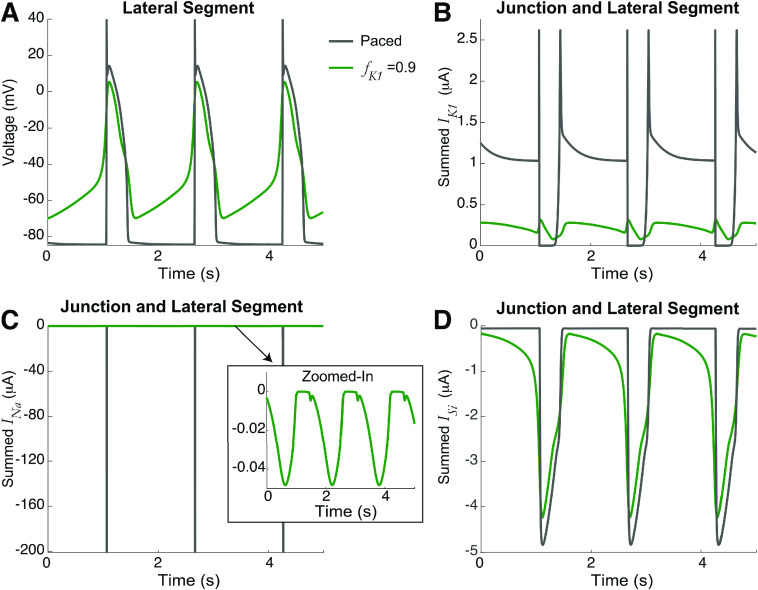
As outlined in Sec. I, we start by analyzing the simplest case: two identical cells only coupled via ephaptic mechanisms to the shared cleft, i.e., no gap junction coupling ( ) and the fraction of at the junctional membrane for both cells are equal, i.e., . Figure 2 illustrates the spontaneous dynamics (i.e., in the absence of any external stimuli) for two values of . For high , the voltage of the lateral segment illustrates spontaneous APs (green). Note that both cells are firing synchronously but only cell-1 is shown for clarity. The cleft voltage similarly oscillates with the APs [Fig. 2(b)]. Consistent with prior work,14 the mechanism underlying this spontaneous activity is as follows: localization of (which is active during diastole [Figs. 2(d)–2(e)], the resting phase between APs) at the junctional membrane drives a gradual accumulation of in the cleft [Fig. 2(c)], which gradually elevates the resting potential of the cells. This, in turn, activates the inward currents on both the lateral membrane and junctional membrane, in particular, the slow-inward current ( ) [Figs. 2(f)–2(h)]. The inward currents ultimately lead to the depolarization that triggers repetitive APs. In contrast, for a lower (black), the localization of does elevate cleft potassium above the bulk concentration of 5.4 mM [Fig. 2(c)], which moderately elevates the resting potential above the baseline of 85 mV. However, this is insufficient to activate the depolarizing inwards currents to drive automaticity. Thus, we identify as a critical parameter regulating the presence or absence of automaticity in coupled ventricular myocytes. We note that in healthy tissue, ventricular myocytes do not regularly exhibit automaticity, suggesting that lower is associated with normal conditions. In the Appendix, for comparison, we show the voltage and ionic currents for spontaneous and paced electrical activity (Fig. 9). We next more broadly investigate how this spontaneous activity can arise by modulation of key cellular and coupling properties.
FIG. 2.
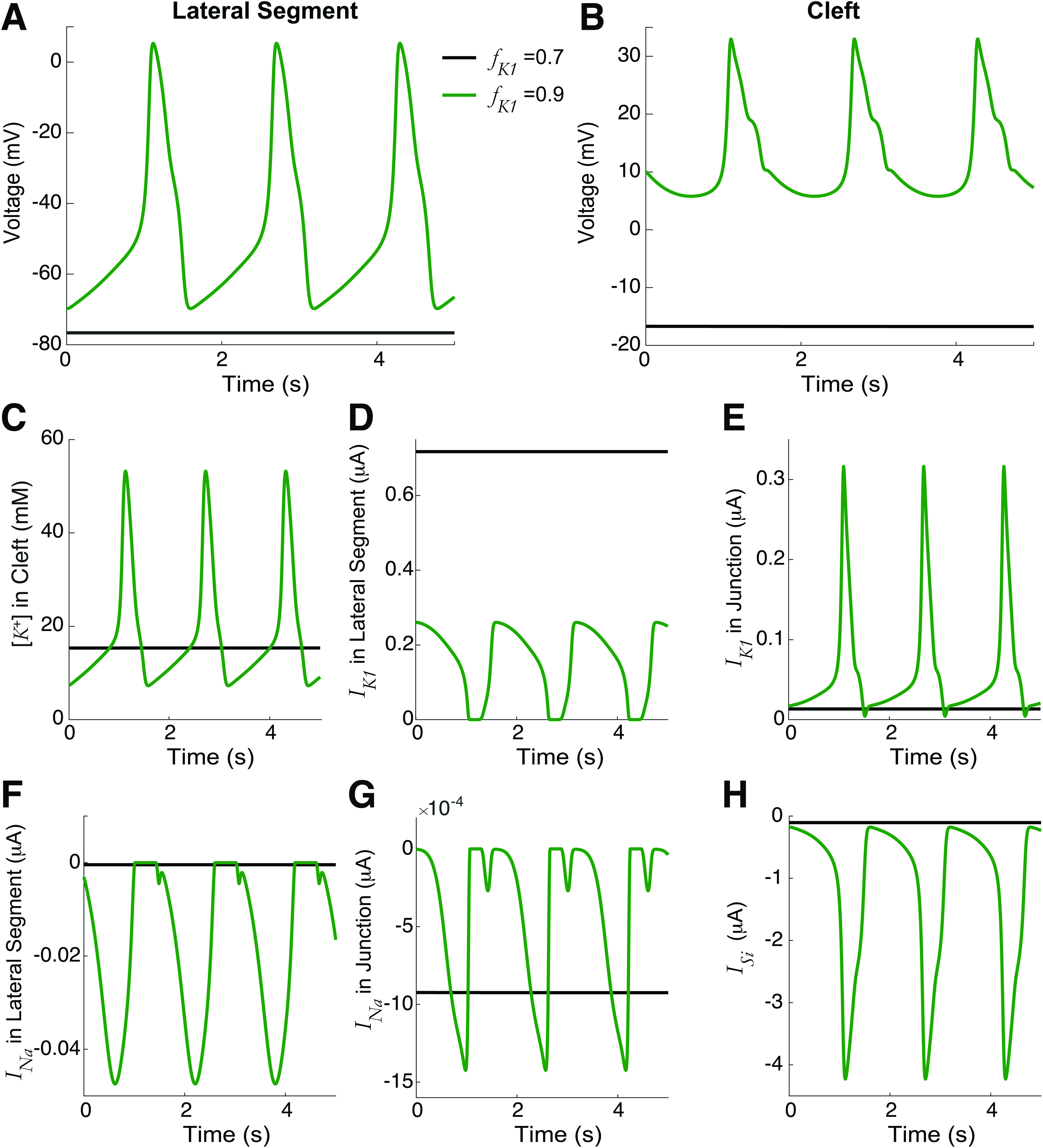
Automaticity in identical cells for high current at the cleft. The time series for the (a) lateral segment voltage, (b) cleft voltage, (c) cleft potassium concentration, at the (d) lateral segment and (e) junctional membrane, sodium current at the (f) lateral segment and (g) junctional membrane, and (h) lateral segment slow-inward current , for the junctional membrane fraction of ( ) of 0.7 (black) and 0.9 (green). Higher triggered automaticity and synchronized APs in both cells, due to cleft potassium accumulation, increasing the resting potential to trigger inward .
B. Automaticity is regulated by junctional membrane IK1 localization and cleft volume
The detailed dynamics of the identical two cell model with ephaptic coupling only via a shared cleft (no gap junction) is shown in Fig. 3. Figure 3(a) is a bifurcation diagram of the lateral segment voltage (vertical axes), varying the parameter that denotes the fraction of current at the junctional membrane; we see a stable fixed point (red) with hyperpolarized values loses stability via an (Andronov–)Hopf bifurcation as increases, resulting in unstable limit cycles (blue) and stable limit cycles (green), corresponding to both cells triggering APs. Note that directly affects the current ( ) in voltage equations in both the lateral segment and junctional membranes.
FIG. 3.
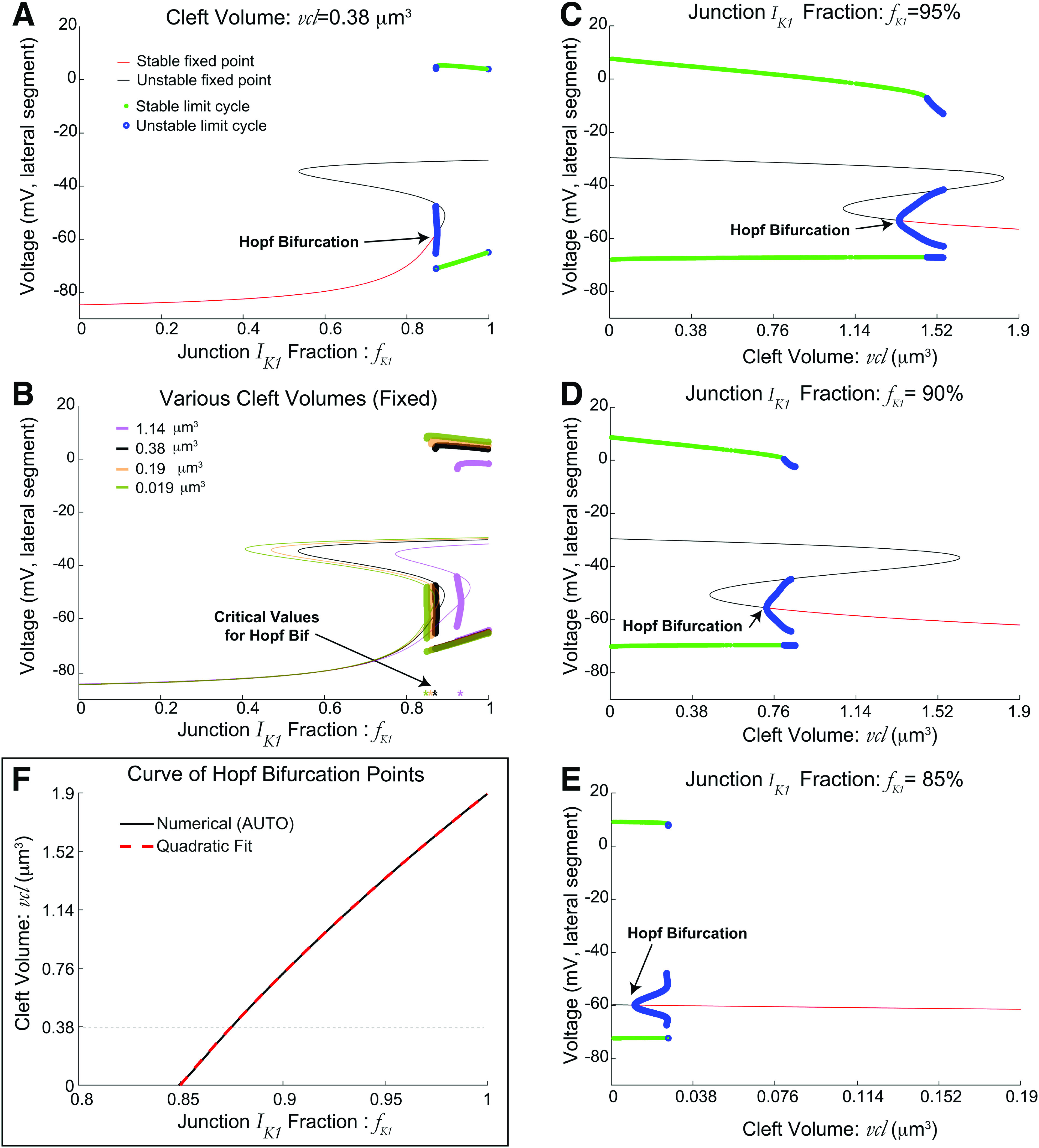
Dynamics of two identical cells with ephaptic coupling only, varying fraction of junctional membranes current, . Increasing leads to automaticity. (a) Bifurcation diagram for the voltage (lateral segment) vs , illustrating regimes of stable (red) and unstable (black) fixed points, and stable (red) and unstable (blue) limit cycles. (b) Bifurcation diagrams with various (fixed) cleft volumes , with all fixed points and limit cycles shown with a single color to illustrate how Hopf bifurcation point varies. (c)–(f) Bifurcation diagrams with fixed values (0.95, 0.9, 0.85, respectively), varying cleft volume . Decreasing the cleft volume leads to automaticity via a Hopf bifurcation. The critical volume decreases as decreases. (f) Summary: two-parameter curve of Hopf bifurcation points computed by XPP-AUTO (black)29,30 is well-fit by a quadratic function: . Note that automaticity occurs in the lower right triangular region of parameter space. Dashed black horizontal line corresponds with value in (a).
Furthermore, the critical that gives rise to automaticity depends on the cleft volume , but the qualitative dynamics are the same. Figure 3(b) shows several bifurcation diagrams with stability and fixed point types suppressed for visual purposes. Notice a leftward shift for smaller cleft volumes (respectively, a rightward shift for larger cleft volumes) of the critical (minimum) fraction for which automaticity occurs. That is, as the cleft volume decreases, the critical fraction of current at the junctional membrane necessary for automaticity is reduced.
We note that the geometry of the cleft is assumed to be a cylinder and that the cleft volume is varied by changing the cleft width while fixing the cleft cross-sectional area. The effects of varying the cleft volume with all other parameters fixed are complicated; this parameter directly changes the conductances of the sodium and potassium currents at the junctional membrane (through changes in cleft width) and the dynamics of the concentrations of sodium and potassium. The bifurcation diagrams in Figs. 3(c)–3(e) show similarly that decreasing the cleft volume promotes automaticity from a stable fixed point losing stability via a Hopf bifurcation. The critical for which this occurs decreases as decreases ( in C, D, E, respectively). Note the smaller values on the axis for in Fig. 3(e), which highlights that for , automaticity only occurs for a very small cleft volume.
Figure 3(f) summarizes these results in a two-parameter curve of Hopf bifurcation points, showing how the critical fraction at the junctional membrane (horizontal) varies with cleft volume (vertical). The curve has a simple monotonic relationship, evidenced by a good fit using a simple quadratic function to relate a given cleft volume to the critical (red dashed). Collectively, these results show the interdependent relationship between cleft volume and the fraction of at the junctional membrane in regulating automaticity.
Prior work has shown that sodium current is a key modulator of AP generation in ephaptic coupling due to the localization of sodium channels at the junctional membrane.19,26 Thus, we considered if the fraction of sodium current at the junctional membrane impacts automaticity. We varied the fractions of the sodium current at the junctional membrane (Fig. 4), with two identical ephaptically coupled cells.
FIG. 4.
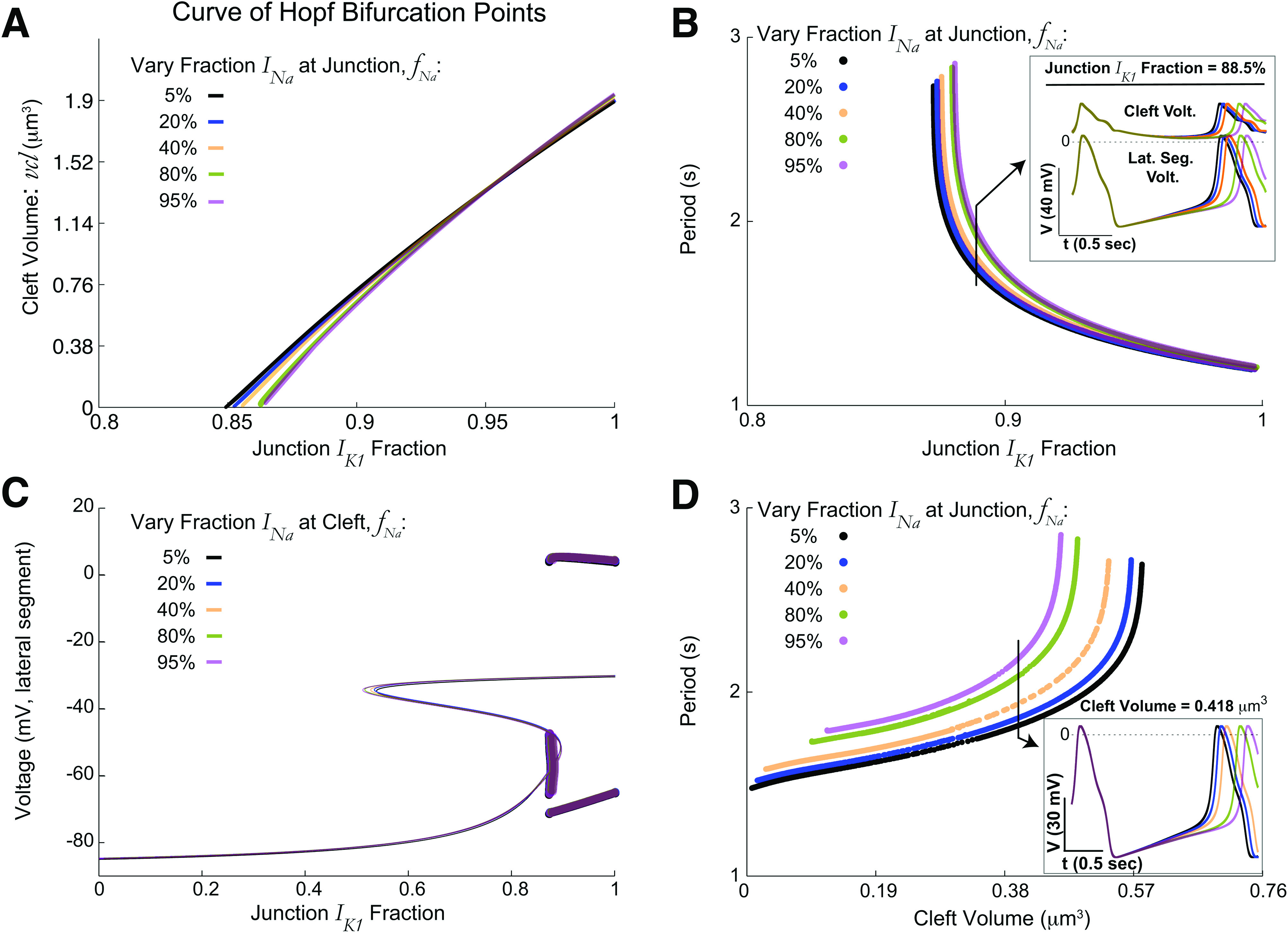
Weak to moderate dependence on fraction of sodium current at the junctional membrane in identical ephaptically coupled cells. (a) The curve of Hopf bifurcation (HB) points shifts slightly over a large range of [cf., Fig. 3(f)]. (b) Period of automaticity as a function of for fixed cleft volume does not significantly vary with . Increasing shortens the period duration for fixed . Inset shows that voltages (cleft on top, lateral segment below) for a fixed value of are similar even with modest differences in period duration. (c) The corresponding bifurcation diagrams of voltage vs for also minimally vary, suppressing stability details as in Fig. 3(b). (d) As a function of for fixed , decreasing the cleft volume shortens the period. Increasing increases period; however, for larger , the variation is minor in the period duration. Inset shows that APs are similar for all five values of with fixed .
Figure 4(a) shows that the two-parameter curve of (Hopf) bifurcation points varies only slightly for various fixed fractions that range from 5% to 95% (at the junctional membrane), with differences relatively larger for smaller cleft volumes. Overall, the regions of automaticity are relatively insensitive to the fraction of sodium channels at the junctional membrane or lateral segment, which demonstrates that the mechanism of automaticity is primarily driven by the localization of potassium, and not sodium, channels. Even for a relatively small cleft width , the bifurcation diagrams of varying do not change much [Fig. 4(c); as before, lateral segment voltage is on vertical axes].
Figure 4(b) shows the corresponding periods ( , as a function of for a wide range of fixed (see inset for AP waveform). First, we find that beyond the critical value, increasing decreases the period. For a given , increasing the sodium fraction at the junctional membrane increased the period of automaticity. Finally, the cleft volume can moderately alter the period duration [Fig. 4(d); here is fixed], with smaller cleft volume decreasing the period duration, while increasing decreased the period duration. The range of with automaticity can significantly change as changes. While the period varied for the near the critical value, for larger , the differences in period duration and values of with automaticity are much smaller than shown in Fig. 4(d). Although can have a weak to moderate effect on the actual period duration (and to a lesser extent on parameters for which automaticity occurs), we fix for the rest of the paper to focus on how the junctional membrane fraction of current, cleft volume, and gap junction coupling alters automaticity for heterogeneous cells.
C. Heterogeneous cells without gap junction coupling
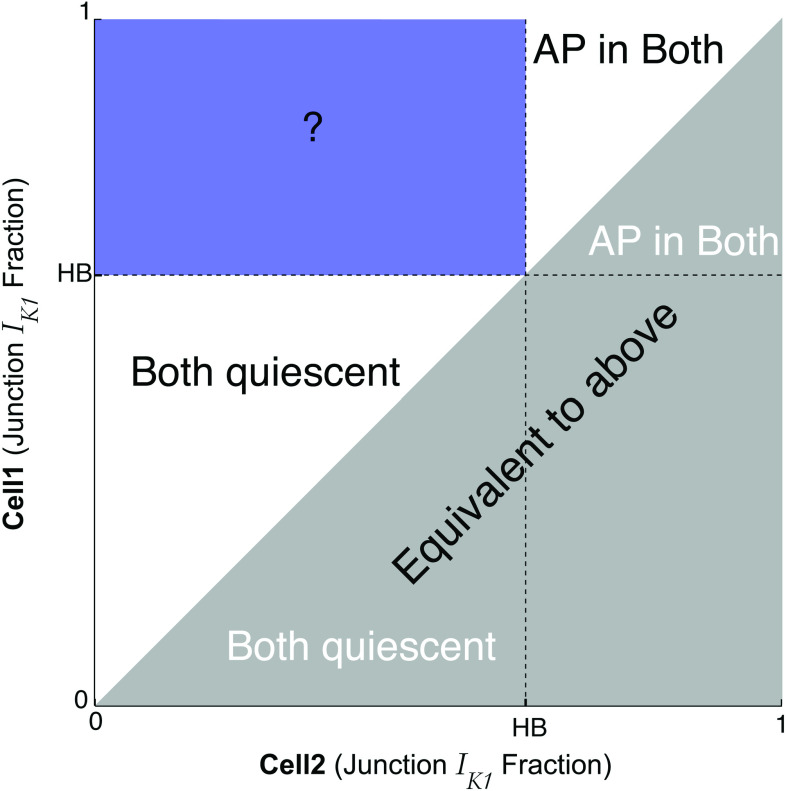
The prior analysis determined the parameter space for which automaticity occurs in identical ventricular cells with ephaptic coupling only, and, therefore, we next consider the dynamics when the fraction of current at the junctional membrane differs between the two cells, i.e., . The prior results can be leveraged in such a way that the region of parameter space can be narrowed to the bluish rectangular region in Fig. 5; the value of the Hopf bifurcation (HB) is a reference point that depends on (among other things) [see Fig. 3(f)]. By convention and without loss of generality, we assume here that cell-1’s fraction of current ( ) is always greater than or equal to ( ) cell-2’s fraction ( ) [see Fig. 5]. For the case of , an AP will occur in both cells, while for , both cells are quiescent (no APs). However, it is not obvious what conditions in the bluish rectangular region correspond to automaticity, quiescence, or something in between. In other words, when and , for what conditions does automaticity occur?
FIG. 5.
Parameter regions of interest varying in both cells. Our analysis focuses on the blue region where fractions of current are heterogeneous; by convention, cell-1 has ( ) values above the Hopf bifurcation (HB) point that trigger action potentials (APs), while cell-2 has ( ) below the HB point.
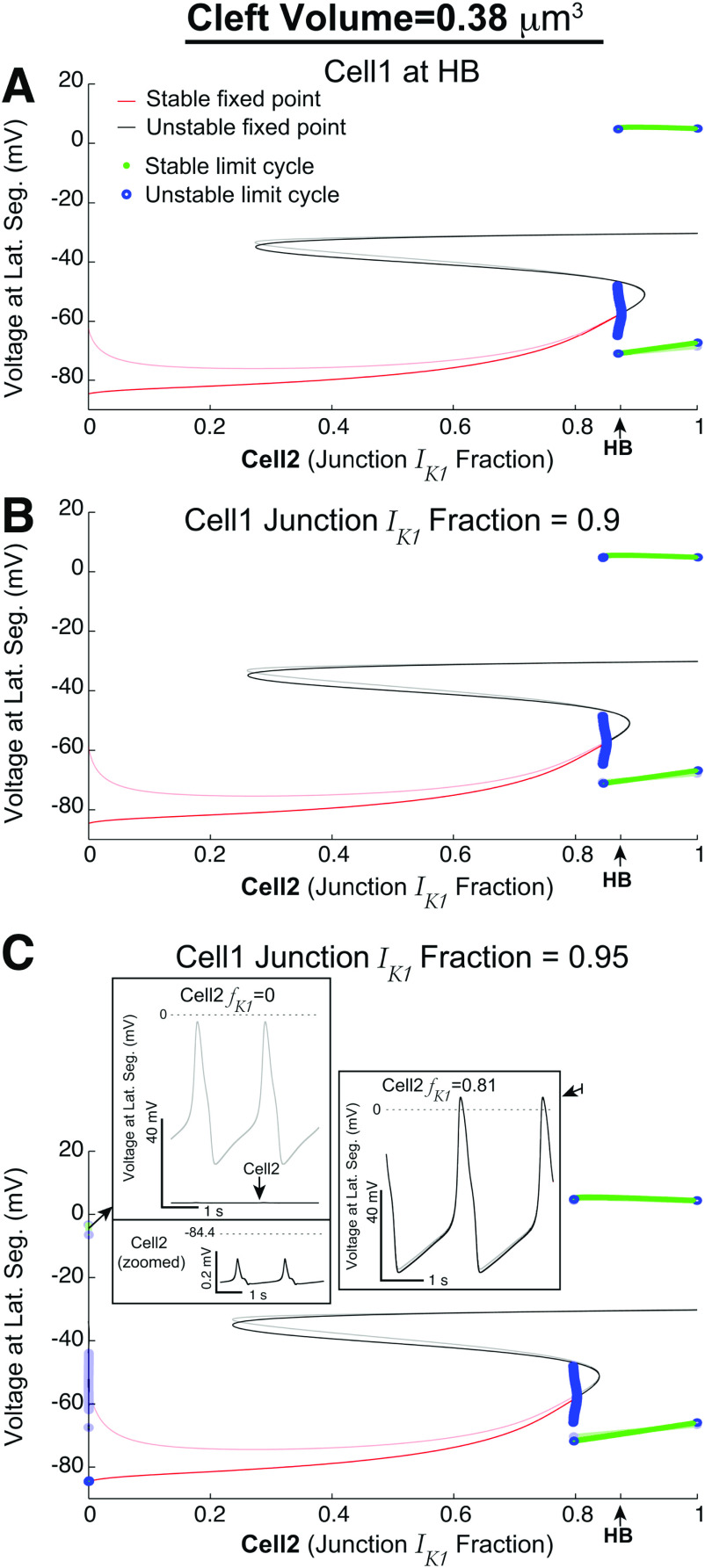
We fix the cleft volume ( ) and also fix at specific values at or above HB ( ) such that the identical cell case would result in automaticity, varying only as the bifurcation parameter (Fig. 6). In Fig. 6(a), the bifurcation diagram shows the lateral segment voltages of cell-1 (transparent) and cell-2 (solid) on the vertical axes. Interestingly, we find that automaticity occurs for (horizontal axis) slightly lesser than the HB value. That is, automaticity can occur in both cells, even if is slightly less than would be necessary for automaticity in the identical case. This “slack” becomes even more apparent as is set to larger values in Figs. 6(b) (0.9) and 6(c) (0.95); the bifurcation point where both cells are triggering APs shifts to the left of the HB value as increases [see also Fig. 7(a)].
FIG. 6.
Detailed bifurcation diagrams for heterogeneous cells, with only ephaptic coupling. The transparent curves are lateral segment voltages in cell-1, and opaque curves are for cell-2. Ephaptic coupling can induce cell-2 to trigger APs in regimes for which, without ephaptic coupling, cell-2 would be quiescent. (a) With cell-1’s fraction of current ( ) at HB, cell-2’s fraction ( ) can be slightly less than HB for both cells to trigger APs. (b) For values larger than HB (0.9), the range for which both cells emit APs is larger. (c) For even larger (0.95), the dynamics are similar as in (b); however, for very small , there is a regime for which cell-1 triggers APs because it is essentially decoupled from cell-2, while cell-2 exhibits sub-threshold oscillations. For other cleft volumes , see Fig. 7(d).
FIG. 7.
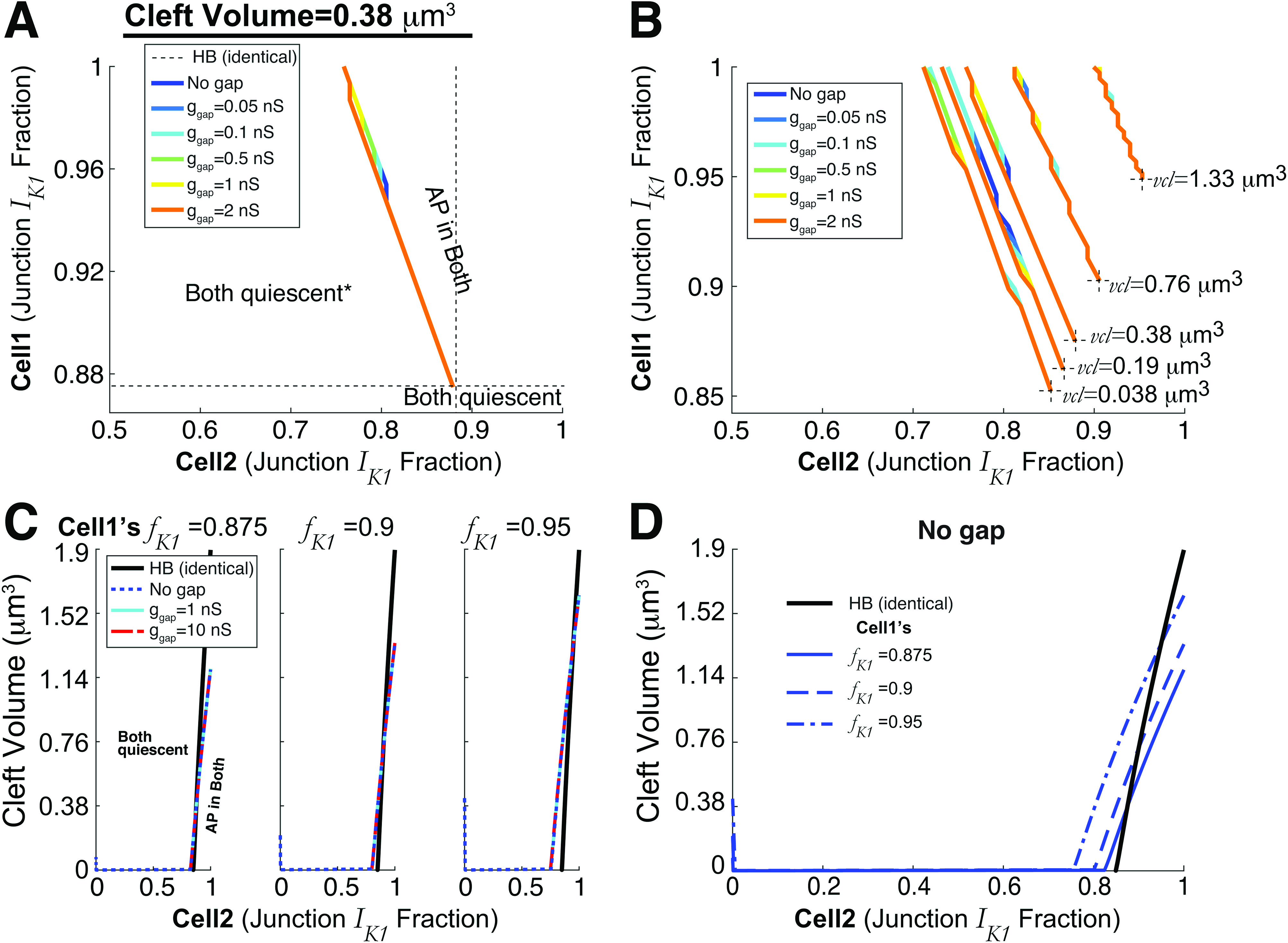
Automaticity regimes in heterogeneous cell pairs with ephaptic and gap junction coupling. (a) Gap junction coupling strength has negligible influence on the regimes for which automaticity occurs. Black dotted lines are the reference point for the Hopf bifurcation (HB) for the minimal for automaticity for identical cells and (cleft volume ). Note that the asterisk in the left region of “both quiescent” indicates that for and small , cell-1 triggers APs and cell-2 has sub-threshold oscillations [recall Fig. 6(c)]. However, this only occurs when ; for , both cells are quiescent in that region. (b) Similar plot as (a) for various cleft volumes —the boundary for automaticity shifts but varying does not significantly change regimes for automaticity. The black dotted lines denoting the HB point are shorter to avoid clutter. (c) Detailed two-parameter bifurcation diagrams, fixing cell-1’s ( ), with cleft volume on the vertical axis and cell-2’s ( ) on horizontal. As in (a) and (b), gap junction coupling does not alter the boundary for which both cells are triggering APs. The near vertical line for (blue dotted) for small is indicative of the dynamics described in Fig. 6(c). (d) The blue curves (no gap junction) in (c) are shown on a single axis, related to Fig. 3(f) (black).
Interestingly, as decreases, we find that cell-1’s voltage is non-monotonic (Fig. 6). In all panels of Fig. 6, cell-1’s voltage (transparent red curve) initially decreases and then rebounds upward as decreases. In fact, for very high [Fig. 6(c)], this gradual depolarization of the cell-1 voltage as decreases results in automaticity for cell-1 (see left inset). Cell-2 exhibits so-called sub-threshold oscillations, below the threshold for AP triggering. However, this regime for cell-1 firing APs but not cell-2 is relatively small (and as we show later, only occurs in the absence of gap junctions). We next consider the impact of the inclusion of gap junctions between the cells and the impact on automaticity.
D. Automaticity in two cells with gap junction and ephaptic coupling
As noted in Sec. I, gap junctions have been shown to synchronize spontaneously firing excitable cells, but the effects of gap junctions on the dynamics described thus far for ephaptically coupled cells are unknown. In particular, we showed that cell-1 exhibiting automaticity (i.e., ) could promote AP firing in an inherently quiescent cell ( ). However, does gap junction coupling between the cells introduce an additional electrical load or “sink” that suppresses synchronized automaticity? Note that investigating gap junction coupling in the identical cell case is trivial, because for all conditions, the voltage difference between the intracellular spaces is always 0 such that gap junctional current ( ) is also always 0 regardless of the value of gap junctional conductance .
In Fig. 7(a), we plot the two-parameter bifurcation curve for and for a fixed cleft volume . As noted above, there exists a regime for which automaticity occurs for cell-1 inherently spontaneously triggering APs and cell-2 inherently quiescent in the absence of gap junctions (blue). Interestingly, incorporating gap junctions has almost no effect on this curve, with increasing gap junctional coupling conductance slightly shifting the curve left. Figure 7(b) illustrates these curves for different . Decreasing left-shifts the curves such that automaticity occurs for a wider range of values in both cells, consistent with the trend for identical cells shown above. Similarly, incorporating gap junctions has minimal impact on the regimes for automaticity. Further, for all parameter sets here, the phase difference for conditions for which both cells are firing APs is less than 0.1 ms, such that cells are always synchronized, independent of .
Note that the parameter space considered here has many dimensions as we vary the cleft volume, fraction of current (ephaptic coupling), and gap junction coupling strength. Thus, we use MATLAB simulations in Figs. 7(a) and 7(b), rather than XPP-AUTO to efficiently analyze the voltage trajectories posthoc to determine when there are actual APs rather than sub-threshold oscillations [see Fig. 6(c)]. In addition, MATLAB simulations enable efficient analyses of the period duration, phase differences, or time-lag when both cells trigger APs.
Figure 7(c) similarly demonstrates the minor effects of gap junction coupling on the regions of automaticity. Here, and are fixed to different values, and the plots illustrate the two-parameter Hopf curves ( vertical, horizontal) that divides the regions with automaticity (lower right) or quiescence (upper left). These plots are analogous to the curve in Fig. 3(f), which represented conditions of identical cells and ; that HB curve (black) is shown for reference. Note, by definition, the colored lines intersect the HB curve for . For all cases, the region of automaticity does not change with Sec. I of gap junctions. Figure 7(d) shows the two-parameter Hopf curves from panel C for different (fixed) on the same axes, where the intersection of the HB curve intersecting the blue curves at is more apparent. As in the prior results, increasing results in a larger regime of automaticity for all values of and .
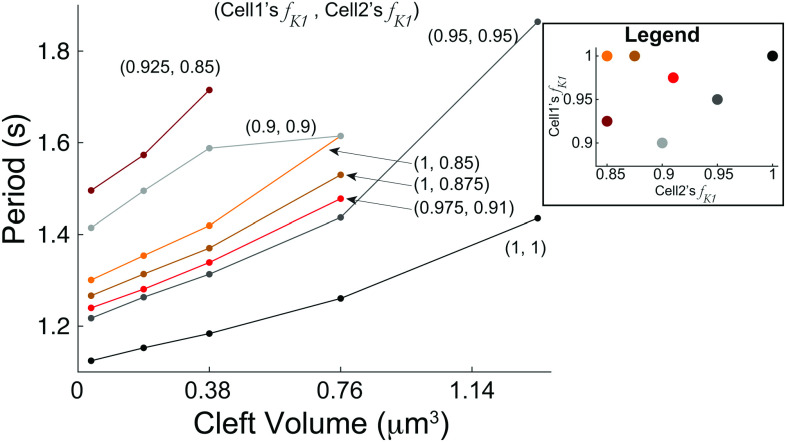
Further, in addition to gap junction coupling not appreciably changing the parameter regions for automaticity, we also find that varying does not change the period of both cells for conditions exhibiting automaticity (not shown). However, we find that the cleft volume can change the period duration. In Fig. 8, we plot the period duration as a function of for different combinations of . Note that we only show cell-1’s period because it is indistinguishable from cell-2. For all conditions, decreasing decreased the period, as we find for the identical case [Fig. 4(d)]. In general, as either or increases, the period tends to shorten for a given , although the period duration dependence is not strictly additive between the two values.
FIG. 8.
The period generally increases as the cleft volume increases for various combinations of fractions for cell 1 and 2 ( , ). Curves that abruptly end, which have less than five dots (e.g., top maroon curve ), indicate that automaticity is extinguished for larger . We considered five total values of . Note that we only show the case of no gap junction coupling ( ), as differences in period duration for values are negligible. Only cell-1’s period is shown, because in all cases, the period duration differences between cells 1 and 2 are less than a fraction of a millisecond.
IV. DISCUSSION
In this study, we demonstrate that synchronized and spontaneous APs can be triggered in a model of identical or heterogeneous ventricular myocyte pairs, coupled via a shared extracellular cleft, i.e., ephaptic coupling. This automaticity arises through a Hopf bifurcation for both high fractions of current at the junctional membrane ( ) and reduced cleft volume ( ). These two properties co-regulate the regimes for spontaneous APs, as smaller supports automaticity for a smaller and vice versa. Further, both higher and smaller trigger APs with a shorter period duration, while a smaller fraction of sodium channels also tended to shorten the period.
In heterogeneous cell pairs, a large can promote automaticity in its neighbor cell that would otherwise be quiescent. Perhaps most interestingly, the presence of gap junction coupling had a near negligible influence on the parameter regimes for automaticity or the period duration of triggered APs. Thus, we have identified how key structural and cellular properties impact the conditions promoting or suppressing automaticity in coupled ventricular myocytes.
In recent years, several studies have demonstrated that ephaptic coupling can play an important role in the formation of cardiac arrhythmias. Tsumoto and colleagues found that the localization of sodium channels at the junctional membrane can impact arrhythmias triggers associated with Brugada syndrome.16 Wei and colleagues showed that conduction defects impacted by cardiac ischemia can be partially recovered via ephaptic coupling.31 Our recent work has shown that cleft volume can also impact the formation of arrhythmias associated with sodium channel gain-of-function and long QT syndrome.18,25,27,32,33 The distribution of gap junctions, ion channels, and tissue structure have been shown to impact cardiac conduction via ephaptic-mediated mechanisms.15,17,26,28,34 Ephaptic coupling was additionally shown to impact electrical conduction in a model of stem cell-derived cardiomyocyte injection.35
Interestingly, the idea that cleft potassium accumulation could play a role in cardiac conduction was theoretically proposed as early as the 1970s by Sperelakis and colleagues.36,37 Yet, in most of the aforementioned studies, ephaptic coupling was primarily mediated via sodium channels at the junctional membrane. Recent experimental identification of potassium channels at the junctional membrane has reinvigorated studies of the potential role of these channels.20,38 Our recent work with Poelzing and Keener predicted that under certain conditions, this potassium accumulation mechanism can facilitate not only AP transmission but also automaticity, suggesting a new role in irregular cardiac rhythms.14 The current study builds upon this prior work to identify the bifurcation that gives rise to spontaneous APs and characterizes how the bifurcation properties change with key structural and cellular properties.
As noted above, gap junctions have previously been predicted to play a critical role in synchronization and conduction in both normal pacemaker electrical rhythms and irregular ventricular ectopic activity.9,22 Interestingly, we find that the inclusion of gap junctions in our coupled cell pair model had minimal influence on both the parameter regimes for automaticity and the characteristics of the spontaneous APs (i.e., the period duration) across nearly two orders of magnitude of gap junction conductance values. We expected this result for the case of identical cells, and, indeed, it was in fact trivially true. Yet, this was unexpected for the case of heterogeneous cells. Indeed, the properties of automaticity are essentially solely defined by the ephaptic-mediated mechanism of a shared cleft. We find that the only significant qualitative difference in dynamics in the presence of gap junctions was the suppression of asynchronous automaticity [i.e., conditions for which cell-1 firing APs and cell-2 exhibit subthreshold oscillations as described in Fig. 6(c)]. It may be the case that in the presence of this ephaptic-mediated automaticity occurring in a larger heterogeneous tissue comprised of many cells, gap junction coupling may play a larger role in the synchronization. Addressing this question is a focus of ongoing work.
Predictions from the current study suggest that ventricular automaticity requires a substantial fraction of current, carried by Kir2.1 channels, to be localized at the cell–cell junction membrane adjacent to the cleft. To our knowledge, the physiological value of this fraction has not been measured experimentally. However, recent evidence suggests that the Kir2.1 channel and the voltage-gated sodium channel (Nav1.5), carrying the current, may form a macromolecular complex such that the expression of these two channels is co-regulated.38 Measures of the sodium channel fraction at the junctional membrane are on the order of 50%–90%,39 which suggests that the fraction under normal conditions may be near but still below the regime required for persistent automaticity. This is consistent with the fact that ventricular automaticity, presenting as PVCs, is overall rare in healthy patients. However, we speculate that potassium channel reorganization, specifically enhanced junctional membrane localization, may be a pathological form of subcellular remodeling that occurs in heart disease that in turn promotes arrhythmias. To our knowledge, this redistribution of Kir2.1 channels has not been identified in disease states, but our study motivates such investigation. Similarly, dynamic changes in cleft volume may also regulate this mechanism of arrhythmia. Further, while the focus of this study is on ventricular myocytes, it is well established that ectopic beats in the atria contribute to the formation of atrial fibrillation40,41 such that similar mechanisms of enhanced automaticity may also occur in this setting.
Finally, we note the limitations of our study. While our cell pair model incorporates key details of ion channel subcellular distribution, this representation is still a simplification of the complex cardiac tissue structure: we assume that the cleft geometry is uniform and represented by a single compartment; however, our recent work has shown that the heterogeneous structure of the cleft can result in variability within the cleft, which in turn can impact ephaptic coupling.28 Further, while the cell pair model enabled a robust and thorough investigation of key cellular and structural properties, this model is a simplification of three-dimensional cardiac tissue structure. It is of interest to investigate how these processes governing automaticity may occur or differ in large tissues (i.e., thousands of coupled cells), in particular, tissues with heterogeneous ion channel distributions, as may occur during pathological remodeling. We speculate that gap junctional coupling may play a larger role in suppressing or maintaining automaticity in heterogeneous tissues (e.g., cells with different values of or clefts with different volumes). Simulations of larger tissues is a focus of future work.
Additionally, our study did not consider the role of ionic pumps and exchangers, in particular, the sodium–potassium ATPase, at the cell–cell junction, which would generally pump ions to oppose the cleft potassium accumulation that drives the automaticity. Interestingly, there is evidence that this pump is present on the junctional membrane,42 although to our knowledge, the relative fraction of the total pump flux at the junction has not been measured. We speculate that the presence and characteristics of automaticity will be highly dependent on the relative localization of and the sodium–potassium pump. Interestingly, this suggests a potential new and critical role for these pumps. In general, the primary role of pumps and exchangers is typically considered to be maintaining intracellular ionic homeostasis; here, our studies suggest that they may similarly play a role in maintaining homeostasis in restricted extracellular spaces, such as the intercellular cleft. Addressing these issues is a focus of ongoing work. Overall, while these limitations may account for quantitative differences, importantly, our simulations demonstrate that this mechanism of ephaptic-mediated enhanced ventricular automaticity is robust over a wide range of conditions.
ACKNOWLEDGMENTS
We acknowledge support from the National Institutes of Health (Grant No. R01-HL138003) (S.H.W.) and from the Simons Foundation (Grant No. 355173) (C.L.).
APPENDIX: SPONTANEOUS VS PACED DYNAMICS
1. Comparison of spontaneous and paced action potentials and currents
A comparison of the action potential and key ionic currents for spontaneous beats and the paced cell is shown in Fig. 9. The spontaneous activity ( , green) is reproduced from Fig. 2. The paced electrical activity (gray) is simulated for conditions of no junctional currents ( , for ) and periodic superthreshold square stimulus (1-ms duration) applied at a period comparable to the spontaneous activity (1.6 s). To compare ionic currents between cases with different distributions (i.e., currents localized on both the lateral segment and junctional membrane), we consider the sum of currents on both membranes for the two cases.
FIG. 9.
Comparison of spontaneous and paced electrical activity. The time series for the (a) lateral segment voltage, and the sum of the currents on the lateral segment and junctional membrane for (b) , (c) , and (d) for spontaneous (green, ) and paced (gray) electrical activity. Spontaneous activity exhibits gradual depolarization between beats and smaller magnitude , while paced activity exhibits a rapid action potential upstroke and large magnitude .
This comparison illustrates both similarities and differences. As illustrated in Fig. 2, the spontaneous activity exhibits a gradual elevation of the resting potential, while for the paced activity, the resting potential remains constant between beats. Most noticeably, the two cases exhibit significantly different sodium current ( ). In the paced cell, the applied stimulus drives a rapid activation of a large magnitude , which triggers the initial upstroke of the action potential. In contrast, for the spontaneous activity, contributes much less, as the gradual voltage increase between beats enhances voltage-dependent inactivation of , ultimately resulting in a much smaller magnitude . In both cases, the slow-inward calcium current is primarily responsible for maintaining the action potential plateau, as the action potential durations are similar between the two cases as well.
Contributor Information
Cheng Ly, Email: mailto:CLy@vcu.edu.
Seth H. Weinberg, Email: mailto:weinberg.147@osu.edu.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Ethics Approval
Ethics approval is not required.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Luo C.-H. and Rudy Y., “A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction,” Circ. Res. 68, 1501–1526 (1991). 10.1161/01.RES.68.6.1501 [DOI] [PubMed] [Google Scholar]
- 2.Silverman M. E. and Hollman A., “Discovery of the sinus node by Keith and Flack: On the centennial of their 1907 publication,” Heart 93, 1184–1187 (2007). 10.1136/hrt.2006.105049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang H., Holden A., Kodama I., Honjo H., Lei M., Varghese T., and Boyett M., “Mathematical models of action potentials in the periphery and center of the rabbit sinoatrial node,” Am. J. Physiol. Heart Circ. Physiol. 279, H397–H421 (2000). 10.1152/ajpheart.2000.279.1.H397 [DOI] [PubMed] [Google Scholar]
- 4.Severi S., Fantini M., Charawi L. A., and DiFrancesco D., “An updated computational model of rabbit sinoatrial action potential to investigate the mechanisms of heart rate modulation,” J. Physiol. 590, 4483–4499 (2012). 10.1113/jphysiol.2012.229435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ly C. and Weinberg S., “Analysis of heterogeneous cardiac pacemaker tissue models and traveling wave dynamics,” J. Theor. Biol. 459, 18–35 (2018). 10.1016/j.jtbi.2018.09.023 [DOI] [PubMed] [Google Scholar]
- 6.Weiss J. N., Karma A., Shiferaw Y., Chen P.-S., Garfinkel A., and Qu Z., “From pulsus to pulseless: The saga of cardiac alternans,” Circ. Res. 98, 1244–1253 (2006). 10.1161/01.RES.0000224540.97431.f0 [DOI] [PubMed] [Google Scholar]
- 7.Laurita K. R. and Rosenbaum D. S., “Mechanisms and potential therapeutic targets for ventricular arrhythmias associated with impaired cardiac calcium cycling,” J. Mol. Cell. Cardiol. 44, 31–43 (2008). 10.1016/j.yjmcc.2007.10.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tse G., “Mechanisms of cardiac arrhythmias,” J. Arrhythmia 32, 75–81 (2016). 10.1016/j.joa.2015.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Xie Y., Sato D., Garfinkel A., Qu Z., and Weiss J. N., “So little source, so much sink: Requirements for after-depolarizations to propagate in tissue,” Biophys. J. 99, 1408–1415 (2010). 10.1016/j.bpj.2010.06.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dukes J. W., Dewland T. A., Vittinghoff E., Mandyam M. C., Heckbert S. R., Siscovick D. S., Stein P. K., Psaty B. M., Sotoodehnia N., Gottdiener J. S. et al., “Ventricular ectopy as a predictor of heart failure and death,” J. Am. Coll. Cardiol. 66, 101–109 (2015). 10.1016/j.jacc.2015.04.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ahn M.-S., “Current concepts of premature ventricular contractions,” J. Lifestyle Med. 3, 26 (2013). [PMC free article] [PubMed] [Google Scholar]
- 12.Hodgkin A. L. and Huxley A. F., “A quantitative description of membrane current and its application to conduction and excitation in nerve,” J. Physiol. 117, 500–544 (1952). 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Livshitz L. M. and Rudy Y., “Regulation of Ca and electrical alternans in cardiac myocytes: Role of CAMKII and repolarizing currents,” Am. J. Physiol. Heart Circ. Physiol. 292, H2854–H2866 (2007). 10.1152/ajpheart.01347.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Poelzing S., Weinberg S. H., and Keener J. P., “Initiation and entrainment of multicellular automaticity via diffusion limited extracellular domains,” Biophys. J. 120, 5279–5294 (2021). 10.1016/j.bpj.2021.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kucera J. P., Rohr S., and Rudy Y., “Localization of sodium channels in intercalated disks modulates cardiac conduction,” Circ. Res. 91, 1176–1182 (2002). 10.1161/01.RES.0000046237.54156.0A [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tsumoto K., Ashihara T., Naito N., Shimamoto T., Amano A., Kurata Y., and Kurachi Y., “Specific decreasing of Na channel expression on the lateral membrane of cardiomyocytes causes fatal arrhythmias in Brugada syndrome,” Sci. Rep. 10, 2849 (2020). 10.1038/s41598-020-76681-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Weinberg S., “Ephaptic coupling rescues conduction failure in weakly coupled cardiac tissue with voltage-gated gap junctions,” Chaos 27, 093908 (2017). 10.1063/1.4999602 [DOI] [PubMed] [Google Scholar]
- 18.Nowak M. B., Greer-Short A., Wan X., Wu X., Deschênes I., Weinberg S. H., and Poelzing S., “Intercellular sodium regulates repolarization in cardiac tissue with sodium channel gain of function,” Biophys. J. 118, 2829–2843 (2020). 10.1016/j.bpj.2020.04.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Veeraraghavan R., Lin J., Hoeker G. S., Keener J. P., Gourdie R. G., and Poelzing S., “Sodium channels in the Cx43 gap junction perinexus may constitute a cardiac ephapse: An experimental and modeling study,” Pflüg. Arch. Eur. J. Physiol. 467, 2093–2105 (2015). 10.1007/s00424-014-1675-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Veeraraghavan R., Lin J., Keener J. P., Gourdie R., and Poelzing S., “Potassium channels in the Cx43 gap junction perinexus modulate ephaptic coupling: An experimental and modeling study,” Pflüg. Arch. Eur. J. Physiol. 468, 1651–1661 (2016). 10.1007/s00424-016-1861-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gourdie R. G., “The cardiac gap junction has discrete functions in electrotonic and ephaptic coupling,” Anat. Rec. 302, 93–100 (2018). 10.1002/ar.24036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cai D., Winslow R. L., and Noble D., “Effects of gap junction conductance on dynamics of sinoatrial node cells: Two-cell and large-scale network models,” IEEE Trans. Biomed. Eng. 41, 217–231 (1994). 10.1109/10.284940 [DOI] [PubMed] [Google Scholar]
- 23.Verheijck E. E., Wilders R., Joyner R. W., Golod D. A., Kumar R., Jongsma H. J., Bouman L. N., and Ginneken A. C. V., “Pacemaker synchronization of electrically coupled rabbit sinoatrial node cells,” J. Gen. Physiol. 111, 95–112 (1998). 10.1085/jgp.111.1.95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Katz B., Nerve, Muscle, and Synapse (McGraw-Hill, New York, 1966). [Google Scholar]
- 25.Greer-Short A., George S. A., Poelzing S., and Weinberg S. H., “Revealing the concealed nature of long-QT type 3 syndrome,” Circ.: Arrhythmia Electrophysiol. 10, e004400 (2017). 10.1161/CIRCEP.116.004400 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ivanovic E. and Kucera J. P., “Localization of Na channel clusters in narrowed perinexi of gap junctions enhances cardiac impulse transmission via ephaptic coupling: A model study,” J. Physiol. 599, 4779–4811 (2021). 10.1113/JP282105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nowak M. B., Poelzing S., and Weinberg S. H., “Mechanisms underlying age-associated manifestation of cardiac sodium channel gain-of-function,” J. Mol. Cell. Cardiol. 153, 60–71 (2021). 10.1016/j.yjmcc.2020.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moise N., Struckman H. L., Dagher C., Veeraraghavan R., and Weinberg S. H., “Intercalated disk nanoscale structure regulates cardiac conduction,” J. Gen. Physiol. 153, 371 (2021). 10.1085/jgp.202112897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ermentrout B., Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students (SIAM, 2002). [Google Scholar]
- 30.Doedel E. J., “Auto: A program for the automatic bifurcation analysis of autonomous systems,” Congr. Numer. 30, 25–93 (1981). [Google Scholar]
- 31.Wei N. and Tolkacheva E. G., “Interplay between ephaptic coupling and complex geometry of border zone during acute myocardial ischemia: Effect on arrhythmogeneity,” Chaos 30, 033111 (2020). 10.1063/1.5134447 [DOI] [PubMed] [Google Scholar]
- 32.Nowak M. B., Veeraraghavan R., Poelzing S., and Weinberg S. H., “Cellular size, gap junctions, and sodium channel properties govern developmental changes in cardiac conduction,” Front. Physiol. 12, 731025 (2021). 10.3389/fphys.2021.731025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu X., Hoeker G. S., Blair G. A., King D. R., Gourdie R. G., Weinberg S. H., and Poelzing S., “Hypernatremia and intercalated disc edema synergistically exacerbate long-QT syndrome type 3 phenotype,” Am. J. Physiol. Heart Circ. Physiol. 321, H1042–H1055 (2021). 10.1152/ajpheart.00366.2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tveito A., Jæger K. H., Kuchta M., Mardal K.-A., and Rognes M. E., “A cell-based framework for numerical modeling of electrical conduction in cardiac tissue,” Front. Phys. 5, 1232 (2017). 10.3389/fphy.2017.00048 [DOI] [Google Scholar]
- 35.Joseph K. Y., Liang J. A., Weinberg S. H., and Trayanova N. A., “Computational modeling of aberrant electrical activity following remuscularization with intramyocardially injected pluripotent stem cell-derived cardiomyocytes,” J. Mol. Cell. Cardiol. 162, 97–109 (2022). 10.1016/j.yjmcc.2021.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.MacDonald R., Hsu D., Mann J., Jr., and Sperelakis N., “An analysis of the problem of K accumulation in the intercalated disk clefts of cardiac muscle,” J. Theor. Biol. 51, 455–473 (1975). 10.1016/0022-5193(75)90074-0 [DOI] [PubMed] [Google Scholar]
- 37.Sperelakis N. and McConnell K., “Electric field interactions between closely abutting excitable cells,” IEEE Eng. Med. Biol. Mag. 21, 77–89 (2002). 10.1109/51.993199 [DOI] [PubMed] [Google Scholar]
- 38.Milstein M. L., Musa H., Balbuena D. P., Anumonwo J. M., Auerbach D. S., Furspan P. B., Hou L., Hu B., Schumacher S. M., Vaidyanathan R. et al., “Dynamic reciprocity of sodium and potassium channel expression in a macromolecular complex controls cardiac excitability and arrhythmia,” Proc. Natl. Acad. Sci. U.S.A. 109, E2134–E2143 (2012). 10.1073/pnas.1109370109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lin X., Liu N., Lu J., Zhang J., Anumonwo J. M., Isom L. L., Fishman G. I., and Delmar M., “Subcellular heterogeneity of sodium current properties in adult cardiac ventricular myocytes,” Heart Rhythm 8, 1923–1930 (2011). 10.1016/j.hrthm.2011.07.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nattel S., Burstein B., and Dobrev D., “Atrial remodeling and atrial fibrillation: Mechanisms and implications,” Circ.: Arrhythmia Electrophysiol. 1, 62–73 (2008). 10.1161/CIRCEP.107.754564 [DOI] [PubMed] [Google Scholar]
- 41.Wijesurendra R. S. and Casadei B., “Mechanisms of atrial fibrillation,” Heart 105, 1860–1867 (2019). 10.1136/heartjnl-2018-314267 [DOI] [PubMed] [Google Scholar]
- 42.Vermij S. H., Abriel H., and van Veen T. A., “Refining the molecular organization of the cardiac intercalated disc,” Cardiovasc. Res. 113, 259–275 (2017). 10.1093/cvr/cvw259 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.