Abstract
The Common Spatial Pattern (CSP) algorithm is the most widely used method for decoding Electroencephalography (EEG) signals from motor imagery (MI) paradigm. However, due to the inter-subject variability, the CSP algorithm heavily relies on the selection of filter bands and extensive analytical processing time required to build an effective model, which has been a challenge in current research. In this paper, we propose a narrow filter bank CSP (NFBCSP) algorithm, which automatically determines the optimal narrow band for two-class motor imagery by band search tree, and a high-performance classification model dedicated to each subject can be obtained in a short time for online processing or further offline analysis. The optimal narrow band is combined with the CSP algorithm to extract the dynamic features in the EEG signals. For the multi-class motor imagery task, it is first transformed into multiple One-Versus-Rest (OVR) tasks and determines the corresponding optimal narrow bands. After extracting the features of each optimal narrow band separately, the Deep Convolutional Neural Network (DCNN) is used for the fusion of band features and classification of multi-class motor imagery. Finally, we verified our method using two different motor imagery datasets, the BCI-VR dataset with two classes of motor imagery and the BCI Competition IV dataset 2a with four classes of motor imagery. The experimental results show that the proposed method achieves an average classification accuracy of 86.43% for the two-class motor imagery task, and 76.87% for the four-class motor imagery task, which outperforms other recent methods.
Supplementary Information
The online version contains supplementary material available at 10.1007/s11571-021-09721-x.
Keywords: Motor imagery, Narrow band, Deep Convolutional Neural Network (DCNN), Feature fusion
Introduction
Motor imagery (MI) is a very important BCI paradigm which has been widely applied in motor rehabilitation and controlling for disabled patients (Wang et al. 2017; Ortner et al. 2012; Lazarou et al. 2018). Several methods have been proposed for EEG-based MI feature extraction, the most classical of which is the CSP algorithm (Kumar et al. 2016), but the effectiveness of the CSP algorithm depends heavily on the selection of the filter band and is only effective in resolving the two-class motor imagery task. In order to improve the classification accuracy, various variants of the CSP algorithm have been proposed, such as the filter bank CSP (FBCSP) algorithm (Ang et al. 2008) and the discriminative filter bank CSP (DFBCSP) algorithm (Thomas et al. 2009). However, these methods still focus on the extraction of static energy features, neglecting the dynamics of the EEG signals during the execution of motor imagery, and even show a decrease in classification accuracy when applied to different subjects.
In addition, recent works for improving CSP performances are employed Convolutional Neural Networks (CNN). EEG signals processing based on Convolutional Neural Networks can be divided into two main categories, raw signal input networks and feature input networks (Wu et al. 2019). The raw signal input network is an end-to-end model where the raw EEG signal is input directly, with (or without) only a little pre-processing. It can automatically learn useful features from raw data, but it is difficult to get satisfactory results for small datasets, and for datasets under different tasks, the model needs to be tuned with relevant background knowledge. By contrast, the feature input network is more suitable for small datasets, and its processing of the EEG signals is divided into two parts: firstly, the EEG signals are converted into feature vectors by feature extraction methods such as wavelet transform and spatial filter, and then the feature vectors are used as input to the CNN for training and classification.
It has been shown (Pfurtscheller et al. 2006; Higashi and Tanaka 2012) that different motor imagery tasks will excite energy on different channels and frequency bands, while the optimal filter band for the same motor imagery task varies among subjects, therefore, it is prone to lose valid information that depends on the subject and the motion patterns when extracting static features. The currently proposed band selection algorithms are determined by grid search, which is still very computationally intensive even for small datasets. Olivas-Padilla and Chacon-Murguia Olivas-Padilla and Chacon-Murguia (2019) proposed a pruning approach to search for pruning by bi-directional iteration and assuming monotonicity in the classification accuracy of EEG signals. Although this method improves the efficiency of the search, the frequency bands obtained by this method are subject to large errors since the classification accuracy of the EEG signals does not show monotonicity as the frequency bands change. To solve this problem, we combine different filter bands in the feature extraction stage to extract the dynamic energy features in the EEG signals by the CSP algorithm, which improves the classification accuracy of EEG signals.
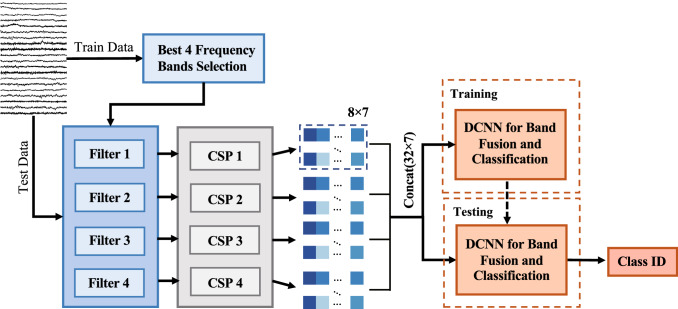
In this paper, we propose a narrow filter bank CSP (NFBCSP) algorithm based on a band search tree, which argues that narrow bands with a step length less than or equal to 4 Hz can remove redundant information to the maximum and retain the most distinguishable dynamic features. Most of the current studies are devoted to finding a better feature selection and feature fusion scheme in the same feature space, such as the L1-Norm and Dempster-Shafer fusion-based algorithms proposed by Jin et al. (2020). However, it relies heavily on the feature space being used, and lacks generalization capability in real scenes. In contrast, the NFBCSP algorithm proposed in this paper is dedicated in selecting the appropriate feature space through dynamic energy features at different frequency bands, which has higher generalization ability in comparison.
Through the NFBCSP algorithm, researchers can obtain the optimal narrow band by fast iteration and construct a high-performance classification model exclusively for each subject, which greatly reduces the time for tuning and data analyzing. Moreover, due to the extraction of dynamic features that distinguish between subjects and motion patterns, the classification accuracy is also greatly improved.
For the multi-class motor imagery task, in order to further improve the classification accuracy, we propose a multi-band feature fusion model based on Deep Convolutional Neural Network by intra-band and inter-band feature fusion on the basis of optimal narrow-band. We apply the proposed method above to two motor imagery datasets, the BCI-VR two-class motor imagery dataset and the BCI Competition IV dataset 2a (Tangermann et al. 2012), which were compared with the results obtained by other recent methods.
Dataset
Two datasets were used for this work, one is the motor imagery dataset collected by the BCI-VR system, which consists of two different motor imagery tasks, left hand grasping and right hand grasping. The other is the BCI Competition IV dataset 2a, which consists of four classes of motor imagery tasks, left hand, right hand, both feet and tongue.
Acquisition of the BCI-VR dataset
Twelve healthy college students, including four females and eight males, with a mean age of 22 (±2) years, were recruited to participate in the experiment. To ensure that the subjects had a good mental state, the experiment was conducted from 9:00 to 11:00 am. During the experiment, subjects sat quietly in a chair in front of a computer screen, wearing an EEG cap and Head Mount Display (HMD). Simulation was presented from a virtual reality environment, including a hospital scene and a pair of virtual arms, and subjects performed motor imagery based on textual cues in the virtual reality, as well as feedback from the virtual arms, as shown in Fig. 1. The study was reviewed and approved by the institutional Ethical Review Committee at Saitama Institute of Technology and the protocol number is 2018-01. Signed informed consent was obtained from each participant.
Fig. 1.

Stimulating presentation of virtual reality scenes
NeuroScan EEG signal acquisition device was used to acquire the subject’s EEG signals, and 64 electrodes were evenly distributed around the motor cortex of the subject’s scalp according to the 10/20 international standard system (Homan et al. 1987), with the grounded electrode REF as the reference electrode, and using a sampling frequency of 250 Hz.
While some channel selection algorithms, such as position priori weight permutation entropy (PPWPE) (Sun et al. 2021), can be effective in improving the signal-to-noise ratio of EEG, it has been shown that small differences exist in the classification accuracy using different numbers of electrodes (Tam et al. 2011; Lo et al. 2016). Most of the currently designed MI-BCI systems require 22–118 electrodes, and to be consistent with the BCI Competition dataset, only the 22 electrodes in the red part of Fig. 2 were used in the experiment.
Fig. 2.

Layout of electrodes. Red circles indicate the used electrodes in this study
Experimental procedure
To avoid eye fatigue caused by wearing the HMD for a long time, each data collection lasted a total of 47 min. The data collection was divided into 8 sessions, each lasting 5 min, with a one-minute break after each session. Each session consists of 30 trials with a duration of 10 s per trial. During each trial, the subjects were in a relaxed state with a rest period of 0–3s in order to allow them proper rest. Since the stimulus presentation is shown through virtual reality, it takes about 2.5 s for the arm to complete the gripping action of the simulation, therefore, 3s-6s are devoted to the presentation of visual stimuli, where the subject can see either a left-handed or right-handed grip in virtual reality. Finally, to ensure the subjects had enough time to complete the motor imagery, 6s-10s were the period of motor imagery, during which subjects imagined their left or right hand grip based on the motion they saw during the stage of stimulus presentation. The experimental paradigm for data collection is shown in Fig. 3.
Fig. 3.
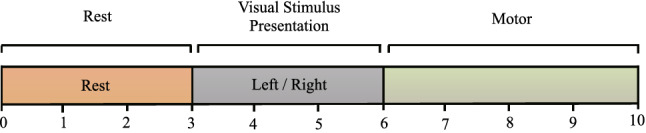
Experimental paradigm for data acquisition
Dataset segmentation and pre-processing
In the BCI Competition IV dataset 2a, 9 different subjects performed 4 classes of motor imagery in 2 experiments. Each experiment consisted of 288 trials, 72 trials of each class of motor imagery, and 3 s of motor imagery duration in each trial. The 288 trials from the previous experiment were used as the training set, and the 288 trials from the subsequent experiment were used as the test set. The BCI-VR motor imagery dataset consisted of the EEG signals acquired from 12 subjects, with a total of 240 valid samples per subject and a duration of 4 s of motor imagery in each trial. 80% of the total dataset was used for training and 20% as a test for accuracy evaluation, data division was determined by 10-fold cross-validation.
In this paper, the EEG signal was preprocessed using the independent component analysis (ICA) method, and the components with obvious blink artifacts and muscle artifacts were analyzed by independent component topographies. After removing the components with artifacts, the remaining components are reconstructed and finally a band-pass filter is applied to the reconstructed EEG signal.
Modified CSP algorithm using optimal narrow band
Most researchers tend to choose the filter band from 7–32 Hz because the Mu and Beta bands lie within this range (Wang et al. 2019; Pfurtscheller and Neuper 2001). It has been experimentally concluded that for different subjects, the energy will be excited in different bands which are not limited to the Mu and Beta bands. Therefore, using fixed filter bands does not effectively remove redundant information, and may even result in the loss of valid information. This paper uses narrow bands to extract dynamic features that depend on the subject and motion patterns, the work of Barry et al. (2007) has shown that narrow bands have an effect on Event-related Potentials (ERP) signals generated by different stimuli, and this paper will further demonstrate the validity of narrow bands for motor imagery.
Feature extraction by CSP algorithm
The CSP algorithm maps the EEG signals to a subspace by constructing a spatial filter that maximizes the difference in variance between the two classes after mapping.
Assume that the band-pass filtered EEG signals is denoted as , where C indicates the number of channels and N indicates the number of samples. The training data were divided into 2 classes, and . indicates the EEG signals corresponding to the samples in the different classes, and indicates the class label.
Denote as , . The time average of is expressed as , and the time variance of after using a spatial filter is denoted as follows.
| 1 |
The maximum value of the variance difference equals the minimum value of one class with variance sum fixed, and the constraints are expressed as follows.
| 2 |
Define as the covariance matrix of the EEG signals labeled d. is expressed as follows.
| 3 |
After introducing the covariance matrix, Eq. (2) can be denoted as follows.
| 4 |
Equation (4) for solving the spatial filter can be derived from Eq. (5) for solving the generalized eigenvalue. By solving the 2r eigenvectors corresponding to the smallest r and the largest r generalized eigenvalues, the spatial filter is constructed.
| 5 |
The EEG signals is mapped to a subspace using spatial filter and the features of the mapped signal are extracted, e.g., variance features are expressed as follows.
| 6 |
represents the eigenvector of the EEG signals that can be used as input to the classifier along with other time-frequency domain features to obtain the classification result.
Band search tree
We propose a method to acquire the optimal narrow band by combining the narrow band with the CSP algorithm. The broadband 0.1–32 Hz is determined as the root node of the band search tree and divided equally into four bands, which are 0.1–8 Hz, 8–16 Hz, 16–24 Hz, and 24–32 Hz. After band-pass filtering through these four bands, features are extracted using the CSP algorithm and then classified using a Support Vector Machine (SVM) (Suykens and Vandewalle 1999) model with linear kernels. The Support Vector Machine is a supervised learning model which finds the hyperplane that best separates one class of data from another, while providing a faster model training speed than neural networks.
Using 80% of the training set as training data and 20% as validation data, the classification accuracy of the four bands is obtained from the SVM model. Find the band with the highest classification accuracy among the four bands and the band adjacent to it with higher classification accuracy, use these two adjacent bands together as the parent node, and divide them into four bands with smaller steps for the next round of search. At the end of each search round, the global classification accuracy is updated to the maximum value, and the band information corresponding to the maximum value is saved. The first 4 rounds of band steps are 8Hz, 4Hz, 2Hz, and 1Hz, and the last round merges the 4th round’s band with step 1 to acquire narrow bands with steps of 3Hz and 2Hz. The number of band iterations for the entire process is 19, which is a significant improvement over the 528 iterations required using the grid search, and the classification accuracy is almost as high as before. The structure of the band search tree is shown in Fig. 4.
Fig. 4.
Band search tree architecture. Dark blue indicates the band with the highest accuracy in the current round, while light blue indicates the band adjacent to the highest accuracy band with higher accuracy in the current round. Gray indicates the removed bands, which will not be calculated in the next round. Orange indicates the band with the highest classification accuracy during the entire search process, and is output at the end of the search
Algorithm 1 describes the process of searching for the optimal narrow band. and denote the lower and upper frequencies of the optimal narrow band, denotes the classification accuracy of the optimal narrow band, denotes the starting band of the current round, step denotes the step size of each band in the current round, and is used to save the classification accuracy of the four bands obtained in each round of search. The function adj(X, Y) is used to return the subscript of the larger value adjacent to Y in the X array, and idx(X, Y) is used to return the subscript of Y in the X array. The nfb is a classification discriminative model which uses the CSP algorithm to extract the features of the filtered EEG signal and classify it using the SVM with a linear kernel.

Comparing the difference between the optimal narrow band and the 7-32Hz broadband for one of the subjects’ EEG signals, the superimposed average effect of C3/C4 channels is shown in Fig. 5. After using the optimal narrow band, the EEG signals from left and right hand motor imagery are more distinguishable in the time-domain, which proves the effectiveness of the narrow band for extracting dynamic energy features.
Fig. 5.
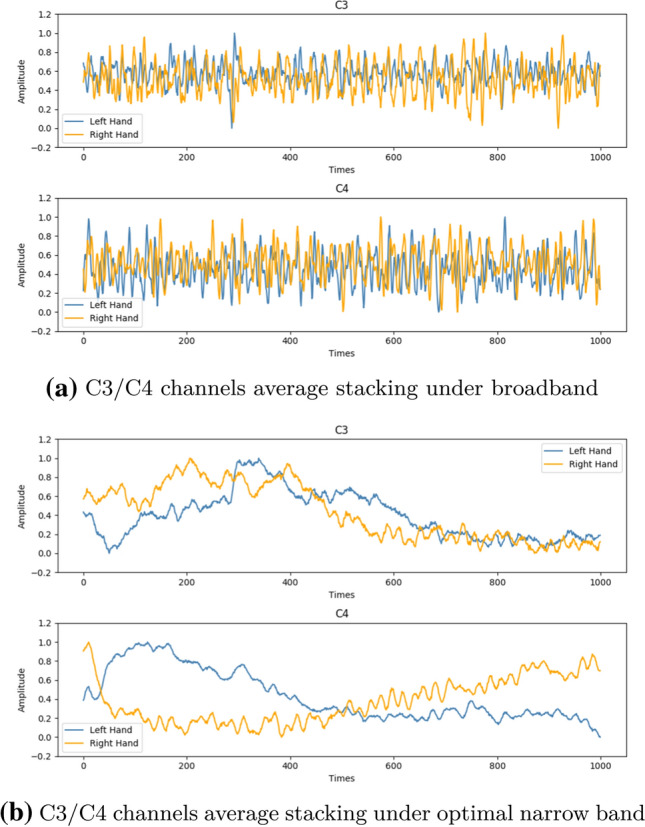
Comparisons on the average stacking with different filter bands using C3/C4 channels
Application of optimal narrow band in online systems
Since the acquisition of the optimal narrow band requires multiple iterations, it is not easy to acquire the optimal narrow band in the processing of the online system in real time, even though only 19 iterations are required.
We acquired the EEG signals of five subjects performing left and right hand motor imagery tasks at different times using the BCI-VR system, and found that the same subject had similar optimal narrow band in two different experiments, as shown in Table 1.
Table 1.
The optimal narrow band of the EEG signals for motor imagery acquired at different times by different subjects
| Subjects | Day1 (Hz) | Day2 (Hz) |
|---|---|---|
| S1 | 11–13 | 11–12 |
| S2 | 11–14 | 10–13 |
| S3 | 22–24 | 22–24 |
| S4 | 12–13 | 11–12 |
| S5 | 24–28 | 26–29 |
Day1 and Day2 are one day apart, and both are in the morning
The experiment shows that in practical applications, the optimal narrow band can be obtained from offline data acquisition, and directly applied to subsequent online systems. Compared with traditional discrimination models, the use of the optimal narrow band can greatly improve the classification accuracy of the EEG signals, which is dependent on the dynamic features of the subjects, and help to accelerate the progress of research such as the online rehabilitation system for motor imagery.
Multi-band feature fusion based on DCNN
Narrow bands for multi-class task
Extending the biclass task to the multiclass task, experiments were conducted using the BCI Competition IV dataset 2a.
The experiment shows that the optimal narrow band for the same category of motor imagery varies greatly among subjects. We analyzed the EEG signals of subjects S1 and S3 in the BCI Competition dataset and found that for subject S1, the optimal narrow band for the left hand with other three classes was 25–26 Hz, while the optimal narrow band for the right hand with other three classes was 12–16Hz. Subject S3 is almost opposite to the above, with the optimal narrow band of 12–13 Hz for the left hand with other three classes, and the optimal narrow band of 20–24 Hz for the right hand with other three classes. Such differences show that in the multiclass motor imagery task, it is difficult to extract highly distinguishable features from a single filter band, while using multiple narrow bands to form a filter bank can extract more discriminating dynamic features compared to a single filter band. At the same time, for the same type of motor imagery task, different subjects need to select different bands individually to maximize the classification performance.
For the four classes of motor imagery task, we construct four OVR classifiers. For each classifier, a certain kind of motor imagery is considered as the first class and all others are considered as the second class, while an optimal narrow band is determined. Since the ratio of the first and second class is 1:3, which is an unbalanced number of classes, F1 Score is used instead of accuracy as a model evaluation metric to optimize the model in the process of determination of the optimal narrow band. For each of the four optimal narrow bands, a spatial filter is constructed. The EEG signals is projected to the subspace with the highest discrimination by the spatial filter, and the eigenvectors corresponding to the first four and the last four eigenvalues are extracted. All algorithms are implemented with python 3.7 and tensorflow 1.15.3.
The input of CNN
The traditional CSP algorithm only acquires the time variance of the EEG signals after mapping by a spatial filter as a feature, but we observe that the EEG signals in the subspace are significantly different in the time and frequency domain. Therefore, for the signal after mapping in subspace, the time domain features are represented by the maximum, minimum, mean, and standard deviation, and the frequency domain features are represented by the frequency mean, frequency variance, and frequency entropy.
The frequency mean is expressed as follows.
| 7 |
denotes the spectral map after Fast Fourier Transform and N denotes half of the highest frequency. The frequency variance is expressed as follows.
| 8 |
The frequency entropy is expressed as follows.
| 9 |
For each EEG signals after the optimal narrow band filtering, four feature matrices are acquired, and the four feature matrices are vertically cascaded to generate a result matrix with dimension as the input of DCNN, finally the Deep Convolutional Neural Network is used to achieve band fusion, as shown in Fig. 6.
Fig. 6.
Multi-Band feature fusion by Deep Convolutional Neural Network (DCNN)
Feature fusion
A feature matrix is obtained as the input to the DCNN after dimensional conversion, and the whole network is divided into three blocks in order to fuse the band features.
The first block contains two convolutional filters with kernel sizes of and , which are used to fuse intra-band features while reducing the size of the feature map. The second block uses convolutional filters with kernel size and to fuse inter-band features, after the second block, the dimension in which the number of features is compressed to 1. Since the input data has already been pre-extracted with features, no pooling layer is added to the entire network, and the network is down-sampled directly through the convolutional layer to enhance the learning capability of the network. Normalization operations are performed on the fused features and input to the third block. The third block is the full connection layer for classification, and to avoid overfitting, dropout layer is used with a rate of 0.5.
In the experiment, we compared the effects of different activation functions, which showed that the Rectified Linear Unit (ReLU) (Hara et al. 2015) activation function performed better in the classification. ReLU is a nonlinear activation function that prevents the gradient from vanishing and makes the network sparse compared to other activation functions, while accelerating the training speed of the network. Therefore, in this paper, the ReLU activation function is applied to the convolutional and fully connected layers. The details of the whole network structure are shown in Fig. 7.
Fig. 7.
Details of intra-band and inter-band feature fusion implemented by DCNN
The network is trained using a cross-entropy loss function, defined as , where p is the target distribution and q is the observed distribution. The network was optimized using Adam optimizer (Kingma and Ba 2014) with learning rate of 1e-3 and decay weights of 1e-7. The normal distribution with zero mean and unit variance was used to initialize the convolutional layer weights, the batch normalization layer was initialized using 1, and the batch size was 16.
Results
The experiment was performed using the BCI-VR dataset and the BCI Competition IV dataset 2a. For the BCI-VR dataset, experiments were conducted using the broadband CSP, FBCSP, DeepConvNet (Schirrmeister et al. 2017), EEGNet (Lawhern et al. 2018), and NFBCSP proposed in this paper, with the test set accounting for 20% of the total dataset, and 10-fold cross-validation was applied for performance analysis. For the BCI Competition IV dataset 2a, the results were evaluated by two metrics, classification accuracy and kappa coefficient (McHugh 2012), which were compared with results obtained from other recent work.
The Kappa coefficient is calculated based on the confusion matrix, which can be used to check the consistency of the results as well as to indicate the classification accuracy. Denote the classification accuracy as , the number of real samples as in each class, the number of predicted samples as in each class, where c denotes the number of classes and the number of samples in the overall class as n. Define as follows.
| 10 |
The Kappa coefficient expression is shown as follows.
| 11 |
The results obtained for each algorithm in the BCI-VR two-class motor imagery dataset are shown in Table 2, where the bolded font indicates the best performance of that subject among all the algorithms compared. The broadband CSP uses 7–32 Hz band-pass filter, FBCSP1 uses 9 non-overlapping filter banks within 4–40 Hz, each filter step is 4 Hz, and FBCSP2 uses 6 non-overlapping filter banks within 4–40 Hz, each filter step is 6Hz. Compared with other classical algorithms, the NFBCSP algorithm has significantly improved the average classification accuracy as well as the average deviation, and most of the subjects achieved the highest classification accuracy.
Table 2.
Comparison of classification accuracy (%) between NFBCSP algorithm and other algorithms on the BCI-VR two-class motor imagery dataset
| Subjects | CSP | FBCSP 1 | FBCSP 2 | EEGNet | DeepConvNet | NFBCSP | Narrow-Band (Hz) |
|---|---|---|---|---|---|---|---|
| S1 | 78.33 | 84.58 | 81.46 | 75.21 | 75.01 | 90.21 | 12–13 |
| S2 | 70.42 | 75.52 | 72.92 | 65.42 | 78.33 | 81.88 | 1–4 Hz |
| S3 | 78.13 | 80.73 | 84.79 | 80.83 | 86.67 | 87.70 | 11–14 |
| S4 | 59.58 | 68.96 | 65.63 | 71.87 | 73.75 | 83.33 | 11–12 |
| S5 | 91.25 | 92.50 | 91.66 | 88.12 | 88.12 | 97.71 | 15–17 |
| S6 | 59.17 | 73.33 | 66.88 | 64.79 | 74.38 | 80.83 | 11–12 |
| S7 | 75.01 | 79.79 | 80.63 | 71.25 | 78.75 | 81.67 | 26–28 |
| S8 | 78.33 | 93.54 | 91.25 | 84.37 | 92.50 | 95.00 | 10–12 |
| S9 | 93.45 | 96.88 | 97.08 | 93.54 | 94.37 | 95.83 | 13–16 |
| S10 | 59.58 | 68.13 | 67.08 | 71.87 | 75.21 | 79.79 | 11–14 |
| S11 | 70.21 | 88.96 | 85.63 | 77.70 | 82.95 | 86.30 | 22–24 |
| S12 | 67.29 | 74.58 | 71.04 | 59.58 | 70.21 | 76.88 | 90 12–13 |
| Mean | 73.40 | 81.46 | 79.67 | 75.38 | 80.85 | 86.43 | |
| Std | 10.94 | 9.39 | 10.35 | 9.62 | 7.59 | 6.61 |
The experiments showed that most of the subjects’ optimal narrow bands were concentrated in the and bands. The optimal narrow band of S2 was 1–4 Hz, probably caused by the 22 channels selected in the experiments did not contain its primary energy information, therefore, the future study can redetermine the optimal narrow band through the channel selection algorithm for subjects with anomalies in the optimal narrow band.
To further demonstrate the effectiveness of the NFBCSP algorithm in the classification of two-class motor imagery task, the four-class motor imagery task in the BCI Competition IV dataset 2a were transformed into 6 two-class motor imagery tasks. The classification accuracy was evaluated using the NFBCSP algorithm by comparing it with the RoCSP-SRIT2NFIS algorithm (Das et al. 2016), which currently performs best on the BCI Competition IV dataset 2a, and the performance analysis of the 6 two-class motor imagery tasks is shown in Table 3. The experiment shows that the motor imagery task with the highest average classification accuracy is the left hand and foot, and the average classification accuracy of the NFBCSP algorithm proposed in this paper is about 1.53% higher than the RoCSP-SRIT2NFIS algorithm, which further demonstrates the effectiveness of the NFBCSP algorithm for the two-class motor imagery task.
Table 3.
Classification accuracy (%) of the RoCSP-SRIT2NFIS algorithm and the NFBCSP algorithm for 6 two-class motor imagery tasks in the BCI Competition IV dataset 2a
| Subjects | Left vs Right | Left vs Foot | Left vs Tongue | Right vs Foot | Right vs Tongue | Foot vs Tongue | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RoCSP | Proposed | RoCSP | Proposed | RoCSP | Proposed | RoCSP | Proposed | RoCSP | Proposed | RoCSP | Proposed | |
| S1 | 93.06 | 91.67 | 99.31 | 97.92 | 99.31 | 97.92 | 100.00 | 97.22 | 100.00 | 98.61 | 78.47 | 81.94 |
| S2 | 68.75 | 65.28 | 83.33 | 90.97 | 73.61 | 83.33 | 84.03 | 96.53 | 72.92 | 79.86 | 79.86 | 94.44 |
| S3 | 97.22 | 96.53 | 95.83 | 100.00 | 96.53 | 97.22 | 95.83 | 97.22 | 99.31 | 99.31 | 79.17 | 95.83 |
| S4 | 75.00 | 77.78 | 90.28 | 90.97 | 92.36 | 92.36 | 90.97 | 91.67 | 88.89 | 87.50 | 73.61 | 80.56 |
| S5 | 65.97 | 93.75 | 70.83 | 77.08 | 78.47 | 83.33 | 72.92 | 72.92 | 77.08 | 84.03 | 75.00 | 68.75 |
| S6 | 72.22 | 70.14 | 72.22 | 79.86 | 75.00 | 72.92 | 70.83 | 77.08 | 74.31 | 78.47 | 75.00 | 75.00 |
| S7 | 86.11 | 81.25 | 98.61 | 97.22 | 97.22 | 94.44 | 99.30 | 100.00 | 98.61 | 97.92 | 86.11 | 84.72 |
| S8 | 97.22 | 96.53 | 91.67 | 93.75 | 96.53 | 92.36 | 90.28 | 88.89 | 91.67 | 88.19 | 90.28 | 82.64 |
| S9 | 93.75 | 90.28 | 97.92 | 92.36 | 97.92 | 99.31 | 89.58 | 84.72 | 95.83 | 89.58 | 95.13 | 93.75 |
| Mean | 83.26 | 84.80 | 88.89 | 91.13 | 89.66 | 90.35 | 88.19 | 89.58 | 88.74 | 89.27 | 81.40 | 84.18 |
| Std | 12.03 | 11.01 | 10.42 | 7.41 | 10.10 | 8.25 | 9.93 | 9.04 | 10.48 | 7.45 | 7.06 | 8.66 |
For the four-class task, the four-class task is transformed into 4 two-class tasks, and determine the optimal narrow band for each two-class task separately with band-pass filtering. Using the CSP algorithm to extract features from the filtered signal, and feature fusion is performed using the DCNN architecture proposed in Sect. 4. Table 4 shows the comparison of the performance between the proposed method in this paper and the method proposed by other work, which includes the results of the competition winner. The average classification accuracy of the proposed method was 76.87% with an average kappa coefficient of 0.69, which is an improvement over the other methods with different degrees and has less mean deviation.
Table 4.
Comparison of classification accuracy and kappa coefficients of the NFBCSP algorithm with other recent algorithms on the BCI Competition IV dataset 2a
| Subjects | Kappa coefficients | Classification accuracy(%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Winer | Ank et al. (Ang et al. 2012) | Sakhavi et al. (Sakhavi et al. 2018) | Raza et al. (Raza et al. 2016) | Sharba et al. (Sharbaf et al. 2017) | Proposed | Aghaei et al. (Aghaei et al. 2015) | Yang et al. (Yang et al. 2015) | Sakhavi et al. (Sakhavi et al. 2015) | Liao et al. (Liao et al. 2020) | Proposed | |
| S1 | 0.68 | 0.78 | 0.83 | 0.88 | 0.75 | 0.85 | 67.88 | 77.14 | 80.55 | 88.60 | 88.39 |
| S2 | 0.42 | 0.41 | 0.54 | 0.22 | 0.31 | 0.57 | 42.18 | 49.82 | 53.82 | 55.70 | 67.71 |
| S3 | 0.75 | 0.76 | 0.87 | 0.88 | 0.82 | 0.88 | 77.87 | 80.41 | 84.72 | 86.70 | 90.63 |
| S4 | 0.48 | 0.53 | 0.56 | 0.39 | 0.56 | 0.64 | 51.77 | 53.88 | 64.58 | 71.00 | 73.61 |
| S5 | 0.40 | 0.42 | 0.50 | 0.53 | 0.47 | 0.59 | 50.17 | 65.47 | 59.03 | 66.50 | 69.09 |
| S6 | 0.27 | 0.19 | 0.27 | 0.33 | 0.38 | 0.43 | 45.97 | 48.70 | 44.10 | 56.00 | 56.94 |
| S7 | 0.77 | 0.80 | 0.86 | 0.38 | 0.75 | 0.87 | 87.50 | 81.37 | 84.03 | 88.40 | 89.93 |
| S8 | 0.75 | 0.74 | 0.78 | 0.85 | 0.74 | 0.74 | 85.79 | 84.39 | 86.80 | 80.09 | 79.86 |
| S9 | 0.61 | 0.54 | 0.73 | 0.81 | 0.67 | 0.68 | 76.31 | 82.29 | 77.77 | 77.10 | 75.69 |
| Mean | 0.57 | 0.57 | 0.66 | 0.58 | 0.61 | 0.69 | 65.05 | 69.27 | 70.60 | 74.60 | 76.87 |
| Std | 0.17 | 0.20 | 0.19 | 0.25 | 0.17 | 0.15 | 16.73 | 14.08 | 14.71 | 12.25 | 10.83 |
It can be found that extracting the dynamic energy features of different subjects under different motor imagery tasks by using narrow filter band can effectively improve the classification accuracy, which proves the effectiveness of narrow filter band for motor imagery. For the biclass motor imagery task, after using CSP algorithm to extract the dynamic features of the optimal narrow band, it is still able to maintain high classification performance by directly applying machine learning algorithms, such as Support Vector Machines, Linear Discriminant Analysis (LDA) (Balakrishnama and Ganapathiraju 1998), etc. For the multi-class motor imagery task, DCNN can be used to fuse and classify multiple band features, but the feature selection scheme still needs to be considered, while the choice of features directly determines the structure of the network.
Conclusion
In this paper, we propose a narrow filter bank CSP (NFBCSP) algorithm, which automatically determines the optimal narrow band by using a band search tree, and uses the CSP algorithm to extract dynamic energy features in the EEG signals that depend on subjects and motion patterns. For the multi-class motor imagery task, the DCNN architecture is designed based on the NFBCSP algorithm, using convolutional operations to fuse and classify features from multiple narrow bands. The experiments show that for the two datasets used in this paper, the average classification accuracy of the left and right hand motor imagery task reached 86.43%, and the average classification accuracy of the four-class motor imagery task reached 76.87%, which is a significant improved than other algorithms. The experiment also shows that the optimal narrow band of motor imagery for the same subject at different times is similar, therefore, it is also an effective potential solution for implementing online systems. Since our method requires the selection of features in advance to construct the feature map as input to the neural network, it may lead to bias in the selection of features for different subjects. Although the two datasets used in this paper have significantly improved the average classification accuracy, there are still some subjects whose classification performance is worse than other methods, which means that better feature selection and band fusion methods are directions for future works.
Supplementary Information
Acknowledgements
This work was supported by National Key R & D Program of China for Intergovernmental International Science and Technology Innovation Cooperation Project (2017YFE0116800), National Natural Science Foundation of China (Grant No.U20B2074, U1909202), Science and Technology Program of Zhejiang Province (2018C04012), Key Laboratory of Brain Machine Collaborative Intelligence of Zhejiang Province (2020E10010).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Aghaei AS, Mahanta MS, Plataniotis KN. Separable common spatio-spectral patterns for motor imagery BCI systems. IEEE Trans Biomed Eng. 2015;63(1):15–29. doi: 10.1109/TBME.2015.2487738. [DOI] [PubMed] [Google Scholar]
- Ang KK, Chin ZY, Zhang H, Guan C (2008) Filter bank common spatial pattern (fbcsp) in brain-computer interface. In 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), pp 2390–2397, IEEE
- Ang KK, Chin ZY, Wang C, Guan C, Zhang H. Filter bank common spatial pattern algorithm on BCI competition iv datasets 2a and 2b. Front Neurosci. 2012;6:39. doi: 10.3389/fnins.2012.00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnama S, Ganapathiraju A. Linear discriminant analysis-a brief tutorial. Inst Signal Inf Process. 1998;18:1–8. [Google Scholar]
- Barry RJ, Rushby JA, Smith JL, Clarke AR, Croft RJ, Wallace MJ. Brain dynamics in the active vs. passive auditory oddball task: exploration of narrow-band EEG phase effects. Clinical Neurophysiol. 2007;118(10):2234–2247. doi: 10.1016/j.clinph.2007.06.059. [DOI] [PubMed] [Google Scholar]
- Das AK, Sundaram S, Sundararajan N. A self-regulated interval type-2 neuro-fuzzy inference system for handling nonstationarities in EEG signals for BCI. IEEE Trans Fuzzy Syst. 2016;24(6):1565–1577. doi: 10.1109/TFUZZ.2016.2540072. [DOI] [Google Scholar]
- Hara K, Saito D, Shouno H (2015) Analysis of function of rectified linear unit used in deep learning. In: 2015 international joint conference on neural networks (IJCNN), pp 1–8, IEEE
- Higashi H, Tanaka T. Simultaneous design of fir filter banks and spatial patterns for EEG signal classification. IEEE Trans Biomed Eng. 2012;60(4):1100–1110. doi: 10.1109/TBME.2012.2215960. [DOI] [PubMed] [Google Scholar]
- Homan RW, Herman J, Purdy P. Cerebral location of international 10–20 system electrode placement. Electroencephalogr Clinical Neurophysiol. 1987;66(4):376–382. doi: 10.1016/0013-4694(87)90206-9. [DOI] [PubMed] [Google Scholar]
- Jin J, Xiao R, Daly I, Miao Y, Wang X, Cichocki A (2020) Internal feature selection method of csp based on l1-norm and dempster-shafer theory. IEEE Trans Neural Netw Learn Syst [DOI] [PubMed]
- Kingma DP, Ba J (2014) Adam: a method for stochastic optimization, arXiv preprint arXiv:1412.6980
- Kumar S, Sharma R, Sharma A, Tsunoda T (2016) Decimation filter with common spatial pattern and fishers discriminant analysis for motor imagery classification. In: 2016 international joint conference on neural networks (IJCNN), pp 2090–2095, IEEE
- Lawhern VJ, Solon AJ, Waytowich NR, Gordon SM, Hung CP, Lance BJ. Eegnet: a compact convolutional neural network for EEG-based brain-computer interfaces. J Neural Eng. 2018;15(5):056013. doi: 10.1088/1741-2552/aace8c. [DOI] [PubMed] [Google Scholar]
- Lazarou I, Nikolopoulos S, Petrantonakis PC, Kompatsiaris I, Tsolaki M. Eeg-based brain-computer interfaces for communication and rehabilitation of people with motor impairment: A novel approach of the 21st century. Front Human Neurosc. 2018;12:14. doi: 10.3389/fnhum.2018.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao JJ, Luo JJ, Yang T, So RQY, Chua MCH (2020) Effects of local and global spatial patterns in EEG motor-imagery classification using convolutional neural network. Brain-Computer Interfaces, pp 1–10
- Lo C-C, Chien T-Y, Chen Y-C, Tsai S-H, Fang W-C, Lin B-S. A wearable channel selection-based brain-computer interface for motor imagery detection. Sensors. 2016;16(2):213. doi: 10.3390/s16020213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHugh ML. Interrater reliability: the kappa statistic. Biochemia Medica: Biochemia Medica. 2012;22(3):276–282. doi: 10.11613/BM.2012.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivas-Padilla BE, Chacon-Murguia MI. Classification of multiple motor imagery using deep convolutional neural networks and spatial filters. Appl Soft Comput. 2019;75:461–472. doi: 10.1016/j.asoc.2018.11.031. [DOI] [Google Scholar]
- Ortner R, Irimia D-C, Scharinger J, Guger C. A motor imagery based brain-computer interface for stroke rehabilitation. Ann Rev Cyber Telemed. 2012;181:319–323. [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C. Motor imagery and direct brain-computer communication. Proc IEEE. 2001;89(7):1123–1134. doi: 10.1109/5.939829. [DOI] [Google Scholar]
- Pfurtscheller G, Brunner C, Schlögl A, Da Silva FL. Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks. NeuroImage. 2006;31(1):153–159. doi: 10.1016/j.neuroimage.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Raza H, Cecotti H, Prasad G (2016) A combination of transductive and inductive learning for handling non-stationarities in motor imagery classification. In: 2016 International Joint Conference on Neural Networks (IJCNN), pp 763–770, IEEE
- Sakhavi S, Guan C, Yan S. Learning temporal information for brain-computer interface using convolutional neural networks. IEEE Trans Neural Netw Learn Syst. 2018;29(11):5619–5629. doi: 10.1109/TNNLS.2018.2789927. [DOI] [PubMed] [Google Scholar]
- Sakhavi S, Guan C, Yan S (2015) Parallel convolutional-linear neural network for motor imagery classification. In: 2015 23rd European Signal Processing Conference (EUSIPCO), pp 2736–2740, IEEE
- Schirrmeister RT, Springenberg JT, Fiederer LDJ, Glasstetter M, Eggensperger K, Tangermann M, Hutter F, Burgard W, Ball T. Deep learning with convolutional neural networks for EEG decoding and visualization. Human Brain Mapping. 2017;38(11):5391–5420. doi: 10.1002/hbm.23730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharbaf M. E, Fallah A, Rashidi S (2017) Shrinkage estimator based common spatial pattern for multi-class motor imagery classification by hybrid classifier. In: 2017 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), pp 26–31, IEEE
- Sun H, Jin J, Kong W, Zuo C, Li S, Wang X. Novel channel selection method based on position priori weighted permutation entropy and binary gravity search algorithm. Cognitive Neurodyn. 2021;15(1):141–156. doi: 10.1007/s11571-020-09608-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suykens JA, Vandewalle J. Least squares support vector machine classifiers. Neural Process Lett. 1999;9(3):293–300. doi: 10.1023/A:1018628609742. [DOI] [Google Scholar]
- Tam W-K, Tong K-Y, Meng F, Gao S. A minimal set of electrodes for motor imagery BCI to control an assistive device in chronic stroke subjects: a multi-session study. IEEE Trans Neural Syst Rehabil Eng. 2011;19(6):617–627. doi: 10.1109/TNSRE.2011.2168542. [DOI] [PubMed] [Google Scholar]
- Tangermann M, Müller K-R, Aertsen A, Birbaumer N, Braun C, Brunner C, Leeb R, Mehring C, Miller KJ, Mueller-Putz G, et al. Review of the BCI competition IV. Front Neurosci. 2012;6:55. doi: 10.3389/fnins.2012.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas KP, Guan C, Lau CT, Vinod AP, Ang KK. A new discriminative common spatial pattern method for motor imagery brain-computer interfaces. IEEE Trans Biomed Eng. 2009;56(11):2730–2733. doi: 10.1109/TBME.2009.2026181. [DOI] [PubMed] [Google Scholar]
- Wang K, Wang Z, Guo Y, He F, Qi H, Xu M, Ming D. A brain-computer interface driven by imagining different force loads on a single hand: an online feasibility study. J Neuroeng Rehabil. 2017;14(1):1–10. doi: 10.1186/s12984-016-0214-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Zhai D-H, Xia Y (2019) Motor imagination eeg recognition algorithm based on dwt, CSP and extreme learning machine. In: 2019 Chinese Control Conference (CCC), pp 4590–4595, IEEE
- Wu H, Li F, Li Y, Fu B, Shi G, Dong M, Niu Y. A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification. Front Neurosci. 2019;13:1275. doi: 10.3389/fnins.2019.01275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Sakhavi S, Ang KK, Guan C (2015) On the use of convolutional neural networks and augmented CSP features for multi-class motor imagery of EEG signals classification. In: 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp 2620–2623, IEEE [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.