Design and aligner-assisted fast fabrication of a microfluidic platform for quasi-3D cell studies on an elastic polymer

Abstract

While most studies of mechanical stimulation of cells are focused on two-dimensional (2D) and three-dimensional (3D) systems, it is rare to study the effects of cyclic stretching on cells under a quasi-3D microenvironment as a linkage between 2D and 3D. Herein, we report a new method to prepare an elastic membrane with topographic microstructures and integrate the membrane into a microfluidic chip. The fabrication difficulty lay not only in the preparation of microstructures but also in the alignment and bonding of the patterned membrane to other layers. To resolve the problem, we designed and assembled a fast aligner that is cost-effective and convenient to operate. To enable quasi-3D microenvironment of cells, we fabricated polydimethylsiloxane (PDMS) microwell arrays (formed by micropillars of a few microns in diameter) with the microwell diameters close to the cell sizes. An appropriate plasma treatment was found to afford a coating-free approach to enable cell adhesion on PDMS. We examined three types of cells in 2D, quasi-3D, and 3D microenvironments; the cell adhesion results showed that quasi-3D cells behaved between 2D and 3D cells. We also constructed transgenic human mesenchymal stem cells (hMSCs); under cyclic stretching, the visualizable live hMSCs in microwells were found to orientate differently from in a 3D Matrigel matrix and migrate differently from on a 2D flat plate. This study not only provides valuable tools for microfabrication of a microfluidic device for cell studies, but also inspires further studies of the topological effects of biomaterials on cells.

Graphical abstract

Highlights

• •A microfluidic platform for quasi-3D cell studies was presented as a linkage between 2D and 3D cell-material research systems.
• •The fabrication difficulty was overcome by designing an effective aligner that can be easily assembled.
• •Cell behaviors can be enhanced with a proper quasi-3D biomaterial microenvironment.
• •A new transgenic cell line and systematic 3D approaches were developed to visualize and digitalize the quasi-3D cells.

1. Introduction

Fundamental studies of interactions between cells and their microenvironment are important to develop biomaterials for tissue engineering etc. [1,2]. Mechanotransduction by which cells sense and respond to mechanical stimuli is also interesting [3,4]. Cyclic cell stretching can significantly influence cell behaviors, such as morphology, proliferation, and differentiation [[5], [6], [7]]. As dimensionality is concerned, the corresponding cell studies are performed under two-dimensional (2D) stretching of cells on an elastic membrane and three-dimensional (3D) stretching of cells in a matrix (such as hydrogel) [8,9]. The 2D and 3D stretchings lead to cell responses in different ways. On 2D, cells orient to the direction with the least disturbance, usually perpendicularly to the stretching direction [[10], [11], [12]]. Further studies showed that cyclic stretching could promote osteoblastic or myogenic differentiation of stem cells [[13], [14], [15]]. In a 3D stretching, cells orient parallelly to the stretching direction [[16], [17], [18]]. The parallel orientation in a 3D matrix should be attributed to three aspects: directional cell protrusion owing to mechano-sensing etc. [19], remodeling of matrix components [20], and boundary constraints [18,21]. Besides, cell behaviors (such as cell adhesion) and diffusion of nutrients are thoroughly different between 2D and 3D environments [22]. As a model system for fundamental research of in vitro mechanotransduction, the 2D cell stretching is relatively easy to be investigated, but the 3D cell stretching mimics in vivo cell behavior that may have a better impact on biomedical and biomaterial researches. It is thus required to establish a quasi-3D model, which can mimic the 3D behaviors of cells to some extent yet bring with us 2D-like convenience.

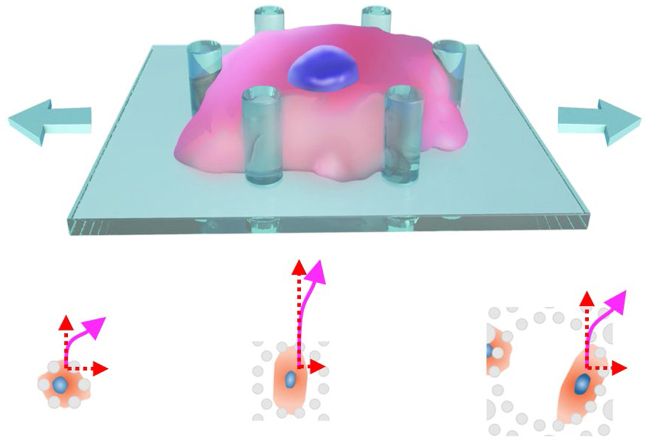
While both 2D and 3D systems have been much investigated, it is rare to study the effects of cyclic stretching on cells under a quasi-3D microenvironment owing to lack of available material platforms. Herein, we report a methodology to prepare an elastic membrane with topographic microstructures and integrate the membrane into a microfluidic chip to decouple the effects of mechanical cues from material cues. The idea is schematically illustrated in Fig. 1A. A cell adheres to, and meanwhile, is constrained by a micropillar array, forming a quasi-3D adhesion. By stretching the elastic membrane, the micropillars on the membrane change their displacements accordingly. Thus, the quasi-3D stimuli would be delivered from the micropillars to cells. Besides, the nutrients and soluble factors could be delivered directly to the cells, thus making it easier to maintain cell viability and regulate other cell behaviors. Such a quasi-3D platform can, if prepared, enable cell observations like on 2D.

Fig. 1.

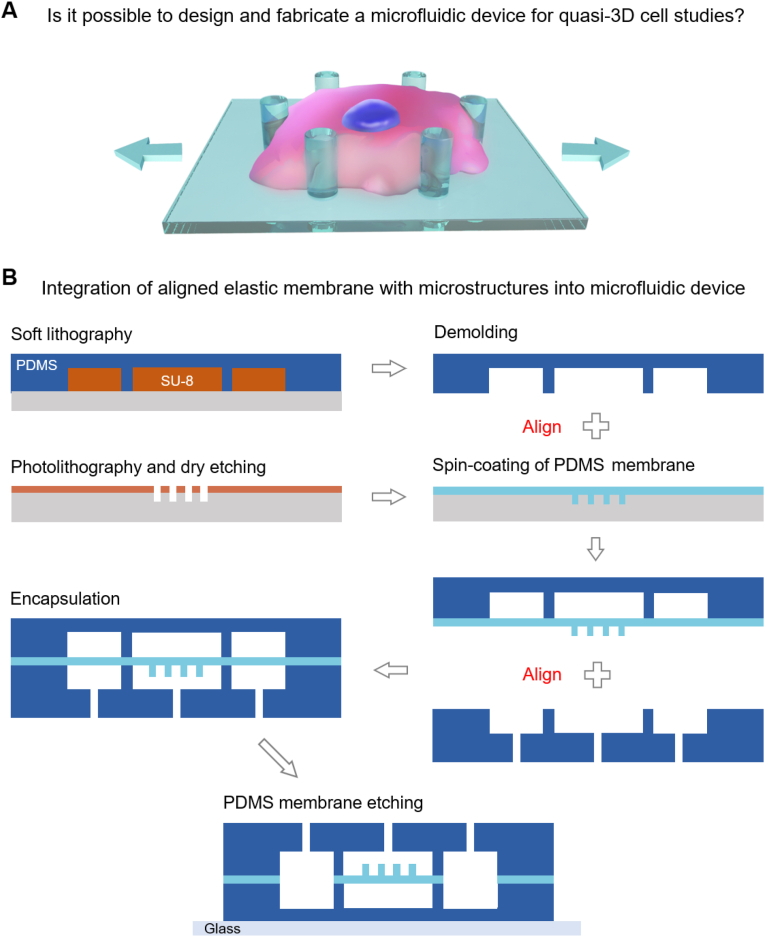
The basic idea of the present study. (A) Schematic presentation of a cell responding to quasi-3D cell stretching. (B) Fabrication of a PDMS membrane with topographic microstructures and its integration into a microfluidic chip. Two alignments were required in this method.

How to integrate such an elastic membrane with micropillars into a stretching platform? Among various cell stretching techniques [23], the microfluidic technology is of many advantages, such as low reagent consumption, precise control, fast analysis, and integration of multiple functions [24]. The microfluidic technology has been applied in many fields, such as biosensing [25,26], organs-on-a-chip [27,28], droplet microfluidics [29,30], and microfiltration [31,32]. Microfluidic chips made of polydimethylsiloxane (PDMS) are particularly suitable for cell culture and real-time observation because of the transparency and gas permeability of the PDMS matrix.

In this work, we present a microfluidic platform for quasi-3D cell stretching. We fabricated topographic microstructures (microwell arrays) on an elastic membrane and integrated such a membrane into a multilayer microfluidic device. An aligner was invented by us to accomplish the fabrication process. To investigate the deformation of the chip under negative pressure, we carried out a numerical simulation with a hyperelastic model. The optimal structural parameters of the chip were predicted by orthogonal experimental design. Subsequently, the microfluidic chips with different topographic microstructures were fabricated experimentally. With the stretching system we built, the microfluidic chips were adaptable to a wide range of stretching ratios and frequencies. To assess the quasi-3D cell adhesion, red fluorescent protein (RFP)-transfected and thus fluorescent human mesenchymal stem cells (hMSCs) in microwell arrays were observed via confocal imaging followed by 3D reconstruction and calculation of 3D sphericity. We performed on-chip quasi-3D cell stretching and examined cell behaviors under the quasi-3D microenvironment. Finally, we studied three types of cells in 2D, quasi-3D, and 3D microenvironments to estimate the effect of spatial dimensions on cells.

2. Material and methods

2.1. Fabrication of microfluidic chips

The fabrication of micropillars on a PDMS membrane and its integration into a microfluidic chip is shown in Fig. 1B. Detailed experimental parameters are released in Supplementary Notes S1 and S2. Briefly, a positive photoresist (AZ ECI 3012, MicroChem) was spin-coated on a silicon wafer and baked. The photoresist was selectively exposed with a photomask on an MA-6 mask aligner (Karl Suss). After a post-bake of the exposed photoresist, the photoresist was developed to obtain the micropattern. The patterned membrane was then used as the mask for dry etching, and an array of cylindrical microholes was thus formed in the silicon wafer. After removing the photoresist, the silicon wafer was treated with oxygen plasma and vapor-deposited with a release agent (1H, 1H, 2H, 2H-perfluorooctyltrichlorosilane, Alfa Aesar). The two components of PDMS (Dow Corning Sylgard 184) were mixed at a 10:1 ratio, degassed, and spin-coated on the silicon templet. After curing PDMS prepolymers, the PDMS membrane with micropillars (10 μm high) was prepared on the silicon templet.

For the creation of microchannel layers, SU-8 (Microchem 2150) was used as a templet. SU-8 prepolymer was spin-coated on a silicon wafer. After baking, the SU-8 was selectively exposed with a photomask and post-baked. The SU-8 templet was created by developing the photoresist in propylene glycol monomethyl ether acetate (PGMEA). After the treatment with the same release agent mentioned above, the SU-8 template with a thickness of ∼300 μm was ready to use. The PDMS components were poured on the SU-8 templets in two 4-inch crystallizing dishes for the fabrication of a thick PDMS microchannel layer and a thin layer. After proper degassing and curing, the PDMS rubber was demolded from the dishes and finely cut. The thick PDMS microchannel layer was punched with holes for the creation of inlets and outlets.

The thin microchannel layer was aligned and bonded (plasma bonding) with the membrane using a homemade aligner. This bonding product was, again, aligned and bonded with the thick microchannel layer. Finally, the bonded chip was fixed on the glass slide. A PDMS etchant (tetrabutylammonium fluoride: 1-methyl-2-pyrrolidinone = 1 : 3) [33] was injected into the side-channels to dissolve the unwanted membrane.

2.2. Design of a fast aligner

The aligner consists of a stereo microscope (XYH model, Shanghai Guangxue Instrument, China) equipped with a top lighting, an upper stage, and a lower stage equipped with a bottom lighting. The upper stage was mounted onto a Z translation stage (LWX4040, Dongguan Shengling Precision Machinery Co., Ltd, China), and equipped with a removable glass sheet. The lower stage was equipped with an X/Y/R (Rotary) stage [34] (LSP40-LM, Dongguan Shengling Precision Machinery Co., Ltd) and a LED pad. The LED pad was controlled by a power source with an electrical current of 0–1000 mA and 24 V. A removable frosted plastic sheet was mounted on the LED pad.

2.3. Numerical simulation and hyperelastic model of PDMS chips

We developed a promising numerical method based on finite element analysis, which precisely predicted the deformation and force distribution of PDMS microfluidic chips under negative pressure (more details can be found in Supplementary Notes S3 and S4). As an elastic polymer, PDMS can proceed 150% strain under a tensile loading; its stress-strain relationship is nonlinear, nearly incompressible, and generally independent of strain rate [35]. As a result, linear elastic models could not describe their stress-strain behaviors, and a hyperelastic model had to be proposed with its stress-strain relationship defined by a strain energy density function [36]. Among all hyperelastic models (neo-Hookean, Mooney-Rivlin, Ogden, Varga, etc.), the Mooney-Rivlin model is a popular one that can predict the large deformation of PDMS accurately [35,37]. We employed an incompressible 5-parameter Mooney-Rivlin model with energy density [38,39],

$$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+C_{20}{\left(I_1-3\right)}^2+C_{02}{\left(I_2-3\right)}^2+C_{11}\left(I_1-3\right)\left(I_2-3\right)$$ (1)

where $C_{10}$ $C_{01}$ $C_{20}$, $C_{02}$, and $C_{11}$ are temperature-dependent characteristic parameters, and I₁ and I₂ are the strain invariants.

In the simulation setting, the geometry was built by replicating the simplified physical structure of the chip. The entire domain was defined as a Mooney-Rivlin hyperelastic material. To find the suitable characteristic parameters for PDMS, we referred to the relevant parameters [[40], [41], [42]] and then tested the parameters with our simulations. The characteristic parameters were finally decided as C₁₀ = 0.255 MPa, C₀₁ = 0.036 MPa, C₂₀ = 0.1 MPa, C₀₂ = 0.312 MPa, and C₁₁ = −0.341 MPa, which were proved to fit with the experimental results. The material density of PDMS was 970 kg m⁻³. A mapping mesh was used with mesh density of maximum and minimum element sizes of 9 μm and 0.13 μm, a maximum element growth rate of 1.1, and a curvature factor of 0.25.

2.4. Characterization of microfluidic chips

The as-fabricated microfluidic chip was transversely cut into a thickness of ∼1 mm for the visualization of the cross-section of the chip. The cut sample was observed under a metallographic microscope (LV100ND, Nikon) with a 5 × objective lens to observe the chip structure and a 20 × one to observe the microstructure. Since the membrane thickness was confirmed by a step profilometer (AlphaStep D-600 KLA Tencor), the sizes of other microstructures can be calculated according to the size ratios.

2.5. Cell culture and construction of a transgenic cell line

Human mesenchymal stem cells (hMSCs), human foreskin fibroblasts (HFFs), and human umbilical vein endothelial cells (HUVECs) were purchased from Cell Bank, Type Culture Collection, Chinese Academy of Sciences. (Note: The uppercase or lowercase of “H” follows the tradition for the pertinent cell types.) The hMSCs were cultured in minimum essential medium Eagle - alpha modification (MEM-α, Gibco). The HFFs and HUVECs were cultured in high-glucose Dulbecco's modified Eagle medium (DMEM, Gibco). All culture media were supplemented with 10% fetal bovine serum (FBS, Gibco) and 100 U mL⁻¹ penicillin/streptomycin (Gibco). After reaching about 90% confluence, cells were detached using 0.25% trypsin/ethylenediaminetetraacetic acid (Gibco) and passed to the next generation. The media were refreshed every two days.

LifeAct-RFP labeled human mesenchymal stem cells (RFP-hMSC) enable the track of live cells (red fluorescence) in micropillar arrays (phase-contrast) under a fluorescence microscope. RFP-tagged LifeAct was transfected into the hMSCs using pCMV-LifeAct-RFP (Ibidi) through the construction of LifeAct-RFP-overexpressed lentivirus vector pH5674-LifeAct-RFP. The transfection principle and some results are presented in Fig. S3.

2.6. PDMS surface treatment and cell adhesion test

PDMS sheets of 1 mm thickness were cut into 1 cm × 1 cm pieces and stuck in 12-well plates using glues (PDMS prepolymer 10:1). Fibronectin was coated on PDMS by sterilizing PDMS pieces with 75% ethanol for 30 min, washing them with phosphate-buffered saline (PBS) solutions three times, and preserving them in a diluted solution of fibronectin (5 μg mL⁻¹, Sigma) at room temperature for 4 h. The plasma treatment of PDMS was carried out at a power of 90 w for 100 s in a DT-03 plasma processor (Suzhou OPS Plasma Technology Co., Ltd., China). The sample was sterilized with 75% ethanol and washed with PBS. Afterwards, cells were seeded on material surfaces with a density of 4 × 10⁴ cells cm⁻².

2.7. Personalized stretching system

The stretching system enables on-chip cell culture, stretching, and real-time observation in a flexible way. It consisted of a computer-controlled pressure controller, a syringe pump, and a live-cell imaging system. The pressure controller (OB1, Elveflow) was supported with a vacuum pump (AP-550V, AutoBo Elec. Technology Co., Ltd, China) using an ultimate vacuum of −100 kPa as the source of negative pressure and a supply of high purity nitrogen at a pressure of 200 kPa as the source of positive pressure. The pressure controller was connected to the two actuation chambers in the microfluidic chip through a “Y” connector to keep pressure equality. The syringe pump (NE-1800, New Era) used two 5 mL syringes per chip to supply culture medium and PBS to the chip's upper and lower culture chambers. The live-cell imaging system was composed of a live-cell culture system equipped with a CO₂ generator and a heating chamber, and an inverted fluorescence microscope (Axiovert 200, Zeiss) with a charge-coupled device (CCD, AxioCam HRC, Zeiss).

2.8. Cell stretching experiments

The microfluidic chip was treated with oxygen plasma (100 w, 90 s), sterilized under ultraviolet light for 30 min, rinsed with 75% ethanol for 15 min, and washed with PBS. The RFP-hMSC cells were detached by 0.25% trypsin/ethylenediaminetetraacetic acid and resuspended at a density of 2 × 10⁵ cells mL⁻¹. The cells were injected into the chip and incubated at 37 °C for 4 h.

During the cell stretching experiment, the microfluidic chip was connected to the pressure controller and the syringe pump, and then it was fixed on the stage of the fluorescence microscope. The syringe pump supplied culture medium and PBS to the microfluidic chip with a flow speed of 1 μL min⁻¹. The stretching ratio was calibrated every time before stretching by tuning the maximum air pressures. Cyclic stretching with sine waves was motivated by the pressure controller. Snapshots of cells (fluorescence) and micropillars (phase contrast) were automatically captured every 10 min with the Zen software (Zeiss).

2.9. Characterization of stretching ratio

The stretching ratio was measured by observing the displacement of the micropillars during cyclic stretching. Before measurement, the high-speed scanning mode of the CCD camera was turned on to capture the quick motion of micropillars. During the measurement, cyclic stretching at a certain frequency and negative pressure was observed under the microscope and was recorded by a personal computer. Individual pictures at special moments were selected from the recorded videos. Distances between two micropillars were measured by ImageJ at the moments when the elastic membrane was completely relaxed (L₀) and stretched (L₁). The stretching ratio is calculated with

$$a=\frac{L_1-L_0}{L_0}$$ (2)

2.10. Confocal microscopy and 3D reconstruction of single cells in microwell arrays

To prepare the RFP-hMSC cells for confocal microscopy, the cells were injected into the microfluidic chip at a density of 2 × 10⁵ cells mL⁻¹. A few drops of cell suspension were reserved at the inlets and outlets of the chip to prevent drying out. After incubation at 37 °C for 4 h, the chip was kept in the dark and transferred to a confocal microscope (C2+, Nikon, Japan) equipped with a CO₂ generator and a heating chamber. Fluorescence images of the cells and phase-contrast images of the micropillars were captured layer-by-layer with 1 μm interval. By importing the image collections into the free software, NIS-Elements Viewer (Nikon, Japan), the fluorescent labeling cells can be viewed in 3D.

To obtain quantitative information about the quasi-3D cell adhesion, we have developed a method to digitally reconstruct the cells. Individual grayscale TIFF images that numbered sequentially were imported from confocal image stacks. Then, a median filter with 3 iterations was used to remove noise from the images. Interactive thresholding was applied to transform the grayscale images into binary images and obtain a proper gray level of the images (usually ∼85% of the whole range of brightness). Since some cells closely adhered that they may be recognized as one cell by the computer program, a separation operation that computed watershed lines on a distance map was applied to separate cells. With a surface generation process, the fluorescent cells were reconstructed and visualized as 3D objects.

The 3D reconstruction process also enabled the acquirement of digital information such as cell volume (V) and surface area (A). Sphericity, a measure of how similar the shape of an object is to a perfect sphere, was calculated by

$$\Psi =\frac{{\pi }^{\frac{1}{3}}{\left(6V\right)}^{\frac{2}{3}}}{A}$$ (3)

Ψ = 1 for a perfect sphere, and the calculated value is usually less than 1.

2.11. Quantification of apparent spreading fraction

The numbers of spreading cells ($N_{\text{spreading}}$) and non-spreading cells ($N_{\text{non}-\text{spreading}}$) were counted from the recorded images, and the apparent spreading fraction of cells was defined as

$$f=\frac{N_{\text{spreading}}}{N_{\text{spreading}}+N_{\text{non}-\text{spreading}}}$$ (4)

To determine whether a cell was “spreading” or “non-spreading”, fluorescence images of cells in microarrays and phase-contrast images of cells on a flat surface were analyzed. If the projection of a cell is large (cell area > 150 μm²) or in a long shape (aspect ratio > 1.3), the cell is considered “spreading” in the present experiment; if a cell is small (cell area ≤ 150 μm²) and round, the cell is considered “non-spreading”.

2.12. Quantification of cell orientation

The orientation angle θ of a cell was measured with ImageJ. It was determined by marking the long axis of a cell with respect to the stretching direction. The order parameter of multiple cells is calculated with [43]

$$R=\sqrt{\sin 2{\theta }^2+\cos 2{\theta }^2}$$ (5)

where 0° < θ ≤ 180°. The formula is explained in Supplementary Note S5. R approaches 0 when cells orient randomly, and R = 1 when all cells orient in the same direction.

2.13. Immunofluorescence staining, observation, and analysis of stained cells

All cells (hMSCs, HFFs, HUVECs) were seeded on PDMS flat surfaces (2D) and PDMS microwells (quasi-3D) for 4 h, and in a 3D Matrigel (growth factor reduced, Corning) for 24 h. All samples were fixed by 4% paraformaldehyde for 15 min and soaked in 0.2% Triton X-100 solution for 10 min. The samples were rinsed with PBS twice whenever a new reagent was used. The specimens were blocked with 5% bovine serum albumin (BSA) solution for 30 min. Then, a vinculin primary antibody (Santa Cruz) at a concentration of 10 μg mL⁻¹ was used to incubate the sample at 4 °C overnight. Afterwards, an Alexa Fluor 488-conjugated goat anti-mouse secondary antibody (Invitrogen) was used at a concentration of 10 μg mL⁻¹. After incubation of the second antibody at room temperature for 2 h, the phalloidin-tetramethyl rhodamine B isothiocyanate (phalloidin-TRITC, Sigma) at 1 μg mL⁻¹ was added and incubated for 30 min at room temperature. Subsequently, a 4’,6- diamidino-2-phenylindole (DAPI, Sigma-Aldrich) at 2 μg mL⁻¹ was used to stain the nuclei in a reaction time of 5 min. The stained cells were observed under a fluorescence microscope (Axiovert 200, Zeiss). To ensure a robust quantitative analysis, the exposure times were kept constant for all groups.

Cells were outlined in the fluorescence images using ImageJ to obtain cell spreading areas and circularity. The integral intensity of F-actin and vinculin per cell was obtained by calculation from the following equation.

$$\text{Intensity}=<S_{\text{cell}}\times \left(I-I_0\right)>$$ (6)

where S_cell is the spreading area of a cell outlined with ImageJ, and I and I₀ are the mean gray values of a whole cell and the background near the cell, respectively.

2.14. Statistical analysis

Four independent experiments were averaged during the data analysis of cell sphericity. For the cell stretching experiment, three independent experiments were averaged. One-way analysis of variance (One-way ANOVA) was carried out to examine the difference between groups using SPSS 20.0 software (SPSS Inc., Chicago, USA). We considered a difference as significant when p < 0.05. Specifically, statistically significant difference was marked as “*” (0.01< p < 0.05), “**” (0.001< p < 0.01), or “***” (p < 0.001).

3. Results

3.1. Efficient fabrication of microfluidic chips using a developed fast aligner system

Two alignments were required for the fabrication of each chip because of the integration of topographic microstructures (Fig. 1B), which increased the failure rate compared to the integration of a flat membrane. What makes the fabrication even harder is that plasma bonding must be made immediately after the plasma treatment, which leaves little time for an alignment [44,45]. We have tried some alternative methods, such as casting PDMS prepolymer or using lubricant (such as deionized water) during bonding, and we found that they were less reliable than direct plasma bonding, as they frequently led to device sealing issues during stretching. Moreover, our fabrication included the alignment of a PDMS layer with a PDMS membrane on a silicon wafer. Since silicon is dark gray, the tiny microhole pattern in silicon was much harder to be detected than the pattern in transparent PDMS material. To tackle these problems, we present the novel chip aligner that is fast for alignment, easy to use, and low-cost.

The structure of the aligner is schematically presented in Fig. 2A, and a prototype is shown in Fig. 2B. A typical example of a PDMS layer aligning with a PDMS membrane on silicon (PDMS-on-silicon layer) is demonstrated in Fig. 2C. The PDMS microchannel layer and the PDMS-on-silicon layer were fixed to the glass sheet and the plastic sheet, respectively. The two sheets were mounted onto the upper stage and the lower stage. The two layers were aligned coarsely by tuning X/Y/R positions under the stereo microscope. After the major alignment, the stage positions were fixed by the knobs of the X/Y/R stage. The sheets were withdrawn from the upper and lower stages (without moving the stages), and then treated with mild plasma oxygen (100 w, 90 s) and loaded back to the stages. After a minor alignment under the stereo microscope, the upper stage was lowered down to complete the bonding. After an annealing process (70 °C, 15 min), the bonded product was sequentially peeled off from the lower plastic sheet, the top glass sheet, and the silicon substrate. The bonding strength was sufficiently strong to resist the peeling forces, thanks to the fast plasma-bonding process. With the advantages of the pre-aligning procedure and effective observation, the alignment and bonding could be done within 1 min as soon as the plasma-treated surfaces were ready.

Fig. 2.

The fast aligning system developed in this study based on a microscope. (A) The 3D structure and (B) the prototype of the fast aligner. (C) A typical aligning procedure of a PDMS microchannel layer with a PDMS membrane with micropillars on a silicon substrate. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

3.2. Optimization of structural parameters by numerical modeling

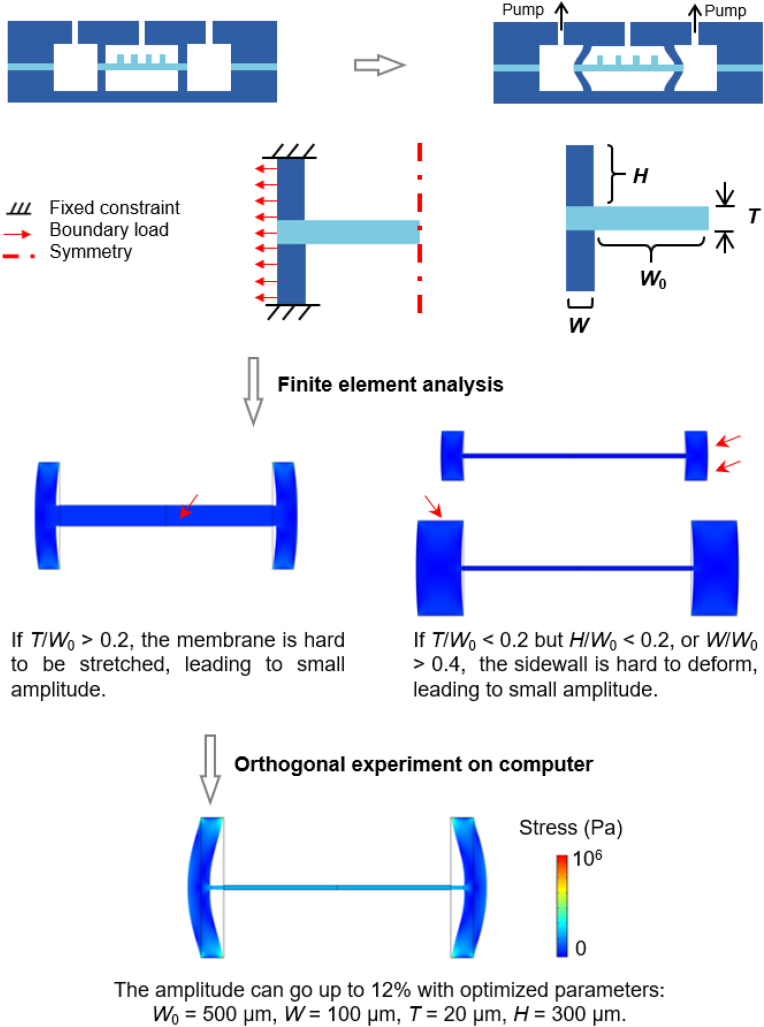
We have developed an effective method to optimize chip structure via numerical simulations. The model was simplified to increase computation convergence and reduce computation time. Since the chip structure and boundary conditions are all symmetrical along the y-axis, only half of the chip is needed for the calculation. The deformations of a bulk PDMS material were small enough to be neglected, and thus the top and bottom boundaries were treated as fixed constraints. The boundary loads are shown by the arrows, which represent the applied forces exerted from negative pressure.

Some representative simulation results are shown in the middle of Fig. 2. If T/W₀ > 0.2, the membrane is hard to be stretched, leading to small amplitude. Even if T/W₀ ≤ 0.2 but H/W₀ < 0.2, or if W/W₀ > 0.4, the sidewall is hard to deform, also leading to small amplitude. Therefore, under inappropriate device parameters, the microfluidic chip would exhibit only small stretching ratios.

We employed orthogonal experimental design (OED) to find out the optimal structural parameters. An OED uses a preset orthogonal table to arrange representative tests based on probability theories [46,47]. By selecting representative combinations of structural parameters arranged by the orthogonal L₉ (3⁴) table, the tests were carried out on computer (finite element analysis) and the results (stretching ratios) were obtained. A complete list of the results under pressure of −40 kPa is shown in Table S1, in which the influence of each factor (H, W, or T) to stretching ratio was estimated. The optimal levels for W, T, and H are 100 μm, 20 μm, and 300 μm, as is displayed at the bottom of Fig. 3. When applying a −40 kPa pressure, the stretching ratio can go up to 12%. There is no obvious stress concentration from the stress distribution (color scale). Using the optimized parameters and various pressures, the model was able to predict experimental results accurately and mimic dynamic stretching actions (Supplementary Movie S1), which proves the successful modeling of PDMS devices.

Fig. 3.

Structure optimization of the microfluidic chip by finite element analysis (FEA) and orthogonal experimental design. The chip structure was refined to obtain a simplified geometry and boundary conditions. The optimal structure was obtained by orthogonal experimental design. The color scale of the simulation results represents the stress distribution. W₀: half width of middle chamber; W: width of sidewall; T: thickness of membrane; H: height of microchannel. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Supplementary data related to this article can be found at https://doi.org/10.1016/j.bioactmat.2021.12.010.

The following is the supplementary data related to this article:

3.3. As-fabricated microfluidic chip and the microwell arrays

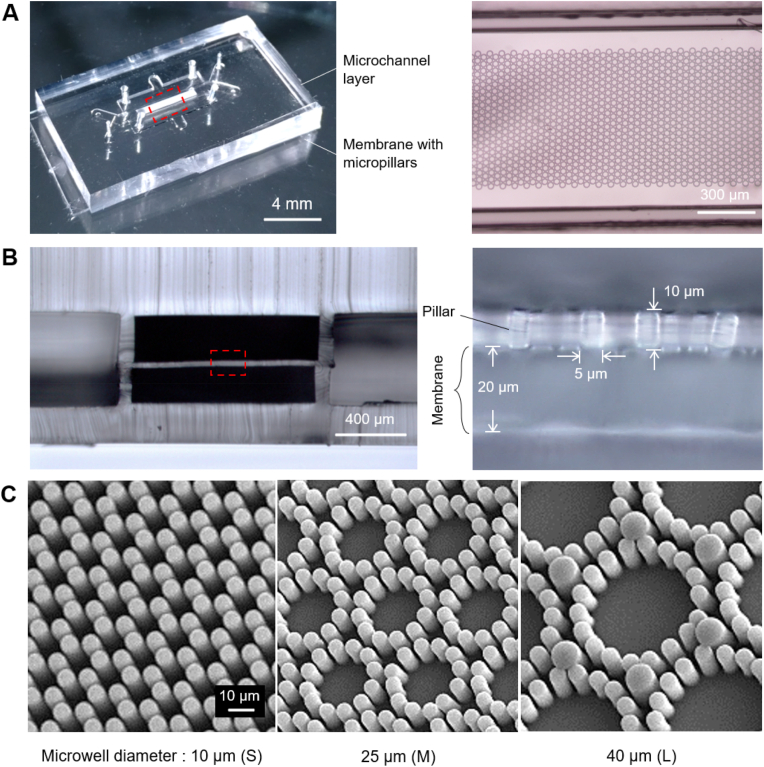
The microfluidic chips were fabricated with the appropriate parameters predicted by finite element analysis. Fig. 4A presents a bonded device prepared following the aligning procedure in Fig. 2C. The right side of Fig. 4A shows the zoom-in image of micropillars located between two microchannel walls. The technical challenge was to accurately place the micropillar pattern (a long strip of 800 μm × 5 mm) paralleled to the microchannel (1 mm wide). The fast aligner was designed to solve the issue effectively.

Fig. 4.

The as-fabricated microfluidic chip and the micropillar arrays. (A) Global view of a bonded chip. The right figure shows a microscopic image of the micropillars aligned in the center of the microchannel. (B) Cross-section of the microfluidic chip, showing a membrane sandwiched by two microchannel layers. The right is a zoom-in image of the micropillars on a membrane. (C) SEM pictures of three kinds of micropillar arrays, namely small microwells, middle microwells, and large microwells.

The cross-sectional view of the chip is shown in Fig. 4B. The elastic membrane was sandwiched between the upper and lower microchannel layers. The membranes in both side-cavities were removed by the PDMS etchant. Since the upper microchannel sidewall with ∼100 μm width was well-aligned with the lower microchannel sidewall, we estimated our alignment accuracy as ±10 μm. The zoomed-in image of the elastic membrane shows that the micropillars stand upright on the ∼20 μm thick membrane. Each micropillar has a diameter of 5 μm (some large micropillars in the L is 10 μm) and a height of ∼10 μm. The gap between each two micropillars is 3 μm.

Fig. 4C shows the SEM pictures of three kinds of microwell arrays with diameters of 10 μm (each with 6 micropillars), 25 μm (each with 12 micropillars), and 40 μm (each with 18 micropillars). The details about the microwell design are shown in Fig. S2. We chose the microwell diameters to match the cell size, which is 15–30 μm for human MSC cells [48,49].

3.4. Customized stretching system and the stretching performance

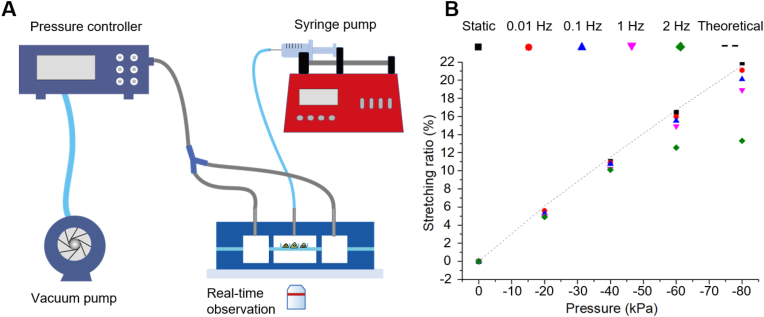
We customized a live-cell stretching and imaging system, as schematically presented in Fig. 5A. The system consisted of a pressure controller for stretching actuation, a syringe pump for medium supply, and a fluorescence microscope equipped with a live-cell culture system.

Fig. 5.

(A) Microfluidic stretching system. (B) The relationship between stretching ratio and pressure at various stretching frequencies. Theoretical results represent the static stretching ratios from finite element analysis.

Stretching ratios were measured at various frequencies and pressures via image analysis of the micropillar displacement. The device worked well in the frequency range of 0–1 Hz with the stretching ratios of 0–19%. It also worked at the frequency of 2 Hz with the stretching ratios of 0–13%. The experimental data matched well with simulation results, which proved the accuracy of our simulation.

3.5. 3D approaches to characterize cells in micropillars

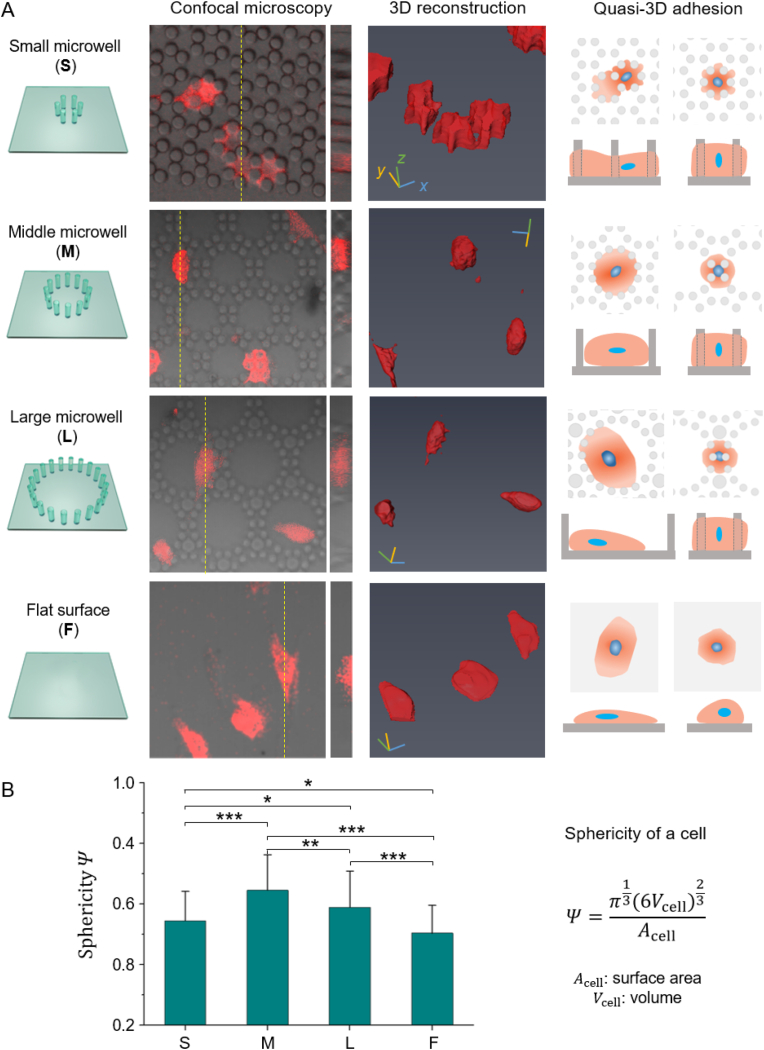
The cells with live fluorescence in micropillars were observed by confocal microscopy. Fig. 6 presents four kinds of membranes, which are small microwells (S), middle microwells (M), large microwells (L), and flat surface (F). We found that the topographic microstructures dramatically modified the cell morphologies: in the S, cells were tightly constrained, and thus the cell surface was rough (low sphericity); in the L, the cells loosely adhered to the bottom and sidewall of the microwells with a spreading morphology (low sphericity); in the M, the cell adhered to the microwells moderately, thus the cells tended to be round (high sphericity); the cells on F were the flattest among the four substrates (lowest sphericity). The sphericity was calculated with the digital information from 3D reconstruction. According to statistics, the cell sphericities were 0.54 (S), 0.65 (M), 0.59 (L), and 0.50 (F). There is a significant difference between any of the two groups.

Fig. 6.

3D characterization of RFP-hMSC cells in micropillars. (A) The morphology of cells in three microwell arrays (S, M, and L) and on a flat surface (F). The four rows from left to right indicate the schematics of the four substrates, typical results of confocal microscopy, 3D reconstruction, schematic diagram of the quasi-3D cell adhesion. Live cells tagged with RFP were detected via red fluorescence, and micropillar arrays were observed in brightfield; confocal results shown are the merged images. (B) Sphericity of cells (n ≥ 80 per group). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

We also schematically present an unignorable fact that there was always a portion of cells reversibly turned into round shapes on all kinds of membranes (the last row of Fig. 6A). This means that cells were not strictly restricted by microwells. Instead, they actively traveled through with the microwells since their sidewalls were made of micropillars.

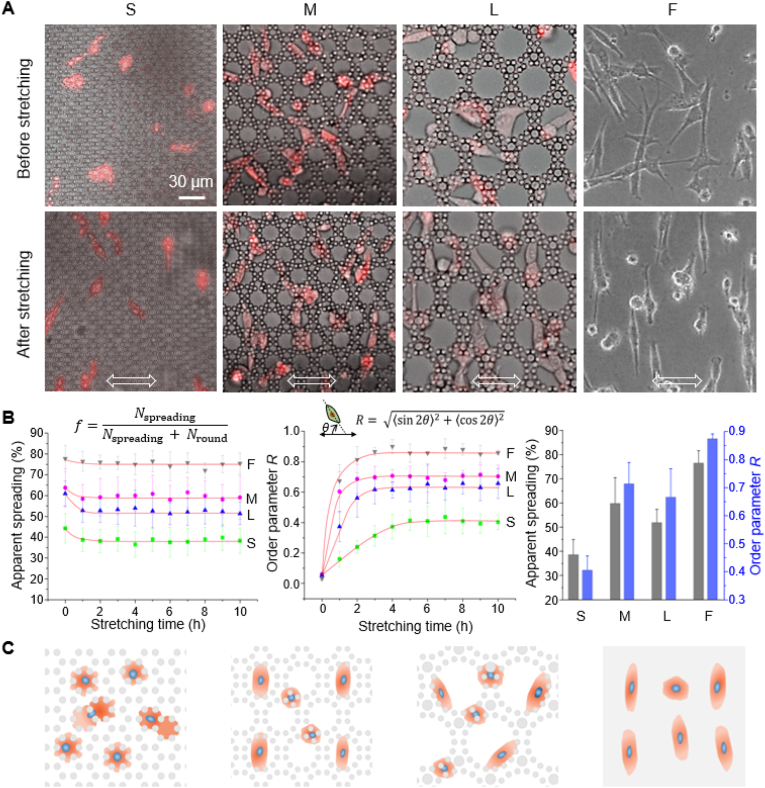
3.6. Cell spreading and orientation during cyclic stretching

The RFP-hMSCs underwent significant changes in cell spreading and orientation during cyclic stretching (1 Hz, 10%), as shown in Fig. 7A and Supplementary Movies S2-S5. Fig. 7B shows the statistics of apparent spreading fraction and order parameters over time. The cell spreading in the S, M, and L arrayed membranes decreased significantly within 0–2 h of stretching (decreased 5–8%), while it is not obvious on the F plane (decreased ∼1%). Under cyclic stretching, some cells contracted in a round shape and adhered to the sidewalls of micropillars to avoid physical disturbance. During 2–10 h, the apparent spreading fraction reached steady states at 39% (S), 58% (M), 53% (L), and 76% (F).

Fig. 7.

Spreading and orientation of RFP-hMSC cells during cyclic stretching (A) Micrographs of cells (n ≥ 300 per time point) in the micropillar arrays after cyclic stretching. The double-sided arrows at the bottom indicated the stretching directions. Live cells tagged with RFP (red fluorescence) were detected via fluorescence mode, and micropillar arrays were observed in phase-contrast mode; shown are the merged images. (B) Apparent spreading fraction and orientational order parameter of cells as functions of stretching time. The red lines in (B) are just for the guidance of view. (C) Schematic presentation of cells in the indicated 2D or quasi-3D material microenvironments under cyclic stretching. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Supplementary data related to this article can be found at https://doi.org/10.1016/j.bioactmat.2021.12.010.

The following is the supplementary data related to this article:

Multimedia component 2

Multimedia component 3

Multimedia component 4

Multimedia component 5

The cells oriented randomly before stretching (t = 0 h). During stretching, the order parameter raised and reached steady states with the values of 0.41 (S), 0.71 (M), 0.63 (L), and 0.86 (F). The time spent to reach the steady states were 5 h (S) and 3 h (M, L, and F). The case of “S” needed longer time to reach equilibrium probably because the cells were restricted by the dense micropillars.

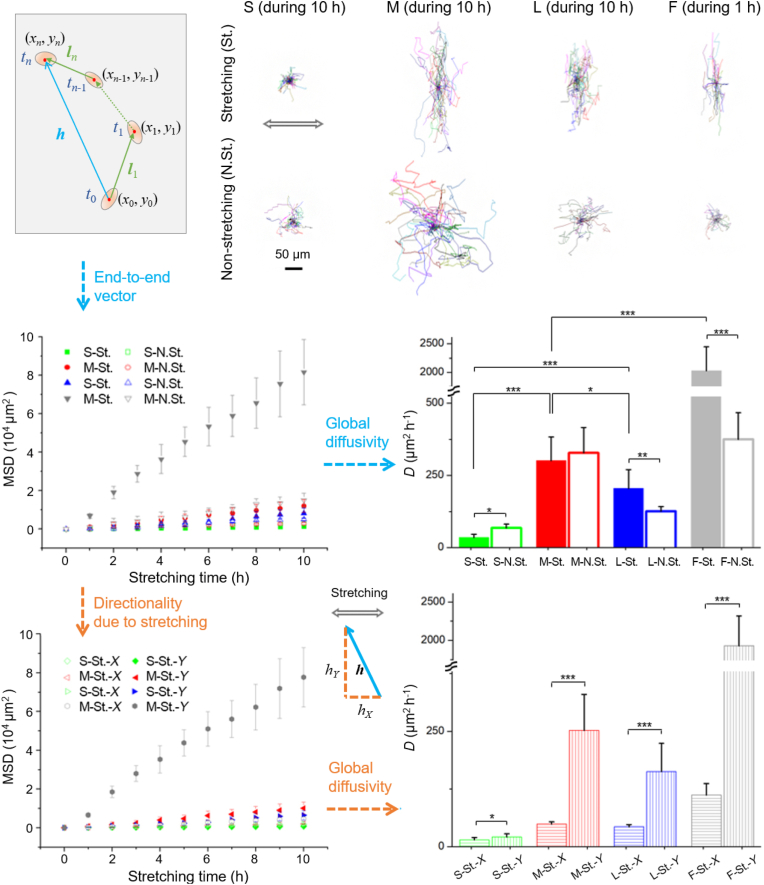
3.7. Cell migration and directionality

It is interesting that cell migration was dramatically changed by the microwell arrays for both stretching and non-stretching cases. Some typical migration trajectories of single cells are demonstrated in the upper of Fig. 8. During stretching, cells sensed strong mechanical disturbances, and to avoid that, they chose to migrate mainly perpendicular to the stretching direction. Furthermore, we quantified cell migration with contour velocity and mean squared displacement (MSD), as the diagram and variables are shown in Fig. 8 (upper-left). The contour velocity is derived from contour length (l) divided by the record time (t),

$$V\left(\text{contour}\right)=\sum _{i=0}^n\frac{l_i}{t}$$ (7)

Fig. 8.

The tracking pathways of single cells under cyclic stretching (St.) and non-stretching (N.St.). The contours show 30 cell traces for each substrate. The MSD was calculated from the end-to-end distance of migration traces every 1 h. The diffusivity D, obtained from the calculation of MSD, was independent upon the time interval. The directionality was characterized based on the calculation of X- and Y- components of MSD.

The MSD was calculated by

$${\mathrm{MSD}}_i={\left(\sum _{j=0}^i{\mathit{l}}_j\right)}^2=4D\left(i\Delta t\right)$$ (8)

or directly via end-to-end vector h,

$${\mathit{h}}^2={\left(\sum _{i=0}^n{\mathit{l}}_i\right)}^2=4D(t_n-t_0)$$ (9)

where D is the diffusivity.

The MSD linearly increased with the stretching time t. It seems that cell migration obeys the random diffusion equation put forward by Einstein in 1905 in studies of Brownian motion of physical particles [50]. Thus, the diffusivity can be calculated with the results of MSD, as shown in the middle of Fig. 8. The diffusivities of cells in the microwell arrays are in sequence of M > L > S, for both stretching and non-stretching cases. The diffusivities of F were larger than the microwell arrays because cells migrated without micropillar obstacles. The ratio of diffusivities between stretching and non-stretching (D_stretching/D_{non-stretching}) is S (0.5) < M (0.9) < L (1.6) < F (5.4), which means that stretching made cell migrate faster than non-stretching for L and F, but slower for S and M.

The contour velocities of RFP-hMSCs on PDMS elastic membranes with varied topological surfaces read V_stretching = 10 μm h⁻¹ (S), 29 μm h⁻¹ (M), 24 μm h⁻¹ (L), 76 μm h⁻¹ (F), and V_{non-stretching} = 14 μm h⁻¹ (S), 33 μm h⁻¹ (M), 17 μm h⁻¹ (L), 35 μm h⁻¹ (F). More details about the contour velocity can be found in Fig. S4.

We found that cell migration showed strong directionality under cyclic stretching. To characterize the directionality, we calculated the X- and Y- components of MSD (MSD_X and MSD_Y), and we define MSD_Y/MSD_X as directionality, which was calculated as 1.4 (S), 5.1 (M), 3.8 (L), and 17.2 (F).

3.8. Adhesion between cells and 2D, quasi-3D, and 3D materials

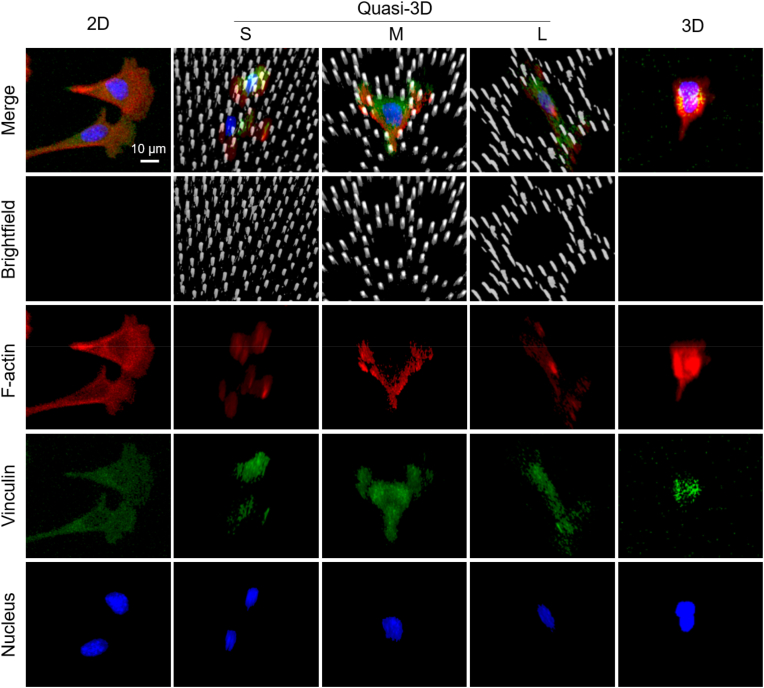
In order to characterize the cell adhesion clearly, hMSC cells were cultured in 2D (on flat PDMS), quasi-3D (in PDMS microwells), and 3D (in Matrigel) microenvironments. After fixation and staining, the cells were scanned layer-by-layer under a confocal microscope. The results are shown in Fig. 9: vinculin and F-actin were significant in all cases, yet the fluorescent intensity of vinculin was relatively weak in the 3D microenvironment (probably due to weak adhesion with the soft hydrogel). Cells were clearly visualized in micropillars and there were obvious adhesion sites in between.

Fig. 9.

Confocal microscopy Z-stacking images of stained hMSC cells with micropillars in gray, F-actin in red, vinculin in green, and nuclei in blue. Here, “2D” means cells on a flat PDMS surface, “3D” means cells in a Matrigel, “quasi-3D”means cells in microwells surrounded by PDMS micropillars, where “S”, “M”, and “L” indicate small, middle and large microwells. Cells were cultured in 2D and quasi-3D for 4 h, and in 3D for 24 h. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

3.9. Different cell behaviors in 2D, quasi-3D, and 3D microenvironments

Three types of cells (hMSCs, HFFs, HUVECs) were cultured in 2D, quasi-3D, and 3D microenvironments. Here topological effects were emphasized free of cyclic stretching. After fixation and immunofluorescence staining, optical micrographs were captured and displayed in Fig. 10A. Cells spread well in 2D within 4 h. But in 3D, cells tended to be round in the Matrigel for 24 h. In quasi-3D, cells exhibited different morphologies: the M membrane shaped the cells rounder than the S and L membranes. Fig. 10B presents the results of the quantitative analysis, and Table S2 lists the global p-values obtained from one-way ANOVA showing a significant difference among all groups. The circularity was indeed 2D < quasi-3D < 3D. Moreover, the integral intensity of vinculin per cell was 2D: quasi-3D: 3D = 5:3:1. Therefore, the quasi-3D microenvironment was between 2D and 3D ones, and relatively closer to a 3D one. Among the quasi-3D (S, M, and L), the M group showed the highest values in three aspects (F-actin, circularity, and cell area) for all three types of cells. Since the diameters of hMSC, HFF, and HUVEC cells were 16.6 ± 2.5 μm, 20.7 ± 5.4 μm, 17.2 ± 2.0 μm (Fig. S5) which were all between the diameters of S and M microwells, all of the three types of cells sensed appropriate quasi-3D microenvironment after entering the medium-sized microwells.

Fig. 10.

Different types of cells cultured in 2D (on flat PDMS), quasi-3D (in PDMS microwells), and 3D (in Matrigel) microenvironments. (A) Fluorescence micrographs of stained hMSC, HFF, and HUVEC with F-actin in red, vinculin in green, and nuclei in blue. (B) Statistic results (n ≥ 90 per group) of integral intensity of F-actin and vinculin, and cell adhesion parameters after 4 h culture of cells in 2D and quasi-3D, and 24 h culture of cells in 3D. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

The 2D cell spreading areas of a single hMSC, HFF, and HUVEC are 982 μm², 1512 μm², and 950 μm²; and the 3D cell project area are 550 μm², 654 μm², 359 μm², respectively. For F-actin and vinculin (labeled with immunofluorescence), the quantities of HFF were 3–4 times more than those of hMSC and HUVEC. This should be related to the inherent properties (e.g., cell size and cell functioning) of different cell types.

4. Discussion

Cells respond to various cues from the surrounding microenvironment, such as nanoscaled cues [51,52], surface topology [53,54], material scaffolding [[55], [56], [57]], biodegradation [[58], [59], [60]], and chemical cues [61,62]. And in many cases, mechanical cues should be taken into consideration [[63], [64], [65]]. It is challenging to reveal responses of individual cells to mechanical cues due to the lack of sufficient innovative material platforms to control mechanical stimulations in single-cell scales. In recent years, the research on the interaction of 3D cells and materials has owned great prospects [[66], [67], [68]]. The present affords a quasi-3D cell-material research platform, which enables observation of live cells of a 3D-like shape yet on a 2D-like plane cultured in a microfluidic chip available for cyclic stretching.

4.1. Design of a fast aligner to assist the fabrication of quasi-3D microfluidic platform

In order to generate a stretchable topographic microstructure, we fabricated micropillars on an elastic polymer membrane and integrated the membrane into a microfluidic chip, as schematically presented in Fig. 1. The key technical challenge not only lay in the creation of micropillars but also in multilayer bonding which required fast and accurate alignment, and the latter is more important. Therefore, we developed a fast aligner system, as presented in Fig. 2. This invention is of the following advantages: 1) increasing the fabrication success rate because each chip required two alignments, 2) enabling fast alignment and bonding processes to avoid the deactivation of plasma-treated surfaces in the atmosphere, 3) leading to vivid alignment of even a dark material owing to the bright front- and back-lightings on samples.

The feature of our aligner comes from the usage of upper and lower stages with removable sheets, so that the two samples for alignment can be attached to the sheets, be coarsely adjusted before plasma treatment, and be finely aligned and quickly bonded under the stereo microscope as soon as the plasma-activated surfaces were ready. The stereo microscope was specifically introduced for visual observations. We have tried a digital microscope (B011, Supereyes) equipped with a monitor instead of the stereo microscope. Both image clarity and operation convenience were inferior to the stereo microscope. The new aligner allowed us to complete the aligning and bonding procedures within 1 min after plasma treatment. The estimated alignment accuracy is ±10 μm, which are suitable for the fabrication of most microfluidic chips. With the strong plasma bonding, the robustness of the chip was greatly improved with fewer leakage issues and fewer chances to be damaged by external forces during experimentation.

4.2. Optimization of structural parameters by theoretical analysis

To optimize the chip structure for maximal stretch ratio, we have combined finite element analysis (FEA) with orthogonal experimental design (OED) as shown in Fig. 3. The whole process can be done on a personal computer. Through the FEA study, we predicted valuable PDMS parameters of the Mooney-Rivlin hyperelastic model that could be used by other researchers. The OED enabled the optimization of chip structure with a few computer experiments (Table S1).

4.3. Moderate-sized microwells triggered the strongest cell responses under quasi-3D microenvironments

For any comprehensive quasi-3D cell study, it is necessary to semi-quantify the cell status. To this end, we established systematic 3D approaches that used confocal microscopy to obtain raw cell data, 3D reconstruction to digitalize the cell morphology, and sphericity to estimate the cell shape (Fig. 6). We found that the cells were modified by the micropillars to different extents: they were constrained severely in the S (relatively small wells surrounded by micropillars), loosely in the L, and moderately in the M. That is, cells formed different levels of quasi-3D adhesion with the mediation of microwells. The use of the self-constructed RFP-transgenic cell line allowed us to observe live cells in the micropillars clearly (Fig. S3).

Cyclic stretching of RFP-hMSC cells was carried out, as seen in Fig. 7 and Supplementary Movies S2-S5. The cells underwent significant changes in spreading and orientation with stretching time. Among the microwell arrays, the middle microwells showed the highest spreading and orientation.

We found no sign of “parallel” orientation (cells oriented parallelly to stretching direction) as it was discovered in previous 3D stretching [[16], [17], [18], [19]]. Since cyclic stretching of a 3D matrix usually causes its vertical shrinkage, cells sensed a strong molding force from the matrix, causing parallel orientation. Foolen et al. [20]. reported that a 3D stretching that constrained the vertical shrinkage can still reproduce the “vertical” orientation of cells at hydrogel surfaces but not in the core. The difference between a 3D stretching and a quasi-3D one enlightened us to revisit the mechanotransduction in different 3D matrixes.

Cell orientation in our quasi-3D stretching was similar to the 2D stretching. Does it imply that most cells adhered to the bottom of microwells so that they mainly sensed 2D mechanical forces? From the 3D analysis (Figs. 6 and 9) and cell stretching results (Fig. 7 and Movies S2-S5), cells could adhere to the micropillars as well as to the microwell bottom. Besides, cell migration was strongly limited by the micropillars compared to a flat surface (Fig. 8). Therefore, these cells did sense the quasi-3D mechanical stimuli. To maintain internal tension in homeostasis, cells oriented towards the least physical disturbance, that is, perpendicular to the stretching direction.

As cell migration is concerned (Fig. 8), we found that the hMSCs migrated faster in moderate-sized microwells (M) than in small-sized microwells (S) and large-sized microwells (L). The quantification of migration directionality revealed that cell stretching largely influenced the direction of cell migration. Interestingly, stretching has made cell migration faster than non-stretching for L and F, but slower for S and M. It has been known that moderate cell adhesion promotes fastest cell migration [69]. For flat surface (F) and sparse micropillars (L), cell adhesion may be weakened by strong mechanical disturbance (10% stretching at 1 Hz), causing cells to be more suitable for migration. As for dense micropillars (S and M), stretching enhanced cell adhesion by increasing cell traction forces [6], thereby hindered cell migration.

The moderate-sized microwells (M) led to the fastest cell migration among the microwell arrays. Is it caused by the different numbers of micropillars? We calculated the ratio of the projection areas of the micropillars to the whole surface area. The pillar projection ratios are 24% (S), 20% (M), and 16% (L) (Fig. S2), so the difference of number or density of micropillars cannot account for the optical migration in the case of M.

Since the cell sphericity was in the same order of M > L > S, we speculate that the quasi-3D cell adhesion altered cell behaviors: The M may act as a “proper scaffold” to help the cells to adhere, reorient, and migrate. It has been reported that pore sizes of scaffolds significantly influenced cell migration [70,71]. Our work can precisely control the “scaffold” size, visualize and digitalize the cells in the “scaffolds”, and provide evidence that cell responses can be enhanced when the scaffold size is comparable to the cell size. In the future, by designing biomaterials with proper microstructures, the activities of certain types of cells could be enhanced for e.g. tissue regeneration.

4.4. Oxygen plasma treatment can serve as a coating-free method to promote cell adhesion and migration on otherwise nonadherent PDMS surfaces

Usually, fibronectin was used to coat PDMS surfaces to promote cell adhesion. However, we found that cell migration was suppressed by fibronectin (data not shown), probably due to the strong cell adhesion brought by fibronectin. We further found that, by applying a mild oxygen plasma treatment on PDMS, cells adhered properly on PDMS surface without the coating of fibronectin (Fig. S6), probably because plasma treatment activated PDMS-protein binding and adsorption. With this easy and effective method, obvious cell migration was observed in both stretching and non-stretching scenarios.

4.5. Study of different types of cells to estimate the similarity of a quasi-3D microenvironment to a 3D one while being convenient to be observed like on 2D

To what extent does the quasi-3D microenvironment mimic a 3D one? We conducted the study of three kinds of cells cultured in 2D, quasi-3D, and 3D microenvironments (Fig. 10). From the quantitative analysis of vinculin and roundness, the quasi-3D was located in between 2D and 3D. And from the data of cell area, the quasi-3D was closer to the 3D than 2D. Besides, quasi-3D cells exhibited uneven spatial distribution of F-actin and vinculin as 3D cells (Fig. 9). Therefore, the quasi-3D approach does show a strong sign of imitating the 3D microenvironment, and meanwhile, it is unique as a linkage between 2D and 3D.

In summary, our experimental results are schematically presented in Fig. S7. With the well-designed microwells surrounded by micropillars, the cells formed different levels of quasi-3D adhesion. By performing the on-chip cell stretching, we discovered totally different cell responses to the microwell arrays. A series of cell responses (spreading, orientation, migration, and directionality) were enhanced in the middle microwells (M), which reflect the proper level of quasi-3D cell characteristics. Different from the work carried out on resting topography [[72], [73], [74]], our work developed a material platform to precisely control the material topography and can meanwhile perform cyclic stretching of an elastic polymer in a microfluidic device; different from the study of cells on tunable micropillar substrates [6,75], we focused on the study of cells with the sizes matching the micropillar lengths. The microwell arrays were designed with their diameters comparable with cell sizes, which influenced cell adhesion and migration and may be expected to further impact other cell behaviors.

5. Conclusions

A microfluidic chip with a stretchable topographic microstructure was designed and successfully prepared, based on which we constructed the quasi-3D adhesion state of the cells and performed cyclic stretching stimulation. An elastic PDMS membrane with micropillars was fabricated and integrated into a microfluidic chip. A novel chip aligner was invented to facilitate the fabrication process. Cells on the miropillared PDMS treated with mild plasma exhibited quasi-3D adhesion. Cyclic stretching of the cells in different micropillar arrays led to different levels of cell spreading, orientation, migration, and directionality. Moderate-sized microwells surrounded by the polymer micropillars triggered the strongest cell responses. We also studied three types of cells in 2D, quasi-3D, and 3D microenvironments; the results confirmed that the quas-3D microenvironment afforded a linkage between 2D and 3D ones, and we found that in many aspects the appropriate quasi-3D cells could imitate the cells in 3D microenvironment while conveniently observed like on 2D. This study provides valuable tools for stretching cells in a quasi-3D microenvironment and revealed complicated effects of topological features of biomaterials on cells, thus opening a new avenue for investigating geometry-controlled cell behaviors statically and dynamically.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is/are the supplementary data to this article: