Abstract
The separation of an object from other objects or the background by selecting the optimal threshold values remains a challenge in the field of image segmentation. Threshold segmentation is one of the most popular image segmentation techniques. The traditional methods for finding the optimum threshold are computationally expensive, tedious, and may be inaccurate. Hence, this paper proposes an Improved Whale Optimization Algorithm (IWOA) based on Kapur’s entropy for solving multi-threshold segmentation of the gray level image. Also, IWOA supports its performance using linearly convergence increasing and local minima avoidance technique (LCMA), and ranking-based updating method (RUM). LCMA technique accelerates the convergence speed of the solutions toward the optimal solution and tries to avoid the local minima problem that may fall within the optimization process. To do that, it updates randomly the positions of the worst solutions to be near to the best solution and at the same time randomly within the search space according to a certain probability to avoid stuck into local minima. Because of the randomization process used in LCMA for updating the solutions toward the best solutions, a huge number of the solutions around the best are skipped. Therefore, the RUM is used to replace the unbeneficial solution with a novel updating scheme to cover this problem. We compare IWOA with another seven algorithms using a set of well-known test images. We use several performance measures, such as fitness values, Peak Signal to Noise Ratio, Structured Similarity Index Metric, Standard Deviation, and CPU time.
Keywords: Image segmentation, Whale optimization algorithm, Linearly convergence, Local Minima, Kapur’s entropy
Introduction
Image segmentation is the practice of splitting an image into several homogeneous and continuous regions that do not overlap so that any two of these regions are heterogeneous. It is a mandatory step in image processing (Kuruvilla et al. 2016) and computer vision (Hu et al. 2016) to facilitate the analysis and understanding of images. Recently, there are various types of images to be processed and analyzed, such as X-ray (Zhang et al. 2020), Nuclear Magnetic Resonance (NMR) (Griswold et al. 2019), computed tomography (Farook et al. 2020; Zhang et al. 2020), sonar (Song and Liu 2020), position emission tomography (Bal et al. 2020), thermal (Al-Musawi et al. 2020), light intensity (gray-scale), and color images. Several image segmentation approaches have been developed, including region detection (Aksac et al. 2017), edge detection (Prathusha and Jyothi 2018), Feature selection-based clustering (Narayanan et al. 2019), and threshold segmentation (Han et al. 2017).
Threshold segmentation is one of the most commonly used approaches categorized into bi-level threshold and multi-level threshold. In the bi-level threshold, we can group image objects into two classes: foreground (object) and background. When the image contains different objects with different intensity, the bi-level threshold couldn’t segment it. Accordingly, we use a more complex threshold segmentation called a multi-level one. The multi-level threshold groups the image objects into more than two classes. Threshold segmentation is simple, accurate, fast, and needs small storage. Unfortunately, time complexity increases exponentially with the multi-level threshold. The used threshold techniques try to find the optimal threshold values based on two approaches: parametric and non-parametric approaches (Dirami et al. 2013). In the parametric approach, each class in the image has some parameters to be calculated using a probability density function. The non-parametric one obtains the threshold values by maximizing some of those functions (Kapur’s entropy (Kapur et al. 1985), fuzzy entropy (Oliva et al. 2019), and Otsu method (Otsu 1979; Bhandari and Kumar 2019)) without using statistical parameters.
The traditional techniques used to find the optimal threshold values are time-consuming. Meta-heuristic algorithms have been used and integrated with threshold segmentation techniques to overcome the high time complexity for a multi-level threshold. Many authors pay attention to employ meta-heuristic algorithms for solving multi-threshold segmentation problems, including Genetic Algorithm (GA) (Elsayed et al. 2014), Particle Swarm Optimization (PSO) (Guo and Li 2007; Xiong et al. 2020; Di Martino and Sessa 2020), ant-colony optimization algorithm (Kaveh and Talatahari 2010), Whale Optimization Algorithm (WOA) (Abd El Aziz et al. 2017), symbiotic organisms search optimization (Chakraborty et al. 2019), and firefly optimization (Erdmann et al. 2015).
Unfortunately, the algorithms in the literature for the ISP suffer at least from one of the following problems:
Falling into local minima,
Low convergence speed,
Not feasible for tackling images having higher threshold levels.
Therefore, in this paper, a new optimization approach based on the improved whale optimization algorithm is proposed to overcome the previous drawbacks for the ISP.
Recently, a new optimization algorithm (Mirjalili and Lewis 2016), namely whale optimization algorithm (WOA), has been proposed for tackling continuous optimization problems. Although the significant performance of the WOA in reaching good outcomes for several real optimization problems (Abdel-Basset et al. 2020; Jafari-Asl et al. 2021; El-Fergany et al. 2019), it still suffers from the local minima and the low convergence speed. Therefore, in this paper, WOA is improved using two strategies to promote its exploration and exploitation capabilities. The first strategy is the linearly convergence increasing and local minima avoidance technique (LCMA) that moves the positions of the worst solutions to be near to the best solution and at the same time randomly within the search space of the problem to avoid falling into local minima. The second strategy is the ranking-based updating method (RUM) to replace the unbeneficial solutions with other better solutions, helping in improving its performance. After then, these strategies are effectively integrated with the standard WOA to maximize Kapur’s entropy for tackling the ISP. Empirically, the improved WOA (IWOA) is validated 13 test images taken from Berkeley Segmentation Dataset (BSD) with threshold levels between 2 and 100 to check the efficacy of IWOA in selecting the optimal thresholds. To see the superiority of the proposed algorithm, it is compared with a number of well-known optimization algorithms under various performance metrics: SSIM, PSNR, STD, fitness value, and CPU time. The empirical outcomes prove the efficacy of IWOA on these images in comparison to the compared optimization algorithms for SSIM, PSNR, STD, and the values of the objective. Unfortunately, the proposed algorithm couldn’t overcome some compared algorithms for the CPU time as our main limitations, but its superiority for the other metrics, such as SSIM, PSNR, and STD makes a better alternative for the existing method proposed for ISP. Finally, we summarize the main contributions of this paper as follows:
We propose an Improved Whale Optimization Algorithm (IWOA) based on Kapur’s entropy for solving the multi-threshold image segmentation.
We improve the performance of IWOA using the LCMA, and RUM.
Several experiments and the Wilcoxon rank-sum test are conducted to prove the efficacy of IWOA in comparison with other well-known algorithms based on some performance metrics, including Peak Signal to Noise Ratio (PSNR), Structured Similarity Index Metric (SSIM), and fitness value metrics using a set of benchmark test images.
We organize the remaining of the paper as follows. Section 2 presents the previous works done for tackling the multi-threshold image segmentation problem. In Sect. 3, we introduce the multi-threshold image segmentation problem using Kapur’s entropy. Moreover, Sect. 4 describes the whale optimization algorithm. Section 5 explains and illustrates the proposed algorithm. Section 6 shows the experiments outcome and their discussions. Finally, Sect. 7 draws the conclusions and the future works about the proposed algorithm.
Related work
Image segmentation groups the pixels of an image according to some specific criteria, including textures, shape, color, and intensity. Many applications exploit image segmentation in understanding and analyzing the acquired images, such as medical diagnosis (Mittal et al. 2020; Zhang et al. 2020; Sinha et al. 2020; Ren et al. 2019), object recognition (Wang et al. 2019), geographical imaging (Chen 2020), satellite image processing (Karydas 2020), remote sensing (Su and Zhang 2017), historical documents (Alberti et al. 2017), and historical newspapers (Naoum et al. 2019; Barman et al. 2020). Although threshold segmentation is easy to implement and has a low computational burden, it is still a challenge for the researchers to determine the optimal n- level threshold. The traditional methods to search for optimal thresholds values such as an exhaustive search can be tedious and computationally expensive. Many authors handled the problem of n- level threshold as an optimization problem solved using meta-heuristic algorithms, which could overcome several optimization problems (Abdel-Basset et al. 2020a, b, [44], Abdel-Basset et al. 2020; Lang and Jia 2019). We will review several attempts done for the optimal threshold selection.
Singla and Patra (2017) selected the initial thresholds by obtaining the mid-points of any two consecutive peaks of the energy curve of an image. Then, the cluster validity measure tries to find the potential thresholds and the bounds that may contain the optimal ones. Finally, the GA algorithm seeks to discover the optimal thresholds from its defined bounds. Also, Manikandan et al. (2014) proposed GA with a simulated binary crossover to maximize the Kapur’s entropy for medical image segmentation. Another meta-heuristic algorithm PSO introduced for image segmentation. Maitra and Chatterjee (2008) integrated PSO with cooperative and comprehensive learning to face the dimensionality curse and to reduce the premature convergence of the swarm, respectively. Consequently, a modified PSO (Liu et al. 2015) employed the adaptive inertia and the adaptive population to improve its performance for maximizing the Otsu’s function to find the optimal thresholds, which will separate homogenous regions within an image. The MPSO has been validated on 12 test images and compared with the standard PSO and GA. Ghamisi et al. (2013) introduced fractional-order Darwinian PSO to solve the problem of the n-level threshold based on Otsu to maximize the variance between the classes.
Another metaheuristic is the Bacterial Foraging Algorithm (BFA). Sanyal et al. (2011) applied an adaptive BFA for gray-scale image segmentation depending on fuzzy entropy, which adaptively switches the bacterium between exploitation and exploration stages. Also, the authors in Sathya and Kayalvizhi (2011) accelerated the convergence of a modified BFA by moving the best bacteria to the subsequent iterations. The results proved that the modified BFA based on Otsu’s function has a high convergence speed in comparison with Kapur’s one. After that, a cooperative BFA (Liu et al. 2015) combined a self-adaptive foraging strategy, which controls the swim amplitude and cell-to-cell communication. The cooperative BFA had higher quality segmentation and less CPU time. Furthermore, BFA (Tang et al. 2017) is incorporated with PSO to support the global search capability in addition to the weak bacterium, which selects a random strong one to reach a location near it. Pan et al. (2017) developed BFA depending on edge-detection for cell image segmentation as the traditional edge-detection techniques are costly expensive and may produce disconnected edges. Lately, BFA (Wang et al. 2019) is integrated with PSO to avoid randomly selecting the direction of the bacterial chemotactic step.
Mostafa et al. (2017) proposed a liver image segmentation using WOA that multiplies the clustered image by the binary one. This clustered image divides the liver image into a predetermined number of clusters. Also, the algorithm used the statistical image to indicate the liver position and converted it into a binary one. The problem of multi-level threshold segmentation (Abd El Aziz et al. 2018) is handled as a multi-objective problem that maximized both the Kapur’s entropy and Otsu’s function. Abd El Aziz et al. (2017) examines the performance of the WOA and Moth-Flame Optimization (MFO) algorithm. WOA traps into local optima while MFO succeeds in balancing the switch between the exploration and the exploitation phases (Sikariwal and Chanak 2018). Ultimately, some of the most recent multilevel thresholds image segmentation method are briefly discussed in Table 1.
Table 1.
Some recent methods proposed for ISP
| Algorithms | Contributions and disadvantages |
|---|---|
| Hybrid slime mould optimizer with whale optimization algorithm (HSMA_WOA) (Abdel-Basset et al. 2020) | Contributions |
| – This paper proposed a new image segmentation algorithm based on integrating the slime mould algorithm (SMA) with the whale optimization algorithm for segmenting the Covid-19 X-ray images | |
| – This approach employed both SMA and WOA together to unify their advantages for overcoming the disadvantages of each one separately | |
| – Afterward, HSMA_WOA has validated 12 chest X-ray images and its outcomes were compared with those of a number of well-known optimization algorithms to see their efficacy | |
| – Finally, the experimental findings show the superiority of the HSMA_WOA over the others | |
| Disadvantages | |
| – Its performance for general test images has not been observed | |
| An equilibrium optimizer (EO) (Abdel-Basset et al. 2021) | Contributions |
| – In this paper, the equilibrium optimizer was adapted for the multilevel thresholding image segmentation problem by maximizing Kapur’s entropy to find the optimal threshold values for various threshold levels | |
| – It has been validated using a number of images and compared to some well-known optimization algorithms to appear its efficacy | |
| Disadvantages | |
| – Still suffers from falling inside local minima which prevents it from reaching the optimal threshold values | |
| Improved marine predators algorithm (IMPA) (Abdel-Basset et al. 2020) | Contributions |
| – Recently, a novel multilevel thresholding image segmentation approach has been proposed for segmenting the Covid-19 X-ray images | |
| – This approach was based on the marine predators algorithm improved by a ranking-based diversity reduction strategy to increase the exploitation capability of the standard marine predators algorithm | |
| – The experimental outcomes proved the superiority of this improved one in terms of PSNR, SSIM, standard deviation, fitness values, and UQI | |
| Disadvantages | |
| – A little expensive in terms of the computational cost compared to the standard MPA and some of the rival algorithms | |
| Antlion optimization (ALO) and multiverse optimization (MVO) algorithms (Chouksey et al. 2020) | Contributions |
| – In this paper, both ALO and MVO have been proposed for overcoming the multilevel thresholding image segmentation problem by maximizing both Kapur’s entropy and the Otsu method | |
| – Those two algorithms were compared with other evolutionary methods in terms of PSNR, SSIM, feature similarity index (FSIM), standard deviation, stability analysis, and fitness values. The experimental results showed that MVO is faster and better than the compared methods | |
| Disadvantages | |
| – Its performance for threshold levels higher than 5 is not known and hence not preferred for the images that have threshold levels higher than that | |
| An improved Bloch quantum artificial bee colony algorithm (ABC) (Huo et al. 2020) | Contributions |
| – The ABC has been improved by the quantum Bloch spherical coordinates of the qubit for reaching better outcomes within a small number of iterations when solving the multilevel thresholding image segmentation problem | |
| – The experimental outcomes show the superiority of the proposed algorithm | |
| Disadvantages | |
| – Low convergence speed | |
| – Falling into local minima | |
| Coyote optimization algorithm (COA)(Moses 2020) | Contributions |
| – In this paper, the COA was adapted to tackle the ISP | |
| – The experimental outcomes showed the superiority of the COA in terms of convergence speed, objective values, and image quality | |
| Disadvantages | |
| – Moves slowly to the near-optimal solution and this will make it consume several function evaluations | |
| Crow search algorithm (CSA) (Moses et al. 2019) | Contributions |
| – Those authors proposed the CSA with the Otsu method as an objective function for selecting the optimal threshold values | |
| – The CSA proved its superiority over the improved particle swarm optimization (PSO), firefly algorithm (FFA), and also the fuzzy version of FA in terms of the quality of the segmented image, and the objective values | |
| Disadvantages | |
| – Low convergence speed | |
| – Not observed for threshold levels greater than 5 | |
| Modified water wave optimization (MWWO) algorithm (Yan et al. 2020) | Contributions |
| – In this paper, the water wave optimization algorithm was modified by the opposition-based learning strategy and ranking-based mutation strategy to find the optimal values for the underwater image segmentation problem | |
| – The opposition-based learning was used to increase the diversity of the individuals to avoid being stuck into local minima and reach better outcomes. While the ranking-based mutation operator was used to improve the selection probability | |
| – The experimental results showed the superiority of MWWO in terms of the segmented images and the objective values over the other compared algorithms | |
| Disadvantages | |
| – Not compared with the recently-published algorithms where the latest compared algorithm was published in 2017 | |
| Modified Red Deer Algorithm (MRDA) (De et al. 2020) | Contributions |
| – The red deer algorithm modified by a few adaptive approaches to improve its efficacy has been proposed in this research for tackling the image segmentation problem | |
| – This algorithm was compared with the standard one and genetic algorithm over a set of real-life test images and could prove its efficacy in terms of fitness value, convergence speed, and standard deviation | |
| Disadvantages | |
| – Not investigated using several test images to check its stability, in addition to using a huge number of iteration up to 1000 which notifies its low convergence speed in the right direction of the near-optimal solution | |
| Modified hybrid bat algorithm (Yue and Zhang 2020) | Contributions |
| – Recently, the bat algorithm has been modified by a genetic crossover operator and a smart inertia weight (SGA-BA) to enhance its performance for maximizing the Otsu method to estimate the optimal thresholds of a set of images | |
| Disadvantages | |
| – Consuming computational cost higher than the other compared algorithm | |
| Improved flower pollination optimizer (IFPA) (Li and Tan 2019) | Contributions |
| – In this paper, the authors improved the flower pollination algorithm for optimizing the Tsallis entropy as an objective function to find the optimal thresholds that separate similar regions within an image | |
| – The experimental results show the superiority of this improved one compared to those three algorithms | |
| Grey Wolf Optimizer (GWO)(Khairuzzaman and Chaudhury 2017) | Contributions |
| – The GWO has been proposed for finding the optimal thresholds to separate similar regions within an image. This algorithm used Kapur’s entropy and Otsu method as objective functions to find those optimal thresholds | |
| – The experimental results show that GWO could be superior in terms of the quality of segmented images and stability and speed | |
| Disadvantages | |
| – Using the intensity of the image to perform the segmentation process | |
| – Not adequate for the images having intensity inhomogeneity problem |
Many other meta-heuristic algorithms are developed for image segmentation, such as cuckoo search (Bhandari et al. 2014), bat algorithm (Yue and Zhang 2020), flower pollination algorithm (Wang et al. 2015), crow search algorithm (Oliva et al. 2017; Upadhyay and Chhabra 2019), Harris hawk optimization algorithm (Bao et al. 2019), grey wolf optimizer (Yao et al. 2019), krill herd algorithm (He and Huang 2020), bee colony algorithm [59], multi-verse optimizer (Kandhway and Bhandari 2019), and locust search algorithm (Cuevas et al. 2020). Unfortunately, the traditional methods for threshold image segmentation are costly in terms of computations and time-consuming. Therefore, many of the researchers find themselves forced to search for new ways to solve this problem in less time and not computationally expensive. One of these ways is to deal with threshold image segmentation as an optimization problem that can be solved using meta-heuristic algorithms. However, the success of meta-heuristic algorithms in obtaining an optimal solution in a reasonable time, the balance between the exploration and exploitation phases and falling into local optima are the biggest problem to face when dealing with theses algorithms. Also, the convergence speed of the algorithms toward the optimal solution may be slow.
As a result, this paper comes to address the aforementioned drawbacks and solve the problem of threshold image segmentation. WOA is one of the meta-heuristic algorithms that are applied to many problems (Mafarja and Mirjalili 2018; Liu et al. 2020; Abdel-Basset et al. 2018). This motivates us to propose an improved whale optimization algorithm that employs the LCMA technique for tackling threshold image segmentation. LCMA works on solving two problems that the WOA suffers from. WOA at the start has high exploration capability and reduces gradually with the iteration; this is considered the first problem due to reducing the convergence speed within the starting of the optimization process. After finishing the exploration capability, which after the first half of the iteration, the WOA will pay attention to the best-so-far solution to find a better solution around it if it is not local minima and this is considered the second problem. Accelerating the convergence speed of the algorithm toward the best-so-far and avoiding falling into local minima motivate us to propose LCMA to move the locations of K worst individuals near to the location of the best one and randomly within the search space according to a certain probability, in addition to using the ranking-based updating method (RUM) to replace the unbeneficial solutions with other solutions generated based on a novel scheme helping the algorithm in exploiting more solutions around the best-so-far solutions. K, at the start, carries a small value, and this value increases gradually with the iteration until getting to the maximum (all the individuals in the population) at the ending of the optimization process. Kapur’s entropy illustrated in the following section is used to evaluate the quality of the solutions.
Mathematical model of Kapur’s entropy
Kapur’s entropy (Kapur et al. 1985) is a method that works on finding the optimal threshold values that will separate the similar regions within an image by maximizing the entropy of the histogram. Let’s start with a bi-level threshold. In bi-level threshold, this method tries to find the threshold value t that divides an image into background and foreground, namely, B and F that maximize the following function:
| 1 |
| 2 |
| 3 |
where determines the number of pixels with a grey value i, and T is the total number of pixels in an image. and refer to the respective probabilities of each class. L is the highest value for a pixel in a grey-scale level and equal 255. The previous function was used for finding the threshold value for the bi-level threshold problem. Also, it can be adapted easily for tackling the multi-level threshold problem by redesigning as follows:
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
where n is the number of threshold levels, and is the threshold values such that: At the end, our proposed algorithm will work on maximizing Eq. (4) to find the optimal threshold values.
Whale optimization algorithm
In WOA, Mirjalili and Lewis (2016) simulates the actions and conducts performed by the humpback whales. The whales surround the victim in a spiral shape swimming up to the surface in a shrinking circle using an astounding feeding method called the bubble-net approach when attacking their victim or prey. WOA simulates this hunting mechanism by making a probability of selecting between a spiral model and a shrinking encircling prey to generate the new position of the current whale. To exchange practically between the spiral model and the shrining encircling mechanism, first, a random number, namely p, is created between 0 and 1 and if this number is less than 0.5, then the encircling mechanism is applied; otherwise; the spiral model is employed. The mathematical formula for the encircling mechanism (exploitation phase) is as follows:
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
where is the position of the current whale, it is the current iteration, is the position of the best whale in the population, rand is a random number in [0, 1], refers to the course of iterations, is computed using Eq. (12) which measures the distance between the best-so-far solution, multiplied by a random number C between 0 and 2, and the current whale and a is a distance control parameter linearly decreased from 2 to 0. The spiral model tries to mimic the helix-shaped movement of whales, so it is proposed between the position of the victim and the whale. The mathematical model of a spiral shape (exploitation phase) is as follows:
| 14 |
| 15 |
where indicates the distance between the position vector of prey and whale, l is a random number between [−1, 1], b is a constant to describe the logarithmic spiral shape. To search for the prey in another direction in the search area, WOA uses a random whale from the population to update the position of the current whale in the exploration phase. If is greater than 1, then the current whale is updated according to a random whale from the population. The mathematical model of the search for the prey (exploration phase) is as follows:
| 16 |
| 17 |
where is a random position vector selected from the current population. The pseudo-code of the standard whale optimization algorithm is described in Algorithm 1.
The proposed approach
In this section, the improved whale optimization algorithm (IWOA) is adapted for tackling multi-threshold image segmentation problems. IWOA is improved using two strategies to promote its exploration and exploitation capabilities:
The first strategy is the linearly convergence increasing and local minima avoidance technique (LCMA) that moves the positions of the worst solutions to the direction of the best-so-far solution or within the search space of the problem to prevent stuck into local minima.
The second strategy is the ranking-based updating method (RUM) to replace the unbeneficial solutions with other better solutions, helping in improving its performance.
The next subsections will illustrate the proposed algorithm in more detail.
Initialization
In this phase, a population of N whales is randomly generated. The dimension of each whale is initialized randomly within the boundaries of gray levels of the image as illustrated in the following equation:
| 18 |
where and is the minimum and maximum of the gray level values in the image histogram, and rand(0, 1) is a random number in the range of [0, 1]. The grey-scale level is represented in 8-bit, where the lowest value in decimal is 0 and the highest is . For representing the positions of the whales within and , Eq. (18) will be used to distribute the position of each whale within this boundary. For example, let’s imagine an image with homogenous regions (n) equal to 10. For finding those threshold values that will separate those regions from each other using the WOA, then WOA will spread its solutions within the search space randomly as shown in Fig. 1 that depicts a solution from among all the solutions to illustrate a representation of the solutions to the image segmentation problem for the grey-scale image.
Fig. 1.
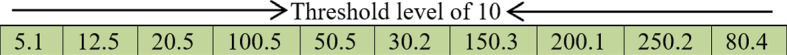
Depiction of a solution to multilevel thresholding
After distributing the solutions within the boundaries of the problem, these values should be transformed into integers because each pixel in the grey image is represented with only 8-bit for an integer value and subsequently each pixel will only load an integer value not decimal. As a result, the values before the dot within Fig. 1 will be used to represent the solution for the image segmentation problem and the numbers after the dot will be truncated as shown in Fig. 2.
Fig. 2.
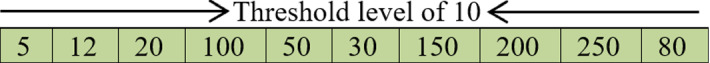
Unordered integer threshold values
Afterward, the integers in Fig. 2 will be arranged as depicted in Fig. 3 and Eq. (4) is called to calculate the quality of those threshold values under Kapur’s entropy.
Fig. 3.
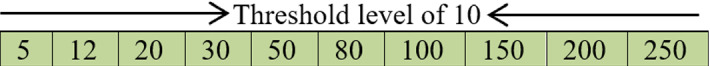
Ordered integer threshold values
The previous steps will distribute the dimensions (number of threshold values required) of the problem within the search space, convert them into integer values, arrange them, and evaluate them using Eq. (4) will be applied for each solution within the initialization step. After that, the initialization step will terminate and the solution created using WOA within the optimization process will be only converted into an integer, arranged, and evaluated using Eq. (4).
Linearly convergence increasing and local minima avoidance strategy
We propose a linearly convergence increasing and local minima avoidance strategy (LCMA) to accelerate the convergence speed of the worst solutions toward the best solution and at the same time to avoid the local minima problem that the optimization algorithms may fall into. LCMA updates a number of K worst individuals, or whales for consistency with the proposed algorithm, in the population towards the best solution found so far and randomly within the search space of the problem based on a certain probability known as exploration rate (ER) to avoid falling into local minima. We can calculate K using the following equation:
| 19 |
where N determines the size of the population, it is the current iteration, maxIter is the maximum number of iterations, and x is a fixed number of the solutions that will be updated within each iteration. round is used to round a number to the nearest integer. After calculating the number of worst individuals K, we update each one of the worst individuals using Eq. (20) to update their positions toward the best solution gradually.
| 20 |
where refers to the worst solution, and is a random numerical vector in the range of [0, 1]. and are two vectors used to contain the upper bound and the lower bound of the search space of the optimization problem, respectively. is a binary vector used to determine if the exploration capability will be applied or not, and will be generated according to the following formula:
| 21 |
In Eq. (21), if the current position in vector corresponding to a value in vector is greater than ER then this position will take a value of 1 (which this position will take an exploration capability), otherwise it will take a value 0. Algorithm 2 illustrates the steps of the LCMA technique.
Typically, at the start, the optimization algorithms give the highest capability for exploration even exploring most of the regions within the search space. This capability may waste most of the iterations within the optimization process without any benefits, although the best current solution may not be a local minima. Subsequently, paying attention to the best-so-far solution will help in reaching the optimal solution in less time. Based on that, we propose this methodology to give the optimization algorithm a high ability on finding a better solution in a reasonable time. On the other side, in some of the meta-heuristic algorithms, its exploration capability is erased at the end of the iterations and subsequently, the possibility of finding a better solution if the current best one is local is impossible. As a result, we support a part within our methodology to dispose of this problem by giving the optimization algorithm ability on searching within the search space of the problem for a better solution. The advantage of LCMA is helping in accelerating the convergence speed toward the best-so-far solution with decreasing falling into the local minima problem.
Our methodology is distinct from the evolutionary population dynamics (EPD) (Saremi et al. 2015) where, in EPD, the worst n/2 solutions are removed from the population and added alternatively n/2 solutions generated randomly around the best-so-far solution. On the other hand, LCMA will select a number of the worst-so-far solution to move them toward the best-so-far randomly with exploration rate within the search space of the problem based on a certain probability (ER) to avoid stuck into local minima. In addition, this number of the worst selected solution will start with a small number and increases with the iteration until reaching the maximum (all the individuals within the population) at the end of the iteration.
Ranking -based updating method (RUM)
Recently, a new strategy (Abdel-Basset et al. 2020) known as a ranking strategy has been proposed to replace the unbeneficial solutions with others helping the algorithm in reaching better outcomes. The main obstacle in front of this strategy is the updating method used to generate a new solution in the form that will improve the performance of the proposed algorithm. Therefore, within our work, a new updating method to promote the exploitation capability gradually with the iteration even reaching the maximum at the end of the iteration is proposed. Mathematically, this updating method is formulated as follows:
| 22 |
Where and are the indices of two whales selected randomly from the population. is a numerical vector generated randomly between 0 and 1.
The pseudo-code of IWOA
To evaluate the solutions, we use Eq. (4) as illustrated before in Sect. 3. This function work on finding the homogenous regions based on maximizing the entropy of the histogram. In our proposed algorithm, this function is used as a fitness function to find the optimal threshold values that maximize the variance of an image. The pseudo-code of the proposed algorithm IWOA to solve the multi-thresholding segmentation problem is shown in Algorithm 3 and the same steps are pictured in Fig. 4. In Algorithm 3 shows the pseudo-code of the proposed algorithm IWOA to solve the multi-thresholding segmentation problem. In Algorithm 3, the standard algorithm is integrated with the LCMA strategy to promote its exploitation in addition to avoiding entrapment into local minima as possible. Furthermore, to utilize the whales in the population within the optimization process as much as possible, the RUM is used as an attempt to increase the exploitation capability of the proposed to find a better solution. Broadly speaking, RUM is employed to replace those solutions which spent a consecutive number, namely Rk, of the failed attempts exceeding the predefined threshold thr recommended 3.
Fig. 4.
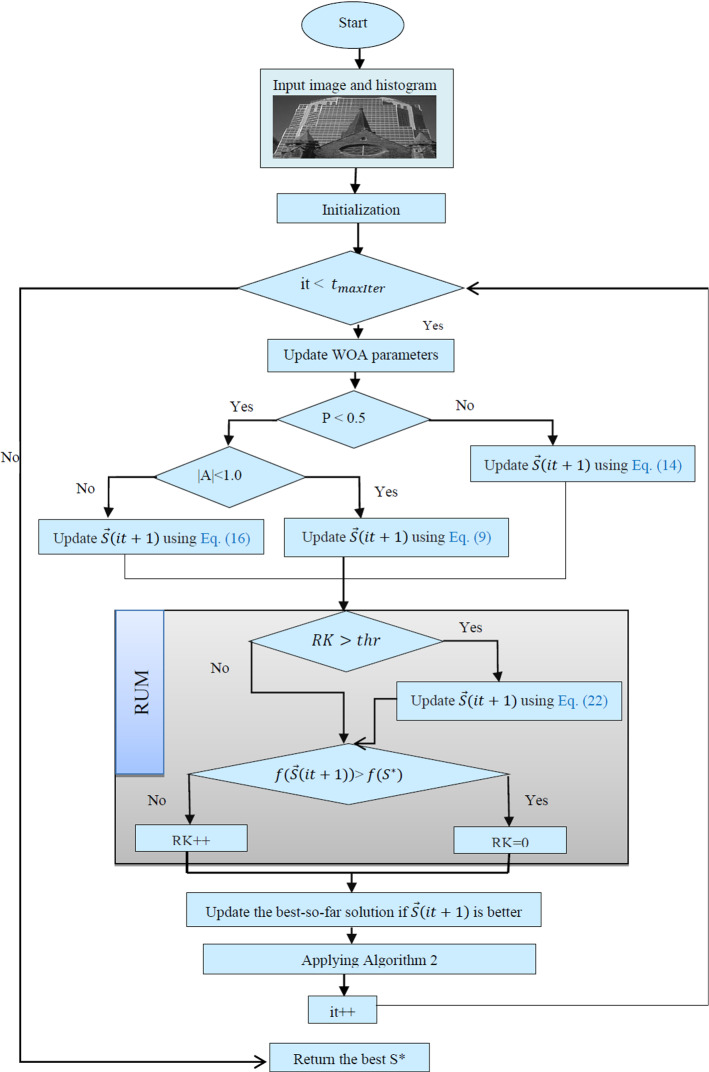
Flowchart of the proposed algorithm IWOA for Multi-threshold image segmentation problem
Since the LCMA moves randomly a number of the worst solution toward the best-so-far solution, a large number of the solutions around the best-so-far may be skipped without exploring although of the possibility of finding better solutions within them. Therefore, the RUM is used with the proposed algorithm to explore gradually the solutions around the best-so-far solutions as an attempt to reach better outcomes.
Figure 4 shows the flowchart of the IWOA. At the start, within this figure, the test images and their histogram are inputted to the proposed algorithm; after that, the initialization step is executed to distribute a number of the solutions within the upper and lower bound values of 255 and 0, respectively. Those initialized solutions will be updated by the standard WOA, LCMA, and RUM as depicted in this figure for reaching better fitness values. Finally, the best-so-far solution is returned to generate the segmented image using algorithm 4.
Our motivations to WOA and segmented image generation algorithm.
At the start, WOA starts with a high exploration capability and this capability gradually reduces with the iteration even fading away after the first half of the iterations. Afterward, the exploitation capability will dominate the whole optimization process to explore most of the regions around the best-so-far solution for finding better if it is not local minima. And this is considered the main advantage of WOA, in addition to the easiness to be understood and implemented, which motivates us to use it. But unfortunately, the WOA suffers from several disadvantages, which are described as follows:
The high exploration capability at the outset may waste a lot of iterations without any beneficial or utilizing optimally for those the wasted iterations.
After the first half of the iterations, the exploration capability will be terminated, and subsequently, the possibility of finding a better solution if the current one is local minima is impossible.
In the second half of the iteration, the exploitation capability will dominate the whole optimization process to explore most of the regions around the best-so-far solution, and subsequently, a lot of the iterations may be wasted if the current best solution is local minima.
To overcome all those drawbacks, we used LCMA and RUM to help in improving the convergence of the WOA and avoiding stuck into local minima problems within the optimization process. The main advantages of our proposed are listed as:
Our proposed has a high ability on the exploitation at the outset to increase the convergence toward the best-so-far solution, and high ability on the exploration within the optimization process to help in disposing of local minima problem.
Utilizing each whale in the population as much as possible for reaching better outcomes.
Also, it helps in exploiting optimally the individuals of the population within the optimization process.
Increase the convergence toward the best solution in a reasonable time.
A small number of parameters for adjustment.
The main drawbacks of our proposed are listed as:
Picking the value for the ER parameter accurately to adjust the performance of the proposed for reaching a better solution.
A little expensive for computational cost compared to some other algorithms.
How the segmented image will be generated under the threshold values obtained? Let’s suppose that an original image is called A with a number of rows and columns of N and M, respectively. And after finding the optimal threshold values under any threshold level, the segmented image will be generated as shown in algorithm 4.
Time complexity for the pseudo-code of IWOA
To show the speedup of the proposed algorithm, in this section, the time complexity in big-O will be designed to see that. At the outset, the main factors that especially affect the speedup of the proposed algorithm are:
The population size: N.
The threshold level: n
The maximum iteration: .
The time complexity of algorithm 2.
In regards to the time complexity formula of the proposed, it is formulated as follows:
| 23 |
Where, the standard WOA is mainly relied only on the former first three factors and that is aggregated in big-O according to algorithm 3 as follows:
| 24 |
Regarding the running time of the LCMA, it also depends on the previous four factors with exception of N, which is replaced by the number of worst whales K extracted using the Quicksort algorithm. Since the Quicksort is utilized, its time complexity is of in the worst case for iteration (Xiang 2011). In general, the time complexity of the LCMA is formulated as follows:
| 25 |
The time complexity of the quick sort for all iterations is of in the worst case, meanwhile, the time complexity of replaing the worst whale is of . By compensating in Eq. (25), the time complexity of the LCMA strategy is as follows:
| 26 |
From Eq. (26), the expression that has the highest growth rate is of . Therefore, the time complexity of the LCMA strategy in the worst case is of . Likewise, for Eq. (22), that is extended as follows:
| 27 |
From Eq. (27), in final. The time complexity of the IWOA in the worst case is of .
Experiments and discussion
Our experimental studies are performed on a desktop computer using Windows 7 ultimate platform with a 32-bit operating system, Intel Core i3-2330M CPU @ 2.20 GHz, and 1 GB of RAM. The proposed algorithm is tested using low memory capacity to validate working under the most constraint conditions. We use the Java programming language for implementing all algorithms used in our comparisons. In this section, we concern with illustrating the results of our experiments. This section organized as follows:
Section 6.1 describes the test images used in our experiments.
Section 6.2 shows the experimental Settings.
Section 6.3 demonstrates valuation Metrics.
Section 6.4 compares the performance Evaluation of IWOA and WOA.
Section 6.5 investigates the performance Evaluation of our proposed algorithm with the others.
Section 6.6 displays the segmented Images produced by IWOA.
Section 6.7 conducts the Wilcoxon rank-sum test.
Test images description
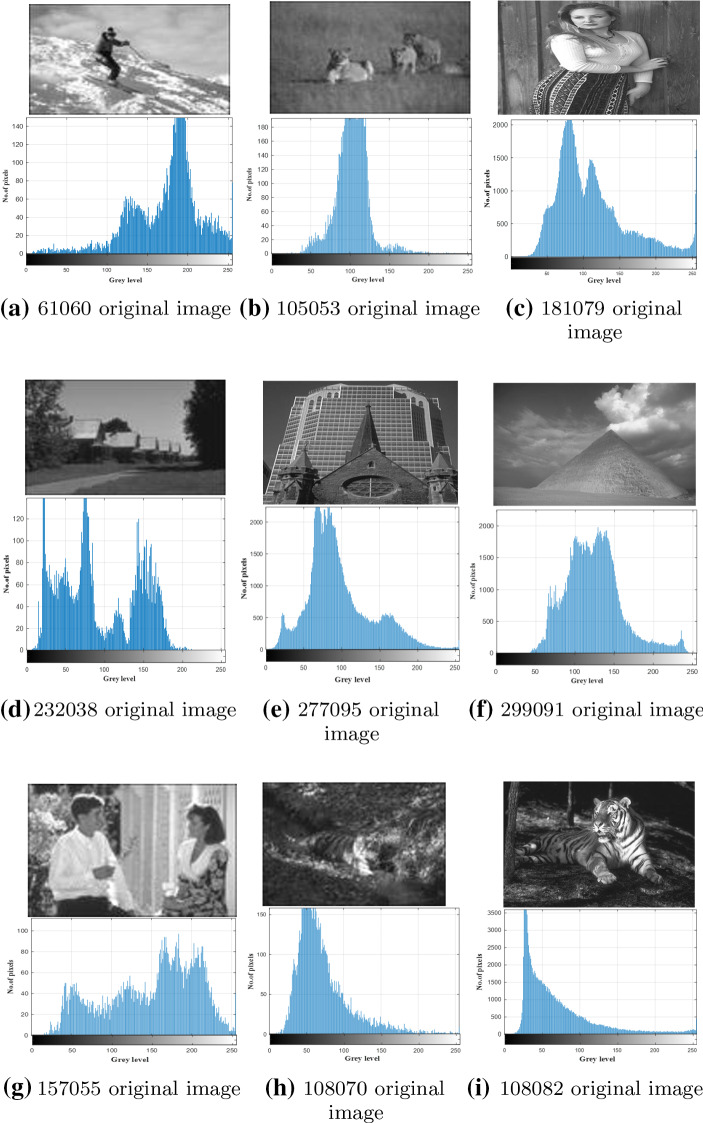
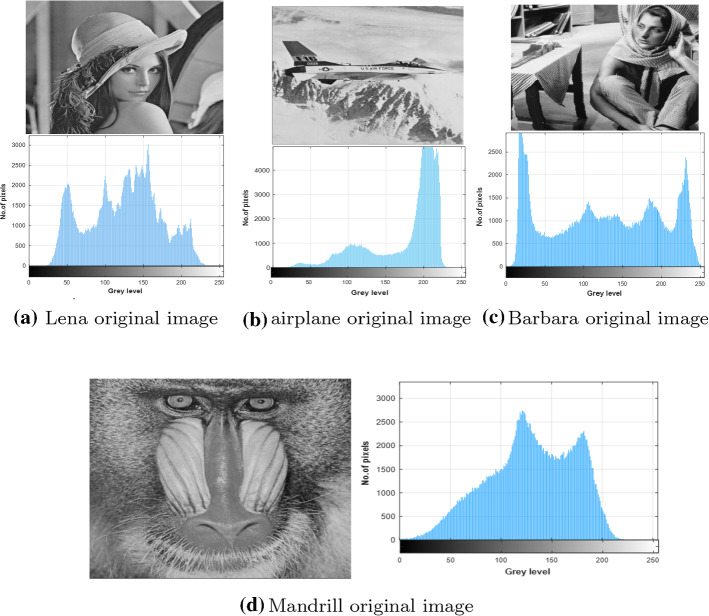
The performance of our proposed algorithm is evaluated on nine test images taken from the Berkeley Segmentation Dataset (BSDS500), and the identifiers (ID) of those images are 61060, 105053, 181079, 232038, 277095, 299091, 157055, 108070, and 108082, in addition to four common test images: Mandrill, Lena, Barbara, and airplane. We used 13 test images in our paper in the same range where the researches in the literature used, for example, whale optimization algorithm (Abd El Aziz et al. 2017) was validated on eight test images, equilibrium optimizer for multi-level thresholding image segmentation used seven test images (Abdel-Basset et al. 2021), and Multi-Level Image Thresholding Based on Modified Spherical Search Optimizer and Fuzzy Entropy Segmentation (Naji Alwerfali et al. 2020) used ten test images. Figures 5, 6 depicts each original image out of the 13 test images and its histogram.
Fig. 5.
Description of the original images and their histograms
Fig. 6.
Description of the original images and their histograms
Parameter settings
Our proposed algorithm is compared with Sine cosine Algorithm (SCA) (Mirjalili 2016), Firefly Algorithm (FFA) (Erdmann et al. 2015), Flower Pollination Algorithm (FPA) (Yang 2012), and standard whale optimization algorithm (Abd El Aziz et al. 2017), L-SHADE (Brest et al. 2016), improved marine predators algorithm (IMPA)(Abdel-Basset et al. 2020), equilibrium optimizer (EO) (Abdel-Basset et al. 2021), crow search algorithm (CSA) (Moses et al. 2019), hybrid WOA (WOA-DE) (Lang and Jia 2019), and salp swarm algorithm (SSA) (Wang et al. 2020). The algorithm parameters are selected based on the standard for these parameters. Also, for a fair comparison, an equal number of function evaluations used with a maximum number of iterations equal 150 and population members set to 30. Additionally, each algorithm runs 30 independently times. Table 2 summarizes the values of the IWOA parameters.
Table 2.
Parameter setting for the proposed IWOA
| Parameter | Value |
|---|---|
| Number of runs | 30 |
| Population size | 30 |
| The maximum number of iterations | 150 |
| X (the number of the redirected particles) | 4 |
| ER | 0.99 |
| thr | 3 |
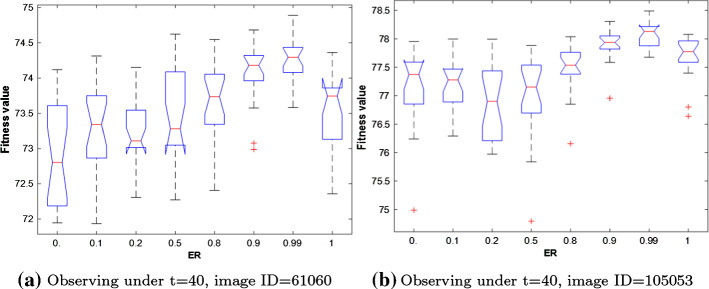
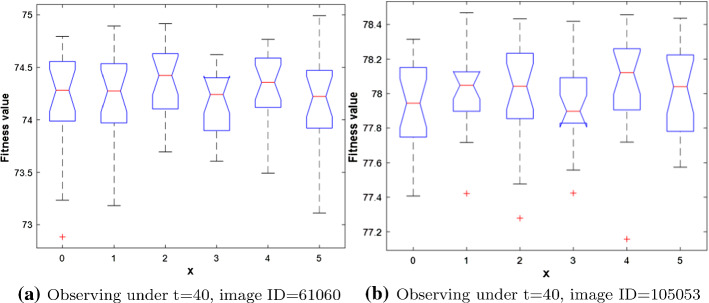
There are two parameters: ER and X in our proposed algorithm needed to be pick accurately for exploiting optimally the performance of our proposed algorithm. Therefore, extensive experiments are performed to extract the best value for those parameters, all those experiments are demonstrated in Figs. 7 and 8 for ER and X parameters, respectively. First, let’s move toward Fig. 7 that depicts the results of our experiments for extracting the best value of the ER parameter. This figure shows the results obtained on two images: 61060 and 105053 with threshold level 40. And inspecting this figure tells us that the best value for ER is 0.99 where it could outperform all the others in the lowest, Quartile-1 (), Quartile-2 (), Quartile-3 (), and the highest values over two images.
Fig. 7.
Depiction of the Boxplot for the outcomes obtained under different value for ER parameter
Fig. 8.
Depiction of the Boxplot for the outcomes obtained under different values for X parameter
Concerning X parameter, an experiment with different values for this parameter involving: 0, 1, 2, 3, 4, and 5 is conducted to extract the best one for this parameter and its results are pictured in Fig. 8 that shows that the best value obtained on two images: 61060 and 105053 with threshold level 40 was by a value of 4, but also for 61060 a value of 2 was competitive with 4. Generally, within our experiments, we used a value of 4 for X parameter. Regarding thr, it is set to as recommended in (Abdel-Basset et al. 2021)
Evaluation Metrics
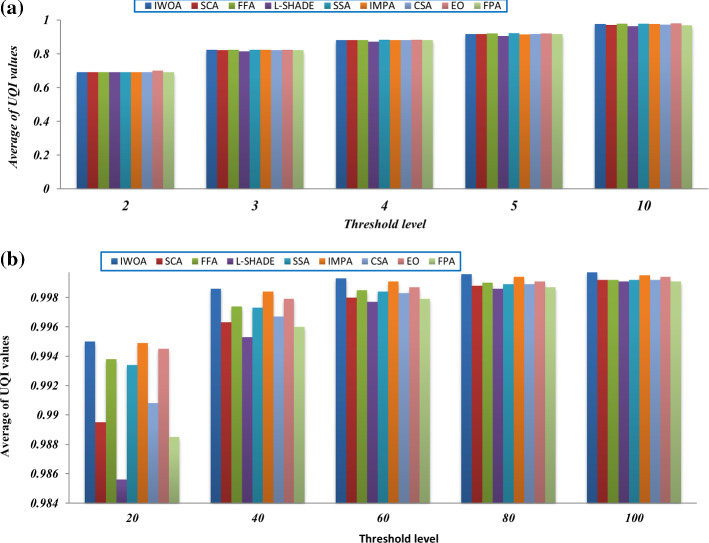
We use six criteria to evaluate the performance of the algorithms, including CPU time, fitness values, Standard Deviation (STD), Peak Signal to Noise Ratio (PSNR), Universal Quality Index (UQI), and Structured Similarity Index Metric (SSIM). We will explain these criteria as follows:
The CPU time is used to calculate the time in seconds taken by each algorithm.
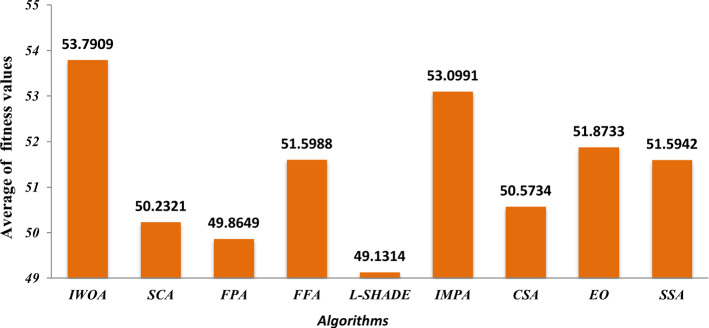
The fitness function is computed using the Kapur’s entropy mentioned above.
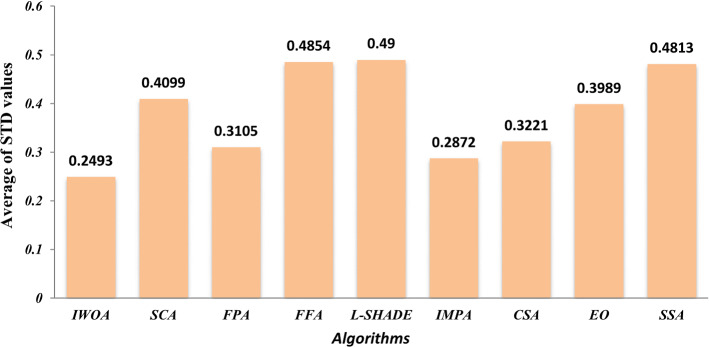
The STD measures the variation and the dispersion of the data of a given algorithm.
- The PSNR (Hore and Ziou 2010) metric measures the quality of the segmented images defined by the following formula:
where 255 determines the maximum pixel value of an image when we represent a pixel in 8 bits, such that: . MSE is the mean squared error and is calculated as follows:28
where O(i, j), S(i, j) represent the original and segmented images, respectively. PSNR is inversely proportional to MSE.29 - The SSIM (Hore and Ziou 2010) metric calculates the difference between the structure of the segmented and original image. The mathematical formula of SSIM is defined as follows:
where and defined the average intensity for both original and segmented images, respectively. and refers to the standard deviation of the original and segmented image, also, stands for the covariance between them. The constant values a and b set to 0.001 and 0.003, respectively.30 - UQI (Egiazarian et al. 2006) is another metric utilized to determine the quality of the segmented image compared to the original one based on three factors: loss of correlation, brightness, and contrast distortion. Mathematically, this model is formulated as follows:
31
The higher value of PNSR and SSIM indicate better performance. PSNR metric work on finding the ratio of the error between the original and the segmented images and don’t focus on the structure of the image after the segmentation on the correlation, luminance distortion, and contrast distortion that specifies the quality of the segmented images. As a result, SSIM is used to pay attention to measure the difference between the structures of the original image and segmented based on the following three factors: loss of correlation, luminance distortion, and contrast distortion between the original and segmented images.
The performance evaluation of IWOA, WOA, and WOA-DE
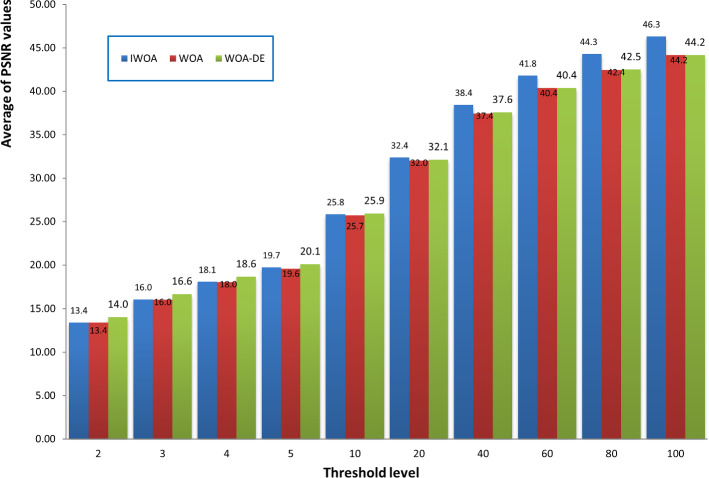
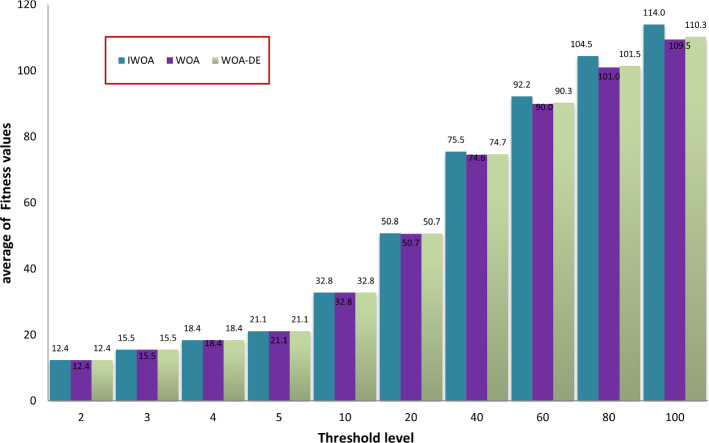
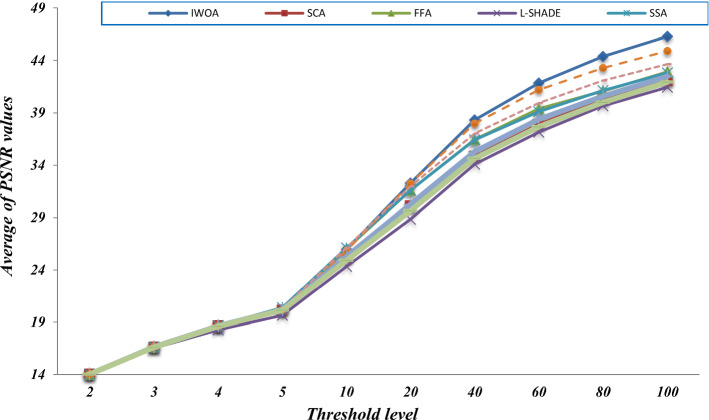
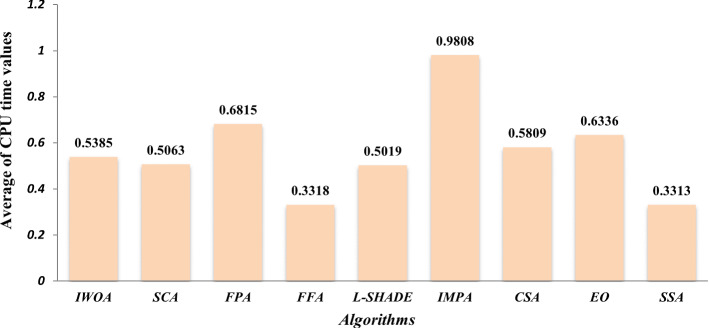
Here, we seek to prove the efficacy of the proposed algorithm in comparison with the standard WOA and WOA-DE. We are interested in studying the effect of using the LCMA technique on the performance of the proposed algorithm. Figure 9 compares the three algorithms using different threshold values, including 2, 3, 4, 5, 10, 40, 60, 80, and 100. The figure shows the average PSNR values obtained by running each algorithm 30 times for all the test images for each threshold level. By observing the figure, we can see that WOA-DE reaches better PSNR for threshold levels of 2, 3, 4, 5, and 10, higher than that, the proposed algorithm could fulfill PSNR values significantly-better than the others. Consequently, IWOA obtains a higher quality segmented image than the other two WOA variants when increasing the threshold levels. Another comparison is presented in Fig. 10 based on the average fitness values of Kapur’s entropy. We use different threshold values, including 2, 3, 4, 5, 10, 20, 40, 60, 80, and 100, to show the consistency of the proposed algorithm within various threshold levels. At first, we obtain the fitness values of running each algorithm 30 times on a given threshold level. Then, we compute the average fitness value for each threshold level as the summation of the fitness values through 30 runs divided by 30. The figure shows that IWOA succeeds in obtaining better fitness values compared to WOA and WOA-DE for all different threshold levels higher than 10 and equal with the rest. In Fig. 11, unfortunately, IWOA couldn’t outperform the WOA and WOA-DE in CPU time for threshold levels higher than 40. However, the proposed algorithm is better as it outperforms WOA based on PSNR and fitness values.
Fig. 9.
Comparison between IWOA, WOA, and WOA-DE based on PSNR
Fig. 10.
Comparison between IWOA, WOA, and WOA-DE based on fitness values
Fig. 11.
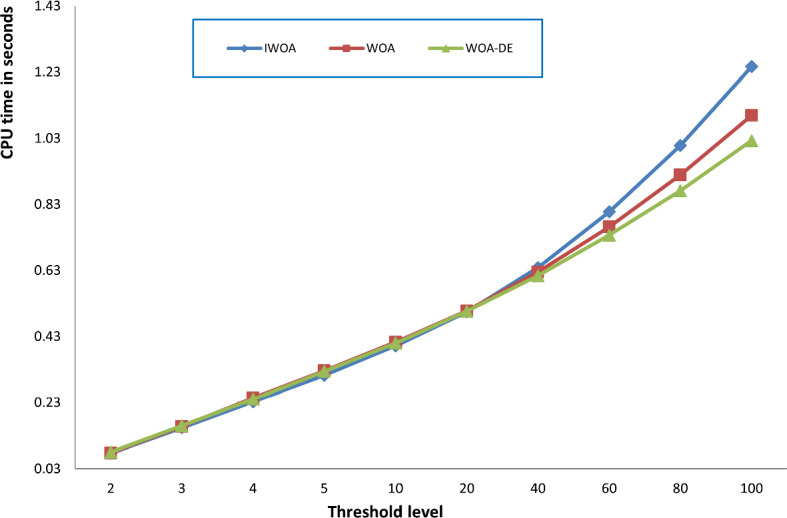
Average CPU time values on each threshold level
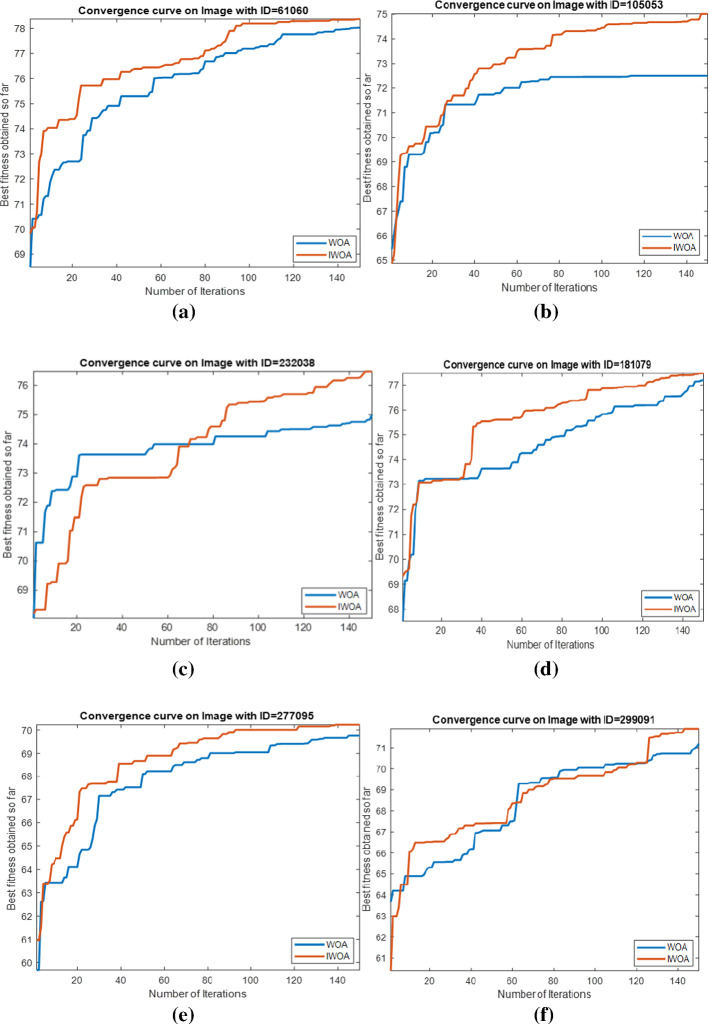
Regarding evaluating the convergence obtained by IWOA and WOA within the optimization process, Figure 12 is introduced to show that on all test images with a threshold level (t) of 40. We selected this threshold level to measure how far each algorithm could perform better with a high threshold level. After inspecting this figure, we found that IWOA could outperform WOA in the convergence within the starting of the optimization process for images: 61060, 105053, 181079, 277095, and 299091 and its superiority move on until the ending. However, for the other images, the convergence curve for WOA appears to be the best at the starting of the optimization process, afterward, this appearance deteriorates due to the local minima problem and our proposed dramatically outperforms.
Fig. 12.
Comparison between IWOA and WOA under convergence curve obtained by each one on each test image under t=40
The performance evaluation of the proposed algorithm and other algorithms
Tables 3, 4, 5 presents a comparison among the algorithms based on the average PSNR values using different Threshold levels (n), including 2-n, 3-n, 4-n,5-n,10-n,20-n,30-n, 40-n, 60-n,80-n, and 100-n. For each threshold level, we compute the average PSNR as follows:
| 32 |
is the summation of the PSNR computed for each run of an algorithm for a given threshold level divided by the number of running the algorithm. R is the number of independent runs for the algorithms, which is 30. Based on the results introduced in the table, the proposed algorithm can outperform the other algorithms in the PSNR metric. For the small threshold levels, we can see that IWOA could be competitive and superior to the others in most of the test images. For the higher threshold values, the performance of the other algorithms is degraded, while IWOA gets the maximum average PSNR for all the test images. Figure 13 shows the total average PSNR values for each algorithm for each threshold level. The total average PSNR can be defined as:
| 33 |
where IN is the number of the used test images, which is 9. is the obtained average PSNR value for an image for a given threshold level. IWOA achieves the best results compared to the other algorithms, especially with the threshold level higher than 10. Also, Fig. 14 shows the summation of the total average PSNR values for all threshold levels. The figure demonstrates the superiority of the proposed algorithm compared with the other algorithm in PSNR results. The higher PSNR values, the lower MSE values.
Table 3.
The PSNR values obtained by each algorithm on different threshold levels
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 61060 | IWOA | 16.2867 | 16.7692 | 18.7869 | 20.2126 | 25.5552 | 31.5556 | 37.6849 | 41.4087 | 43.9277 | 45.7956 |
| IMPA (Abdel-Basset et al. 2020) | 16.2867 | 16.6497 | 18.7869 | 20.6893 | 25.5117 | 30.9022 | 35.6584 | 38.2204 | 40.3062 | 42.026 | |
| FFA (Erdmann et al. 2015) | 16.2867 | 16.5289 | 18.7641 | 20.1954 | 25.1383 | 29.8495 | 32.9637 | 35.2004 | 37.0466 | 38.3628 | |
| SCA (Mirjalili 2016) | 16.2624 | 16.5125 | 18.528 | 20.6307 | 25.1069 | 29.8977 | 35.0462 | 37.6503 | 39.7634 | 41.5877 | |
| FPA(Yang 2012) | 16.2855 | 16.4567 | 18.5627 | 20.5322 | 24.7915 | 29.0752 | 34.3168 | 36.9882 | 39.1574 | 41.2035 | |
| L-SHADE(Brest et al. 2016) | 15.7974 | 16.1315 | 18.1156 | 19.4022 | 23.7514 | 28.5646 | 33.5875 | 35.8807 | 38.6393 | 40.8016 | |
| SSA (Wang et al. 2020) | 16.2867 | 16.617 | 18.7624 | 20.3786 | 24.5493 | 29.4472 | 32.431 | 35.6409 | 37.4665 | 38.9306 | |
| EO(Abdel-Basset et al. 2021) | 16.2867 | 16.7095 | 18.7869 | 20.2083 | 25.0504 | 29.7666 | 33.1060 | 35.3548 | 37.1199 | 38.9897 | |
| CSA(Moses et al. 2019) | 16.2795 | 16.4914 | 18.7005 | 20.6590 | 25.0777 | 29.7559 | 34.2771 | 37.0703 | 39.5528 | 41.3172 | |
| 105053 | IWOA | 8.1763 | 17.4895 | 17.7293 | 20.7808 | 26.6813 | 32.7199 | 39.1301 | 42.3156 | 44.6779 | 46.881 |
| IMPA(Abdel-Basset et al. 2020) | 8.1763 | 17.4895 | 17.4435 | 21.0702 | 26.2227 | 33.191 | 39.2632 | 41.6234 | 43.8625 | 45.9313 | |
| FFA (Erdmann et al. 2015) | 8.1763 | 17.4753 | 17.6355 | 21.3868 | 27.0934 | 32.8384 | 37.7095 | 40.9477 | 42.5877 | 44.4127 | |
| SCA (Mirjalili 2016) | 8.1633 | 17.3352 | 17.341 | 21.4962 | 25.5527 | 30.0635 | 35.0526 | 38.3385 | 40.5995 | 42.028 | |
| FPA(Yang 2012) | 8.174 | 17.3413 | 17.3105 | 21.3455 | 25.6217 | 30.1868 | 35.4511 | 38.3075 | 40.0721 | 42.6076 | |
| L-SHADE(Brest et al. 2016) | 9.6425 | 16.1628 | 17.5898 | 19.2213 | 23.7277 | 28.802 | 34.3476 | 37.5381 | 39.6678 | 42.1126 | |
| SSA (Wang et al. 2020) | 8.1763 | 17.4679 | 17.407 | 20.94 | 27.0642 | 32.8371 | 37.7193 | 40.7466 | 43.158 | 44.9611 | |
| EO(Abdel-Basset et al. 2021) | 9.4004 | 17.4895 | 18.1580 | 21.7813 | 26.6968 | 33.3049 | 39.5285 | 42.8861 | 45.2782 | 46.3812 | |
| CSA(Moses et al. 2019) | 8.1695 | 17.3392 | 17.2921 | 21.5001 | 25.8554 | 30.9389 | 35.9129 | 39.2477 | 41.1463 | 43.2806 | |
| 181079 | IWOA | 10.9408 | 13.5952 | 18.6509 | 19.7918 | 26.1093 | 31.742 | 37.8592 | 41.5339 | 43.7337 | 45.9791 |
| IMPA(Abdel-Basset et al. 2020) | 10.9408 | 13.5952 | 18.6295 | 19.8006 | 26.1567 | 31.7284 | 37.4946 | 39.9403 | 41.6452 | 42.9932 | |
| FFA (Erdmann et al. 2015) | 10.9408 | 13.5956 | 18.7702 | 19.8336 | 26.0867 | 30.7462 | 34.7174 | 36.4639 | 39.3715 | 40.7335 | |
| SCA (Mirjalili 2016) | 10.9647 | 13.6067 | 18.5867 | 19.6452 | 25.1353 | 29.5348 | 34.453 | 37.5382 | 39.8938 | 41.1671 | |
| FPA(Yang 2012) | 10.9408 | 13.5314 | 18.6755 | 19.7329 | 24.7949 | 29.4295 | 34.3434 | 37.1452 | 39.9103 | 41.5033 | |
| L-SHADE(Brest et al. 2016) | 11.3971 | 15.075 | 17.0602 | 19.0854 | 23.5204 | 28.6653 | 34.0922 | 36.5777 | 39.0134 | 41.2603 | |
| SSA (Wang et al. 2020) | 10.9408 | 13.596 | 18.7222 | 19.8396 | 26.1203 | 30.9164 | 34.8317 | 37.5808 | 38.8031 | 40.7615 | |
| EO(Abdel-Basset et al. 2021) | 10.9408 | 13.8211 | 18.7563 | 19.8096 | 26.0668 | 31.5504 | 36.1967 | 38.7301 | 40.5557 | 41.9747 | |
| CSA(Moses et al. 2019) | 10.9489 | 13.6335 | 18.6553 | 19.7121 | 25.3675 | 29.9050 | 35.0332 | 38.2055 | 39.8197 | 41.8183 | |
| 232038 | IWOA | 13.0048 | 15.1266 | 18.1124 | 19.8585 | 24.2759 | 31.987 | 38.0154 | 41.3027 | 43.691 | 45.7513 |
| IMPA(Abdel-Basset et al. 2020) | 13.0048 | 15.1266 | 18.8365 | 19.7179 | 24.4223 | 31.7808 | 37.5034 | 40.6755 | 42.4778 | 44.4932 | |
| FFA (Erdmann et al. 2015) | 13.0048 | 15.1302 | 18.9594 | 20.0016 | 25.0449 | 31.0259 | 35.9598 | 38.979 | 41.2838 | 43.1382 | |
| SCA (Mirjalili 2016) | 12.9986 | 15.1485 | 19.0294 | 19.7184 | 23.7883 | 29.3839 | 34.9091 | 37.2016 | 39.8539 | 41.5944 | |
| FPA(Yang 2012) | 13.004 | 15.1197 | 19.385 | 19.547 | 24.3978 | 29.7331 | 34.3111 | 37.7972 | 39.6273 | 41.4956 | |
| L-SHADE(Brest et al. 2016) | 13.004 | 15.6361 | 17.4787 | 18.6656 | 23.2296 | 27.4646 | 33.3554 | 36.6544 | 39.1189 | 40.7351 | |
| SSA (Wang et al. 2020) | 13.0048 | 15.1287 | 18.945 | 19.7159 | 24.9574 | 31.3648 | 36.4699 | 39.5262 | 41.7867 | 42.8996 | |
| EO(Abdel-Basset et al. 2021) | 13.0048 | 15.1266 | 19.2749 | 19.7192 | 25.0847 | 31.6771 | 37.4857 | 41.1474 | 43.1810 | 44.6525 | |
| CSA(Moses et al. 2019) | 13.0030 | 15.1346 | 19.3847 | 19.6840 | 24.1848 | 29.5117 | 34.9319 | 37.7080 | 40.2279 | 42.1482 | |
| 277095 | IWOA | 17.2331 | 19.5955 | 20.0944 | 22.2815 | 27.9087 | 34.1189 | 40.4472 | 44.0415 | 46.5726 | 48.872 |
| IMPA(Abdel-Basset et al. 2020) | 17.2331 | 19.3947 | 20.0944 | 22.3408 | 28.0279 | 34.3134 | 40.3225 | 43.4826 | 44.9598 | 46.6855 | |
| FFA (Erdmann et al. 2015) | 17.2331 | 19.4469 | 20.3817 | 22.3397 | 28.0926 | 34.372 | 39.6988 | 41.8509 | 43.2272 | 44.6291 | |
| SCA (Mirjalili 2016) | 17.2592 | 19.4005 | 20.1383 | 22.0145 | 26.9085 | 31.9687 | 36.0582 | 39.435 | 42.0242 | 43.736 | |
| FPA(Yang 2012) | 17.2462 | 19.3746 | 20.339 | 22.1086 | 26.469 | 30.7319 | 35.1382 | 38.7162 | 41.2978 | 42.7415 | |
| L-SHADE(Brest et al. 2016) | 16.6452 | 18.3082 | 19.6956 | 20.6929 | 24.0195 | 29.1134 | 33.9374 | 37.4709 | 39.4088 | 41.6076 | |
| SSA (Wang et al. 2020) | 17.2331 | 19.5076 | 20.3945 | 22.3716 | 28.1538 | 34.2436 | 39.4361 | 41.4285 | 43.6577 | 45.6107 | |
| EO(Abdel-Basset et al. 2021) | 17.2331 | 19.5318 | 20.0944 | 22.2582 | 27.8796 | 34.0662 | 39.5489 | 42.6040 | 44.9147 | 46.7984 | |
| CSA(Moses et al. 2019) | 17.2495 | 19.5695 | 20.3456 | 22.0283 | 27.0782 | 31.2230 | 36.4326 | 39.4172 | 42.0179 | 43.4224 | |
Bold values indicate the best value
Table 4.
The PSNR values obtained by each algorithm on different threshold levels
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 299091 | IWOA | 12.7506 | 14.7732 | 17.4413 | 19.4405 | 26.649 | 33.2916 | 39.4496 | 42.9397 | 45.4949 | 47.2838 |
| IMPA(Abdel-Basset et al. 2020) | 12.7506 | 14.7732 | 17.4413 | 18.5549 | 26.7035 | 33.3705 | 39.9062 | 42.8988 | 44.9928 | 46.5953 | |
| FFA (Erdmann et al. 2015) | 12.7506 | 14.7732 | 17.5053 | 20.8595 | 27.2694 | 33.0254 | 37.5475 | 40.406 | 42.5489 | 43.7756 | |
| SCA (Mirjalili 2016) | 12.6001 | 14.6274 | 17.5049 | 19.6115 | 25.8008 | 30.2924 | 35.3947 | 38.2696 | 40.6356 | 42.4988 | |
| FPA(Yang 2012) | 12.7343 | 14.6982 | 17.5 | 19.1003 | 26.0155 | 30.5486 | 35.0727 | 38.1241 | 40.4536 | 42.9055 | |
| L-SHADE(Brest et al. 2016) | 12.7018 | 14.3751 | 16.9103 | 19.2296 | 24.4079 | 29.2449 | 34.1894 | 37.4026 | 39.5417 | 41.8211 | |
| SSA (Wang et al. 2020) | 12.7506 | 14.7732 | 17.4821 | 19.3247 | 27.3287 | 32.7439 | 37.8646 | 40.2891 | 42.6772 | 44.775 | |
| EO(Abdel-Basset et al. 2021) | 12.7506 | 14.7732 | 17.4413 | 19.4697 | 27.3109 | 33.5670 | 38.3367 | 41.4319 | 43.7787 | 45.0486 | |
| CSA(Moses et al. 2019) | 12.7343 | 14.7640 | 17.4171 | 19.6498 | 26.1747 | 31.1799 | 36.1748 | 39.0938 | 41.5331 | 43.4786 | |
| 157055 | IWOA | 14.8685 | 16.82 | 18.7981 | 19.4275 | 26.274 | 31.916 | 38.0734 | 41.5321 | 43.9867 | 45.9721 |
| IMPA(Abdel-Basset et al. 2020) | 14.8685 | 16.8202 | 18.8129 | 19.4275 | 26.1992 | 31.9554 | 37.4332 | 40.7193 | 42.6234 | 44.3435 | |
| FFA (Erdmann et al. 2015) | 14.8685 | 16.8252 | 18.827 | 19.4485 | 26.2039 | 31.0721 | 35.6588 | 38.2036 | 40.3306 | 41.8274 | |
| SCA (Mirjalili 2016) | 14.8616 | 16.8316 | 18.7873 | 19.2676 | 25.0025 | 29.7745 | 34.6014 | 37.391 | 39.77 | 41.5039 | |
| FPA(Yang 2012) | 14.8641 | 16.8188 | 18.4205 | 19.3255 | 24.8499 | 29.2591 | 34.2189 | 37.2836 | 39.6526 | 41.4933 | |
| L-SHADE(Brest et al. 2016) | 14.637 | 16.4629 | 17.7539 | 18.7346 | 23.3999 | 28.056 | 33.2929 | 36.4933 | 39.0554 | 40.9173 | |
| SSA (Wang et al. 2020) | 14.8685 | 16.8223 | 18.8185 | 19.4271 | 26.1326 | 31.041 | 35.8873 | 38.0579 | 39.9067 | 41.7728 | |
| EO(Abdel-Basset et al. 2021) | 14.8685 | 16.8190 | 18.8086 | 19.4363 | 26.2407 | 31.2912 | 36.0481 | 38.4696 | 40.5889 | 42.1586 | |
| CSA(Moses et al. 2019) | 14.8652 | 16.8220 | 18.6925 | 19.3459 | 25.3089 | 29.9455 | 34.8648 | 37.8973 | 40.0332 | 41.9029 | |
| 108070 | IWOA | 12.8967 | 14.2363 | 15.7475 | 17.7623 | 25.9934 | 32.5243 | 38.4528 | 41.1617 | 43.6999 | 45.4801 |
| IMPA(Abdel-Basset et al. 2020) | 12.8967 | 14.2363 | 15.7304 | 17.0121 | 25.1283 | 32.5107 | 38.0452 | 40.4146 | 42.2708 | 44.3453 | |
| FFA (Erdmann et al. 2015) | 12.8967 | 14.2363 | 15.833 | 17.8724 | 24.7973 | 32.1232 | 36.7794 | 39.4306 | 41.6915 | 42.5833 | |
| SCA (Mirjalili 2016) | 12.8869 | 14.3027 | 15.5702 | 17.9583 | 24.9282 | 30.1214 | 34.2607 | 37.4506 | 39.7926 | 41.2647 | |
| FPA(Yang 2012) | 12.8965 | 14.2737 | 15.6903 | 17.7294 | 24.9322 | 29.9455 | 35.0972 | 37.6076 | 39.905 | 42.0306 | |
| L-SHADE(Brest et al. 2016) | 12.7868 | 14.1071 | 16.2789 | 17.7593 | 23.7576 | 29.0393 | 33.9972 | 36.9642 | 39.1351 | 41.158 | |
| SSA (Wang et al. 2020) | 12.8967 | 14.2363 | 15.7986 | 17.758 | 24.8294 | 32.3343 | 37.0911 | 39.0282 | 41.5582 | 42.2324 | |
| EO(Abdel-Basset et al. 2021) | 12.8965 | 14.2737 | 15.6903 | 17.7294 | 24.9322 | 29.9455 | 35.0972 | 37.6076 | 39.9050 | 42.0306 | |
| CSA(Moses et al. 2019) | 12.7868 | 14.1071 | 16.2789 | 17.7593 | 23.7576 | 29.0393 | 33.9972 | 36.9642 | 39.1351 | 41.1580 | |
| 108082 | IWOA | 14.5453 | 16.0075 | 17.1678 | 18.0151 | 23.1348 | 31.4783 | 36.7836 | 40.1501 | 42.9475 | 44.8308 |
| IMPA(Abdel-Basset et al. 2020) | 14.5423 | 16.0369 | 17.1311 | 17.8325 | 21.7034 | 30.9698 | 36.2668 | 39.3682 | 41.373 | 43.4287 | |
| FFA (Erdmann et al. 2015) | 14.5423 | 16.0368 | 17.197 | 18.1359 | 22.7504 | 30.7971 | 34.7235 | 38.0501 | 39.706 | 42.2618 | |
| SCA (Mirjalili 2016) | 14.534 | 15.9818 | 17.2315 | 17.9926 | 22.7623 | 29.145 | 33.9605 | 37.0217 | 39.8852 | 41.1458 | |
| FPA(Yang 2012) | 14.5423 | 15.9806 | 17.1285 | 17.924 | 22.792 | 29.495 | 33.6834 | 37.5135 | 39.2886 | 41.6687 | |
| L-SHADE(Brest et al. 2016) | 14.5417 | 16.0231 | 16.9894 | 18.1094 | 22.606 | 27.9576 | 33.2503 | 36.4203 | 38.3674 | 40.6714 | |
| SSA (Wang et al. 2020) | 14.5423 | 16.0259 | 17.196 | 18.1525 | 22.1649 | 31.0065 | 35.359 | 38.3042 | 40.0028 | 41.9553 | |
| EO(Abdel-Basset et al. 2021) | 14.5453 | 16.0369 | 17.1931 | 18.0947 | 23.5194 | 31.0019 | 35.9745 | 39.5162 | 41.5182 | 42.6250 | |
| CSA(Moses et al. 2019) | 14.5489 | 15.9921 | 17.2301 | 18.0076 | 22.2066 | 29.5041 | 34.6427 | 37.7308 | 40.2057 | 42.3192 | |
Bold values indicate the best value
Table 5.
The PSNR values obtained by each algorithm on different threshold levels
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| Barbara | IWOA | 14.9240 | 17.3240 | 19.0009 | 20.6601 | 25.1294 | 31.2820 | 37.3790 | 40.9505 | 43.4813 | 45.0693 |
| IMPA | 14.9240 | 17.3240 | 19.0009 | 20.6529 | 25.0946 | 30.8266 | 37.3247 | 40.5081 | 42.3595 | 44.1365 | |
| FFA | 14.9240 | 17.3243 | 18.9989 | 20.6374 | 24.9916 | 30.9267 | 36.3082 | 39.1633 | 40.8988 | 42.4291 | |
| SCA | 14.9343 | 17.3251 | 18.9987 | 20.6534 | 24.6423 | 28.9304 | 33.6535 | 37.4021 | 39.3181 | 41.1608 | |
| FPA | 14.9253 | 17.3223 | 18.9569 | 20.5960 | 24.3680 | 28.9210 | 34.0246 | 36.9185 | 39.2672 | 41.2625 | |
| L-SHADE | 14.8961 | 17.2009 | 18.7727 | 20.2293 | 23.9052 | 28.4566 | 33.3502 | 36.7070 | 38.8824 | 40.6336 | |
| SSA | 14.9240 | 17.3245 | 18.9967 | 20.6365 | 24.9814 | 30.9075 | 35.8686 | 38.6984 | 41.1878 | 42.6449 | |
| EO | 14.9240 | 17.3240 | 19.0009 | 20.6494 | 25.1599 | 30.7916 | 35.7825 | 38.7773 | 41.0402 | 42.7376 | |
| CSA | 14.9249 | 17.3239 | 19.0022 | 20.6149 | 24.5367 | 29.1929 | 34.4222 | 37.6804 | 39.9503 | 41.6369 | |
| Airplane | IWOA | 16.0751 | 18.8125 | 20.4488 | 21.3370 | 27.3730 | 32.3476 | 38.4140 | 41.9920 | 45.0835 | 46.6236 |
| IMPA | 16.0751 | 18.8125 | 20.4488 | 21.4567 | 27.2478 | 31.8160 | 38.0477 | 42.0791 | 44.2614 | 45.9047 | |
| FFA | 16.0751 | 18.8129 | 20.4452 | 21.4559 | 26.2709 | 29.5272 | 34.9981 | 38.8658 | 41.2281 | 42.7745 | |
| SCA | 16.0827 | 18.8924 | 20.4463 | 21.5307 | 27.1930 | 31.1098 | 35.8470 | 39.0601 | 41.1149 | 42.5819 | |
| FPA | 16.0768 | 18.8461 | 20.4374 | 21.4167 | 26.3792 | 30.1531 | 35.1931 | 38.0125 | 39.9903 | 42.4332 | |
| L-SHADE | 16.0179 | 18.6636 | 19.8807 | 21.5476 | 25.4422 | 29.3645 | 34.5157 | 37.3993 | 39.6480 | 41.5033 | |
| SSA | 16.0751 | 18.8125 | 20.4440 | 21.4246 | 26.6092 | 29.5688 | 34.5122 | 38.8826 | 40.4920 | 43.6145 | |
| EO | 16.0751 | 18.8125 | 20.4488 | 21.3566 | 26.7137 | 30.6354 | 35.0350 | 37.0585 | 39.6525 | 41.4923 | |
| CSA | 16.0748 | 18.8629 | 20.3635 | 21.4873 | 26.7369 | 30.6653 | 35.2753 | 38.6441 | 40.5772 | 42.1391 | |
| Mandrill | IWOA | 16.0224 | 18.6845 | 20.4448 | 22.1853 | 26.3722 | 32.3825 | 38.6526 | 42.5150 | 44.7773 | 46.9402 |
| IMPA | 16.0224 | 18.6644 | 20.4448 | 22.1853 | 26.3530 | 32.6721 | 39.2602 | 42.3941 | 44.5893 | 46.1535 | |
| FFA | 16.0224 | 18.6593 | 20.4327 | 22.1853 | 26.3572 | 32.1962 | 38.0196 | 40.9025 | 42.0967 | 43.7755 | |
| SCA | 16.0217 | 18.6987 | 20.3928 | 22.0788 | 25.6647 | 30.5413 | 35.5081 | 38.6804 | 40.2669 | 42.4611 | |
| FPA | 16.0223 | 18.7418 | 20.3279 | 22.0176 | 25.8664 | 29.9430 | 34.5191 | 37.3315 | 39.8083 | 41.9171 | |
| L-SHADE | 15.9707 | 18.5610 | 19.8114 | 21.0192 | 24.6964 | 28.9577 | 34.2195 | 37.0521 | 40.1598 | 41.6228 | |
| SSA | 16.0224 | 18.6543 | 20.4310 | 22.1887 | 26.5805 | 31.9945 | 38.0775 | 40.5521 | 42.3196 | 43.7486 | |
| EO | 16.0224 | 18.6795 | 20.4439 | 22.1817 | 26.0229 | 31.9824 | 37.8365 | 41.1402 | 42.9315 | 44.8846 | |
| CSA | 16.0222 | 18.7012 | 20.3947 | 21.9913 | 26.0366 | 30.5380 | 35.5805 | 38.6316 | 40.9571 | 42.9933 | |
| Lena | IWOA | 14.5905 | 17.2956 | 18.9878 | 19.9951 | 26.2791 | 32.7712 | 38.6962 | 42.2773 | 44.6147 | 46.7193 |
| IMPA | 14.5905 | 17.2956 | 19.0590 | 19.9951 | 26.5888 | 32.8846 | 38.8096 | 42.2573 | 44.1450 | 46.0416 | |
| FFA | 14.5905 | 17.2956 | 18.9663 | 20.0024 | 27.0062 | 32.5039 | 37.7317 | 40.2838 | 41.9336 | 44.4400 | |
| SCA | 14.5806 | 17.3046 | 18.9222 | 19.8514 | 24.8959 | 30.2306 | 35.2764 | 38.0468 | 40.4707 | 41.7868 | |
| FPA | 14.5894 | 17.2792 | 18.9582 | 19.7769 | 24.4228 | 29.6579 | 35.0304 | 37.8850 | 39.9406 | 42.0798 | |
| L-SHADE | 14.5626 | 17.1384 | 18.5966 | 19.2063 | 23.8421 | 29.0641 | 33.7940 | 37.5096 | 39.6289 | 41.4567 | |
| SSA | 14.5905 | 17.2956 | 19.0217 | 19.9985 | 26.9547 | 32.8229 | 37.8615 | 40.1590 | 42.6289 | 43.8999 | |
| EO | 14.5905 | 17.2956 | 19.0163 | 19.9951 | 26.8761 | 32.5363 | 37.8972 | 40.8029 | 42.8185 | 44.4948 | |
| CSA | 14.5905 | 17.2796 | 18.9372 | 19.9300 | 25.0691 | 30.7963 | 35.7561 | 38.9216 | 41.2209 | 42.8667 | |
Bold values indicate the best value
Fig. 13.
Average PSNR values on each threshold level
Fig. 14.
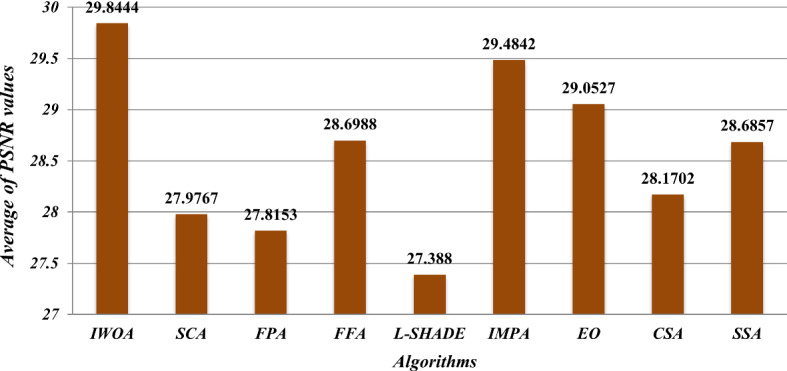
PSNR values Comparison of the total average for all the test images
Tables 6, 7, and 8 provides the average SSIM values obtained by the algorithms on ten different threshold levels for all the test images. The SSIM metric is employed for assessing the structural similarity between the original image and the segmented image. According to the results, the proposed algorithm can also outperform the other algorithms for most of the test images on the different threshold values. Additionally, Fig. 15 inspects a comparison in terms of the total average SSIM for all the test images on each threshold level. The figure proves the efficacy of the proposed algorithm compared to the other algorithms with threshold levels higher than 10. With threshold levels smaller than 10, all algorithms seem to be converged.
Table 6.
The SSIM values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 61060 | IWOA | 0.8476 | 0.8627 | 0.9413 | 0.9499 | 0.9839 | 0.9939 | 0.9968 | 0.9973 | 0.9976 | 0.9976 |
| IMPA(Abdel-Basset et al. 2020) | 0.8476 | 0.8574 | 0.9413 | 0.953 | 0.9839 | 0.993 | 0.9956 | 0.9964 | 0.9968 | 0.9972 | |
| FFA (Erdmann et al. 2015) | 0.8476 | 0.8521 | 0.9409 | 0.9497 | 0.9815 | 0.9905 | 0.9922 | 0.9942 | 0.9955 | 0.9958 | |
| SCA (Mirjalili 2016) | 0.8476 | 0.8511 | 0.9386 | 0.952 | 0.9805 | 0.9908 | 0.9953 | 0.9963 | 0.9969 | 0.9972 | |
| FPA(Yang 2012) | 0.8476 | 0.8497 | 0.9394 | 0.9508 | 0.9791 | 0.9888 | 0.9947 | 0.9961 | 0.9967 | 0.9971 | |
| L-SHADE(Brest et al. 2016) | 0.8357 | 0.8453 | 0.9205 | 0.94 | 0.9706 | 0.9876 | 0.9941 | 0.9952 | 0.9965 | 0.997 | |
| SSA (Wang et al. 2020) | 0.8476 | 0.856 | 0.9409 | 0.9508 | 0.9776 | 0.9894 | 0.9916 | 0.9948 | 0.9957 | 0.9962 | |
| EO(Abdel-Basset et al. 2021) | 0.8476 | 0.8600 | 0.9413 | 0.9499 | 0.9824 | 0.9913 | 0.9933 | 0.9948 | 0.9955 | 0.9963 | |
| CSA(Moses et al. 2019) | 0.8475 | 0.8510 | 0.9386 | 0.9532 | 0.9803 | 0.9905 | 0.9948 | 0.9958 | 0.9967 | 0.9971 | |
| 105053 | IWOA | 0.0771 | 0.7117 | 0.7268 | 0.8263 | 0.95 | 0.9847 | 0.9943 | 0.9956 | 0.9965 | 0.9969 |
| IMPA(Abdel-Basset et al. 2020) | 0.0771 | 0.7117 | 0.7179 | 0.8352 | 0.9461 | 0.986 | 0.9943 | 0.9956 | 0.9964 | 0.9967 | |
| FFA (Erdmann et al. 2015) | 0.0771 | 0.7119 | 0.724 | 0.8449 | 0.954 | 0.9842 | 0.992 | 0.9946 | 0.9953 | 0.9961 | |
| SCA (Mirjalili 2016) | 0.0739 | 0.7093 | 0.711 | 0.8442 | 0.9312 | 0.9665 | 0.9856 | 0.9919 | 0.9938 | 0.9947 | |
| FPA(Yang 2012) | 0.0764 | 0.7099 | 0.7113 | 0.8418 | 0.9272 | 0.9673 | 0.9868 | 0.992 | 0.9932 | 0.9952 | |
| L-SHADE(Brest et al. 2016) | 0.1771 | 0.643 | 0.6982 | 0.7632 | 0.8796 | 0.9548 | 0.9838 | 0.9903 | 0.993 | 0.9949 | |
| SSA (Wang et al. 2020) | 0.0771 | 0.7124 | 0.717 | 0.8322 | 0.9535 | 0.9834 | 0.9916 | 0.9942 | 0.9956 | 0.9962 | |
| EO(Abdel-Basset et al. 2021) | 0.1586 | 0.7117 | 0.7403 | 0.8577 | 0.9512 | 0.9858 | 0.9942 | 0.9955 | 0.9964 | 0.9966 | |
| CSA(Moses et al. 2019) | 0.0750 | 0.7097 | 0.7114 | 0.8489 | 0.9340 | 0.9719 | 0.9876 | 0.9928 | 0.9940 | 0.9956 | |
| 181079 | IWOA | 0.5938 | 0.7673 | 0.909 | 0.929 | 0.982 | 0.9928 | 0.9957 | 0.9963 | 0.9964 | 0.9966 |
| IMPA(Abdel-Basset et al. 2020) | 0.5938 | 0.7673 | 0.9088 | 0.929 | 0.982 | 0.9925 | 0.9955 | 0.996 | 0.9961 | 0.9963 | |
| FFA (Erdmann et al. 2015) | 0.5938 | 0.7673 | 0.9008 | 0.9296 | 0.9813 | 0.9907 | 0.9938 | 0.9945 | 0.9956 | 0.9958 | |
| SCA (Mirjalili 2016) | 0.5966 | 0.7683 | 0.9087 | 0.9278 | 0.977 | 0.989 | 0.9939 | 0.9953 | 0.996 | 0.9961 | |
| FPA(Yang 2012) | 0.5938 | 0.7655 | 0.9089 | 0.9294 | 0.9746 | 0.9884 | 0.9936 | 0.9951 | 0.996 | 0.9961 | |
| L-SHADE(Brest et al. 2016) | 0.6263 | 0.8113 | 0.8702 | 0.9124 | 0.9628 | 0.9868 | 0.9936 | 0.9949 | 0.9957 | 0.9961 | |
| SSA (Wang et al. 2020) | 0.5938 | 0.7672 | 0.9005 | 0.93 | 0.9812 | 0.9907 | 0.994 | 0.995 | 0.9954 | 0.9959 | |
| EO(Abdel-Basset et al. 2021) | 0.5938 | 0.7741 | 0.9105 | 0.9291 | 0.9816 | 0.9919 | 0.9947 | 0.9955 | 0.9958 | 0.9961 | |
| CSA(Moses et al. 2019) | 0.5947 | 0.7704 | 0.9093 | 0.9284 | 0.9777 | 0.9895 | 0.9942 | 0.9955 | 0.9958 | 0.9961 | |
| 232038 | IWOA | 0.6517 | 0.7972 | 0.8863 | 0.9338 | 0.9735 | 0.9941 | 0.9969 | 0.9973 | 0.9976 | 0.9977 |
| IMPA(Abdel-Basset et al. 2020) | 0.6517 | 0.7972 | 0.9065 | 0.932 | 0.9748 | 0.9934 | 0.9965 | 0.9972 | 0.9974 | 0.9976 | |
| FFA (Erdmann et al. 2015) | 0.6517 | 0.7972 | 0.9114 | 0.9357 | 0.9779 | 0.9923 | 0.9959 | 0.9969 | 0.9973 | 0.9975 | |
| SCA (Mirjalili 2016) | 0.6512 | 0.8004 | 0.9134 | 0.9309 | 0.9702 | 0.9895 | 0.9955 | 0.9964 | 0.997 | 0.9973 | |
| FPA(Yang 2012) | 0.6516 | 0.7982 | 0.9238 | 0.9278 | 0.9733 | 0.9902 | 0.9951 | 0.9966 | 0.997 | 0.9973 | |
| L-SHADE(Brest et al. 2016) | 0.6514 | 0.8155 | 0.8704 | 0.9047 | 0.9635 | 0.9843 | 0.9941 | 0.9962 | 0.9968 | 0.9972 | |
| SSA (Wang et al. 2020) | 0.6517 | 0.7972 | 0.911 | 0.9344 | 0.977 | 0.9929 | 0.9961 | 0.997 | 0.9973 | 0.9975 | |
| EO(Abdel-Basset et al. 2021) | 0.6517 | 0.7972 | 0.9187 | 0.9320 | 0.9782 | 0.9934 | 0.9966 | 0.9973 | 0.9975 | 0.9976 | |
| CSA(Moses et al. 2019) | 0.6516 | 0.7988 | 0.9235 | 0.9306 | 0.9720 | 0.9900 | 0.9955 | 0.9966 | 0.9971 | 0.9974 | |
| 277095 | IWOA | 0.7949 | 0.8825 | 0.8953 | 0.9286 | 0.9709 | 0.9833 | 0.9862 | 0.9868 | 0.9869 | 0.987 |
| IMPA(Abdel-Basset et al. 2020) | 0.7949 | 0.8766 | 0.8953 | 0.9304 | 0.9716 | 0.9833 | 0.986 | 0.9866 | 0.9868 | 0.9869 | |
| FFA (Erdmann et al. 2015) | 0.7941 | 0.8845 | 0.9006 | 0.9298 | 0.9717 | 0.9832 | 0.9858 | 0.9862 | 0.9865 | 0.9867 | |
| SCA (Mirjalili 2016) | 0.7949 | 0.8778 | 0.8958 | 0.9258 | 0.9647 | 0.979 | 0.9832 | 0.9854 | 0.9863 | 0.9866 | |
| FPA(Yang 2012) | 0.7952 | 0.8771 | 0.899 | 0.9261 | 0.9604 | 0.9761 | 0.9826 | 0.9852 | 0.9861 | 0.9864 | |
| L-SHADE(Brest et al. 2016) | 0.766 | 0.8328 | 0.8741 | 0.8923 | 0.9372 | 0.97 | 0.9811 | 0.9846 | 0.9854 | 0.9861 | |
| SSA (Wang et al. 2020) | 0.7941 | 0.8806 | 0.9008 | 0.931 | 0.9721 | 0.9831 | 0.9857 | 0.9861 | 0.9866 | 0.9868 | |
| EO(Abdel-Basset et al. 2021) | 0.7949 | 0.8835 | 0.8953 | 0.9277 | 0.9708 | 0.9829 | 0.9858 | 0.9865 | 0.9868 | 0.9869 | |
| CSA(Moses et al. 2019) | 0.7952 | 0.8820 | 0.8995 | 0.9261 | 0.9651 | 0.9769 | 0.9839 | 0.9854 | 0.9863 | 0.9865 | |
Bold values indicate the best value
Table 7.
The SSIM values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 299091 | IWOA | 0.671 | 0.7613 | 0.8346 | 0.8808 | 0.9737 | 0.9932 | 0.9966 | 0.9972 | 0.9975 | 0.9976 |
| IMPA(Abdel-Basset et al. 2020) | 0.671 | 0.7613 | 0.8346 | 0.8619 | 0.9735 | 0.993 | 0.9967 | 0.9972 | 0.9974 | 0.9975 | |
| FFA (Erdmann et al. 2015) | 0.671 | 0.7613 | 0.8366 | 0.911 | 0.9736 | 0.992 | 0.9952 | 0.9964 | 0.9969 | 0.9971 | |
| SCA (Mirjalili 2016) | 0.6621 | 0.7554 | 0.8374 | 0.8854 | 0.9693 | 0.9855 | 0.9935 | 0.9956 | 0.9964 | 0.997 | |
| FPA(Yang 2012) | 0.67 | 0.7582 | 0.8367 | 0.8724 | 0.9703 | 0.9866 | 0.9936 | 0.9957 | 0.9964 | 0.9971 | |
| L-SHADE(Brest et al. 2016) | 0.664 | 0.7316 | 0.8143 | 0.8729 | 0.9527 | 0.9824 | 0.9925 | 0.9951 | 0.9962 | 0.9968 | |
| SSA (Wang et al. 2020) | 0.671 | 0.7612 | 0.8358 | 0.8779 | 0.9735 | 0.9916 | 0.9953 | 0.9962 | 0.997 | 0.9973 | |
| EO(Abdel-Basset et al. 2021) | 0.6710 | 0.7613 | 0.8346 | 0.8812 | 0.9783 | 0.9934 | 0.9960 | 0.9968 | 0.9972 | 0.9973 | |
| CSA(Moses et al. 2019) | 0.6700 | 0.7610 | 0.8337 | 0.8847 | 0.9704 | 0.9881 | 0.9945 | 0.9960 | 0.9968 | 0.9972 | |
| 157055 | IWOA | 0.8733 | 0.919 | 0.9408 | 0.9479 | 0.9825 | 0.9888 | 0.9909 | 0.9912 | 0.9914 | 0.9914 |
| IMPA(Abdel-Basset et al. 2020) | 0.8733 | 0.9191 | 0.9409 | 0.9479 | 0.9821 | 0.9888 | 0.9908 | 0.9911 | 0.9913 | 0.9913 | |
| FFA (Erdmann et al. 2015) | 0.8733 | 0.9195 | 0.9411 | 0.9486 | 0.9821 | 0.9877 | 0.9899 | 0.9906 | 0.9909 | 0.9911 | |
| SCA (Mirjalili 2016) | 0.8733 | 0.9184 | 0.9405 | 0.9457 | 0.9777 | 0.9861 | 0.9896 | 0.9905 | 0.9909 | 0.9911 | |
| FPA(Yang 2012) | 0.8732 | 0.9188 | 0.9359 | 0.9466 | 0.9767 | 0.9857 | 0.9895 | 0.9905 | 0.9909 | 0.9911 | |
| L-SHADE(Brest et al. 2016) | 0.8686 | 0.911 | 0.9268 | 0.9367 | 0.9686 | 0.9832 | 0.9889 | 0.9903 | 0.9908 | 0.9911 | |
| SSA (Wang et al. 2020) | 0.8733 | 0.9193 | 0.9411 | 0.9484 | 0.9817 | 0.9879 | 0.9901 | 0.9906 | 0.9909 | 0.9911 | |
| EO(Abdel-Basset et al. 2021) | 0.8733 | 0.9190 | 0.9409 | 0.9481 | 0.9822 | 0.9884 | 0.9902 | 0.9907 | 0.9910 | 0.9912 | |
| CSA(Moses et al. 2019) | 0.8733 | 0.9191 | 0.9394 | 0.9470 | 0.9787 | 0.9865 | 0.9898 | 0.9906 | 0.9909 | 0.9912 | |
| 108070 | IWOA | 0.3955 | 0.5708 | 0.6933 | 0.7969 | 0.9592 | 0.9846 | 0.9897 | 0.9904 | 0.9909 | 0.9911 |
| IMPA(Abdel-Basset et al. 2020) | 0.3955 | 0.5708 | 0.692 | 0.7712 | 0.9522 | 0.9847 | 0.9894 | 0.9901 | 0.9906 | 0.9909 | |
| FFA (Erdmann et al. 2015) | 0.3955 | 0.5708 | 0.6998 | 0.8001 | 0.965 | 0.9838 | 0.9881 | 0.9897 | 0.9904 | 0.9905 | |
| SCA (Mirjalili 2016) | 0.3954 | 0.58 | 0.685 | 0.8021 | 0.9488 | 0.9782 | 0.9859 | 0.9887 | 0.9897 | 0.9903 | |
| FPA(Yang 2012) | 0.3955 | 0.5764 | 0.6913 | 0.7953 | 0.9463 | 0.9774 | 0.9869 | 0.9888 | 0.9897 | 0.9905 | |
| L-SHADE(Brest et al. 2016) | 0.3855 | 0.5523 | 0.7178 | 0.7786 | 0.9297 | 0.9724 | 0.9852 | 0.9884 | 0.9895 | 0.9902 | |
| SSA (Wang et al. 2020) | 0.3955 | 0.5707 | 0.6975 | 0.8179 | 0.9546 | 0.9839 | 0.9887 | 0.9894 | 0.9903 | 0.9905 | |
| EO(Abdel-Basset et al. 2021) | 0.3955 | 0.5708 | 0.6920 | 0.8147 | 0.9692 | 0.9855 | 0.9895 | 0.9902 | 0.9908 | 0.9910 | |
| CSA(Moses et al. 2019) | 0.3955 | 0.5756 | 0.7023 | 0.7837 | 0.9487 | 0.9780 | 0.9870 | 0.9894 | 0.9900 | 0.9907 | |
| 108082 | IWOA | 0.5318 | 0.6676 | 0.7614 | 0.8068 | 0.935 | 0.9901 | 0.9954 | 0.9967 | 0.9971 | 0.9974 |
| IMPA(Abdel-Basset et al. 2020) | 0.5318 | 0.6703 | 0.7613 | 0.7947 | 0.9198 | 0.9886 | 0.995 | 0.9964 | 0.9968 | 0.9972 | |
| FFA (Erdmann et al. 2015) | 0.5318 | 0.6703 | 0.7615 | 0.8144 | 0.933 | 0.9883 | 0.9936 | 0.9957 | 0.9963 | 0.997 | |
| SCA (Mirjalili 2016) | 0.5318 | 0.6703 | 0.7612 | 0.8031 | 0.9296 | 0.9831 | 0.9929 | 0.9954 | 0.9965 | 0.9967 | |
| FPA(Yang 2012) | 0.5318 | 0.6701 | 0.7554 | 0.7999 | 0.9263 | 0.9844 | 0.9927 | 0.9956 | 0.9962 | 0.9969 | |
| L-SHADE(Brest et al. 2016) | 0.5313 | 0.6701 | 0.7386 | 0.8039 | 0.9248 | 0.9768 | 0.9917 | 0.995 | 0.9958 | 0.9966 | |
| SSA (Wang et al. 2020) | 0.5318 | 0.6693 | 0.7616 | 0.8152 | 0.9289 | 0.9887 | 0.9942 | 0.9959 | 0.9964 | 0.9969 | |
| EO(Abdel-Basset et al. 2021) | 0.5318 | 0.6703 | 0.7616 | 0.8122 | 0.9429 | 0.9889 | 0.9948 | 0.9963 | 0.9968 | 0.9971 | |
| CSA(Moses et al. 2019) | 0.5319 | 0.6714 | 0.7611 | 0.8049 | 0.9218 | 0.9846 | 0.9936 | 0.9956 | 0.9965 | 0.9970 | |
Bold values indicate the best value
Table 8.
The SSIM values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| Barbara | IWOA | 0.8834 | 0.9356 | 0.9574 | 0.9710 | 0.9879 | 0.9954 | 0.9974 | 0.9977 | 0.9979 | 0.9979 |
| IMPA | 0.8834 | 0.9356 | 0.9574 | 0.9710 | 0.9879 | 0.9951 | 0.9973 | 0.9977 | 0.9978 | 0.9979 | |
| FFA | 0.8834 | 0.9356 | 0.9574 | 0.9710 | 0.9876 | 0.9952 | 0.9971 | 0.9975 | 0.9977 | 0.9978 | |
| SCA | 0.8836 | 0.9356 | 0.9574 | 0.9707 | 0.9865 | 0.9930 | 0.9962 | 0.9973 | 0.9975 | 0.9977 | |
| FPA | 0.8834 | 0.9356 | 0.9560 | 0.9700 | 0.9854 | 0.9931 | 0.9964 | 0.9972 | 0.9975 | 0.9977 | |
| L-SHADE | 0.8813 | 0.9320 | 0.9533 | 0.9668 | 0.9838 | 0.9926 | 0.9961 | 0.9971 | 0.9975 | 0.9976 | |
| SSA | 0.8834 | 0.9356 | 0.9573 | 0.9710 | 0.9876 | 0.9951 | 0.9970 | 0.9975 | 0.9977 | 0.9978 | |
| EO | 0.8834 | 0.9356 | 0.9574 | 0.9710 | 0.9880 | 0.9951 | 0.9970 | 0.9975 | 0.9977 | 0.9978 | |
| CSA | 0.8834 | 0.9356 | 0.9573 | 0.9703 | 0.9862 | 0.9933 | 0.9966 | 0.9973 | 0.9976 | 0.9977 | |
| Airplane | IWOA | 0.9019 | 0.9486 | 0.9613 | 0.9664 | 0.9883 | 0.9948 | 0.9970 | 0.9975 | 0.9977 | 0.9978 |
| IMPA | 0.9019 | 0.9486 | 0.9613 | 0.9668 | 0.9881 | 0.9943 | 0.9969 | 0.9975 | 0.9977 | 0.9978 | |
| FFA | 0.9019 | 0.9486 | 0.9613 | 0.9668 | 0.9854 | 0.9900 | 0.9951 | 0.9967 | 0.9972 | 0.9974 | |
| SCA | 0.9013 | 0.9488 | 0.9610 | 0.9673 | 0.9871 | 0.9927 | 0.9958 | 0.9968 | 0.9973 | 0.9974 | |
| FPA | 0.9018 | 0.9486 | 0.9605 | 0.9665 | 0.9843 | 0.9907 | 0.9953 | 0.9966 | 0.9969 | 0.9974 | |
| L-SHADE | 0.8995 | 0.9455 | 0.9541 | 0.9630 | 0.9794 | 0.9891 | 0.9952 | 0.9963 | 0.9969 | 0.9972 | |
| SSA | 0.9019 | 0.9486 | 0.9612 | 0.9666 | 0.9866 | 0.9899 | 0.9947 | 0.9967 | 0.9971 | 0.9976 | |
| EO | 0.9019 | 0.9486 | 0.9613 | 0.9665 | 0.9870 | 0.9930 | 0.9956 | 0.9962 | 0.9969 | 0.9973 | |
| CSA | 0.9018 | 0.9487 | 0.9604 | 0.9671 | 0.9861 | 0.9918 | 0.9953 | 0.9967 | 0.9971 | 0.9973 | |
| Mandrill | IWOA | 0.8637 | 0.9184 | 0.9405 | 0.9613 | 0.9835 | 0.9941 | 0.9971 | 0.9975 | 0.9977 | 0.9978 |
| IMPA | 0.8637 | 0.9183 | 0.9405 | 0.9613 | 0.9835 | 0.9944 | 0.9971 | 0.9975 | 0.9977 | 0.9977 | |
| FFA | 0.8637 | 0.9182 | 0.9405 | 0.9614 | 0.9829 | 0.9936 | 0.9966 | 0.9972 | 0.9973 | 0.9975 | |
| SCA | 0.8636 | 0.9187 | 0.9400 | 0.9598 | 0.9792 | 0.9908 | 0.9954 | 0.9967 | 0.9969 | 0.9974 | |
| FPA | 0.8637 | 0.9191 | 0.9389 | 0.9586 | 0.9794 | 0.9894 | 0.9945 | 0.9960 | 0.9968 | 0.9973 | |
| L-SHADE | 0.8602 | 0.9131 | 0.9295 | 0.9439 | 0.9717 | 0.9859 | 0.9942 | 0.9959 | 0.9970 | 0.9972 | |
| SSA | 0.8637 | 0.9182 | 0.9405 | 0.9614 | 0.9838 | 0.9932 | 0.9967 | 0.9971 | 0.9974 | 0.9975 | |
| EO | 0.8637 | 0.9184 | 0.9405 | 0.9613 | 0.9819 | 0.9936 | 0.9966 | 0.9972 | 0.9975 | 0.9977 | |
| CSA | 0.8637 | 0.9185 | 0.9398 | 0.9588 | 0.9806 | 0.9907 | 0.9953 | 0.9966 | 0.9971 | 0.9975 | |
| Lena | IWOA | 0.8295 | 0.9017 | 0.9296 | 0.9400 | 0.9823 | 0.9949 | 0.9969 | 0.9975 | 0.9976 | 0.9978 |
| IMPA | 0.8295 | 0.9017 | 0.9307 | 0.9400 | 0.9842 | 0.9949 | 0.9969 | 0.9975 | 0.9976 | 0.9978 | |
| FFA | 0.8295 | 0.9017 | 0.9292 | 0.9400 | 0.9858 | 0.9943 | 0.9966 | 0.9971 | 0.9973 | 0.9977 | |
| SCA | 0.8298 | 0.9025 | 0.9284 | 0.9384 | 0.9745 | 0.9906 | 0.9954 | 0.9965 | 0.9972 | 0.9973 | |
| FPA | 0.8295 | 0.9016 | 0.9289 | 0.9371 | 0.9706 | 0.9896 | 0.9954 | 0.9965 | 0.9971 | 0.9973 | |
| L-SHADE | 0.8294 | 0.8978 | 0.9214 | 0.9279 | 0.9675 | 0.9885 | 0.9945 | 0.9963 | 0.9970 | 0.9972 | |
| SSA | 0.8295 | 0.9017 | 0.9301 | 0.9400 | 0.9854 | 0.9947 | 0.9966 | 0.9971 | 0.9973 | 0.9976 | |
| EO | 0.8295 | 0.9017 | 0.9300 | 0.9400 | 0.9857 | 0.9945 | 0.9967 | 0.9973 | 0.9974 | 0.9977 | |
| CSA | 0.8295 | 0.9015 | 0.9283 | 0.9387 | 0.9750 | 0.9919 | 0.9958 | 0.9968 | 0.9972 | 0.9974 | |
Bold values indicate the best value
Fig. 15.
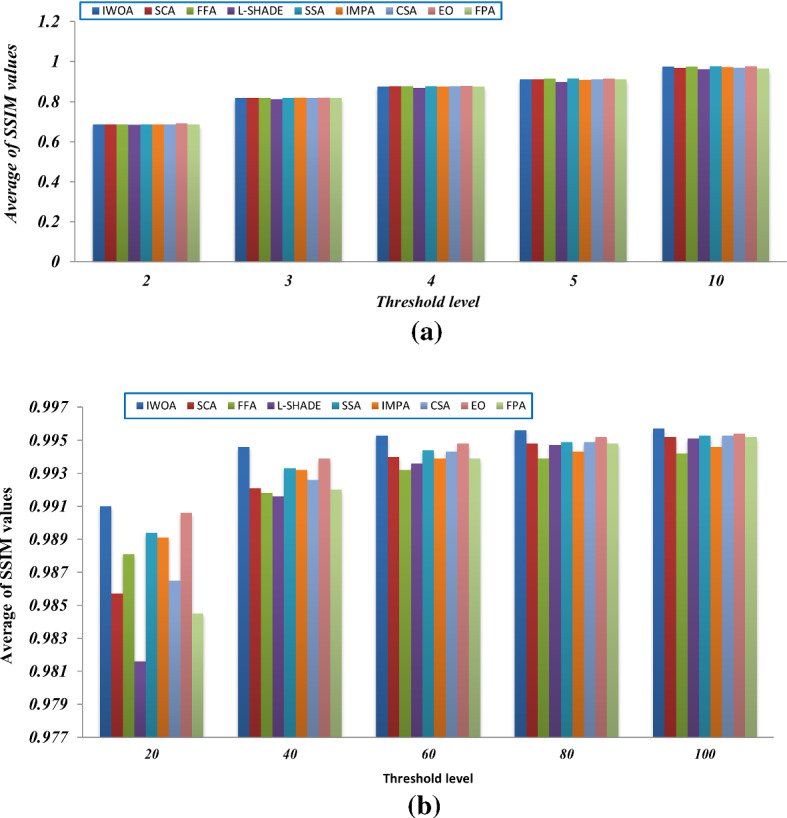
Comparison among algorithms of the SSIM values
Tables 9, 10, and 11 provides the average UQI values obtained by the algorithms on ten different threshold levels for all the test images. The UQI metric is also employed for assessing the structural similarity between the original image and the segmented image. According to the results, the proposed algorithm can also outperform the other algorithms for most of the test images on the different threshold values. Additionally, Fig. 16 inspects a comparison in terms of the total average SSIM for all the test images on each threshold level. The figure proves the efficacy of the proposed algorithm compared to the other algorithms with threshold levels higher than 10. With threshold levels smaller than 10, all algorithms seem to be converged.
Table 9.
The UQI values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 61060 | IWOA | 0.8494 | 0.8722 | 0.9431 | 0.9521 | 0.9861 | 0.9960 | 0.9989 | 0.9994 | 0.9996 | 0.9997 |
| IMPA | 0.8494 | 0.8696 | 0.9431 | 0.9549 | 0.9865 | 0.9951 | 0.9981 | 0.9984 | 0.9991 | 0.9993 | |
| FFA | 0.8494 | 0.8537 | 0.9425 | 0.9540 | 0.9820 | 0.9918 | 0.9950 | 0.9967 | 0.9976 | 0.9983 | |
| SCA | 0.8494 | 0.8523 | 0.9411 | 0.9535 | 0.9836 | 0.9924 | 0.9971 | 0.9985 | 0.9991 | 0.9993 | |
| FPA | 0.8494 | 0.8523 | 0.9406 | 0.9526 | 0.9790 | 0.9919 | 0.9967 | 0.9984 | 0.9989 | 0.9993 | |
| L-SHADE | 0.8456 | 0.8465 | 0.9292 | 0.9402 | 0.9711 | 0.9893 | 0.9963 | 0.9980 | 0.9987 | 0.9992 | |
| SSA | 0.8494 | 0.8535 | 0.9428 | 0.9520 | 0.9796 | 0.9894 | 0.9940 | 0.9962 | 0.9976 | 0.9981 | |
| EO | 0.8494 | 0.8722 | 0.9431 | 0.9509 | 0.9832 | 0.9934 | 0.9952 | 0.9969 | 0.9976 | 0.9987 | |
| CSA | 0.8494 | 0.8526 | 0.9411 | 0.9544 | 0.9808 | 0.9922 | 0.9969 | 0.9982 | 0.9989 | 0.9991 | |
| 61060 | IWOA | 0.0823 | 0.7153 | 0.7204 | 0.8283 | 0.9485 | 0.9867 | 0.9965 | 0.9979 | 0.9987 | 0.9991 |
| IMPA | 0.0823 | 0.7153 | 0.7204 | 0.8549 | 0.9456 | 0.9880 | 0.9965 | 0.9981 | 0.9987 | 0.9987 | |
| FFA | 0.0823 | 0.7154 | 0.7202 | 0.8438 | 0.9513 | 0.9871 | 0.9955 | 0.9967 | 0.9977 | 0.9982 | |
| SCA | 0.0801 | 0.7115 | 0.7124 | 0.8440 | 0.9329 | 0.9673 | 0.9899 | 0.9940 | 0.9958 | 0.9975 | |
| FPA | 0.0821 | 0.7130 | 0.7145 | 0.8458 | 0.9248 | 0.9652 | 0.9877 | 0.9929 | 0.9964 | 0.9974 | |
| L-SHADE | 0.0803 | 0.6889 | 0.7314 | 0.7901 | 0.9152 | 0.9600 | 0.9864 | 0.9944 | 0.9961 | 0.9976 | |
| SSA | 0.0823 | 0.7155 | 0.7201 | 0.8543 | 0.9547 | 0.9871 | 0.9953 | 0.9964 | 0.9976 | 0.9982 | |
| EO | 0.2041 | 0.7153 | 0.7429 | 0.8593 | 0.9543 | 0.9884 | 0.9960 | 0.9979 | 0.9983 | 0.9988 | |
| CSA | 0.0813 | 0.7148 | 0.7144 | 0.8486 | 0.9467 | 0.9755 | 0.9912 | 0.9951 | 0.9972 | 0.9979 | |
| 181079 | IWOA | 0.6007 | 0.7729 | 0.9136 | 0.9338 | 0.9855 | 0.9962 | 0.9989 | 0.9995 | 0.9997 | 0.9998 |
| IMPA | 0.6007 | 0.7729 | 0.9132 | 0.9338 | 0.9855 | 0.9961 | 0.9986 | 0.9992 | 0.9994 | 0.9996 | |
| FFA | 0.6007 | 0.7729 | 0.9140 | 0.9338 | 0.9849 | 0.9941 | 0.9967 | 0.9981 | 0.9988 | 0.9992 | |
| SCA | 0.6020 | 0.7722 | 0.9128 | 0.9332 | 0.9806 | 0.9926 | 0.9971 | 0.9985 | 0.9992 | 0.9993 | |
| FPA | 0.6007 | 0.7720 | 0.9113 | 0.9318 | 0.9777 | 0.9919 | 0.9971 | 0.9984 | 0.9991 | 0.9994 | |
| L-SHADE | 0.6141 | 0.7846 | 0.9081 | 0.9226 | 0.9722 | 0.9894 | 0.9969 | 0.9983 | 0.9990 | 0.9994 | |
| SSA | 0.6007 | 0.7729 | 0.9147 | 0.9338 | 0.9848 | 0.9933 | 0.9968 | 0.9982 | 0.9986 | 0.9991 | |
| EO | 0.6007 | 0.7729 | 0.9137 | 0.9337 | 0.9851 | 0.9955 | 0.9979 | 0.9987 | 0.9989 | 0.9994 | |
| CSA | 0.6013 | 0.7738 | 0.9133 | 0.9324 | 0.9805 | 0.9930 | 0.9973 | 0.9987 | 0.9990 | 0.9994 | |
| 232038 | IWOA | 0.6524 | 0.8012 | 0.9097 | 0.9233 | 0.9769 | 0.9960 | 0.9988 | 0.9995 | 0.9997 | 0.9998 |
| IMPA | 0.6524 | 0.8012 | 0.9055 | 0.9335 | 0.9759 | 0.9953 | 0.9985 | 0.9993 | 0.9995 | 0.9997 | |
| FFA | 0.6524 | 0.8015 | 0.9104 | 0.9363 | 0.9798 | 0.9948 | 0.9981 | 0.9991 | 0.9995 | 0.9996 | |
| SCA | 0.6519 | 0.8025 | 0.9139 | 0.9279 | 0.9741 | 0.9931 | 0.9968 | 0.9988 | 0.9991 | 0.9994 | |
| FPA | 0.6524 | 0.8020 | 0.9242 | 0.9298 | 0.9721 | 0.9911 | 0.9972 | 0.9986 | 0.9991 | 0.9994 | |
| L-SHADE | 0.6550 | 0.7978 | 0.8787 | 0.9313 | 0.9704 | 0.9889 | 0.9965 | 0.9980 | 0.9990 | 0.9994 | |
| SSA | 0.6524 | 0.8019 | 0.9190 | 0.9375 | 0.9784 | 0.9950 | 0.9980 | 0.9991 | 0.9994 | 0.9996 | |
| EO | 0.6524 | 0.8012 | 0.9055 | 0.9339 | 0.9802 | 0.9956 | 0.9987 | 0.9993 | 0.9996 | 0.9997 | |
| CSA | 0.6523 | 0.8018 | 0.9261 | 0.9325 | 0.9738 | 0.9923 | 0.9976 | 0.9988 | 0.9993 | 0.9995 | |
| 277095 | IWOA | 0.8066 | 0.8883 | 0.9077 | 0.9422 | 0.9833 | 0.9960 | 0.9988 | 0.9994 | 0.9997 | 0.9998 |
| IMPA | 0.8066 | 0.8944 | 0.9077 | 0.9441 | 0.9841 | 0.9960 | 0.9987 | 0.9993 | 0.9995 | 0.9996 | |
| FFA | 0.8066 | 0.8931 | 0.9118 | 0.9437 | 0.9844 | 0.9955 | 0.9984 | 0.9988 | 0.9992 | 0.9994 | |
| SCA | 0.8070 | 0.8888 | 0.9072 | 0.9387 | 0.9789 | 0.9911 | 0.9968 | 0.9982 | 0.9989 | 0.9993 | |
| FPA | 0.8072 | 0.8895 | 0.9104 | 0.9372 | 0.9743 | 0.9880 | 0.9955 | 0.9976 | 0.9986 | 0.9990 | |
| L-SHADE | 0.8042 | 0.8754 | 0.9004 | 0.9186 | 0.9560 | 0.9826 | 0.9941 | 0.9969 | 0.9983 | 0.9988 | |
| SSA | 0.8066 | 0.8958 | 0.9133 | 0.9423 | 0.9843 | 0.9956 | 0.9982 | 0.9988 | 0.9991 | 0.9995 | |
| EO | 0.8066 | 0.8948 | 0.9116 | 0.9411 | 0.9837 | 0.9955 | 0.9985 | 0.9992 | 0.9994 | 0.9996 | |
| CSA | 0.8081 | 0.8897 | 0.9120 | 0.9404 | 0.9770 | 0.9900 | 0.9961 | 0.9982 | 0.9988 | 0.9992 | |
Bold values indicate the best value
Table 10.
The UQI values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 299091 | IWOA | 0.6720 | 0.7634 | 0.8357 | 0.8863 | 0.9761 | 0.9949 | 0.9987 | 0.9993 | 0.9996 | 0.9997 |
| IMPA | 0.6720 | 0.7634 | 0.8357 | 0.8706 | 0.9750 | 0.9947 | 0.9987 | 0.9993 | 0.9995 | 0.9996 | |
| FFA | 0.6720 | 0.7634 | 0.8376 | 0.8931 | 0.9794 | 0.9942 | 0.9976 | 0.9986 | 0.9991 | 0.9994 | |
| SCA | 0.6669 | 0.7622 | 0.8441 | 0.8797 | 0.9652 | 0.9861 | 0.9953 | 0.9978 | 0.9987 | 0.9992 | |
| FPA | 0.6716 | 0.7622 | 0.8376 | 0.8754 | 0.9656 | 0.9880 | 0.9958 | 0.9979 | 0.9987 | 0.9992 | |
| L-SHADE | 0.6722 | 0.7293 | 0.8215 | 0.8779 | 0.9561 | 0.9829 | 0.9947 | 0.9975 | 0.9985 | 0.9989 | |
| SSA | 0.6720 | 0.7634 | 0.8363 | 0.9089 | 0.9793 | 0.9943 | 0.9974 | 0.9984 | 0.9991 | 0.9992 | |
| EO | 0.6720 | 0.7634 | 0.8357 | 0.9021 | 0.9802 | 0.9955 | 0.9983 | 0.9989 | 0.9993 | 0.9995 | |
| CSA | 0.6704 | 0.7611 | 0.8383 | 0.8880 | 0.9733 | 0.9899 | 0.9965 | 0.9984 | 0.9989 | 0.9992 | |
| 157055 | IWOA | 0.8813 | 0.9272 | 0.9485 | 0.9564 | 0.9908 | 0.9972 | 0.9992 | 0.9996 | 0.9998 | 0.9998 |
| IMPA | 0.8813 | 0.9275 | 0.9487 | 0.9563 | 0.9907 | 0.9972 | 0.9992 | 0.9996 | 0.9997 | 0.9998 | |
| FFA | 0.8813 | 0.9275 | 0.9487 | 0.9567 | 0.9903 | 0.9964 | 0.9983 | 0.9990 | 0.9993 | 0.9995 | |
| SCA | 0.8808 | 0.9271 | 0.9488 | 0.9549 | 0.9865 | 0.9945 | 0.9977 | 0.9990 | 0.9994 | 0.9996 | |
| FPA | 0.8813 | 0.9262 | 0.9448 | 0.9539 | 0.9843 | 0.9942 | 0.9980 | 0.9988 | 0.9993 | 0.9995 | |
| L-SHADE | 0.8797 | 0.9235 | 0.9403 | 0.9502 | 0.9804 | 0.9926 | 0.9976 | 0.9988 | 0.9992 | 0.9995 | |
| SSA | 0.8813 | 0.9275 | 0.9480 | 0.9567 | 0.9897 | 0.9964 | 0.9983 | 0.9990 | 0.9994 | 0.9995 | |
| EO | 0.8813 | 0.9274 | 0.9486 | 0.9564 | 0.9903 | 0.9966 | 0.9986 | 0.9991 | 0.9994 | 0.9996 | |
| CSA | 0.8812 | 0.9268 | 0.9475 | 0.9548 | 0.9868 | 0.9948 | 0.9981 | 0.9989 | 0.9994 | 0.9996 | |
| 108070 | IWOA | 0.4139 | 0.5808 | 0.7064 | 0.8151 | 0.9666 | 0.9923 | 0.9979 | 0.9989 | 0.9993 | 0.9995 |
| IMPA | 0.4139 | 0.5808 | 0.7064 | 0.7739 | 0.9627 | 0.9933 | 0.9975 | 0.9985 | 0.9991 | 0.9993 | |
| FFA | 0.4139 | 0.5808 | 0.7093 | 0.8241 | 0.9724 | 0.9930 | 0.9970 | 0.9982 | 0.9987 | 0.9991 | |
| SCA | 0.4130 | 0.5897 | 0.7078 | 0.8157 | 0.9592 | 0.9848 | 0.9939 | 0.9972 | 0.9982 | 0.9989 | |
| FPA | 0.4139 | 0.5836 | 0.6943 | 0.8219 | 0.9621 | 0.9855 | 0.9947 | 0.9971 | 0.9985 | 0.9989 | |
| L-SHADE | 0.4056 | 0.5866 | 0.6849 | 0.8005 | 0.9569 | 0.9781 | 0.9938 | 0.9973 | 0.9982 | 0.9987 | |
| SSA | 0.4139 | 0.5808 | 0.7065 | 0.8249 | 0.9726 | 0.9927 | 0.9968 | 0.9980 | 0.9987 | 0.9991 | |
| EO | 0.4139 | 0.5808 | 0.7064 | 0.8211 | 0.9758 | 0.9942 | 0.9979 | 0.9988 | 0.9992 | 0.9994 | |
| CSA | 0.4139 | 0.5872 | 0.6996 | 0.7916 | 0.9600 | 0.9876 | 0.9956 | 0.9976 | 0.9985 | 0.9990 | |
| 108082 | IWOA | 0.5366 | 0.6803 | 0.7643 | 0.8129 | 0.9345 | 0.9929 | 0.9980 | 0.9989 | 0.9994 | 0.9996 |
| IMPA | 0.5366 | 0.6839 | 0.7628 | 0.8043 | 0.9295 | 0.9915 | 0.9967 | 0.9984 | 0.9991 | 0.9994 | |
| FFA | 0.5369 | 0.6836 | 0.7665 | 0.8181 | 0.9458 | 0.9901 | 0.9960 | 0.9982 | 0.9989 | 0.9992 | |
| SCA | 0.5419 | 0.6799 | 0.7665 | 0.8091 | 0.9286 | 0.9858 | 0.9957 | 0.9974 | 0.9987 | 0.9990 | |
| FPA | 0.5368 | 0.6793 | 0.7697 | 0.8191 | 0.9284 | 0.9836 | 0.9956 | 0.9981 | 0.9986 | 0.9991 | |
| L-SHADE | 0.5451 | 0.6711 | 0.7714 | 0.8105 | 0.9252 | 0.9837 | 0.9953 | 0.9973 | 0.9987 | 0.9989 | |
| SSA | 0.5376 | 0.6852 | 0.7665 | 0.8165 | 0.9470 | 0.9893 | 0.9972 | 0.9983 | 0.9988 | 0.9992 | |
| EO | 0.5366 | 0.6839 | 0.7655 | 0.8149 | 0.9554 | 0.9896 | 0.9972 | 0.9984 | 0.9991 | 0.9994 | |
| CSA | 0.5382 | 0.6772 | 0.7658 | 0.8124 | 0.9315 | 0.9885 | 0.9963 | 0.9980 | 0.9985 | 0.9991 | |
Bold values indicate the best value
Table 11.
The UQI values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| Barbara | IWOA | 0.8840 | 0.9366 | 0.9585 | 0.9728 | 0.9899 | 0.9974 | 0.9993 | 0.9997 | 0.9998 | 0.9999 |
| IMPA | 0.8840 | 0.9366 | 0.9585 | 0.9727 | 0.9898 | 0.9971 | 0.9993 | 0.9997 | 0.9997 | 0.9998 | |
| FFA | 0.8840 | 0.9366 | 0.9584 | 0.9726 | 0.9895 | 0.9970 | 0.9991 | 0.9995 | 0.9996 | 0.9998 | |
| SCA | 0.8841 | 0.9367 | 0.9585 | 0.9724 | 0.9884 | 0.9952 | 0.9985 | 0.9992 | 0.9995 | 0.9997 | |
| FPA | 0.8841 | 0.9366 | 0.9579 | 0.9720 | 0.9874 | 0.9951 | 0.9984 | 0.9991 | 0.9995 | 0.9997 | |
| L-SHADE | 0.8838 | 0.9348 | 0.9558 | 0.9687 | 0.9862 | 0.9947 | 0.9981 | 0.9990 | 0.9994 | 0.9996 | |
| SSA | 0.8840 | 0.9366 | 0.9584 | 0.9726 | 0.9895 | 0.9970 | 0.9989 | 0.9994 | 0.9997 | 0.9997 | |
| EO | 0.8840 | 0.9366 | 0.9585 | 0.9727 | 0.9900 | 0.9971 | 0.9990 | 0.9994 | 0.9996 | 0.9997 | |
| CSA | 0.8841 | 0.9366 | 0.9580 | 0.9721 | 0.9883 | 0.9958 | 0.9985 | 0.9993 | 0.9996 | 0.9997 | |
| Airplane | IWOA | 0.9039 | 0.9510 | 0.9634 | 0.9689 | 0.9905 | 0.9968 | 0.9991 | 0.9995 | 0.9997 | 0.9998 |
| IMPA | 0.9039 | 0.9510 | 0.9634 | 0.9694 | 0.9902 | 0.9963 | 0.9989 | 0.9995 | 0.9997 | 0.9997 | |
| FFA | 0.9039 | 0.9510 | 0.9633 | 0.9689 | 0.9872 | 0.9925 | 0.9969 | 0.9986 | 0.9994 | 0.9994 | |
| SCA | 0.9035 | 0.9509 | 0.9635 | 0.9697 | 0.9892 | 0.9951 | 0.9977 | 0.9988 | 0.9992 | 0.9993 | |
| FPA | 0.9039 | 0.9509 | 0.9627 | 0.9687 | 0.9864 | 0.9928 | 0.9973 | 0.9986 | 0.9990 | 0.9994 | |
| L-SHADE | 0.9033 | 0.9467 | 0.9553 | 0.9632 | 0.9805 | 0.9926 | 0.9968 | 0.9983 | 0.9985 | 0.9993 | |
| SSA | 0.9039 | 0.9510 | 0.9633 | 0.9692 | 0.9887 | 0.9919 | 0.9968 | 0.9987 | 0.9991 | 0.9996 | |
| EO | 0.9039 | 0.9510 | 0.9634 | 0.9689 | 0.9892 | 0.9951 | 0.9973 | 0.9984 | 0.9990 | 0.9994 | |
| CSA | 0.9038 | 0.9510 | 0.9634 | 0.9688 | 0.9881 | 0.9946 | 0.9977 | 0.9989 | 0.9992 | 0.9995 | |
| Mandrill | IWOA | 0.8643 | 0.9202 | 0.9426 | 0.9630 | 0.9855 | 0.9960 | 0.9989 | 0.9995 | 0.9997 | 0.9998 |
| IMPA | 0.8643 | 0.9199 | 0.9426 | 0.9630 | 0.9854 | 0.9964 | 0.9991 | 0.9994 | 0.9996 | 0.9997 | |
| FFA | 0.8643 | 0.9202 | 0.9424 | 0.9632 | 0.9850 | 0.9959 | 0.9986 | 0.9991 | 0.9994 | 0.9996 | |
| SCA | 0.8643 | 0.9204 | 0.9417 | 0.9622 | 0.9816 | 0.9924 | 0.9970 | 0.9984 | 0.9990 | 0.9993 | |
| FPA | 0.8643 | 0.9210 | 0.9407 | 0.9604 | 0.9813 | 0.9914 | 0.9965 | 0.9980 | 0.9988 | 0.9992 | |
| L-SHADE | 0.8617 | 0.9118 | 0.9287 | 0.9414 | 0.9736 | 0.9869 | 0.9960 | 0.9981 | 0.9988 | 0.9992 | |
| SSA | 0.8643 | 0.9198 | 0.9425 | 0.9631 | 0.9857 | 0.9952 | 0.9986 | 0.9991 | 0.9994 | 0.9995 | |
| EO | 0.8643 | 0.9202 | 0.9425 | 0.9630 | 0.9835 | 0.9956 | 0.9987 | 0.9991 | 0.9995 | 0.9996 | |
| CSA | 0.8643 | 0.9208 | 0.9415 | 0.9611 | 0.9810 | 0.9927 | 0.9974 | 0.9986 | 0.9992 | 0.9994 | |
| Lena | IWOA | 0.8330 | 0.9045 | 0.9319 | 0.9424 | 0.9845 | 0.9970 | 0.9991 | 0.9996 | 0.9997 | 0.9998 |
| IMPA | 0.8330 | 0.9045 | 0.9328 | 0.9424 | 0.9864 | 0.9970 | 0.9991 | 0.9995 | 0.9997 | 0.9998 | |
| FFA | 0.8330 | 0.9046 | 0.9322 | 0.9425 | 0.9879 | 0.9967 | 0.9986 | 0.9993 | 0.9995 | 0.9996 | |
| SCA | 0.8329 | 0.9045 | 0.9326 | 0.9412 | 0.9749 | 0.9933 | 0.9978 | 0.9987 | 0.9990 | 0.9994 | |
| FPA | 0.8330 | 0.9043 | 0.9317 | 0.9396 | 0.9730 | 0.9918 | 0.9975 | 0.9986 | 0.9991 | 0.9994 | |
| L-SHADE | 0.8307 | 0.9000 | 0.9241 | 0.9351 | 0.9707 | 0.9906 | 0.9969 | 0.9983 | 0.9991 | 0.9994 | |
| SSA | 0.8330 | 0.9045 | 0.9324 | 0.9425 | 0.9877 | 0.9967 | 0.9987 | 0.9992 | 0.9995 | 0.9996 | |
| EO | 0.8330 | 0.9045 | 0.9313 | 0.9424 | 0.9879 | 0.9966 | 0.9988 | 0.9993 | 0.9995 | 0.9997 | |
| CSA | 0.8330 | 0.9040 | 0.9318 | 0.9413 | 0.9785 | 0.9936 | 0.9979 | 0.9989 | 0.9993 | 0.9995 | |
Bold values indicate the best value
Fig. 16.
Comparison among algorithms of the UQI values
Here, we are interested in comparing the algorithms in terms of maximizing Kapur’s entropy function (Eq. 4). Regarding the results, we can observe that the proposed algorithm could be superior in most cases, especially cases with the high threshold levels, shown in Tables 12, 13, 14 and competitive in the other cases. Additionally, Fig. 17 illustrates the superiority of the proposed algorithm compared with the other algorithm in the Fitness values. The figure inspects the average fitness values for all the test images for each algorithm. IWOA achieves the highest fitness value of 53.7909, while IMPA comes in the second rank with 53.099. L-SHADE shows the lowest fitness value of 49.13.
Table 12.
The Fitness values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 61060 | IWOA | 12.776 | 15.9511 | 19.0715 | 21.789 | 33.8015 | 52.3957 | 78.3952 | 96.322 | 109.6184 | 120.0533 |
| IMPA(Abdel-Basset et al. 2020) | 12.776 | 15.9561 | 19.0715 | 21.8197 | 33.8031 | 52.2547 | 77.7866 | 95.1371 | 107.3739 | 116.0695 | |
| FFA (Erdmann et al. 2015) | 12.776 | 15.9611 | 19.0712 | 21.788 | 33.7471 | 51.8177 | 75.8089 | 91.5198 | 103.0224 | 111.9054 | |
| SCA (Mirjalili 2016) | 12.7756 | 15.957 | 19.0357 | 21.7388 | 33.45 | 50.6662 | 73.1764 | 88.8787 | 100.2654 | 109.332 | |
| FPA(Yang 2012) | 12.776 | 15.9529 | 19.0336 | 21.7037 | 33.3017 | 50.2076 | 72.8298 | 88.225 | 100.0461 | 109.6068 | |
| L-SHADE(Brest et al. 2016) | 12.7402 | 15.848 | 18.7631 | 21.3867 | 32.6433 | 49.0551 | 70.8876 | 86.3258 | 98.1304 | 107.4438 | |
| SSA (Wang et al. 2020) | 12.776 | 15.9574 | 19.0712 | 21.7995 | 33.6629 | 51.7207 | 76.1782 | 91.5312 | 103.1833 | 112.8129 | |
| EO(Abdel-Basset et al. 2021) | 12.7760 | 15.9536 | 19.0715 | 21.7891 | 33.7511 | 51.7728 | 76.2052 | 92.0687 | 103.9213 | 113.4531 | |
| CSA(Moses et al. 2019) | 12.7759 | 15.9574 | 19.0516 | 21.7625 | 33.4716 | 50.8725 | 73.7686 | 89.3058 | 101.4225 | 110.6946 | |
| 105053 | IWOA | 11.8823 | 15.122 | 18.0216 | 20.6712 | 32.3523 | 50.3743 | 74.7683 | 91.2218 | 102.9993 | 112.056 |
| IMPA(Abdel-Basset et al. 2020) | 11.8823 | 15.122 | 18.0383 | 20.6791 | 32.3437 | 50.2377 | 74.2076 | 89.9192 | 100.9974 | 108.9814 | |
| FFA (Erdmann et al. 2015) | 11.8823 | 15.122 | 18.0247 | 20.6791 | 32.1936 | 49.4224 | 71.4182 | 85.7842 | 95.8659 | 104.189 | |
| SCA (Mirjalili 2016) | 11.881 | 15.113 | 17.9904 | 20.6263 | 31.9543 | 48.4581 | 69.2537 | 83.0938 | 93.5198 | 101.607 | |
| FPA(Yang 2012) | 11.8822 | 15.1112 | 17.9834 | 20.6066 | 31.7961 | 47.7961 | 68.4096 | 82.1473 | 92.5227 | 100.9397 | |
| L-SHADE(Brest et al. 2016) | 11.7392 | 14.8633 | 17.589 | 20.1722 | 30.8293 | 45.98 | 66.0778 | 79.8543 | 90.5128 | 98.9473 | |
| SSA (Wang et al. 2020) | 11.8823 | 15.1219 | 18.0358 | 20.6664 | 32.2229 | 49.4192 | 71.5406 | 85.3184 | 95.8636 | 104.4071 | |
| EO(Abdel-Basset et al. 2021) | 11.8482 | 15.1220 | 17.9966 | 20.6998 | 32.3109 | 49.7221 | 72.1895 | 86.1353 | 97.3854 | 104.7356 | |
| CSA(Moses et al. 2019) | 11.8821 | 15.1161 | 17.9991 | 20.6338 | 32.0011 | 48.5745 | 69.8052 | 84.2199 | 94.7203 | 103.0389 | |
| 181079 | IWOA | 12.5194 | 15.6559 | 18.5605 | 21.2831 | 33.0229 | 51.7113 | 77.6138 | 95.1912 | 108.2282 | 118.3517 |
| IMPA(Abdel-Basset et al. 2020) | 12.5194 | 15.6559 | 18.5607 | 21.2833 | 33.0227 | 51.5554 | 77.0396 | 93.8592 | 105.3401 | 114.4753 | |
| FFA (Erdmann et al. 2015) | 12.5194 | 15.6559 | 18.5596 | 21.2816 | 32.9363 | 51.0539 | 74.4852 | 89.7446 | 101.5361 | 110.4897 | |
| SCA (Mirjalili 2016) | 12.5193 | 15.6528 | 18.5481 | 21.2574 | 32.7656 | 50.0573 | 72.2192 | 87.5166 | 98.8036 | 107.7341 | |
| FPA(Yang 2012) | 12.5194 | 15.6525 | 18.5463 | 21.2322 | 32.5791 | 49.4161 | 71.6639 | 86.8136 | 98.6199 | 107.5495 | |
| L-SHADE(Brest et al. 2016) | 12.5021 | 15.5605 | 18.3787 | 20.9216 | 31.8685 | 48.2518 | 69.8864 | 84.675 | 96.4386 | 105.7433 | |
| SSA (Wang et al. 2020) | 12.5194 | 15.6559 | 18.56 | 21.2813 | 32.9585 | 51.1506 | 74.8946 | 90.6978 | 101.2136 | 110.3164 | |
| EO(Abdel-Basset et al. 2021) | 12.5194 | 15.6530 | 18.5598 | 21.2829 | 32.9412 | 51.0342 | 74.8979 | 90.8307 | 102.4668 | 111.2834 | |
| CSA(Moses et al. 2019) | 12.5194 | 15.6545 | 18.5530 | 21.2561 | 32.7245 | 49.9210 | 72.6653 | 88.2450 | 99.7304 | 109.0304 | |
| 232038 | IWOA | 11.9894 | 15.2615 | 18.0564 | 20.8226 | 32.5819 | 50.9049 | 76.2528 | 93.5106 | 106.3026 | 116.2968 |
| IMPA(Abdel-Basset et al. 2020) | 11.9894 | 15.2615 | 18.0657 | 20.8512 | 32.5896 | 50.6511 | 75.6467 | 92.4374 | 104.1028 | 112.7034 | |
| FFA (Erdmann et al. 2015) | 11.9894 | 15.2606 | 18.0551 | 20.7902 | 32.4147 | 50.1182 | 73.7958 | 89.8715 | 100.9383 | 109.7447 | |
| SCA (Mirjalili 2016) | 11.9891 | 15.249 | 18.022 | 20.7231 | 32.1319 | 49.1496 | 71.225 | 85.6759 | 96.8546 | 105.4877 | |
| FPA(Yang 2012) | 11.9893 | 15.2502 | 18.025 | 20.7002 | 31.9145 | 48.6638 | 70.3656 | 85.5129 | 96.7159 | 105.5622 | |
| L-SHADE(Brest et al. 2016) | 11.9613 | 15.0528 | 17.7702 | 20.3541 | 31.1784 | 47.232 | 68.699 | 83.3479 | 94.5921 | 103.6789 | |
| SSA (Wang et al. 2020) | 11.9894 | 15.261 | 18.0619 | 20.8162 | 32.4102 | 50.1126 | 74.0407 | 90.1449 | 101.0976 | 110.3437 | |
| EO(Abdel-Basset et al. 2021) | 11.9894 | 15.2615 | 18.0687 | 20.8512 | 32.5406 | 50.1159 | 74.1409 | 90.2424 | 101.5987 | 110.4611 | |
| CSA(Moses et al. 2019) | 11.9894 | 15.2547 | 18.0412 | 20.7296 | 32.2061 | 49.0106 | 71.4365 | 86.6975 | 98.2346 | 106.9818 | |
| 277095 | IWOA | 11.9706 | 14.9796 | 17.802 | 20.4036 | 31.6016 | 48.2872 | 70.2967 | 84.8372 | 95.0545 | 102.9802 |
| IMPA(Abdel-Basset et al. 2020) | 11.9706 | 14.9795 | 17.802 | 20.4091 | 31.5793 | 48.2265 | 69.9503 | 83.2584 | 91.978 | 98.399 | |
| FFA (Erdmann et al. 2015) | 11.9706 | 14.9793 | 17.7932 | 20.3993 | 31.5387 | 47.9795 | 68.6196 | 80.9031 | 89.0562 | 95.4017 | |
| SCA (Mirjalili 2016) | 11.9703 | 14.9777 | 17.7794 | 20.3582 | 31.2482 | 46.4847 | 65.0903 | 77.2917 | 86.0844 | 92.7041 | |
| FPA(Yang 2012) | 11.9706 | 14.9763 | 17.7676 | 20.3349 | 30.9178 | 45.3584 | 62.8773 | 74.6368 | 83.5616 | 90.2943 | |
| L-SHADE(Brest et al. 2016) | 11.9036 | 14.8163 | 17.5314 | 19.8222 | 29.1678 | 42.401 | 59.4692 | 71.5032 | 79.9929 | 86.9559 | |
| SSA (Wang et al. 2020) | 11.9706 | 14.9791 | 17.7927 | 20.4005 | 31.5368 | 47.8578 | 67.9296 | 80.6834 | 89.2749 | 96.6264 | |
| EO(Abdel-Basset et al. 2021) | 11.9706 | 14.9797 | 17.8020 | 20.4010 | 31.5495 | 47.7624 | 68.4138 | 81.7316 | 90.9752 | 98.3387 | |
| CSA(Moses et al. 2019) | 11.9704 | 14.9777 | 17.7781 | 20.3590 | 31.1246 | 46.0247 | 64.5108 | 76.7458 | 85.4095 | 92.4490 | |
Bold values indicate the best value
Table 13.
The Fitness values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| 299091 | IWOA | 12.1936 | 15.2182 | 18.06 | 20.6625 | 32.037 | 48.9849 | 72.2013 | 87.63 | 98.821 | 107.3364 |
| IMPA(Abdel-Basset et al. 2020) | 12.1936 | 15.2182 | 18.06 | 20.6617 | 32.0308 | 48.8686 | 71.6678 | 86.1093 | 96.4726 | 103.7719 | |
| FFA (Erdmann et al. 2015) | 12.1936 | 15.2182 | 18.0594 | 20.6612 | 31.8862 | 47.9939 | 68.2067 | 81.2467 | 90.8543 | 98.5 | |
| SCA (Mirjalili 2016) | 12.1935 | 15.2127 | 18.0461 | 20.6218 | 31.6553 | 46.9312 | 66.3038 | 79.1904 | 88.7332 | 96.069 | |
| FPA(Yang 2012) | 12.1936 | 15.2134 | 18.0392 | 20.6098 | 31.3523 | 46.2153 | 65.2326 | 78.1287 | 87.5557 | 95.305 | |
| L-SHADE(Brest et al. 2016) | 12.1758 | 15.1165 | 17.7635 | 20.2311 | 29.9142 | 43.4662 | 61.9724 | 75.148 | 84.9238 | 92.8362 | |
| SSA (Wang et al. 2020) | 12.1936 | 15.218 | 18.0595 | 20.6608 | 31.8082 | 47.9178 | 68.1283 | 81.1228 | 91.3473 | 98.9493 | |
| EO(Abdel-Basset et al. 2021) | 12.1936 | 15.2182 | 18.0600 | 20.6615 | 31.9104 | 48.1877 | 68.5090 | 81.7795 | 91.5729 | 99.0036 | |
| CSA(Moses et al. 2019) | 12.1936 | 15.2150 | 18.0423 | 20.6216 | 31.6156 | 47.0079 | 66.6733 | 79.8625 | 89.8023 | 97.4248 | |
| 157055 | IWOA | 12.7329 | 15.8481 | 18.7846 | 21.5883 | 33.58 | 51.5129 | 76.3282 | 93.3345 | 105.7084 | 115.3345 |
| IMPA(Abdel-Basset et al. 2020) | 12.7329 | 15.8481 | 18.7846 | 21.5883 | 33.5438 | 51.4185 | 75.8986 | 91.9737 | 103.1469 | 111.9807 | |
| FFA (Erdmann et al. 2015) | 12.7329 | 15.8481 | 18.7841 | 21.5846 | 33.5169 | 50.5955 | 73.2913 | 87.9072 | 99.147 | 107.5119 | |
| SCA (Mirjalili 2016) | 12.7324 | 15.8465 | 18.7767 | 21.5452 | 33.0927 | 49.846 | 71.1477 | 85.6086 | 96.1502 | 105.1024 | |
| FPA(Yang 2012) | 12.7327 | 15.8464 | 18.7693 | 21.5363 | 32.9778 | 49.1333 | 70.239 | 84.7424 | 95.9082 | 104.5418 | |
| L-SHADE(Brest et al. 2016) | 12.7131 | 15.7919 | 18.6232 | 21.2728 | 32.1838 | 47.8387 | 68.3398 | 82.6632 | 93.9342 | 102.6285 | |
| SSA (Wang et al. 2020) | 12.7329 | 15.8481 | 18.7843 | 21.5851 | 33.5003 | 50.5414 | 73.4454 | 87.7362 | 98.669 | 107.3931 | |
| EO(Abdel-Basset et al. 2021) | 12.7329 | 15.8481 | 18.7845 | 21.5880 | 33.5399 | 50.8141 | 73.7899 | 88.6606 | 99.8075 | 108.0157 | |
| CSA(Moses et al. 2019) | 12.7326 | 15.8470 | 18.7751 | 21.5526 | 33.1433 | 49.8022 | 71.5882 | 86.0455 | 97.1117 | 105.9712 | |
| 108070 | IWOA | 12.5289 | 15.7032 | 18.5777 | 21.2449 | 32.9399 | 50.7339 | 74.9149 | 91.1513 | 103.1007 | 112.4513 |
| IMPA(Abdel-Basset et al. 2020) | 12.5289 | 15.7032 | 18.5786 | 21.2508 | 32.9194 | 50.6107 | 74.2717 | 89.7181 | 100.1829 | 108.4918 | |
| FFA (Erdmann et al. 2015) | 12.5289 | 15.7032 | 18.5733 | 21.24 | 32.8684 | 50.017 | 72.3464 | 86.2931 | 96.7648 | 104.4112 | |
| SCA (Mirjalili 2016) | 12.5284 | 15.6982 | 18.5556 | 21.22 | 32.6078 | 48.9772 | 69.7404 | 83.4832 | 93.6996 | 101.6287 | |
| FPA(Yang 2012) | 12.5289 | 15.6973 | 18.5418 | 21.1986 | 32.4195 | 48.3326 | 69.3536 | 83.2895 | 93.5883 | 101.5344 | |
| L-SHADE(Brest et al. 2016) | 12.495 | 15.6113 | 18.4059 | 20.9844 | 31.7188 | 47.1881 | 67.1581 | 81.5701 | 91.8702 | 100.0146 | |
| SSA (Wang et al. 2020) | 12.5289 | 15.7031 | 18.575 | 21.2338 | 32.8494 | 50.0621 | 71.945 | 86.1112 | 96.6926 | 104.2336 | |
| EO(Abdel-Basset et al. 2021) | 12.5289 | 15.7032 | 18.5786 | 21.2380 | 32.8913 | 50.1531 | 72.7822 | 87.1156 | 97.9495 | 106.3171 | |
| CSA(Moses et al. 2019) | 12.5289 | 15.6980 | 18.5549 | 21.2202 | 32.6136 | 48.9436 | 70.3134 | 84.5232 | 95.2522 | 103.4803 | |
| 108082 | IWOA | 12.5693 | 15.8063 | 18.8163 | 21.5944 | 33.5664 | 52.3813 | 78.7126 | 96.9154 | 110.5434 | 121.0727 |
| IMPA(Abdel-Basset et al. 2020) | 12.5693 | 15.8063 | 18.8167 | 21.5958 | 33.5708 | 52.1202 | 77.9697 | 95.755 | 107.9924 | 117.6285 | |
| FFA (Erdmann et al. 2015) | 12.5693 | 15.8063 | 18.8159 | 21.5932 | 33.4895 | 51.6847 | 75.954 | 92.9873 | 104.651 | 114.27 | |
| SCA (Mirjalili 2016) | 12.5693 | 15.8046 | 18.8083 | 21.5741 | 33.2802 | 50.6619 | 73.6094 | 89.4522 | 101.3693 | 110.538 | |
| FPA(Yang 2012) | 12.5693 | 15.8043 | 18.8031 | 21.5577 | 33.1035 | 50.2587 | 73.2679 | 89.2795 | 101.1707 | 110.884 | |
| L-SHADE(Brest et al. 2016) | 12.5569 | 15.7491 | 18.6537 | 21.3417 | 32.5185 | 49.0634 | 71.6566 | 87.5361 | 99.5521 | 109.1102 | |
| SSA (Wang et al. 2020) | 12.5693 | 15.8062 | 18.8158 | 21.593 | 33.466 | 51.7307 | 76.3116 | 93.0452 | 104.5969 | 113.8966 | |
| EO(Abdel-Basset et al. 2021) | 12.5693 | 15.8063 | 18.8160 | 21.5936 | 33.4811 | 51.7049 | 76.5644 | 93.0660 | 105.0594 | 114.6498 | |
| CSA(Moses et al. 2019) | 12.5693 | 15.8049 | 18.8087 | 21.5746 | 33.2841 | 50.7958 | 74.0185 | 89.8674 | 102.3192 | 111.9132 | |
Bold values indicate the best value
Table 14.
The Fitness values obtained by each algorithm
| ID | Algorithm | Threshold level (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-n | 3-n | 4-n | 5-n | 10-n | 20-n | 40-n | 60-n | 80-n | 100-n | ||
| Barbara | IWOA | 12.8944 | 16.0776 | 19.0524 | 21.8663 | 33.9123 | 52.4601 | 79.0757 | 97.5044 | 111.1390 | 121.6892 |
| IMPA | 12.8944 | 16.0776 | 19.0524 | 21.8663 | 33.8879 | 52.2651 | 78.4649 | 96.2442 | 108.8346 | 119.0990 | |
| FFA | 12.8944 | 16.0775 | 19.0523 | 21.8658 | 33.8054 | 51.8108 | 76.8774 | 93.3866 | 105.6021 | 114.8431 | |
| SCA | 12.8944 | 16.0758 | 19.0482 | 21.8492 | 33.6107 | 50.7942 | 73.8078 | 89.7958 | 101.6265 | 111.2091 | |
| FPA | 12.8944 | 16.0756 | 19.0413 | 21.8341 | 33.3758 | 50.3978 | 73.7337 | 89.6948 | 102.0421 | 111.8403 | |
| L-SHADE | 12.8922 | 16.0579 | 18.9910 | 21.7421 | 33.0279 | 49.9484 | 72.8420 | 88.7265 | 100.7691 | 110.3752 | |
| SSA | 12.8944 | 16.0775 | 19.0523 | 21.8659 | 33.7984 | 51.7781 | 76.6527 | 93.2786 | 105.3635 | 114.6159 | |
| EO | 12.8944 | 16.0776 | 19.0524 | 21.8663 | 33.8446 | 51.9086 | 76.6778 | 93.4764 | 106.5393 | 115.7284 | |
| CSA | 12.8944 | 16.0764 | 19.0476 | 21.8471 | 33.5953 | 50.8853 | 74.2599 | 90.3407 | 103.0055 | 112.4235 | |
| Airplane | IWOA | 12.2274 | 15.5081 | 18.3280 | 20.9303 | 32.1921 | 49.4457 | 73.3265 | 89.5468 | 101.3674 | 110.3298 |
| IMPA | 12.2274 | 15.5081 | 18.3280 | 20.9443 | 32.1938 | 49.3655 | 72.9529 | 88.3452 | 99.0658 | 107.5168 | |
| FFA | 12.2274 | 15.5081 | 18.3277 | 20.9426 | 32.1144 | 48.7340 | 71.0379 | 85.4506 | 95.3996 | 103.3912 | |
| SCA | 12.2271 | 15.5060 | 18.3131 | 20.9008 | 31.8910 | 47.6428 | 68.1025 | 81.4938 | 91.3694 | 99.3757 | |
| FPA | 12.2274 | 15.5050 | 18.3041 | 20.8828 | 31.5846 | 46.8968 | 66.7783 | 80.3438 | 90.4299 | 98.7316 | |
| L-SHADE | 12.2193 | 15.4624 | 18.1729 | 20.6912 | 31.0167 | 45.4572 | 65.3350 | 78.7339 | 89.0651 | 97.3590 | |
| SSA | 12.2274 | 15.5081 | 18.3276 | 20.9398 | 32.1214 | 48.8001 | 70.8753 | 85.1912 | 95.0733 | 103.6766 | |
| EO | 12.2274 | 15.5081 | 18.3280 | 20.9323 | 32.1053 | 48.7336 | 71.1307 | 85.3082 | 96.0334 | 104.1792 | |
| CSA | 12.2273 | 15.5069 | 18.3155 | 20.9039 | 31.8410 | 47.6095 | 68.4197 | 82.4731 | 93.1874 | 101.3812 | |
| Mandrill | IWOA | 12.2772 | 15.3757 | 18.2736 | 20.9959 | 32.9155 | 51.1552 | 76.0453 | 92.9924 | 105.3956 | 114.9888 |
| IMPA | 12.2772 | 15.3757 | 18.2736 | 20.9959 | 32.9143 | 51.1099 | 75.6127 | 91.7131 | 103.1385 | 112.2372 | |
| FFA | 12.2772 | 15.3757 | 18.2736 | 20.9950 | 32.7840 | 50.5569 | 73.9999 | 89.7650 | 100.2964 | 108.6361 | |
| SCA | 12.2772 | 15.3750 | 18.2694 | 20.9754 | 32.5856 | 49.3850 | 70.8031 | 85.1097 | 95.4408 | 103.8036 | |
| FPA | 12.2772 | 15.3742 | 18.2574 | 20.9455 | 32.3696 | 48.6056 | 69.7875 | 83.8852 | 94.5511 | 103.5075 | |
| L-SHADE | 12.2716 | 15.3496 | 18.1481 | 20.7558 | 31.8418 | 47.5229 | 68.1328 | 82.4165 | 93.4220 | 102.1532 | |
| SSA | 12.2772 | 15.3757 | 18.2735 | 20.9946 | 32.7925 | 50.3889 | 73.9087 | 89.0713 | 100.4362 | 108.8014 | |
| EO | 12.2772 | 15.3757 | 18.2736 | 20.9956 | 32.8209 | 50.6321 | 74.1493 | 89.5809 | 100.6387 | 109.2418 | |
| CSA | 12.2772 | 15.3748 | 18.2661 | 20.9636 | 32.5732 | 49.4223 | 71.0083 | 85.4344 | 96.6188 | 105.3668 | |
| Lena | IWOA | 12.4048 | 15.4167 | 18.1576 | 20.8085 | 32.0524 | 49.6385 | 74.1868 | 90.5829 | 102.7917 | 112.0831 |
| IMPA | 12.4048 | 15.4167 | 18.1610 | 20.8085 | 32.0648 | 49.5704 | 73.5401 | 89.6584 | 100.5093 | 109.4049 | |
| FFA | 12.4048 | 15.4167 | 18.1575 | 20.8062 | 31.9091 | 48.9252 | 71.3114 | 85.7903 | 95.9802 | 104.9155 | |
| SCA | 12.4044 | 15.4150 | 18.1452 | 20.7724 | 31.6910 | 47.8182 | 68.6007 | 82.6401 | 92.7791 | 100.4986 | |
| FPA | 12.4048 | 15.4150 | 18.1412 | 20.7472 | 31.4874 | 47.2013 | 67.6995 | 81.6370 | 92.0589 | 100.1660 | |
| L-SHADE | 12.3984 | 15.3854 | 18.0679 | 20.5629 | 31.0228 | 46.3283 | 66.1567 | 80.2060 | 90.6329 | 99.0467 | |
| SSA | 12.4048 | 15.4167 | 18.1581 | 20.8081 | 31.9273 | 48.7946 | 71.3387 | 85.9434 | 96.7511 | 104.2898 | |
| EO | 12.4048 | 15.4167 | 18.1593 | 20.8085 | 31.9498 | 49.0792 | 71.6291 | 86.3202 | 97.0603 | 105.3507 | |
| CSA | 12.4048 | 15.4154 | 18.1476 | 20.7676 | 31.6884 | 47.9890 | 69.2904 | 83.6876 | 94.4701 | 102.7164 | |
Bold values indicate the best value
Fig. 17.
Comparison of the Fitness values results from each algorithm
Figure 18 demonstrates the average of the STD for the fitness values by running each algorithm 30 times on all test images for all threshold levels. Based on those results, the proposed algorithm could also outperform all the algorithms with an average value for STD of 0.2493. Figure 19 shows a comparison among the algorithms in terms of the CPU time. The figure provides the total CPU time for running each algorithm 30 using different threshold values for all the test images. Although IWOA doesn’t obtain the minimum CPU time, it can achieve the best results for PSNR, SSIM, fitness, and STD. IWOA takes CPU time of 0.5385 seconds, while IMPA takes the most CPU time with a value of 0.9808. FFA succeeds to attain less time in 0.3318 seconds. We can conclude that IWOA attains the best results with less STD at a reasonable time when compared with other algorithms.
Fig. 18.
Average STD for fitness values of all test images on all threshold levels
Fig. 19.
Average CPU Time values for all test images on all threshold levels
The segmented Images
Figure 20 presents the segmented images generated by the proposed algorithm using ten different threshold levels. We can see that using more threshold levels makes the segmented image to be better and close to the original one. For using a 100-threshold level, we can see that the segmented image is the best compared to other threshold levels as it succeeds to separate more objects.
Fig. 20.
The segmented images were obtained by the proposed algorithm using threshold levels 2, 3,4,5,10, 20, 40, and 100, respectively
Wilcoxon rank-sum test
In this section, the results obtained by our proposed algorithm are compared with the results obtained by the other algorithms using the statistical test called the Wilcoxon rank-sum test (Haynes 2013). This test is based on the null hypothesis and the alternative hypothesis. In the null hypothesis, this test supposes that there is no difference between the ranks of the results obtained by a pair of algorithms. On the other hand, the alternative hypothesis considers that there is a difference between the ranks obtained by a pair of algorithms. The significant level used in our test is . Tables 15, 16, and 17 show the P and S values obtained by comparing the fitness values obtained by the proposed algorithm with those of each compared algorithm on nine test images: 61060, 105053, 181079, 232038, 277095, 299091, 157055, 108070, and 108082. If or (), then the null hypothesis is true, whereas if or (), then the alternative hypothesis is true. Inspecting those tables appears that our proposed algorithm could be significantly different from the others for most test images under threshold levels greater than 5 however, for threshold levels smaller than that, it could almost reach the same outcomes of some compared algorithms. Based on that, our proposed algorithm can outperform all other algorithms for most of the threshold levels with all the test images.
Table 15.
Results of the Wilcoxon rank-sum test between IWOA and each algorithm on images from 61060:105053 under fitness values
| Test image | h | SCA | WOA | SSA | FPA | FFA | L-SHADE | IMPA | EO | CSA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | ||
| 61060 | 2 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 |
| 3 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 105053 | 2 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
Table 16.
Results of the Wilcoxon rank-sum test between IWOA and each algorithm on images from 181079:157055 under fitness values
| Test image | h | SCA | WOA | SSA | FPA | FFA | L-SHADE | IMPA | EO | CSA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | ||
| 181079 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 232038 | 2 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 277095 | 2 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 299091 | 2 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 157055 | 2 | <0.05 | 1 | <,0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
Table 17.
Results of the Wilcoxon rank-sum test between IWOA and each algorithm on images from 108070:med3 under fitness values
| Test image | h | SCA | WOA | SSA | FPA | FFA | L-SHADE | IMPA | EO | CSA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | P | S | ||
| 108070 | 2 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 108082 | 2 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | >0.05 | 0 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | >0.05 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | >0.05 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 10 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 20 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 40 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 60 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 80 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 100 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
Conclusion and future directions
Image segmentation is considered a significant problem that attracts many researchers those days. Due to using image segmentation in solving many problems in the real world, researchers have been tried to find a better technique that enables them to extract the required information from the image. Many techniques were proposed, such as threshold-based, region-based, feature-based clustering, and, edge-based to resolve this research challenge. The threshold-based segmentation is used for analyzing the image segmentation due to its ease in use. To tackle the image segmentation problem using the threshold technique, we proposed an improvement on the standard whale optimization algorithm by proposing two strategies, namely linearly convergence increasing and local minima avoidance strategy (LCMA), and ranking-based updating method (RUM) that help the whale optimization algorithm (WOA) in accelerating the convergence toward the best-so-far solution and avoiding local minima that fall into at the end of the optimization process. LCMA moves the worst K particle towards the best so-far solution for accelerating the convergence and avoiding falling into local minima by updating them within the search space based on a certain probability. K starts with a small value at the start of the optimization and increases gradually with the increasing number of the iteration even reaching the maximum at the end of the iteration. Meanwhile, RUM utilizes each individual in the population as possible in an effective way that will gradually explore the solutions around the best-so-far solution as an attempt to reach better outcomes. The experiments are performed to observe the performance of IWOA with thresholds level between 2 and 100: the first one is based on a set of the normal images taken from Berkeley Segmentation Dataset (BSD). To see the superiority of IWOA, through these two experiments, it was compared with other existing algorithms like the standard whale optimization algorithm (WOA), sine-cosine algorithm (SCA), slap swarm algorithm (SSA), flower pollination algorithm (FPA), and L-SHADE algorithm, Firefly algorithm (FFA), Equilibrium optimizer (EO), and Crow search algorithm (CSA). The quality of segmented images, fitness values, and STD metrics obtained from each algorithm through these two experiments demonstrate that the proposed algorithm outperforms all algorithms integrated with the comparison. Despite these promising results, our algorithm could not outperform some algorithms in CPU time, as our main limitation. Therefore, our future extensin will be applying the LCMA technique with other evolutionary algorithms for reducing the running time and improving the quality of results. In addition, a version of the IWOA for solving the multi-objective and single-objective optimization problems is included in our future work. Moreover, a binary version of IWOA for overcoming the feature selection problem will be given as a work in the future.
Funding
This research has no funding source.
Declarations
Conflict of interest
The authors declare that there is no conflict of interest about the research.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Mohamed Abdel-Basset, Email: mohamedbasset@ieee.org.
Reda Mohamed, Email: redamoh@zu.edu.eg.
Mohamed Abouhawwash, Email: saleh1284@mans.edu.eg, Email: abouhaww@msu.edu.
References
- Abd El Aziz M, Ewees AA, Hassanien AE. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst Appl. 2017;83:242–256. doi: 10.1016/j.eswa.2017.04.023. [DOI] [Google Scholar]
- Abd El Aziz M, Ewees AA, Hassanien AE, Mudhsh M, Xiong S (2018) Multi-objective whale optimization algorithm for multilevel thresholding segmentation. In: Advances in soft computing and machine learning in image processing. Springer, Cham, pp. 23–39
- Abdel-Basset M, Manogaran G, El-Shahat D, Mirjalili S. Integrating the whale algorithm with tabu search for quadratic assignment problem: a new approach for locating hospital departments. Appl Soft Comput. 2018;73:530–546. doi: 10.1016/j.asoc.2018.08.047. [DOI] [Google Scholar]
- Abdel-Basset M, Chang V, Mohamed R. Hsma\_woa: a hybrid novel slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest x-ray images. Appl Soft Comput. 2020;95:106642. doi: 10.1016/j.asoc.2020.106642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abdel-Basset M, Mohamed R, Mirjalili S, Chakrabortty RK, Ryan MJ. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol Energy. 2020;209:694–708. doi: 10.1016/j.solener.2020.09.032. [DOI] [Google Scholar]
- Abdel-Basset M, Mohamed R, Sallam KM, Chakrabortty RK, Ryan MJ. An efficient-assembler whale optimization algorithm for DNA fragment assembly problem: analysis and validations. IEEE Access. 2020;8:222 144–222 167. doi: 10.1109/ACCESS.2020.3044857. [DOI] [Google Scholar]
- Abdel-Basset M, Mohamed R, Elhoseny M, Chakrabortty RK, Ryan M. A hybrid covid-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE Access. 2020;8:521–540. doi: 10.1109/ACCESS.2020.2990893. [DOI] [Google Scholar]
- Abdel-Basset M, Chang V, Mohamed R. A novel equilibrium optimization algorithm for multi-thresholding image segmentation problems. Neural Comput Appl. 2021;33(17):10 685–10 718. doi: 10.1007/s00521-020-04820-y. [DOI] [Google Scholar]
- Abdel-Basset M, Mohamed R, Abouhawwash M. Balanced multi-objective optimization algorithm using improvement based reference points approach. Swarm Evol Comput. 2021;60:100791. doi: 10.1016/j.swevo.2020.100791. [DOI] [Google Scholar]
- Abdel-Basset M, Mohamed R, Mirjalili S. A binary equilibrium optimization algorithm for 0–1 knapsack problems. Comput Ind Eng. 2020;151:106946. doi: 10.1016/j.cie.2020.106946. [DOI] [Google Scholar]
- Aksac A, Ozyer T, Alhajj R. Complex networks driven salient region detection based on superpixel segmentation. Pattern Recogn. 2017;66:268–279. doi: 10.1016/j.patcog.2017.01.010. [DOI] [Google Scholar]
- Alberti M, Seuret M, Pondenkandath V, Ingold R, Liwicki M (2017) “Historical document image segmentation with lda-initialized deep neural networks,” In: Proceedings of the 4th international workshop on historical document imaging and processing, pp 95–100
- Al-Musawi AK, Anayi F, Packianather M. Three-phase induction motor fault detection based on thermal image segmentation. Infra Phys Technol. 2020;104:103140. doi: 10.1016/j.infrared.2019.103140. [DOI] [Google Scholar]
- Bal A, Banerjee M, Sharma P, Maitra M (2020) Gray matter segmentation and delineation from positron emission tomography (pet) image. In: Emerging technology in modelling and graphics. Springer, Singapore, pp 359–372
- Bao X, Jia H, Lang C. A novel hybrid harris hawks optimization for color image multilevel thresholding segmentation. Ieee Access. 2019;7:76 529–76 546. doi: 10.1109/ACCESS.2019.2921545. [DOI] [Google Scholar]
- Barman R, Ehrmann M, Clematide S, Oliveira SA, Kaplan F (2020) “Combining visual and textual features for semantic segmentation of historical newspapers,” arXiv preprintarXiv:2002.06144
- Bhandari AK, Kumar IV. A context sensitive energy thresholding based 3D OTSU function for image segmentation using human learning optimization. Appl Soft Comput. 2019;82:105570. doi: 10.1016/j.asoc.2019.105570. [DOI] [Google Scholar]
- Bhandari AK, Singh VK, Kumar A, Singh GK. Cuckoo search algorithm and wind driven optimization based study of satellite image segmentation for multilevel thresholding using kapur’s entropy. Expert Syst Appl. 2014;41(7):3538–3560. doi: 10.1016/j.eswa.2013.10.059. [DOI] [Google Scholar]
- Brest J, Maučec MS, Bošković B (2016) “il-shade: improved l-shade algorithm for single objective real-parameter optimization,” In: 2016 IEEE congress on evolutionary computation (CEC). IEEE, pp 1188–1195
- Chakraborty F, Nandi D, Roy PK. Oppositional symbiotic organisms search optimization for multilevel thresholding of color image. Appl Soft Comput. 2019;82:105577. doi: 10.1016/j.asoc.2019.105577. [DOI] [Google Scholar]
- Chen G. Image segmentation algorithm combined with regularized pm de-noising model and improved watershed algorithm. J Med Imag Health Informat. 2020;10(2):515–521. doi: 10.1166/jmihi.2020.2899. [DOI] [Google Scholar]
- Chouksey M, Jha RK, Sharma R. A fast technique for image segmentation based on two meta-heuristic algorithms. Multimed Tools Appl. 2020;79(27):19075–19127. doi: 10.1007/s11042-019-08138-3. [DOI] [Google Scholar]
- Cuevas E, Fausto F, González A (2020) Locust search algorithm applied to multi-threshold segmentation. In: New advancements in swarm algorithms: operators and applications. Springer, Cham, pp 211–240
- De S, Dey S, Debnath S, Deb A (2020) “A new modified red deer algorithm for multi-level image thresholding,” In: 2020 Fifth international conference on research in computational intelligence and communication networks (ICRCICN). IEEE, pp 105–111
- Di Martino F, Sessa S. Pso image thresholding on images compressed via fuzzy transforms. Inf Sci. 2020;506:308–324. doi: 10.1016/j.ins.2019.07.088. [DOI] [Google Scholar]
- Dirami A, Hammouche K, Diaf M, Siarry P. Fast multilevel thresholding for image segmentation through a multiphase level set method. Signal Process. 2013;93(1):139–153. doi: 10.1016/j.sigpro.2012.07.010. [DOI] [Google Scholar]
- Egiazarian K, Astola J, Ponomarenko N, Lukin V, Battisti F, Carli M (2006) “New full-reference quality metrics based on hvs,” In: Proceedings of the second international workshop on video processing and quality metrics, vol. 4
- El-Fergany AA, Hasanien HM, Agwa AM. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers Manage. 2019;201:112197. doi: 10.1016/j.enconman.2019.112197. [DOI] [Google Scholar]
- Elsayed SM, Sarker RA, Essam DL. A new genetic algorithm for solving optimization problems. Eng Appl Artif Intell. 2014;27:57–69. doi: 10.1016/j.engappai.2013.09.013. [DOI] [Google Scholar]
- Erdmann H, Wachs-Lopes G, Gallão C, Ribeiro MP, Rodrigues PS (2015) A study of a firefly meta-heuristics for multithreshold image segmentation. In: Developments in medical image processing and computational vision. Springer, Cham, pp 279–295
- Farook TH, Mousa MA, Jamayet NB. Method to control tongue position and open source image segmentation for cone-beam computed tomography of patients with large palatal defect to facilitate digital obturator design. J Oral Maxillofac Surg Med Pathol. 2020;32(1):61–64. doi: 10.1016/j.ajoms.2019.09.009. [DOI] [Google Scholar]
- Ghamisi P, Couceiro MS, Martins FM, Benediktsson JA. Multilevel image segmentation based on fractional-order darwinian particle swarm optimization. IEEE Trans Geosci Remote Sens. 2013;52(5):2382–2394. doi: 10.1109/TGRS.2013.2260552. [DOI] [Google Scholar]
- Griswold M, Jiang Y, Ma D, Deshmane A, Badve C, Gulani V, Sunshine JL (2019) U.S. Patent No. 10,261,154. U.S. Patent and Trademark Office, Washington, DC
- Guo C, Li H (2007) “Multilevel thresholding method for image segmentation based on an adaptive particle swarm optimization algorithm,” In: Australasian joint conference on artificial intelligence. Springer, pp 654–658
- Han J, Yang C, Zhou X, Gui W. A new multi-threshold image segmentation approach using state transition algorithm. Appl Math Model. 2017;44:588–601. doi: 10.1016/j.apm.2017.02.015. [DOI] [Google Scholar]
- Haynes W (2013) Wilcoxon rank sum test. Encyclopedia of systems biology, 2354–2355
- He L, Huang S. An efficient krill herd algorithm for color image multilevel thresholding segmentation problem. Appl Soft Comput. 2020;89:106063. doi: 10.1016/j.asoc.2020.106063. [DOI] [Google Scholar]
- Hore A, Ziou D (2010) “Image quality metrics: Psnr versus ssim,” In: 2010 20th international conference on pattern recognition. IEEE, pp 2366–2369
- Huo F, Sun X, Ren W. Multilevel image threshold segmentation using an improved bloch quantum artificial bee colony algorithm. Multimed Tools Appl. 2020;79(3):2447–2471. doi: 10.1007/s11042-019-08231-7. [DOI] [Google Scholar]
- Hu R, Rohrbach M, Venugopalan S, Darrell T (2016) “Utilizing large scale vision and text datasets for image segmentation from referring expressions,” arXiv preprintarXiv:1608.08305
- Jafari-Asl J, Seghier MEAB, Ohadi S, van Gelder P. Efficient method using whale optimization algorithm for reliability-based design optimization of labyrinth spillway. Appl Soft Comput. 2021;101:107036. doi: 10.1016/j.asoc.2020.107036. [DOI] [Google Scholar]
- Kandhway P, Bhandari AK. Spatial context cross entropy function based multilevel image segmentation using multi-verse optimizer. Multimed Tools Appl. 2019;78(16):22 613–22 641. doi: 10.1007/s11042-019-7506-7. [DOI] [Google Scholar]
- Kapur JN, Sahoo PK, Wong AK. A new method for gray-level picture thresholding using the entropy of the histogram. Computer Vis Gr Image Process. 1985;29(3):273–285. doi: 10.1016/0734-189X(85)90125-2. [DOI] [Google Scholar]
- Karydas CG. Optimization of multi-scale segmentation of satellite imagery using fractal geometry. Int J Remote Sens. 2020;41(8):2905–2933. doi: 10.1080/01431161.2019.1698071. [DOI] [Google Scholar]
- Kaveh A, Talatahari S (2010) An improved ant colony optimization for constrained engineering design problems. Engineering Computations
- Khairuzzaman AKM, Chaudhury S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst Appl. 2017;86:64–76. doi: 10.1016/j.eswa.2017.04.029. [DOI] [Google Scholar]
- Kuruvilla J, Sukumaran D, Sankar A, Joy SP (2016) “A review on image processing and image segmentation,” In: 2016 international conference on data mining and advanced computing (SAPIENCE). IEEE, pp 198–203
- Lang C, Jia H. Kapur’s entropy for color image segmentation based on a hybrid whale optimization algorithm. Entropy. 2019;21(3):318. doi: 10.3390/e21030318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Tan Z. An improved flower pollination optimizer algorithm for multilevel image thresholding. IEEE Access. 2019;7:165 571–165 582. doi: 10.1109/ACCESS.2019.2953494. [DOI] [Google Scholar]
- Liu Y, Mu C, Kou W, Liu J. Modified particle swarm optimization-based multilevel thresholding for image segmentation. Soft Comput. 2015;19(5):1311–1327. doi: 10.1007/s00500-014-1345-2. [DOI] [Google Scholar]
- Liu M, Yao X, Li Y. Hybrid whale optimization algorithm enhanced with lévy flight and differential evolution for job shop scheduling problems. Appl Soft Comput. 2020;87:105954. doi: 10.1016/j.asoc.2019.105954. [DOI] [Google Scholar]
- Liu Y, Hu K, Zhu Y, Chen H (2015) “Color image segmentation using multilevel thresholding-cooperative bacterial foraging algorithm,” In: 2015 IEEE International conference on cyber technology in automation, control, and intelligent systems (CYBER). IEEE, pp 181–185
- Mafarja M, Mirjalili S. Whale optimization approaches for wrapper feature selection. Appl Soft Comput. 2018;62:441–453. doi: 10.1016/j.asoc.2017.11.006. [DOI] [Google Scholar]
- Maitra M, Chatterjee A. A hybrid cooperative-comprehensive learning based pso algorithm for image segmentation using multilevel thresholding. Expert Syst Appl. 2008;34(2):1341–1350. doi: 10.1016/j.eswa.2007.01.002. [DOI] [Google Scholar]
- Manikandan S, Ramar K, Iruthayarajan MW, Srinivasagan K. Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm. Measurement. 2014;47:558–568. doi: 10.1016/j.measurement.2013.09.031. [DOI] [Google Scholar]
- Mirjalili S. Sca: a sine cosine algorithm for solving optimization problems. Knowl-Based Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
- Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- Mittal M, Arora M, Pandey T, Goyal LM (2020) “Image segmentation using deep learning techniques in medical images,” In: Advancement of machine intelligence in interactive medical image analysis. Springer, pp 41–63
- Moses MML (2020) “Coyote optimization algorithm based multilevel thresholding approach for image segmentation,” J Soft Comput Eng Appl 1(2)
- Mostafa A, Hassanien AE, Houseni M, Hefny H. Liver segmentation in mri images based on whale optimization algorithm. Multimed Tools Appl. 2017;76(23):24 931–24 954. doi: 10.1007/s11042-017-4638-5. [DOI] [Google Scholar]
- Naji Alwerfali HS, Al-qaness MA, Abd Elaziz M, Ewees AA, Oliva D, Lu S. Multi-level image thresholding based on modified spherical search optimizer and fuzzy entropy. Entropy. 2020;22(3):328. doi: 10.3390/e22030328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naoum A, Nothman J, Curran J (2019) “Article segmentation in digitised newspapers with a 2d markov model,” In: 2019 International conference on document analysis and recognition (ICDAR). IEEE, pp 1007–1014
- Narayanan BN, Hardie RC, Kebede TM, Sprague MJ. Optimized feature selection-based clustering approach for computer-aided detection of lung nodules in different modalities. Pattern Anal Appl. 2019;22(2):559–571. doi: 10.1007/s10044-017-0653-4. [DOI] [Google Scholar]
- Oliva D, Hinojosa S, Cuevas E, Pajares G, Avalos O, Gálvez J. Cross entropy based thresholding for magnetic resonance brain images using crow search algorithm. Expert Syst Appl. 2017;79:164–180. doi: 10.1016/j.eswa.2017.02.042. [DOI] [Google Scholar]
- Oliva D, Abd Elaziz M, Hinojosa S (2019) Fuzzy entropy approaches for image segmentation. In: Metaheuristic algorithms for image segmentation: theory and applications. Springer, Cham, pp 141–147
- Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;9(1):62–66. doi: 10.1109/TSMC.1979.4310076. [DOI] [Google Scholar]
- Pan Y, Xia Y, Zhou T, Fulham M. Cell image segmentation using bacterial foraging optimization. Appl Soft Comput. 2017;58:770–782. doi: 10.1016/j.asoc.2017.05.019. [DOI] [Google Scholar]
- Prathusha P, Jyothi S (2018) A novel edge detection algorithm for fast and efficient image segmentation. In: Data engineering and intelligent computing. Springer, Singapore, pp 283–291
- Ren T, Wang H, Feng H, Xu C, Liu G, Ding P. Study on the improved fuzzy clustering algorithm and its application in brain image segmentation. Appl Soft Comput. 2019;81:105503. doi: 10.1016/j.asoc.2019.105503. [DOI] [Google Scholar]
- Sanyal N, Chatterjee A, Munshi S. An adaptive bacterial foraging algorithm for fuzzy entropy based image segmentation. Expert Syst Appl. 2011;38(12):15 489–15 498. doi: 10.1016/j.eswa.2011.06.011. [DOI] [Google Scholar]
- Saremi S, Mirjalili SZ, Mirjalili SM. Evolutionary population dynamics and grey wolf optimizer. Neural Comput Appl. 2015;26(5):1257–1263. doi: 10.1007/s00521-014-1806-7. [DOI] [Google Scholar]
- Sathya P, Kayalvizhi R. Modified bacterial foraging algorithm based multilevel thresholding for image segmentation. Eng Appl Artif Intell. 2011;24(4):595–615. doi: 10.1016/j.engappai.2010.12.001. [DOI] [Google Scholar]
- Shahabi F, Pourahangarian F, Beheshti H. A multilevel image thresholding approach based on crow search algorithm and Otsu method. J Dec Op Res. 2019;4(1):33–41. [Google Scholar]
- Sikariwal P, Chanak P (2018) “An efficient moth flame optimization algorithm based multi level threshoding for segmentation of satellite images,” In: 2018 Second international conference on intelligent computing and control systems (ICICCS). IEEE, pp 269–274
- Singla A, Patra S. A fast automatic optimal threshold selection technique for image segmentation. SIViP. 2017;11(2):243–250. doi: 10.1007/s11760-016-0927-0. [DOI] [Google Scholar]
- Sinha P, Tuteja M, Saxena S. Medical image segmentation: hard and soft computing approaches. SN Appl Sci. 2020;2(2):1–8. doi: 10.1007/s42452-020-1956-4. [DOI] [Google Scholar]
- Song Y, Liu P. Segmentation of sonar images with intensity inhomogeneity based on improved mrf. Appl Acoust. 2020;158:107051. doi: 10.1016/j.apacoust.2019.107051. [DOI] [Google Scholar]
- Su T, Zhang S. Local and global evaluation for remote sensing image segmentation. ISPRS J Photogramm Remote Sens. 2017;130:256–276. doi: 10.1016/j.isprsjprs.2017.06.003. [DOI] [Google Scholar]
- Tang K, Xiao X, Wu J, Yang J, Luo L. An improved multilevel thresholding approach based modified bacterial foraging optimization. Appl Intell. 2017;46(1):214–226. doi: 10.1007/s10489-016-0832-9. [DOI] [Google Scholar]
- Upadhyay P, Chhabra JK. Kapur’s entropy based optimal multilevel image segmentation using crow search algorithm. Applied soft computing. 2020;97:105522. doi: 10.1016/j.asoc.2019.105522. [DOI] [Google Scholar]
- Wang R, Zhou Y, Zhao C, Wu H. A hybrid flower pollination algorithm based modified randomized location for multi-threshold medical image segmentation. Bio-Med Mater Eng. 2015;26(s1):S1345–S1351. doi: 10.3233/BME-151432. [DOI] [PubMed] [Google Scholar]
- Wang S, Jia H, Peng X. Modified salp swarm algorithm based multilevel thresholding for color image segmentation. Math Biosci Eng. 2020;17:700–724. doi: 10.3934/mbe.2020036. [DOI] [PubMed] [Google Scholar]
- Wang E, Tu D, Chen Y, Zhang F (2019) “An improved bacterial foraging strategy for image segmentation,” In: 2019 International conference on intelligent transportation, big data & smart city (ICITBS). IEEE, pp 544–547
- Wang X, Wang X, Wilkes DM (2019) Machine learning-based natural scene recognition for mobile robot localization in an unknown environment. Springer
- Xiang W (2011) Analysis of the time complexity of quick sort algorithm, In: 2011 international conference on information management, innovation management and industrial engineering, vol 1, pp 408–410
- Xiong L, Tang G, Chen YC, Hu YX, Chen RS (2020) Color disease spot image segmentation algorithm based on chaotic particle swarm optimization and FCM. J Supercomput 76(11), 8756–8770
- Yang X-S (2012) “Flower pollination algorithm for global optimization,” In: International conference on unconventional computing and natural computation. Springer, pp 240–249
- Yan Z, Zhang J, Tang J. Modified water wave optimization algorithm for underwater multilevel thresholding image segmentation. Multimed Tools Appl. 2020;79(43):32415–32448. doi: 10.1007/s11042-020-09664-1. [DOI] [Google Scholar]
- Yao X, Li Z, Liu L, Cheng X (2019) “Multi-threshold image segmentation based on improved grey wolf optimization algorithm,” In: IOP Conference series: earth and environmental science, vol. 252, no. 4. IOP Publishing, p 042105
- Yue X, Zhang H. Modified hybrid bat algorithm with genetic crossover operation and smart inertia weight for multilevel image segmentation. Appl Soft Comput. 2020;90:106157. doi: 10.1016/j.asoc.2020.106157. [DOI] [Google Scholar]
- Zhang Y, Miao S, Mansi T, Liao R. Unsupervised x-ray image segmentation with task driven generative adversarial networks. Med Image Anal. 2020;62:101664. doi: 10.1016/j.media.2020.101664. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Wu C, Coleman S, Kerr D. Dense-inception u-net for medical image segmentation. Comput Methods Programs Biomed. 2020;192:105395. doi: 10.1016/j.cmpb.2020.105395. [DOI] [PubMed] [Google Scholar]
- Zhang H, Essa E, Xie X. Automatic vessel lumen segmentation in optical coherence tomography (oct) images. Appl Soft Comput. 2020;88:106042. doi: 10.1016/j.asoc.2019.106042. [DOI] [Google Scholar]