Characterization and Absolute Calibration of an AERONET-OC Radiometer

Abstract

The Ocean Color component of the global Aerosol Robotic Network (AERONET-OC) utilizes CE-318 sun photometers modified for above-water radiometry from fixed structures such as oil rigs, lighthouses and service platforms. Primarily, AERONET-OC measurements allow determination of the water-leaving radiance required for the validation of ocean color satellite data products. One instrument from the AERONET-OC network, identified as AERONET #080, was studied in this work. A laser-illuminated integrating sphere of known radiance enabled determination of the linearity with flux and absolute radiance responsivity at multiple wavelengths within 7 of the AERONET #080 filter bands. We compared the results to calibrations from the AERONET facility at the Goddard Space Flight Center of the National Aeronautics and Space Administration and from the Joint Research Centre of the European Commission. These results agree within the estimated mean comparison uncertainty of 1.88 % (k = 2). We also assessed these results using calibrated lamp-illuminated integrating spheres and observed a spectral dependence to the comparison results that is unexplained.

1. Introduction

Ocean color satellite sensors such as the Visible Infrared Imaging Radiometer Suite (VIIRS) measure the radiant flux from the solar-illuminated oceans at selected wavelengths in order to determine the water-leaving spectral radiance, L_w(λ), the normalized water-leaving spectral radiance, nL_w(λ), or the remote sensing reflectance R_rs(λ) [1–3]. These primary radiometric data allow for the determination of higher level products such as the chlorophyll a concentration, the absorption coefficient of colored dissolved organic matter, or the water diffuse attenuation coefficient that are relevant for ocean ecology, biogeochemistry, and climate investigations [4]. As implied by the name, L_w(λ) is the spectral radiance scattered out of the upper sunlit layer of the water. The spectral radiance at the entrance aperture of an ocean color satellite sensor L_T(λ) is the sum of L_w(λ) and contributions from the atmosphere and the ocean surface. These latter contributions dominate the at-satellite signal and need to be removed through an atmospheric correction process to determine L_w(λ) [5]. However, errors in the satellite sensor calibration and the atmospheric correction process may not support the required uncertainties in L_w(λ) [6, 7]. Consequently, L_w(λ) is measured at an instrumented ocean site to quantify and minimize biases that may adversely affect L_w(λ) measurements from different missions [8, 9]. These in situ values of L_w(λ) are used to correct the satellite gain coefficients through a procedure termed System Vicarious Calibration (SVC) [6] that determines bias contributions from both residual errors in sensor calibration and inaccurate determination of atmospheric effects. As documented by Zibordi et al. [7], the requirement to create climate data records across different ocean color satellite missions is best served by locating the SVC site in ocean waters similar to the majority of the ocean area – clear waters with marine atmospheres.

Coastal regions have spatially and temporally complex atmospheres and water columns whose variability is not fully captured by the sun-synchronous polar orbiting ocean color satellites. The spectral shape of L_w(λ) and the atmospheric radiance differs from the open ocean SVC sites. Sound practice mandates validation of the satellite-derived coastal data products using in situ measurements from multiple sites with a variety of measurement conditions. One approach, typically applied in coastal waters, relies on the use of modified CE-318 sun photometers by CIMEL Electronique (Paris, France) [10] for the execution of autonomous above-water radiometric measurements.

CE-318 sun photometers are filter radiometers designed and utilized world-wide in the Aerosol Robotic Network (AERONET) [11] for measurements of the direct solar irradiance, used to determine the aerosol optical depth, and measurements of the sky radiance, used to determine aerosol optical properties; these derived quantities are needed for accurate modeling of radiative transfer processes in the atmosphere. Leveraging the benefits of the AERONET infrastructure and CE-318 autonomous measurement capabilities, the SeaWiFS Photometer Revision for Incident Surface Measurements (SeaPRISM) was designed to enable above-water radiometric measurements [12]. The SeaPRISM spectral bands have central wavelengths suitable for ocean color investigations; spectral discrimination is obtained with interference filters characterized by low spectral out-of-band (OOB) response and stabilized interference coatings. In agreement with consolidated above-water radiometry protocols (e.g. chapter 5 of Zibordi et al. [13]), the SeaPRISM instrument gathers radiance data of the sea and sky from fixed offshore platforms. These instruments, deployed around the world, form the basis of the Ocean Color component of AERONET (i.e., AERONET-OC). The AERONET-OC network relies on measurements by these standardized instruments using established measurement protocols, and benefits from the instrument characterizations and calibrations performed at the AERONET central facility located at the National Aeronautics and Space Administration’s Goddard Space Flight Center (NASA/GSFC) as well as data processing performed with the same code and quality assurance/control scheme [14]. Lastly, a key component of the data quality control process is radiometric calibrations performed at both NASA/GSFC and the Joint Research Center (JRC) of the European Commission. The standard uncertainty in L_w(λ) at 412 nm, 443 nm, 488 nm, and 551 nm is estimated to be within 5 % (k = 1) in moderately turbid waters [14].

Currently there are two VIIRS sensors in orbit: one on board the Suomi National Polar-orbiting Partnership (SNPP) satellite and the other on National Oceanic and Atmospheric Administration’s (NOAA’s) NOAA-20 satellite (formerly known as the Joint Polar Satellite System-1, or JPSS-1 satellite). To support VIIRS, NOAA performs annual calibration/validation cruises [15], and has collaborated with the community to establish four new AERONET-OC sites: i) in Long Island Sound operated by the City College of the City University of New York [16]; ii) in the Gulf of Mexico operated by Louisiana State University and the Naval Research Laboratory [17]; iii) in the Southern California Bight operated by the University of Southern California and Oregon State University [18]; and iv) in western Lake Erie operated by the University of New Hampshire and NOAA [19].

To comprehensively assess the radiometric performance of SeaPRISM instruments, NOAA collaborated with the National Institute of Standards and Technology (NIST) with the specific objective to characterize and calibrate these instruments. In this paper, we present the results of a study of a SeaPRISM instrument hereafter referred to as AERONET #080 from the JRC that has been utilized in multiple deployments at the Acqua Alta Oceanographic Tower in the northern Adriatic Sea and represents the instrument model most deployed within AERONET-OC [20]. The primary aim of the study was to assess the relative spectral response functions provided by the filter manufacturer, provide system level absolute spectral radiance calibration coefficients, and validate the GSFC and JRC absolute calibration factors. We do not report on other possible influencing factors, such as temperature sensitivity, radiometric stability, field-of-view (FOV), polarization sensitivity, etc., some of which are addressed in the literature [11, 14, 21, 22]. In addition, the study offered the opportunity to gain additional experience at NIST in performing absolute calibrations of sun photometers using the Spectral Irradiance and Radiance responsivity Calibrations using Uniform Sources (SIRCUS) facility [23, 24]. While not relevant for this study, it is noted that sun photometers designed to make direct solar irradiance measurements, applied to determine the spectral exo-atmospheric solar irradiance, may undergo absolute laboratory calibrations such as those described in this work as an alternative to the determination of coefficients from Langley plots [25–27].

2. Experimental

2.1. AERONET #080

AERONET #080, originally part of the CE-318 AERONET suite of instruments, with digital sensor head utilizing the CE2405B electronic card, was modified to meet AERONET-OC requirements by adding firmware for executing the above-water measurements and replacing existing spectral channels with ones suitable for ocean color applications such as the 412 nm, 531 nm, and 551 nm bands. Equivalent to any AERONET sun photometer [28], it has two foreoptics, one for direct solar irradiance measurements with a 1.5° full angle FOV that is defined by a pair of apertures, and the other for sky and sea radiance measurements with an ≈1.25° FOV that is defined by a lens and a field stop. These foreoptics are mounted in two cylindrical baffle tubes. A silicon photodiode quadrant detector is used for solar tracking. Light from each foreoptic is focused onto a corresponding 2.5 mm square silicon photodiode detector, but only one type of measurement – radiance or irradiance – can be made at a time. Internal baffles are installed in the baffle tubes, and 1.9 mm diameter apertures are located close to the detector front surfaces. The photocurrent from the silicon detectors is converted to voltage by two transimpedance amplifiers co-located with the detectors. The radiance channel has a single feedback resistor providing high (sky, sea) gain, while the irradiance channel has either medium (aureole) or low (sun) gain, selectable using relays. The electronic gains are complemented by a software gain that controls the output from the 16 bit analog-to-digital converter (ADC). A filter wheel, located between the foreoptic and the detector, selects the measurement spectral band; it can also be positioned to block incoming flux on both detectors simultaneously. The same filter is used for the radiance and irradiance measurements. A complete AERONET-OC installation for autonomous operation includes the CE-318 (comprising sensor head, automated mount for sun tracking, and control unit), a satellite transmitter, and solar panels.

AERONET #080 is calibrated for spectral radiance responsivity at GSFC using two different lamp-illuminated integrating spheres: Eris and Slick. Eris is a 50.8-cm diameter sphere with barium sulfate type coating that is in a trailer on the roof of Building 33 at the GSFC AERONET cross-calibration facility [11]. Slick is a 91.4-cm diameter sphere with a polytetrafluoroethylene (PTFE) type wall material that is in the GSFC Code 618 Radiometric Calibration Facility. Both sphere sources have spectral radiance values that are traceable to NIST FEL lamp standards of spectral irradiance [29]. JRC uses FEL lamps calibrated by Optronic Laboratories to illuminate PTFE type diffuse reflectance standards to realize spectral radiance values [14].

Figure 1 illustrates a part of the calibration history for AERONET #080. The factors, in units of spectral radiance per output counts, are normalized by the average at each band. The colors represent wavelength and the symbols represent method. The agreement is within ±1.5 % for most results over this 18-month interval (October 2012 to March 2014). The outliers are the 413 nm band with Eris in May of 2013 and the 870 nm and 1020 nm bands with Eris in 2014 and JRC in 2013 and 2014. JRC attributes these results to decreased opacity in the blocking curtains in the NIR, which was rectified in the spring of 2015 when the focus at JRC expanded outside the visible domain.

Fig. 1.

Temporal history of spectral radiance responsivity calibrations for AERONET #080: ○, ◻, and ▽ represent JRC, Eris, and Slick, respectively.

During AERONET-OC calibrations at GSFC or JRC and operations in the field, the CIMEL control unit is utilized. A pre-programmed command sequence of filter selections, foreoptic mode, and gain selections, termed “PRS,” defines the SeaPRISM measurement protocol. At NIST, it was necessary to have a direct interface to the AERONET #080 sensor head for technical reasons. This was accomplished utilizing a manufacturer-supplied protocol. We term this mode of operation, which was implemented in LabVIEW [30], the SeaPRISM LabVIEW (SPLV) measurement protocol.

The SeaPRISM software gain is adjustable by factors of 2ⁿ⁻¹, where n is an integer indicating the software gain, according to which bits are read out from the readout register. For band i, the net signal for gain n from a broadband source with spectral radiance L(λ) will follow the measurement equation given by

$$S_i=2^{n-1}{\xi }_i\underset{i}{{\displaystyle \int }}L(\lambda )r_i(\lambda )d\lambda ,$$ (1)

where S_i is the net signal for the band in digital number (DN) from measurements of the broadband source, ξ_i is a constant for the band in units of signal per radiance, and r_i(λ) is the relative spectral responsivity (RSR) for the band. Note the absolute radiance responsivity (ASR) is $R_i(\lambda )={\xi }_i{r}_i(\lambda )$. Knowledge of n is necessary for comparing the GSFC or JRC results to the SIRCUS results. For GSFC or JRC, all bands had n = 5 except for the 870 nm and 1020 nm band, which had n = 4. At NIST, all bands had n = 5.

2.2. Measurements

AERONET #080 was at NIST on two occasions – from August 2010 to October 2011 and from September 2013 to January 2014. Between these intervals, the instrument was serviced. The system-level studies at NIST with the AERONET #080 radiance foreoptic used laser- or lamp-illuminated integrating sphere sources. In addition, the normal transmittance of representative AERONET-OC filters was determined to investigate the spectral OOB as part of the uncertainty analysis.

The NIST SIRCUS facility performs absolute spectral radiance or irradiance responsivity measurements using fiber-coupled, monochromatic flux from tunable lasers to illuminate integrating sphere sources that have known exit aperture areas. A broadband reference detector, calibrated for spectral flux responsivity using an absolute cryogenic radiometer and equipped with a known aperture, determines the radiance in the exit aperture of the laser-illuminated sphere or the irradiance at the plane of the detector’s aperture by knowing the separation between the two apertures [24]. The SIRCUS protocol is to illuminate the sphere with monochromatic flux from the laser and measure the radiance with both the reference standard NIST detector and the AERONET #080. The measurement sequence is to open a shutter in the beam path, acquiring ‘light’ signals, closing the shutter and acquiring ‘dark’ signals, then changing the laser wavelength and repeating the process. The net signal is the difference between the ‘light’ and ‘dark’ measurements of the integrating sphere. The SPLV code was integrated with the SIRCUS acquisition system for automated data acquisition.

The AERONET #080 was calibrated on SIRCUS in January and February of 2011 and in December 2013. Measurements of the laser-illuminated sphere, with the laser scanned over the in-band spectral region of the bands, gave Ri(λ) values; linearity with radiance was determined for the 870 nm band in 2011.

The NIST Remote Sensing Laboratory (RSL) is configured for spectral radiance intercomparisons. Several lamp-illuminated integrating sphere sources are arranged linearly at fixed positions, and several types of filter or hyperspectral radiometers are mounted on translation tables for computer-controlled alignment to each source.

The RSL sources utilized were the laboratory version of the NIST Portable Radiance (NPR) source [31], designated NII, and an Optronic Laboratories OL455–18 integrating sphere source [32]. NII is a 30 cm diameter sphere with PTFE-type wall material and a 10-cm exit aperture. It was calibrated for spectral radiance in September 2013 on the NIST Facility for Automated Spectroradiometric Calibrations (FASCAL) [33] from 250 nm to 2500 nm in steps of 10 nm at the four-lamp level. However, this level saturated some of the AERONET #080 bands. The OL455–18, which did not saturate any of the AERONET #080 bands, was used to validate the SPLV protocol and both spheres were used to validate the SIRCUS results. The OL455–18 has a 45.7 cm diameter sphere, a barium-sulfate based interior coating, an external lamp, and a shutter and iris between the lamp and the sphere to control the radiance level at the 15.2 cm diameter exit aperture. Mounted on the sphere wall is a silicon photodiode fitted with a photopic filter for luminance monitoring. The front panel displays the output of this monitor photodiode in luminance or photocurrent values.

Multiple radiometers on two separate occasions were used to assign spectral radiance values to the OL455–18. In January 2014, four radiometers at NIST transferred the NII radiance scale to the OL455–18. In March 2015, the LuMOS channel of Marine Optical BuoY (MOBY) buoy 256 transferred the radiance scale of two MOBY integrating sphere sources, the OL425 and OL420 to the OL455–18. The MOBY project is operated by Moss Landing Marine Laboratories (MLML) and the University of Miami for NOAA for SVC of ocean color satellites [6, 9]. The MOBY lamp-illuminated integrating sphere sources are routinely calibrated in FASCAL as part of NIST’s collaboration with the project.

The radiometers utilized at NIST were the Visible Transfer Radiometer (VXR) filter radiometer [34], two filter radiometers from the MOBY project (Standard Lamp Monitors (SLMs) [35]), and a Spectral Evolution SR4500 commercial hyperspectral fiber-coupled spectroradiometer [36]. Initial tests also included an ASD FieldSpec 4 fiber-coupled spectroradiometer [37]; these results had to be eliminated when we determined its internal shutter was sticking. The VXR has six ocean color filter bands, approximately 10 nm wide, from 412 nm to 870 nm. The SLMs are single channel filter radiometers with bands at 412 nm and 664 nm. The SLM filters came from the same lot as the filters used in the commensurate VXR bands. The spectral OOB of these filters is low, so any bias related to differences in the spectral distribution of the two sphere sources is negligible [38]. The SR4500 covers the spectral range from 340 nm to 2500 nm with a spectral resolution of 3 nm in the visible and near infrared (VNIR) spectral range. A 2° FOV lens coupled light from the spheres into the SR4500 fiber optic. It has been characterized for stray light using a tunable, quasi-cw laser with measurements every 10 nm across the VNIR array [39]. The efficacy of the stray light correction was validated using measurements of LED sources. The LuMOS channel of MOBY, utilized in March 2015, focuses light into the two MOBY hyperspectral spectrographs, which cover from 340 nm to 955 nm and have narrow instrument bandpasses (0.85 nm to 1.2 nm, depending on spectral region) [9]. The data are corrected for stray light and sensitivity to ambient temperature.

Additionally, an ancillary study of representative AERONET-OC bandpass filters was performed using a Cary-14 prism-grating scanning monochromator and a calibrated tungsten ribbon filament lamp [40]. The detector chamber of the Cary-14 was modified to collimate the output beam and the filters were placed in front of the silicon detector. A stable tungsten ribbon filament lamp illuminated the Cary-14. The spectral range was 300 nm to 1100 nm. For the in-band regions, the bandpass and wavelength sampling were 1 nm; for the OOB region, these parameters were 2.2 nm and 10 nm, respectively.

3. Analysis

3.1. Corrected Output Counts

The SIRCUS results from 2011 were initially analyzed by utilizing the following measurement equation

$$R_i(\lambda )=\frac{A\text{Ω}}{\text{Φ}(\lambda )}\left[S_{i,\text{open}}(\lambda )-S_{i,\text{closed}}(\lambda )\right].$$ (2)

In Eq. (2), the ASR, or R_i (λ), is expressed as the AERONET #080 output per radiance in the exit aperture of the sphere. The radiance is the optical flux in watts divided by the SIRCUS throughput factor in area times steradian, $\text{Φ}(\lambda )/(A\text{Ω})$. The radiance at each laser wavelength is determined using a calibrated, unfiltered, irradiance radiometer [24]. The quantity in brackets is the net signal in DN determined with the SIRCUS laser shutter open, S_i,open(λ), and closed, S_i,closed(λ). The shutter closed measurement is designed to remove internal offsets or ambient flux.

The initial analysis gave anomalous results for these SIRCUS data. As illustrated in Fig. 2, the ASR values at the edges of the filter bandpass were negative for some bands, which is unphysical. Additionally, the linearity of AERONET #080, as measured in SIRCUS for the 870 nm band, exhibited a large departure from unity over four decades of input radiance, see Sec. 4.1. Testing with broadband sources using the PRS protocol did not exhibit such a large departure from linearity. The root cause of these anomalies was determined to be acquisition using the SPLV mode, which can result in “shutter open” output values smaller than “shutter closed” values. Application of Eq. (2) to data acquired using the SPLV protocol therefore leads to incorrect results, including negative ASR and incorrect assessment of the device’s linearity. As a result, a revised measurement equation was necessary.

Fig. 2.

Correction example for the 530 nm band: ○, ◁, ▷, and solid line represent Open − Closed, Open + Closed, Closed − Open, and Final, respectively.

In the Sky electronic gain mode used here, internal background subtraction is automatic. This led us to consider the specifics of internal processing in the AERONET #080 for the SPLV mode. Writing S_i,flux(λ_b) to represent counts proportional to input radiance from the laser-illuminated sphere for band “b”, with B_int the internal offset in counts, equivalent for all bands, then the net signal is

$$S_{i,\text{net}}\left({\lambda }_{\text{b}}\right)=S_{i,\text{flux}}\left({\lambda }_{\text{b}}\right)-B_{\text{int}}-S_{i,\text{closed}}\left({\lambda }_{\text{b}}\right).$$ (3)

For regions of low responsivity, Eq. (3) leads to negative values of the net signal.

The addition of a constant offset to net signals using Eq. (3) does not remove undershoots observed in the initial results at the band edges. However, we determined an algorithm exists for the SPLV mode that explains the results if we assume the only source of measured flux is the laser-illuminated sphere. This is reasonable because the laser was fiber coupled to the sphere, the cladding was opaque, and the sphere and the AERONET #080 were inside a light-tight enclosure. The algorithm is summarized as:

1. There is an internal offset B_int, a positive value in units of DN, that is always subtracted prior to outputting the measurement result.

2. The output is the absolute value of the result of this internal subtraction.

3. S_i,closed(λ_b) is a good approximation to B_int.

Unfortunately, this algorithm for S_i,flux is multivalued, see Table 1 (dropping the band reference for clarity). Both the offset of 2B_int and correction factor of −1 apply when negative values of S_i,net occur. Therefore, a manual algorithm was employed: an offset of 2S_i,closed was added to S_i,net for all the data and the correction factor was applied only to negative S_i,net results. For multivalued results, on a point-by-point basis, the result that produced the smoothest shape was chosen.

Table 1.

Summary of AERONET #80 output and corrections or offsets applied to S_i,net from Eq. (2).

Condition	S i,open	S i,closed	S i,net	Offset or Correction Factor
Si,flux > Bint	Si,flux – Bint	B int	Si,flux – 2Bint	+2Bint
Si,flux = 2Bint	B int	B int	0	+2Bint
Si,flux = Bint	0	B int	−Bint	+2Bint
Si,flux < Bint	−Si,flux + Bint	B int	−Si,flux	Multiply by −1

Figure 2 illustrates the procedure for the 530 nm band. Note the offset solution corresponds to S_i,open + S_i,closed and the multiplicative solution corresponds to S_i,closed − S_i,open for determination of S_i,flux. The wavelengths corresponding to the conditions stated in row 2 of Table 1 occur at approximately 524.27 nm and 536.95 nm for the blue and red shoulders; for row 3 the corresponding wavelengths are approximately 528.8 nm and 537.3 nm. Note it is possible to miss the inflection points if the wavelength coverage is too sparse.

The internal background subtraction limits the measurements in the OOB spectral region because regions with S_i,net close to zero have the largest ambiguity. When S_i,net is zero, S_i,flux can be zero or 2B_int. In Fig. 2, this condition applies to the results below ≈522 nm and above ≈539 nm. In the OOB region, assumptions about spectral shape are not reliable indicators of the correct solution because of noise, sparse data, or the possibility of real features. The uncertainty for measurements in the OOB region is increased because B_int and S_i,closed are each uncertain as is their equivalence in time.

3.2. Spectral Data

The 2011 SIRCUS data were reprocessed for the internal background effect after the correction model was developed. The 2013 SIRCUS data were manually corrected for the internal background effect as the measurements progressed. For both data sets, multiple measurements at laser wavelengths separated by ≈0.005 nm or less were combined to a single value, excluding outliers by visual inspection and averaging the remaining values. Eight bands were measured in 2011, see Table 2; in 2013 the 936 nm band was not measured, and, as the tunable laser systems necessary for the 490 nm band were not operational, only one value using an Argon ion laser at 487.988 nm was determined. In 2011, this line was also measured, and the final SIRCUS results at this band were scaled to the argon ion laser measurement values. The band center wavelengths λ_b in Table 2 were determined by NASA/GSFC as the mean wavelength of the wavelengths that correspond to 50 % of the peak transmittance.

Table 2.

Filter identification and gain factors for AERONET #080 ASR measurements: SPLV vs PRS.

SPLV Commanded Position	Gain n SPLV	λb, nm	PRS Band Number	Gain n PRS	Year ASR Measured
1	5	413.2	6	5	2011, 2013
2	5	936	7	5	2011
3	5	489.9	8	5	2011
4	5	550.7	9	5	2011, 2013
5	5	1020	1	4
6	5	870.0	2	4	2011, 2013
7	5	668.2	3	5	2011, 2013
8	5	440.7	4	5	2011, 2013
9	5	530.6	5	5	2011, 2013

Including both SIRCUS data sets, the number of values determined for each band varied (between 23 and 230), as did the mean wavelength spacing (from 0.10 nm to 0.98 nm), with the three blue bands having coarser wavelength coverage as a result of the laser system characteristics. When normalized to the moment wavelength (see Eq. (4)), graphical inspection indicated the band shapes and wavelength scales for the 413 nm, 441 nm, 531 nm, 551 nm, and 870 nm bands from the 2011 and 2013 ASR values were the same. The final ASRs for these five bands were determined by combining the normalized SIRCUS results for both data sets and then rescaling to the 2013 ASR levels.

The transmittance of the filters installed in AERONET #080 were determined by the manufacturer and delivered to GSFC for all nine bands. These transmittance data are equally spaced in wavelength with 0.1 nm sampling at all bands except for the 551 nm and 441 nm bands, where the sampling was 0.25 nm and 0.2 nm, respectively. These data include spectral regions centered on the band covering between 1.5 and 4.5 decades; no data were provided over the full sensitivity range of the instrument’s silicon photodiode detector, denoted the OOB spectral region. For four of the bands (413, 870, 936, and 1020) nm, the filter vendor reported a wavelength shift to be applied to the supplied transmittance data. We implemented the corrections (+0.2 nm, +0.4 nm, and +0.7 nm) for the 413 nm, 870 nm, and 936 nm, bands, respectively.

To assess possible significance of the lack of OOB data in the SIRCUS ASR and manufacturer RSR values, six representative AERONET-OC 12.7 mm diameter filters were measured as described in Sec. 2.2 using the Cary-14 spectroradiometer. The measurements were validated by comparison to the NIST reference transmittance spectrophotometer Lambda™ 1050 [41] using three larger diameter NIST interference filters at 430 nm, 560 nm, and 610 nm.

The AERONET #080 absolute SIRCUS ASR R_i(λ) values and the manufacturer-supplied transmittance data t_i(λ), along with the ancillary AERONET-OC filter t_j(λ), data were utilized according to Eqs. (4) and (5) from reference [38]. The system-level RSR values, r_i(λ), were approximated as the filter transmittance data, which is valid as long as spectral dependencies in optical elements and the silicon photodiode’s responsivity are nearly constant within the in-band spectral region, and the beam geometry in the AERONET #080 is similar to that used to measure the filter transmittances.

$${\lambda }_i=\frac{\int \lambda R_i(\lambda )L(\lambda )d\lambda }{\int R_i(\lambda )L(\lambda )d\lambda }=\frac{\int \lambda r_i(\lambda )L(\lambda )d\lambda }{\int r_i(\lambda )L(\lambda )d\lambda }$$ (4)

$$\text{Δ}{\lambda }_i=\frac{\int R_i(\lambda )L(\lambda )d\lambda }{R_i\left({\lambda }_i\right)L\left({\lambda }_i\right)}=\frac{\int r_i(\lambda )L(\lambda )d\lambda }{r_i\left({\lambda }_i\right)L\left({\lambda }_i\right)}$$ (5)

$$C_i=\text{Δ}{\lambda }_i{R}_i\left({\lambda }_i\right)$$ (6)

The band wavelength λ_i is recognized as the moment wavelength weighted by the product of spectral responsivity and spectral radiance, see Eq. (4). In Eq. (5) the integral $\int R_i(\lambda )L(\lambda )d\lambda$ is equated to be the product of a square profile with width (bandpass) Δλ_i and height $R_i\left({\lambda }_i\right)L\left({\lambda }_i\right)$. With the calibration coefficient C_i as output signal over spectral radiance, then combining Eqs. (1) (with signals normalized to soft gain n = 1) and (5) yields Eq. (6). The band wavelengths and bandpasses depend only on the relative spectral distribution of the response functions and the source spectral radiance L(λ), while the calibration coefficient depends on these parameters in addition to the ASR at λ_i, R_i(λ_i).

Sources of spectral radiance include calibration values for NII, the OL455–18, other lamp-illuminated sources, and during field operation, sunlit sources. For integration, values for r_i(λ), R_i(λ), and L(λ) were interpolated onto a uniform wavelength grid with 0.10 nm spacing using smoothing splines with no weighting and the smoothing parameter set to 0.995. The integrals were evaluated using trapezoidal numerical integration (MATLAB, see [42]). The limits of the integrals were given by the available ASR or transmittance data.

4. Results

In this section, we present results from the analysis method described in Sec. 3. We consider the efficacy of the adopted measurement equation that incorporates the background correction model and state results of the SIRCUS calibrations. Then we describe the uncertainties for the radiometric calibration of the OL-455 used to validate the AERONET-OC #080 calibration. The AERONET-OC #080 calibration coefficients are derived and used to compare to the NASA/GSFC and JRC calibration coefficients.

4.1. Validation of Correction Model

The background correction model was validated by modeling the effect using simulated data and by performing experimental tests. In the first experiment, we compared measurements using the PRS or SPLV mode for observations of the OL455–18 sphere. Measurements were taken with the sphere shutter open and closed for all bands (however, the PRS mode excludes the 936 nm band). The SPLV data were analyzed by adding the shutter closed value to the shutter open value (see the first row of Table 1), since no shutter open values were smaller than the shutter closed values. The PRS data were zero when the sphere shutter was closed. Daily means and standard deviations were determined for the three measurement days and the ratios of the PRS to SPLV outputs determined. Combined over all bands and days, the mean ratio is 1.0033 ± 0.0032 (k = 1). (All uncertainties in this paper are stated as standard uncertainties, with k = 1 or ≈68 % confidence level.) If the correction is not applied, bands with small DN (e.g. 412 nm and 443 nm) result in ratios that differ from unity by 11 % and 5.4 %, respectively and the mean ratio for all bands increases to 1.029.

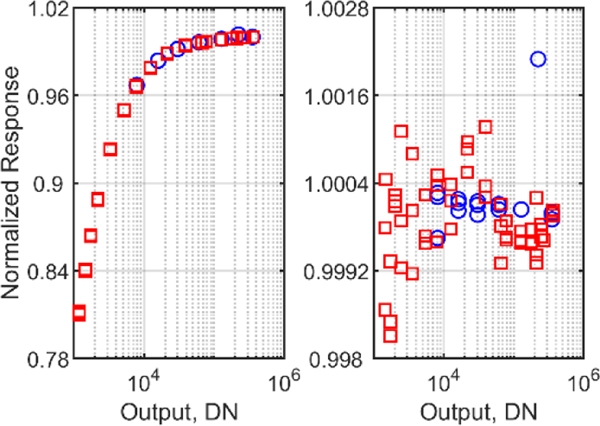
The second experimental method of validating the SPLV background model was to measure the output as a function of input radiance and reference the results to detector standards. Linearity measurements were done in SIRCUS for the 870 nm band. The laser flux was varied by a factor of 240 and the reference detector was the silicon photodiode mounted in the wall of the laser-illuminated sphere. The AERONET #080 output was normalized by the monitor value and this ratio was normalized to the maximum observed ratio and plotted as a function of AERONET #080 output, see Fig. 3. The left panel utilizes S_870,net while the right panel utilizes S_870,net + 2B_int. The uncorrected normalized ratios indicate a departure from unity up to 0.81, which is inconsistent with SeaPRISM performance.

Fig. 3.

Inferred linearity with optical flux measured in SIRCUS for the 870 nm band on 21-Jan-2011 and 24-Feb-2011, blue ◻ and red ○, respectively, for uncorrected (left panel) and corrected (right panel) method of analysis.

With the correction applied, the average normalized ratio is 1.0034 ± 0.0062. Linearity tests were also performed for the 413 nm and 870 nm bands with the OL455–18 by varying the iris setting and using the internal illuminance monitor photodiode for the reference detector. Results at 413 nm were satisfactory, but at 870 nm the correction model did not fully eliminate the apparent nonlinearity. We attribute this to the failure of the illuminance monitor to capture any change in the relative spectral distribution of the OL455–18 as the iris, which has a different reflectance than the sphere wall, was varied. Finally, the ASR of the 870 nm channel was determined in 2011 in SIRCUS with the laser at low and high power, respectively. In this case the reference detector was a silicon trap detector calibrated using cryogenic radiometry. In the uncorrected results, the ASR for the low power illumination was negative at the band edges and disagreed with the high-power results by 4.4 % ± 0.9 % over the in-band region. With correction, the ASR is positive, and the in-band agreement between the low- and high-power test improved to 0.11 % ± 0.01 %. All these results support the efficacy of the background correction model.

4.2. Results for the RSR and ASR values

A visual comparison of the AERONET #080, manufacturer-supplied, normalized transmittance data and normalized SIRCUS results is shown in Figs. 4 to 10 for the seven AERONET-OC bands that were measured on SIRCUS. The symbols represent measurements, while the solid lines are illustrative. For this graphical comparison, the normalization was to the transmittance or ASR value at the band wavelength from Eq. (4) with constant L(λ) = L₀. The normalized values are sensitive to the density and scatter of the input data. Table 3 reports the results of Eqs. (4) and (5) using the NII spectral radiance for the weighting. The band wavelength λ_b values supplied by JRC are also reported. In Figs. 4 to 10, only the in-band region is plotted in the linear graphs, but all the data (excepting any negative values) are plotted in the logarithmic graphs. The typical dynamic range is 10⁴.

Fig. 4.

Normalized ASR (blue ○) and transmittance data (red +) for the 413 nm band.

Fig. 10.

Normalized ASR (blue ○) and transmittance data (red +) for the 870 nm band.

Table 3.

AERONET #080 calculated spectral parameters, in nanometers, using the NII spectral distribution.

Wavelength	Manufacturer filter τ(λ)		NIST, SIRCUS		Application
λb	λi	Δλi	λi	Δλi
413.2	413.24	7.93	413.06	8.08	AERONET OC
440.7	440.85	9.76	440.96	9.90	AERONET OC
489.9	489.95	10.4	489.73	10.4	AERONET OC
530.6	530.65	9.45	530.64	9.54	AERONET OC
550.7	550.75	9.82	550.76	9.91	AERONET OC
668.2	668.00	8.40	667.96	8.45	AERONET OC
870.0	869.95	9.60	869.90	9.79	AERONET OC
936	935.93	9.01	934.57	9.09	AERONET
1020.0	1020.2	10.7	NaN	NaN	AERONET OC

The qualitative agreement of the band shapes in Figs. 4 to 10 is good. Differences occur within the in-band region near regions of curvature; these regions will be affected by the density of measurements and the bandpass of the source for the filter transmittance data. There are slight differences in the in-band shape for some bands. The transmittance data have increased noise in the OOB for the 413 nm and 870 nm bands (Figs. 4 and 10), as well as the in band for the 870 nm band (Fig. 10). In some cases, there is disagreement in the OOB results, see Figs. 7 and 10. The 490 nm ASR data (Fig. 6) are sparse in the density of wavelengths measured over the spectral range. The quantitative agreement (Table 3) for the measured ocean color band wavelengths is also good. The mean absolute difference in moment vs band wavelength for the seven bands from 413 nm to 870 nm is 0.089 nm, with magnitudes between 0.009 nm (at 551 nm) and 0.21 nm (at 490 nm). Differences in the integral $\int R_i(\lambda )L(\lambda )d\lambda$ evaluated with a NII source distribution and unity-normalized transmittance or responsivity for R_i(λ) are described by comparing the bandpasses Δλ_i in Table 3. The mean ratio of the bandpasses for the transmittance to SIRCUS results, using Eq. (5), is 0.989 nm ± 0.006 nm.

Fig. 7.

Normalized ASR (blue ○) and transmittance data (red +) for the 531 nm band.

Fig. 6.

Normalized ASR (blue ○) and transmittance data (red +) for the 490 nm band.

4.3. OL455–18 Spectral Radiance

The spectral radiance of the OL55–18 was determined by comparison with the NIST transfer radiometers to NII in December 2013 and January 2014 over five measurement days, and by comparison with MOBY256 to two MOBY spheres in March 2015. The measurement equation for either the filter radiometers or the spectrographs as transfer radiometers is

$$L_{\text{OL}455}(\lambda )=\frac{S_{\text{OL}455}}{S_{\text{ref}}}{L}_{\text{ref}}(\lambda ).$$ (7)

The ratio of signals is for a single pixel in the spectrographs or the same band in the filter radiometers. For the spectrographs, with their narrow bandpasses and stray light corrections, the wavelength to evaluate the reference spectral radiance is the calibrated wavelength for the pixel in question. For the filter radiometers, the reference-source weighted moment wavelength was used following Eq. (4).

The uncertainties in the OL455–18 spectral radiance determined at NIST arise from the measurements and the NII reference source. For the measurements, we evaluated the signal measurement uncertainty as the uncertainty in the mean, e.g. the standard deviation divided by the square root of the number of measurements. The size-of-source effect, or the fraction of signal that arises from outside the geometric target area and is a function of source diameter, was estimated by comparison of net signals calculated two ways – one using a lens cap covering the foreoptic and the other with it removed but an on-axis occulting disc blocking the geometric target area. Optical linearity with flux was estimated to be 0.1 %. The effect of slightly different source distributions for the NII and the OL455–18 was estimated for the filter radiometers by estimating the coefficient C_i for the different lamp-based distributions mentioned in Sec. 3.2. For the SR4500, the uncertainty associated with the stray light correction was taken to be 10 % of the difference between corrected and uncorrected signal spectra and assessed in terms of the ratios of the calibration and unknown source spectral distributions.

Three uncertainty components for the NII spectral radiance values were evaluated. The first is the uncertainty in the calibration values; these are in the FASCAL calibration report [43]. The second is an estimate of the amount of drift between the calibration and use with the AERONET #080. For this, we compared the following FASCAL calibration of NII that took place in September 2015 and used a uniform probability distribution with the absolute difference for the limits. The third is the uncertainty of the wavelength in the transfer radiometers. For the filter radiometers calibrated on SIRCUS, the wavelength uncertainty is negligible. For the SR4500, the stray light characterization in April 2015 provided data to evaluate the wavelength calibration, and the results were fitted to a polynomial. The magnitude of the difference from the native wavelength calibration was used to bound a uniform probability distribution to give the uncertainty in the wavelength, and a Taylor series expansion of the NII spectral radiances was used to evaluate the spectral radiance uncertainty.

The results for the combined standard uncertainty in the OL455–18 spectral radiance from the NIST measurements are illustrated in Fig. 11. For the SR4500, the dominant components are the measurement uncertainty and the uncertainty in the NII L(λ) values, which are comparable from 425 nm to 700 nm; outside of this region the measurement uncertainty dominates and is responsible for the “U” shape to the curve. In the 400 nm to 700 nm spectral region, the wavelength uncertainty is the third most significant component, but beyond 700 nm, that attribute switches to the size-of-source effect. For the filter radiometers, the dominant uncertainty component is the uncertainty in the NII L(λ) values, with the NII temporal stability next in significance, except for the 870 nm band of the VXR, where the size-of-source uncertainty is the dominant component.

Fig. 11.

Combined standard uncertainty for the RSL OL455–18 L(λ) values: ○, ◇, and solid line, represent VXR, SLMs and SR4500, respectively.

The combined standard uncertainty in the OL455–18 spectral radiance from the March 2015 measurements at MOBY were determined from the measurement uncertainty, the reference source uncertainty, source stability from 2014 to 2015, the uncertainty in the stray light correction, and the uncertainty in the responsivity correction with ambient temperature. The OL455–18 was calibrated with the MOBY OL425 sphere on March 11, and with the MOBY OL420 sphere on March 12. Each time, six scan sets were acquired, where a scan set was a camera acquisition with the shutter closed, five scans with the shutter cycling open, and a final scan with the shutter closed. The results were corrected for the dark offset, integration time, bin factor, stray light, thermal sensitivity, and to the average monitor photodiode reading for the OL455–18 in March 2015. The monitor photodiode on the OL425 was used to correct the signals according to its reading during the calibration in FASCAL. The average monitor photodiode readings for the NIST OL455–18 agreed to 0.26 % between the 2014 in and 2015 measurements and no correction was applied.

4.4. Calibration Coefficients

In this section we present comparisons of the NIST SIRCUS and GSFC and JRC calibrations and the NIST internal validations. Equations (1) and (4) to (6) illustrate the two methods used to determine the AERONET #080 calibration coefficients – detector-based as the product of the bandpass and ASR at the band wavelength, and source-based as the ratio of measured signal to the spectral radiance of a calibrated reference source. For the source-based method, we further divide the results between GSFC and JRC or NIST sources.

The SIRCUS ASRs are independent of a source’s relative spectral distribution. To compare to the source-based calibration coefficients, we follow the suggestion in [38] to utilize a typical lamp-based spectral distribution and the SIRCUS ASR values to calculate the wavelength, bandpass, and calibration coefficients. The source spectral distribution utilized in Eqs. (4) and (5) corresponded to the FASCAL L(λ) values for NII.

The detector-based calibration coefficients using Eq. (6) with the NII L(λ) source distribution are given in Table 4 along with the combined standard uncertainties. The SIRCUS component for the ASR values for the in-band region are between 0.18 % and 0.29 %. The uncertainty in the AERONET #080 linearity, also from the SIRCUS measurements, is 0.05 % or smaller. The standard deviation of the calibration coefficients derived with five different broadband source calibration data (JRC’s FEL lamp F1159, NII, OL455–18, MOBY’s OL425, and NIST’s F431 reflected by a sintered PTFE diffuse reflectance standard) provided an estimate of the uncertainty arising from using the NII source distribution to compare the detector-based calibration coefficients to the GSFC and JRC source-based ones. Interpolation in the ASR and L(λ) input values with smoothing parameters between 0.8 and 1 for the ASR data and 0 to 1 for the L(λ) gave reasonable estimates of the range of calibration coefficient values, and from these a Type B uncertainty was determined using a uniform probability distribution. The uncertainties from both the source spectral shape and the interpolation parameters are negligible, 0.03 % or smaller. Finally, for an estimate of bias due to insufficient OOB SIRCUS data, the Cary-14 transmittance data from the ancillary set of AERONET-OC filters were processed with the same five source calibration data to determine the fraction of total signal due to the OOB transmittance. (The OOB cutoff was set at 0.1 % of the maximum transmittance.) The OOB fraction is between 0.04 % and 0.33 %, resulting in a negative bias for the SIRCUS C_i values. No values are available at 870 nm because a filter for this band was not measured on the Cary-14. This source-dependent uncertainty component, which is assumed to apply to AERONET #080, is the leading component for the 551 nm and 668 nm bands.

Table 4.

AERONET #080 detector-based calibration coefficients using NII source distribution.

λi, nm	Ci, (DN cm2 sr nm) / μW	u(Ci), %
413.06	5790.9	0.27
440.96	7873.2	0.36
489.73	11,321	0.21
530.64	11,918	0.19
550.76	13,075	0.38
667.96	15,923	0.31
869.90	19,804	0.19*

^*OOB uncertainty component not available.

Figure 12 illustrates the ratio of the GSFC and JRC source-based to the NII-weighted detector-based calibration coefficients distinguished by source; e.g. the mean of the Eris calibration coefficients in time (Fig. 1) normalized by the SIRCUS-weighted calibration coefficient as a function of AERONET #080 band. For GSFC, the vertical lines are the combined standard uncertainties of the spectral radiance sources [44, 45], the standard deviation of repeat calibrations on the respective sphere source, and the uncertainties in the NII-weighted detector-based coefficients from Table 4. For JRC, the vertical lines are the combined standard uncertainties from a rigorous evaluation of their lamp/plaque uncertainty budget, the standard deviation of repeat calibrations, and the uncertainties in the NII-weighted detector-based calibration coefficients.

Fig. 12.

Ratio of AERONET #080 source-based calibration coefficients to the NII-weighted SIRCUS detector-based calibration coefficients: ○, ◻, and Δ represent Eris, Slick, and lamp/plaque, respectively.

AERONET #080 measured the NII at three bands and the OL455–18 at 8 bands on January 16 and 17, 2014. The NII spectral radiance is known from FASCAL, and the OL455–18 spectral radiance was determined multiple ways as explained in Sec. 4.3. We evaluate the source-based calibration coefficients and compare to the NII-weighted SIRCUS ASR results. For the spectrometers, these calibration coefficients are the measured signals divided by the spectral radiance evaluated at source-weighted wavelength, see (4). Except for one band in the VXR, the band wavelengths of the filter radiometers are close (within 7 nm) to the AERONET #080 band wavelengths and allow for estimates of the OL455–18 spectral radiance. A band shift correction was applied to the filter radiometer-determined spectral radiances using the slope from the SR4500 calibration of the OL455–18. The ratio of the source-based to detector-based calibration coefficients is shown in Fig. 13, with the vertical lines representing the combined standard uncertainty in the calibration coefficient ratios.

Fig. 13.

AERONET #080 source-based calibration coefficients using the NII or the OL455–18 ratioed to the NII-weighted SIRCUS detector-based calibration coefficients, where ○, ◻, ◊, Δ, and ▽ represent NII and the four methods for the OL455–18: MOBY LuMOS, SR4500, VXR, and SLMs, respectively.

5. Discussion

The necessity of developing a model of the background, or offset, DN for the AERONET #080 when used in the SPLV mode was not expected, requiring extra time and effort to reconcile the results. It is emphasized this issue does not occur during normal AERONET-OC operations. It does, however, serve as an example of why it is critical to accurately assess offset values. In the SPLV mode with AERONET #080 the traditional interpretation of subtracting shutter closed from shutter open results in negative responsivity and large departures from linearity. It also led to issues with probing the OOB spectral region. In 2011 and 2013, SIRCUS lasers did not have enough power to maintain an output greater than 130 DN to 140 DN over the OOB spectral region, thus avoiding ambiguity in interpreting the data acquired with the SPLV protocol. This restricted the dynamic range of the measurements. Currently in SIRCUS, higher power lasers are utilized, so future efforts may be useful for OOB studies. To facilitate such studies, it would be helpful to first acquire OOB filter transmittance data to identify regions to avoid or concentrate on.

The visual comparison of the AERONET #080 filter transmittance data from the filter manufacturer to the SIRCUS ASR data, both normalized to unity, is good. For some bands, e.g. the 490 nm band, the SIRCUS density of measurements was low, being driven by the laser characteristics. Insufficient density of coverage can cause interpolation error in regions of strong curvature; see the 480 nm to 485 nm region in Fig. 6. Filter transmittance data can be acquired with dense wavelength coverage but require the bandpass of the filtering spectroradiometer to be narrow compared to the filter bandpass. If the bandpass is too narrow, SNR can be compromised; if it is too broad, features are not fully resolved, see Figs. 4, 7, and 8.

Fig. 8.

Normalized ASR (blue ○) and transmittance data (red +) for the 551 nm band.

The differences in band wavelength between the manufacturer transmittance data and the SIRCUS data were largest for the 413 nm and 490 nm bands. The impact of wavelength error for calibration using a broadband source or interrogation of the spectral radiance of an unknown source depends on the local slope of the spectral radiance distribution. A wavelength difference of 0.18 nm for the 413 nm band and 0.21 nm for the 490 nm band applied to a representative lamp-based calibration source (NII) results in bias of 0.33 % and 0.23 %, respectively.

Some of the observed differences in spectral shape over the in-band region may be due to spectral dependencies in AERONET #080 such as window and lens transmittances, or the silicon photodiode responsivity. Using Eq. (5) and both the lamp-based and flat spectral distributions gives a ratio of bandpasses (transmittance data over ASR data) of 0.989 ± 0.005 averaged over all bands, e.g. the bandpass with the transmittance data is less than the bandpass with the ASR data. Modeling of the effect of silicon photodiode responsivity, which increases with increasing wavelength, changed the moment wavelength by 0.03 nm or less. Choice of interpolation parameters also had a negligible effect.

The OL455–18 was used as a validation source, for both the background model and the SIRCUS calibration. It was calibrated by comparison to three different spectral radiance standards using four different transfer radiometers. This additional effort was motivated by discrepancies between the SR4500 and the ASD in the blue spectral region, before we were aware of the shutter problem, and because the SR4500 validation results indicated a spectral dependence, which is discussed next.

The comparison to the GSFC and JRC source-based calibration coefficients, Fig. 12, shows the ratios to the detector-based calibration coefficients are independent of wavelength – an unweighted linear fit results in a small F-value with the probability that 39 % of the time this value could be drawn from a random set compared to data drawn from the linear model. However, it is biased high, with a mean and standard deviation of 1.0144 ± 0.0060 for the 413 nm to 870 nm bands; if the 870 nm band is excluded, the result is 1.0137 ±0.0050. Previous reported calibrations using absolute laser-based methods showed good comparison of NIR bands of a CE318 sun-sky radiometer to GSFC’s Eris sphere [46] but not for Vis/NIR bands of a SimbadA to GSFC’s Hardy sphere, where the bias was between 4 % to 6 % [23].

One explanation for the bias shown in Fig. 12 could be a size-of-source effect in the AERONET #080, as the source dimensions for GSFC and JRC are larger than the exit aperture of the SIRCUS laser-illuminated sphere. A second possibility is sphere loading that occurs when the source to radiometer separation is small; however, this would not be expected to impact the JRC results. Size-of-source effects, which arise from non-ideal FOV functions, can be assessed using on axis baffles as describe in Sec. 4.3, by mapping the FOV, by a differential scheme [47], or simply by verifying the signal is independent of the source to radiometer separation as long as the entrance pupil is overfilled.

In contrast to Fig. 12, the comparison to the NII and OL455, Fig. 13, shows a dependence with wavelength. In this case the unweighted linear fit has an adjusted R-squared of 0.797, a large F-value, and negligible probability of a draw from a random set. The fitted slope over the 413 nm to 870 nm spectral region corresponds to 0.586 % ± 0.064 % per 100 nanometers. We note previous results using SIRCUS in 2002 with the SimbadA sun photometer, when validated using the RSL NIST Portable Radiance (NPR) source (also calibrated on FASCAL), did not exhibit any spectral dependence and agreed with the source-based method to ±1 % except for 2 bands [23].

The traceability paths to primary radiometric standards for the GSFC, JRC, RSL, and MOBY realizations of the reference source spectral radiance values differ. GSFC values are traceable to FEL lamp standards of spectral irradiance because the transfer spectrometer is operated in irradiance mode, and it is calibrated with FEL lamps. JRC is traceable via irradiance values for FEL lamp standards and reflectance values for their PTFE reflectance standards. All the FEL lamps used had spectral irradiance values traceable to NIST’s FASCAL 2 facility [48]. FASCAL 2 utilizes detector standards with responsivity values traceable to SIRCUS. In contrast, the NII, OL425 and OL420 spheres are all calibrated on FASCAL [33]. FASCAL utilizes blackbody source standards traceable to temperature standards. An interpretation of the validation results is that there is spectral consistency within detector-based methods, see Fig. 12, but a spectral bias exists between SIRCUS and FASCAL, see Fig. 13, that is unexplained.

6. Conclusion

The CE-318 AERONET-OC instrument identified as AERONET #080 was characterized for linearity and calibrated for absolute radiance responsivity using the SIRCUS facility, resulting in low uncertainties for these detector-based calibration coefficients. The normalized results were compared to filter transmittance data from the AERONET #080 filter manufacturer and the agreement was good. To perform the SIRCUS calibrations, AERONET #080 had to be operated using the custom protocol and this led to anomalous results unless a specific background model was implemented.

The SIRCUS results were used to evaluate the AERONET #080 band wavelength, bandpass, and calibration coefficients using a source-weighted approach. It is fully appropriate when the ratio of the in-band signal to the total signal is near unity, that is, when the OOB response is low and the source presents measurable spectral radiance over the band. In the field, depending on the optical properties of the water, this may not always be the case, e.g. in-water measurements of up-welling spectral radiance in Case 1 waters in the near-infrared where the source distribution is heavily weighted to blue wavelengths. In the ideal case – where environmental sources of noise and bias are negligible – the OOB response must be quantified and possibly corrected for. Although above-water measurements such as AERONET-OC are in coastal waters, and the source distributions of the sky and water-reflected measurements are influenced by the solar spectrum, one should still investigate potential bias from OOB effects. The comparison of the source-weighted SIRCUS results to the AERONET-OC calibration coefficients from GSFC and JRC agreed within the combined expanded uncertainties (k = 2), but there is a bias of 1.4 % ± 0.6 % that although not explained, does not have a substantial impact on the overall uncertainty budget of AERONET-OC products. The SIRCUS uncertainties are smaller than those from measurements of spectral radiance standards and provide a pathway to improved overall uncertainty in AERONET-OC field measurements for cases where environmental uncertainties are well understood and do not dominate the uncertainty budget.

The validation component of this effort, where we compared spectral radiance reference sources traceable to temperature and detector standards, indicates a spectral discrepancy. The discrepancy is near zero at the 668 nm band but increases away from this region. Previous unpublished work, using the VXR and other filter radiometers to validate SIRCUS responsivity assignments and FASCAL spectra radiance assignments, has also observed this effect. The source of these biases is unknown and is under investigation. If the magnitude of the differences observed in this validation exercise represent existing bias in NIST scales, then the potential exists to affect the remote sensing community and other customer’s calibration results.

Fig. 5.

Normalized ASR (blue ○) and transmittance data (red +) for the 441 nm band.

Fig. 9.

Normalized ASR (blue ○) and transmittance data (red +) for the 668 nm band.